Fractal turtles
| March, 2014 |
Here we build upon what we previously did in . In order to quickly
load it a good method is to use
For our first example we start with a simple case: we paint dots at each of the vertices of an equilateral triangle.
(define (three-dots sz)
(let ((x _posx)
(y _posy))
(map (lambda (ang)
(go (list x y))
(look ang)
(forward sz)
(fill (circle 1) "black"))
'(90 -30 210))))
Scheme]
(draw (three-dots 4))
Scheme]
It is obvious that one could paint anything at the vertices. For
instance an ugly gnu (
) or the figure resulting
of a recursion step as we next do. First we slightly generalize the
previous code to draw any three things (this in turn may be easily
generalized to an arbitrary regular polygon). Then we do the recursion
in the function
(define (three-things thing sz)
(let ((x _posx)
(y _posy))
(map (lambda (ang)
(go (list x y))
(look ang)
(forward sz)
(thing))
'(90 -30 210))))
Scheme]
(define (pinski fig count sz)
(if (> count 1)
(three-things
(lambda () (pinski fig (- count 1) (* sz 0.5))) sz)
(three-things fig sz)))
Scheme]
(draw (pinski (lambda () (fill (circle 0.2)
"black")) 5 25))
Scheme]
Yes, that was (or should've been) the Sierpinsky triangle. As
promised, we now generalize the previous code to a general regular
polygon with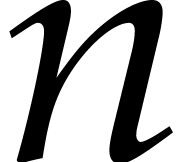 
vertices. We want to place these
polygons recursively at the vertices of the previous polygon and for
this we need a little computation for the scaling factor 
(the 
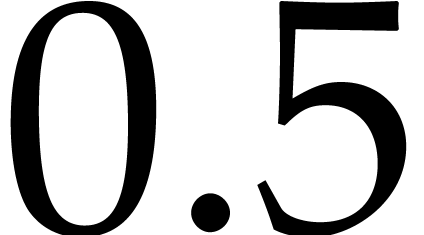that we silently introduced
in
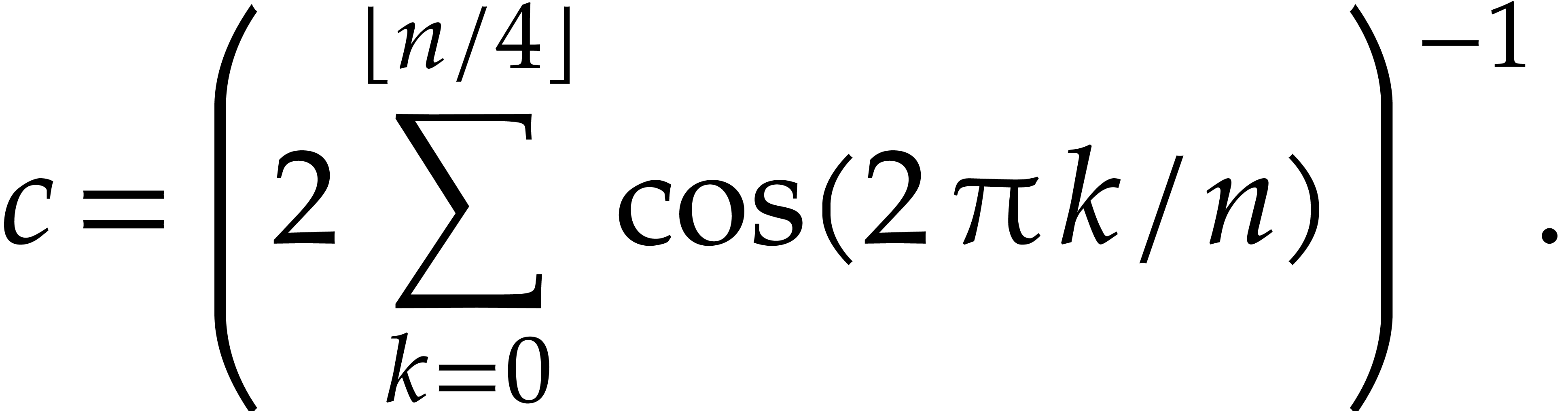
We also implement in a straightforward way the generalizations to 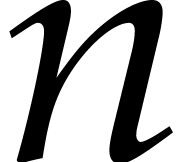polygons.
(define (n-factor n)
(with a_k (lambda (k) (cos (/ (* 2 pi k) n)))
(/ 1 (* 2 (apply + (map a_k (.. 0 (+ 1 (floor (/ n
4))))))))))
Scheme]
(define (n-angles n)
(with ang (/ 360 n)
(map (lambda (x) (floor (+ (- 90 ang) x)))
(map (lambda (x) (* x ang)) (.. 1 (+ 1 n))))))
Scheme]
(define (n-things n thing sz)
(let ((x _posx)
(y _posy))
(map (lambda (ang)
(go (list x y))
(look ang)
(forward sz)
(thing))
(n-angles n))))
Scheme]
(define (n-pinski n fig cnt sz)
(with nextfig (lambda ()(n-pinski n fig (- cnt 1) (* sz
(n-factor n))))
(if (> cnt 1)
(n-things n nextfig sz)
(n-things n fig sz))))
Scheme]
(draw (n-pinski 7 (lambda () (fill (circle 0.2)
"black")) 4 30))
Scheme]
Just one more thing: you might want your output inline, but our
previous
Scheme]
(define (plot* . l)
; Remember the drawing contract:
; Drawing functions (such as turn) with no graphics output
return '()
(cond ((nlist? l) '(graphics "" ""))
((== l '()) (noop))
((list? (car l)) ‘(graphics "" ,@(car
l)))
(else ‘(graphics "" ,@l))))
(define (plot l)
(stree->tree (plot* (simplify l 0))))
Scheme]
(plot (n-pinski 5 (lambda () (fill (circle 0.2)
"black")) 5 30))
Scheme]
Now try your own figures. Have fun!
Bonus: try redefining