| Complexity bounds for zero-test algorithms |
|
| November 4, 2023 |
|
Abstract
In this paper, we analyze the complexity of a zero test for expressions built from formal power series solutions of first order differential equations with non degenerate initial conditions. We will prove a doubly exponential complexity bound. This bound establishes a power series analogue for “witness conjectures”.
Zero equivalence is a major issue on the analysis side of symbolic computation. Standard mathematical notation provides a way of representing many transcendental functions. However, trivial cases apart, this notation gives rise to the following problems:
Expressions may not be defined: consider  ,
,  or
or  .
.
Expressions may be ambiguous: what values should we take for  or
or  ?
?
Expressions may be redundant:  and
and  are different expressions
are different expressions
, but they represent the same function.
Often, one is interested in expressions which represent functions in a ring. In that case, the third problem reduces to deciding when a given expression represents the zero function.
As to the first two problems, one has to decide where and how we want our functions to be defined. In this paper, we will mainly be concerned with expressions that represent multivariate power series. The expressions will then be formed from the constants and the indeterminates using the ring operations and power series solutions to first-order differential equations. The correctness and non-ambiguity of expressions may then be ensured by structural induction. This may involve zero-testing for the series represented by subexpressions.
In order to evaluate the complexity of algorithms, one needs a
reasonable notion for the size of an expression. In this paper, the size
of an expression will always be the number of nodes in the corresponding
“expression tree”. For instance the size of  is
is  . In section 3.1,
we will also introduce the alternative notion of the
“pseudo-norm” of an expression. Roughly speaking, all
expressions in this paper may be represented by polynomials in a tower
of field extensions
. In section 3.1,
we will also introduce the alternative notion of the
“pseudo-norm” of an expression. Roughly speaking, all
expressions in this paper may be represented by polynomials in a tower
of field extensions  . Such
towers start with a field
. Such
towers start with a field  of constants and each
of constants and each
 with
with  is of the form
is of the form

where  is a solution to an algebraic differential
equations over
is a solution to an algebraic differential
equations over  and the
and the  are polynomials over
are polynomials over  . The
pseudo-norm of an element in
. The
pseudo-norm of an element in  is defined
recursively in terms of its degree in
is defined
recursively in terms of its degree in  and the
pseudo-norms of its coefficients.
and the
pseudo-norms of its coefficients.
As a first step, one would like to be able to solve zero-equivalence for the elementary constants, that is to say the smallest field of constants closed under the application of the exponential, trigonometric and (for non-zero argument) logarithmic functions. Alas no such algorithm is known and it is clear that some formidable problems in transcendental number theory would need to be solved before one was found. In the face of this dilemma implementers have used heuristic methods generally involving floating-point computations.
Theoreticians have often resorted to the use of an oracle; in other words they pre-supposed a solution to the problem for constants. They have then gone on to develop other algorithms, for example to decide zero equivalence of functions, on this basis. However for elementary constants one can do better than merely invoke an oracle.
The Schanuel Conjecture may be stated as follows: Let  be complex numbers which are linearly independent over
the rational numbers
be complex numbers which are linearly independent over
the rational numbers  .
Then the transcendence degree of
.
Then the transcendence degree of

is at least  . Many
special cases of this are well known unsolved conjectures in
transcendental number theory. Following work by Lang, [Lang(1971)],
algorithms for deciding the signs of elementary constants based on
the Schanuel Conjecture have been given by Caviness and Prelle, [Caviness and Prelle(1978)] and Richardson, [Richardson(1997)].
The conjecture has been shown to imply the decidability of the real
exponential field, [Macintyre and Wilkie(1995)].
. Many
special cases of this are well known unsolved conjectures in
transcendental number theory. Following work by Lang, [Lang(1971)],
algorithms for deciding the signs of elementary constants based on
the Schanuel Conjecture have been given by Caviness and Prelle, [Caviness and Prelle(1978)] and Richardson, [Richardson(1997)].
The conjecture has been shown to imply the decidability of the real
exponential field, [Macintyre and Wilkie(1995)].
There are definite advantages in using a conjecture from number theory rather than heuristic methods, in that it is clear what is being assumed and any counter example found would be of considerable mathematical interest. However in a practical situation, a zero equivalence method for constants is generally needed very often, and here the algorithms based on the Schanuel Conjecture are really rather slow.
Another limitation of the above approach is that it is very hard to see how to generalize the Schanuel Conjecture to cover constants given by Liouvillian or Pfaffian functions. For the substance of the conjecture is that the relations between exponentials and logarithms of numbers are just the ones we already know about, but it seems impossible to even formulate such a claim when integrals and solutions of differential equations are involved.
In [van der Hoeven(2001b)], the following witness
conjectures was made. Let  and consider the
set
and consider the
set  of real exp-log expressions such that
for each subexpression of the form
of real exp-log expressions such that
for each subexpression of the form  or
or  , we have
, we have  resp.
resp.  ,
where
,
where  denotes the value of
denotes the value of  as a real constant. Then there exists a witness function of
the form
as a real constant. Then there exists a witness function of
the form  (strong witness conjectures) or
(strong witness conjectures) or
 (weak witness conjecture) such that for any
(weak witness conjecture) such that for any
 of size
of size  ,
it suffices to evaluate
,
it suffices to evaluate  up to
up to  digits in order to determine whether it vanishes.
digits in order to determine whether it vanishes.
Earlier versions and variants of witness conjectures appeared in [van der Hoeven(1997), van der Hoeven(2001a), Richardson(2001), van der Hoeven(2001b)]. Also,
Dan Richardson has accumulated numerical evidence and worked out some
number-theoretic consequences. It should be noticed that these
conjectures are apparently independent of the Schanuel conjecture.
Indeed, there might exist non zero elementary constants, which yet
evaluate to extremely small numbers. On the other hand, there might
exist counterexamples to the Schanuel conjecture which can be
“detected” to be zero by evaluating a reasonable number of
digits. The interest of witness conjectures is that they potentially
provide us with fast zero tests, if they can be proved to to hold for
“reasonably small” witness functions  .
.
Remark

The variable  occurs only twice in the function,
but
occurs only twice in the function,
but  has valuation
has valuation  as a
power series. Therefore, the
as a
power series. Therefore, the  -th
iterate
-th
iterate  of
of  has size
has size
 , but valuation
, but valuation  . Consequently, the constant
. Consequently, the constant  yields a counterexample to the strong witness conjecture for
sufficiently large
yields a counterexample to the strong witness conjecture for
sufficiently large  . This
counterexample has been generalized in [van der
Hoeven(2003)] to all polynomial witness functions. Nevertheless, no
counterexamples to the weak witness conjecture are currently known.
. This
counterexample has been generalized in [van der
Hoeven(2003)] to all polynomial witness functions. Nevertheless, no
counterexamples to the weak witness conjecture are currently known.
Although zero-test algorithms for constants are extremely hard to design, more progress has been made on zero-tests for functions [Shackell(1989), Shackell(1993), Péladan-Germa(1995)]. Unfortunately, no reasonable complexity bounds (i.e. less that the Ackermann function) for these algorithms were known up till now. In this paper, we both generalize the algorithm from [Shackell(1989), Shackell(2004)] to the multivariate setting and provide complexity bounds. A recent survey on the theoretical complexity of calculations involving Pfaffian functions is given in [Gabrielov and Vorobjov(2004)].
Now it is interesting to study the significance of such bounds for the exp-log constant conjecture. Indeed, since number theoretical questions about transcendence or Diophantine approximation are usually very hard, a first step usually consists of formulating analogue questions in the setting of function fields. A deep and well-known theorem of Ax [Ax(1971)] states that the power series version of Schanuel's conjecture does hold.
The exp-log conjecture also admits a natural power series analogue.
Given a field  , consider the
set
, consider the
set  of multivariate power series expressions
constructed from
of multivariate power series expressions
constructed from  and
and  using
using  and left composition of infinitesimal
series by
and left composition of infinitesimal
series by  ,
,  and
and  . Now let
. Now let  be such an expression of size
be such an expression of size  and
let
and
let  be the power series represented by
be the power series represented by  . Then we expect that there exists
a constant
. Then we expect that there exists
a constant  , such that
, such that  if and only if the coefficient of
if and only if the coefficient of  in
in  vanishes for all
vanishes for all  .
.
As a side effect of our complexity bounds, we will be able to prove a
weaker result: with the above notation, there exists a constant  , such that
, such that  vanishes if and only if the coefficient of
vanishes if and only if the coefficient of  in
in
 vanishes for all
vanishes for all  .
Just as the Ax theorem gives theoretical evidence that for the numerical
Schanuel conjecture, our result thereby gives evidence that the
numerical witness conjecture might be true.
.
Just as the Ax theorem gives theoretical evidence that for the numerical
Schanuel conjecture, our result thereby gives evidence that the
numerical witness conjecture might be true.
In section 2, we describe our setup of effective local domains for doing computations on power series. Such computations may either be effective zero-tests or the extraction of coefficients. We will next consider the extension of effective local domains by solutions of first order partial differential equations. In section 5, we will show that such extensions are again effective local domains.
In section 3, we recall the Bareiss method for Gaussian elimination of matrices with coefficients in an integral domain. This method has the advantage of limiting the expression swell. More precisely, we give bounds in terms of pseudo-norms on integral domains. In the sequel, the Bareiss method is applied to the efficient g.c.d. computation of several polynomials. This is an essential improvement with respect to [Shackell(1989)], which allows us to obtain “reasonable” complexity bounds for our zero test.
In section 4, we prove four key lemmas which ensure the correctness of
our zero test. We also corrected a small mistake in the original
correctness proof in [Shackell(1989)]. In section 5
we present the actual algorithm and complexity bounds. The main idea
behind the algorithm is as follows: consider a polynomial  , where
, where  are solutions
to given algebraic differential equations. Then
are solutions
to given algebraic differential equations. Then  is zero-equivalent if and only if any differentially algebraic
consequence of
is zero-equivalent if and only if any differentially algebraic
consequence of  and the defining equations of
and the defining equations of
 is zero-equivalent. Using g.c.d.
computations, we first compute a particularly simple such consequence.
Next, it will suffice to check the zero-equivalence of this consequence
up to a certain order.
is zero-equivalent. Using g.c.d.
computations, we first compute a particularly simple such consequence.
Next, it will suffice to check the zero-equivalence of this consequence
up to a certain order.
In the case of power series over the real numbers, it is possible to obtain better theoretical bounds using techniques from [Khovanskii(1991)]. Nevertheless, we think that the results of this paper are interesting from several point of views:
The framework is more general, because we show how to obtain complexity bounds in a relative way for extensions of effective local domains.
We presented an improved version of an actual zero-test algorithm, which might have a better average complexity than Khovanskii's complexity bounds in non-degenerate cases, although we have not yet proved a better bound for the worst case.
Our methods are likely to generalize to higher order differential equations, by adapting the algorithms from [Shackell(1993), van der Hoeven(2002a)].
We plan to improve our complexity bounds in a forthcoming paper, with
the hope of obtaining bounds closer to those in [Khovanskii(1991),
Theorem 1.2], i.e. of the form  instead of
instead of  .
.
Let  be an effective field of constants, which
means that all field operations can be performed algorithmically and
that we have an effective zero test. The ring
be an effective field of constants, which
means that all field operations can be performed algorithmically and
that we have an effective zero test. The ring  is
a differential ring for the partial differentiations
is
a differential ring for the partial differentiations  w.r.t.
w.r.t.  on
on  .
.
We will frequently consider multivariate power series in  as recursive power series in
as recursive power series in  .
For this reason, it is convenient to introduce the partial evaluation
mappings
.
For this reason, it is convenient to introduce the partial evaluation
mappings  with
with

for all  . We re-obtain the
total evaluation mappings
. We re-obtain the
total evaluation mappings  as special cases.
Notice that
as special cases.
Notice that

for every  and
and  .
.
Definition 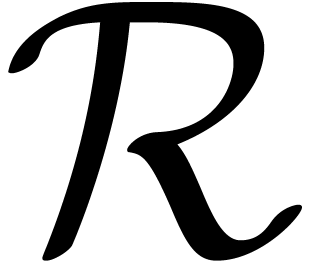 of
of  is called an
effective power series domain, if we have algorithms for
is called an
effective power series domain, if we have algorithms for  and an algorithm to test whether
and an algorithm to test whether  for each
for each  and
and  .
.
Remark  , we
observe that
, we
observe that  may be considered as an effective
power series domain for each
may be considered as an effective
power series domain for each  .
Indeed, this follows from the fact that
.
Indeed, this follows from the fact that  commutes
with
commutes
with  .
.
Let  be an effective power series domain and let
be an effective power series domain and let
 be a power series in
be a power series in  , which satisfies partial differential equations
, which satisfies partial differential equations
 |
(1) |
where  are such that
are such that  for
each
for
each  . Then the ring
. Then the ring

is a differential subring of  ,
which is called a regular D-algebraic extension of
,
which is called a regular D-algebraic extension of  . The main aim of this paper is to show that
. The main aim of this paper is to show that
 is also an effective power series domain and to
give complexity bounds for the corresponding algorithms.
is also an effective power series domain and to
give complexity bounds for the corresponding algorithms.

Elements in  are naturally represented by
polynomials
are naturally represented by
polynomials  in a formal variable
in a formal variable  , via the unique
, via the unique  -algebra
morphism
-algebra
morphism  with
with  .
This mapping
.
This mapping  naturally extends to a mapping
naturally extends to a mapping
 , where
, where

The structure of  may be transported to
may be transported to  in a natural way. The partial differentiations
in a natural way. The partial differentiations  on
on  extend uniquely to
extend uniquely to  by setting
by setting  for each
for each  (so that
(so that  ).
Each partial evaluation mapping
).
Each partial evaluation mapping  induces a
natural evaluation mapping
induces a
natural evaluation mapping  on
on  , which we will also denote by
, which we will also denote by  . Since
. Since  is an effective
local domain, the operations
is an effective
local domain, the operations  can clearly be
performed algorithmically on
can clearly be
performed algorithmically on  .
Our main problem will therefore be to design a zero-test for
.
Our main problem will therefore be to design a zero-test for  , which amounts to deciding whether
, which amounts to deciding whether
 for a given rational function
for a given rational function  .
.
Actually, it is more convenient to work with polynomials in  instead of rational functions in
instead of rational functions in  . Our main problem will then be to decide whether
. Our main problem will then be to decide whether
 for
for  ,
since a rational function
,
since a rational function  represents zero if and
only if
represents zero if and
only if  does. Unfortunately, the ring
does. Unfortunately, the ring  is not necessarily stable under the derivations
is not necessarily stable under the derivations  . For this reason, we introduce the
derivations
. For this reason, we introduce the
derivations

which do map  into itself.
into itself.
In order to determine whether  for polynomials
for polynomials
 , we will consider the roots
of such polynomials in the algebraic closure
, we will consider the roots
of such polynomials in the algebraic closure  of
of
 . Now it is classical that
the algebraic closure of the ring
. Now it is classical that
the algebraic closure of the ring  of univariate
power series over a field
of univariate
power series over a field  is the field
is the field  of Puiseux series over the algebraic closure
of Puiseux series over the algebraic closure  of
of  .
Interpreting multivariate power series in
.
Interpreting multivariate power series in  as
recursive power series in
as
recursive power series in  ,
we may thus view elements in
,
we may thus view elements in  as recursive
Puiseux series in
as recursive
Puiseux series in  .
.
In what follows, it will convenient to use vector notation. We define
the anti-lexicographical ordering  on
on  by
by

for  .
.
Consider a Puiseux series  .
We will write
.
We will write

for the power series expansion of  w.r.t.
w.r.t.  . Each coefficient may recursively
be expanded in a similar way w.r.t.
. Each coefficient may recursively
be expanded in a similar way w.r.t.  .
Alternatively, we may expand
.
Alternatively, we may expand  at once w.r.t. all
variables using the anti-lexicographical ordering:
at once w.r.t. all
variables using the anti-lexicographical ordering:

where  . If
. If  , then the minimal
, then the minimal  with
with
 is called the valuation of
is called the valuation of  and we denote it by
and we denote it by  . If
. If
 , then may we define
, then may we define  to be the coefficient of
to be the coefficient of  in
in
 , for each
, for each  . As usual, we denote
. As usual, we denote  .
.
If  is a non zero polynomial, then we define the
valuation
is a non zero polynomial, then we define the
valuation 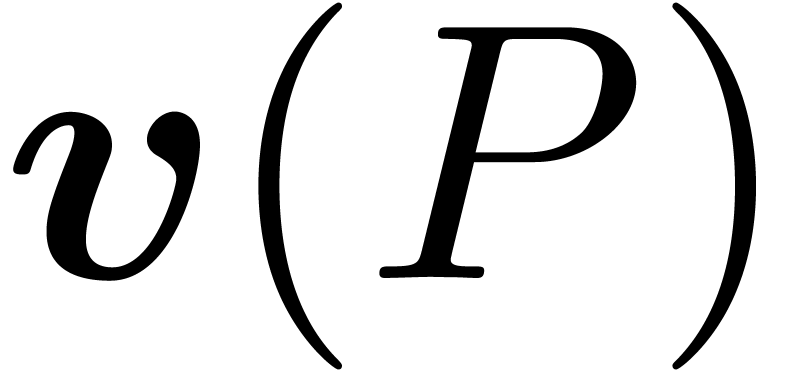 of
of  to be the
minimum of the valuations of its non zero coefficients. Suppose that
to be the
minimum of the valuations of its non zero coefficients. Suppose that
 . Then we recall that
. Then we recall that  are power series and define
are power series and define

for each  .
.
It should be noticed that the recursive extraction of coefficients can
be done effectively in an effective power series domain  , because
, because

for all  and
and  .
More generally, if
.
More generally, if  , then we
may formally represent the coefficient
, then we
may formally represent the coefficient  of
of  by polynomials in
by polynomials in  .
Such representations are best derived through relaxed evaluation of
formal power series [van der Hoeven(2002b)], by using the
partial differential equations satisfied by
.
Such representations are best derived through relaxed evaluation of
formal power series [van der Hoeven(2002b)], by using the
partial differential equations satisfied by  .
.
Let  be an effective integral domain. In what
follows, we will describe algorithms to triangulate matrices with
entries in
be an effective integral domain. In what
follows, we will describe algorithms to triangulate matrices with
entries in  and compute g.c.d.s of polynomials
with coefficients in
and compute g.c.d.s of polynomials
with coefficients in  . In
order to state complexity bounds, it is convenient to measure the
“sizes” of coefficients in
. In
order to state complexity bounds, it is convenient to measure the
“sizes” of coefficients in  in terms
of a pseudo-norm, which is a function
in terms
of a pseudo-norm, which is a function  with the following properties:
with the following properties:
 .
.
 .
.
If  is actually a differential ring with
derivations
is actually a differential ring with
derivations  , then we also
assume the existence of a constant
, then we also
assume the existence of a constant  with
with
 .
.
As remarked in the introduction, the pseudo-norm of an expression should not be confused with its “natural size”, i.e. the number of nodes of the corresponding expression tree.
Example  , then we may take
, then we may take  to
be the maximum of the degrees of
to
be the maximum of the degrees of  in
in  and
and  .
.
Example 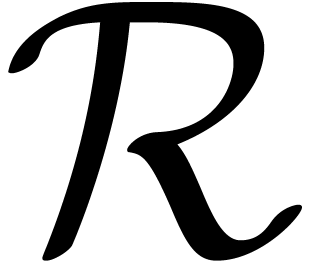 and
and  are as in section 2
and assume that we have a pseudo-norm
are as in section 2
and assume that we have a pseudo-norm  on
on 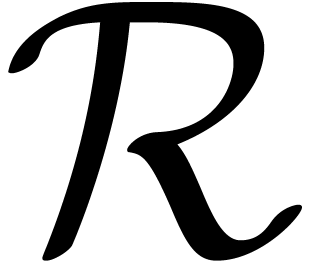 . Then we define a pseudo-norm on
. Then we define a pseudo-norm on
 by
by

This pseudo-norm induces a pseudo-norm on  by
by

Notice that we may take

Let  still be an effective integral domain with a
pseudo-norm
still be an effective integral domain with a
pseudo-norm  and quotient field
and quotient field  . Consider an
. Consider an  matrix
matrix
 with entries in
with entries in  (i.e. a matrix with
(i.e. a matrix with  rows and
rows and  columns). For all indices
columns). For all indices  and
and
 , we will also write
, we will also write  for the
for the  minor of
minor of  when we only keep the rows
when we only keep the rows  and
columns
and
columns  .
.
It is classical that we may upper triangulate  using Gaussian elimination. This leads to a formula
using Gaussian elimination. This leads to a formula

where  is a matrix with determinant one and
is a matrix with determinant one and  an upper triangular matrix. Unfortunately, this
process usually leads to a fast coefficient growth for the numerators of
the entries of the successive matrices. In order to remove this
drawback, we will rather do all computations over
an upper triangular matrix. Unfortunately, this
process usually leads to a fast coefficient growth for the numerators of
the entries of the successive matrices. In order to remove this
drawback, we will rather do all computations over  instead of
instead of  . In this section,
we will briefly recall this approach, which is due to Bareiss [Bareiss(1968),
Loos(1983)].
. In this section,
we will briefly recall this approach, which is due to Bareiss [Bareiss(1968),
Loos(1983)].
So let us now be given an  matrix
matrix  with entries in
with entries in  .
For simplicity, we will first assume that the usual triangulation of
.
For simplicity, we will first assume that the usual triangulation of
 as a matrix with entries in
as a matrix with entries in  does not involve row permutations. This usual triangulation of
does not involve row permutations. This usual triangulation of  gives rise to a sequence of identities
gives rise to a sequence of identities

with  , where
, where  is the matrix obtained from
is the matrix obtained from  after
after  steps. More precisely,
steps. More precisely,  is obtained
from
is obtained
from  by leaving the first
by leaving the first  rows invariant and by adding multiples of the
rows invariant and by adding multiples of the  -th row to the others (in particular, the
-th row to the others (in particular, the  will be lower triangular throughout the process). If there
exists a
will be lower triangular throughout the process). If there
exists a  with
with  ,
then let
,
then let  be the minimal such
be the minimal such  , so that
, so that  for all
for all  and
and  . Each
. Each
 may be rewritten as a product
may be rewritten as a product

of an invertible diagonal matrix  and another
matrix
and another
matrix  with entries in
with entries in  . Our aim is to show that we may choose the
. Our aim is to show that we may choose the  and
and  of small pseudo-norms. In
fact, we claim that we may take
of small pseudo-norms. In
fact, we claim that we may take  for each
for each  , where
, where  .
.
In order to see this, let  ,
,
 and
and  .
Then
.
Then

since  is a lower triangular matrix. Moreover,
this matrix has only ones on its diagonal, whence
is a lower triangular matrix. Moreover,
this matrix has only ones on its diagonal, whence

Since  is upper triangular, we also have
is upper triangular, we also have

By our choice of  , we finally
have
, we finally
have

Putting this together, we see that each coefficient of  (whence in particular
(whence in particular  ) may
be written as the determinant of a minor of
) may
be written as the determinant of a minor of  :
:
 |
(2) |
Hence, we have not only shown that the  and
and  have coefficients in
have coefficients in  ,
but even that they may be written explicitly as determinants of minors
of
,
but even that they may be written explicitly as determinants of minors
of  . This result remains so
(up to a factor
. This result remains so
(up to a factor  ) if row
permutations were needed in the triangulation process, since we may
always permute the rows of
) if row
permutations were needed in the triangulation process, since we may
always permute the rows of  a priori, so
that no further row permutations are necessary during the
triangulations. This proves the following theorem:
a priori, so
that no further row permutations are necessary during the
triangulations. This proves the following theorem:
Theorem  matrix
matrix  with entries in
with entries in 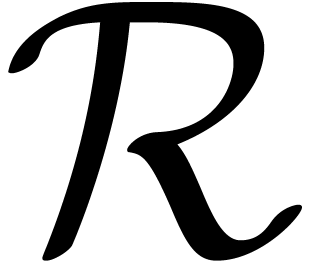 on input, and
which computes an invertible
on input, and
which computes an invertible  diagonal matrix
diagonal matrix
 and an
and an  upper triangular
matrix
upper triangular
matrix  with entries in
with entries in 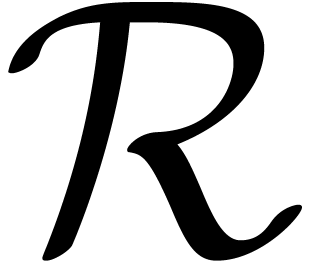 , such that there exists a matrix
, such that there exists a matrix  with entries in
with entries in  , of
determinant one, and so that
, of
determinant one, and so that  .
Moreover,
.
Moreover,  and
and  .
Here
.
Here  .
.
By way of comment, we note that the actual computation of  involves
involves  elementary operations. If
we do have an algorithm for exact division in
elementary operations. If
we do have an algorithm for exact division in  , then this is also the time complexity of the
algorithm in terms of operations in
, then this is also the time complexity of the
algorithm in terms of operations in  .
Otherwise, it may be necessary to compute the entries of the
intermediate matrices
.
Otherwise, it may be necessary to compute the entries of the
intermediate matrices  by formula (2),
which yields an overall complexity of
by formula (2),
which yields an overall complexity of  .
.
Let  still be an effective integral domain with a
pseudo-norm
still be an effective integral domain with a
pseudo-norm  and quotient field
and quotient field  . Consider a finite number
. Consider a finite number  of polynomials in
of polynomials in  . In this
section, we address the question of computing a g.c.d.
. In this
section, we address the question of computing a g.c.d.  of
of  and a corresponding Bezout
relation. Since we are only computing over an integral domain, we call
and a corresponding Bezout
relation. Since we are only computing over an integral domain, we call
 a g.c.d., if
a g.c.d., if  is
a scalar multiple of the g.c.d. of
is
a scalar multiple of the g.c.d. of  , when considered as polynomials over the
quotient field
, when considered as polynomials over the
quotient field  . Accordingly,
a Bezout relation for
. Accordingly,
a Bezout relation for  has the form
has the form
 |
(3) |
where  and
and  .
From the computational point of view, we are interested in minimizing
the pseudo-norms of
.
From the computational point of view, we are interested in minimizing
the pseudo-norms of  and
and  . As to the degrees, such “small Bezout
relations” always exist. In fact quite a lot of research has been
done in this area, see [Kollar(1999)] for example. Here we
give a relatively simple result which is sufficient for our purposes.
. As to the degrees, such “small Bezout
relations” always exist. In fact quite a lot of research has been
done in this area, see [Kollar(1999)] for example. Here we
give a relatively simple result which is sufficient for our purposes.
Proposition  be more than one non-zero polynomial. Then there exists a
Bezout relation
be more than one non-zero polynomial. Then there exists a
Bezout relation  .
.
Proof. Assume the contrary and choose a Bezout relation
(3) of minimal degree  and such that
the number
and such that
the number  of indices
of indices  with
with  is minimal. Since
is minimal. Since  , we must have
, we must have  ,
and modulo a permutation of indices, we may assume that
,
and modulo a permutation of indices, we may assume that  for each
for each  . Let
. Let  be the leading coefficient of
be the leading coefficient of  and
and
 the leading coefficient of
the leading coefficient of  . Then for
. Then for  ,
we have
,
we have

is again a Bezout relation, which contradicts our minimality
hypothesis.
Let  . In order to actually
find a Bezout relation of degree
. In order to actually
find a Bezout relation of degree  ,
we now consider the matrix
,
we now consider the matrix  with
with  rows and
rows and  columns, which is the vertical
superposition of all matrices of the form
columns, which is the vertical
superposition of all matrices of the form

where  . Now triangulate
. Now triangulate  as in the section above
as in the section above
 |
(4) |
and let  be the number of non-zero rows in
be the number of non-zero rows in  . The
. The  -th
row of
-th
row of  corresponds to a polynomial linear
combination of
corresponds to a polynomial linear
combination of  of minimal degree. In other
words, it contains the coefficients of a g.c.d. of
of minimal degree. In other
words, it contains the coefficients of a g.c.d. of  .
.
Moreover, we may obtain a Bezout relation when considering the matrix
 with an
with an  identity matrix
glued at its right hand side. When triangulating this matrix, we obtain
a relation of the form
identity matrix
glued at its right hand side. When triangulating this matrix, we obtain
a relation of the form

such that the additional part  of the
triangulated matrix gives us the transformation matrix
of the
triangulated matrix gives us the transformation matrix  in (4) up to the diagonal matrix
in (4) up to the diagonal matrix  :
:

The finite sum which leads to the  -th
row in the product
-th
row in the product  now yields the desired Bezout
relation. Notice that
now yields the desired Bezout
relation. Notice that  in this Bezout relation.
in this Bezout relation.
From the complexity point of view, we also notice that at most  rows in
rows in  may actually have
contributed to the first
may actually have
contributed to the first  rows of
rows of  . When replacing
. When replacing  with
its restriction to these rows, the above triangulations will therefore
yield the same g.c.d. and the same Bezout relation. We have
proved
with
its restriction to these rows, the above triangulations will therefore
yield the same g.c.d. and the same Bezout relation. We have
proved
Theorem  be more than one non-zero polynomials. Then there
exists an algorithm to compute a g.c.d. of
be more than one non-zero polynomials. Then there
exists an algorithm to compute a g.c.d. of  as well as a Bezout relation
as well as a Bezout relation  , such that
, such that

Let  be an effective integral domain and let
be an effective integral domain and let  be polynomials over
be polynomials over  with
with
 . If
. If  were actually an effective field, then we might have used the Euclidean
division algorithm to obtain the unique expression for
were actually an effective field, then we might have used the Euclidean
division algorithm to obtain the unique expression for  of the form
of the form

with  and
and  .
However, this algorithm involves divisions and can no longer be used if
.
However, this algorithm involves divisions and can no longer be used if
 is an integral domain but not a field.
Nevertheless, pseudo-division may always be used to obtain the unique
expression for
is an integral domain but not a field.
Nevertheless, pseudo-division may always be used to obtain the unique
expression for  of the form
of the form

where  is the leading coefficient or
initial of
is the leading coefficient or
initial of  and
and  are such that
are such that  . We also call
. We also call
 the pseudo-quotient and
the pseudo-quotient and  the pseudo-remainder of the division of
the pseudo-remainder of the division of  by
by  .
.
Algorithm pdiv
Input  with
with  .
.
Output the pseudo-quotient resp. pseudo-remainder of
the division of  by
by  .
.
Set  and
and 
For  do
do


Return 
In particular, we may use pseudo-division to make a polynomial  square-free. Namely, if
square-free. Namely, if  ,
then we take sqfree
,
then we take sqfree to be the
square-free part of
to be the
square-free part of  .
.
Proposition  of
of  as above. Then
as above. Then  .
.
Proof. Let  and
and  . Then
. Then  ,
by Theorem 8. Also,
,
by Theorem 8. Also,  for
for  . Hence,
. Hence,  .
.
We recall that derivations on integral domains extend uniquely to their algebraic closures.
Lemma  be a square-free polynomial and
be a square-free polynomial and

Consider the factorization

with  and
and  .
Then each of the
.
Then each of the  satisfies the partial
differential equations
satisfies the partial
differential equations
Proof. Consider one of the factors  of
of  and write
and write

For each  , we have
, we have

Since  both divides
both divides  and
and
 , it also divides
, it also divides  . Now
. Now  is
square-free, so that
is
square-free, so that  does not divide
does not divide  . Therefore
. Therefore  divides
divides  . Consequently,
. Consequently,  for each
for each  ,
i.e.
,
i.e.  satisfies (1).
satisfies (1).
Lemma  be a Puiseux series with
be a Puiseux series with  . Assume that
. Assume that  satisfies the
same equations
satisfies the
same equations  and the same initial condition
and the same initial condition  . Then
. Then  .
.
Proof. Let us prove by induction over  that
that  for all
for all  .
We have
.
We have  by assumption. Assume therefore that
by assumption. Assume therefore that
 and
and  .
Then
.
Then  is a Puiseux series in
is a Puiseux series in  of the form
of the form
 |
(5) |
Since  and
and  commute,
commute,  satisfies the partial differential equation
satisfies the partial differential equation
 |
(6) |
In particular, extraction of the coefficient in  yields
yields
 |
(7) |
for every  . Now
. Now

since  . Consequently, we may
see (7) as a recurrence relation which uniquely determines
. Consequently, we may
see (7) as a recurrence relation which uniquely determines
 as a function of other
as a function of other  with
with  . Hence
. Hence  is the unique solution to (6) of the form (5).
The lemma now follows by induction.
is the unique solution to (6) of the form (5).
The lemma now follows by induction.
Lemma  be a polynomial in
be a polynomial in  .
Given
.
Given  with
with
 |
(8) |
there exists a root  of
of  with
with  and
and  .
.
Proof. Intuitively speaking, this lemma follows from
the Newton polygon method: the existence of a solution  to (8) implies that the Newton polygon associated to the
equation
to (8) implies that the Newton polygon associated to the
equation  admits a horizontal slope and that
admits a horizontal slope and that  is a solution to the associated Newton polynomial.
Therefore,
is a solution to the associated Newton polynomial.
Therefore,  is the first term of a solution to
is the first term of a solution to
 , the full solution being
obtained using the Newton polygon method. If
, the full solution being
obtained using the Newton polygon method. If  , then the Newton polygon admits a “strictly
positive slope” and a similar argument applies.
, then the Newton polygon admits a “strictly
positive slope” and a similar argument applies.
More precisely, we may apply the results from chapter 3 in [van der Hoeven(2004)] (see also [van der Hoeven(1997)]). We first note that

is a field of grid-based power series. Now setting  , the Newton degree
, the Newton degree  of
of
 |
(9) |
is strictly positive. Indeed, this is clear if  , and this follows from Lemma 3.6 in [van
der Hoeven(2004)] if
, and this follows from Lemma 3.6 in [van
der Hoeven(2004)] if  .
Now our lemma follows from the fact that the algorithm
polynomial_solve returns
.
Now our lemma follows from the fact that the algorithm
polynomial_solve returns  solutions to
(9).
solutions to
(9).
Lemma

Proof. Assuming that  ,
we have
,
we have  for
for  .
It follows that
.
It follows that  divides both
divides both  and
and  , whence
, whence  and
and  . Since
. Since  , it follows in particular that
, it follows in particular that  .
.
Assume now that  . Lemma 12 implies that
. Lemma 12 implies that  admits a root
admits a root  with
with  and
and  . This root
. This root  satisfies
the equations (1), by Lemma 10. Hence
satisfies
the equations (1), by Lemma 10. Hence  , by Lemma 11. We
conclude that
, by Lemma 11. We
conclude that  and
and  .
.
The lemmas from the previous section yield the following zero-test algorithm:
Algorithm zero_test
Input  .
.
Output result of the test  .
.
Step 1. [trivial case]
If  then return true.
then return true.
Step 2. [g.c.d. computations]
Replace  .
.
Let  .
.
Step 3. [compute the valuation  of
of
 ]
]
Denote  .
.
For  , compute
, compute  as a function of
as a function of  as follows:
as follows:
Expand each coefficient  (
( ) w.r.t.
) w.r.t.  .
.
Stop at the least  , such
that there exists a
, such
that there exists a  with
with  .
.
Step 4. [evaluate and conclude]
Return  .
.
Remark  in step 3 may be done efficiently using the technique
of relaxed evaluation [van der Hoeven(2002b)].
in step 3 may be done efficiently using the technique
of relaxed evaluation [van der Hoeven(2002b)].
In order to derive complexity bounds, we will have to assume that we
have a pseudo-norm  on
on  and that there exists a function
and that there exists a function  ,
which gives a bound
,
which gives a bound  on the valuation
on the valuation  , for each
, for each  . Here we understand that
. Here we understand that

for each  . It is also
reasonable to also assume that
. It is also
reasonable to also assume that  is increasing and
that it grows sufficiently fast such that
is increasing and
that it grows sufficiently fast such that  ,
,
 and
and  for all
for all  . Notice that we may take
. Notice that we may take  for all
for all  when
when  .
.

Then for any  , we have
, we have

Proof. Assume first that  can be
represented by a square-free polynomial
can be
represented by a square-free polynomial  .
Then
.
Then  does not change in step 2 of
zero_test and for
does not change in step 2 of
zero_test and for  ,
we have
,
we have

Then Theorem 8 yields

Since  for each non-zero coefficient
for each non-zero coefficient  of
of  , it follows
that
, it follows
that

in step 3 of zero_test. Since we assumed  , we must have
, we must have  in the last
step of zero_test. Considering the Taylor series expansion
in the last
step of zero_test. Considering the Taylor series expansion

in the infinitesimal power series  ,
we observe that
,
we observe that  .
.
By Theorem 8,  also satisfies a
Bezout relation of the form
also satisfies a
Bezout relation of the form

Now  for all
for all  (recall that
(recall that
 ), so that
), so that

We conclude that

This gives a bound for  in the case when
in the case when  is square-free.
is square-free.
Let us now turn to the more general situation in which  is represented by a polynomial
is represented by a polynomial  which is no
longer square-free. Setting
which is no
longer square-free. Setting  ,
the above discussion yields the bound
,
the above discussion yields the bound

since  by Proposition 9. Now
by Proposition 9. Now  divides
divides  when we understand
these polynomials to have coefficients in the quotient field of
when we understand
these polynomials to have coefficients in the quotient field of 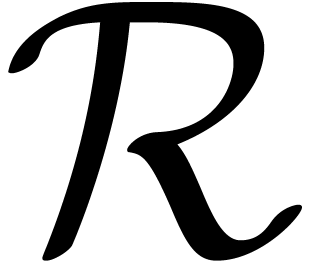 . If
. If  is the
leading coefficient of
is the
leading coefficient of  , we
thus have
, we
thus have  in
in  ,
as is seen by pseudo-dividing
,
as is seen by pseudo-dividing  by
by  . It follows that
. It follows that

since  .
.
Let us finally consider the case when  is
represented by a general element
is
represented by a general element  .
Then we may rewrite
.
Then we may rewrite  as a fraction
as a fraction  with
with  and
and  , and we have
, and we have

Since  , we thus get
, we thus get

since  or
or  .
.
Remark  to
to  . In the second part, one might for
instance consider the factorization of
. In the second part, one might for
instance consider the factorization of  instead
of gcd
instead
of gcd as in the zero-test algorithm.
as in the zero-test algorithm.
As a consequence of the above bound for the valuations of non-zero
series  , we have a
straightforward zero-test algorithm for series
, we have a
straightforward zero-test algorithm for series  which consists of testing whether all coefficients of
which consists of testing whether all coefficients of  up to the bound vanish using relaxed evaluation [van der
Hoeven(2002b)]. This algorithm satisfies the following complexity
bound:
up to the bound vanish using relaxed evaluation [van der
Hoeven(2002b)]. This algorithm satisfies the following complexity
bound:
Theorem  . With the notation from Theorem 15,
we may test whether
. With the notation from Theorem 15,
we may test whether  represents zero in time
represents zero in time
 .
.
Remark
Consider a tower of regular D-algebraic ring extensions  starting with
starting with  . We have
natural representations
. We have
natural representations

for all  . The repeated
application of Theorem 15 yields
. The repeated
application of Theorem 15 yields
Corollary  , such that for all
, such that for all
 , we have either
, we have either  or
or  .
.
Remark  , we have a polynomial
time algorithm zero-test in
, we have a polynomial
time algorithm zero-test in  .
Theoretically speaking, we already knew this, because
.
Theoretically speaking, we already knew this, because  for a certain ideal
for a certain ideal  of
of  . Hence, it would suffice to reduce a polynomial in
. Hence, it would suffice to reduce a polynomial in
 with respect to a Groebner basis for
with respect to a Groebner basis for  in order to know whether it represents zero.
Unfortunately, we do not know of any algorithm to compute such a
Groebner basis for
in order to know whether it represents zero.
Unfortunately, we do not know of any algorithm to compute such a
Groebner basis for  .
Nevertheless, even without such a Groebner basis the above corollary
tells us that we still have a polynomial time zero-test.
.
Nevertheless, even without such a Groebner basis the above corollary
tells us that we still have a polynomial time zero-test.
Let us now return to exp-log series in the ring  considered in the introduction. Recall that the size of an element in
considered in the introduction. Recall that the size of an element in
 is the number of nodes in the corresponding
expression tree. Repeated application of Theorem 15 yields
is the number of nodes in the corresponding
expression tree. Repeated application of Theorem 15 yields
Corollary  , which can be
represented by an expression of size
, which can be
represented by an expression of size  .
Then either
.
Then either  or
or  .
.
Proof. Let  be an expression
which represents
be an expression
which represents  and let
and let  be its subexpressions listed in the order of a postfix traversal. We
construct a tower
be its subexpressions listed in the order of a postfix traversal. We
construct a tower  with representations
with representations  , such that
, such that  for all
for all  and
and  .
We construct the tower by induction over
.
We construct the tower by induction over  .
For
.
For  we have nothing to show, so suppose
we have nothing to show, so suppose  and that we have performed the construction up to
stage
and that we have performed the construction up to
stage  .
.
If  or
or  ,
then we clearly have
,
then we clearly have  . If
. If
 ,
,  ,
,  or
or  with
with  , then
, then  . Assume finally that
. Assume finally that  with
with  , where
, where  . Then we take
. Then we take  if
if  or
or  otherwise, and one the
relations
otherwise, and one the
relations

holds for all  . Notice that
the pseudo-norm of
. Notice that
the pseudo-norm of  is bounded by
is bounded by  (whence by
(whence by  )
for all
)
for all  . Consequently, the
. Consequently, the
 from Theorem 15 is bounded by
from Theorem 15 is bounded by  at each stage. By induction over
at each stage. By induction over  , it therefore follows that
, it therefore follows that  for all
for all  . If
. If  , we conclude that
, we conclude that  .
.
Ax, J., 1971. On Schanuel's conjecture. Ann. of Math. 93, 252–268.
Bareiss, E., 1968. Sylvester's identity and multistep integer-preserving Gaussian elimination. Math. Comp. 22 22, 565–578.
Caviness, B., Prelle, M., 1978. A note on algebraic independence of logarithmic and exponential constants. SIGSAM Bull. 12/2, 18–20.
Gabrielov, A., Vorobjov, N., April 2004. Complexity of computations with Pfaffian and Noetherian functions. In: et al, Y. I. (Ed.), Normal forms, bifurcations and finiteness problems in differential equations. Vol. 137 of NATO Science series II. Kluwer, to appear.
Khovanskii, A., 1991. Fewnomials. Vol. 88 of Translations of Mathematical Monographs. A.M.S., Providence RI.
Kollar, J., 1999. Effective nullstellensatzn for arbitrary ideals. Vol. 1. pp. 313–337.
Lang, S., 1971. Transcendental numbers and diophantine approximation. Bull. Amer. Math. Soc. 77/5, 635–677.
Loos, R., 1983. Generalized polynomial remainder sequences. In: Buchberger, B., Collins, G., Loos, R. (Eds.), Computer Algebra: Symbolic and Algebraic Computation. Springer-Verlag, Wien/New York, pp. 115–137.
Macintyre, A., Wilkie, A., 1995. On the decidability of the real exponential field. In: Odifreddi, P. (Ed.), Kreisel 70th birthday volume. CLSI. A.K. Peters.
Péladan-Germa, A., 1995. Testing identities of series defined by algebraic partial differential equations. In: Cohen, G., Giusti, M., Mora, T. (Eds.), Proc. of AAECC-11. Vol. 948 of Lect. Notes in Comp. Science. Springer, Paris, pp. 393–407.
Richardson, D., 1997. How to recognise zero. JSC 24, 627–645.
Richardson, D., 2001. The uniformity conjecture. In: Lecture Notes in Computer Science. Vol. 2064. Springer Verlag, pp. 253–272.
Shackell, J., 1989. A differential-equations approach to functional equivalence. In: Proc. ISSAC '89. ACM Press, Portland, Oregon, A.C.M., New York, pp. 7–10.
Shackell, J., 1993. Zero equivalence in function fields defined by differential equations. Proc. of the A.M.S. 336 (1), 151–172.
Shackell, J., 2004. Symbolic asymptotics. Vol. 12 of Algorithms and computation in Mathematics. Springer-Verlag.
van der Hoeven, J., 1997. Automatic asymptotics. Ph.D. thesis, École polytechnique, France.
van der Hoeven, J., 2001a. Fast evaluation of holonomic functions near and in singularities. JSC 31, 717–743.
van der Hoeven, J., 2001b. Zero-testing, witness conjectures and differential diophantine approximation. Tech. Rep. 2001-62, Prépublications d'Orsay.
van der Hoeven, J., July 2002a. A new zero-test for formal power series. In: Mora, T. (Ed.), Proc. ISSAC '02. Lille, France, pp. 117–122.
van der Hoeven, J., 2002b. Relax, but don't be too lazy. JSC 34, 479–542.
van der Hoeven, J., 2003. Counterexamples to witness conjectures. Tech. Rep. 2003-43, Université Paris-Sud, Orsay, France, to appear in JSC.
van der Hoeven, J., 2004. Transseries and real differential algebra. Tech. Rep. 2004-47, Université Paris-Sud, Orsay, France, to appear in Lecture Notes in Mathematics, Springer-Verlag.