| Modular composition via complex
roots |
|
Joris van der Hoevena,
Grégoire Lecerfb
|
|
Laboratoire d'informatique de l'École
polytechnique, CNRS UMR 7161
École polytechnique
91128 Palaiseau Cedex, France
|
|
a. Email: vdhoeven@lix.polytechnique.fr
|
|
b. Email: lecerf@lix.polytechnique.fr
|
|
| Preprint version, March 27, 2017 |
|
Modular composition is the problem to compute the composition of
two univariate polynomials modulo a third one. For polynomials
with coefficients in a finite field, Kedlaya and Umans proved in
2008 that the theoretical complexity for performing this task
could be made arbitrarily close to linear. Unfortunately, beyond
its major theoretical impact, this result has not led to
practically faster implementations yet. In this paper, we explore
the particular case when the ground field is the field of
computable complex numbers. Ultimately, when the precision becomes
sufficiently large, we show that modular compositions may be
performed in softly linear time.
|
1.Introduction
Let  be an effective field, and let
be an effective field, and let  be polynomials in
be polynomials in  .
The problem of modular composition is to compute
.
The problem of modular composition is to compute  modulo
modulo  .
Modular composition is an important problem in complexity theory because
of its applications to polynomial factorization [14–16]. It also occurs very naturally whenever one wishes to
perform polynomial computations over
.
Modular composition is an important problem in complexity theory because
of its applications to polynomial factorization [14–16]. It also occurs very naturally whenever one wishes to
perform polynomial computations over  inside an
algebraic extension of
inside an
algebraic extension of  . In
addition, given two different representations
. In
addition, given two different representations  of
an algebraic extension of
of
an algebraic extension of  ,
the implementation of an explicit isomorphism actually boils down to
modular composition.
,
the implementation of an explicit isomorphism actually boils down to
modular composition.
Denote by  the number of operations in
the number of operations in  required to multiply two polynomials of degree
required to multiply two polynomials of degree  in
in  . Let
. Let  and
and  be polynomials in
be polynomials in  of respective degrees
of respective degrees  ,
,
 and
and  .
The naive modular composition algorithm takes
.
The naive modular composition algorithm takes  operations in
operations in  . In 1978,
Brent and Kung [3] gave an algorithm with cost
. In 1978,
Brent and Kung [3] gave an algorithm with cost  . It uses the baby-step giant-step
technique due to Paterson and Stockmeyer [21], and even
yields a sub-quadratic cost
. It uses the baby-step giant-step
technique due to Paterson and Stockmeyer [21], and even
yields a sub-quadratic cost  when using fast
linear algebra (see [13, p. 185]). The constant
when using fast
linear algebra (see [13, p. 185]). The constant  is such that a
is such that a  matrix over
matrix over  can be multiplied with another
can be multiplied with another  rectangular matrix in time
rectangular matrix in time  .
The best current bound
.
The best current bound  is due to Huang and Pan
[12, Theorem 10.1].
is due to Huang and Pan
[12, Theorem 10.1].
A major breakthrough has been achieved by Kedlaya and Umans [15,
16] in the case when  is the finite
field
is the finite
field  . For any positive
. For any positive
 , they showed that the
composition
, they showed that the
composition  modulo
modulo  could
be computed with bit complexity
could
be computed with bit complexity  .
Unfortunately, it remains a major open problem to turn this theoretical
complexity bound into practically useful implementations.
.
Unfortunately, it remains a major open problem to turn this theoretical
complexity bound into practically useful implementations.
Quite surprisingly, the existing literature on modular composition does
not exploit the simple observation that composition modulo a separable
polynomial  that splits over
that splits over  can be reduced to the well known problems of multi-point evaluation and
interpolation [6, Chapter 10]. More precisely, assume that
can be reduced to the well known problems of multi-point evaluation and
interpolation [6, Chapter 10]. More precisely, assume that
 is separable, which means that
is separable, which means that  . If
. If  are of degree
are of degree
 , then
, then  can be computed by evaluating
can be computed by evaluating  at
at  , by evaluating
, by evaluating  at
at
 , and by interpolating the
evaluations
, and by interpolating the
evaluations  to yield
to yield  .
.
Whenever  is algebraically closed and a
factorization of
is algebraically closed and a
factorization of  is known, the latter
observation leads to a softly-optimal algorithm for composition modulo
is known, the latter
observation leads to a softly-optimal algorithm for composition modulo
 . More generally, if the
computation of a factorization of
. More generally, if the
computation of a factorization of  has a
negligible or acceptable cost, then this approach leads to an efficient
method for modular composition. In this paper, we prove a precise
complexity result in the case when
has a
negligible or acceptable cost, then this approach leads to an efficient
method for modular composition. In this paper, we prove a precise
complexity result in the case when  is the field
of computable complex numbers. In a separate paper [11], we
also consider the case when
is the field
of computable complex numbers. In a separate paper [11], we
also consider the case when  is a finite field
and
is a finite field
and  has composite degree; in that case,
has composite degree; in that case,  can be factored over suitable field extensions, and
similar ideas lead to improved complexity bounds.
can be factored over suitable field extensions, and
similar ideas lead to improved complexity bounds.
In the special case of power series composition (i.e.
composition modulo  ), our
approach is similar in spirit to the analytic algorithm designed by
Ritzmann [22]; see also [8]. In order to keep
the exposition as simple as possible in this paper, we only study
composition modulo separable polynomials. By handling multiplicities
with Ritzmann's algorithm, we expect our algorithm to extend to the
general case.
), our
approach is similar in spirit to the analytic algorithm designed by
Ritzmann [22]; see also [8]. In order to keep
the exposition as simple as possible in this paper, we only study
composition modulo separable polynomials. By handling multiplicities
with Ritzmann's algorithm, we expect our algorithm to extend to the
general case.
The organization of the present paper is as follows. In section 2,
we specify the complexity model to be used, and various standard
notations. In section 3, we give a detailed version of the
modular composition algorithm that we sketched above for a separable
modulus that splits over  . In
order to instantiate this algorithm for the field
. In
order to instantiate this algorithm for the field  of computable complex numbers, we need additional concepts. In section
4, we recall basic results about ball arithmetic
[9]. In section 5, we recall the computation
model of straight-line programs [4]. In section 6, we introduce a new ultimate complexity model that
is convenient for proving complexity results at a “sufficiently
large precision”. This model has the advantage that complexity
results over an abstract effective field
of computable complex numbers, we need additional concepts. In section
4, we recall basic results about ball arithmetic
[9]. In section 5, we recall the computation
model of straight-line programs [4]. In section 6, we introduce a new ultimate complexity model that
is convenient for proving complexity results at a “sufficiently
large precision”. This model has the advantage that complexity
results over an abstract effective field  can
naturally be turned into ultimate complexity results over
can
naturally be turned into ultimate complexity results over  . In section 7, we apply this
transfer principle to the modular composition algorithm from section 3—we expect our framework to be useful in many other
situations.
. In section 7, we apply this
transfer principle to the modular composition algorithm from section 3—we expect our framework to be useful in many other
situations.
One disadvantage of ultimate complexity analysis is that it does not
provide us with any information about the precision from which the
ultimate complexity is reached. In practical applications, the input
polynomials  and
and  often
admit integer or rational coefficients. In these cases, the required bit
precision is expected to be of order
often
admit integer or rational coefficients. In these cases, the required bit
precision is expected to be of order  in the
worst case, where
in the
worst case, where  and
and  is
the largest bit size of the coefficients: in fact, this precision allows
to compute all the complex roots of
is
the largest bit size of the coefficients: in fact, this precision allows
to compute all the complex roots of  efficiently
using algorithms from [18, 19, 24].
This precision should also be sufficient to perform the multi-point
polynomial evaluations of
efficiently
using algorithms from [18, 19, 24].
This precision should also be sufficient to perform the multi-point
polynomial evaluations of  and
and  by asymptotically fast algorithms. We intend to work out more such
detailed bit complexity bounds for this situation in a forthcoming
paper.
by asymptotically fast algorithms. We intend to work out more such
detailed bit complexity bounds for this situation in a forthcoming
paper.
2.Preliminaries
In the sequel, we consider both the algebraic and bit complexity models
for analyzing the costs of our algorithms. The algebraic complexity
model expresses the running time in terms of the number of
operations in some abstract ground ring or field [4,
Chapter 4]. The bit complexity model relies on Turing machines
with a sufficient number of tapes [20].
Fundamental algebraic complexity bounds
Let

be an effective field. We write

for a function that bounds the total cost of a
polynomial product algorithm in terms of the number operations in
 .
. In other words, two
polynomials of degrees

in

can be multiplied using at most

arithmetic
operations in
 .
. The
schoolbook algorithm allows us to take
 .
.
The fastest currently known algorithm [
5] yields
 .
. Here, the
soft-Oh
notation

means that

(we refer the reader to [
6, Chapter 25, Section 7] for
technical details). In order to simplify the cost analysis of our
algorithms we make the customary assumption that

for all
 .
. Notice that this
assumption implies the
super-additivity of
 ,
, namely

for all

and
 .
.
Fundamental bit complexity bounds
For bit complexity analyses, we consider Turing machines with
sufficiently many tapes. We write

for a
function that bounds the bit-cost of an algorithm which multiplies two
integers of bit sizes at most
 ,
,
for the usual binary representation. The best known bound [
7]
for

is
 .
.
Again, we make the customary assumption that

is nondecreasing.
Multipoint evaluation and interpolation
Let

again be an effective field. The
remainder (resp.
quotient) of the Euclidean division
of

by

in

is denoted by

(resp. by
 ).
). It may be computed using

operations in
 ,
,
if

and

have degrees
 .
. We recall that the gcd of
two polynomials of degrees at most

over

can be computed using

operations in

[
6, Algorithm
11.4]. Given polynomials

and

over

with

and
 ,
, all the remainders

may be computed simultaneously in cost

using a
subproduct tree [
6, Chapter 10]. The
inverse problem, called
Chinese remaindering, can be solved
with a similar cost
 ,
,
assuming that the

are pairwise coprime. The
fastest known algorithms for these tasks can be found in [
1,
2,
10].
3.Abstract modular composition in
the separable case
For any field  and
and  ,
we denote
,
we denote

In this section,  represents an abstract
algebraically closed field of constants. Let
represents an abstract
algebraically closed field of constants. Let  be
a separable monic polynomial, so
be
a separable monic polynomial, so  admits
admits  pairwise distinct roots
pairwise distinct roots  in
in
 . Then we may use the
following algorithm for composition modulo
. Then we may use the
following algorithm for composition modulo  :
:
-
Input
Polynomials
 and pairwise distinct
and pairwise distinct
 .
.
-
Output
-
 , where
, where  .
.
-
Compute  using fast multi-point
evaluation.
using fast multi-point
evaluation.
-
Compute  using fast multi-point
evaluation.
using fast multi-point
evaluation.
-
Retrieve  with
with  using fast interpolation.
using fast interpolation.
-
Return  .
.
Theorem 1. Algorithm 1 is correct and requires  operations in
operations in  .
.
Proof. By construction,  for
for  . Since
. Since  and the
and the  are pairwise distinct, it follows that
are pairwise distinct, it follows that
 . This proves the correctness
of the algorithm. The complexity bound follows from the fact that steps
1, 2 and 3 take
. This proves the correctness
of the algorithm. The complexity bound follows from the fact that steps
1, 2 and 3 take  operations in
operations in  .
.
We wish to apply the theorem in the case when  . Of course, on a Turing machine, we can only
approximate complex numbers with arbitrarily high precision, and
likewise for the field operations in
. Of course, on a Turing machine, we can only
approximate complex numbers with arbitrarily high precision, and
likewise for the field operations in  .
For given numbers
.
For given numbers  and
and  , approximations at precision
, approximations at precision 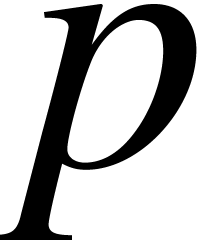 for
for  ,
,  ,
,  and
and  (whenever
(whenever  ) can all be
computed in time
) can all be
computed in time  . In view of
Theorem 1, it is therefore natural to ask whether
. In view of
Theorem 1, it is therefore natural to ask whether 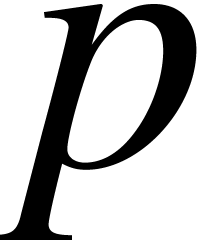 -bit approximations of the
coefficients of
-bit approximations of the
coefficients of  may be computed in time
may be computed in time  .
.
In the remainder of this paper we give a positive answer to a carefully
formulated version of this question. Our first task is to make the
concept of “approximations at precision 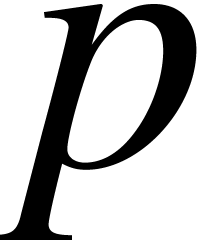 ” more precise and to understand the way
errors accumulate when performing a sequence of computations at
precision
” more precise and to understand the way
errors accumulate when performing a sequence of computations at
precision 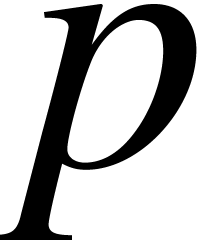 . We rely on
“fixed point ball arithmetic” for this matter, as described
in the next subsection. At a second stage, we prove a complexity bound
for modular composition that holds for a fixed modulus
. We rely on
“fixed point ball arithmetic” for this matter, as described
in the next subsection. At a second stage, we prove a complexity bound
for modular composition that holds for a fixed modulus  with known roots
with known roots  and for sufficiently large
working precisions
and for sufficiently large
working precisions 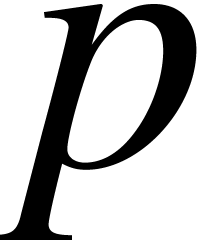 .
.
The assumption that the roots  of
of  are known is actually quite harmless in this context for
the following reason: as soon as approximations for
are known is actually quite harmless in this context for
the following reason: as soon as approximations for  are known at a sufficiently high precision, the computation of even
better approximations can be done fast using Newton's method combined
with multi-point evaluation. Since we are only interested in the
complexity for “sufficiently large working precisions”, the
computation of the initial approximations of
are known at a sufficiently high precision, the computation of even
better approximations can be done fast using Newton's method combined
with multi-point evaluation. Since we are only interested in the
complexity for “sufficiently large working precisions”, the
computation of the initial approximations of  can
therefore be regarded as a precomputation of negligible cost.
can
therefore be regarded as a precomputation of negligible cost.
4.Ball arithmetic and straight-line
programs
4.1.Fixed point numbers
Let  be a real number, we write
be a real number, we write  for the largest integer less or equal to
for the largest integer less or equal to  and
and
 for the closest integer to
for the closest integer to  .
.
Given a precision  , we denote
by
, we denote
by  the set of fixed point numbers with
the set of fixed point numbers with
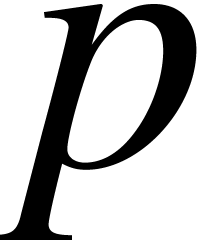 binary digits after the dot. This set
binary digits after the dot. This set  is clearly stable under addition and subtraction. We can
also define approximate multiplication
is clearly stable under addition and subtraction. We can
also define approximate multiplication  on
on  using
using  , so
, so
 for all
for all  .
.
For any fixed constant  and
and  , we notice that
, we notice that  and
and
 can be computed in time
can be computed in time  , whereas
, whereas  can be computed in
time
can be computed in
time  . Similarly, one may
define an approximate inversion
. Similarly, one may
define an approximate inversion  on
on  by
by  . For any
fixed constant
. For any
fixed constant  and
and  ,
we may compute
,
we may compute  in time
in time  .
.
4.2.Fixed point ball arithmetic
Ball arithmetic is used for providing reliable error bounds for
approximate computations. A ball is a set  with
with  and
and  .
From the computational point of view, we represent such balls by their
centers
.
From the computational point of view, we represent such balls by their
centers  and radii
and radii  .
We denote by
.
We denote by  the set of balls with centers in
the set of balls with centers in
 and radii in
and radii in  .
Given vectors
.
Given vectors  and
and  we
write
we
write  to mean
to mean  ,
and we also set
,
and we also set  .
.
Let  be an open subset of
be an open subset of  . We say that
. We say that  is a
domain lift at precision
is a
domain lift at precision 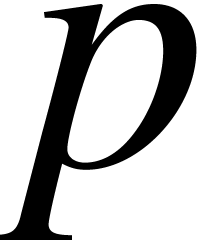 if
if  for all
for all  . The
maximal such lift is given by
. The
maximal such lift is given by  .
Given a function
.
Given a function  , a ball
lift of
, a ball
lift of  at precision
at precision 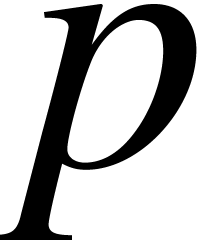 is a function
is a function  , where
, where  is a domain lift of
is a domain lift of  at
precision
at
precision 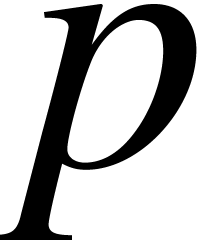 , that satisfies
the inclusion property: for any
, that satisfies
the inclusion property: for any  and
and
 , we have
, we have

A ball lift  of
of  is a computable sequence
is a computable sequence  of ball lifts at every
precision such that for any sequence
of ball lifts at every
precision such that for any sequence  with
with  , we have
, we have

This condition implies the following:

We say that  is maximal if
is maximal if  is the maximal domain lift for each
is the maximal domain lift for each 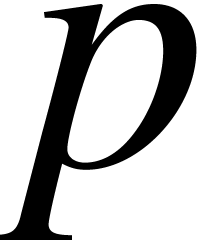 . Notice that a function
. Notice that a function  must be continuous in order to admit a maximal ball lift.
must be continuous in order to admit a maximal ball lift.
The following formulas define maximal ball lifts  ,
,  and
and  at precision
at precision 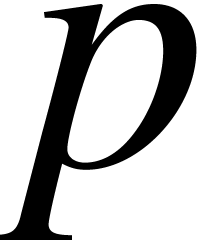 for the ring operations
for the ring operations  ,
,  and
and  :
:

The extra  in the formula for multiplication is
needed in order to counter the effect of rounding errors that might
occur in the three multiplications
in the formula for multiplication is
needed in order to counter the effect of rounding errors that might
occur in the three multiplications  ,
,
 and
and  .
For
.
For  with
with  ,
the following formula also defines a maximal ball lift
,
the following formula also defines a maximal ball lift  at precision
at precision 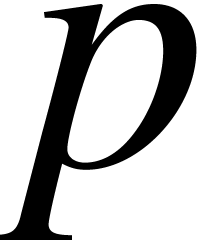 for the inversion:
for the inversion:

For any fixed constant  and
and  , we notice that
, we notice that  ,
,
 ,
,  and
and
 can be computed in time
can be computed in time  .
.
Let  be the ball lift of a function
be the ball lift of a function  with
with  . Consider
a second ball lift
. Consider
a second ball lift  of a function
of a function  with
with  . Then we
may define a ball lift
. Then we
may define a ball lift  of the composition
of the composition  as follows. For each precision
as follows. For each precision 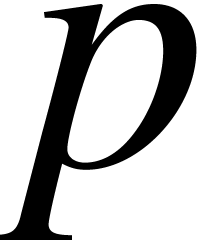 , we take
, we take  ,
where
,
where  is the restriction of
is the restriction of  to the set
to the set  .
.
We shall use ball arithmetic for the computation of complex functions
 simply through the consideration of real and
imaginary parts. This point of view is sufficient for the asymptotic
complexity point of view of the present paper. Of course, it would be
more efficient to directly compute with complex balls (i.e.
balls with a complex center and a real radius), but this would involve
approximate square roots and ensuing technicalities.
simply through the consideration of real and
imaginary parts. This point of view is sufficient for the asymptotic
complexity point of view of the present paper. Of course, it would be
more efficient to directly compute with complex balls (i.e.
balls with a complex center and a real radius), but this would involve
approximate square roots and ensuing technicalities.
4.3.The Lipschitz property
Assume that we are given the ball lift  of a
function
of a
function  with
with  .
Given a subset
.
Given a subset  and constants
and constants  , we say that the ball lift
, we say that the ball lift  is
is  -Lipschitz on
-Lipschitz on
 if
if

For instance, the ball lifts  and
and  of addition and subtraction are
of addition and subtraction are  -Lipschitz on
-Lipschitz on  .
Similarly, the ball lift
.
Similarly, the ball lift  of multiplication is
of multiplication is
 -Lipschitz on
-Lipschitz on  (by taking
(by taking  ),
whereas the ball lift
),
whereas the ball lift  of
of  is
is  -Lipschitz on
-Lipschitz on  .
.
Given  and
and  as above, we
say that
as above, we
say that  is locally
is locally  -Lipschitz on
-Lipschitz on  if
if  is
is  -Lipschitz
on each compact subset of
-Lipschitz
on each compact subset of  .
We define
.
We define  to be
to be  -Lipschitz
(resp. locally
-Lipschitz
(resp. locally  -Lipschitz) on
-Lipschitz) on
 if there exists a constant
if there exists a constant  for which
for which  is
is  -Lipschitz
(resp. locally
-Lipschitz
(resp. locally  -Lipschitz).
If
-Lipschitz).
If  is locally
is locally  -Lipschitz
on
-Lipschitz
on  , then it is not hard to
see that
, then it is not hard to
see that  is necessarily locally Lipschitz on
is necessarily locally Lipschitz on
 , with Lipschitz constant
, with Lipschitz constant
 . That is,
. That is,

In fact, the requirement that a computable ball lift  is
is  -Lipschitz implies that we
have a means to compute high quality error bounds. We finally define
-Lipschitz implies that we
have a means to compute high quality error bounds. We finally define
 to be Lipschitz (resp. locally Lipschitz) on
to be Lipschitz (resp. locally Lipschitz) on
 if there exists a constant
if there exists a constant  for which
for which  is
is  -Lipschitz
(resp. locally
-Lipschitz
(resp. locally  -Lipschitz).
-Lipschitz).
Proof. Consider a compact subset  . Since this implies
. Since this implies  to
be a compact subset of
to
be a compact subset of  , it
follows that there exists an
, it
follows that there exists an  such that
such that  . Let
. Let  ,
,
 and
and  be such that for any
be such that for any
 ,
,  and
and
 , we have
, we have

Given  with
with  and
and  , it follows that
, it follows that  satisfies
satisfies  , whence
, whence  . If we also assume that
. If we also assume that  , then it also follows that
, then it also follows that  , whence
, whence  and
and  . In other words, if
. In other words, if  and
and 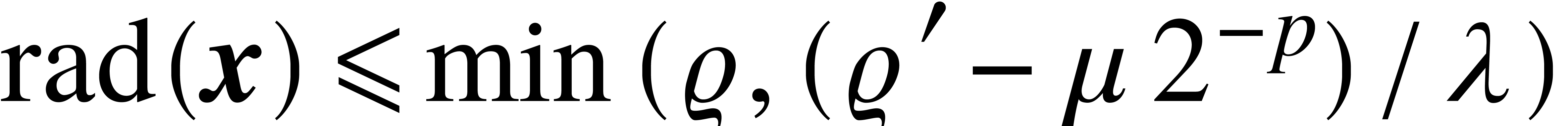 , then
, then
 and
and  .
.
5.Straight-line programs
A signature is a finite or countable set of function symbols
 together with an arity
together with an arity  for each
for each  . A model
for
. A model
for  is a set
is a set  together
with a function
together
with a function  with
with  for
each
for
each  . If
. If  is a topological space, then
is a topological space, then  is required to be
an open subset of
is required to be
an open subset of  . Let
. Let  be a countable and ordered set of variable symbols.
be a countable and ordered set of variable symbols.
A straight-line program  with signature
with signature
 is a sequence
is a sequence  of
instructions of the form
of
instructions of the form

where  and
and  ,
together with a subset
,
together with a subset  of output
variables. Variables that appear for the first time in the sequence
in the right-hand side of an instruction are called input
variables. We denote by
of output
variables. Variables that appear for the first time in the sequence
in the right-hand side of an instruction are called input
variables. We denote by  the set of input
variables. The number
the set of input
variables. The number  is called the
length of
is called the
length of  .
.
There exist unique sequences  and
and  with
with  and
and  . Given a model
. Given a model  of
of  we can run
we can run  for inputs in
for inputs in  , provided that the arguments
, provided that the arguments  are always in the domain of
are always in the domain of  when executing the instruction
when executing the instruction  .
Let
.
Let  be the set of tuples
be the set of tuples  on which
on which  can be run. Given
can be run. Given  , let
, let  denote the value
of
denote the value
of  at the end of the program. Hence
at the end of the program. Hence  gives rise to a function
gives rise to a function  .
.
Now assume that  is a model for
is a model for  and that we are given a ball lift
and that we are given a ball lift  of
of  for each
for each  . Then
. Then
 is also a model for
is also a model for  at
each precision
at
each precision 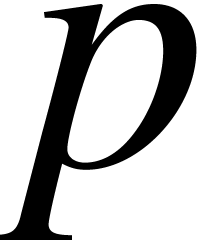 , by taking
, by taking
 for each
for each  .
Consequently, any SLP
.
Consequently, any SLP  as above gives rise to
both a function
as above gives rise to
both a function  and a ball lift
and a ball lift  at each precision
at each precision 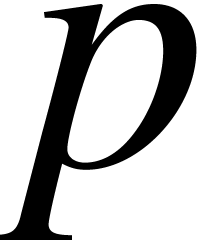 . The
sequence
. The
sequence  thus provides us with a ball lift
thus provides us with a ball lift  for
for  .
.
Proof. For each model  of
of
 , for each variable
, for each variable  and each input
and each input  ,
let
,
let  denote the value of
denote the value of  after step
after step  . We may regard
. We may regard
 as a function from
as a function from  to
to
 . In particular, we obtain a
computable sequence of functions
. In particular, we obtain a
computable sequence of functions  that give rise
to a ball lift
that give rise
to a ball lift  of
of  .
Let us show by induction over
.
Let us show by induction over  that
that  is Lipschitz for every
is Lipschitz for every  .
This is clear for
.
This is clear for  , so let
, so let
 . If
. If  , then we have
, then we have  ;
otherwise, we have
;
otherwise, we have

In both cases, it follows from Lemma 2 that  is again a Lipschitz ball lift. We conclude by noticing
that
is again a Lipschitz ball lift. We conclude by noticing
that  .
.
6.Computable numbers and ultimate
complexity
A real number  is said to be computable
if there exists an approximation algorithm
is said to be computable
if there exists an approximation algorithm  that takes
that takes  on input and produces
on input and produces  on output with
on output with  (we say that
(we say that  is a
is a  -approximation
of
-approximation
of  ). We denote by
). We denote by  the field of computable real numbers.
the field of computable real numbers.
Let  be a nondecreasing function. We say that a
computable real number
be a nondecreasing function. We say that a
computable real number  has ultimate
complexity
has ultimate
complexity  if it admits an approximation
algorithm
if it admits an approximation
algorithm  that computes
that computes  in time
in time  for some fixed constant
for some fixed constant  . The fact that we allow
. The fact that we allow  to be computed in time
to be computed in time  and not
and not  is justified by the observation that the position of the “binary
dot” is somewhat arbitrary in the approximation process of a
computable number.
is justified by the observation that the position of the “binary
dot” is somewhat arbitrary in the approximation process of a
computable number.
The notion of approximation algorithm generalizes to vectors with real
coefficients: given  , an
approximation algorithm for
, an
approximation algorithm for  as a whole is an
algorithm
as a whole is an
algorithm  that takes
that takes  on
input and returns
on
input and returns  on output with
on output with  for
for  . This
definition naturally extends to any other mathematical objects that can
be encoded by vectors of real numbers: complex numbers (by their real
and complex parts), polynomials and matrices (by their vectors of
coefficients), etc. The notion of ultimate complexity also extends to
any of these objects.
. This
definition naturally extends to any other mathematical objects that can
be encoded by vectors of real numbers: complex numbers (by their real
and complex parts), polynomials and matrices (by their vectors of
coefficients), etc. The notion of ultimate complexity also extends to
any of these objects.
A ball lift  is said to be computable if
there exists an algorithm for computing
is said to be computable if
there exists an algorithm for computing  for all
for all
 . A computable ball lift
. A computable ball lift  of a function
of a function  with
with  allows us to compute the restriction of
allows us to compute the restriction of  to
to  : given
: given  with approximation algorithm
with approximation algorithm  ,
by taking
,
by taking  , we have
, we have  ,
,  ,
and
,
and  .
.
Let  be a nondecreasing function and assume that
be a nondecreasing function and assume that
 is open. We say that
is open. We say that  has
ultimate complexity
has
ultimate complexity  if for every
compact set
if for every
compact set  , there exist
constants
, there exist
constants  ,
,  and
and  such that for any
such that for any  and
and  with
with  and
and  , we can compute
, we can compute  in time
in time  . For instance,
. For instance,  and
and  have ultimate complexity
have ultimate complexity
 , whereas
, whereas  and
and  have ultimate complexity
have ultimate complexity  .
.
Proof. Let  be an
approximation algorithm for
be an
approximation algorithm for  of complexity
of complexity  , where
, where  . There exist
. There exist  and a compact
ball
and a compact
ball  around
around  with
with  and such that
and such that  is included in
is included in
 for all
for all  .
There also exists a constant
.
There also exists a constant  such that
such that  can be computed in time
can be computed in time  for all
for all
 . Since
. Since  is locally Lipschitz, there exists yet another constant
is locally Lipschitz, there exists yet another constant  such that
such that  for
for  .
For
.
For  and
and  ,
this shows that we may compute a
,
this shows that we may compute a  -approximation
of
-approximation
of  in time
in time  .
.
Proof. In a similar way as in the proof of Lemma
2, the evaluation of  for
for  with
with  and
and  boils down to the evaluation of
boils down to the evaluation of  at
at  and the evaluation of
and the evaluation of  at
at  with
with  . Modulo a
further lowering of
. Modulo a
further lowering of  and
and  if necessary, these evaluations can be done in time
if necessary, these evaluations can be done in time  and
and  for suitable
for suitable  and
sufficiently large
and
sufficiently large  .
.
Proof. This is a direct consequence of
Proposition 5.
Proof. We use the ball lifts of section 4
for each  : they are locally
Lipschitz and computable with ultimate complexity
: they are locally
Lipschitz and computable with ultimate complexity  . We may thus apply the Theorem 6 to
obtain
. We may thus apply the Theorem 6 to
obtain  .
.
7.Ultimate modular composition for
separable moduli
Proof. The algorithm for fast multi-point
evaluation of a polynomial  at
at  can be regarded as an SLP over
can be regarded as an SLP over  of length
of length  that takes
that takes  on input and that
produces
on input and that
produces  on output. Similarly, the algorithm for
interpolation can be regarded as an SLP over
on output. Similarly, the algorithm for
interpolation can be regarded as an SLP over  of
length
of
length  that takes
that takes  on
input and that produces
on
input and that produces  on output with
on output with  . Altogether, we may regard the
entire Algorithm 1 as an SLP
. Altogether, we may regard the
entire Algorithm 1 as an SLP  over
over
 of length
of length  that takes
that takes
 on input and that produces
on input and that produces  on output with
on output with  . It follows
from Corollary 7 that
. It follows
from Corollary 7 that  admits a ball
lift
admits a ball
lift  of ultimate complexity
of ultimate complexity  . The conclusion now follows from Proposition
4.
. The conclusion now follows from Proposition
4.
According to the above lemma, we notice that the time complexity for
computing  is
is  for some
constant
for some
constant  that depends on
that depends on  ,
, 
 , and the
, and the  .
.
Proof. There are many algorithms for the
certified computation of the roots of a separable complex polynomial. We
may use any of these algorithms as a “fall back” algorithm
in the case that we only need a  -approximation
of
-approximation
of  at a low precision
at a low precision  determined by
determined by  only.
only.
For general precisions  , we
use the following strategy in order to compute a ball
, we
use the following strategy in order to compute a ball  with
with  and
and  for some fixed
threshold
for some fixed
threshold  . For some suitable
. For some suitable
 and
and  ,
we use the fall back algorithm. For
,
we use the fall back algorithm. For  and for a
second fixed constant
and for a
second fixed constant  , we
first compute a ball enclosure
, we
first compute a ball enclosure  at the lower
precision
at the lower
precision  using a recursive application of the
method. We next compute
using a recursive application of the
method. We next compute  using a ball version of
the Newton iteration, as explained below. If this yields a ball
using a ball version of
the Newton iteration, as explained below. If this yields a ball  with acceptable radius
with acceptable radius  ,
then we are done. Otherwise, we resort to our fall-back method. Such
calls of the fall-back method only occur if the default threshold
precision
,
then we are done. Otherwise, we resort to our fall-back method. Such
calls of the fall-back method only occur if the default threshold
precision  was chosen too low. Nevertheless, we
will show that there exists a threshold
was chosen too low. Nevertheless, we
will show that there exists a threshold  such
that the computed
such
that the computed  by the Newton iteration always
satisfies
by the Newton iteration always
satisfies  for
for  .
.
Let us detail how we perform our ball version of the Newton iteration.
Recall that  with
with  and
and
 is given. We also assume that we computed once
and for all a
is given. We also assume that we computed once
and for all a  -approximation
of
-approximation
of  , in the form of a ball
polynomial
, in the form of a ball
polynomial  of radius
of radius  that contains
that contains  . Now we
evaluate
. Now we
evaluate  and
and  at each of
the points
at each of
the points  using fast multi-point evaluation.
Let us denote the results by
using fast multi-point evaluation.
Let us denote the results by  and
and  . Let
. Let  ,
,
 and
and  denote the balls
with radius zero and whose centers are the same as for
denote the balls
with radius zero and whose centers are the same as for  ,
,  and
and  . Using vector notation, the Newton iteration
now becomes:
. Using vector notation, the Newton iteration
now becomes:

If  , then it is well-known
[17, 23] that
, then it is well-known
[17, 23] that  .
Since
.
Since  , the fact that
multi-point ball evaluation (used for
, the fact that
multi-point ball evaluation (used for  and
and  ) is locally Lipschitz implies the
existence of a constant
) is locally Lipschitz implies the
existence of a constant  with
with  and
and  . Since
. Since  for
for  , there also exists a
constant
, there also exists a
constant  with
with  .
Altogether, this means that there exists a constant
.
Altogether, this means that there exists a constant  with
with  . Let
. Let  . Then for any
. Then for any  ,
the Newton iteration provides us with a
,
the Newton iteration provides us with a  with
with
 .
.
Let us now analyze the ultimate complexity  of
our algorithm. For large
of
our algorithm. For large  ,
the algorithm essentially performs two multi-point evaluations of
ultimate cost
,
the algorithm essentially performs two multi-point evaluations of
ultimate cost  for some constant
for some constant  that does not depend on
that does not depend on  , and
a recursive call. Consequently,
, and
a recursive call. Consequently,

We finally obtain an other constant  such that
such that

by summing up the geometric progression and using the fact that  is nondecreasing. The conclusion now follows from
Lemma 4.
is nondecreasing. The conclusion now follows from
Lemma 4.
Remark 10. A remarkable
feature of the above proof is that the precision  at which the Newton iteration can safely be used does not need to be
known in advance. In particular, the proof does not require any a
priori knowledge about the Lipschitz constants.
at which the Newton iteration can safely be used does not need to be
known in advance. In particular, the proof does not require any a
priori knowledge about the Lipschitz constants.
Proof. This is an immediate consequence of the
combination of the two above lemmas.
8.Conclusion and final remarks
With some more work, we expect that all above bounds of the form  can be lowered to
can be lowered to  .
Notice that
.
Notice that  for
for  ,
when taking
,
when taking  [7]. In order to prove
this stronger bound using our framework, one might add an auxiliary
operation
[7]. In order to prove
this stronger bound using our framework, one might add an auxiliary
operation  for the product of two polynomials of
degrees
for the product of two polynomials of
degrees  to the set of signatures
to the set of signatures  . Polynomial products of this kind can be
implemented for coefficients in
. Polynomial products of this kind can be
implemented for coefficients in  with
with  using Kronecker substitution. For bounded coefficients,
this technique allows for the computation of one such product in time
using Kronecker substitution. For bounded coefficients,
this technique allows for the computation of one such product in time
 . By using Theorem 6,
a standard complexity analysis should show that multi-point evaluation
and interpolation have ultimate complexity
. By using Theorem 6,
a standard complexity analysis should show that multi-point evaluation
and interpolation have ultimate complexity  .
.
By Theorem 11, the actual bit complexity of modular
composition is of the form  for some value of
for some value of
 that depends on
that depends on  (hence
of
(hence
of  ). An interesting problem
is to get a better grip on this value
). An interesting problem
is to get a better grip on this value  ,
which mainly depends on the geometric proximity of the roots of
,
which mainly depends on the geometric proximity of the roots of  .
.
If  belong to
belong to  ,
then
,
then  and we may wish to bound
and we may wish to bound  as a function of
as a function of  and the maximum bit size
and the maximum bit size  of the coefficients of
of the coefficients of  ,
,
 and
and  .
This would involve bit complexity results for root isolation [18,
19, 24], for multi-point evaluation, and for
interpolation. The overal complexity should then be compared with the
maximal size of the output, namely
.
This would involve bit complexity results for root isolation [18,
19, 24], for multi-point evaluation, and for
interpolation. The overal complexity should then be compared with the
maximal size of the output, namely  ,
which is in general much larger than the input size.
,
which is in general much larger than the input size.
If  is not separable, but if a separable
decomposition is known, then the techniques developed in this paper
could be combined with Ritzmann's algorithm for the composition of
formal power series [22]. If such a separable decomposition
is not known, then it is an interesting problem to obtain a general
algorithm for modular composition with a similar complexity (but this
seems far beyond the scope of this paper).
is not separable, but if a separable
decomposition is known, then the techniques developed in this paper
could be combined with Ritzmann's algorithm for the composition of
formal power series [22]. If such a separable decomposition
is not known, then it is an interesting problem to obtain a general
algorithm for modular composition with a similar complexity (but this
seems far beyond the scope of this paper).
Bibliography
-
[1]
-
D. Bernstein. Scaled remainder trees. Available from
https://cr.yp.to/arith/scaledmod-20040820.pdf,
2004.
-
[2]
-
A. Bostan, G. Lecerf, and É. Schost.
Tellegen's principle into practice. In Hoon Hong, editor,
Proceedings of the 2003 International Symposium on Symbolic
and Algebraic Computation, ISSAC '03, pages 37–44, New
York, NY, USA, 2003. ACM.
-
[3]
-
R. P. Brent and H. T. Kung. Fast algorithms for
manipulating formal power series. J. ACM,
25(4):581–595, 1978.
-
[4]
-
P. Bürgisser, M. Clausen, and M. A. Shokrollahi.
Algebraic complexity theory, volume 315 of Grundlehren
der Mathematischen Wissenschaften. Springer-Verlag, 1997.
-
[5]
-
D. G. Cantor and E. Kaltofen. On fast multiplication
of polynomials over arbitrary algebras. Acta Infor.,
28(7):693–701, 1991.
-
[6]
-
J. von zur Gathen and J. Gerhard. Modern computer
algebra. Cambridge University Press, New York, 2 edition,
2003.
-
[7]
-
D. Harvey, J. van der Hoeven, and G. Lecerf. Even
faster integer multiplication. J. Complexity,
36:1–30, 2016.
-
[8]
-
J. van der Hoeven. Fast composition of numeric power
series. Technical Report 2008-09, Université Paris-Sud,
Orsay, France, 2008.
-
[9]
-
J. van der Hoeven. Ball arithmetic. Technical report,
CNRS & École polytechnique, 2011. https://hal.archives-ouvertes.fr/hal-00432152/.
-
[10]
-
J. van der Hoeven. Faster Chinese remaindering.
Technical report, CNRS & École polytechnique, 2016.
http://hal.archives-ouvertes.fr/hal-01403810.
-
[11]
-
J. van der Hoeven and G. Lecerf. Modular composition
via factorization. Technical report, CNRS & École
polytechnique, 2017. http://hal.archives-ouvertes.fr/hal-01457074.
-
[12]
-
Xiaohan Huang and V. Y. Pan. Fast rectangular matrix
multiplication and applications. J. Complexity,
14(2):257–299, 1998.
-
[13]
-
E. Kaltofen and V. Shoup. Fast polynomial
factorization over high algebraic extensions of finite fields.
In Proceedings of the 1997 International Symposium on
Symbolic and Algebraic Computation, ISSAC '97, pages
184–188, New York, NY, USA, 1997. ACM.
-
[14]
-
E. Kaltofen and V. Shoup. Subquadratic-time factoring
of polynomials over finite fields. Math. Comp.,
67(223):1179–1197, 1998.
-
[15]
-
K. S. Kedlaya and C. Umans. Fast modular composition
in any characteristic. In FOCS'08: IEEE Conference on
Foundations of Computer Science, pages 146–155,
Washington, DC, USA, 2008. IEEE Computer Society.
-
[16]
-
K. S. Kedlaya and C. Umans. Fast polynomial
factorization and modular composition. SIAM J. Comput.,
40(6):1767–1802, 2011.
-
[17]
-
R. Krawczyk. Newton-Algorithmen zur Bestimmung von
Nullstellen mit Fehler-schranken. Computing,
4:187–201, 1969.
-
[18]
-
C. A. Neff and J. H. Reif. An efficient algorithm for
the complex roots problem. J. Complexity,
12(2):81–115, 1996.
-
[19]
-
V. Y. Pan. Univariate polynomials: nearly optimal
algorithms for numerical factorization and root-finding. J.
Symbolic Comput., 33(5):701–733, 2002.
-
[20]
-
C. H. Papadimitriou. Computational Complexity.
Addison-Wesley, 1994.
-
[21]
-
M. S. Paterson and L. J. Stockmeyer. On the number of
nonscalar multiplications necessary to evaluate polynomials.
SIAM J.Comput., 2(1):60–66, 1973.
-
[22]
-
P. Ritzmann. A fast numerical algorithm for the
composition of power series with complex coefficients.
Theoret. Comput. Sci., 44:1–16, 1986.
-
[23]
-
S. M. Rump. Kleine Fehlerschranken bei
Matrixproblemen. PhD thesis, Universität Karlsruhe,
1980.
-
[24]
-
A. Schönhage. The fundamental theorem of algebra
in terms of computational complexity. Technical report,
Preliminary Report of Mathematisches Institut der
Universität Tübingen, Germany, 1982.
 be an effective field, and let
be an effective field, and let  be polynomials in
be polynomials in  .
The problem of modular composition is to compute
.
The problem of modular composition is to compute  modulo
modulo  .
Modular composition is an important problem in complexity theory because
of its applications to polynomial factorization [14–16]. It also occurs very naturally whenever one wishes to
perform polynomial computations over
.
Modular composition is an important problem in complexity theory because
of its applications to polynomial factorization [14–16]. It also occurs very naturally whenever one wishes to
perform polynomial computations over  inside an
algebraic extension of
inside an
algebraic extension of  . In
addition, given two different representations
. In
addition, given two different representations  of
an algebraic extension of
of
an algebraic extension of  ,
the implementation of an explicit isomorphism actually boils down to
modular composition.
,
the implementation of an explicit isomorphism actually boils down to
modular composition.
 the number of operations in
the number of operations in  in
in  and
and  .
. operations in
operations in  .
. when using fast
linear algebra (see [
when using fast
linear algebra (see [ is such that a
is such that a  matrix over
matrix over  rectangular matrix in time
rectangular matrix in time  .
. is due to Huang and Pan
[
is due to Huang and Pan
[ .
. ,
, .
. that splits over
that splits over  is separable, which means that
is separable, which means that  .
. are of degree
are of degree
 can be computed by evaluating
can be computed by evaluating  at
at  ,
, at
at
 ,
, to yield
to yield  ),
), of computable complex numbers, we need additional concepts. In section
of computable complex numbers, we need additional concepts. In section
 in the
worst case, where
in the
worst case, where  and
and  is
the largest bit size of the coefficients: in fact, this precision allows
to compute all the complex roots of
is
the largest bit size of the coefficients: in fact, this precision allows
to compute all the complex roots of  for a function that bounds the total cost of a
polynomial product algorithm in terms of the number operations in
for a function that bounds the total cost of a
polynomial product algorithm in terms of the number operations in
 .
. .
. means that
means that  (we refer the reader to [
(we refer the reader to [ for all
for all  .
. ,
, for all
for all  and
and  .
. for a
function that bounds the bit-cost of an algorithm which multiplies two
integers of bit sizes at most
for a
function that bounds the bit-cost of an algorithm which multiplies two
integers of bit sizes at most  .
. is nondecreasing.
is nondecreasing.
 (resp. by
(resp. by  ).
). operations in
operations in  .
. operations in
operations in  over
over  and
and  ,
, may be computed simultaneously in cost
may be computed simultaneously in cost  using a subproduct tree [
using a subproduct tree [ are pairwise coprime. The
fastest known algorithms for these tasks can be found in [
are pairwise coprime. The
fastest known algorithms for these tasks can be found in [ ,
,
 be
a separable monic polynomial, so
be
a separable monic polynomial, so  and pairwise distinct
and pairwise distinct
 .
. ,
, using fast multi-point
evaluation.
using fast multi-point
evaluation.
 using fast multi-point
evaluation.
using fast multi-point
evaluation.
 with
with  using fast interpolation.
using fast interpolation.
 .
. .
. for
for  .
. and the
and the  are pairwise distinct, it follows that
are pairwise distinct, it follows that
 .
.
 .
. .
. and
and  ,
,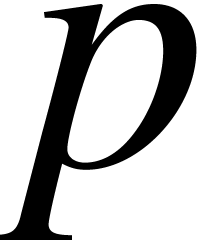 for
for  ,
, ,
, and
and  (whenever
(whenever  )
) .
. may be computed in time
may be computed in time  .
. be a real number, we write
be a real number, we write  for the largest integer less or equal to
for the largest integer less or equal to  for the closest integer to
for the closest integer to  ,
, the set of fixed point numbers with
the set of fixed point numbers with
 is clearly stable under addition and subtraction. We can
also define approximate multiplication
is clearly stable under addition and subtraction. We can
also define approximate multiplication  on
on  ,
, for all
for all  .
. and
and  ,
, ,
, can be computed in
time
can be computed in
time  .
. on
on  by
by  .
. ,
, in time
in time  with
with  and
and  .
. and radii
and radii  .
. the set of balls with centers in
the set of balls with centers in
 .
. and
and  we
write
we
write  to mean
to mean  ,
, .
. be an open subset of
be an open subset of  .
. is a
domain lift at precision
is a
domain lift at precision  for all
for all  .
. .
. ,
, ,
, is a domain lift of
is a domain lift of  and
and

 of
of  of ball lifts at every
precision such that for any sequence
of ball lifts at every
precision such that for any sequence  with
with  ,
,

 is the maximal domain lift for each
is the maximal domain lift for each  ,
, and
and  at precision
at precision  ,
, and
and  :
:
 in the formula for multiplication is
needed in order to counter the effect of rounding errors that might
occur in the three multiplications
in the formula for multiplication is
needed in order to counter the effect of rounding errors that might
occur in the three multiplications  ,
, and
and  .
. with
with  ,
, at precision
at precision 
 ,
, ,
, ,
, and
and
 can be computed in time
can be computed in time  .
. of a function
of a function  with
with  .
. of the composition
of the composition  as follows. For each precision
as follows. For each precision  ,
, is the restriction of
is the restriction of  to the set
to the set  .
. simply through the consideration of real and
imaginary parts. This point of view is sufficient for the asymptotic
complexity point of view of the present paper. Of course, it would be
more efficient to directly compute with complex balls (i.e.
balls with a complex center and a real radius), but this would involve
approximate square roots and ensuing technicalities.
simply through the consideration of real and
imaginary parts. This point of view is sufficient for the asymptotic
complexity point of view of the present paper. Of course, it would be
more efficient to directly compute with complex balls (i.e.
balls with a complex center and a real radius), but this would involve
approximate square roots and ensuing technicalities.
 and constants
and constants  ,
, -
- if
if

 and
and  of addition and subtraction are
of addition and subtraction are  -Lipschitz
-Lipschitz .
. of multiplication is
of multiplication is
 -Lipschitz
-Lipschitz (by taking
(by taking  ),
), of
of  is
is  -Lipschitz
-Lipschitz .
. as above, we
say that
as above, we
say that  -Lipschitz
-Lipschitz for which
for which 
 for which
for which  be a locally
be a locally  -Lipschitz
-Lipschitz .
. be a locally
be a locally
 -Lipschitz
-Lipschitz .
. and
and  ,
, is a locally
is a locally  -Lipschitz
-Lipschitz on
on
 .
. to
be a compact subset of
to
be a compact subset of  such that
such that  .
. ,
, and
and  be such that for any
be such that for any
 ,
, and
and
 ,
,
 with
with  and
and  ,
, satisfies
satisfies  ,
, .
. ,
, ,
, and
and  .
.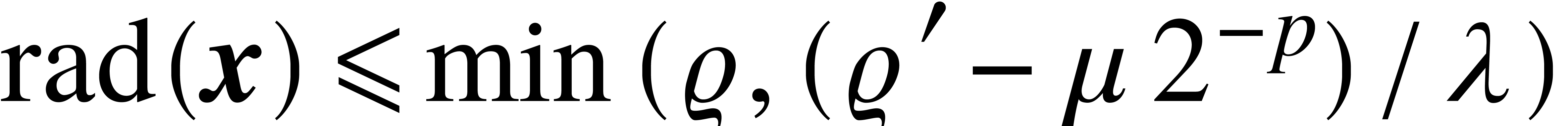 ,
, and
and  .
. together with an arity
together with an arity  for each
for each  .
. together
with a function
together
with a function  with
with  for
each
for
each  .
. is required to be
an open subset of
is required to be
an open subset of  .
. be a countable and ordered set of variable symbols.
be a countable and ordered set of variable symbols.
 with signature
with signature
 of
instructions of the form
of
instructions of the form

 and
and  ,
, of output
variables. Variables that appear for the first time in the sequence
in the right-hand side of an instruction are called input
variables. We denote by
of output
variables. Variables that appear for the first time in the sequence
in the right-hand side of an instruction are called input
variables. We denote by  the set of input
variables. The number
the set of input
variables. The number  is called the
length of
is called the
length of  and
and  with
with  and
and  .
. are always in the domain of
are always in the domain of  when executing the instruction
when executing the instruction  .
. be the set of tuples
be the set of tuples  on which
on which  ,
, denote the value
of
denote the value
of  at the end of the program. Hence
at the end of the program. Hence  .
. is a model for
is a model for  for each
for each  for each
for each  and a ball lift
and a ball lift  at each precision
at each precision  thus provides us with a ball lift
thus provides us with a ball lift  for
for  .
. ,
, is again Lipschitz.
is again Lipschitz.
 of
of
 ,
, and each input
and each input  ,
, denote the value of
denote the value of  after step
after step  .
. as a function from
as a function from  that give rise
to a ball lift
that give rise
to a ball lift  of
of  .
. ,
, .
. ,
, ;
;
 .
. is said to be computable
if there exists an approximation algorithm
is said to be computable
if there exists an approximation algorithm  that takes
that takes  on output with
on output with  (we say that
(we say that  is a
is a  -approximation
-approximation the field of computable real numbers.
the field of computable real numbers.
 be a nondecreasing function. We say that a
computable real number
be a nondecreasing function. We say that a
computable real number  has ultimate
complexity
has ultimate
complexity  for some fixed constant
for some fixed constant  .
. ,
, as a whole is an
algorithm
as a whole is an
algorithm  that takes
that takes  on output with
on output with  for
for  .
. :
: with approximation algorithm
with approximation algorithm  ,
, ,
, ,
, .
. be a nondecreasing function and assume that
be a nondecreasing function and assume that
 if for every
compact set
if for every
compact set  ,
, and
and  and
and  ,
, in time
in time  .
. has ultimate complexity
has ultimate complexity  .
. be an
approximation algorithm for
be an
approximation algorithm for  of complexity
of complexity  .
. around
around  and such that
and such that  such that
such that  for all
for all
 such that
such that  for
for  and
and  ,
, -approximation
-approximation .
. and
and  that can be composed. If
that can be composed. If
 ,
, .
. for
for  and the evaluation of
and the evaluation of  at
at  with
with  .
. and
and  if necessary, these evaluations can be done in time
if necessary, these evaluations can be done in time  for suitable
for suitable  and
sufficiently large
and
sufficiently large  .
. is a model for the
function symbols
is a model for the
function symbols  be a nondecreasing function such that
be a nondecreasing function such that  .
. be an SLP over
be an SLP over  .
.
 be an SLP of length
be an SLP of length  over
over  (where
(where  and
and  are naturally seen as constant fonctions
of arity zero). Then, there exists a ball lift
are naturally seen as constant fonctions
of arity zero). Then, there exists a ball lift  .
. :
: .
. such that the following
assertion holds. Let
such that the following
assertion holds. Let  ,
, has ultimate complexity
has ultimate complexity  .
. .
. at
at  can be regarded as an SLP over
can be regarded as an SLP over  on input and that
produces
on input and that
produces  on output. Similarly, the algorithm for
interpolation can be regarded as an SLP over
on output. Similarly, the algorithm for
interpolation can be regarded as an SLP over  on
input and that produces
on
input and that produces  on output with
on output with  .
. on input and that produces
on input and that produces  on output with
on output with  .
. is
is  for some
constant
for some
constant  that depends on
that depends on 
 be separable and monic of
degree
be separable and monic of
degree  ,
, by
by  .
. has ultimate
complexity
has ultimate
complexity  .
. with
with  and
and  for some fixed
threshold
for some fixed
threshold  .
. ,
, and for a
second fixed constant
and for a
second fixed constant  ,
, at the lower
precision
at the lower
precision  using a recursive application of the
method. We next compute
using a recursive application of the
method. We next compute  using a ball version of
the Newton iteration, as explained below. If this yields a ball
using a ball version of
the Newton iteration, as explained below. If this yields a ball  was chosen too low. Nevertheless, we
will show that there exists a threshold
was chosen too low. Nevertheless, we
will show that there exists a threshold  such
that the computed
such
that the computed  .
. and
and
 is given. We also assume that we computed once
and for all a
is given. We also assume that we computed once
and for all a  of radius
of radius  and
and  at each of
the points
at each of
the points  using fast multi-point evaluation.
Let us denote the results by
using fast multi-point evaluation.
Let us denote the results by  and
and  .
. ,
, denote the balls
with radius zero and whose centers are the same as for
denote the balls
with radius zero and whose centers are the same as for  ,
, and
and  .
.
 with
with  and
and  .
. for
for  with
with  .
. with
with  .
. .
. of
our algorithm. For large
of
our algorithm. For large  for some constant
for some constant  that does not depend on
that does not depend on 
 such that
such that

 is nondecreasing. The conclusion now follows from
Lemma
is nondecreasing. The conclusion now follows from
Lemma  has
ultimate complexity
has
ultimate complexity  .
. for
for  ,
, [
[ for the product of two polynomials of
degrees
for the product of two polynomials of
degrees  with
with  .
. for some value of
for some value of
 ,
, and we may wish to bound
and we may wish to bound