Factoring sparse polynomials
fast  |
|
December 28, 2023 |
| Final version of February 23, 2025 |
|
 . This work has
partly been supported by the French ANR-22-CE48-0016
NODE project.
. This work has
partly been supported by the French ANR-22-CE48-0016
NODE project.
 . This article has
been written using GNU TeXmacs [47].
. This article has
been written using GNU TeXmacs [47].
Consider a sparse polynomial in several variables given explicitly as a sum of non-zero terms with coefficients in an effective field. In this paper, we present several algorithms for factoring such polynomials and related tasks (such as gcd computation, square-free factorization, content-free factorization, and root extraction). Our methods are all based on sparse interpolation, but follow two main lines of attack: iteration on the number of variables and more direct reductions to the univariate or bivariate case. We present detailed probabilistic complexity bounds in terms of the complexity of sparse interpolation and evaluation. |
Let  be an effective field. Consider a sparse
polynomial
be an effective field. Consider a sparse
polynomial 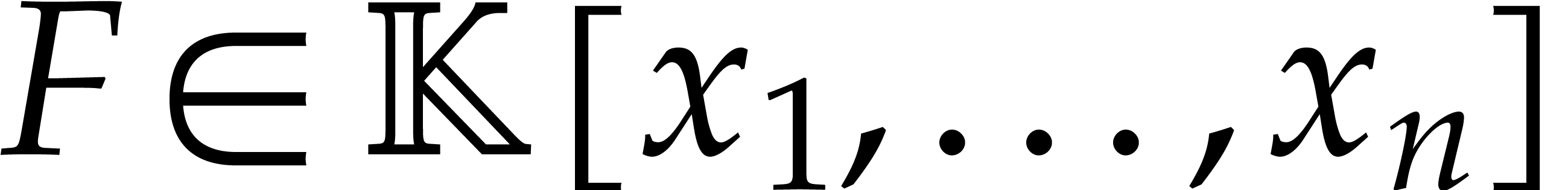 , represented as
, represented as
 |
(1.1) |
where  ,
, 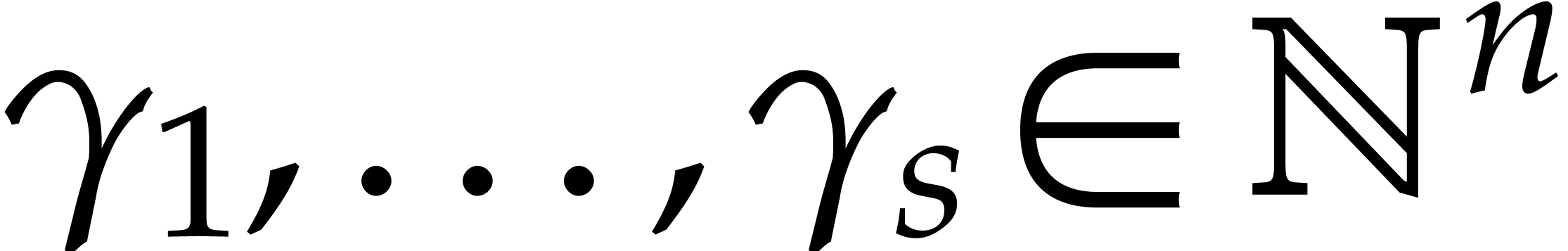 , and
, and  for any
for any  . We call
. We call  the size of
the size of  and
and  its support. The aim of this paper is to factor
its support. The aim of this paper is to factor  into a product of irreducible sparse polynomials.
into a product of irreducible sparse polynomials.
All algorithms that we will present are based on the approach of sparse evaluation and interpolation. Instead of directly working with sparse representations (1.1), the idea is to evaluate input polynomials at a sequence of well-chosen points, do the actual work on these evaluations, and then recover the output polynomials using sparse interpolation. The evaluation-interpolation approach leads to very efficient algorithms for many tasks, such as multiplication [48, 46], division, gcd computations [51], etc. In this paper, we investigate the complexity of factorization under this light.
One particularly good way to choose the evaluation points is to take
them in a geometric progression: for a fixed  , we evaluate at
, we evaluate at 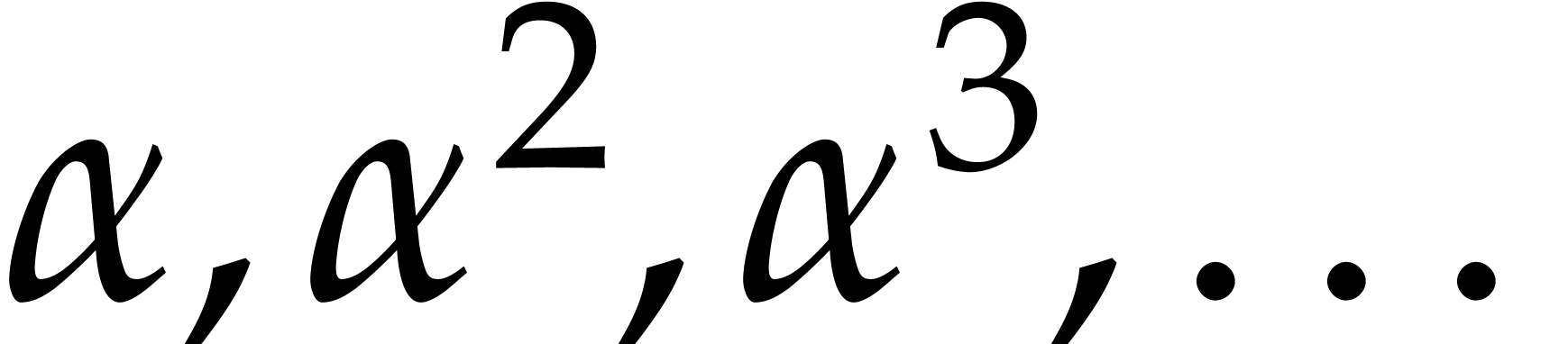 ,
where
,
where 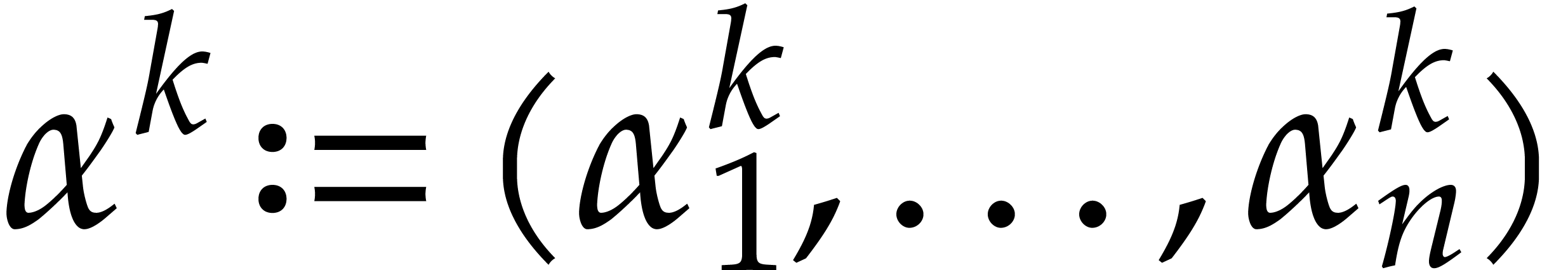 . This idea goes back
to Prony [91] and was rediscovered, extended, and
popularized by Ben Or and Tiwari [5]. We refer to [92]
for a nice survey. If
. This idea goes back
to Prony [91] and was rediscovered, extended, and
popularized by Ben Or and Tiwari [5]. We refer to [92]
for a nice survey. If  is a finite field, then a
further refinement is to use suitable roots of unity, in which case both
sparse evaluation and interpolation essentially reduce to discrete
Fourier transforms [52, 46].
is a finite field, then a
further refinement is to use suitable roots of unity, in which case both
sparse evaluation and interpolation essentially reduce to discrete
Fourier transforms [52, 46].
In this paper, we do not specify the precise algorithms that should be
used for sparse evaluation and interpolation, but we will always assume
that the evaluation points form geometric progressions. Then the cost
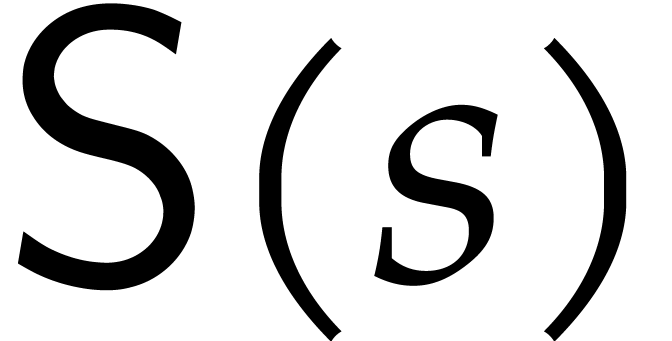 of sparse evaluation or interpolation at
of sparse evaluation or interpolation at  such points is quasi-linear in
such points is quasi-linear in 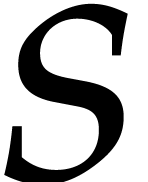 . We refer to Sections 2.1, 2.3,
and 2.4 for more details on this cost function
. We refer to Sections 2.1, 2.3,
and 2.4 for more details on this cost function 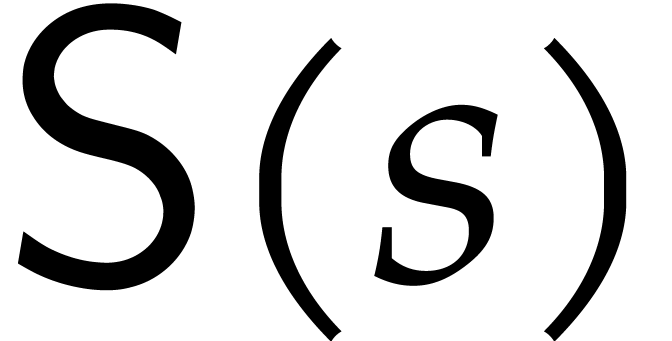 and the algebraic complexity model that we assume.
and the algebraic complexity model that we assume.
One important consequence of relying on geometric progressions is that
this constraints the type of factorization algorithms that will be
efficient. For instance, several existing methods start with the
application of random shifts 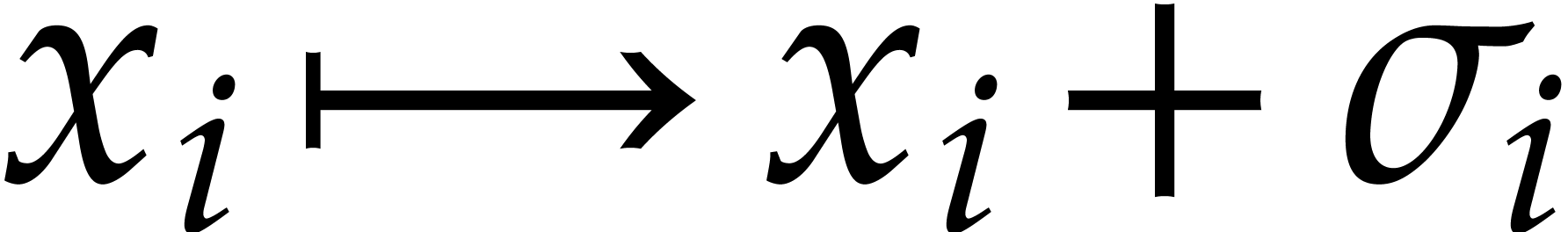 for one or more
variables
for one or more
variables  . Since such shifts
do not preserve geometric progressions, this is a technique that we must
avoid. On the other hand, monomial transformations like
. Since such shifts
do not preserve geometric progressions, this is a technique that we must
avoid. On the other hand, monomial transformations like  do preserve geometric progressions and we will see how to make use of
this fact.
do preserve geometric progressions and we will see how to make use of
this fact.
The main goal of this paper is to develop fast algorithms for factoring sparse polynomials under these constraints. Besides the top-level problem of factorization into irreducibles, we also consider several interesting subtasks, such as gcd computations, Hensel lifting, content-free and square-free factorization, and the extraction of multiple roots. While relying on known techniques, we shall show how to conciliate them with the above constraints.
Our complexity bounds are expressed in terms of the maximal size and total degree of the input and output polynomials. In practical applications, total degrees often remain reasonably small, so we typically allow for a polynomial dependence on the total degree times the required number of evaluation/interpolation points. In this particular asymptotic regime, our complexity bounds are very sharp and they improve on the bounds from the existing literature.
Concerning the top-level problem of decomposing sparse polynomials into irreducible factors, we develop two main approaches: a recursive one on the dimension and a more direct one based on simultaneous lifting with respect to all but one variables. We will present precise complexity bounds and examples of particularly difficult cases.
The factorization of polynomials is a fundamental problem in computer algebra. Since we are relying on sparse interpolation techniques, it is also natural to focus exclusively on randomized algorithms of Monte Carlo type. For some deterministic algorithms, we refer to [61, 101, 72].
Before considering multivariate polynomials, we need an algorithm for
factoring univariate polynomials. Throughout this paper, we assume that
we have an algorithm for this task (it can be shown that the mere
assumption of  being effective is not sufficient
[27, 28]).
being effective is not sufficient
[27, 28]).
In practice, we typically have  ,
,
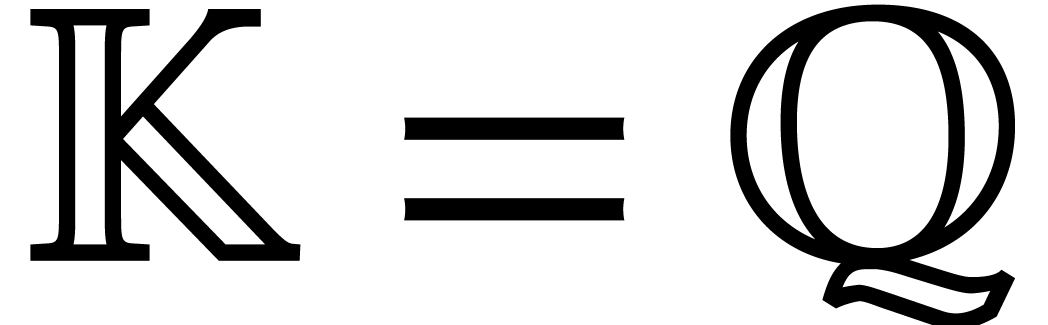 ,
,  , or
, or  for some prime
for some prime  and
and 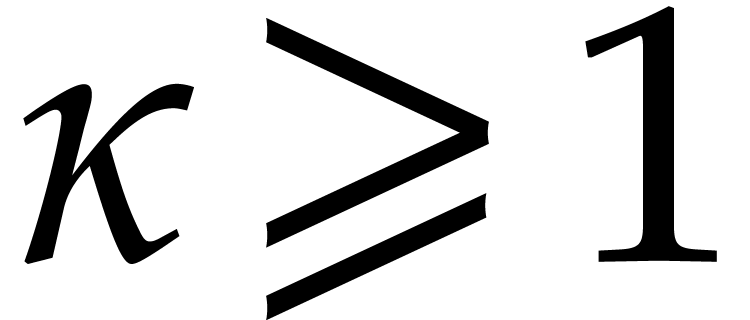 . Most
basic is the case when
. Most
basic is the case when  is a finite field, and
various efficient probabilistic methods have been proposed for this
case. An early such method is due to Berlekamp [6, 7].
A very efficient algorithm that is also convenient to implement is due
to Cantor and Zassenhaus [16]. Asymptotically more
efficient methods have been developed since [67, 70]
as well as specific improvements for the case when
is a finite field, and
various efficient probabilistic methods have been proposed for this
case. An early such method is due to Berlekamp [6, 7].
A very efficient algorithm that is also convenient to implement is due
to Cantor and Zassenhaus [16]. Asymptotically more
efficient methods have been developed since [67, 70]
as well as specific improvements for the case when  is composite [53]. See also [31, Chapter 14]
and [65].
is composite [53]. See also [31, Chapter 14]
and [65].
Rational numbers can either be regarded as a subfield of  or
or  . For
asymptotically efficient algorithms for the approximate factorizations
of univariate polynomials over
. For
asymptotically efficient algorithms for the approximate factorizations
of univariate polynomials over  ,
we refer to [98, 87, 83]. When
reducing a polynomial in
,
we refer to [98, 87, 83]. When
reducing a polynomial in  modulo
modulo  for a sufficiently large random prime, factorization over
for a sufficiently large random prime, factorization over  reduces to factorization over
reduces to factorization over 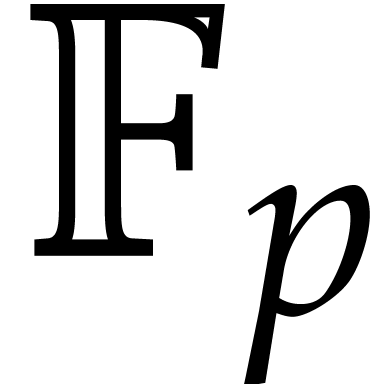 via
Hensel lifting [97, 42, 107]. For
more general factorization methods over
via
Hensel lifting [97, 42, 107]. For
more general factorization methods over  ,
we refer to [26, 20, 82, 39,
3].
,
we refer to [26, 20, 82, 39,
3].
Now let  and assume that we have an irreducible
factorization
and assume that we have an irreducible
factorization 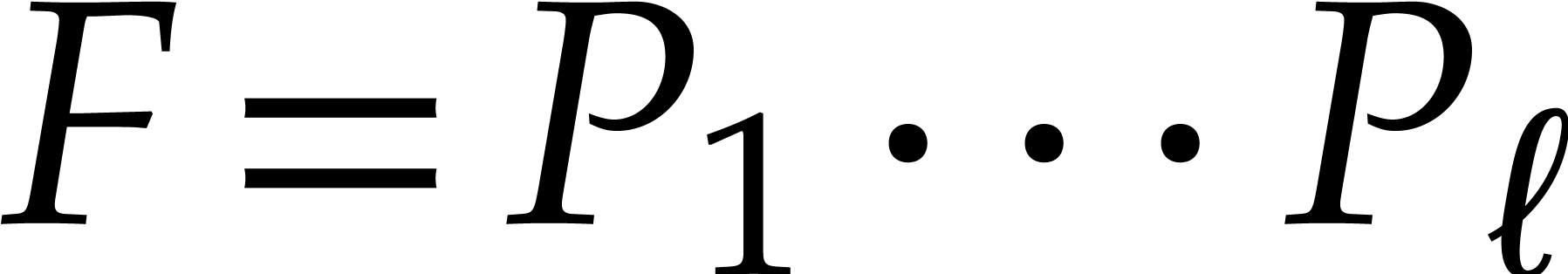 with
with 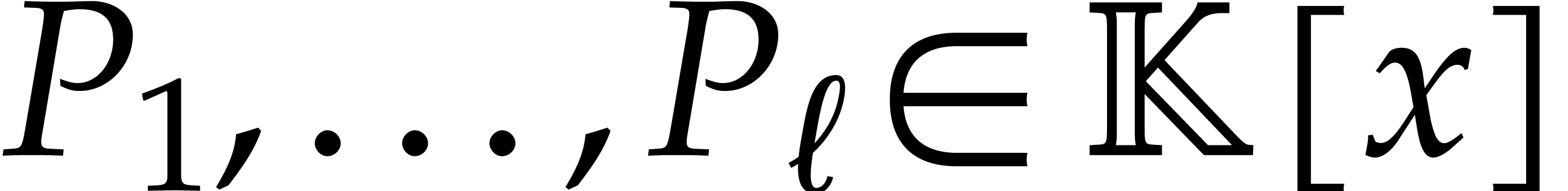 for
for
 or
or 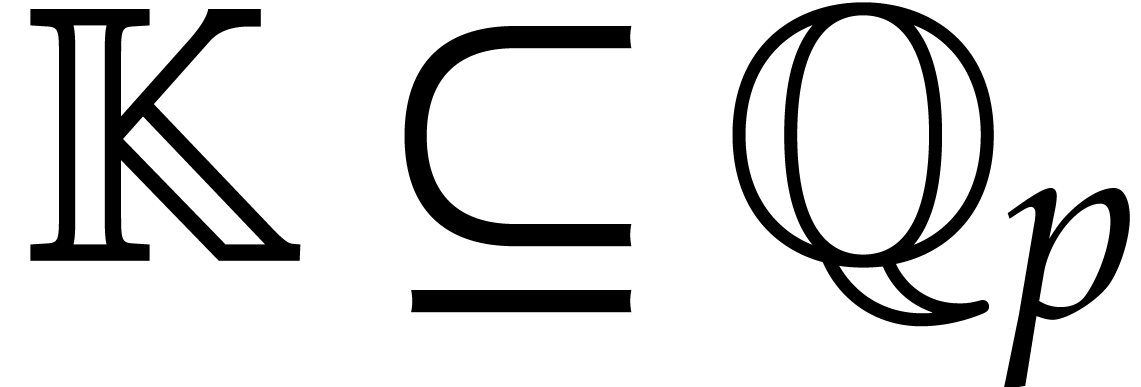 .
(In practice, we require that
.
(In practice, we require that  are known with
sufficient precision.) In order to turn this into a factorization over
are known with
sufficient precision.) In order to turn this into a factorization over
 , we need a way to recombine
the factors, i.e., to find the subsets
, we need a way to recombine
the factors, i.e., to find the subsets 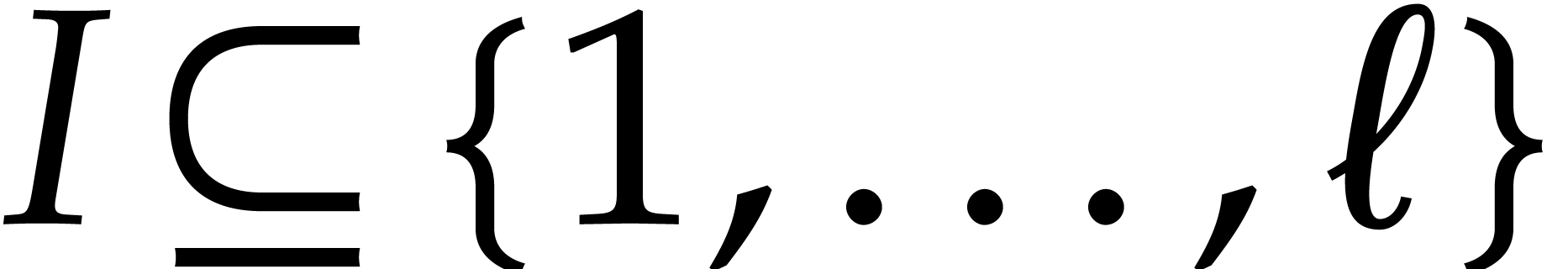 for which
for which  . Indeed, if
. Indeed, if  is irreducible in
is irreducible in  and
and 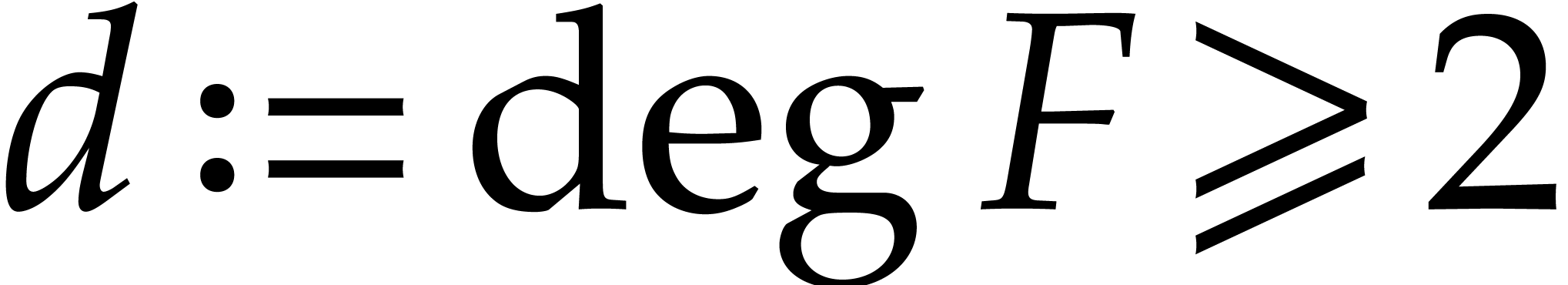 , then
, then  is
never irreducible in
is
never irreducible in  and irreducible with
probability
and irreducible with
probability 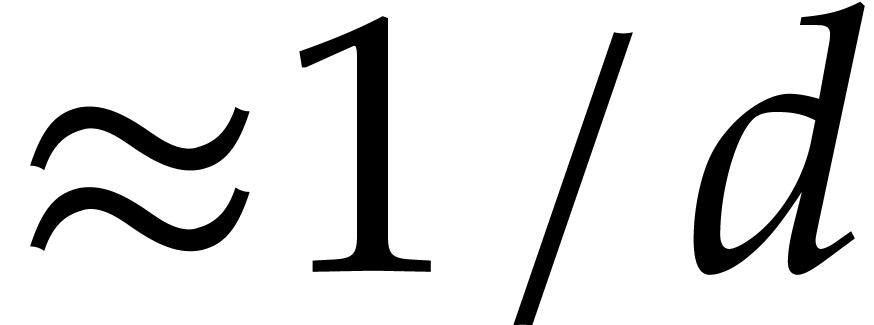 in
in  for a
large random prime
for a
large random prime  . The
first recombination method that runs in polynomial time is due to
Lenstra-Lenstra-Lovasz [77]. Subsequently, many
improvements and variants of this LLL-algorithm have been developed [44, 4, 85, 86, 94].
. The
first recombination method that runs in polynomial time is due to
Lenstra-Lenstra-Lovasz [77]. Subsequently, many
improvements and variants of this LLL-algorithm have been developed [44, 4, 85, 86, 94].
The problem of factoring a bivariate polynomial  over
over  is similar in many regards to factoring
polynomials with rational coefficients. Indeed, for a suitable random
prime
is similar in many regards to factoring
polynomials with rational coefficients. Indeed, for a suitable random
prime  , we have seen above
that the latter problem reduces to univariate factorization over
, we have seen above
that the latter problem reduces to univariate factorization over 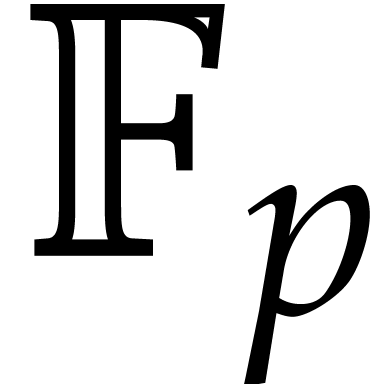 , Hensel lifting, and factor
combination. In a similar way, after factoring
, Hensel lifting, and factor
combination. In a similar way, after factoring  for a sufficiently random
for a sufficiently random  (possibly in an
extension field of
(possibly in an
extension field of  , whenever
, whenever
 is a small finite field), we may use Hensel
lifting to obtain a factorization in
is a small finite field), we may use Hensel
lifting to obtain a factorization in  ,
and finally recombine the factors. The precise algorithms for factor
recombination are slightly different in this context [29,
71, 4, 74] (see also [93,
95] for earlier related work), although they rely on
similar ideas.
,
and finally recombine the factors. The precise algorithms for factor
recombination are slightly different in this context [29,
71, 4, 74] (see also [93,
95] for earlier related work), although they rely on
similar ideas.
Hensel lifting naturally generalizes to polynomials in three or more
variables  . Many algorithms
for multivariate polynomial factorization rely on it [84,
104, 103, 109, 60,
32, 33, 62, 61, 8, 72, 80, 81, 17],
as well as many implementations in computer algebra systems. One
important property of higher dimensional Hensel lifting is that factor
recombination can generally be avoided with high probability, contrary
to what we saw for
. Many algorithms
for multivariate polynomial factorization rely on it [84,
104, 103, 109, 60,
32, 33, 62, 61, 8, 72, 80, 81, 17],
as well as many implementations in computer algebra systems. One
important property of higher dimensional Hensel lifting is that factor
recombination can generally be avoided with high probability, contrary
to what we saw for  -adic and
bivariate Hensel lifting. This is due to Hilbert and Bertini's
irreducibility theorems [43, 10]:
-adic and
bivariate Hensel lifting. This is due to Hilbert and Bertini's
irreducibility theorems [43, 10]:
 is irreducible and of
total degree
is irreducible and of
total degree  . Let
. Let  be the set of points
be the set of points  for
which
for
which
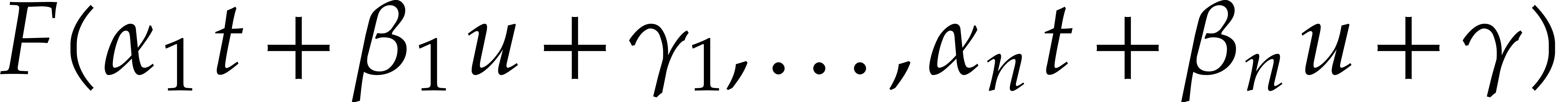 |
(1.2) |
is irreducible in 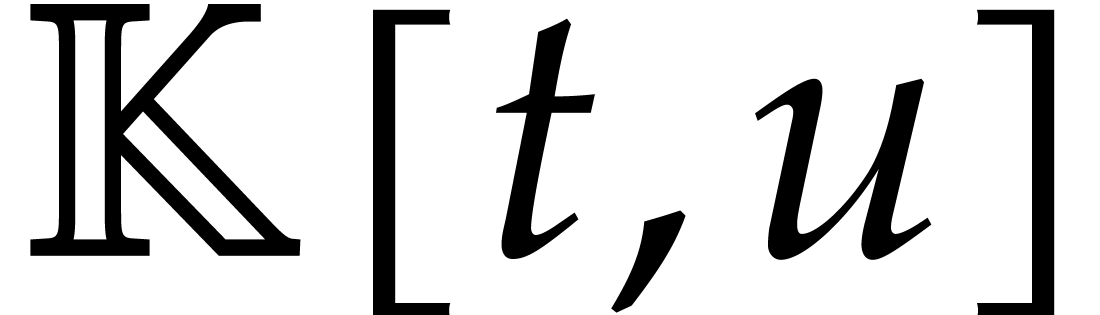 . Then
. Then
 is a Zariski open subset of
is a Zariski open subset of  , which is dense over the algebraic closure
of
, which is dense over the algebraic closure
of  .
.
Effective versions of these theorems can be used to directly reduce the
factorization problem in dimension 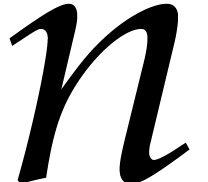 to a
bivariate problem (and even to a univariate problem if
to a
bivariate problem (and even to a univariate problem if 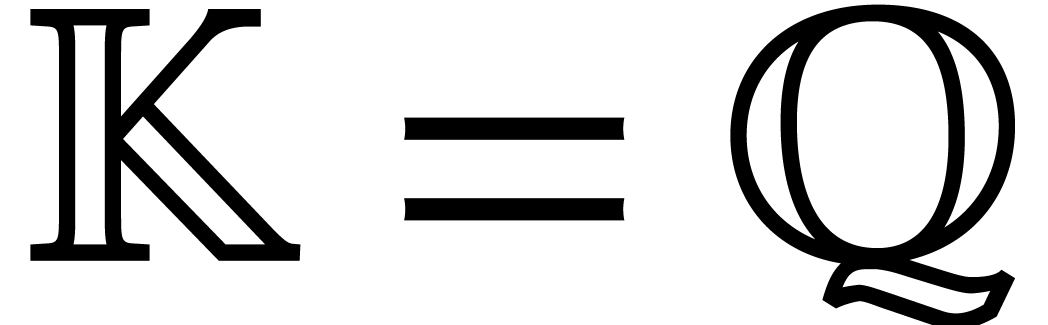 , using similar ideas). We refer to [74]
and [75, Chapître 6] for a recent presentation of how
to do this and to [100, Section 6.1] for the mathematical
background.
, using similar ideas). We refer to [74]
and [75, Chapître 6] for a recent presentation of how
to do this and to [100, Section 6.1] for the mathematical
background.
In order to analyze the computational complexity of factorization, we
first need to specify the precise way we represent our polynomials. When
using a dense representation (e.g. storing all monomials of
total degree 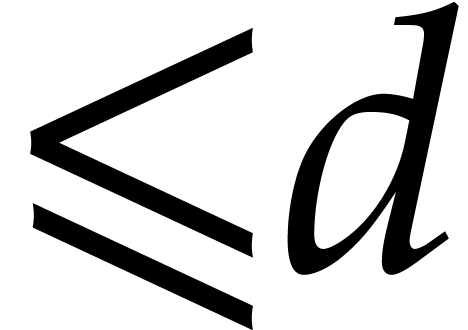 with their (possibly zero)
coefficients), Theorem 1.1 allows us to directly reduce to
the bivariate case (if
with their (possibly zero)
coefficients), Theorem 1.1 allows us to directly reduce to
the bivariate case (if  is very small, then one
may need to replace
is very small, then one
may need to replace  by a suitable algebraic
extension). The first polynomial time reduction of this kind was
proposed by Kaltofen [60]. More recent bounds that exploit
fast dense polynomial arithmetic can be found in [72].
by a suitable algebraic
extension). The first polynomial time reduction of this kind was
proposed by Kaltofen [60]. More recent bounds that exploit
fast dense polynomial arithmetic can be found in [72].
Another popular representation is the “black box
representation”, in which case we are only given an algorithm for
the evaluation of our polynomial  .
Often this algorithm is actually a straight line program (SLP) [14],
which corresponds to the “SLP representation”. In these
cases, the relevant complexity measure is the length of the SLP or the
maximal number of steps that are needed to compute one black box
evaluation. Consequently, affine changes of variables (1.2)
only marginally increase the program size. This has been exploited in
order to derive polynomial time complexity bounds for factoring in this
model [63, 68]; see also [30, 17, 18]. Here we stress that the output factors
are also given in black box or SLP representation.
.
Often this algorithm is actually a straight line program (SLP) [14],
which corresponds to the “SLP representation”. In these
cases, the relevant complexity measure is the length of the SLP or the
maximal number of steps that are needed to compute one black box
evaluation. Consequently, affine changes of variables (1.2)
only marginally increase the program size. This has been exploited in
order to derive polynomial time complexity bounds for factoring in this
model [63, 68]; see also [30, 17, 18]. Here we stress that the output factors
are also given in black box or SLP representation.
Plausibly the most common representation for multivariate polynomials in
computer algebra is the sparse one (1.1). Any sparse
polynomial naturally gives rise to an SLP of roughly the same size.
Sparse interpolation also provides a way to convert in the opposite
direction. However, for an SLP 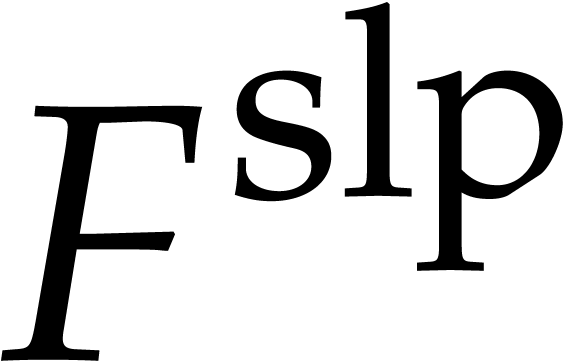 of length
of length  , it takes
, it takes  time to recover its sparse representation
time to recover its sparse representation  ,
where
,
where  . A priori,
the back and forth conversion
. A priori,
the back and forth conversion 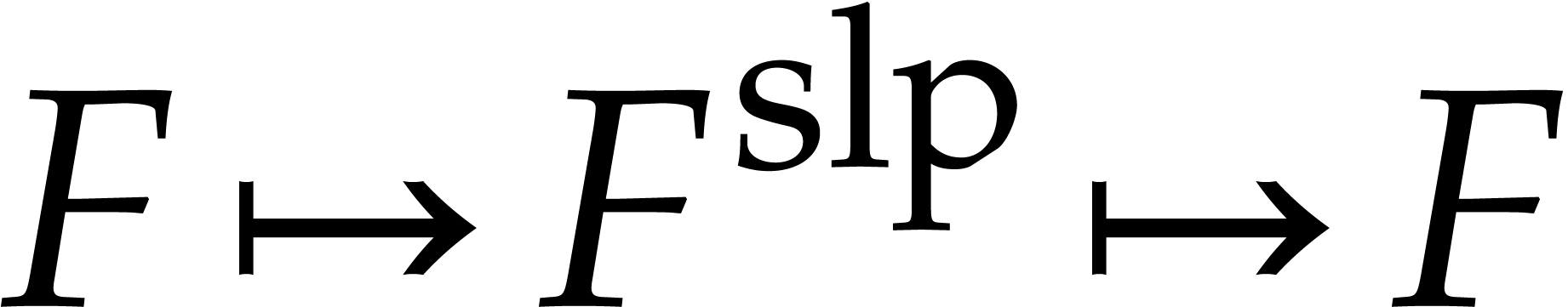 therefore takes
quadratic time
therefore takes
quadratic time 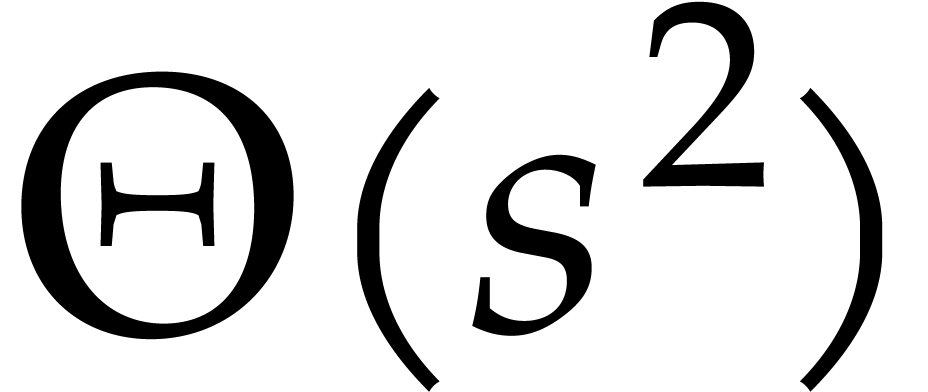 . While it is
theoretically possible to factor sparse polynomials using the above
black box methods, this is suboptimal from a complexity perspective.
. While it is
theoretically possible to factor sparse polynomials using the above
black box methods, this is suboptimal from a complexity perspective.
Unfortunately, general affine transformations (1.2) destroy
sparsity, so additional ideas are needed for the design of efficient
factorization methods based on Hilbert-Bertini-like irreducibility
theorems. Dedicated algorithms for the sparse model have been developed
in [32, 8, 79, 81].
There are two ways to counter the loss of sparsity under affine
transformations, both of which will be considered in the present paper.
One possibility is to successively use Hensel lifting with respect to
 . Another approach is to use
a more particular type of changes of variables, like
. Another approach is to use
a more particular type of changes of variables, like 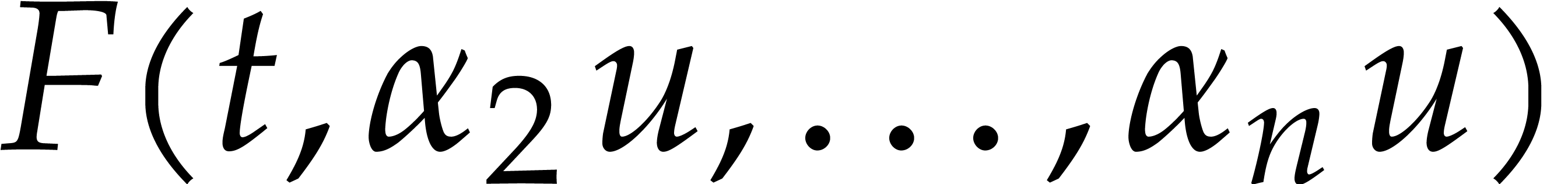 . However, both approaches require
. However, both approaches require  to be of a suitable form to allow for Hensel lifting. Some
reference for Hensel lifting in the context of sparse polynomials are
[62, 8, 78, 80, 81, 17].
to be of a suitable form to allow for Hensel lifting. Some
reference for Hensel lifting in the context of sparse polynomials are
[62, 8, 78, 80, 81, 17].
For most applications in computer algebra, the total degree of large sparse polynomials is typically much smaller than the number of terms. The works in the above references mainly target this asymptotic regime. The factorization of “supersparse” polynomials has also been considered in [40, 37]. The survey talk [96] discusses the complexity of polynomial factorizations for yet other polynomial representations.
The theory of polynomial factorization involves several other basic algorithmic tasks that are interesting for their own sake. We already mentioned the importance of Hensel lifting. Other fundamental operations are gcd computations, multiple root extractions, square-free factorizations, and determining the content of a polynomial. We refer to [31] for classical univariate algorithms. As to sparse multivariate polynomials, there exist many approaches for gcd computations [21, 108, 68, 66, 59, 22, 56, 76, 51, 58].
Whenever convenient, we will assume that the characteristic of  is either zero or sufficiently large. This will allow us
to avoid technical non-separability issues; we refer to [34,
102, 73] for algorithms to deal with such
issues. A survey of multivariate polynomial factorization over finite
fields (including small characteristic) can be found in [65].
Throughout this paper, factorizations will be done over the ground field
is either zero or sufficiently large. This will allow us
to avoid technical non-separability issues; we refer to [34,
102, 73] for algorithms to deal with such
issues. A survey of multivariate polynomial factorization over finite
fields (including small characteristic) can be found in [65].
Throughout this paper, factorizations will be done over the ground field
 . Some algorithms for
“absolute factorization” over the algebraic closure
. Some algorithms for
“absolute factorization” over the algebraic closure 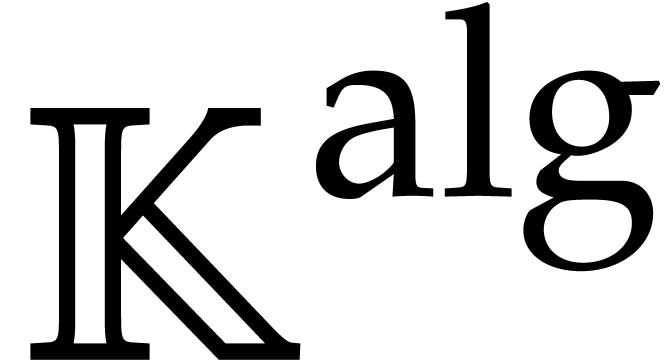 of
of  can be found in [64,
19, 23]; alternatively, one may mimic
computations in
can be found in [64,
19, 23]; alternatively, one may mimic
computations in 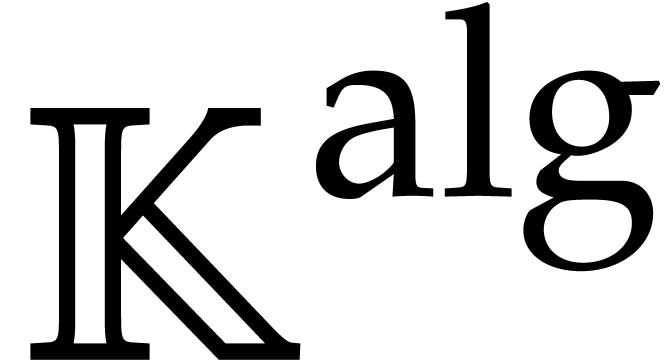 using dynamic evaluation [24, 49].
using dynamic evaluation [24, 49].
The goal of this paper is to redevelop the theory of sparse polynomial factorization, by taking advantage as fully as possible of evaluation-interpolation techniques at geometric sequences. The basic background material is recalled in Section 2. We recall that almost all algorithms in the paper are randomized, of Monte Carlo type. We also note that the correctness of a factorization can easily be verified, either directly or with high probability, by evaluating the polynomial and the product of the potential factors at a random point. (On the other hand, this approach does not yield a probabilistic irreducibility test.)
As an appetizer, we start in Section 3 with the problem of
multivariate gcd computation. This provides a nice introduction for the
main two approaches used later in the paper: induction on dimension and
direct reduction to the univariate (or bivariate or low dimensional)
case. It also illustrates the kind of complexity bounds that we are
aiming for. Consider the computation of the gcd  of two sparse polynomials
of two sparse polynomials  .
Ideally speaking, setting
.
Ideally speaking, setting 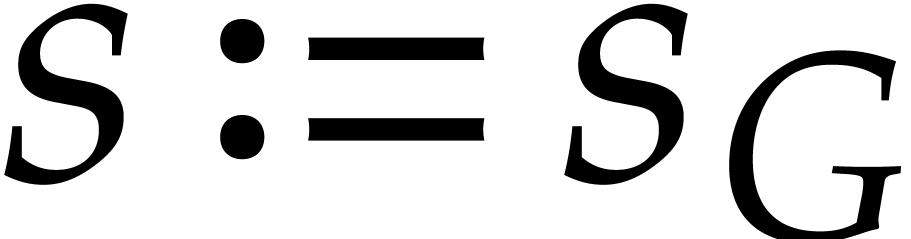 ,
,
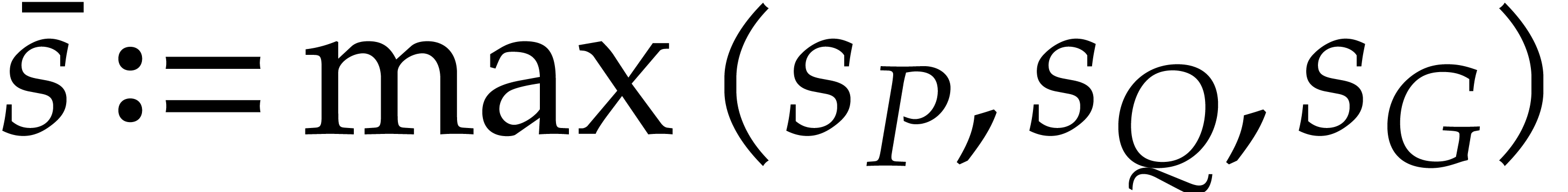 ,
, 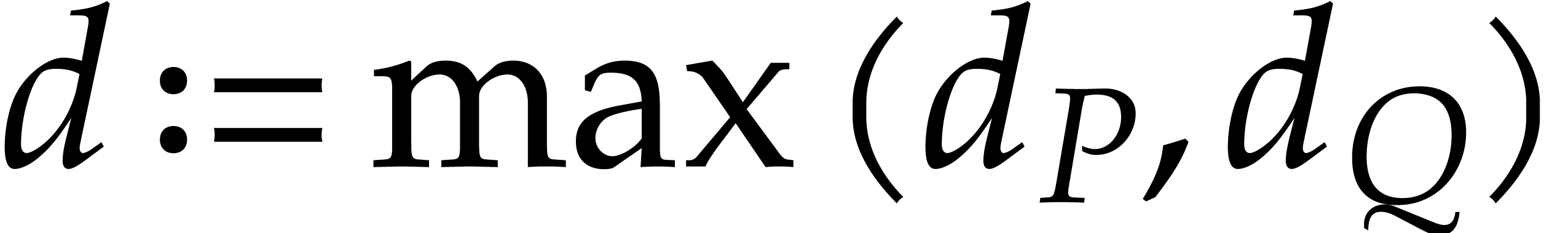 , we are aiming for a complexity bound of the form
, we are aiming for a complexity bound of the form
 |
(1.3) |
where  is a constant. Since
is a constant. Since  is typically much smaller than
is typically much smaller than  ,
we can afford ourselves the non-trivial overhead with respect to
,
we can afford ourselves the non-trivial overhead with respect to  in the term
in the term 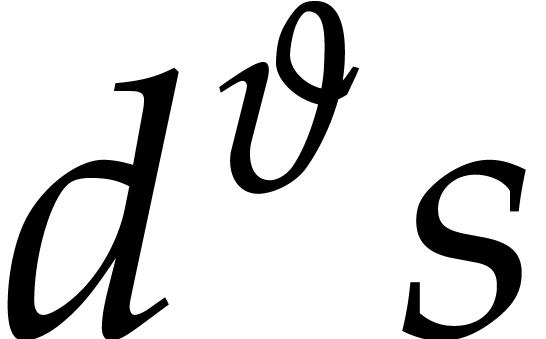 .
The inductive approach on the dimension
.
The inductive approach on the dimension 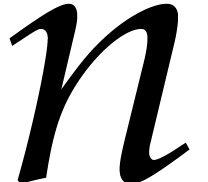 achieves
the complexity (1.3) with
achieves
the complexity (1.3) with 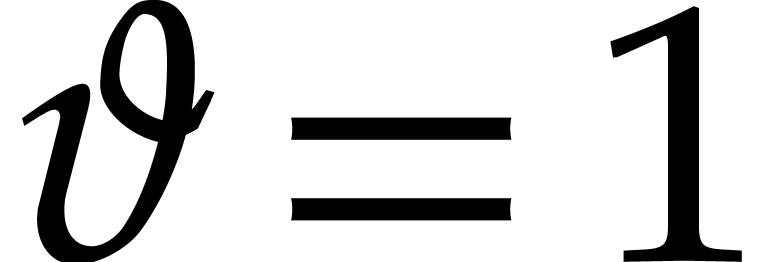 ,
but its worst case complexity is
,
but its worst case complexity is 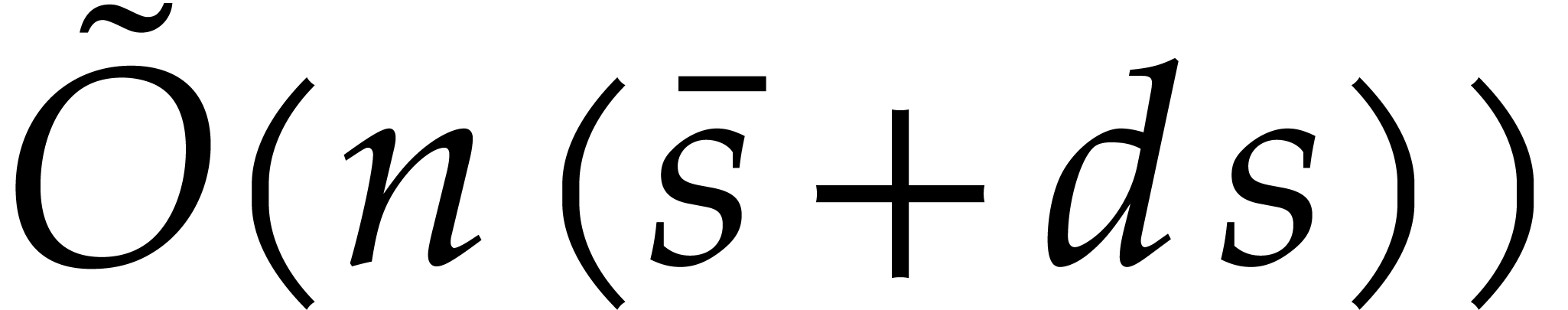 .
This algorithm seems to be new. The second approach uses a direct
reduction to univariate gcd computations via so-called
“regularizing weights” and achieves the complexity (1.3)
with
.
This algorithm seems to be new. The second approach uses a direct
reduction to univariate gcd computations via so-called
“regularizing weights” and achieves the complexity (1.3)
with 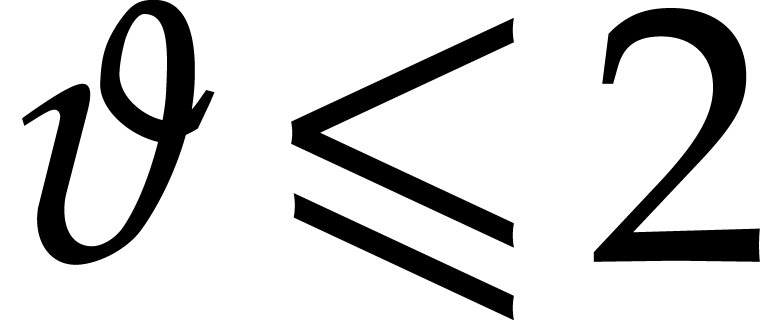 , and even
, and even 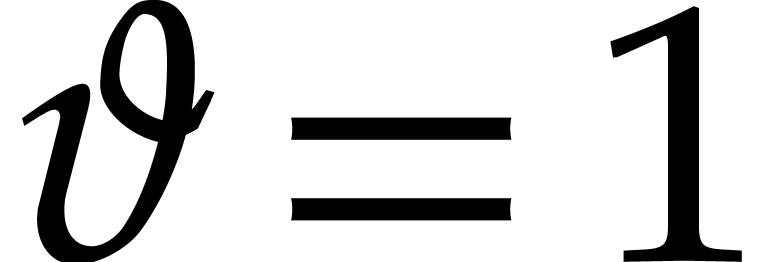 for some practical examples (e.g., when the gcd is monic
in one of the variables). This algorithm is a sharpened version of the
algorithm from [51, Section 4.3].
for some practical examples (e.g., when the gcd is monic
in one of the variables). This algorithm is a sharpened version of the
algorithm from [51, Section 4.3].
Most existing algorithms for multivariate polynomial factorization
reduce to the univariate or bivariate case. Direct reduction to the
univariate case is only possible for certain types of coefficients, such
as integers, rational numbers, or algebraic numbers. Reduction to the
bivariate case works in general, thanks to Theorem 1.1, and
this is even interesting when 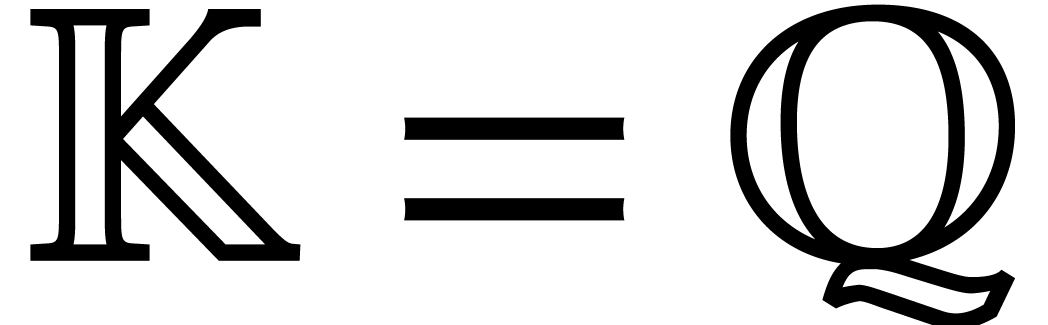 :
first reduce modulo a suitable prime
:
first reduce modulo a suitable prime  ,
then factor over
,
then factor over 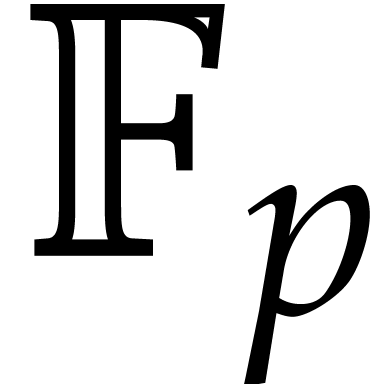 , and
finally Hensel lift to obtain a factorization over
, and
finally Hensel lift to obtain a factorization over  . In this paper, we will systematically opt for
the bivariate reduction strategy. For this reason, we have included a
separate Section 4 on bivariate factorization and related
problems. This material is classical, but recalled for
self-containedness and convenience of the reader.
. In this paper, we will systematically opt for
the bivariate reduction strategy. For this reason, we have included a
separate Section 4 on bivariate factorization and related
problems. This material is classical, but recalled for
self-containedness and convenience of the reader.
If  is a finite field, then we already noted that
multivariate factorization does not directly reduce to the univariate
case. Nevertheless, such direct reductions are possible for some special
cases of interest: content-free factorization, extraction of multiple
roots, and square-free factorization. In Section 5, we
present efficient algorithms for these tasks, following the
“regularizing weights” approach that was introduced in
Section 3.2 for gcd computations. All complexity bounds are
of the form (1.3) for the relevant notions of output size
is a finite field, then we already noted that
multivariate factorization does not directly reduce to the univariate
case. Nevertheless, such direct reductions are possible for some special
cases of interest: content-free factorization, extraction of multiple
roots, and square-free factorization. In Section 5, we
present efficient algorithms for these tasks, following the
“regularizing weights” approach that was introduced in
Section 3.2 for gcd computations. All complexity bounds are
of the form (1.3) for the relevant notions of output size
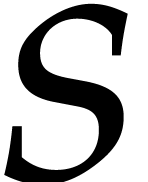 , input-output size
, input-output size  , and total degree
, and total degree  .
.
In Section 6, we turn to the factorization of a
multivariate polynomial 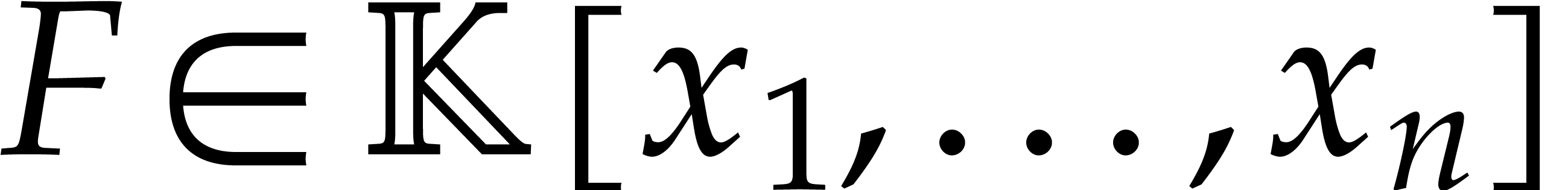 using induction on the
dimension
using induction on the
dimension 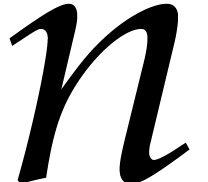 . Starting with a
coprime factorization of a bivariate projection
. Starting with a
coprime factorization of a bivariate projection 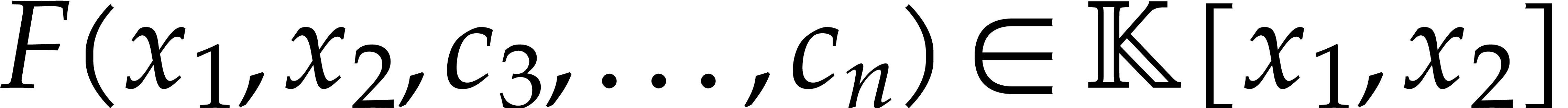 of
of  for random
for random  ,
we successively Hensel lift this factorization with respect to
,
we successively Hensel lift this factorization with respect to  . Using a suitable
evaluation-interpolation strategy, the actual Hensel lifting can be done
on bivariate polynomials. This leads to complexity bounds of the form
. Using a suitable
evaluation-interpolation strategy, the actual Hensel lifting can be done
on bivariate polynomials. This leads to complexity bounds of the form
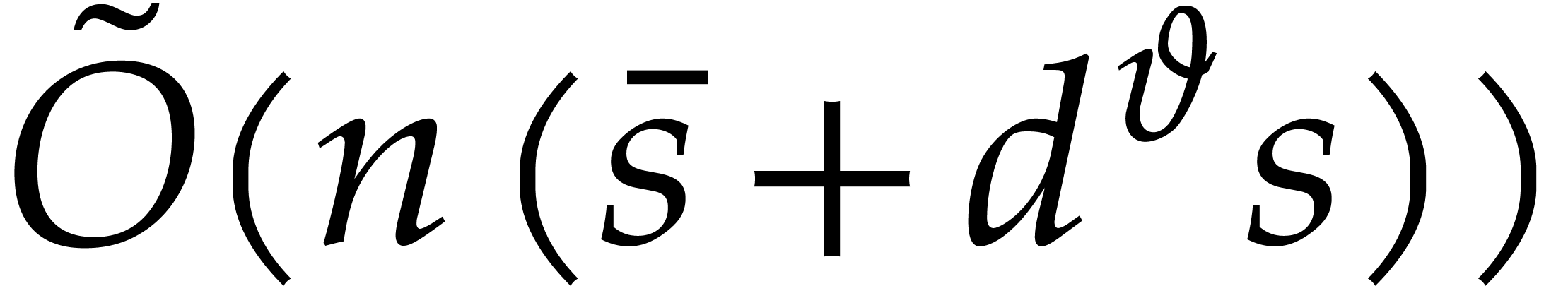 with
with 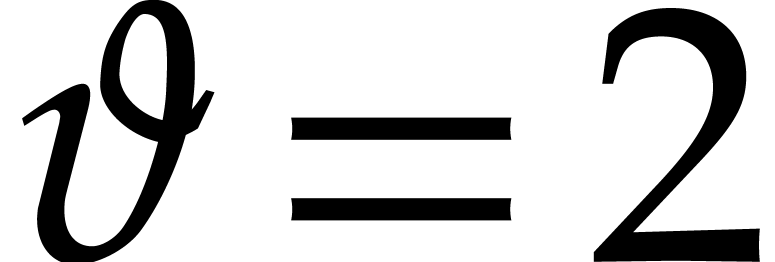 .
In fact, we separately consider factorizations into two or more factors.
In the case of two factors, it is possible to first determine the
smallest factor and then perform an exact division to obtain the other
one. In the complexity bound, this means that
.
In fact, we separately consider factorizations into two or more factors.
In the case of two factors, it is possible to first determine the
smallest factor and then perform an exact division to obtain the other
one. In the complexity bound, this means that 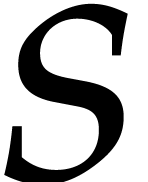 should really be understood as the number of evaluation-interpolation
points, i.e. the minimum of the sizes of the two factors.
It depends on the situation whether it is faster to lift a full coprime
factorization or one factor at a time, although we expect the first
approach to be fastest in most cases.
should really be understood as the number of evaluation-interpolation
points, i.e. the minimum of the sizes of the two factors.
It depends on the situation whether it is faster to lift a full coprime
factorization or one factor at a time, although we expect the first
approach to be fastest in most cases.
Due to the fact that projections such as  are
only very special types of affine transformations, Theorem 1.1
does not apply. Therefore, the direct inductive approach from Section 6 does not systematically lead to a full irreducible
factorization of
are
only very special types of affine transformations, Theorem 1.1
does not apply. Therefore, the direct inductive approach from Section 6 does not systematically lead to a full irreducible
factorization of  . In Remarks
6.14 and 6.15, we give an example where our
approach fails, together with two different heuristic remedies (which
both lead to similar complexity bounds, but with
. In Remarks
6.14 and 6.15, we give an example where our
approach fails, together with two different heuristic remedies (which
both lead to similar complexity bounds, but with  or higher).
or higher).
In the last Section 7, we present another approach, which
avoids induction on the dimension 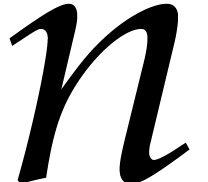 and the
corresponding overhead in the complexity bound. The idea is to exploit
properties of the Newton polytope of
and the
corresponding overhead in the complexity bound. The idea is to exploit
properties of the Newton polytope of  and
“face factorizations” (e.g. factorizations of
restrictions of
and
“face factorizations” (e.g. factorizations of
restrictions of  to faces of its Newton
polytope). In the most favorable case, there exists a coprime edge
factorization, which can be Hensel lifted into a full factorization, and
we obtain a complexity bound of the form (1.3). In less
favorable cases, different face factorizations need to be combined.
Although this yields a similar complexity bound, the details are more
technical. We refer to [1, 105] for a few
existing ways to exploit Newton polytopes for polynomial factorization.
to faces of its Newton
polytope). In the most favorable case, there exists a coprime edge
factorization, which can be Hensel lifted into a full factorization, and
we obtain a complexity bound of the form (1.3). In less
favorable cases, different face factorizations need to be combined.
Although this yields a similar complexity bound, the details are more
technical. We refer to [1, 105] for a few
existing ways to exploit Newton polytopes for polynomial factorization.
In very unfavorable cases (see Section 7.6), the
factorization of  cannot be recovered from its
face factorizations at all. In Section 7.7, we conclude
with a fully general algorithm for irreducible factorization. This
algorithm is not as practical, but addresses pathologically difficult
cases through the introduction of a few extra variables. Its cost is
cannot be recovered from its
face factorizations at all. In Section 7.7, we conclude
with a fully general algorithm for irreducible factorization. This
algorithm is not as practical, but addresses pathologically difficult
cases through the introduction of a few extra variables. Its cost is
 plus the cost of one univariate factorization of
degree
plus the cost of one univariate factorization of
degree 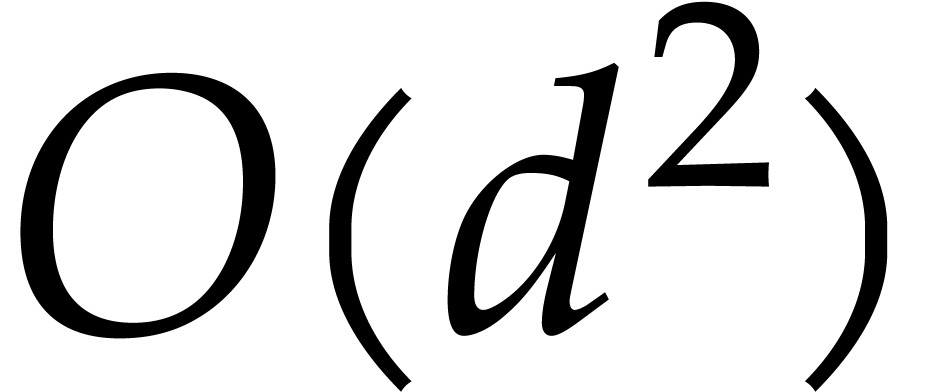 .
.
In this paper, we will measure the complexity of algorithms using the
algebraic complexity model [14]. In addition, we assume
that it is possible to sample a random element from  (or a subset of
(or a subset of  ) in constant
time. We will use
) in constant
time. We will use 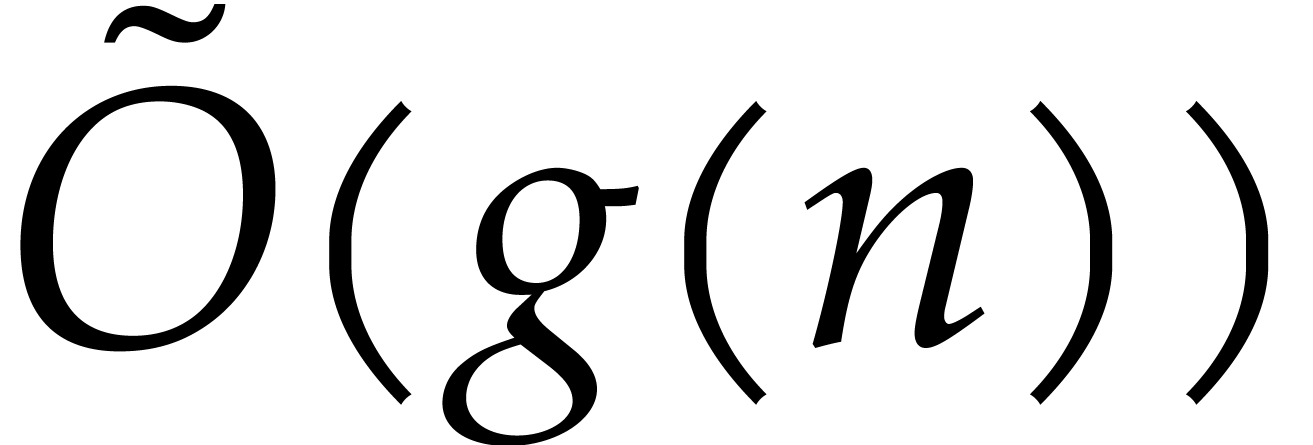 as a shorthand for
as a shorthand for 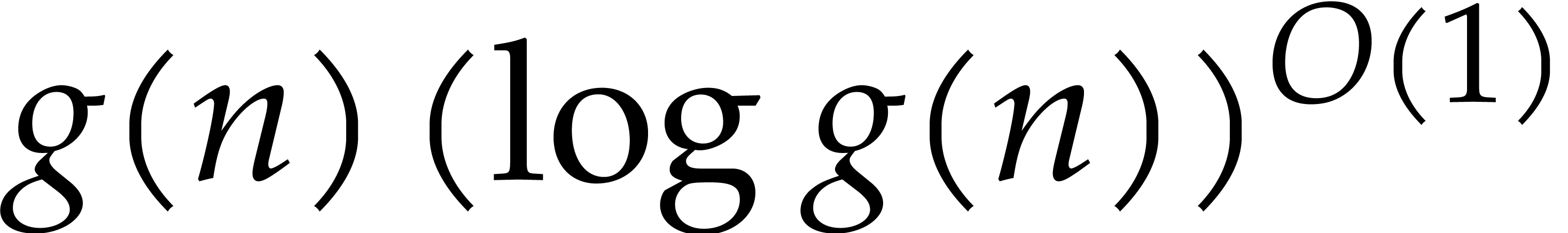 .
.
We let 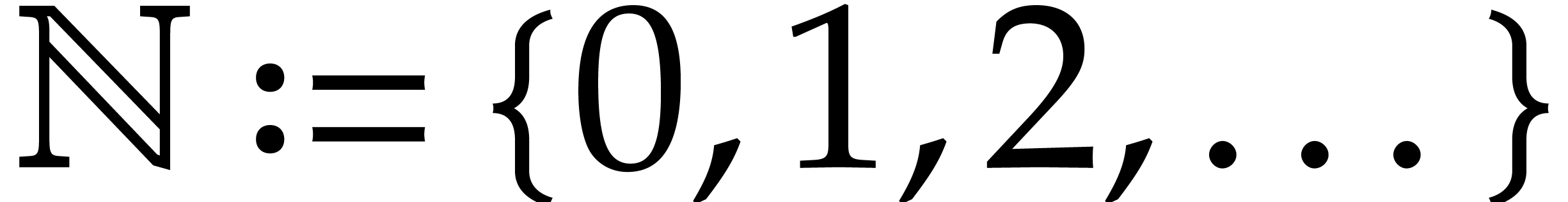 and
and  .
We also define
.
We also define 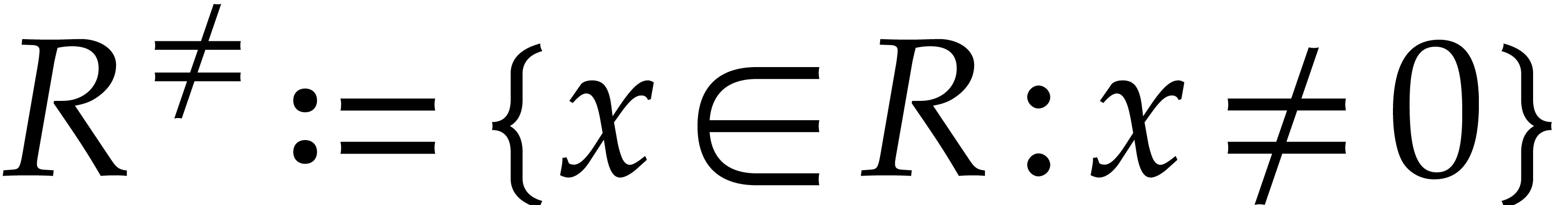 , for any ring
, for any ring
 . Given a multivariate
polynomial
. Given a multivariate
polynomial 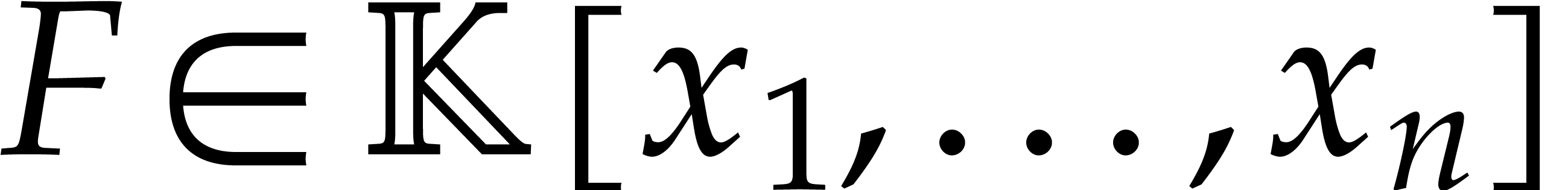 and
and  ,
we write
,
we write 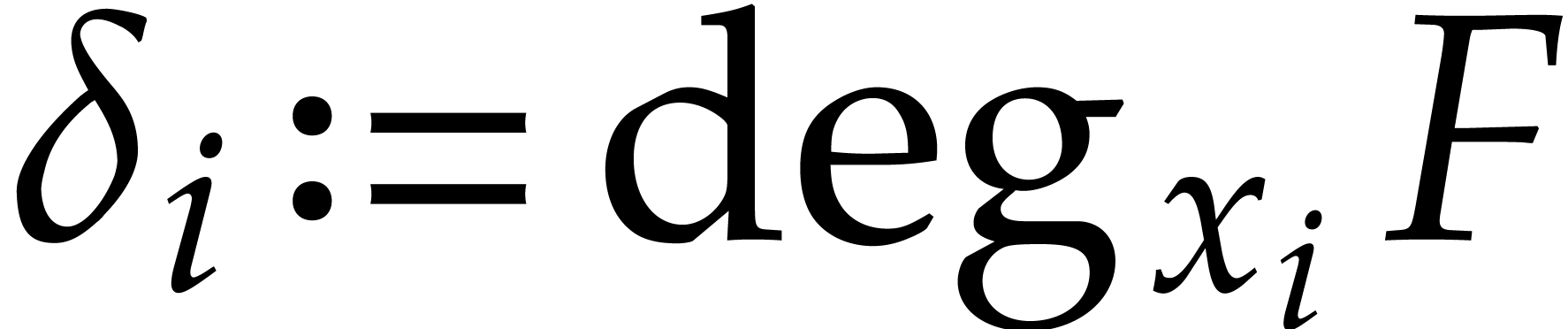 (resp.
(resp. 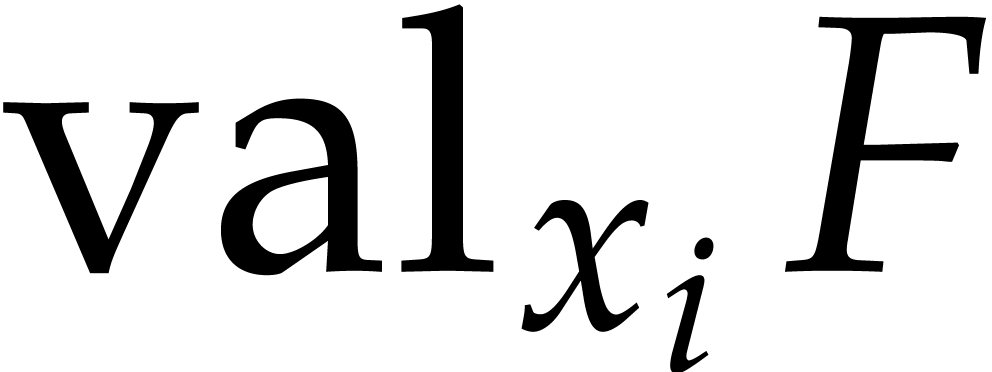 ) for the degree (resp. valuation)
of
) for the degree (resp. valuation)
of  in
in  .
We also write
.
We also write 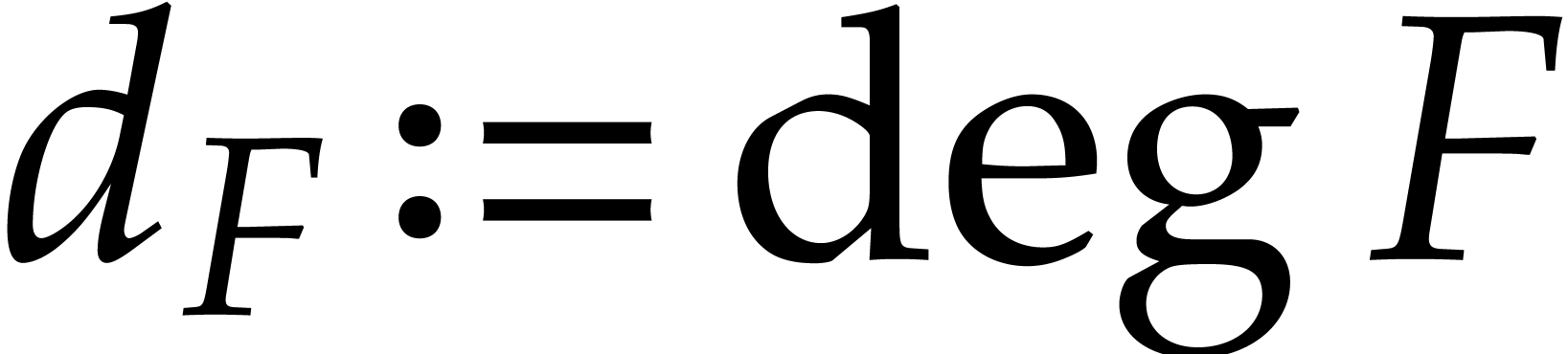 (resp.
(resp.  ) for the total degree (resp.
valuation of
) for the total degree (resp.
valuation of  ), and we set
), and we set
 . Recall that
. Recall that 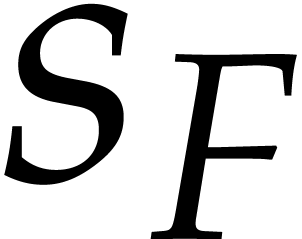 stands for the number of terms of
stands for the number of terms of  in its sparse representation (1.1).
in its sparse representation (1.1).
Acknowledgment. We wish to thank Grégoire Lecerf for useful discussions during the preparation of this paper and the first anonymous referee for helpful comments and suggestions.
Let  (or
(or  )
be the cost to multiply two dense univariate polynomials of degree
)
be the cost to multiply two dense univariate polynomials of degree 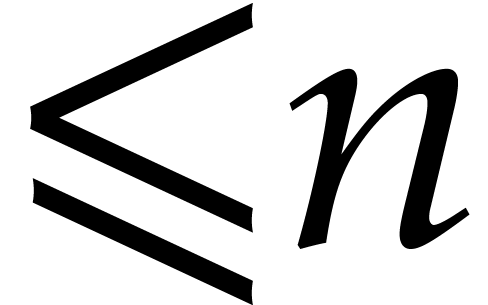 in
in 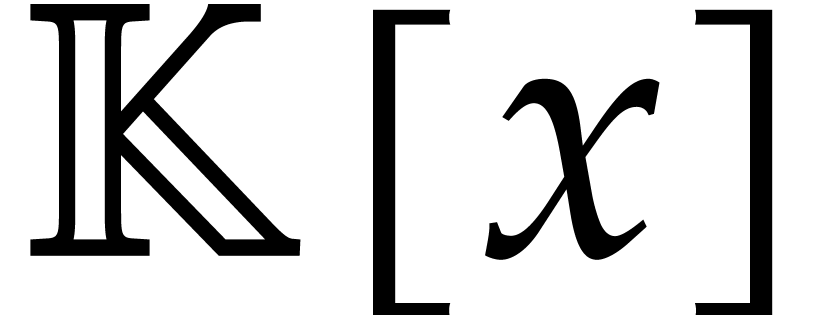 .
Throughout the paper, we make the assumption that
.
Throughout the paper, we make the assumption that  is a non-decreasing function. In the algebraic complexity model [14], when counting the number of operations in
is a non-decreasing function. In the algebraic complexity model [14], when counting the number of operations in  , we may take
, we may take 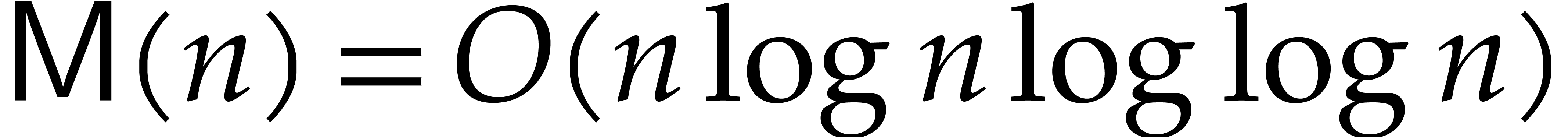 [15].
If
[15].
If  is a finite field
is a finite field 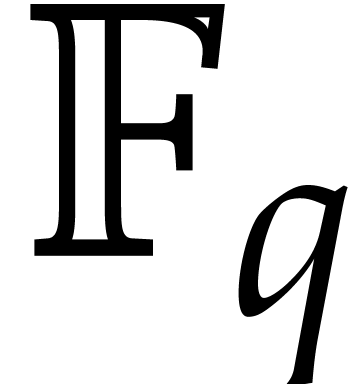 , then one has
, then one has 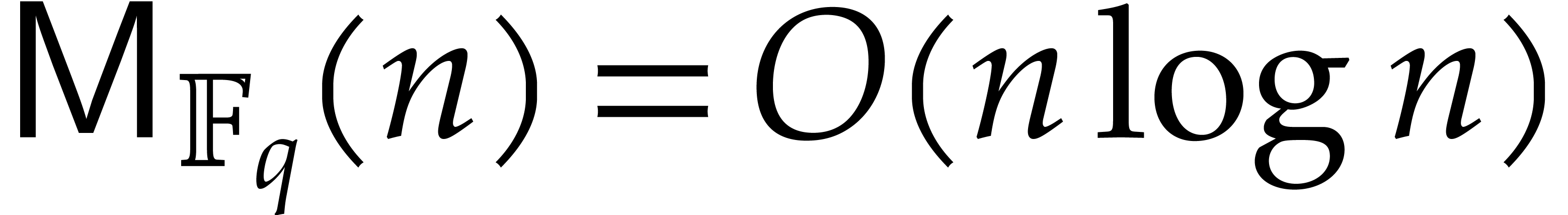 ,
under suitable number theoretic assumption [41]. In this
case, the corresponding bit complexity (when counting the number of
operations on a Turing machine [88]) is
,
under suitable number theoretic assumption [41]. In this
case, the corresponding bit complexity (when counting the number of
operations on a Turing machine [88]) is 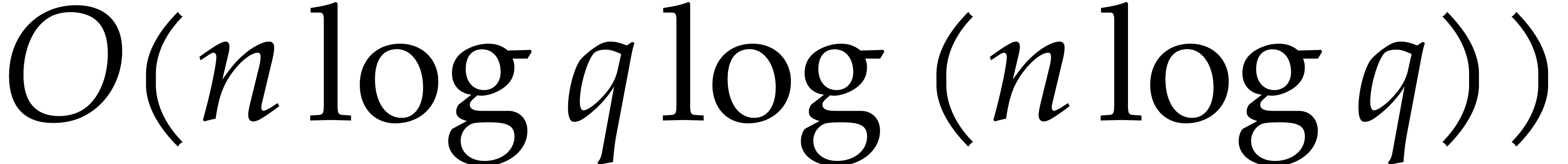 .
.
For polynomials 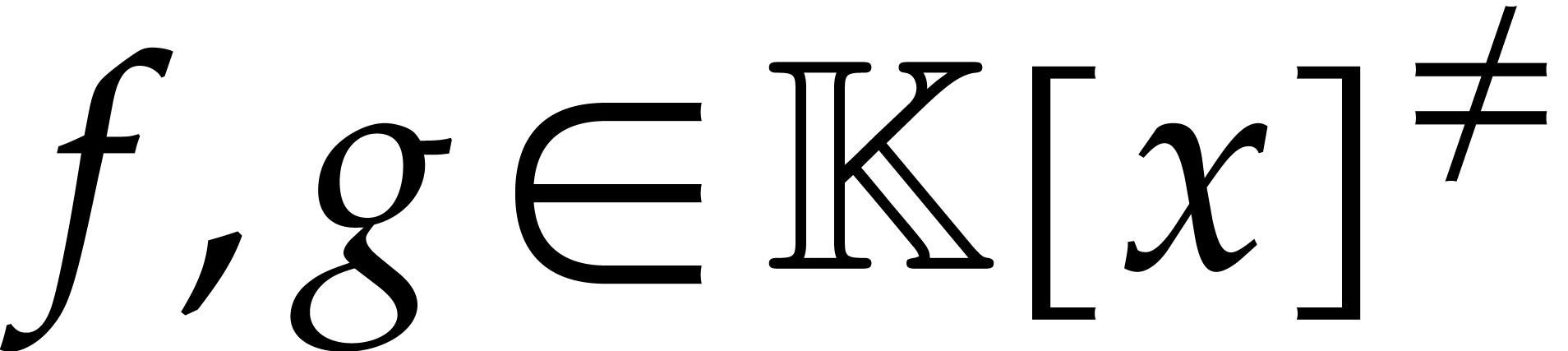 of degree
of degree 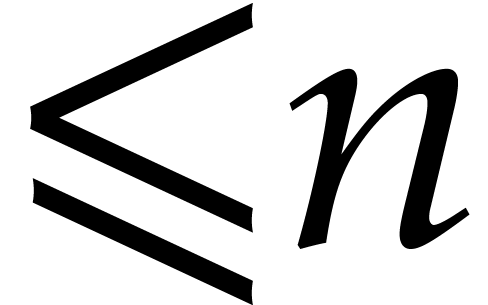 it is possible to find the unique
it is possible to find the unique  ,
such that
,
such that 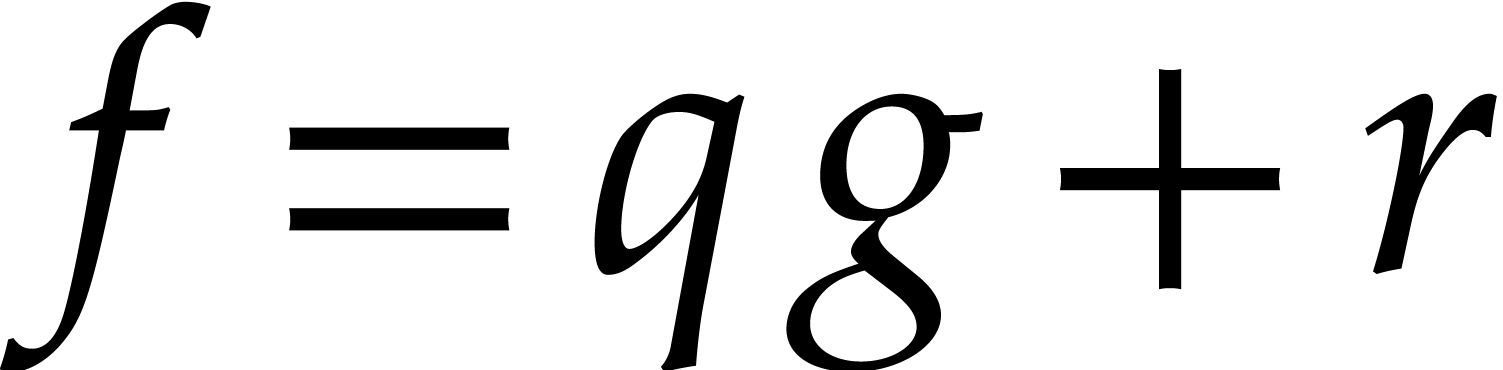 with
with  .
This is the problem of univariate division with remainder, which
can be solved in time
.
This is the problem of univariate division with remainder, which
can be solved in time 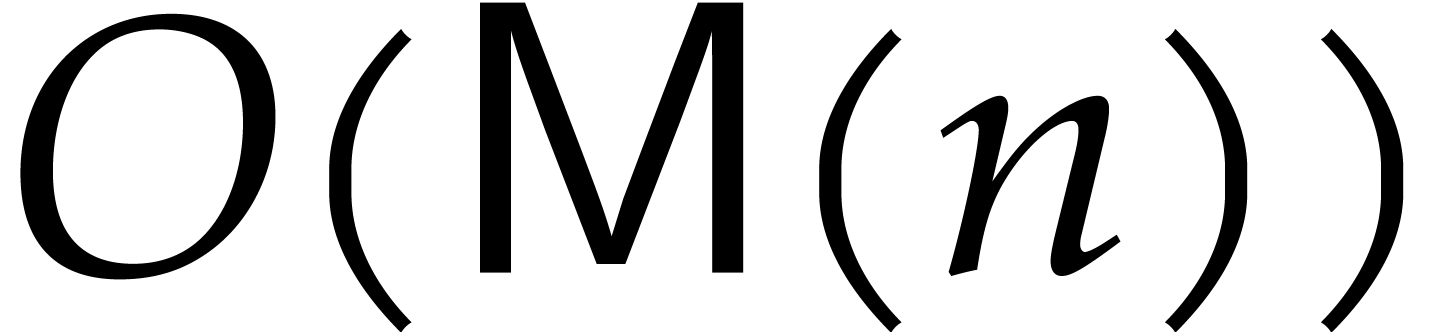 by applying Newton
iteration [31, Section 9.1]. A related task is
univariate root extraction: given
by applying Newton
iteration [31, Section 9.1]. A related task is
univariate root extraction: given 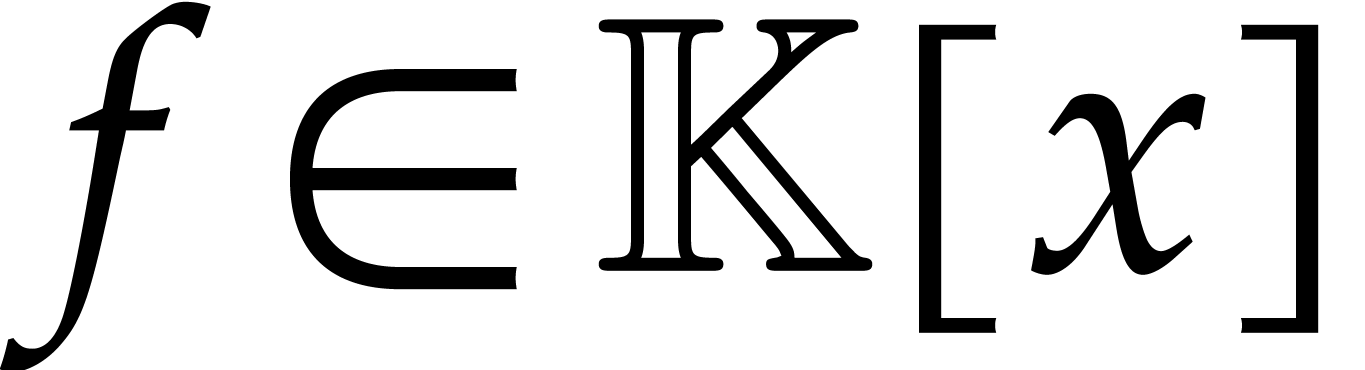 and
and
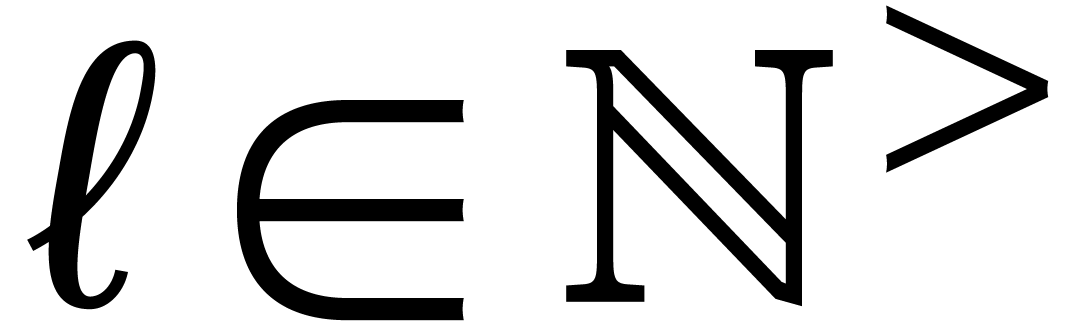 , check whether
, check whether  is of the form
is of the form 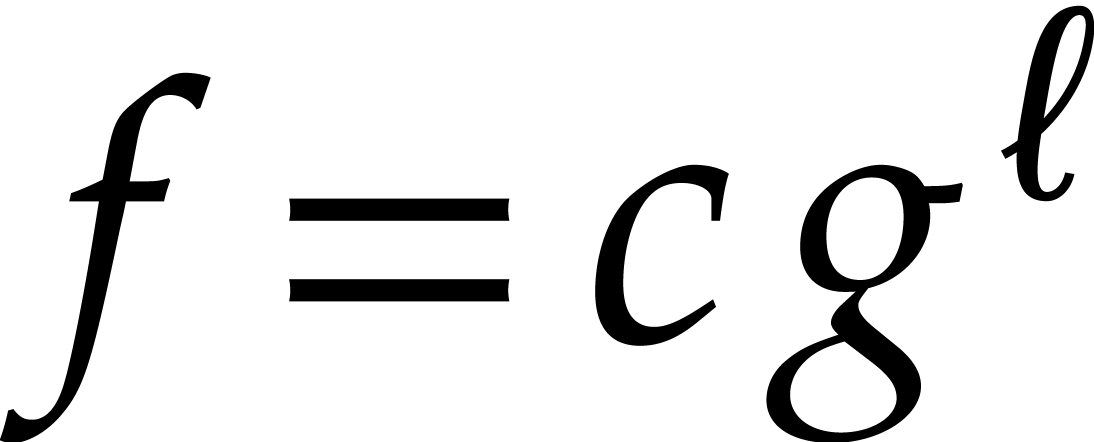 for some
for some 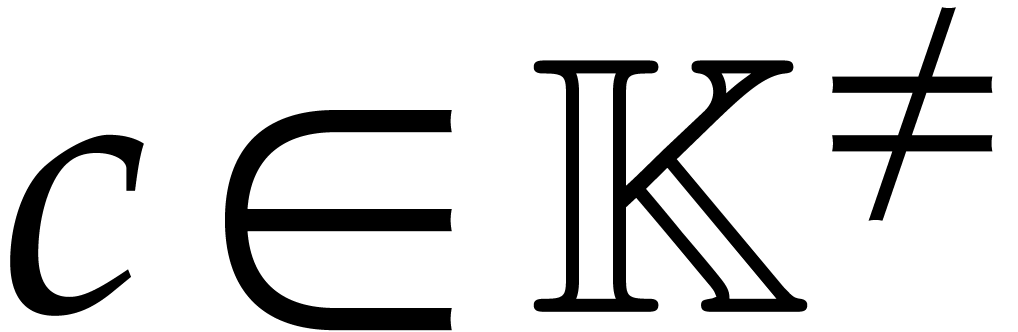 and monic
and monic  , and
determine
, and
determine  and
and  if so. For
a fixed
if so. For
a fixed  , this can be
checked, and the unique
, this can be
checked, and the unique  can be found in
can be found in 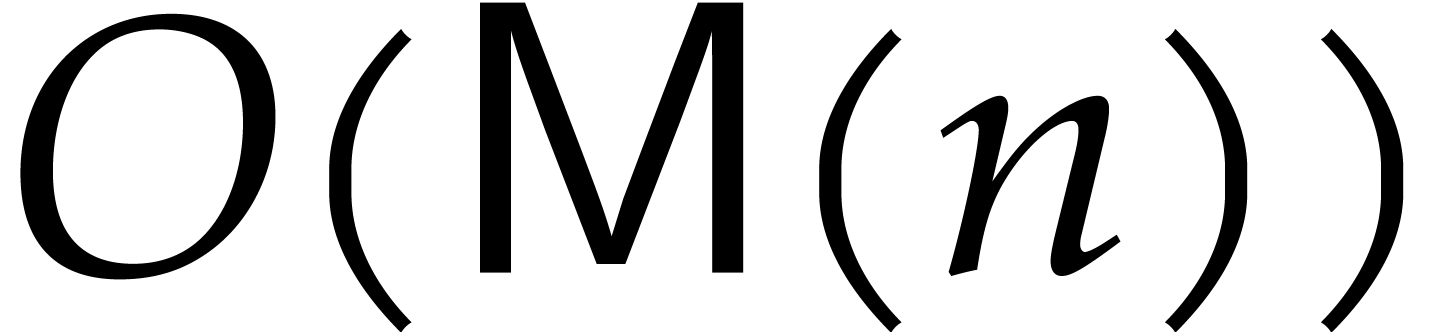 arithmetic operations in
arithmetic operations in  by
applying Newton iteration [31, polynomial analogue of
Theorem 9.28].
by
applying Newton iteration [31, polynomial analogue of
Theorem 9.28].
Consider the Vandermonde matrix
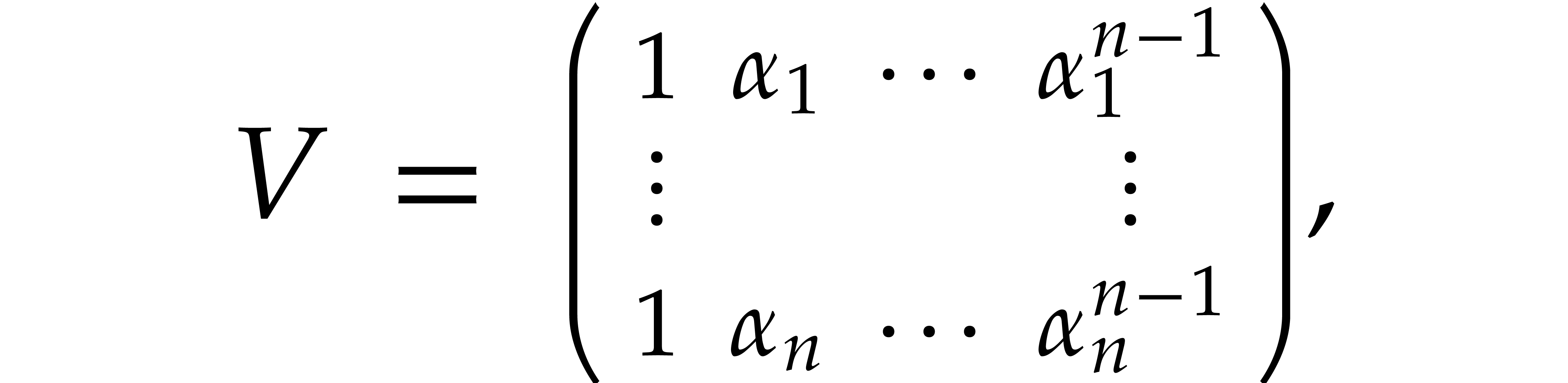
where 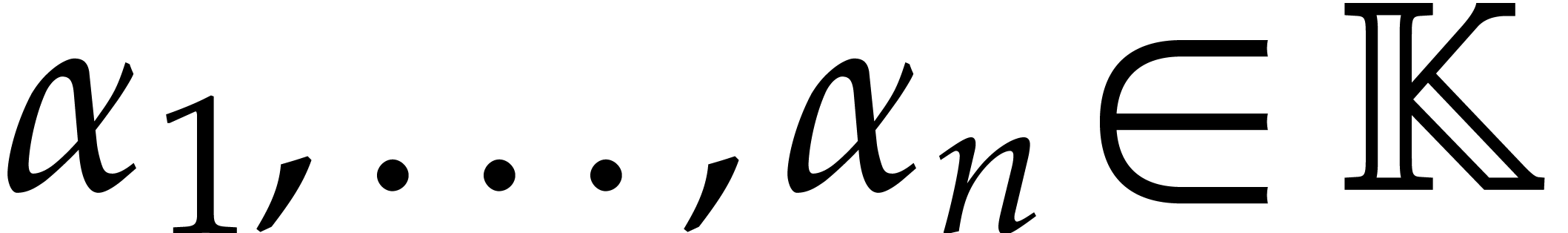 are pairwise distinct. Given a column
vector
are pairwise distinct. Given a column
vector  with entries
with entries  , it is well known [11, 69,
12, 9, 45] that the products
, it is well known [11, 69,
12, 9, 45] that the products
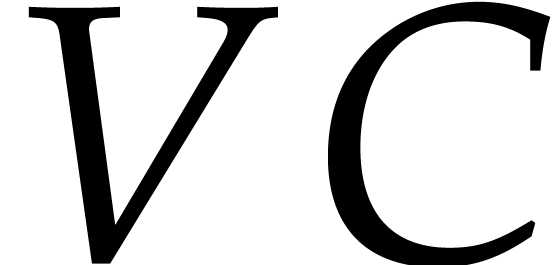 ,
, 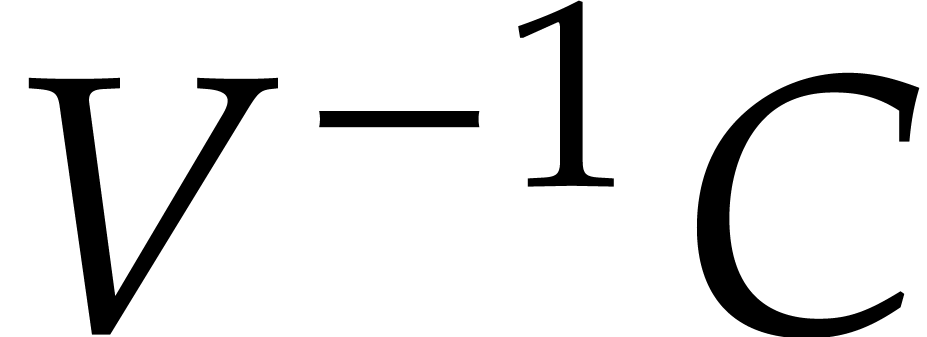 ,
,  , and
, and
 can all be computed in time
can all be computed in time 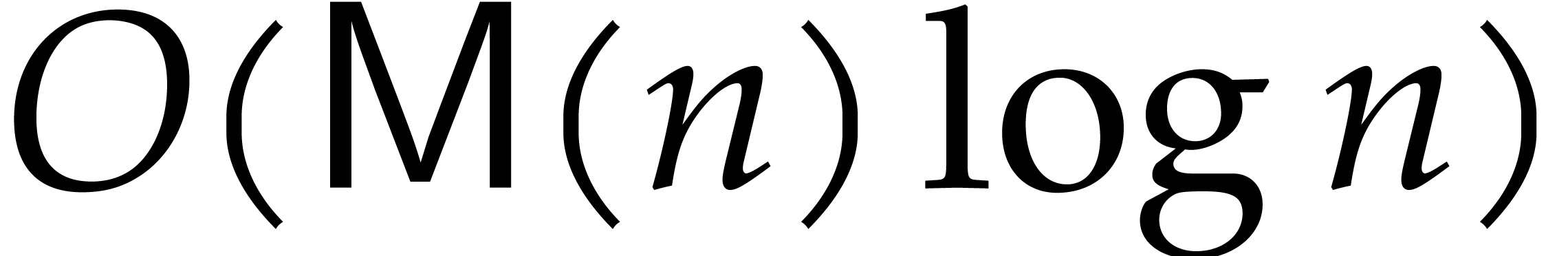 . These are respectively the problems of
multi-point evaluation, (univariate) interpolation,
transposed multi-point evaluation, and transposed
interpolation. For fixed
. These are respectively the problems of
multi-point evaluation, (univariate) interpolation,
transposed multi-point evaluation, and transposed
interpolation. For fixed  ,
these complexities can often be further reduced to
,
these complexities can often be further reduced to  using techniques from [45].
using techniques from [45].
For our factorization algorithms, we will sometimes need to assume the
existence of an algorithm to factor univariate polynomials in 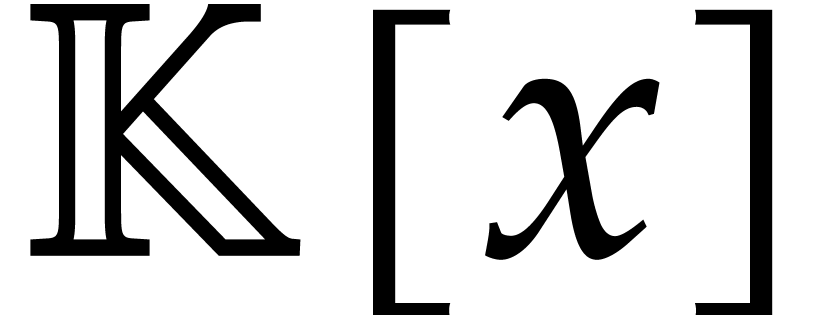 into irreducible factors. We will denote by
into irreducible factors. We will denote by 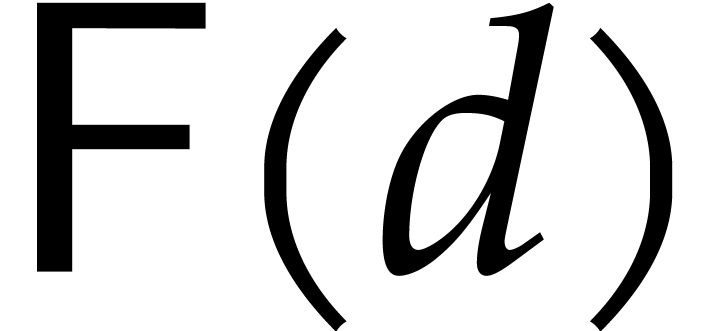 the cost of such a factorization as a function of degree
the cost of such a factorization as a function of degree
 . We will always assume that
. We will always assume that
 is non-decreasing. In particular
is non-decreasing. In particular 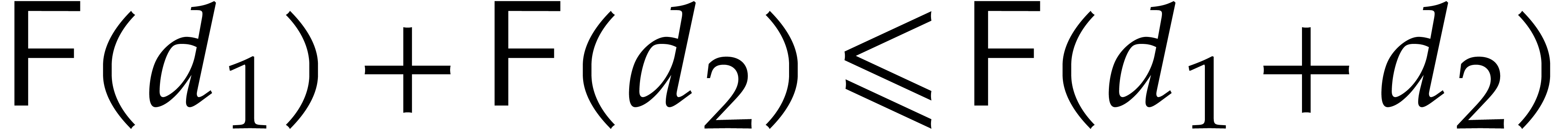 for all
for all 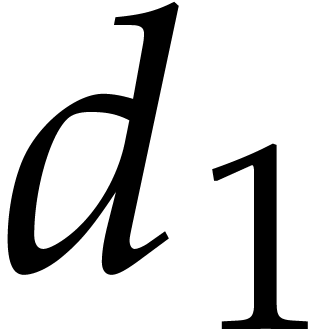 and
and  .
.
If  is the finite field
is the finite field 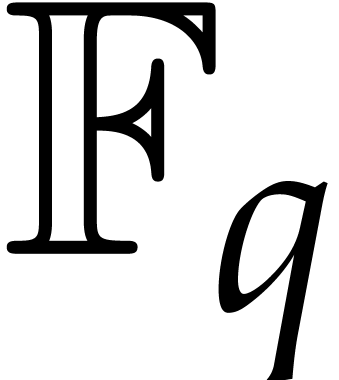 with
with 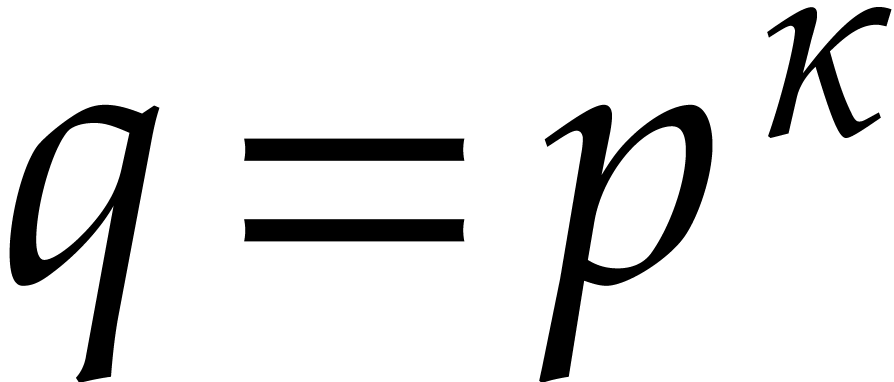 elements for some odd
elements for some odd 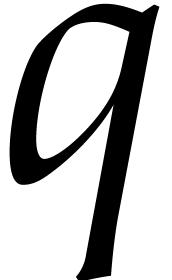 , then the best univariate factorization
methods are randomized of Las Vegas type. When allowing for such
algorithms, we may take
, then the best univariate factorization
methods are randomized of Las Vegas type. When allowing for such
algorithms, we may take 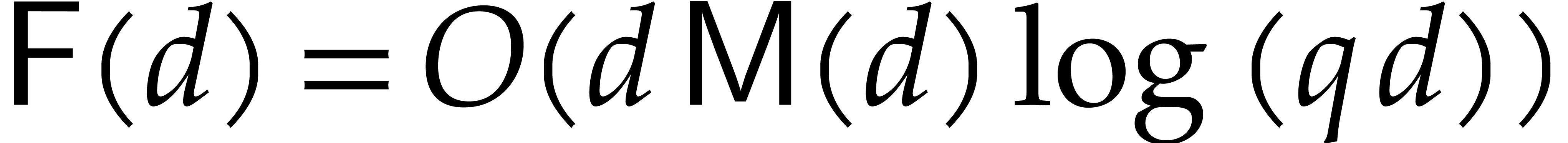 , by
using Cantor and Zassenhaus' method from [16]. With the use
of fast modular composition [70], we may take
, by
using Cantor and Zassenhaus' method from [16]. With the use
of fast modular composition [70], we may take

but this algorithm is only relevant in theory, for the moment [50].
If the extension degree  is composite, then this
can be exploited to lower the practical complexity of factorization [53].
is composite, then this
can be exploited to lower the practical complexity of factorization [53].
In all probabilistic algorithms in this paper,  will stand for a sufficiently large integer such that “random
elements in
will stand for a sufficiently large integer such that “random
elements in  ” are
chosen in some fixed subset of
” are
chosen in some fixed subset of  of size at least
of size at least
 . In the case when
. In the case when  is larger than the cardinality
is larger than the cardinality 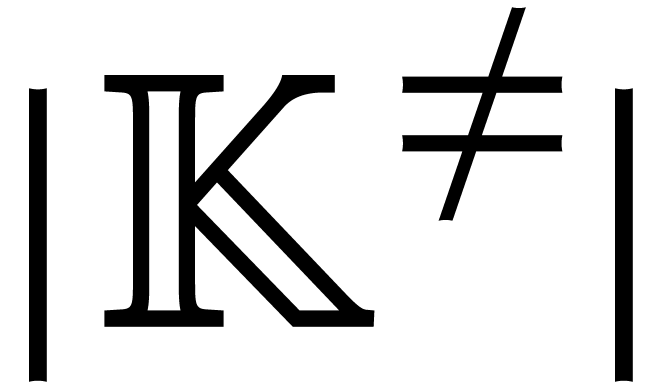 of
of
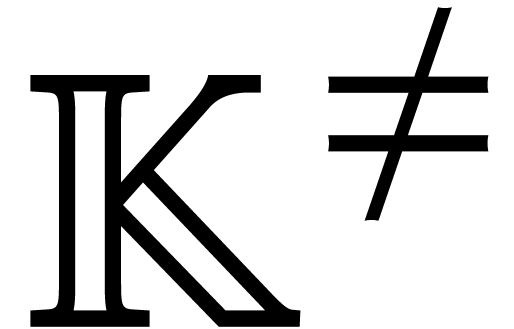 , this means that
, this means that  needs to be replaced by an algebraic extension of degree
needs to be replaced by an algebraic extension of degree
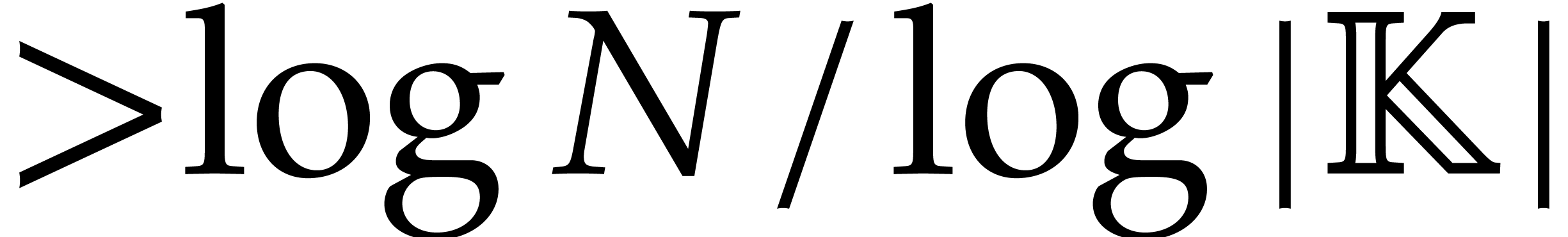 , which induces a logarithmic
, which induces a logarithmic
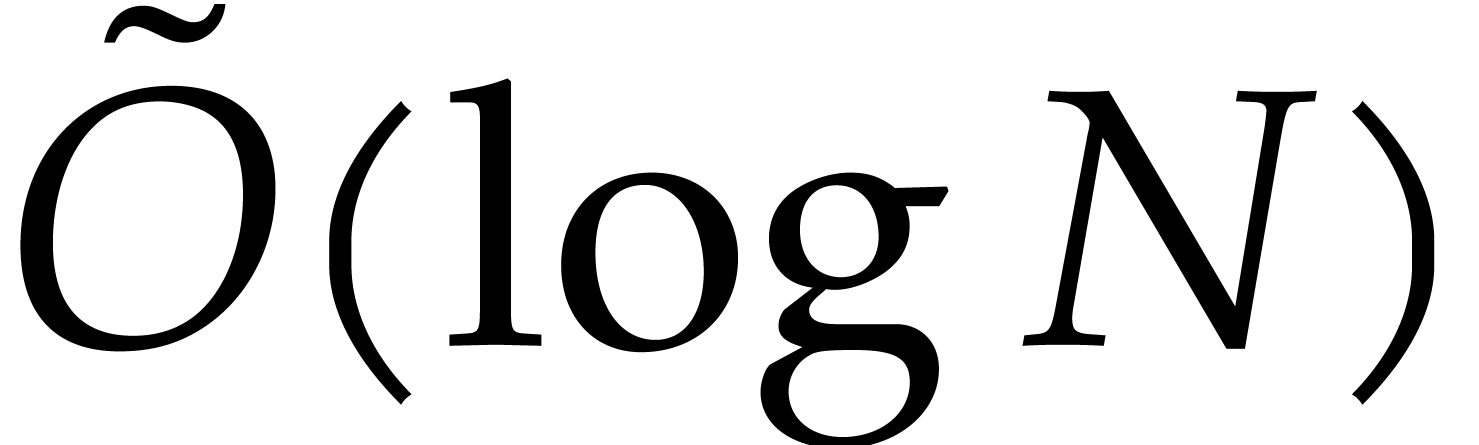 overhead for the cost of field operations in
overhead for the cost of field operations in
 . We will frequently use the
following well-known lemma:
. We will frequently use the
following well-known lemma:
Proof. We apply the lemma to  .
.
 .
Let
.
Let 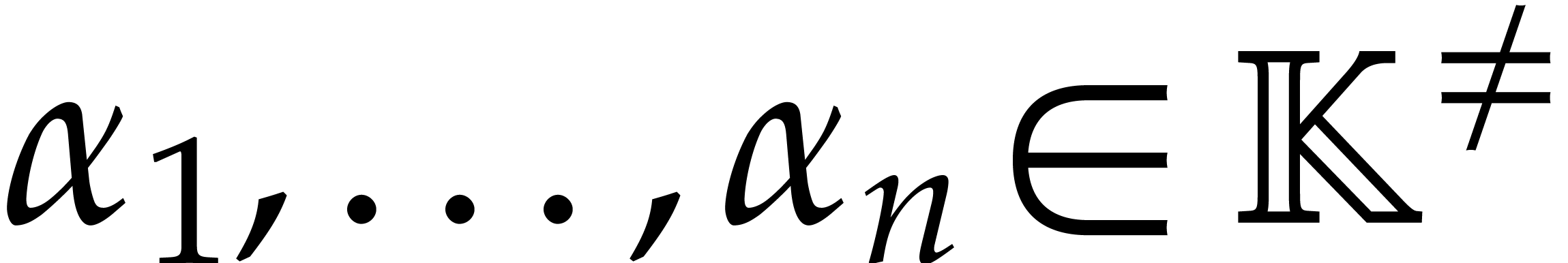 and let
and let 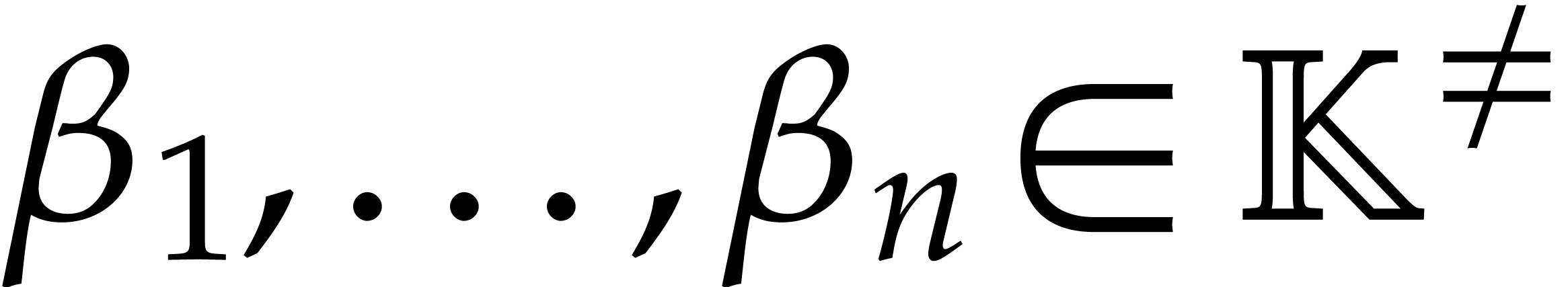 be chosen
independently at random. Then the probability that
be chosen
independently at random. Then the probability that 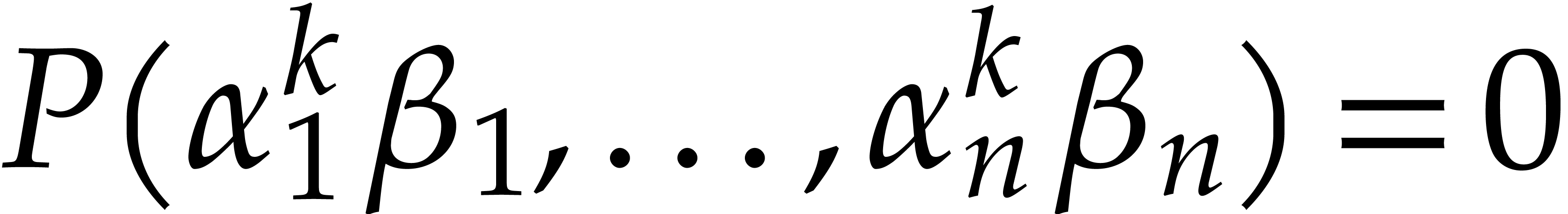 for some
for some  is at most
is at most  .
.
Proof. We apply the lemma to  .
.
Consider a polynomial 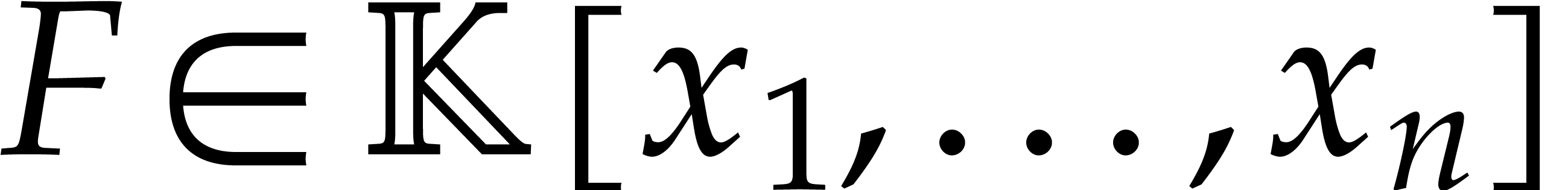 that is presented as a
blackbox function. The task of sparse interpolation is to
recover the sparse representation (1.1) from a sufficient
number of blackbox evaluations of
that is presented as a
blackbox function. The task of sparse interpolation is to
recover the sparse representation (1.1) from a sufficient
number of blackbox evaluations of  .
One may distinguish between the cases when the exponents
.
One may distinguish between the cases when the exponents  of
of  are already known or not. (Here
“known exponents” may be taken liberally to mean a superset
of reasonable size of the set of actual exponents.)
are already known or not. (Here
“known exponents” may be taken liberally to mean a superset
of reasonable size of the set of actual exponents.)
One popular approach for sparse interpolation is based on Prony's
geometric sequence technique [91, 5]. This
approach requires an admissible ratio  , such that for any
, such that for any 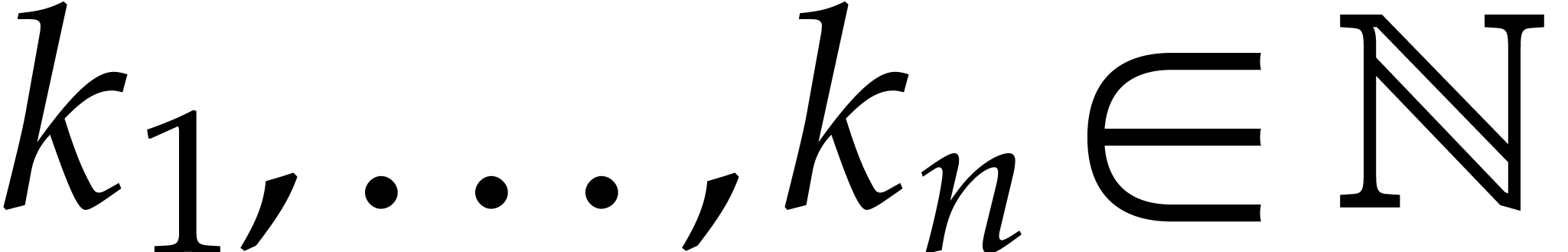 ,
there is an algorithm to recover
,
there is an algorithm to recover  from
from  . If
. If 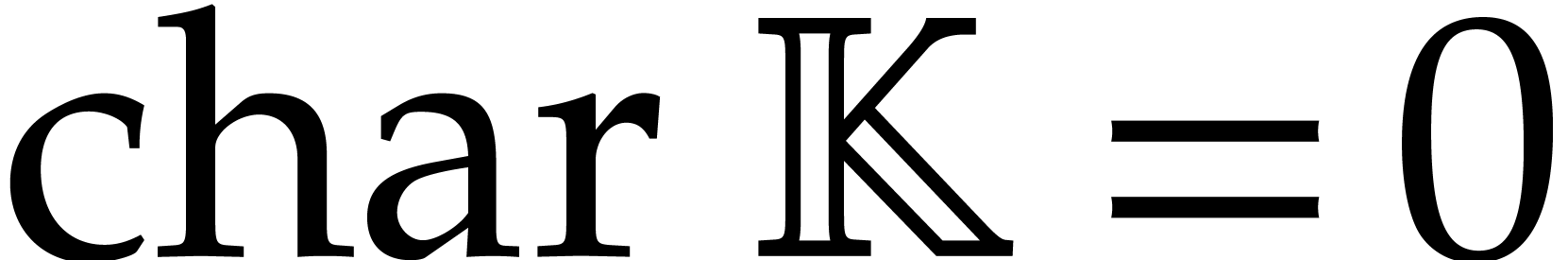 ,
then we may take
,
then we may take  to be the
to be the  -th prime number, and use prime factorization
in order to recover
-th prime number, and use prime factorization
in order to recover  . If
. If  is a finite field, where
is a finite field, where  is a
smooth prime (i.e.
is a
smooth prime (i.e. 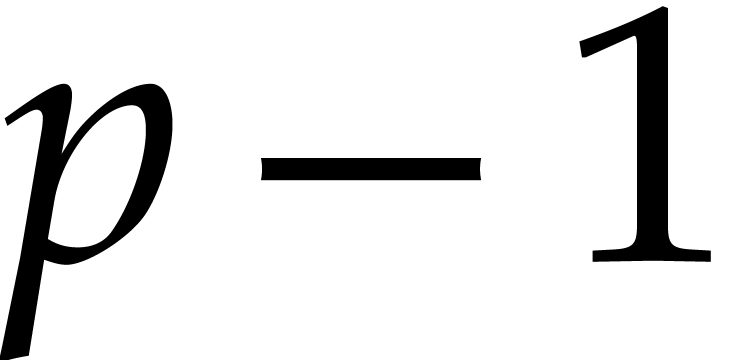 has many small
prime divisors), then one may recover exponents using the tangent
Graeffe method [38].
has many small
prime divisors), then one may recover exponents using the tangent
Graeffe method [38].
Given an admissible ratio  ,
Prony's method allows for the sparse interpolation of
,
Prony's method allows for the sparse interpolation of  using
using 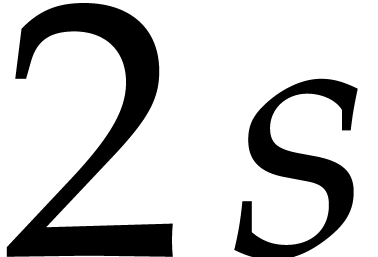 evaluations of
evaluations of  at
at
 for
for  ,
as well as
,
as well as 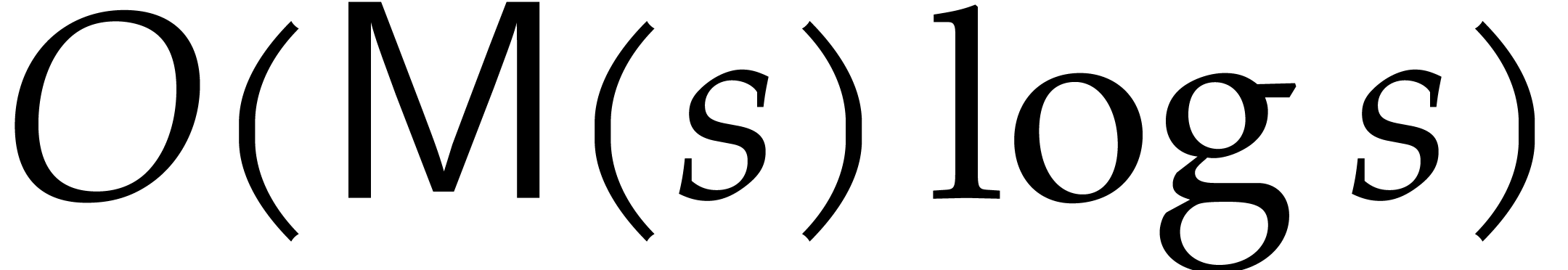 operations in
operations in  for determining
for determining  , and
, and 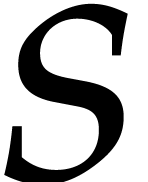 subsequent exponent recoveries. If
subsequent exponent recoveries. If 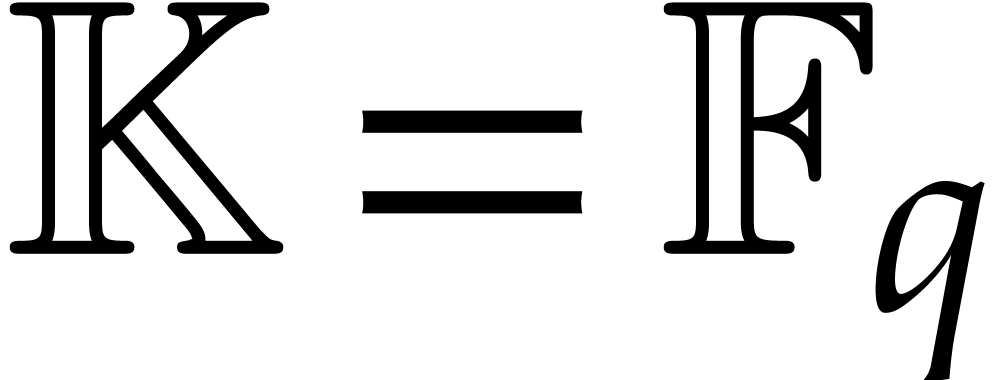 , then the exponents can be recovered if
, then the exponents can be recovered if 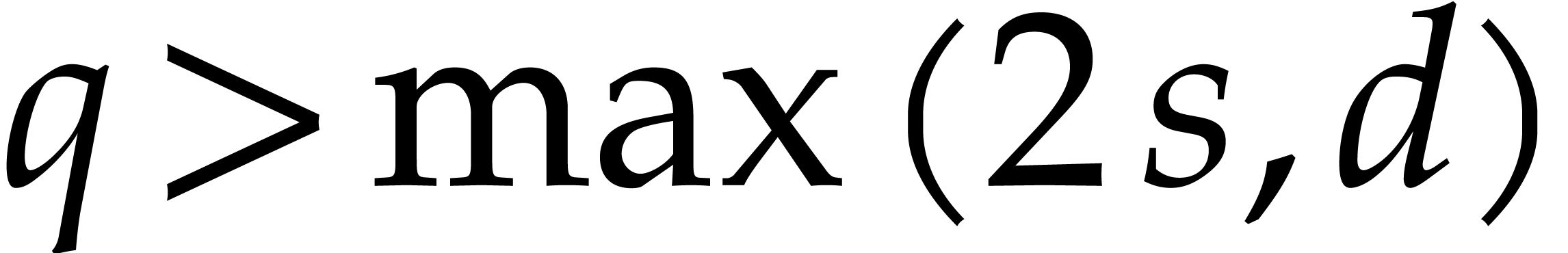 , which can be ensured by working
over a field extension
, which can be ensured by working
over a field extension 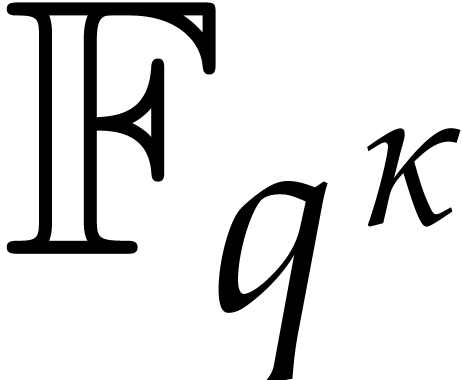 of
of  with
with  . If the exponents
. If the exponents  are already known, then the coefficients can be
obtained from
are already known, then the coefficients can be
obtained from 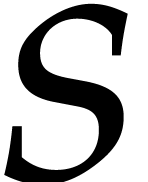 evaluations of
evaluations of  at
at  using one transposed univariate interpolation
of cost
using one transposed univariate interpolation
of cost 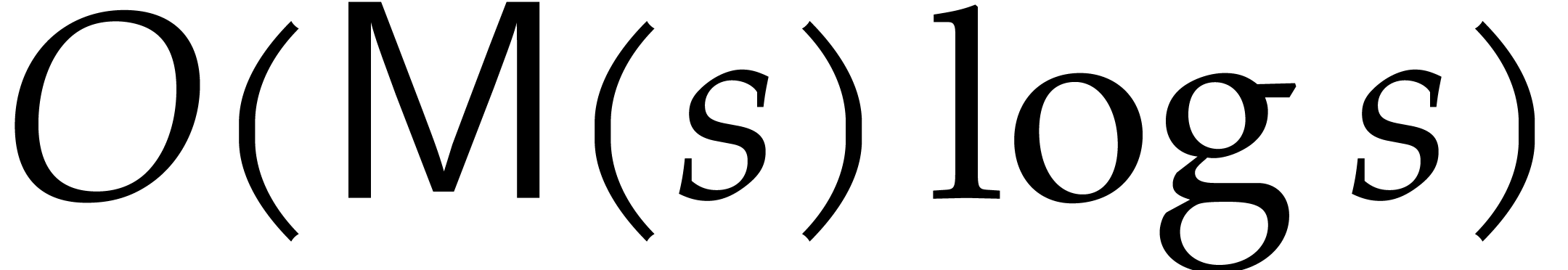 .
.
If  is a finite field, then it can be more
efficient to consider an FFT ratio
is a finite field, then it can be more
efficient to consider an FFT ratio  for
which
for
which  are roots of unity. When choosing these
roots of unity with care, possibly in an extension field of
are roots of unity. When choosing these
roots of unity with care, possibly in an extension field of  , sparse interpolation can often be done in
time
, sparse interpolation can often be done in
time 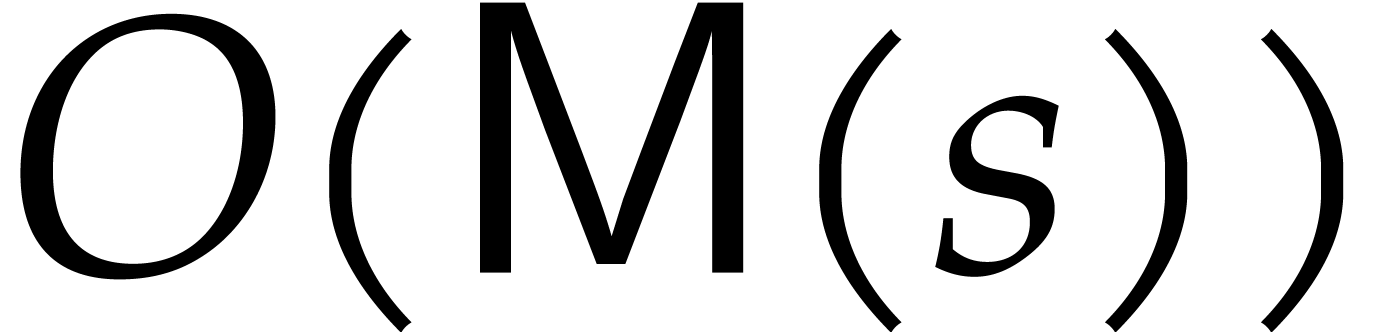 from
from 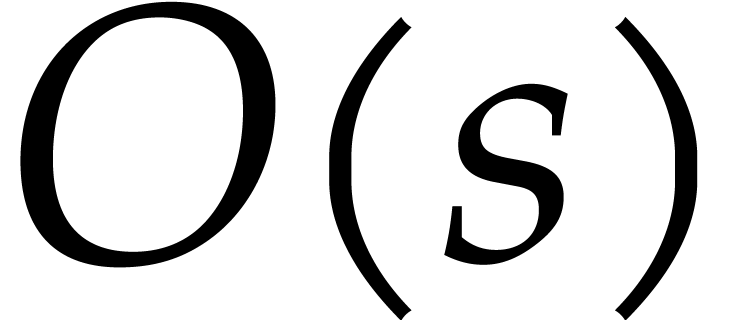 values of
values of
 , using discrete Fourier
transforms; see [52, 46] for details.
, using discrete Fourier
transforms; see [52, 46] for details.
In what follows, we will denote by 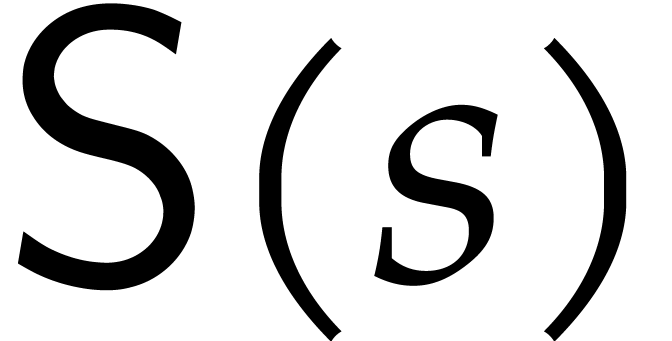 the cost of
sparse interpolation of size
the cost of
sparse interpolation of size  ,
given
,
given 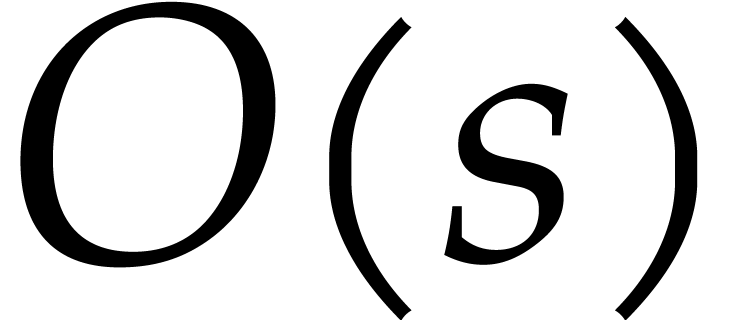 values of
values of  at a
suitable geometric sequence. When using Prony's approach, we may thus
take
at a
suitable geometric sequence. When using Prony's approach, we may thus
take 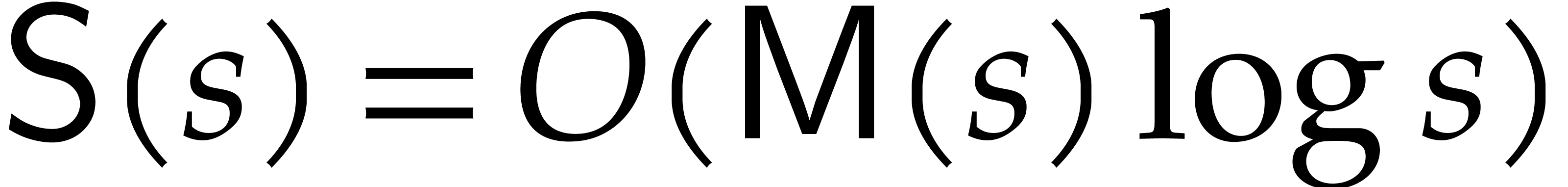 , whenever the cost to
recover the exponents
, whenever the cost to
recover the exponents  from
from  is negligible. If the discrete Fourier approach is applicable, then we
may even take
is negligible. If the discrete Fourier approach is applicable, then we
may even take 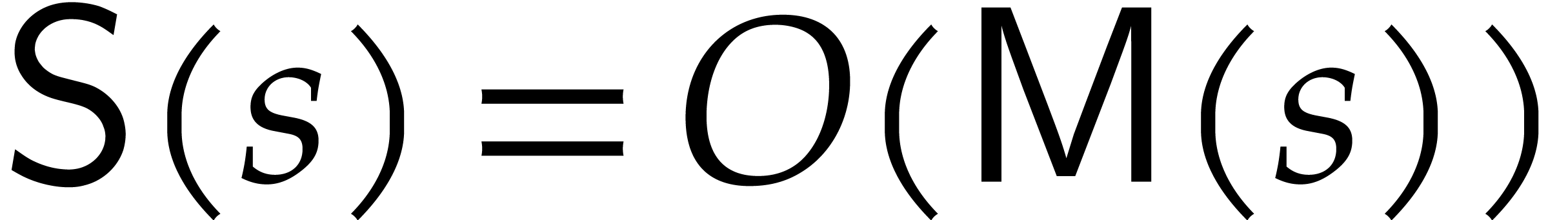 .
.
Remark  for the cost of
sparse interpolation, since this cost may also depend on the dimension
for the cost of
sparse interpolation, since this cost may also depend on the dimension
 and the total degree
and the total degree  . In particular, manipulations of the exponent
vectors typically add
. In particular, manipulations of the exponent
vectors typically add 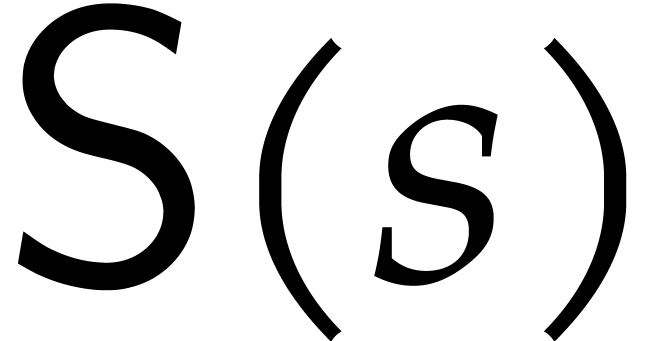 to the bit complexity.
Nonetheless, in our algebraic complexity model, this cost can often be
discarded: if
to the bit complexity.
Nonetheless, in our algebraic complexity model, this cost can often be
discarded: if 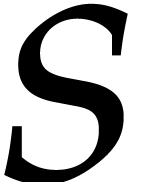 , then the
sparse interpolation of the exponents only gives rise to a constant
overhead using the derivative trick from [57]. In practice,
this remains true as long as the exponent vectors can be packed into
small integers, such as 64 bit machine integers. In order to enhance the
readability of our complexity analyses, we therefore assume that we are
in a regime where the cost
, then the
sparse interpolation of the exponents only gives rise to a constant
overhead using the derivative trick from [57]. In practice,
this remains true as long as the exponent vectors can be packed into
small integers, such as 64 bit machine integers. In order to enhance the
readability of our complexity analyses, we therefore assume that we are
in a regime where the cost  of sparse
interpolation can be modeled in terms of the sole parameter
of sparse
interpolation can be modeled in terms of the sole parameter  . For recent theoretical work on sparse
interpolation when
. For recent theoretical work on sparse
interpolation when  and/or
and/or  are allowed to become large, we refer to [36, 54].
are allowed to become large, we refer to [36, 54].
Remark 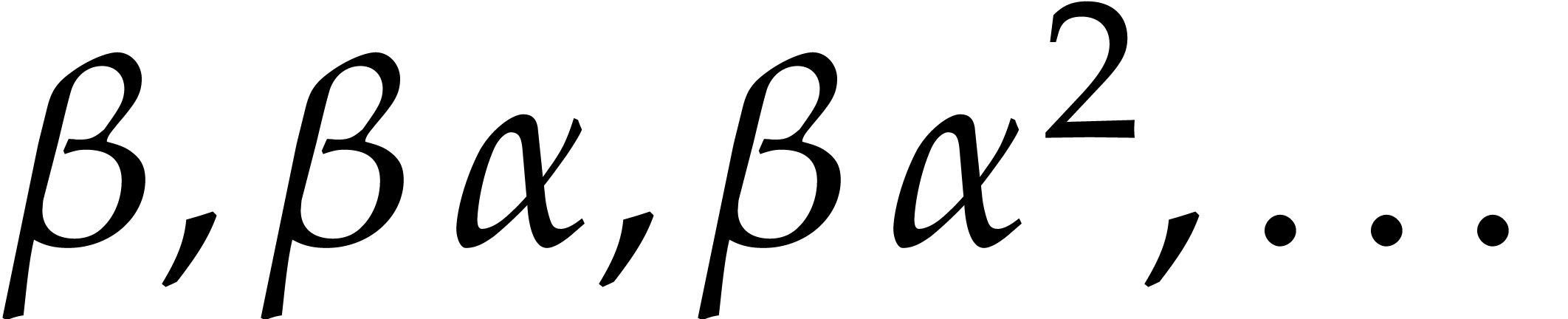 for the number of terms of
for the number of terms of  , then we assume that our sparse
interpolation method is deterministic and that it interpolates
, then we assume that our sparse
interpolation method is deterministic and that it interpolates  in time
in time  . If we
do not know the number of terms of
. If we
do not know the number of terms of  ,
then we may run the interpolation method for a guessed number of
,
then we may run the interpolation method for a guessed number of  terms. We may check the correctness of our guessed
interpolation
terms. We may check the correctness of our guessed
interpolation 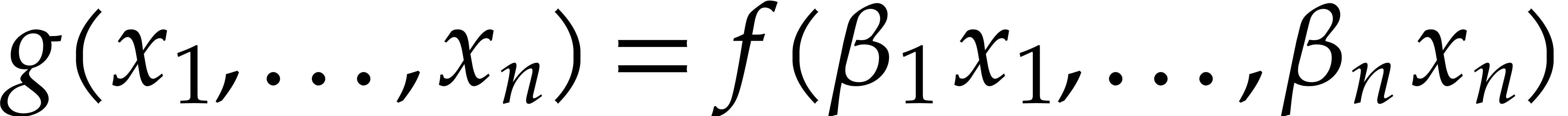 by verifying that the evaluations
of
by verifying that the evaluations
of  and
and  coincide at a
randomly chosen point. By the Schwartz-Zippel lemma, this strategy
succeeds with probability at least
coincide at a
randomly chosen point. By the Schwartz-Zippel lemma, this strategy
succeeds with probability at least  .
.
Remark  with
with  as the evaluation points, by considering the function
as the evaluation points, by considering the function  instead of
instead of 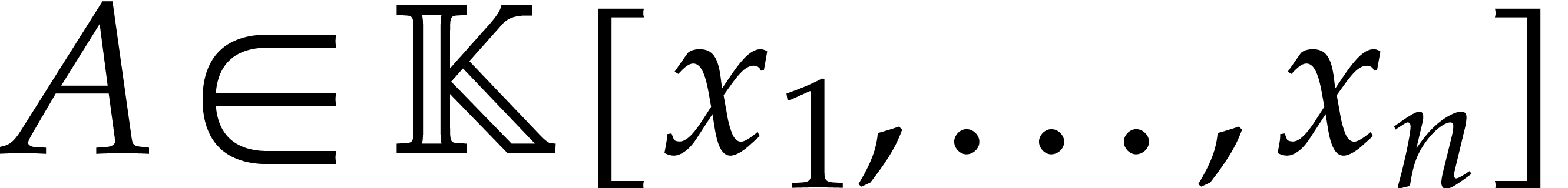 .
Taking a random
.
Taking a random  avoids certain problems due to
degeneracies; this is sometimes called “diversification” [35]. If
avoids certain problems due to
degeneracies; this is sometimes called “diversification” [35]. If  is itself chosen at random,
then it often suffices to simply take
is itself chosen at random,
then it often suffices to simply take  .
We will occasionally do so without further mention.
.
We will occasionally do so without further mention.
Remark  of geometric progressions to be picked at random, which
excludes FFT ratios. Alternatively, we could have relied on Corollary 2.3 and diversification of all input and output polynomials
for a fixed random scaling factor
of geometric progressions to be picked at random, which
excludes FFT ratios. Alternatively, we could have relied on Corollary 2.3 and diversification of all input and output polynomials
for a fixed random scaling factor  (see the above
remark).
(see the above
remark).
Assume for instance that we wish to factor 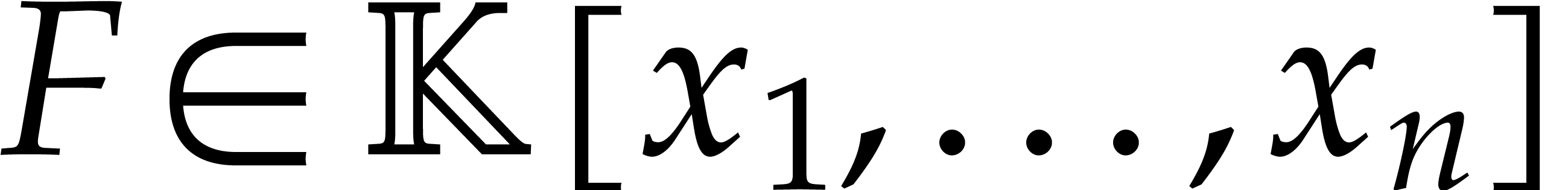 .
Then the factors
.
Then the factors  of
of  are
in one-to-one correspondence with the factors
are
in one-to-one correspondence with the factors  of
of
 . If we rely on Corollary 2.3 instead of 2.2 in our complexity bounds for
factoring
. If we rely on Corollary 2.3 instead of 2.2 in our complexity bounds for
factoring  (like the bounds in Theorems 6.11
or 7.2 below), then the cost of diversification adds an
extra term
(like the bounds in Theorems 6.11
or 7.2 below), then the cost of diversification adds an
extra term 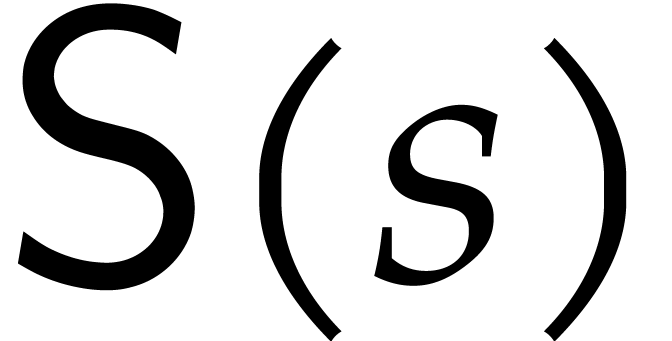 , where
, where  and
and  is the total size of
is the total size of  and the computed factors. On the positive side, in the
corresponding bounds for the probability of failure, the quadratic
dependence
and the computed factors. On the positive side, in the
corresponding bounds for the probability of failure, the quadratic
dependence  on the number
on the number  of evaluation points reduces to a linear one. Similar adjustments apply
for other operations such as gcd computations.
of evaluation points reduces to a linear one. Similar adjustments apply
for other operations such as gcd computations.
Opposite to sparse interpolation, one may also consider the evaluation
of  at
at 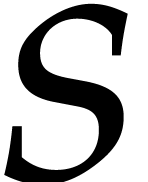 points
points  in a geometric progression. In general, this can be done
in time
in a geometric progression. In general, this can be done
in time 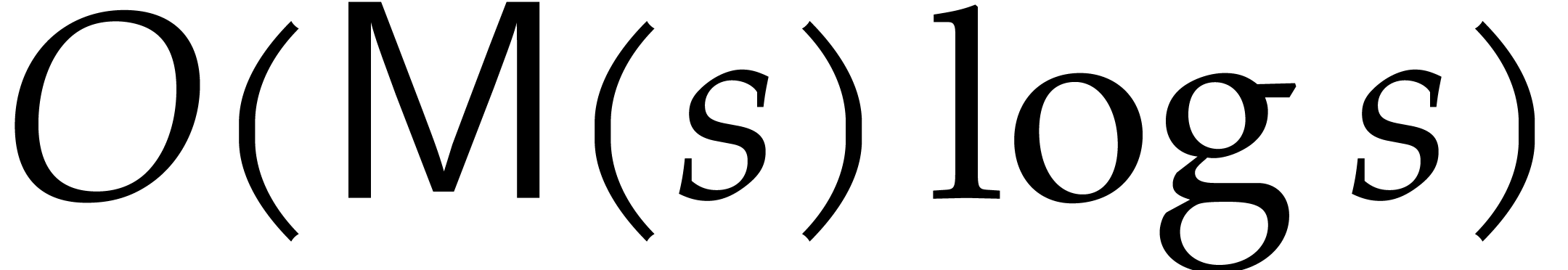 , using one
transposed multi-point evaluation of size
, using one
transposed multi-point evaluation of size 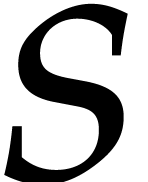 .
If
.
If  is a suitable FFT ratio, then this complexity
drops to
is a suitable FFT ratio, then this complexity
drops to 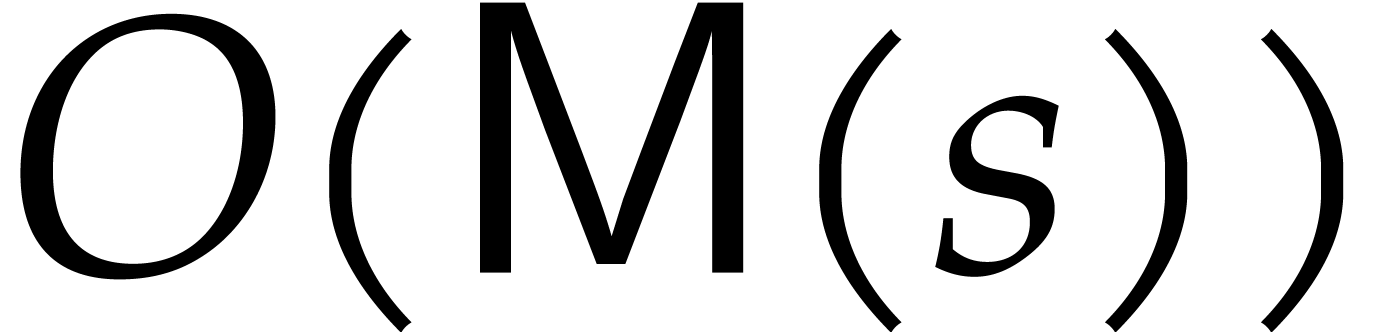 , using a discrete
Fourier transform of size
, using a discrete
Fourier transform of size 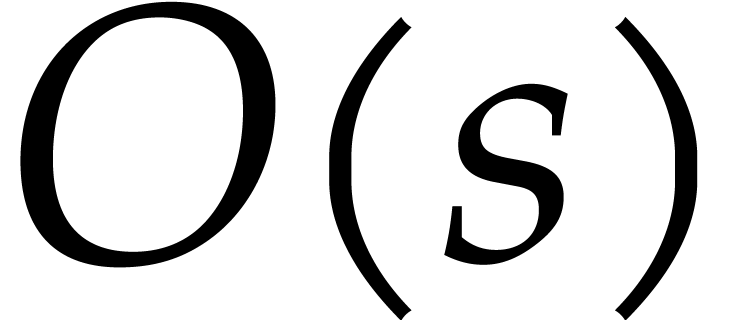 .
In what follows, we will assume that this operation can always be done
in time
.
In what follows, we will assume that this operation can always be done
in time  .
.
Remark  and
and  ,
so similar observations as in Remark 2.4 apply.
,
so similar observations as in Remark 2.4 apply.
More generally, we may consider the evaluation of  at
at  points
points  in a geometric
progression. If
in a geometric
progression. If  , we may do
this in time
, we may do
this in time 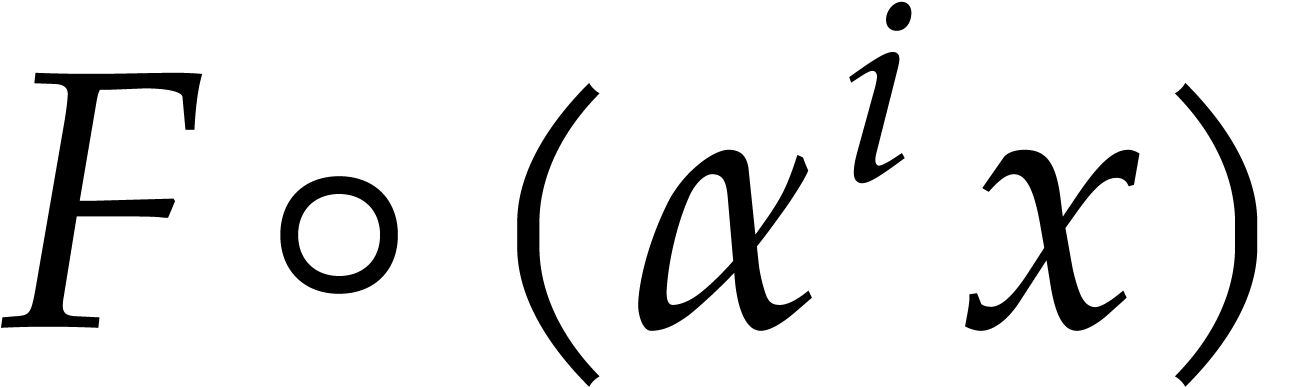 , by reducing to
the evaluation of
, by reducing to
the evaluation of  at
at  progressions of size
progressions of size 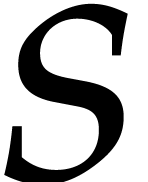 . To
obtain the evaluations of
. To
obtain the evaluations of  at
at 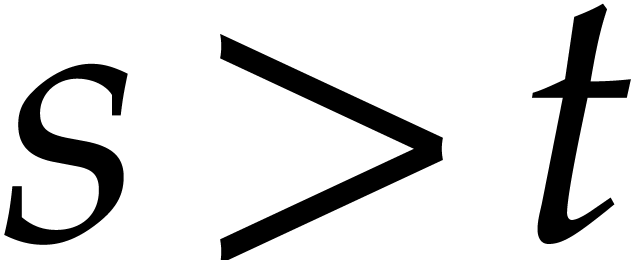 for
for  , we can evaluate
, we can evaluate  at
at  . If
. If
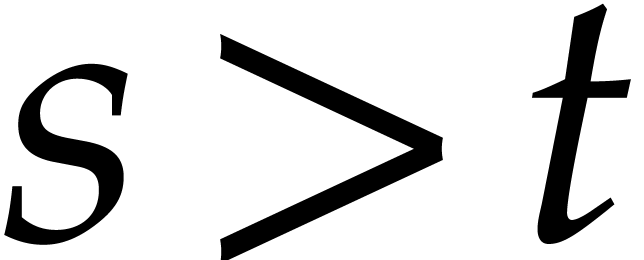 , then we may cut
, then we may cut  into
into  polynomials of size
polynomials of size 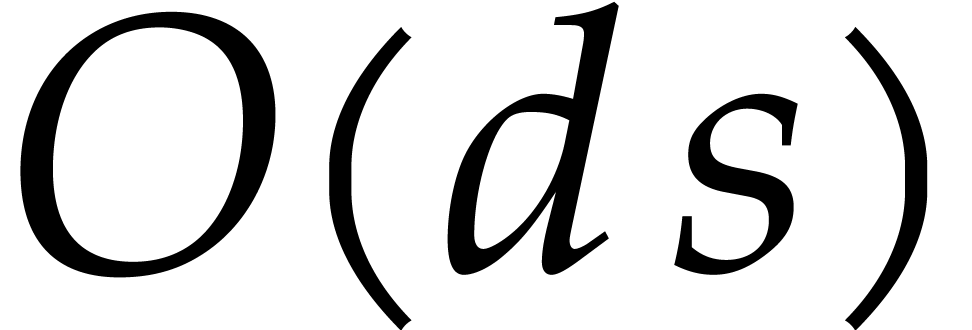 , and do the evaluation in time
, and do the evaluation in time
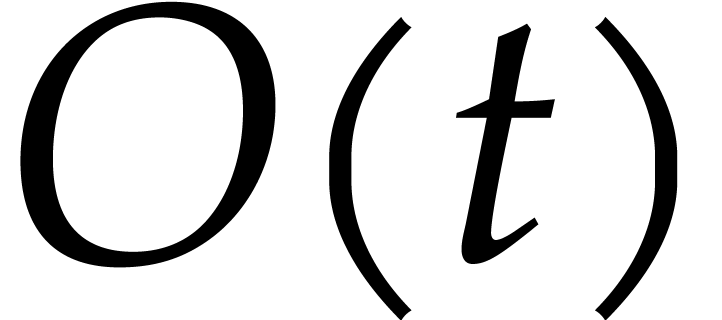 .
.
Remark  is an FFT-ratio, then the bound for the case when
is an FFT-ratio, then the bound for the case when  further reduces to
further reduces to 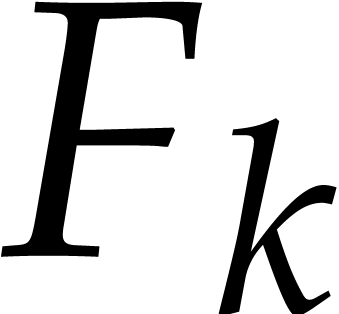 plus
plus 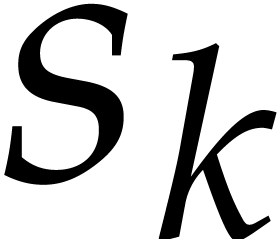 bit operations on exponents, since the cyclic
projections from [46, 52] reduce
bit operations on exponents, since the cyclic
projections from [46, 52] reduce  in linear time to cyclic polynomials with
in linear time to cyclic polynomials with 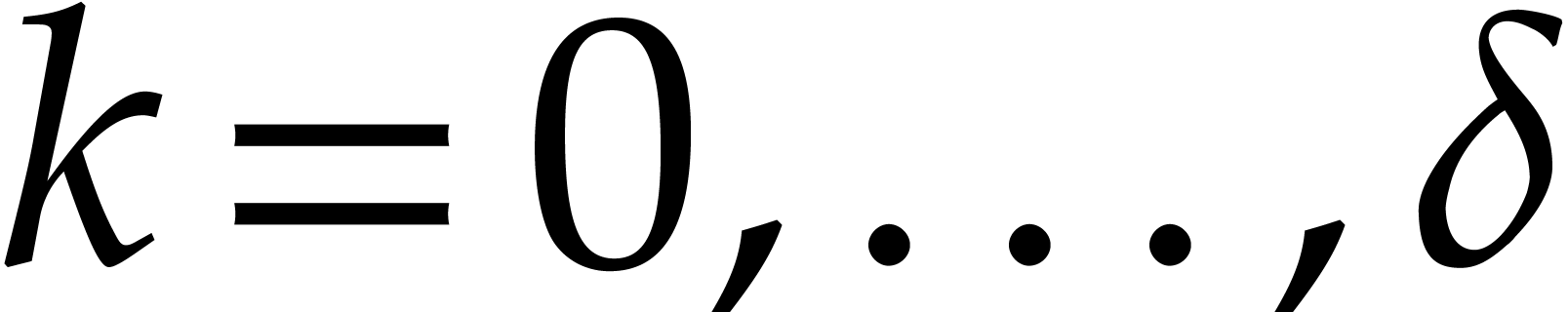 terms before applying the FFTs. We did not exploit this optimization for
the complexity bounds in this paper, since we preferred to state these
bounds for general ratios
terms before applying the FFTs. We did not exploit this optimization for
the complexity bounds in this paper, since we preferred to state these
bounds for general ratios  ,
but it should be straightforward to adapt them to the specific FFT case.
,
but it should be straightforward to adapt them to the specific FFT case.
In this paper, we will frequently need to evaluate  at all but one or two variables. Assume for instance that
at all but one or two variables. Assume for instance that
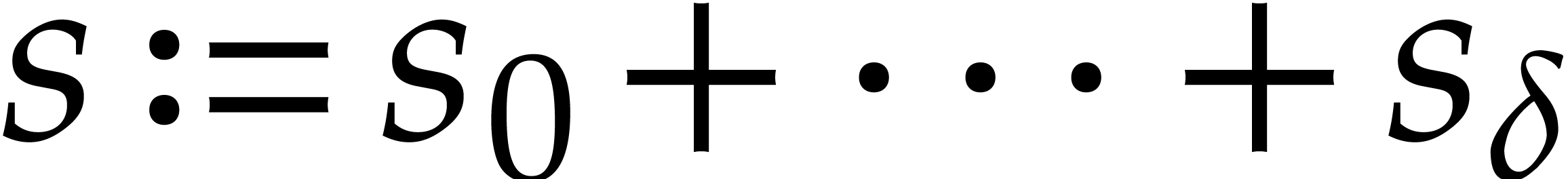
where  has
has  terms for
terms for  and
and 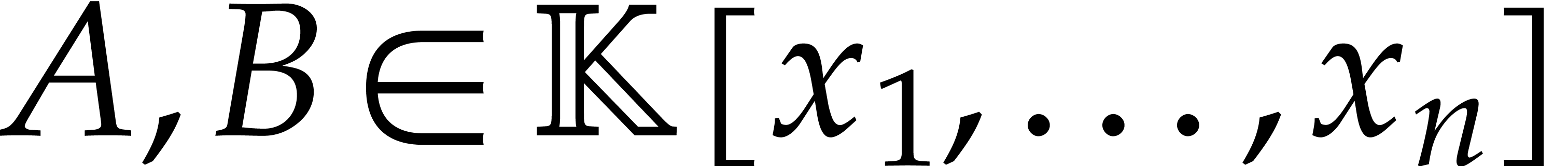 . Then
using the above method, we can compute
. Then
using the above method, we can compute  for
for 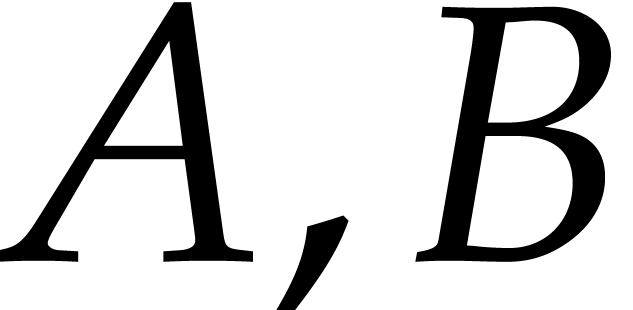 using
using  operations.
operations.
One traditional application of the combination of sparse evaluation and
interpolation are probabilistic algorithms for multiplication and exact
division of sparse multivariate polynomials. For the given  , we can compute the product
, we can compute the product 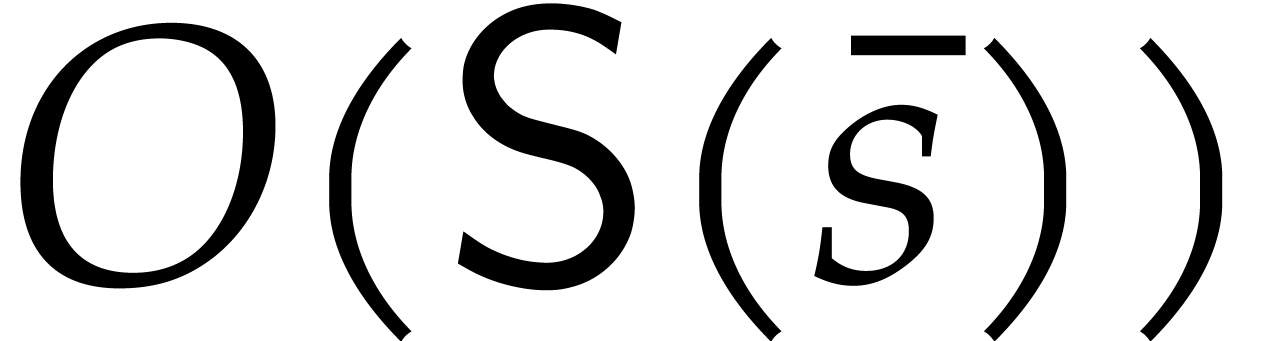 by evaluating
by evaluating  , and
, and  at a geometric progression
at a geometric progression  with
with
 and recovering of
and recovering of  in the
sparse representation (1.1) via sparse interpolation. The
total cost of this method is bounded by
in the
sparse representation (1.1) via sparse interpolation. The
total cost of this method is bounded by  operations in
operations in  , where
, where  . If
. If  and
and
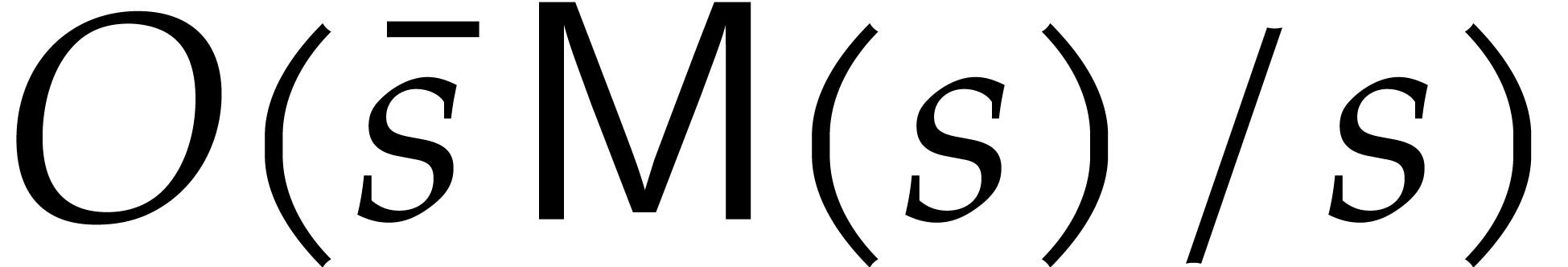 are known, then the exact quotient
are known, then the exact quotient 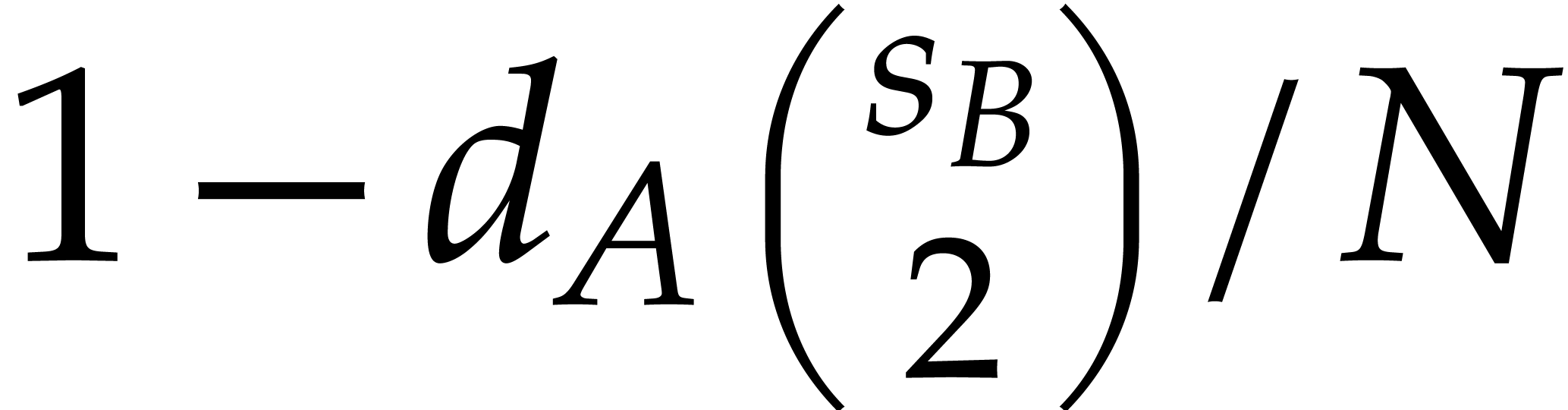 can be computed in a similar fashion and with the same
complexity. If
can be computed in a similar fashion and with the same
complexity. If 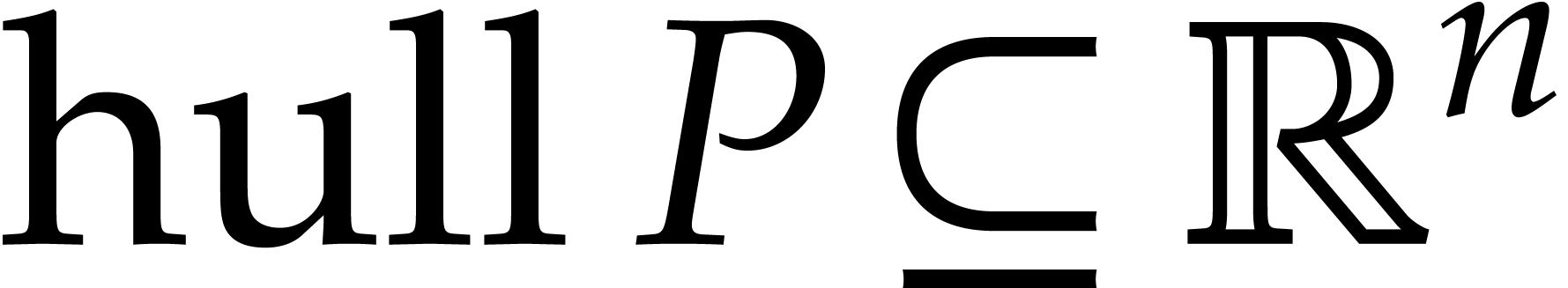 , then the
quotient
, then the
quotient  can actually be computed in time
can actually be computed in time  . Divisions by zero are avoided
through diversification, with overhead
. Divisions by zero are avoided
through diversification, with overhead  and
probability at least
and
probability at least 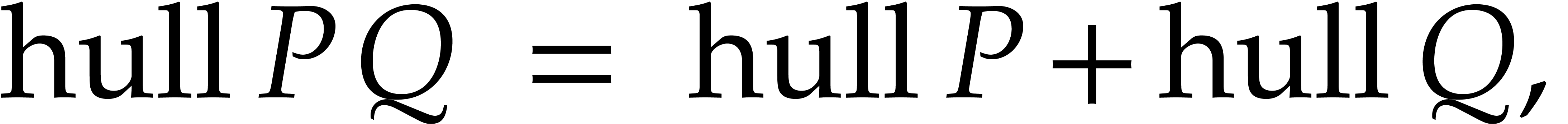 , by
Corollary 2.2.
, by
Corollary 2.2.
Consider a multivariate polynomial 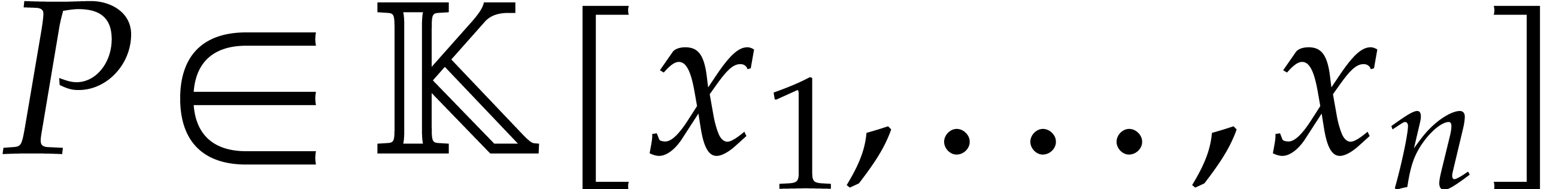 .
We define
.
We define  to be the convex hull of
to be the convex hull of 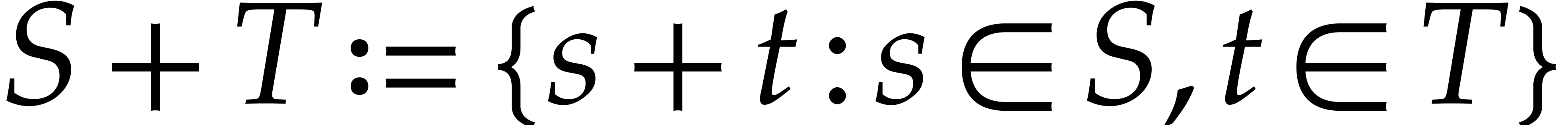 and we call it the Newton polytope of
and we call it the Newton polytope of  . Given another polynomial
. Given another polynomial  , it is well known that
, it is well known that
where the Minkowski sum of two subsets  is
is  .
.
Let 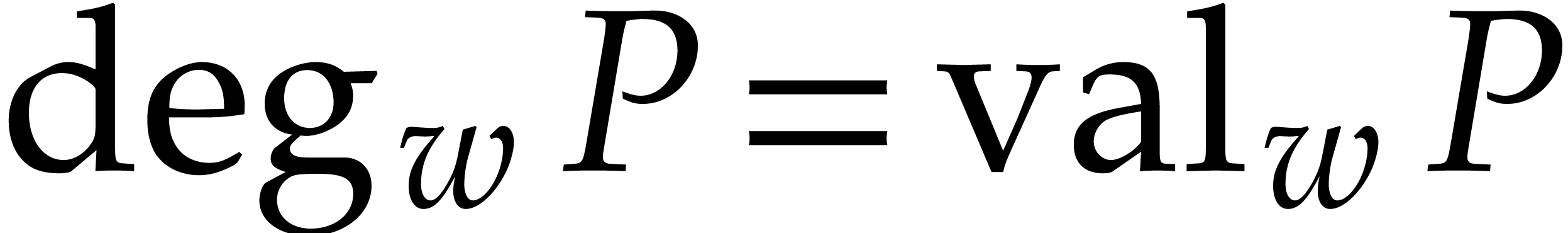 be a non-zero weight vector. We define the
be a non-zero weight vector. We define the
 -degree,
-degree,  -valuation, and
-valuation, and  -ecart of a non-zero
polynomial
-ecart of a non-zero
polynomial 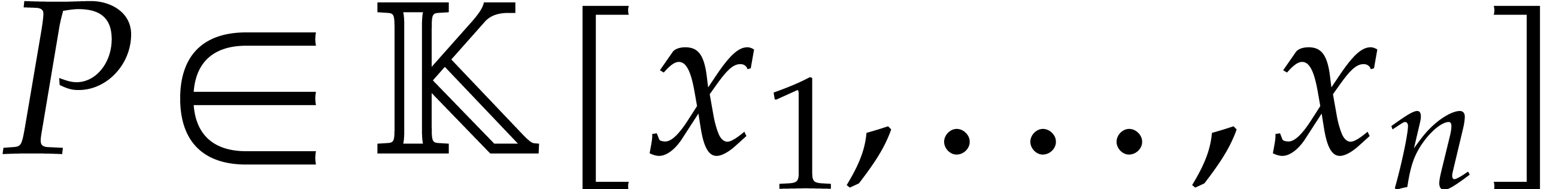 by
by
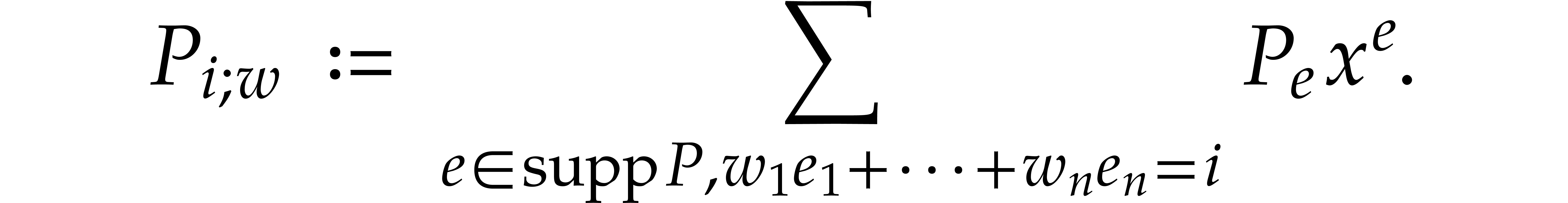
Note that 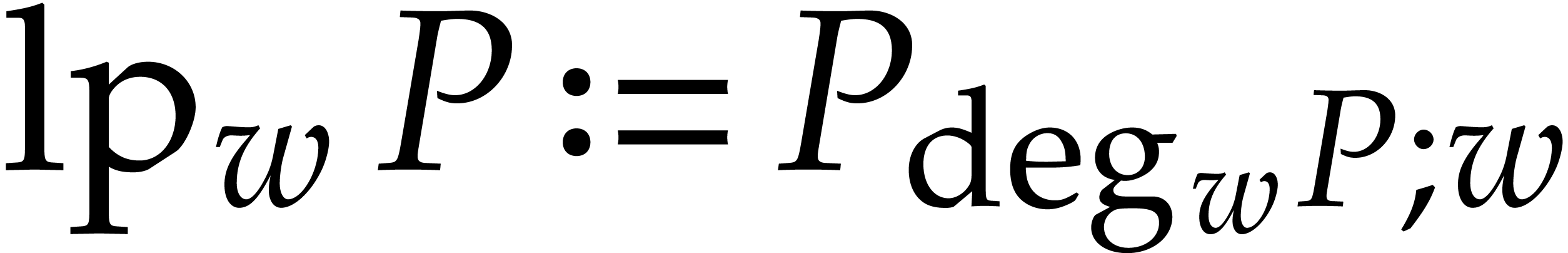 and
and  ,
where we exploit the fact that we allow for negative weights. We say
that
,
where we exploit the fact that we allow for negative weights. We say
that  is
is  -homogeneous
if
-homogeneous
if  . Any
. Any  can uniquely be written as a sum
can uniquely be written as a sum
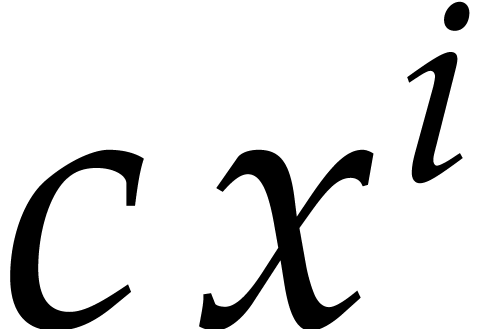
of its  -homogeneous
parts
-homogeneous
parts
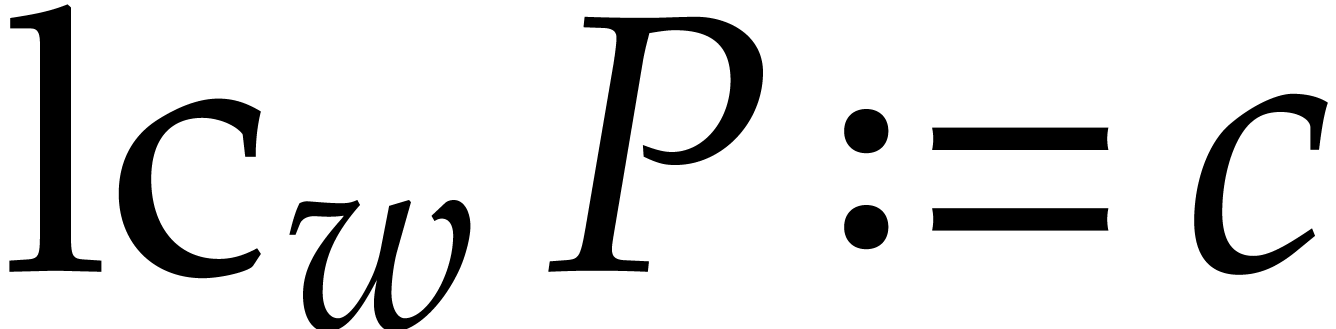
We call  and
and  the
the
 -leading and
-leading and
 -trailing parts of
-trailing parts of
 . We say that
. We say that  is
is  -regular
if
-regular
if  consists of a single term
consists of a single term  . In that case, we denote
. In that case, we denote  and we say that
and we say that  is
is  -monic if
-monic if  .
Given another non-zero polynomial
.
Given another non-zero polynomial  ,
we have
,
we have

Setting  , we also have
, we also have
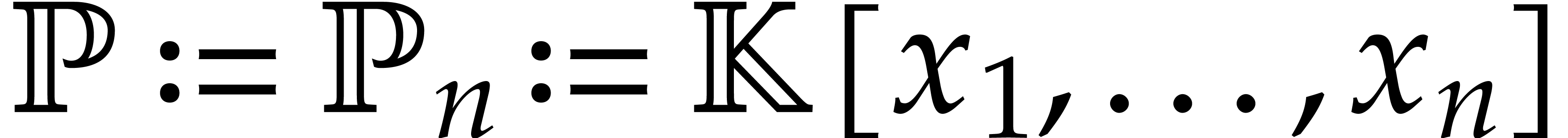
The Newton polytopes  and
and  are facets of
are facets of  . In
particular, they are contained in the boundary
. In
particular, they are contained in the boundary 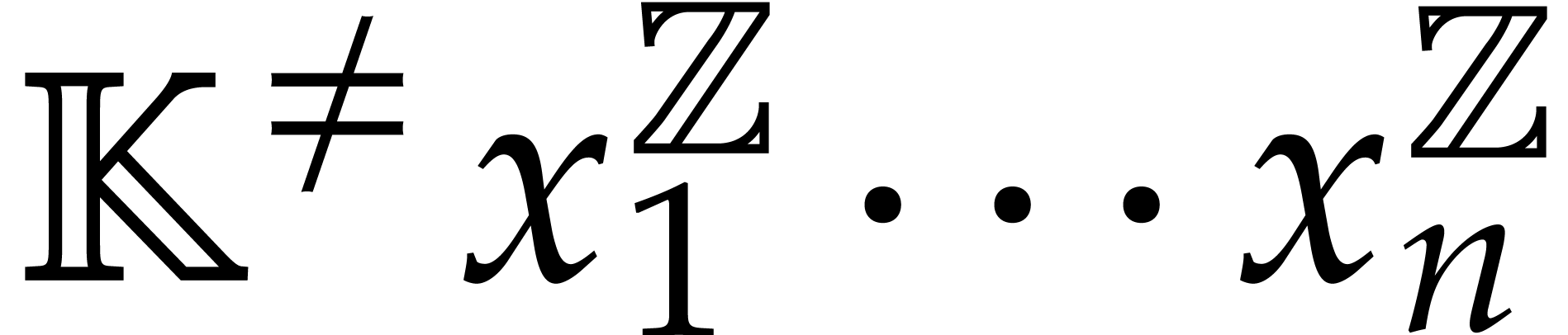 .
.
Consider the rings  and
and  of ordinary polynomials and Laurent polynomials. Both rings are
unique factorization domains, but the group of units of
of ordinary polynomials and Laurent polynomials. Both rings are
unique factorization domains, but the group of units of 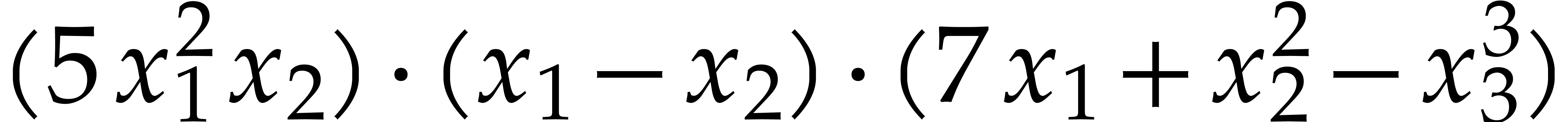 is
is 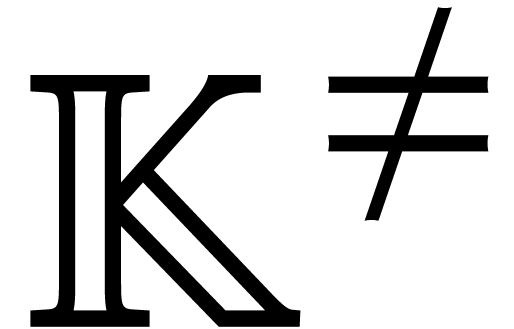 , whereas the group of
units of
, whereas the group of
units of 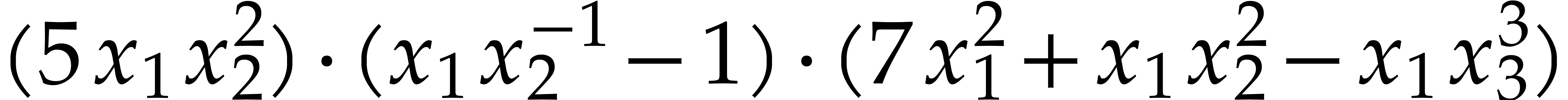 is
is  .
Factoring in
.
Factoring in 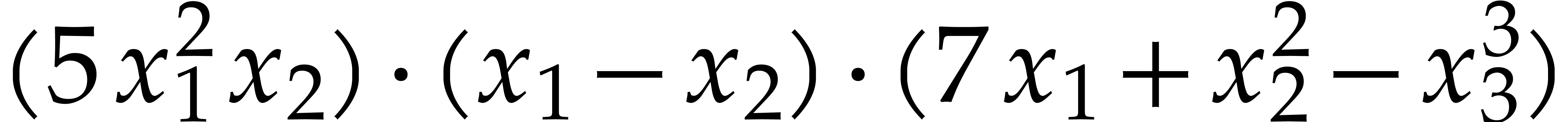 is therefore essentially the same
as factoring in
is therefore essentially the same
as factoring in 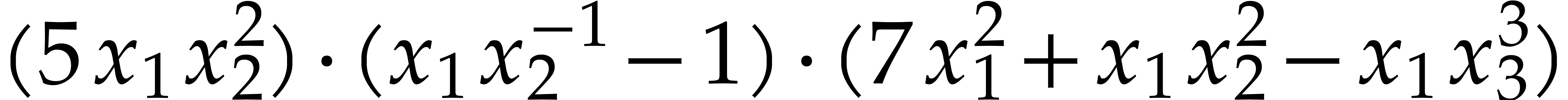 up to multiplications with
monomials in
up to multiplications with
monomials in  . For instance,
the factorization
. For instance,
the factorization  in
in 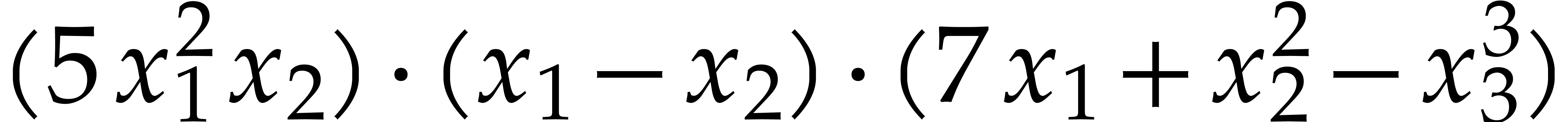 gives rise to the factorization
gives rise to the factorization  in
in 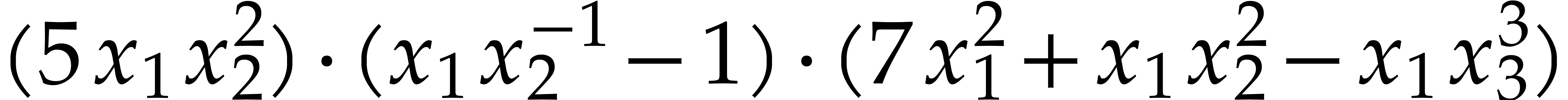 . Conversely, the factorization
. Conversely, the factorization  in
in 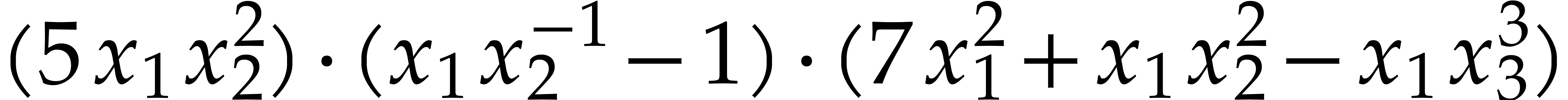 gives rise to the factorization
gives rise to the factorization
 in
in 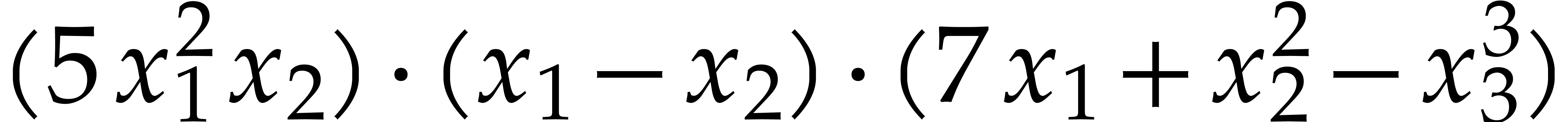 .
Similarly, computing gcds in
.
Similarly, computing gcds in 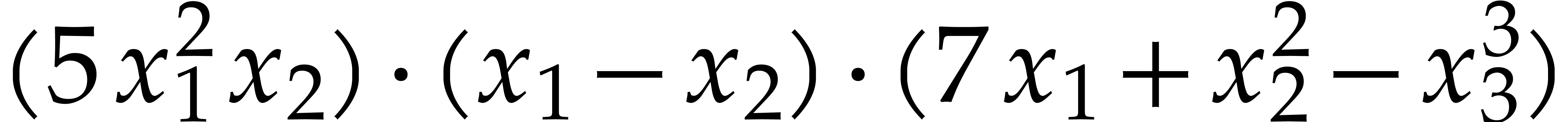 is essentially the
same problem as computing gcds in
is essentially the
same problem as computing gcds in 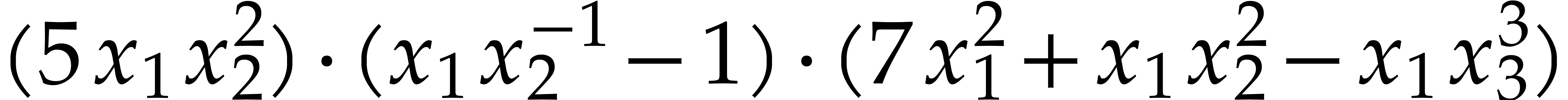 .
.
Given any  matrix
matrix 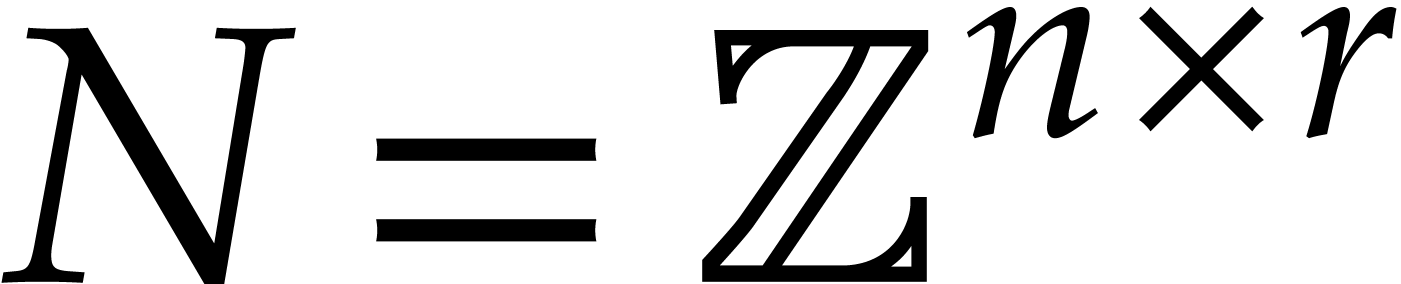 ,
we define the monomial map
,
we define the monomial map  by
by
This is clearly a homomorphism, which is injective (or surjective) if
the linear map  is injective (or surjective).
Note also that
is injective (or surjective).
Note also that 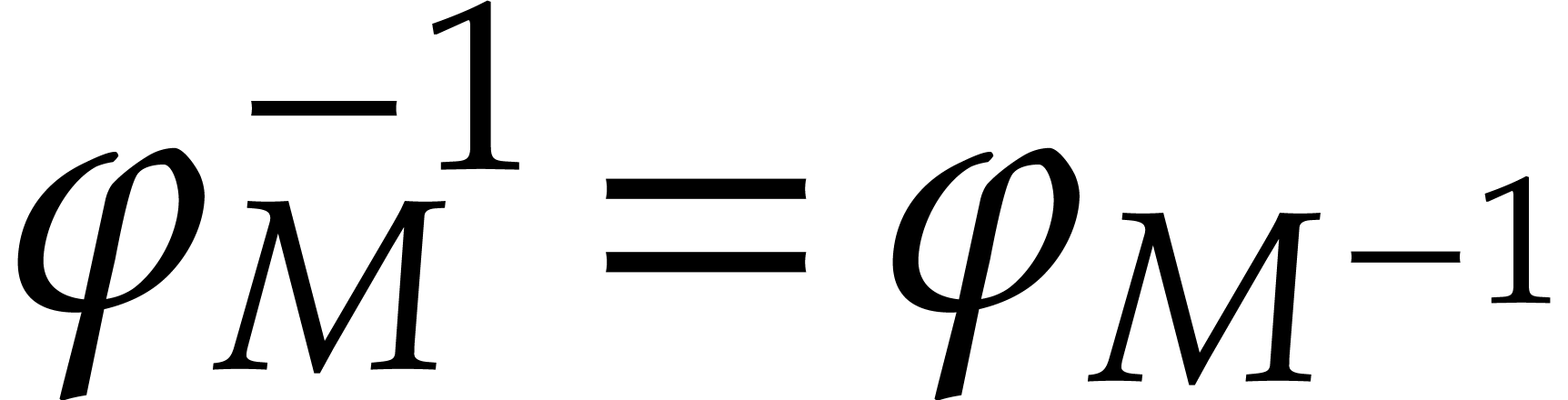 for any matrices
for any matrices 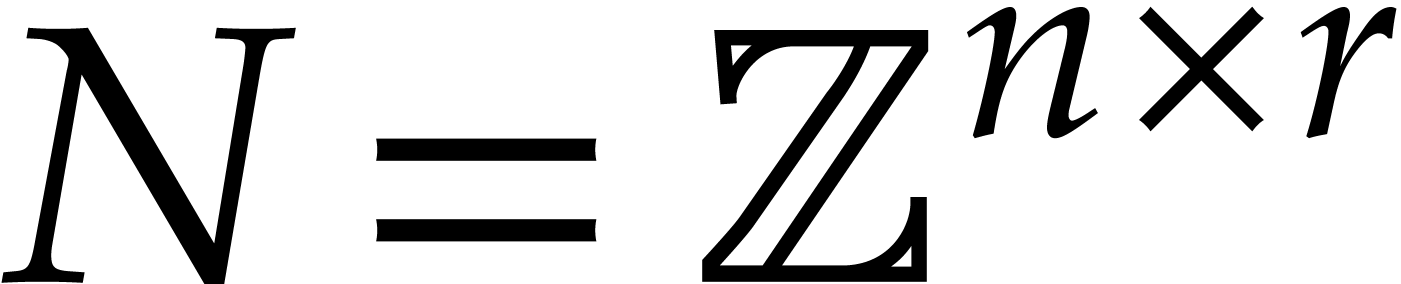 and
and  . In particular, if
. In particular, if 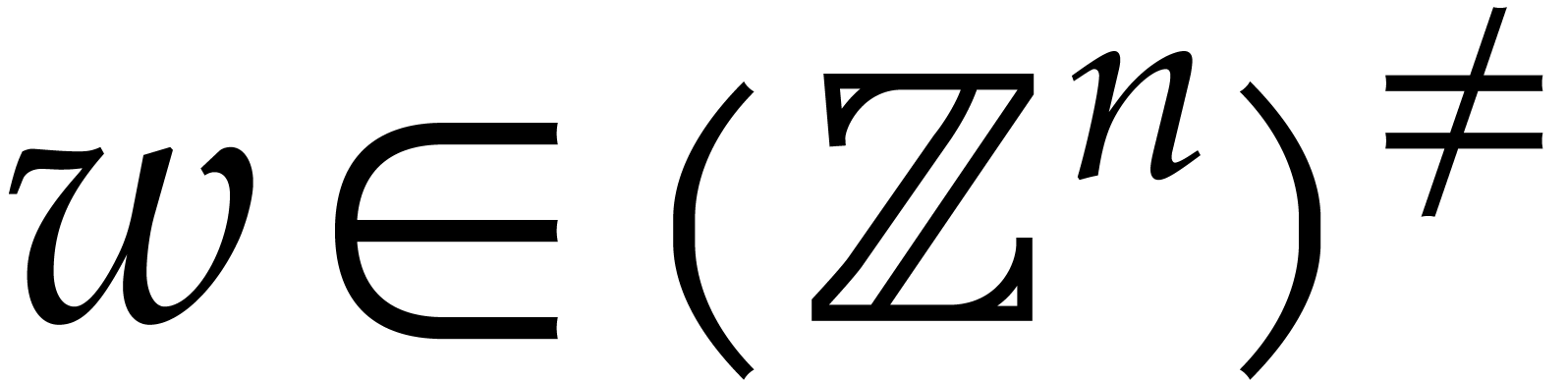 is unimodular, then
is unimodular, then 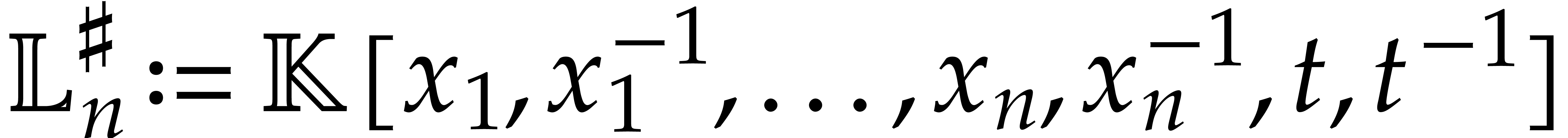 is an
automorphism of
is an
automorphism of 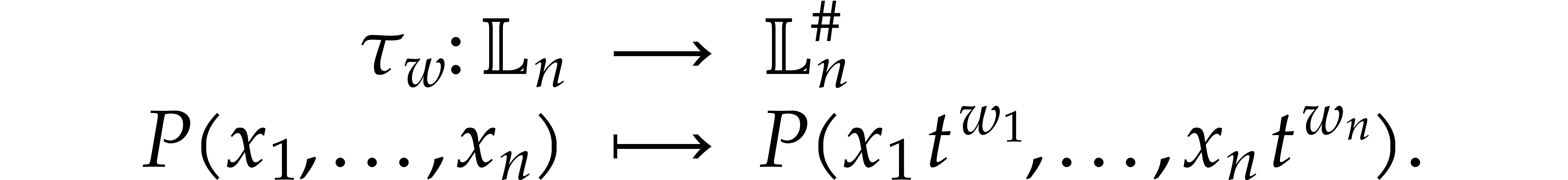 with
with  .
.
Laurent polynomials are only slightly more general than ordinary
polynomials and we already noted above that factoring in  is essentially the same problem as factoring in
is essentially the same problem as factoring in 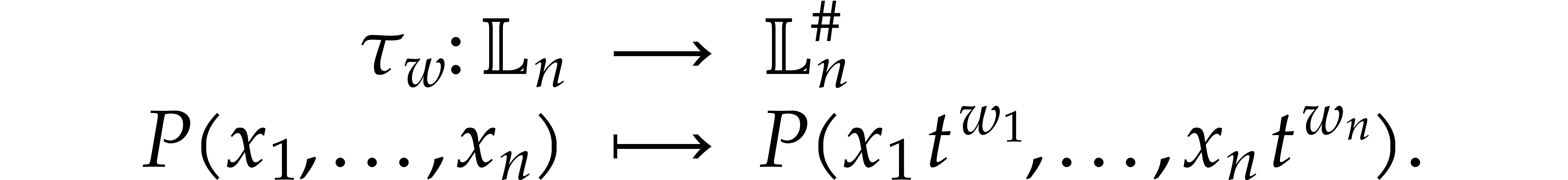 (and similarly for gcd computations). It is also
straightforward to adapt the definitions from Section 2.5
and most algorithms for sparse interpolation to this slightly more
general setting. The main advantage of Laurent polynomials is that they
are closed under monomial maps, which allows us to change the geometry
of the support of a polynomial without changing its properties with
respect to factorization.
(and similarly for gcd computations). It is also
straightforward to adapt the definitions from Section 2.5
and most algorithms for sparse interpolation to this slightly more
general setting. The main advantage of Laurent polynomials is that they
are closed under monomial maps, which allows us to change the geometry
of the support of a polynomial without changing its properties with
respect to factorization.
Let  be a non-zero weight vector and let
be a non-zero weight vector and let  . We define the
. We define the  -tagging map by
-tagging map by

This map is an injective monomial map. For any  , we have
, we have  ,
,
 ,
,  , and
, and  .
Divisibility and gcds are preserved as follows:
.
Divisibility and gcds are preserved as follows:
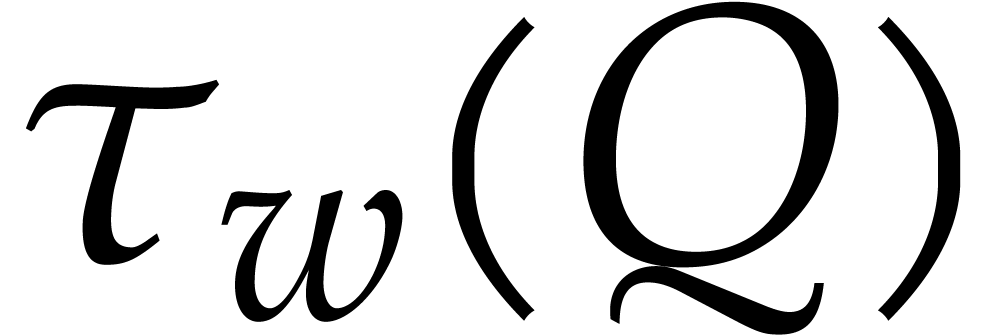 with
with  for
for 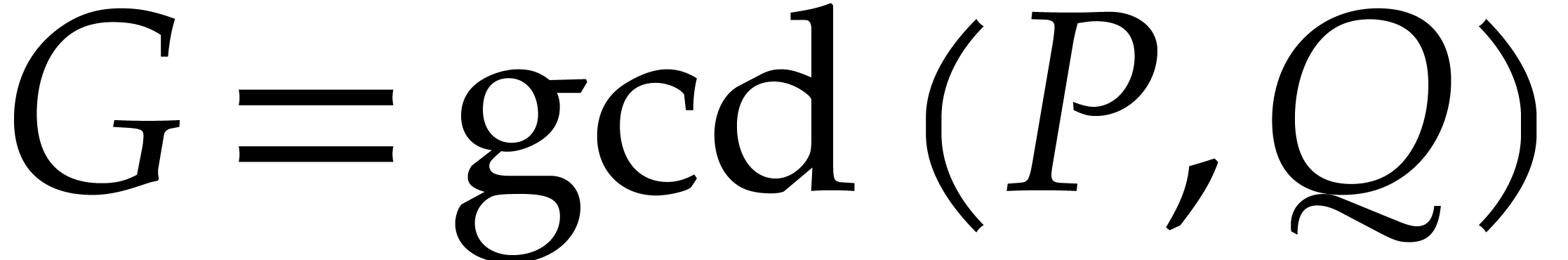 . Then
. Then
 divides
divides 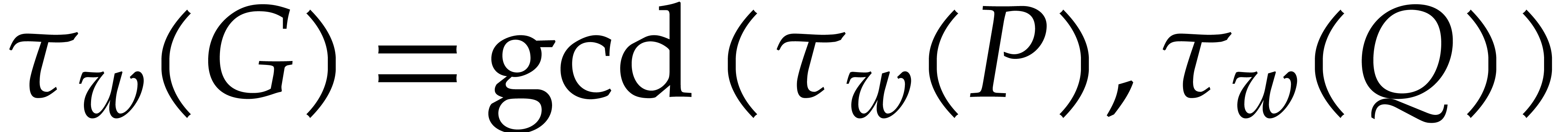 in
in  if and only if
if and only if 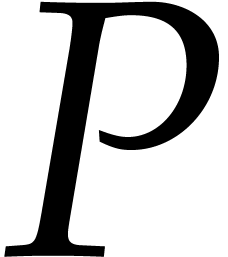 divides
divides  in
in  .
.
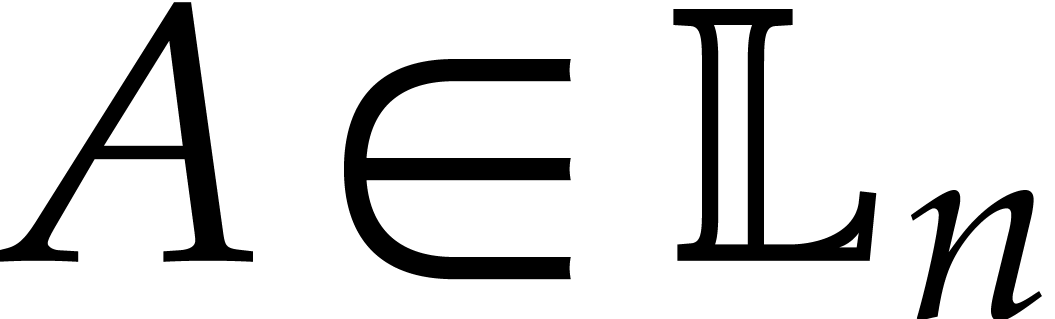 in
in  if and only
if
if and only
if 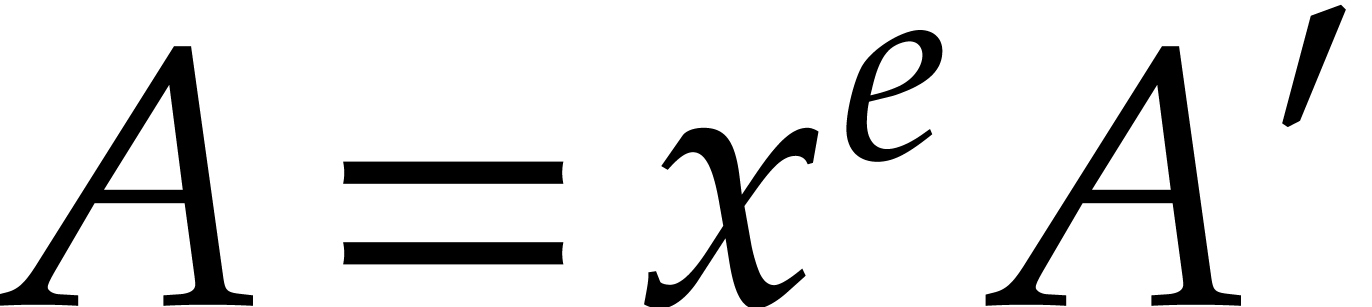 in
in  .
.
Proof. We claim that  divides
divides 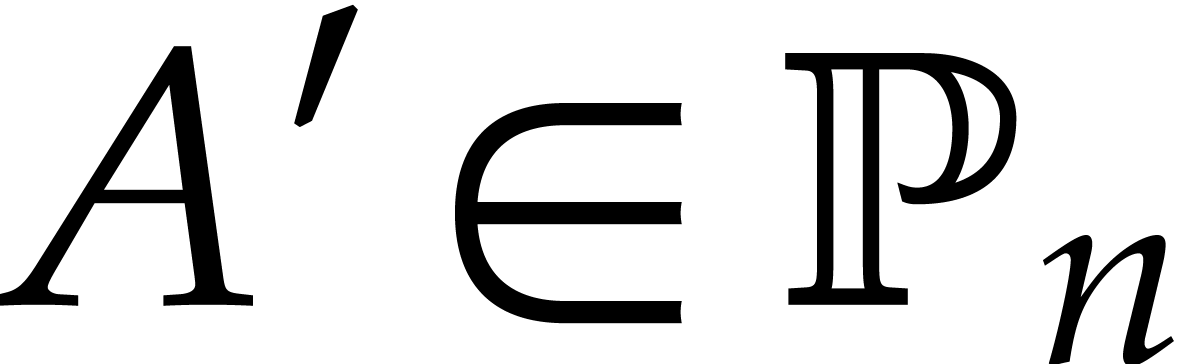 in
in  if and only
if
if and only
if  divides
divides 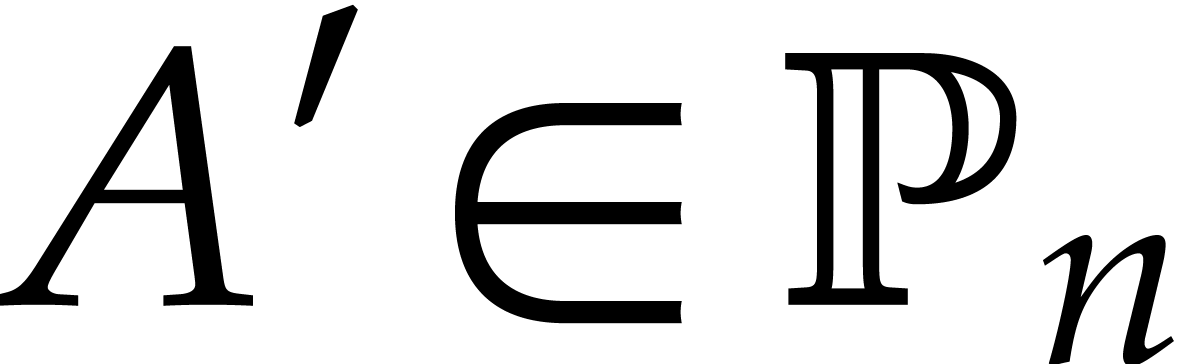 in
in 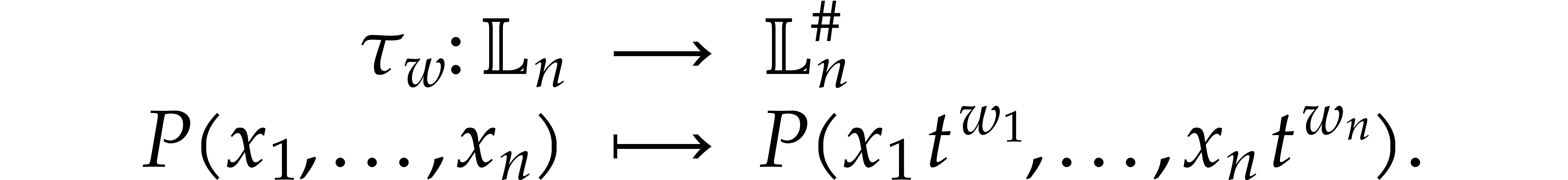 . One direction is clear. Assume
that
. One direction is clear. Assume
that  divides
divides 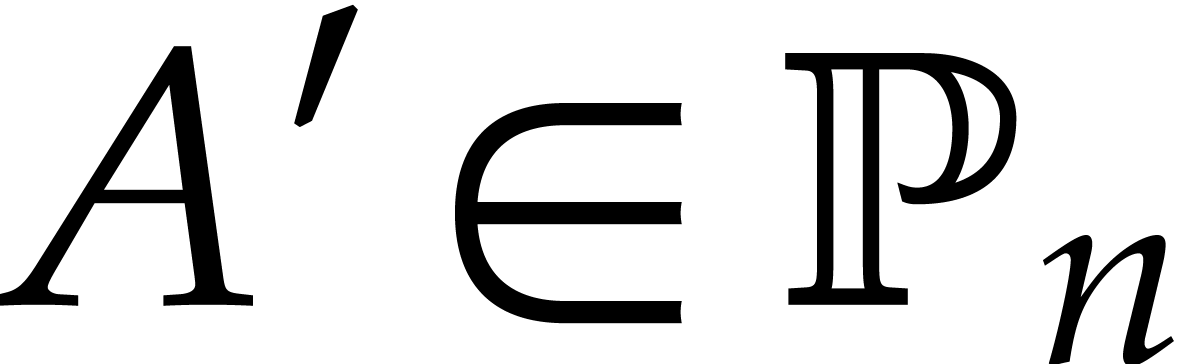 in
in 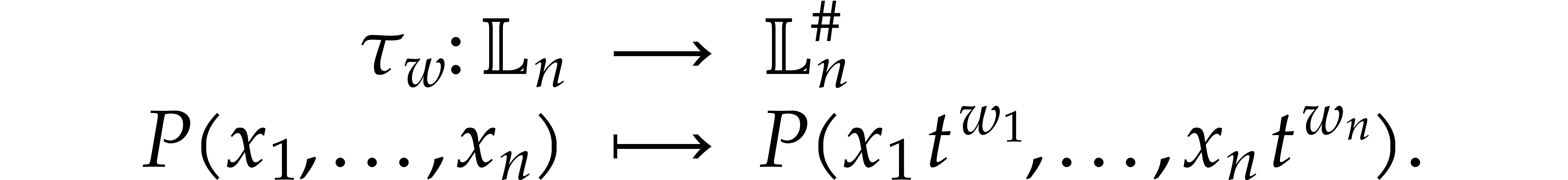 , so that
, so that  with
with  . We may uniquely write
. We may uniquely write
 with
with  and
and  such that
such that  for
for 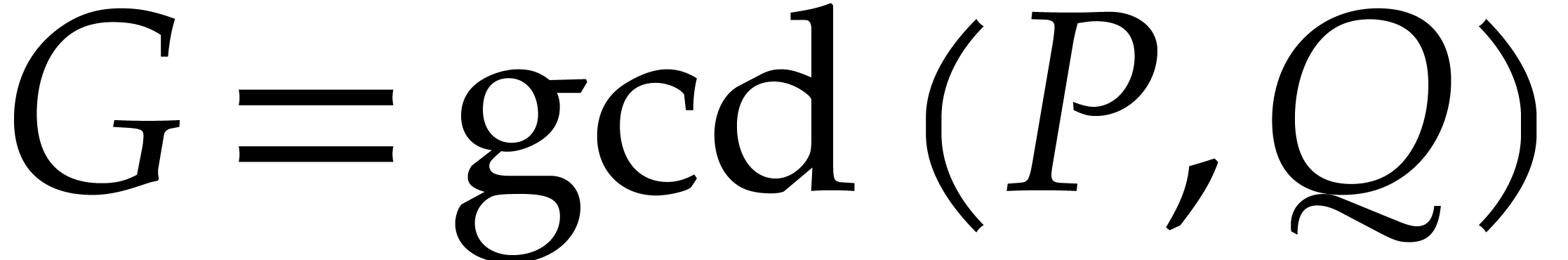 . Since
. Since  for
for 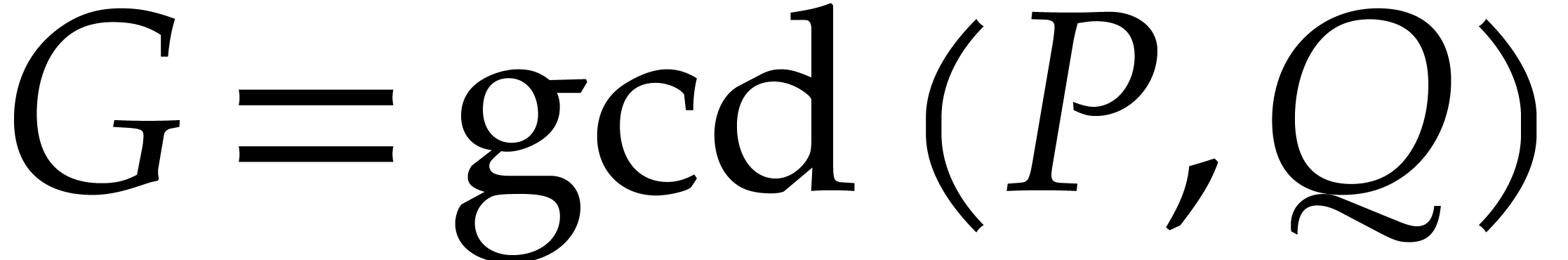 , it follows that
, it follows that 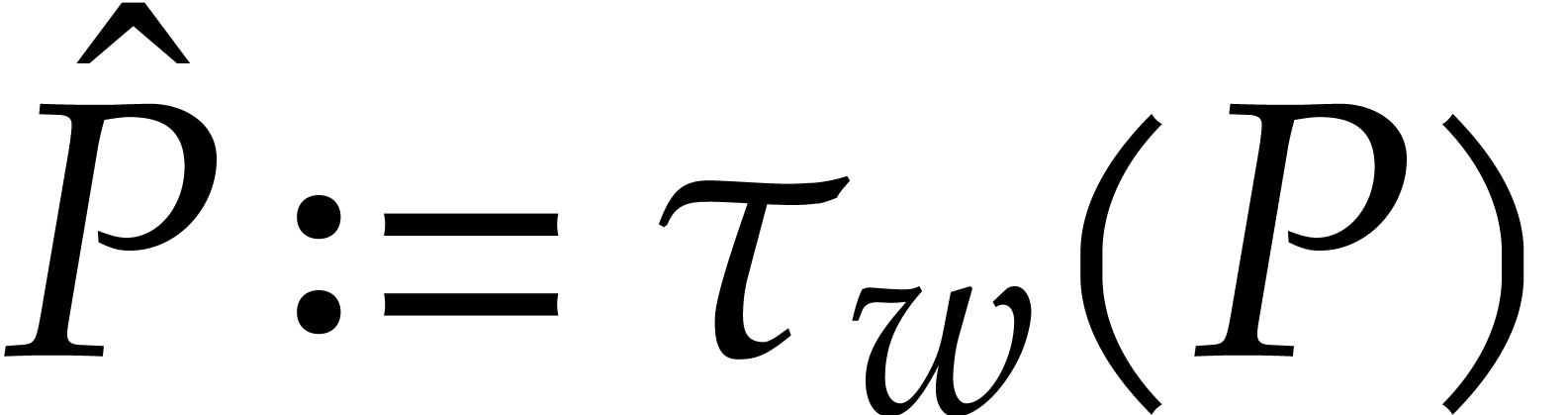 . Hence
. Hence  divides
divides 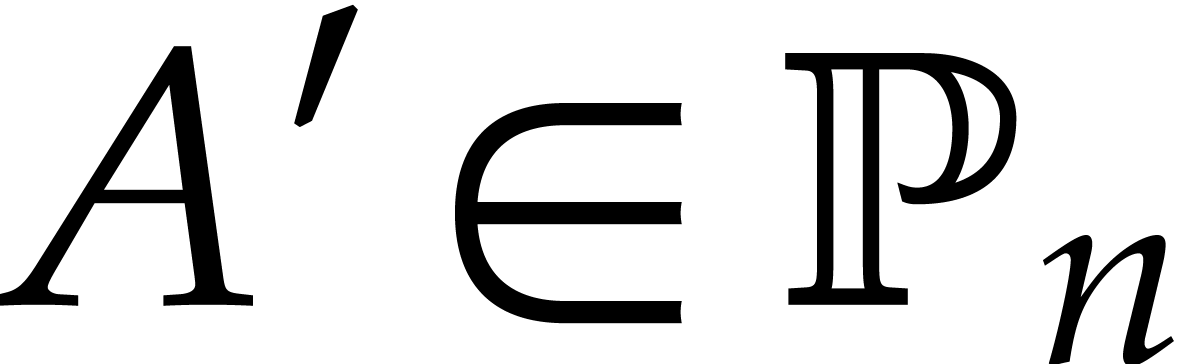 in
in  . Our
claim implies that
. Our
claim implies that  divides
divides 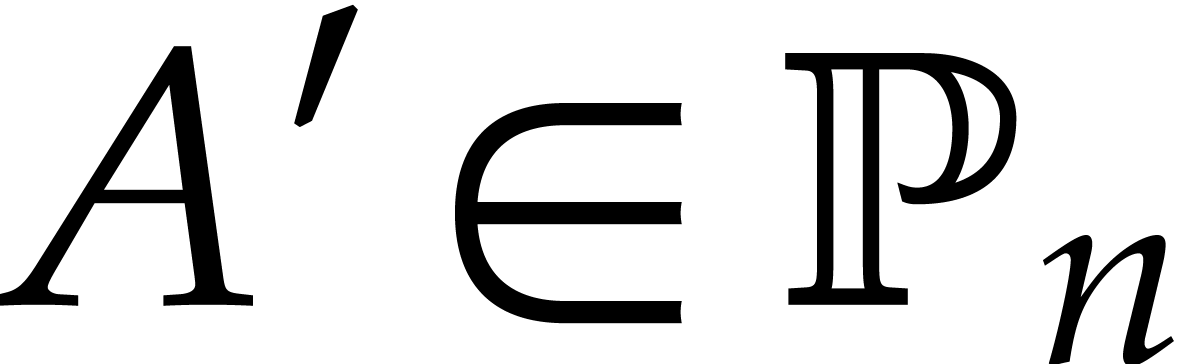 in
in  if and only if
if and only if  divides
divides 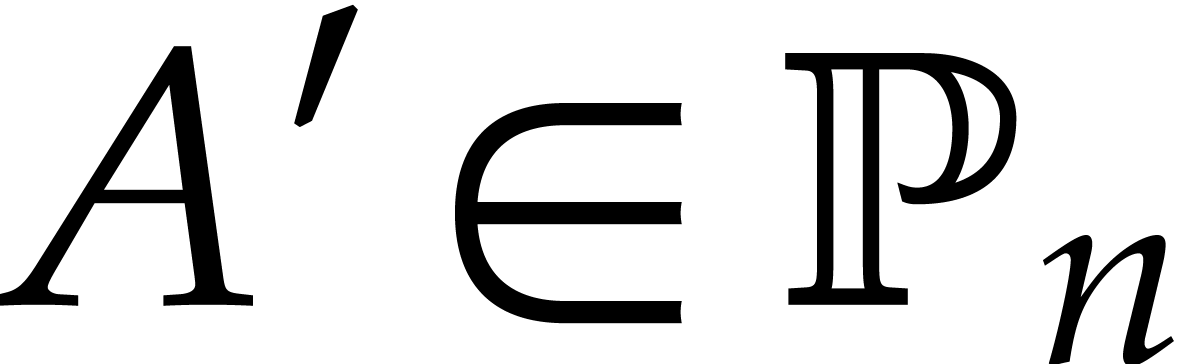 in
in  .
Now we may further extend
.
Now we may further extend  to a monomial
automorphism of
to a monomial
automorphism of  by sending
by sending 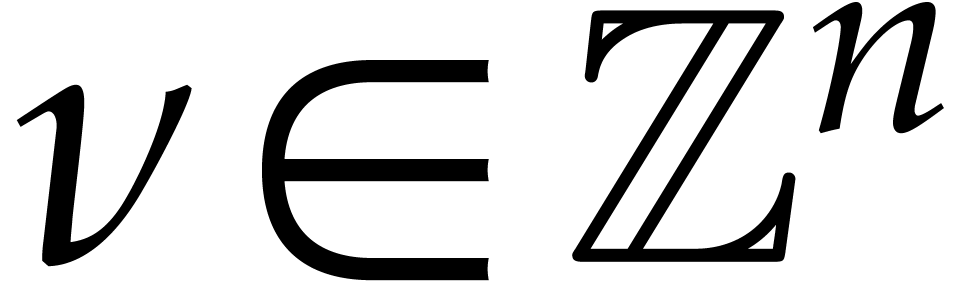 to itself. This yields (a). The second property is an easy
consequence.
to itself. This yields (a). The second property is an easy
consequence.
Given a  -regular polynomial
-regular polynomial
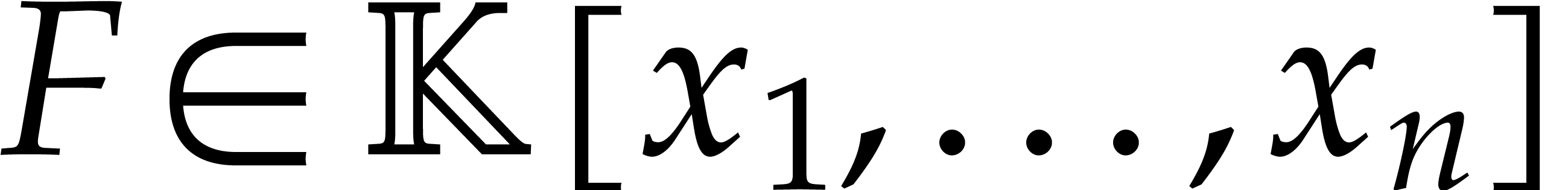 , we note that any divisor
, we note that any divisor
 must again be
must again be  -regular.
Hence, modulo multiplication with a suitable constant in
-regular.
Hence, modulo multiplication with a suitable constant in  , we may always normalize such a divisor to
become
, we may always normalize such a divisor to
become  -monic. In the setting
of Laurent polynomials, we may further multiply
-monic. In the setting
of Laurent polynomials, we may further multiply  by a monomial in
by a monomial in  such that
such that  . Similarly, when applying
. Similarly, when applying  , we can always normalize
, we can always normalize  to be monic as a Laurent polynomial in
to be monic as a Laurent polynomial in  by
considering
by
considering  .
.
Both for gcd computations and factorization, this raises the question of
how to find weights  for which a given non-zero
polynomial
for which a given non-zero
polynomial 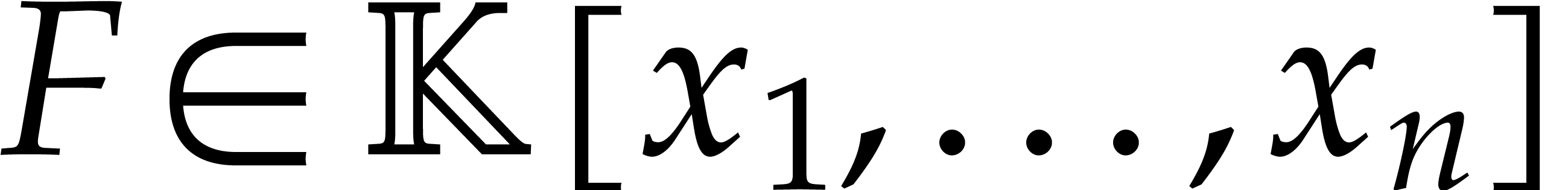 is
is  -regular.
In [51, Section 4.3], a way was described to compute such a
regularizing weight
-regular.
In [51, Section 4.3], a way was described to compute such a
regularizing weight  :
let
:
let 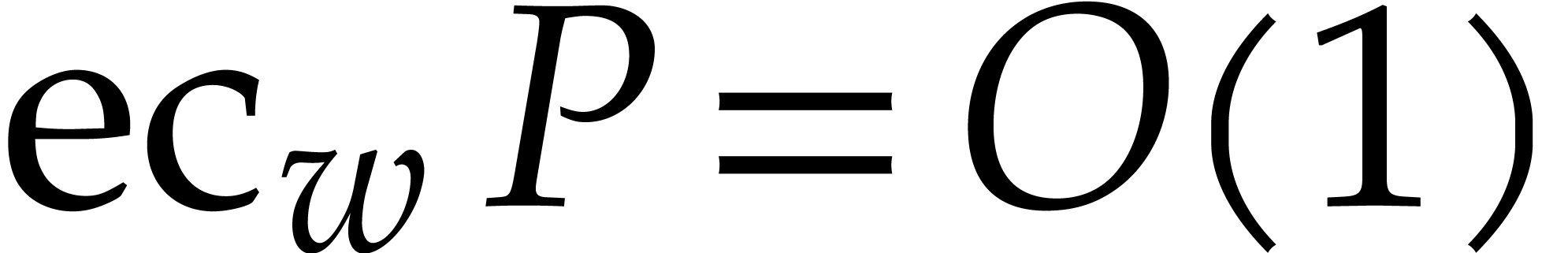 be such that
be such that 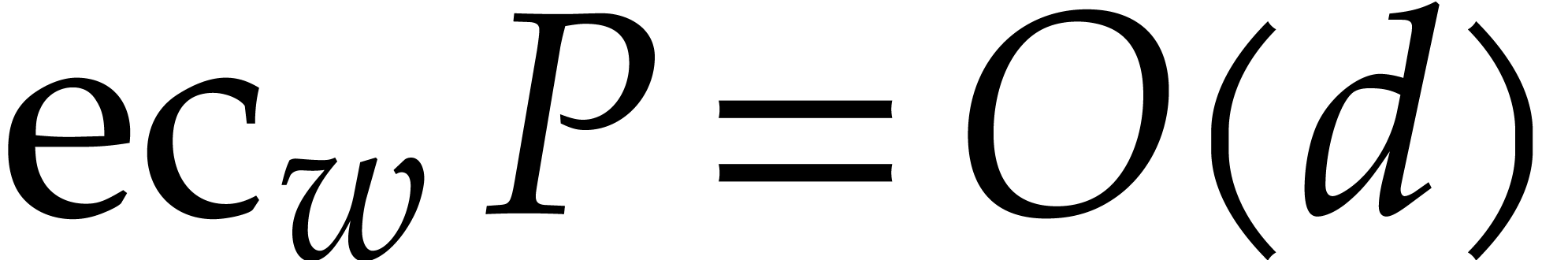 is
maximal. In that case, it suffices to take
is
maximal. In that case, it suffices to take 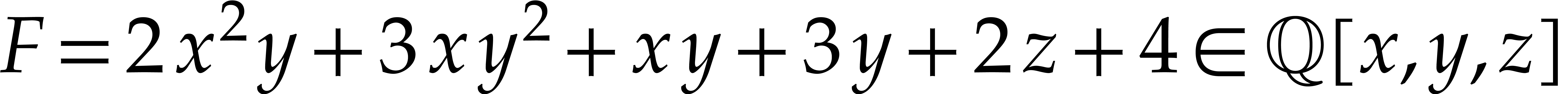 ,
and we note that
,
and we note that  , where
, where  is the total degree of
is the total degree of  .
For our applications in Sections 3.2 and 5 it
is often important to find a
.
For our applications in Sections 3.2 and 5 it
is often important to find a  for which
for which 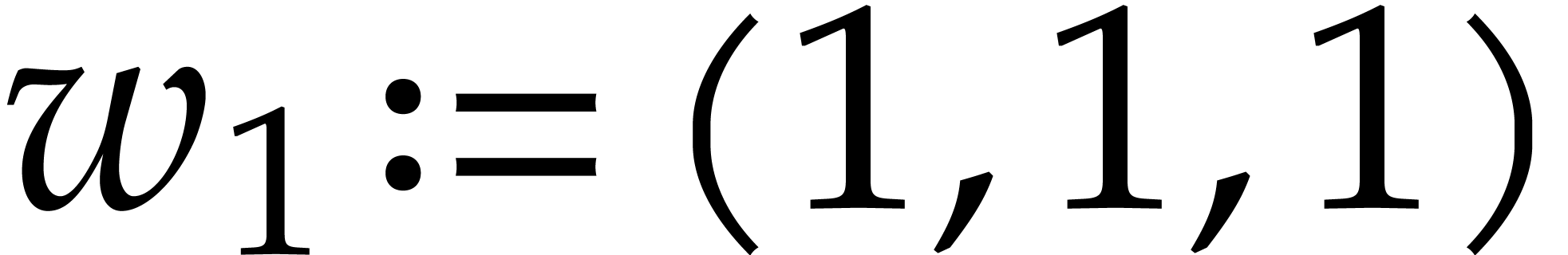 is small. By trying a few random weights with small
(possibly negative) entries, it is often possible to find a regularizing
weight
is small. By trying a few random weights with small
(possibly negative) entries, it is often possible to find a regularizing
weight  with
with 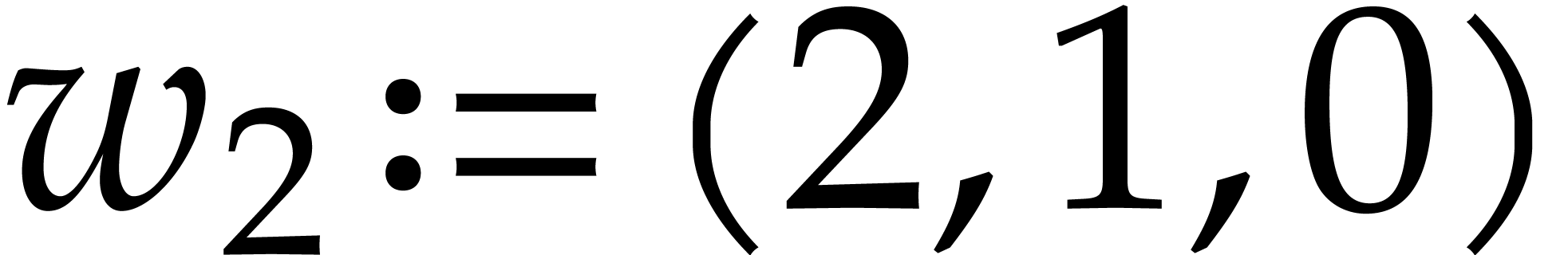 or
or 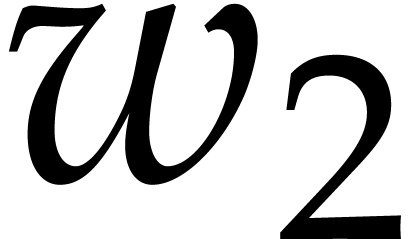 .
.
Example  . Then,
. Then,  is not
is not  -regular for the
natural weight
-regular for the
natural weight  . If we take
. If we take
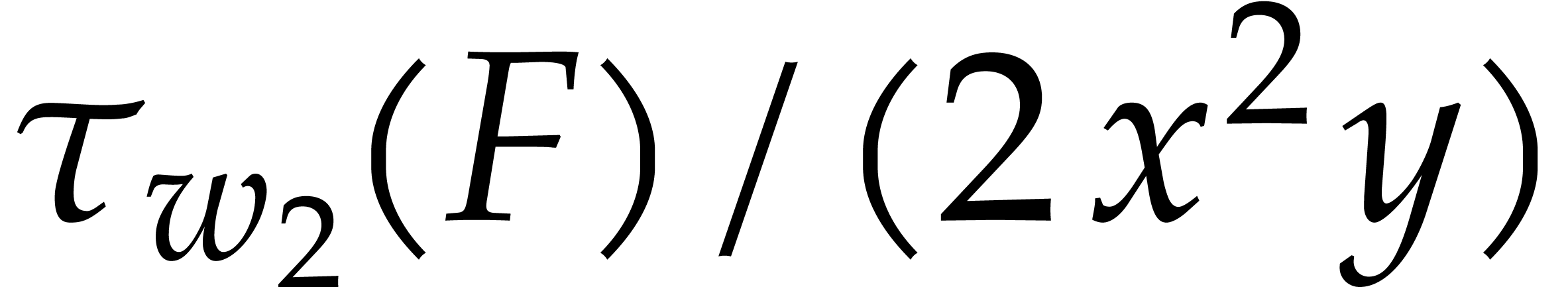 instead, then
instead, then  is
is 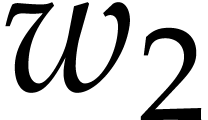 -regular with
-regular with 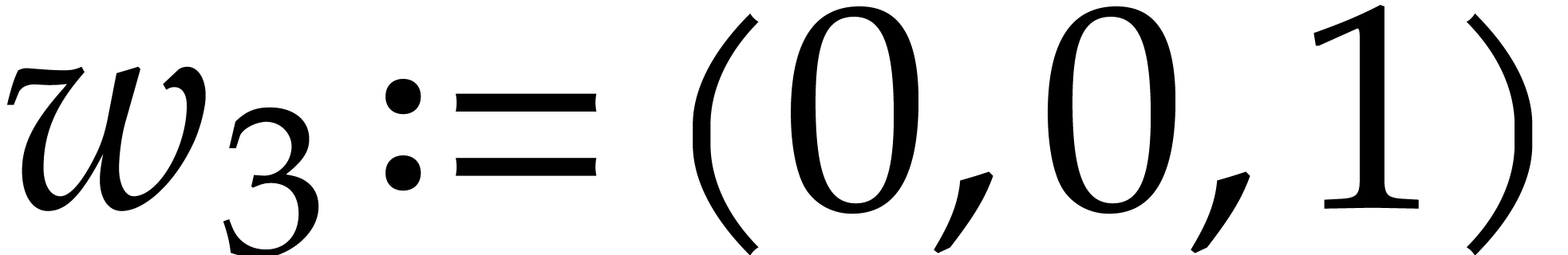 , and we arrive at
, and we arrive at

Furthermore,  can be normalized to be monic as a
Laurent polynomial in
can be normalized to be monic as a
Laurent polynomial in  by considering
by considering 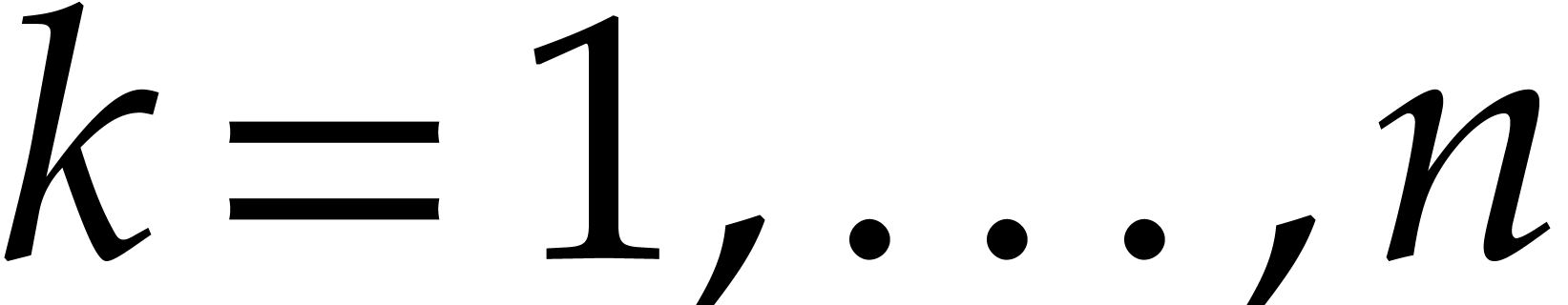 . Note that
. Note that 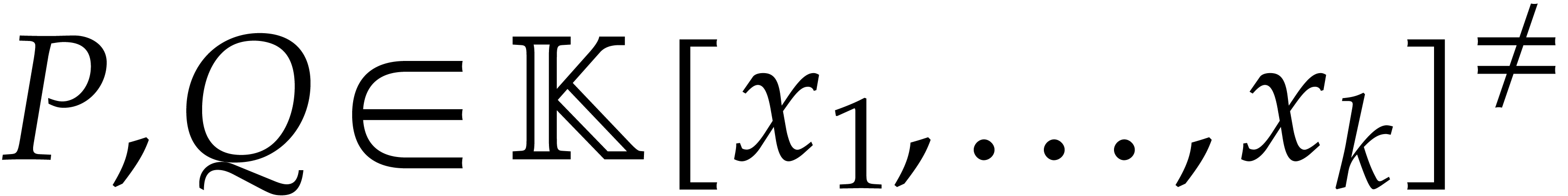 is also a regularizing weight for
is also a regularizing weight for  with
with 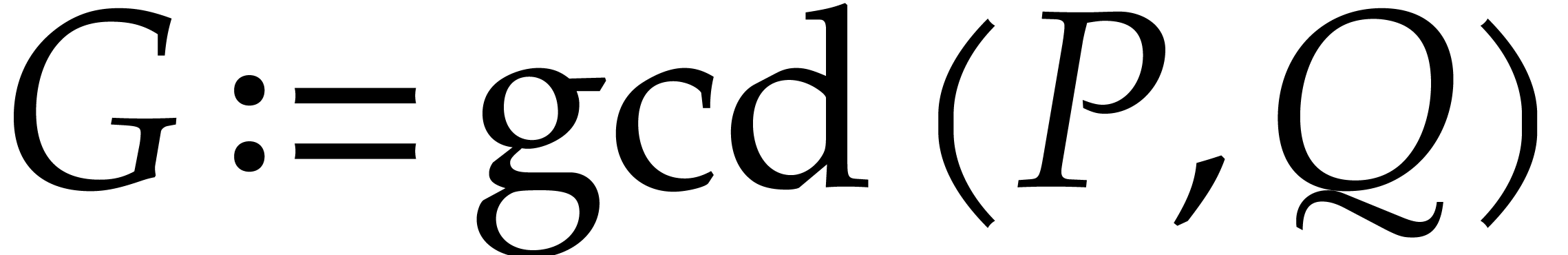 .
.
Before studying the factorization problem for multivariate polynomials, it is interesting to consider the easier problem of gcd computations. In this section we introduce two approaches for gcd computations that will also be useful later for factoring polynomials.
The first approach is iterative on the number of variables. It will be adapted to the factorization problem in Section 6. The second approach is more direct, but requires a regularizing weight (see Section 2.7). Square-free factorization can be accomplished using a similar technique, as we shall see in Section 5. The algorithms from Section 7 also draw some of their inspiration from this technique, but also rely on Newton polygons instead of regularizing weights.
Let 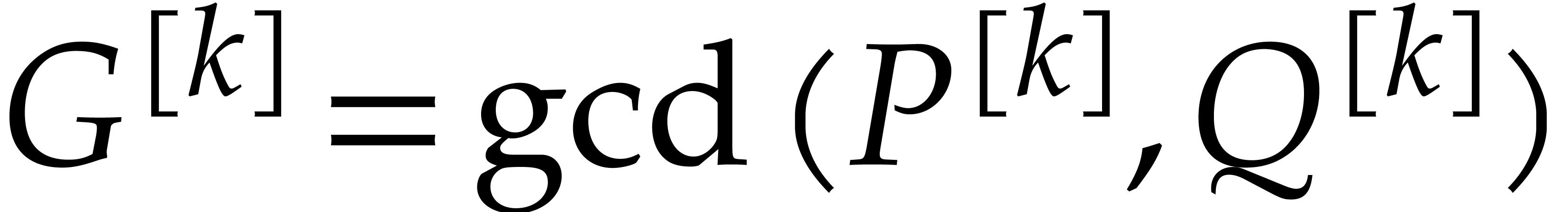 be random elements of
be random elements of  . For any
. For any  and
and  , we define
, we define
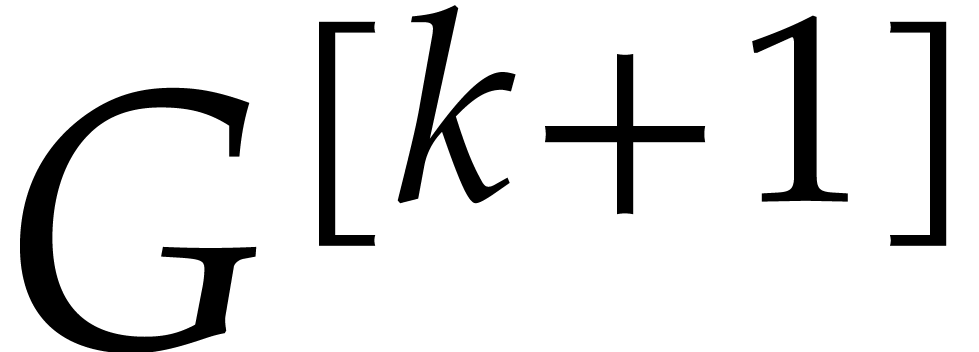
Let 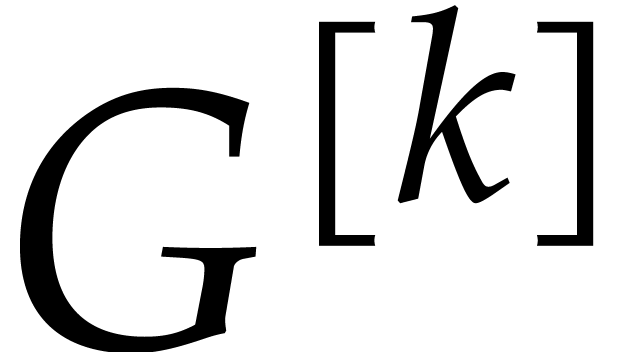 and
and  . As we will see below,
. As we will see below,  for
for  with high probability. We may easily compute
the univariate greatest common divisor
with high probability. We may easily compute
the univariate greatest common divisor  .
In this subsection, we shall describe an iterative algorithm to compute
.
In this subsection, we shall describe an iterative algorithm to compute
 from
from 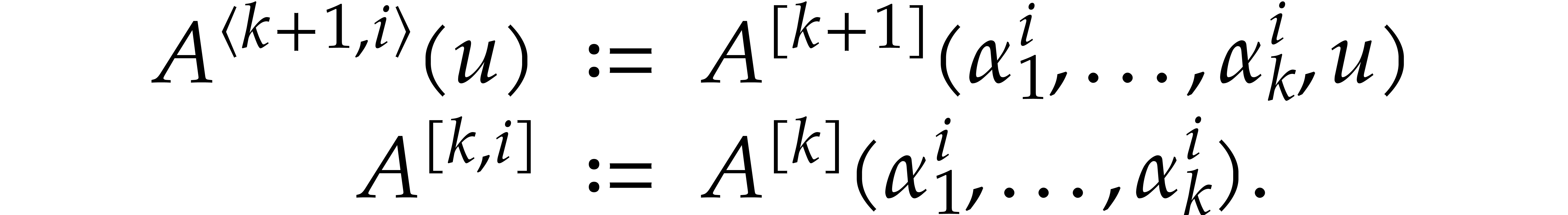 for
for  . Eventually, this yields
. Eventually, this yields  .
.
Let  be an admissible ratio or an FFT ratio. For
any
be an admissible ratio or an FFT ratio. For
any  and any
and any  ,
let
,
let

For any  , we have
, we have  with high probability. Now these greatest common divisors
are only defined up to non-zero scalar multiples in
with high probability. Now these greatest common divisors
are only defined up to non-zero scalar multiples in  . Nevertheless, there exists a unique greatest
common divisor
. Nevertheless, there exists a unique greatest
common divisor  of
of  and
and
 whose evaluation at
whose evaluation at  coincides with
coincides with 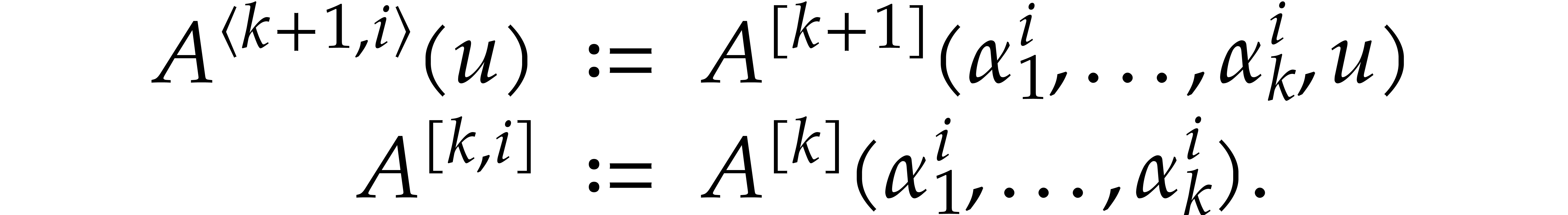 .
.
If 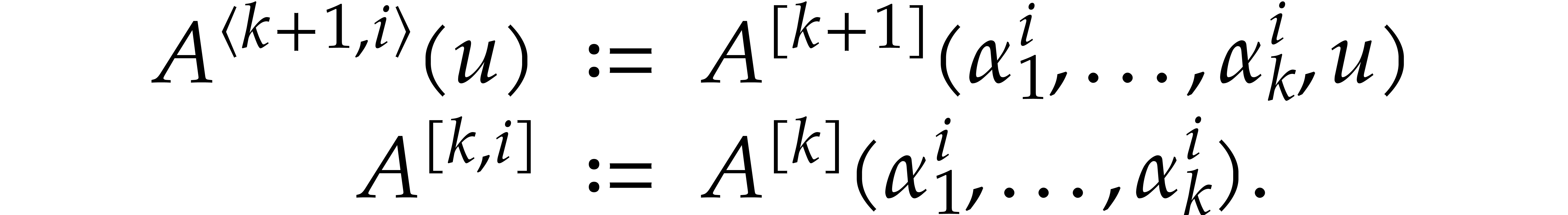 is known, then
is known, then 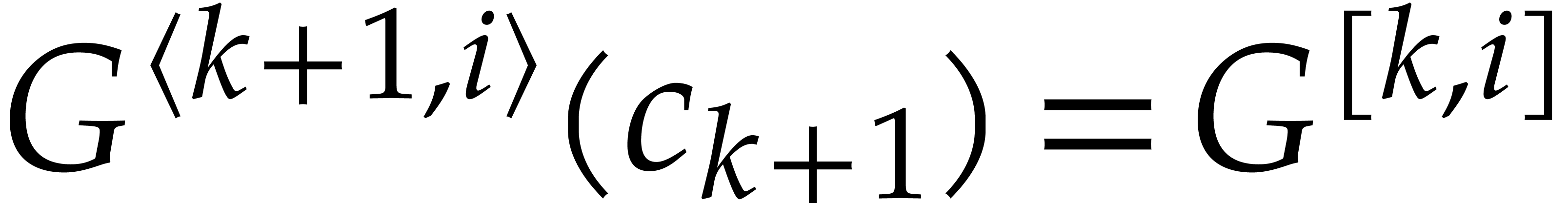 ,
,
 , and
, and  can be computed for successive
can be computed for successive  using fast
evaluation at geometric progressions. For any
using fast
evaluation at geometric progressions. For any  , we may then compute the univariate gcd
, we may then compute the univariate gcd  of
of  and
and  , under the normalization constraint that
, under the normalization constraint that  . It finally suffices to
interpolate
. It finally suffices to
interpolate  from sufficiently many
from sufficiently many  . This yields the following algorithm:
. This yields the following algorithm:
Algorithm
Output:  ,
such that
,
such that 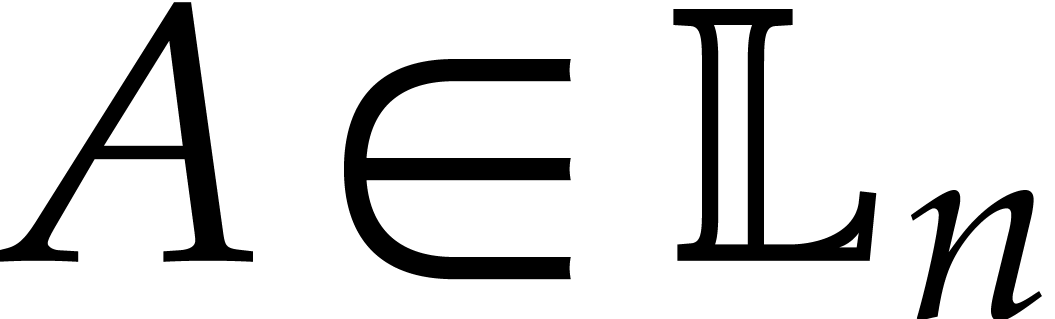
If  , then compute
, then compute 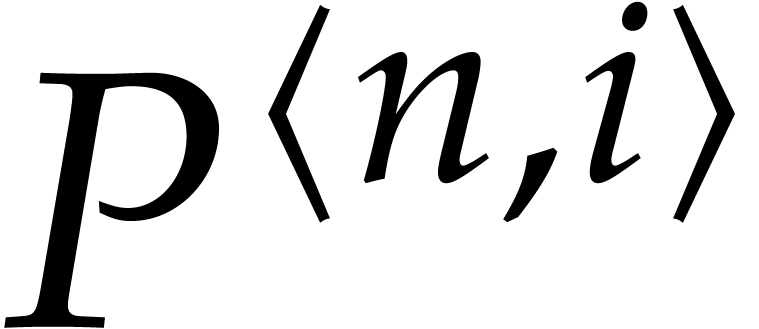 using a univariate algorithm and return it
using a univariate algorithm and return it
Compute 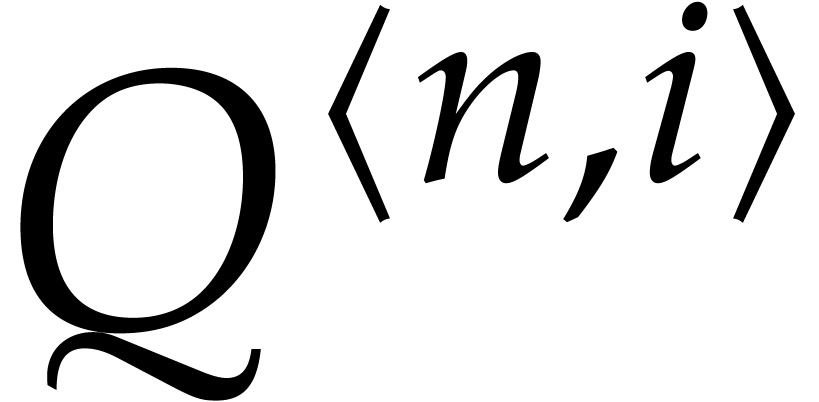 by recursively applying the algorithm
to
by recursively applying the algorithm
to  and
and 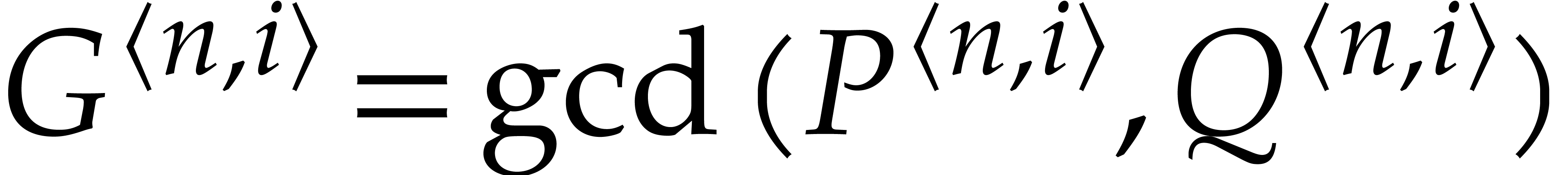
Let 
Compute  ,
,  ,
,  for
for 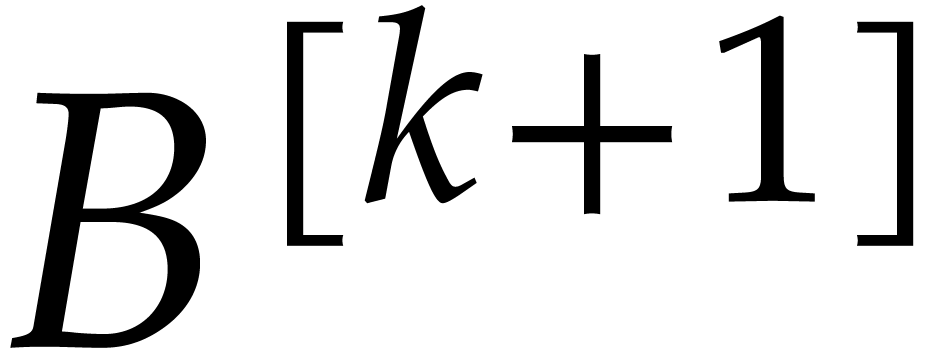 using sparse evaluation
using sparse evaluation
Compute 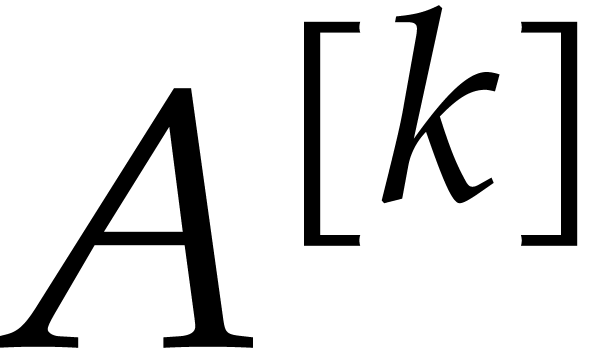 with
with 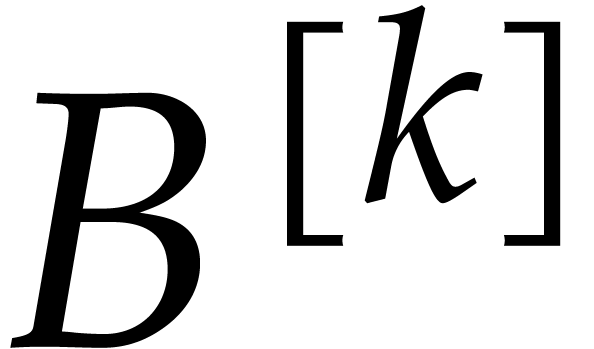 for
for 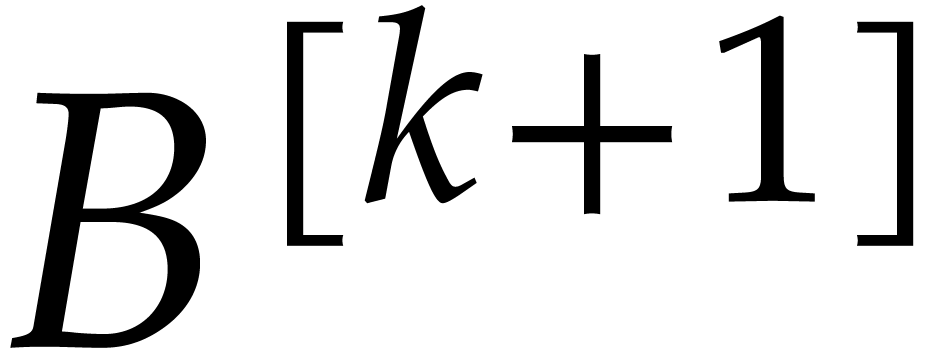
Recover  from
from 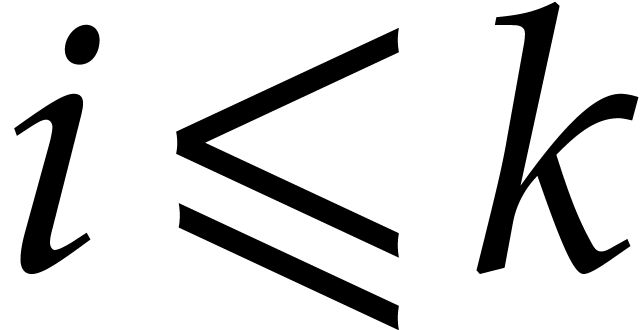 using
sparse interpolation
using
sparse interpolation
Return 
Before we analyze this algorithm, we will need a few probabilistic
lemmas. Assume that 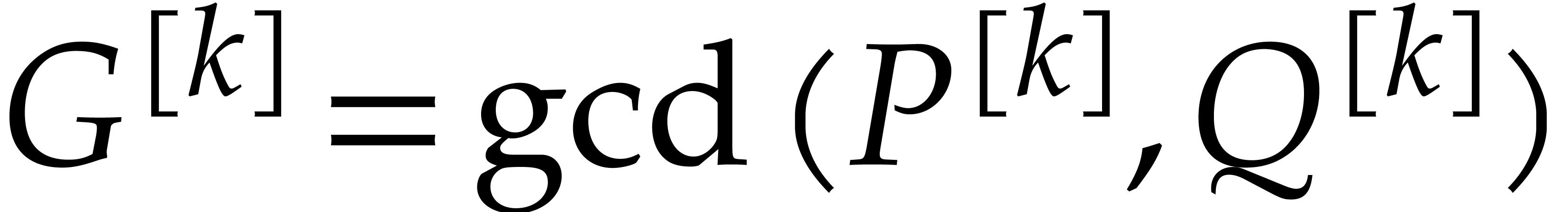 and
and  are independently chosen at random from a subset of
are independently chosen at random from a subset of 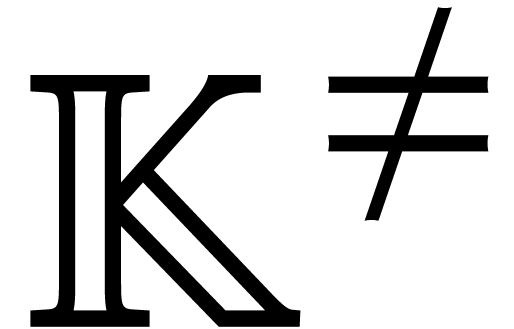 of size at least
of size at least  (if
(if  is
a small finite field, this forces us to move to a field extension).
is
a small finite field, this forces us to move to a field extension).
 be such that
be such that 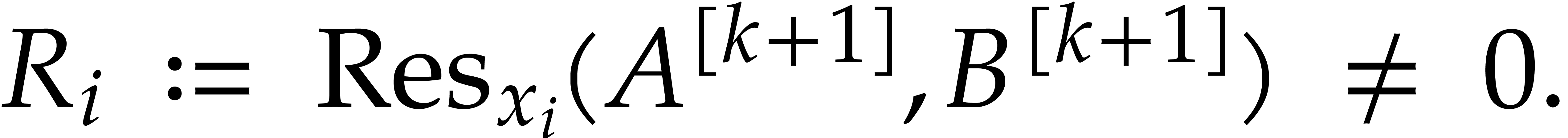 and
and 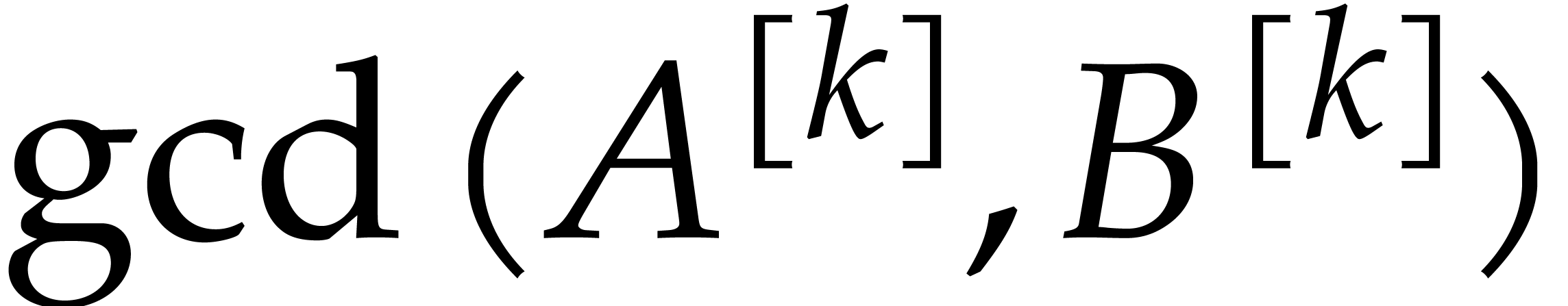 are coprime. Then the probability that
are coprime. Then the probability that
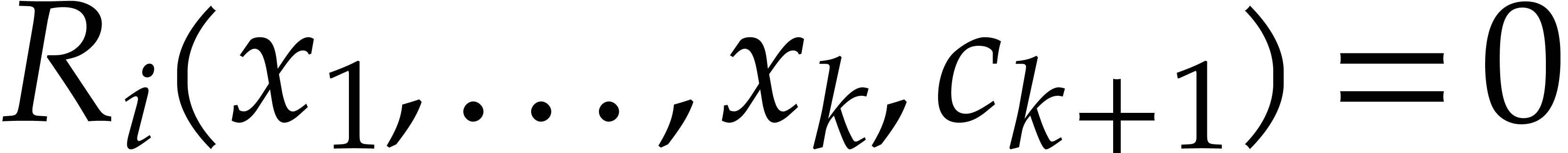 and
and  are not coprime is
bounded by
are not coprime is
bounded by  .
.
Proof. Let  with
with 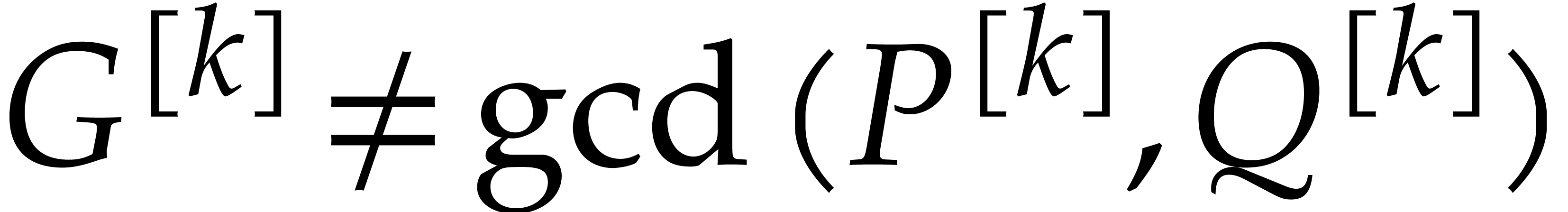 be a variable that occurs both in
be a variable that occurs both in 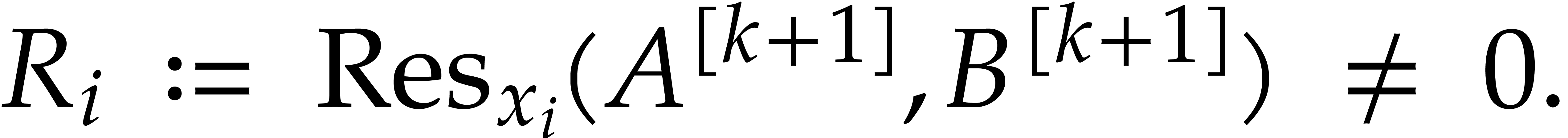 and in
and in 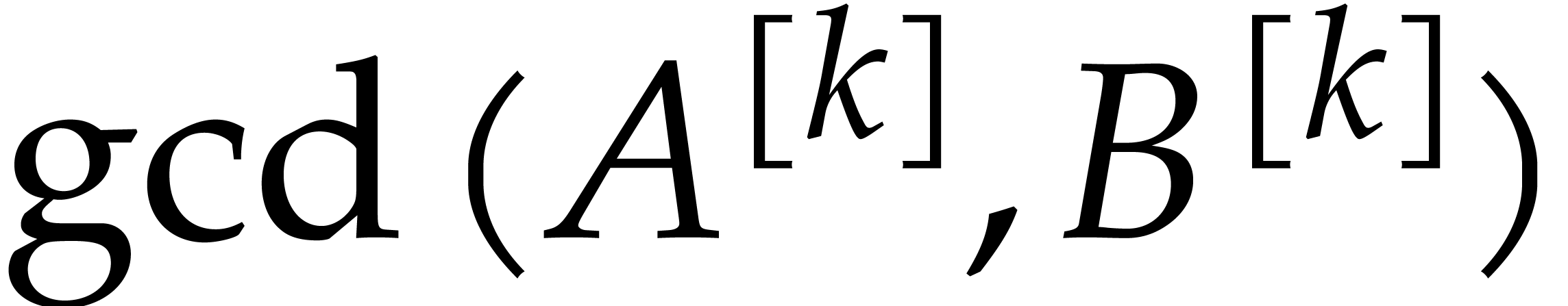 . Then
. Then
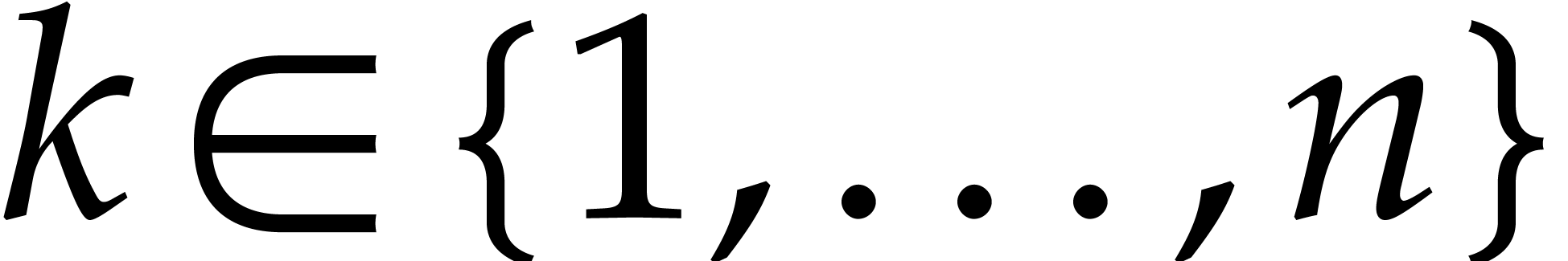
If  occurs in
occurs in  ,
then
,
then  , which can happen for
at most
, which can happen for
at most  values of
values of  .
.
Proof. Let us write 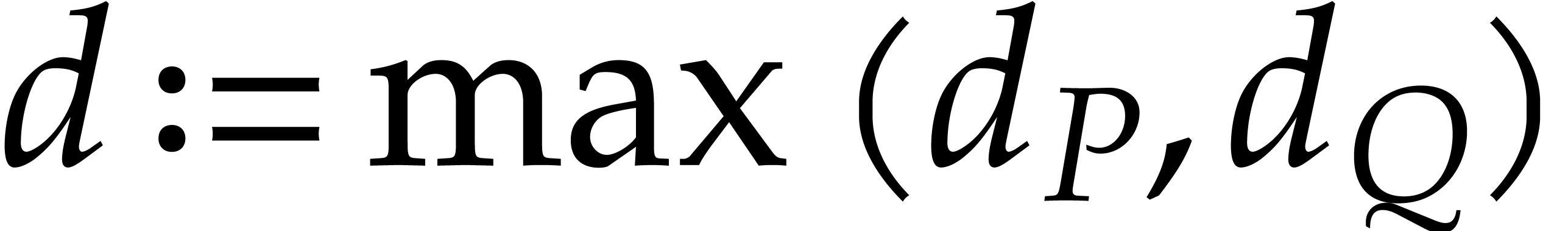 and
and
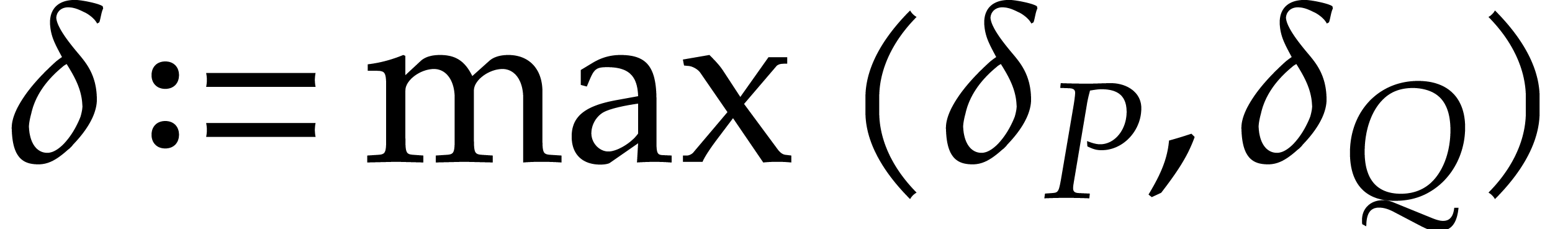 , where
, where 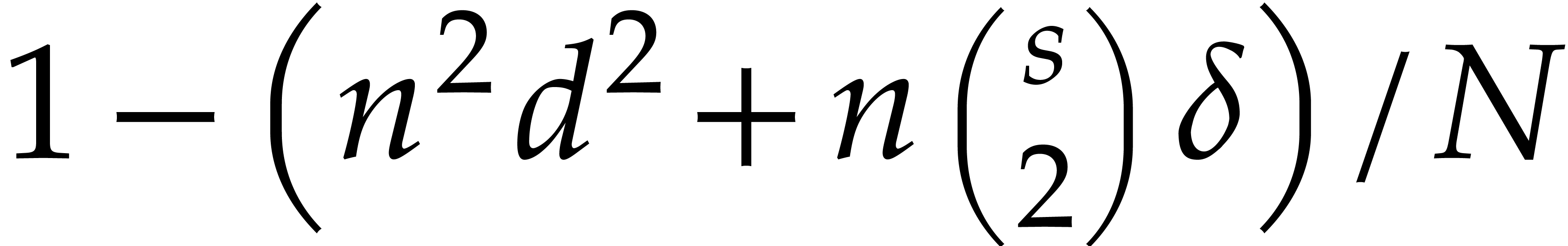 and
and 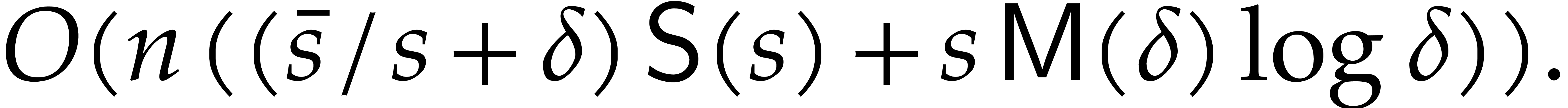 are coprime. Then we have
are coprime. Then we have  if and only if
if and only if 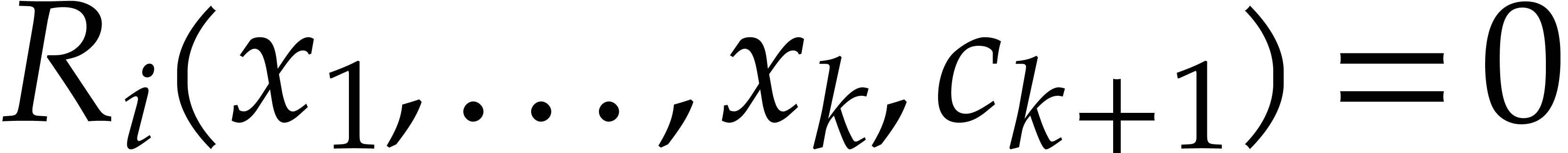 and
and  are
not coprime. The result now follows by applying the previous lemma for
are
not coprime. The result now follows by applying the previous lemma for
 .
.
 ,
,  ,
, 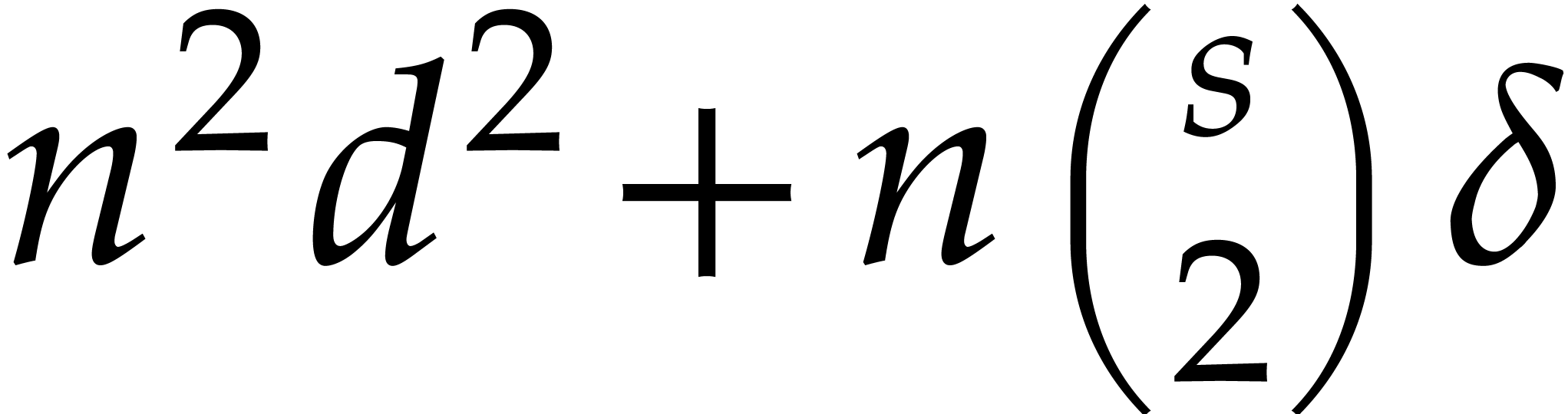 ,
and
,
and 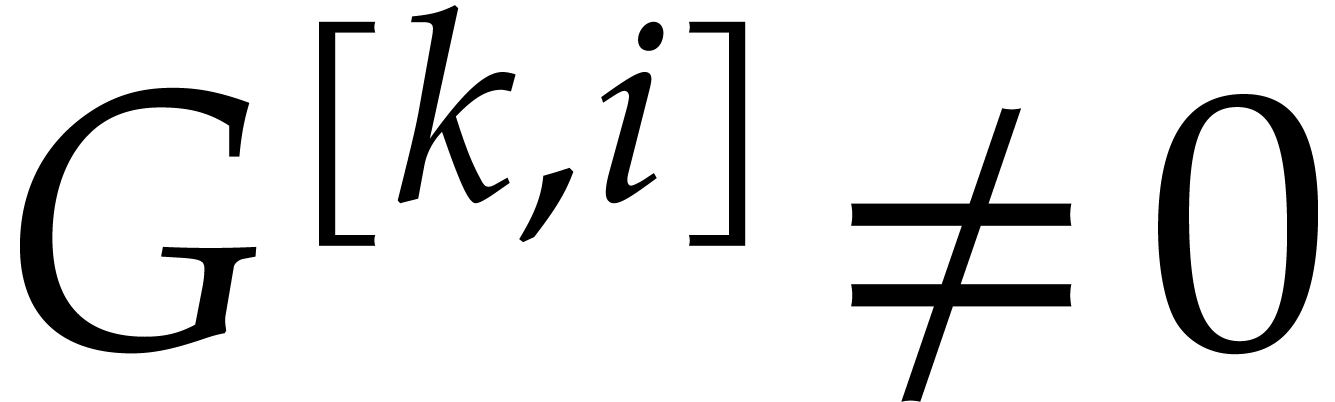 . Then Algorithm 3.1 is correct with probability at least
. Then Algorithm 3.1 is correct with probability at least  and it runs in time
and it runs in time

Remark. The probability bound implicitly assumes
that  , since the statement
becomes void for smaller
, since the statement
becomes void for smaller  . In
particular, we recall that this means that the cardinality of
. In
particular, we recall that this means that the cardinality of  should be at least
should be at least  .
.
Proof. Assuming that  and
and
 for
for 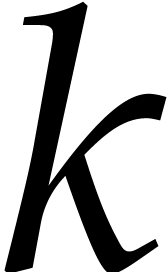 and
and 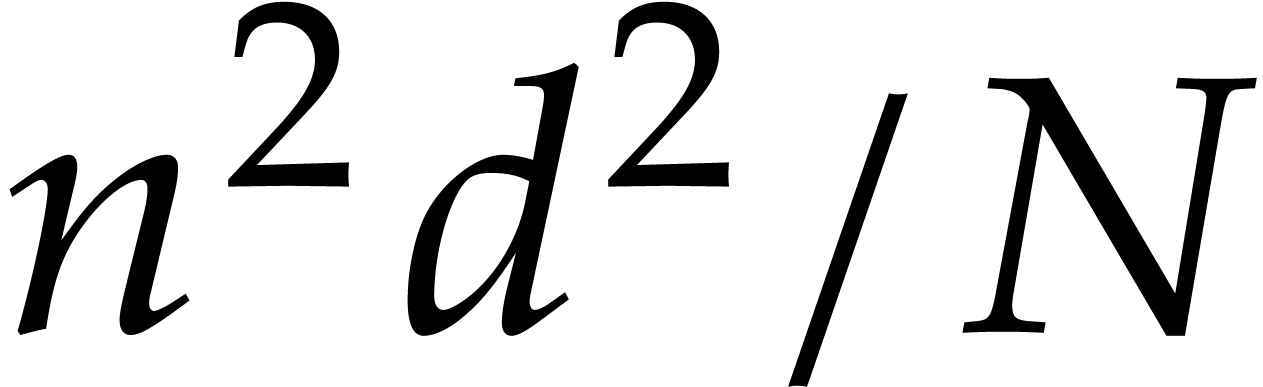 , let us prove that Algorithm 3.1
returns the correct answer. Indeed, these assumptions imply that
, let us prove that Algorithm 3.1
returns the correct answer. Indeed, these assumptions imply that  can be normalized such that
can be normalized such that  and that the unique such
and that the unique such  must coincide with
must coincide with
 . Now
. Now 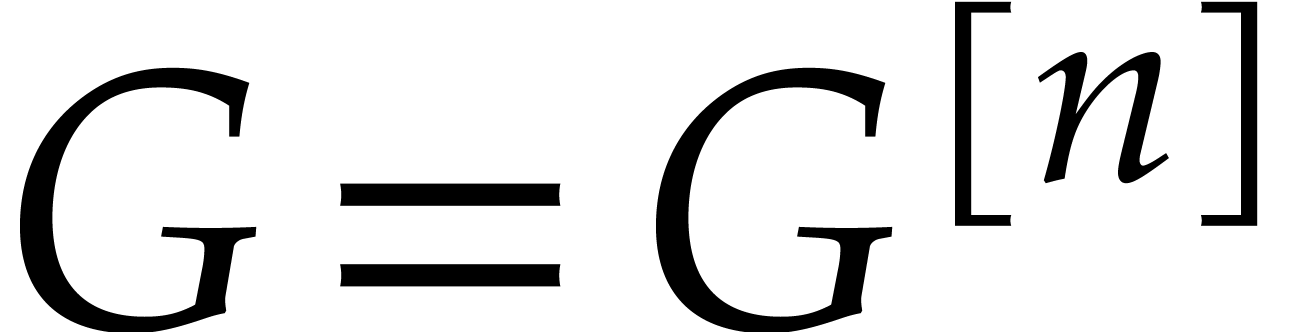 fails for some
fails for some  with probability at most
with probability at most  , by Lemma 3.2. Since
, by Lemma 3.2. Since
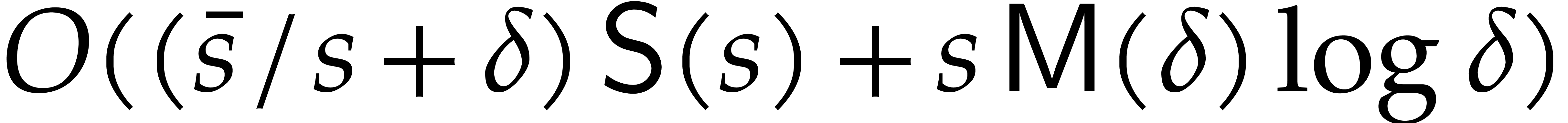 , the condition
, the condition 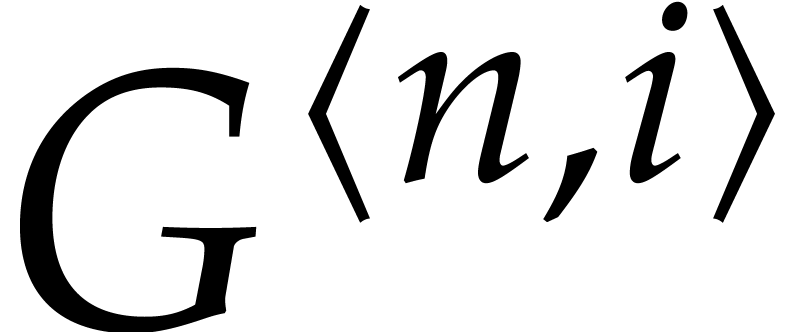 fails with probability at most
fails with probability at most 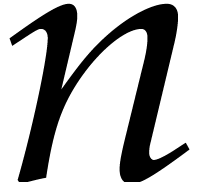 for
some
for
some  and
and  ,
by Corollary 2.2. This completes the probabilistic
correctness proof.
,
by Corollary 2.2. This completes the probabilistic
correctness proof.
As to the complexity, let us first ignore the cost of the recursive
call. Then the sparse evaluations of  ,
,
 , and
, and  can be done in time
can be done in time  : see
Section 2.4. The univariate gcd computations take
: see
Section 2.4. The univariate gcd computations take  operations. Finally, the recovery of
operations. Finally, the recovery of  using sparse interpolation can be done in time
using sparse interpolation can be done in time  . Altogether, the complexity without the recursive
calls is bounded by
. Altogether, the complexity without the recursive
calls is bounded by 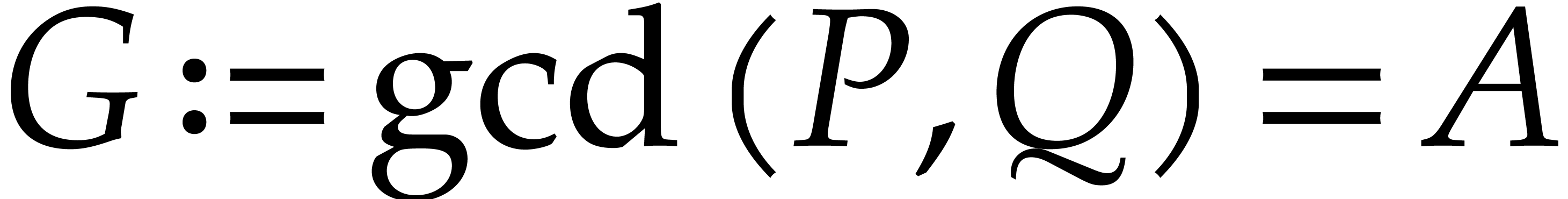 . We
conclude by observing that the degrees and numbers of terms of
. We
conclude by observing that the degrees and numbers of terms of  ,
, 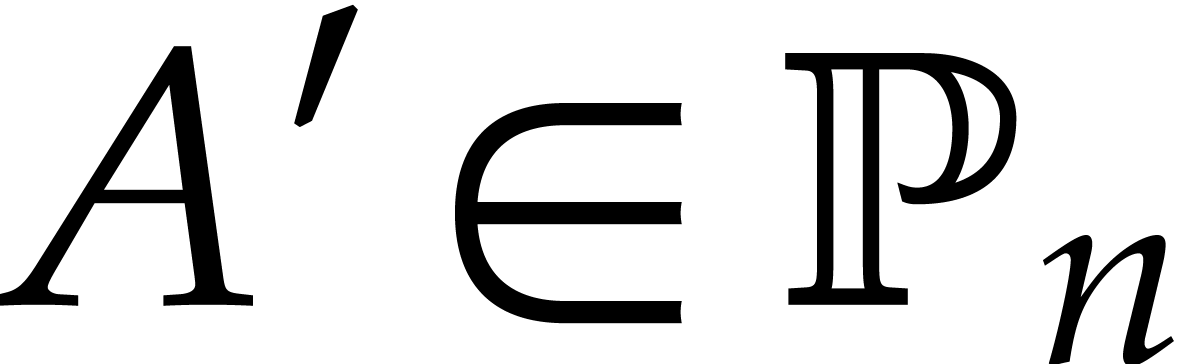 ,
and
,
and  can only decrease during recursive calls.
Since the recursive depth is
can only decrease during recursive calls.
Since the recursive depth is  ,
the complexity bound follows.
,
the complexity bound follows.
Remark  from
from 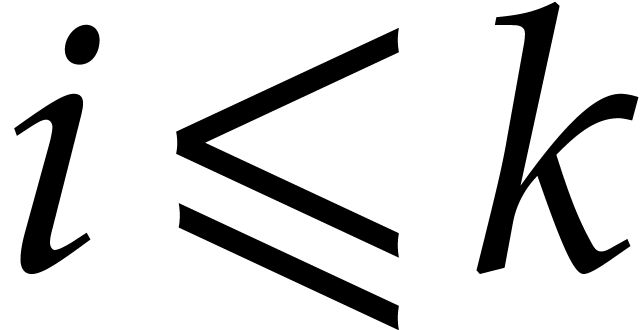 using
sparse interpolation, one may exploit the fact that the exponents of
using
sparse interpolation, one may exploit the fact that the exponents of
 in
in  are already known.
are already known.
Example 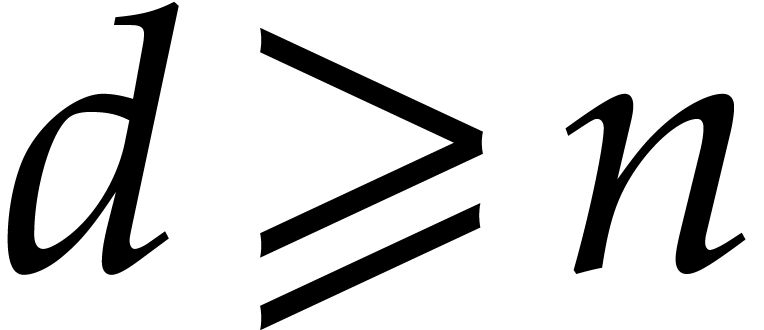 be random polynomials of total degree
be random polynomials of total degree  and consider
and consider  ,
, 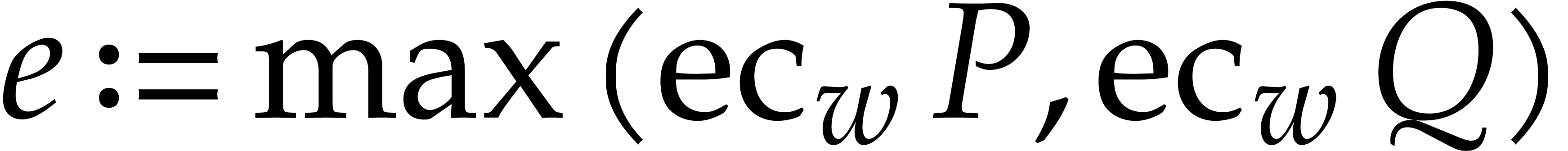 . With high probability,
. With high probability,  . Let us measure the overhead of recursive calls in
Algorithm 3.1 with respect to the number of variables
. Let us measure the overhead of recursive calls in
Algorithm 3.1 with respect to the number of variables  . With high probability, we have
. With high probability, we have
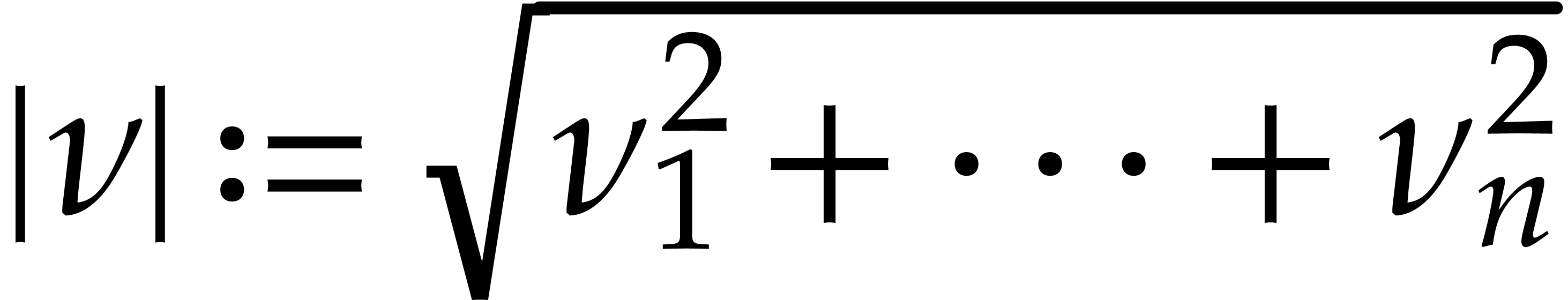
and

Assuming that  , it follows
that
, it follows
that
This shows that the sizes of the supports of the input and output polynomials in Algorithm 3.1 become at least twice as small at every recursive call. Consequently, the overall cost is at most twice the cost of the top-level call, roughly speaking.
Algorithm 3.1 has the disadvantage that the complexity
bound in Theorem 3.3 involves a factor  . Let us now present an alternative algorithm
that avoids this pitfall, but which may require a non-trivial monomial
change of variables. Our method is a variant of the algorithm from [51, Section 4.3].
. Let us now present an alternative algorithm
that avoids this pitfall, but which may require a non-trivial monomial
change of variables. Our method is a variant of the algorithm from [51, Section 4.3].
Given  , we first compute a
regularizing weight
, we first compute a
regularizing weight  for
for  or
or 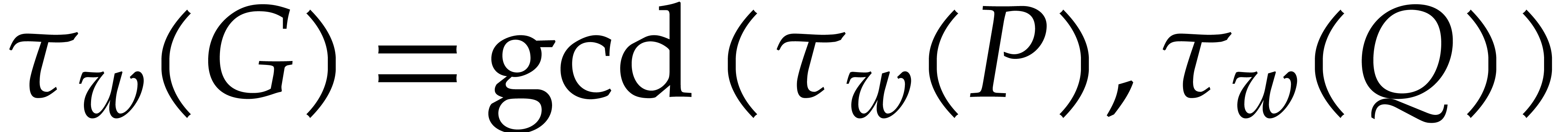 , for which
, for which 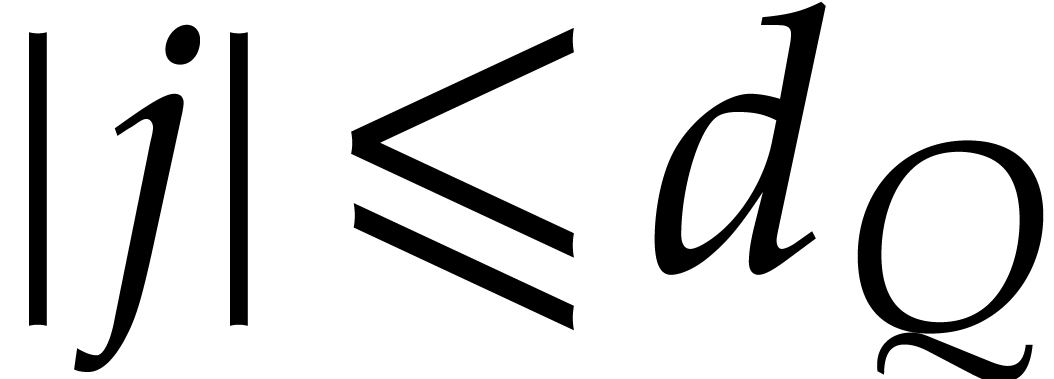 is as small as possible. From a practical point of view,
as explained in Section 2.7, we first try a few random
small weights
is as small as possible. From a practical point of view,
as explained in Section 2.7, we first try a few random
small weights  . If no
regularizing weight is found in this way, then we may always revert to
the following choice:
. If no
regularizing weight is found in this way, then we may always revert to
the following choice:
 , let
, let  . Let
. Let 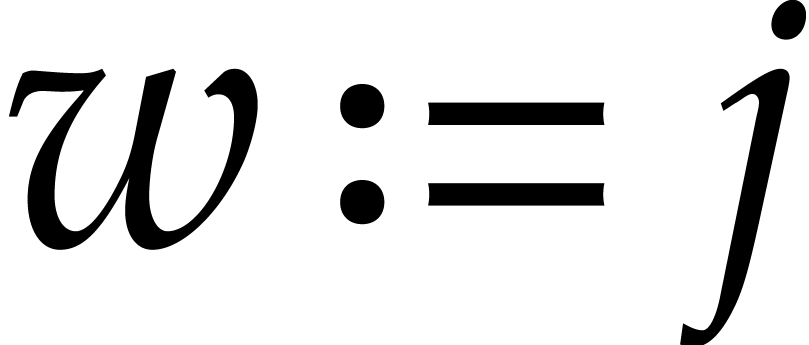 be such that
be such that
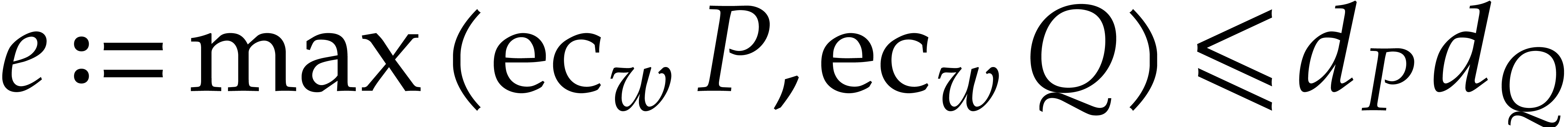 is maximal. Let
is maximal. Let 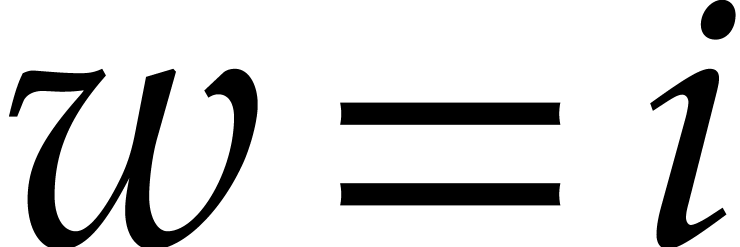 be
such that
be
such that  is maximal. Let
is maximal. Let 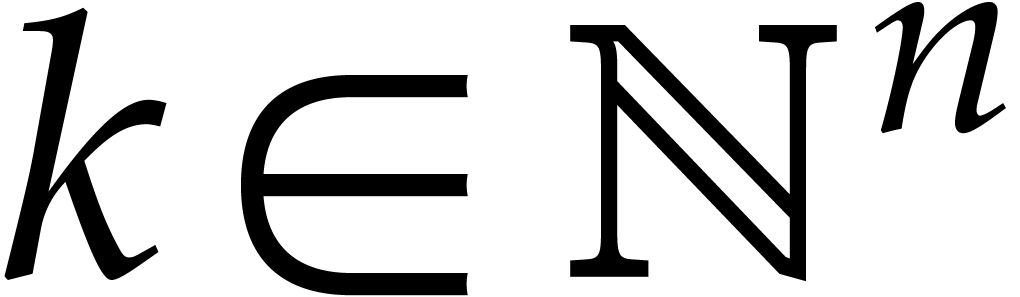 if
if 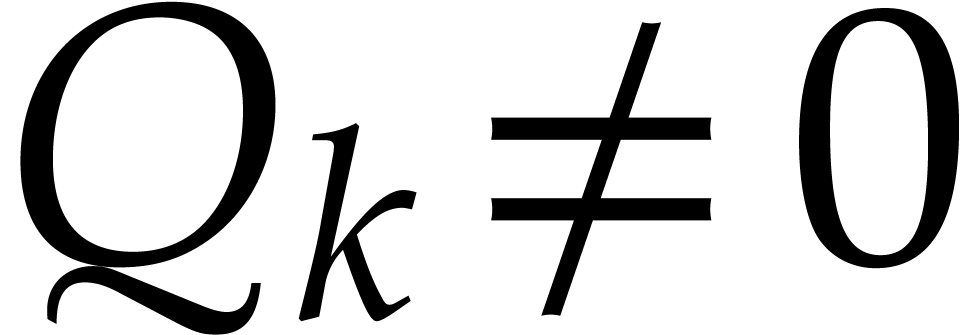 and
and  otherwise. Then
otherwise. Then
 .
.
Proof. Assume that  . Then
. Then  for any
for any  with
with  . The case
when
. The case
when  is handled similarly.
is handled similarly.
Now consider  ,
,  , and
, and  in
in 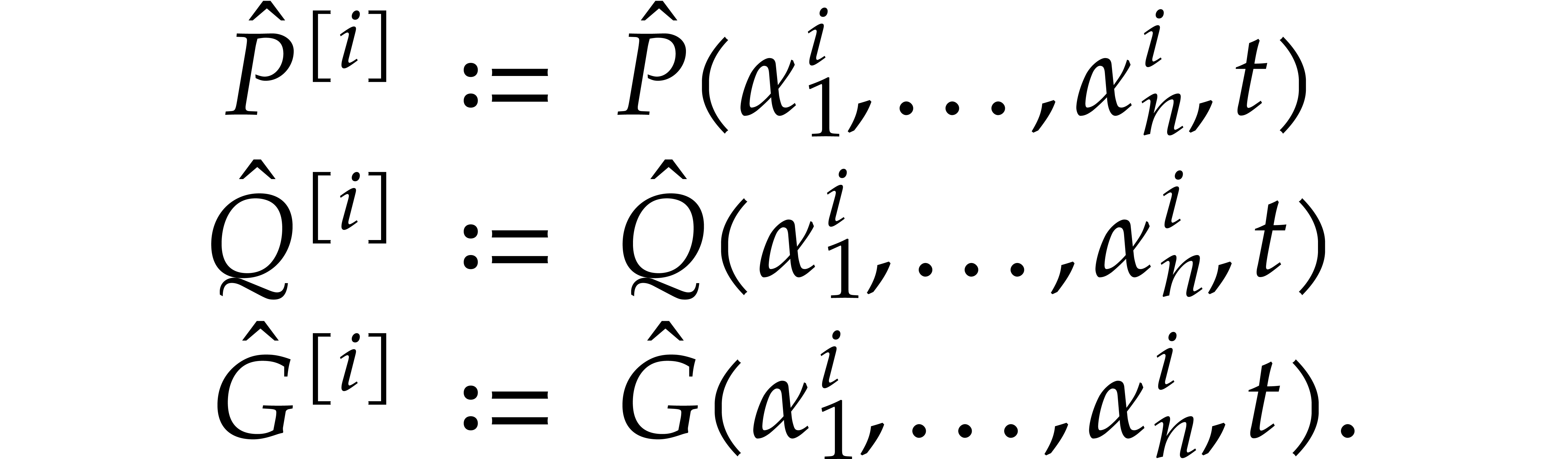 . We normalize
. We normalize  in such
a way that
in such
a way that  and such that
and such that  is monic as a polynomial in
is monic as a polynomial in  ;
this is always possible since
;
this is always possible since 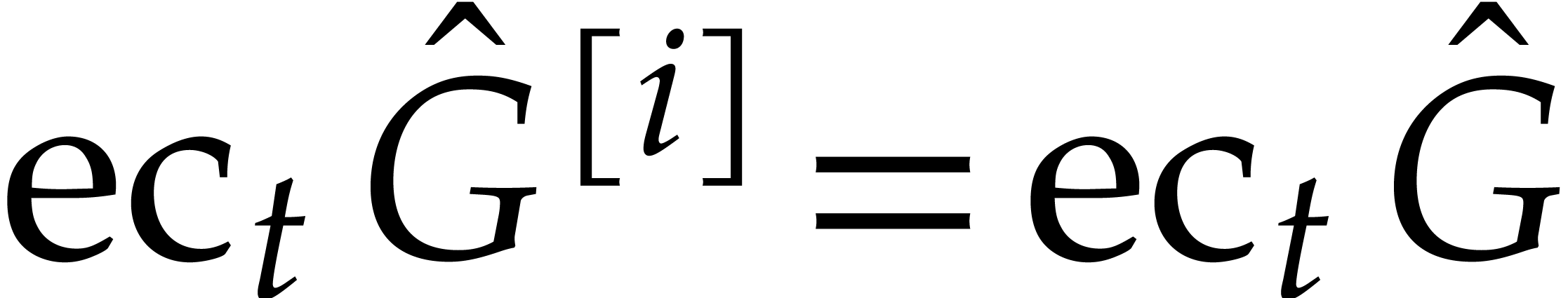 is
is  -regular. Let
-regular. Let 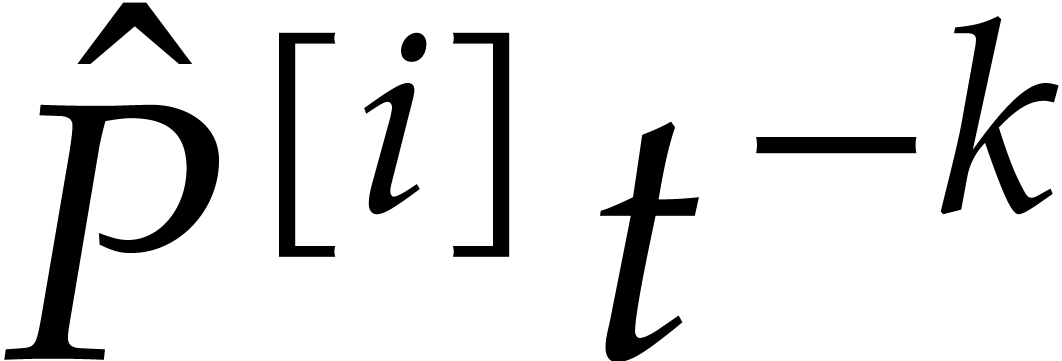 be an
admissible ratio or an FFT ratio. For any
be an
admissible ratio or an FFT ratio. For any  ,
we evaluate at
,
we evaluate at 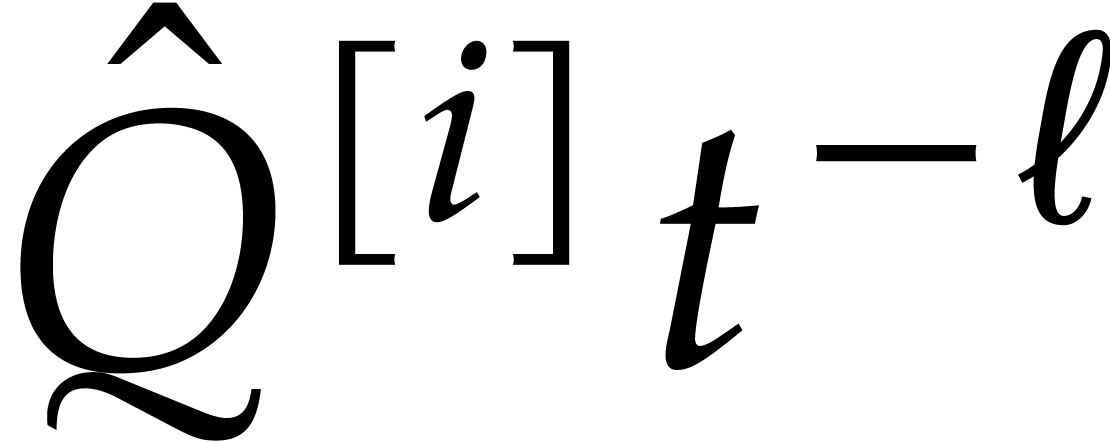 and
and  ,
which leads us to define the univariate polynomials
,
which leads us to define the univariate polynomials
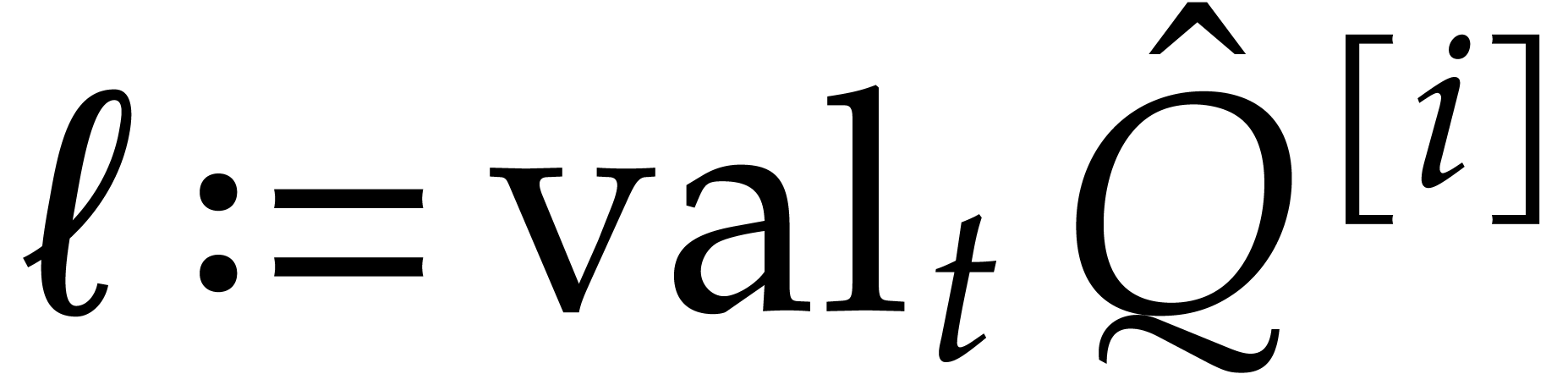
With high probability,  , and
, and
 is the monic gcd of
is the monic gcd of  and
and
 , where
, where 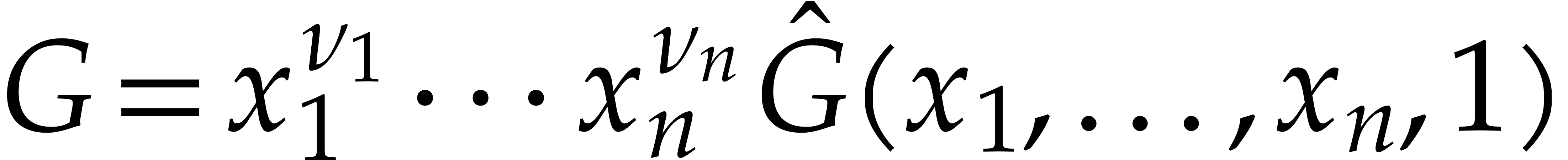 and
and  . For sufficiently large
. For sufficiently large
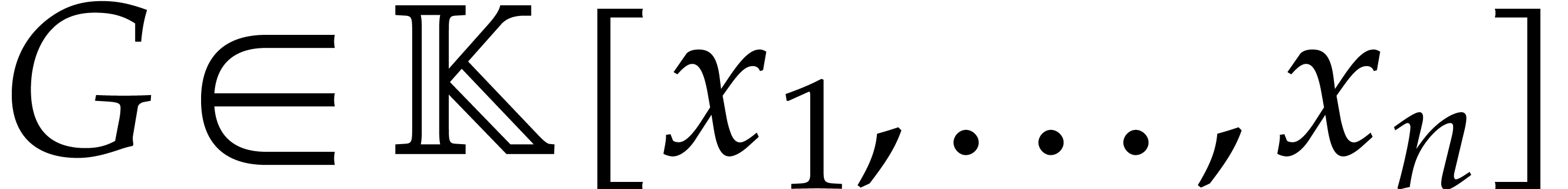 (with
(with  ),
we may thus recover
),
we may thus recover 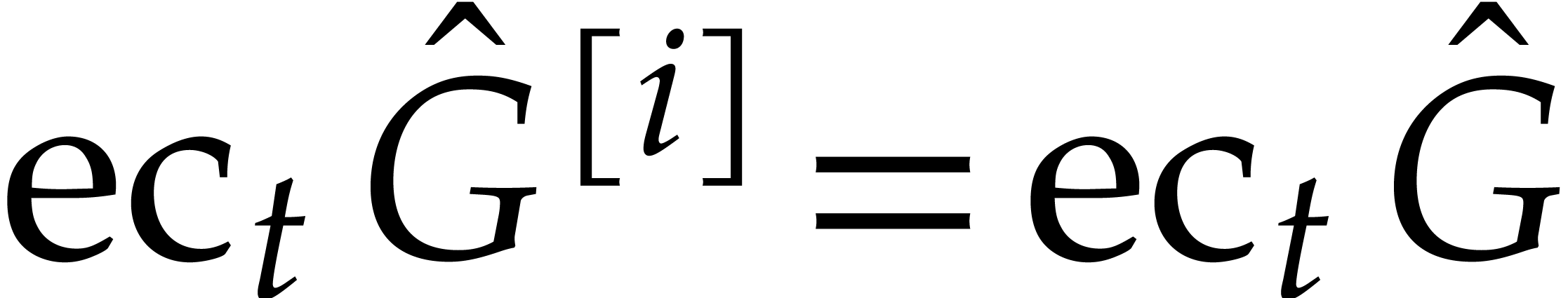 from
from  using sparse interpolation. Finally, for
using sparse interpolation. Finally, for 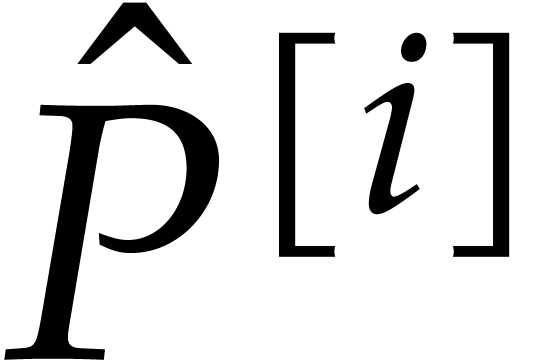 ,
we obtain
,
we obtain  , where
, where 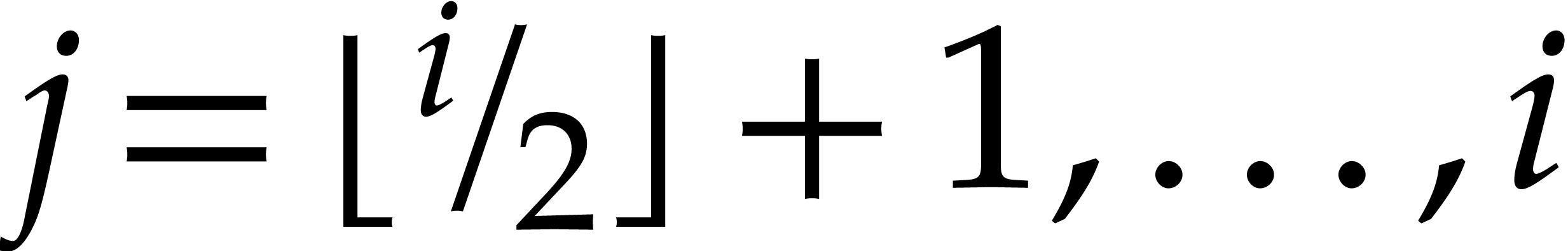 for
for  . This
leads to the following algorithm:
. This
leads to the following algorithm:
Algorithm
Output: 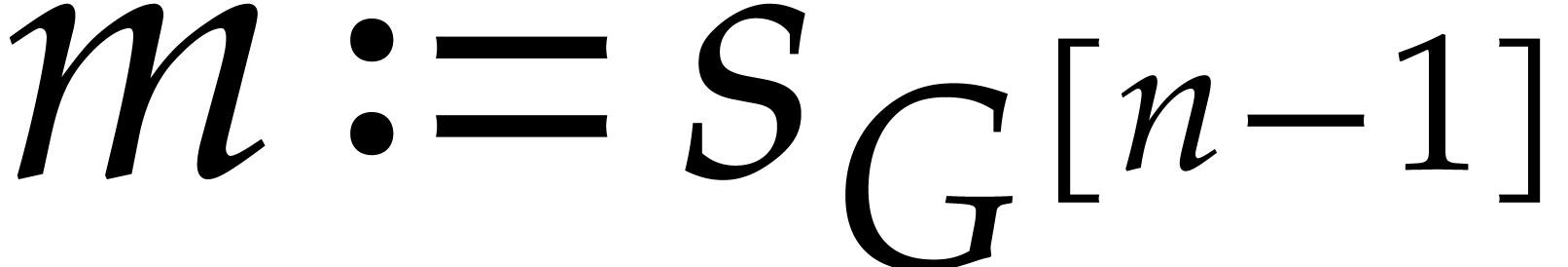 ,
such that
,
such that 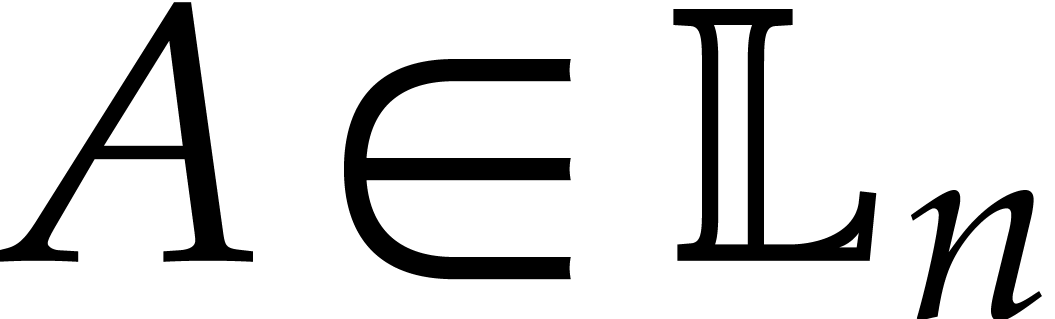
Find a regularizing weight  for
for  or
or 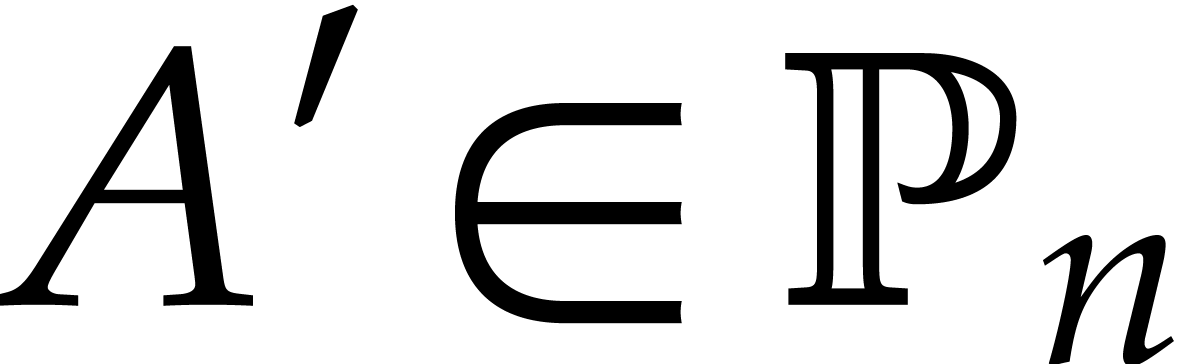
For  do
do
Compute  ,
,  for
for 
Compute  with
with  monic and
monic and
 for
for 
If  yield
yield  through
sparse interpolation, then
through
sparse interpolation, then
Let  for
for 
Return 
Remark  is normalized in
is normalized in  to be monic as a
polynomial in
to be monic as a
polynomial in 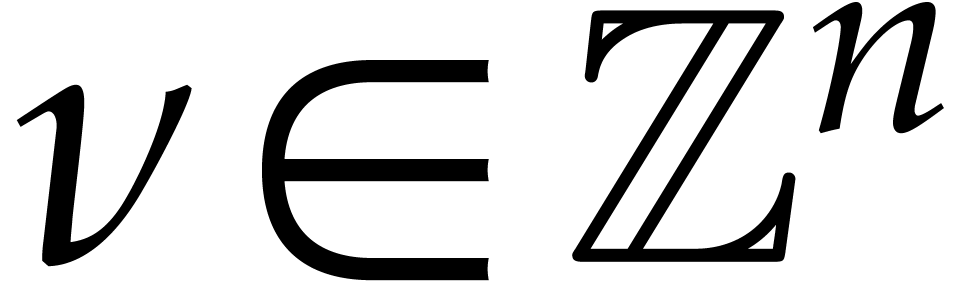 , then we may
need to interpolate multivariate polynomials with negative exponents in
order to recover
, then we may
need to interpolate multivariate polynomials with negative exponents in
order to recover 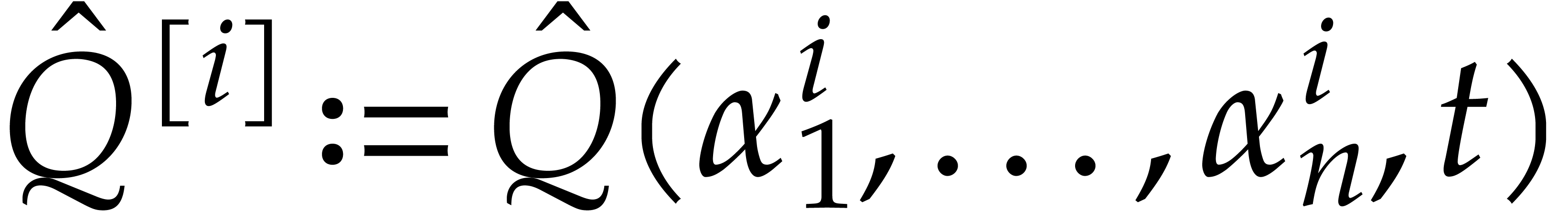 from
from  . In practice, many interpolation algorithms based
on geometric sequences, like Prony's method, can be adapted to do this.
. In practice, many interpolation algorithms based
on geometric sequences, like Prony's method, can be adapted to do this.
As in the previous subsection, assume that  are
independently chosen at random from a subset of
are
independently chosen at random from a subset of  of size at least
of size at least  . We let
. We let
 ,
, 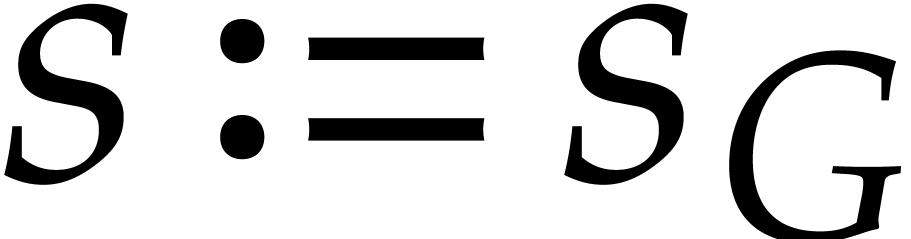 , and
, and  .
.
 or
or  is
is  -regular. Let
-regular. Let  with
with 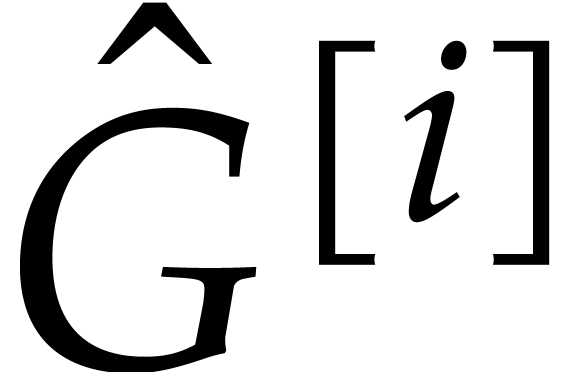 be monic as a polynomial in
be monic as a polynomial in
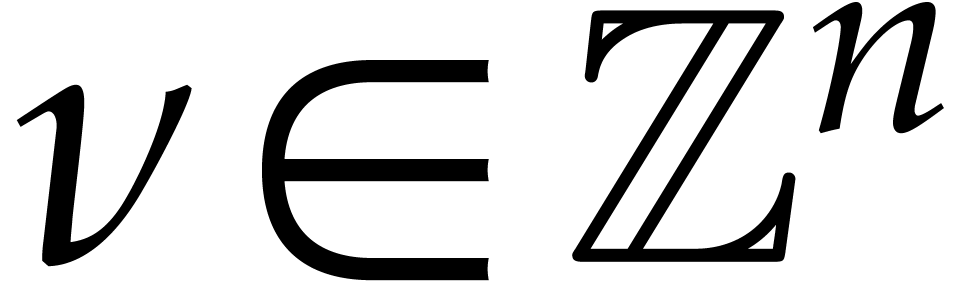 . Take
. Take  ,
,  ,
and
,
and  . The probability that
. The probability that
 for all
for all  is at least
is at least
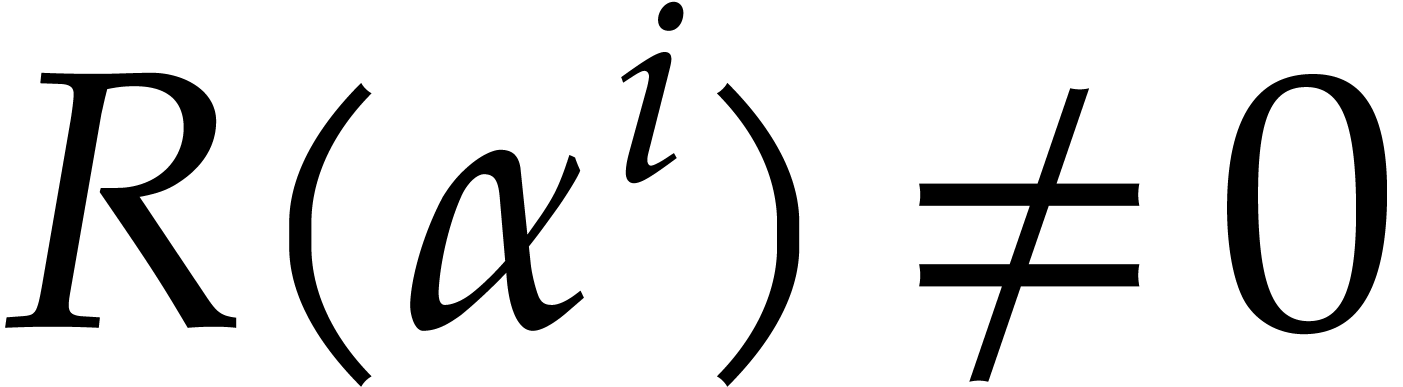
Proof. We have  if and
only if
if and
only if 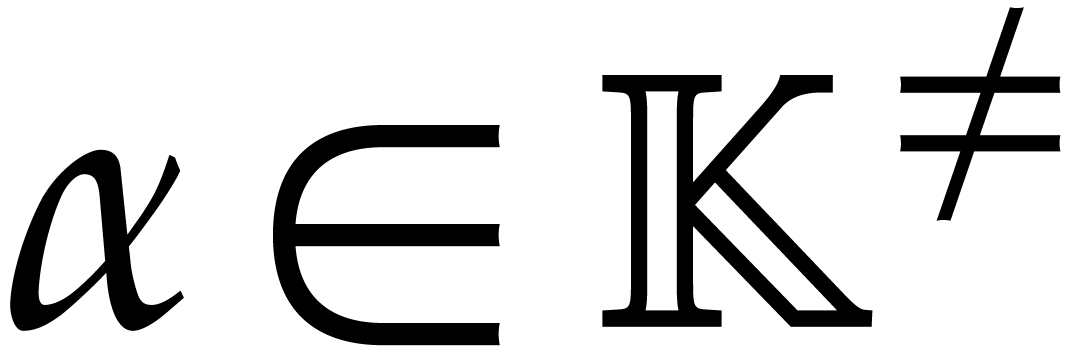 does not vanish at
does not vanish at 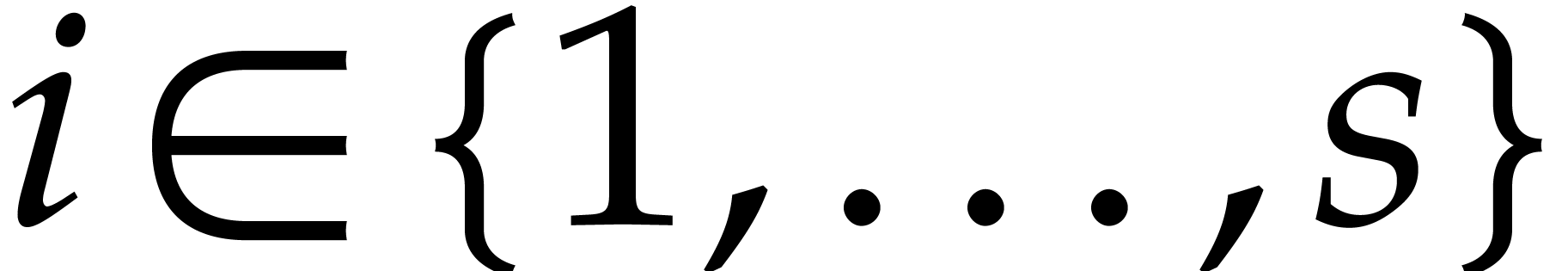 . Now the degree of
. Now the degree of 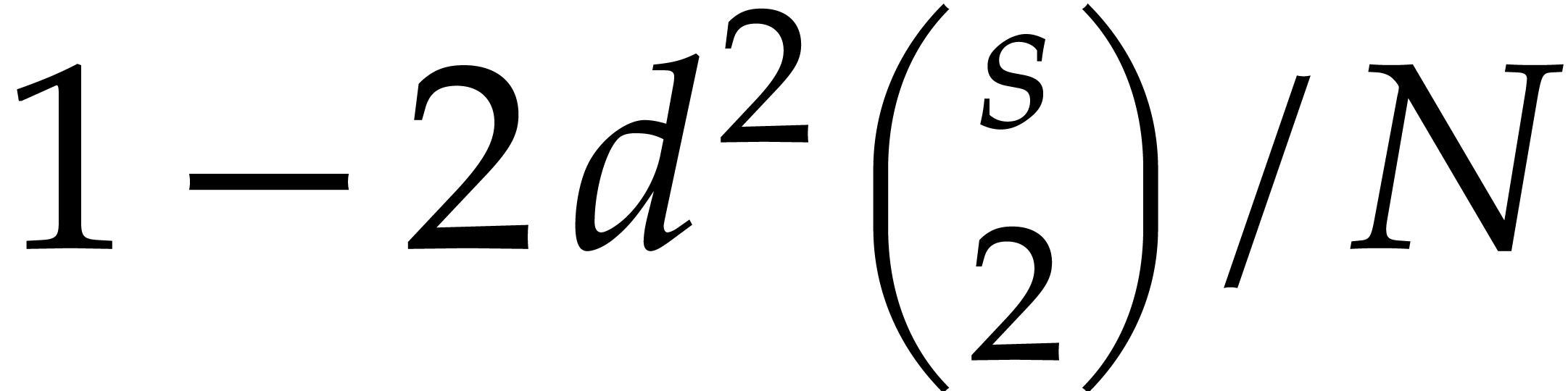 is
at most
is
at most 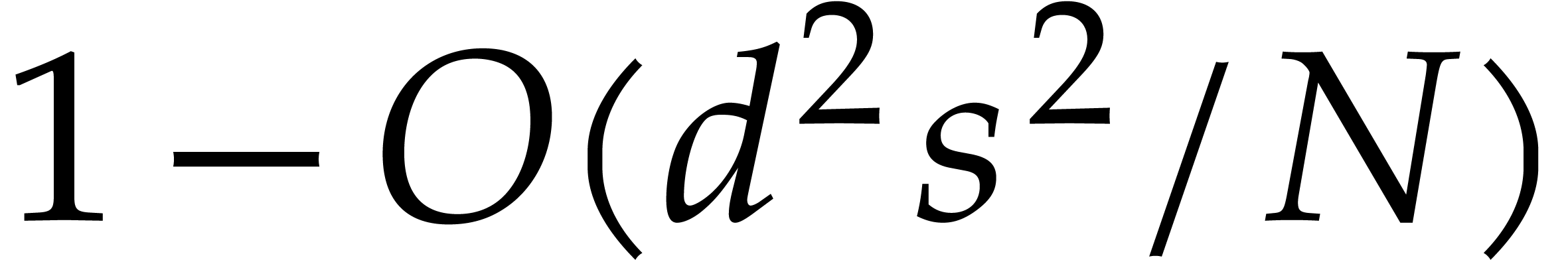 , so the probability
that
, so the probability
that 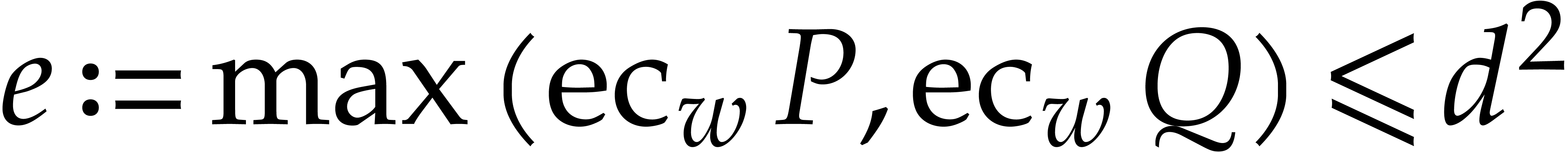 for a randomly chosen
for a randomly chosen  and all
and all  is at least
is at least  , by Corollary 2.2.
, by Corollary 2.2.
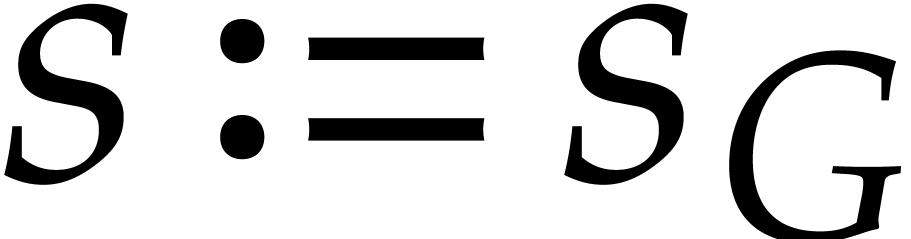 ,
, 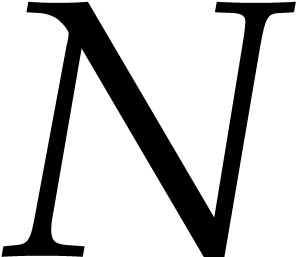 ,
, 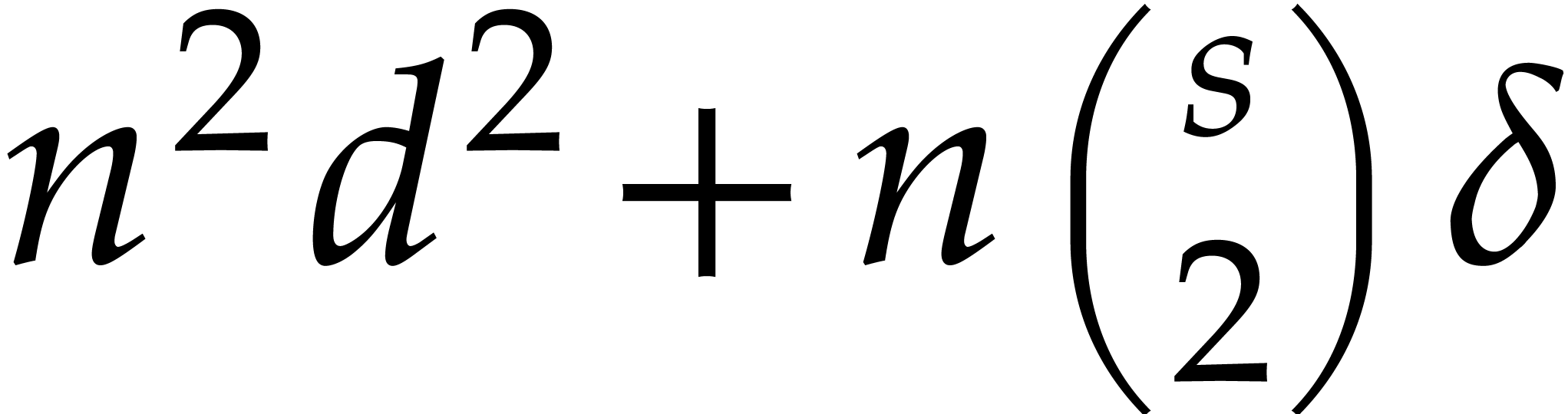 ,
and
,
and  . Algorithm 3.2
is correct with probability at least
. Algorithm 3.2
is correct with probability at least 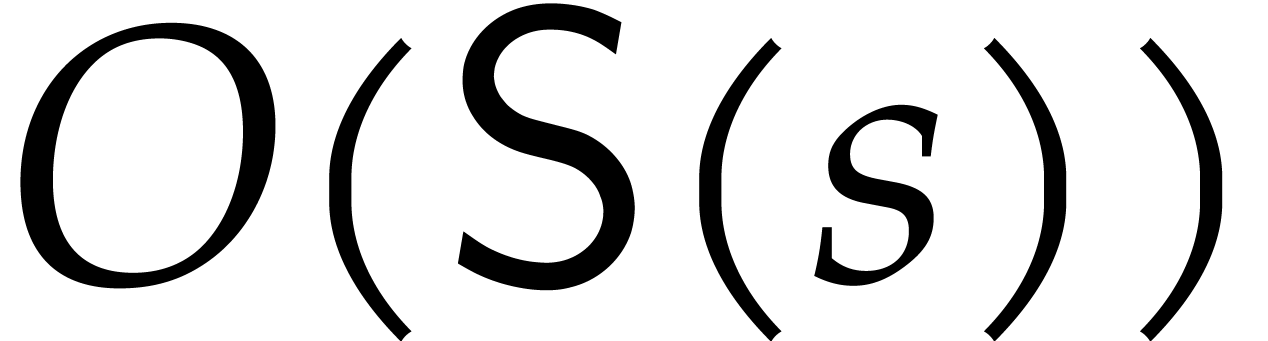 and it
runs in time
and it
runs in time
 |
(3.1) |
Proof. The correctness with the announced
probability follows from Corollaries 2.11 and 3.9,
while also using Remark 2.5. The computation of  and
and  through sparse evaluation at
geometric progressions requires
through sparse evaluation at
geometric progressions requires  operations (see
Section 2.4). The univariate gcd computations take
operations (see
Section 2.4). The univariate gcd computations take  further operations. The final interpolation of
further operations. The final interpolation of 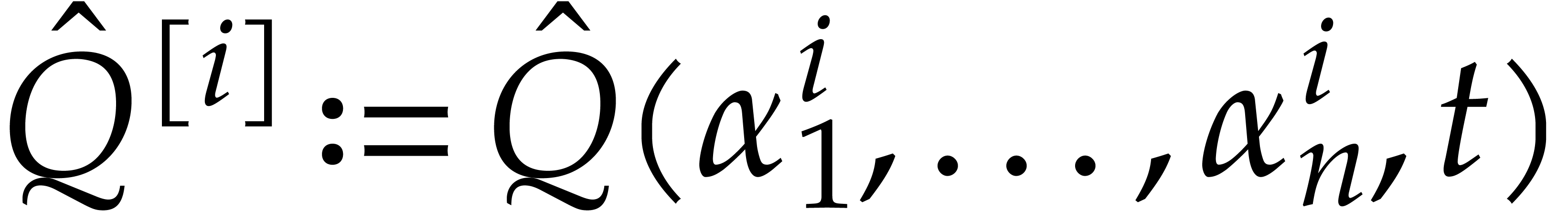 from
from  can be done in time
can be done in time
 .
.
Example 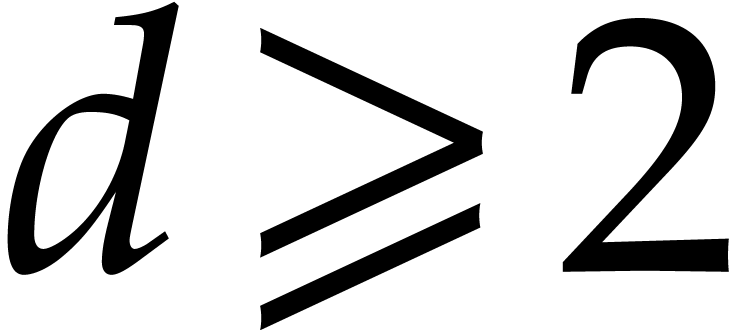 . Consider the particular case when
. Consider the particular case when
 is monic as a polynomial in
is monic as a polynomial in 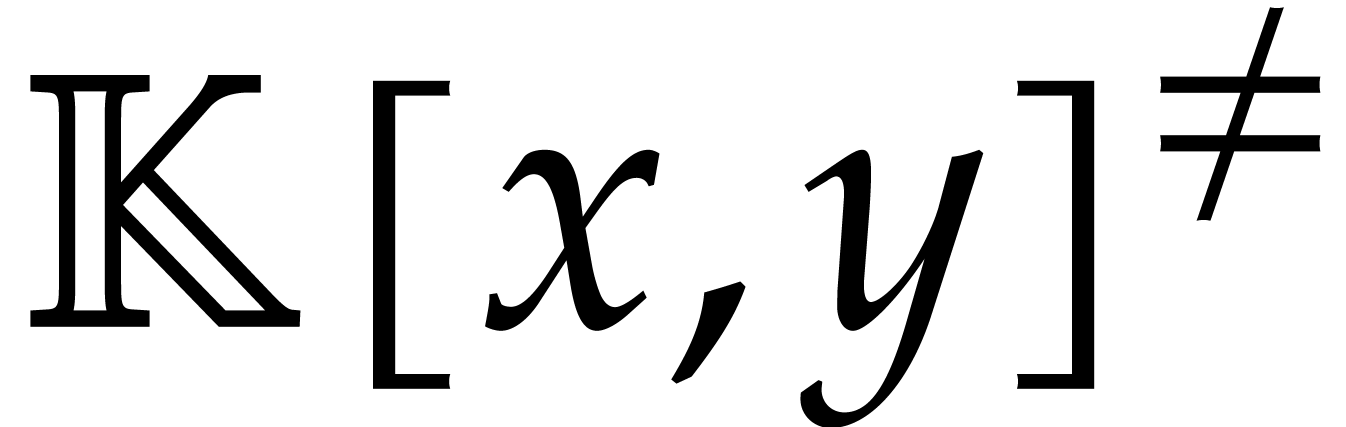 . Then,
. Then,  is a
regularizing weight for
is a
regularizing weight for  , and
therefore also for
, and
therefore also for  . This
situation can be readily detected and, in this case, we have
. This
situation can be readily detected and, in this case, we have  in the complexity bound (3.1).
in the complexity bound (3.1).
Remark 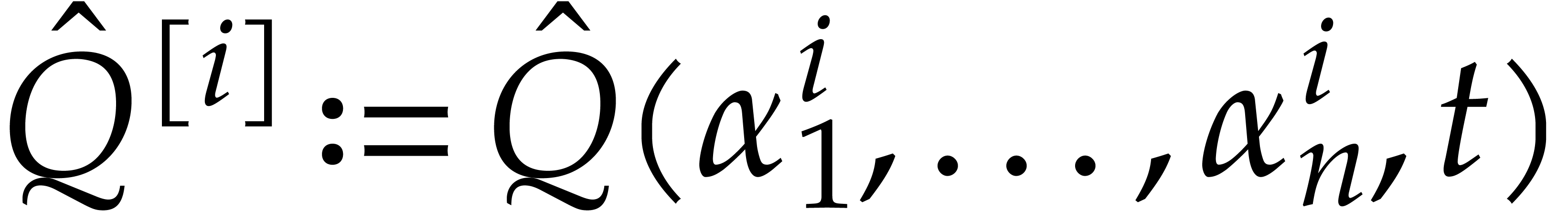 in Algorithm 3.2 in case the terms of
in Algorithm 3.2 in case the terms of 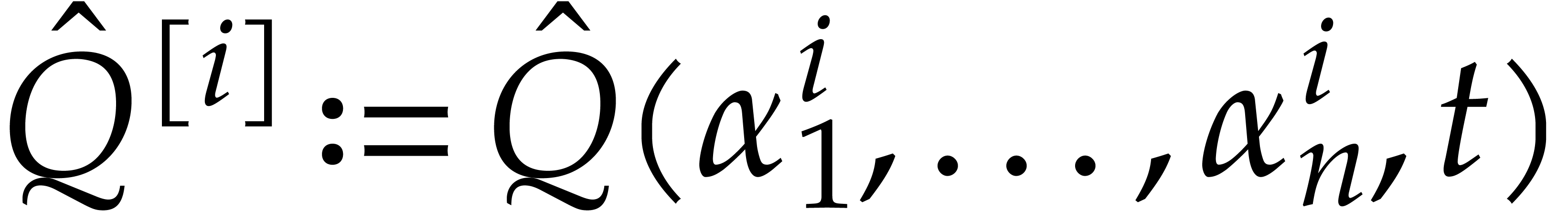 are distributed over the powers of
are distributed over the powers of  .
For instance, if the terms are distributed evenly, then we have
.
For instance, if the terms are distributed evenly, then we have 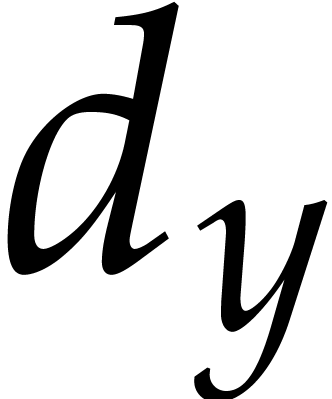 in the complexity bound (3.1).
in the complexity bound (3.1).
Lemma 3.2 allows us to project the general problem of
multivariate gcd computations down to the univariate case. For the
polynomial factorization problem, no such reduction exists: given a
random univariate polynomial of degree 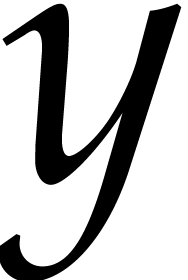 over a
finite field, there is a non-zero probability that this polynomial is
not irreducible. For this reason, it is customary to project down to
bivariate instead of the univariate polynomials (when applicable, an
alternative is to project down to univariate polynomials with integer
coefficients; see [79], for instance).
over a
finite field, there is a non-zero probability that this polynomial is
not irreducible. For this reason, it is customary to project down to
bivariate instead of the univariate polynomials (when applicable, an
alternative is to project down to univariate polynomials with integer
coefficients; see [79], for instance).
This explains why it is interesting to study the factorization of
bivariate polynomials in more detail. Throughout this section,  is a bivariate polynomial in
is a bivariate polynomial in 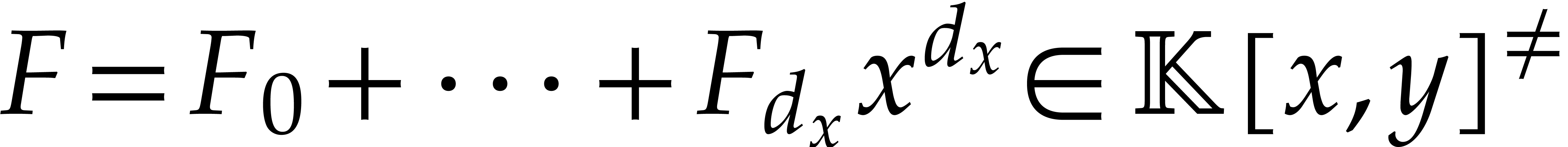 of
degree
of
degree 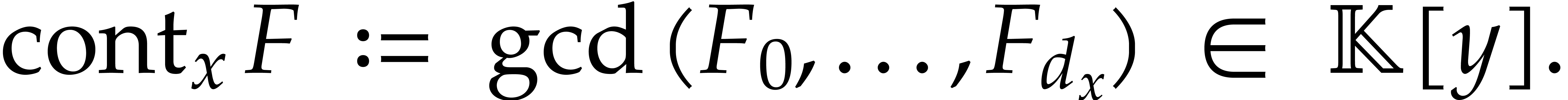 in
in  and of degree
and of degree
 in
in 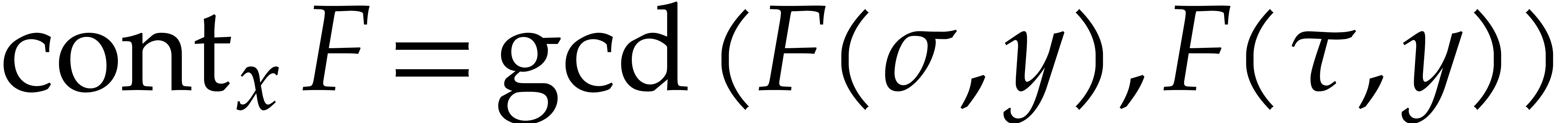 .
As in Sections 2.2 and 3, random numbers will
be drawn from a subset of
.
As in Sections 2.2 and 3, random numbers will
be drawn from a subset of  of size at least
of size at least  . We will recall some classical
results concerning the complexity of bivariate factorization, important
techniques, and special cases: content-free factorization, root
extraction, Hensel lifting, and square-free factorization.
. We will recall some classical
results concerning the complexity of bivariate factorization, important
techniques, and special cases: content-free factorization, root
extraction, Hensel lifting, and square-free factorization.
Recall that the content of 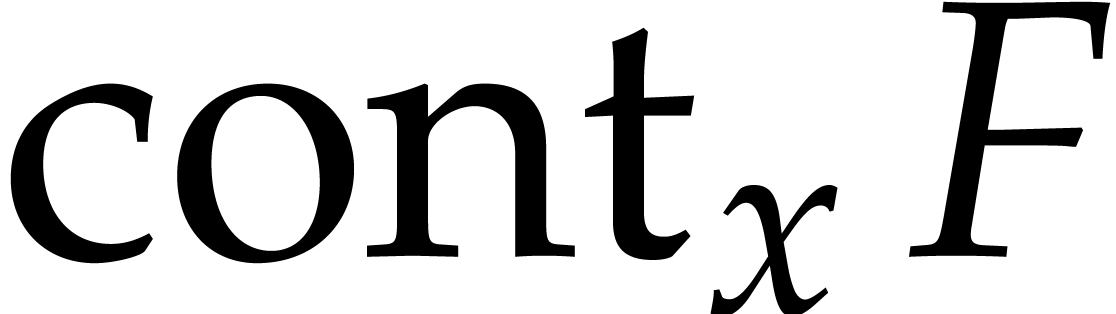 in
in  is defined by
is defined by
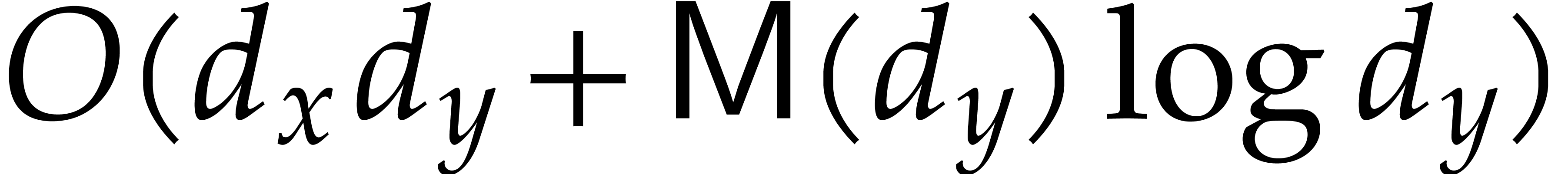
We say that  is content-free (or
primitive) in
is content-free (or
primitive) in  if
if 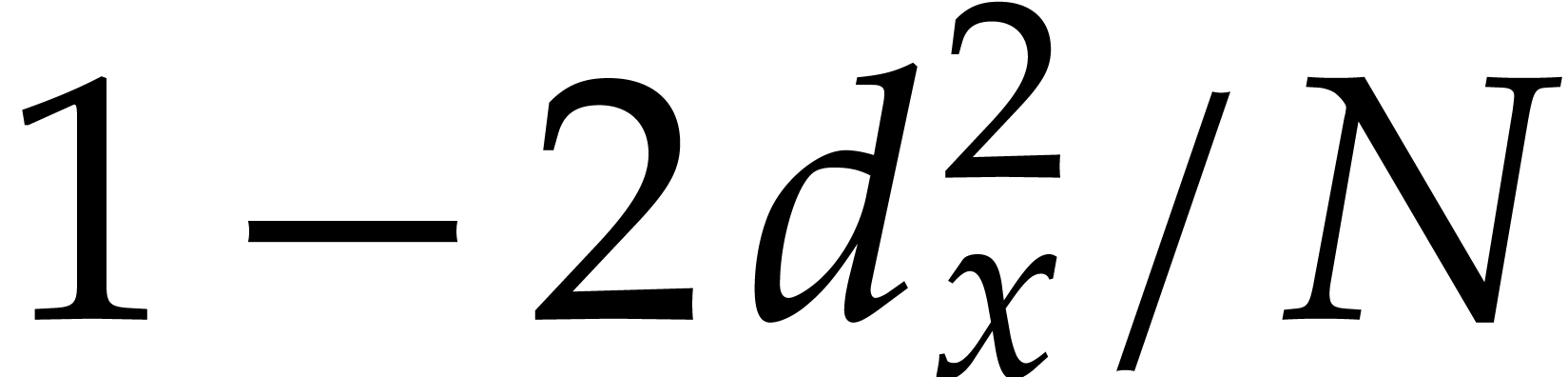 . Given two random shifts
. Given two random shifts 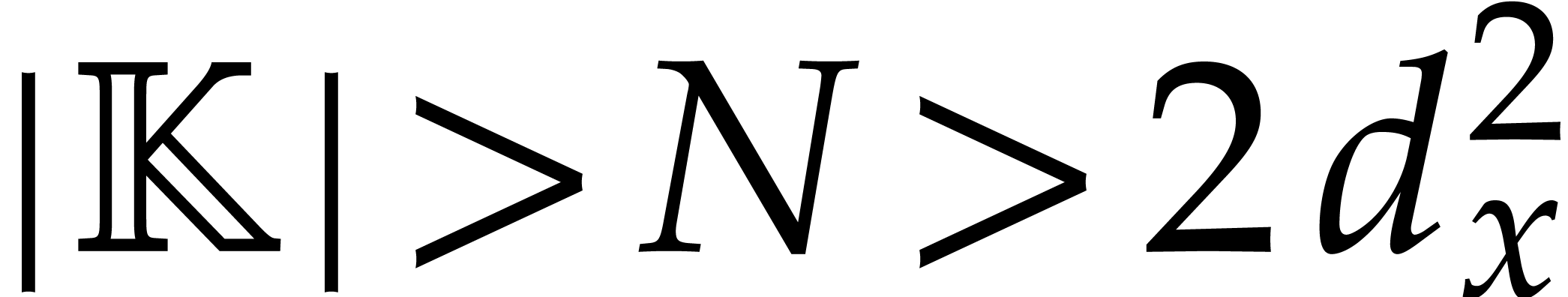 , we have
, we have 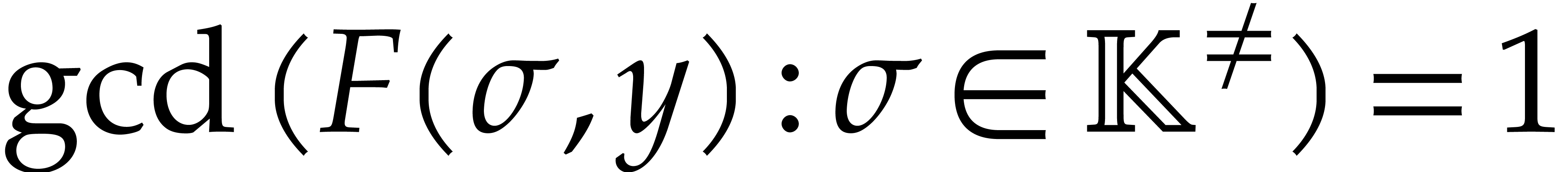 with high
probability. More precisely:
with high
probability. More precisely:
Proof. Without loss of generality, we may assume
that 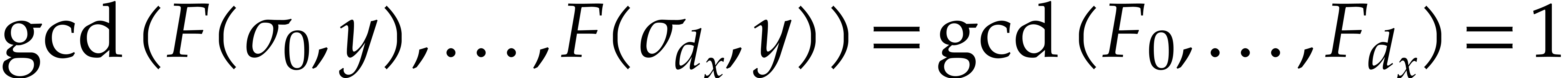 . Let us first consider
the case when
. Let us first consider
the case when 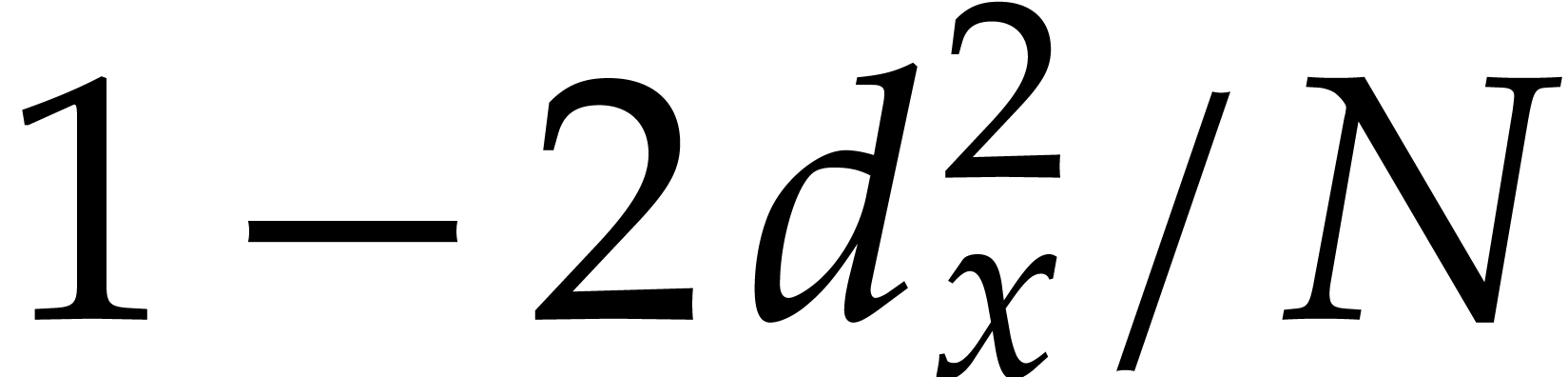 . Then we claim
that
. Then we claim
that  . Indeed, for
. Indeed, for 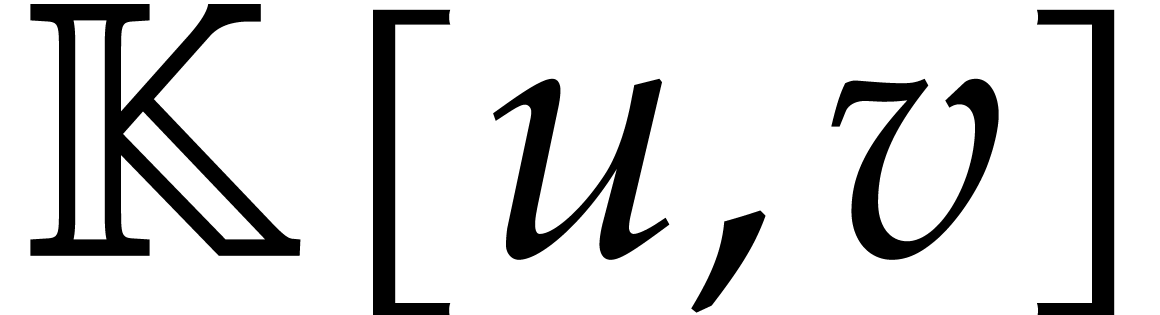 pairwise distinct
pairwise distinct 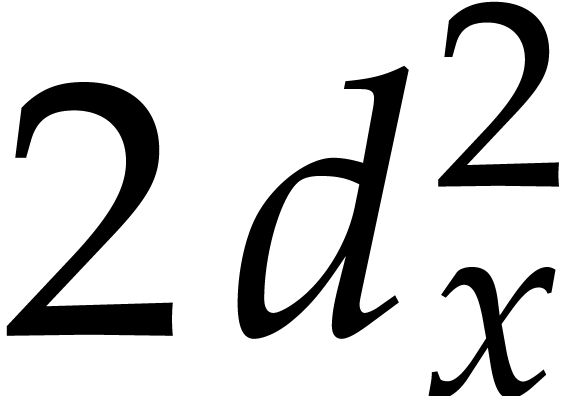 ,
the Vandermonde matrix
,
the Vandermonde matrix 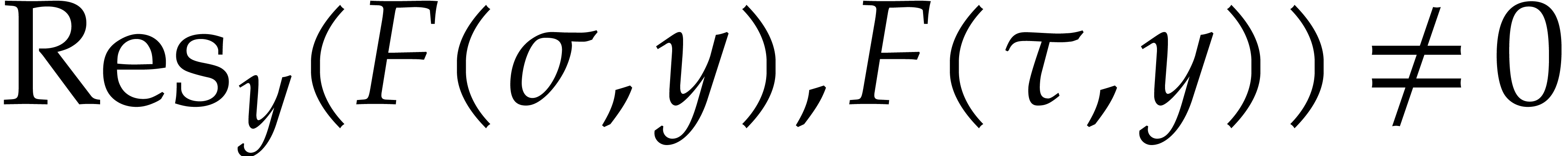 is invertible, so
is invertible, so 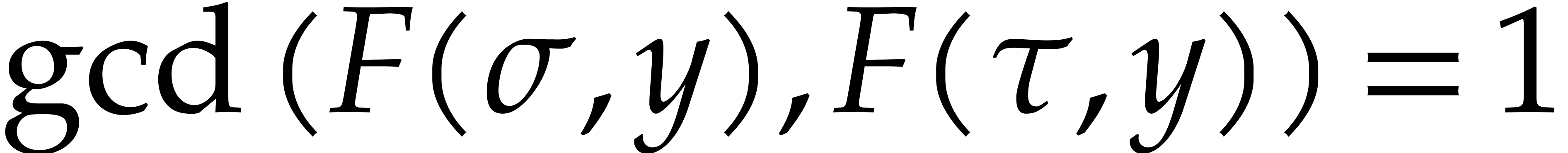 . It follows that
. It follows that 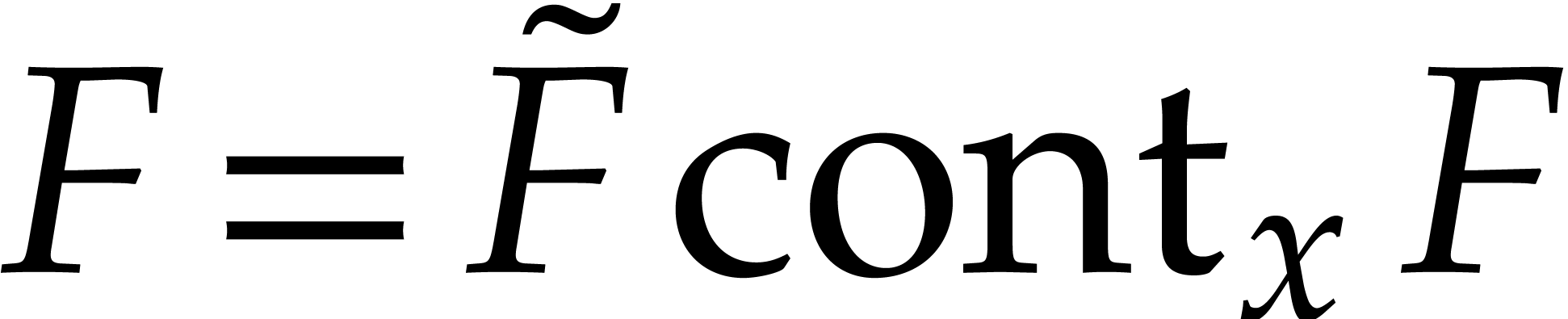 , regarded as an element of
, regarded as an element of 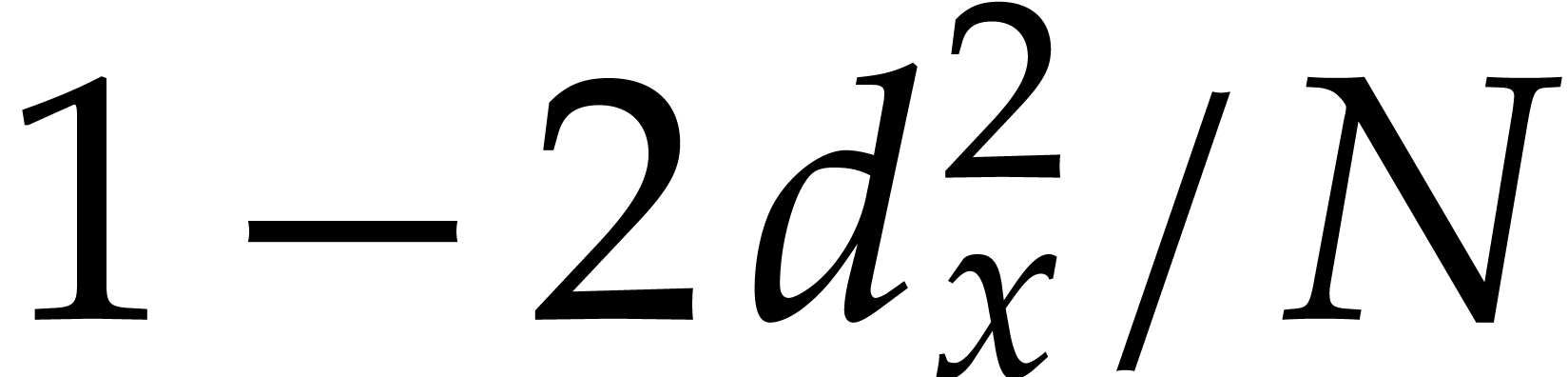 , is non-zero, and its total degree is bounded
by
, is non-zero, and its total degree is bounded
by  . By Lemma 2.1,
it follows that
. By Lemma 2.1,
it follows that 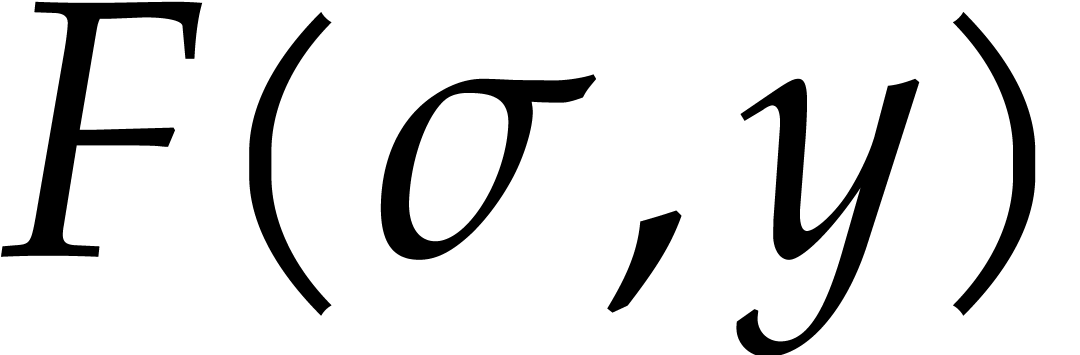 with probability at least
with probability at least 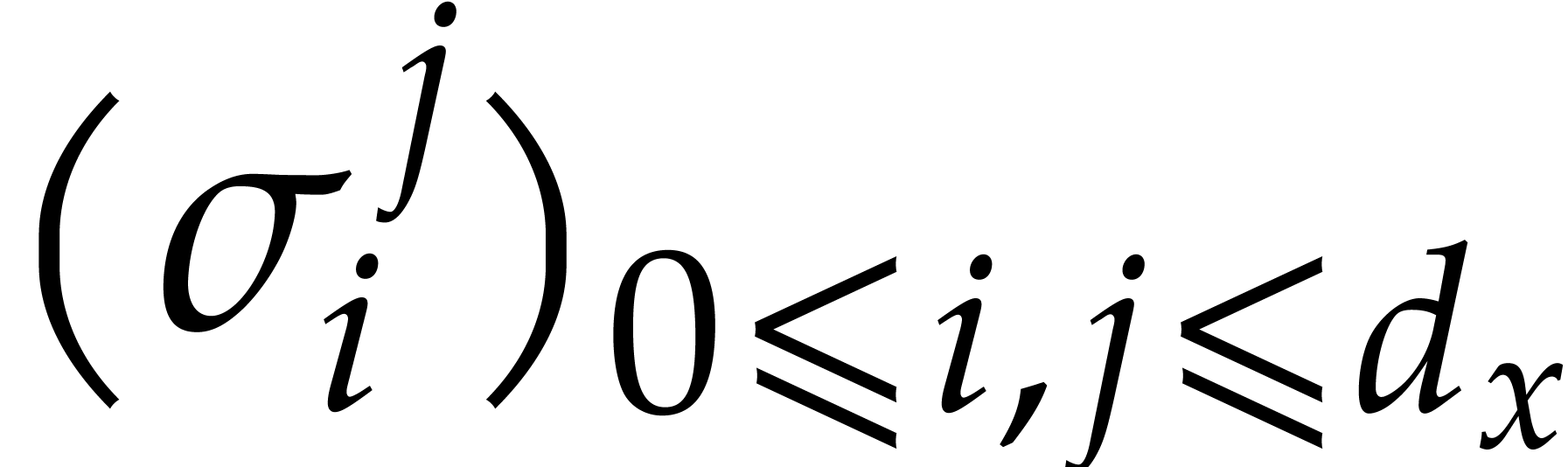 . In that case,
. In that case, 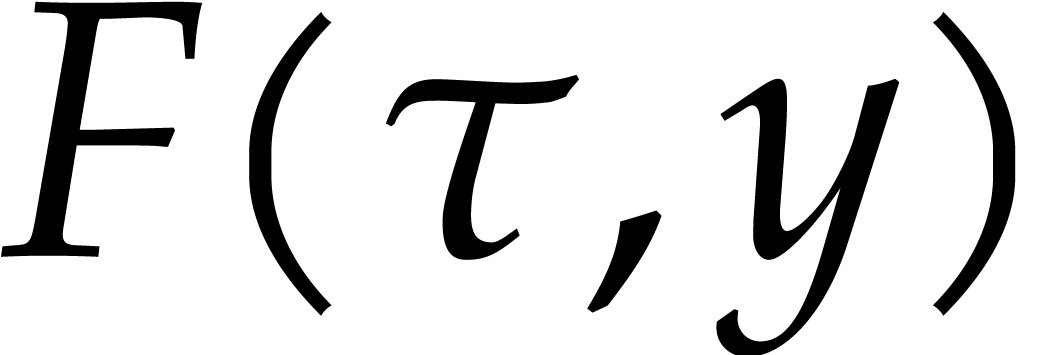 .
.
We have proved our probabilistic correctness claim in the particular
case when 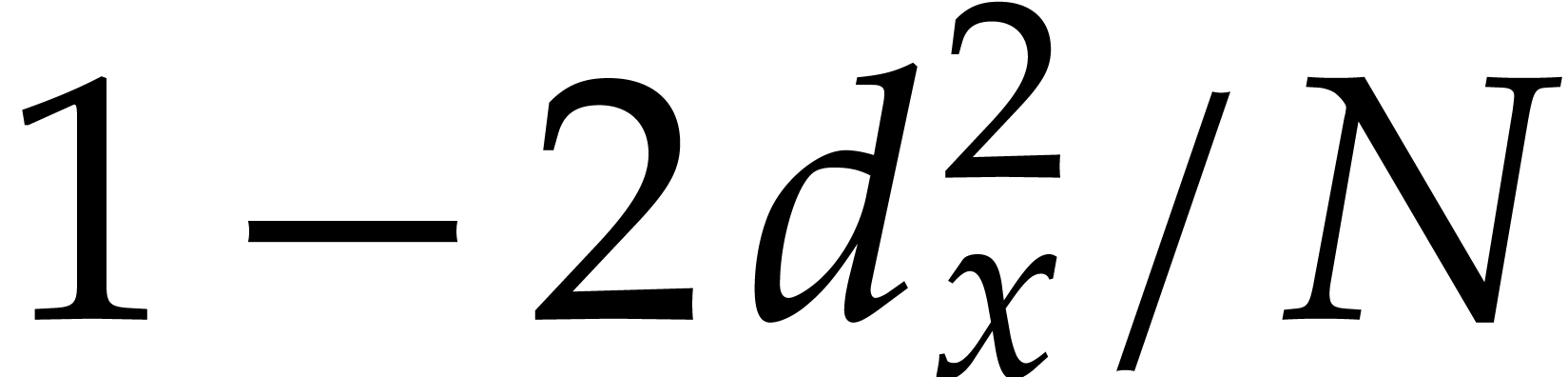 . In general, we
factor
. In general, we
factor  . With probability at
least
. With probability at
least 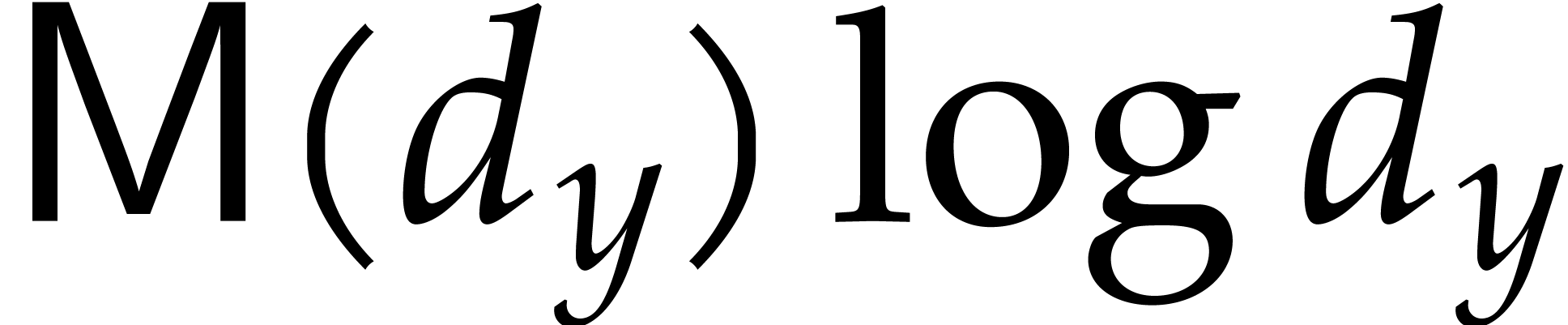 , we have
, we have  .
.
As to the complexity bound, the evaluations  and
and
 require
require 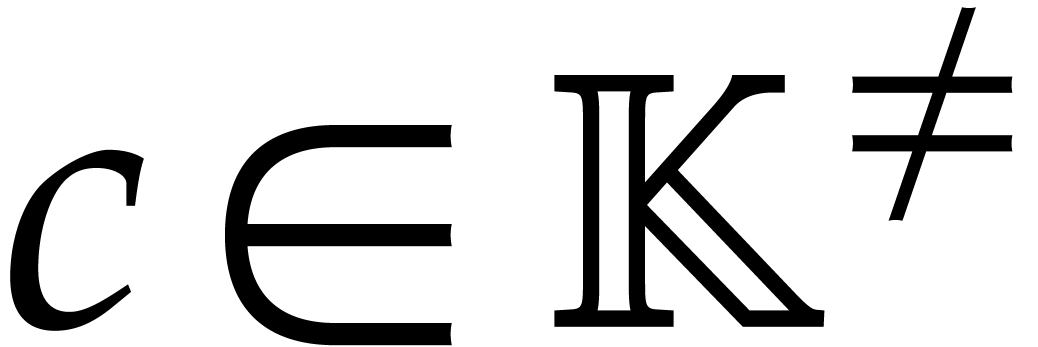 operations and
the univariate gcd computation can be done in time
operations and
the univariate gcd computation can be done in time 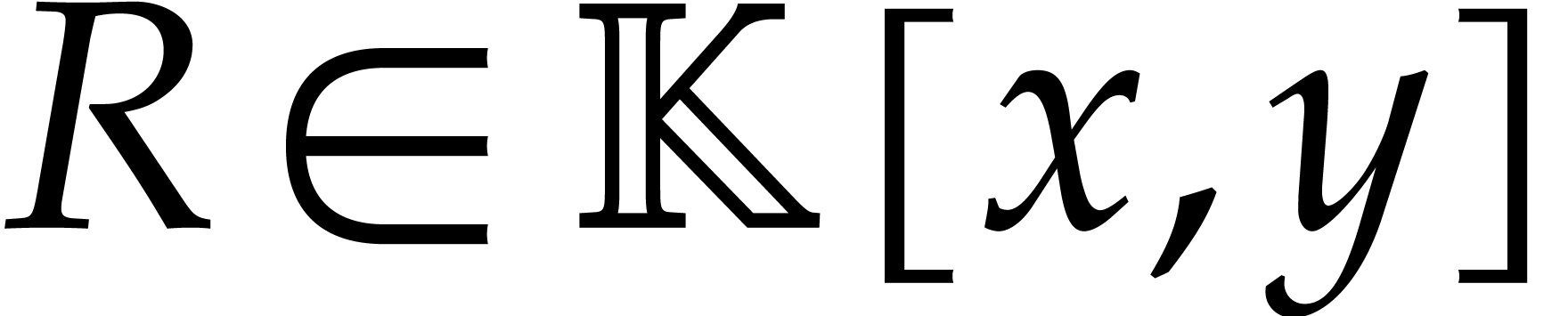 .
.
Let  and
and  .
Assume that
.
Assume that 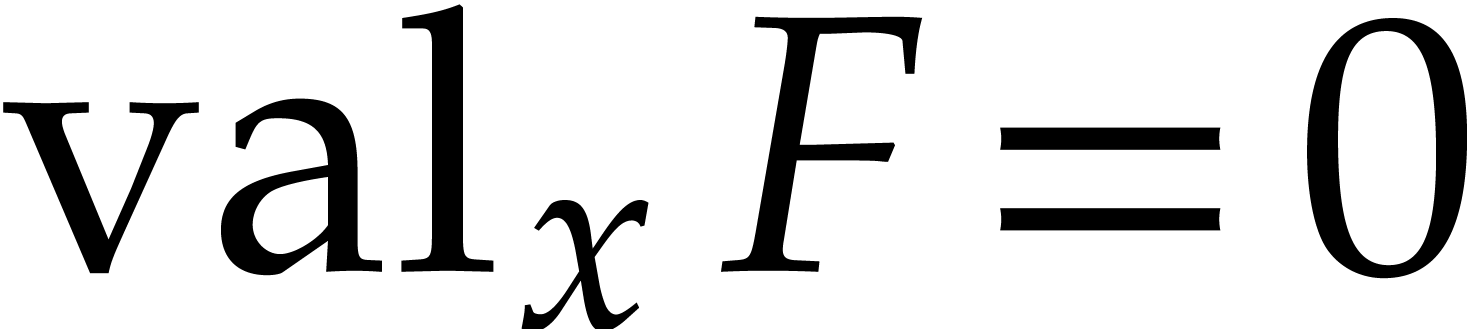 for some
for some  and
and
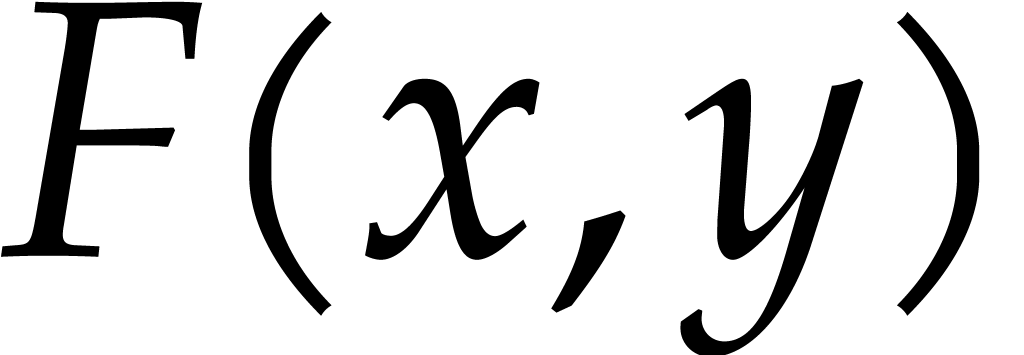 . Assume that
. Assume that  . Then
. Then  can be computed
efficiently as follows.
can be computed
efficiently as follows.
After dividing out a suitable power of 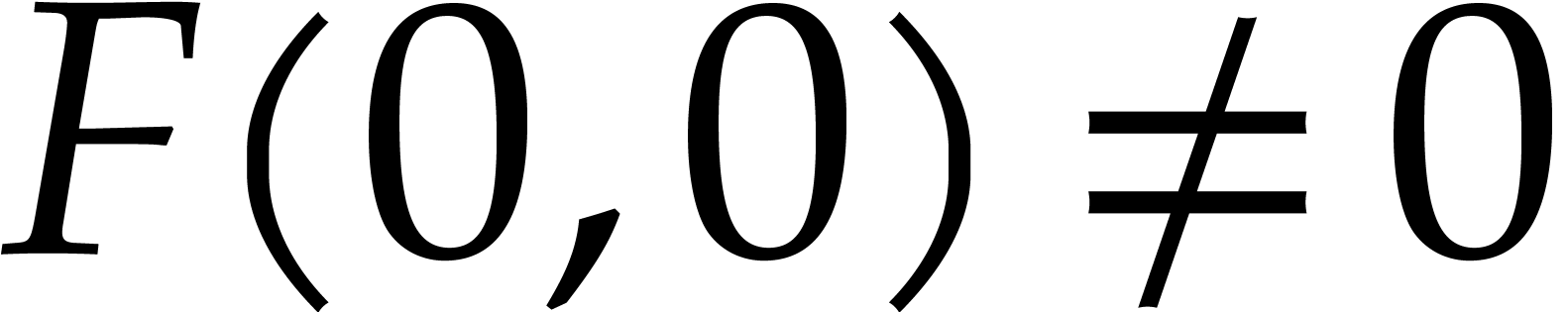 ,
we may assume without loss of generality that
,
we may assume without loss of generality that 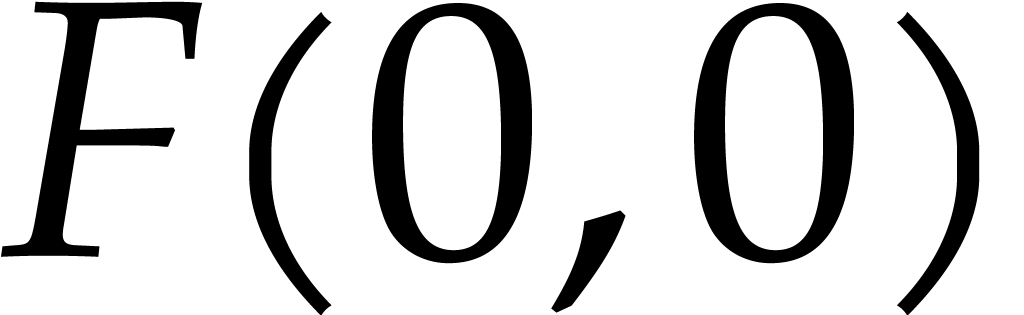 . For a random shift
. For a random shift 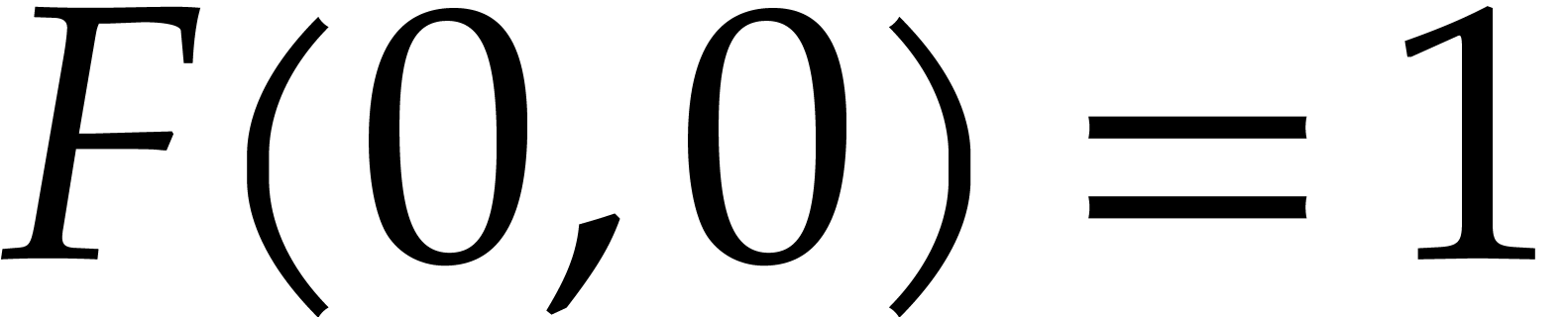 ,
we next replace
,
we next replace  with
with  . With high probability, this ensures that
. With high probability, this ensures that 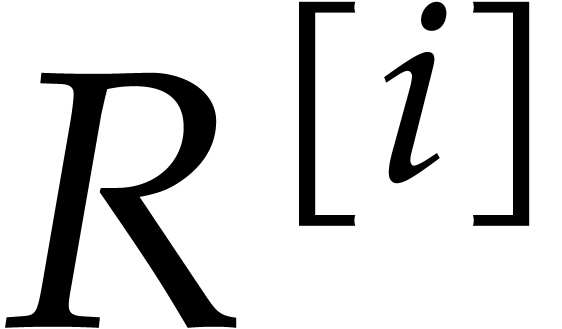 . Modulo division of
. Modulo division of  by
by 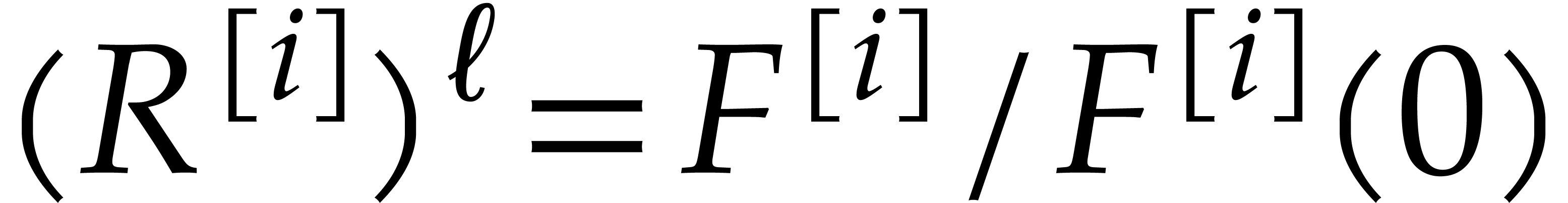 , we may
then assume without loss of generality that
, we may
then assume without loss of generality that 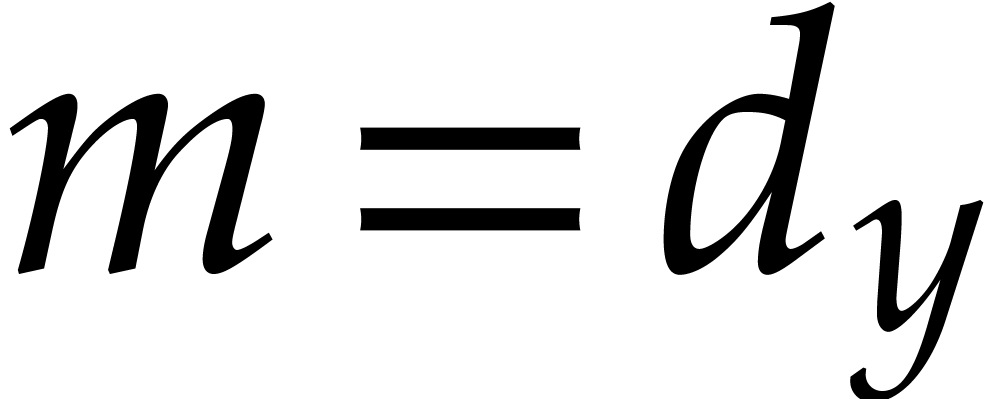 , and we will show how to compute the unique
, and we will show how to compute the unique 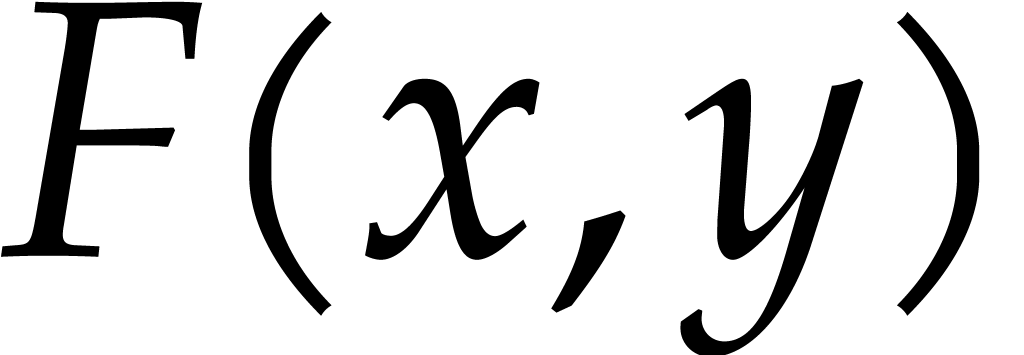 with
with  and
and  . Since
. Since  is a univariate
polynomial, we may efficiently compute
is a univariate
polynomial, we may efficiently compute 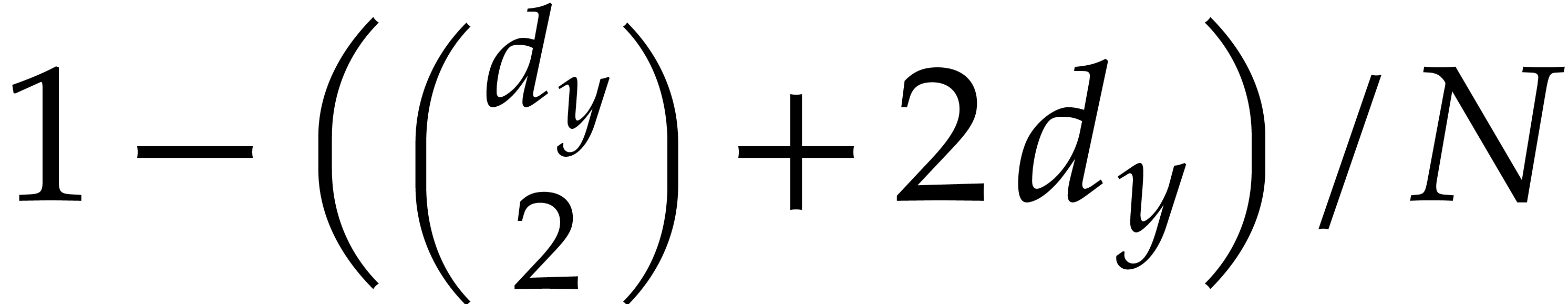 using
univariate root extraction.
using
univariate root extraction.
Let  be an admissible ratio or an FFT ratio. For
any
be an admissible ratio or an FFT ratio. For
any  , we define the
univariate polynomial
, we define the
univariate polynomial 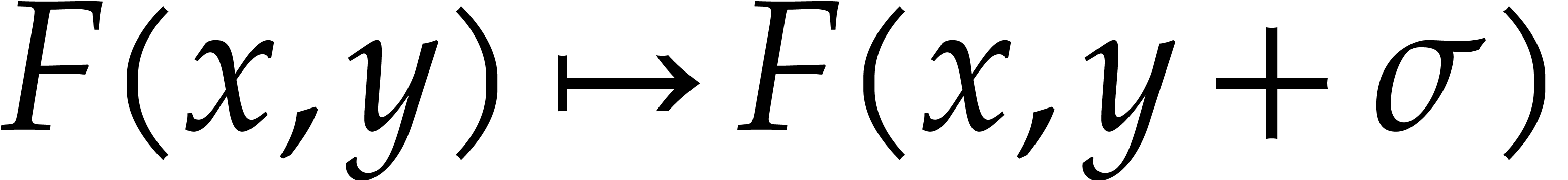 . With
high probability, we have
. With
high probability, we have 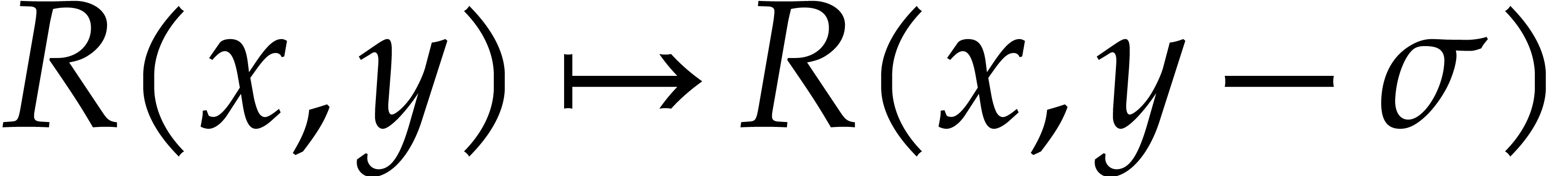 .
Let
.
Let  be the unique univariate polynomial such
that
be the unique univariate polynomial such
that 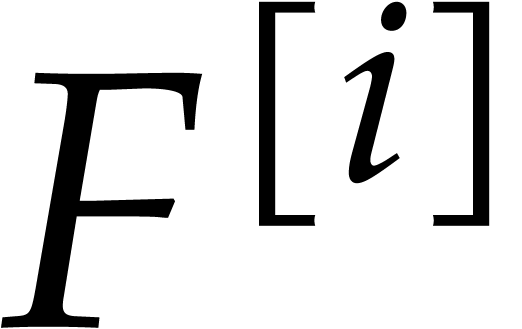 and
and  .
Such
.
Such  can be found efficiently using univariate
root extraction. For
can be found efficiently using univariate
root extraction. For 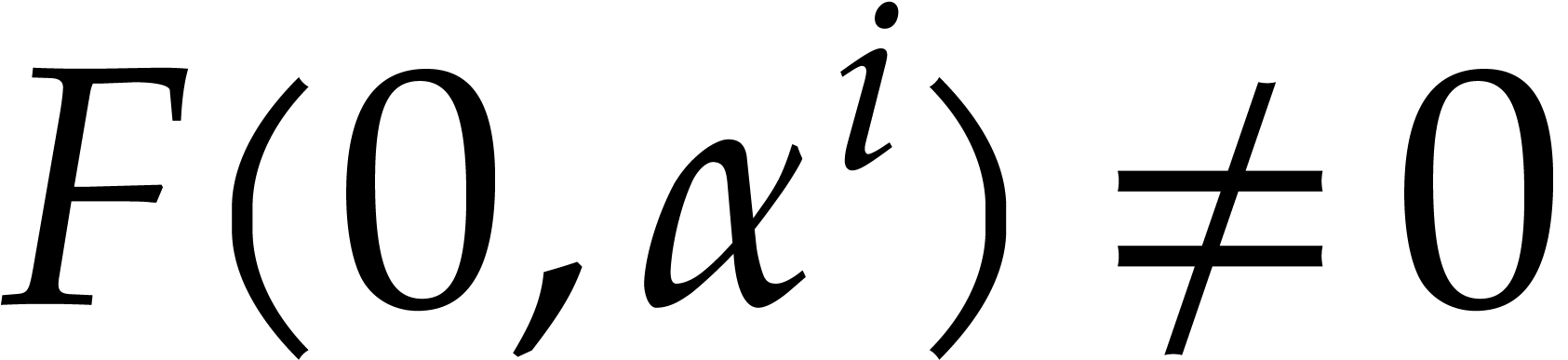 , we may
recover
, we may
recover  from
from  using
interpolation.
using
interpolation.
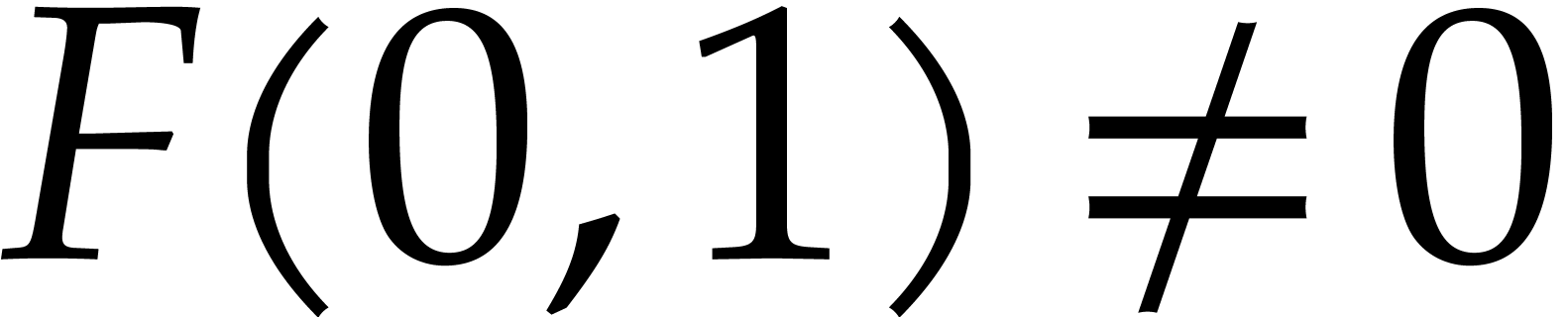 and
and 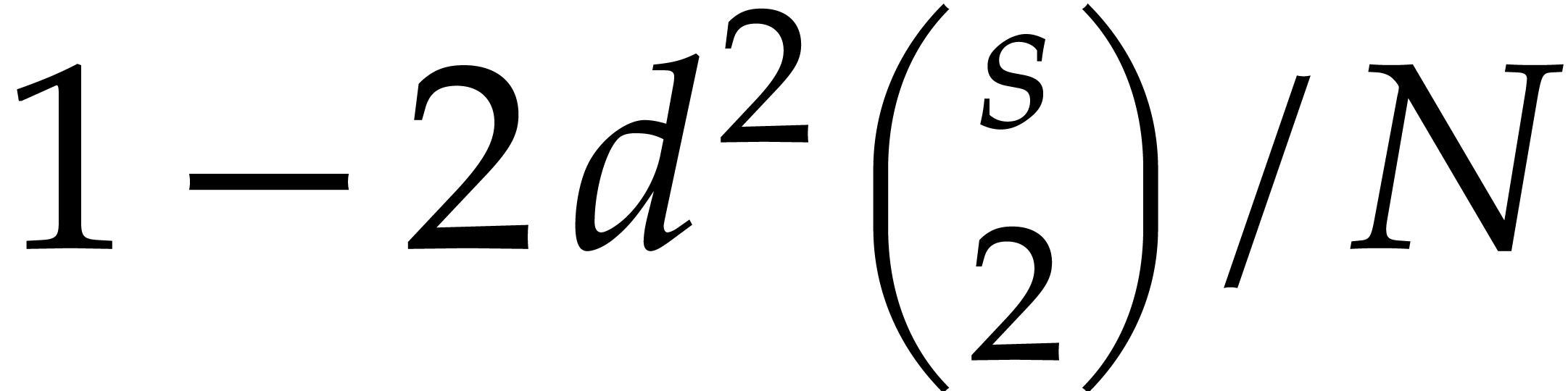 in time
in time  , with a probability of success
of at least
, with a probability of success
of at least 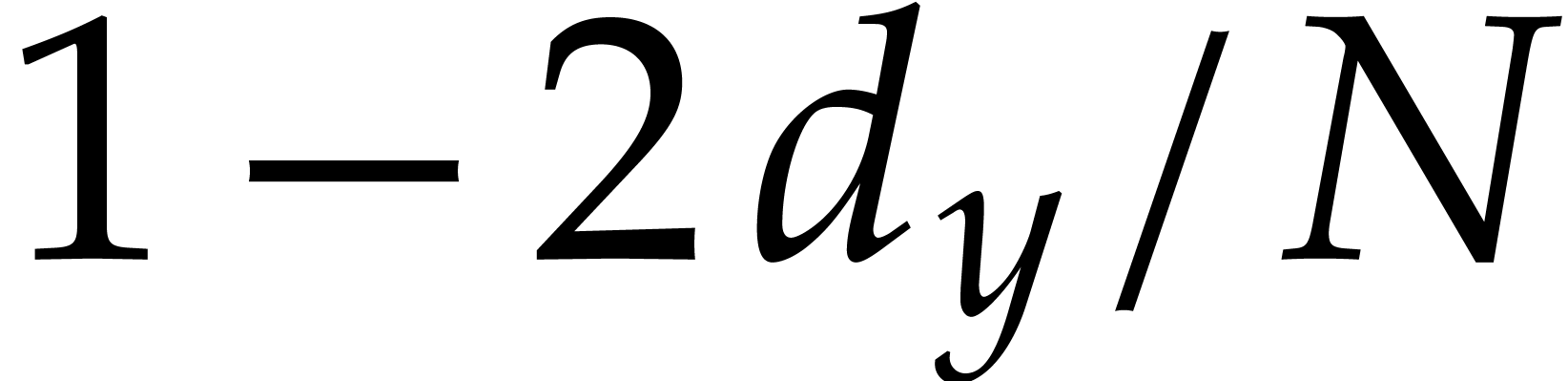 .
.
Proof. The random shift 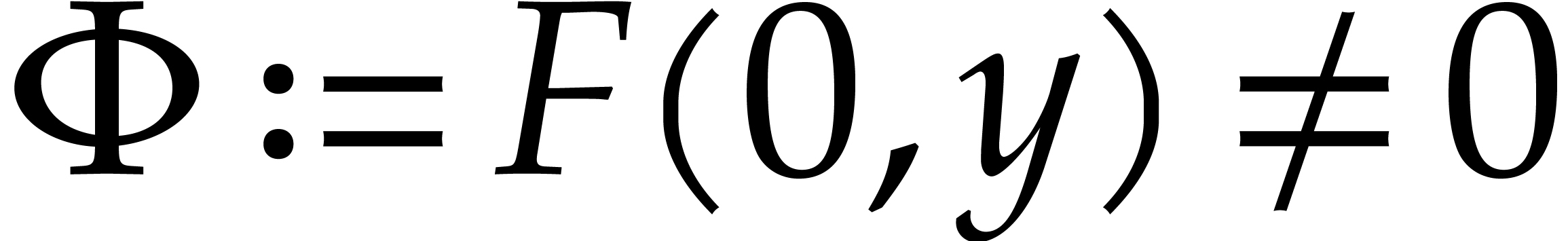 and the corresponding backshift
and the corresponding backshift 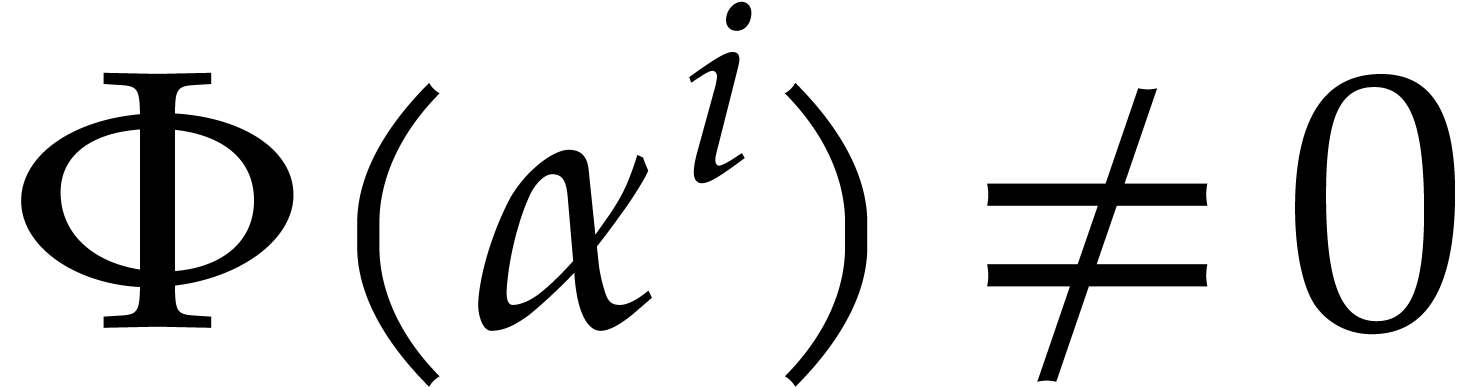 can be computed
in time
can be computed
in time  using the so-called convolution method
[2, Theorem 5]. The computation of
using the so-called convolution method
[2, Theorem 5]. The computation of 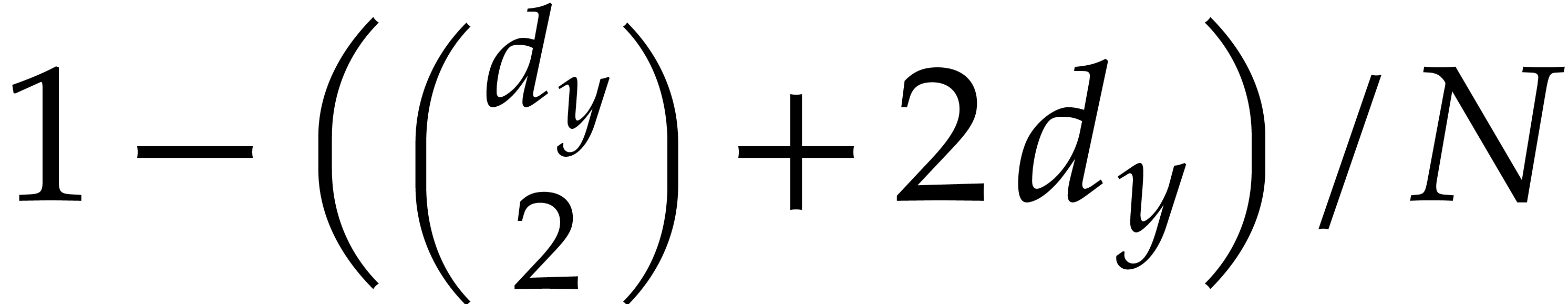 for
for 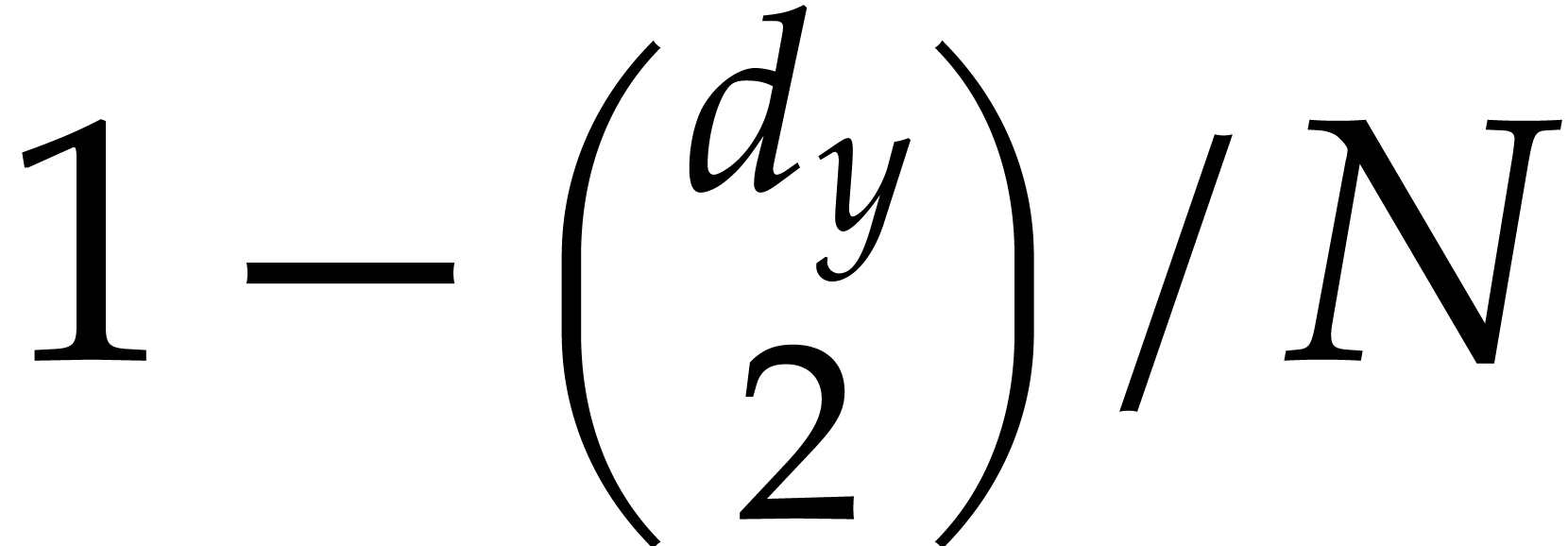 can be done in time
can be done in time  using fast root extraction. We may compute
using fast root extraction. We may compute 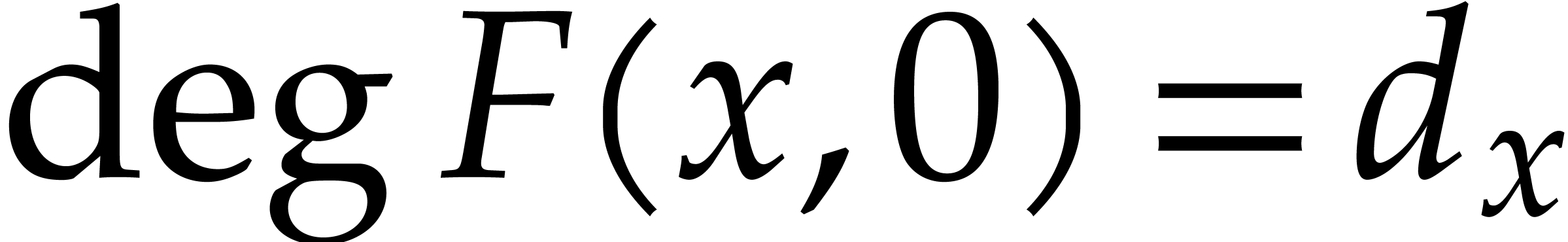 and
and
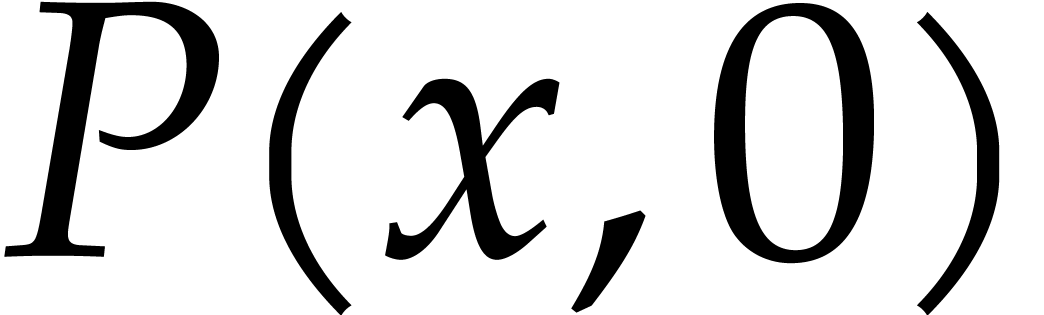 for
for 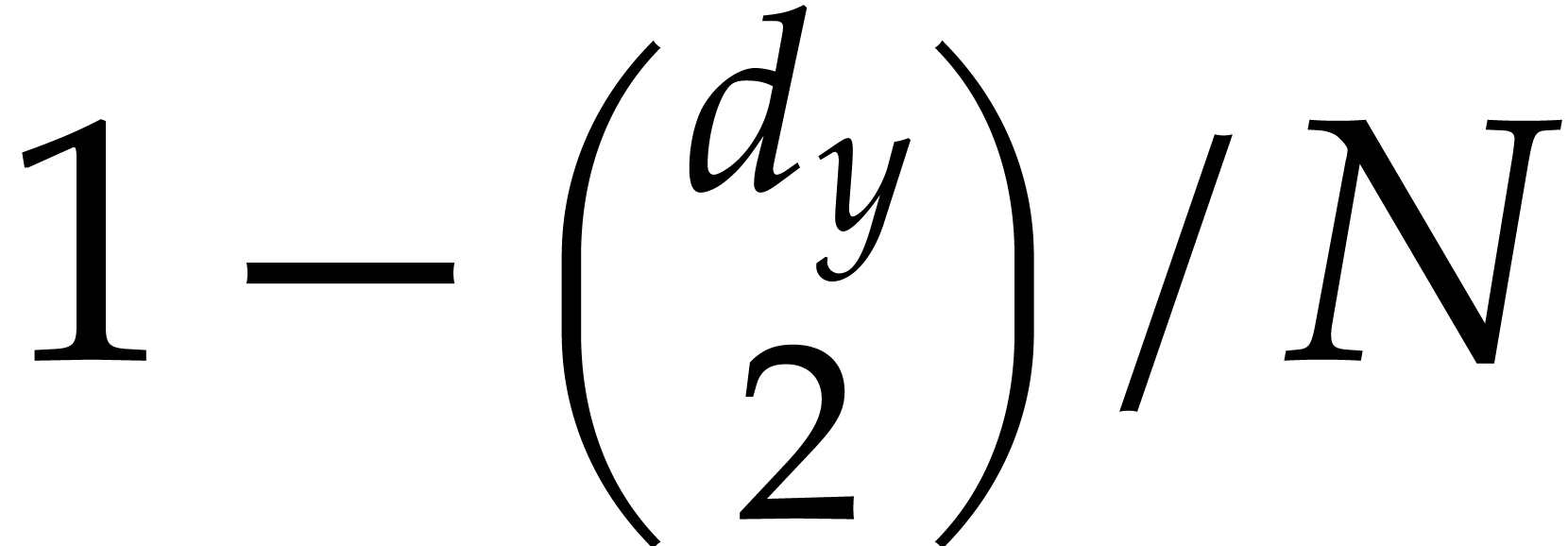 in time
in time  using fast multipoint evaluation at geometric sequences
[2, 13]. The same holds for the interpolation
of
using fast multipoint evaluation at geometric sequences
[2, 13]. The same holds for the interpolation
of 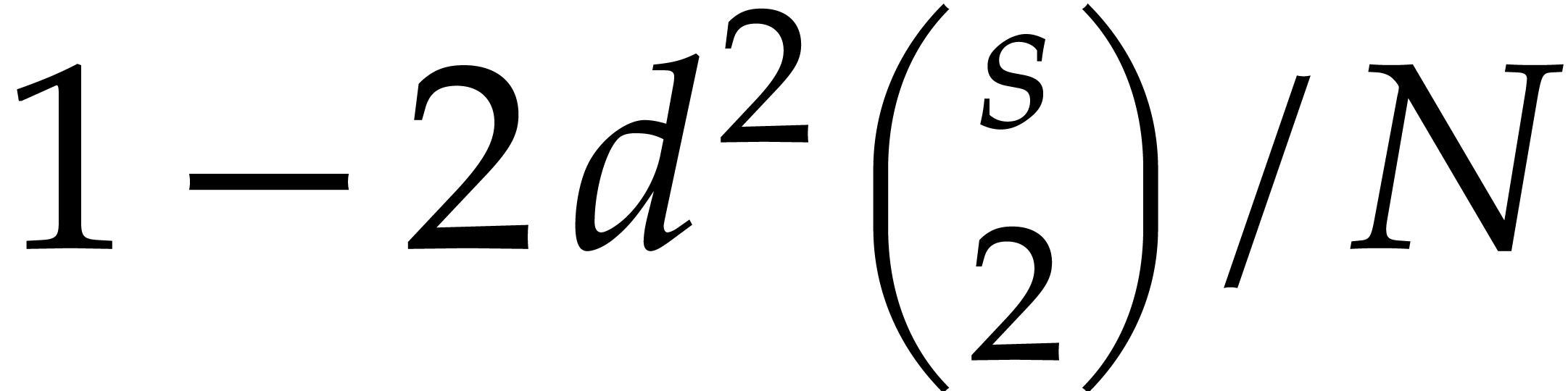 from the
from the  .
Finally, the
.
Finally, the  -th roots
-th roots  of the univariate polynomials
of the univariate polynomials 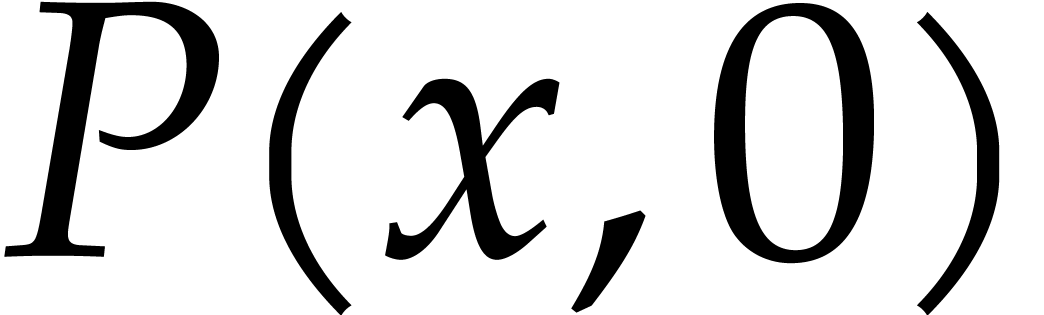 can be computed in time
can be computed in time 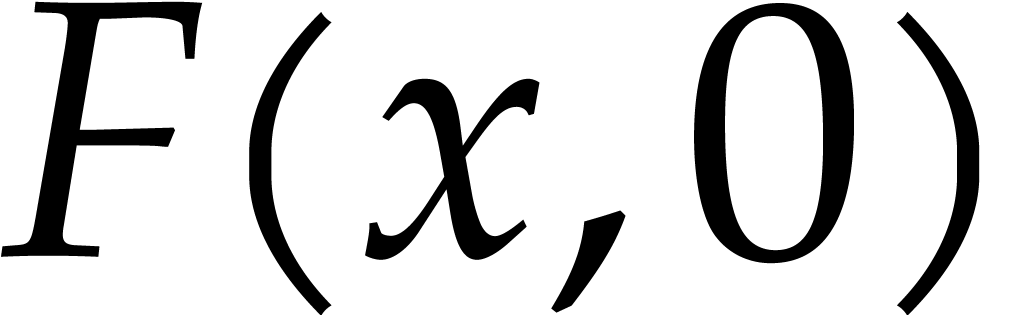 . The
algorithm is correct as long as
. The
algorithm is correct as long as 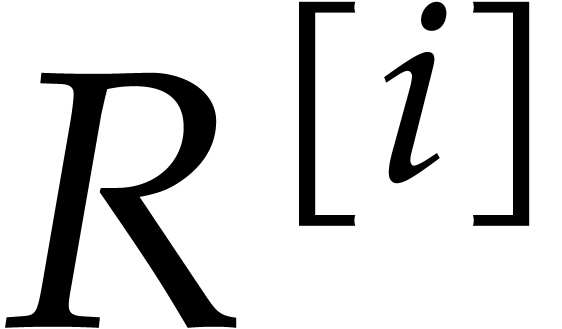 and
and  for
for 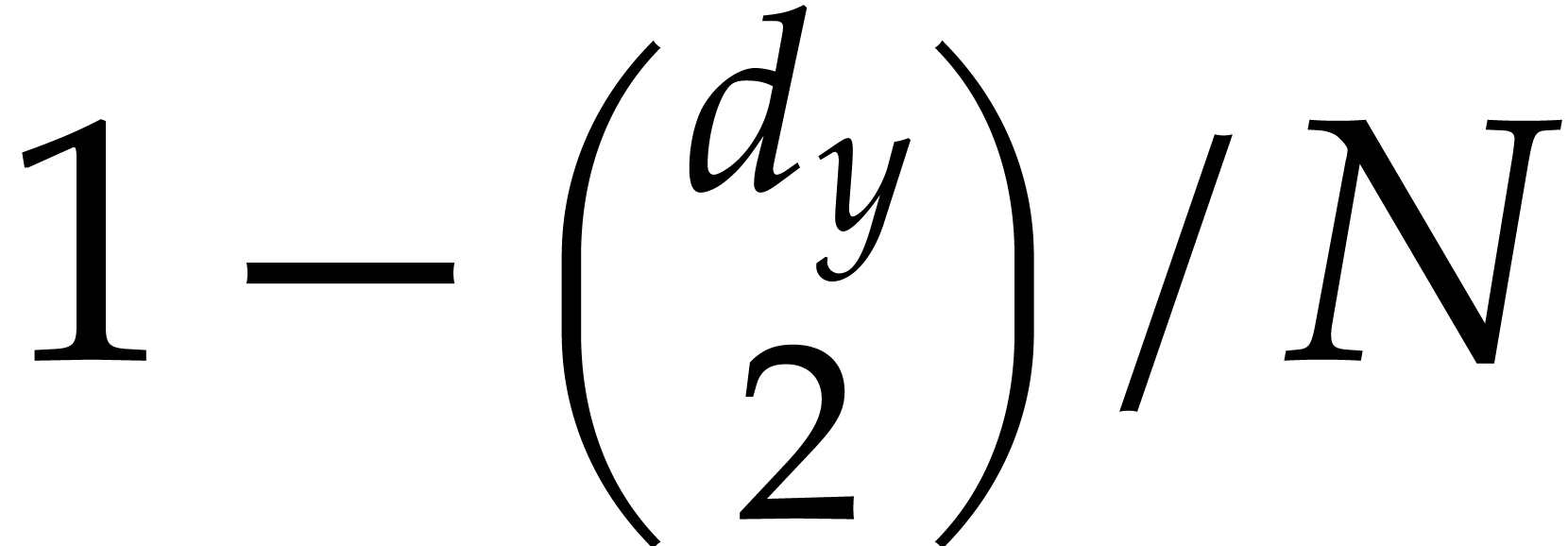 . The
probability that
. The
probability that 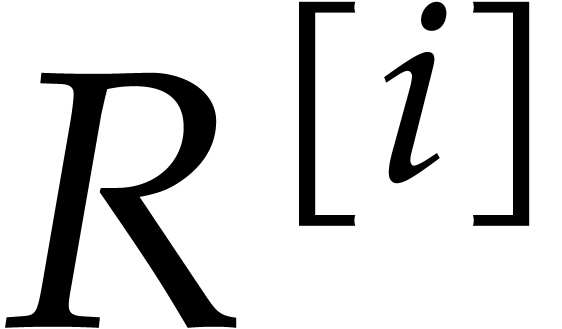 and
and 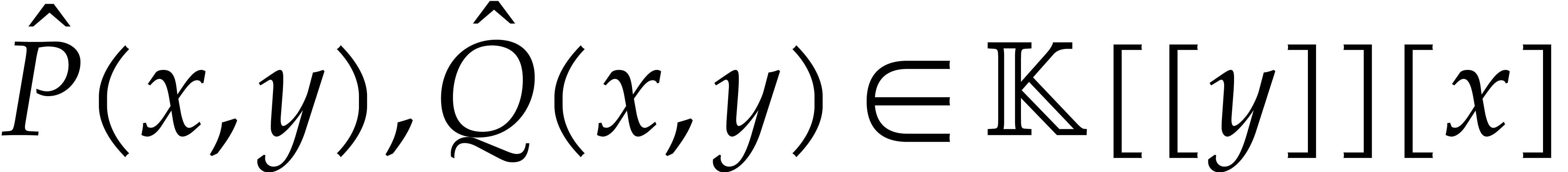 for
a random choice of
for
a random choice of 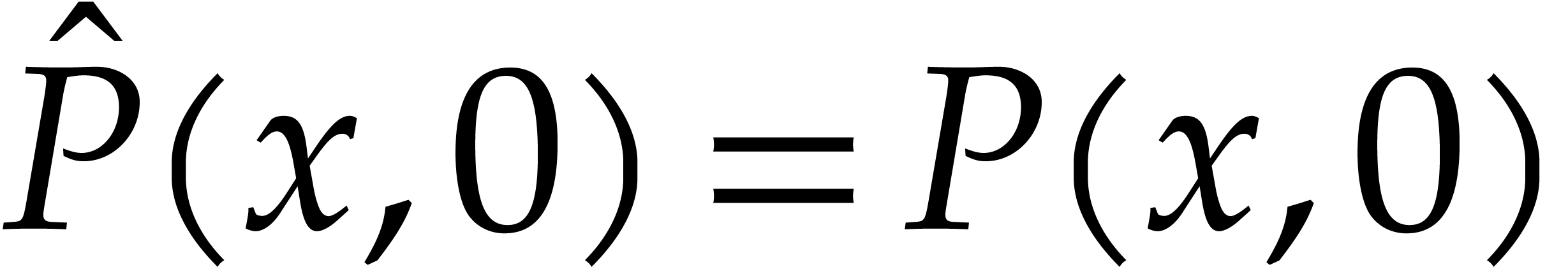 is at least
is at least 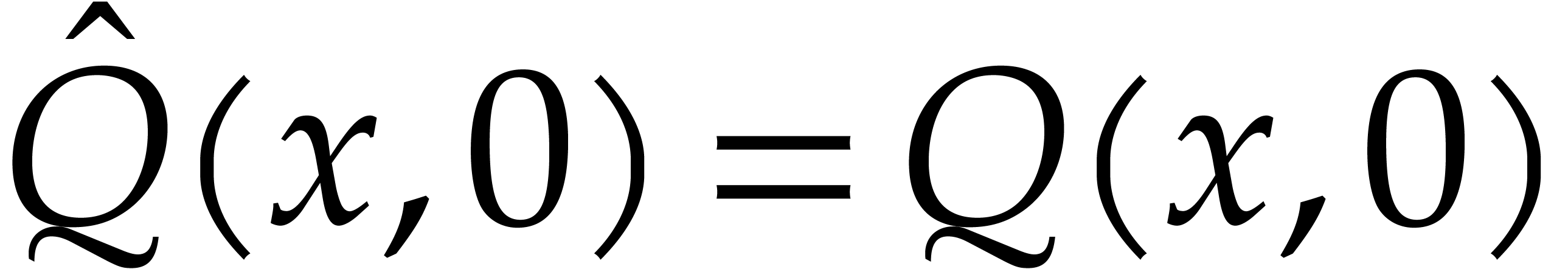 , by Lemma 2.1. In that case,
, by Lemma 2.1. In that case,  and the probability that
and the probability that  for
for
 is at least
is at least  ,
by Corollary 2.2.
,
by Corollary 2.2.
Let  be content-free in
be content-free in  and assume that
and assume that  has a non-trivial factorization
has a non-trivial factorization
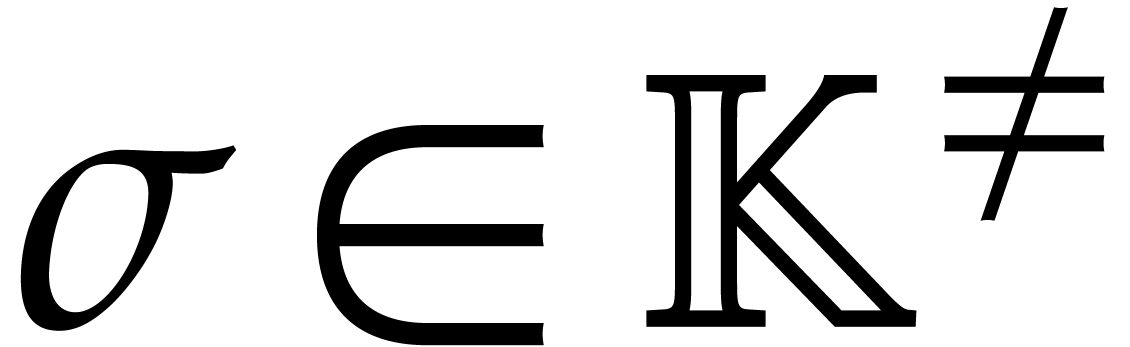 , and
, and 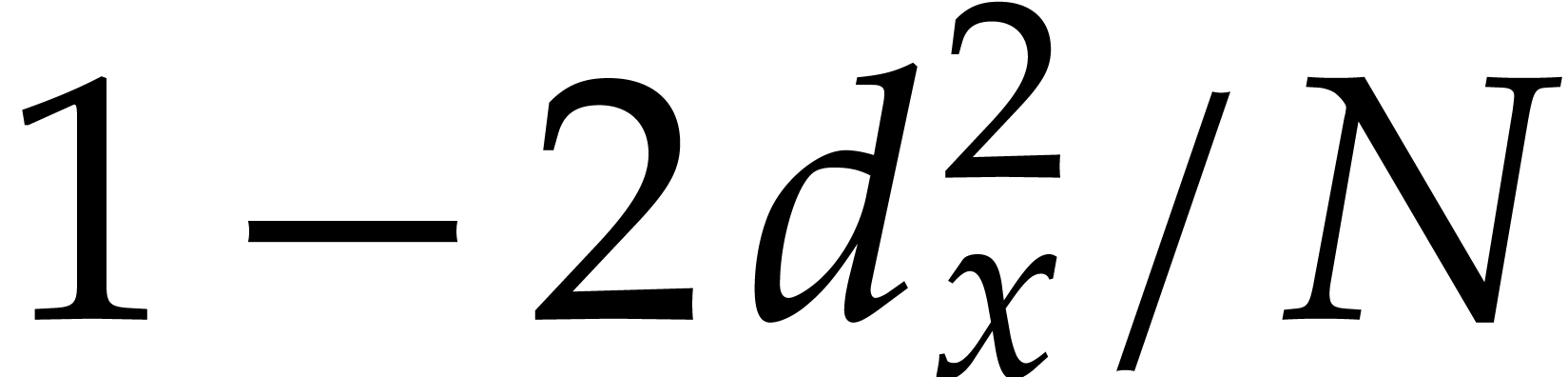 . Assume that
. Assume that 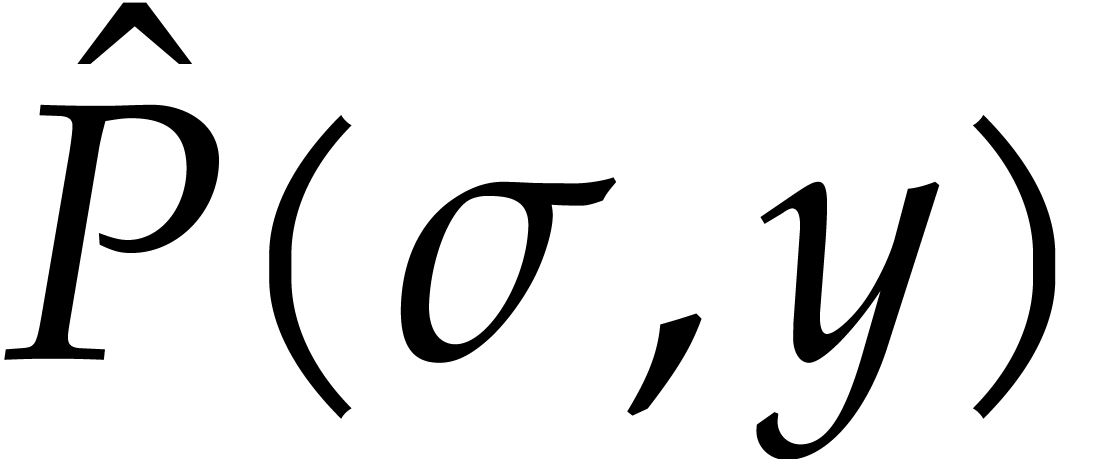 and that
and that 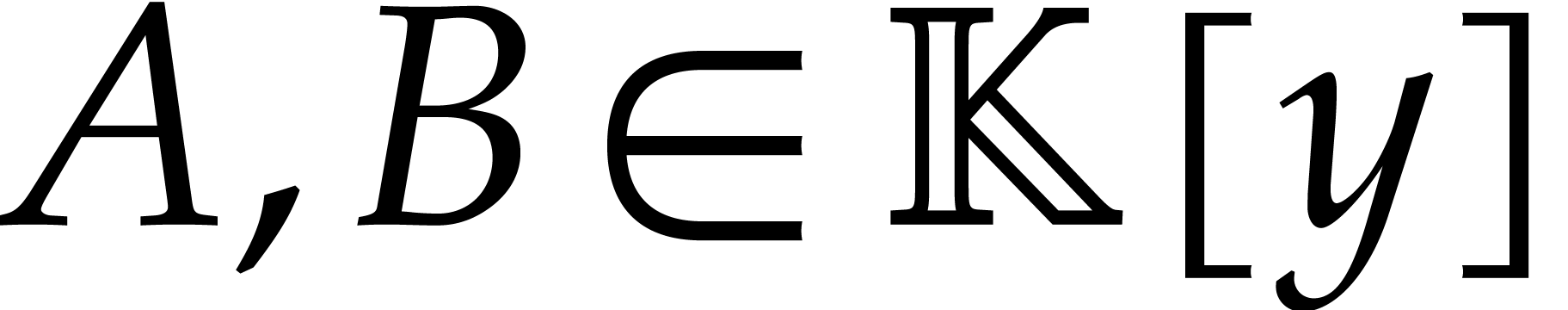 and
and 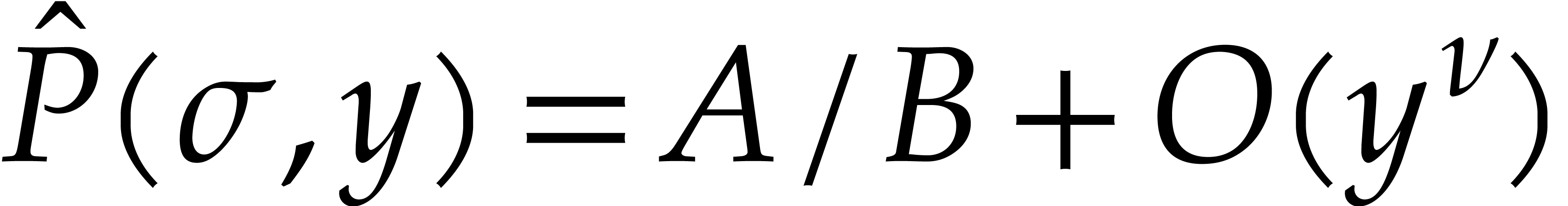 are known and coprime (in
particular
are known and coprime (in
particular  and
and 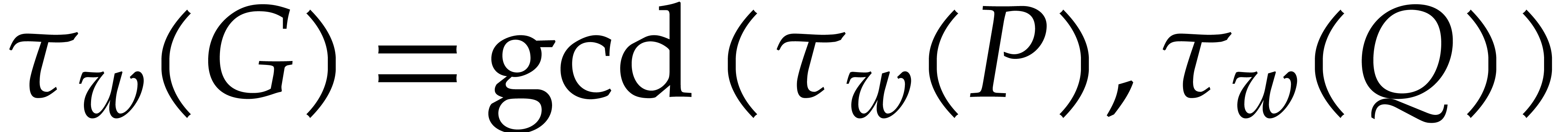 are
coprime). Using a random shift
are
coprime). Using a random shift 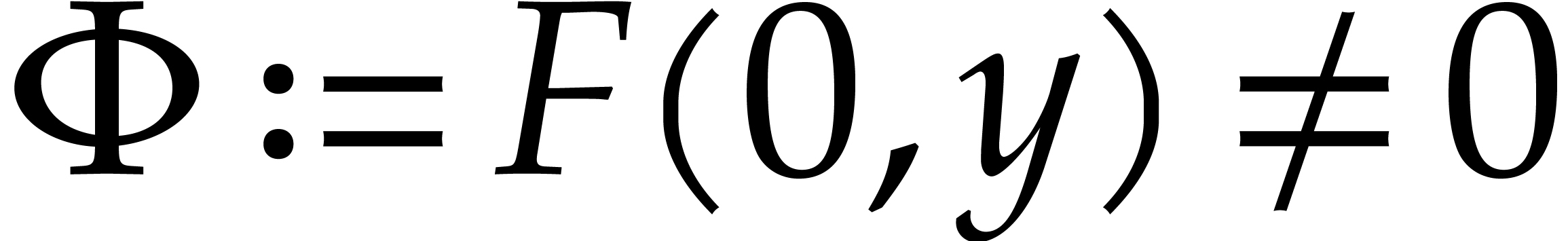 ,
these assumptions can be enforced with high probability, provided that
,
these assumptions can be enforced with high probability, provided that
 and
and 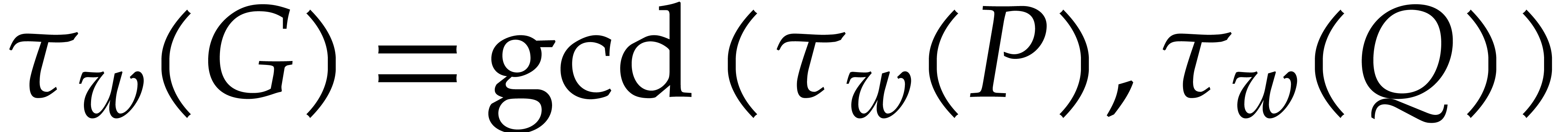 are coprime. Without
loss of generality we may also assume that we normalized the
factorization of
are coprime. Without
loss of generality we may also assume that we normalized the
factorization of 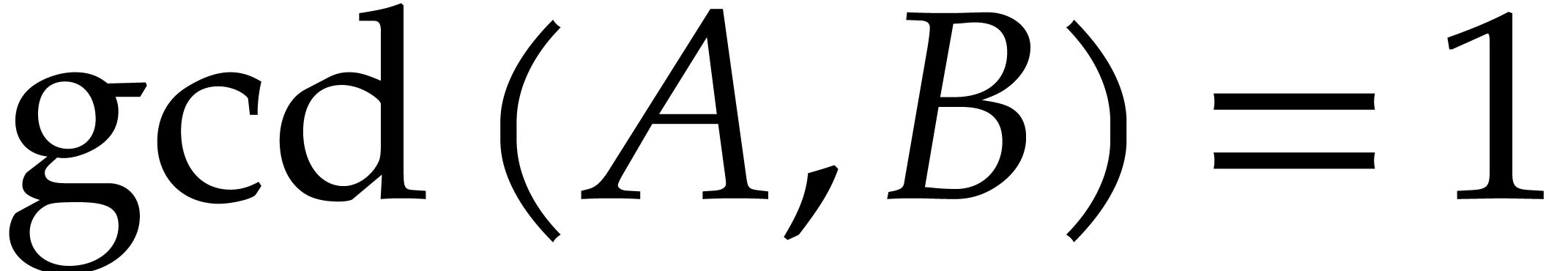 such that
such that 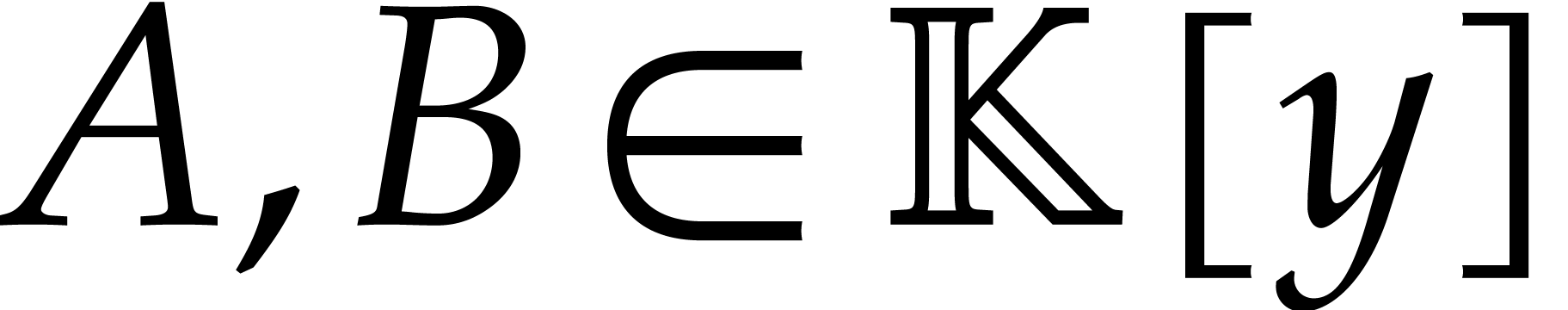 is monic. Under these assumptions, we may compute
is monic. Under these assumptions, we may compute  and
and 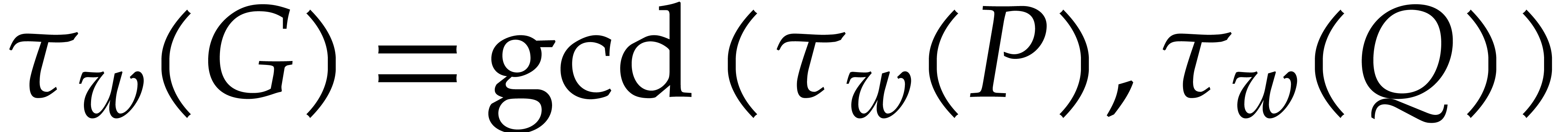 as follows:
as follows:
We first use Hensel lifting to obtain a factorization 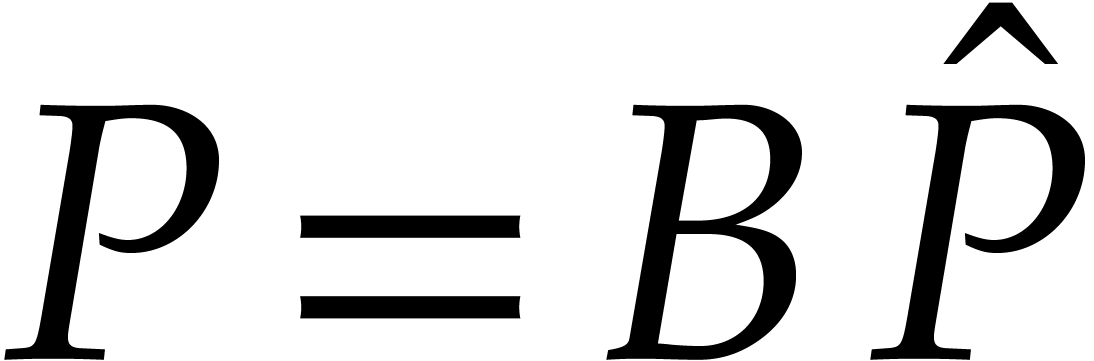 with
with 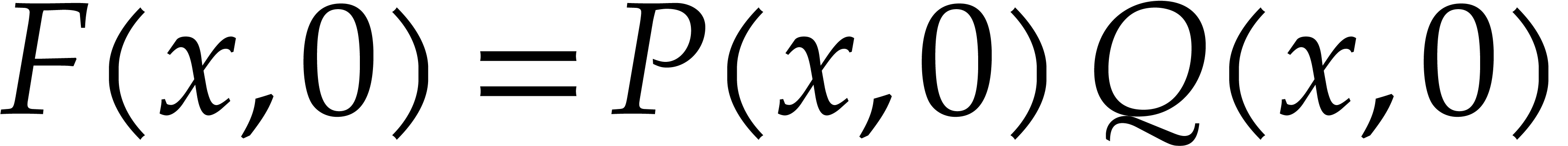 and
and  ,
,  ,
and such that
,
and such that 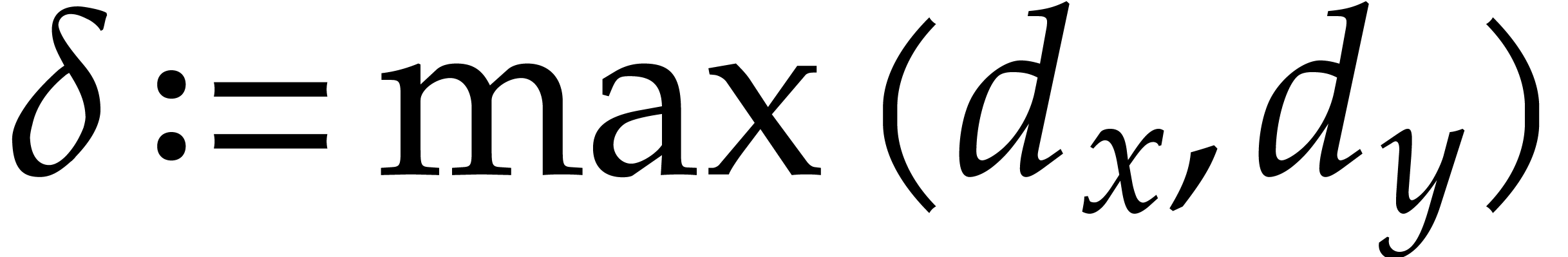 is monic in
is monic in  . We compute
. We compute 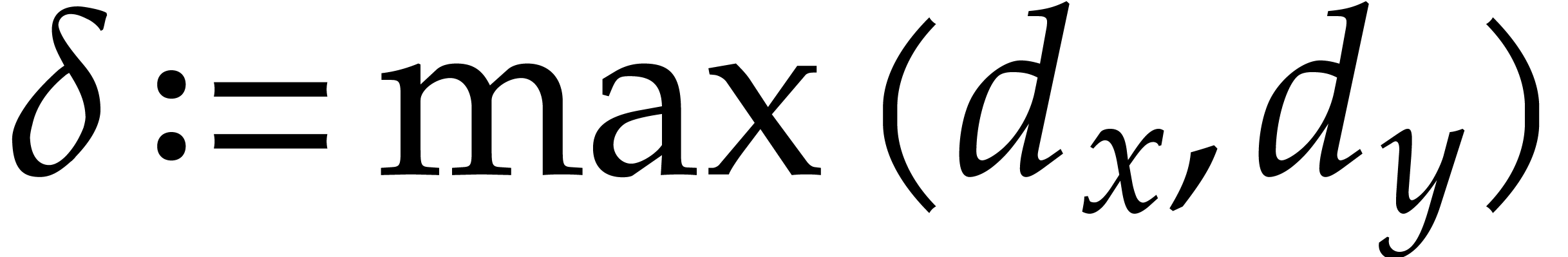 and
and
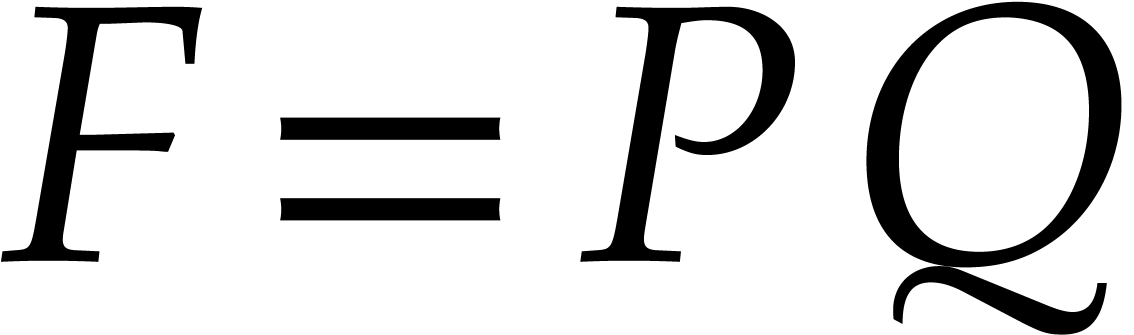 modulo
modulo  for
for  .
.
For a random shift 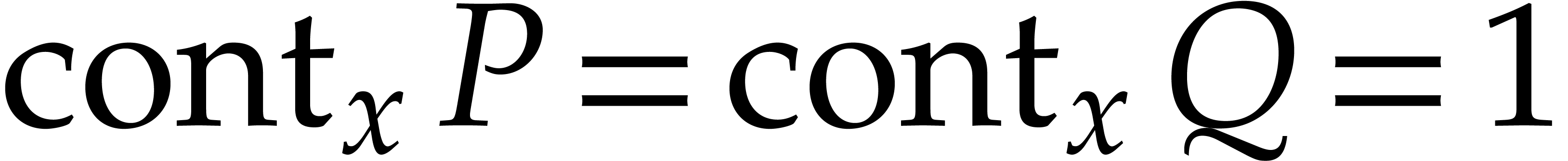 , we
apply rational function reconstruction [31, Section
5.7] to
, we
apply rational function reconstruction [31, Section
5.7] to  to obtain
to obtain 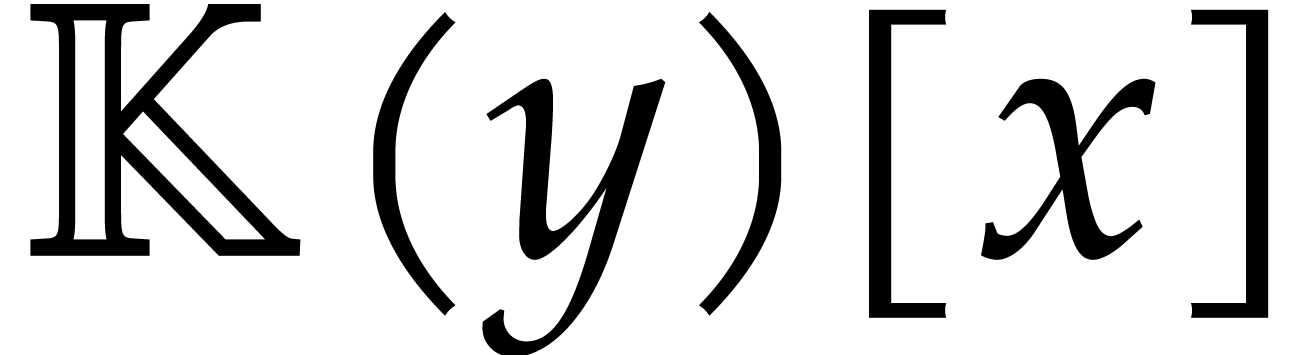 with
with  and
and  and
and  of the smallest possible degree with these
properties. With high probability, we then have
of the smallest possible degree with these
properties. With high probability, we then have 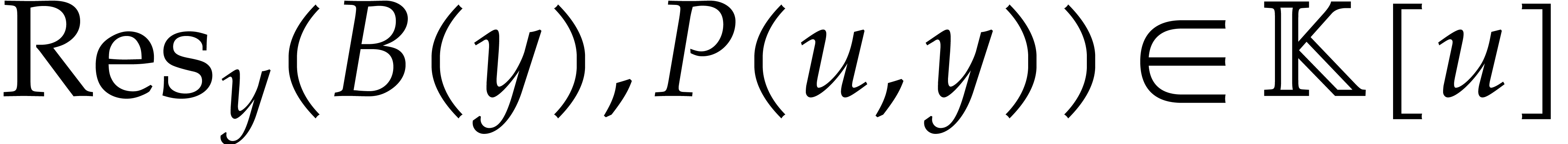 . We may compute
. We may compute 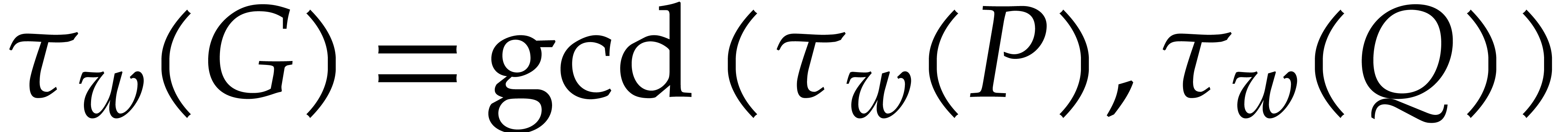 in
a similar way.
in
a similar way.
 and
and  satisfying the above assumptions, let
satisfying the above assumptions, let 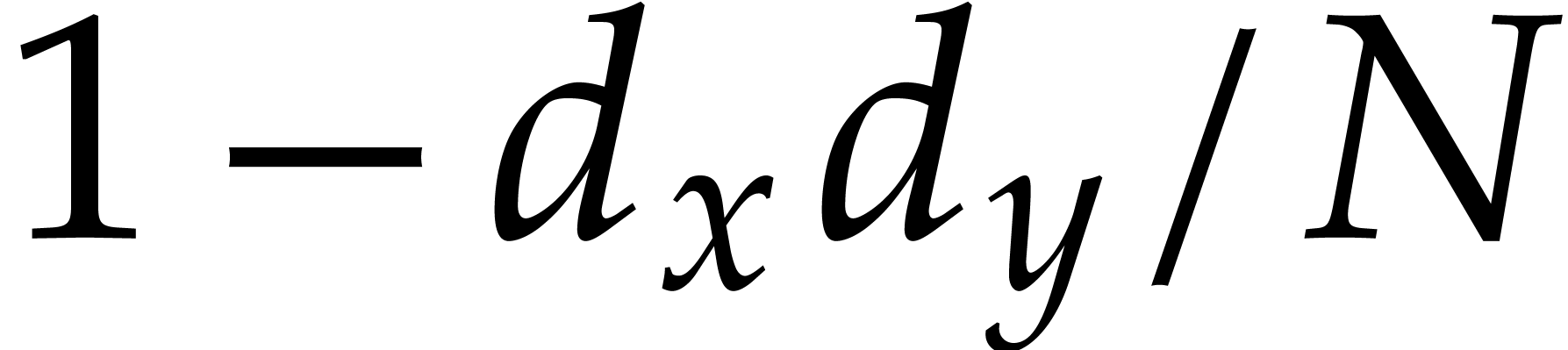 ,
, 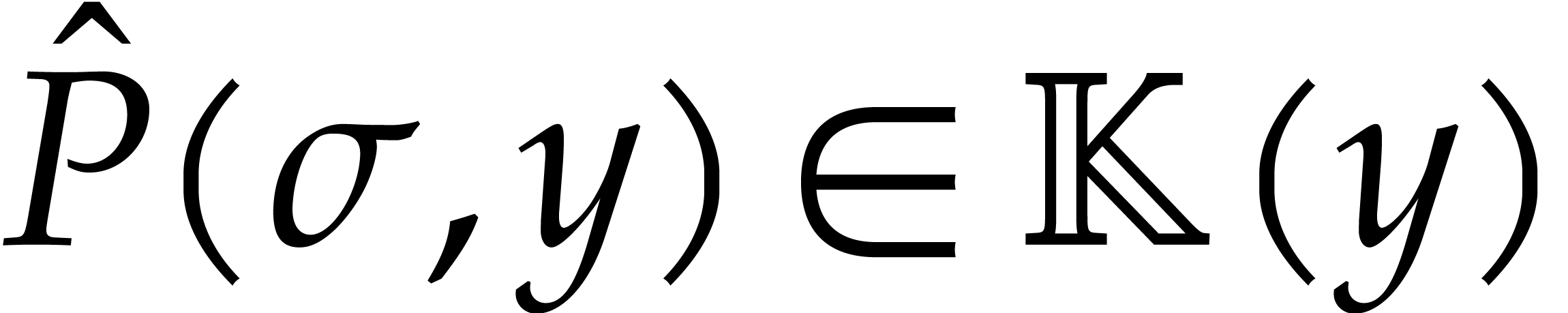 ,
and
,
and 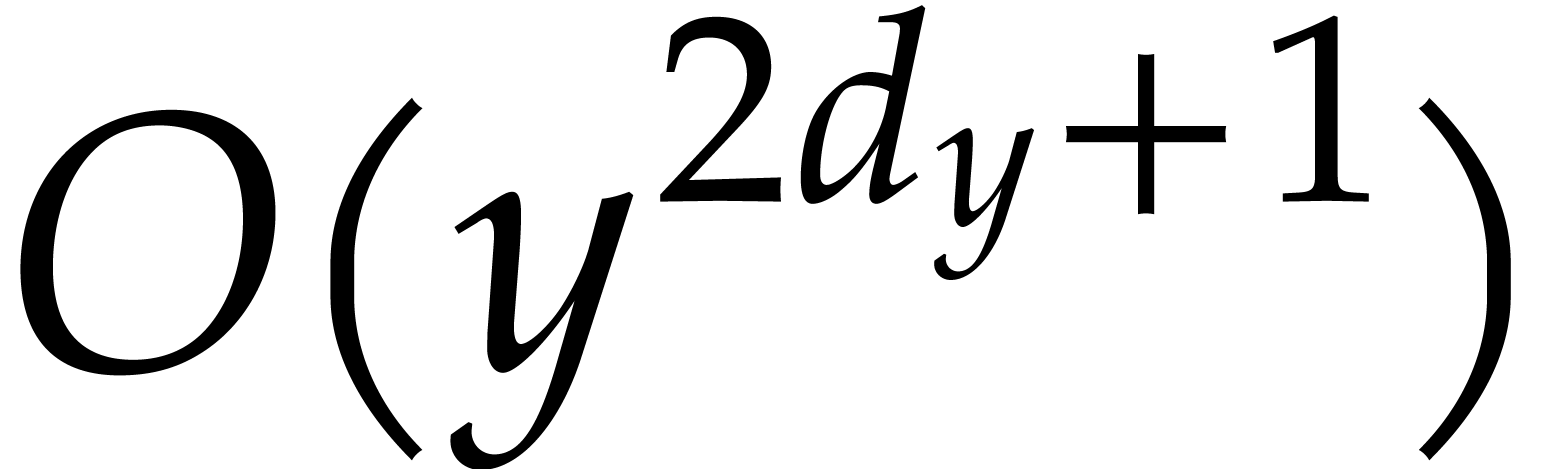 . We may lift the
factorization of
. We may lift the
factorization of 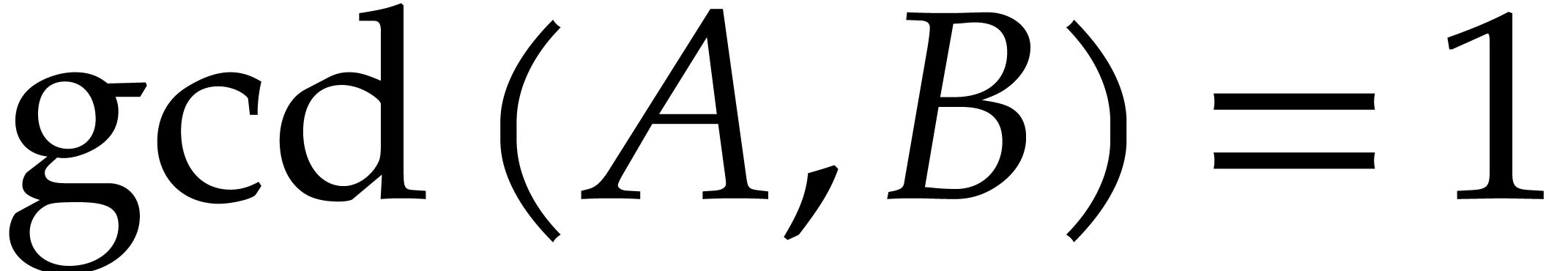 into a factorization
into a factorization 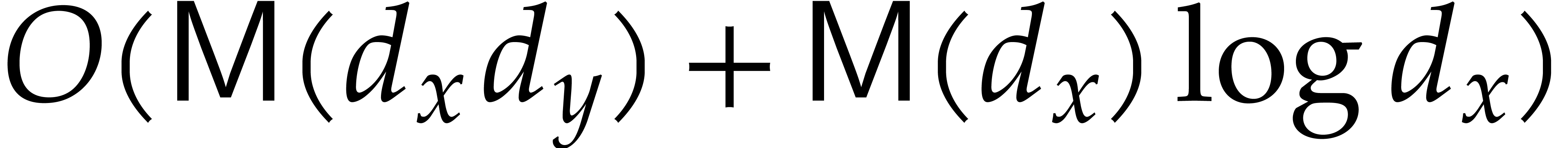 in time
in time
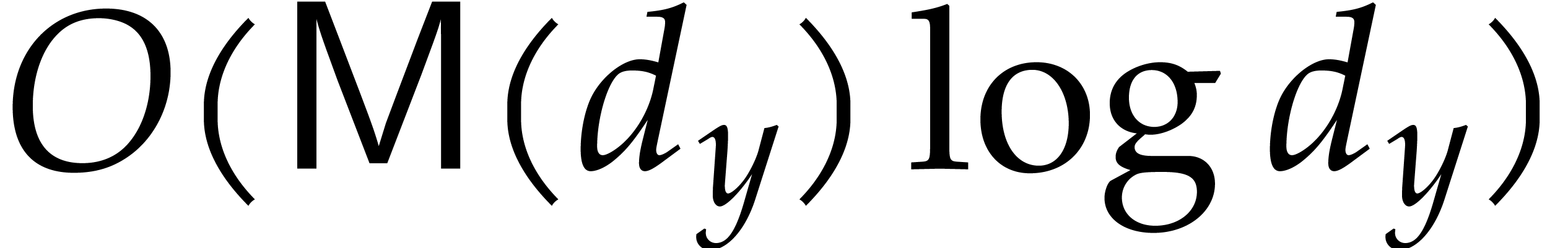
with a probability of success of at least  .
.
Proof. We first observe that there is a unique
factorization 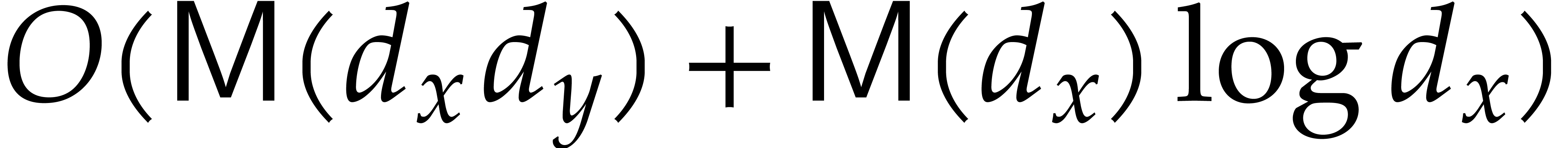 that lifts the factorization of
that lifts the factorization of
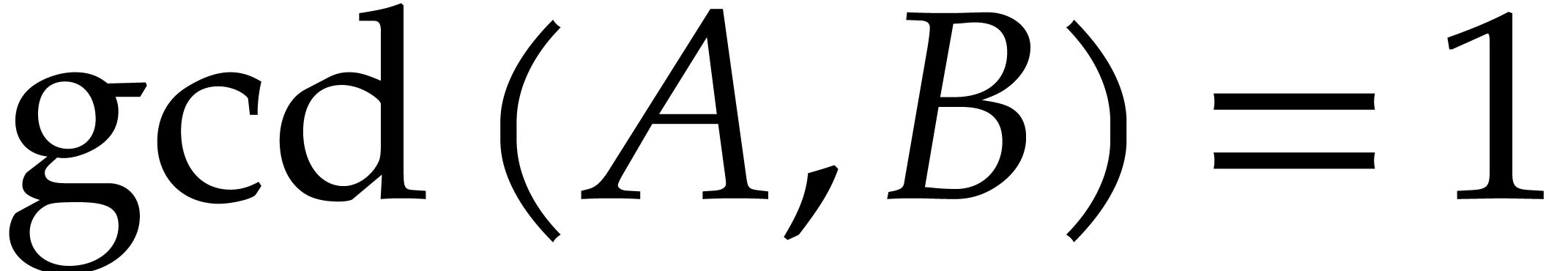 , thanks to our hypothesis
that
, thanks to our hypothesis
that 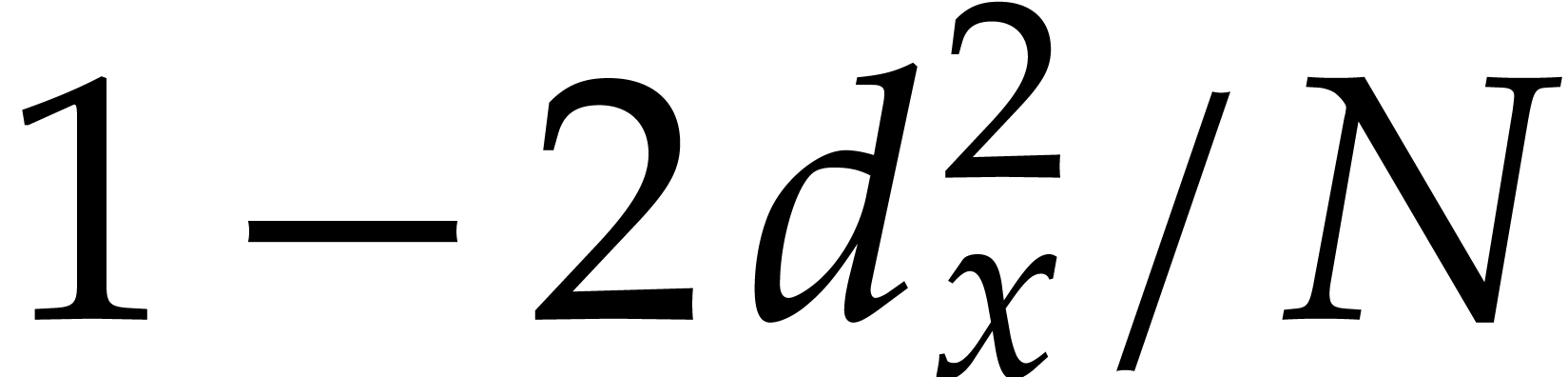 . Since this hypothesis
also implies that
. Since this hypothesis
also implies that  , the
denominator
, the
denominator 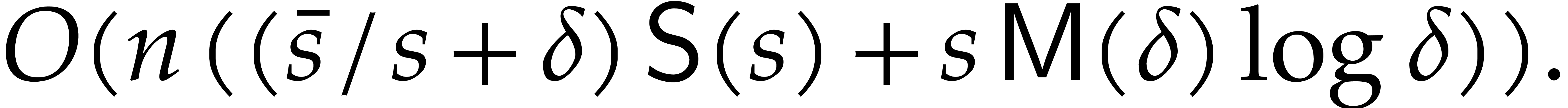 of
of 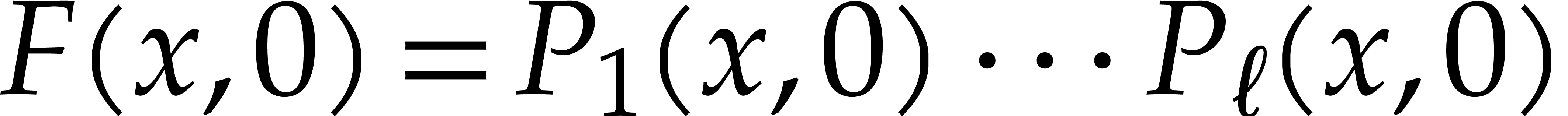 as an
element of
as an
element of  coincides with the leading
coefficient of
coincides with the leading
coefficient of  as a polynomial in
as a polynomial in 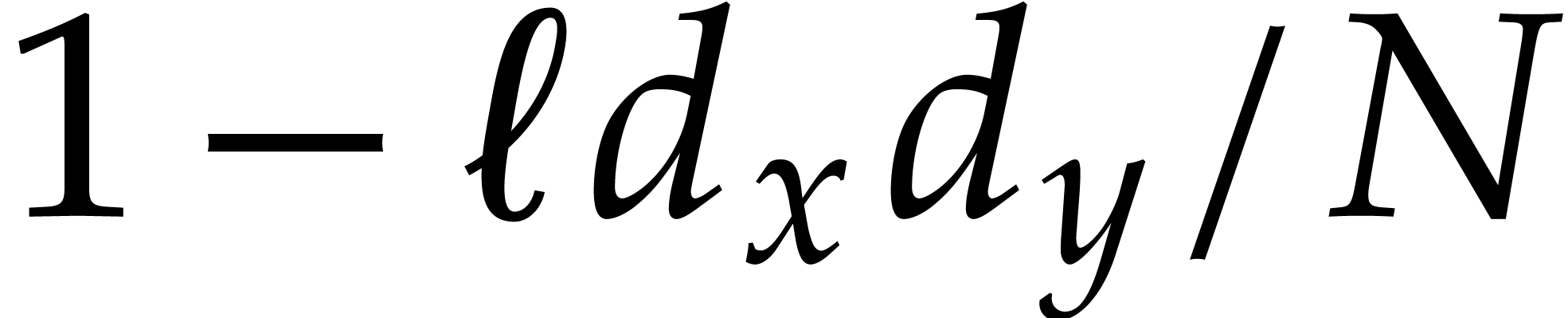 . Consequently, the denominator of
. Consequently, the denominator of  equals
equals 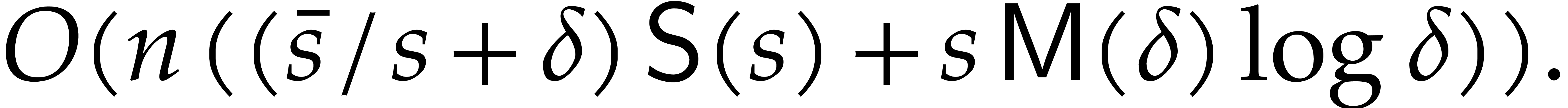 if and only if
if and only if  . Since the degree of
. Since the degree of  is bounded by
is bounded by  , this happens
with probability at least
, this happens
with probability at least  .
Since the degrees of the numerator
.
Since the degrees of the numerator 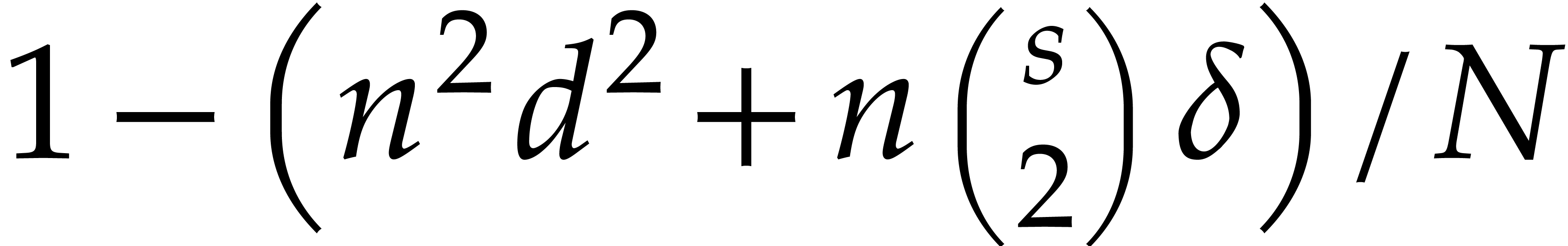 and
denominator
and
denominator 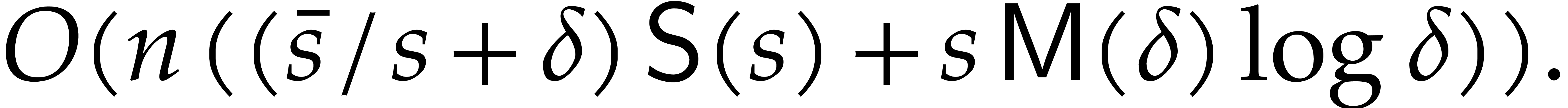 of
of  do not
exceed
do not
exceed  , it suffices to
compute
, it suffices to
compute 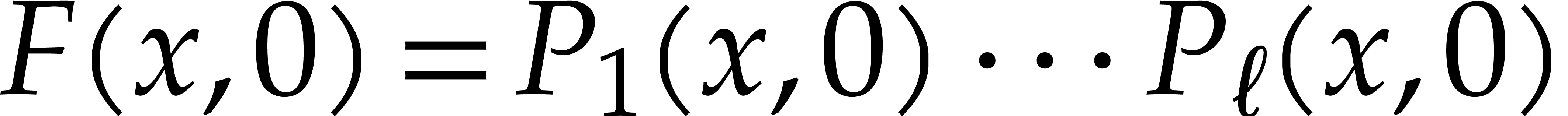 modulo
modulo 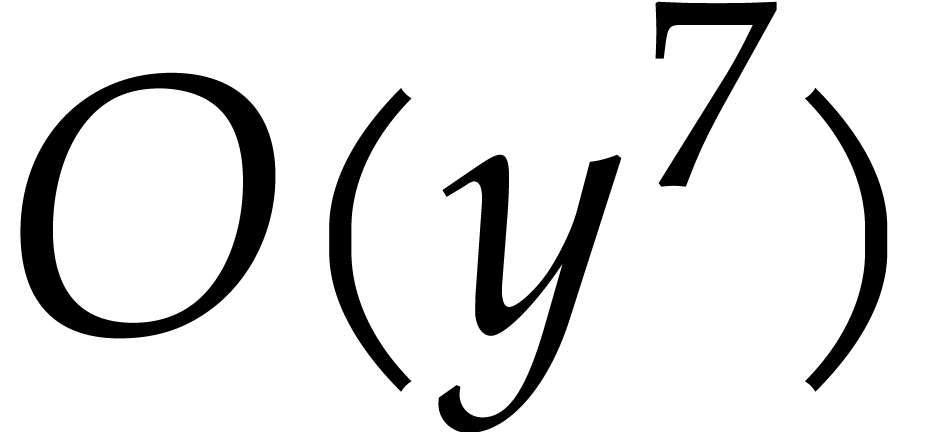 in order
to recover
in order
to recover 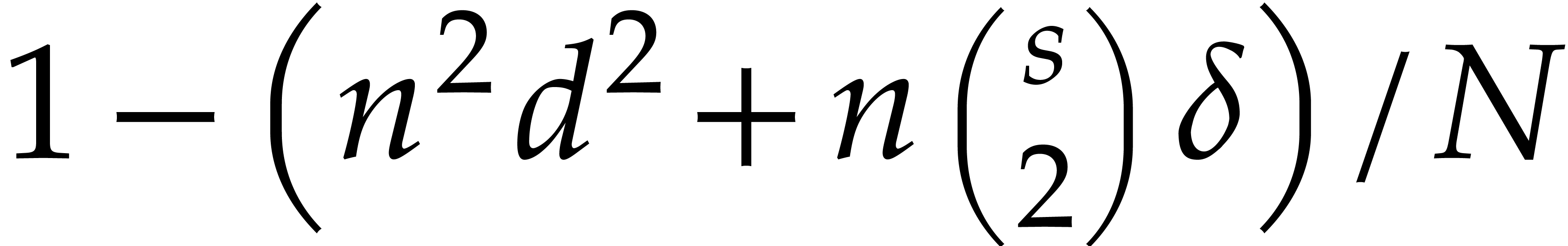 and
and 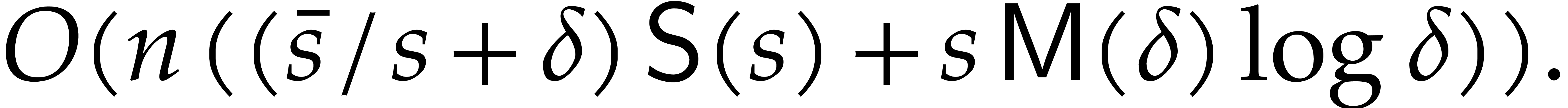 .
This completes the probabilistic correctness proof.
.
This completes the probabilistic correctness proof.
As to the complexity bound, the Hensel lifting requires 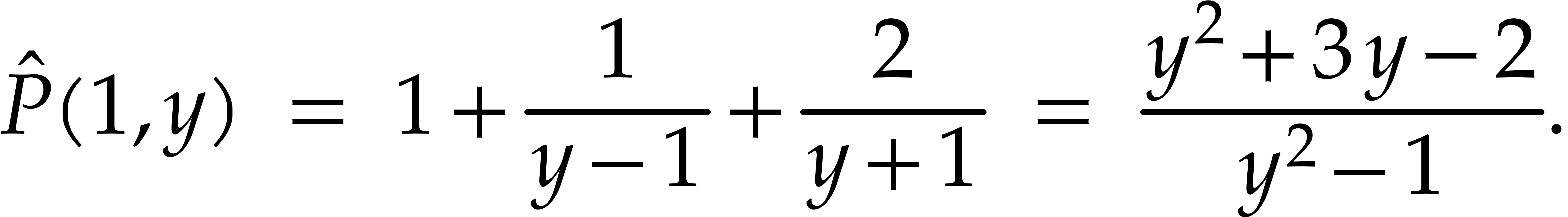 operations in
operations in  , when using a
fast Newton iteration [31, Theorem 15.18, two factors]. The
computation of
, when using a
fast Newton iteration [31, Theorem 15.18, two factors]. The
computation of  requires
requires 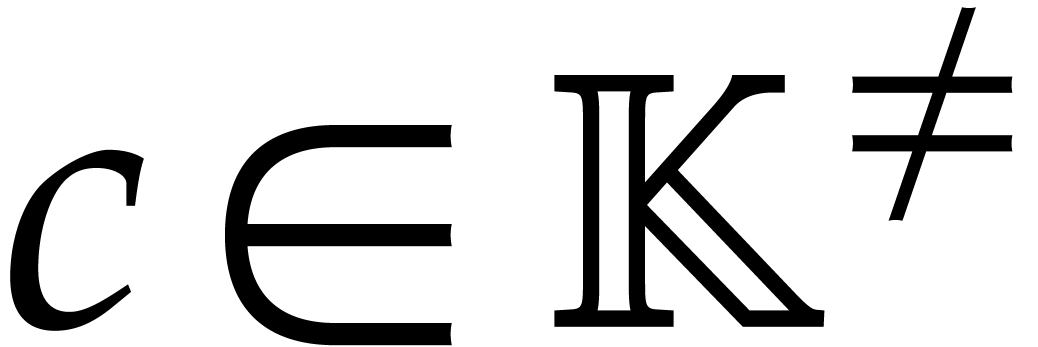 further operations and the rational function reconstruction can be done
in time
further operations and the rational function reconstruction can be done
in time 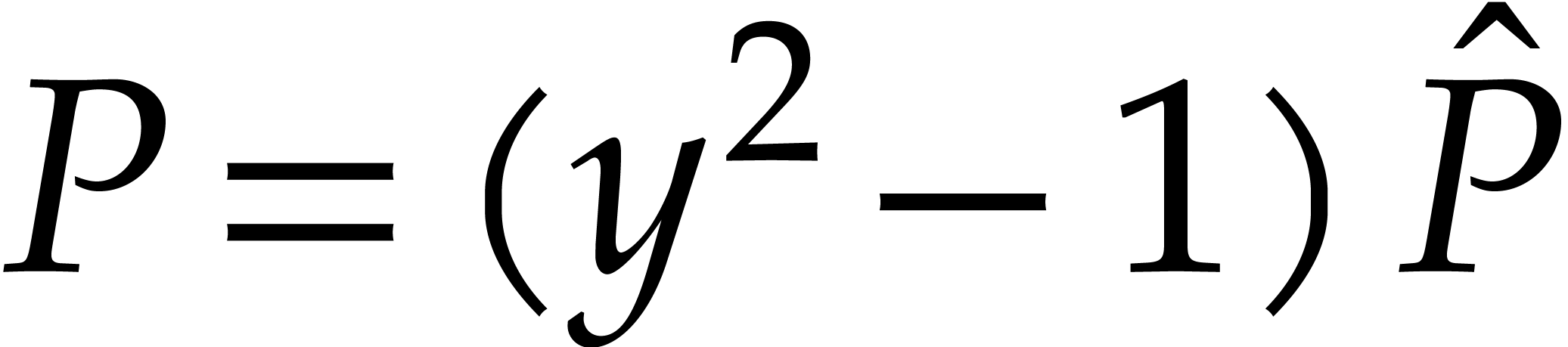 using the technique of half gcds [31, Chapter 11].
using the technique of half gcds [31, Chapter 11].
The proposition generalizes in a straightforward way to the case when
 has
has  pairwise coprime
factors
pairwise coprime
factors  . In that case, one
may use fast multifactor Hensel lifting [31, Theorem
15.18], to obtain the following:
. In that case, one
may use fast multifactor Hensel lifting [31, Theorem
15.18], to obtain the following:
 be such that
be such that  and
and  .
Assume that
.
Assume that  can be factored as
can be factored as 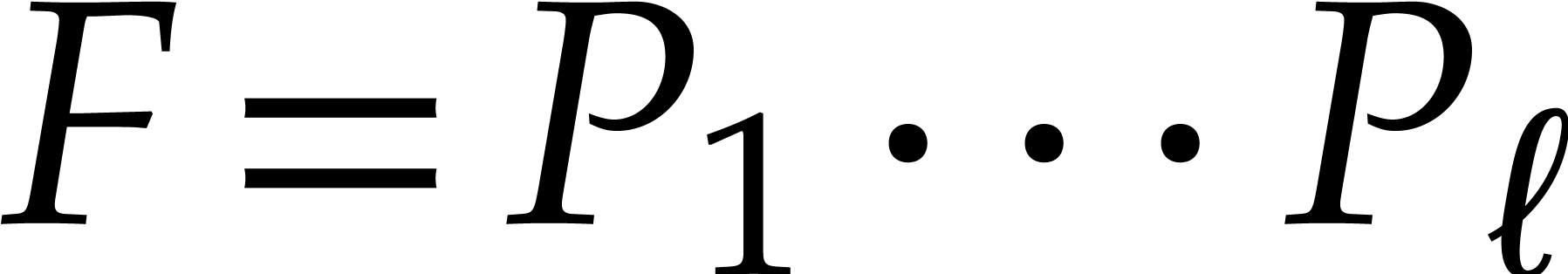 , where
, where  are pairwise
coprime and known. Assume also that
are pairwise
coprime and known. Assume also that  are monic.
Then we may lift the factorization
are monic.
Then we may lift the factorization  into a
factorization
into a
factorization 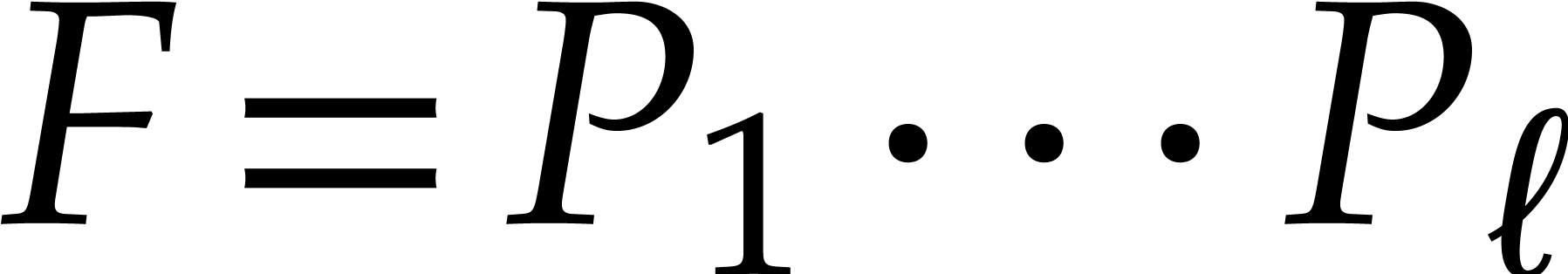 in time
in time
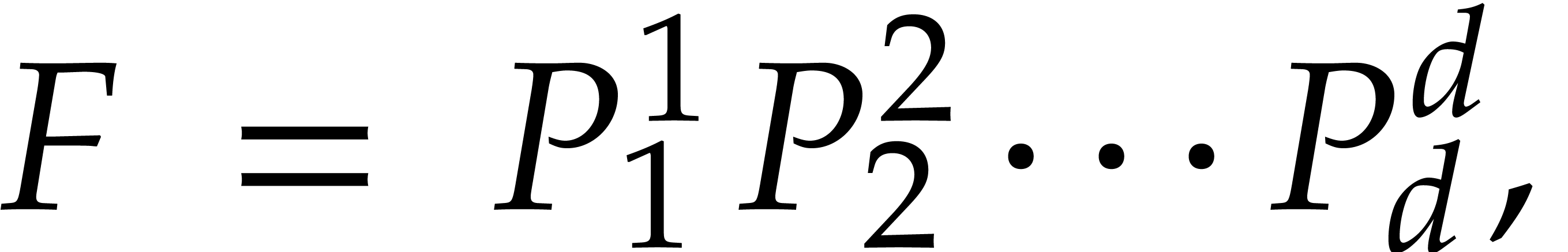
 .
.

Example

with
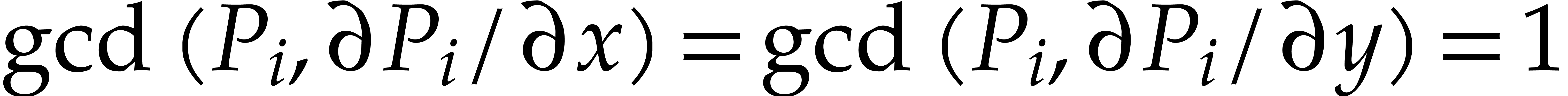
This factorization lifts to the following factorization of  in
in  :
:
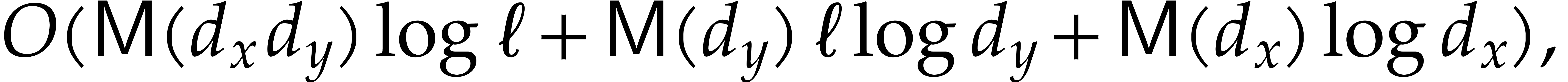
Taking 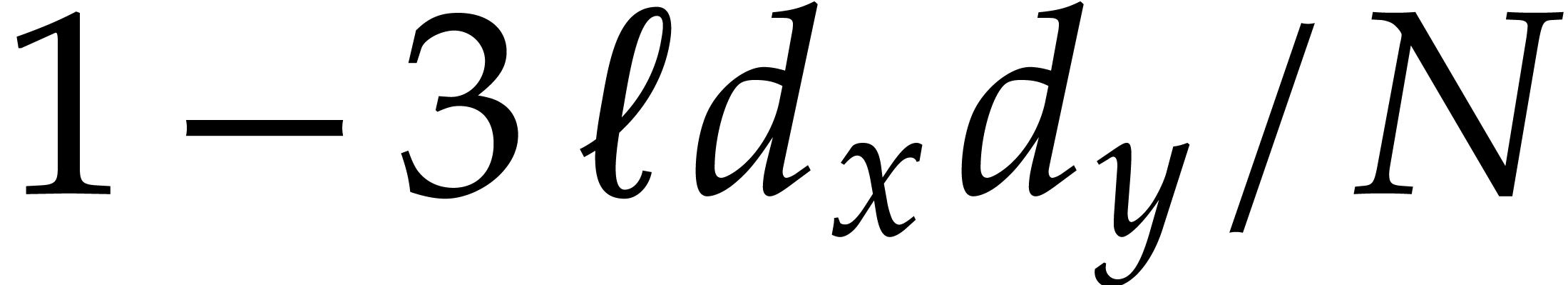 , we obtain the
following rational reconstruction of
, we obtain the
following rational reconstruction of  up to the
order
up to the
order  :
:
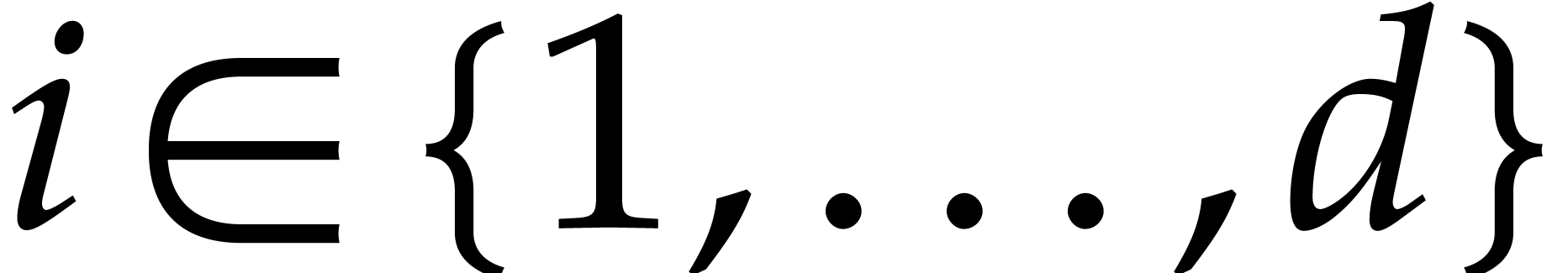
Consequently,  is the sought factor of
is the sought factor of  in
in 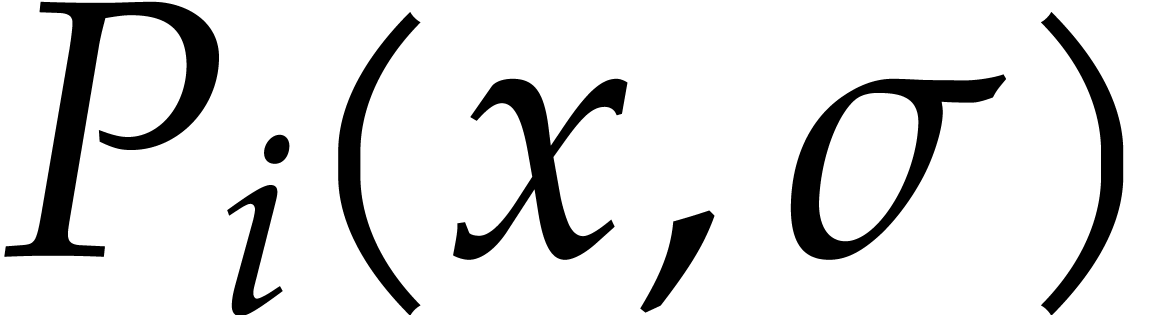 . In a
similar way, we find that
. In a
similar way, we find that  .
.
Assume that  is content-free in
is content-free in 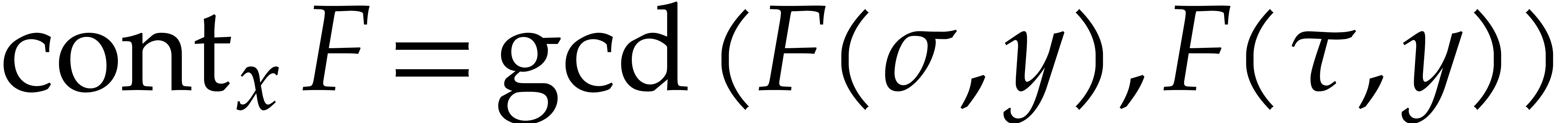 and of total degree
and of total degree  . Assume
also that
. Assume
also that  . Recall that the
square-free factorization of
. Recall that the
square-free factorization of  is of the
form
is of the
form
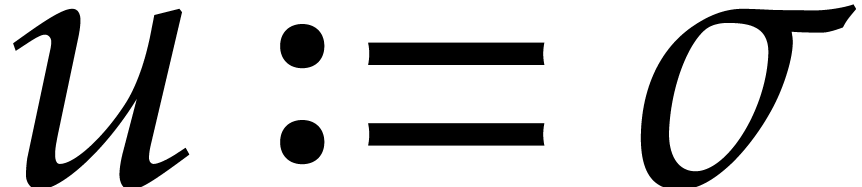
where each 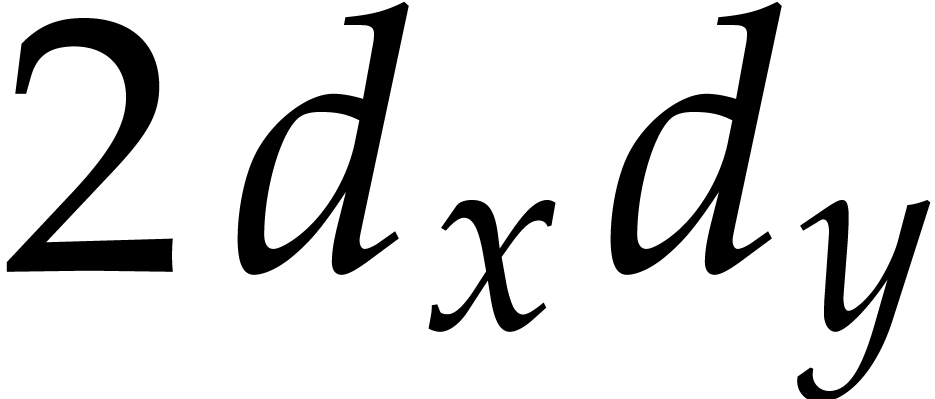 is the product of all irreducible
factors of
is the product of all irreducible
factors of  that occur with multiplicity
that occur with multiplicity  . Note that some of the
. Note that some of the 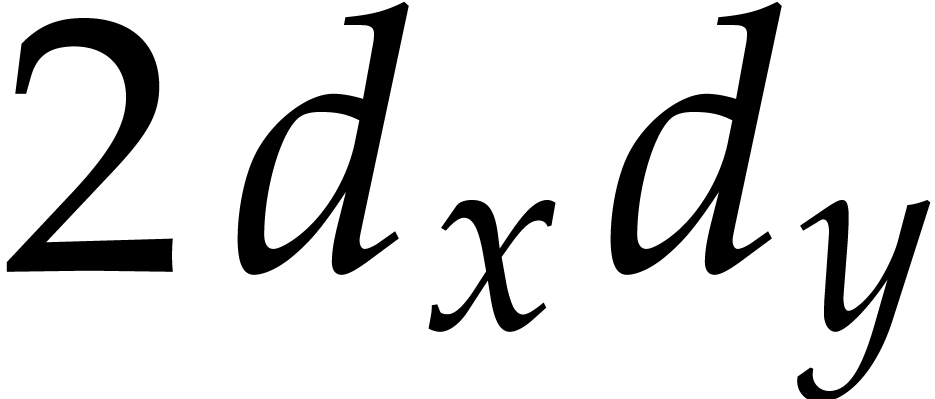 are allowed to be units in
are allowed to be units in  and
that the
and
that the 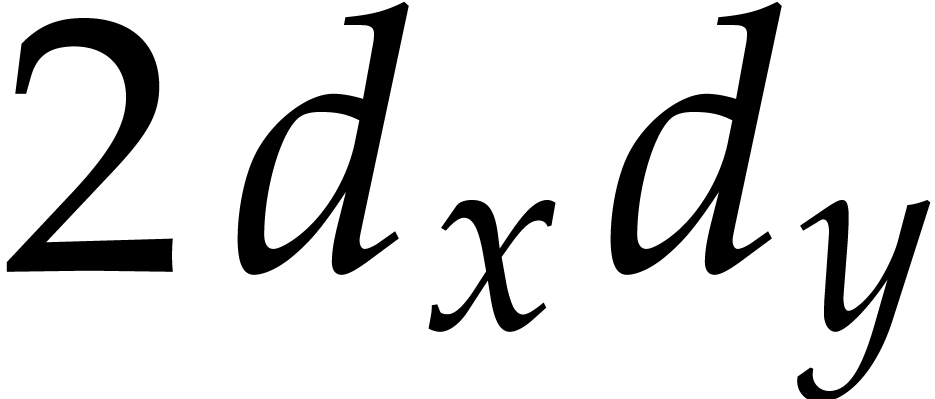 are unique up to multiplication by such
units. The polynomials
are unique up to multiplication by such
units. The polynomials 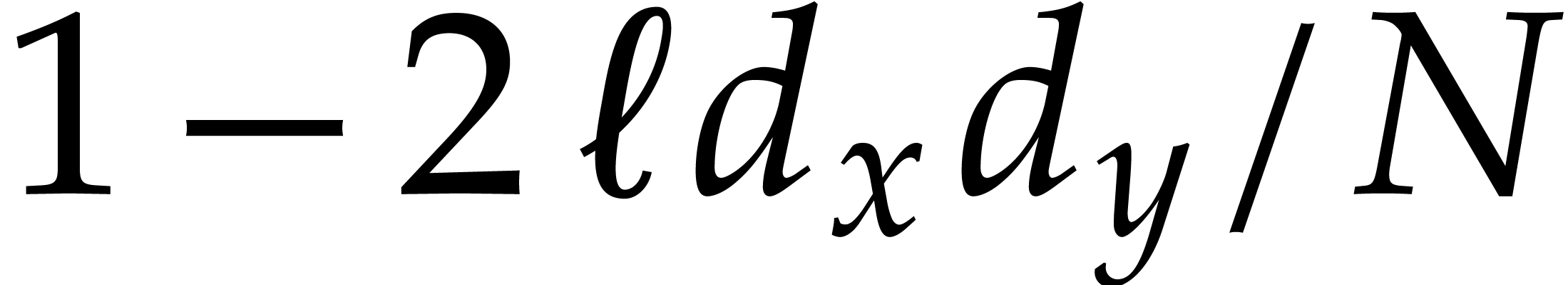 are pairwise coprime.
Since
are pairwise coprime.
Since  , they must also be
separable in both
, they must also be
separable in both  and
and 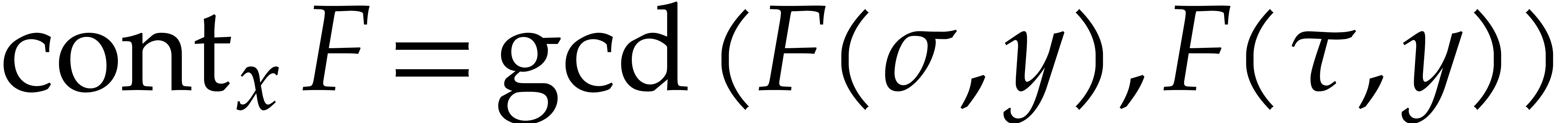 (i.e.
(i.e. 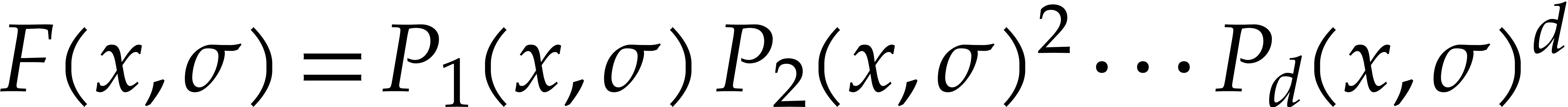 ). The
square-free factorization of
). The
square-free factorization of  can be computed
efficiently as follows:
can be computed
efficiently as follows:
For a random shift  ,
replace
,
replace  by
by  .
.
Compute the square-free factorization of 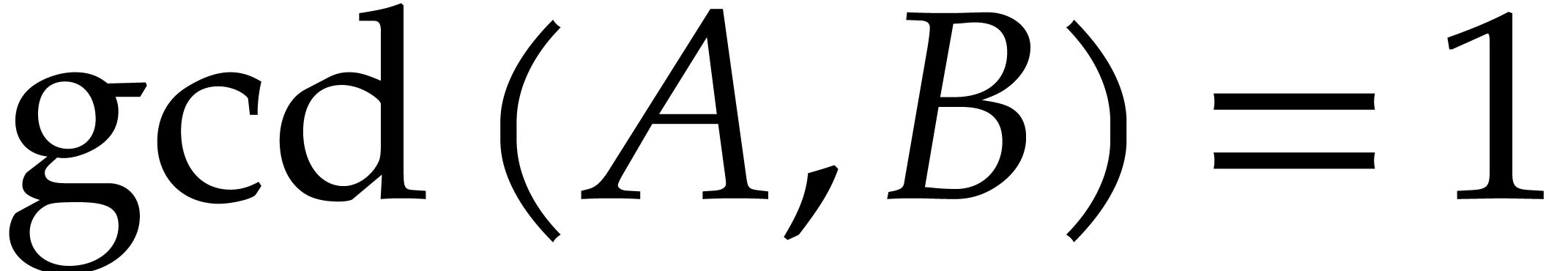 .
.
Hensel lift this into the square-free factorization of  using Proposition 4.4.
using Proposition 4.4.
Apply the shift in the opposite direction.
 is
content-free in
is
content-free in 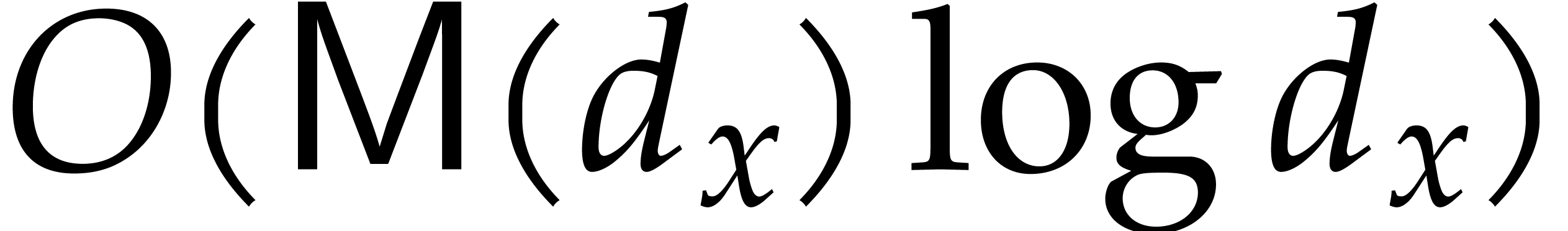 and that
and that  . We can compute the square-free
factorization of
. We can compute the square-free
factorization of  in time
in time

with a probability of success of at least  , where
, where  .
.
Proof. Given 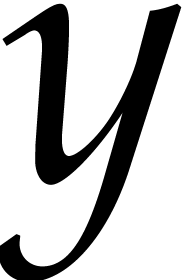 ,
consider
,
consider 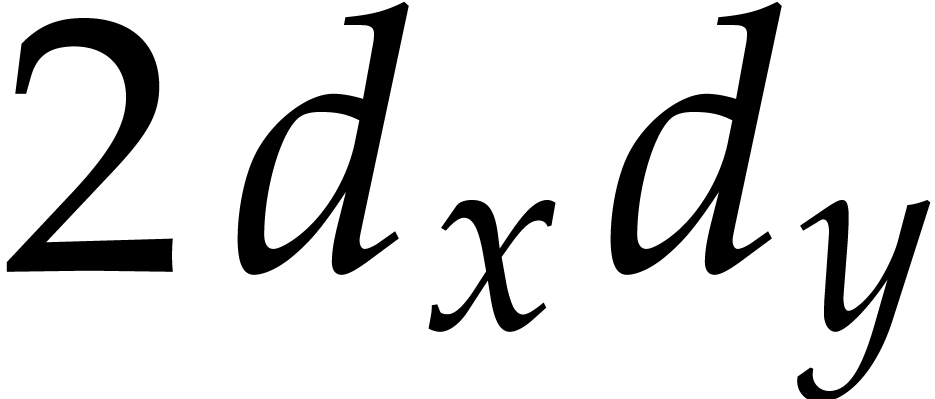 and
and 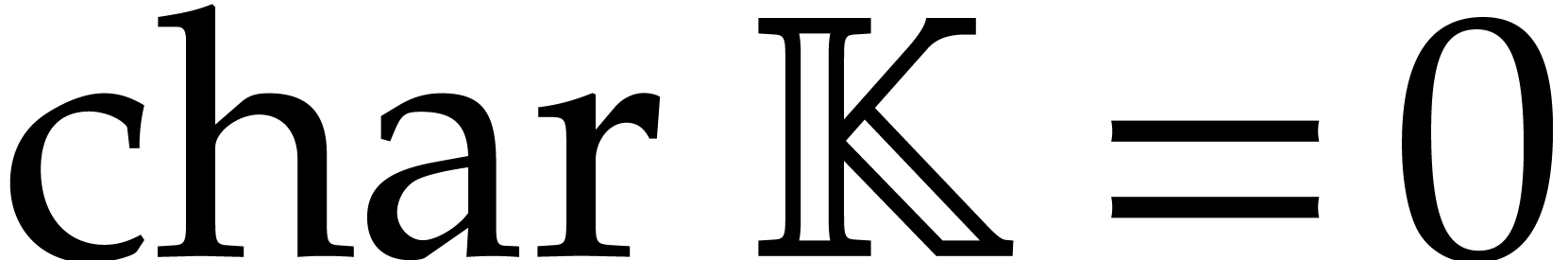 .
The polynomials
.
The polynomials 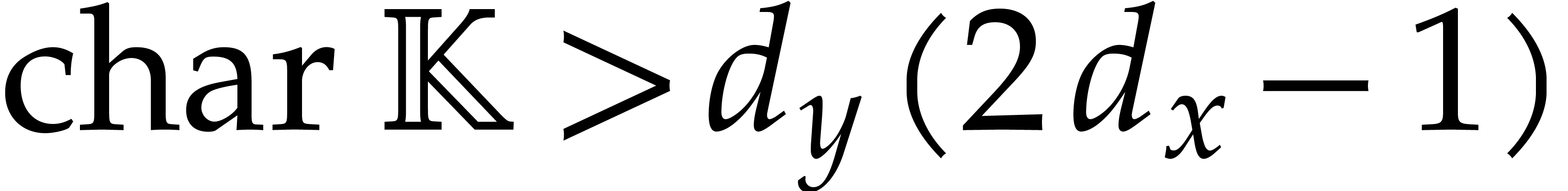 and
and  are
coprime if and only if
are
coprime if and only if 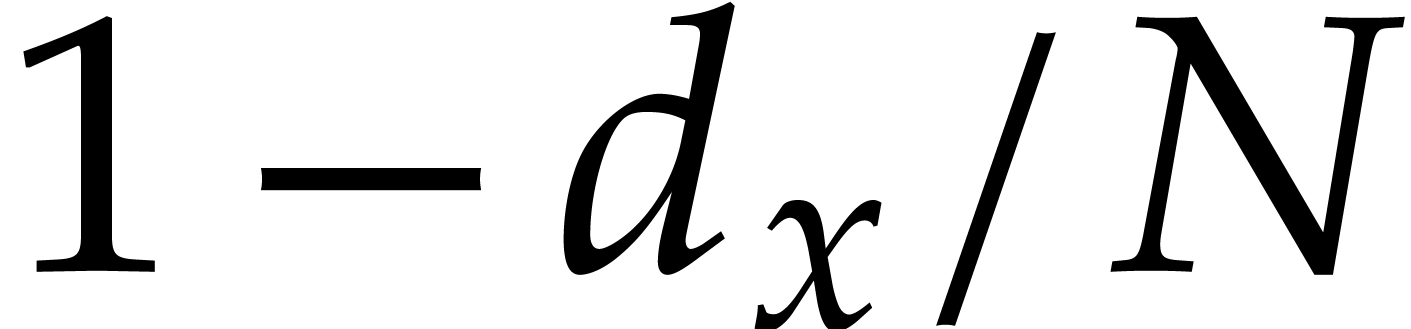 does not vanish at
does not vanish at  . Since this resultant has degree
at most
. Since this resultant has degree
at most 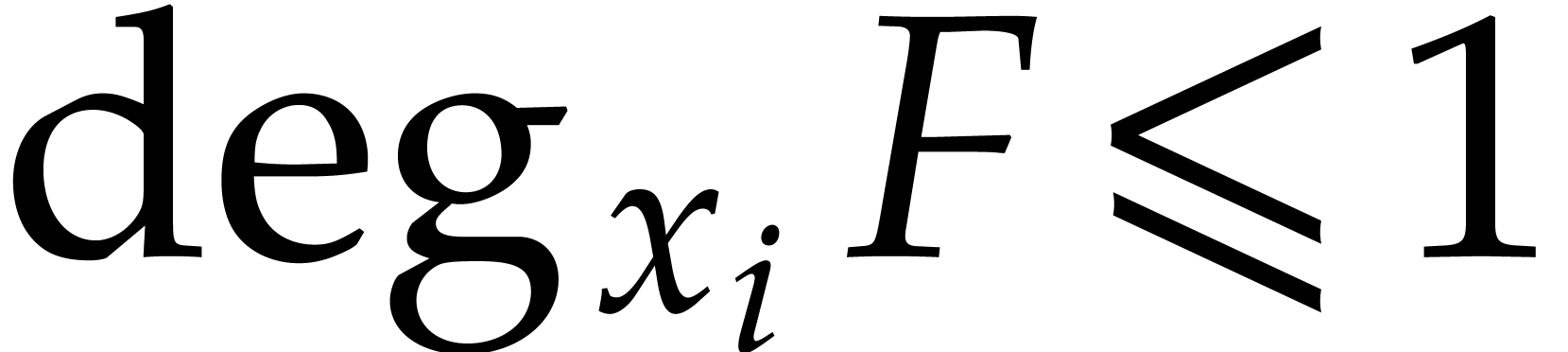 , this happens with
probability
, this happens with
probability  . Therefore, the
probability that all
. Therefore, the
probability that all 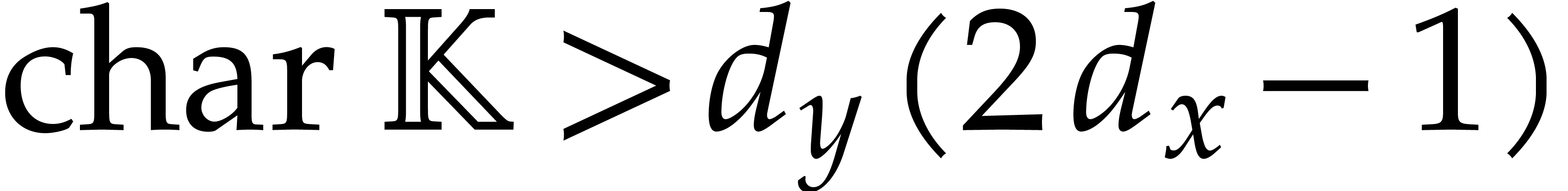 are pairwise coprime and
all
are pairwise coprime and
all 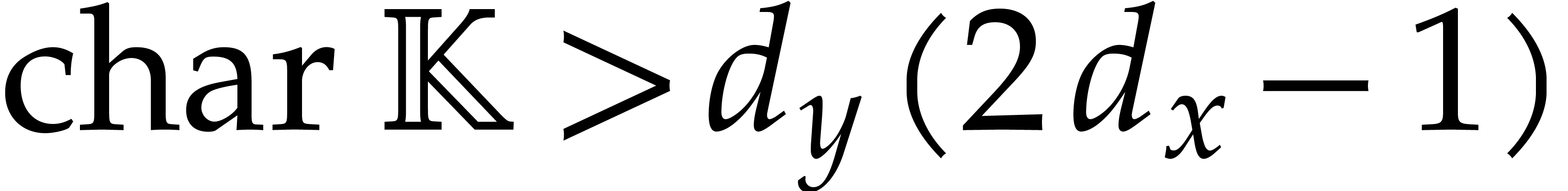 are separable is at least
are separable is at least  . In that case,
. In that case,  is the
square-free decomposition of
is the
square-free decomposition of  .
Modulo normalization, we are thus in the position to apply Proposition
4.4. This proves the probabilistic correctness of the
algorithm.
.
Modulo normalization, we are thus in the position to apply Proposition
4.4. This proves the probabilistic correctness of the
algorithm.
The computation of the shift 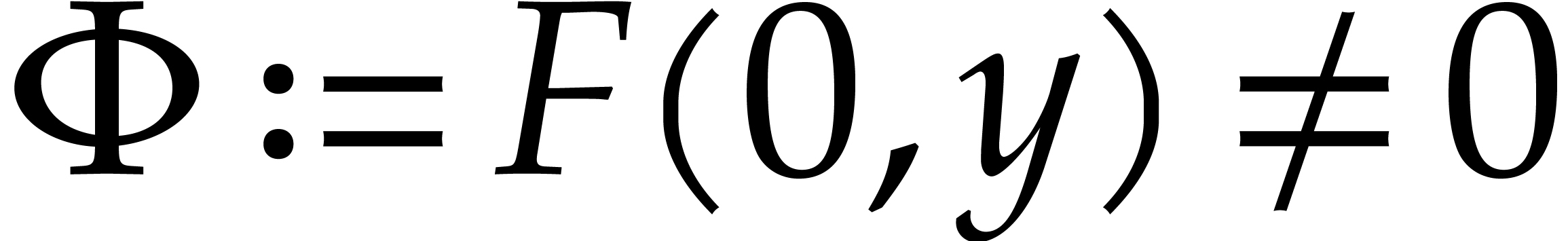 can be done in time
can be done in time
 using the algorithm from [2,
Theorem 5] and the same holds for the shifts in the opposite direction
in the last step. The square-free factorization of the univariate
polynomial
using the algorithm from [2,
Theorem 5] and the same holds for the shifts in the opposite direction
in the last step. The square-free factorization of the univariate
polynomial 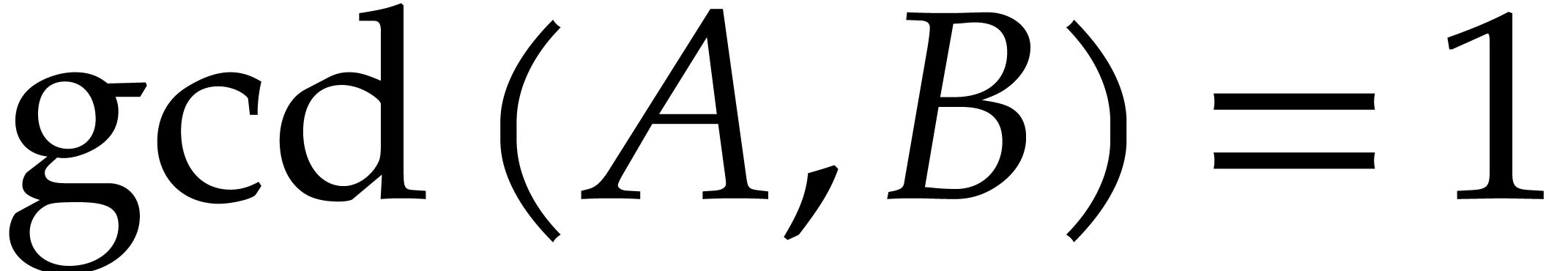 can be done in time
can be done in time 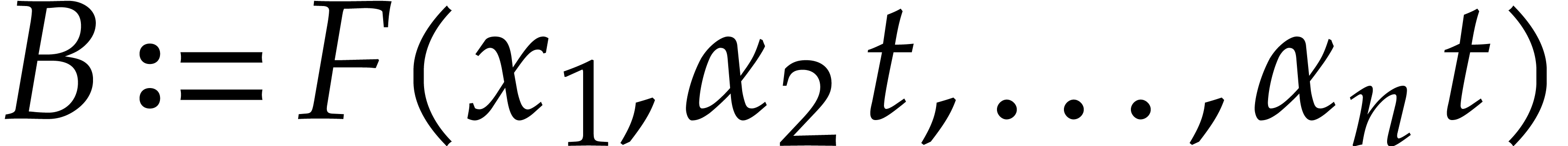 : see [106] and [31,
Theorem 14.23]. We conclude with Proposition 4.4.
: see [106] and [31,
Theorem 14.23]. We conclude with Proposition 4.4.
General bivariate factorization of 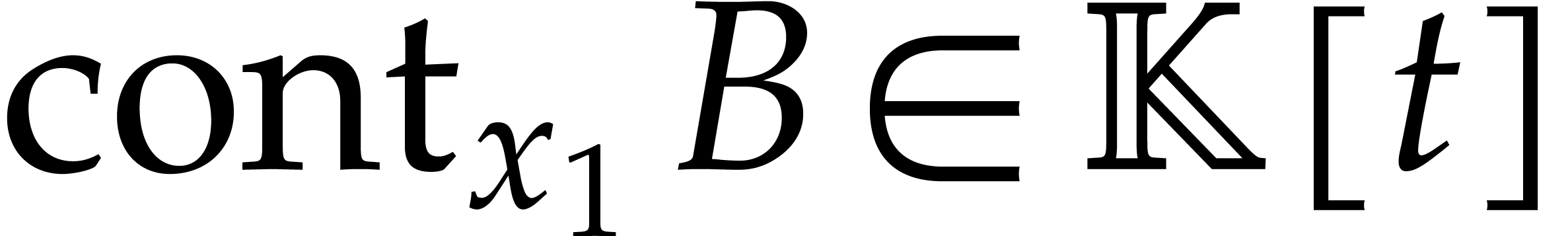 can often be
reduced to Hensel lifting as in Section 4.3 using a random
shift
can often be
reduced to Hensel lifting as in Section 4.3 using a random
shift 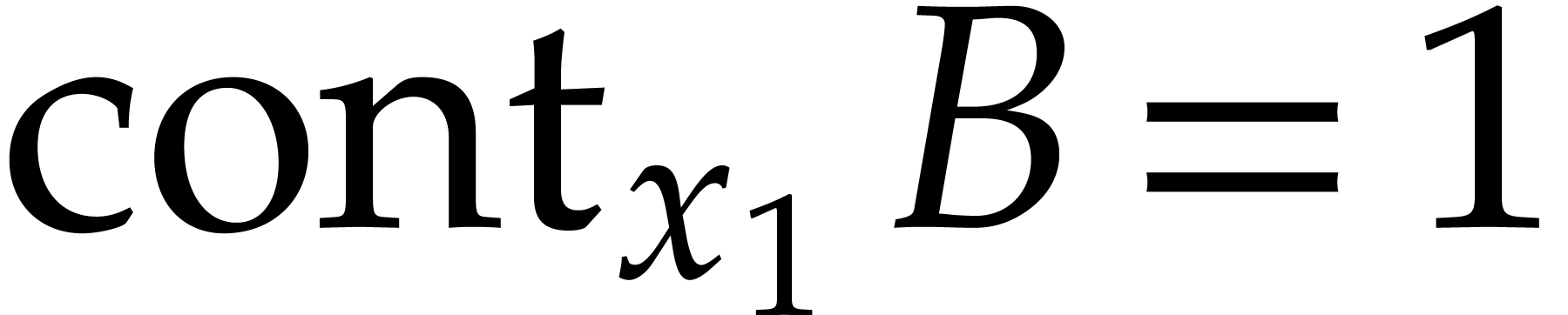 and diversification
and diversification  ,
,  . Let
. Let
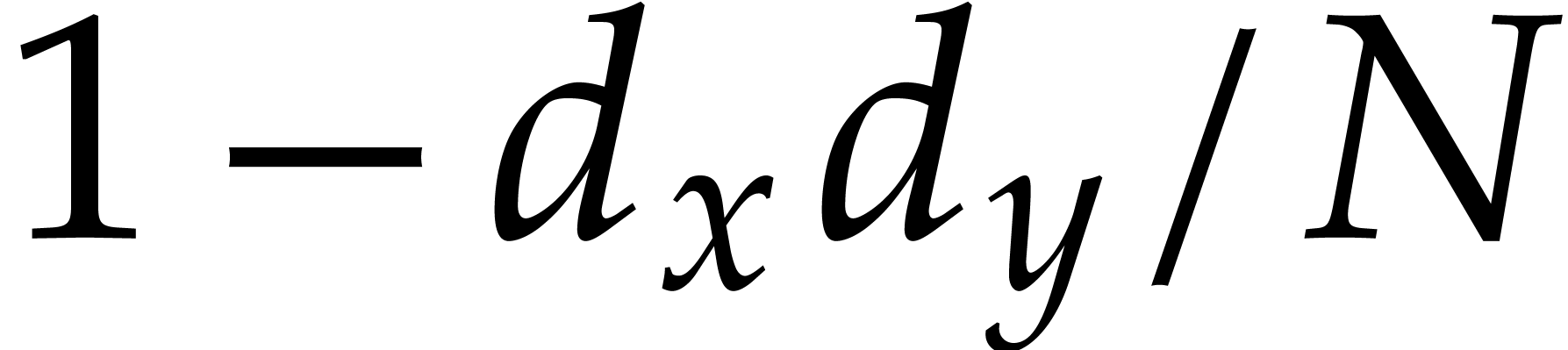 ,
, 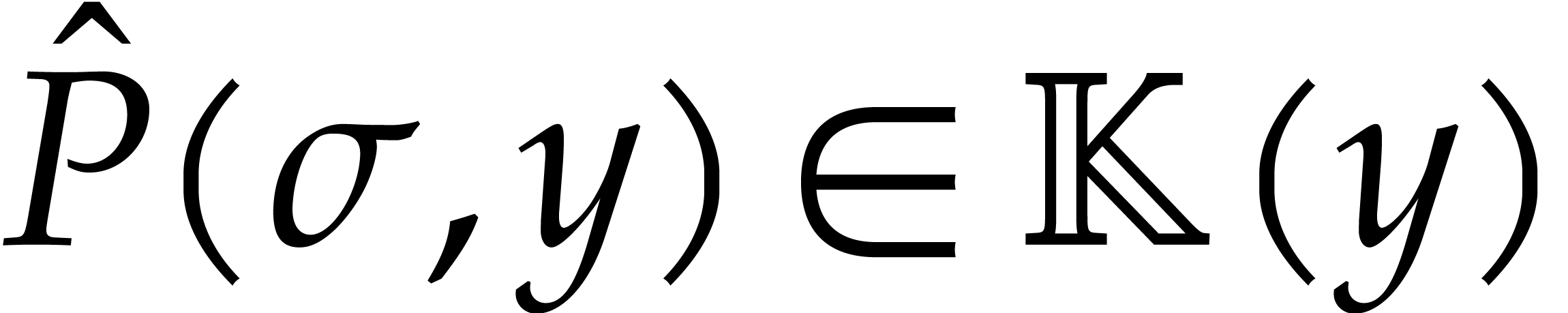 . The best currently known complexity bound is the
following:
. The best currently known complexity bound is the
following:
 be square-free and content-free in both
be square-free and content-free in both 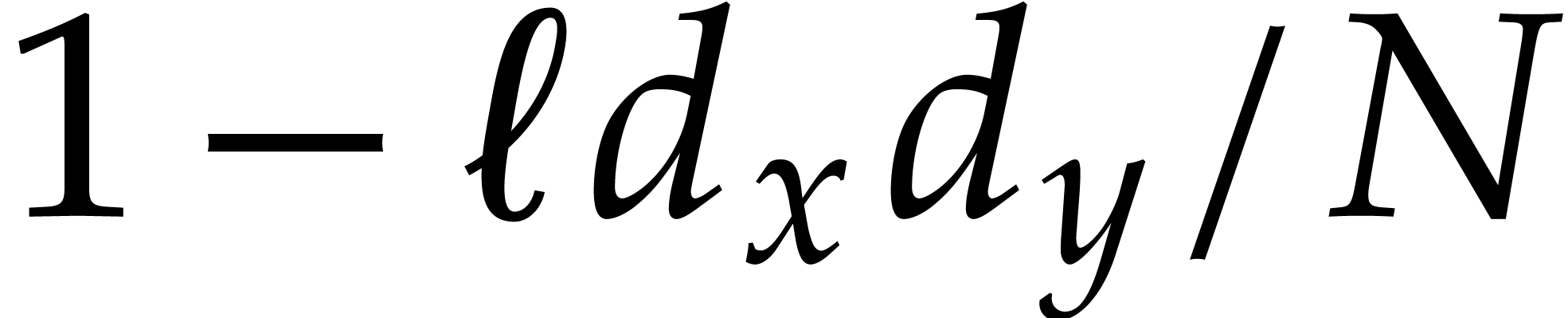 and
and 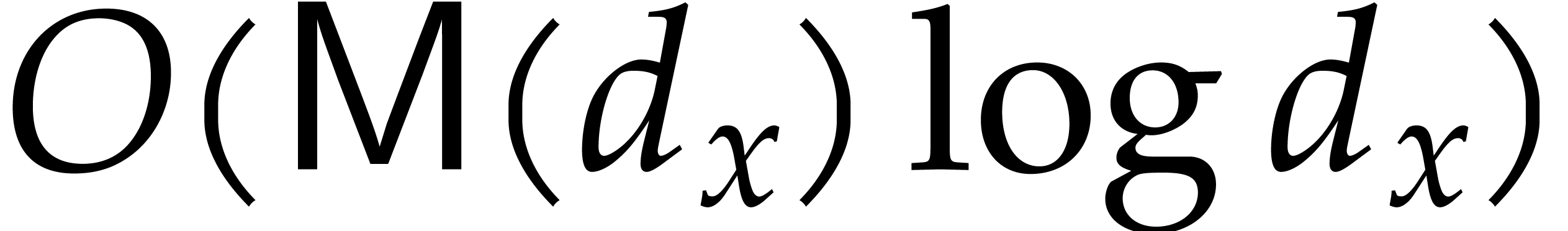 .
Assume that
.
Assume that  or
or 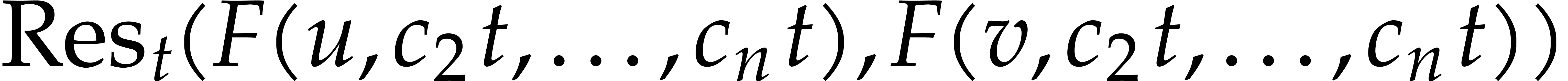 .
Then we can compute the irreducible factorization of
.
Then we can compute the irreducible factorization of  in time
in time
 .
.

The actual proposition in [74] also contains a similar
result for finite fields of small characteristic. For  as in Theorem 4.7, square-freeness and content-freeness can
be achieved with high probability and negligible cost using the
algorithms from Sections 4.1 and 4.4.
as in Theorem 4.7, square-freeness and content-freeness can
be achieved with high probability and negligible cost using the
algorithms from Sections 4.1 and 4.4.
In the bivariate setting of the previous section, we have presented several efficient algorithms for the computation of partial factorizations. In this section, we will generalize three of them to the multivariate setting: removal of content, root extraction, and square-free factorizations. The common feature of these generalizations is that they recover the answer directly from the corresponding univariate specializations of the problem, in a similar fashion as the gcd algorithm from Section 3.2.
Consider a polynomial  and a variable
and a variable  . If, for every non-trivial
factorization
. If, for every non-trivial
factorization 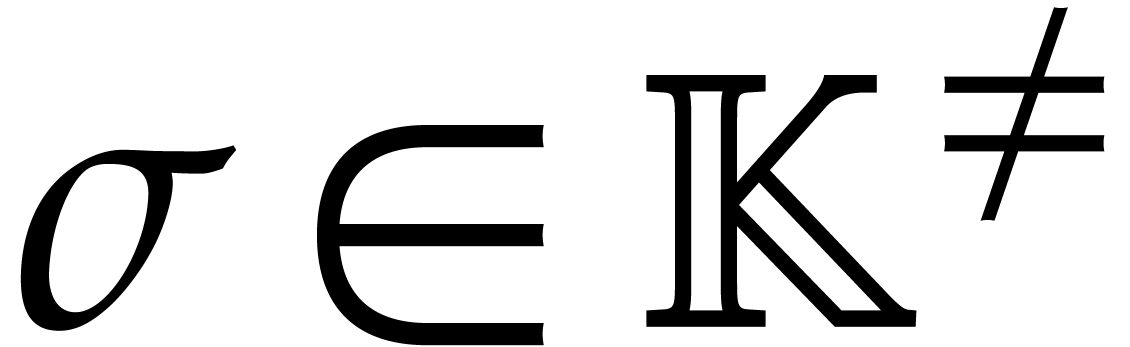 with
with  ,
both
,
both  and
and 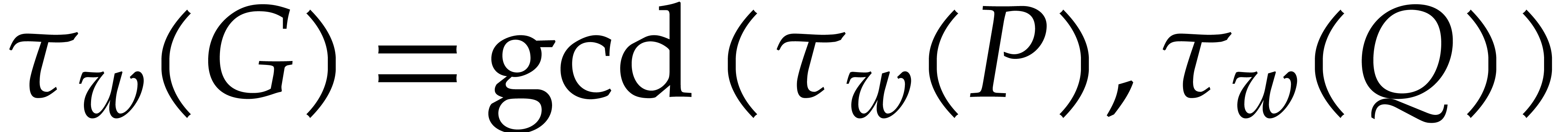 depend on
depend on  , then we say that
, then we say that  is content-free (or primitive) in
is content-free (or primitive) in  . Note that this is always the case if
. Note that this is always the case if  . If
. If  is
content-free in
is
content-free in  for all
for all  , then we say that
, then we say that  is
content-free.
is
content-free.
For a given variable  , say
, say
 , we can efficiently test
whether
, we can efficiently test
whether  is content-free with respect to
is content-free with respect to  : for random
: for random  , we form the bivariate polynomial
, we form the bivariate polynomial  and compute
and compute 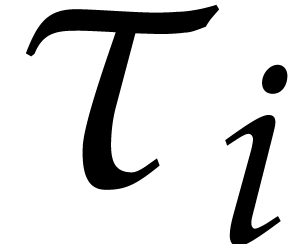 using the method from Section 4.1. With high probability,
using the method from Section 4.1. With high probability,  is
content-free with respect to
is
content-free with respect to 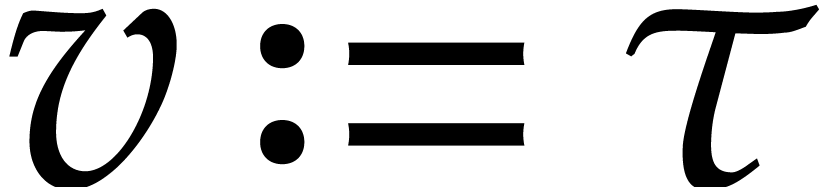 if and only if
if and only if
 . Performing this test for
each of the variables
. Performing this test for
each of the variables  yields:
yields:
 is
content-free (and, if not, determine all variables
is
content-free (and, if not, determine all variables  with respect to which
with respect to which  is not content-free) in
time
is not content-free) in
time  and with a probability of success of at
least
and with a probability of success of at
least 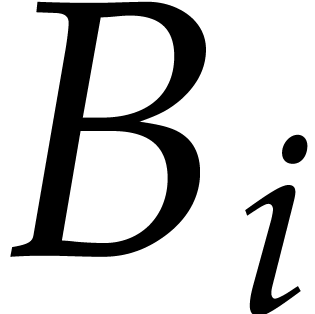 .
.
Proof. The proof is similar to the one of
Proposition 4.1. This time, for the probability bound, we
consider the resultant 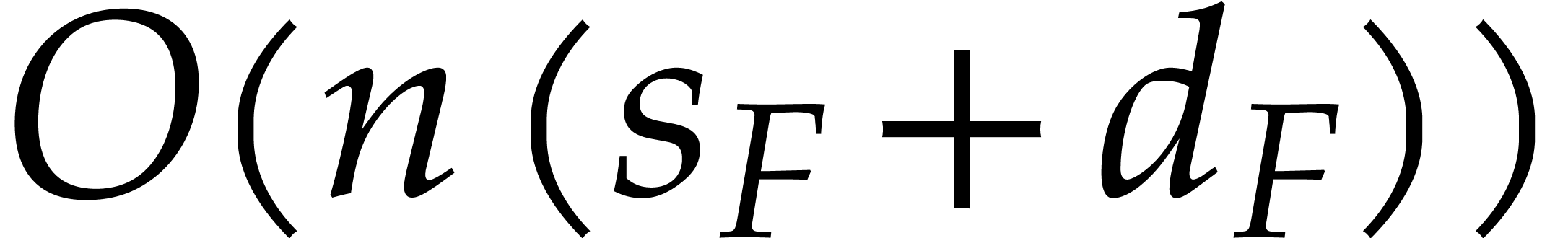 as a polynomial in
as a polynomial in  , of total degree at most
, of total degree at most 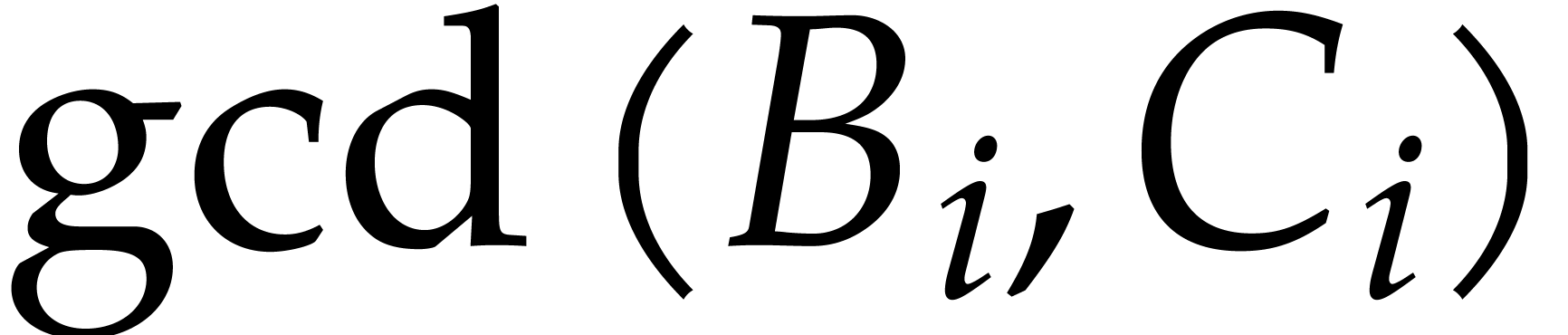 . If
. If  ,
then this resultant does not vanish with probability at least
,
then this resultant does not vanish with probability at least 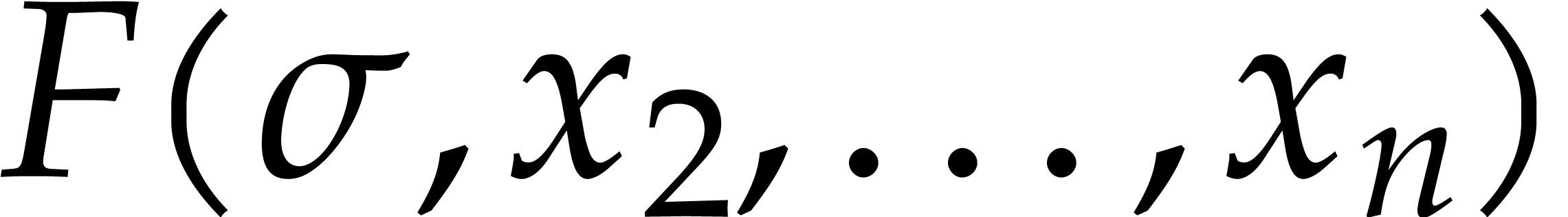 for random
for random 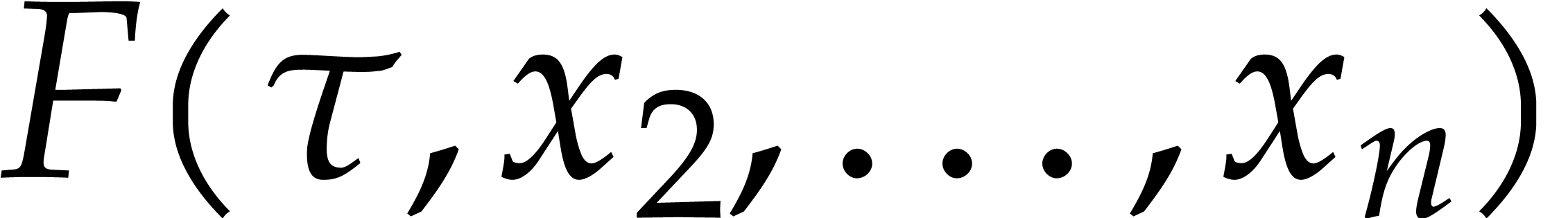 ,
,
 ,
,  .
.
As to the complexity bound, for 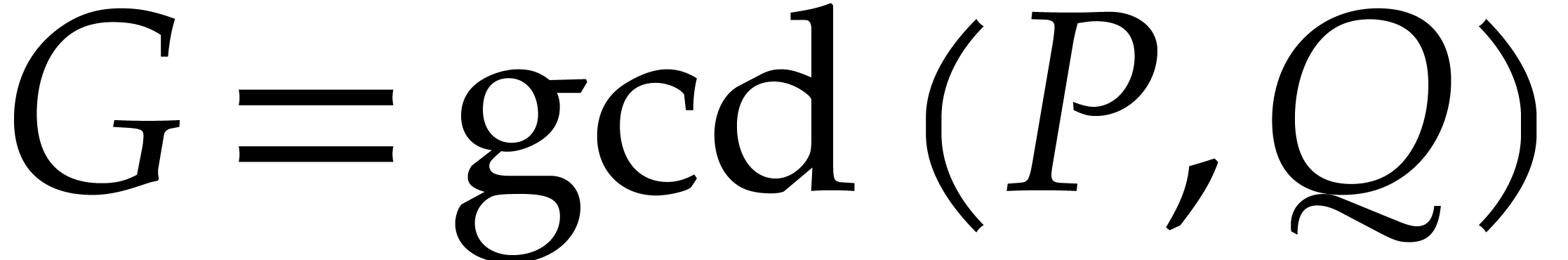 ,
let
,
let  and
and  be random and
consider
be random and
consider 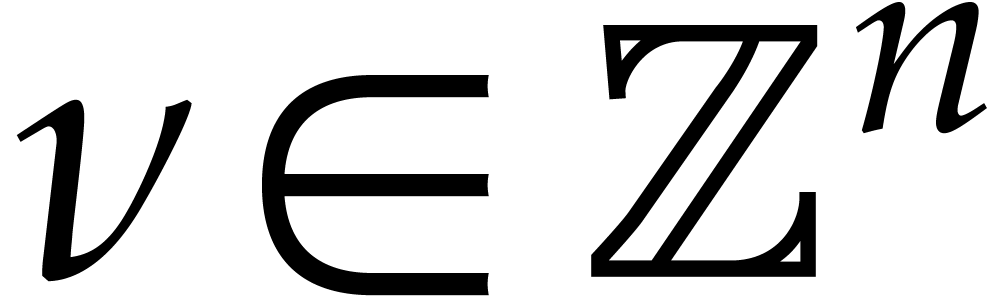 and
and  .
We compute the
.
We compute the  simultaneously for
simultaneously for 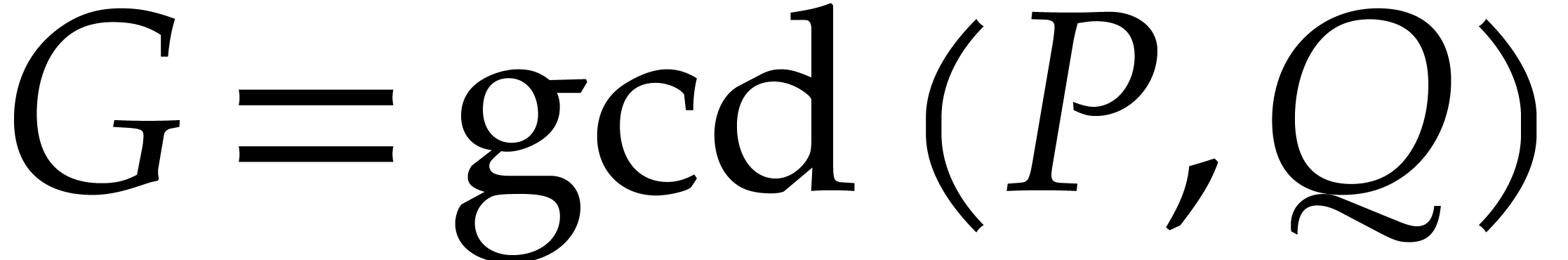 in time
in time  and similarly for the
and similarly for the
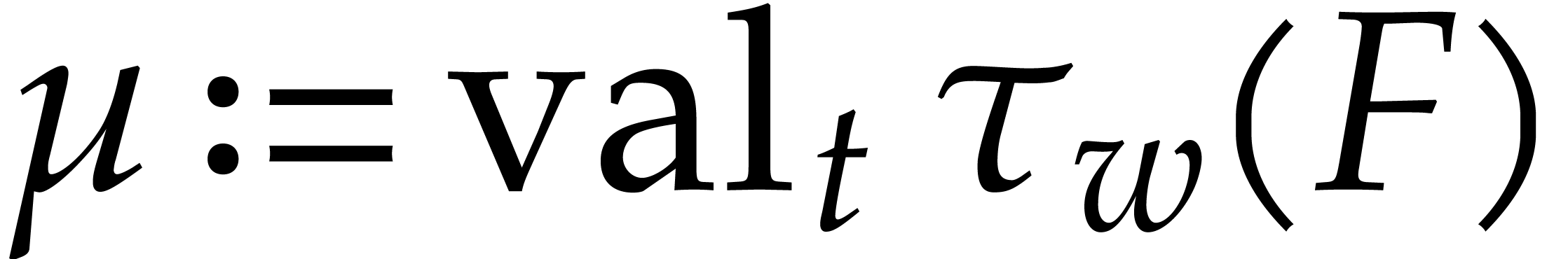 . Finally, the computation of
. Finally, the computation of
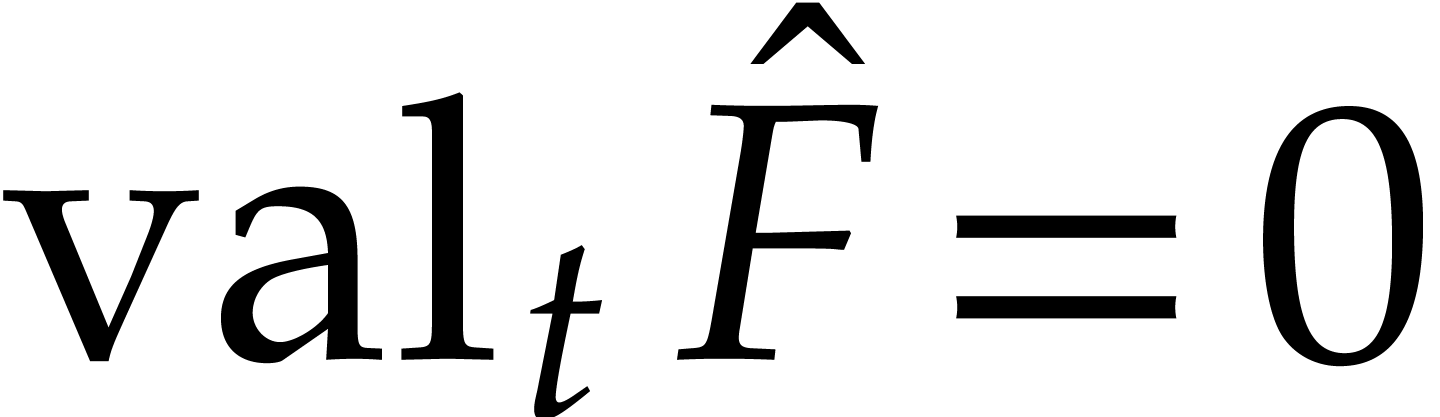 for
for 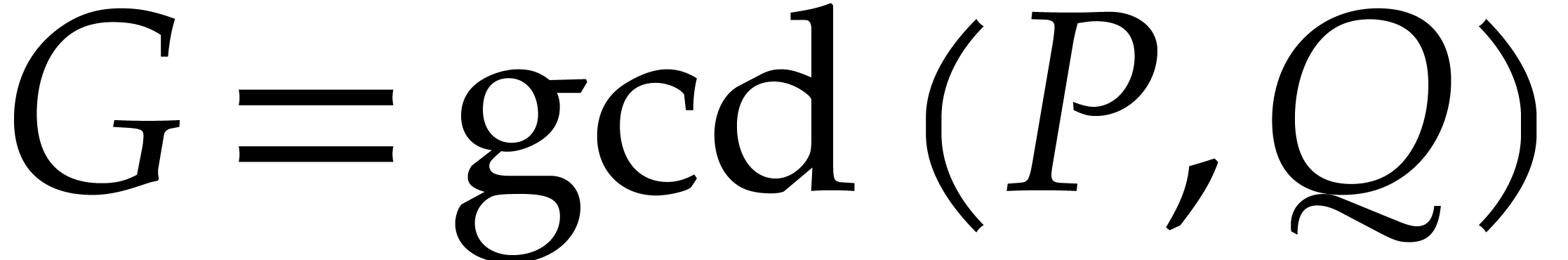 takes
takes  operations.
operations.
Assume now that  is not content-free, say with
respect to
is not content-free, say with
respect to  . With high
probability, the content of
. With high
probability, the content of  with respect to
with respect to  then equals the gcd of
then equals the gcd of 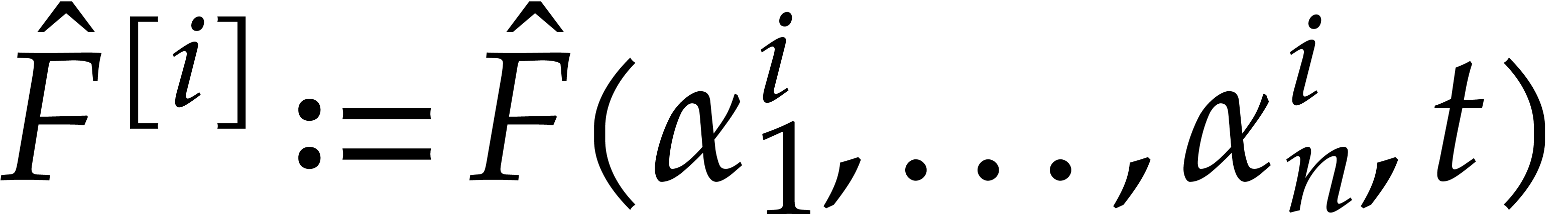 and
and
 , for two random shifts
, for two random shifts 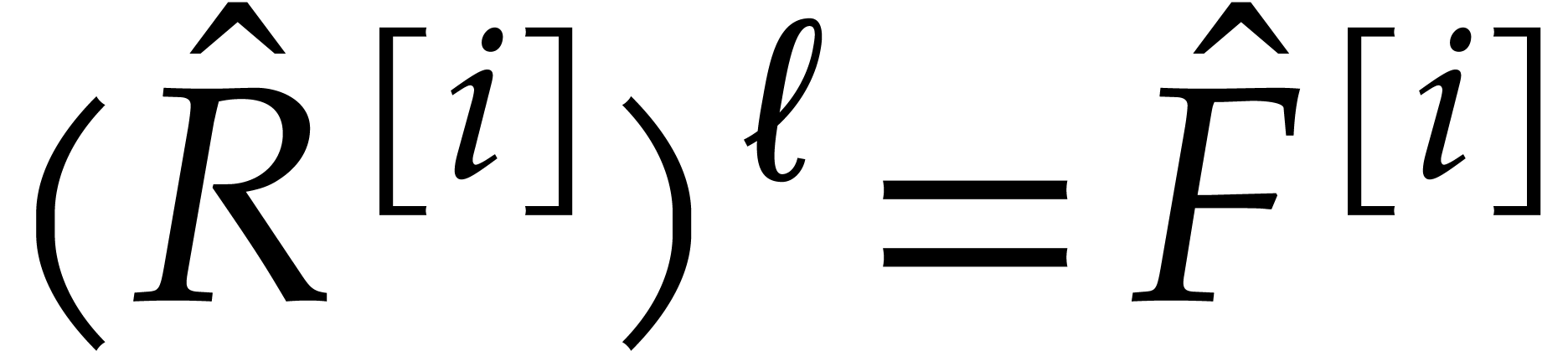 . This leads to a non-trivial
factorization of
. This leads to a non-trivial
factorization of  for the cost of one gcd
computation and one exact division.
for the cost of one gcd
computation and one exact division.
Given  and
and  ,
multivariate
,
multivariate  -th root
extraction is the problem of determining
-th root
extraction is the problem of determining  and
and
 , such that
, such that 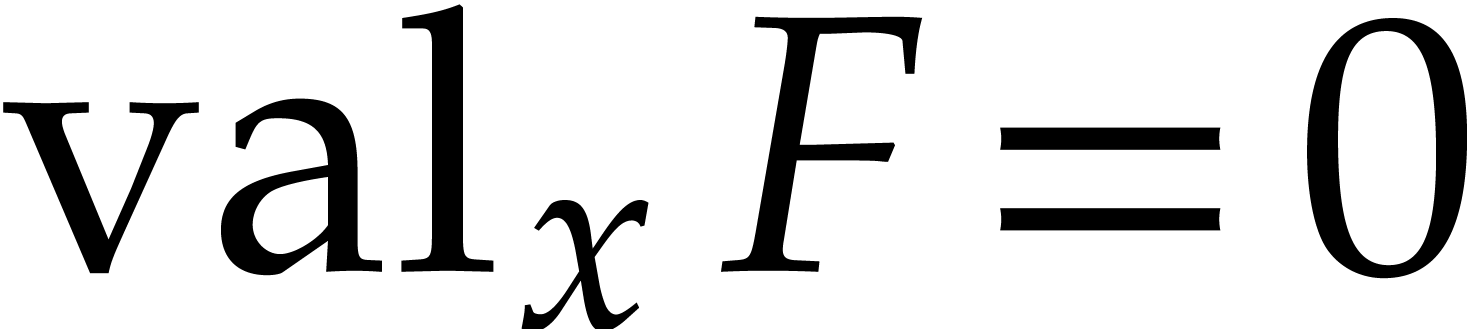 , whenever such
, whenever such  and
and
 exist. We devise an algorithm in the same vein
as the algorithm for gcd computations from Section 3.2.
exist. We devise an algorithm in the same vein
as the algorithm for gcd computations from Section 3.2.
We first compute a regularizing weight  for
for  such that
such that 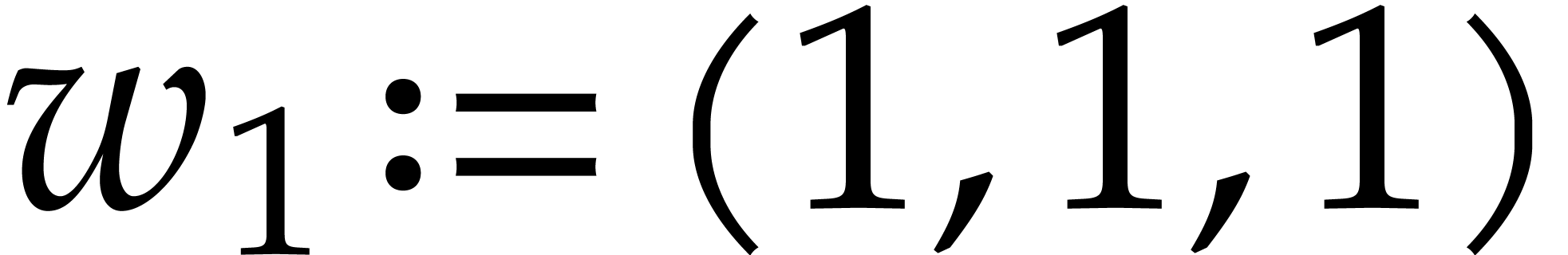 is small. Recall
that the regularity of
is small. Recall
that the regularity of  ensures that
ensures that  for some
for some  and
and  . We take
. We take  and note that
we then must have
and note that
we then must have 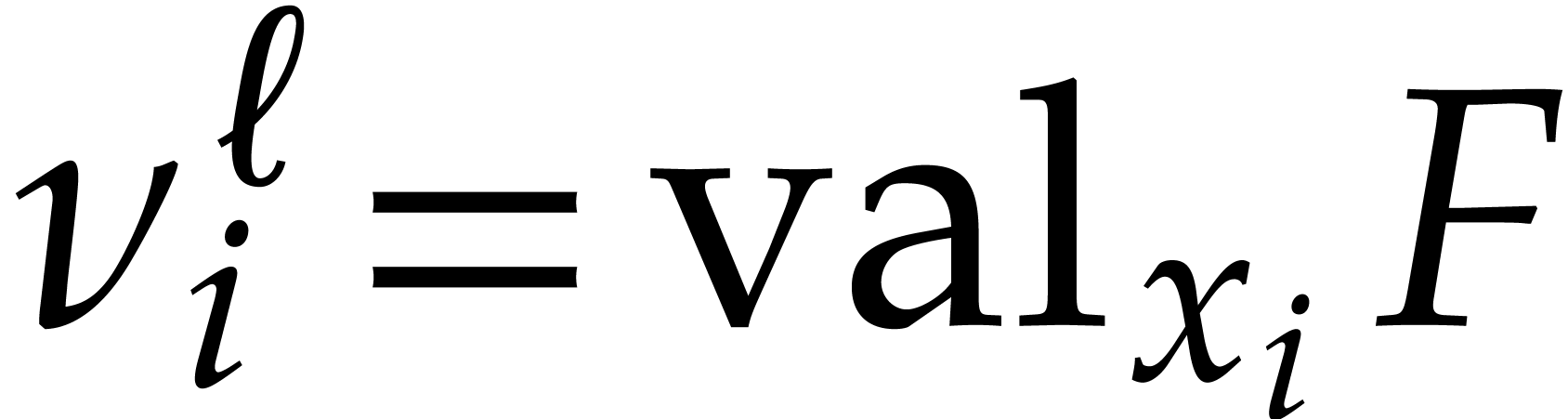 .
.
Now let 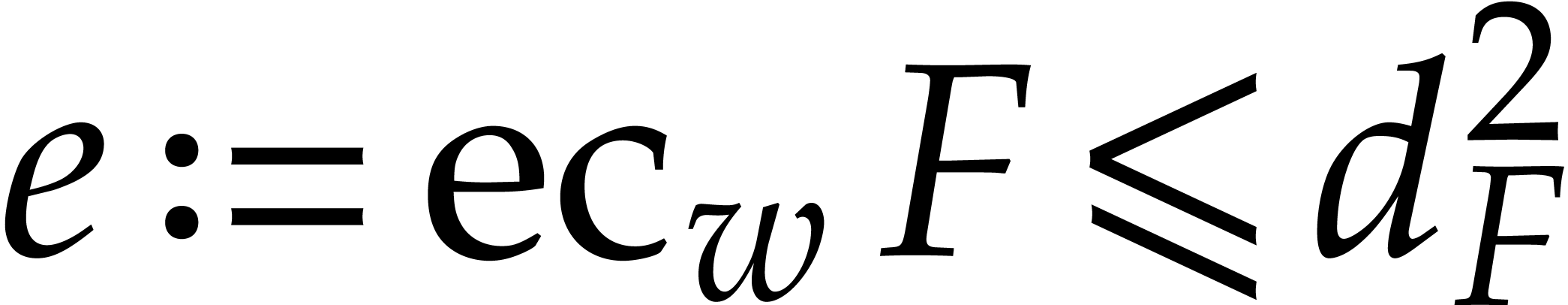 with
with 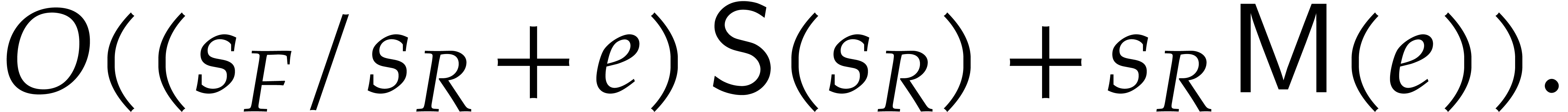 ,
so that
,
so that 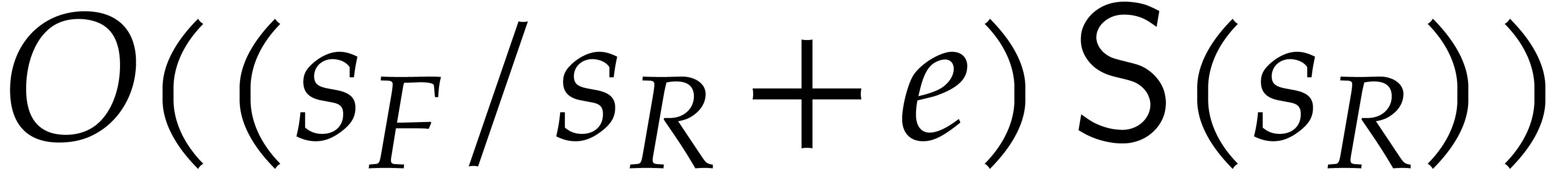 and
and  is monic as
a polynomial in
is monic as
a polynomial in  . Let
. Let 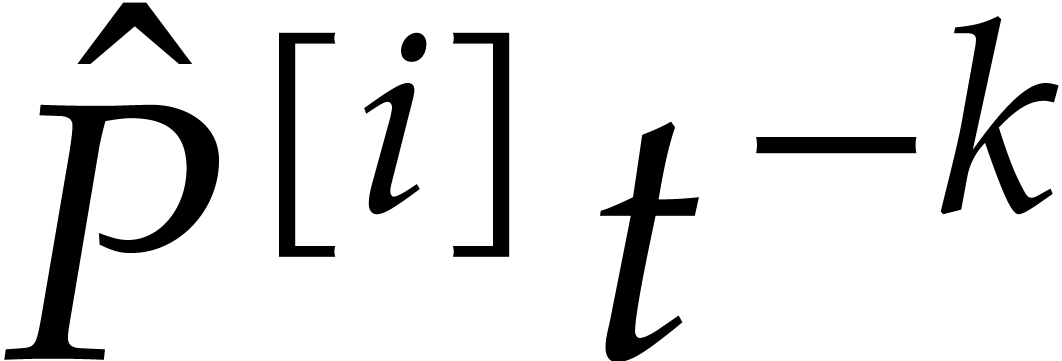 be an admissible ratio or an FFT ratio. For any
be an admissible ratio or an FFT ratio. For any  , we define the univariate
polynomial
, we define the univariate
polynomial  . Let
. Let  be the unique monic polynomial with
be the unique monic polynomial with  . For sufficiently large
. For sufficiently large 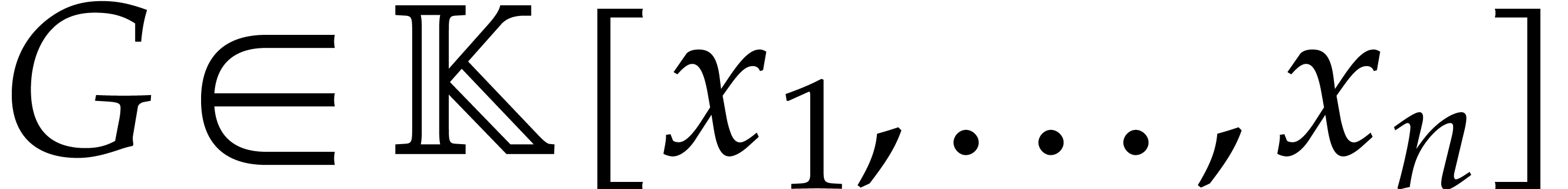 (with
(with  ), we may recover
), we may recover  from
from  using sparse
interpolation. Finally, we have
using sparse
interpolation. Finally, we have 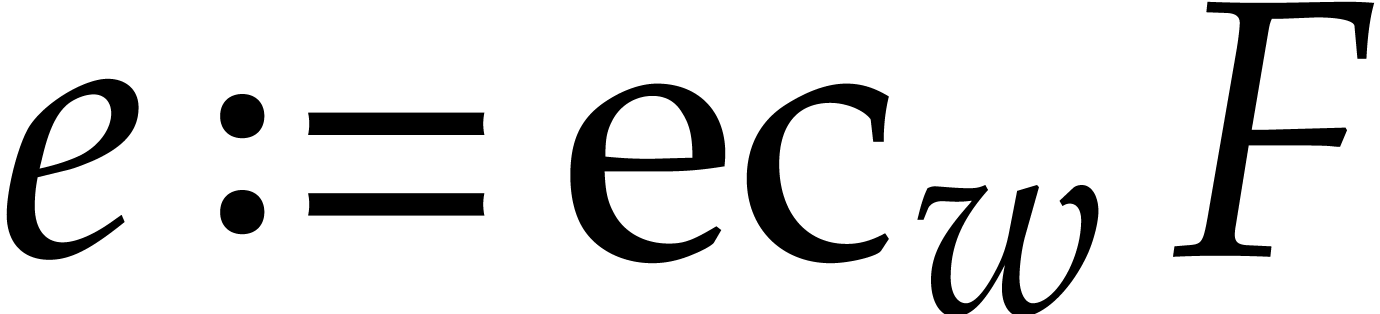 ,
where
,
where 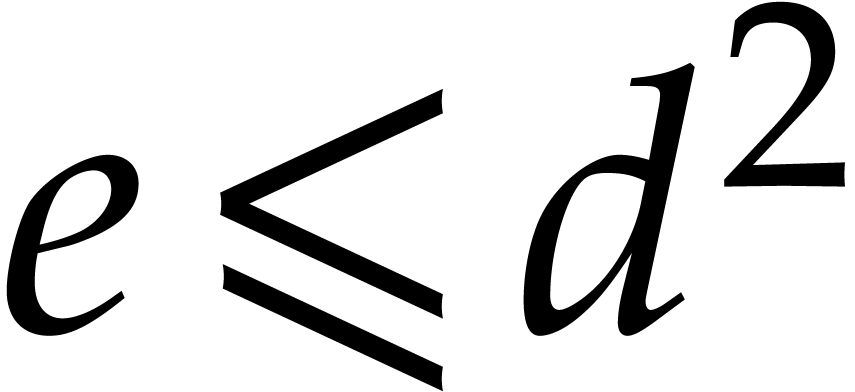 is such that
is such that 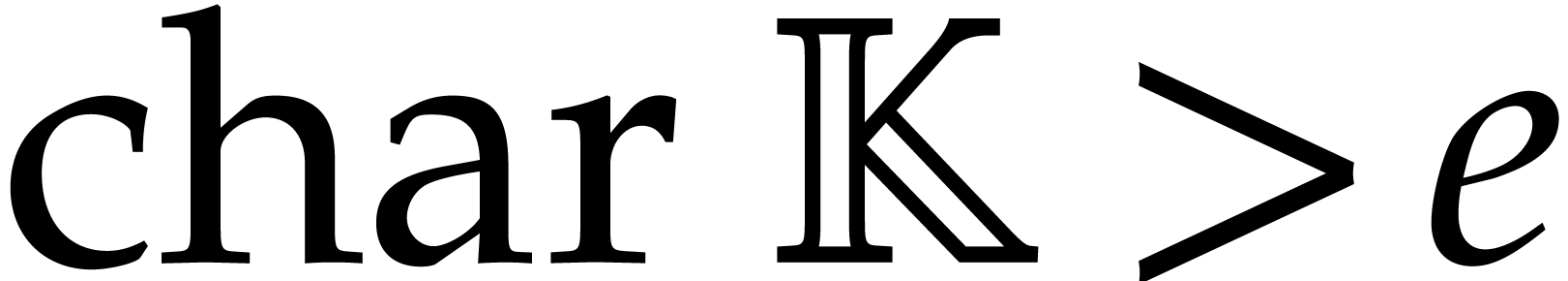 for
for
 .
.
 is
is  -regular with
-regular with  .
Then we may compute
.
Then we may compute  and
and  with
with 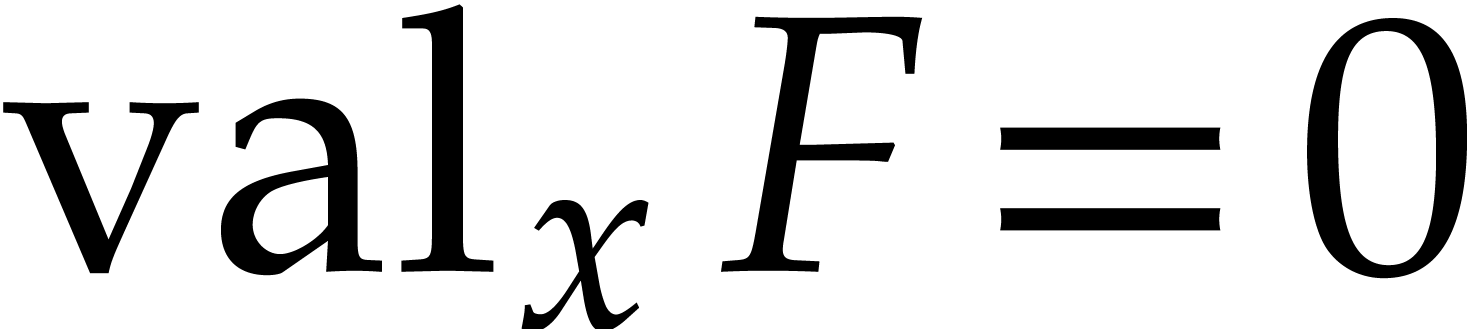 , whenever such
, whenever such 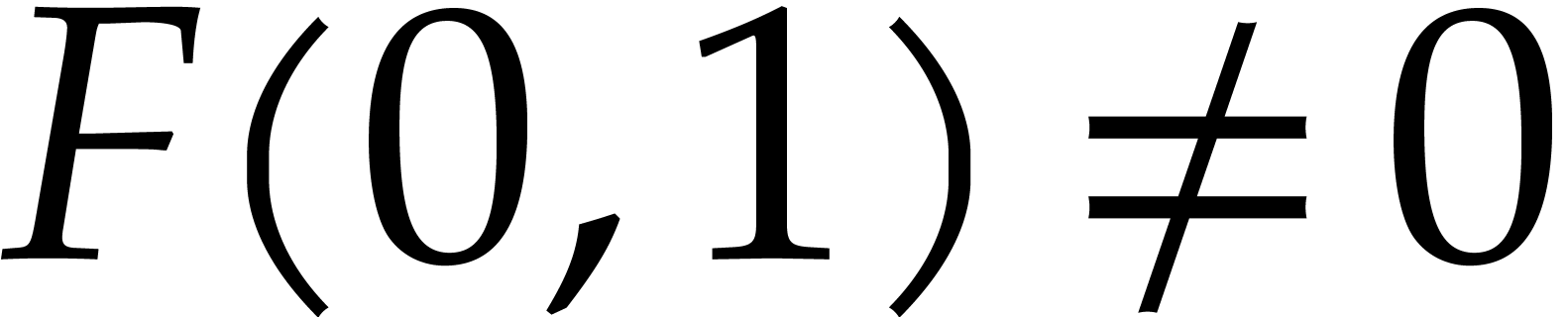 and
and 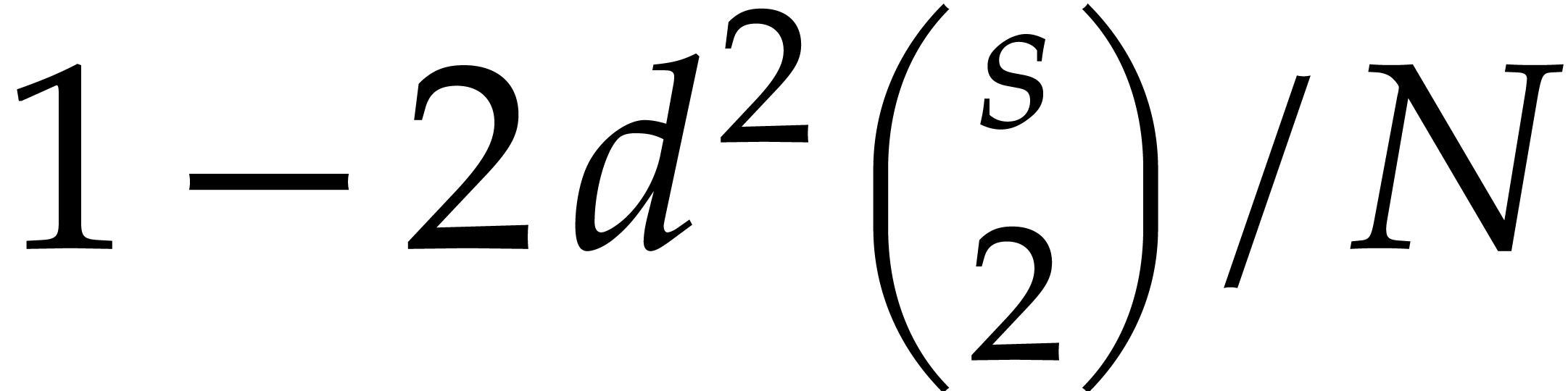 exist, in time
exist, in time

Proof. The evaluations  take
take  operations, whereas the sparse
interpolation of
operations, whereas the sparse
interpolation of  from the
from the  can be done in time
can be done in time  . The
cost of the univariate
. The
cost of the univariate  -th
root extractions
-th
root extractions 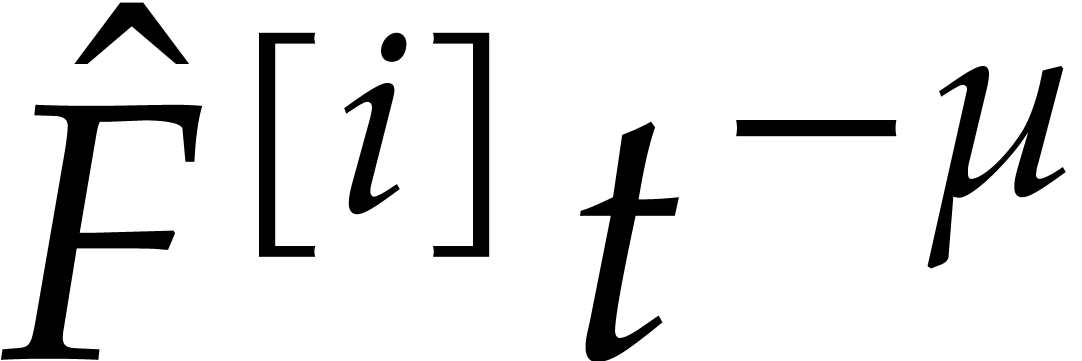 is bounded by
is bounded by  .
.
Consider 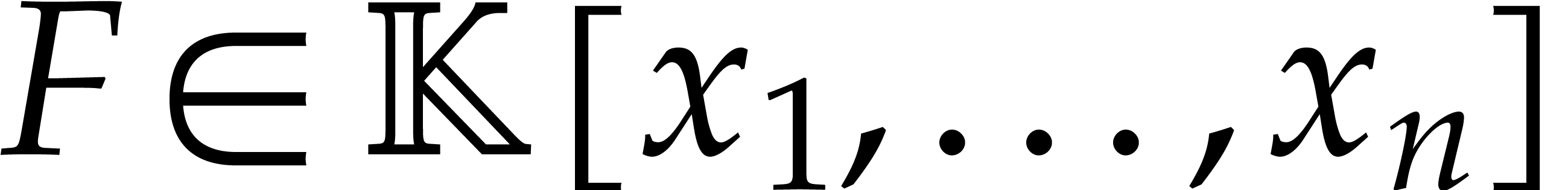 of total degree
of total degree  . Assume that
. Assume that  is
content-free and that
is
content-free and that 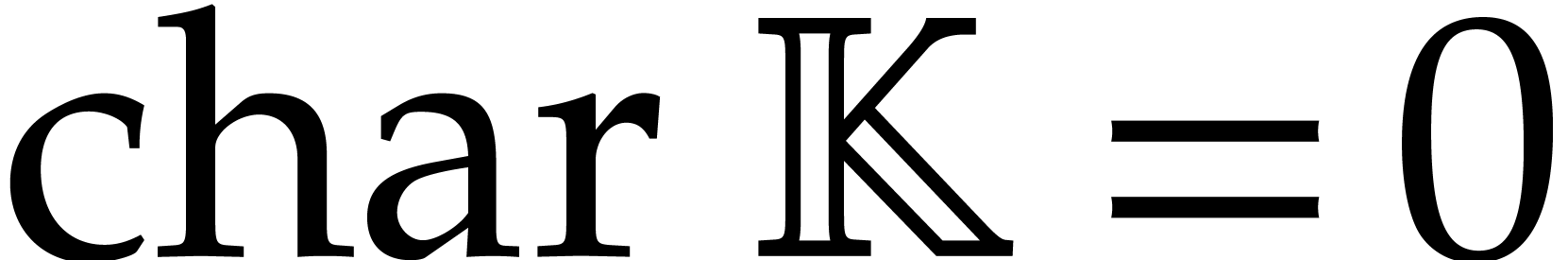 or
or 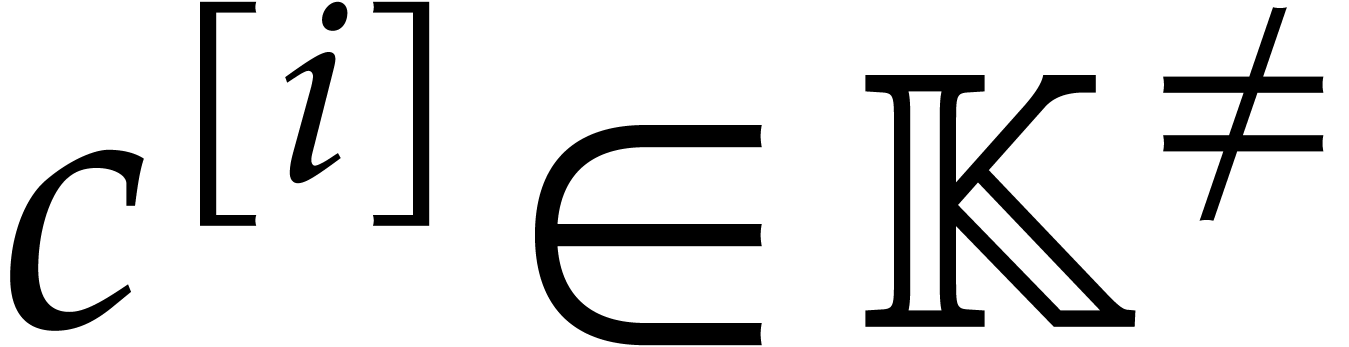 . The factorization of
. The factorization of

into square-free parts can be done using a similar technique as for gcd
computations in Section 3.2. We start with the computation
of a regularizing weight  for
for  . Setting
. Setting 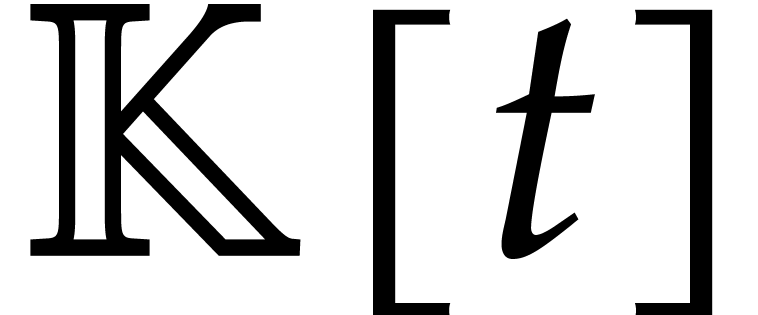 ,
we recall that
,
we recall that  , whence
, whence 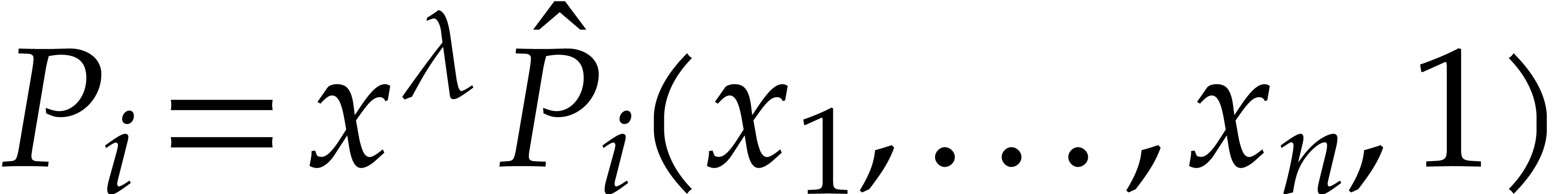 . Let
. Let
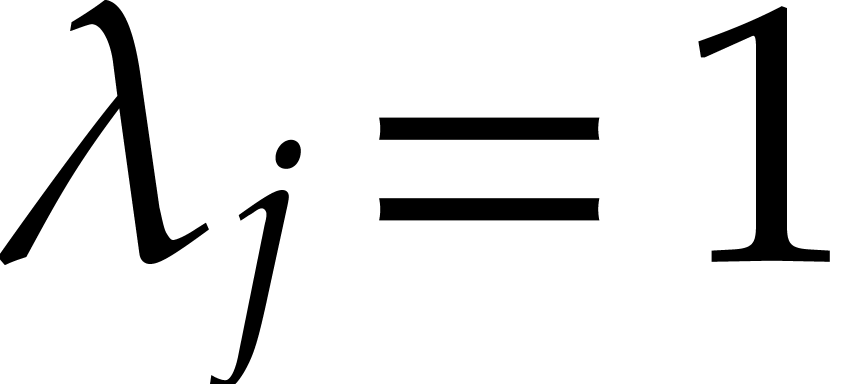
and consider the normalized square-free factorization

where  ,
,  ,
, 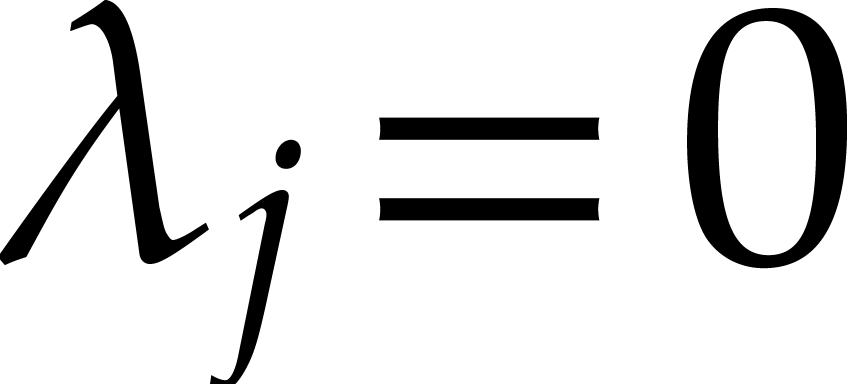 ,
and where
,
and where 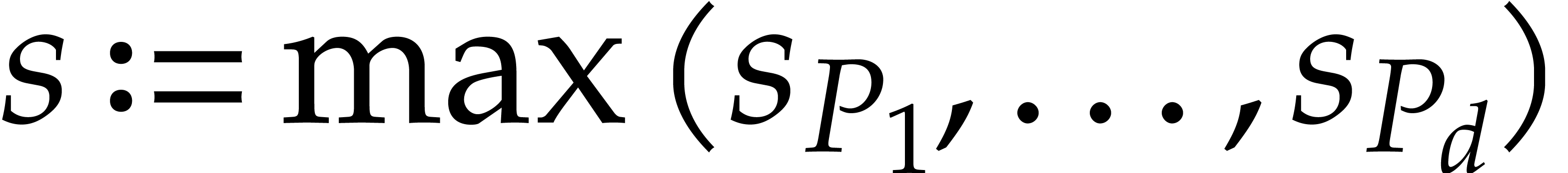 are monic and of valuation zero in
are monic and of valuation zero in
 . Let
. Let 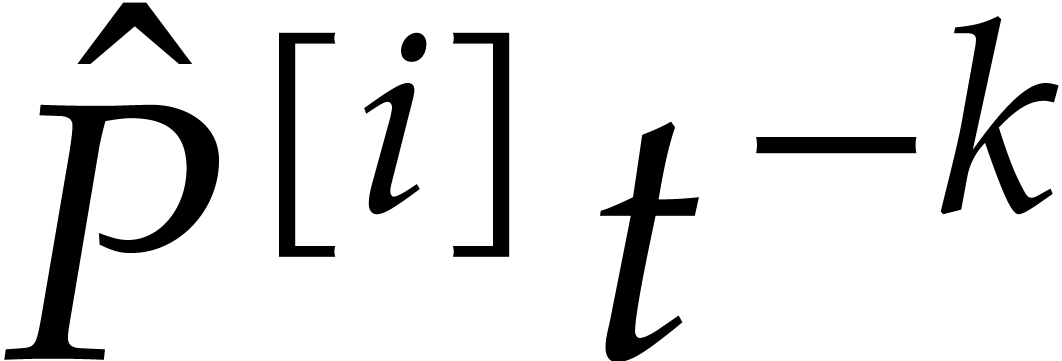 be an admissible ratio or an FFT ratio. For any
be an admissible ratio or an FFT ratio. For any  , we define the univariate polynomials
, we define the univariate polynomials
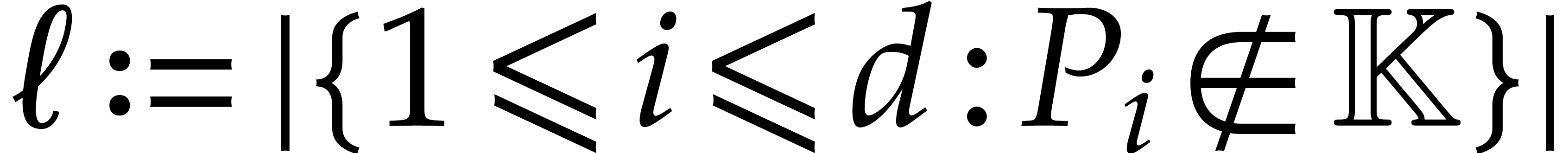
The normalized square-free factorization of  is
of the form
is
of the form
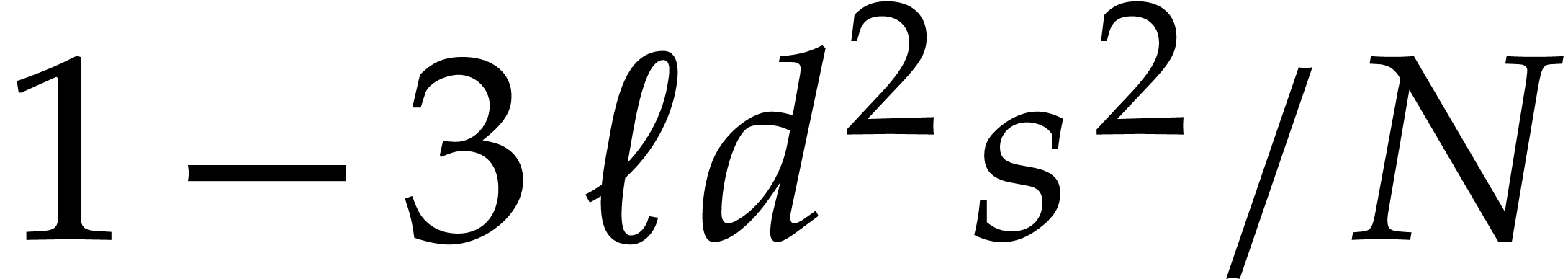
where  , and
, and 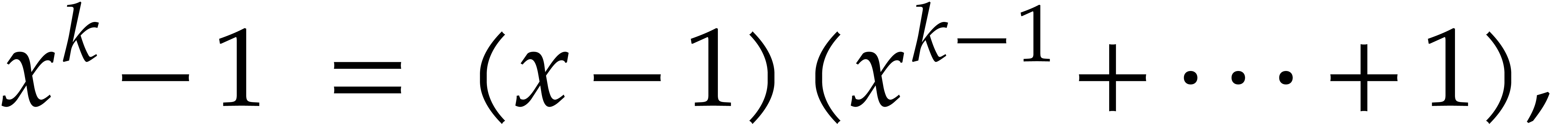 are monic polynomials in
are monic polynomials in  . We
recover
. We
recover 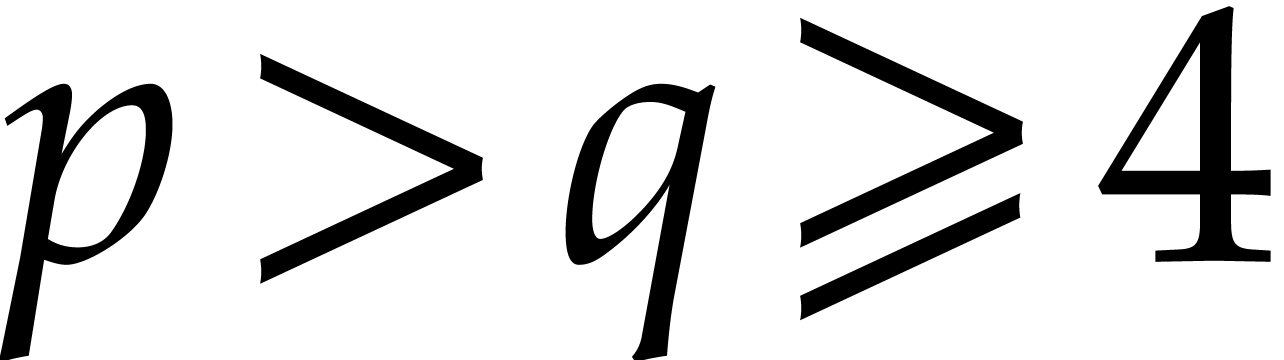 using sparse interpolation and then
using sparse interpolation and then 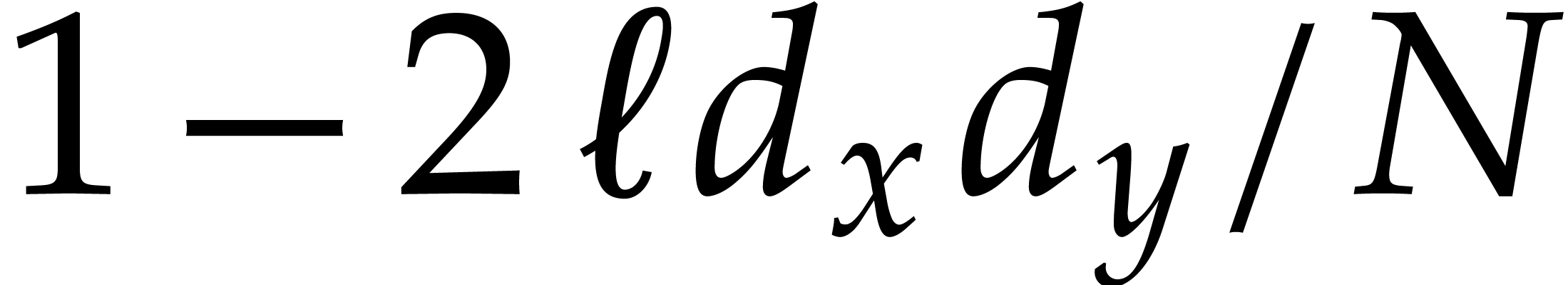 by setting
by setting  and multiplying by
appropriate monomials in
and multiplying by
appropriate monomials in  .
More precisely,
.
More precisely,  , where
, where  if
if  and
and  otherwise.
otherwise.
 is
is  -regular with
-regular with  .
Let
.
Let 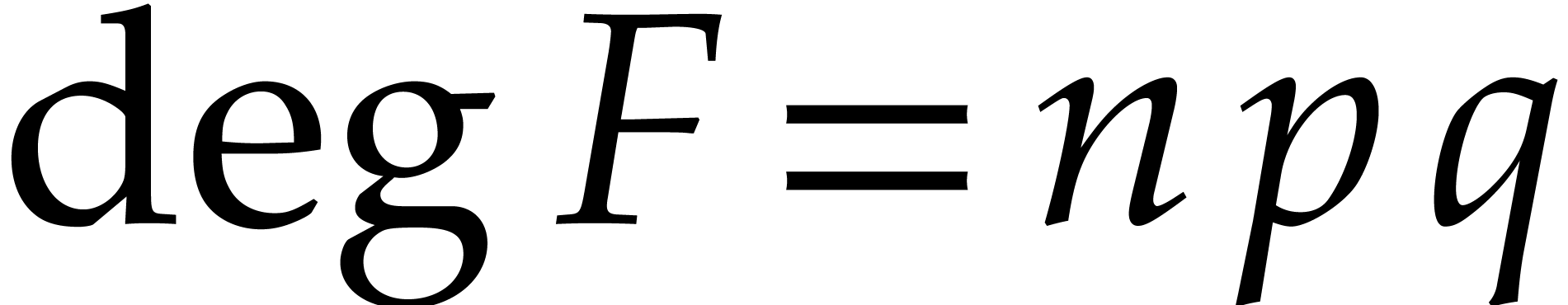 and
and  .
Then we may compute a square-free factorization of in time
.
Then we may compute a square-free factorization of in time

with a probability of success of at least  .
.
Proof. The probabilistic correctness is proved
in a similar way as in the bivariate case (see Proposition 4.6),
while also using Corollary 2.2. The sparse evaluation and
interpolation at a geometric sequence require 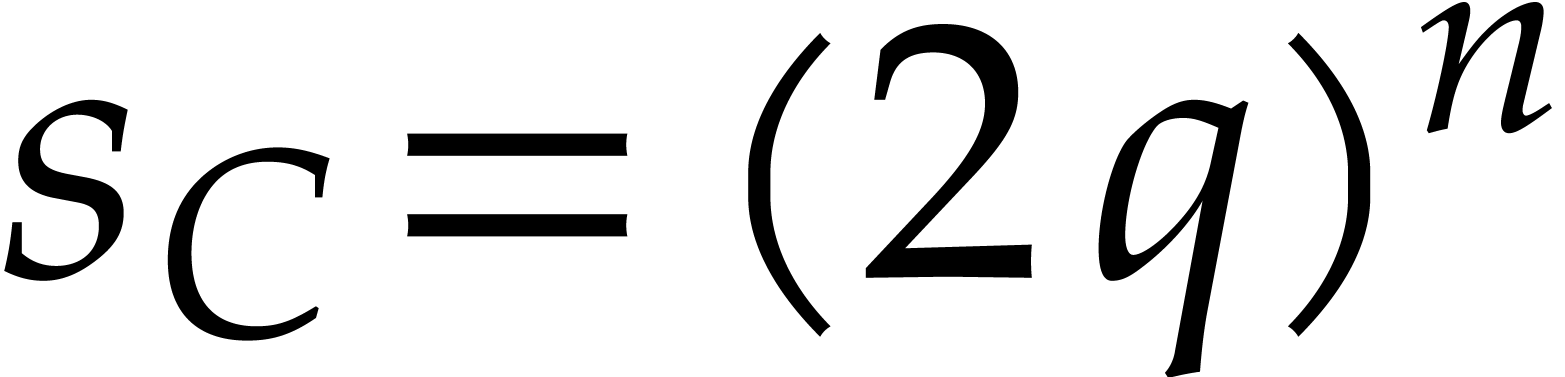 operations. The univariate square-free factorizations can be done in
time
operations. The univariate square-free factorizations can be done in
time  , using [106]
and [31, Theorem 14.23].
, using [106]
and [31, Theorem 14.23].
It is well known that a divisor of a sparse polynomial can have far more terms than the polynomial itself, because of the identity
 |
(5.1) |
and the possibility to replace  by any other
sparse polynomial. For this reason, many problems on sparse polynomials
turn out to be NP-hard [89, 90]. In a way that
has been made precise in [25], this fundamental example is
actually the main cause for such hardness results.
by any other
sparse polynomial. For this reason, many problems on sparse polynomials
turn out to be NP-hard [89, 90]. In a way that
has been made precise in [25], this fundamental example is
actually the main cause for such hardness results.
The example (5.1) is less dramatic if we consider sparse polynomials for which the total degree is much smaller than the total number of terms, which is often the case in practice. But even then, it still has some unpleasant consequences. Recall from [25] that

for coprime  ,
,  with
with 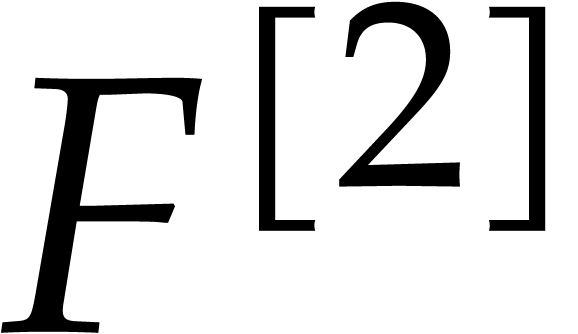 . This gcd
contains exactly
. This gcd
contains exactly  terms. Such gcds can also occur
during content-free factorizations. For instance, the content of
terms. Such gcds can also occur
during content-free factorizations. For instance, the content of

in 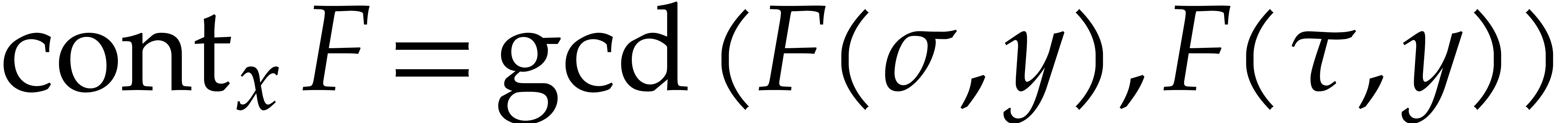 is
is  .
Now consider
.
Now consider

Then  and
and  .
The size of each individual factor in any irreducible factorization of
.
The size of each individual factor in any irreducible factorization of
 is bounded by
is bounded by  ,
which is sharp with respect to
,
which is sharp with respect to 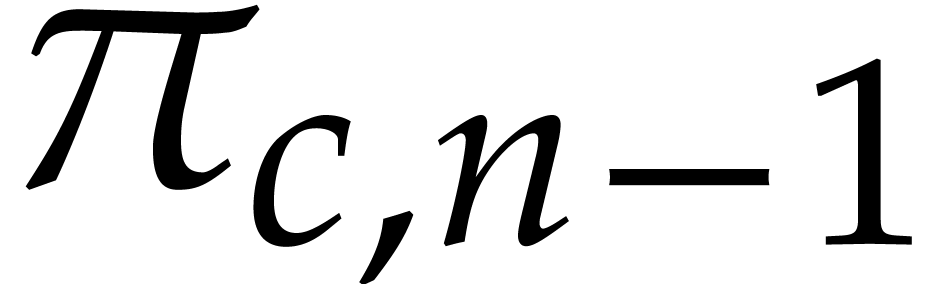 .
However, the content
.
However, the content  of
of  in
in 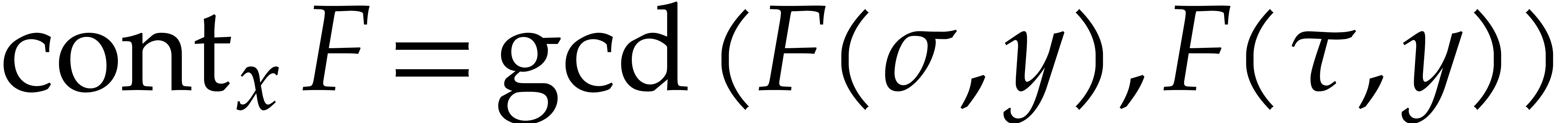 has size
has size 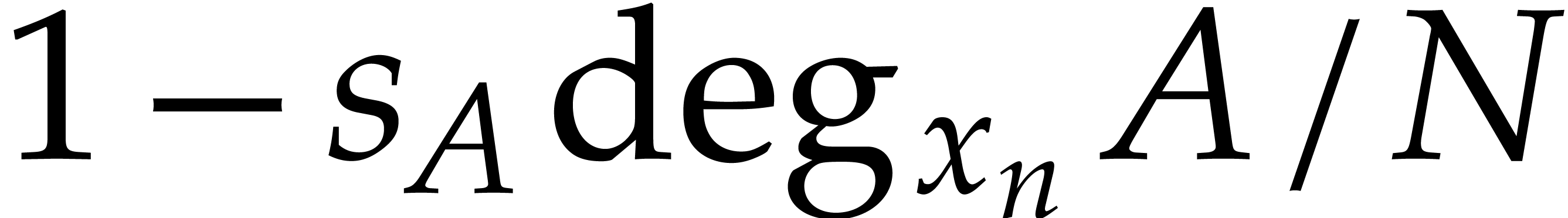 .
This means that content-free factorization as a preparation step (before
launching a “more expensive” factorization method) is a bad
idea on this particular example.
.
This means that content-free factorization as a preparation step (before
launching a “more expensive” factorization method) is a bad
idea on this particular example.
Let 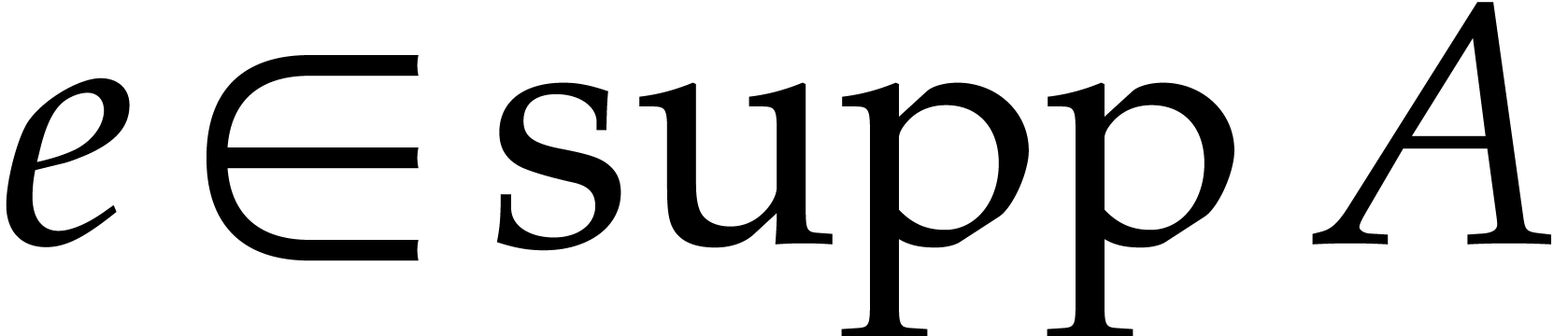 be a content-free polynomial and recall that
any factor of
be a content-free polynomial and recall that
any factor of  is again content-free. Let
is again content-free. Let 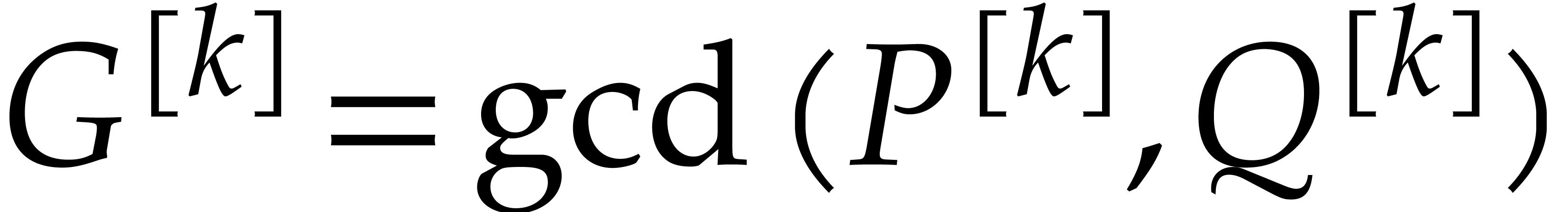 be random non-zero elements of
be random non-zero elements of  . For any
. For any  and
and 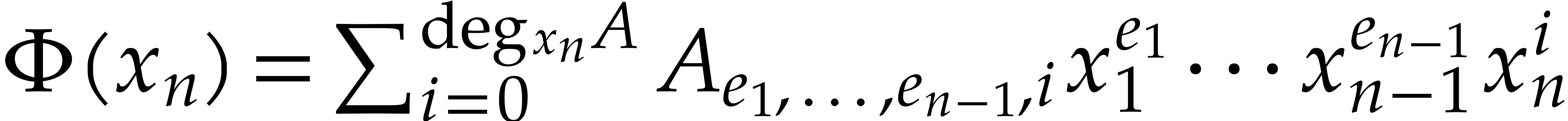 , we define
, we define
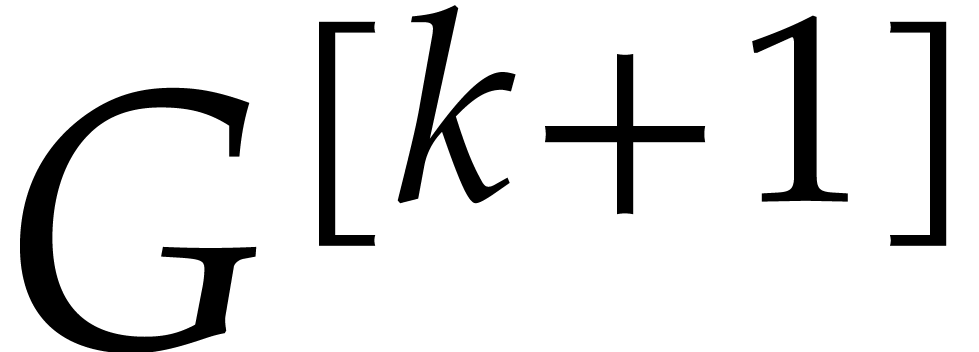
In this section, we describe several algorithms for the factorization of
 , following a similar
recursive approach as for the computations of gcds in Section 3.1.
This time, we start with the computation of a non-trivial factorization
of the bivariate polynomial
, following a similar
recursive approach as for the computations of gcds in Section 3.1.
This time, we start with the computation of a non-trivial factorization
of the bivariate polynomial  .
From this, we will recursively obtain non-trivial factorizations of
.
From this, we will recursively obtain non-trivial factorizations of
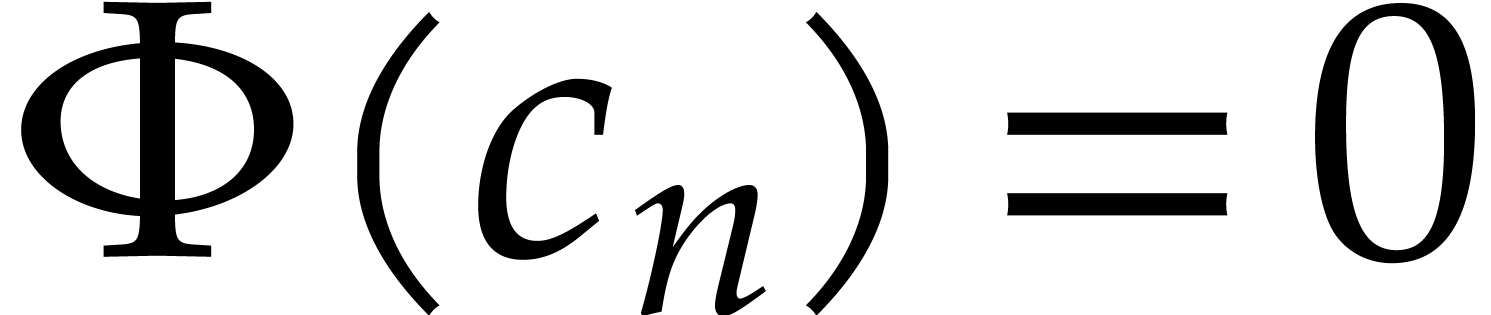 . This will in particular
yield a non-trivial factorization of
. This will in particular
yield a non-trivial factorization of  .
We will separately study the cases when
.
We will separately study the cases when  has a
factorization into two or more coprime factors.
has a
factorization into two or more coprime factors.
In order to reconstruct factorizations of  from
factorizations of
from
factorizations of 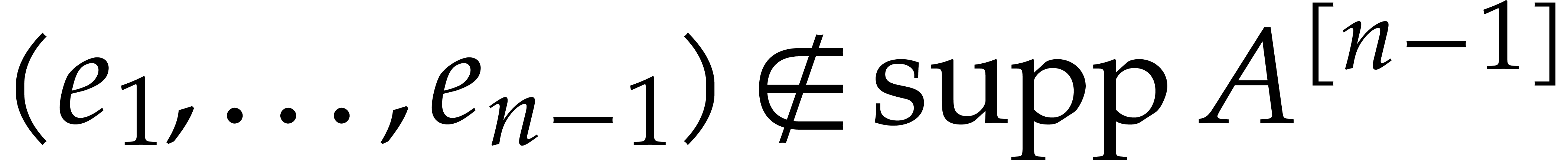 , it is
important that the projection
, it is
important that the projection  be sufficiently
generic. For
be sufficiently
generic. For 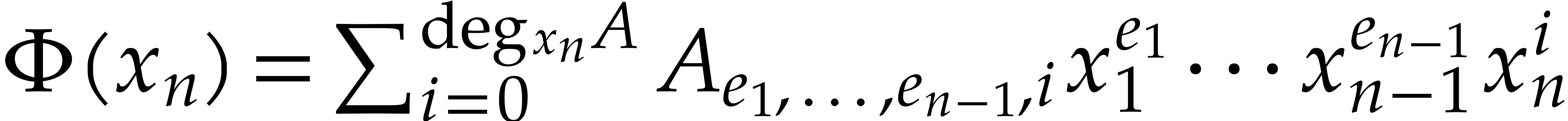 , let us denote
by
, let us denote
by  the projection
the projection  .
We say that
.
We say that  is faithful for
is faithful for  if
if  for
for  .
.
As usual, we assume that 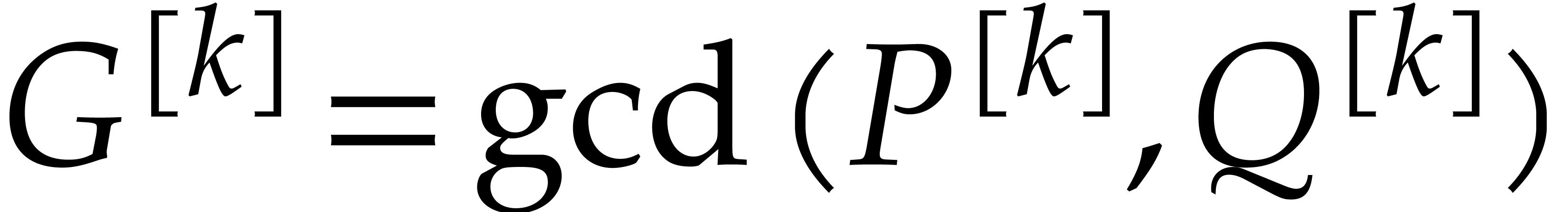 are independently
chosen at random from a subset of
are independently
chosen at random from a subset of  of size at
least
of size at
least  .
.
 , the probability that
, the probability that  is faithful for
is faithful for  is at least
is at least
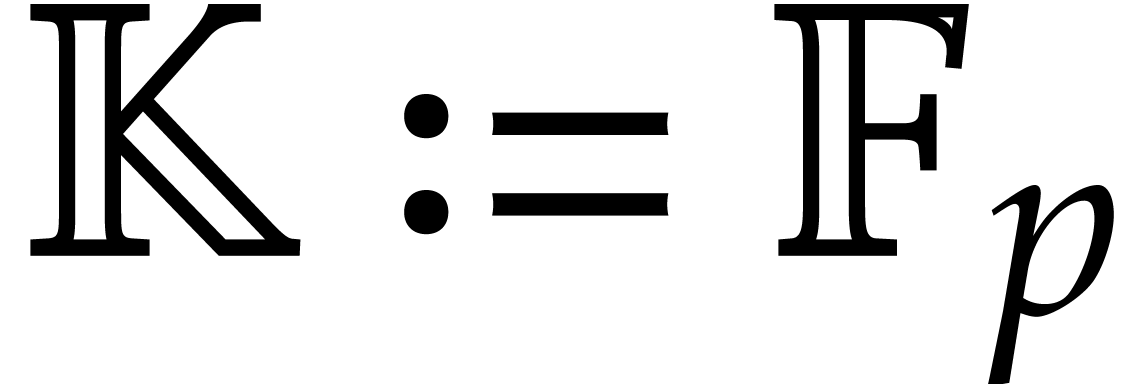 .
.
Proof. Given  ,
let
,
let 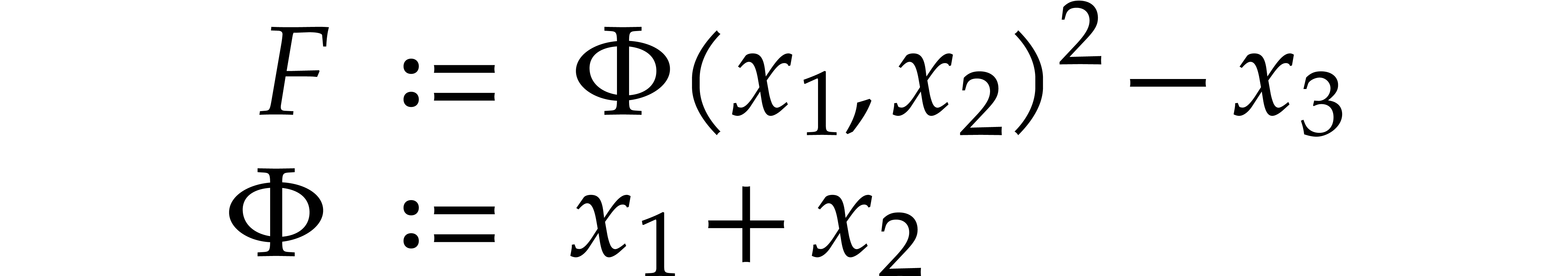 . Then
. Then 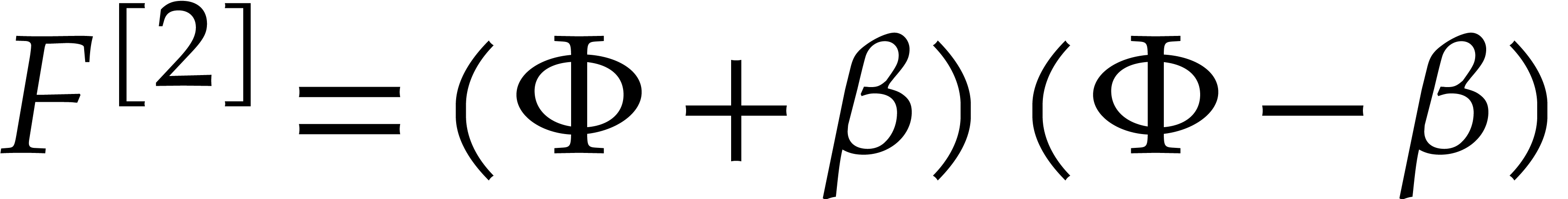 if and only if
if and only if 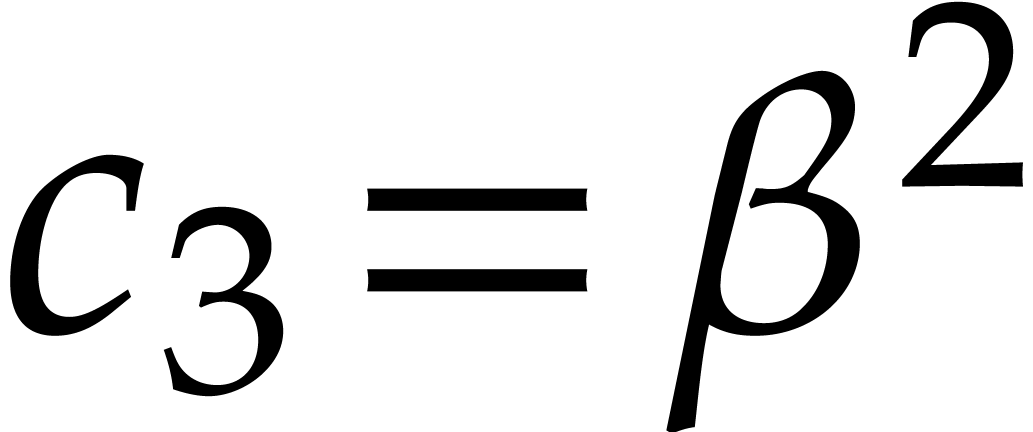 , which
happens with probability at most
, which
happens with probability at most  .
.
Now consider a factorization 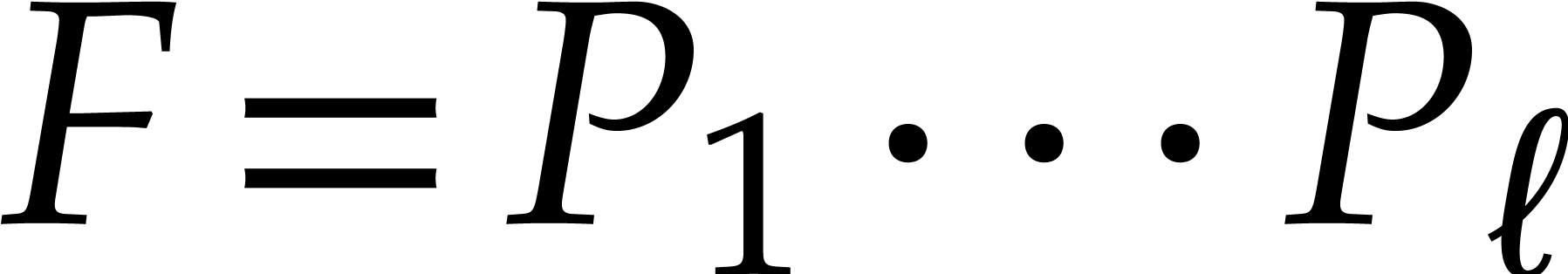 such that
such that  are pairwise coprime. We say that
are pairwise coprime. We say that  is faithful for this factorization if
is faithful for this factorization if  is faithful for
is faithful for  and
and  are
pairwise coprime.
are
pairwise coprime.
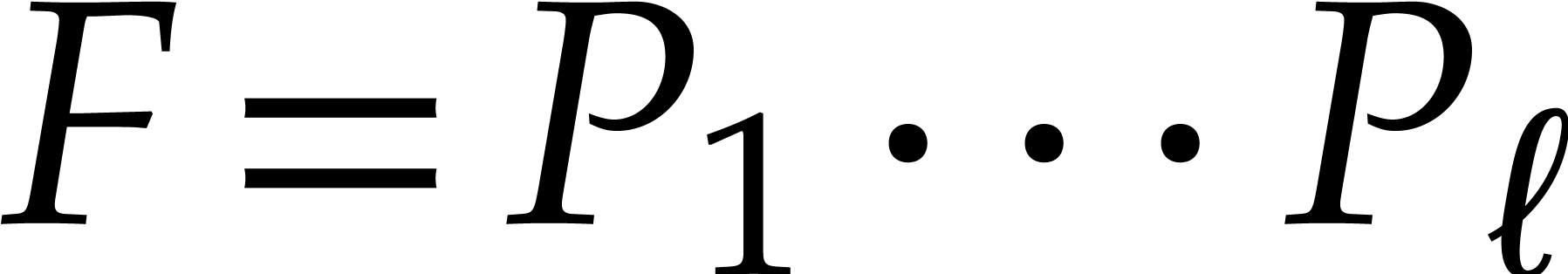 and
and  , the probability that
, the probability that  is faithful for this factorization is at least
is faithful for this factorization is at least  .
.
Proof. This directly follows from Lemma 3.2
(while using that  ) and the
previous lemma (using induction on
) and the
previous lemma (using induction on  ).
).
While faithful mappings preserve coprime factorizations in a predictable
way, it may still happen that an irreducible polynomial is projected to
a reducible one. In fact this may even happen with probability 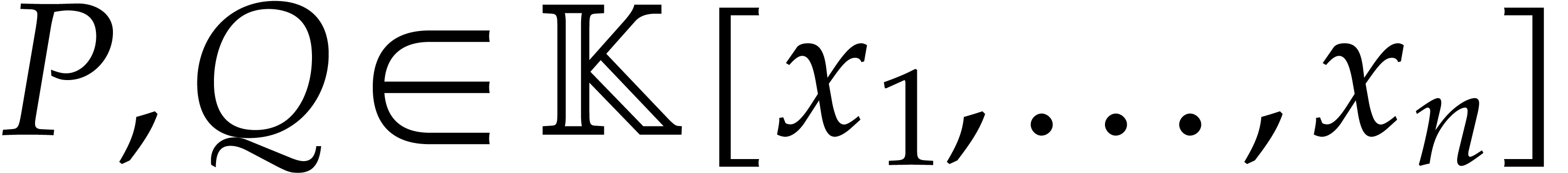 for a random choice of
for a random choice of 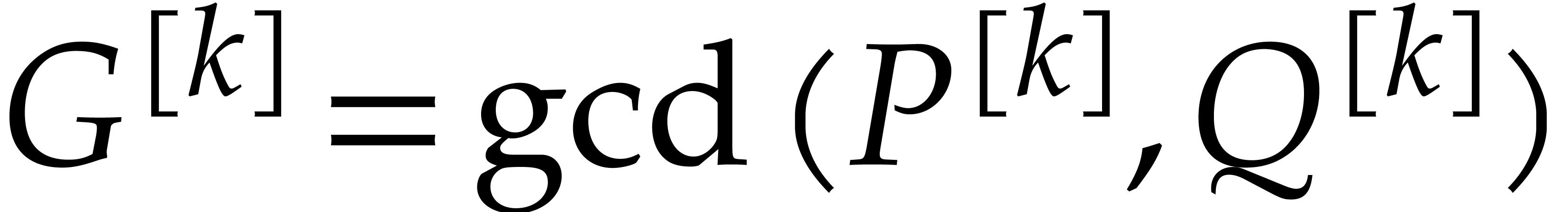 .
.
Example 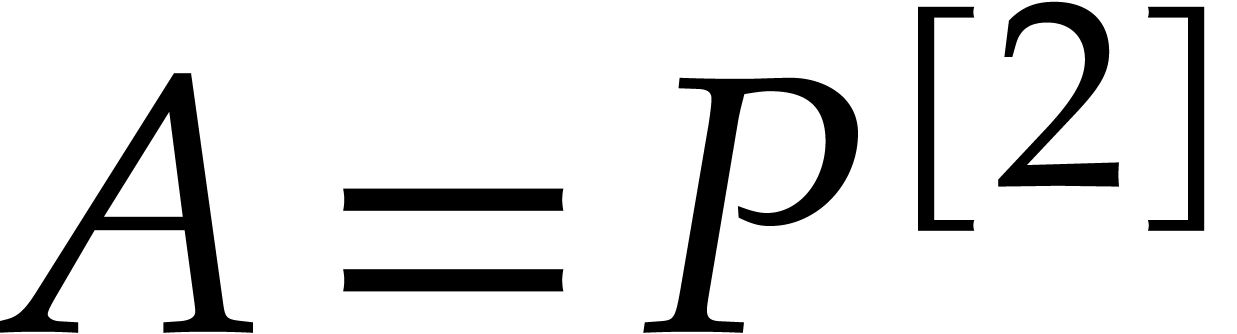 and
and  for an odd prime
for an odd prime
 . Consider
. Consider
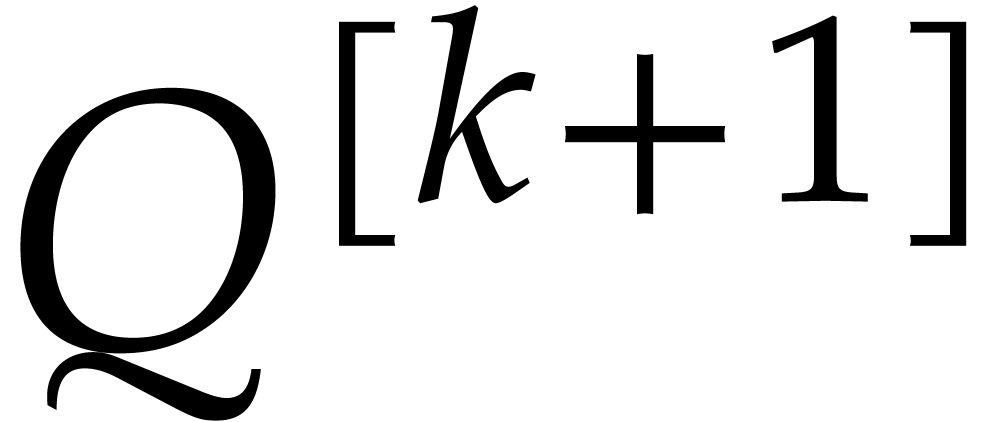
Then  is irreducible, but
is irreducible, but 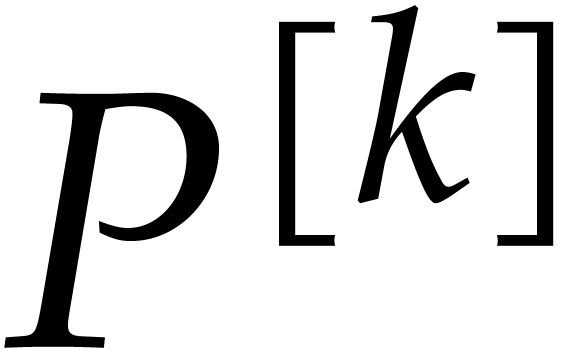 whenever
whenever  is a square in
is a square in  . If
. If  is a random element of
is a random element of
 , then this happens with
probability
, then this happens with
probability 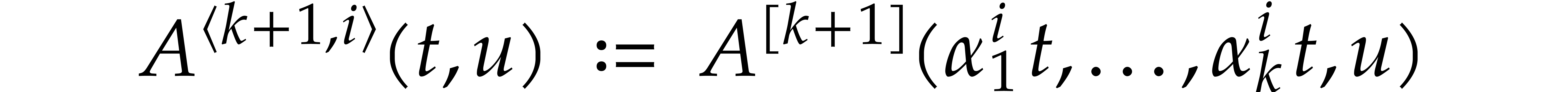 . (Note that we
may replace
. (Note that we
may replace 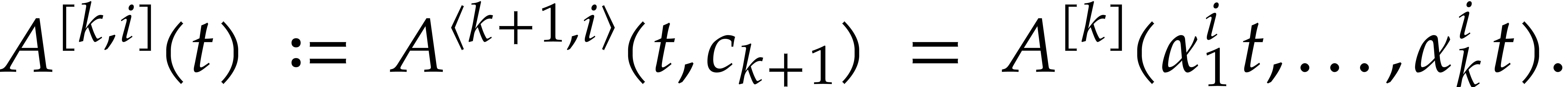 by any other irreducible polynomial
that involves both
by any other irreducible polynomial
that involves both  and
and 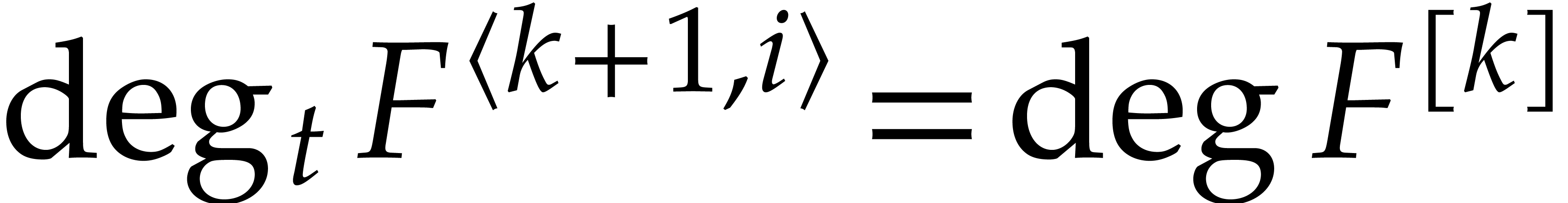 .)
.)
This phenomenon is not so much of a problem if we want to recursively
Hensel lift a coprime factorization 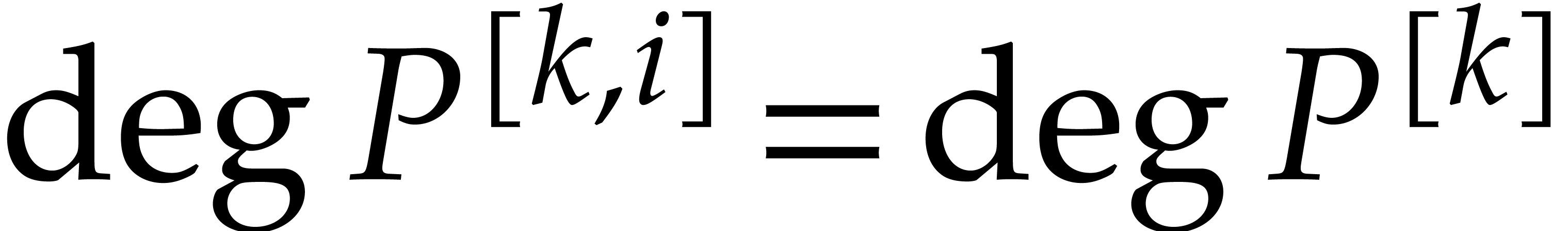 for which we
know that there exist
for which we
know that there exist 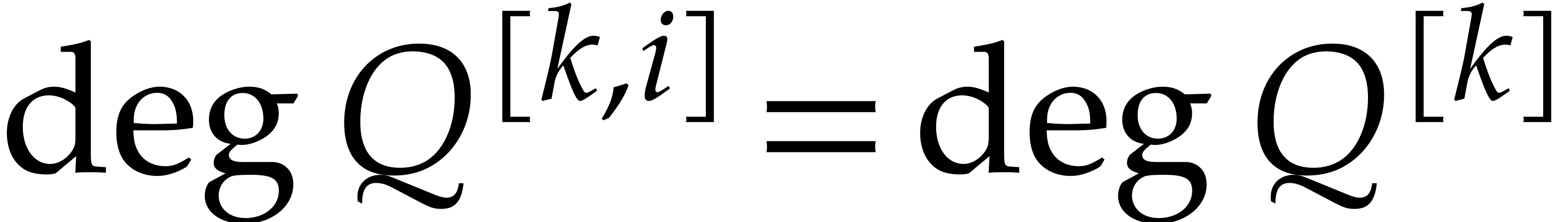 with
with  and
and 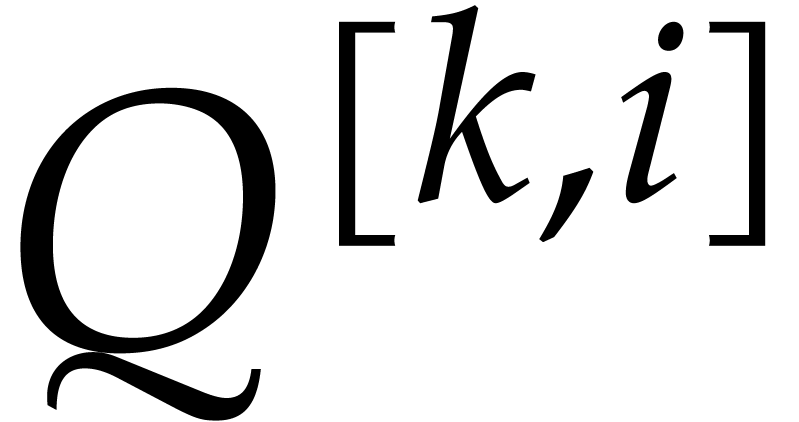 (see Algorithms 6.1
and 6.2 below). However, any algorithm for Hensel lifting
will fail if
(see Algorithms 6.1
and 6.2 below). However, any algorithm for Hensel lifting
will fail if  is irreducible or, more generally,
if no such
is irreducible or, more generally,
if no such  and
and 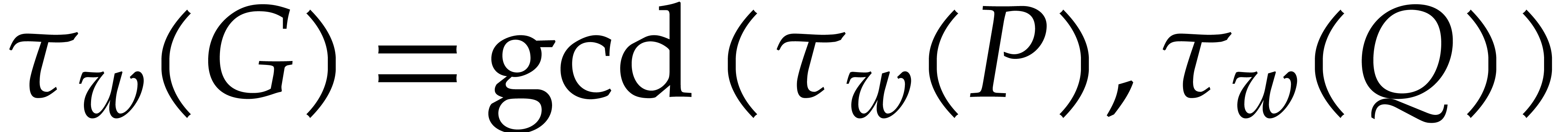 exist
(Algorithm 6.3 below for the irreducible factorization of
exist
(Algorithm 6.3 below for the irreducible factorization of
 may therefore fail on Example 6.3).
may therefore fail on Example 6.3).
Consider a non-trivial factorization  ,
where
,
where  are coprime. Assume that
are coprime. Assume that  is faithful for this factorization. Let us show how to recover
is faithful for this factorization. Let us show how to recover  and
and 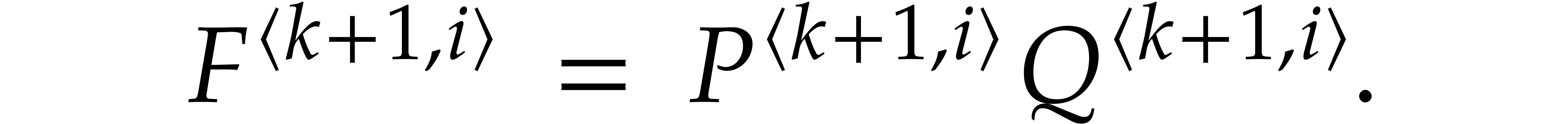 from
from 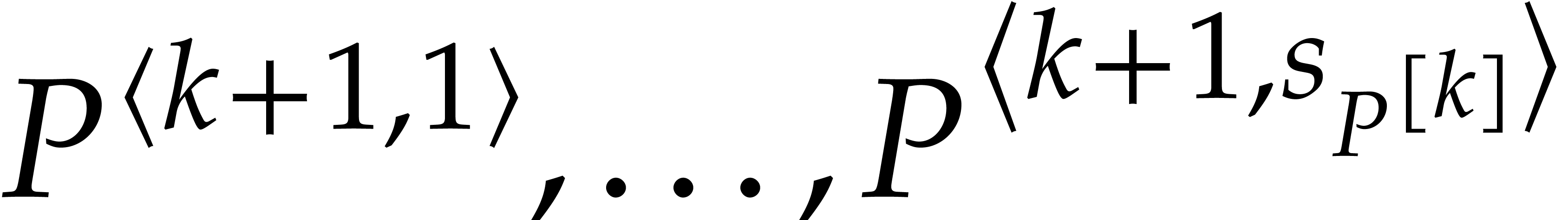 and
and  , for
, for 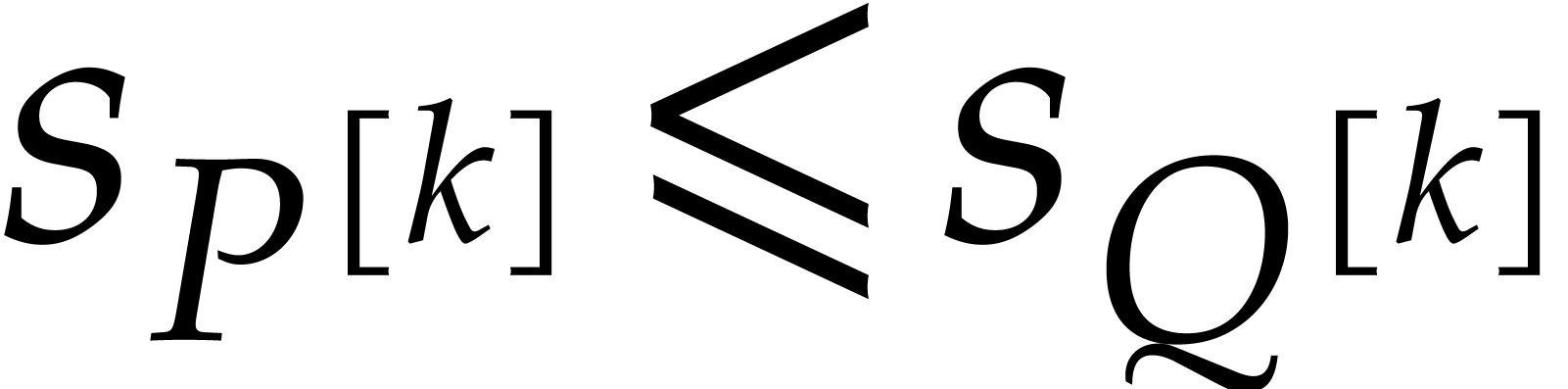 .
.
Let  be an admissible ratio or an FFT ratio. For
any
be an admissible ratio or an FFT ratio. For
any  and any
and any  ,
let
,
let

and

With high probability, we have  ,
,
 ,
,  , and the polynomials
, and the polynomials 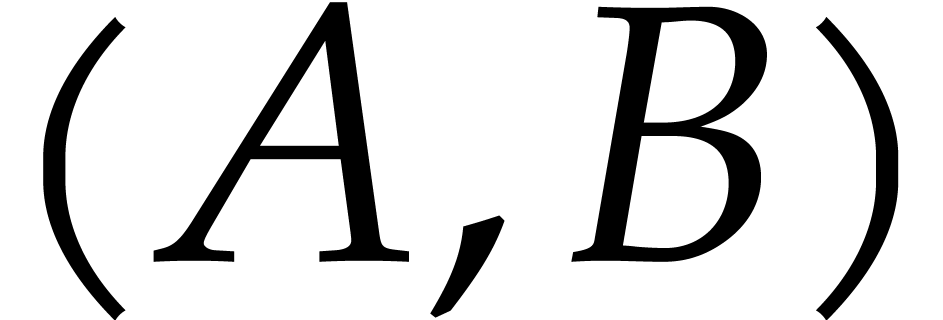 and
and
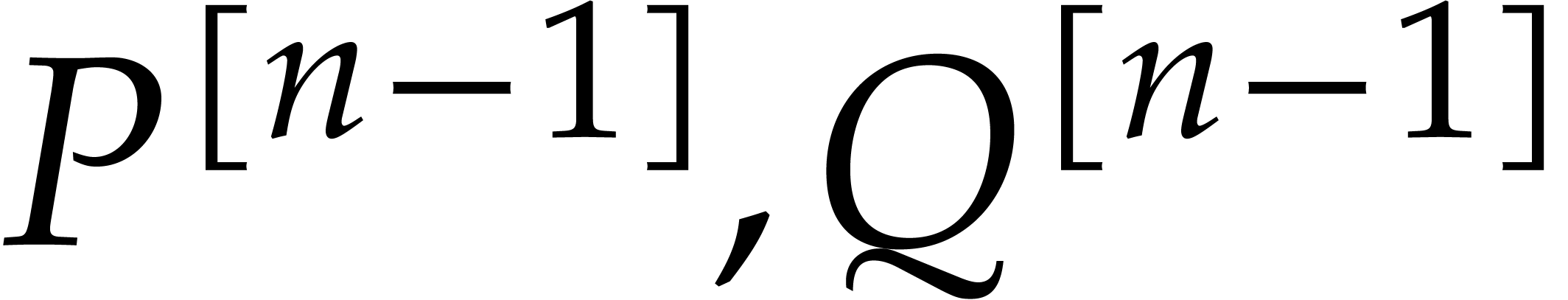 are again coprime. It follows that each
factorization
are again coprime. It follows that each
factorization

can be Hensel-lifted (see Section 4.3) into a factorization

We now recover 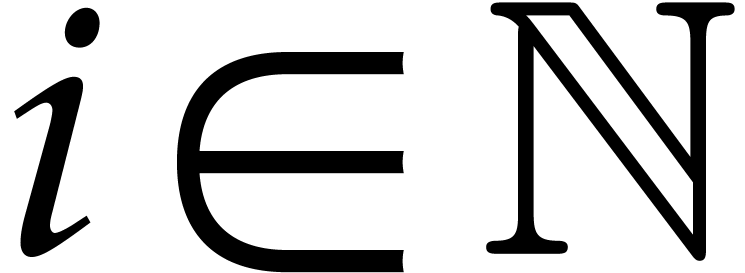 and
and 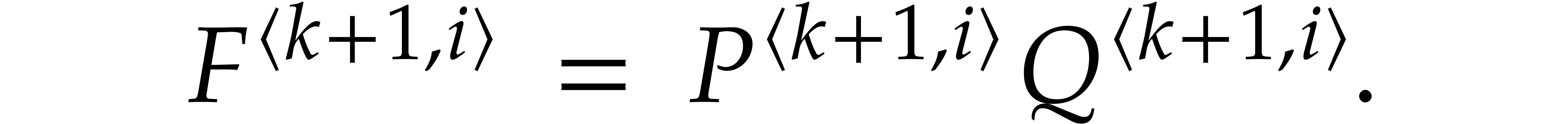 from
from
 and
and  ,
respectively, using sparse interpolation. In fact, if
,
respectively, using sparse interpolation. In fact, if  , then we may interpolate
, then we may interpolate 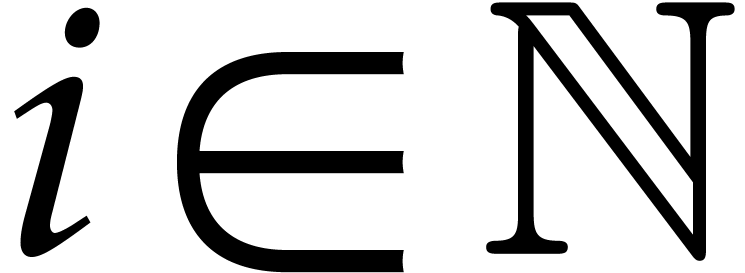 and recover
and recover 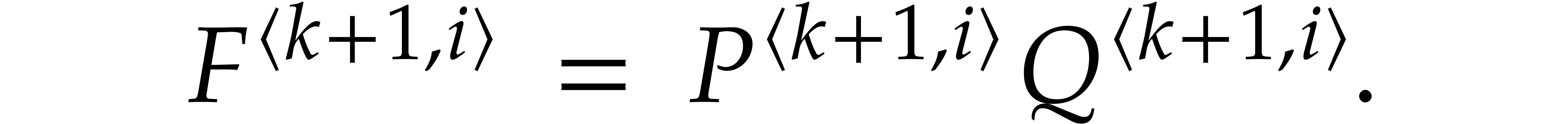 using one exact division.
using one exact division.
Moreover, we may exploit the assumption that the supports of 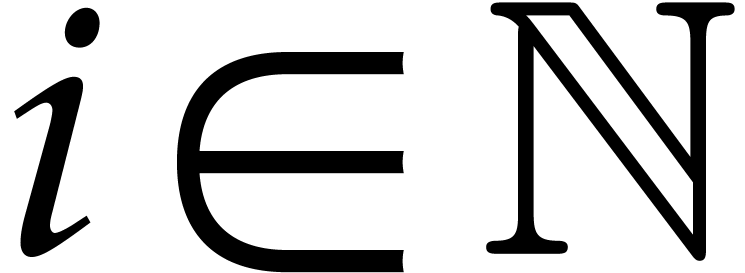 and
and 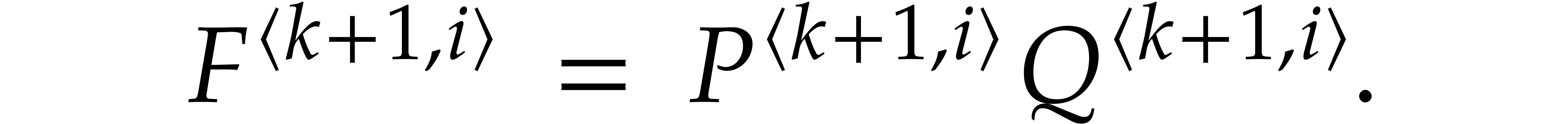 with respect to
with respect to 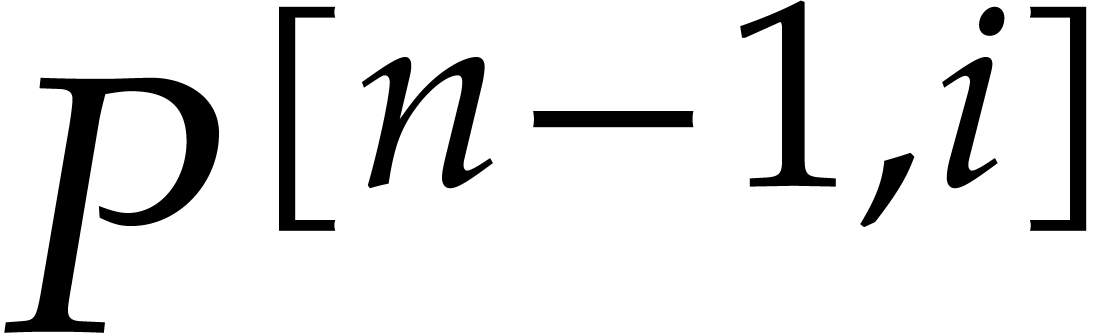 coincide with the supports of
coincide with the supports of 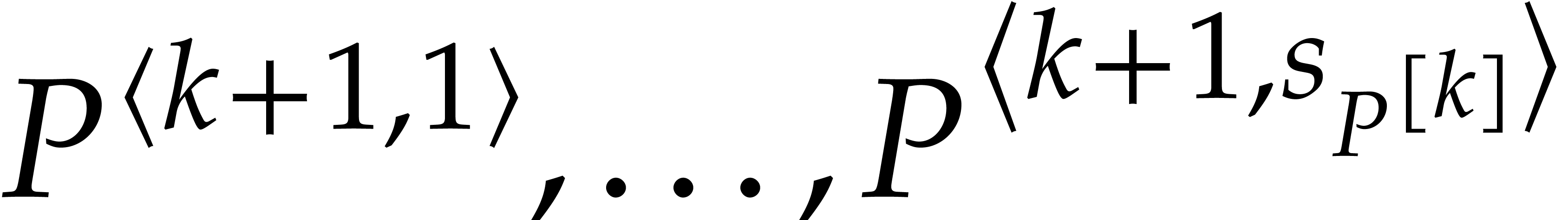 and
and
 . In the algorithm below,
this explains why
. In the algorithm below,
this explains why 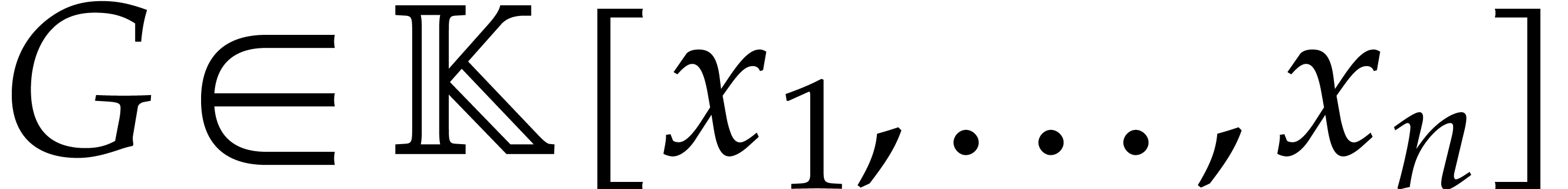 evaluation points indeed
suffice:
evaluation points indeed
suffice:
Algorithm
| Input: |
|
| Output: |
|
If  , then return
, then return 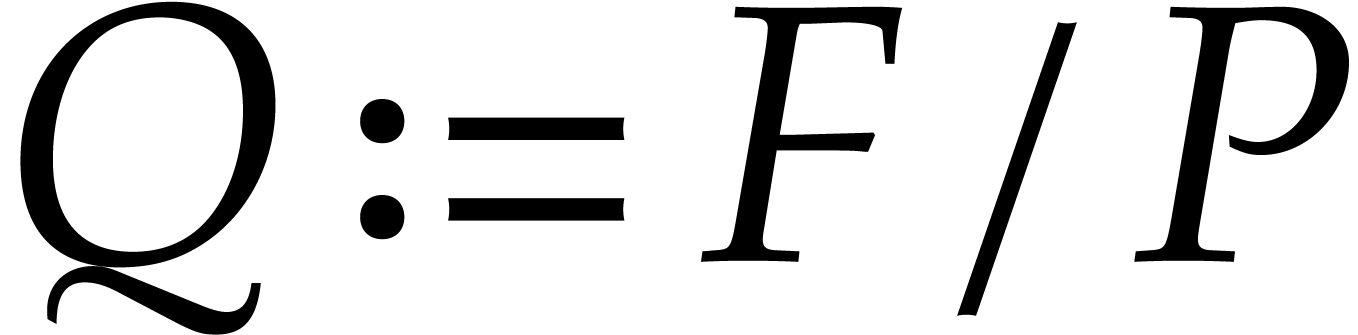
Compute 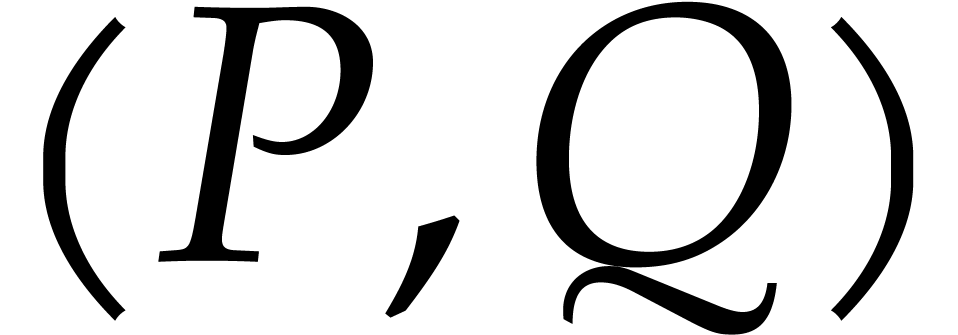 by recursively applying the algorithm
to
by recursively applying the algorithm
to 
Permute 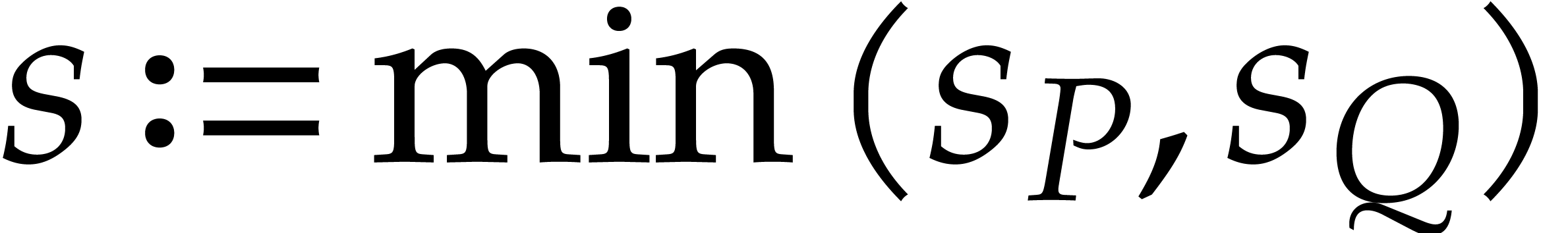 if necessary to ensure that
if necessary to ensure that 
Compute 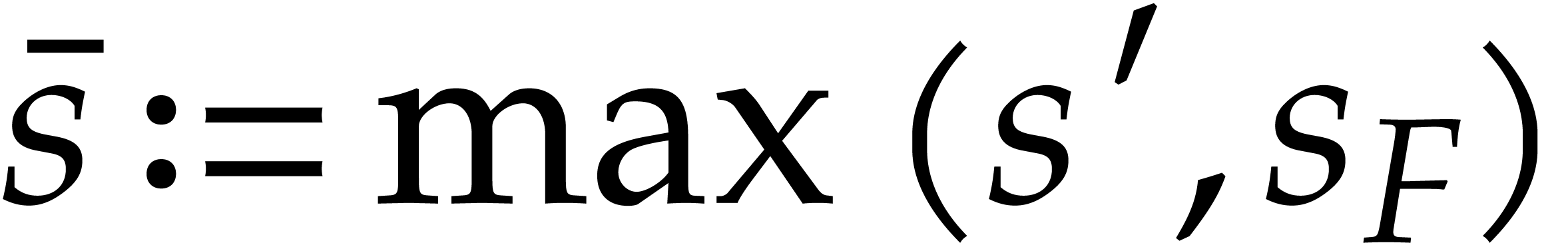 ,
, 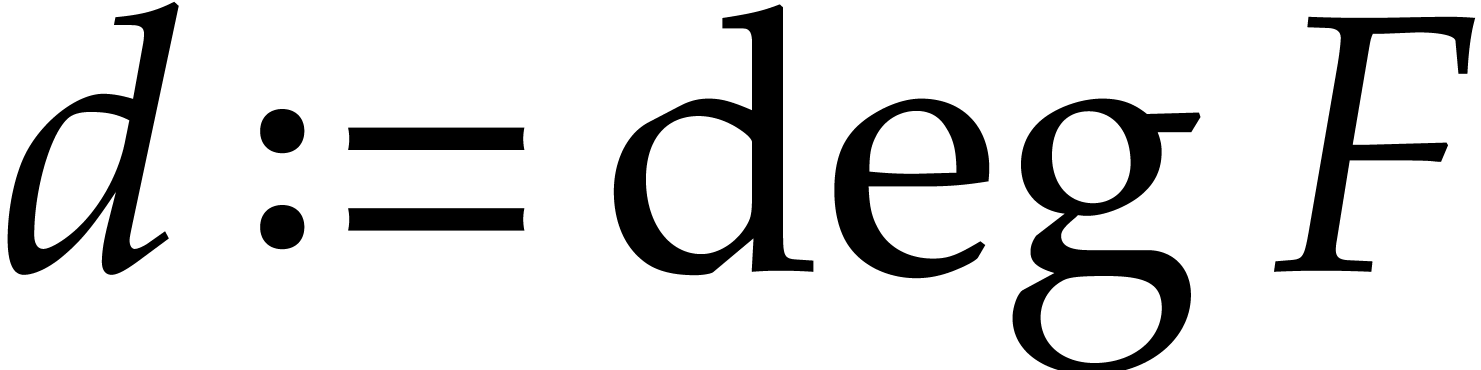 , and
, and 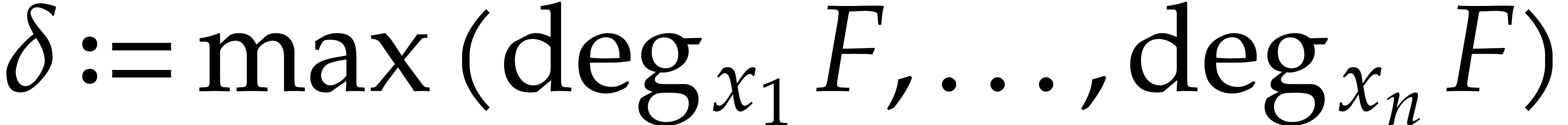 for
for  , using sparse evaluation
, using sparse evaluation
Deduce  for
for 
For 
Compute  with
with  using
Hensel lifting (Section 4.3)
using
Hensel lifting (Section 4.3)
Raise an error if this fails
Recover  from
from  using
sparse interpolation
using
sparse interpolation
Let  and return
and return 
Remark 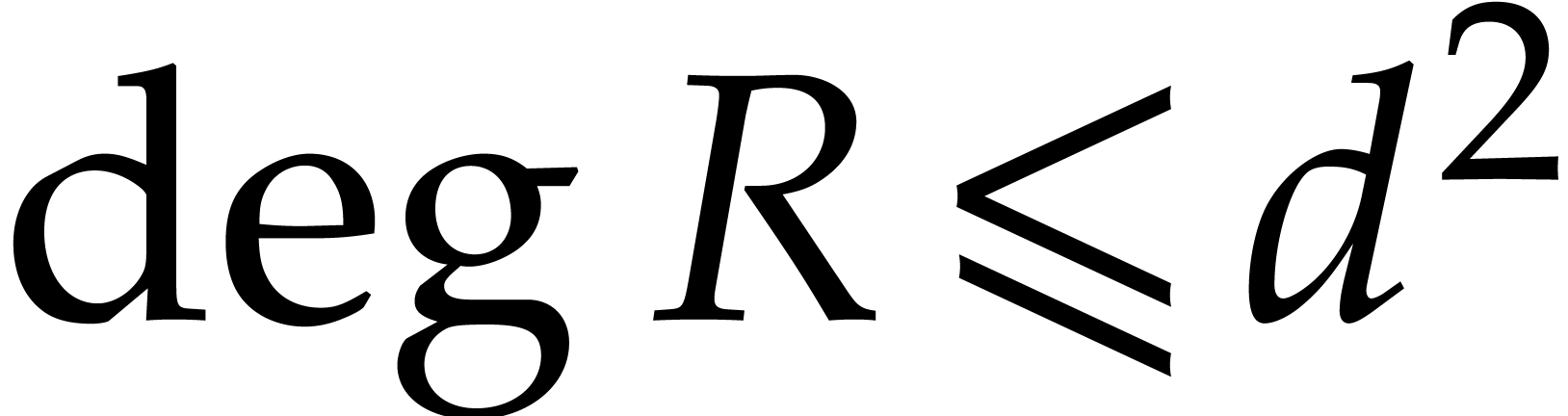 .
If
.
If  is small, then this support bound is
reasonably tight. Consequently, we may use sparse interpolation with
known supports in order to recover
is small, then this support bound is
reasonably tight. Consequently, we may use sparse interpolation with
known supports in order to recover  .
.
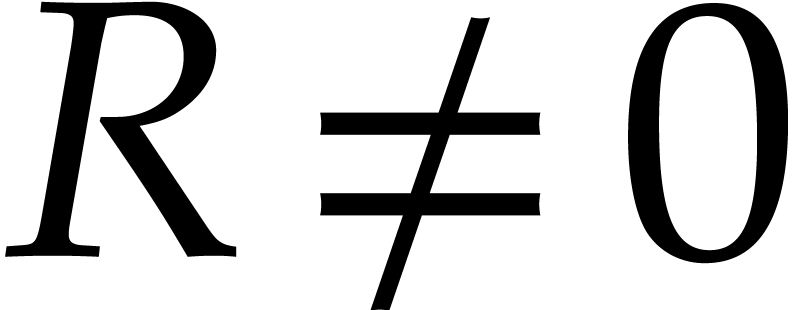 ,
, 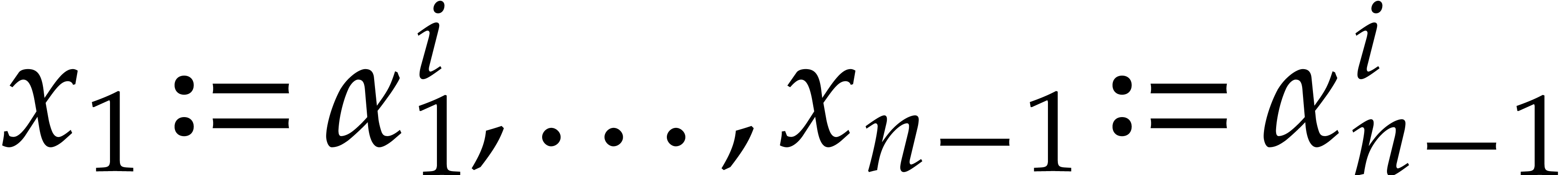
 ,
,  , and
, and 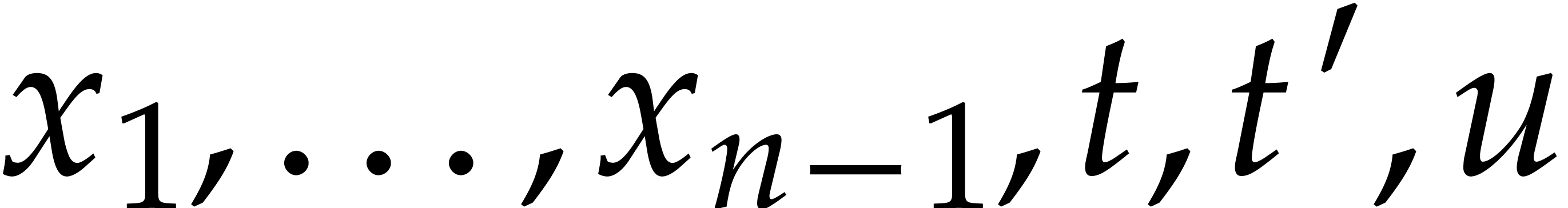 . Then Algorithm 6.1 runs in time
. Then Algorithm 6.1 runs in time

and returns the correct result with probability at least
Proof. Assume that we correctly recovered 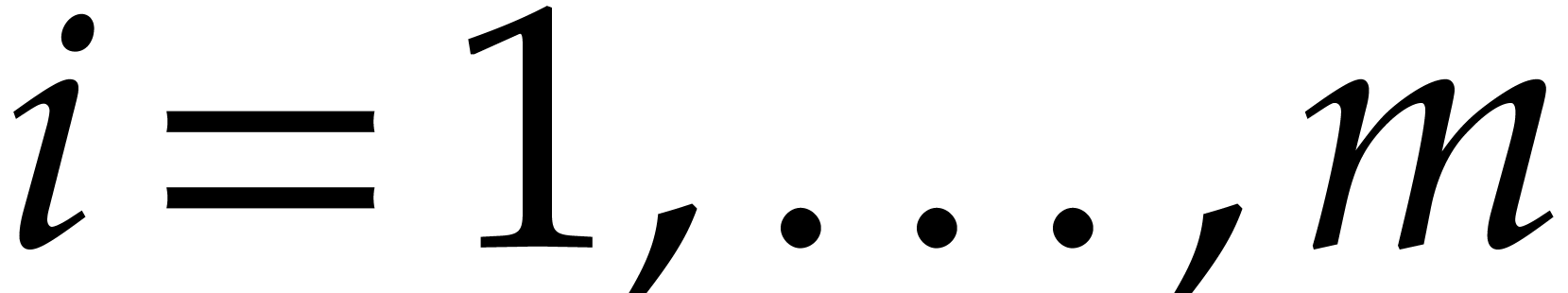 and
and 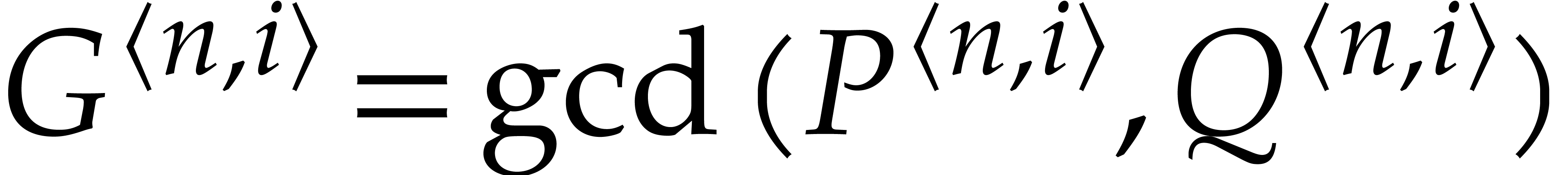 and let us investigate
the probability that the results
and let us investigate
the probability that the results  and
and 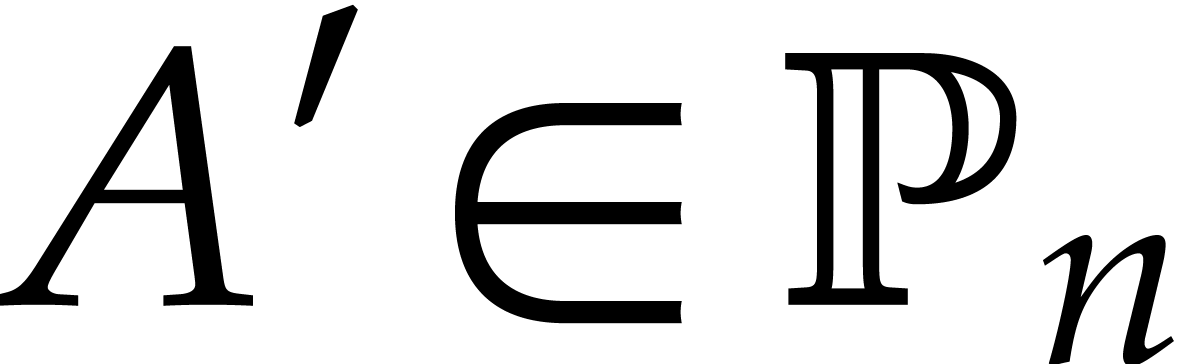 are correct.
are correct.
Let us first examine the probability that the Hensel lifting method from
Section 4.3 works correctly. This is the case whenever the
following three conditions are satisfied for 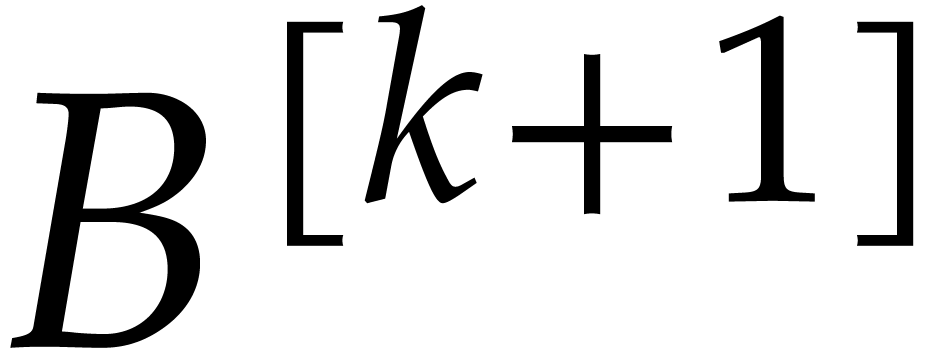 :
:
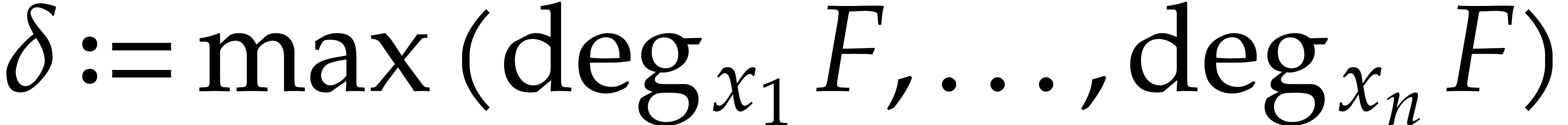 and
and 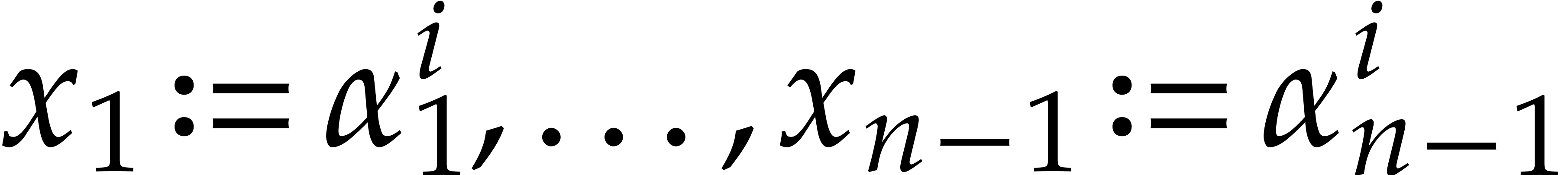 are coprime;
are coprime;
We have 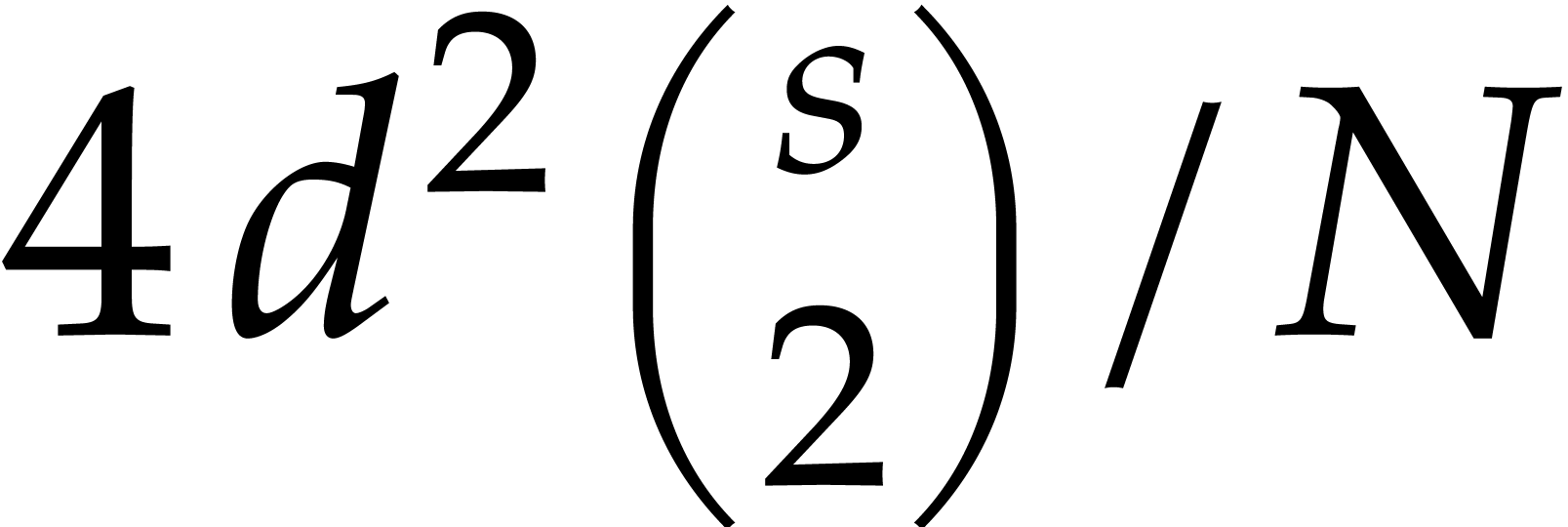 ;
;
We have 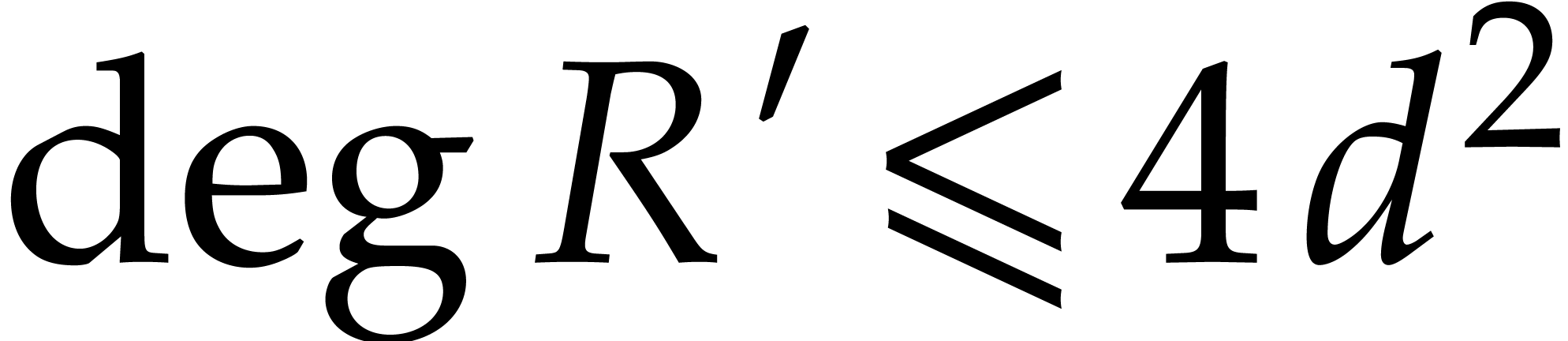 .
.
Consider
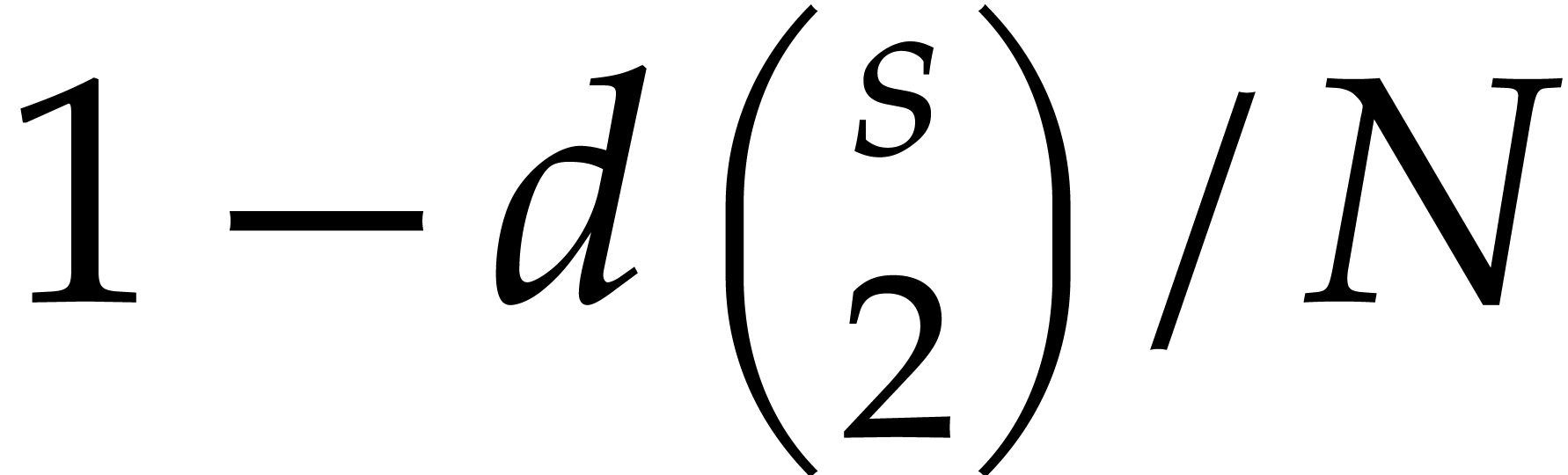 |
(6.1) |
with  . We have
. We have 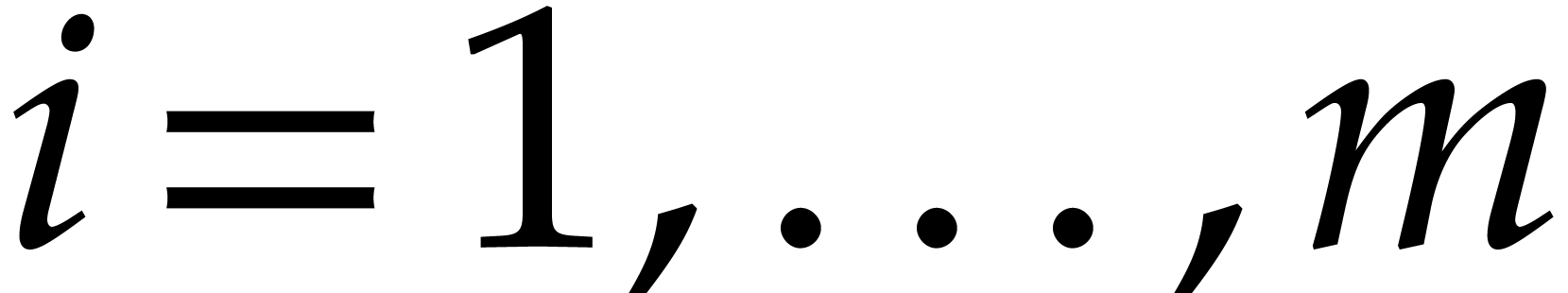 since
since 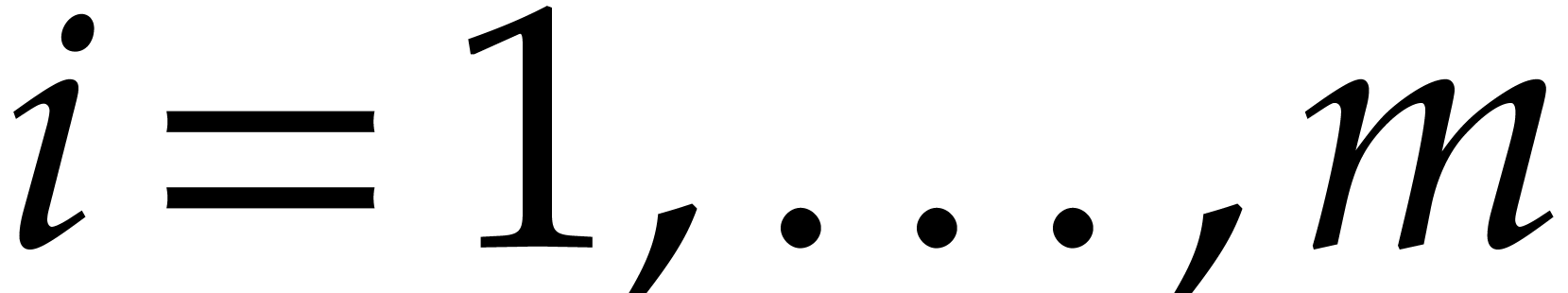 and
and 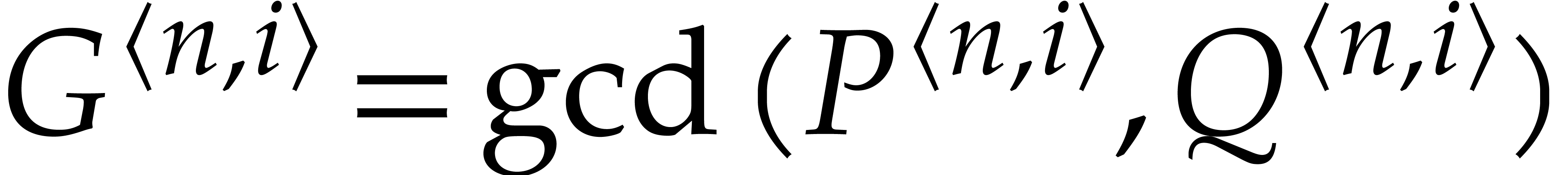 are coprime. The first condition fails for a given
are coprime. The first condition fails for a given  if and only if
if and only if 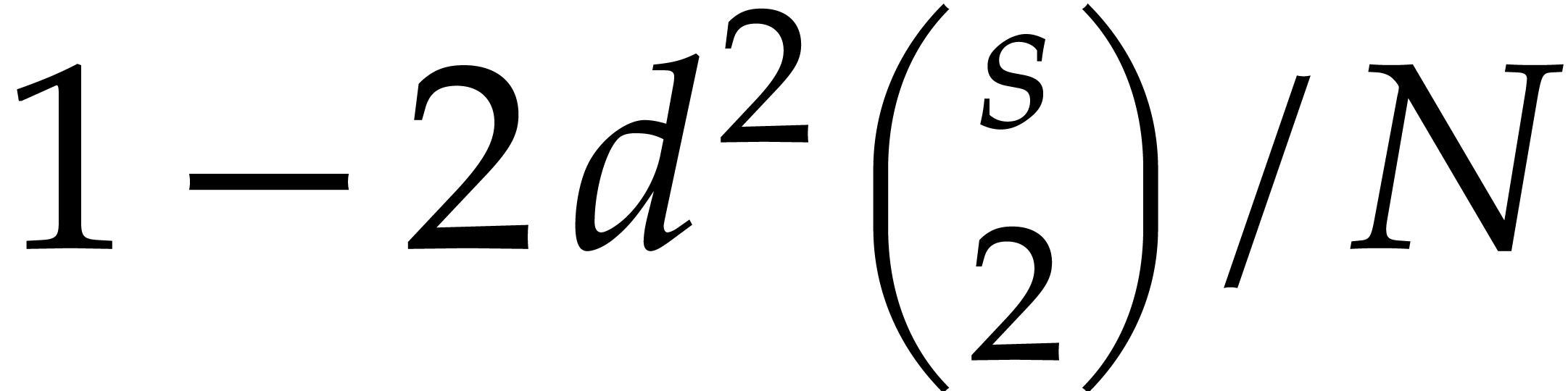 vanishes under the substitutions
vanishes under the substitutions
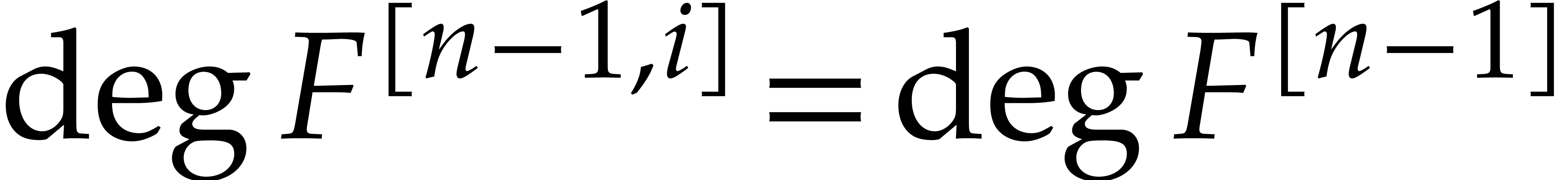 . This happens with
probability at most
. This happens with
probability at most 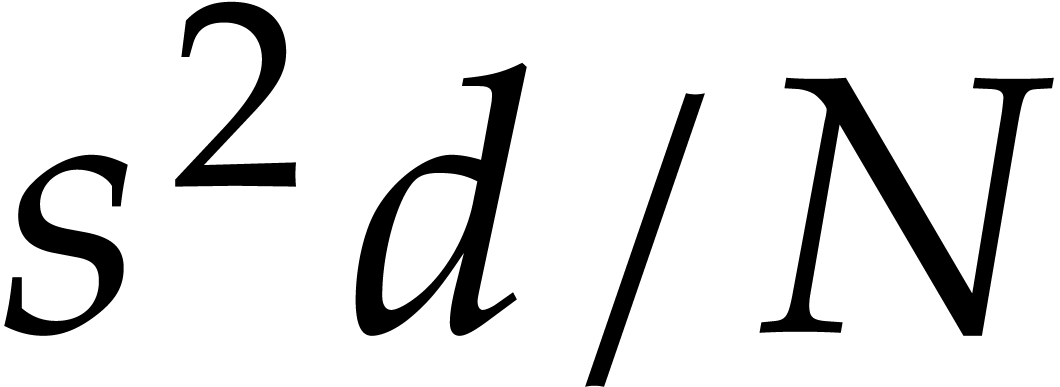 for some
for some  , by Corollary 2.2. Let us next
consider
, by Corollary 2.2. Let us next
consider
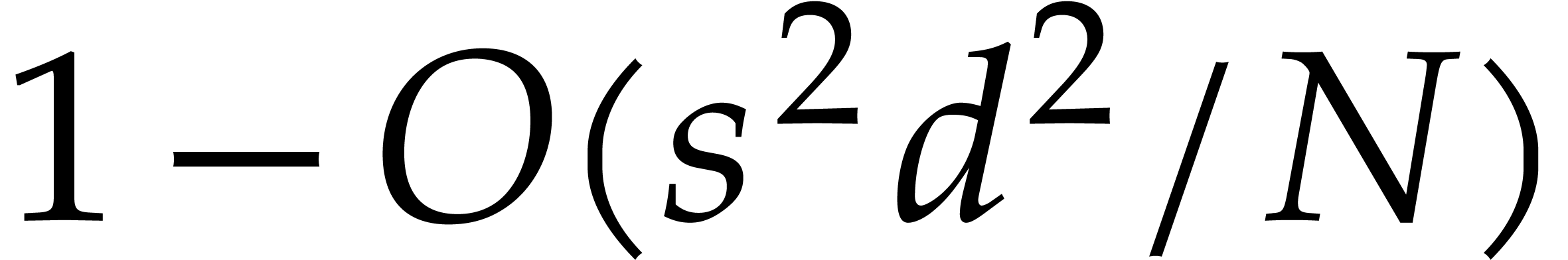
where  are formal indeterminates. Since
are formal indeterminates. Since  is content-free, we have
is content-free, we have 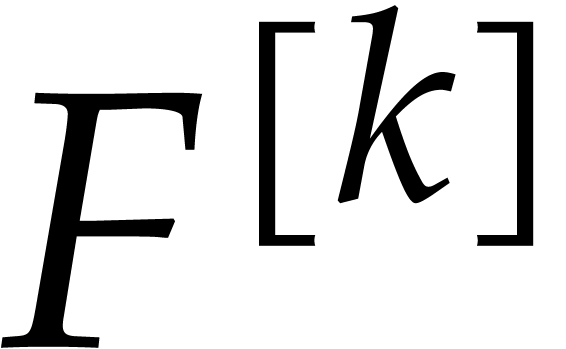 .
Now
.
Now 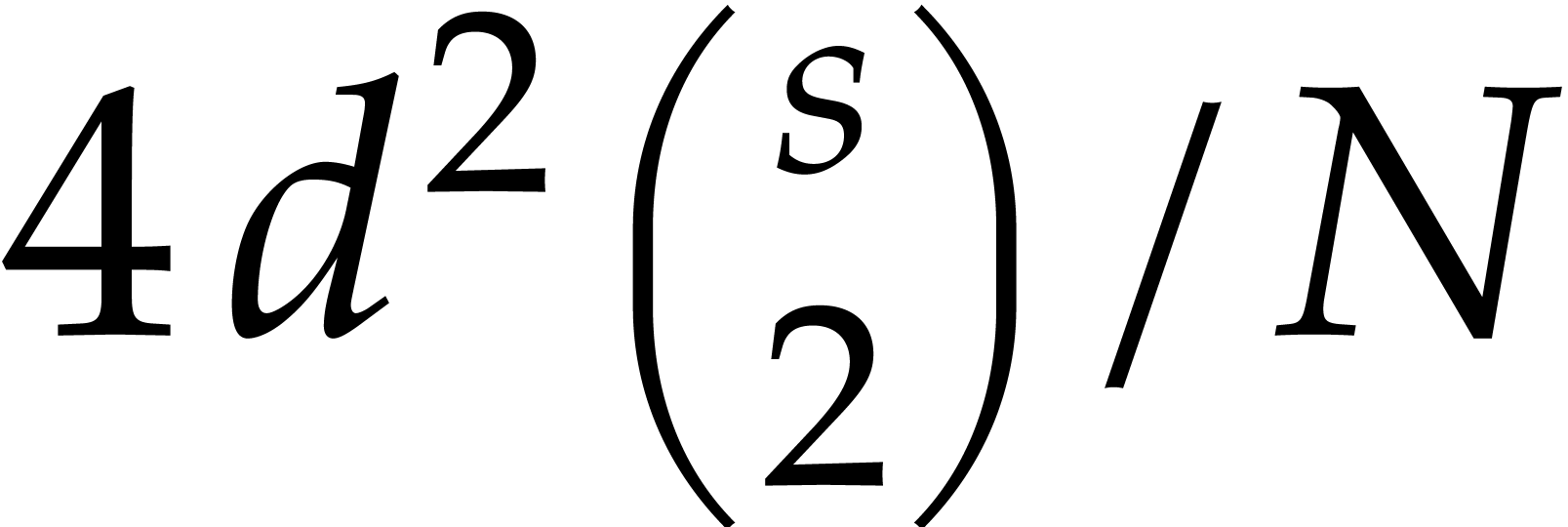 whenever
whenever  does not
vanish under the substitutions
does not
vanish under the substitutions  .
The second condition therefore fails for some
.
The second condition therefore fails for some  with probability at most
with probability at most  , by
Corollary 2.2 and using the fact that
, by
Corollary 2.2 and using the fact that 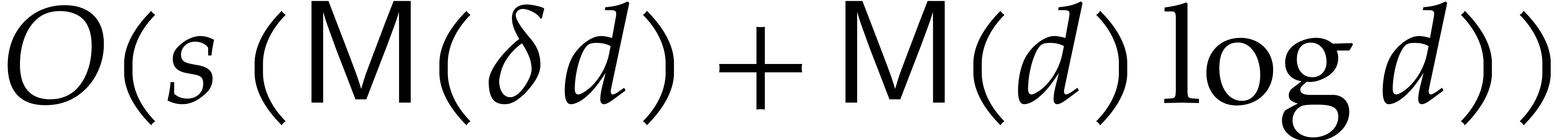 . Finally, with probability at least
. Finally, with probability at least  , we have
, we have

for  , by Corollary 2.2.
, by Corollary 2.2.
Let us now return to the correctness of the overall algorithm. Concerning the top-level call, we have the following:
Obtaining  from the evaluations
from the evaluations 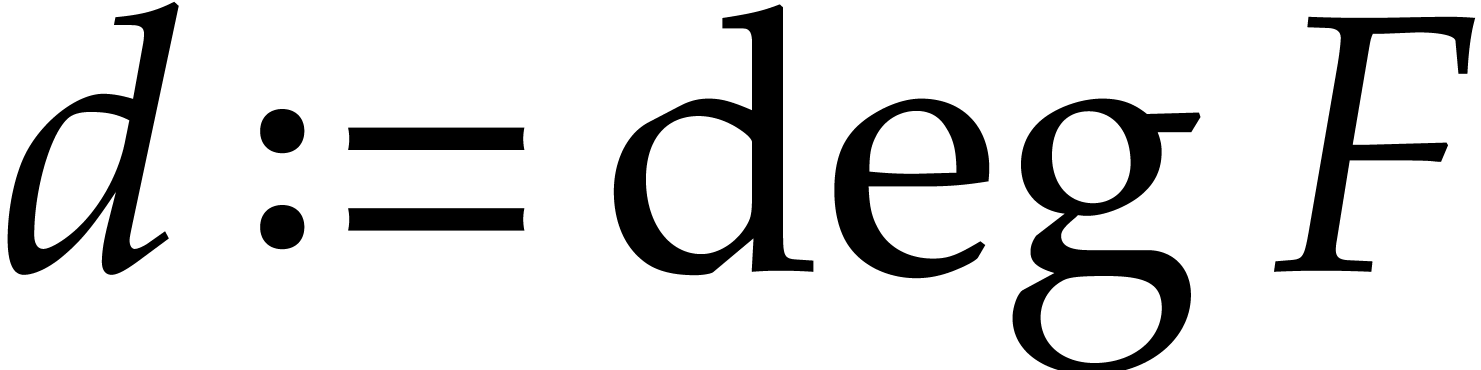 ,
, 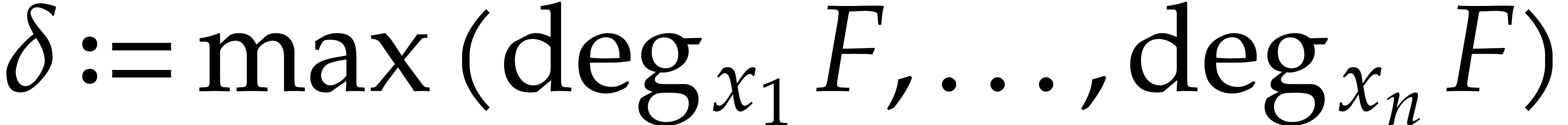 for
for  by exact univariate polynomial division is possible as
long as
by exact univariate polynomial division is possible as
long as  . This condition
fails with probability at most
. This condition
fails with probability at most  by Corollary
2.2.
by Corollary
2.2.
We have shown above that the Hensel lifting strategy from Section
4.3 can be applied with probability at least  . By adapting the proof of
Proposition 4.3 such that we can apply Corollary 2.2, the Hensel lifting itself also succeeds with
probability at least
. By adapting the proof of
Proposition 4.3 such that we can apply Corollary 2.2, the Hensel lifting itself also succeeds with
probability at least 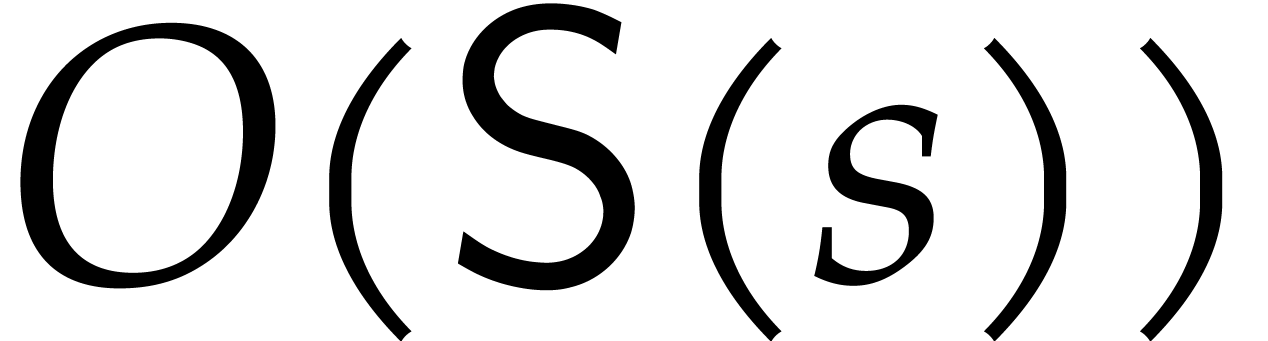 ,
for
,
for 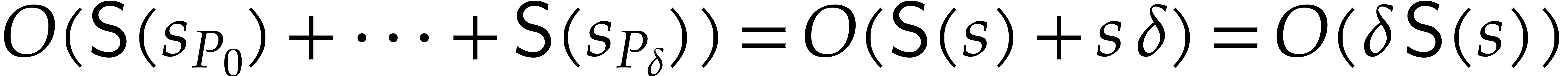 .
.
Altogether, we correctly determine  and
and  with probability at least
with probability at least 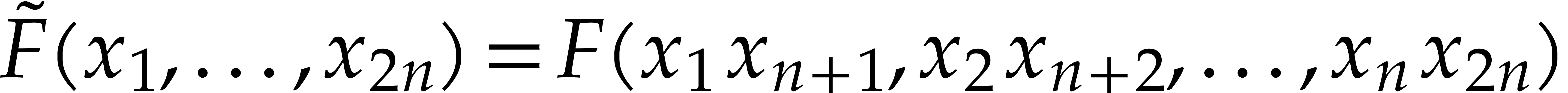 .
Since there are
.
Since there are  recursive levels and since the
sizes of the supports of
recursive levels and since the
sizes of the supports of  ,
,
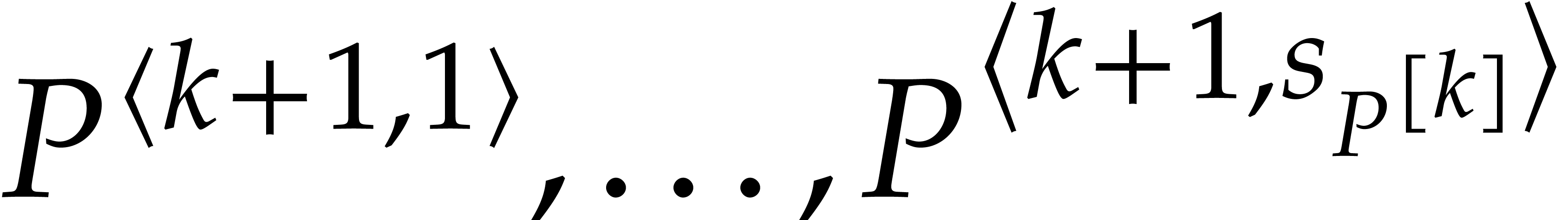 , and
, and  are all smaller than those of
are all smaller than those of  ,
,
 , and
, and 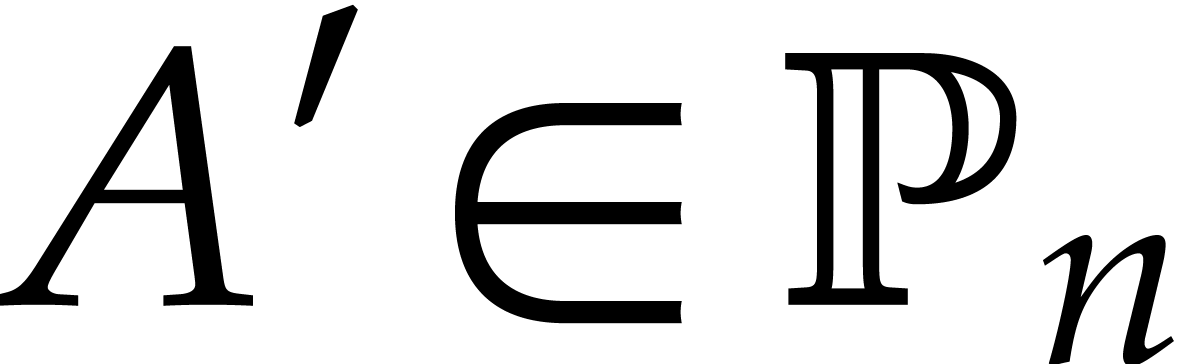 , the probabilistic correctness claim follows.
, the probabilistic correctness claim follows.
As to the complexity bound, let us now study the cost when not counting the recursive calls:
The computation of the 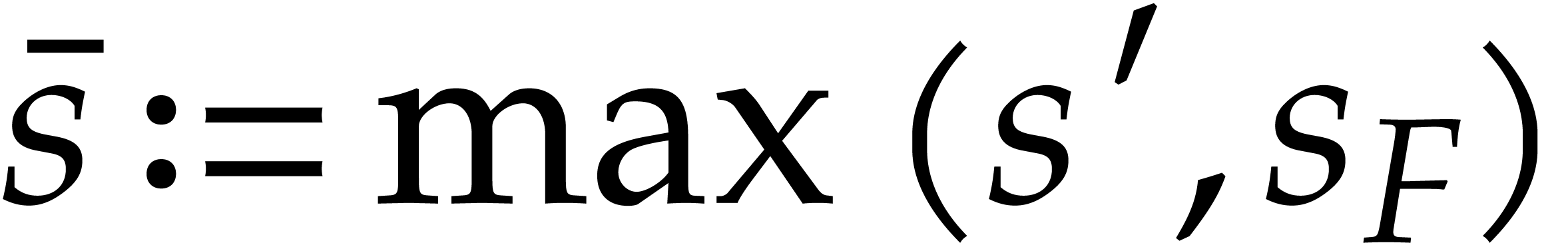 ,
,
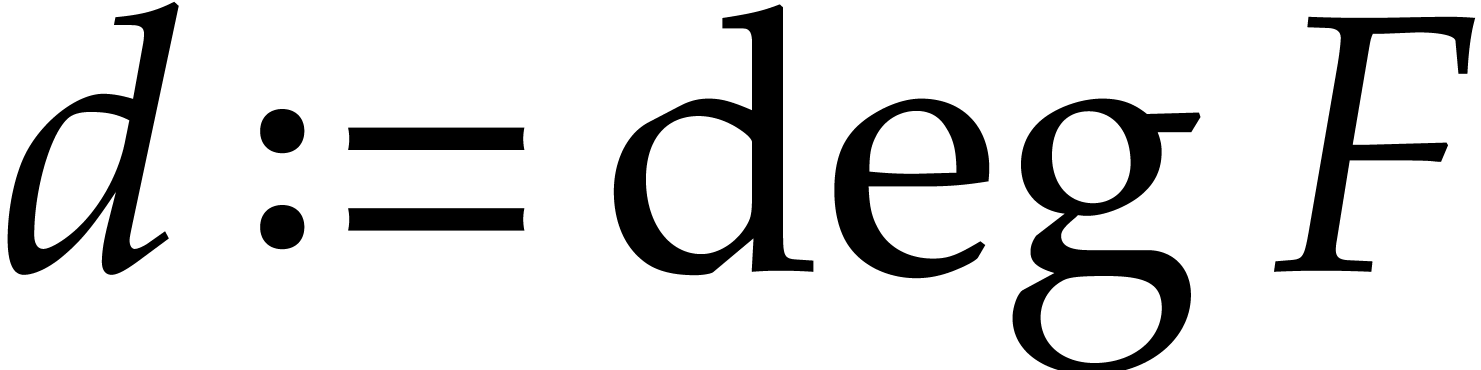 , and
, and 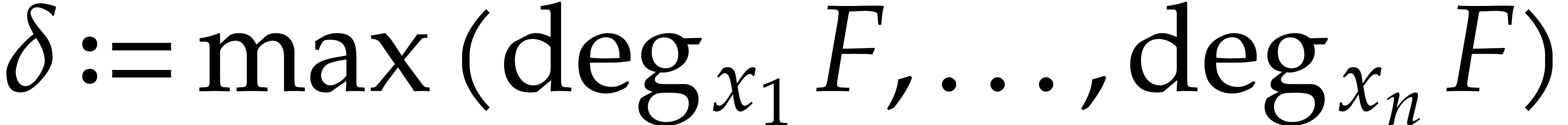 , using sparse evaluation at geometric
sequences requires
, using sparse evaluation at geometric
sequences requires 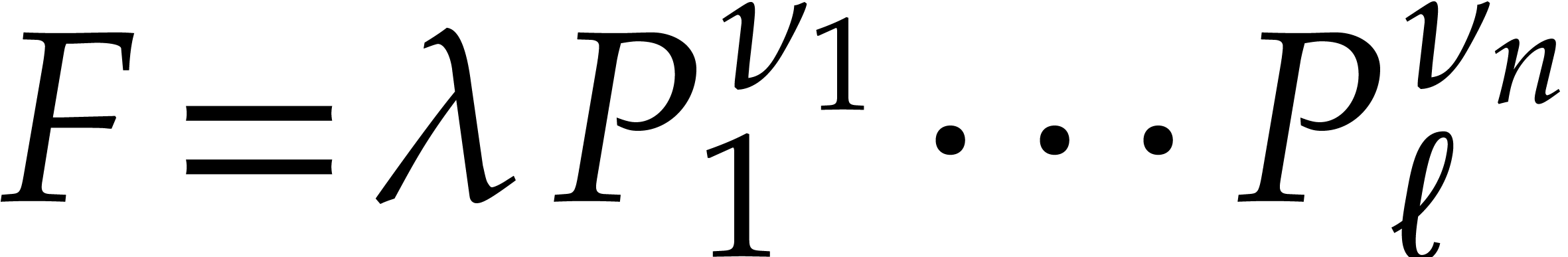 operations in
operations in  .
.
The evaluations of  are obtained by exact
univariate polynomial division and require
are obtained by exact
univariate polynomial division and require  operations in total.
operations in total.
Lifting the factorization for all of the evaluations requires  further operations, by Proposition 4.3.
further operations, by Proposition 4.3.
We obtain  from
from  using
sparse interpolation of the coefficients
using
sparse interpolation of the coefficients  in
time
in
time  .
.
The recovery of 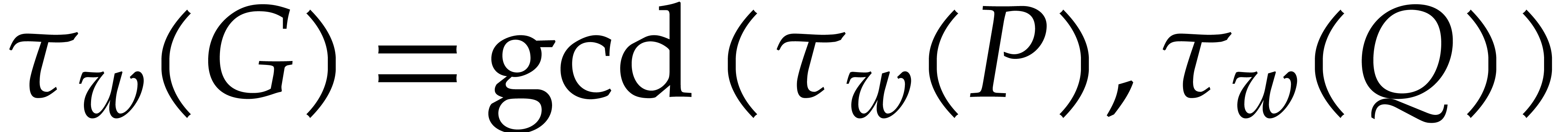 through sparse polynomial
division takes
through sparse polynomial
division takes 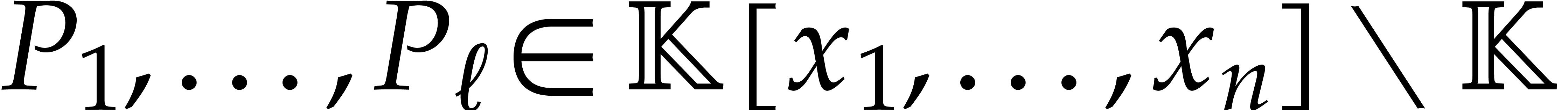 further operations, as
explained in Section 2.4.
further operations, as
explained in Section 2.4.
We conclude that the cost is  ,
when not counting the recursive calls. Since there are
,
when not counting the recursive calls. Since there are  recursive levels and since the sizes of the supports of
recursive levels and since the sizes of the supports of 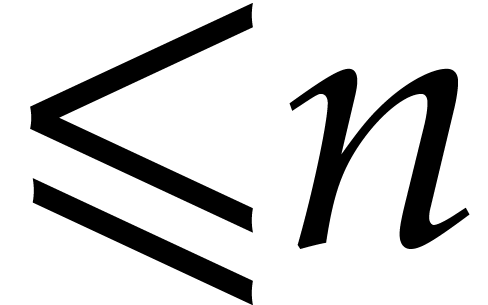 ,
, 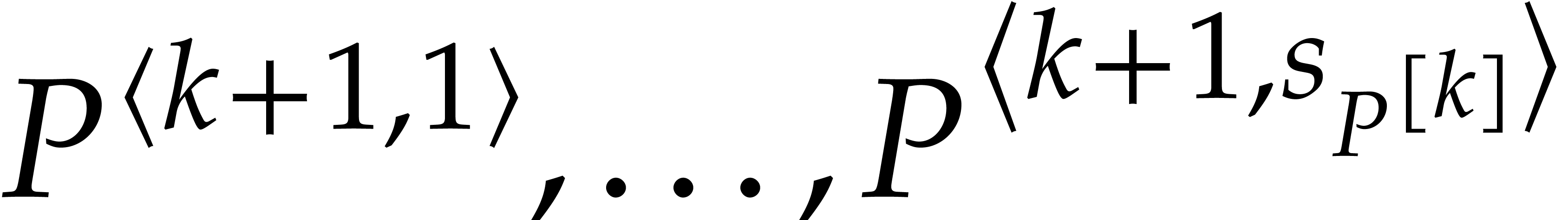 ,
and
,
and  are all smaller than those of
are all smaller than those of  ,
,  ,
and
,
and  , the complexity bound
follows.
, the complexity bound
follows.
Example 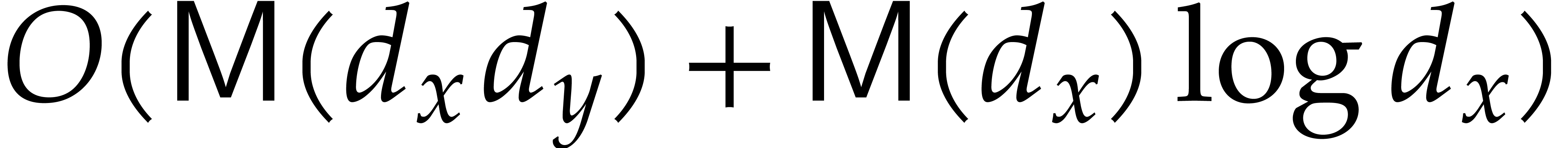 , where
, where  are
coprime. Now consider the polynomial
are
coprime. Now consider the polynomial  .
When factoring
.
When factoring  using Algorithm 6.1,
the last
using Algorithm 6.1,
the last  lifting steps with respect to
lifting steps with respect to  all operate on a projection
all operate on a projection 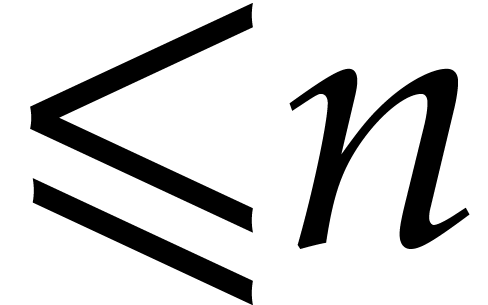 of
size
of
size  . This is an example
when the overhead
. This is an example
when the overhead  in the complexity bound is
sharp. However, the support of
in the complexity bound is
sharp. However, the support of  is very special,
since it is contained in an affine subspace of dimension
is very special,
since it is contained in an affine subspace of dimension  . It is easy to detect this situation and
directly obtain the exponents in the last
. It is easy to detect this situation and
directly obtain the exponents in the last  variables as affine combinations of the known exponents in the first
variables as affine combinations of the known exponents in the first
 variables.
variables.
More generally, it may happen that the fibers of the support under the
projection with respect to the last  variables
are all small. It would be interesting to develop specific optimizations
for this situation, e.g. directly apply sparse
interpolation on the fibers.
variables
are all small. It would be interesting to develop specific optimizations
for this situation, e.g. directly apply sparse
interpolation on the fibers.
The lifting algorithm generalizes in a straightforward way to the case
when  is a product of more than two factors. This
time, we wish to recover a factorization
is a product of more than two factors. This
time, we wish to recover a factorization  from
from
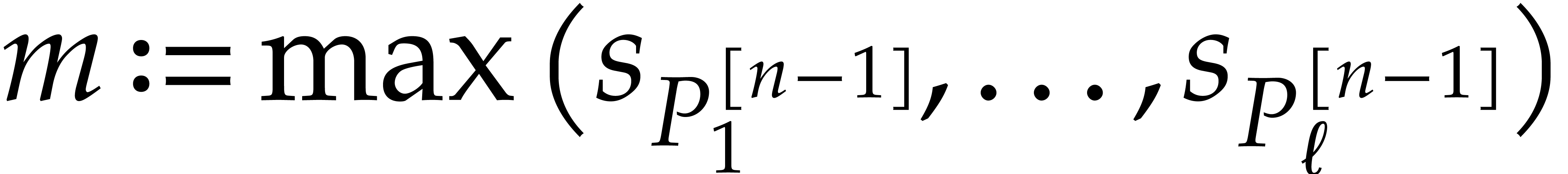 , assuming that
, assuming that  (hence
(hence  ) are
pairwise coprime.
) are
pairwise coprime.
Algorithm
Input: |
|
Output: |
irreducible and pairwise coprime |
If  , then return
, then return 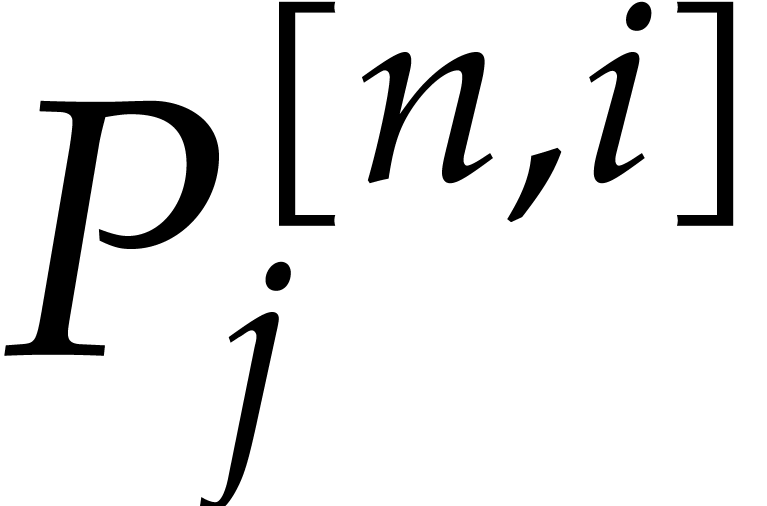
Recursively apply the algorithm to 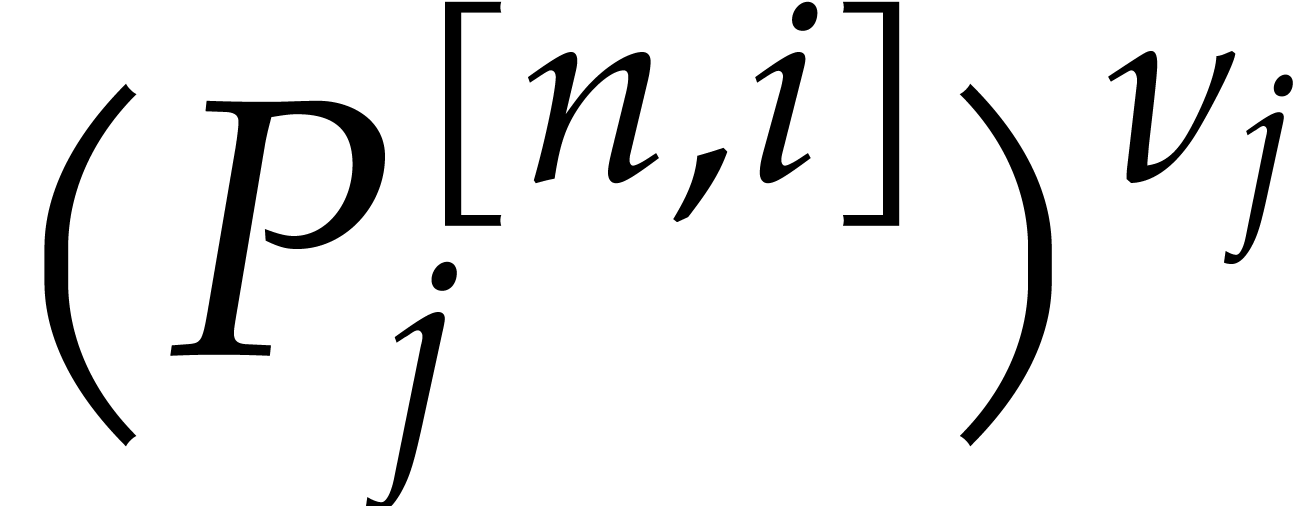 to compute
to compute
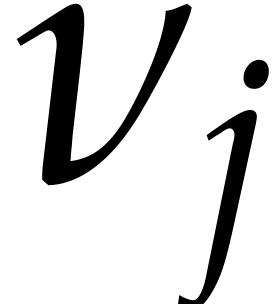
Let 
Compute 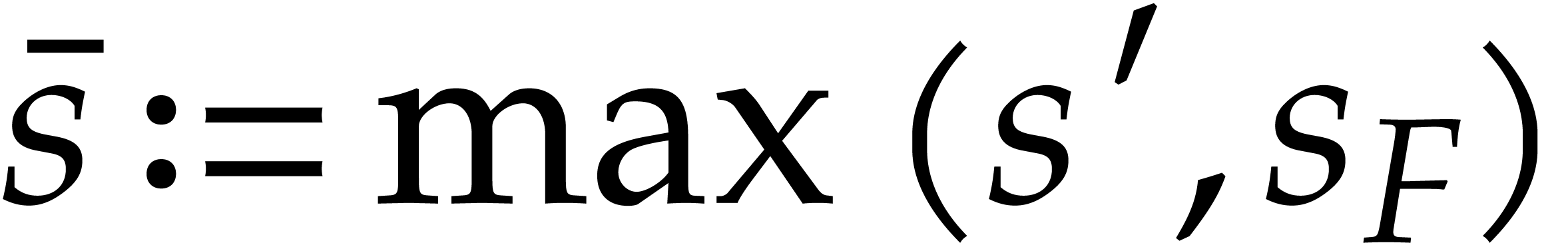 ,
, 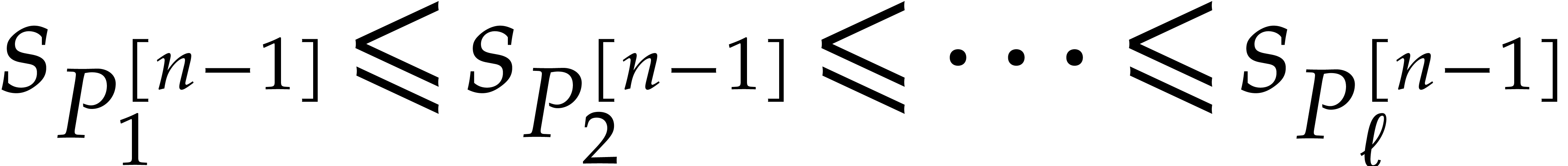 for
for 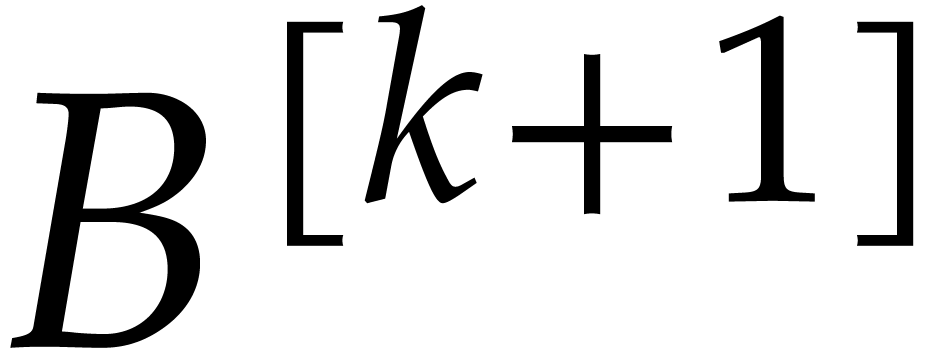 , using sparse
evaluation
, using sparse
evaluation
Deduce 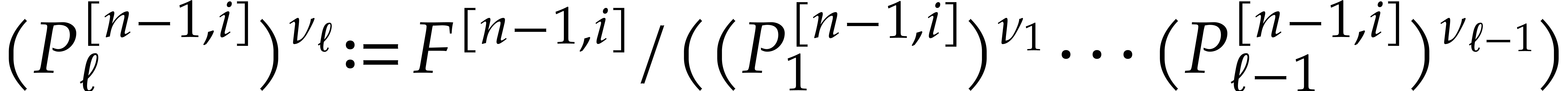 for
for 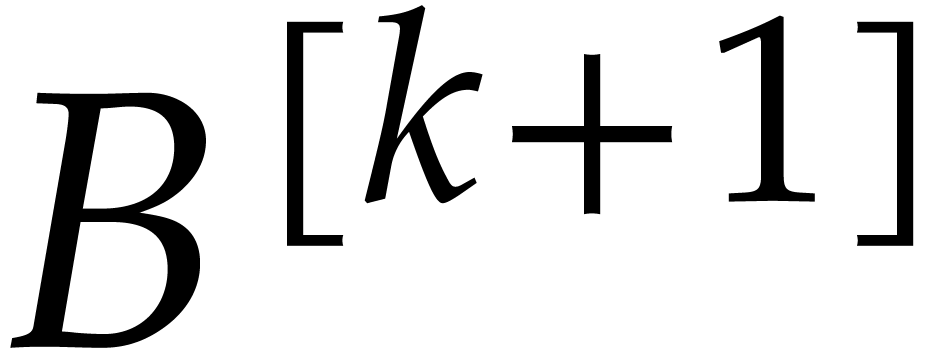
For 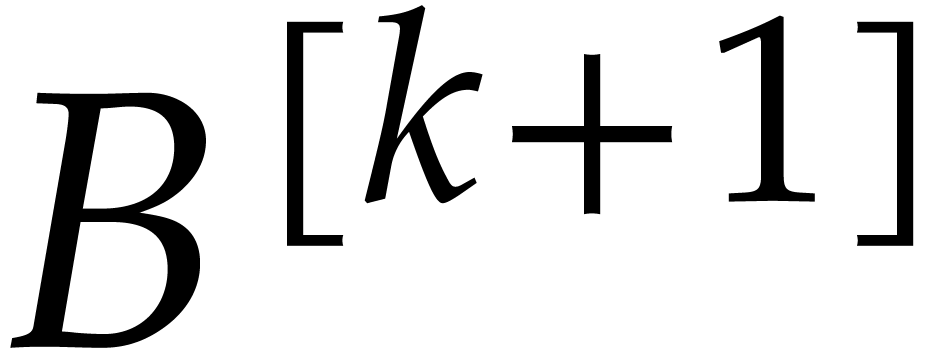
Compute 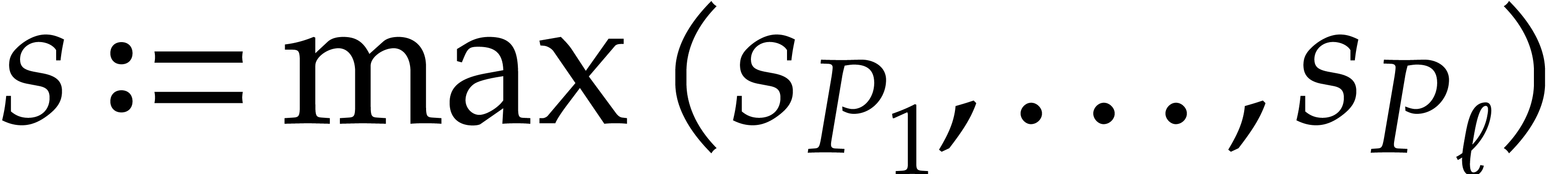 with
with 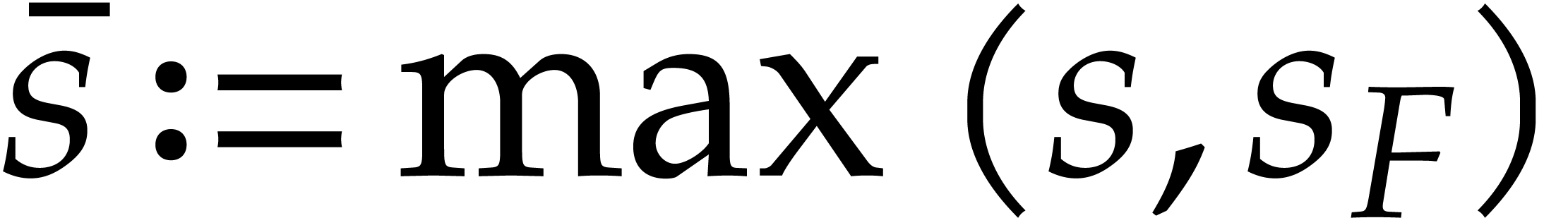 using
Hensel lifting
using
Hensel lifting
Raise an error if this fails
Recover  from the
from the 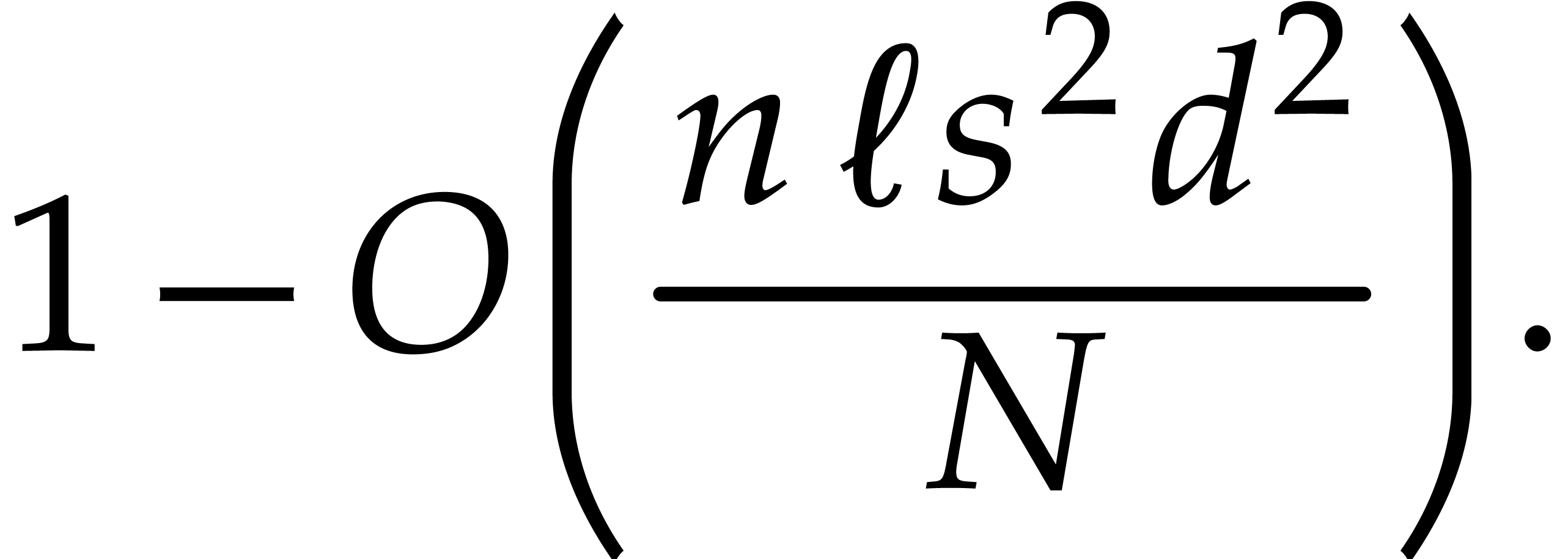 using
sparse interpolation, for
using
sparse interpolation, for 
Return ( )
)
Remark 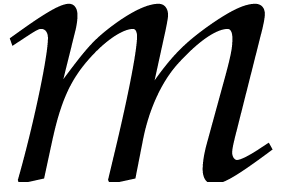 using binary powering and
using binary powering and
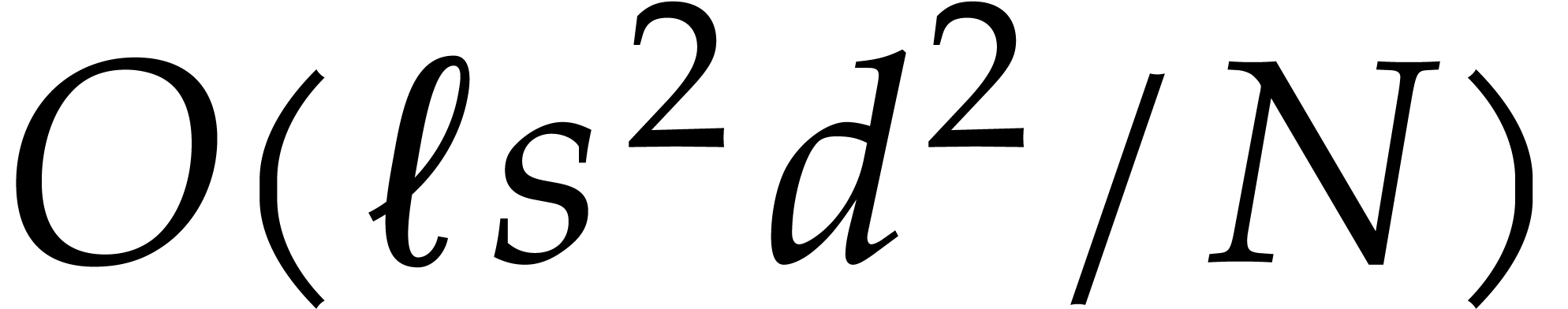 from
from  using dense
bivariate
using dense
bivariate  -th root
extraction, for
-th root
extraction, for  . As an
optimization, we may first sort the factors of
. As an
optimization, we may first sort the factors of 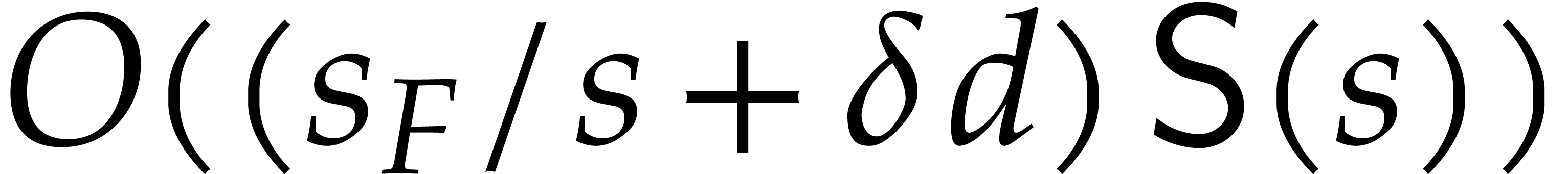 such that
such that  and then compute
and then compute 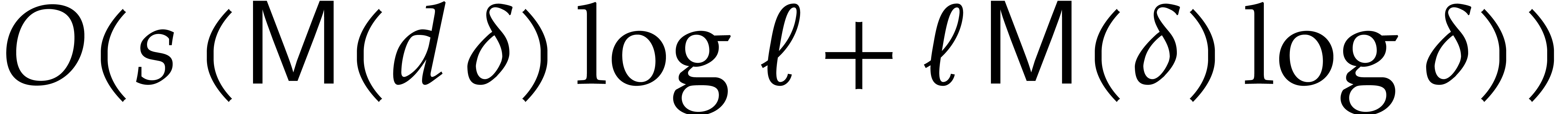 using exact division.
using exact division.
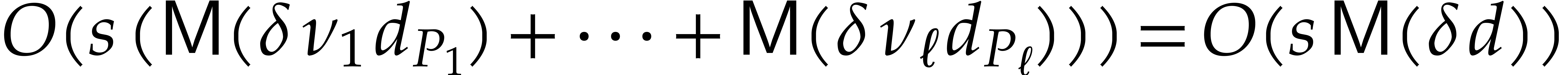 ,
, 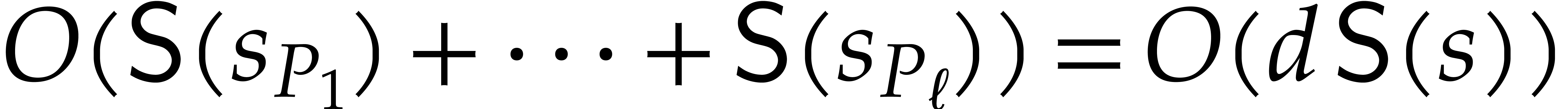 ,
, 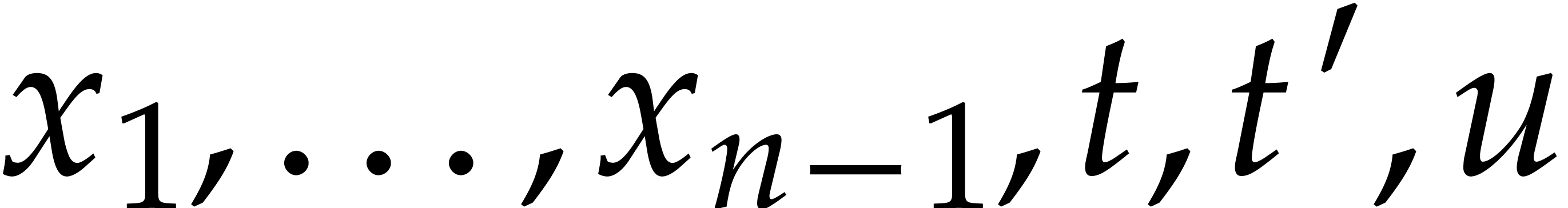 ,
and
,
and  . Then Algorithm 6.2 runs in time
. Then Algorithm 6.2 runs in time
and returns the correct result with probability at least
Proof. The proof is similar to that of Algorithm
6.1. Assume now that we correctly recovered 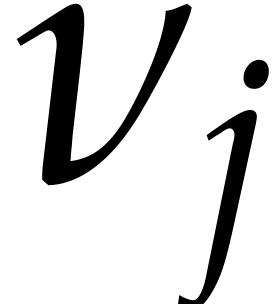 and let us investigate the probability that the results
and let us investigate the probability that the results
 are correct. To apply the Hensel lifting method
from Section 4.3, the following three conditions must be
satisfied for
are correct. To apply the Hensel lifting method
from Section 4.3, the following three conditions must be
satisfied for 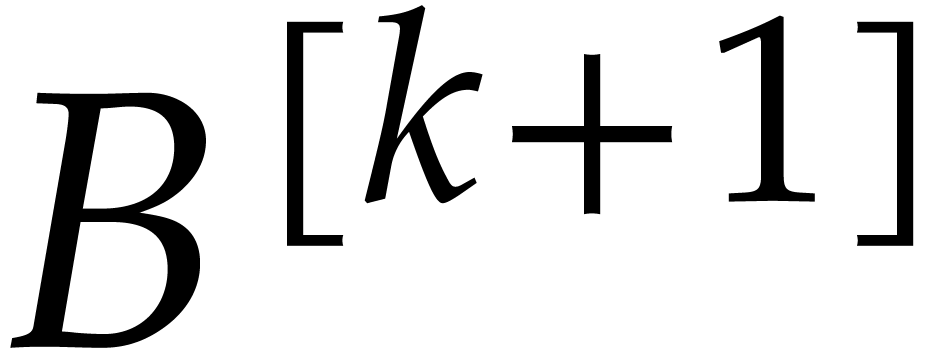 :
:
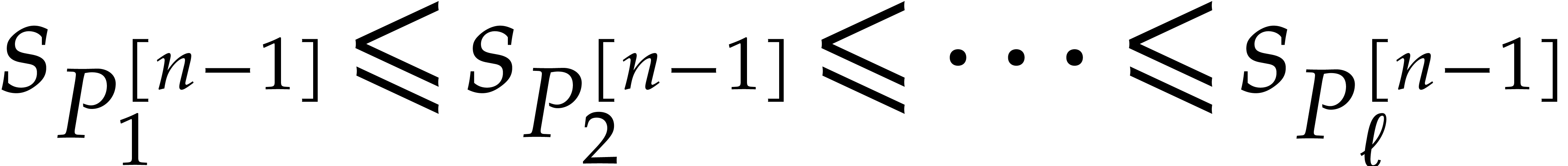 are pairwise coprime;
are pairwise coprime;
We have 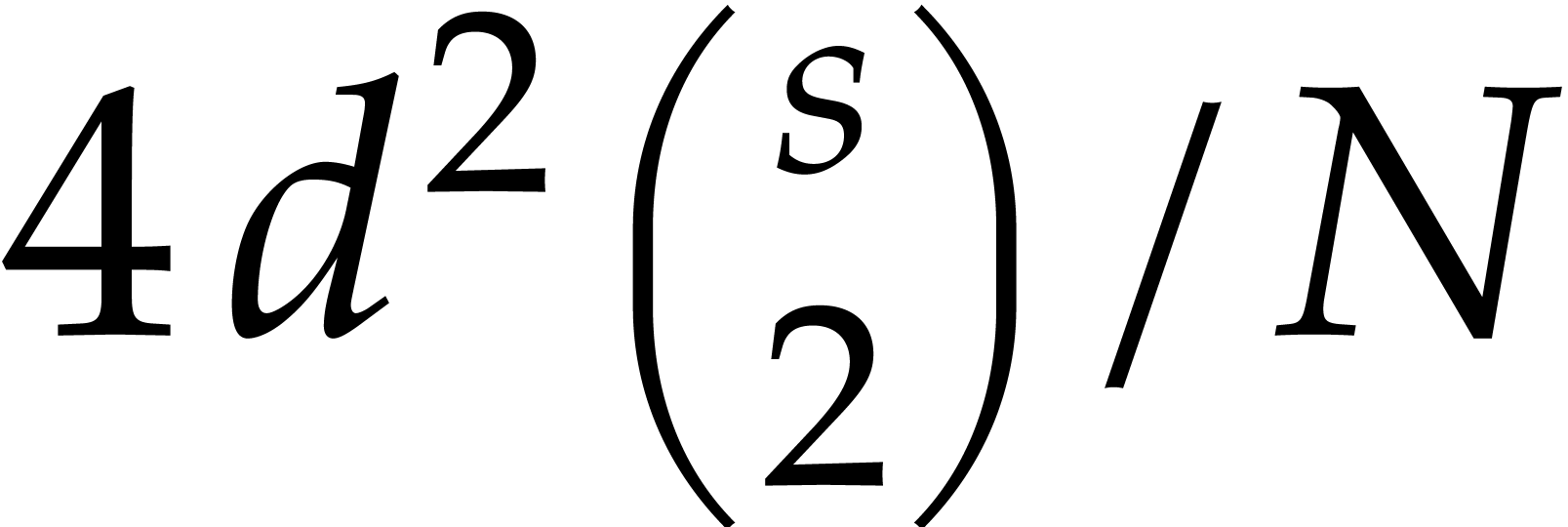 ;
;
We have 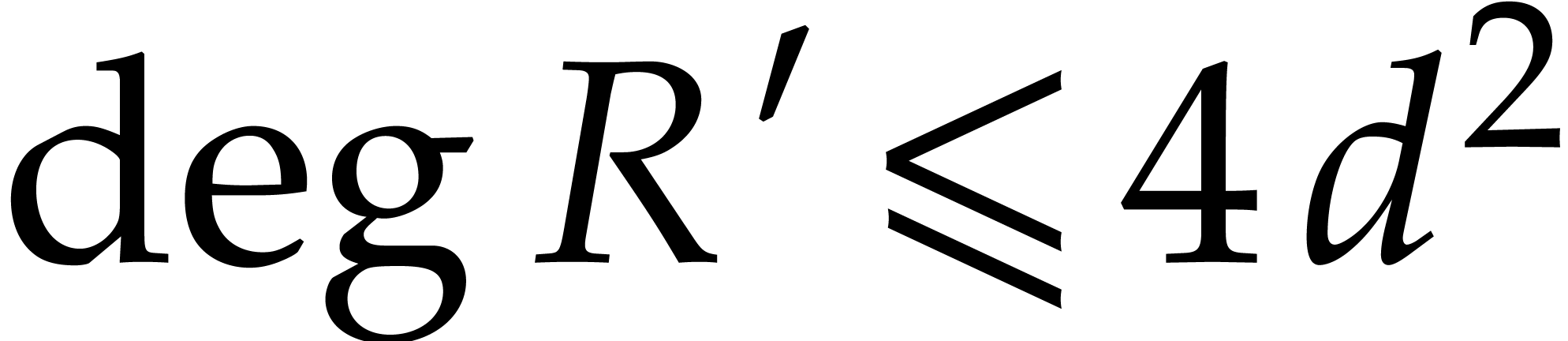 .
.
The analysis is similar as in the proof of Theorem 6.5, except that (6.1) now becomes
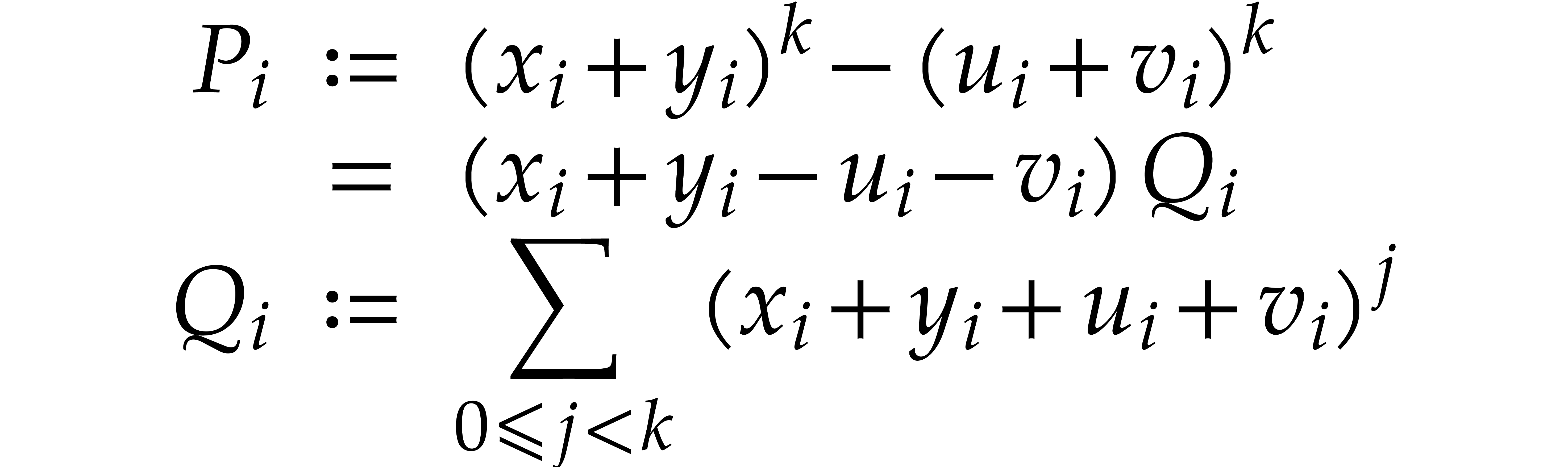
and the probability that 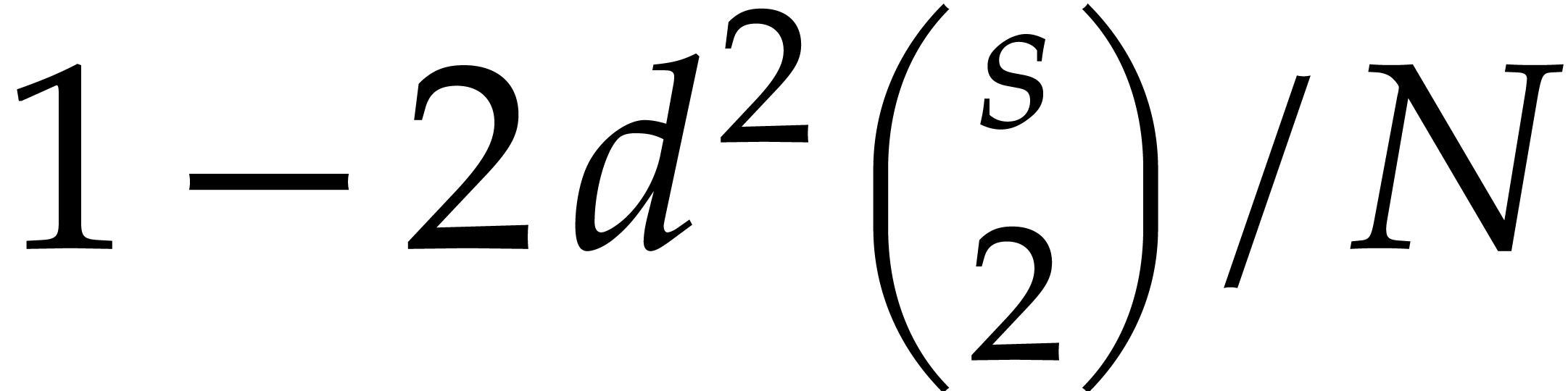 vanishes for one of the
vanishes for one of the
 substitutions is now bounded by
substitutions is now bounded by 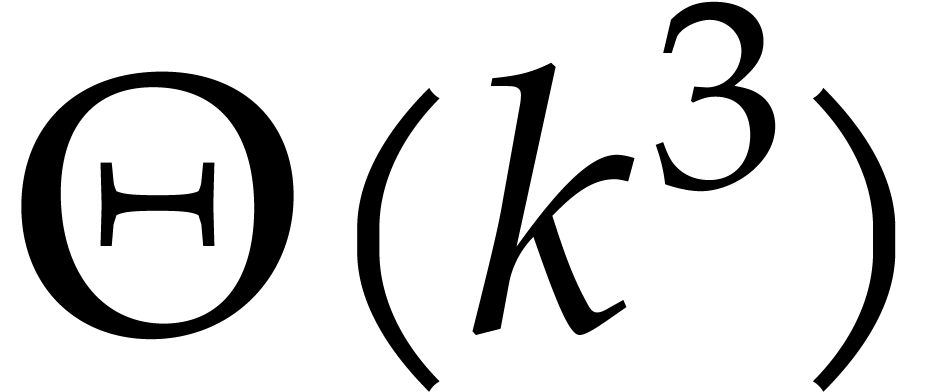 , since
, since 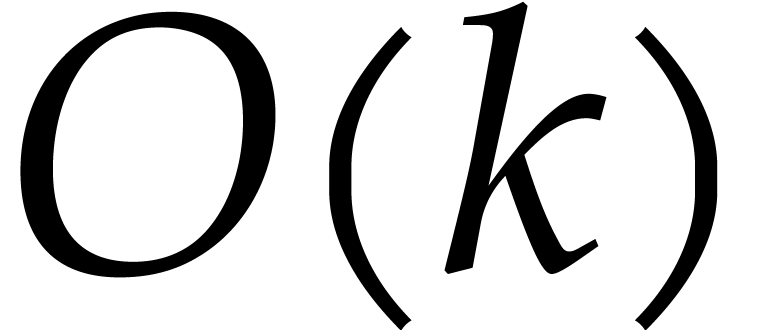 .
Using the fact there are
.
Using the fact there are  recursive levels, this
completes the probabilistic correctness proof.
recursive levels, this
completes the probabilistic correctness proof.
For the cost analysis, we again start by analyzing the cost of the algorithm without the recursive calls:
The evaluation of the factors 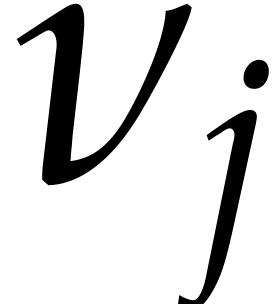 on the
geometric sequence can be done in time
on the
geometric sequence can be done in time 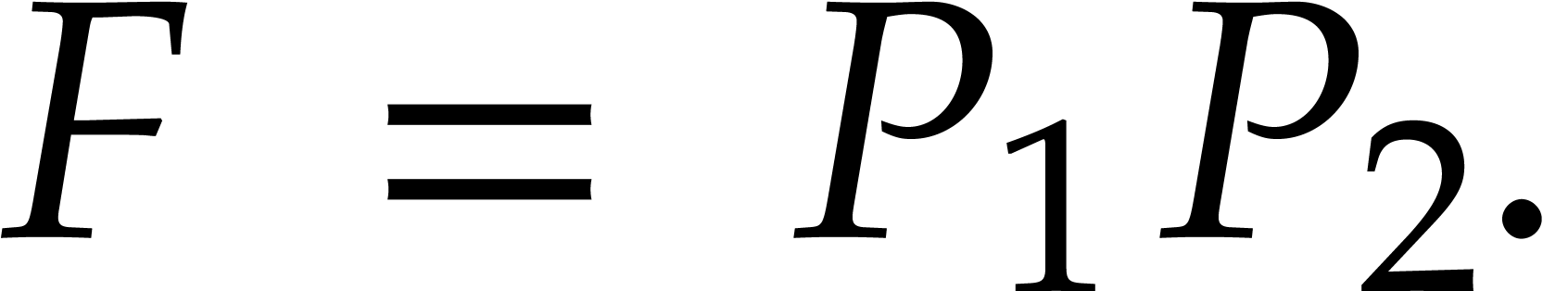 .
.
The computation of the 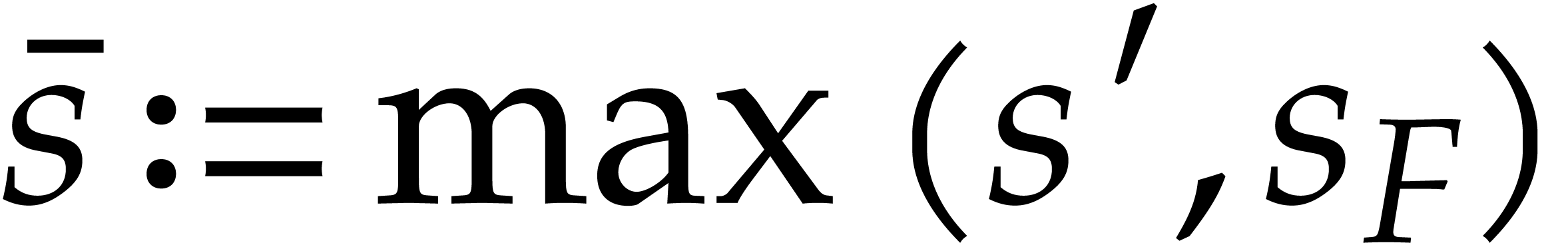 and
and 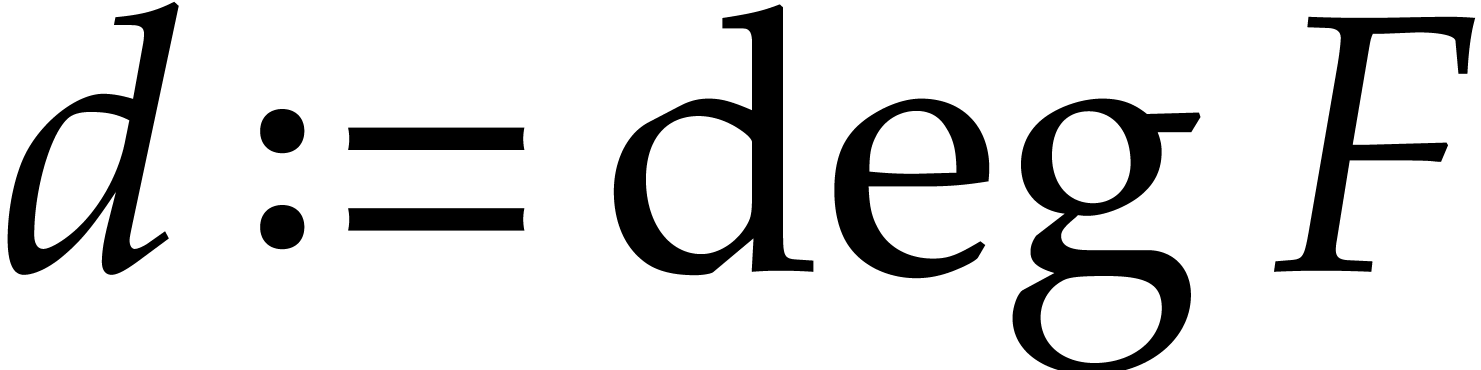 takes
takes 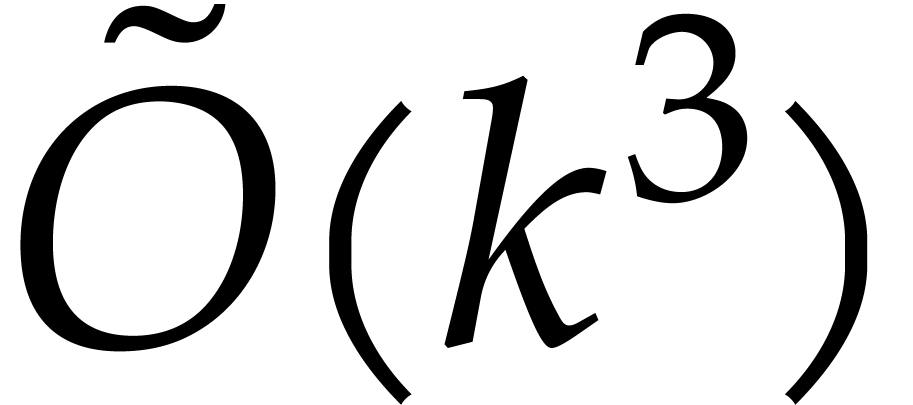 operations.
operations.
The powers 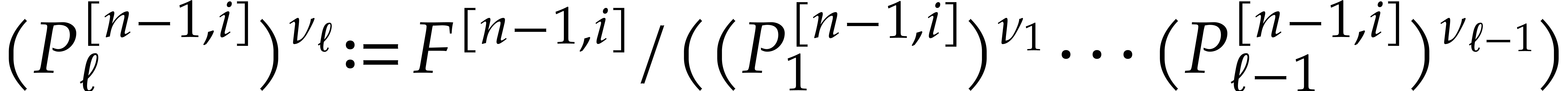 can be obtained in time
can be obtained in time  , using binary powering.
, using binary powering.
The Hensel lifting is done using Proposition 4.4
instead of Proposition 4.3, which contributes  to the cost.
to the cost.
The bivariate root extractions take  operations, by Proposition 4.2.
operations, by Proposition 4.2.
The recovery of the  from the
from the 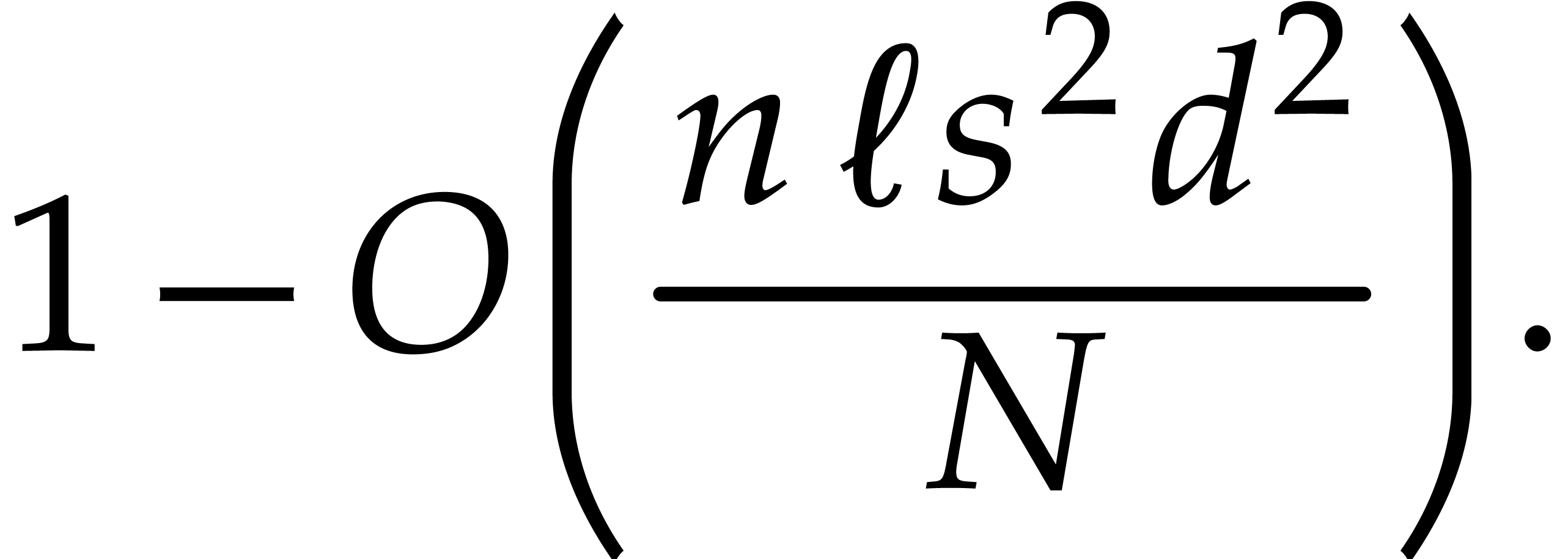 using sparse interpolation requires
using sparse interpolation requires 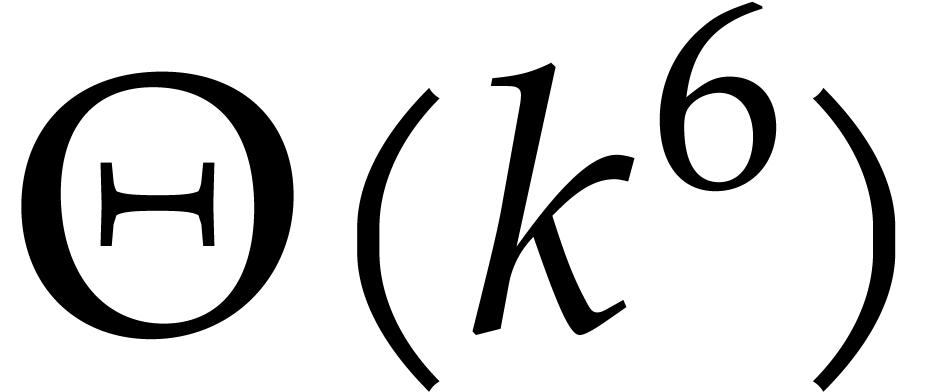 operations.
operations.
Summing these costs and multiplying with the recursive depths  yields the desired complexity bound.
yields the desired complexity bound.
Example 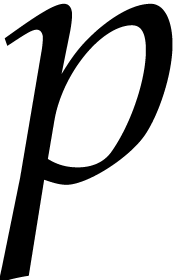 and
and  , consider
the polynomials
, consider
the polynomials
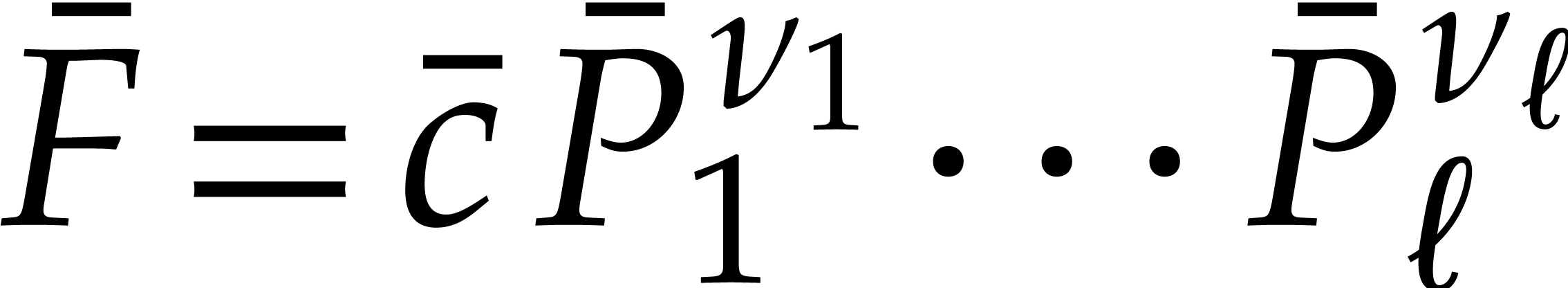
and note that  has
has  terms,
whereas
terms,
whereas  has only
has only  terms.
Now consider
terms.
Now consider

Then a direct factorization of  into irreducibles
can be done in time
into irreducibles
can be done in time 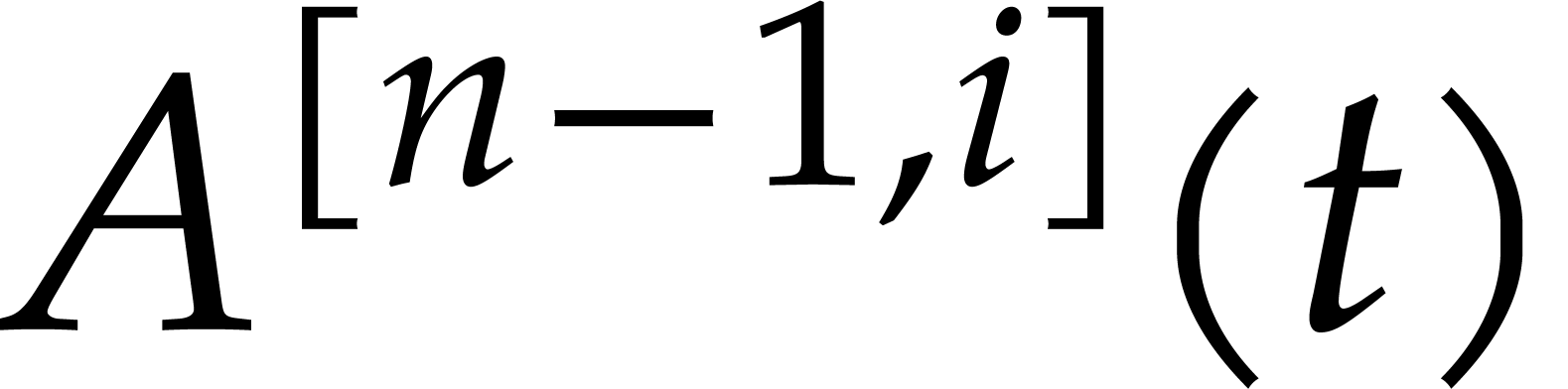 , whereas
recursively factoring out
, whereas
recursively factoring out 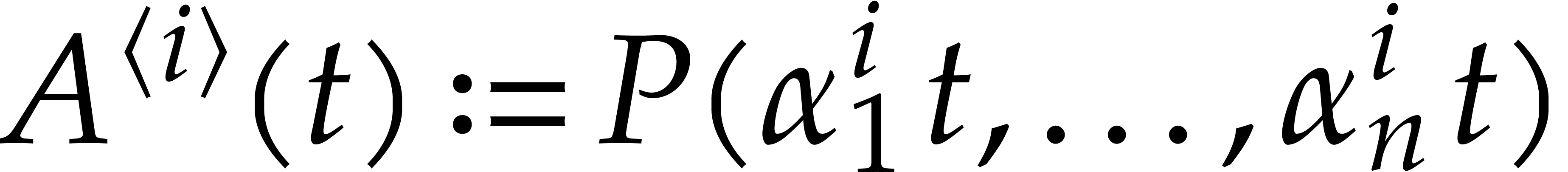 and then
and then 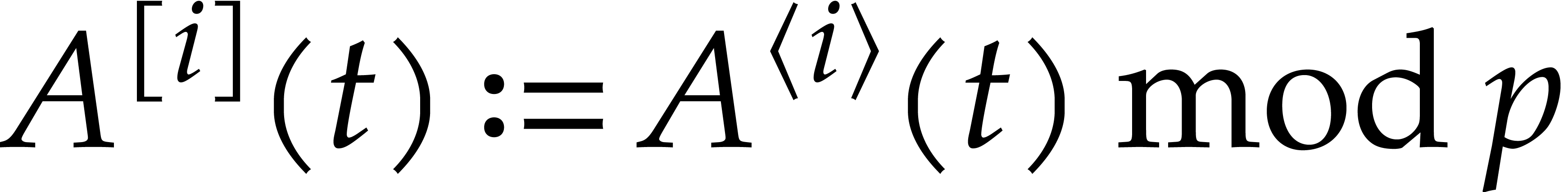 may lead us to consider intermediate expressions like
may lead us to consider intermediate expressions like  of size
of size  .
.
Remark 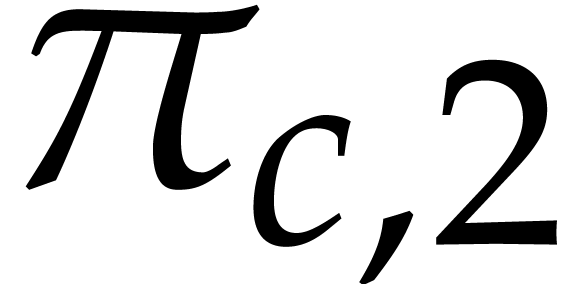 -adic lifting, in order to factor a polynomial
-adic lifting, in order to factor a polynomial
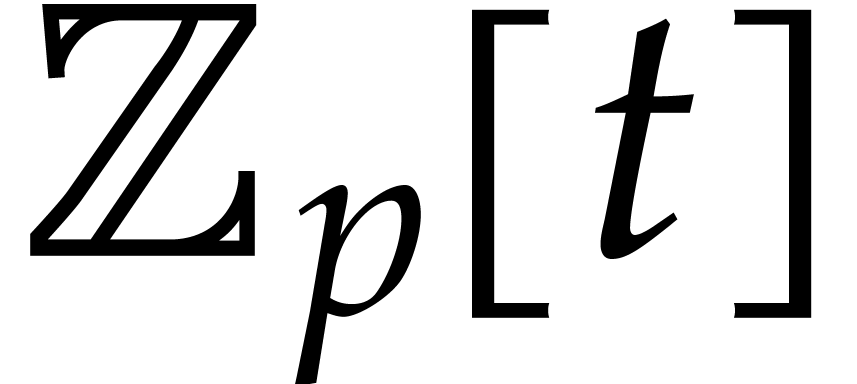 with rational coefficients. In that case, we
start with a factorization
with rational coefficients. In that case, we
start with a factorization  of
of 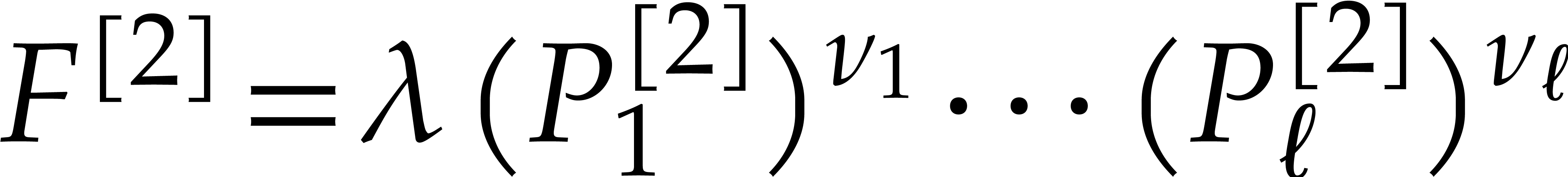 for some sufficiently large prime
for some sufficiently large prime 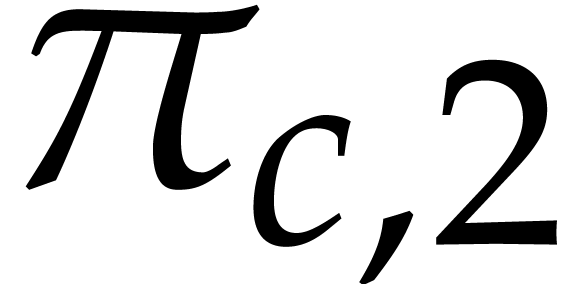 .
The goal is to lift this into a factorization of
.
The goal is to lift this into a factorization of  for some sufficiently large
for some sufficiently large  and then to recover
a factorization of
and then to recover
a factorization of  using rational number
reconstruction [31, Section 5.10]. The relevant analogues
of
using rational number
reconstruction [31, Section 5.10]. The relevant analogues
of  and
and 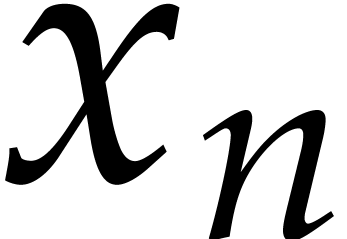 are
are  and
and  , where the
prime number
, where the
prime number 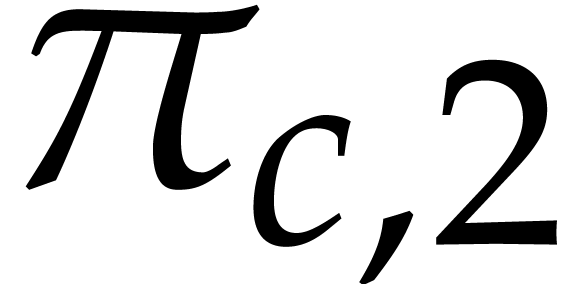 plays a similar role as the formal
indeterminate
plays a similar role as the formal
indeterminate  . The bivariate
Hensel lifting in
. The bivariate
Hensel lifting in  is replaced by traditional
univariate Hensel lifting in
is replaced by traditional
univariate Hensel lifting in 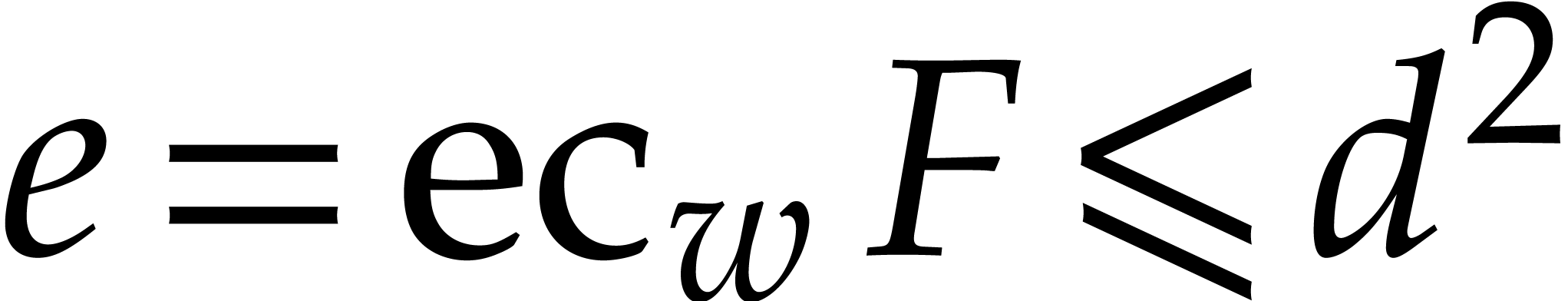 .
.
In lucky cases, given an irreducible factorization 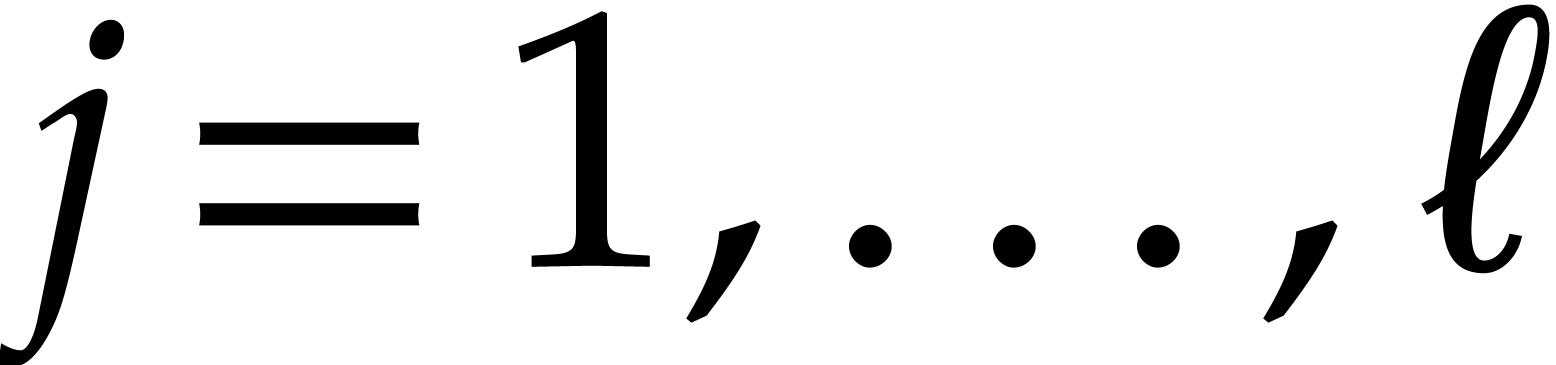 , random choices of
, random choices of 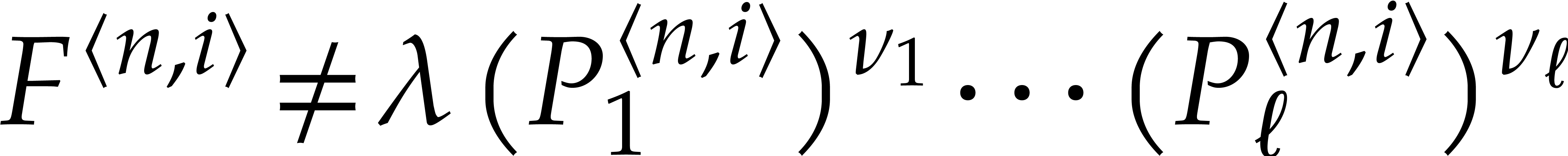 give rise with high probability to an irreducible factorization
give rise with high probability to an irreducible factorization 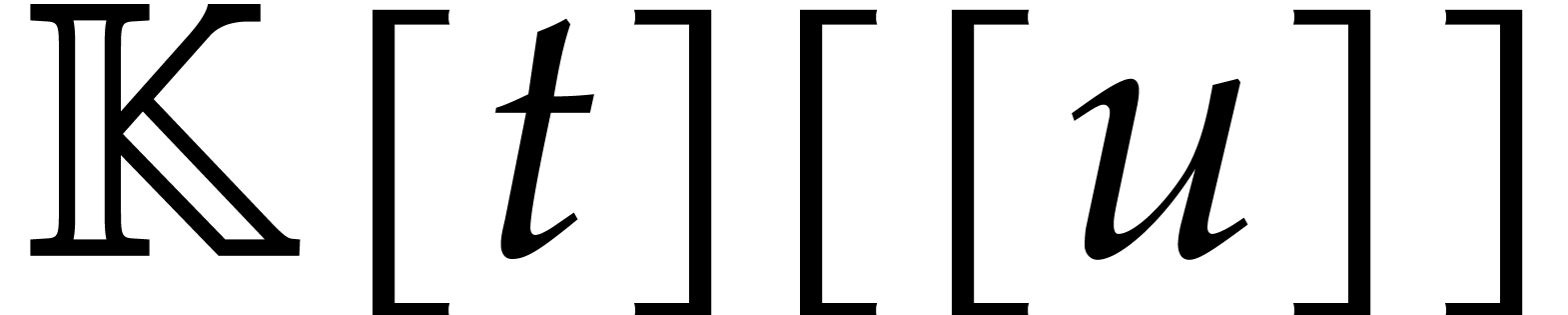 . For such
. For such  , we may use the following algorithm to compute its
irreducible factorization:
, we may use the following algorithm to compute its
irreducible factorization:
Algorithm
Output: an irreducible factorization  or an error
or an error
If  , then return the result
of a univariate irreducible factorization
, then return the result
of a univariate irreducible factorization
Let 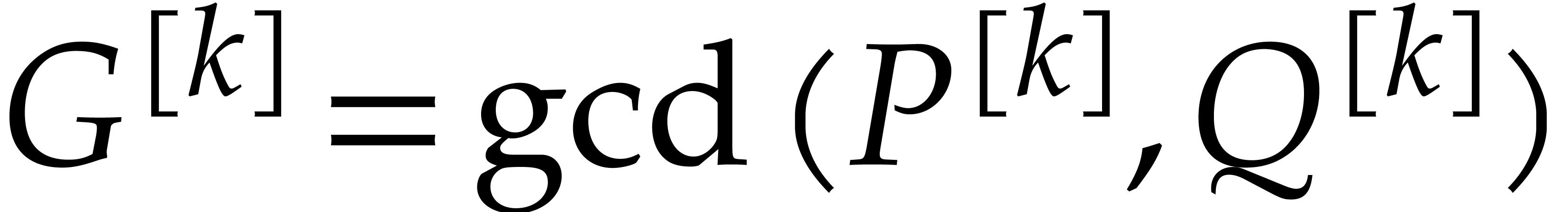 be random elements of
be random elements of 
Compute an irreducible factorization 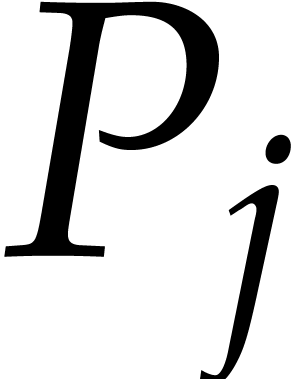 of
of 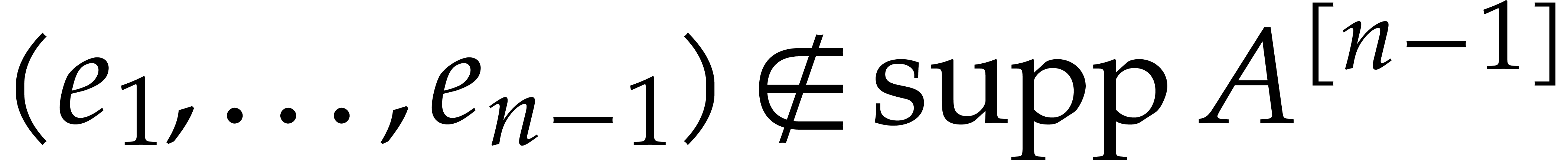
Apply Algorithm 6.2 to  and this
factorization
and this
factorization
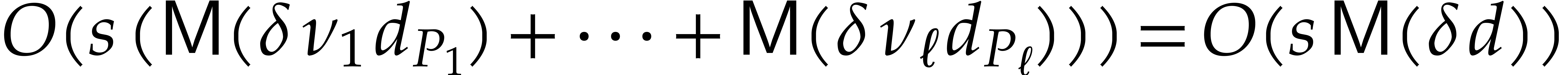 ,
, 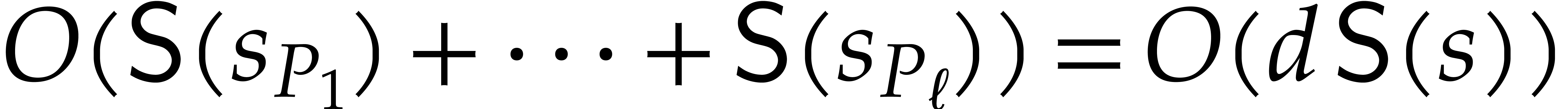 ,
, 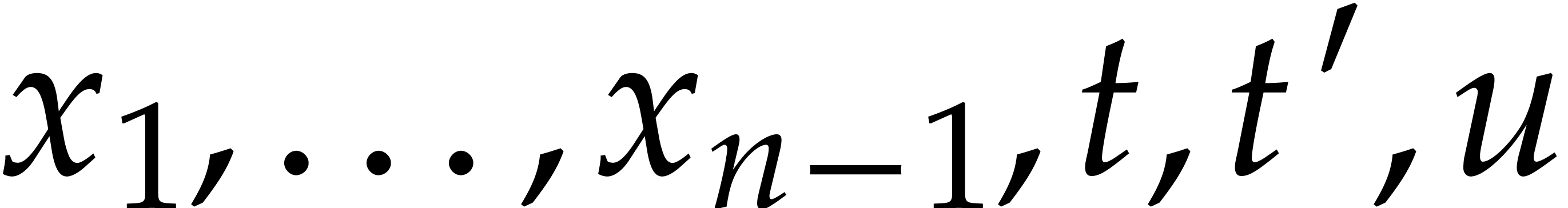 ,
and
,
and  . Then Algorithm 6.3 runs in time
. Then Algorithm 6.3 runs in time

and returns the correct result (when no error is raised) with probability at least

Proof. This follows from Theorems 6.8,
4.7, and Lemma 6.2.
Remark  in
in 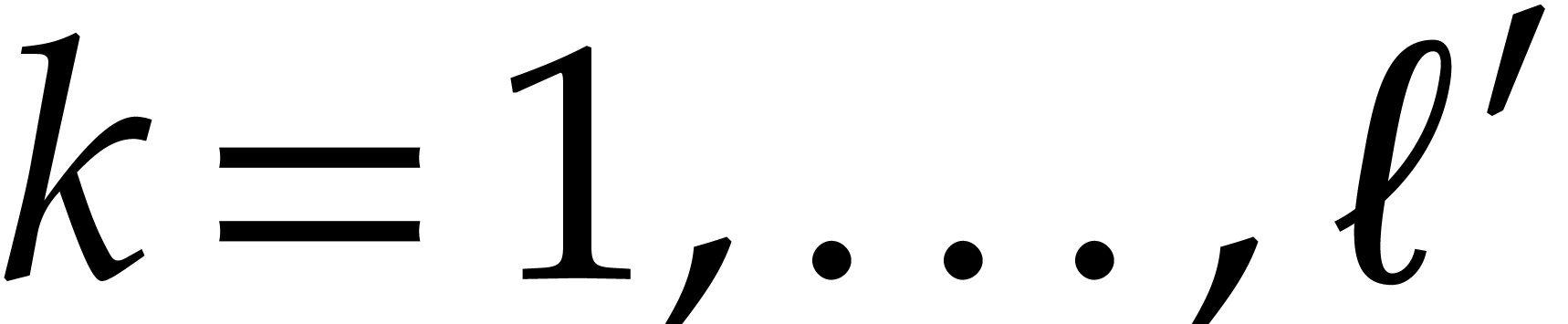 at the top-level and performing
the recursive call and bivariate lifting to
at the top-level and performing
the recursive call and bivariate lifting to  instead of
instead of  . Incorporating
the content-free factorization directly into the main algorithm in this
way yields a similar complexity bound as in Theorem 6.11,
but with
. Incorporating
the content-free factorization directly into the main algorithm in this
way yields a similar complexity bound as in Theorem 6.11,
but with 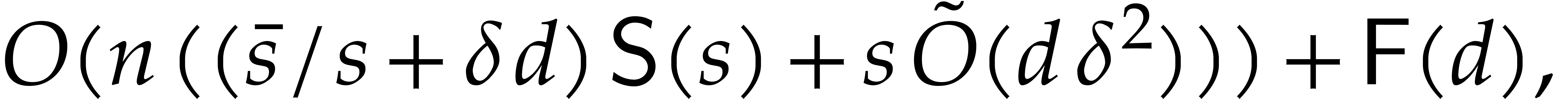 instead of
instead of  .
.
Remark  according to a regularizing weight
according to a regularizing weight  . This has the advantage of
“exposing” the entire factorization of
. This has the advantage of
“exposing” the entire factorization of  with respect to the tagging variable
with respect to the tagging variable 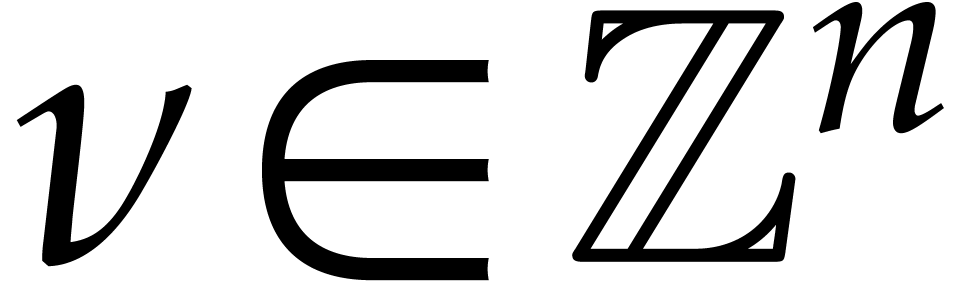 .
Of course, this requires to replace the degree
.
Of course, this requires to replace the degree 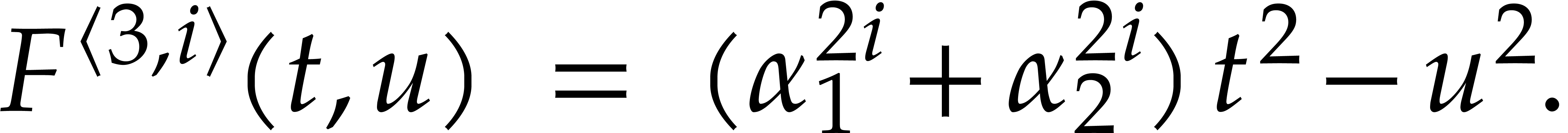 in the complexity bound by
in the complexity bound by  .
.
Remark 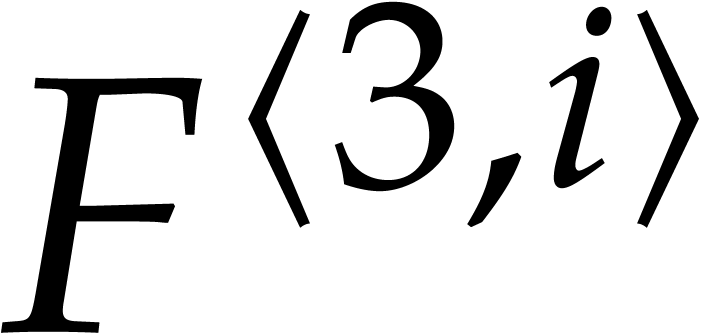 , we may continue the Hensel
lifting to a higher precision (the
, we may continue the Hensel
lifting to a higher precision (the 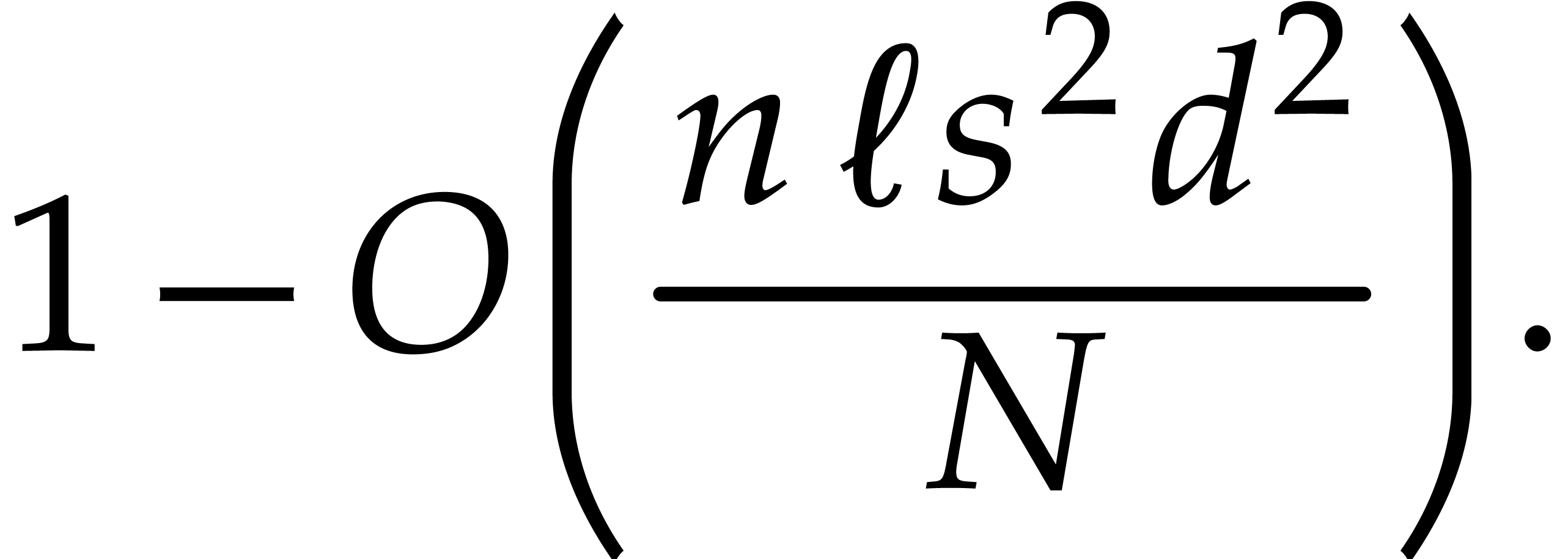 are now power
series in
are now power
series in  ) and determine
which factors need to be combined in order to obtain a factorization of
) and determine
which factors need to be combined in order to obtain a factorization of
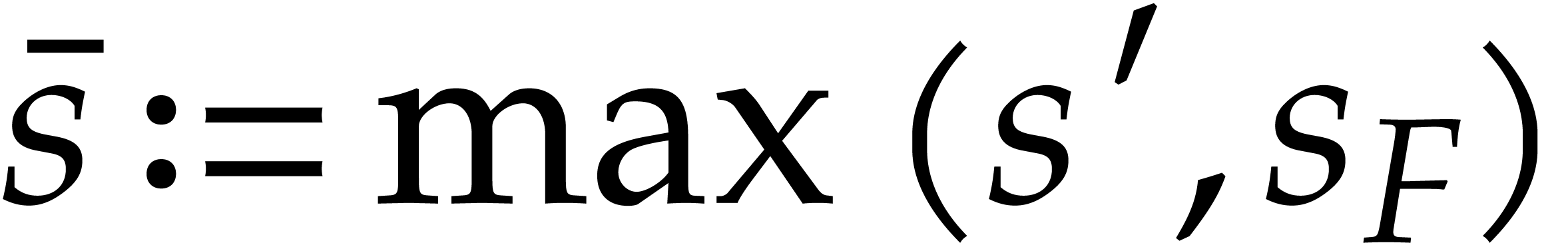 (using the techniques from [74]).
Doing this for all
(using the techniques from [74]).
Doing this for all  leads to a finest partition
leads to a finest partition
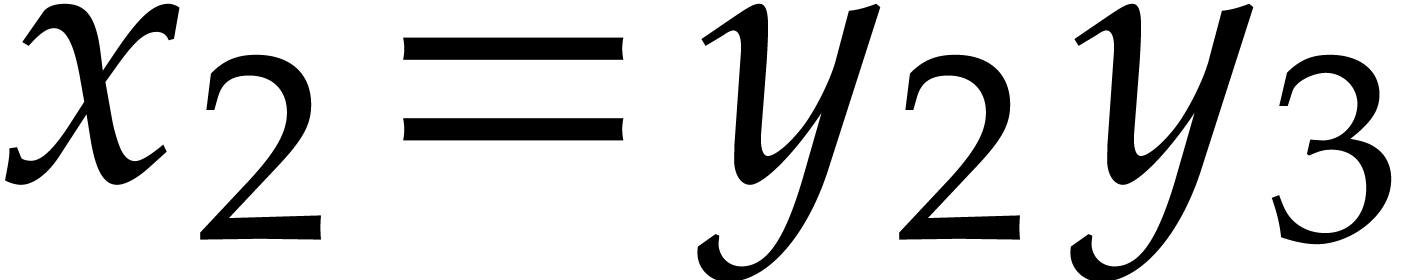 of
of  such that
such that 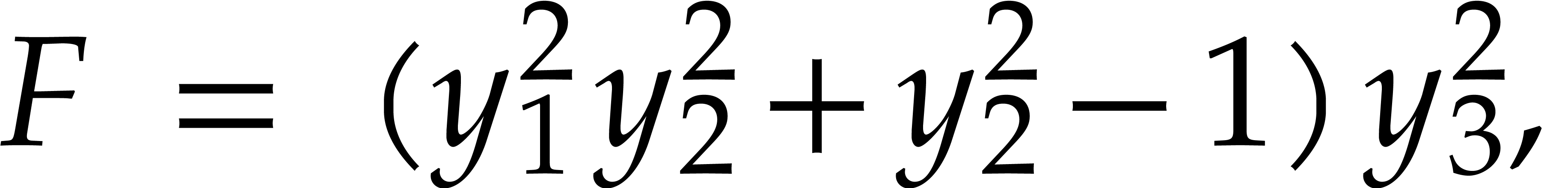 is a polynomial factor of
is a polynomial factor of 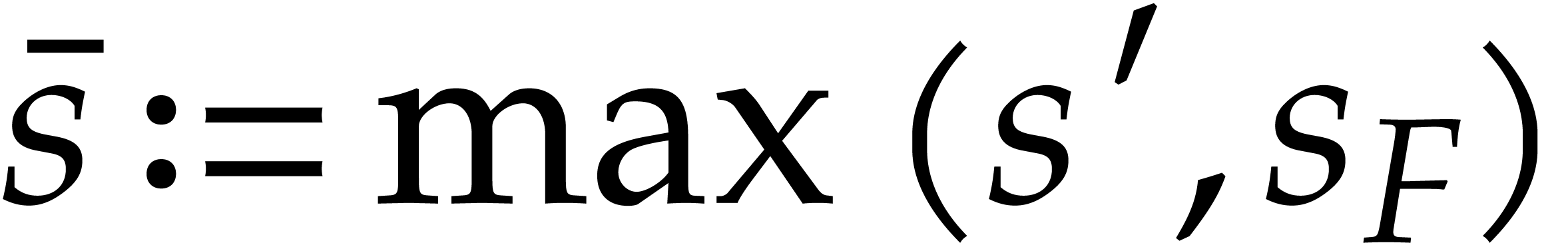 for
for 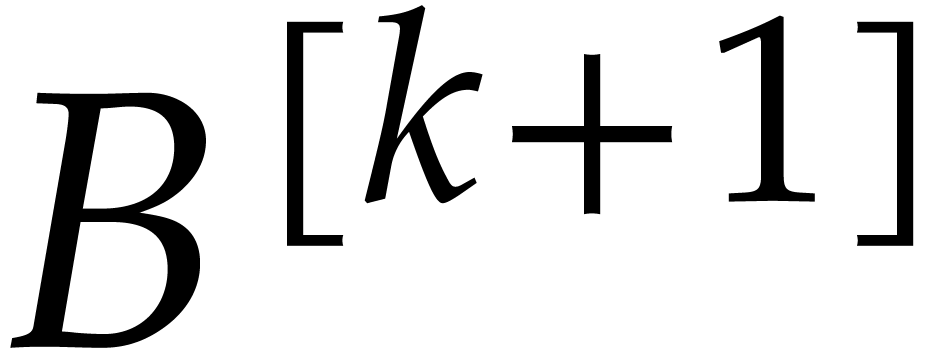 and
and 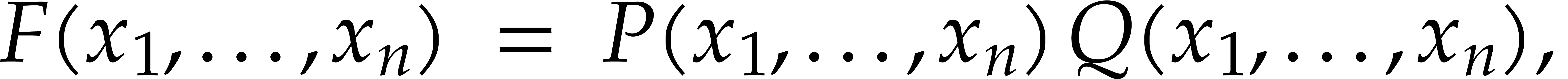 . We
next apply the sparse interpolation to the polynomials
. We
next apply the sparse interpolation to the polynomials  instead of the series
instead of the series  . This
may require more than
. This
may require more than  interpolation points, so
we also double
interpolation points, so
we also double  until the interpolation step
succeeds. Combined with Remark 6.12, this yields to an
algorithm of complexity
until the interpolation step
succeeds. Combined with Remark 6.12, this yields to an
algorithm of complexity

where  is the maximal size of an irreducible
factor of
is the maximal size of an irreducible
factor of  for
for 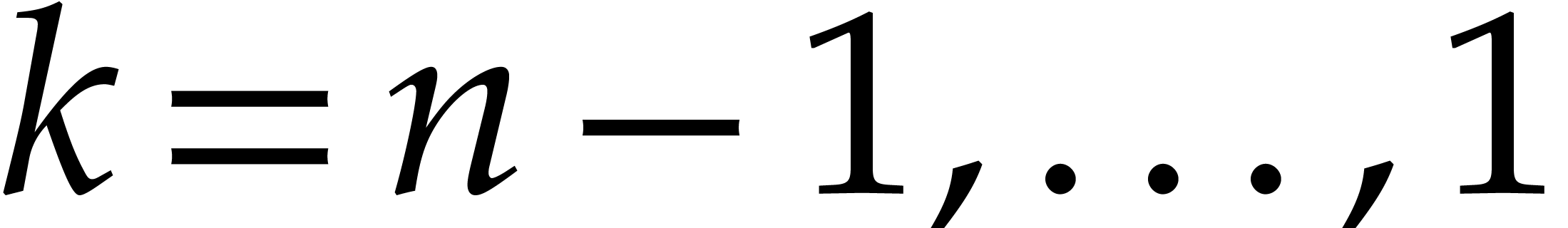 .
.
Unfortunately, we have not yet been able to perform a clean probabilistic analysis for this method. Indeed, we still need to prove that the algorithm terminates in reasonable expected time for irreducible polynomials. Now consider the example
 |
(6.2) |
for which we obtain
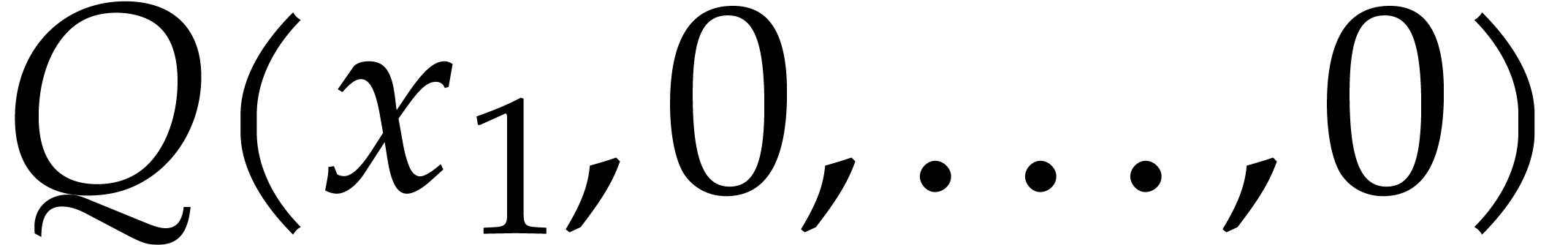
Whenever  with
with 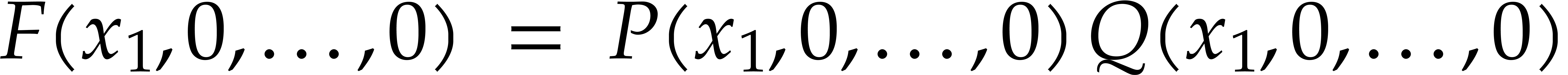 and
and  is a square in
is a square in  ,
the projected polynomial
,
the projected polynomial 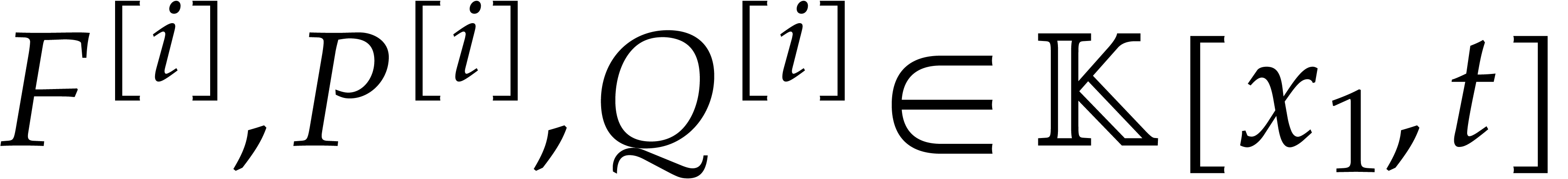 is not irreducible. In
principle, this only happens with probability
is not irreducible. In
principle, this only happens with probability 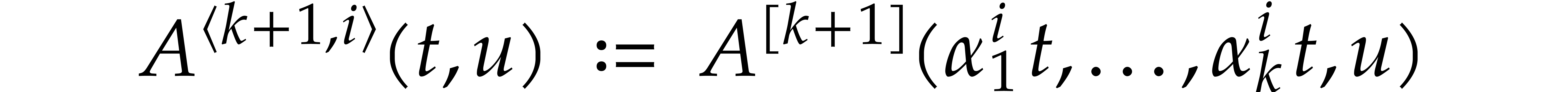 , so this is unlikely to happen for all
, so this is unlikely to happen for all  values of
values of 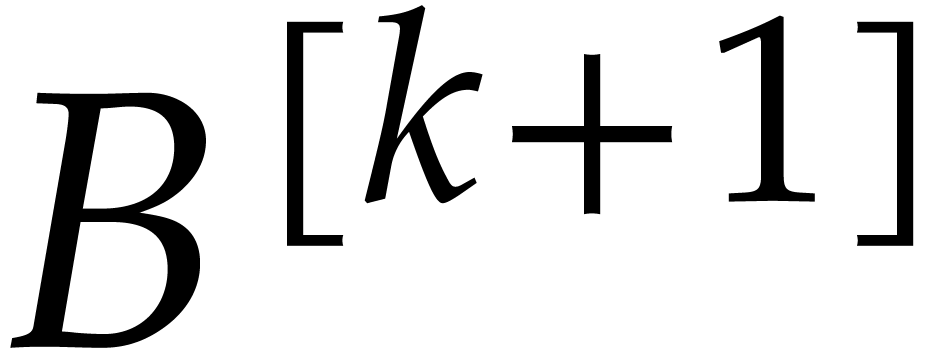 .
However, we were unable so far to prove a general bound. We also note
that this probabilistic argument is different from traditional
Hilbert–Bertini style arguments [100, Section 6.1];
see also [74] and [75, Chapître 6].
.
However, we were unable so far to prove a general bound. We also note
that this probabilistic argument is different from traditional
Hilbert–Bertini style arguments [100, Section 6.1];
see also [74] and [75, Chapître 6].
Remark  . For
instance, after the change of variables
. For
instance, after the change of variables  ,
,
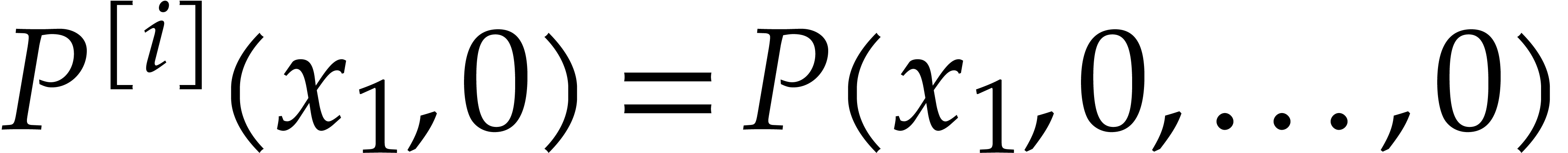 ,
, 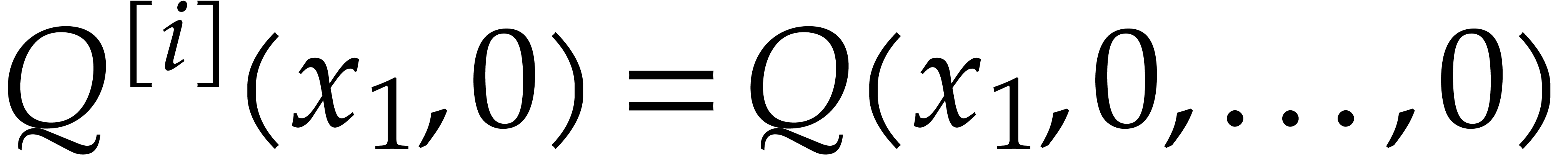 , we have
, we have
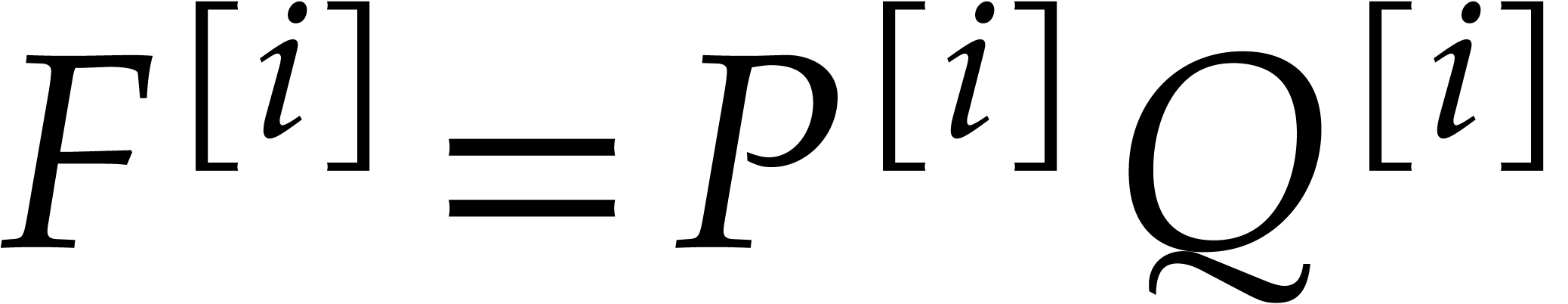
for the polynomial  from example (6.2).
With high probability, Algorithm 6.3 returns the correct
irreducible factorization of
from example (6.2).
With high probability, Algorithm 6.3 returns the correct
irreducible factorization of  after this
rewriting.
after this
rewriting.
The iterative approach from Sections 3.1 and 6
has the disadvantage of introducing a dependence on the dimension  in the complexity bounds. In the case of gcd
computations, the idea of regularizing weights allowed for the more
direct approach in Section 3.2.
in the complexity bounds. In the case of gcd
computations, the idea of regularizing weights allowed for the more
direct approach in Section 3.2.
Unfortunately, direct adaptations of this approach to factorization only
work in very special cases, because it is unclear how to recombine the
factors found at different evaluation points. One notable exception is
when  factors, say, into two irreducible factors
of degrees one and two in one of the variables; in that case, we can
recombine based on degree information.
factors, say, into two irreducible factors
of degrees one and two in one of the variables; in that case, we can
recombine based on degree information.
In this section, we will develop another “direct” approach
for the factorization of  that avoids iteration
on the dimension
that avoids iteration
on the dimension  . Except for
precomputations in the algorithm from Section 7.7, the
algorithms in this section do not rely on regularizing weights, but
exploits more subtle properties of the Newton polytope of
. Except for
precomputations in the algorithm from Section 7.7, the
algorithms in this section do not rely on regularizing weights, but
exploits more subtle properties of the Newton polytope of  . We will present three versions of our
approach in order to deal with Newton polytopes of increasing
complexity. For simplicity, we only present them in the case when
. We will present three versions of our
approach in order to deal with Newton polytopes of increasing
complexity. For simplicity, we only present them in the case when  is the product of two factors. As we shall see in
Section 7.6, even the last and most elaborate version of
our approach is not fully general. We will conclude with a theoretical
variant that is less efficient in practice, but which has the advantage
of providing a full algorithm for the computation of irreducible
factorizations.
is the product of two factors. As we shall see in
Section 7.6, even the last and most elaborate version of
our approach is not fully general. We will conclude with a theoretical
variant that is less efficient in practice, but which has the advantage
of providing a full algorithm for the computation of irreducible
factorizations.
Assume that the unique factorization of  contains
exactly two factors
contains
exactly two factors
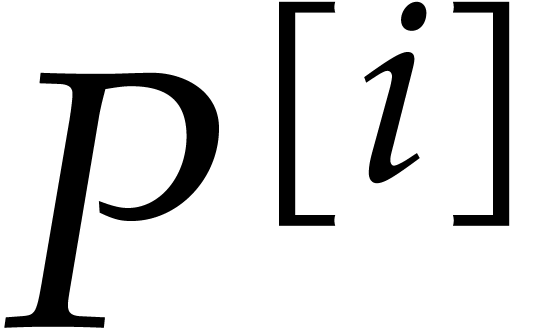 |
(7.1) |
where  are irreducible and distinct and both
depend on the “main” variable, say,
are irreducible and distinct and both
depend on the “main” variable, say,  . In particular, this implies that
. In particular, this implies that  is content-free and square-free. Assume also that the following
conditions hold:
is content-free and square-free. Assume also that the following
conditions hold:
 .
.
 and
and  are coprime.
are coprime.
Note that H1 allows us to normalize the factorization

by requiring that 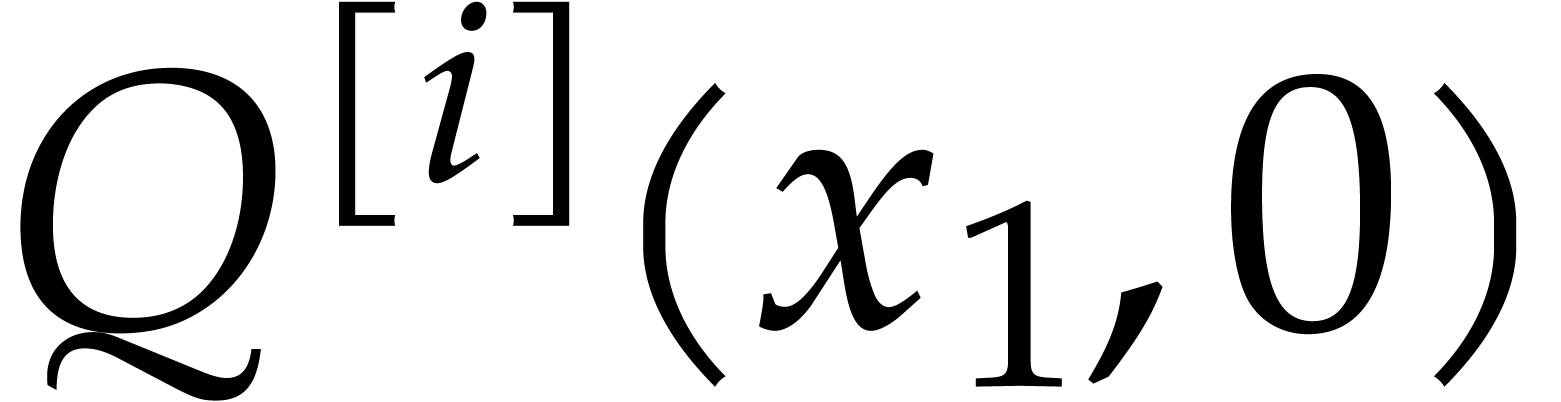 is monic. From now on we will
always assume that we have done this.
is monic. From now on we will
always assume that we have done this.
Under these assumptions, we claim that  and
and 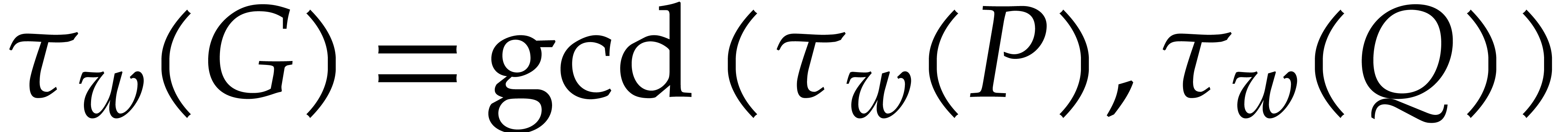 can be computed from
can be computed from 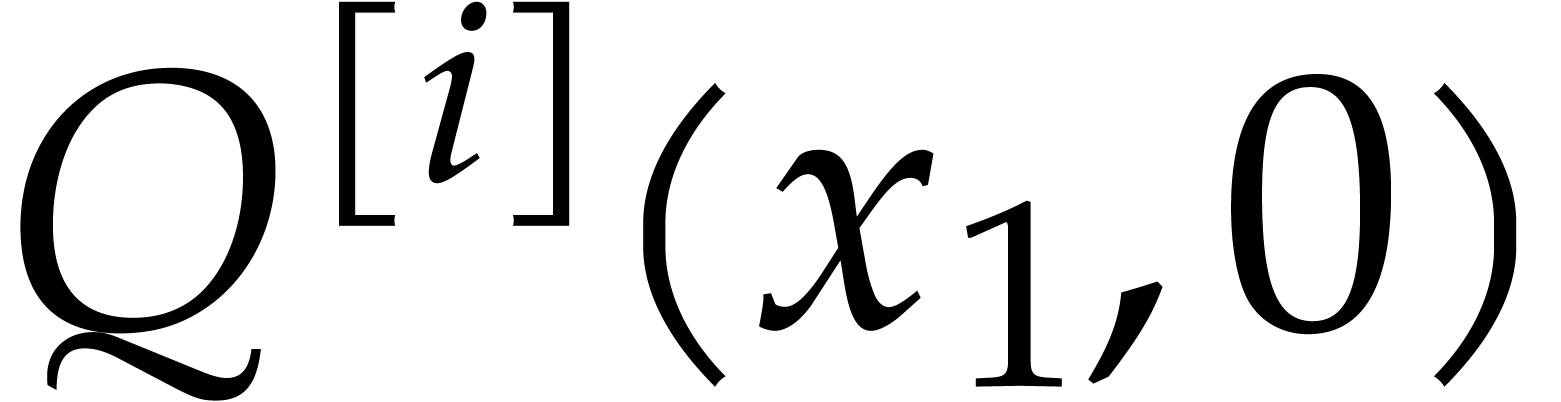 and
and  using Hensel lifting and sparse interpolation. In
order to see this, let
using Hensel lifting and sparse interpolation. In
order to see this, let  be an admissible ratio or
an FFT ratio. For each
be an admissible ratio or
an FFT ratio. For each  , we
define bivariate polynomials
, we
define bivariate polynomials  by
by
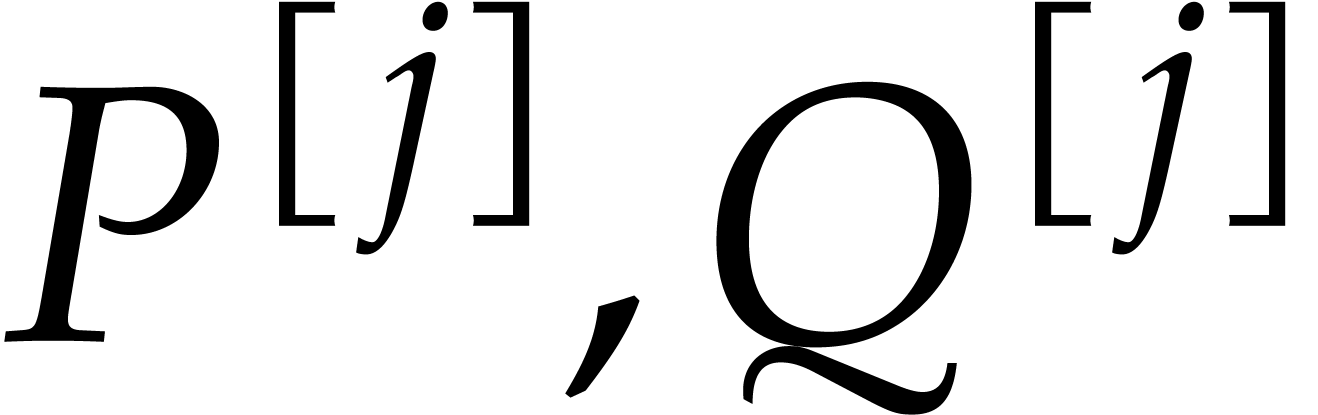
Then 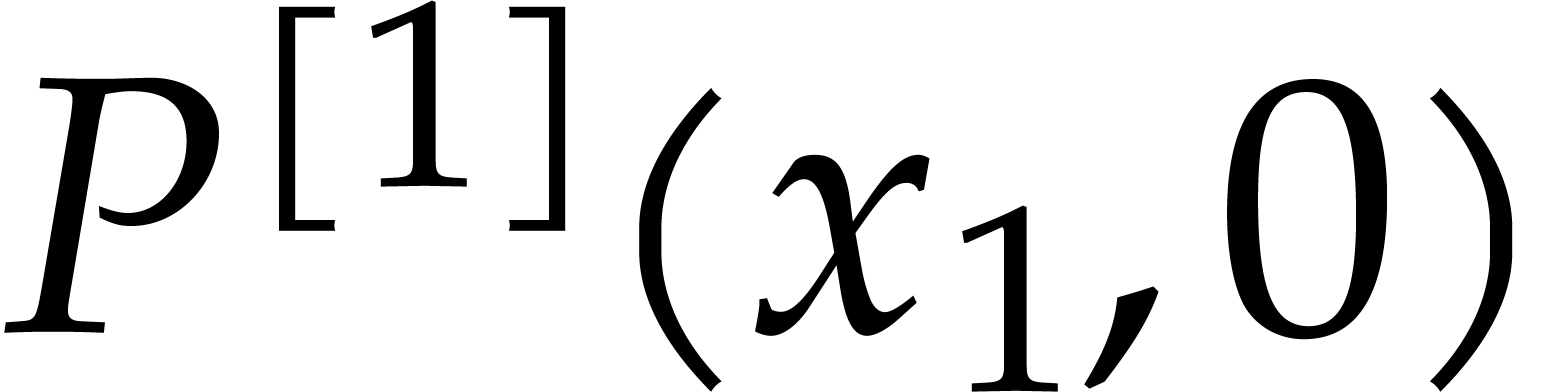 and
and 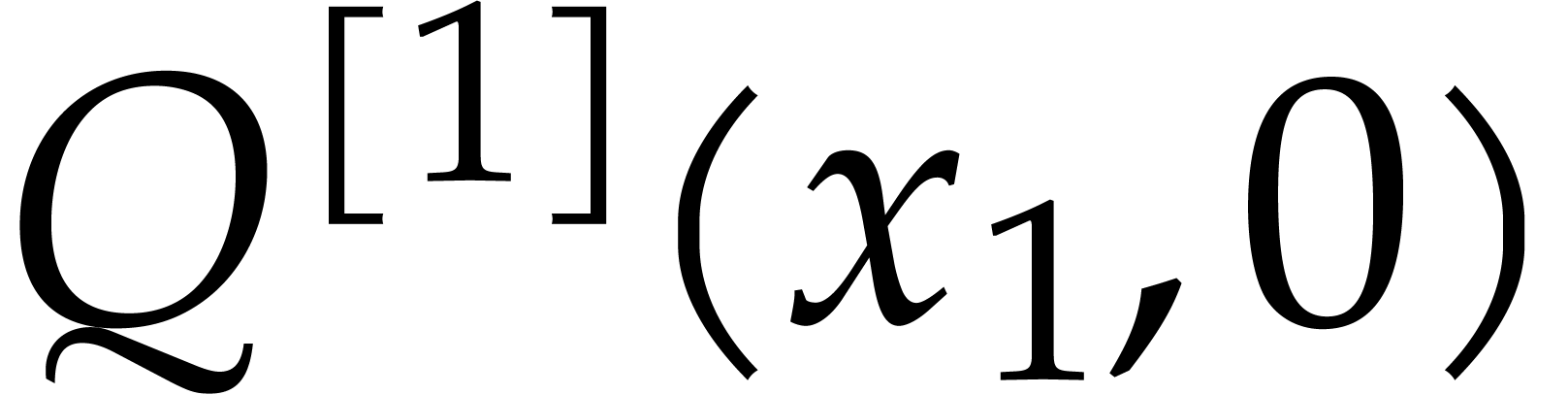 are coprime and
we have
are coprime and
we have  . This allows us to
compute
. This allows us to
compute  and
and  from
from 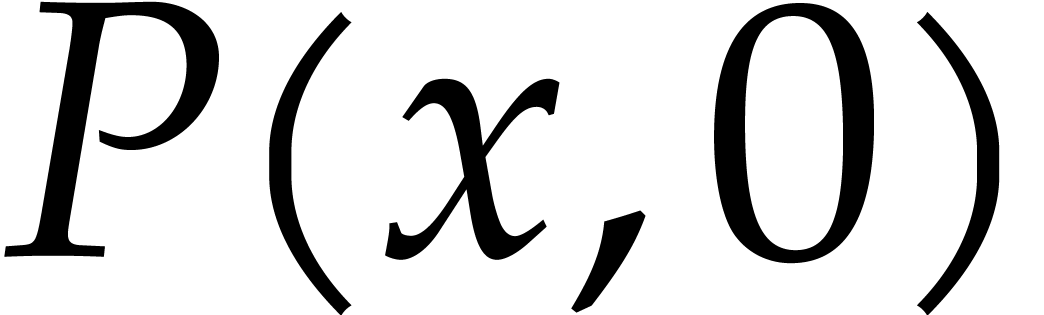 ,
,  ,
and
,
and 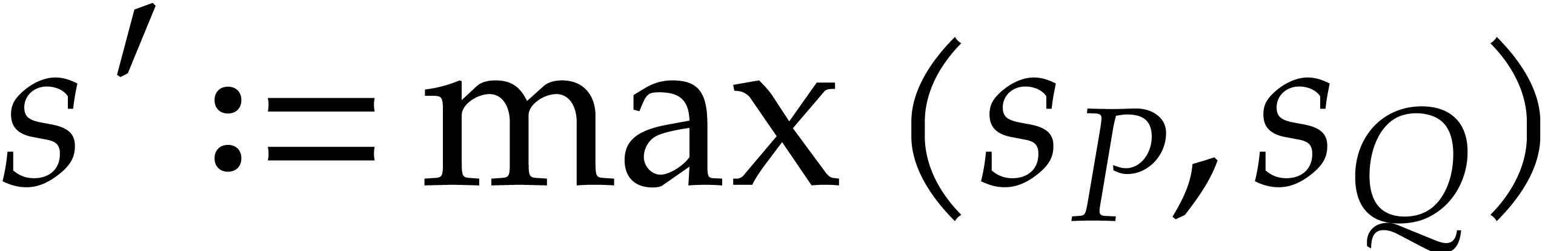 using Hensel lifting. For sufficiently large
using Hensel lifting. For sufficiently large
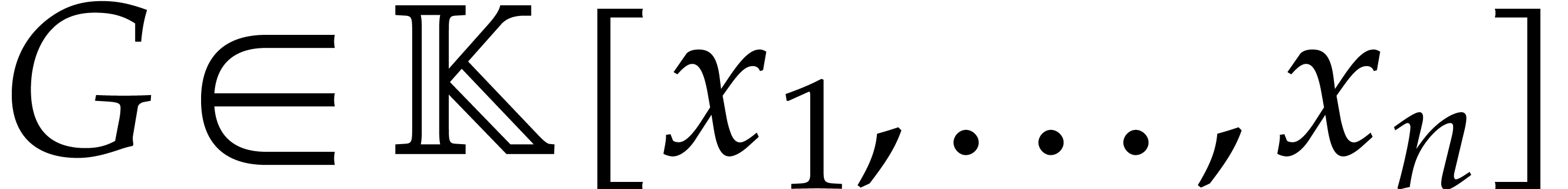 , with
, with 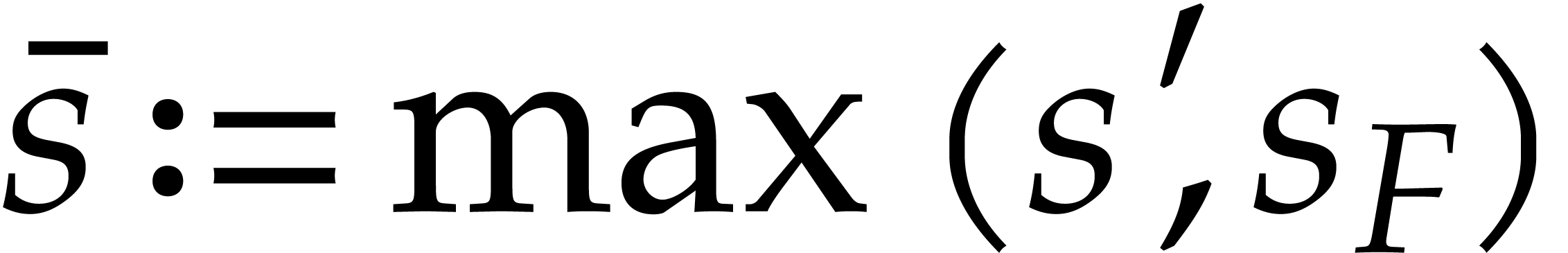 , we may then use sparse interpolation to recover
, we may then use sparse interpolation to recover
 from
from  or
or 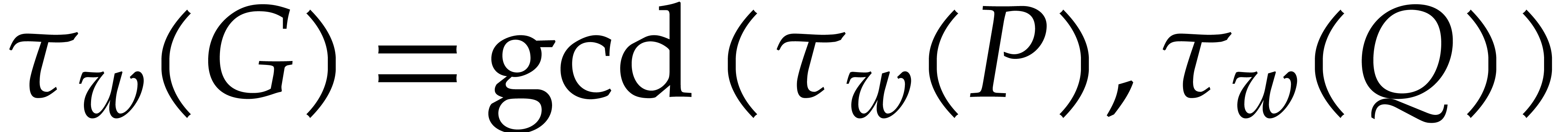 from
from  . This leads to the
following algorithm:
. This leads to the
following algorithm:
Algorithm
|
|
Output: |
|
For 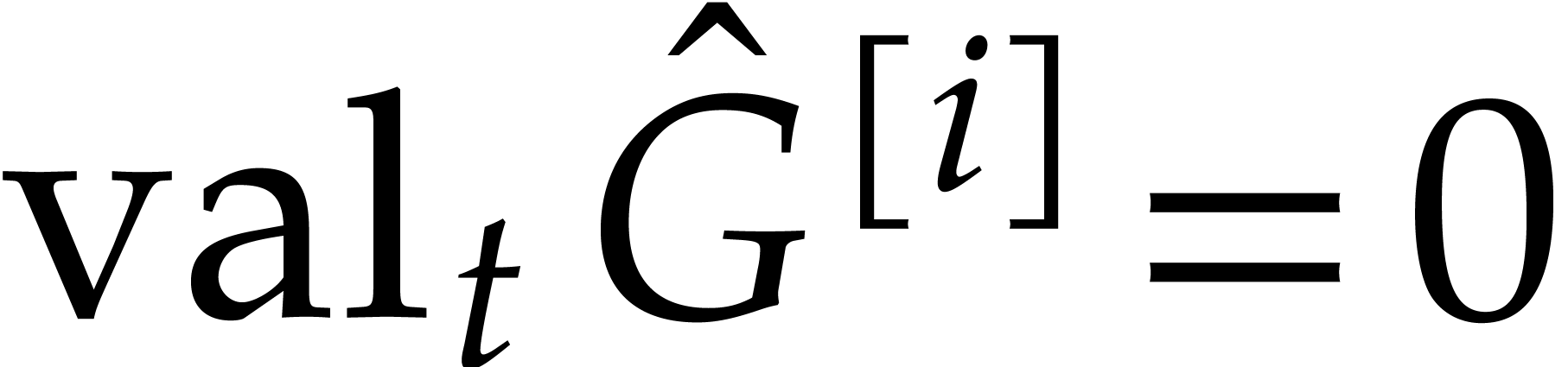 do
do
Compute 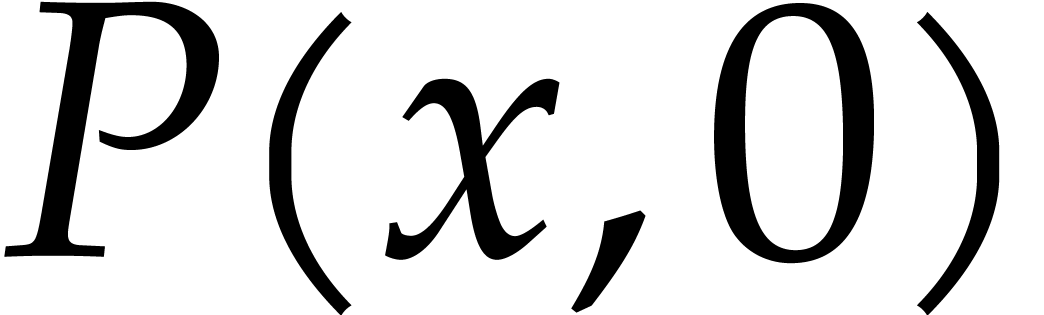 for
for 
Compute  for
for  ,
,
using bivariate Hensel lifting for 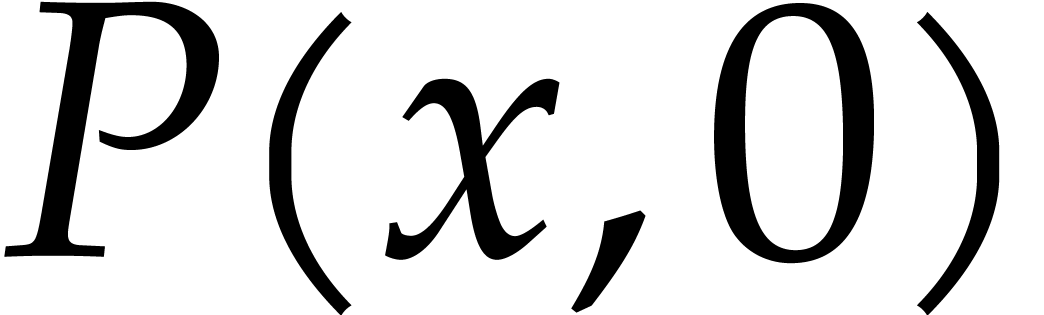 ,
,
 ,
, 
If  yield
yield  through
sparse interpolation, then return
through
sparse interpolation, then return 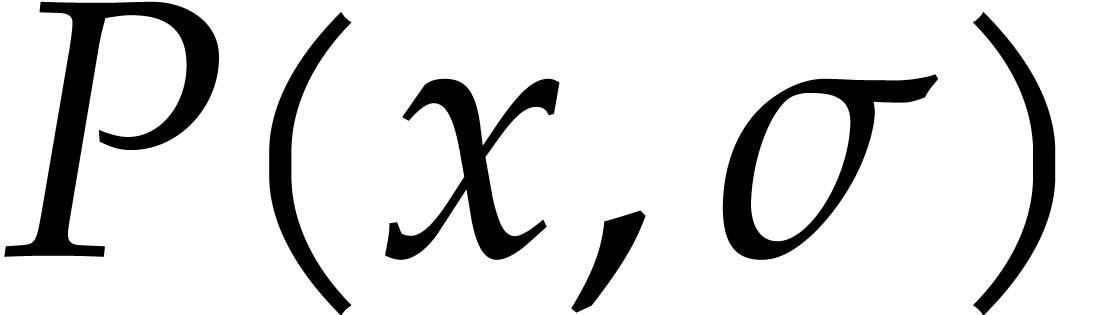
If  yield
yield 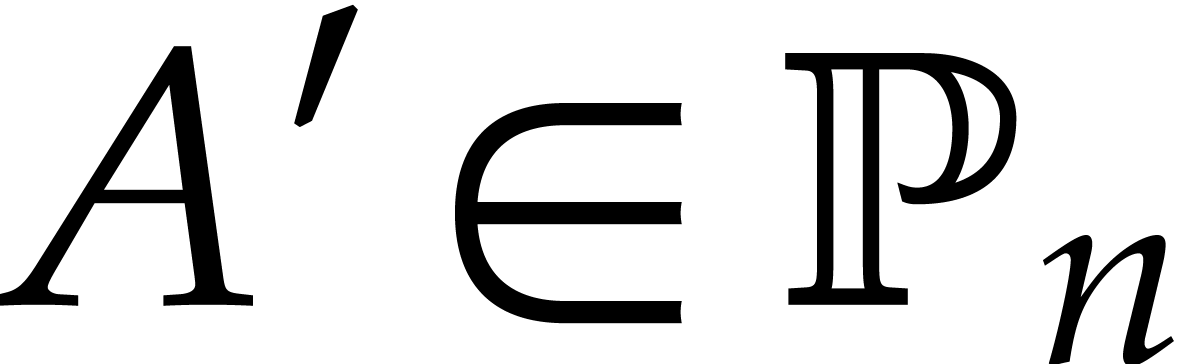 through
sparse interpolation, then return
through
sparse interpolation, then return 
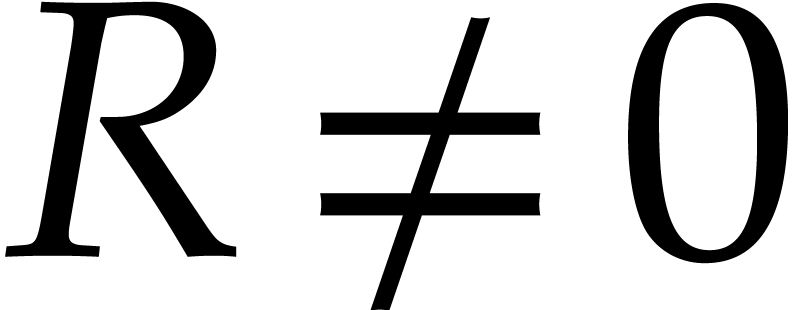 ,
, 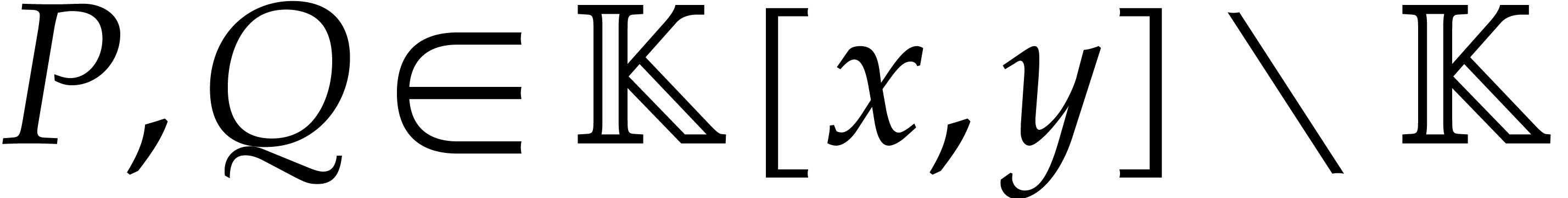 ,
,  ,
,
 , and
, and  . Then Algorithm 7.1 is correct
with probability at least
. Then Algorithm 7.1 is correct
with probability at least 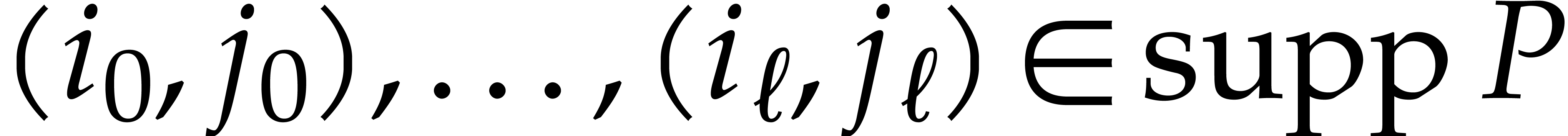 and runs in time
and runs in time
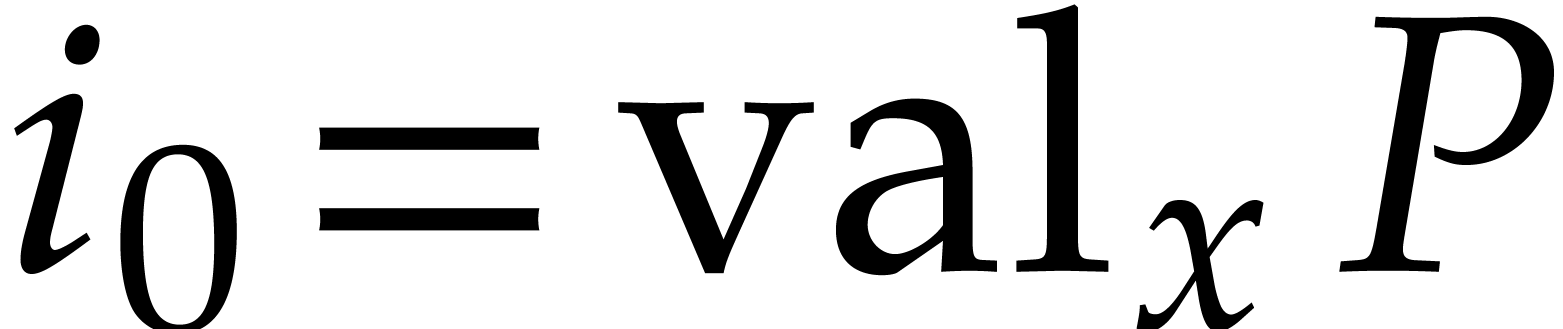
Proof. The correctness is clear. Let us analyze the cost of the main steps of the algorithm:
The computation of the 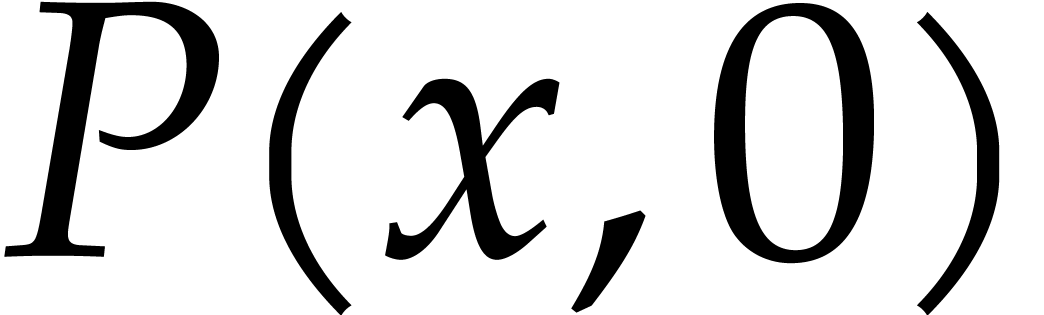 takes
takes 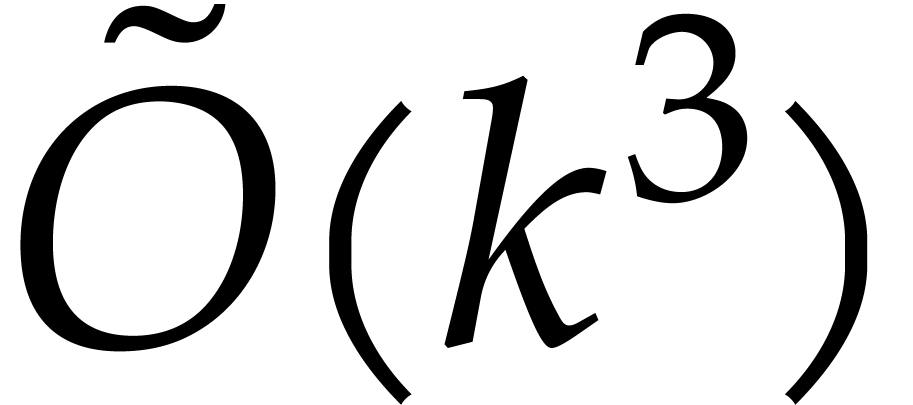 operations.
operations.
The Hensel lifting has a total cost of  .
.
The sparse interpolation of  (or
(or 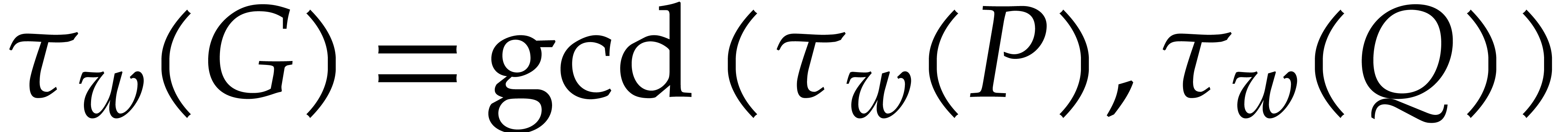 ) takes
) takes  operations.
operations.
The sparse polynomial division to recover 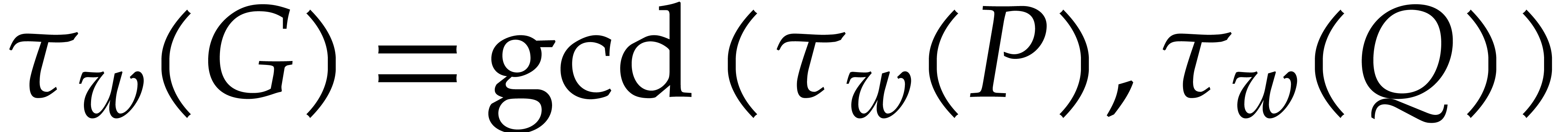 (or
(or  ) requires
) requires  operations.
operations.
Adding up these costs, the complexity bound follows. The algorithm is
correct as long as the final division succeeds, which is the case with
probability at least 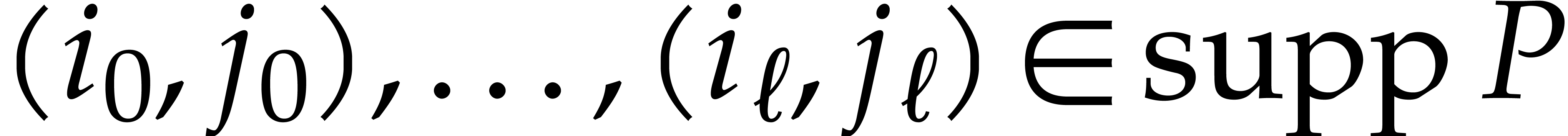 .
.
The assumptions H1 and H2 are fairly
strong: they are never satisfied both if  is a
homogeneous polynomial. Now the assumptions H1 and
H2 essentially allow us to perform the bivariate Hensel
lifting using the method from Section 4.3. The problem that
we face in order to extend the approach from Algorithm 7.1
is that random shifts
is a
homogeneous polynomial. Now the assumptions H1 and
H2 essentially allow us to perform the bivariate Hensel
lifting using the method from Section 4.3. The problem that
we face in order to extend the approach from Algorithm 7.1
is that random shifts  are not allowed for the
bivariate Hensel lifting from Section 4.3: we only have an
efficient algorithm to compute
are not allowed for the
bivariate Hensel lifting from Section 4.3: we only have an
efficient algorithm to compute 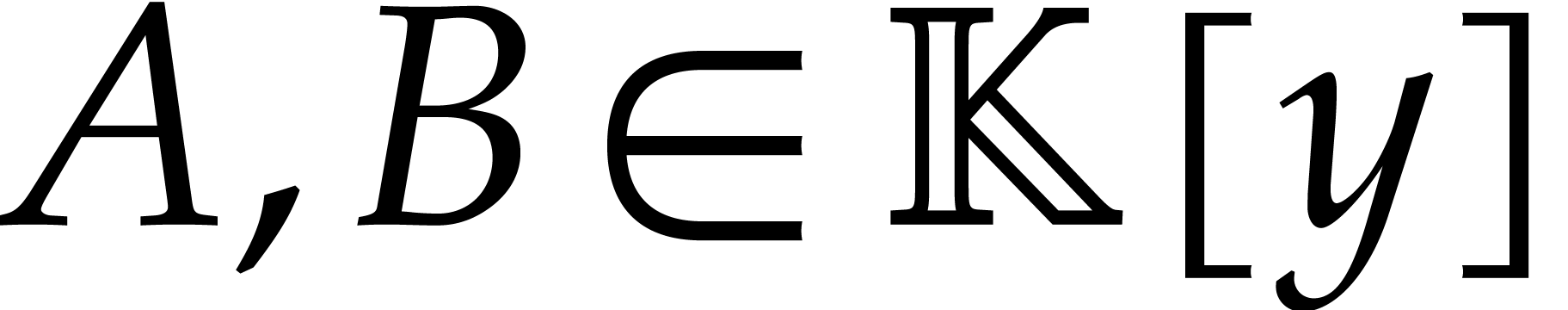 and
and 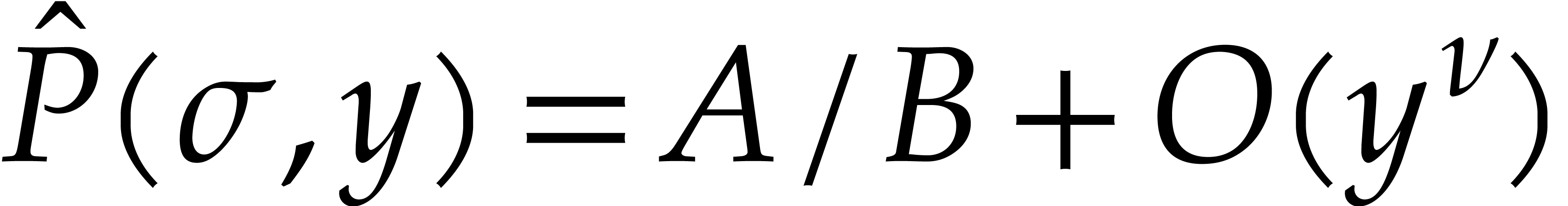 are given, not
are given, not 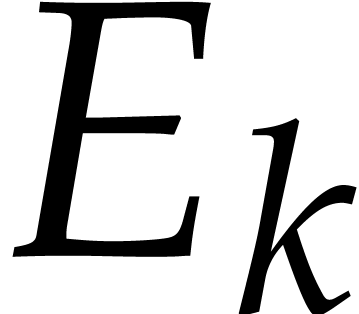 and
and  .
.
Instead, we need a way to generalize the algorithm from Section 4.3
to the case when the Newton polygon of  is
non-trivial. In this subsection, we start with the simplest
“single slope” case. Since this material is a supplement to
Section 4.3, we adopt the notation from there.
is
non-trivial. In this subsection, we start with the simplest
“single slope” case. Since this material is a supplement to
Section 4.3, we adopt the notation from there.
Assume that  has a non trivial factorization
has a non trivial factorization 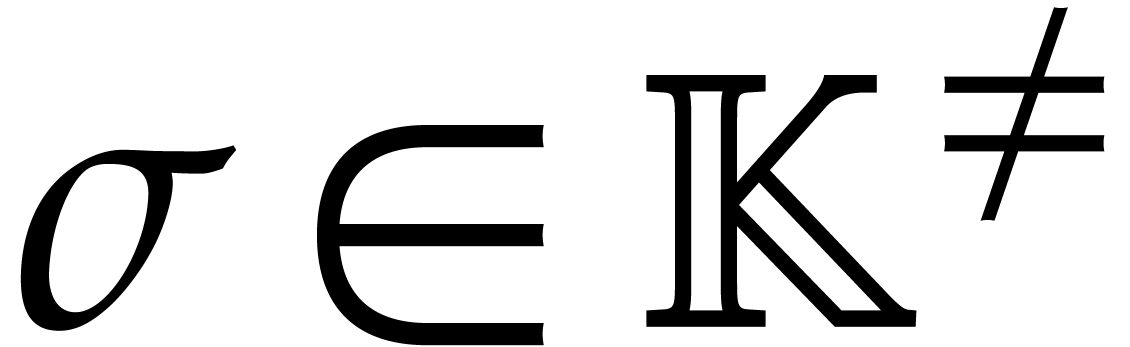 with
with 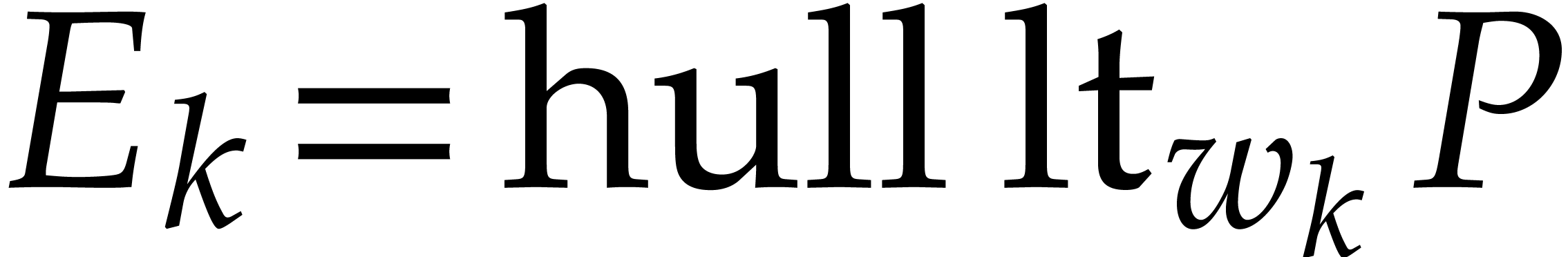 . We
define the Newton polygon of
. We
define the Newton polygon of  to be the
“lower border” of its Newton polytope:
to be the
“lower border” of its Newton polytope:

It is the union of a finite number of edges 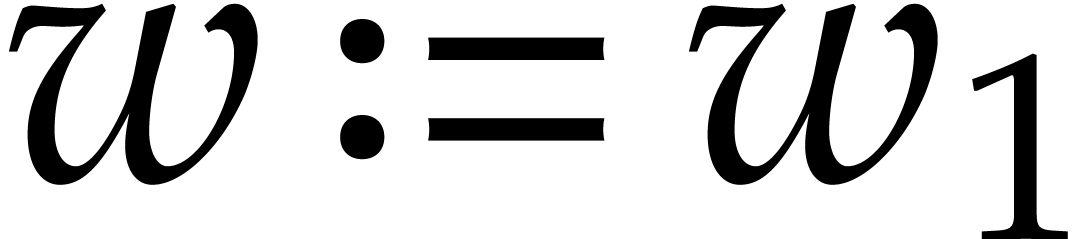 between
between 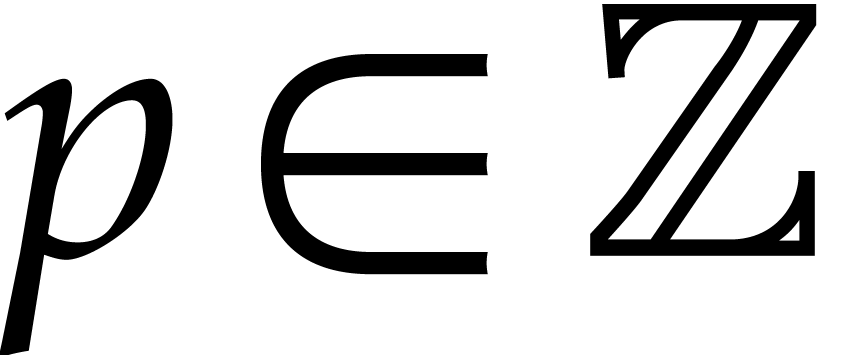 with
with 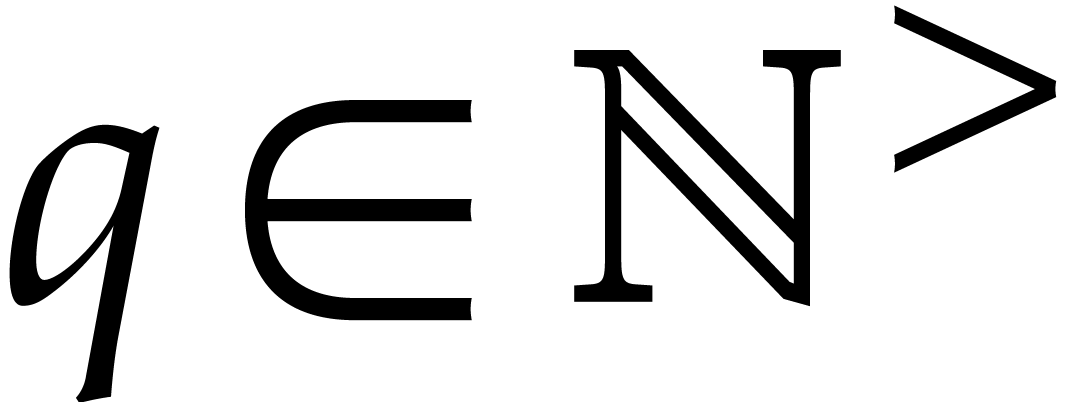 ,
,
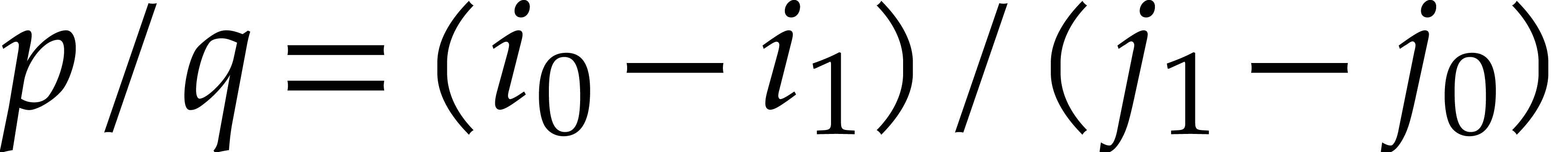 , and
, and  . For each edge
. For each edge  ,
there is a corresponding weight
,
there is a corresponding weight 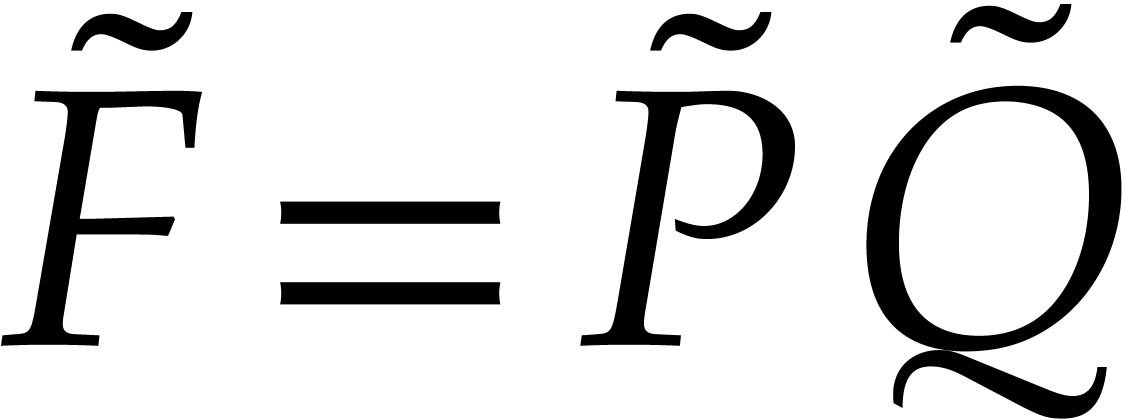 such that
such that 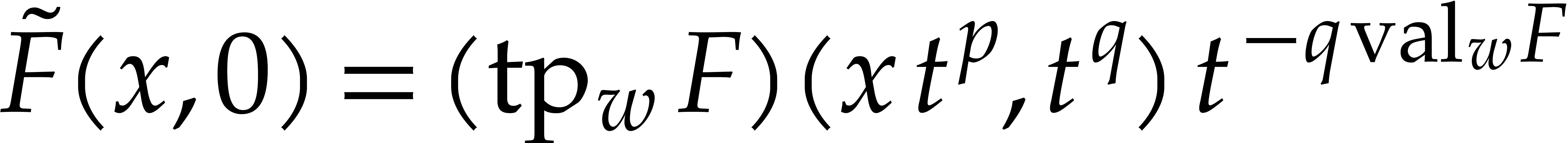 .
.
Assume that 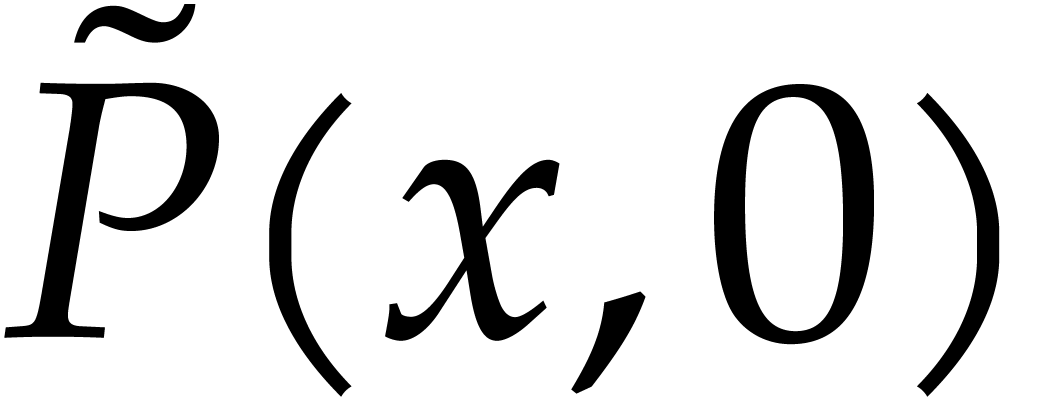 has a single edge, let
has a single edge, let  , and let
, and let  and
and  be coprime such that
be coprime such that  .
Now consider
.
Now consider

Then  and
and 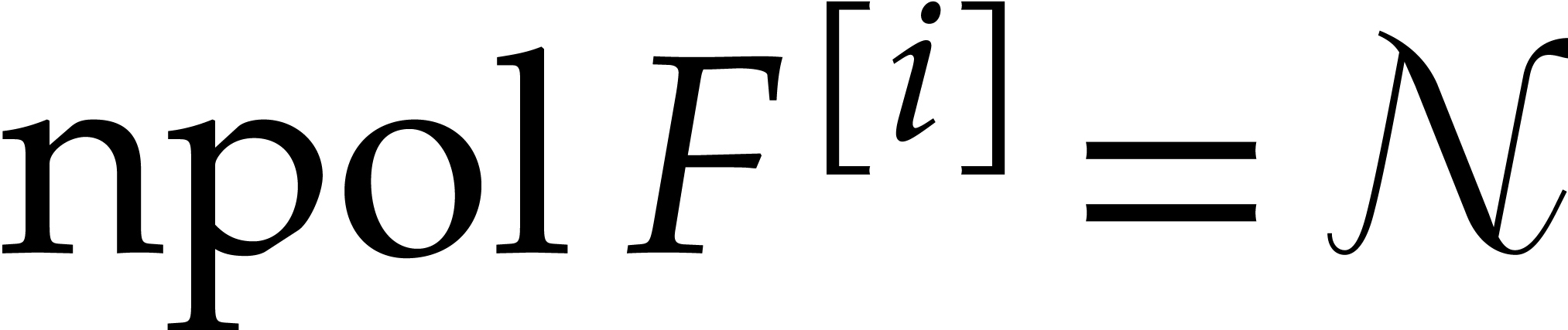 .
Moreover,
.
Moreover,  , and we have
similar expressions for
, and we have
similar expressions for  and
and  . If
. If  and
and 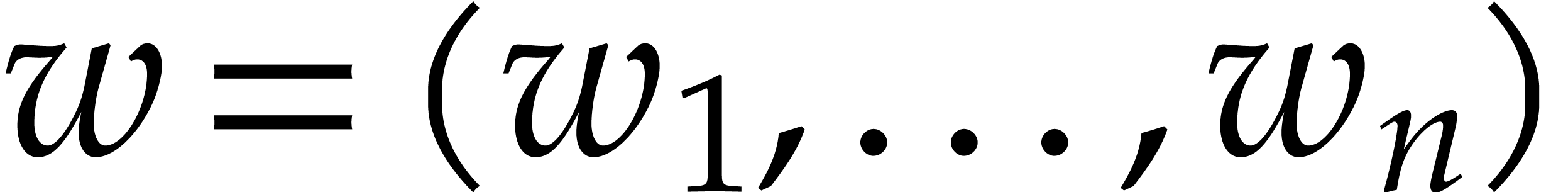 are known and if their transforms
are known and if their transforms 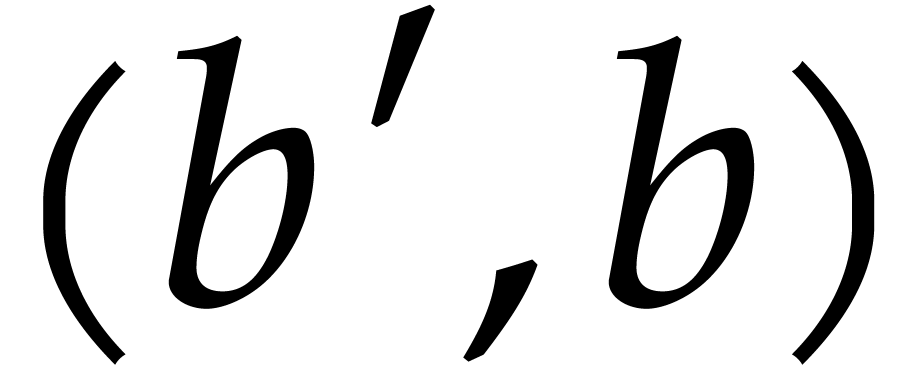 and
and 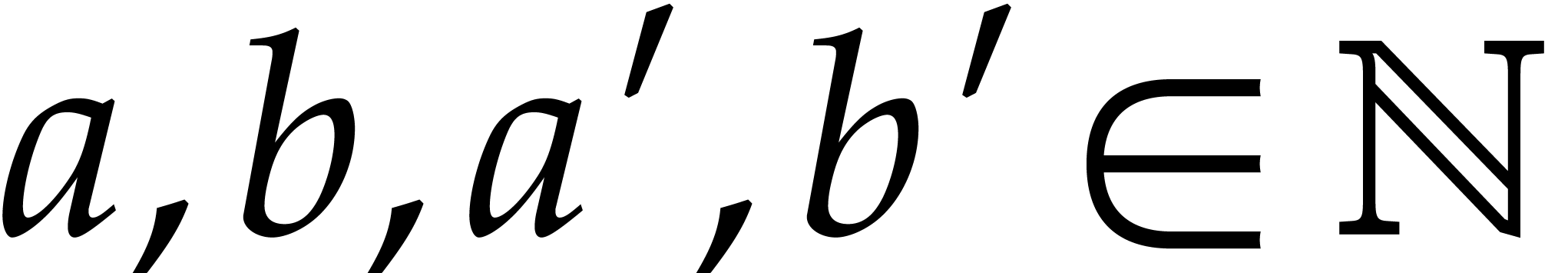 are coprime, then this enables us to compute
are coprime, then this enables us to compute
 and
and 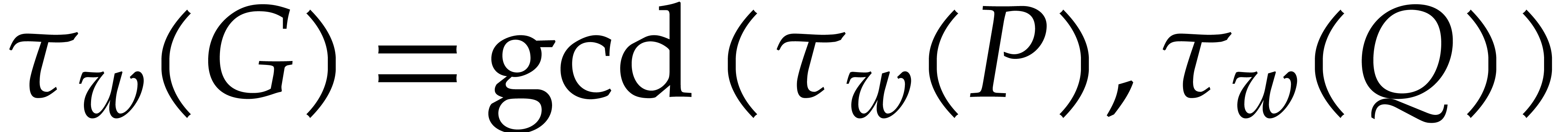 by applying the
Hensel lifting method from Section 4.3 to
by applying the
Hensel lifting method from Section 4.3 to  ,
, 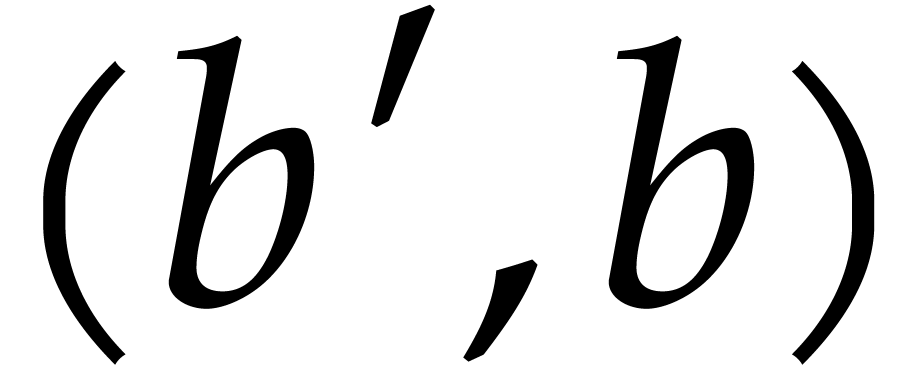 ,
and
,
and 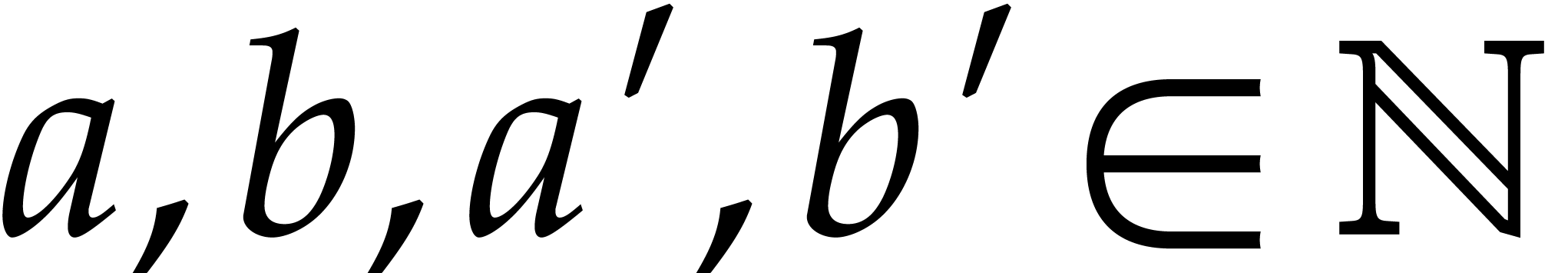 .
.
Let us now return to the factorization problem from Section 7.1 and let us show how to generalize Algorithm 7.1 using the material from the previous subsection.
Let  and let
and let 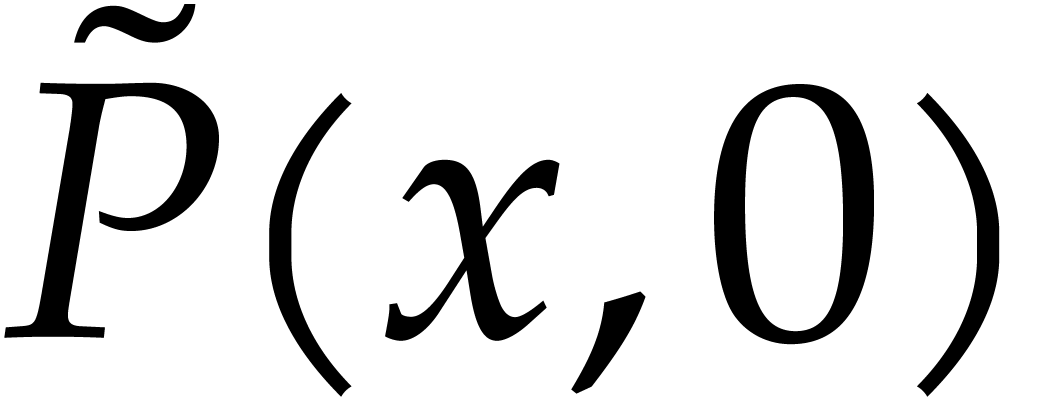 be the lower
boundary of its convex hull. With high probability, we have
be the lower
boundary of its convex hull. With high probability, we have  and
and 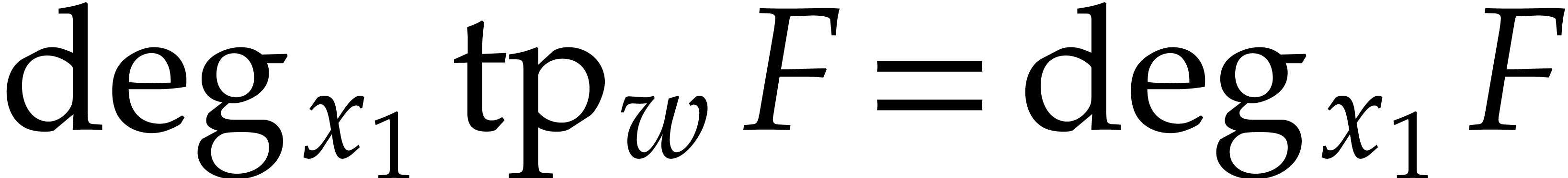 , for any
given
, for any
given  . The last edge of
. The last edge of 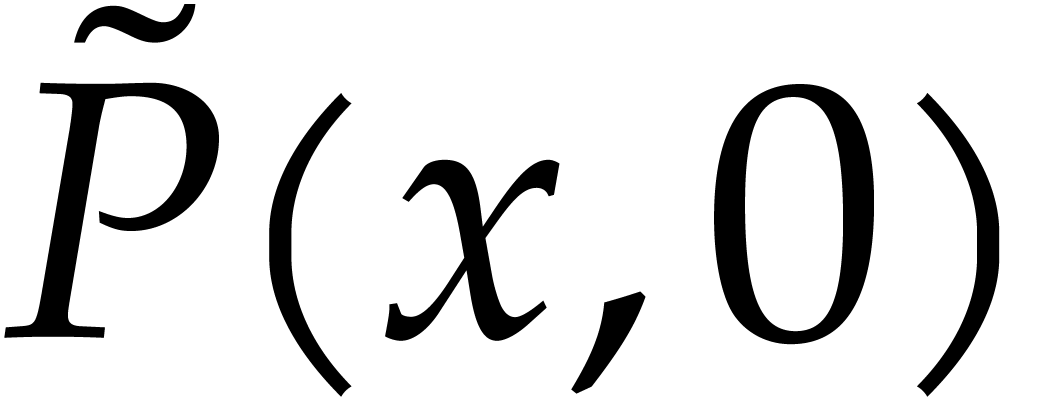 joins the points
joins the points 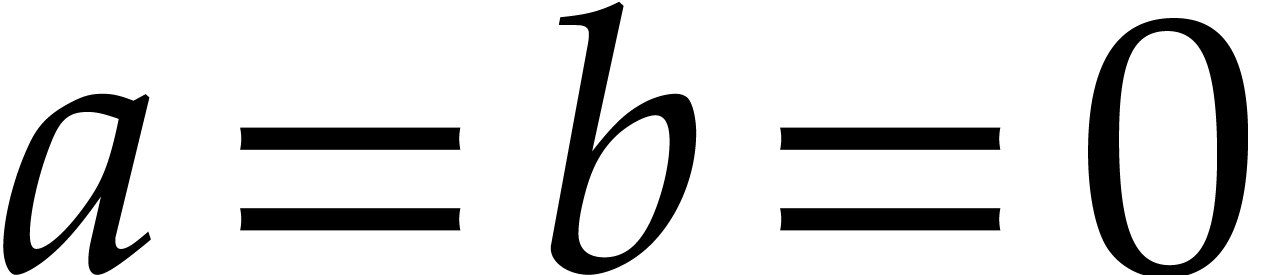 and
and  for
for 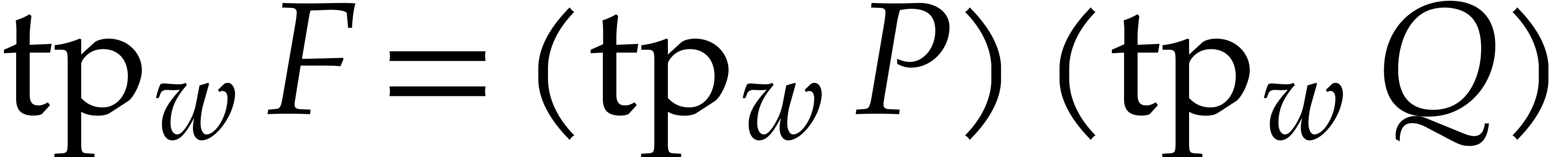 with
with  . Let
. Let 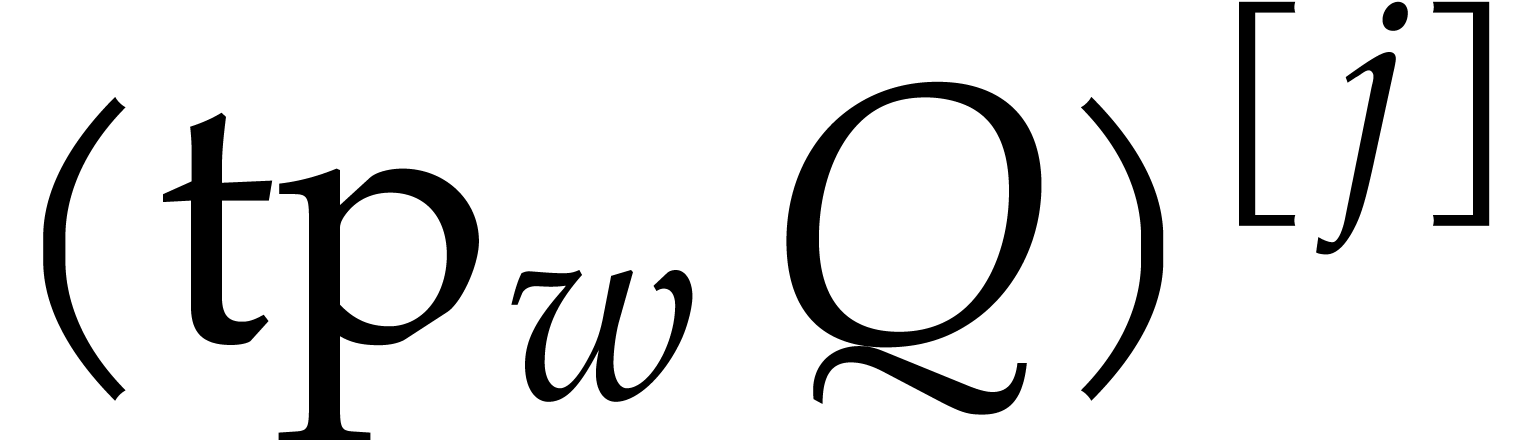 with
with 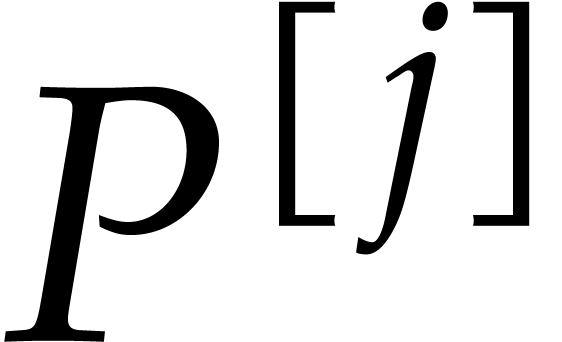 and
and  , where
, where
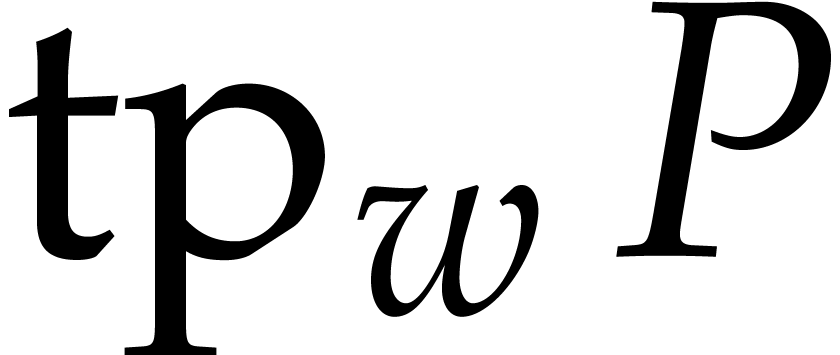 ,
, 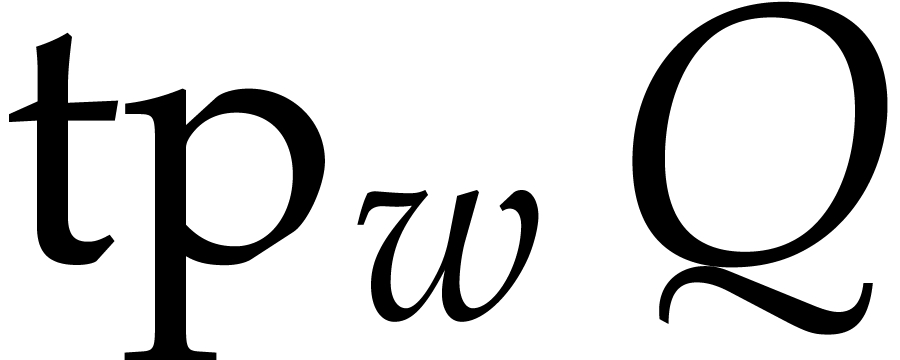 , and
, and  .
Now consider the assumptions
.
Now consider the assumptions
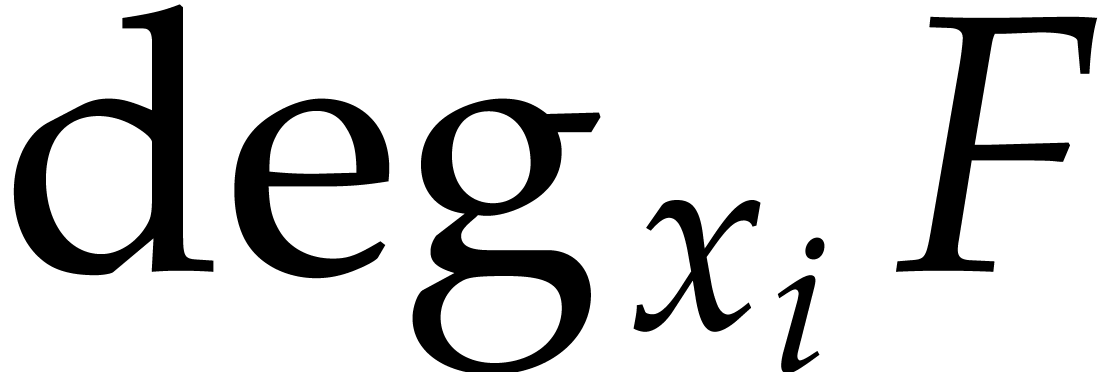 .
.
 and
and 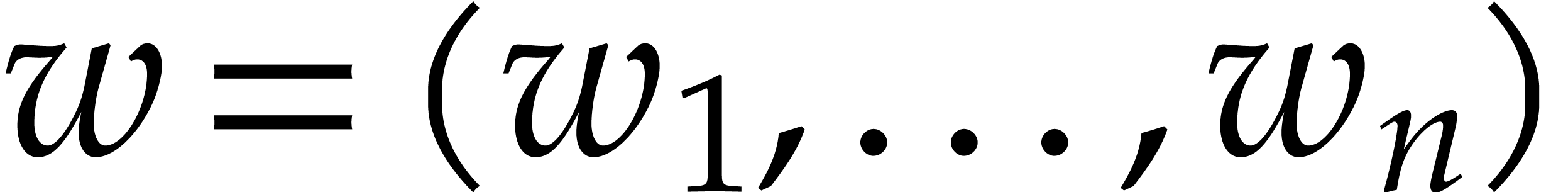 are coprime.
are coprime.
The hypotheses H1 and H2 correspond to
the special case when  . If
. If
 and
and 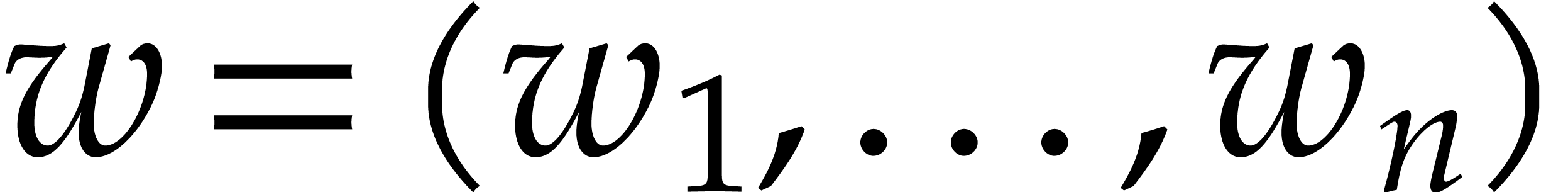 are known
(e.g. through the recursive factorization of
are known
(e.g. through the recursive factorization of 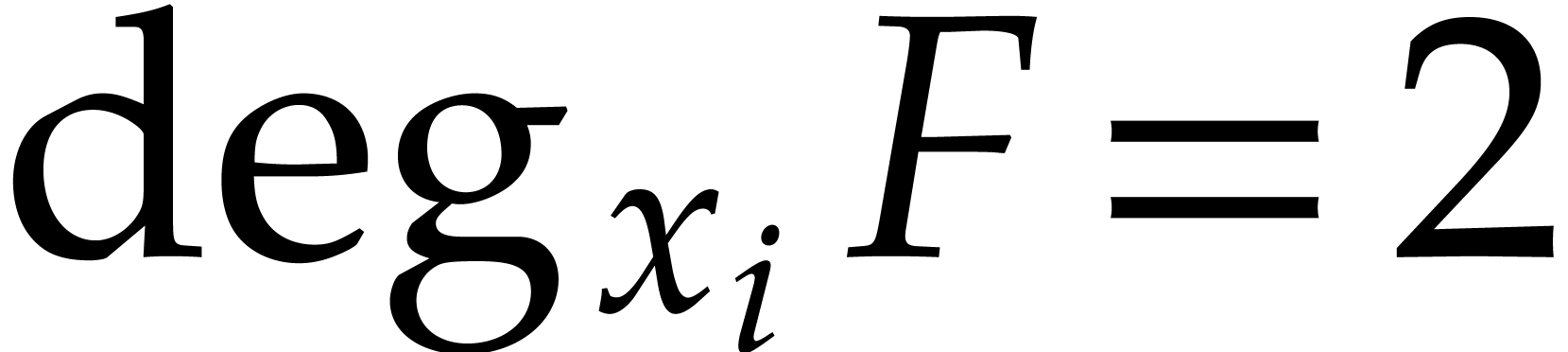 if
if  is not
is not  -homogeneous), then the algorithm from Section 7.2 allows us to Hensel lift the factorization
-homogeneous), then the algorithm from Section 7.2 allows us to Hensel lift the factorization  into a factorization
into a factorization  .
This leads to the following generalization of Algorithm 7.1:
.
This leads to the following generalization of Algorithm 7.1:
Algorithm
|
|
Output: |
|
For 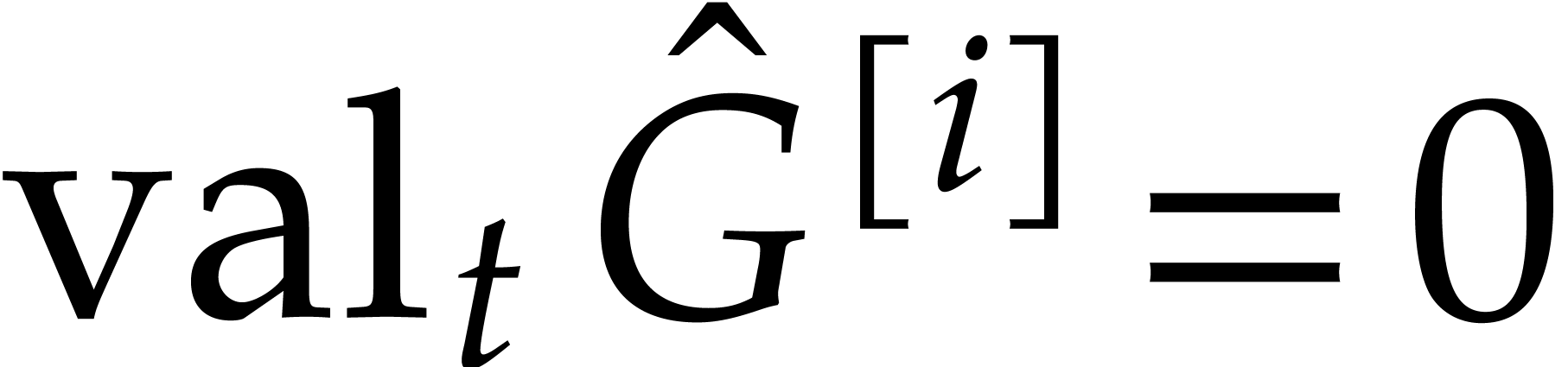 do
do
Compute  ,
, 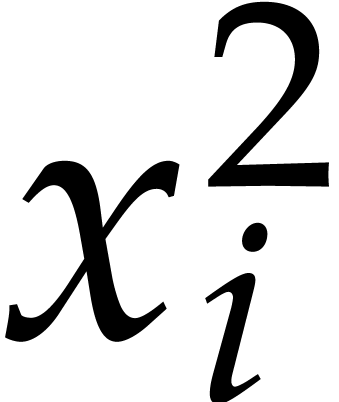 ,
,  for
for 
Compute  ,
,  for
for  ,
,
using bivariate Hensel lifting from Section 7.2 for 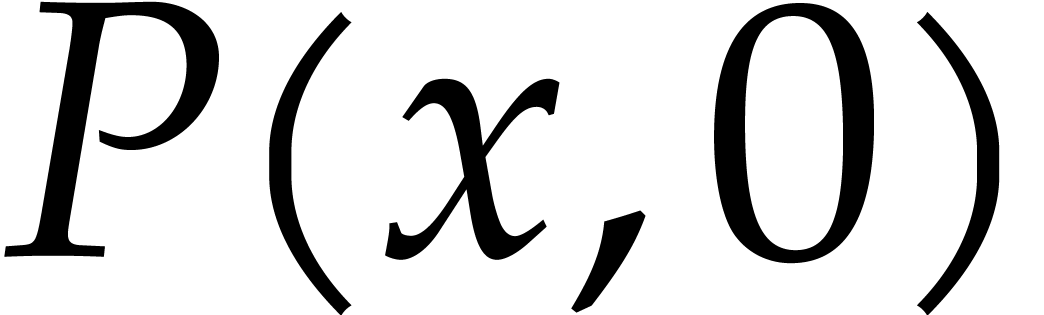 ,
, 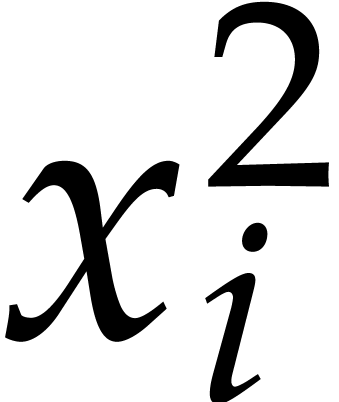 ,
,

If  yield
yield  through
sparse interpolation, then return
through
sparse interpolation, then return 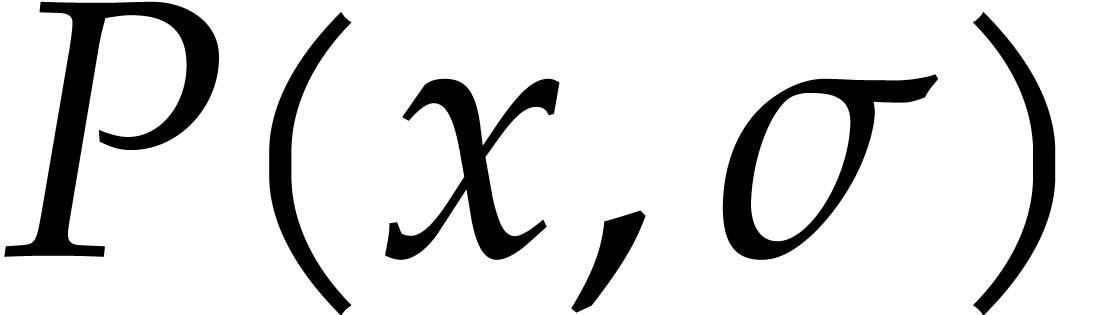
If  yield
yield 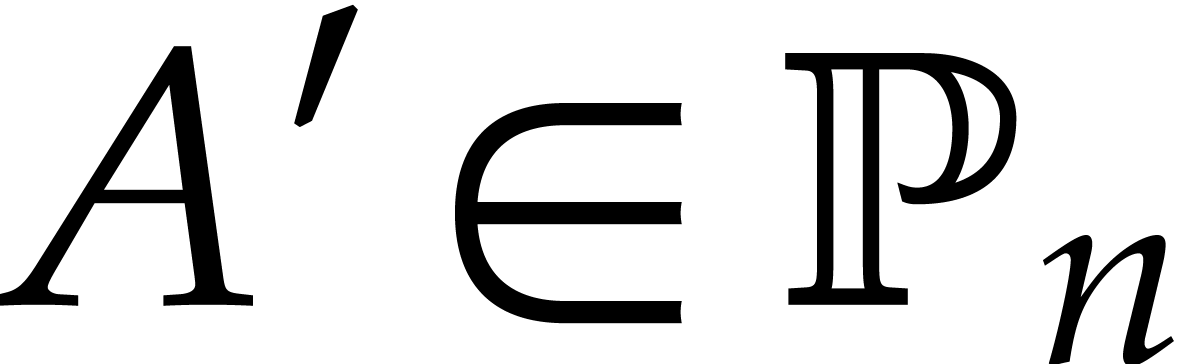 through
sparse interpolation, then return
through
sparse interpolation, then return 
 ,
, 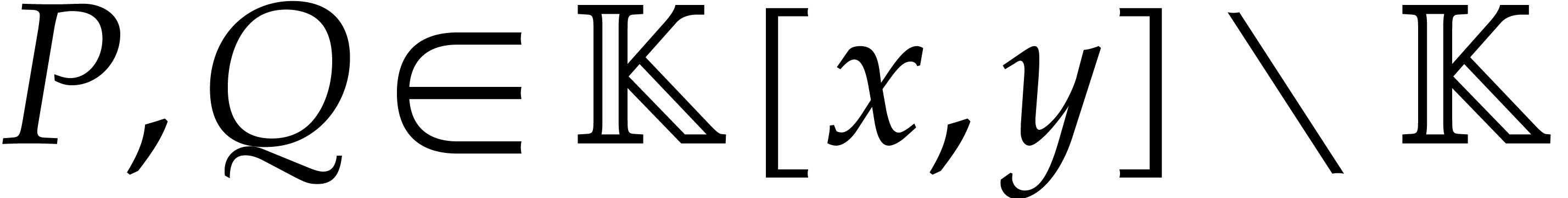 ,
,  ,
,
 , and
, and  . Then Algorithm 7.2 is correct
with probability at least
. Then Algorithm 7.2 is correct
with probability at least 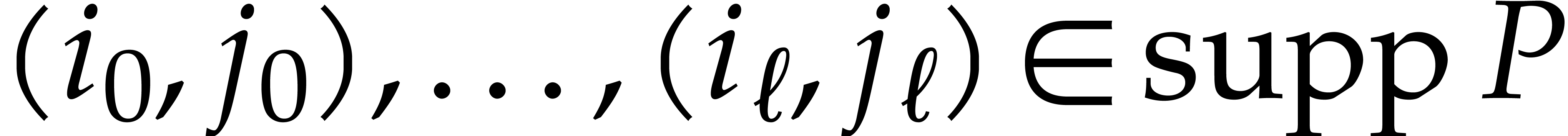 and runs in time
and runs in time
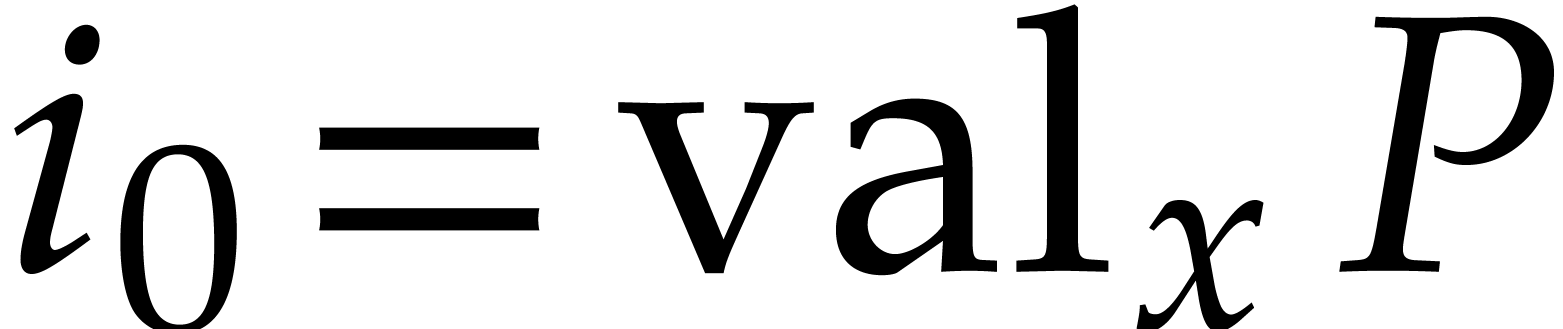
Proof. The proof is similar to the proof of
Theorem 7.1. The main change is that the generalized
algorithm also requires the evaluations of  and
and
 on our sequence. This takes
on our sequence. This takes 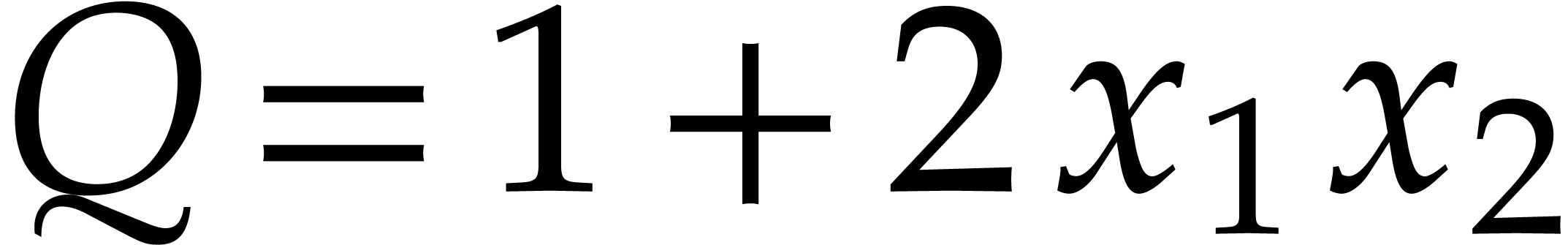 additional operations, which is absorbed by the complexity bound.
additional operations, which is absorbed by the complexity bound.
Note that the assumptions H1' and H2'
are actually slightly more liberal than the statement that the Newton
polygon should have a single edge. For this reason, Algorithm 7.2
is very likely to apply as soon as there exists a variable  for which
for which 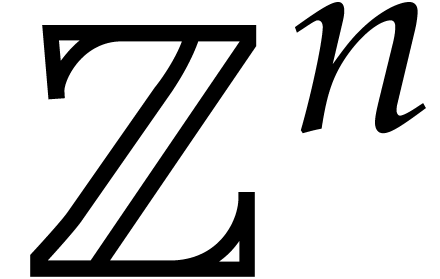 is small (of course, we
may then assume
is small (of course, we
may then assume 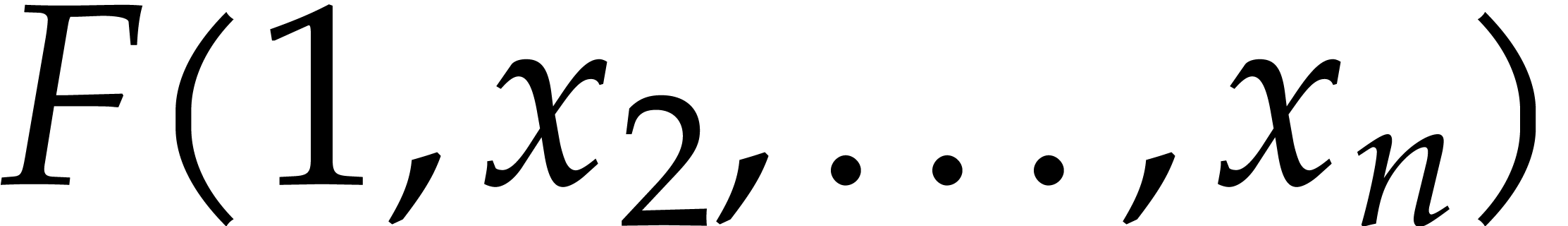 modulo a permutation of
variables). This in particular the case when
modulo a permutation of
variables). This in particular the case when 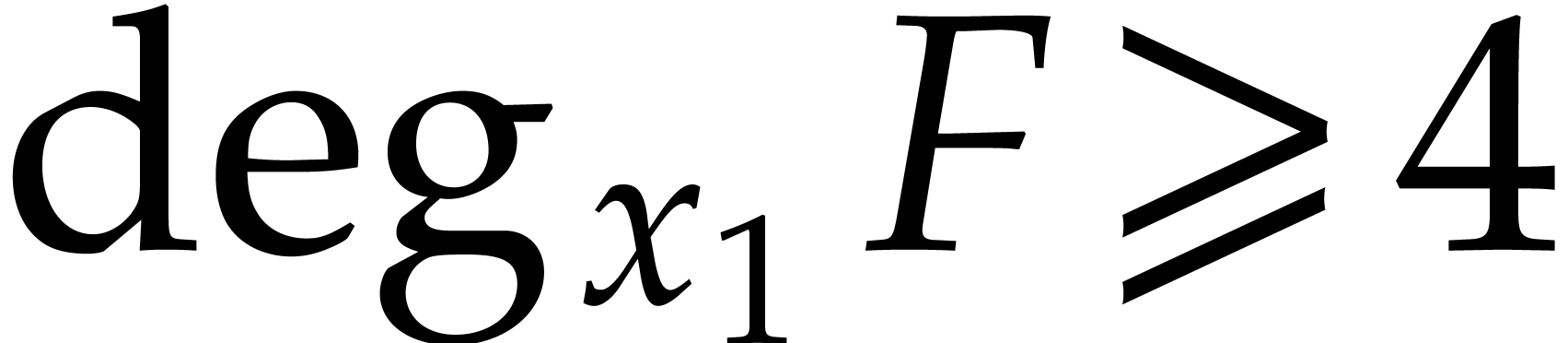 , unless
, unless 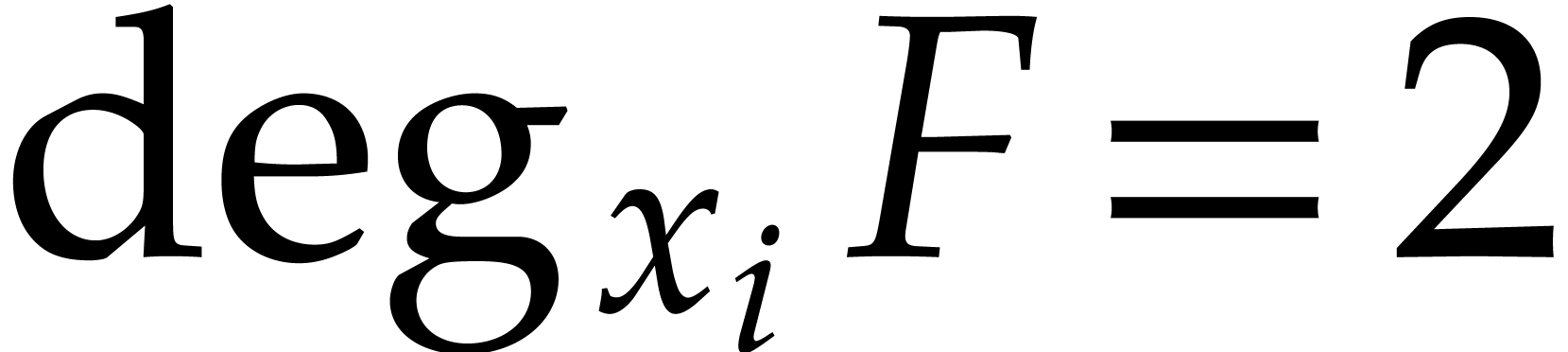 is not square-free
(one may need to replace
is not square-free
(one may need to replace 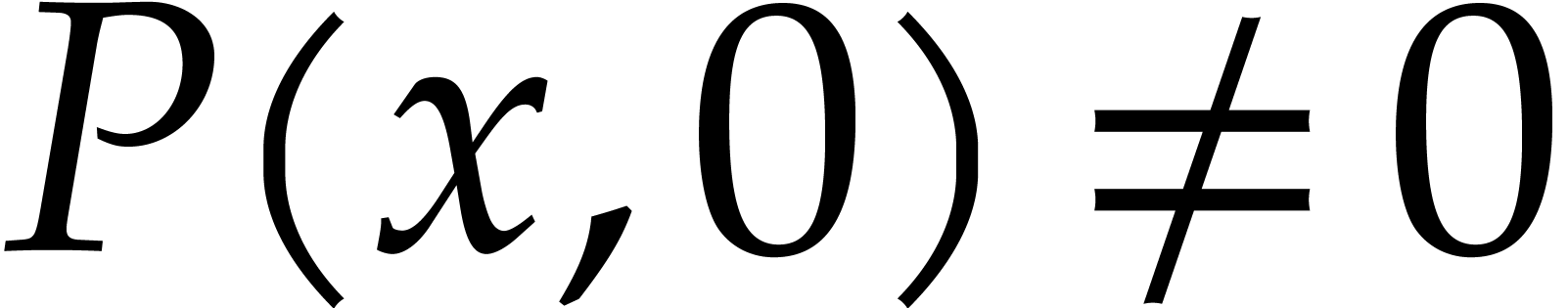 and multiply
and multiply  with
with  ). Note
that a single “good” variable
). Note
that a single “good” variable  suffices.
suffices.
Remark
Remark 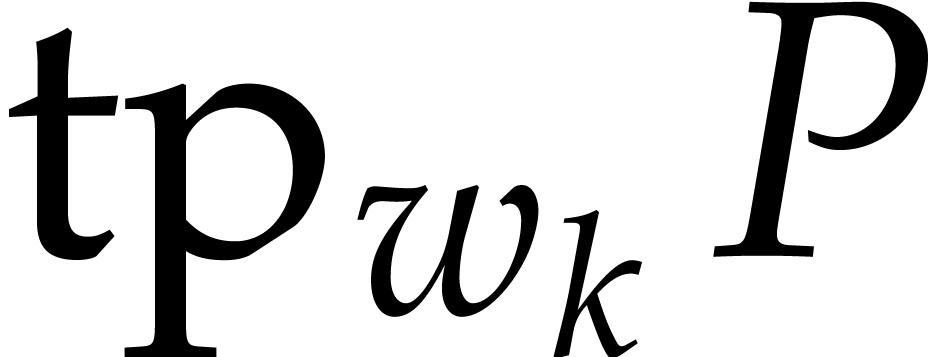 and
and  .
Then
.
Then 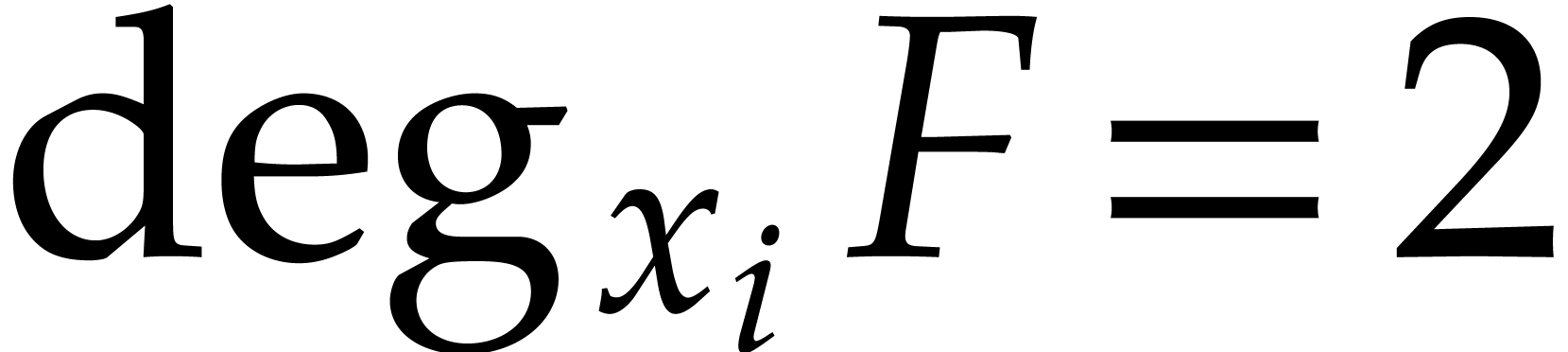 coincides with
coincides with  , so the requested factorization of
, so the requested factorization of 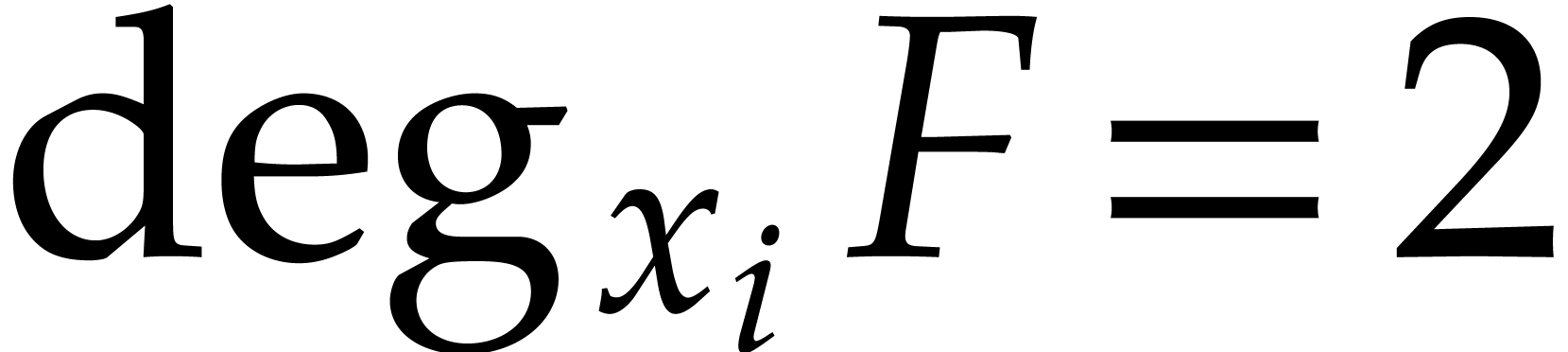 is not simpler than the desired factorization of
is not simpler than the desired factorization of  . This is due to the fact that the exponents of
. This is due to the fact that the exponents of  all lie in a linear subspace of
all lie in a linear subspace of 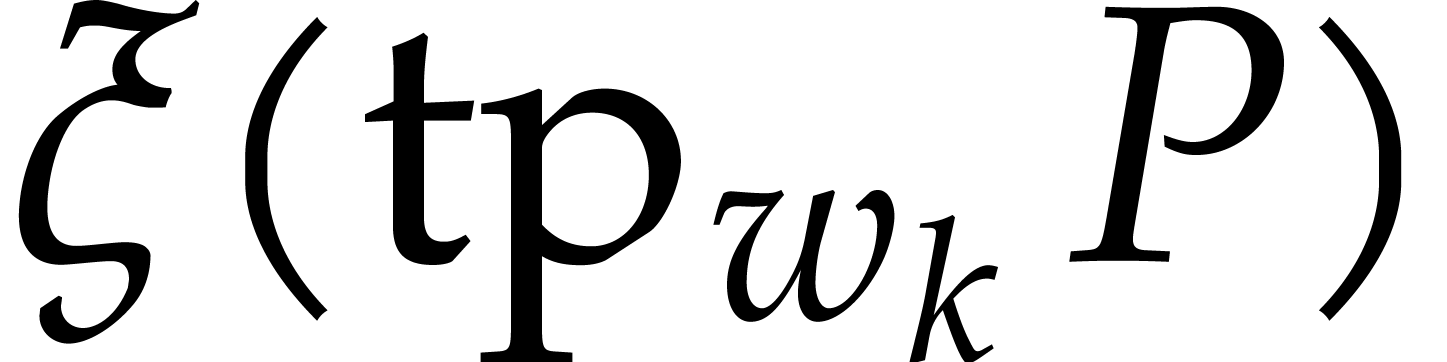 . In particular, the degree in
. In particular, the degree in  of any term of
of any term of  can be determined as a function
of the degrees of the other variables. In particular, we may recover a
factorization of
can be determined as a function
of the degrees of the other variables. In particular, we may recover a
factorization of  from a factorization of
from a factorization of 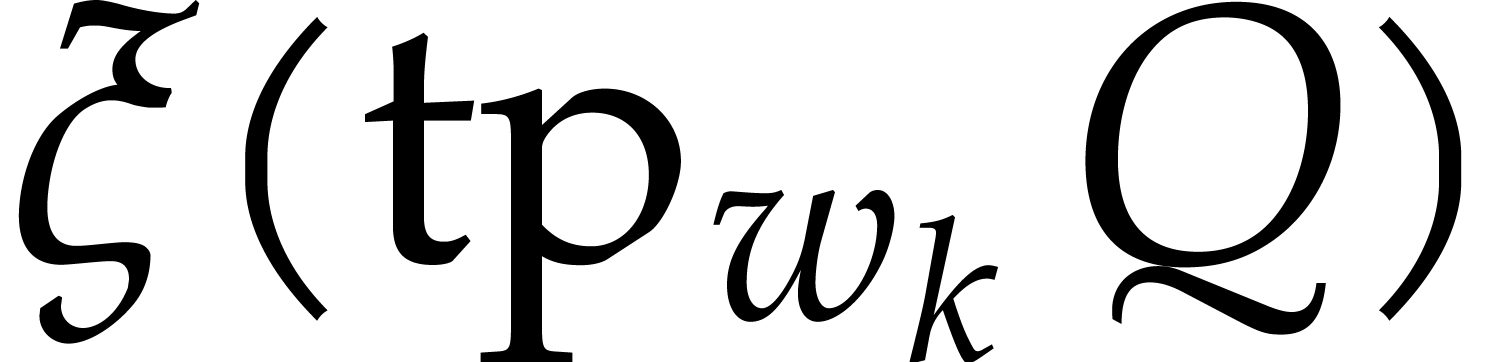 . Using a straightforward induction
on
. Using a straightforward induction
on  , this allows us to ensure
that
, this allows us to ensure
that 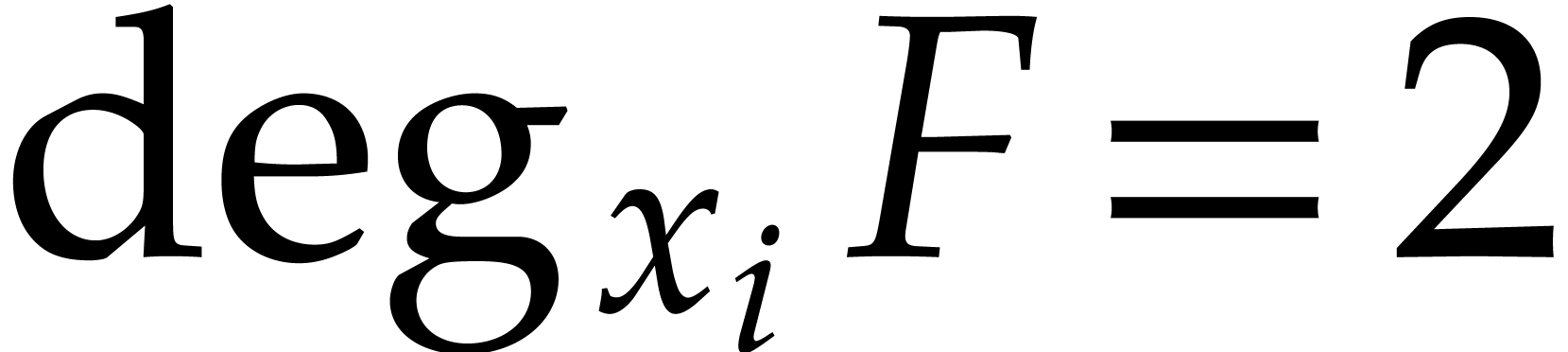 has strictly less terms than
has strictly less terms than  .
.
As soon as  , it can happen
that every factor of
, it can happen
that every factor of  has a Newton polygon with
at least two edges. In order to deal with this situation, the algorithm
from Section 7.2 may be further generalized to accommodate
Newton polygons with multiple slopes. In order to explain how, we again
adopt the notation from Sections 4.3 and 7.2.
has a Newton polygon with
at least two edges. In order to deal with this situation, the algorithm
from Section 7.2 may be further generalized to accommodate
Newton polygons with multiple slopes. In order to explain how, we again
adopt the notation from Sections 4.3 and 7.2.
So assume that 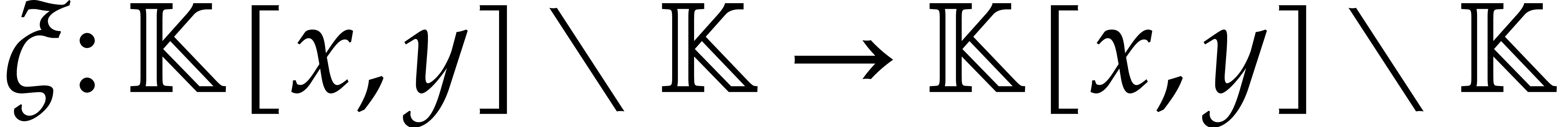 and
and 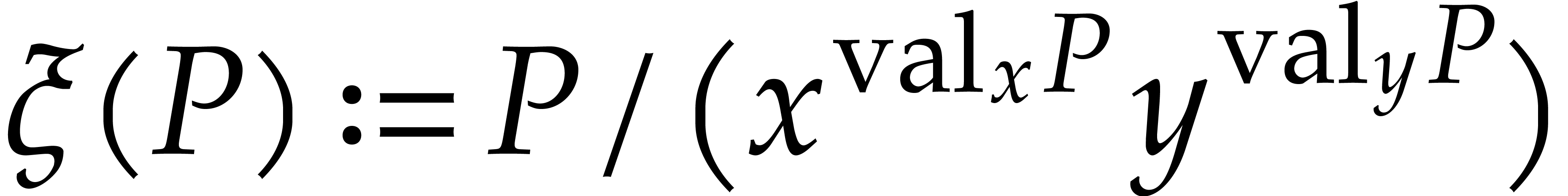 ,
that
,
that 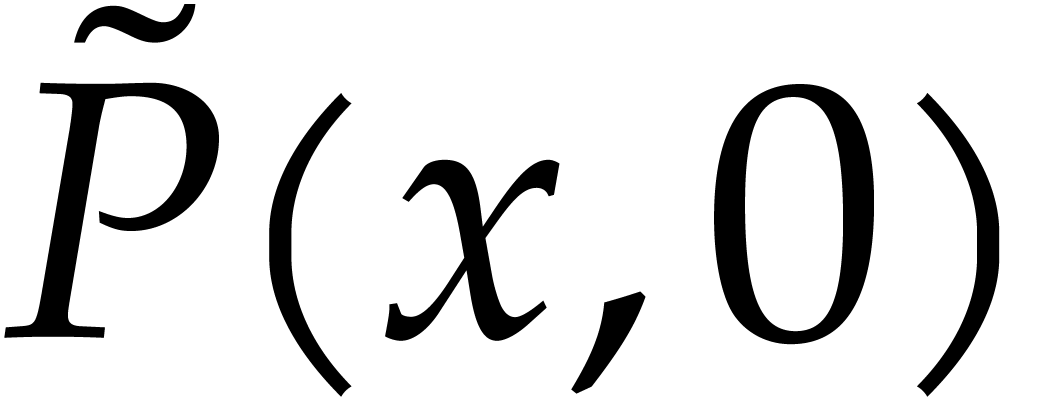 has an arbitrary number of edges, and that
has an arbitrary number of edges, and that
 and
and 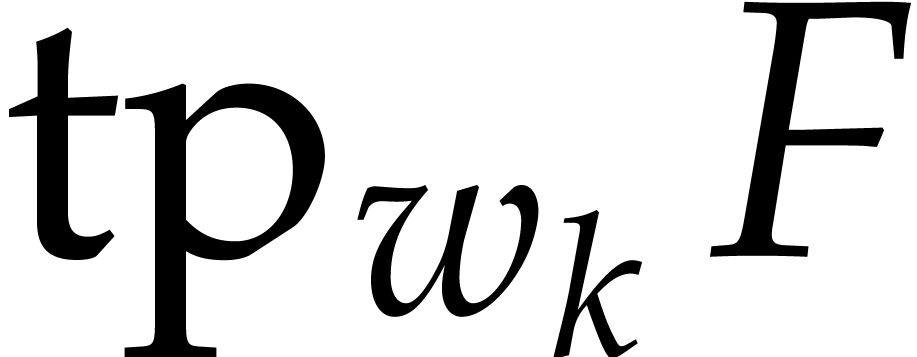 are known for each
edge
are known for each
edge  . Assume also that
. Assume also that  and
and  are coprime for
are coprime for 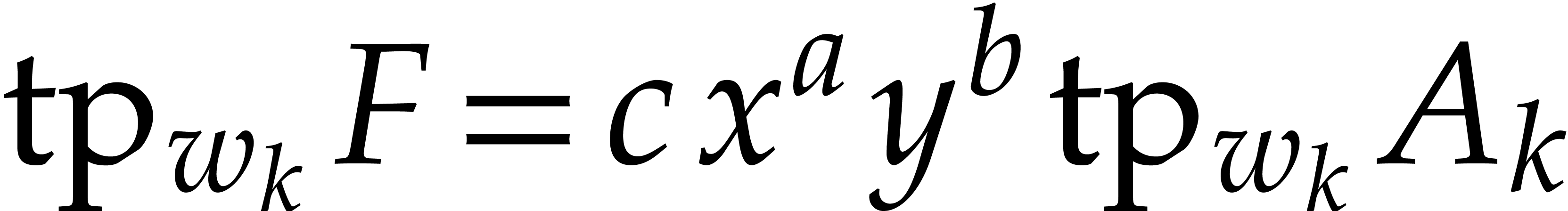 , where
, where 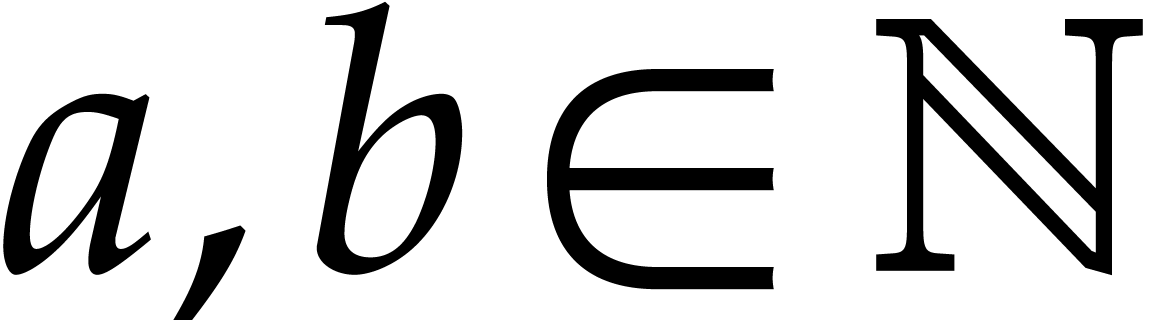 is
the normalization mapping with
is
the normalization mapping with  .
We will say that
.
We will say that 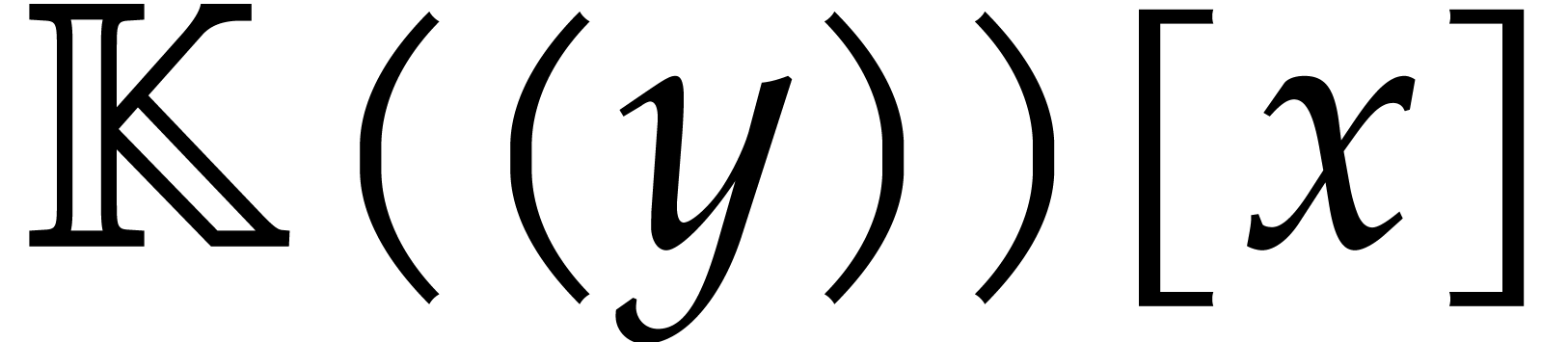 is a coprime edge
factorization of
is a coprime edge
factorization of  . The
aim of this subsection is to lift these factorizations efficiently into
the global factorization
. The
aim of this subsection is to lift these factorizations efficiently into
the global factorization 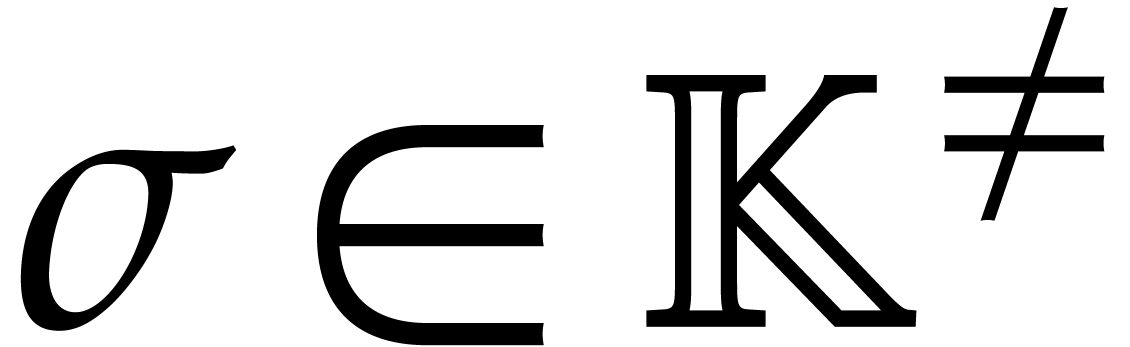 .
.
It is well known that a variant of the Newton polygon method can be used
in order to factor  over the ring
over the ring 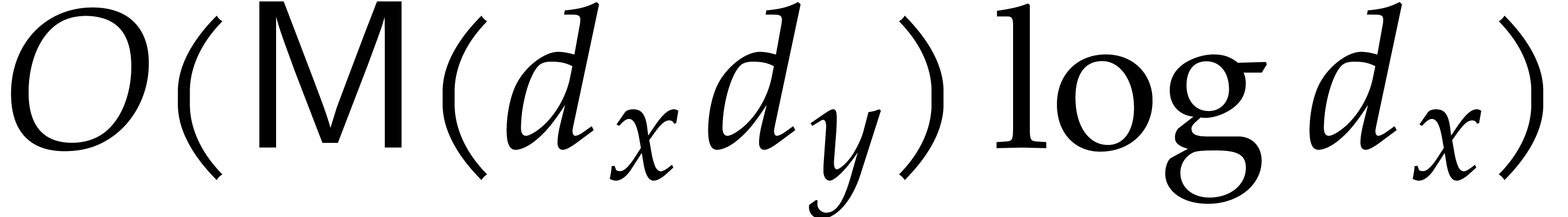 of Laurent series. An efficient algorithm for this task
was described in [55]. One important subtask is distinct
slope factorization: each edge
of Laurent series. An efficient algorithm for this task
was described in [55]. One important subtask is distinct
slope factorization: each edge  gives rise to a
unique monic factor
gives rise to a
unique monic factor  of
of  such that
such that 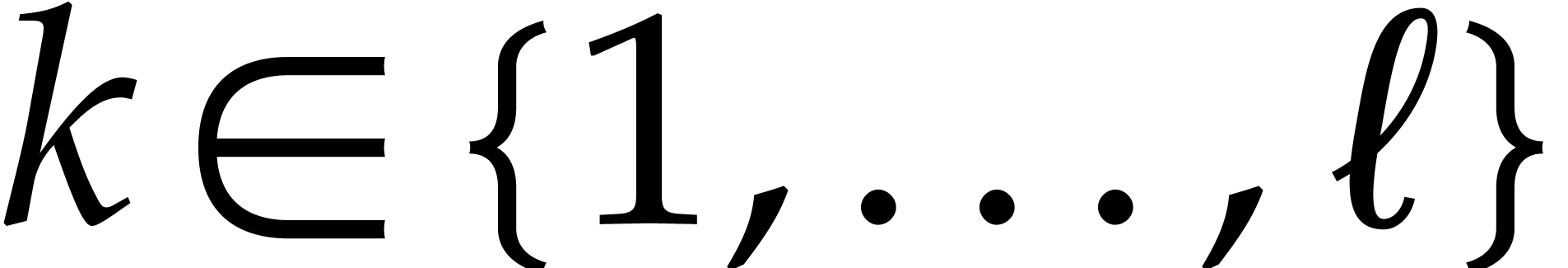 for
for  ,
,
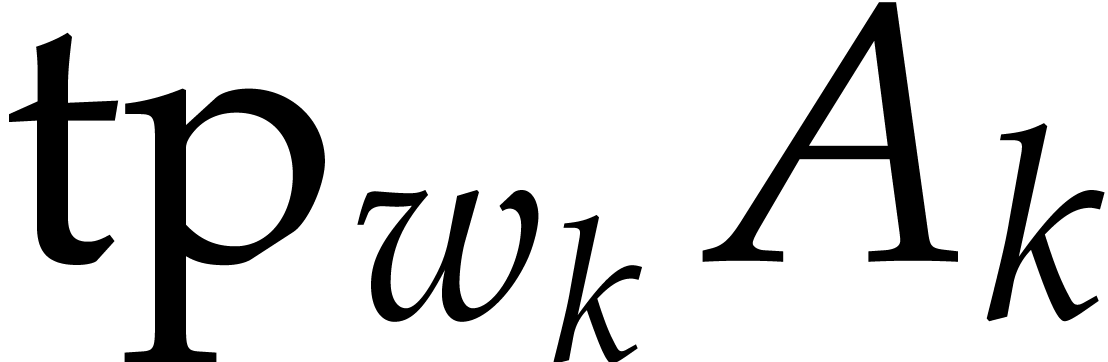 , and the natural
generalization of the notation
, and the natural
generalization of the notation 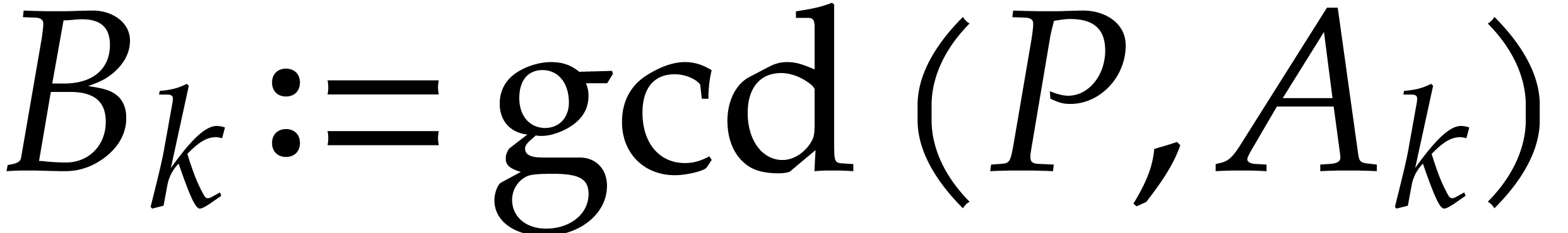 to
to 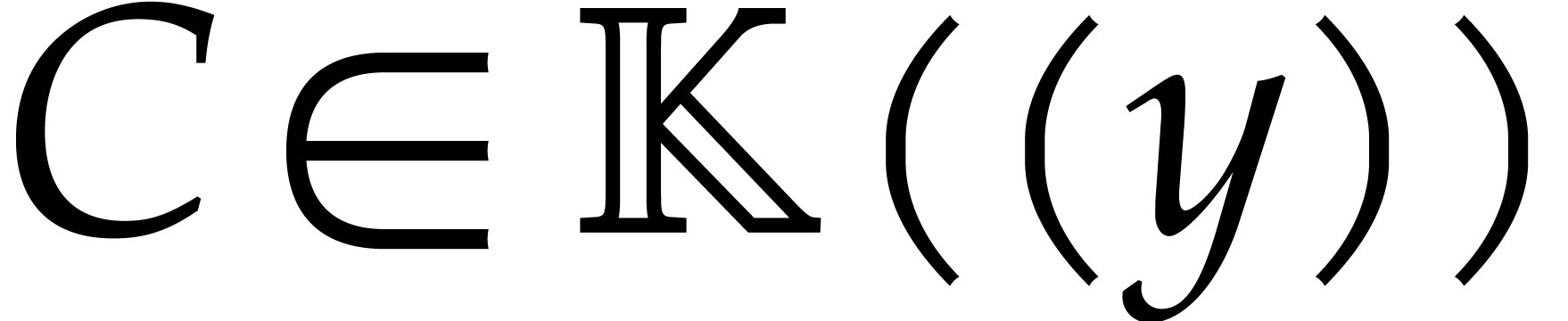 . The methods from [55] allow for
the efficient computation of the
. The methods from [55] allow for
the efficient computation of the 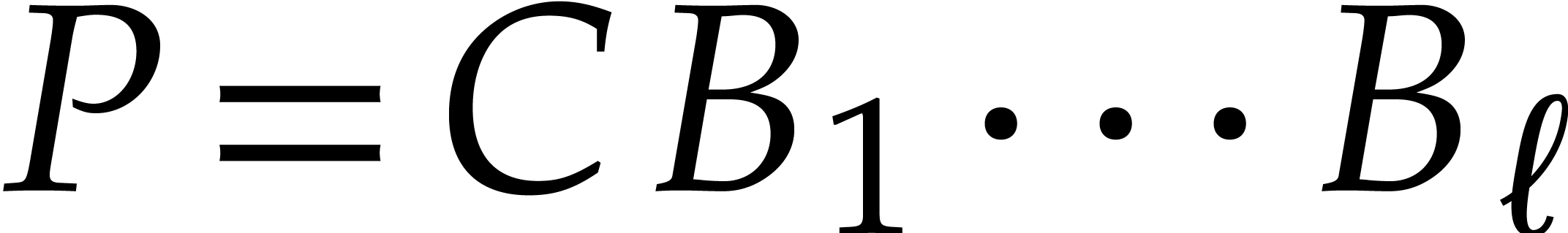 :
it takes time
:
it takes time  to compute
to compute  at order
at order  for
for  .
.
Now for each 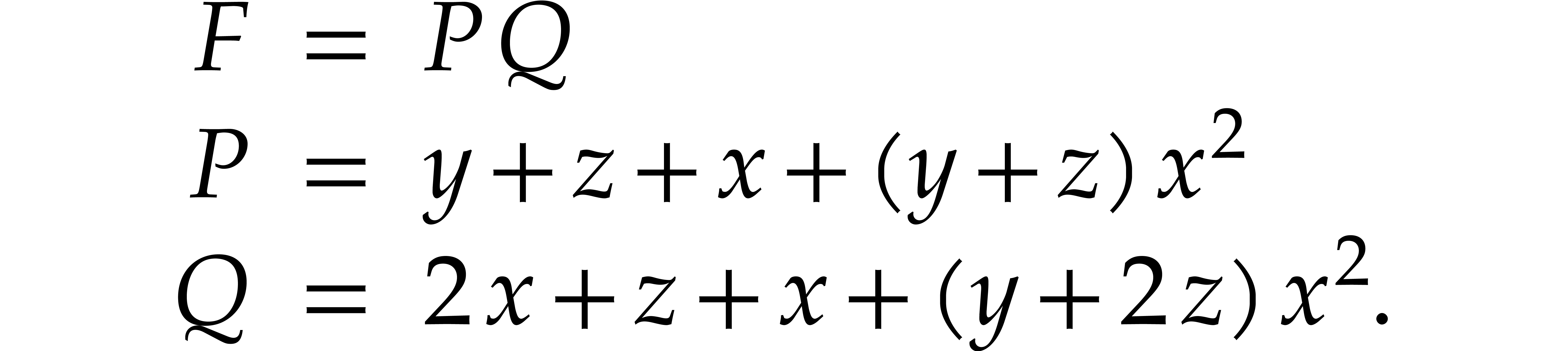 , the known
factor
, the known
factor  of
of  induces a
factor of
induces a
factor of 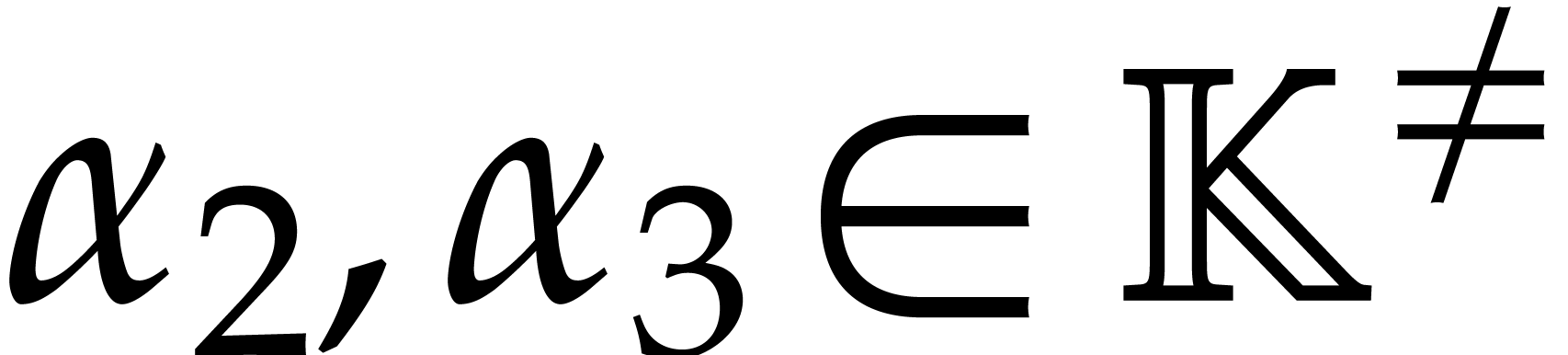 that can be Hensel lifted into the
factor
that can be Hensel lifted into the
factor 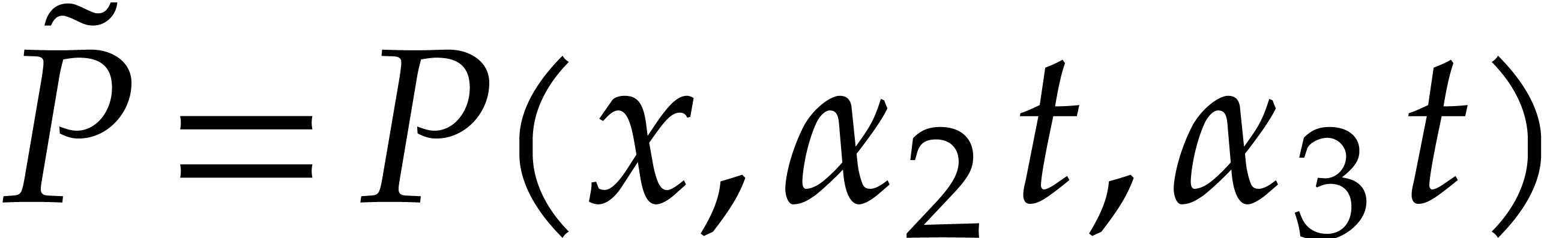 of
of 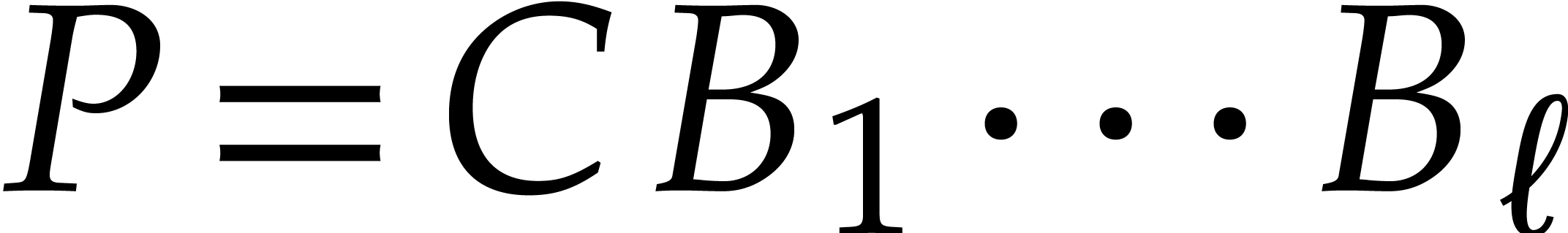 ,
by adapting the techniques from Section 4.3 to Laurent
series coefficients. For some
,
by adapting the techniques from Section 4.3 to Laurent
series coefficients. For some 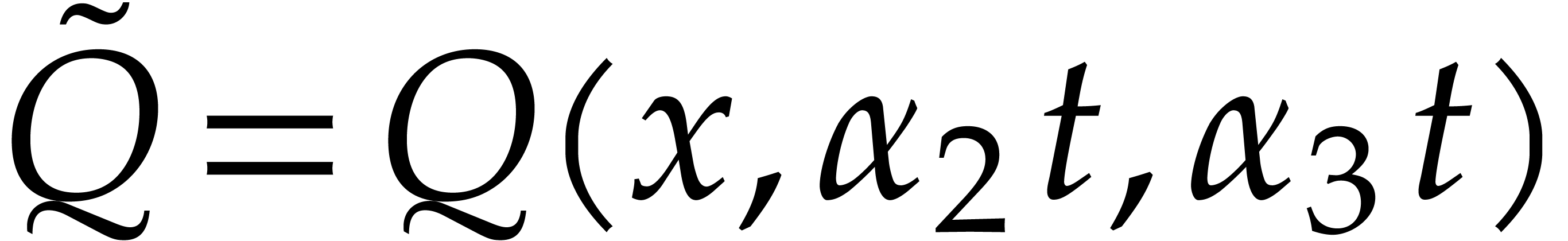 ,
we then have
,
we then have  . We may
determine
. We may
determine  in a similar way as in Section 4.3. The other factor
in a similar way as in Section 4.3. The other factor  can be obtained
using one bivariate division. The total cost of this method to compute
can be obtained
using one bivariate division. The total cost of this method to compute
 and
and 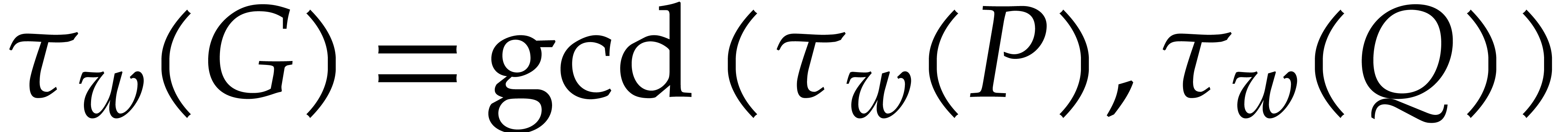 is bounded by
is bounded by  .
.
We are now in a position to generalize Algorithm 7.2 to the case when the bivariate Hensel lifting is done using the multiple slope method from the previous subsection. The general algorithm is fairly technical, so we found it more instructive to illustrate the main ideas on an example. Let

For generic  , consider
, consider  ,
, 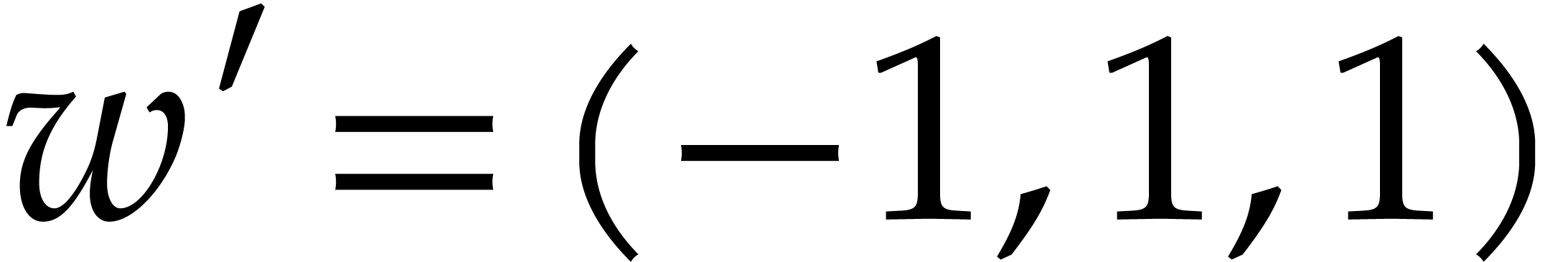 ,
and
,
and 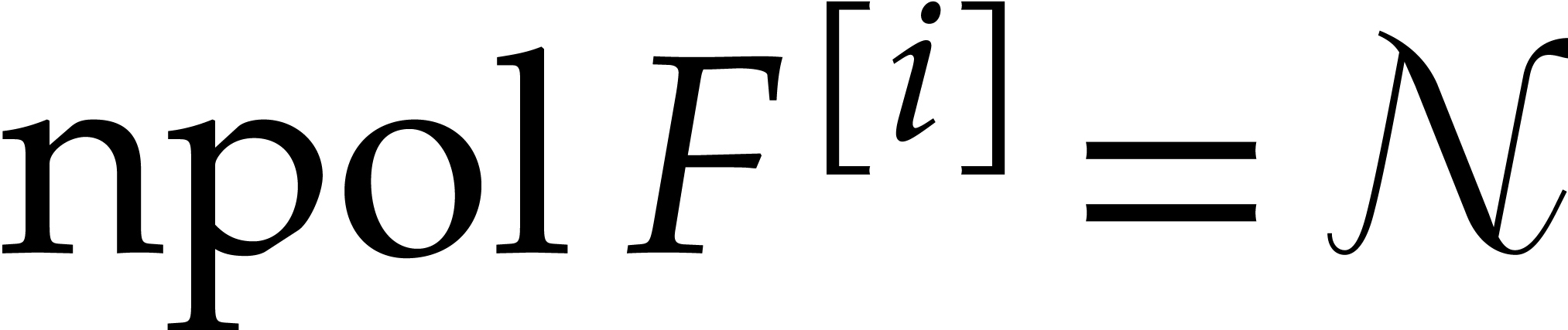 . Then
. Then

whence  is the closed triangle with vertices
is the closed triangle with vertices
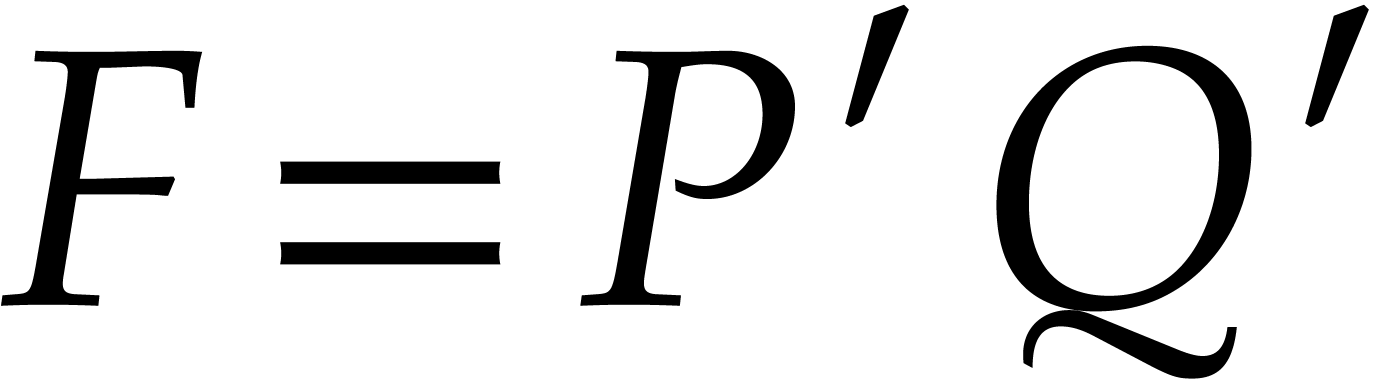 ,
,  , and
, and  .
Its lower boundary consists of the edge from
.
Its lower boundary consists of the edge from 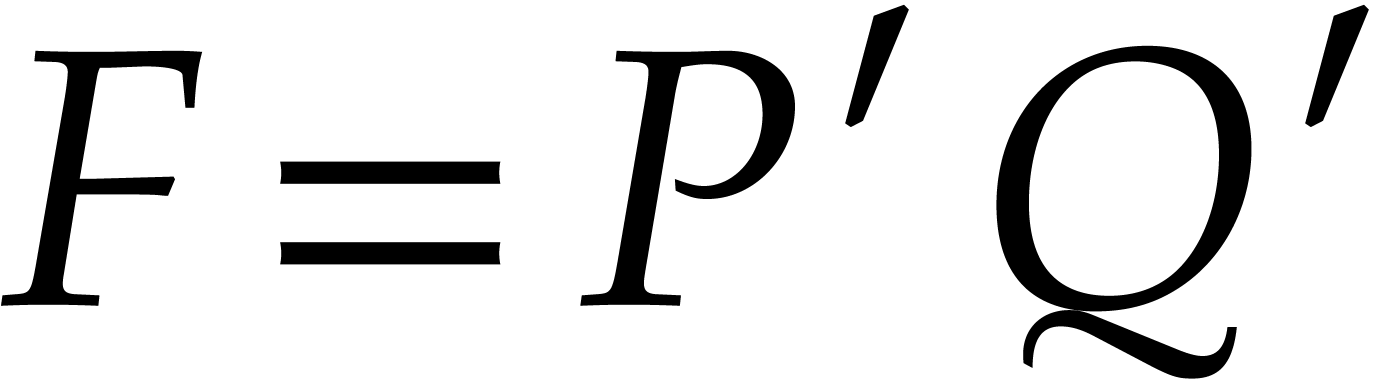 to
to
 and the edge from
and the edge from  to
to
 , which correspond to the
weights
, which correspond to the
weights 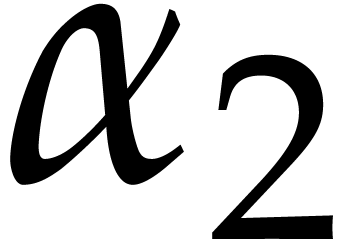 and
and  respectively. The generalized algorithm starts with the recursive
factorizations of
respectively. The generalized algorithm starts with the recursive
factorizations of 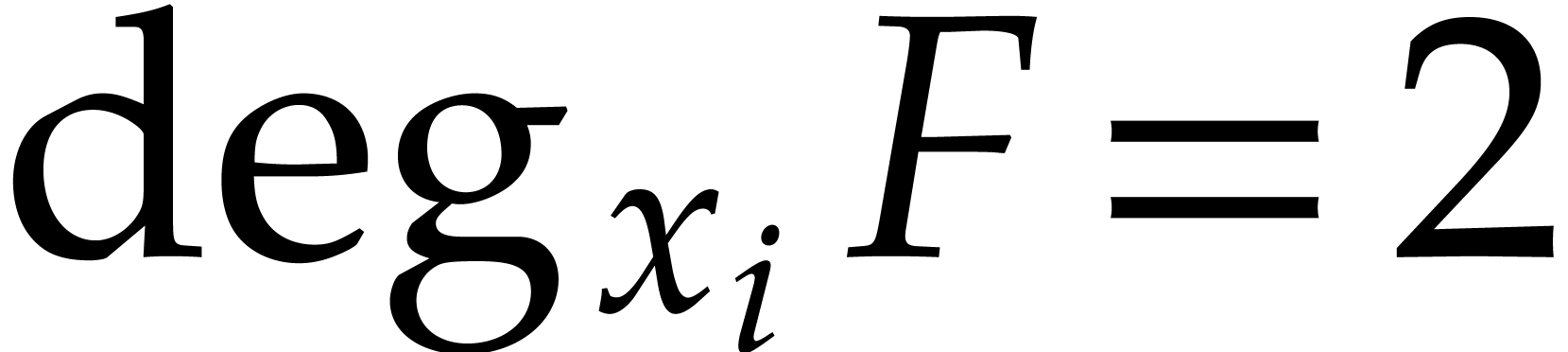 and
and 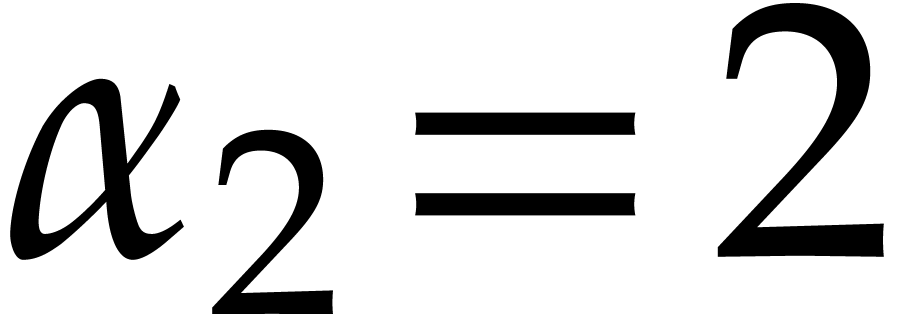 , which yields
, which yields

However, these factorizations do not tell us from which factors of  they originate: the factorization of
they originate: the factorization of  could have been of the form
could have been of the form  ,
with
,
with  and
and  .
In order to obtain the correct matches, the next idea is to consider the
bivariate factorization of
.
In order to obtain the correct matches, the next idea is to consider the
bivariate factorization of  for some sufficiently
generic values of
for some sufficiently
generic values of  and
and 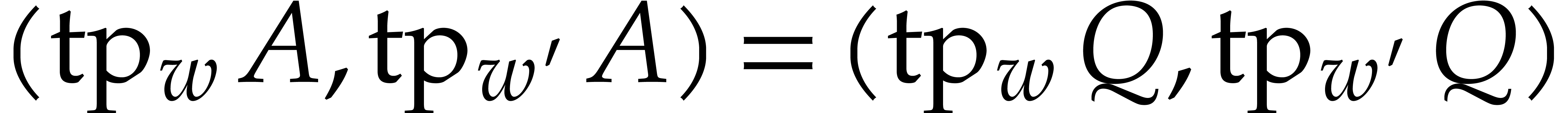 . For instance, for
. For instance, for  and
and
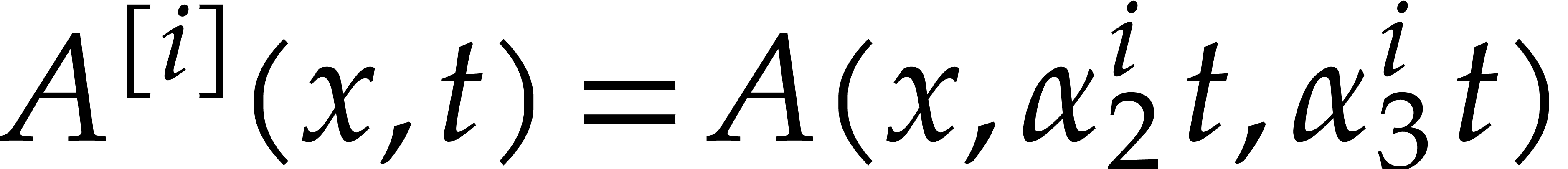 , we obtain
, we obtain
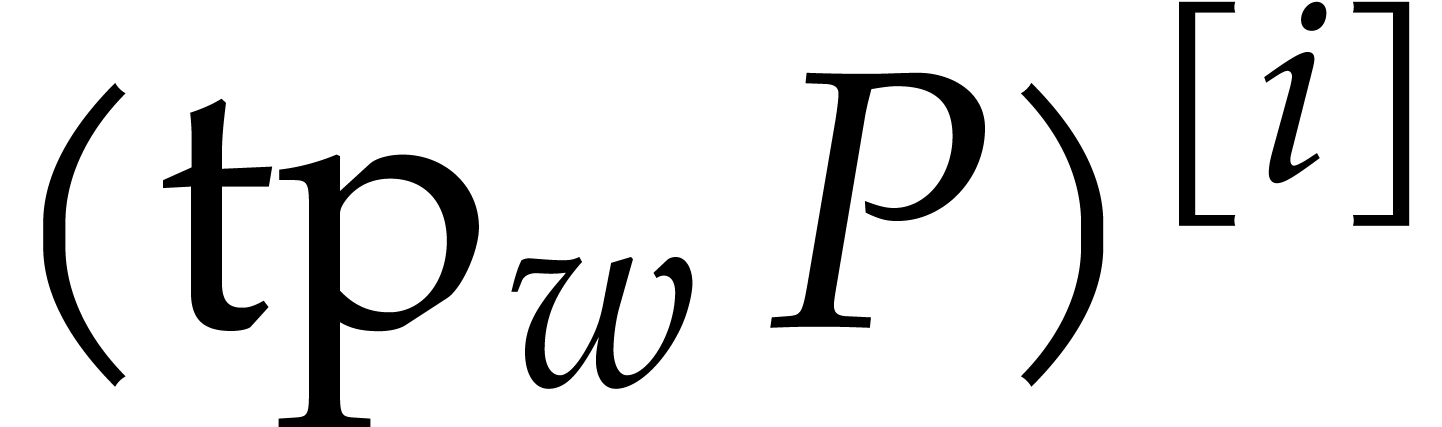
From these computations, we deduce that the factor  of
of 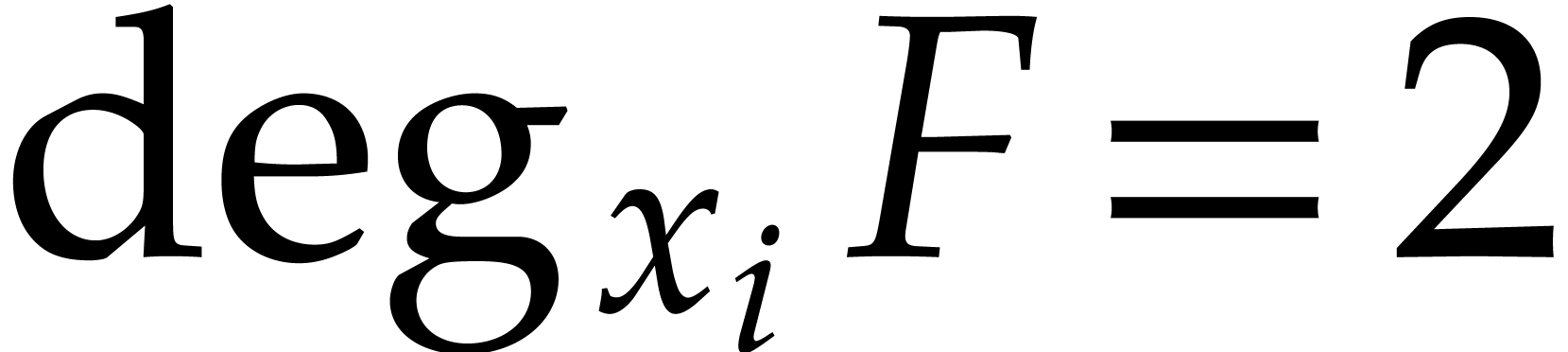 comes from the same factor of
comes from the same factor of  as the factor
as the factor  of
of  . We say that we have managed to match
the factors
. We say that we have managed to match
the factors  and
and  of the
different slopes. In other words, if
of the
different slopes. In other words, if 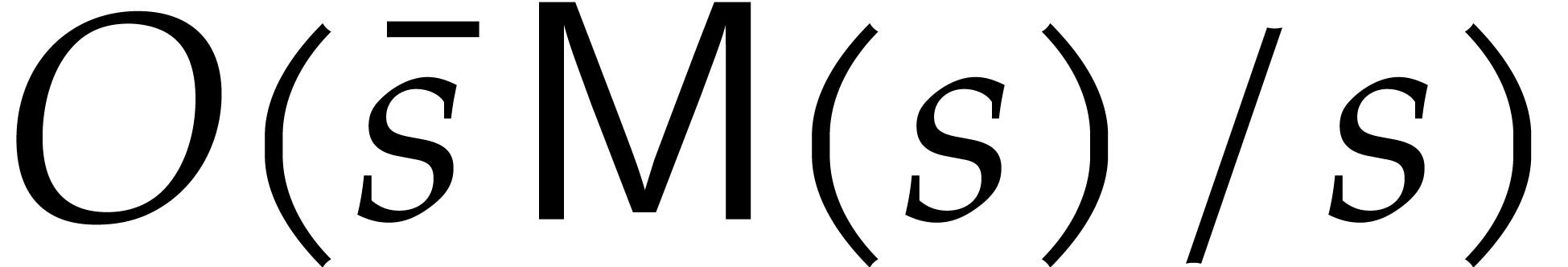 is a
non-trivial factor of
is a
non-trivial factor of  , then,
up to constant scaling, we now know that either
, then,
up to constant scaling, we now know that either 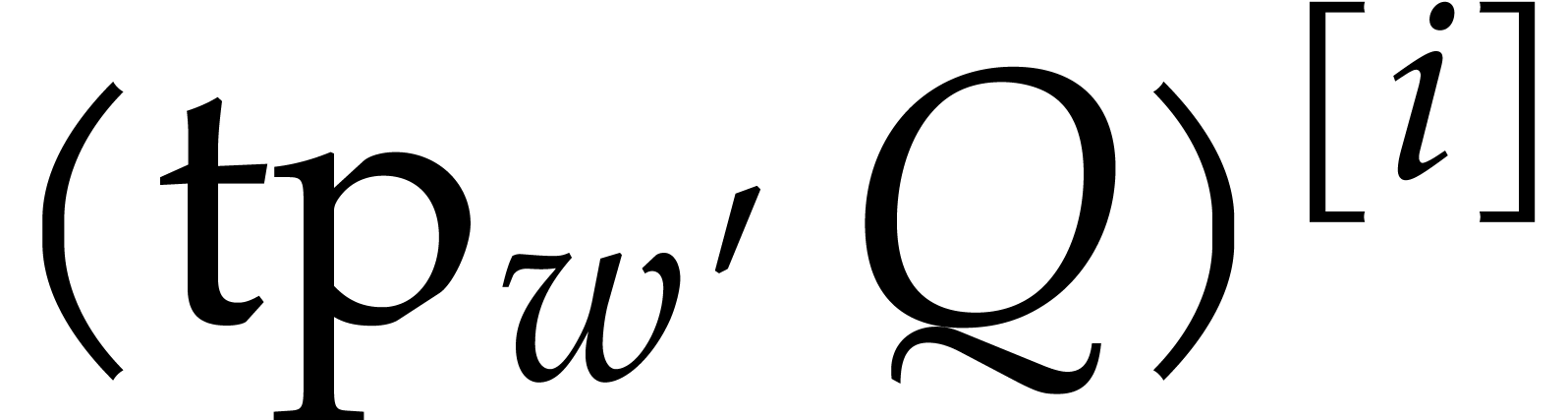 or
or 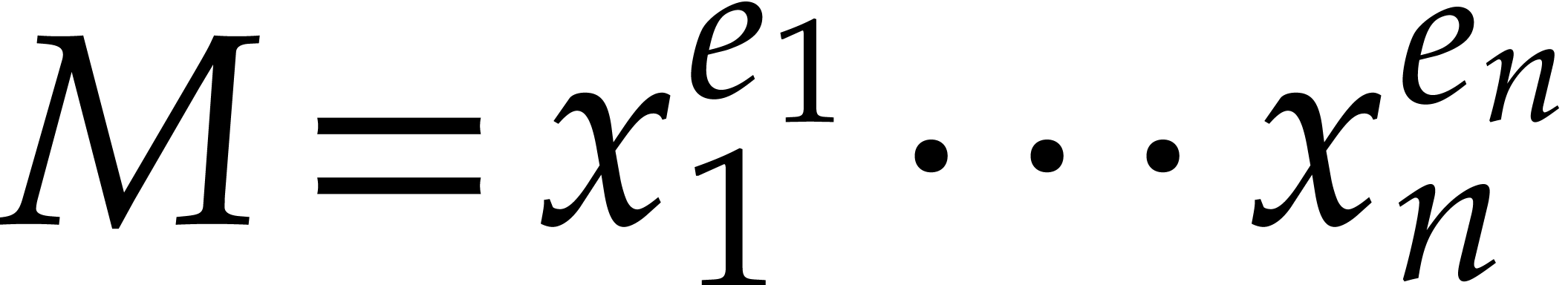 .
.
For any  and
and  ,
let
,
let  . Having completed the
above matching, we may now use the lifting algorithm from Section 7.4 to deduce
. Having completed the
above matching, we may now use the lifting algorithm from Section 7.4 to deduce  and
and  from
from  ,
, 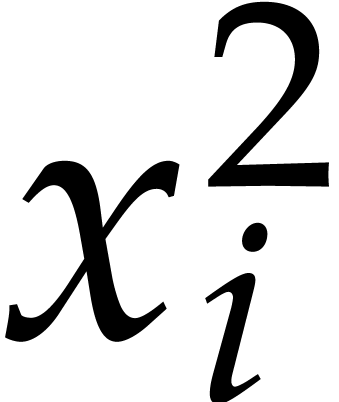 ,
,  ,
,  , and
, and 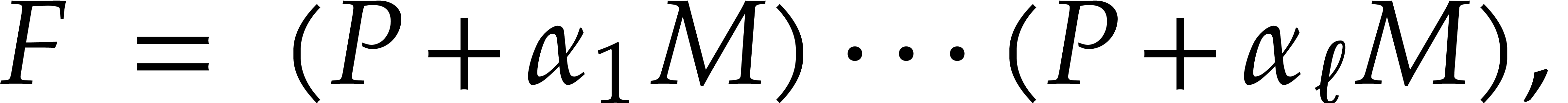 .
Doing this for sufficiently many
.
Doing this for sufficiently many  ,
we may finally recover
,
we may finally recover  and
and 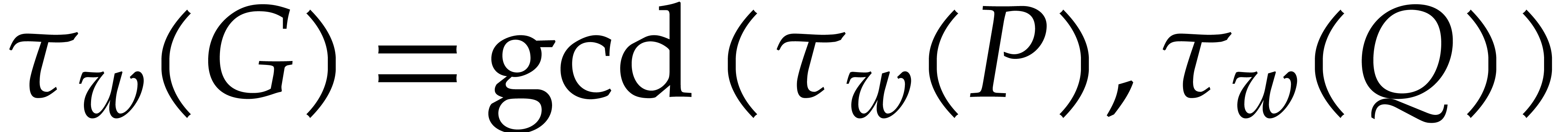 using sparse interpolation.
using sparse interpolation.
The approach from Section 7.5 is fairly general. However, as we will show now, it is possible to construct pathological examples that can still not be treated with this method.
Example 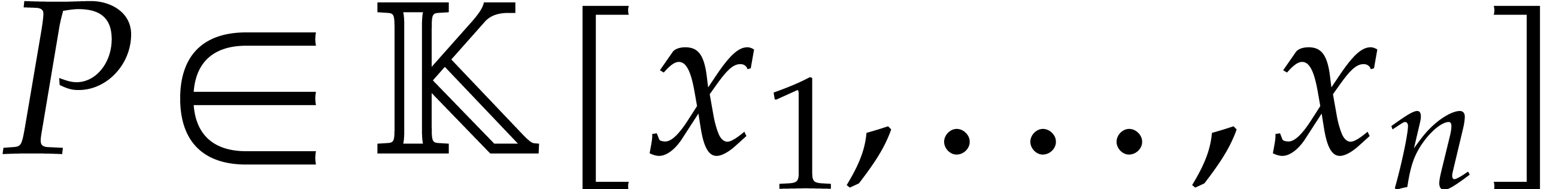 and a monomial
and a monomial  such that
such that  lies in the interior of the Newton
polytope
lies in the interior of the Newton
polytope  . For instance, we
may take
. For instance, we
may take

Now consider
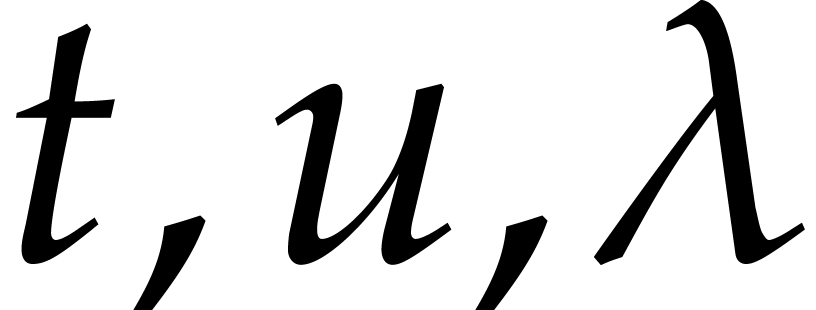
for pairwise distinct  . This
polynomial cannot be factored using the techniques from this section, so
far.
. This
polynomial cannot be factored using the techniques from this section, so
far.
In fact, it is not so much the factorization of the bivariate 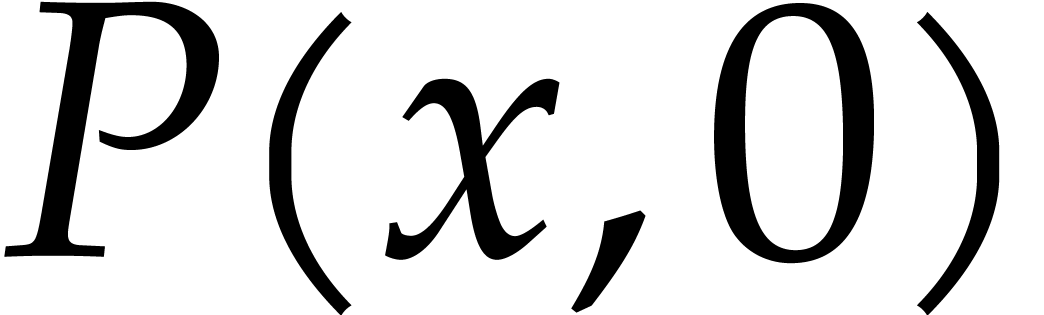 polynomials that is a problem: instead of Hensel lifting,
we may very well rely on Theorem 4.7 (this only increases
the exponent in
polynomials that is a problem: instead of Hensel lifting,
we may very well rely on Theorem 4.7 (this only increases
the exponent in  in Theorems 7.1 and
7.2, which is subdominant anyway if
in Theorems 7.1 and
7.2, which is subdominant anyway if  ). The true problem is matching corresponding
factors of
). The true problem is matching corresponding
factors of 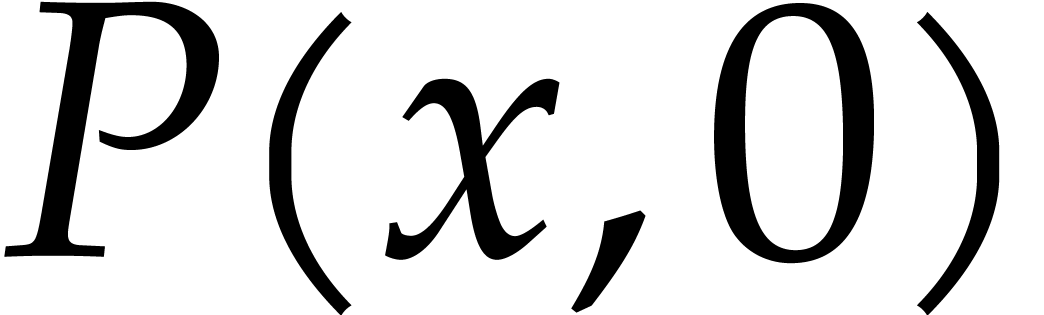 for different
for different  , especially in the most difficult cases like
Example 7.5. We conclude this section with an approach that
completely solves this problem, modulo a polynomial overhead in
, especially in the most difficult cases like
Example 7.5. We conclude this section with an approach that
completely solves this problem, modulo a polynomial overhead in  .
.
Let  ,
, 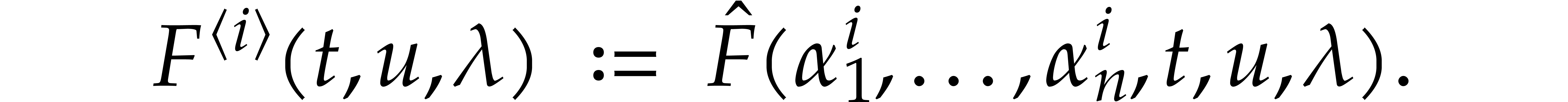 ,
, 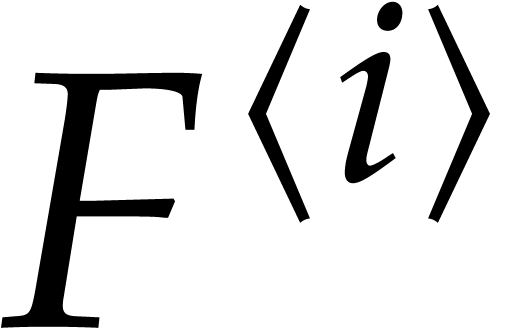 be random elements of
be random elements of  and let
and let  be new
indeterminates. We define
be new
indeterminates. We define
For 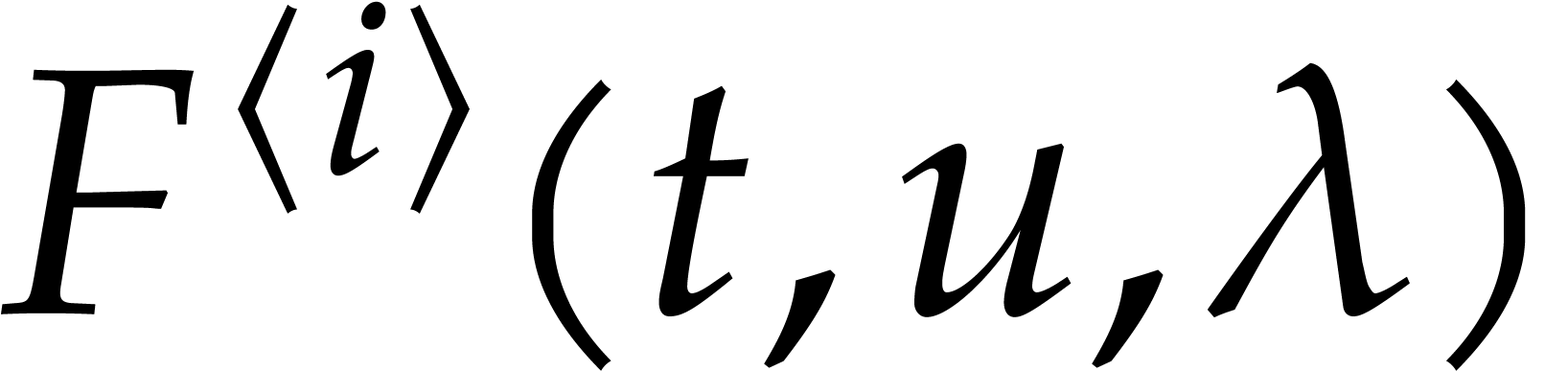 , we also define
, we also define
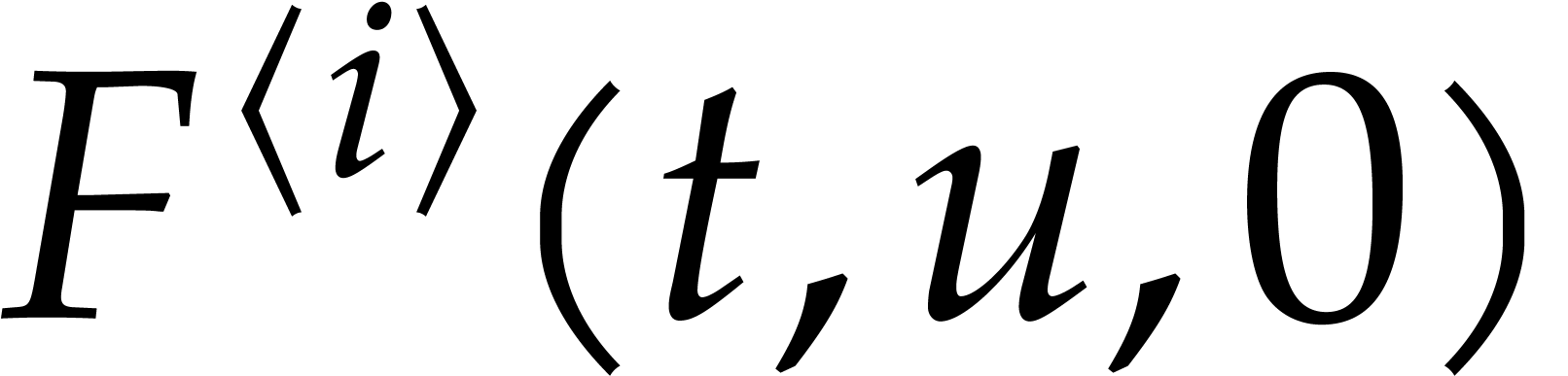
If  is irreducible, then
is irreducible, then 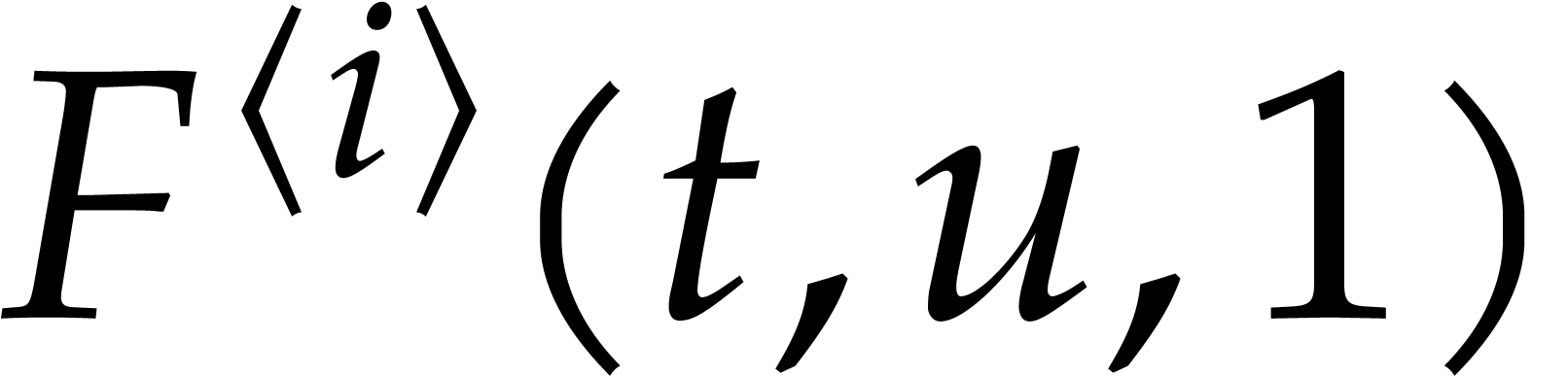 is irreducible with high probability, by Theorem 1.1, and
so are
is irreducible with high probability, by Theorem 1.1, and
so are 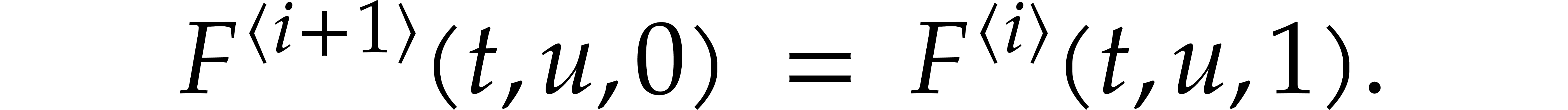 and
and  .
For general
.
For general  , this also means
that the factors of
, this also means
that the factors of 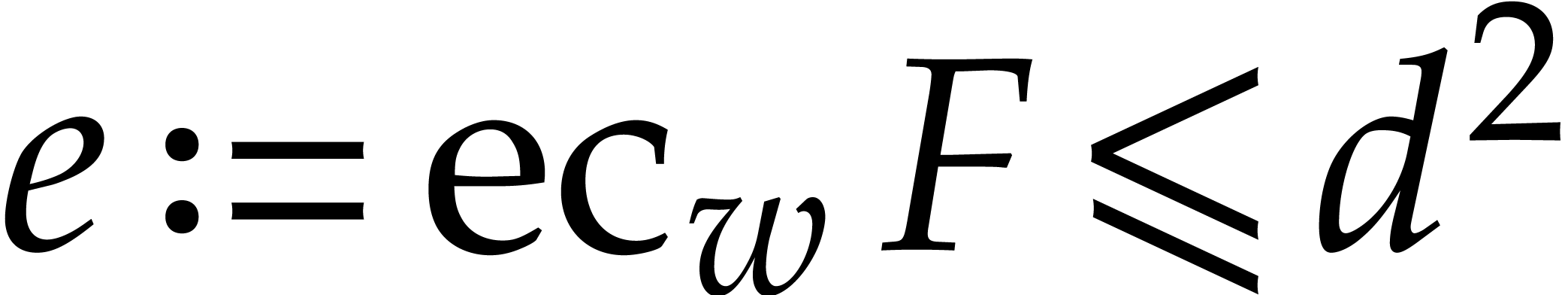 ,
, 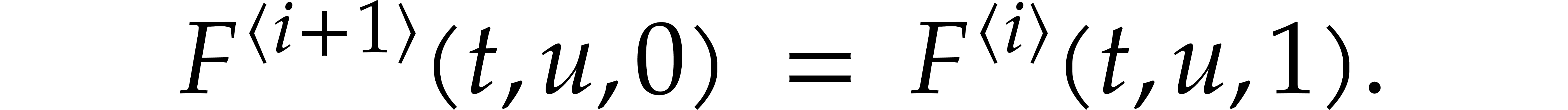 , and
, and  are
in effective one to one correspondence, with high probability. Moreover,
by construction,
are
in effective one to one correspondence, with high probability. Moreover,
by construction,

Using this relation, we may therefore match corresponding factors of
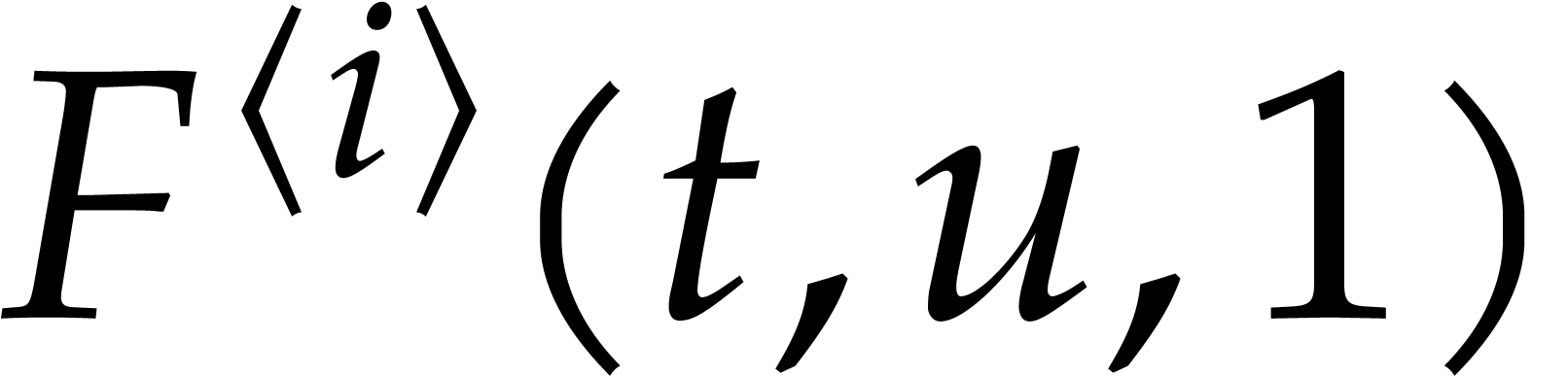 and
and  with high
probability.
with high
probability.
Having solved the matching problem, we still need to ensure that the
factorizations of the 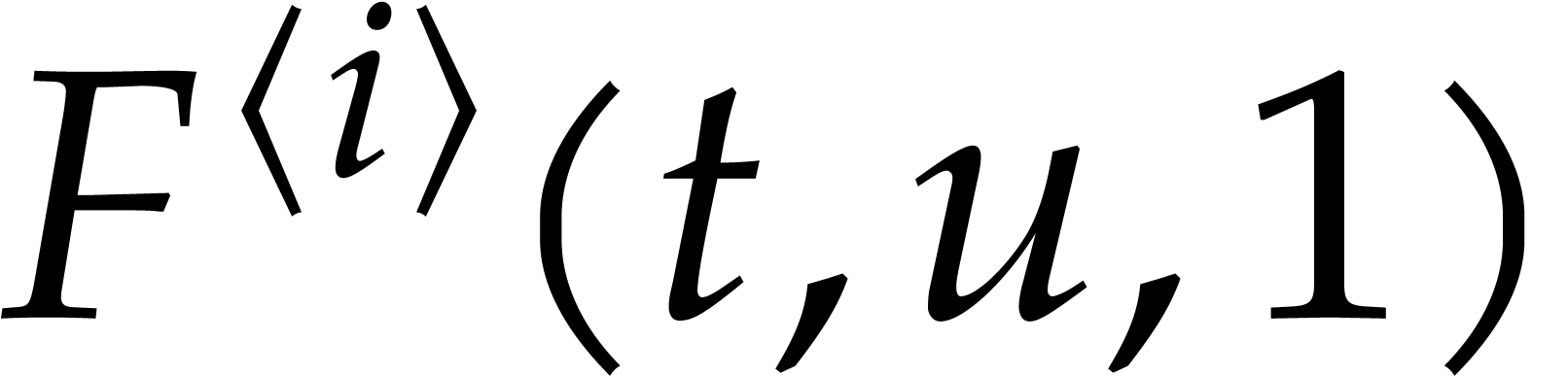 are normalized in a
suitable way such that we can recover the factors of
are normalized in a
suitable way such that we can recover the factors of  using sparse interpolation. For this, let
using sparse interpolation. For this, let  be a
regularizing weight for
be a
regularizing weight for  with
with  . Let
. Let 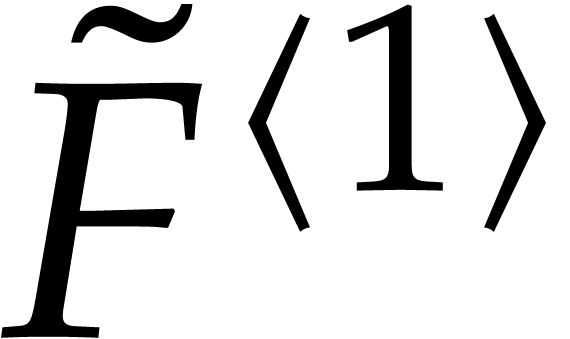 be yet another
indeterminate and consider
be yet another
indeterminate and consider

By construction, any factor  of
of 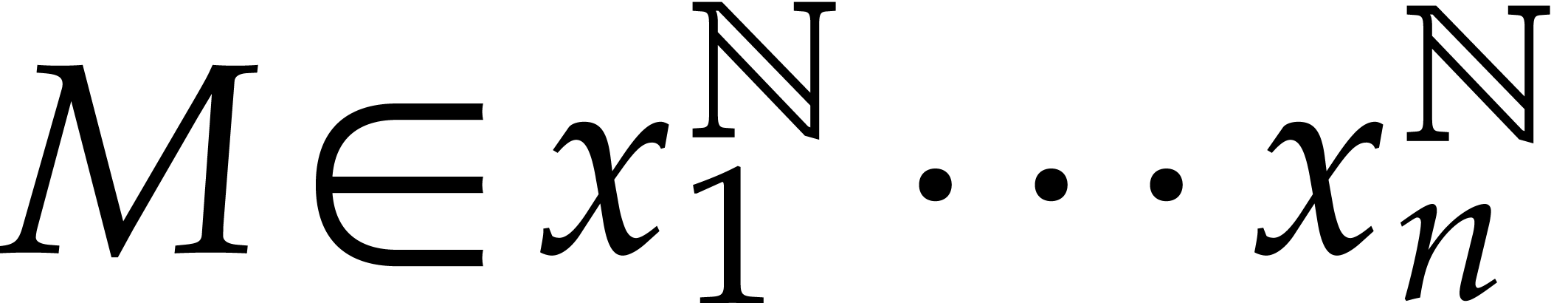 has leading coefficient
has leading coefficient  with respect to
with respect to 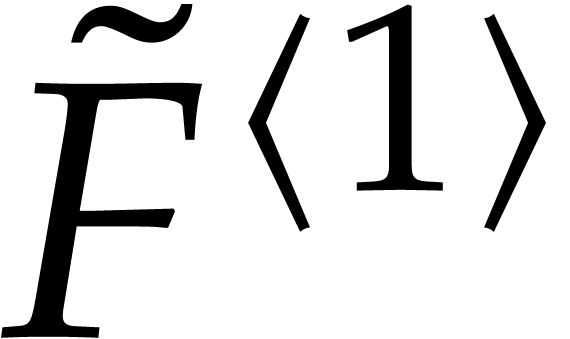 , for some
, for some 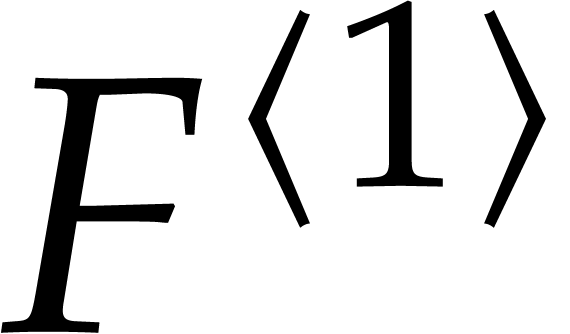 ,
, 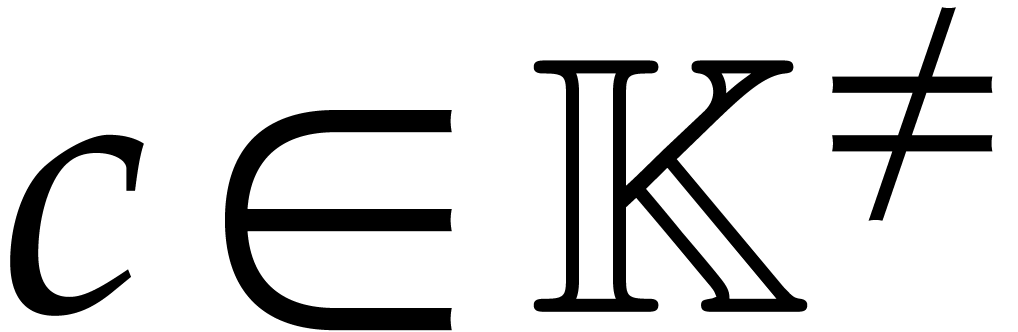 , and
some monomial
, and
some monomial 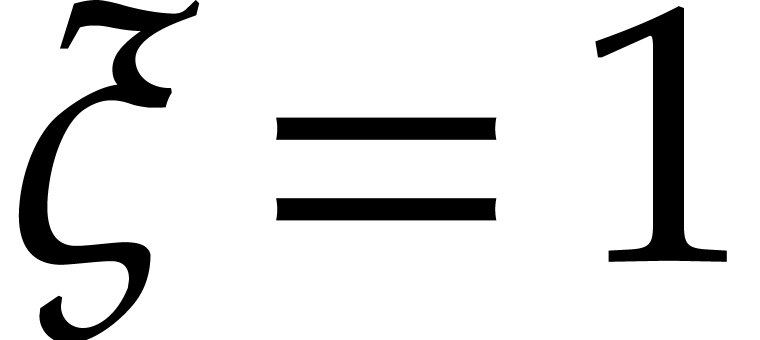 . Thus, any
such factor
. Thus, any
such factor  can be normalized by dividing out
the constant
can be normalized by dividing out
the constant 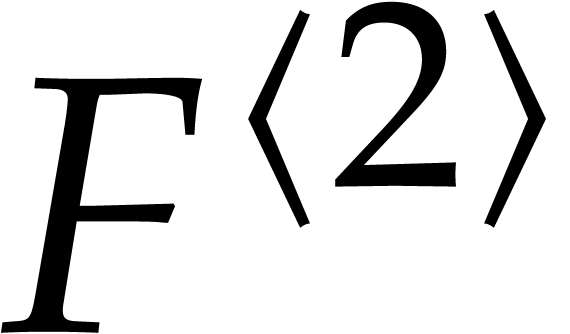 in
in 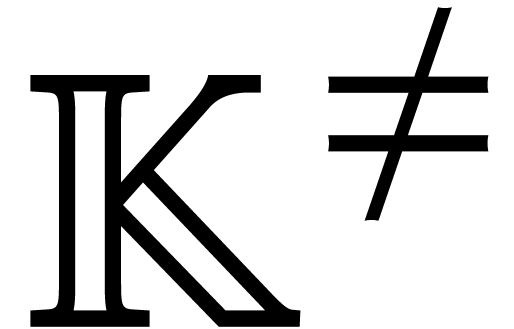 .
Now consider the unique factorization of
.
Now consider the unique factorization of 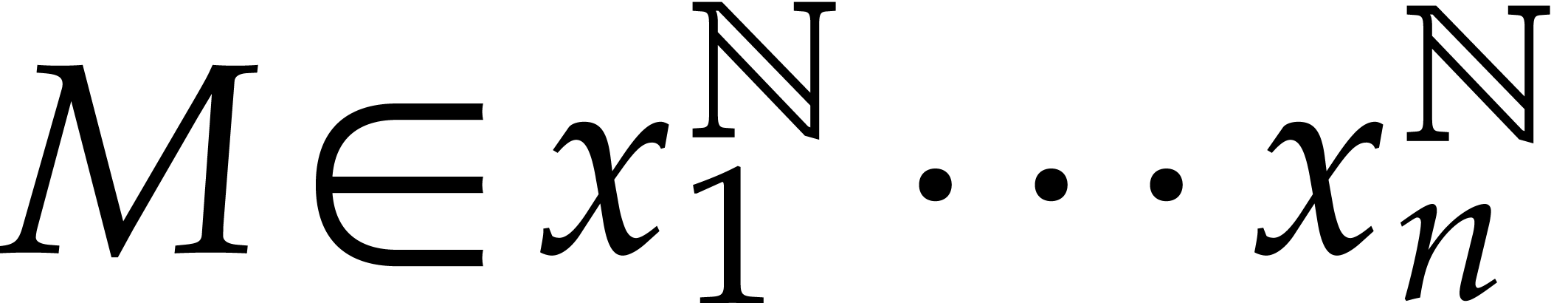 into a
product of normalized factors times a non-zero scalar in
into a
product of normalized factors times a non-zero scalar in  . This yields a factorization of
. This yields a factorization of  by setting
by setting  .
.
The factorization of  can be lifted to the
factorization of
can be lifted to the
factorization of  , which is,
in turn, lifted to the factorization of
, which is,
in turn, lifted to the factorization of  ,
and so on. An irreducible factorization of
,
and so on. An irreducible factorization of  is
recovered via interpolation from the factorizations of
is
recovered via interpolation from the factorizations of 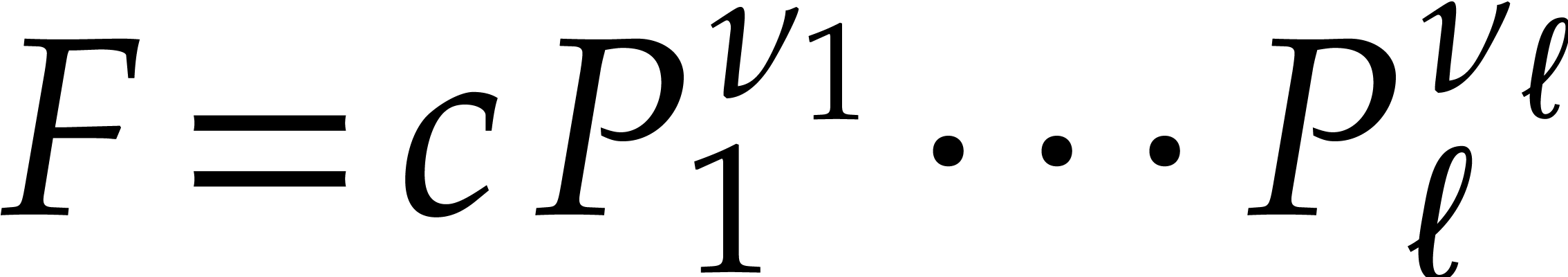 for sufficiently large
for sufficiently large 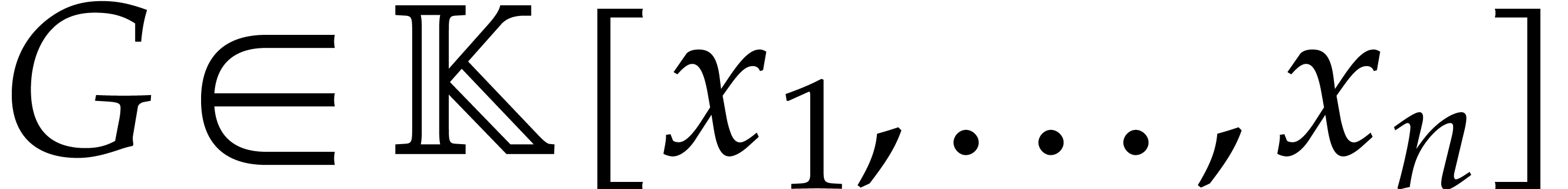 .
Finally, to obtain a factorization of
.
Finally, to obtain a factorization of  from a
factorization of
from a
factorization of  , we can set
, we can set
 , and apply the map
, and apply the map  .
.
This leads to the following algorithm:
Algorithm
Output: an irreducible factorization  of
of 
Compute 
Let  be a regularizing weight for
be a regularizing weight for 
Compute an irreducible factorization  ,
normalized as above
,
normalized as above
For 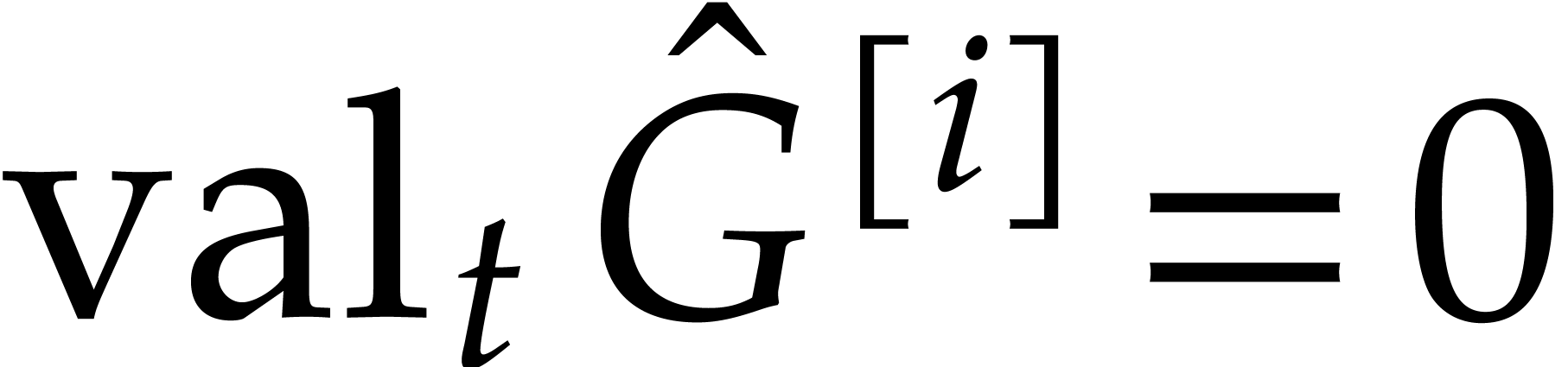 do
do
Compute 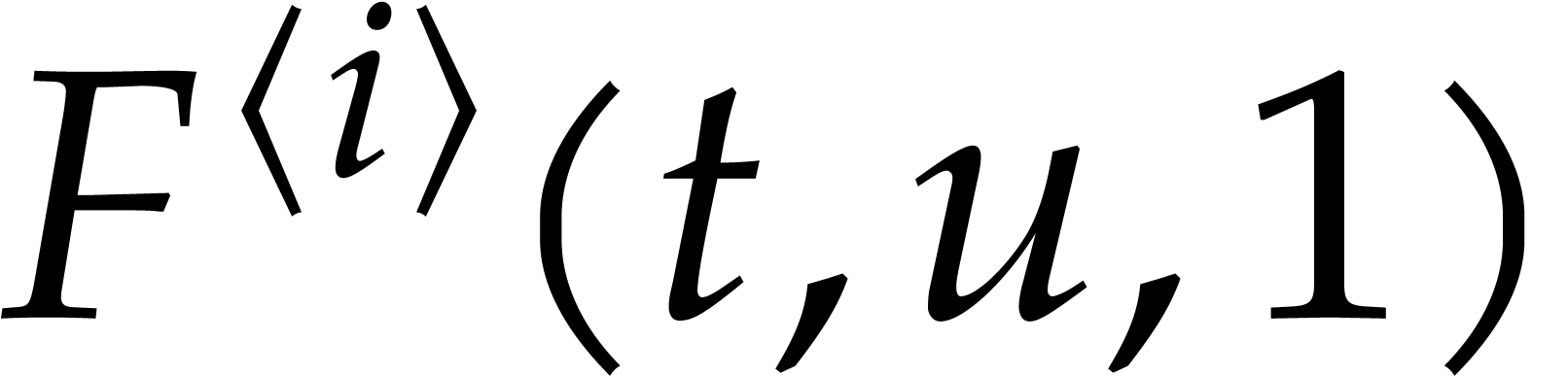 for
for 
For  do
do
Hensel lift 
into an irreducible factorization 
Deduce  from
from  via root
extraction
via root
extraction
Try to determine  from
from  (
(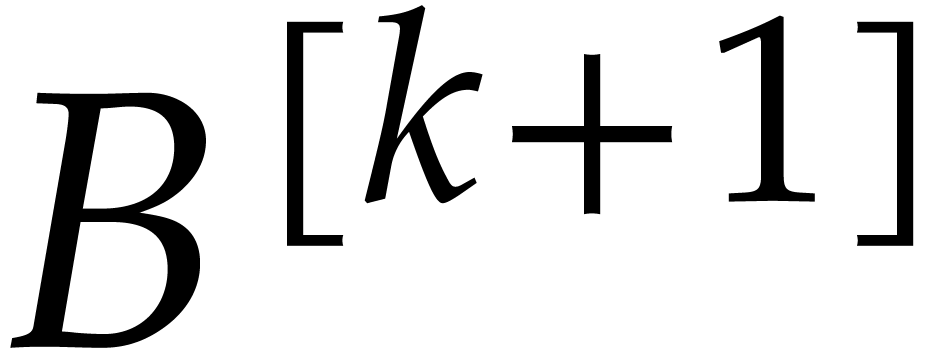 ) using sparse
interpolation
) using sparse
interpolation
If successful, then set  ,
,
 and return
and return 
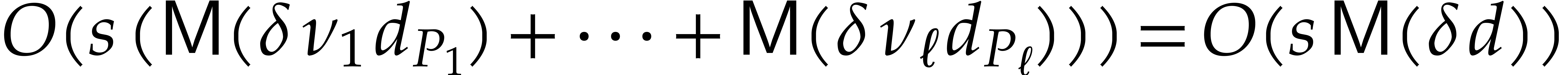 ,
, 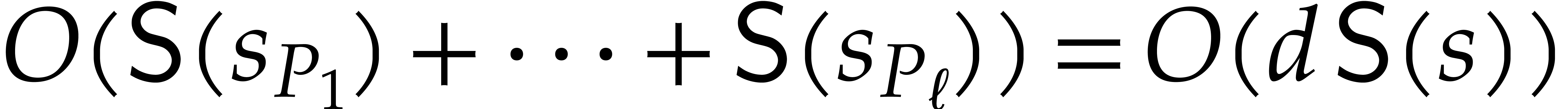 ,
,  ,
and
,
and  . Assume that
. Assume that 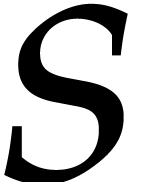 or
or 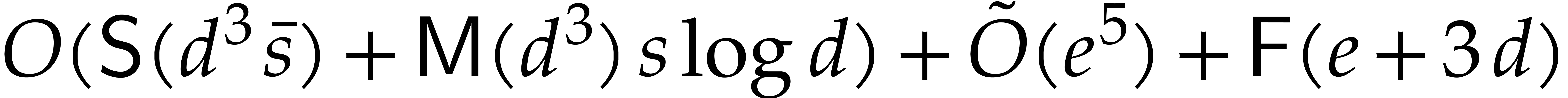 . Then
Algorithm 7.3 runs in time
. Then
Algorithm 7.3 runs in time
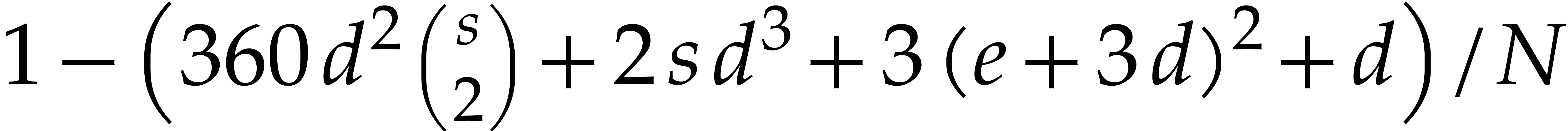
and succeeds with probability at least  .
.
Proof. We factor  as a
dense polynomial in four variables of degree
as a
dense polynomial in four variables of degree  (after division by a suitable power of
(after division by a suitable power of 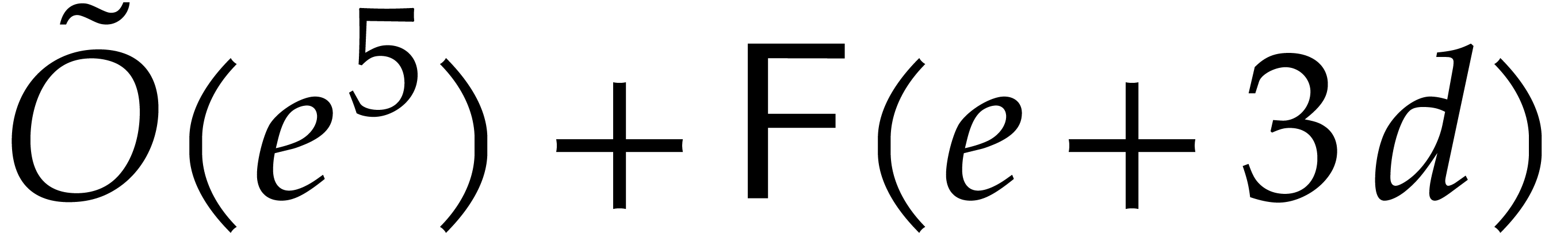 )
using the algorithm from [72, Proposition 5]. This requires
)
using the algorithm from [72, Proposition 5]. This requires
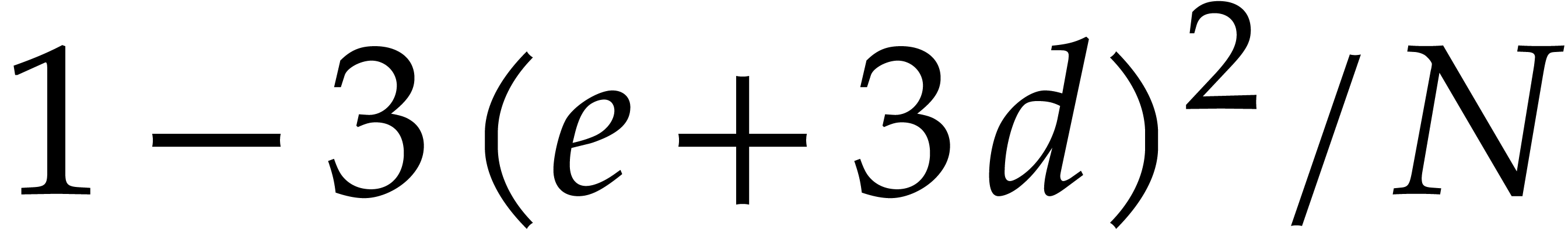 operations in
operations in  and the
probability of success is at least
and the
probability of success is at least 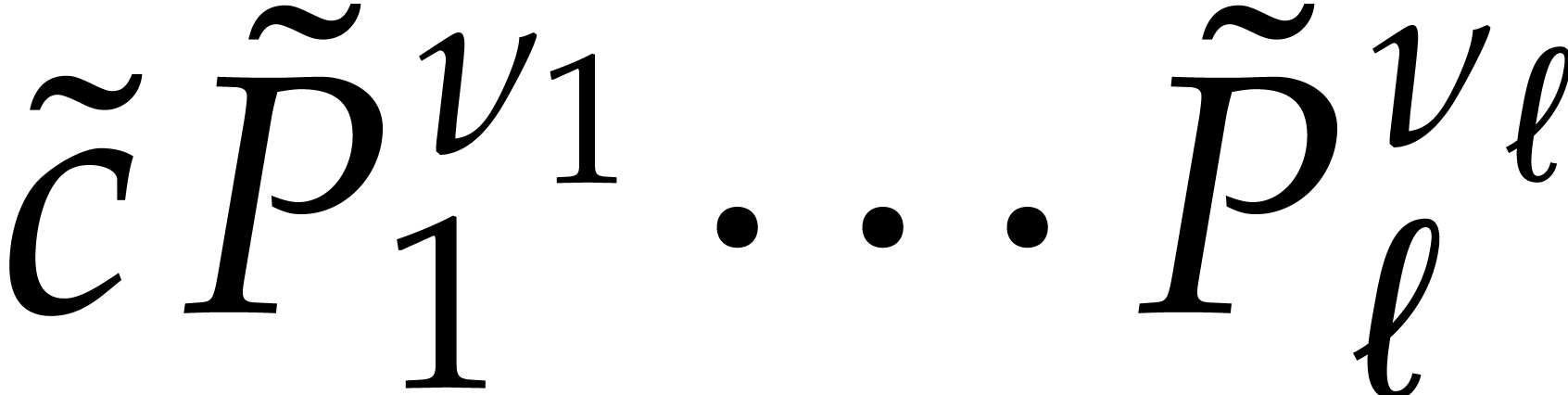 .
.
Let  be an irreducible factorization of
be an irreducible factorization of  . By our assumption on the
characteristic, the factors
. By our assumption on the
characteristic, the factors  are all separable.
We will apply [75, Théorème 6.9] for each of
the points in our geometric progression. By using Corollary 2.2
instead of the Schwartz-Zippel lemma in the proof of [75,
Théorème 6.9], we deduce that the specializations
are all separable.
We will apply [75, Théorème 6.9] for each of
the points in our geometric progression. By using Corollary 2.2
instead of the Schwartz-Zippel lemma in the proof of [75,
Théorème 6.9], we deduce that the specializations  ,
,  ,
and thus
,
and thus  are irreducible for
are irreducible for 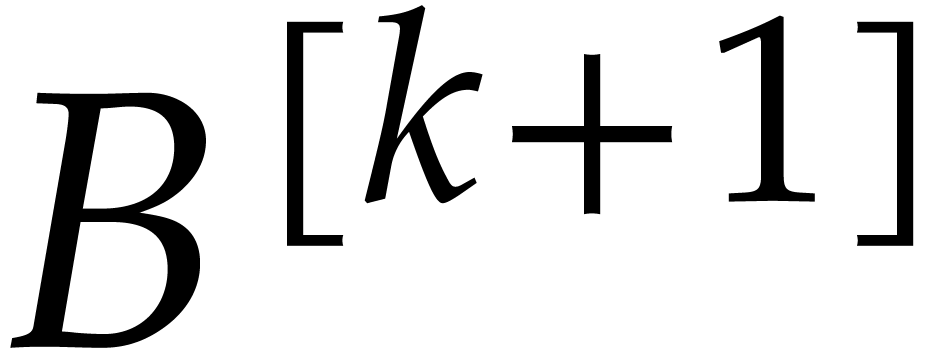 and
and  , with probability at
least
, with probability at
least 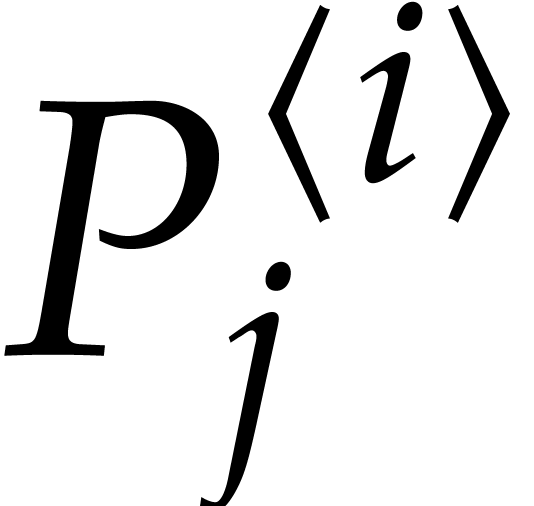 . Under this
assumption, and modulo reordering the factors, the computed
. Under this
assumption, and modulo reordering the factors, the computed 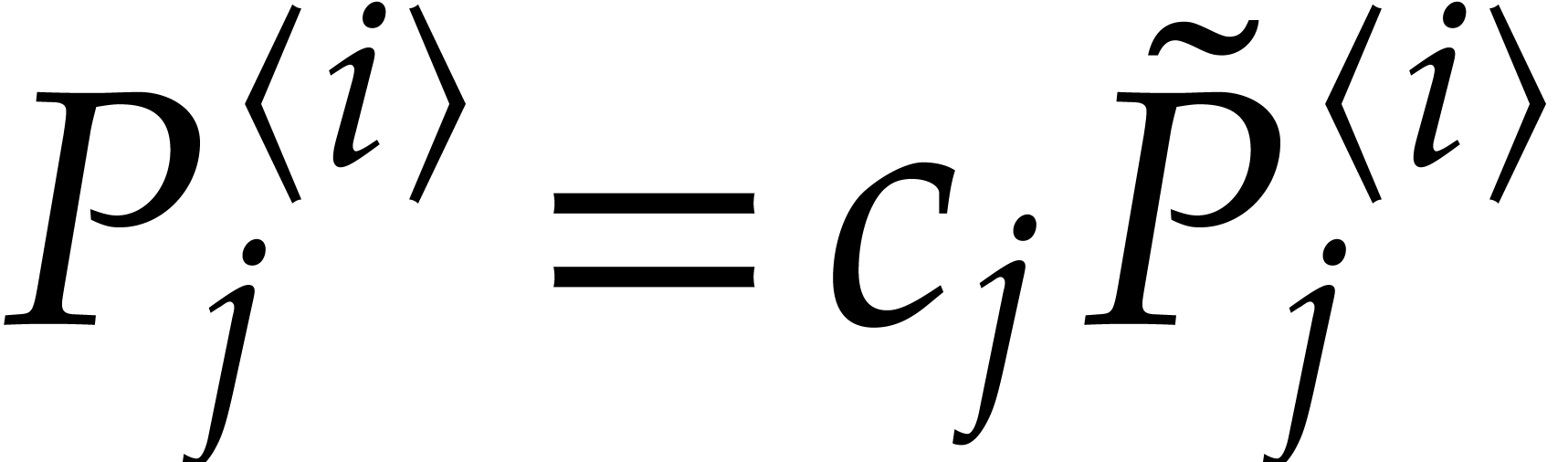 are of the form
are of the form  for suitable
scaling factors
for suitable
scaling factors  that do not depend on
that do not depend on  . The check whether the computed
factorization of
. The check whether the computed
factorization of  is correct reports a false
positive with probability at most
is correct reports a false
positive with probability at most  ,
by Remark 2.5 or the Schwarz-Zippel lemma.
,
by Remark 2.5 or the Schwarz-Zippel lemma.
Let us now analyze the complexity. We first observe that  , since
, since  when
when  consists of a single monomial of total degree
consists of a single monomial of total degree 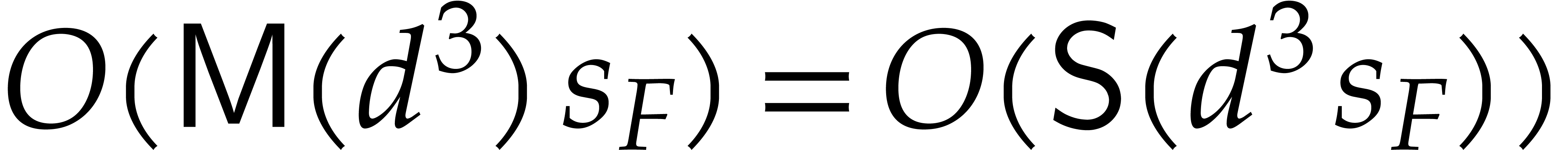 . Using [2, Theorem 5] in a
recursive manner, we may compute
. Using [2, Theorem 5] in a
recursive manner, we may compute  from
from  in time
in time 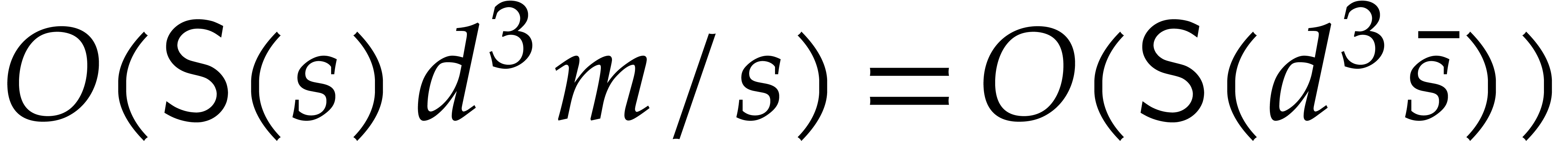 . We
saw above that the factorization of
. We
saw above that the factorization of  requires at
most
requires at
most 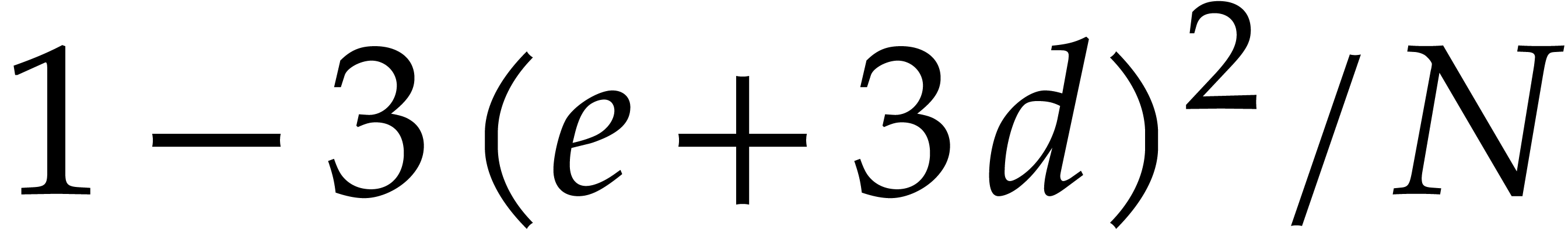 operations in
operations in  .
The computation of the specializations
.
The computation of the specializations 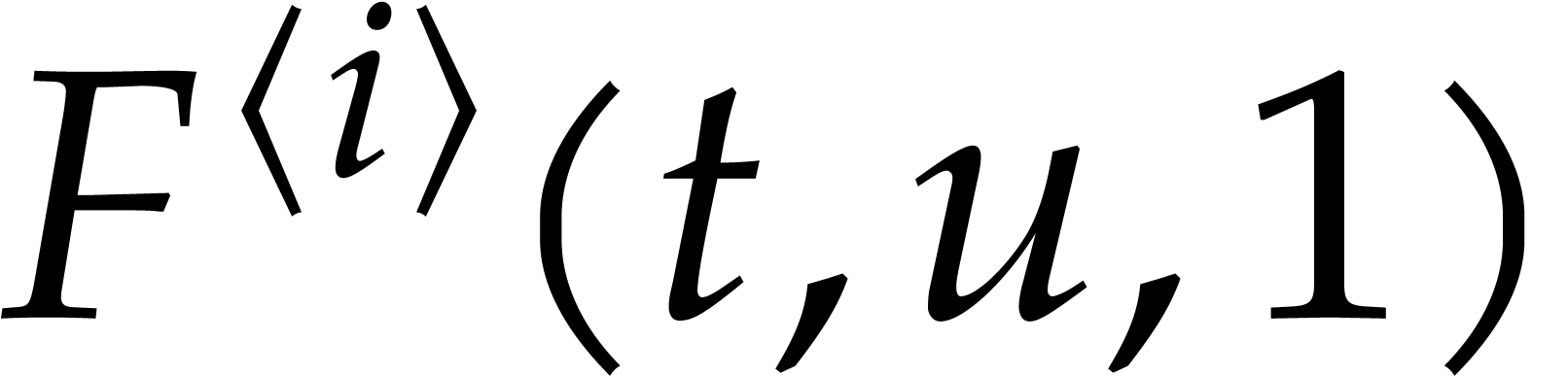 for
for 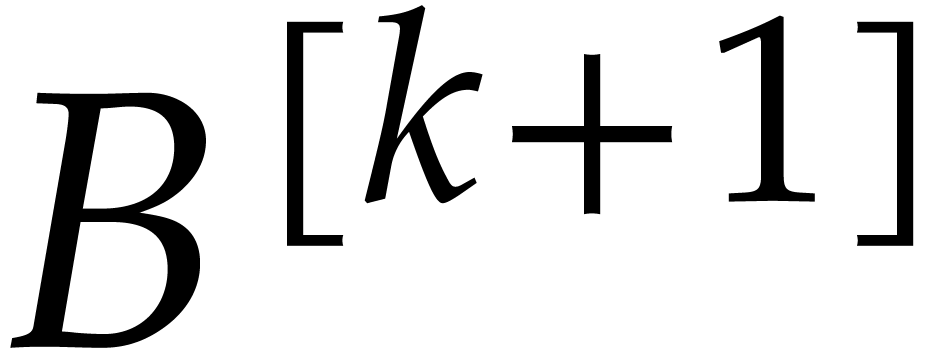 requires
requires  further operations.
The Hensel lifting of the
further operations.
The Hensel lifting of the 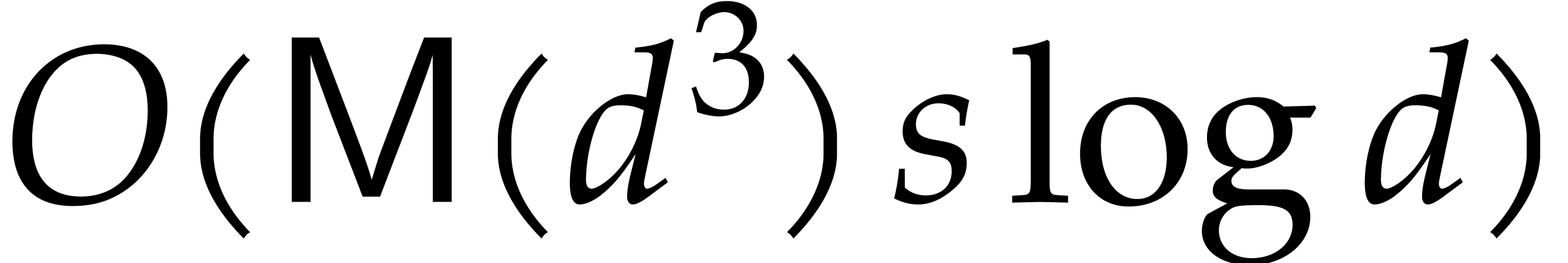 can be done in time
can be done in time
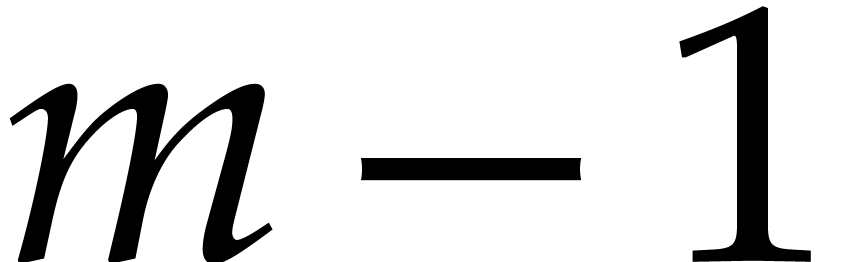 using Proposition 4.4 and
evaluation-interpolation in the remaining variable. The
using Proposition 4.4 and
evaluation-interpolation in the remaining variable. The  Hensel lifts succeed with probability at least
Hensel lifts succeed with probability at least 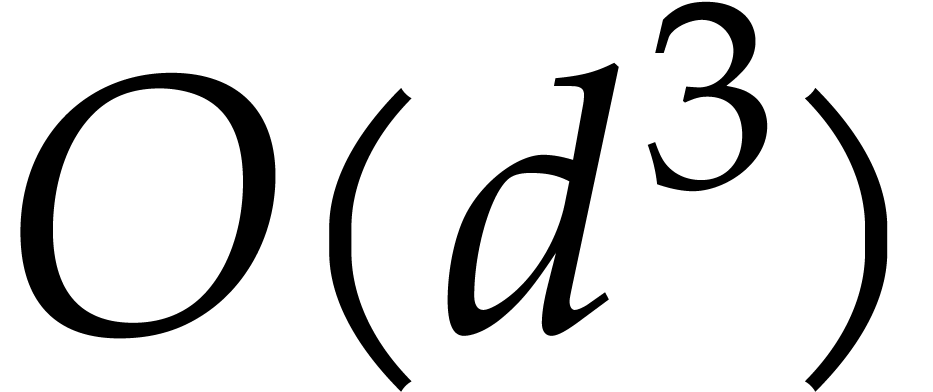 . Adding up, we obtain the desired complexity bound,
as well as the claimed bound for the probability of success.
. Adding up, we obtain the desired complexity bound,
as well as the claimed bound for the probability of success.
Remark  overhead, Algorithm 7.3 is mainly
of theoretical interest. It is plausible that (7.2) can be
replaced by a less, but still sufficiently, generic formula. This would
reduce the overhead in
overhead, Algorithm 7.3 is mainly
of theoretical interest. It is plausible that (7.2) can be
replaced by a less, but still sufficiently, generic formula. This would
reduce the overhead in  . In
practice, one may use Algorithm 7.3 as a last resort, in
the unlikely case that all other strategies from Sections 6
and 7 fail.
. In
practice, one may use Algorithm 7.3 as a last resort, in
the unlikely case that all other strategies from Sections 6
and 7 fail.
F. Abu Salem, S. Gao, and A. G. B. Lauder. Factoring polynomials via polytopes. In Proc. ISSAC '04, pages 4–11. New York, NY, USA, 2004. ACM.
A. V. Aho, K. Steiglitz, and J. D. Ullman. Evaluating polynomials on a fixed set of points. SIAM Journ. of Comp., 4:533–539, 1975.
M. Alberich-Carramiñana, J. Guàrdia, E. Nart, A. Poteaux, J. Roé, and M. Weimann. Polynomial factorization over henselian fields. Technical Report, arXiv, 2022. https://doi.org/10.48550/arXiv.2207.02139.
K. Belabas, M. van Hoeij, J. Klüners, and A. Steel. Factoring polynomials over global fields. J. Théor. Nombres Bordeaux, 21(1):15–39, 2009.
M. Ben-Or and P. Tiwari. A deterministic algorithm for sparse multivariate polynomial interpolation. In Proc. ACM STOC '88, pages 301–309. New York, NY, USA, 1988.
E. R. Berlekamp. Factoring polynomials over finite fields. Bell System Tech. J., 46:1853–1859, 1967.
E. R. Berlekamp. Factoring polynomials over large finite fields. Math. Comp., 24:713–735, 1970.
L. Bernardin. Factorization of multivariate polynomials over finite fields. PhD thesis, ETH, Zürich, 1999.
D. J. Bernstein. Scaled remainder trees. Available from https://cr.yp.to/arith/scaledmod-20040820.pdf, 2004.
E. Bertini. Introduzione alla geometria proiettiva degli iperspazi con appendice sulle curve algebriche e loro singolarità. Giuseppe Principato, 1923.
A. Borodin and R. T. Moenck. Fast modular transforms. Journal of Computer and System Sciences, 8:366–386, 1974.
A. Bostan, G. Lecerf, and É. Schost. Tellegen's principle into practice. In Proc. ISSAC '03, pages 37–44. Philadelphia, USA, August 2003.
A. Bostan and É. Schost. Polynomial evaluation and interpolation on special sets of points. J. of Complexity, 21(4):420–446, August 2005. Festschrift for the 70th Birthday of Arnold Schönhage.
P. Bürgisser, M. Clausen, and M. A. Shokrollahi. Algebraic complexity theory. Springer-Verlag, Berlin, 1997.
D. G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Informatica, 28:693–701, 1991.
D. G. Cantor and H. Zassenhaus. A new algorithm for factoring polynomials over finite fields. Math. Comp., 36(154):587–592, 1981.
T. Chen and M. Monagan. The complexity and parallel implementation of two sparse multivariate Hensel lifting algorithms for polynomial factorization. In Proc. CASC 2020, pages 150–169. Springer-Verlag, 2020.
T. Chen and M. Monagan. Factoring multivariate polynomials represented by black boxes: a maple + C implementation. JSC, 16, 2022.
G. Chèze and G. Lecerf. Lifting and recombination techniques for absolute factorization. J. of Complexity, 23(3):380–420, 2007.
A. L. Chistov. Efficient factoring polynomials over local fields and its applications. In Proceedings of the International Congress of Mathematicians, Kyoto, Japan, 1990, volume 1, pages 1509–1519. Springer-Verlag, 1991.
G. E. Collins. Subresultants and reduced polynomial remainder sequences. JACM, 14(1):128–142, 1967.
A. Cuyt and W.-S. Lee. Sparse interpolation of multivariate rational functions. TCS, 412:1445–1456, 2011.
W. Decker, G. Lecerf, and G. Pfister. Absolute
factorization for characteristic 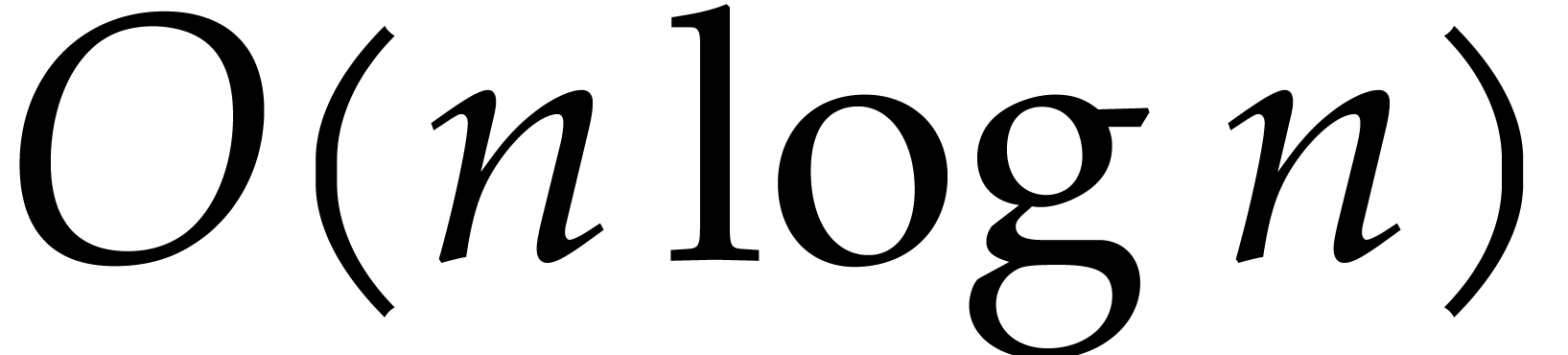 .
Singular library absfact.lib, 2005.
.
Singular library absfact.lib, 2005.
J. Della Dora, C. Dicrescenzo, and D. Duval. A new method for computing in algebraic number fields. In Eurocal'85 (2), volume 174 of Lect. Notes in Comp. Science, pages 321–326. Springer, 1985.
M. Filaseta, A. Granville, and A. Schinzel. Irreducibility and greatest common divisor algorithms for sparse polynomials. London Math. Soc. Lect. Note Series, 352:155–176, 2008.
D. Ford. On the computation of the maximal order in a Dedekind domain. PhD thesis, Ohio State University, 1978.
A. Fröhlich and J. C. Shepherdson. On the factorisation of polynomials in a finite number of steps. Math. Z., 62:331–334, 1955.
A. Fröhlich and J. C. Shepherdson. Effective procedures in field theory. Philos. Trans. Soc. London. Ser. A., 248:407–432, 1956.
S. Gao. Factoring multivariate polynomials via partial differential equations. Math. Comp., 72(242):801–822, 2003.
J. von zur Gathen. Irreducibility of multivariate polynomials. J. Comp. System Sci., 31:225–264, 1985.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, New York, NY, USA, 3rd edition, 2013.
J. von zur Gathen and E. Kaltofen. Factoring sparse multivariate polynomials. J. Comput. System Sci., 31(2):265–287, 1983. Proc. FOCS.
J. von zur Gathen and E. Kaltofen. Factorization of multivariate polynomials over finite fields. Math. Comp., 45(171):251–261, 1985.
P. Gianni and B. Trager. Square-free algorithms in positive characteristic. AAECC, 7(1):1–14, 1996.
M. Giesbrecht and D. S. Roche. Diversification improves interpolation. In Proc. ISSAC '11, pages 123–130. New York, NY, USA, 2011. ACM.
P. Giorgi, B. Grenet, A. Perret Du Cray, and D. S. Roche. Sparse polynomial interpolation and division in soft-linear time. In Proc. ISSAC'22, pages 459–468. Lille, France, 2022. ACM Press.
B. Grenet. Bounded-degree factors of lacunary multivariate polynomials. JCS, 75:171–192, 2016.
B. Grenet, J. van der Hoeven, and G. Lecerf. Randomized root finding over finite fields using tangent Graeffe transforms. In Proc. ISSAC '15, pages 197–204. New York, NY, USA, 2015. ACM.
J. Guàrdia, J. Montes, and E. Nart. Newton polygons of higher order in algebraic number theory. Trans. Amer. Math. Soc., 364(1):361–416, 2012.
Jr. H. W. Lenstra. Finding small degree factors of lacunary polynomials. In In Number theory in progress, volume 1, pages 267–276. De Gruyter, Zakopane-Kościelisko, 1999.
D. Harvey and J. van der Hoeven. Polynomial
multiplication over finite fields in time 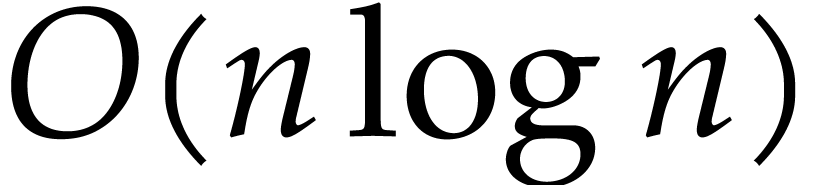 . Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02070816.
. Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02070816.
K. Hensel. Neue Grundlagen der Arithmetik. J. Reine Angew. Math., 127:51–84, 1904.
D. Hilbert. Über die Irreducibilität ganzer rationaler Functionen mit ganzzahligen Coefficienten. J. reine angew. Math., 110:104–129, 1892.
M. van Hoeij. Factoring polynomials and the knapsack problem. Journal of Number theory, 95(2):167–189, 2002.
J. van der Hoeven. Faster Chinese remaindering. Technical Report, HAL, 2016. https://hal.archives-ouvertes.fr/hal-01403810.
J. van der Hoeven. Probably faster multiplication of sparse polynomials. Technical Report, HAL, 2020. https://hal.archives-ouvertes.fr/hal-02473830.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
J. van der Hoeven and G. Lecerf. On the bit-complexity of sparse polynomial multiplication. JSC, 50:227–254, 2013.
J. van der Hoeven and G. Lecerf. Directed evaluation. J. of Complexity, 60, 2020. Article ID 101498.
J. van der Hoeven and G. Lecerf. Fast multivariate multi-point evaluation revisited. J. of Complexity, 56, 2020. Article ID 101405, 38 pages.
J. van der Hoeven and G. Lecerf. On sparse interpolation of rational functions and gcds. ACM SIGSAM Commun. Comput. Algebra, 55(1):1–12, 2021.
J. van der Hoeven and G. Lecerf. Sparse polynomial interpolation: faster strategies over finite fields. AAECC, 2024. https://doi.org/10.1007/s00200-024-00655-5.
J. van der Hoeven and G. Lecerf. Univariate polynomial factorization over large finite fields. AAECC, 35:121–149, 2024.
J. van der Hoeven and G. Lecerf. Fast interpolation of multivariate polynomials with sparse exponents. J. of Complexity, 87, 2025. Article ID 101922.
J. van der Hoeven and G. Lecerf. Plane curve germs and contact factorization. AAECC, 36:5–106, 2025.
J. Hu and M. B. Monagan. A fast parallel sparse polynomial GCD algorithm. In S. A. Abramov, E. V. Zima, and X.-S. Gao, editors, Proc. ISSAC '16, pages 271–278. ACM, 2016.
Q.-L. Huang. Sparse polynomial interpolation over fields with large or zero characteristic. In Proc. ISSAC '19, pages 219–226. ACM, 2019.
Q.-L. Huang and X.-S. Gao. Bit complexity of polynomial gcd on sparse representation. Preprint available from https://arxiv.org/abs/2207.13874, 2022.
M. Javadi and M. Monagan. A sparse modular gcd algorithm for polynomial gcd computation over algebraic function fields. In Proc. ISSAC '07, pages 187–194. 2007.
E. Kaltofen. A polynomial reduction from multivariate to bivariate integral polynomial factorization. In Proc. STOC '82, pages 261–266. ACM, 1982.
E. Kaltofen. Polynomial-time reductions from multivariate to bi- and univariate integral polynomial factorization. SIAM J. Comput., 14(2):469–489, 1985.
E. Kaltofen. Sparse Hensel lifting. In Proc. EUROCAL '85, pages 4–17. Berlin, Heidelberg, 1985. Springer.
E. Kaltofen. Factorization of polynomials given by straight-line programs. In S. Micali, editor, Randomness and Computation, volume 5 of Advances in Computing Research, pages 375–412. JAI Press Inc., Greenwhich, Connecticut, 1989.
E. Kaltofen. Effective noether irreducibility forms and applications. J. Computer and System Sciences, 50(2):274–295, 1995.
E. Kaltofen and G. Lecerf. Handbook of finite fields, chapter Factorization of multivariate polynomials, pages 383–392. Discrete Mathematics and its Applications. Chapman and Hall/CRC, 2013.
E. Kaltofen and M. B. Monagan. On the genericity of the modular polynomial gcd algorithm. In Proc. ISSAC '99, pages 59–66. 1999.
E. Kaltofen and V. Shoup. Subquadratic-time factoring of polynomials over finite fields. Math. Comp., 67(223):1179–1197, 1998.
E. Kaltofen and B. M. Trager. Computing with polynomials given by black boxes for their evaluations: greatest common divisors, factorization, separation of numerators and denominators. JSC, 9(3):301–320, 1990.
E. Kaltofen and L. Yagati. Improved sparse multivariate polynomial interpolation algorithms. In ISSAC '88: Proceedings of the International Symposium on Symbolic and Algebraic Computation, pages 467–474. Springer Verlag, 1988.
K. S. Kedlaya and C. Umans. Fast polynomial factorization and modular composition. SIAM J. Comput., 40(6):1767–1802, 2011.
G. Lecerf. Sharp precision in Hensel lifting for bivariate polynomial factorization. Mathematics of Computation, 75:921–933, 2006.
G. Lecerf. Improved dense multivariate polynomial factorization algorithms. JSC, 42(4):477–494, 2007.
G. Lecerf. Fast separable factorization and applications. Applicable Algebra in Engineering, Communication and Computing, 19(2), 2008.
G. Lecerf. New recombination algorithms for bivariate polynomial factorization based on Hensel lifting. AAECC, 21(2):151–176, 2010.
G. Lecerf. Journées Nationales de Calcul Formel (2013), volume 3 of Les cours du CIRM, chapter Factorisation des polynômes à plusieurs variables. CEDRAM, 2013. Exp. No. 2, 85 pages, https://ccirm.centre-mersenne.org/articles/10.5802/ccirm.18.
G. Lecerf. On the complexity of the Lickteig–Roy subresultant algorithm. JSC, 92:243–268, 2019.
A. K. Lenstra, H. W. Lenstra, and L. Lovász. Factoring polynomials with rational coefficients. Math. Ann., 261:515–534, 1982.
M. Monagan and B. Tuncer. Using sparse interpolation in Hensel lifting. In Proceedings of CASC 2016, volume 9890 of LNCS, pages 381–400. Springer, 2016.
M. Monagan and B. Tuncer. Factoring multivariate polynomials with many factors and huge coefficients. In Computer Algebra in Scientific Computing, pages 319–334. Cham, 2018. Springer International Publishing.
M. Monagan and B. Tuncer. Sparse multivariate Hensel lifting: a high-performance design and implementation. In Proc. ICMS 2018, volume 10931 of LNCS, pages 359–368. Springer, 2018.
M. Monagan and B. Tuncer. The complexity of sparse Hensel lifting and sparse polynomial factorization. Journal of Symbolic Computation, 99:189–230, 2020.
J. Montes. Polígonos de Newton de orden superior y aplicaciones aritméticas. PhD thesis, Universitat de Barcelona, Spain, 1999.
G. Moroz. New data structure for univariate polynomial approximation and applications to root isolation, numerical multipoint evaluation, and other problems. In Proc. IEEE FOCS '21. Denver, United States, 2022.
D. R. Musser. Multivariate polynomial factorization. JACM, 22(2):291–308, 1975.
A. Novocin. Factoring Univariate Polynomials over the Rationals. PhD thesis, Florida State University at Tallahassee, 2008.
A. Novocin, D. Stehlé, and G. Villard. An LLL-Reduction algorithm with quasi-linear time complexity: extended abstract. In Proc. ACM STOC '11, pages 403–412. New York, NY, USA, 2011.
V. Y. Pan. Univariate polynomials: nearly optimal algorithms for numerical factorization and root-finding. JSC, 33(5):701–733, 2002.
C. H. Papadimitriou. Computational Complexity. Addison-Wesley, 1994.
D. A. Plaisted. Sparse complex polynomials and polynomial reducibility. J. of Computer and System Sciences, 14(2):210–221, 1977.
D. A. Plaisted. New NP-hard and NP-complete polynomial and integer divisibility problems. TCS, 31(1-2):125–138, 1984.
R. Prony. Essai expérimental et analytique sur les lois de la dilatabilité des fluides élastiques et sur celles de la force expansive de la vapeur de l'eau et de la vapeur de l'alkool, à différentes températures. J. de l'École Polytechnique Floréal et Plairial, an III, 1:24–76, 1795. Cahier 22.
D. S. Roche. What can (and can't) we do with sparse polynomials? In Proc. ISSAC '18, pages 25–30. New York, NY, USA, 2018. ACM.
W. M. Ruppert. Reduzibilität ebener kurven. J. Reine Angew. Math., 396:167–191, 1986.
K. Ryan and N. Heninger. Fast practical lattice reduction through iterated compression. In Advances in Cryptology – CRYPTO 2023, pages 3–36. 2023.
T. Sasaki and M. Sasaki. A unified method for multivariate polynomial factorizations. Japan J. Indust. Appl. Math., 10(1):21–39, 1993.
N. Saxena. Closure of algebraic classes under factoring. https://www.cse.iitk.ac.in/users/nitin/talks/Sep2023-paris.pdf, 2023. Talk at Recent Trends in Computer Algebra, Institut Henri Poincar´e, Paris.
Th. Schönemann. Von denjenigen Moduln, welche Potenzen von Primzahlen sind. J. Reine Angew. Math., 32:93–105, 1846. See §59.
A. Schönhage. Asymptotically fast algorithms for the numerical multiplication and division of polynomials with complex coefficients. In J. Calmet, editor, EUROCAM '82: European Computer Algebra Conference, volume 144 of Lect. Notes Comp. Sci., pages 3–15. Marseille, France, April 1982. Springer.
J. T. Schwartz. Fast probabilistic algorithms for verification of polynomial identities. JACM, 27(4):701–717, 1980.
I. R. Shafarevich. Basic Algebraic Geometry 1. Springer, 3rd edition, 2013.
V. Shoup. On the deterministic complexity of factoring polynomials over finite fields. Information Processing Letters, pages 261–267, 1990.
A. Steel. Conquering inseparability: primary decomposition and multivariate factorization over algebraic function fields of positive characteristic. JSC, 40(3):1053–1075, 2005.
P. S. Wang. An improved multivariate polynomial factoring algorithm. Math. Comp., 32(144):1215–1231, 1978.
P. S. Wang and L. P. Rothschild. Factoring multivariate polynomials over the integers. Math. Comp., 29:935–950, 1975.
W. Wu, J. Chen, and Y. Feng. Sparse bivariate polynomial factorization. Science China Mathematics, 57:2123–2142, 2014.
D. Y. Y. Yun. On square-free decomposition algorithms. In Proc. SYMSAC '76, pages 26–35. New York, NY, USA, 1976. ACM.
H. Zassenhaus. On Hensel factorization, I. Journal of Number Theory, 1(3):291–311, 1969.
R. Zippel. Probabilistic algorithms for sparse polynomials. In Proc. EUROSAM '79, pages 216–226. Springer, 1979.
R. Zippel. Newton's iteration and the sparse Hensel algorithm (extended abstract). In Proc. SYMSAC '81, pages 68–72. New York, NY, USA, 1981. ACM.