In this paper, we present new algorithms for the computation of
fast Fourier transforms over complex numbers for
“medium” precisions, typically in the range from
G.1.0 Computer-arithmetic |
|
In this paper, we present new algorithms for the computation of
fast Fourier transforms over complex numbers for
“medium” precisions, typically in the range from
G.1.0 Computer-arithmetic |
Multiple precision arithmetic [4] is crucial in areas such as computer algebra and cryptography, and increasingly useful in mathematical physics and numerical analysis [2]. Early multiple precision libraries appeared in the seventies [3], and nowadays GMP [11] and MPFR [8] are typically very efficient for large precisions of more than, say, 1000 bits. However, for precisions which are only a few times larger than the machine precision, these libraries suffer from a large overhead. For instance, the MPFR library for arbitrary precision and IEEE-style standardized floating point arithmetic is typically about a factor 100 slower than double precision machine arithmetic.
This overhead of multiple precision libraries tends to further increase
with the advent of wider SIMD (Single Instruction, Multiple
Data) arithmetic in modern processors, such as the 
AVX technology. Indeed, it is hard to take advantage
of wide SIMD instructions when implementing basic arithmetic for integer
sizes of only a few words. In order to fully exploit SIMD instructions,
one should rather operate on vectors of integers of a few words. A
second problem with current SIMD arithmetic is that CPU vendors tend to
privilege wide floating point arithmetic over wide integer arithmetic,
which would be most useful for speeding up multiple precision libraries.
In order to make multiple precision arithmetic more useful in areas such as numerical analysis, it is a major challenge to reduce the overhead of multiple precision arithmetic for small multiples of the machine precision, and to build libraries with direct SIMD arithmetic for multiple precision numbers.
One existing approach is based on the
“TwoSum” and
“TwoProduct” algorithms [7, 22], which allow for the exact computation of sums and
products of two machine floating point numbers. The results of these
operations are represented as sums 
where 
and 
have no
“overlapping bits” (e.g. 
or 
). The
TwoProduct algorithm can be implemented using only two
instructions when hardware features the fused-multiply-add
(FMA) and fused-multiply-subtract (FMS) instructions, as is for
instance the case for
It is classical that double machine precision arithmetic can be implemented reasonably efficiently in terms of the TwoSum and TwoProduct algorithms [7, 22, 23]. The approach has been further extended in [24] to higher precisions. Specific algorithms are also described in [21] for triple-double precision, and in [15] for quadruple-double precision. But these approaches tend to become inefficient for large precisions.
For certain applications, efficient fixed point arithmetic is actually sufficient. One good example is the fast discrete Fourier transform (FFT) [6], which is only numerically accurate if all input coefficients are of the same order of magnitude. This means that we may scale all input coefficients to a fixed exponent and use fixed point arithmetic for the actual transform. Moreover, FFTs (and especially multi-dimensional FFTs) naturally benefit from SIMD arithmetic.
In this paper, we will show how to efficiently implement FFTs using
fixed point arithmetic for small multiples of the machine precision. In
fact, the actual working precision will be of the form 
, where 
,
for a small integer 
(typically, 
), and 
denotes the number of fractional bits of the mantissa
(also known as the trailing significant field, so that 
for IEEE double precision numbers).
Allowing for a small number of
“nail” bits makes it easier to handle carries efficiently.
On the downside, we sacrifice a few bits and we need an additional
routine for normalizing our numbers. Fortunately, normalizations can
often be delayed. For instance, every complex butterfly operation during
an FFT requires only four normalizations (the real and imaginary parts
of the two outputs).
Redundant representations with nail bits, also known as carry-save representations, are very classical in hardware design, but rarely used in software libraries. The term “nail bits” was coined by the GMP library [11], with a different focus on high precisions. However, the GMP code which uses this technology is experimental and disabled by default. Redundant representations have also found some use in modular arithmetic. For instance, they recently allowed to speed up modular FFTs [13].
Let 
denote the time spent to compute an FFT of
length 
at a precision of 
bits. For an optimal implementation at precision 
, we would expect that 
.
However, the naive implementation of a product at precision requires at least 
machine
multiplications, so 
is a more realistic goal for
small 
. The first
contribution of this paper is a series of optimized routines for basic
fixed point arithmetic for small .
These routines are vectorial by nature and therefore well suited to
current , our timings seem to indicate that 
. For 
,
we compared our implementation with 
when using the built-in type __float128 of GCC) and a
home-made double-double implementation along the same lines as
[23] (in which case we got 
).
Although the main ingredients of this paper (fixed point arithmetic and
nail bits) are not new, we think that we introduced a novel way to
combine them and demonstrate their efficiency in conjunction with modern
wide SIMD technology. There has been recent interest in efficient
multiple precision FFTs for the accurate integration of partial
differential equations from hydrodynamics [5]. Our new
algorithms should be useful in this context, with special emphasis on
the case when . We also
expect that the ideas in this paper can be adapted for some other
applications, such as efficient computations with truncated numeric
Taylor series for medium working precisions.
Our paper is structured as follows. Section 2 contains a
detailed presentation of fixed point arithmetic for the important
precision 
. In Section 3, we show how to apply this arithmetic to the computation of
FFTs, and we provide timings. In Section 4, we show how our
algorithms generalize to higher precisions with
, and present further timings
for the cases when 
and 
. In our last section, we discuss possible speed-ups
if certain SIMD instructions were hardware-supported, as well as some
ideas on how to use asymptotically faster algorithms in this context.
Throughout this paper, we assume IEEE arithmetic with correct rounding
and we denote by 
the set of machine floating
point numbers. We let 
be the machine precision
minus one (which corresponds to the number of fractional bits of the
mantissa) and let 
and 
be
the minimal and maximal exponents of machine floating point numbers. For
IEEE double precision numbers, this means that , 
and 
.
The algorithms in this paper are designed to work with all possible
rounding modes. Given 
and 
, we denote by 
the rounding
of 
according to the chosen rounding mode. If
is the exponent of and
(i.e. in absence of overflow and
underflow), then we notice that 
.
Modern processors usually support fused-multiply-add (FMA) and
fused-multiply-subtract (FMS) instructions, both for scalar and SIMD
vector operands. Throughout this paper, we assume that these
instructions are indeed present, and we denote by 
and 
the roundings of 
and
according to the chosen rounding mode.
Let 
. In this section, we are
interested in developing efficient fixed point arithmetic for a bit
precision . Allowing 
to be smaller than makes it
possible to efficiently handle carries during intermediate computations.
We denote by 
the number of extra
“nail” bits.
We denote by 
the set of fixed point numbers
which can be represented as
where 
are such that
It will be convenient to write 
for numbers of
the above form. Since contains all numbers 
with 
and 
, this means that can
be thought of as a fixed point type of precision .
Remark 
and 
,
but the extra flexibility provided by (2) and (3)
will be useful during intermediate computations. In addition, for
efficiency reasons, we do not require that 
.
An important subalgorithm for efficient fixed point arithmetic computes the truncation of a floating point number at a given exponent:
Algorithm Split |
return |
Proof. Let 
.
Since 
, we have
Since 
is obtained by rounding 
, it follows that
whence the exponent of is 
and 
, for any rounding mode.
Since 
also has exponent , it follows that 
satisfies
. Furthermore, and are both integer multiples of
, whence so is 
. Finally, 
.□
Remark 
suffices in Proposition 2. Indeed, this weaker condition
implies 
, and therefore 
, with the rest of the proof
unchanged. The same remark holds for Proposition 7 below
and allows several of the subsequent bounds to be slightly improved. As
a consequence, this sometimes allows us to decrease 
by one. However, in this paper, we prefer to avoid hypotheses on the
rounding mode, for the sake of portability, efficiency, and simplicity.
Nevertheless, our observation may be useful on some recent processors
(such as
Let 
. We will write 
for the subset of of all numbers
with
Numbers in 
are said to be in normal
form.
Remark 
and 
are in normal form, and both
and 
represent the number
. Consequently, our fixed
point representation is still redundant under this
normalization (this is reminiscent from Avižienis'
representations [1]).
Algorithm Normalize( |
return |
Proof. Since 
,
using Proposition 2 with 
,
we have 
and 
.
Using the fact that 
, this
entails 
and therefore 
. Hence 
,
so that 
. Finally, implies 
, so
that 
.□
Non normalized addition and subtraction of fixed point numbers are straightforward:
|
|
|
Proof. Since both 
and
are multiple of 
,
the addition 
is exact. Furthermore, the
exponents of 
and 
are
both strictly bounded by 
.
Consequently, 
and 
.
Finally 
. The statement for
the subtraction follows by replacing by 
.□
Our multiplication algorithm of fixed point numbers is based on a
subalgorithm LongMul
which computes the exact product of two numbers
in the form of a sum 
, with
the additional constraint that 
.
Without this additional constraint (and in absence of overflow and
underflow), 
and 
can be
computed using the classical “Two Product” algorithm: 
, 
.
Our LongMul algorithm
exploits the FMA and FMS instructions in a similar way.
|
|
|
and 
be such that 
. Then the
algorithm 
computes a pair 
with , 
, and 
.
In addition, if 
, then 
and 
.
Proof. In a similar way as in the proof of
Proposition 2, one shows that and
. It follows that and 
. If , then the subtraction 
is exact, whence 
.□
Proof. Let us write 
, 
and 
for the successive values of 
taken during the
execution of the algorithm. Since 
,
Proposition 7 implies that 
,
, and 
. Using that 
and 
, we next obtain 
and 
. We also get that 
and 
.
Finally we obtain:
 |
 |
 |
|
|
 |
||
 |
 |
□ |
For our C++ implementation inside
template<typename C, typename V> fixed_quadruple;
The parameter C corresponds to a built-in numeric type
such as double. The parameter V is a
“traits” type (called the “variant” in
(see [18] for details). When instantiating for C=double
and the default variant V, the type fixed_quadruple<double>
corresponds to with 
(see
the file numerix/fixed_quadruple.hpp).
Since all algorithms from this section only use basic arithmetic
instructions (add, subtract, multiply, FMA, FMS) and no branching, they
admit straightforward SIMD analogues.
In this section we describe how to use the fixed point arithmetic
functions to compute FFTs. The number of nail bits
is adjusted to perform a single normalization stage per butterfly. In
the next paragraphs we follow the classical Cooley and Tukey in place
algorithm [6].
We implement complex analogues ComplexNormalize,
ComplexAdd, ComplexSubtract and
ComplexMultiply of Normalize,
Add, Subtract and
Multiply in a naive way. We have fully specified
ComplexMultiply below, as an example. The three other
routines proceed componentwise, by applying the real counterparts on the
real and imaginary parts. Here 
and 
represent the real and imaginary parts of 
respectively. The norm 
of the complex number
is defined as 
.
Algorithm ComplexMultiply( |
return |
The basic building block for fast discrete Fourier transforms is the
complex butterfly operation. Given a pair 
and a
precomputed root of unity 
,
the butterfly operation computes a new pair 
. For inverse transforms, one rather computes the
pair 
instead. For simplicity, and without loss
of generality, we may assume that the approximation of 
in 
satisfies 
.
|
|
|
Proof. Let 
be as in
ComplexMultiply with 
and 
as arguments. From Proposition 8, it
follows that 
and 
,
and we have similar bounds for 
and 
. From Proposition 6, we next get
and 
.
Applying Proposition 6 again, we obtain 
, 
and 
. The conclusion now follows from Proposition
5.□
Proof. Proposition 6 yields 
and 
, and
. Proposition 5
then gives us 
, 
. Let be as in
ComplexMultiply with 
and 
as arguments. From Proposition 8, it
follows that 
, 
, and we have similar bounds for and . From
Proposition 6 again, we get 
and
. Finally Proposition 5 gives us 
, 
.□
For reason of space, we will not go into more details concerning the
total precision loss in the FFT, which is of the order of 
bits at size .
We refer the reader to the analysis in [14], which can be
adapted to the present context thanks to the above propositions.
Throughout this article, timings are measured on a platform equipped
with an kernel version 3.14 in 64
bit mode. We measured average timings, while taking care to avoid
|
|||||||||||||||||||||||||||||||||||||||||
For the sake of comparison, Table 1 displays timings to
compute
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Our 
.
Timings are reported in Table 2. We have implemented the
split-radix algorithm [19]. The configuration
process of
The three first rows concern the same built-in numerical types as in the
previous table. The row quadruple makes use of our own
non IEEE compliant implementation of the algorithms of [23],
sometimes called double-double arithmetic (see file numerix/quadruple.hpp).
The row fixed_quadruple corresponds to the new
algorithms of this section with nail bits. In the rows double,
quadruple, and fixed_quadruple, the
computations fully benefit from
Let us mention that our type quadruple requires 
arithmetic operations (counting FMA and FMS for 
) for a product, and 
for an addition or subtraction. A direct butterfly thus
amounts to 
elementary operations. On the other
hand, our type fixed_quadruple needs only 48 such
operations. It is therefore satisfying to observe that these estimates
are reflected in practice for small sizes, where the cost of memory
caching is negligible.
The representation with nail bits and the algorithms designed so far for doubled precision can be extended to higher precisions, as explained in the next paragraphs.
Given 
and an integer 
, we denote by 
the set of
numbers of the form
where 
are such that
We write 
for numbers of the above form and
abbreviate 
. Numbers in 
are said to be in normal form. Of course, we
require that 
is smaller than 
. For this, we assume that 
. The normalization procedure generalizes as
follows (of course, the loop being unrolled in practice):
Algorithm Normalize( |
for
return |
Proof. During the first step of the loop, when
, by Proposition 2
we have 
and 
.
Using the fact that 
, this
entails 
and therefore 
. Hence 
,
so that 
. Using similar
arguments for 
, we obtain
and 
.
Finally, since we have 
, which concludes the proof.□
The generalizations of Add and
Subtract are straightforward: 
, and 
.
Proof. Since both 
and
are integer multiples of 
for 
, the additions 
are exact. Furthermore, the exponents of 
and 
are both strictly bounded by 
. Consequently, 
and
. The statement for the
subtraction follows by replacing by .□
Multiplication can be generalized as follows (all loops again being unrolled in practice):
Algorithm Multiply( |
for
for
for
return |
Proof. Let us write 
for
the pair returned by 
, for
. Since 
, Proposition 7 implies that 
, 
,
and 
. At the end of the
algorithm we have 
and 
for all 
, and therefore 
for all 
.
In particular no overflow occurs and these sums are all exact. Let 
represent the value of 
before
entering the second loop. Then let 
for 
, so that 
holds at the end of the algorithm. We have 
,
and 
for all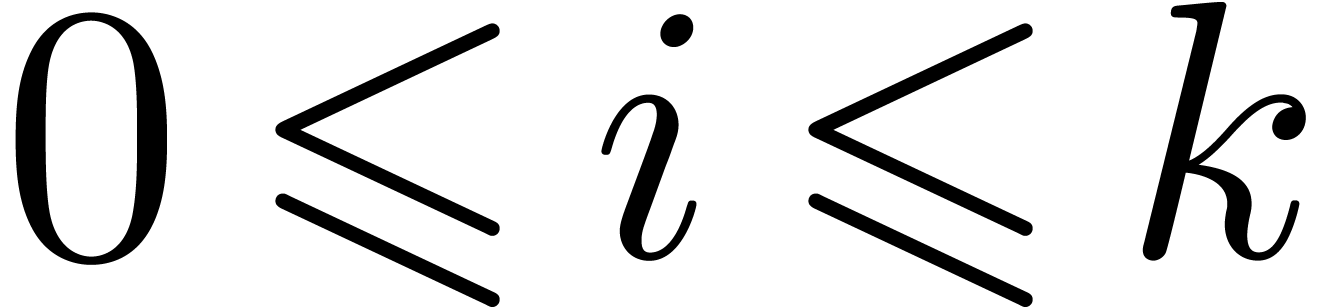 
.
For the precision loss, from 
,
we deduce that
The proof follows from 
,
while using that 
and 
.□
We can use the same butterfly implementations as in Section 3.2.
The following generalization of Proposition 9 shows that we
may take as long as 
, and 
as long as 
for the direct butterfly operation.
Proof. Let be as in
ComplexMultiply with and as arguments. From Proposition 13, it
follows that 
and 
,
and we have similar bounds for and . From Proposition 12, we next get
and 
.
Applying Proposition 12 again, we obtain 
, 
and 
. The conclusion now follows from Proposition
11.□
The following generalization of Proposition 9 shows that we
may take as long as 
, as long as 
, and 
as long as 
for the inverse butterfly operation.
Proof. Proposition 12 yields 
and 
, and
. Proposition 11
then gives us 
, 
. Let be as in
ComplexMultiply with and as arguments. From Proposition 13, it
follows that 
, 
, and we have similar bounds for and . From
Proposition 12 again, we get 
and
. Finally Proposition 11 gives us 
, 
.□
Remark replaced by 
. In our code for 
and 
, we have decided to keep
by performing one additional normalization of
in 
.
Remark
by one: instead of normalizing the entries of an FFT to be of norm 
, we rather normalize them to be of
norm 
for some small constant 
. This should allow us to turn the conditions
and 
in the Propositions
14 and 10 into 
and
. One could also investigate
what happens if we additionally assume 
.
It is interesting to compute the number of operations in which are needed for our various fixed point operations,
the allowed operations in being addition,
subtraction, multiplication, FMA and FMS. For larger precisions, it may
also be worth it to use Karatsuba's method [20] for the
complex multiplication, meaning that we compute 
using the formula 
. This
saves one multiplication at the expense of three additions/subtractions
and an additional increase of .
The various operation counts are summarized in Table 3.
|
||||||||||||||||||||||||||||||||||||||||||||||||
For our C++ implementation inside
template<typename C, typename V> fixed_hexuple;
template<typename C, typename V> fixed_octuple;
with similar semantics as fixed_quadruple. When
instantiating for C=double and the default variant V, these types correspond to 
and
with .
In the future, we intend to implement a more general template type which
also takes as a parameter.
Table 4 shows our timings for FFTs over the above types. Although the butterflies of the split-radix algorithm are a bit different from the classical ones, it is pleasant to observe that our timings roughly reflect operation counts of Table 3. For comparison, let us mention that the time necessary to perform (essentially) the same computations with MPFR are roughly the same as in Table 2, even in octuple precision. In addition (c.f. Table 2), we observe that the performance of our fixed_hexuple FFT is of the same order as FFTW's long double implementation.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Thanks to the genericity of our
.
Alternatively, we may regard such numbers as polynomials
in the “indeterminate” ,
with 
and 
.
It can be checked that the algorithms of this paper can be adapted to
this setting with no penalty (except for multiplication which may
require one additional instruction). Roughly speaking, every time that
we need to add a “high” part and a
“low” part of two long products, it
suffices to use a fused-multiply-add instruction 
instead of a simple addition 
.
For naive multiplication, the polynomial representation may become
slightly more efficient for 
,
when the hardware supports an SIMD instruction for rounding floating
point numbers to the nearest integer. In addition, when
becomes somewhat larger, say 
,
then the polynomial representation makes it possible to use pair-odd
Karatsuba multiplication [12, 16] without any
need for special carry handling (except that has
to be chosen a bit larger). Finally, the restriction 
is no longer necessary, so the approach can in principle be extended to
much larger values of .
In order to develop an efficient GMP-style library for SIMD multiple precision integers, it would be useful to have an instruction for multiplying two vectors of 64 bit integers and obtain the lower and higher parts of the result in two other vectors of 64 bit integers. For multiple precision additions and subtractions, it is also important to have vector variants of the “add with carry” and “subtract with borrow” instructions.
Assuming the above instructions, a 
bit unsigned
truncated integer multiplication can be done in SIMD fashion using
approximately 
instructions. Furthermore, in this
setting, there is no need for normalizations. However, signed
multiplications are somewhat harder to achieve. The best method for
performing a signed integer multiplication 
with
is probably to perform the unsigned
multiplication 
with 
and
use the fact that 
. We expect
that the biggest gain of using integer arithmetic comes from the fact
that we achieve a instead of a 
bit precision (for small , we
typically have ).
One potential problem with GMP-style SIMD arithmetic is that
asymptotically faster algorithms, such as Karatsuba multiplication (and
especially the even-odd variant), are harder to implement. Indeed, we
are not allowed to ressort to branching for carry handling. One remedy
would be to use expansions 
with coefficients
for a suitable number of
nail bits and a suitable “multiplexer” 
.
and 
on input and which computes numbers 
with 
,
and 
.
In that case, normalization would only require two instructions
instead of four. Besides speeding up the naive algorithms, it would
also become less expensive to do more frequent normalizations, which
makes the use of asymptotically more efficient multiplication
algorithms more tractable at lower precisions and with fewer nail
bits. More efficient normalization is also important for efficient
shifting of mantissas, which is the main additional ingredient for the
implementation of multiple precision arithmetic.
denote the
bit complexity of 
bit integer multiplication.
It has recently been proved [14] that 
, where 
.
Under mild assumptions on and
it can also be shown [14] that an FFT of size and bit precision can be
performed in time 
. For
and large ,
this means that 
scales linearly with . In a future paper, we intend to
investigate the best possible (and practically achievable) constant
factor involved in this bound.
A. Avizienis. Signed-digit number representations for fast parallel arithmetic. IRE Transactions on Electronic Computers, EC-10(3):389–400, 1961.
D. H. Bailey, R. Barrio, and J. M. Borwein. High precision computation: Mathematical physics and dynamics. Appl. Math. Comput., 218:10106–10121, 2012.
R. P. Brent. A Fortran multiple-precision arithmetic package. ACM Trans. Math. Software, 4:57–70, 1978.
R. P. Brent and P. Zimmermann. Modern Computer Arithmetic. Cambridge University Press, 2010.
S. Chakraborty, U. Frisch, W. Pauls, and Samriddhi S. Ray. Nelkin scaling for the Burgers equation and the role of high-precision calculations. Phys. Rev. E, 85:015301, 2012.
J. W. Cooley and J. W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Comp., 19:297–301, 1965.
T. J. Dekker. A floating-point technique for extending the available precision. Numer. Math., 18(3):224–242, 1971.
L. Fousse, G. Hanrot, V. Lefèvre, P. Pélissier, and P. Zimmermann. MPFR: A multiple-precision binary floating-point library with correct rounding. ACM Trans. Math. Software, 33(2), 2007. Software available at http://www.mpfr.org.
M. Frigo and S. G. Johnson. The design and implementation of FFTW3. Proc. IEEE, 93(2):216–231, 2005.
GCC, the GNU Compiler Collection. Software available at http://gcc.gnu.org, from 1987.
T. Granlund et al. GMP, the GNU multiple precision arithmetic library. http://www.swox.com/gmp, from 1991.
G. Hanrot and P. Zimmermann. A long note on Mulders' short product. J. Symbolic Comput., 37(3):391–401, 2004.
D. Harvey. Faster arithmetic for number-theoretic transforms. J. Symbolic Comput., 60:113–119, 2014.
D. Harvey, J. van der Hoeven, and G. Lecerf. Even faster integer multiplication, 2014. http://arxiv.org/abs/1407.3360.
Yozo Hida, Xiaoye S. Li, and D. H. Bailey. Algorithms for quad-double precision floating point arithmetic. In Proc. 15th IEEE Symposium on Computer Arithmetic, pages 155–162. IEEE, 2001.
J. van der Hoeven and G. Lecerf. On the complexity of multivariate blockwise polynomial multiplication. In J. van der Hoeven and M. van Hoeij, editors, Proc. 2014 International Symposium on Symbolic and Algebraic Computation, pages 211–218. ACM, 2012.
J. van der Hoeven, G. Lecerf, B. Mourrain, et al. Mathemagix, from 2002. http://www.mathemagix.org.
J. van der Hoeven, G. Lecerf, and G. Quintin. Modular SIMD arithmetic in Mathemagix, 2014. http://hal.archives-ouvertes.fr/hal-01022383.
S. G. Johnson and M. Frigo. A modified split-radix FFT with fewer arithmetic operations. IEEE Trans. Signal Process., 55(1):111–119, 2007.
A. Karatsuba and J. Ofman. Multiplication of multidigit numbers on automata. Soviet Physics Doklady, 7:595–596, 1963.
C. Lauter. Basic building blocks for a triple-double intermediate format. Technical Report RR2005-38, LIP, ENS Lyon, 2005.
J.-M. Muller, N. Brisebarre, F. de Dinechin, C.-P. Jeannerod, V. Lefèvre, G. Melquiond, N. Revol, D. Stehlé, and S. Torres. Handbook of Floating-Point Arithmetic. Birkhäuser Boston, 2010.
T. Nagai, H. Yoshida, H. Kuroda, and Y. Kanada. Fast quadruple precision arithmetic library on parallel computer SR11000/J2. In Computational Science - ICCS 2008, 8th International Conference, Kraków, Poland, June 23-25, 2008, Proceedings, Part I, pages 446–455, 2008.
D. M. Priest. Algorithms for arbitrary precision floating point arithmetic. In Proc. 10th Symposium on Computer Arithmetic, pages 132–145. IEEE, 1991.
until 
bits. On the one
hand, such precisions are usually not supported by hardware. On
the other hand, asymptotically fast algorithms for multiple
precision arithmetic do not pay off yet. The main idea behind our
algorithms is to develop efficient vectorial multiple precision
fixed point arithmetic, capable of exploiting SIMD instructions in
modern processors.
.
and 
such that 
with 
and 
.
with 
,
with 
.
and 
with 
.
,
with
.
,
with 
.
,
and 
and 
.
)
with 
and assume that 
.
and 
.
and assume that 
and 
.
,
from
down to 
with 
,
.
with 
with 
.
,
with 
.
)
do
from 
to 
do
to 
.
with 
.
with 
and assume that 
and 
.
and 
.
.