Plane curve germs and contact
factorization  |
|
| September 17, 2024 |
|
. This paper is
part of a project that has received funding from the French
“Agence de l'innovation de défense”.
. This article has
been written using GNU TeXmacs [49].
Given an algebraic germ of a plane curve at the origin, in terms of a bivariate polynomial, we analyze the complexity of computing an irreducible decomposition up to any given truncation order. With a suitable representation of the irreducible components, and whenever the characteristic of the ground field is zero or larger than the degree of the germ, we design a new algorithm that involves a nearly linear number of arithmetic operations in the ground field plus a small amount of irreducible univariate polynomial factorizations.
|
Algebraic curves play a central role in algebraic geometry and various
applications in effective algebra. In particular, efficient algorithms
are needed to compute topological or analytic invariants, arithmetic
genus, desingularized models, integral closures, Riemann–Roch
spaces, etc. Usual applications in computer algebra concern the
irreducible factorization of multivariate polynomials, the integration
of rational functions, the construction of algebraic geometry error
correcting codes, the bi-linear complexity of polynomial multiplication,
etc. In the present paper, we are interested in computing the
irreducible factorization of any given polynomial 
, where 
denotes an
effective field. Here “effective” means that
algorithms are at our disposal for the arithmetic operations and the
zero test in .
Historically, the first local factorization methods focused on root
computations. More precisely, let 
denote the
fraction field of 
of Laurent series in 
. The field
of power series with fractional exponents is called the field of
Puiseux series (or Puiseux expansions) over . Let 
denote a fixed algebraic closure of .
If has characteristic zero, then 
is the algebraic closure of .
In other words, any polynomial 
in 
splits into linear factors in 
. Computations of Puiseux expansions of roots of
go back to Newton [70], and were
rediscovered by Puiseux [90]; see [7,
p. 198] and [98, 102]. The well
known Newton polygon method turns out to be effective whenever
is effective. When adopting a suitable algebraic
complexity model (in which running times are measured in terms of the
required number of arithmetic operations in or
), the complexity is easily
seen to be polynomial in the degree of and in
the required precision.
Another line of works, that directly concerns the actual factorization
of , goes back to Ore [75–77] and Mac Lane [62]. For
the last two decades, Montes and his collaborators have designed
polynomial time algorithms in this line.
For both Puiseux series and irreducible factorization it is classical
that complexity bounds become softly linear whenever the requested
precision becomes “sufficiently large”: this property
essentially follows from fast multi-factor Newton–Hensel lifting
algorithms [31]. In both cases, the state of the art
algorithms are due to Poteaux and Weimann [87, 89]:
quasi-linear complexity is achieved whenever the requested precision is
larger than the valuation of the discriminant of , assuming that is separable
and that the characteristic of is zero or
sufficiently large.
However, we are not aware of any algorithm with a softly linear cost for
arbitrary precisions. In particular, no such algorithm seems to exist
for precisions below the valuation of the discriminant of . For the design of such an algorithm, it is
important to carefully state the problem that needs to be solved and to
pay attention to the way approximate factors are represented. Modulo
these precautions and assuming that the characteristic of is zero or sufficiently large, we present the first
quasi-linear algorithm to solve this factorization problem. This result
assumes that the cost of univariate factorizations over algebraic
extensions of is sufficiently low in a way that
will be made precise.
So, the goal of the present paper is to perform local irreducible
factorization at any given precision in quasi-linear time. More
specifically, we extend and improve the recent result of [89]
for factoring a polynomial that is given modulo
for a finite precision 
, assuming that we already have an algorithm for
decomposing polynomials in 
into irreducible
factors.
Below the valuation of the discriminant of ,
the factorization of is not always well defined,
and the problem is commonly called “approximate
factorization”. Approximate factorization is an important problem
in computer algebra. List decoding of geometric error correcting codes
is one typical application [9]; a fast algorithm for linear
factors can be found in [69]. Other applications concern
the computation of Igusa zeta functions [24] and the
computation of the divisor of a polynomial at the singular branches of a
plane curve [1]. We also expect that approximate
factorization could play a role in bivariate polynomial factorization,
e.g. in the vein of [61]. Note that
approximate factorization of polynomials in 
is a
similar problem that has received a lot of attention during the last
decades [81, 93]; see [66] for
some recent advances.
For complexity analyses, we consider algebraic complexity models (such as computation trees). In other words we simply count numbers of arithmetic operations and zero tests in specified algebraic structures.
Until the end of the paper, 
is a fixed rational
number that can be taken arbitrarily close to zero. For complexity
estimates we often use the soft-Oh notation: 
means that 
; see [31,
chapter 25, section 7] for technical details. The least integer larger
or equal to 
is written 
; the largest one smaller or equal to is written 
.
For randomized algorithms over a finite effective ring 
, we assume a special instruction that
uniformly generates random elements in with
constant cost. For a given input, the cost of a randomized algorithm is
thus a random variable. The expected cost for input size 
is defined as the maximum of the averages of these
random variables over all possible inputs of size 
.
For a finite field 
of characteristic 
and with 
elements, the usual
primitive element representation will be used, so elements in will be regarded in 
where 
is an irreducible polynomial of degree 
.
as a notation for the cost of
multiplying two polynomials of degree 
,
in terms of the number of operations in the coefficient ring. We
assume that 
is a non-decreasing function in
. It is known [15,
92] that one can take 
.
For rings of positive characteristic, one even has 
, modulo a plausible number-theoretic
conjecture [40]. We will also denote
for a separable irreducible monic polynomial 
and
. We set
Products and inversions in 
take 
operations in . This was
first proved in [51] in the case when
is a field and 
. The result
was extended to more general algebraic towers in [52].
Whenever 
, we may work in an
algebraic extension 
of degree 
such that 
. The computation
of such an extension can be done using 
operations in the prime subfield 
of , thanks to [94, Theorem 4.1]. For
a fixed field , this can be
regarded as a precomputation, whereas computations with elements in instead of induce only a
logarithmic overhead 
.
to be an upper bound for the cost
(expected or not) of irreducible factorization of a polynomial in
. It is convenient to
introduce
so 
is a non-decreasing function in 
.
For example, if is the finite field , then a well known probabilistic algorithm due
to Cantor and Zassenhaus [16] factors univariate
polynomials in 
using an expected number of 
bit operations.
The currently best known algorithm is obtained as a combination of results due to von zur Gathen, Kaltofen and Shoup [32, 54, 55], and Kedlaya and Umans [57]: it takes an expected number of
bit operations; see [53, Corollary 5.1].
The case of a tower 
over 
(with the above notation) reduces to the case of 
by means of the fast change of representation of [85,
Theorem 1.2], that applies whenever
 |
(1.1) |
In terms of bit complexity, and for a “random access memory” computational model, this yields
Details can be found in [53, Corollary 5.3]. Whenever
condition
When the tower has small degrees 
,
optimized factorization procedures can be found in [50, 53, 54]. In particular, if
is smooth, then polynomials of small degree can even be factored in
quasi-optimal time. Note that these optimizations do not depend on
Kedlaya–Umans' algorithm for modular composition.
For an abstract effective field ,
there does not exist a general algorithm to factor polynomials in into irreducible ones [29, 30].
Throughout this paper, we will therefore need to assume that such an
algorithm is provided by the computational model:
In practice, this property holds whenever is
effectively finitely generated over its prime subfield. Once
factorization is available in ,
it is also available in 
,
with a complexity that depends on those of resultants and gcds [97].
Let still denote an effective field, let 
be monic as a polynomial in , and assume that 
.
So 
defines a germ of curve at the origin. In
practice, we always truncate at a finite order
in . For the discussion in
the following paragraphs, we therefore take 
and
assume that is monic, primitive, and separable
in , of total degree 
, and of partial degrees 
in and 
in
.
is zero or
sufficiently large, then Puiseux expansions to any given precision can
be computed in polynomial time when considering an algebraic
complexity model over —this
result belongs to the folklore.
Consider a Puiseux series 
that is a root of
. The shortest truncation of
this series which is different from any truncation of a distinct Puiseux
series root of is called the singular
part of . In 1978, Kung
and Traub [58] showed that the Puiseux expansion of can be computed efficiently using Newton's method,
once its singular part is known.
The complexity of the computation of singular parts started to be
studied in the eighties. In [41], Henry and Merle showed
that the embedded resolution of an irreducible germ of curve defined by
at the origin can be computed with 
operations in .
In [23], Duval introduced the notion of rational
Puiseux expansions, that allowed computations over
to be replaced by computations over .
She adapted the usual Newton polygon algorithm to such a rational
representation, and made use of dynamic evaluation to handle
algebraic extensions without polynomial factorization. She achieved a
total cost of operations in , whenever the characteristic is zero or
sufficiently large. This analysis was based on slow arithmetic for
polynomials and series.
In his PhD thesis [83], Poteaux showed that Duval's
algorithm takes at most 
operations in in order to obtain all the singular parts of the Puiseux
expansions. In [84], Poteaux and Rybowicz also proved that
the singular parts of the rational Puiseux expansions centered at a
single point can be computed using 
operations in
, in the case when 
; this bound relies on fast
polynomial arithmetic. In [87], Poteaux and Weimann finally
gave a probabilistic algorithm that allows singular parts to be computed
with 
operations in ,
assuming that the characteristic of is zero or
sufficiently large. This bound is quasi-optimal in worst cases, when we
need order about 
before root separation takes
place [87, Example 8.1]. Their algorithm makes use of
dynamic evaluation and the singular parts are represented by truncations
of rational Puiseux expansions. These algorithms by Poteaux et
al. also extend efficiently to obtain the collection of all
singular parts at each of the singularities of the algebraic curve
defined by . As a byproduct,
Poteaux and Weimann proved the expected complexity bound 
for the irreducible factors of at
precision , still under the
assumption that the characteristic of is 
; see [87, Theorem
1.6].
When 
, a polynomial bit
complexity for Puiseux series was first achieved by Chistov [17].
The complexity bound for this case was subsequently detailed and
improved by Walsh [99, 100]. Since the
complexity exponents are rather large, multi-modular approaches turn out
to be of practical interest [83].
Once singular parts are known, we have already mentioned that Puiseux expansions can be extended by means of the Newton operator, as described in [58]; see also [45] for recent optimizations. For small and moderate expansion orders, it is often more efficient to use lazy or relaxed arithmetic to expand algebraic power series [44, 101]. For very large expansion orders, yet another method is to compute a differential operator that annihilates the expansions [19, 20]; see [11] for complexity bounds. It is also worth mentioning that individual terms of algebraic Puiseux series over a finite field can be computed even faster than with the Newton iteration [10].
;
see for instance [56]. Hamburger–Noether expansions
constitute a natural extension of Puiseux series in positive
characteristic [13].
In his 1989 article [2], Abhyankar addressed a question
from Kuo about an algorithm to decide the irreducibility of a germ of
curve, without using blowups or Puiseux series. In characteristic zero,
Abhyankar gave a positive answer to this question, by using expansions
of the defining polynomial of the germ with respect to so-called
approximate roots. These approximate roots can be determined
recursively by means of a generalized Newton polygon, previously
introduced in [3, 4]. They generalize the
Tschirnhaus transform [95, 96], which was also
used in the Newton polygon algorithm from [43, chapter 3].
Complexity analyses for ordinary power series coefficients can be found
in [86, 88]: in favorable cases irreducibility
tests take softly linear time (plus a justifiable amount of
irreducibility tests in ).
Abhyankar's work has been completed and extended to arbitrary characteristic by Cossart and Moreno-Socías in [22], where they present another construction based on valuation theory. The mathematical relationship between approximate roots, Puiseux expansions, and Hamburger–Noether expansions can be found in [88, 91].
is a local ring different from , factorization in 
is a more difficult problem, for which Puiseux
expansions cannot be used. The first interesting case is when is the field 
of the -adic numbers. Let 
be a monic primitive square-free polynomial in 
. A first series of contributions
concern the Round Four algorithm due to Zassenhaus, and
dedicated to the construction of integral bases modulo ; see [21, 26, 27] for instance. The first polynomial time algorithm for
factoring over was
given by Chistov [18], and then improved by Cantor and
Gordon in [14].
After that, Pauli [82] designed a factorization algorithm
over an algebraic extension of degree 
of with bit complexity
 |
(1.2) |
Another approach for local factorization was initiated by Ore during
1920–1930, but it was restricted to sufficiently generic
polynomials (essentially the case of contact towers of height 
in our context); see [37] for a summary of
Ore's result. Ore's ideas have been generalized to factor any input
polynomial by Montes in his PhD thesis [64]: Montes took
advantage of mathematical constructions to classify the valuations of
, due to Mac Lane [62].
In particular, Montes designed an irreducibility test that was
subsequently shown [28] to have a complexity similar to
Based on Montes' PhD thesis, the next complexity improvements are due to Guàrdia, Montes, and Nart [35, 36]. Then, in [8], Bauch, Nart, and Stainsby proved the bit complexity bound
for an algebraic extension of degree of . Further refinements and
applications, including the computation of integral closures, can be
found in [25, 37, 38]. In their
recent article [89] Poteaux and Weimann improved the latter
complexity bound to
(discarding factorization costs in 
)
whenever 
: they made use of
Abhyankar's approximate roots, the natural “divide and
conquer” extension of the generalized Hensel lifting of [39],
and also applied the same “increase of precision” strategy
as in [87].
Since Montes' algorithm is in the vein of works by Ore, Mac Lane, Okutsu, it is often refered to as the “OM algorithm” [5, 37]. The relationship between Mac Lane's theory and Okutsu's method for computing integral bases [71–74] is discussed in [34, Corollary 4.6]; see also [25, Theorems 6.7 and 6.9], and [68] for a survey.
Recently, the Poteaux–Weimann variant of Montes' algorithm [89] has been generalized to the more general context of henselian fields [5]. Note that [5] also contains an up-to-date survey of the “OM algorithm” and links with related mathematical results in valuation theory.
of generalized power series instead of .
One natural example is to take 
,
where is an effective subfield of another
field of Laurent series 
.
In this case, the underlying value group of
becomes non-archimedean, and the issue arises how to conduct exact
computations with truncated power series. This is easy if 
, but less trivial if
contains transcendental power series such as 
, because of the required zero test. We refer to
[47, 48] for some recent perspectives on
this type of computations.
The resolution of algebraic equations over fields
of generalized power series is still based on the Newton polygon method.
However, the complexity can no longer be analyzed in terms of the
truncation order in a non-archimedean context. Instead, one may consider
the resolution of equations in Hensel position as a natural building
block. In [43], van der Hoeven showed how to reduce the
resolution of a general algebraic equation of degree
to at most 
applications of Hensel's lemma. It
would be interesting to analyze the complexity of this algorithm in the
special cases that were considered above.
Non-archimedean value groups are not merely a theoretical curiosity. Until recently, effective counterparts of Hironaka's theory of standard bases for power series were only known in the case of algebraic power series [6, 65]. In [48], generalized Puiseux series have been put to develop elimination theories for more general power series, such as differentially algebraic power series. Non-archimedean value groups actually arise in a natural way when studying algebraic differential equations, and the Newton polygon method can be generalized to this context; see [7] for recent progress and further references.
The main purpose of this paper is a self-contained and quasi-optimal
algorithm for the approximate factorization of univariate polynomials
over rings of formal power series. We show how to efficiently factor
into irreducible polynomials, and for each
irreducible factor 
we construct generators of
the valuation group of 
in a form of a
contact tower; see Definition 3.1. An
irreducible factorization of modulo
is a list of factors 
of
modulo ,
along with their associated multiplicity and contact tower; see
Definition 7.6. In particular the
are irreducible, pairwise coprime, and we have
for some integers 
. The
contact tower associated to allows the
computation of the valuation in in softly linear
time. The following main result will be proved at the end of section 8.2:
be a fixed positive value, and
assume be monic of degree 
in 
, known modulo , and such that the characteristic of 
is zero or 
.
Then, an irreducible factorization of 
modulo
can be computed using
operations in .
Example 
, 
,
and 
. Then 
, 
,
and 
is an irreducible factorization of modulo . Taking
, 
, 
, 
, we obtain another such
factorization. This shows that approximate factorizations are not unique
in general.
Note that the term 
is negligible with respect to
as soon as the precision 
is sufficiently large. By using our approximate factorization algorithm
with a sufficiently large precision, as a corollary, we deduce the
following complexity bound for the actual irreducible factorization of
; see section 9.5.
be a fixed positive value, and
assume be monic and separable of degree
in and known at precision 
in 
with 
.
Assume that the characteristic of is zero or
. Then, the irreducible
factors of can be computed modulo 
using
operations in .
Theorem 1.3 considers as part of
the input. This is not very restrictive in characteristic zero or 
thanks to [67, Theorem 1]. On the other
hand, if belongs 
then
can be computed with 
operations in .
Theorem 1.1 is new while Theorem 1.3 essentially corresponds to a slightly improved version of [89, Theorem 4]: we detail the cost analysis of the factorizations and we do not need extra irreducibility tests. Theorem 1.3 may also be regarded as a counterpart of [87, Theorem 1.6], where field extensions are represented in terms of primitive elements and local factors in terms of uniformizing parameters. Note also that Theorem 1.3 is deterministic while [87, Theorem 1.6] is probabilistic (although footnote 2 on page 1062 sketches how to get rid of the probabilistic aspects). Technically speaking, the algorithms presented in this paper share several ingredients with [89], but also include new ones. Below we detail the differences and improvements.
by means of Gröbner bases, which is convenient for
implementations in computer algebra systems. Note that Mac Lane's
theory and Montes' algorithm are restricted to valuations (their
“key polynomials” are irreducible). On the contrary, our
framework does not rely on Puiseux expansions or on the data
structures of the “OM algorithm”. The philosophy behind
contact calculus consists in extending usual calculus with
multivariate polynomials by taking care of carries. The
“contact” terminilogy brings a convenient geometric point
of view. Computing over contact towers involves a major difficulty:
how to compute efficiently in small relative precision? In this paper
we overcome this difficulty by doing most of the actual work within
the original ring 
with a sufficiently high
precision.
While Mac Lane and later Montes focused on constructing augmented valuations over polynomial rings, our down-to-earth and self-contained approach begins with designing efficient data structures in the vein of triangular sets and Hironaka's standard bases [42].
In [35] Guardia, Montes, and Nart address the computation of uniformizing parameters. In this paper we only need the initial part of uniformized representations, along with a rewriting algorithm for homogeneous polynomials. Section 6 contains an algorithm with quasi-linear time for these initial parts and conversions.
according to the slopes of its Newton polygon. Equal-slope
factorizations serve a similar purpose for polynomials with a single
slope. We achieve these computations in softly linear time by means of
the contact Hensel lifting of section 4.
In Ore's work the distinct and equal-slope factorization were already known and called “dissections”. These “dissections” were generalized by Montes to higher order Newton polygons [64, Capítulo 2]. Note that Montes' “high order Newton” polygon was previously used by Abhyankar [2]. These Newton polygons are still a cornerstone of the “OM algorithm”: for instance [36, Theorem 3.1] corresponds to the distinct-slope factorization and [36, Theorem 3.7] to the equal-slope factorization. The generalization of the Ostrowski theorem to higher order Newton polynomials can be found in [25, Theorem 2.8] or [36, Theorem 2.26]. Our Lemma 7.8 is a mild extension of it to the context of contact towers. The main advantage of our approch is the ability to compute the factors directly in terms of the contact coordinates.
is discovered as a tree of partial factorizations.
The leaves are the irreducible factors. When this tree is not
sufficiently well balanced, the total complexity moves away from
quasi-linearity.
Poteaux and Weiman circumvent the equilibration issue of the partial
factorization tree by using a divide-and-conquer approach on the
precision. This approach yields a quasi-linear complexity bound [87, 89] under the condition that the precision
exceeds the valuation of the discriminant of .
In order to prove Theorem 1.1, we use a divide and conquer strategy on the degree rather than the truncation order. For this, we developed the central shift algorithm, which is another main contribution of this paper: see section 7.7. The top level algorithm is described in section 8. Note that approximate factorizations in the sense of Theorem 1.1 (especially for truncation orderes below the valuation of the discriminant) are not addressed in [87, 89].
Approximate roots can indeed be regarded as special elements of contact towers. Our contact factorization algorithm does not rely on such roots: as explained in section 8.3, these roots may be useful in practice, but it is a drawback that they are not preserved during factorizations. In fact, our central shift strategy behaves as an algorithmic improvement upon approximate roots: see section 2.6.
Finally, we also analyze the cost of all univariate factorizations over
algebraic extensions of that occur during the
factorization over . We
expect that it should be possible to avoid such univariate
factorizations using the technique of directed evaluation [52].
However, the technical details are not obvious, especially when it comes
to computing Newton polygons in quasi-linear time. In [89,
section 5.4], Poteaux and Weimann indicate how dynamic evaluation might
be combined with their algorithm.
In order to highlight the complexity issues that arise in local factorization, we dedicate our next section to introductory examples. These key examples illustrate the main computational difficulties that are common to all known approaches.
At the end of the paper, a glossary is dedicated to the specific mathematical notations, and an index gathers references to the main definitions.
Before we give the formal definition of a contact factorization, we review a few motivating examples from the complexity perspective.
Let 
be a totally ordered abelian group and let
be a monoid embedded in . A graded ring 
with respect to the grading 
is a direct
sum
where the 
are abelian groups such that 
for all 
and 
in . An element of is said to be homogeneous if it belongs to one of
the . Any element 
in can be uniquely written 
, where 
is called the homogeneous component of degree of . If
and 
,
then we also denote
The initial form of a non-zero element 
, written 
, is the non-zero homogeneous component 
with the smallest index .
By convention we set 
.
An ideal 
of is said to
be homogeneous whenever it can be generated by homogeneous
elements, or equivalently whenever the homogenous components of any
element of also belong to .
To each non-zero element
we may associate the smallest index
such that
;
we set
.
The map
is a
semi-valuation
, which means that it satisfies
and
for all
.
Given
,
we call
the
truncation
of
at
relative precision
.
The Newton polygon of a non-zero polynomial
of degree 
is the lower border of the convex hull
in 
of the set of points
Figure 2.1 illustrates this definition with 
and 
. The
Newton polygon is thus a broken line with edges 
, with 
,
such that:
,
for 
,
, for all and 
with 
,
, for all and 
or 
with .
Intuitively speaking, these conditions mean that 
lies on or above the Newton polygon. If 
,
then we have 
and 
.
Any 
determines an edge 
with vertices 
and 
.
The Newton polynomial associated to
is
Whenever 
, the slope
of is 
.
The first slope is 
whenever . Two consecutive edges have different slopes.
In order to illustrate computations in algebraic extensions of or , let us
first consider applying the Newton polygon method to an input polynomial
of the form
where 
is a monic separable irreducible
polynomial of degree and 
has degree 
in .
We then consider
 |
(2.1) |
as a polynomial equation in .
The Newton polygon of consists of a single edge
starting at 
and ending at 
; its slope is 
.
Equation 
, where 
. Indeed, let 
be the
class of in 
.
Replacing by 
in
 |
(2.2) |
The separability of 
implies 
, which allows us to apply Hensel's lemma:
there exists a unique solution 
with valuation
in .
This is the point of view of factoring in terms
of Puiseux expansions.
In terms of space complexity, we note that computations in typically require times more space
than in . Fortunately, this
is compensated by the fact that the “unique” solution 
to solutions to 
.
Indeed, any solution in is obtained by
substituting a root 
of
for in the expression of .
From a time complexity point of view, the resolution of 
, where . These give in turn rise to modular
compositions (with modulus ).
Over general coefficient fields ,
no quasi-optimal algorithm (of complexity 
)
is currently known for this task, so it is preferable to avoid such
operations whenever possible. In particular, it is better to avoid
working over algebraic extensions of the field
of coefficients.
In order to avoid modular compositions, one idea is to consider that
equation as “solved” if and only if the Newton polygon
of with respect to suitable “contact
coordinates” has a single slope for which the associated Newton
polynomial is separable (and technically, irreducible).
The problem of solving a general equation with
then reduces to the problem of factoring as a product of “solved” polynomials.
From this perspective, expressing the solutions of
as Puiseux series becomes a rewriting problem for “solved”
polynomials, which is independent from the main resolution of the
equation itself.
Consider the polynomial equation in over 
given by
 |
(2.3) |
When solving this equation by means of the Newton polygon method, we see
that the Newton polygon of has a single slope
with associated Newton polynomial
In other words, all solutions of 
, where 
. Usually, the Newton polygon
method proceeds by performing a change of variable
while imposing the constraint .
So we are reduced to solving
The Newton polygon has two edges: 
and 
. Therefore 
and we have 
, so 
, where 
.
We proceed with the change of variable
while imposing the constraint 
.
So we are now led to solving
The unique value of 
can therefore be computed
efficiently by means of the Newton iteration as a regular root of 
. However, this means that we have
to work over the algebraic extension 
.
The idea behind contact calculus is to avoid computing over this type of
algebraic extensions, by working with respect to so-called contact
coordinates instead. In the present example, the idea is to rewrite
We next reinterpret this equation as
 |
(2.4) |
where 
and 
are two new
variables that are subject to the following constraints:
, 
,
and 
.
The variables and can be
regarded as unknowns, with values in the ring of Puiseux series in . These unknowns satisfy the system
of equations
In other words, computing Puiseux expansions of solutions to is equivalent to computing Puiseux expansions of solutions
to the latter system. We note that 
is separable
in and that the solutions for
begin with 
. Then 
is separable in for each solution
, so the system admits the
following solutions:
After the change of variable 
,
these solutions are regular roots of the following map modulo 
:
By means of the Newton iteration, these roots may be lifted efficiently
to any required precision, and so may the corresponding solutions of
.
The variables and are
called contact coordinates. Note that
so the germ of the curve defined by 
approximates
the one defined by 
. From a
geometric point of view, the two germs are “in contact”.
Informally speaking, the Newton polygon of equation has a single edge of
vertices 
and 
,
with associated Newton polynomial ,
whence 
. The precise meaning
of this “generalized Newton polygon” will be the purpose of
section 7. Since the polynomial 
is
separable in 
, we consider
the polynomial to be “solved”.
Working with contact coordinates is a little bit tricky, since and are related by the equation
. Basic arithmetic operations
and the Newton polygon method therefore have to be adapted with care. It
turns out that “contact calculus” with respect to contact
coordinates has a double flavor. At small orders
in , it boils down to working
in towers of algebraic extensions of 
.
At large orders in , we may
convert between polynomials in 
and 
through the mechanism of 
-adic
expansions.
In this paper, we have chosen to do most actual computations in , since fast algorithms for basic
arithmetic operations in this ring are well known. However, conversions
between the “plain coordinates” 
and
the “contact coordinates” 
incur some
precision loss. Fortunately, this precision loss can be controlled for
the applications in this paper. Of course, it would be interesting to
design a genuine fast arithmetic for contact coordinates without
precision loss.
Example
 |
(2.5) |
In that case, the contact coordinates would rather be 
and . This illustrates that
we do not systematically take ,
although we always do have 
when working over
.
Let us next consider the equation
 |
(2.6) |
In this case, we start with the same contact coordinates and as for 
,
subject to 
. In general, we
may need to introduce as many as 
contact
coordinates.
Yet another variant of
 |
(2.7) |
We again use the same contact coordinates and
as for rewrites into 
, that can be factored:
In general, these types of factorizations can be expensive to compute with respect to the original coordinates and become more transparent for the contact coordinates.
Let us first consider the equation
 |
(2.8) |
When solving this equation using the usual Newton polygon method, we
find that there is a single slope ,
with , for which the
associated Newton polynomial 
has a single root
of multiplicity 
.
This means that the leading terms of the Puiseux expansions are and that the remaining terms can be found by
performing the change of variable 
and solving
the resulting equation for :
In a similar way, we find the leading term of
, which has again
multiplicity . We have to go
on like this for 
steps until reaching the
equation
At this point there are two possible dominant terms for 
(namely 
and 
),
each of multiplicity one, and we consider that we essentially solved the
equation (more terms can be obtained efficiently using Newton's method).
From the complexity point of view, the problem is that we need to
recompute a new equation at every step where we discover one more term
of the expansion, which is quite expensive. A well known trick to
replace the 50 steps by a single one is to compute the solution 
to the derivative of the equation, that is
and directly set 
instead of . The new equation in
then becomes
after which the resolution process directly splits into two branches
and 
.
In general, for a -fold
leading term, we need to consider a solution 
to
the 
-fold derivative of the
equation. In that case, the change of variables
is called a Tschirnhaus transform.
For general contact coordinates, things become more technical, but
similar strategies apply. In general, if is a
ring with unity, if is a monic polynomial of
degree in 
,
if divides ,
and if is invertible in , then there exists a unique monic polynomial 
of degree 
such that 
has degree 
;
see section 8.3. The polynomial 
is
called the -th
approximate root of .
If 
, then the -th approximate root 
corresponds to the Tschirnhaus transform .
In general, the -adic
expansion of writes as 
where the 
are polynomials in
of degree 
, so is the -th
approximate root of if and only if
.
Let us now consider yet another type of equation with an almost -fold multiple solution
 |
(2.9) |
When solving the equation naively with the Newton polygon method, we
obtain a -fold branch 
at the first step, a single branch 
and a -fold branch 
at the second step, a single branch 
and a 
-fold branch 
at the third step, and so on. From the complexity point of
view, factoring out a single branch at every step leads to a cost
as a function of , which is
not quasi-linear in .
Using Tschirnhaus transforms is not really of any help. For instance,
the -fold derivative of the
equation yields
with solution 
. After the
change of variable , we still
obtain one single branch and one -fold
branch.
What really helps in this situation is a way to determine the series
 |
(2.10) |
This series has the property that, after the change of variable , we obtain the equivalent equation
whose Newton polygon has 
edges. In particular,
the resolution process now branches into
distinct parts of multiplicity one.
Computing the series .
But instead of peeling off factors of degree one from the left-hand side
of with precision about 
in a
recursive manner. This allows to factor as the
product of two polynomials of degree close to , and to repeat this process in a recursive manner.
Series such as , even within contact coordinates, the central
shift will allow us to guarantee a suitably balanced factorization 
for which 
and 
can recursively be factored with good complexity.
This section formalizes the concept of contact towers. The effective
ground field is written and the contact
coordinates will be denoted by 
.
We endow 
with the weighted valuation, simply
written “
”,
defined by 
and 
for . With
this valuation induces a grading
where 
is the set of polynomials made only of
terms of valuation ; notice
that 
. When no confusion is
possible, we drop “weighted”.
Let 
be the least common multiple of the
denominators of 
. Then, the
Chinese remainder theorem implies the following identity for the group
completion 
of 
:
The integer is called the ramification
index of the valuation.
The following definition is central for the rest of this paper.
consists of:
Rational numbers ,
called weights.
These data are required to satisfy the following properties:
is monic in 
of
degree 
;
, for 
and 
;
and 
for ;
We endow with the weighted valuation
defined by and 
for
. We demand that:
, for ;
, for 
.
The tower is said to be reduced when
for 
.
Unless explicitly stated, the towers in this paper will be
almost reduced in the sense that
for 
.
The weights will also be called the contact
slopes, in reference to the slopes of the corresponding Newton
polygons; see section 7.3. When a contact tower is almost
reduced then 
holds. The degree
of the tower is 
.
Example 
, 
,
form a contact tower of height 
.
Example 
, 
and
form a contact tower with contact slopes , 
.
Here we got 
and 
from
and 
.
We introduce another independent variable 
of
weight 
and subject to the constraint 
. We also define the ideal
and the corresponding quotient ring
In the following paragraphs, we show that 
is
effective for computations with finite truncation orders in and . For this,
we adopt the point of view of standard bases, while doing the proofs
from scratch for completeness. We recall that the lexicographic
ordering 
on 
is
defined as follows:
We also introduce a total ordering 
with
on the group 
by
The ordering is a monomial ordering in
the sense that
implies
for all 
. The leading
monomial 
of 
with
respect to this ordering is defined to be the largest monomial with a
non-zero coefficient in . The
set of monomials spanned by the leading monomials of the elements of an
ideal is written 
.
Note that 
. With the
terminology of [33], the ordering
is called a negative weighted degree lexicographic local
ordering.
A standard basis of an ideal 
with respect to the monomial ordering is a set
of generators 
such that the leading monomial of
any polynomial in is a multiple of the leading
monomial of at least one of the 
.
In other words, is generated by 
. A standard basis is said to be reduced
whenever none of the non-leading monomials in the
belong to .
For the completeness, we now prove two well known lemmas from the theory of standard bases.
is a reduced standard basis of 
for 
.
Proof. Since 
are
independent of , it suffices
to prove the lemma in .
According to the assumptions, 
is monic of degree
in ,
and for all 
and 
. Therefore,
for . The lemma follows from
general standard basis theory since the leading monomials of the 
share no variable. For completeness, we give a
dedicated proof.
Let us prove by induction on 
that 
is a standard basis for the ideal 
in 
. This clearly holds for
. Let us assume that the
induction hypothesis holds for some and consider
. If 
, then 
is a multiple of
. Otherwise, we write
with 
and 
.
Then
so 
belongs to the ideal 
of 
. By the induction
hypothesis, 
is a multiple of 
for some 
, whence so is . It follows that
is a standard basis. The fact that it is reduced is clear from degree
considerations.
For 
, we define
where 
stands at position
and 
at position 
.
Note that the dot product 
is identically zero.
For 
, the initial form of
, still written 
, is defined as 
.
Proof. We prove the lemma by induction on . For 
,
we have nothing to prove, so assume that 
.
Extracting homogeneous components, we may assume without loss of
generality that
whenever 
and 
.
By the induction hypothesis, we may also assume that 
. Long division of 
by
yields
for homogeneous polynomials 
with 
, for 
.
Reducing the relation 
modulo 
, we obtain
Since 
is monic in 
,
it follows that 
, and thus
that 
. Consequently, we
obtain
which implies
Let . If 
, then 
is homogeneous.
Otherwise, we have
so 
is also homogeneous. Each
can be expanded with respect to :
with 
. Then we have
which implies 
for all 
. We conclude by applying the induction
hypothesis.
Proof. We expand each 
with respect to the variable :
For all , we get
so Lemma 3.5 ensures the existence of homogeneous
polynomials 
in such that
Letting 
, we deduce that
Since the are homogeneous, up to replacing the
by their homogeneous components of suitable
valuation, we may assume that
the are homogeneous,
holds for all with
and 
,
holds for all with
and .
For 
, we introduce the
vectors
where 
stands at position 
and 
at position 
,
so the dot product 
is identically zero. We set
Using the fact that 
, we
conclude that
Proof. Let 
,
so there exist 
with
We repeat the following operations:
Let 
. Since 
, we always have 
. If 
,
then we obtain a relation
where 
is the non-empty subset of indices
such that 
,
so we are done.
Otherwise 
, hence 
. The latter relation can be
lifted to 
with 
for
, by Lemma 3.6.
Replace the vector 
by 
, and go to step 1.
Thanks again to the assumption ,
the relation 
holds after each iteration.
Furthermore, the value of 
strictly increases, so
the process converges. We conclude that 
.
Proof. Assume that 
belongs to 
. Then 
, so Lemma 3.7 implies
that 
for some 
.
From Proposition 3.8, we know that an element of can be uniquely represented by
a polynomial 
of partial degree 
in for .
We call the canonical
representative of .
We introduce contact towers as a tool for the local resolution of polynomial equations. For this, we will often reduce to the case when all the roots of the polynomial are in the local region of interest. Such polynomials are said to be “clustered”:
in is a clustered polynomial if
its canonical representative is monic in of
degree 
and if 
.
Example is a clustered polynomial regarded in 
for 
.
The theory of standard bases comes with algorithms to compute modulo
ideals given by standard bases. We now detail how to perform such
computations in the case of .
Additions, subtractions and scalar multiplications are straightforward,
but other operations require an appropriate treatment of
“carries” within -adic
expansions. For the contact coordinates of Example 3.3, let
us briefly illustrate how carries occur during multiplications.
Example and
form a contact tower with contact slopes , .
Let us first illustrate the computation of a product modulo 
:
Doing a direct polynomial multiplication, we obtain
which is not in canonical representation since the degrees in and are too high. We thus have to
rewrite
and
At the end, this leads to the following canonical representation for
modulo :
The canonical representative of an element in can uniquely be written as
where 
satisfies 
for
. Similarly, the canonical
representative of another element 
can be written as
Now assume that 
for sufficiently large values of
. Then we may regard 
as a univariate polynomial in : the “degree of in
”, written 
, is defined as the largest integer
such that 
.
We say that is “monic of degree
in ”
when 
and for 
.
Now we ask whether we can define and compute a generalized Euclidean
division of by .
The answer is “yes” under suitable assumptions. More
generally, the following lemma shows that there exists a unique -adic expansion of .
is clustered at 
and has degree 
in . Then,
there exist unique elements 
in satisfying
and such that 
for all 
.
Proof. This lemma is a reformulation of what we have already proved with contact coordinates. In fact, it suffices to increase the height of the tower by one, to set
, and to assign any weight
to the new variable 
. Therefore, the canonical representative of the
image of in 
is given by
where 
for 
.
Consequently the above -adic
expansion of exists with 
.
As for uniqueness, let the be as in the
statement of the lemma, and let us write them
with 
. The 
must satisfy
that implies
It follows that the do exist and are uniquely
determined by the canonical representative of in
.
and 
are respectively
called the quotient and remainder of
the Euclidean division of by , and are written 
and
.
Example
We have
Therefore the division of by
writes 
with 
and 
.
In what follows, we will restrict ourselves to computations with “polynomials” in
instead of “series” in .
Elements in can be
represented canonically by polynomials 
of
partial degrees in for
. In order to alleviate
terminology, we call elements in contact
polynomials, in which case we always assume that
is represented canonically as a polynomial 
in
with 
;
we will also call this the contact representation.
At the same time, we will keep the terminology of “canonical
representatives” whenever we need to carefully distinguish between
and its actual polynomial representative .
By what precedes, we may recursively expand elements in
with respect to 
until . However, from a computational point of view such
recursive 
-adic
expansions are expensive. Indeed such expansions are reminiscent of
computations modulo triangular sets, so it would be interesting to
examine whether the algorithms of [51] could be adapted or
not. In this subsection we follow another direction that leads to
efficient algorithms. The key idea is to rewrite elements in with respect to the plain coordinates
and .
For this purpose, we introduce the following polynomials:
Note that 
is monic of degree 
. The change of representation is presented in
the following lemma:
Proof. We introduce the following auxiliary
evaluation morphism over :
For , we have
so 
and 
is well defined.
Let us prove by induction on that is bijective. This is clear when , so assume that .
Let be of degree 
for
some integer 
. The 
-adic expansion of
yields a polynomial
such that 
and 
for 
. Next we recursively compute 
for . This
yields
with 
. This proves that is surjective.
Now let 
be non-zero. Since 
, we must have 
,
that is 
. The induction
hypothesis implies that 
.
As seen in the proof of Lemma 3.15, the isomorphism corresponds to a cascade of -adic expansions for .
We begin with recalling known costs for univariate expansions over an
effective ring .
and let be
monic of degree 
. The 
-adic expansion of 
can be computed using 
operations
in 
.
Proof. Without loss of generality, we may assume
that 
for some integer 
. We compute 
using 
operations in .
We divide by 
,
so 
with 
and 
. Then we compute the -adic expansion of 
and 
in a recursive manner so the expansion of is obtained by merging those of
and . The depth of the
recursive calls is 
. The sum
of the costs of the operations at depth is , whence the claimed bound.
be polynomials in 
and let be a monic polynomial of degree in .
Then, 
can be computed using
operations in , where 
.
Proof. Without loss of generality, we may assume
that 
for some integer . We compute with operations in .
In a recursive manner we compute 
and 
, and finally we compute 
with operations in . The rest of the complexity analysis follows
as in the proof of Lemma 3.16.
Remark 
in
Lemmas 3.16 and 3.17; see [46].
,
and write 
. One evaluation
of modulo at an
element of degree 
in 
(for the canonical representation), and one evaluation of 
modulo at a polynomial of degree
in ,
both take 
operations in .
Proof. Let be of degree
. Its -adic expansion takes 
operations in by Lemma 3.16. Then,
we perform 
calls to 
in
degree 
. A straightforward
induction gives a total complexity bound
The backward conversion makes use of Lemma 3.17, and the
complexity analysis is similar.
,
and let and be two
contact polynomials in of degree in and given with precision
. Then, the product 
can be computed modulo with
operations in ,
where 
.
Proof. The product is computed via the following formula:
By Proposition 3.19 the cost of the conversions amounts to
. Multiplying 
and 
modulo
incurs 
.
For actual machine computations, we only work with truncated power
series. The decision of whether it is more efficient to use contact
representations or the plain representations in
depends on the truncation order. For sufficiently small orders, the
“carries” can be neglected, which makes it more efficient to
conduct computations directly in the contact representation. For large
orders, and thus for asymptotic complexity analyses, the overhead of the
conversions using isomorphism . Until the end of the
paper we perform most of the computations directly in , and thereby minimize the number of
conversions.
The isomorphism with respect to
, in the sense of Lemma 3.12. In fact, let and be as in the lemma, and compute the division of by :
where 
. The degree in of the canonical representative of 
is therefore 
. It follows
that equals the remainder 
of Definition 3.13. Since both and
have finite degree in , we note that this also yields an easier way to
define the division in comparison to Lemma 3.12. In
particular, the assumption that 
is not needed.
,
and let and be two
contact polynomials in of degree in , and
given with precision . If
is monic in ,
then the division of by
can be computed modulo with
operations in , where .
Proof. The division is
computed as above via
By Proposition 3.19 the conversions take . Dividing by modulo incurs .
Recall that 
represents the valuation semi-group
of the contact tower
stand for the image of in . The
valuation 
extends to a semi-valuation 
with 
for 
, and such that
inherits the weighted grading of 
.
Proof. For 
of canonical
representative 
, we set
We need to verify that 
actually defines a
semi-valuation in .
If is another element of
of canonical representative 
,
then it is straightforward to verify that .
As for the product, we compute the long division by the standard basis
thanks to Proposition 3.8:
where 
is the canonical representative of , so 
.
The latter long division begins with setting 
and
then it successively subtracts polynomials of the form 
from where 
,
, 
, and 
.
Since the monomials in 
have valuation 
, it follows that
This shows that 
. Since 
, we deduce that .
We write 
for the partial
valuation in of 
. The valuation in of an
element of will be the valuation in of its canonical representative. In the canonical
representation, the degrees of the being
bounded, the valuation in of an element in can be related to 
in terms of
the 
. The following bounds
will be useful when converting between the canonical and plain
representations.
Proof. Assume 
.
There exists a monomial of the form 
in . Using and
for ,
we verify that
and then that
 |
 |
 |
|
|
 |
||
 |
 |
||
|
 |
||
 |
|||
|
 |
|
The following lemma asserts that preserves the
valuation in .
Proof. For any element 
, the inequality 
clearly
holds. Conversely, for any 
,
we have 
. It follows that
whence the first assertion. The second assertion is a consequence of the
fact that is a -isomorphism;
see Lemma 3.15.
The next lemma relates valuations and precisions of approximations of
and .
Proof. Lemmas 3.23 and 3.24 give us
 |
(3.4) |
In particular, if 
then 
. As for the second assertion, the inequalities
In particular, if 
then 
.
Remark
For simplicity we will not use this refinement in the sequel.
The usual Hensel lemma asserts that if a monic polynomial factors into two monic coprime polynomials 
and 
modulo , then there exist unique monic polynomials 
and 
in
such that 
, 
, and 
.
In addition, and can be
obtained with a softly linear cost in the output size.
A variant of Hensel lifting is the Weierstraß preparation theorem,
in which case and are no
longer monic, but is invertible as a power
series in . We will
generalize these two kinds of lifting to the contact coordinate
framework.
Throughout this section, ,
are elements in ,
regarded informally as “polynomials” in the main variable
. We will assume that 
holds for a “sufficient” initial
precision, and that are “pairwise
coprime”. We want to lift into 
so that 
holds up to a required
precision. The case when is monic and
corresponds to the multi-factor Hensel lifting. The case when
and
is called the Weierstraß normalization of
.
Let 
be the canonical representative of . We recall that 
, 
,
and is the image of 
in
. If
is a non-zero element in that is monic in , then 
represents the remainder in the division of by
, as specified in Definition
3.13.
Let be clustered (see Definition 3.9)
at and of degree 
in
. Given 
with 
, its inverse modulo
, whenever it exists, belongs
to 
for some 
.
In order to determine a bound for 
,
consider 
satisfying
,
is an integer 
,
.
Lemma 3.23 yields
If 
, then setting 
leads to
So we may divide 
by 
and
subtract 
from in order
to get a “simplified” modular inverse
of that satisfies
 |
(4.1) |
If 
, so that 
, then multiplication of
by 
also reduces to the case when (4.1)
holds. In general, this shows that modular inverses can always be
normalized in the sense of the following definition:
be clustered at of degree in , and let be of
degree in .
A normalized inverse of
modulo with relative
precision 
is an element 
with 
such that:
,
satisfies 
,
.
If 
, then we say that
is the normalized initial
inverse of modulo
.
The existence and the computation of such inverses are postponed in
section 7.1. The next definition concerns the special case
when belongs to 
.
be of degree 
in (
is in ). A normalized
initial inverse of is a homogeneous
element 
such that:
satisfies 
,
.
Proof. We have 
.
Definition 4.2 also yields
Concerning the uniqueness, if 
represents a
normalized initial inverse of then
and therefore 
, whence 
.
has a normalized inverse modulo
with relative precision , as in Definition 4.1, then it is
unique and 
holds for all 
.
Proof. We extend the contact tower with 
and apply Lemma 4.3 in order to obtain
the equality for the valuation. As for the uniqueness let represent another normalized inverse modulo . We have 
and thus
, whence .
We explain how to increase the relative precision of a normalized modular inverse, in terms of the contact coordinates.
,
and ,
be such that
is clustered at of
degree in ,
,
is a normalized inverse of modulo with relative
precision 
.
Then, there exists a unique normalized modular inverse 
of with relative precision 
such that 
.
More precisely, with and
we have 
and
Proof. Let 
represent an
unknown in 
with 
,
and which satisfies
 |
(4.2) |
This equation is equivalent to
and, by Lemma 4.4, to
Hence
We have 
, and therefore 
. Lemma 3.23 implies
that
so 
can actually be divided by 
. We conclude that 
is
the unique solution of (4.2), whence 
fulfills all requirements.
be clustered at of degree in . If admits an
initial inverse modulo , then there exists a unique 
such that 
and 
.
Proof. Thanks to repeated applications of
Proposition 4.5 we can construct the initial inverse of
modulo with any finite
relative precision. The existence of 
follows
from the completeness of .
The next corollary addresses the precision loss of the initial inverse
of modulo when and are truncated modulo .
be clustered at of degree in . If admits an
initial inverse modulo , then (as defined in
Corollary 4.6) can be computed modulo 
from the truncations of and
modulo , whenever 
.
Proof. Let
represent the truncations of of and modulo , and
let be the smallest element of
larger or equal to 
. Thanks
to repeated applications of Proposition 4.5 we can compute
the initial inverse of 
modulo 
with relative precision .
Since 
and ,
we have 
and therefore 
. From
we deduce that
It follows that 
and then that
Using 
, we obtain that
hence
Lemma 3.23 implies that
Thanks to the value taken for it follows that
whence 
.
We now turn to the Weierstraß normalization of an element . The following definition gathers
the necessary technical conditions and data structures.
be of degree in . A
Weierstraß context for with relative precision consists
of elements 
in and
that satisfy the following properties:
If 
, then we say that
is an initial
Weierstraß context for .
The Weierstraß lifting step summarizes as follows.
be monic of degree
in and let denote a Weierstraß context for
with relative precision .
Then, there exists a unique Weierstraß context 
for with relative precision
such that 
, 
, and 
.
More precisely, with
we have 
and
Letting
we also have 
and
Proof. Consider the unknowns 
and 
such that 
and
It follows that
Lemma 4.4 and the constraints on valuations and precisions equivalently yield
whence
Then Lemma 3.23 gives
This shows that 
exists and is uniquely
determined by
The formula for 
is straightforward and the one
for 
follows from Proposition 4.5.
be monic of degree
in and let denote an initial Weierstraß context for . Then, there exist unique 
such that 
,
, and 
. We call 
(that is
clustered at ) the Weierstraß
part of .
Proof. This follows from Proposition 4.9
and the completeness of .
be monic of degree
in .
If there exists an initial Weierstraß context
for , then
and 
(as defined in Corollary 4.10)
can be computed modulo 
from the truncation of
modulo .
Proof. We introduce the truncation 
of modulo , and set to the smallest
element of larger or equal to 
. The quadruple 
,
, 
, 
is an initial
Weierstraß context for .
From Proposition 4.9 we know that we can compute the
Weierstraß context 
,
, , for
with relative precision , so
that 
and
According to Corollary 4.6 we may consider the modular
inverse 
of modulo , so that 
. Hence
and
Lemma 3.23 implies that
Since and are monic of
the same degree in we deduce that 
.
The above formulas for the Weierstraß lifting can be applied
directly in , but for the
sake of efficiency it is worth using plain coordinates. As a technical
complication, conversions between contact and plain coordinates result
in precision loss. Fortunately, this loss is sufficiently small so that
it has no serious impact on the complexity of our top-level
factorization algorithm. In the following algorithm, the input and
output polynomials use plain coordinates. However, the relative
precision , to be doubled
during a lifting step, refers to the contact coordinates.
Algorithm
and degree
as above, a rational number
.
A monic polynomial
modulo
,
where
,
and polynomials
in
modulo
.
The elements
for
,
,
and
form a Weierstraß context for
with relative precision
,
as in Definition
4.8
.
in modulo , such that the elements
for ,
, and form a Weierstraß context for with relative precision 
such that 
for
and 
.
Set 
.
Compute 
in 
.
Compute 
and 
in
.
Compute 
in .
Compute 
in .
Compute 
and 
in
.
Return .
Proof. The hypotheses of Proposition 4.9 are satisfied. We let
Lemma 3.25 implies
We have seen in Proposition 4.9 that , whence 
by Lemma 3.24.
Consequently 
is well defined. With the notation
of Proposition 4.9 we verify that
and
By Proposition 4.9, properties 
, and relative
precision .
In a similar fashion we verify that
so we have
By Proposition 4.5, property 
.
Applying successively Algorithm 4.1 several times enables us to lift any such initial context to any requested precision. The cost is summarized in the following corollaries.
be of degree in and let
be an initial Weierstraß context for . Then, given ,
we may compute a Weierstraß context for
with relative precision
using
operations in , where
and 
is the degree of
the contact tower.
Proof. We convert the input data into the plain
representation modulo using Proposition 3.19,
with 
operations in .
We successively apply Algorithm 4.1 to increase the
relative precision from 
to 
, for 
.
By Proposition 4.12, the total cost of the lifting
contributes to
At the end of the lifting, we convert the polynomials to contact
coordinates modulo via Proposition 3.19,
again with operations in .
be of degree in and let
form an initial Weierstraß context for . Then, given with
precision with 
,
we can compute its Weierstraß part (as
defined in Corollary 4.10) with precision using
operations in , where
is the degree of the contact tower.
Proof. The truncation of
at precision does not depend on , as long as the initial Weierstraß
context properties are preserved. In particular we may set 
to the largest slope of (which is
if is a power of ), so we have 
where 
, whence
 |
(4.3) |
We use Corollary 4.13 with relative precision 
, as in the proof of Corollary 4.11.
The running time is
which yields the claimed bound thanks to inequality
We now turn to the lifting of a factorization of an element , assuming that suitable approximate modular
inverses are known. The following definition gathers the necessary
technical conditions and data structures.
be clustered at of degree in . A Hensel
context for with relative precision
consists of elements 
in and integers 
that
satisfy the following properties:
Informally speaking, the assumption that 
admits
a normalized initial inverse modulo 
for 
corresponds to the idea that
are “initially coprime”. We revisit the classical Chinese
theorem in this context.
Proof. Let us write
By construction this yields
 |
(4.4) |
for . Assume by induction
that there exists 
such that
 |
(4.5) |
holds for some , which is
indeed the case for by 
, there exists 
such
that
 |
(4.6) |
Since 
is initially invertible modulo 
, Corollary 4.6 yields
the existence of the initial inverse 
of modulo ,
so there exists such that
Combining the latter equality to
thanks to Lemma 4.4 and with 
.
At the end of the induction equality 
, and since 
, we finally deduce that 
.
Given clustered at ,
we can increase 
with and
. The contact tower 
obtained in this way corresponds to the quotient ring
: in the sequel is endowed with the semi-valuation induced by 
.
is a -linear isomorphism
and we have 
, where
Proof. It is clear from the assumptions that the
map is well defined and -linear.
Let
From Lemma 4.4 we have
so Lemma 3.23 implies
If follows that 
belongs to
and that 
. By construction we
have
that proves that 
is surjective.
Let 
be in the kernel of . There exists 
such that
for .
By Lemma 4.16 we deduce that
whence 
. Consequently is injective.
The Hensel lifting step goes as follows.
be clustered at of degree in . Let 
represent a
Hensel context for with relative precision
. Then, there exists a
unique Hensel context 
for
with relative precision such that 
and 
for . More precisely, letting
for , we have 
,
Letting 
and
we also have 
and
Proof. For ,
let us consider unknowns 
in 
such that 
and
After expanding the right-hand side of the latter equation, we obtain equivalently that
 |
(4.7) |
By Proposition 4.17, equality
For , Lemma 4.4
and the constraints on valuations and precisions then yield
whence
Then Lemma 3.23 gives
For , this shows that is uniquely determined by
whence satisfy the required properties. We
finally remark that
for , so the formulas for the
follow from Proposition 4.5.
be clustered at of degree in and let represent an initial
Hensel context for . Then,
there exist unique 
such that 
, for ,
and 
.
Proof. This follows from a repeated use of
Proposition 4.18 with increasing precision.
be clustered at of degree in and let represent an initial
Hensel context for . Then
(as defined in Corollary 4.19)
can be computed modulo 
for
from the truncation of modulo .
Proof. We introduce the truncation of modulo
and let be the smallest element of larger or equal to 
.
By assumption, form an initial Hensel context
for . From Proposition 4.18 we know that we can compute the Hensel context for with relative precision , so that 
and
Since 
is the initial inverse of 
modulo , Corollary 4.6
ensures the existence of the modular inverse 
of
modulo ,
which satisfies
It follows that
whence
Lemma 3.23 implies that
Since 
and are monic of
the same degree in we deduce that 
.
Hensel lifting is performed by the following algorithm that is dedicated to doubling the relative precision of a Hensel context.
Algorithm
and degree
as above, a rational number
.
A monic polynomial
modulo
,
where
,
and polynomials
in
modulo
.
Integers
in
.
The elements
,
,
and
for
form a Hensel context for
with relative precision
as in Definition
4.15
.
in modulo , such that the elements
, 
, and for form a Hensel context for
with relative precision .
Set , and 
.
Compute 
in 
,
for .
For :
Compute 
in 
,
Compute 
and 
in .
Compute 
in .
Compute 
in for
.
For , compute 
in .
For , compute 
and 
in .
Return .
Proof. The hypotheses of Proposition 4.18 are satisfied. We let
Lemma 3.25 implies
We have seen in Proposition 4.18 that , whence 
by Lemma 3.24. Consequently 
is well defined for
. With the notation of
Proposition 4.18 we verify that
By Proposition 4.18, properties and relative precision .
In a similar fashion we verify that
From Proposition 4.18 we know that 
divides 
, so it divides 
. Consequently 
is well defined for , and we
have
By Proposition 4.5, property
Concerning complexities, from Definition 4.2 we first observe that
for . Consequently steps 2,
4, and 5 take
operations in using the sub-product tree
technique; see [31, chapter 10, Theorems 10.6 and 10.10],
for instance. The other steps require 
further
operations in .
Applying successively Algorithm 4.2 several times enables us to lift an initial Hensel context to any requested precision. The cost is summarized in the following corollary.
be clustered at of degree in , and let be an
initial Hensel context for .
Then, given and 
,
we may compute a Hensel context for with relative precision
using
operations in , where
is the degree of the contact tower.
Proof. We convert the input data into the plain
representation modulo using Proposition 3.19,
with operations in .
We successively apply Algorithm 4.2 to increase the
relative precision from to , for .
By Proposition 4.21, the total cost of the lifting
contributes to
At the end of the lifting, we convert the polynomials to contact
coordinates modulo using Proposition 3.19,
again with operations in .
be clustered at of degree in , and let be an
initial Hensel context for .
Then, given at precision
we can compute (as defined in Corollary 4.20) at precision for 
, using
operations in , where
is the degree of the contact tower.
Proof. We use Corollary 4.22 with
the relative precision 
as in the proof of
Corollary 4.20. The running time is
Then we verify that
Using 
the cost of the lifting simplifies to
.
In this section we introduce the notion of “separability” for contact towers. This will allow the construction of derivations on contact towers, which will be the key ingredient of the central shift algorithm in section 7.7.
Informally speaking, a contact tower is said to be separable when the
initial forms of the its defining polynomials
are separable. The precise definition is as follows.
of contact
coordinates as in Definition 3.1 is said to be separable
when 
is initially invertible in 
, for .
It is said to be effectively separable if
the normalized initial inverses of the are
known for algorithmic purpose.
Throughout this section, we assume that is
effectively separable. For ,
represents the initial inverse of 
modulo . More
precisely, we assume that 
is homogeneous and
satisfies 
, where 
. From Definition 4.1
we know that
since 
.
Example by
taking , , ,
, and 
. Indeed,
where 
stands for remainder with respect to the
variable .
Example
and form a contact tower of height with contact slopes ,
. We get
and from and . As for the modular inverses we
may take , 
,
Indeed, we verify that
Since the map 
is a -isomorphism,
from Lemma 3.15, the derivation 
on
induces a derivation on
(that is still denoted by for simplicity):
The separability assumption ensures that this derivation satisfies several convenient properties.
Proof. We prove the result by induction on . For we
have
and
For we have
By Lemma 4.3, the separability assumption yields
Combined with the induction hypothesis we deduce
On the other hand, for we have
and therefore
 |
|||
 |
 |
||
|
 |
||
|
 |
||
 |
 |
|
We now study the effect of several consecutive differentiations in .
Proof. The inequality follows from
Lemma 5.4, and the inequality
for .
Proof. Writing 
,
we have
Then, for 
, we have 
so Lemma 5.5 yields
On the other hand,
 |
(5.1) |
so Lemma 5.4 implies
and
Proof. First note that
holds for all 
. We prove the
lemma by induction on . The
result is clear for 
, so
assume that 
. The induction
hypothesis implies that
 |
(5.2) |
for some such that
Differentiating 
yields
 |
(5.3) |
Since 
does not depend on , the initial form of 
also
does not depend on . It
follows that
whence
 |
(5.4) |
Equation , and the definition of imply that
 |
(5.5) |
By combining
 |
(5.6) |
On the other hand Lemma 5.6 gives us
 |
(5.7) |
We conclude the proof by combining equations
Canonical representations are not always the most efficient ones for
computations with initial forms. This can be already observed in the
case when 
. Indeed, let us
write
with 
and for 
. Let and
be coprime integers such that
Then, the coefficient 
is zero whenever 
is not a multiple of 
.
This shows that 
is sparse in the sense that it
contains at most 
non-zero terms besides 
. In particular, computations that
use the dense representation are deemed to be suboptimal.
Assume for instance that we need to compute the valuation and the
initial inverse of 
. We first
extract the initial part of its canonical representative ; there exist 
and 
such that
where 
. Note that is again sparse. We now have to compute the Bézout
relation of the specializations at 
of and in 
. Without exploiting the sparsity, this computation
takes 
operations in . In this particular case, the remedy is to compute
with respect to 
instead of , while exploiting the fact that 
and are dense polynomials in .
In order to generalize this remedy to the case when 
, we show in this section how to rewrite sparse
homogeneous polynomials in 
into suitable
products of coefficients in “algebraic towers” over and “monomials”.
In all computations below, will be an
effectively separable contact tower (as in Definition 5.1)
that satisfies the following additional property.
is said to be regular
when 
has valuation 
and
is initially invertible, for .
It is said to be effectively regular if
the normalized initial inverse of is known for
algorithm purpose, for .
This regularity assumption implies that is
determined by
An algebraic tower over is a sequence
with 
and 
, for and monic
polynomials 
. We will write
for the image of 
in 
and set 
for . The tower is said to be effectively
separable when we are given and 
in 
of respective degree 
and 
such that the Bézout
relation
holds, for . The next
definition concerns the alternative representation of homogeneous
polynomials modulo 
.
An effectively separable tower
where 
is monic of degree 
in .
The class of in
is written . For 
the inverse of exists
and is known.
A tower of purely ramified extensions of 
, written
where 
are positive integers called ramification indices,
for , and 
is invertible in 
for 
. The class of 
in 
is written 
.
and a uniformizing parameter 
such that 
,
where 
, for .
coprime with 
along with integers and 
such that 
and 
, for .
The construction of an initial expansion associated to a contact tower
is achieved by induction on .
This subsection is devoted to the case when . As in the introduction of this section, we write
with and for . Note that 
because the tower is regular. As before, we let
and be coprime integers such that
We define
where . Note that 
whenever is not a multiple of
. The inverse of 
is:
With 
and 
,
the map
is well defined because
Let us now show how to compute conversions via 
. Let 
be homogeneous of
valuation 
and write
with . Then the formula
allows for the computation of 
without any
arithmetic operations or zero tests. This also shows that is an isomorphism.
Assume that two elements 
and 
in 
with 
have the same
valuation, that is
If 
(that corresponds to 
), then 
so 
and therefore 
. Otherwise we
have
and and are coprime. So
divides 
,
whence 
and 
.
In other words, any homogeneous element in 
can
be written in a unique way as 
with 
, 
,
and 
.
Now consider the Bézout relation 
between
and ,
with 
and 
.
The element
has valuation 
. From
and
we obtain formulas to rewrite and 
in terms of 
:
Consequently is a uniformizing
parameter of , whose
valuation group is
and 
. In particular, 
is a purely ramified extension of 
. It remains to make 
effectively separable. To this end, we first compute
Let 
and 
be such that
and let 
be such that
. Then we have
Necessarily 
and 
is the
inverse of 
. From this
inverse we easily recover the Bézout relation of 
and 
, that makes the tower
effectively separable.
The next lemma deals with the construction of an initial expansion
associated to a contact tower. We extend the above construction for
.
, there exists an initial
expansion such that each divides , and
is a -algebra
isomorphism, for . We set
. In addition, with , 
has
valuation group
The algebra inherits the grading of 
. We still write
for the semi-valuation induced over ,
so 
and 
for . Any homogeneous element of can uniquely be written as 
, where 
and
Proof. We prove the lemma by induction on 
The case has been addressed
in the previous subsection, so we assume that 
and recall that 
is a uniformizing parameter of
. We write
where 
is homogeneous for 
. Then we define
where 
and 
,
for 
. We introduce
so we have
 |
(6.2) |
Since the tower is regular, 
is invertible. Since
is homogeneous, we have
whenever 
is not a multiple of 
and
for 
. The latter equation is
equivalent to
We define 
as
and
 |
(6.3) |
The inverse of 
is then given by
 |
(6.4) |
From the induction hypothesis, 
can uniquely be
rewritten as
where 
is invertible in 
and 
. We also have
so Lemma 3.23 further yields
Inside 
, the following
equalities hold:
which shows that 
is well defined.
Let 
be homogeneous of valuation 
, such that 
for , and let us write it in the form
with 
homogeneous in 
and
. Then
shows that it is straightforward to compute
recursively, and that is a -algebra isomorphism; an explicit recursive
formula for 
will be given in the proof of
Proposition 6.4 below.
Now assume that two elements 
and 
, with 
,
have the same valuation, that is
or, equivalently
Since , from Definition 3.1, 
, and since
and 
are coprime, divides 
,
whence 
and 
.
In other words, any homogeneous element in 
can
be uniquely written 
with 
, 
and 
.
Let
be the Bézout relation of and , with 
and
. The element
has valuation
On the other hand we verify that
 |
(6.5) |
and
 |
(6.6) |
Consequently, the valuation group of is
and 
is a uniformizing parameter. In addition we
have
whence
 |
(6.7) |
In order to show that is separable, we verify
that
Let 
and 
be such that
and let 
be such that
. Then we have
It follows that 
and
whence
 |
(6.8) |
From this inverse we easily recover the Bézout relation of 
and so the tower is effectively separable.
Before turning the above construction of the initial expansion into an
algorithm, we study the costs of the conversions
and . We recall from section
1.2 that products in take operations in .
be homogeneous of
valuation in 
.
Recall that 
. Then we can
compute 
in the form 
with 
using
operations in .
Conversely, given with , we can compute
with the same cost bound. In addition, if
has degree in and if
divides 
,
then we can compute 
using
operations in .
Proof. Let us first assume that 
. Let denote the
canonical representative of .
There exists such that 
and
Note that 
. Hence, for 
, we may recursively compute 
with .
Then we verify
Recall that the inverse of is at our disposal
and that the belong to . So we need to compute 
using binary powering and fast tower arithmetic. Then, we multiply this
quantity by 
. These products
take
operations in . Since and 
, we
may simplify
Let 
be the cost of evaluating
at any valuation 
. We have
shown that
whence
The above formulas can be read in reverse order for performing a
backward conversion , with a
similar cost; note that 
.
Assume now that 
. Then we
replace by 
and use 
to obtain
This contributes 
operations in .
The second assertion of the proposition corresponds to the special case
where , which leads to the
cost 
via the following formulas:
 |
|
 |
|
|
 |
||
|
 |
|
Having shown how the conversions and can be computed efficiently, let us now turn to the
incremental construction of an initial expansion. We keep the same
notation as in section 6.3.
of an effectively separable and regular contact tower, an initial
expansion can be computed using
operations in .
Proof. The case has been
detailed in section 6.1: it takes
arithmetic operations in . By
induction on we may assume that the initial
expansion has been computed up to height 
.
We write
with the 
homogeneous in . Since 
and 
, Proposition 6.4 allows us to
compute 
for using
 |
(6.9) |
operations in . This is
sufficient to obtain .
If 
stands for the normalized initial inverse of
, then we can compute 
. Hence
so the computation of the inverse of 
requires
one evaluation of 
at 
and
products in .
The inverse of is then obtained via 
operations in . The cost of
these two tasks does not exceed the bound
The computation of the inverse 
of modulo then requires one
evaluation of at the initial inverse of 
, then 
products in , and 
products in ,
by using formula 
and
, namely 
, requires 
further
operations in .
By using formula 
from 
takes
operations in , that is 
operations in .
The sum of the costs for all levels of the tower is bounded by
 |
|||
|
 |
|
In this section we apply the lifting algorithms of section 4
in order to compute so-called Newton factorizations of a
polynomial that is clustered at
(Definition 3.9). These are partial factorizations that are
related to the contact Newton polygon of
with respect to the current contact coordinates (Definition 7.7).
Until the end of the paper, contact towers will be effectively separable (Definition 5.1) and regular (Definition 6.1). Since we occasionally will have to manipulate multiple contact towers at multiple levels, it is convenient to
regard an element as an element in any other
via the natural isomorphism 
;
write
for the initial form, the valuation, and the truncation of , when regarded as an element
in ;
given 
, write
for the initial form and the valuation of 
in
.
Since we assumed from the outset that we have an algorithm or oracle for
factoring univariate polynomials over ,
we are interested in factoring elements of into
irreducible factors. There is a corresponding notion of irreducible
contact towers and, thanks to our oracle, all contact towers that we
will need for our main factoring algorithm can be forced to be of this
type.
is said to be initially
reducible if there exists and homogeneous in 
such that
. A contact tower is irreducible if 
is initially irreducible for .
In view of the initial expansion and 
of a contact tower ,
we observe from Lemma 6.3 that is
irreducible if and only if is a field.
Equivalently, is a tower of field extensions. In
this case, any non-zero element in admits a
unique normalized initial inverse.
Proof. If is reducible
then their exists a smallest index such that
admits an initial factorization regarded in
. This initial factorization
yields an initial Hensel context that can be lifted into a non trivial
factorization of 
by Corollary 4.19.
Conversely assume that is irreducible and let
be a factor of .
Then, 
initially divides , hence cannot be a non
trivial factor of .
The next lemmas are devoted to the complexity of initial inversions.
be an effectively separable,
regular, and irreducible contact tower, and assume that its initial
expansion has been precomputed. Let 
be
homogeneous and of valuation in . Then, admits a
unique normalized initial inverse, that can be computed with
operations in .
Proof. From Lemma 3.23 we know that
. The computation of
takes
operations in by Proposition 6.4.
Then we compute 
in time
Proposition 6.4 allows us to obtain
with 
further operations. Since 
, Lemma 3.23 implies 
. We verify that
by using identity stated in Definition 6.2.
It follows that 
. After
multiplying or dividing by a suitable power of
we obtain the normalized initial inverse of
.
be an effectively separable,
regular, and irreducible contact tower, and assume that its initial
expansion has been precomputed. Let be
clustered at of degree
in such that does not
divide , and let be homogeneous of degree in and of valuation in . We can test whether admits a normalized initial inverse modulo or not, and if so compute this initial inverse with 
operations in .
Proof. We increment the tower
with 
. The extended tower is
not necessarily separable or irreducible because of its top level, but
this does not prevent from building the corresponding incremented
initial expansion with the difference that 
is
not a field extension of ,
that is not even necessarily separable. By Proposition 6.5
this “almost initial expansion” incurs
operations in . The
conclusion follows from Lemma 7.3: still writing 
, the required initial modular
inverse exists if and only if is invertible in
.
The following lemma asserts that is clustered at
any for 
as soon as it is
clustered at .
be clustered as in Definition 3.9, of degree in . Then, for 
,
the polynomial is clustered at , and we have 
where
.
Proof. Note that is
monic in of degree 
.
Therefore is monic in 
of
degree 
when regarded in , for 
.
The rest of the proof is done by induction on
from down to .
The case 
corresponds to the hypothesis of the
lemma. Now let us assume that 
holds for some
, and consider the contact
representation
in , with
for 
. It follows that
where the second inequality is strict for 
.
Consequently, 
.
be an effectively
separable, regular, and irreducible contact tower and let be clustered at .
An irreducible contact factorization of
at precision is a
sequence of pairs 
modulo
for 
, such that:
is an effectively separable, regular,
and irreducible contact tower for 
;
and 
for ;
is a power of the last contact
coordinate 
of 
modulo for ;
(this equality can be regarded
equivalently in any for 
).
Consider a contact polynomial
with 
for 
and 
. The Newton
polygon 
of is the
lower border of the convex hull of the set of pairs 
with 
and 
.
More precisely, 
is a broken line with vertices
, where
,
for ,
for all such that 
, the point 
is on or
above the Newton polygon.
Any determines an edge 
between the vertices and , of slope .
The set of points above the Newton polygon is convex. When 
we have 
, so
the slope of the first edge is .
In order to establish the usual relationship between
and the Newton polygons of the factors of ,
we introduce the following definition.
of is said to be effectively
regular when the elements 
are
initially invertible in ,
and we are given the normalized initial inverses 
of for 
.
If then we set 
by
convention.
The following lemma extends a special case of a classical result about Minkowski sums of polytopes due to Ostrowski [78] (translated in [80], and revisited later in [79]). In our variant we need to take care of “carries” involved by the contact arithmetic.
and 
be
contact polynomials in .
Their respective Newton polygons 
and 
are assumed to be regular, the slopes of 
are strictly smaller than the ones of 
, and all slopes are 
. If 
,
, 
, and 
,
then the Newton polygon 
of
equals
In addition, the contact polynomial
satisfies 
for 
and
for 
.
Proof. First of all, note that the hypothesis on the slopes guarantees that the region of the plane above the Newton polygon
is actually convex.
Let 
be a point above . For all 
,
we have
 |
(7.1) |
Similarly, for any point 
above
and for all 
we have
 |
(7.2) |
Since the slope of the edge 
is smaller than the
slope of 
, for , we obtain
Combining the latter inequality with
which means that 
is above the line spanned by
and 
.
Similarly, since 
and since the slope of the edge
is smaller than the one of 
, we obtain
for . In combination with
so is above the line spanned by 
and 
. So far, we have proved
that 
is above 
,
for all 
and 
.
Since 
and 
are
invertible, for in 
,
Lemma 4.3 yields
Now consider the contact polynomial 
with 
, so we have 
and 
. Because the slopes of
are 
,
the point 
is strictly above .
Let us fix 
to a value different from the slopes
of and .
Let us assume first that 
is less than the
smallest slope of . If is less than the largest slope of
we let to be the largest integer such that is less than the slope of 
, otherwise we let 
.
Let 
be the corresponding valuation induced in
: 
for
and 
;
we write 
for the corresponding initial part. We
verify that
Consequently, Lemma 4.3 implies
belongs to the Newton polygon of ,
and .
Assume now that is greater than the smallest
slope of then we let to
be the first integer such that is greater than
the slope of 
. Using a
similar argument as above, we may prove that
 |
(7.3) |
belongs to the Newton polygon of ,
and that 
. This concludes the
proof.
be an effectively separable,
regular, and irreducible contact tower and let
be a contact polynomial with the and
truncated modulo with 
. Then, the effectively regular Newton polygon of
can be computed using
operations in .
Proof. We first compute the initial expansion of
, that contributes to 
from Proposition 6.5. Set in 
. In order
to compute the valuation of we run over all its
homogeneous components in in increasing
valuation order. Up to precision 
,
the number of such components is 
.
Each such component has 
terms. Overall the
number of zero tests in is 
.
From the valuations of the ,
the computation of the Newton polygon 
does not
involve arithmetic operations in ,
but 
bit operations (with the usual “divide
and conquer” algorithm). Finally, for a vertex of abscissa of the Newton polygon we need to compute the initial
inverse of . For this purpose
we extract 
and appeal to Lemma 7.3.
Let be clustered at
given with its effectively regular Newton polygon . We are to show that each edge of
gives rise to a factor of .
Algorithm
along with its initial expansion; a contact polynomial
given modulo
with
and clustered at
;
the effectively regular Newton polygon of
(whose slopes are all
).
Let 
be the abscissas of the vertices of the
Newton polygon, as in Definition 7.7. The normalized
initial inverse of
is part of the input for .
Contact polynomials 
modulo , clustered at , such that 
,
admits a single Newton polynomial that
coincides with the -th
one of , for 
.
If 
then return .
Let 
and set 
, where 
is the slope
of the edge between abscissas 
and 
.
Compute 
, 
, 
, 
.
Via Corollary 4.14 called with precision 
, compute contact
polynomials and
in modulo such
that 
, is clustered at ,
, and 
.
Recursively call the algorithm with input : the vertices of the Newton polygon of are 
and the
normalized initial inverses are 
rescaled
by suitable powers of .
Recursively call the algorithm with input : the vertices of the Newton polygon of are 
,
with normalized initial inverses 
.
Return the union of the sets of factors returned by the above recursive calls.
Proof. If then the
algorithm is clearly correct. From now assume 
. By definition of the effectively regular Newton
polygon, the value of 
occurring in step 3 writes
as
From 
and 
for 
, Lemma 4.3 yields
Then Lemma 3.23 implies 
,
hence step 3 computes an initial Weierstraß context for .
Let and be as in
Corollary 4.14: ,
, and 
hold in step 4. From Lemma 7.8 we know that the Newton
polygon of a is the Minkowski sum of those of
and (up to the occasional vertex at infinity of
and ).
Since the vertices of the Newton polygon of have
valuation in 
(or
infinity), so are those of the polygons of and
.
Let 
be the first index such that 
. From 
,
Lemma 3.23 implies 
,
whence
 |
(7.4) |
It follows that the Newton polygon of coincides
with the one of for 
, and that these polygons are effectively regular,
with the initial inverses as in steps 4 and 5.
In step 3, for 
, we compute
with 
operations in thanks to Proposition 3.20. The same
cost applies to the computation of 
in step 5. By
Corollary 4.14, and since 
,
the cost of the lifting in step 4 is
The depth of the recursive calls is 
,
so the complexity bound follows from a standard induction.
be a contact tower,
and let a be a contact polynomial clustered at . The distinct-slope
factorization of is made of contact
polynomials clustered at
such that 
, the Newton
polygon of admits a single edge for 
and the sequence of the slopes of these edges is
strictly increasing.
be an effectively
separable, regular, and irreducible contact tower, and let a be a
contact polynomial clustered at .
Then, there exists a unique distinct-slope factorization of .
Proof. Since the tower is irreducible, the
Newton polygon of can be made effectively
regular, thanks to Lemma 7.3. Consequently the existence of
the distinct-slope factorization of follows from
Proposition 7.10.
Given a distinct-slope factorization ,
by Lemma 7.8 the slopes of the are
those of the Newton polygon of .
If is set to the opposite of the slope of then 
is a Newton polynomial
of of slope (up to a
power of and up to a factor in ). The uniqueness of the
thus follows from the uniqueness of the lifting of the distinct slope
factors.
Consider the factorization of an element whose
Newton polygon has a single edge with finite slope. We have already seen
that an initial factorization into pairwise coprime factors of lifts into a factorization of . We now explain how to obtain this initial
factorization. The contact polynomial is assumed
to be truncated modulo with .
We assume that the initial expansion of the contact tower has already
been computed. We extend the map (defined in
Lemma 6.3) as follows:
We set to be the opposite of the unique slope of
the Newton polygon of
Note that . Let
 |
(7.5) |
with 
prime to 
and let
. Note that 
is an integer. In the next subsection we shall see that the notation is
consistent since 
will be the “next
ramification index”.
We compute 
with 
,
for 
, and construct
so we have
 |
(7.6) |
We factor
where each 
is a power of a monic irreducible
factor and the are pairwise coprime. For 
, we let 
and
 |
(7.7) |
We compute 
using
where 
stands for the coefficient of 
in .
, the polynomial defined in , and
of valuation 
. In addition,
we have
Proof. The first assertion is clear by
construction. The second assertion follows from the fact that is a ring isomorphism that preserves the valuation.
We next compute the modular inverses
for . Let us write the
expansion of 
as follows
let 
be the smallest integer such that 
is a multiple of and set
From
Recall from Definition 6.2 that . We further set
so we have
From
we deduce that
whence
After a division by a suitable power of ,
we deduce the normalized initial inverse of 
modulo for .
The following algorithm makes use of the separable factorization of univariate polynomials: see [60]. In the case of characteristic zero or sufficiently large, that holds in the present paper, the separable factorization coincides with the squarefree factorization.
Algorithm
along with its initial expansion; a contact polynomial
modulo
clustered at
,
with
;
the Newton polygon of
,
with a single edge of finite slope
.
A factorization of into clustered
polynomials at
modulo , each has a single edge of slope
in its Newton polygon and the associated Newton polygon is the
initial power of an irreducible polynomial.
The characteristic of is zero or 
.
Compute 
and 
such
that 
.
Factor 
, where 
are pairwise coprime powers of irreducible
factors of 
: this can
be done by computing the separable factorization of and then the irreducible factors of the separable
ones.
For compute 
.
For compute as
defined in
For compute 
as
defined in 
.
Lift the initial factorization of 
into
to precision by
using Corollary 4.23 at precision 
.
Return modulo .
operations in , where
is the degree of the separable part of 
.
Proof. From the above discussion the required initial Hensel context is known when entering step 6, so lifting is possible thanks to Corollary 4.23. Using Lemma 3.23 we verify that
It follows that the Newton polygon of modulo
has a single edge of slope . We are done with the correctness of the
algorithm.
Let 
. Steps 1, 4, and 5 take
by Proposition 6.4. For the factorization of in step 2, as indicated we first compute the separable
factorization 
using 
operations in by [60], and then
factor 
(which are pairwise coprime).
Consequently the cost of factoring over is
Step 3 contributes to
operations in : this includes
the computation of 
via [31, chapter
10, Theorem 10.10], the remainders by the via
[31, chapter 10, Theorem 10.6], and 
modular inversions. Finally, the cost of step 6 follows from Corollary
4.23 and 
.
be an effectively
separable, regular, and irreducible contact tower, and let a be a
contact polynomial clustered at having a
single edge in its Newton polygon. The equal-slope
factorization of is made of contact
polynomials clustered at
such that , the Newton
polygon of admits a single edge of the same
slope as and its Newton polynomial is the
initial of a power of an irreducible homogeneous polynomial for . These irreducible homogeneous
polynomials are pairwise distinct.
be an effectively
separable, regular, and irreducible contact tower, and let a be a
contact polynomial clustered at having a
single edge in its Newton polygon. Then, there exists a unique
equal-slope factorization of ,
up to a permutation of the factors.
Proof. The existence follows from Proposition 7.14. As for the uniqueness, assume that
is an equal-slope factorization of .
In the same way as we constructed from in equation 
of degree 
by
for . The 
are powers of pairwise distinct irreducible polynomials, so they
coincide with those computed in Algorithm 7.2.
After distinct-slope and equal-slope factorizations, we have reduced the
general situation to the case where the Newton polygon of has a single edge and the associated Newton polynomial is
an initial power of an irreducible homogeneous polynomial. This allows
us to increment the underlying contact tower with a new contact
coordinate at level 
and then to pursue the
factorization of with respect to the extended
tower. In order to ensure that the extended contact tower is separable,
we assume from now on that the characteristic of
is zero or sufficiently large.
Algorithm
along with its initial expansion; a contact polynomial
clustered at
modulo
with
,
whose Newton polygon has a single edge of finite slope
,
and such that the associated Newton polynomial is the initial power
of an irreducible homogeneous polynomial.
An extended tower 
modulo , still effectively separable, regular,
and irreducible, and such that is
clustered at it of degree 
in .
The characteristic of is zero or .
Compute 
into the form 
, with .
Compute the separable factorization 
, where 
is
irreducible and separable, according to the assumptions.
Set 
, 
as above, and compute
Extend the contact tower with 
and extend
the initial expansion accordingly.
Make level of the tower effectively
separable by computing the inverse of 
modulo .
Proof. By construction,
is homogeneous of valuation 
in 
, and satisfies all the
requirements of Definition 3.1. The incremented tower
remains effectively regular, since the known initial inverse of straightforwardly yields an initial inverse of 
. We extend the initial expansion
at level 
accordingly. The initial inverse in
step 5 does exist because 
is separable.
Steps 1 and 3 contribute to
by Proposition 6.4. Step 2 takes 
operations in by [60]. The cost of
step 5 is 
by Lemma 7.4. Finally,
is initially equal to 
whenever , which means that
is clustered at .
In principle, Algorithm 7.3 might introduce a new contact
coordinate of degree one in . For complexity reasons it is better to avoid
this from happening. As outlined in the introductory sections 2.5
and 2.6, we now work out the central shift algorithm.
Let be an effectively separable, regular, and
irreducible contact tower. Let 
be clustered at
. An initial
root of is an element 
such that
If 
is a Newton polynomial of , then an initial root of is an initial root of regarded
with set to the opposite of the slope of . One key idea behind the central
shift algorithm is the following lemma, that will be used in a
“divide and conquer” fashion in the subsequent algorithm.
be a contact polynomial clustered
at , and let be a non-zero initial root of of
multiplicity . If the
characteristic of is zero or 
, then is an initial
root of 
of multiplicity 
, for 
.
Proof. Set 
.
Lemma 5.7 implies
 |
(7.10) |
Since the tower is separable, we know from Lemma 5.4 that
is initially invertible, hence
is an initial root of 
of multiplicity 
.
Algorithm
An effectively separable, regular, and irreducible tower ; a contact polynomial clustered at and of
degree in modulo
, with ; we assume that 
, where is initially
invertible in .
An effectively separable, regular, and irreducible tower 
such that 
for , and the non-zero initial
roots of the Newton polynomials of have
multiplicity 
.
If 
then replace
by 
and return .
Let 
and compute the Weierstraß
normalization of 
modulo via Corollary 4.14.
The initial context is made of
and the normalized initial inverse 
of
in .
Call the algorithm recursively with input
and modulo .
Let 
be the tower obtained in return.
Compute the effectively regular Newton polygon of in 
modulo
via Lemma 7.9.
Compute the distinct-slope factorization of
in modulo with
Algorithm 7.1.
If all the non-zero initial roots of the Newton polynomials of
have multiplicity , then return modulo
.
Otherwise, compute the factor 
modulo
of of degree
in
whose initial is the -th power of a linear factor 
with 
,
non-zero, and where 
is set to 
.
Let 
and compute the Weierstraß
normalization 
of 
modulo via Corollary 4.14.
The initial context is made of
and the normalized initial inverse 
of
in .
Call the algorithm recursively with input
and modulo .
Return the tower obtained in the output.
Proof. If the algorithm exits at step 1, then
when regarded in the returned tower. Since 
the initial form of the returned
is the same as the initial form of the input value of , hence the returned tower is effectively
separable, regular, and irreducible. The Newton polynomial of cannot have non-zero initial roots with respect to the
returned contact tower, so the output is correct.
The initial Weierstraß context in step 2 follows from equation
In step 7, Lemma 7.18 ensures that 
is a non-zero initial root of a Newton polynomial of
of multiplicity 
, regarded in
. Since 
, is a non-zero initial
root of a Newton polynomial of of multiplicity
. As a non-zero initial root
of a Newton polynomial of modulo we necessarily have 
,
hence
by Lemma 3.23. From Lemma 4.3, we deduce that
and consequently that
It follows that is a non-zero initial root of a
Newton polynomial of of multiplicity modulo , hence
that 
. Consequently,
 |
(7.11) |
We verify that 
, so 
. In step 8, the contact polynomial
has degree 
in 
. By Lemma 7.18,
inequality , a
non-zero initial root of a Newton polynomial of 
in 
has multiplicity
Let us now examine the Newton polynomials of in
. For this purpose, by means
of Corollaries 7.12 and 7.16, we may decompose
into
where 
has Newton polynomials with slopes 
, where 
has
Newton polynomials with slope 
,
and where 
has a single Newton polynomial of
slope 
but that does not admit
for initial root.
The initial of 
is ,
so its valuation is .
Therefore the Newton polygon of in has a single edge of slope .
We also verify that the Newton polygon of in
admits a single edge of slope . Then, the Newton polygon of
in is the same as in . Finally the Newton polygon of
in has slopes .
Consequently the non-zero initial roots of the Newton polynomials of
in cannot have
multiplicities 
. We are done
with the proof of the correctness.
From Lemma 5.4 we have
Therefore, by using Proposition 3.20, the initial inverse
of can be obtained with 
operations in from the precomputations attached
to . The needed initial
Weierstraß contexts in steps 2 and 8 can be obtained with 
operations in thanks to
Proposition 3.20 again. The corresponding Weierstraß
normalizations take further operations in by Corollary 4.14.
Let 
represent the cost of the algorithm with
input of degree .
In step 1, the cost is 
. In
step 4 the effectively regular Newton polygon can be determined with
cost 
by Lemma 7.9. Step 5 amounts
to by using distinct-slope factorization and
Proposition 7.10. In step 6, we appeal to the equal-slope
factorization but discarding the irreducible factorizations: in fact,
having a root of multiplicity is equivalent to
having a separable factor of multiplicity ,
that can thus be read off from the separable factorization. So
Proposition 7.14 provides us with a cost
for steps 6 and 7. Consequently the cost 
of the
algorithm in degree in
satisfies
We conclude by a standard induction.
We are now in a position to present our top level algorithm for contact factorization. The distinct-slope and equal-slope factorizations are intertwined in order to increase the current contact tower and split the input polynomials. The process finishes once the polynomial to be factored is a power of the top level contact coordinate, up to the input precision. The central shift algorithm ensures that the “divide and conquer” approach only incurs a logarithmic complexity overhead.
The main step of the contact factorization is summarized in the following algorithm.
Algorithm
effectively separable, regular, and
irreducible; a contact polynomial modulo
clustered at , with .
A set 
of contact factors 
with precision for such that:
, for ;
;
is clustered at 
, for ;
The Newton polygon of with respect
to 
has a single edge whose Newton
polynomial is an initial power of an homogeneous polynomial
of degree in ;
If the Newton polygon of has a
non-zero initial root, then its multiplicity is
.
The characteristic of is zero or .
Initialize with the empty
set.
Compute the effectively regular Newton polygon of modulo via Lemma 7.9,
and then the distinct-slope factorization of
modulo by using Algorithm 7.1.
Let 
be the set of factors obtained in
return.
For each in , compute the equal-slope factorization of
over by using
Algorithm 7.2. Let 
be the
set of all resulting factors along with their multiplicities.
For each in of
multiplicity written :
If 
, then insert
in .
If 
(so is an
initial power of a polynomial of degree one in ), then call Algorithm 7.4
and append the resulting factorization to .
Return .
Proof. Properties (a) to (e) are satisfied by
construction. Step 2 takes by Lemma 7.9
and Proposition 7.10. Step 3 totalizes 
by Proposition 7.14. Step 4 contributes to
by Proposition 7.19.
Our top level algorithm finally makes a repeated use of Algorithm 8.1.
Algorithm
Initialize and
with the empty set.
Call Algorithm 8.1 and let
denote the returned contact factors for .
For :
If is a power of 
then insert into .
Otherwise, call Algorithm 7.3 with and and let 
be the returned tower.
If equals 
then insert 
into .
If has degree
in and writes 
, then replace 
by 
and insert the pair into .
Otherwise insert the pair into .
Call the algorithm recursively for each element of . Include the returned factors into
.
Return .
Proof. On the one hand, if the initial of is a power of a degree one polynomial, then according
to the specification of Algorithm 8.1 we have
On the other hand, if is an initial power of a
polynomial of degree 
, then
Consequently the depth of the recursive calls is 
. Let us analyze the valuation of 
. If comes from a
proper distinct-slope factor or a proper equal-slope factor of then inequalities
Otherwise has a single slope and its initial is
separable, so 
, 
and this case does not yield a recursive call. We conclude
that the algorithm behaves as specified.
Discarding factorization costs, step 2 takes
operations in , by
Proposition 8.1. In step 3, by Proposition 6.5,
for each the initial expansion of takes 
, where
represents the degree of 
. By Proposition 7.17, the cost of
Algorithm 7.3 is 
,
where 
denotes the degree of
in its main variable 
. The
total cost of steps 3 is
Let 
for 
denote the
elements of 
when entering step 4. By
construction we have
If 
represents the cost function of the algorithm
(still discarding factorizations), we have shown that
and that 
. Unrolling the
recursion times leads to
Let us now turn to the cumulated cost 
of
factoring separable polynomials over algebraic extensions of during the execution of Algorithm 8.2. Let us
show by induction on and 
that
 |
(8.1) |
This is easy if 
, so assume
that 
. We recall that
holds for any positive integers 
.
Assume first that has a non-trivial
distinct-slope factorization 
during Algorithm 8.1 and let be the degrees of 
in . Then
the induction hypothesis implies
Assume next that the Newton polygon of has a
unique slope and that the associated Newton polynomial is the 
-th power of an irreducible
polynomial of degree , for
some 
. Then the induction
hypothesis yields
Assume finally that the Newton polygon of has a
unique slope and that the associated Newton polynomial
has at least two distinct prime factors. Consider the separable
factorization
and let be the degrees of 
in . Note that 
and
Applying the induction hypothesis, this again yields
We conclude by induction that (8.1) indeed holds.
Proof of Theorem 1.1. Theorem 1.1 is a consequence of Proposition 8.2 by
applying Algorithm 8.2 with input 
and the trivial contact tower of height zero.
We explain how Abhyankar's approximate roots theory could improve our
contact factorization algorithm in some cases. If 
is a monic polynomial of degree and if is a divisor of that is invertible
in , then there exists a
unique polynomial of degree 
such that
 |
(8.2) |
This polynomial is called the -th approximate root of . In particular, is
monic and the -adic expansion
of is of the form
where 
. Let 
, that is the reverse of , and 
.
Condition
which means that is uniquely determined by 
, whenever
is a perfect field. The computation of the -th
approximate root of can be done using the Newton
operator if is not in
: we define the sequence 
A standard computation shows that this sequence converges quadratically
to 
. The computation of 
by this method takes 
operations in . Let us now
extend this construction to contact coordinates.
be monic of degree in , and let
be a divisor of that
is invertible in . Then,
there exists a unique monic of degree 
in such that
Proof. The condition rewrites
and we have 
, 
. Therefore is uniquely
determined as the -th
approximate root of .
In the context of Lemma 8.3, the -adic expansion of has the
form
The algorithmic purpose of approximate roots is as follows. Suppose that
for some monic in .
We can add one level to with
We write 
for the image of
in and examine the Newton polygon of . If we had
with some , this would mean
that
for some sufficiently small positive value of 
. In particular, the -adic
expansion of would be
whence
The latter equality is not possible since it contradicts the fact that
is an approximate root of .
Consequently, the Newton polygon of cannot have
a single edge with a Newton polynomial of the form 
. Either it has at least two edges, or a single
edge but the initial factors of the Newton polynomial have multiplicity
. For the situations similar
to the one of section 2.5 these computations are expected
to be faster and easier than the central shift method.
In this section we consider a monic and separable polynomial . We are interested in computing
the irreducible factorization of modulo for some requested precision . Our strategy naturally relies on computing a
contact factorization of for a sufficiently
large precision. We begin with analyzing the precision loss induced by
the distinct slope and equal-slope factorizations.
Let be monic and separable, and let be a contact tower. Let ()¯
denote an algebraic closure of ,
we still write 
for the extended valuation.
Proof. From Lemma 7.5 we know that
is clustered at 
,
hence
where 
. Since 
, necessarily 
holds.
Assume that the lemma holds up to some index 
. From Lemma 7.5, the contact
polynomial 
is clustered at . Let us canonically write
where 
and 
.
By induction we have
for 
. Since
necessarily 
holds. Let 
be canonically written
with 
. Thanks to the
induction hypothesis, we verify that
Finally the lemma holds for index .
If is a separable, regular, and irreducible
contact tower, then Lemmas 4.3 and 7.3 imply
that is a valuation of
that extends .
be a separable,
regular, and irreducible contact tower and let 
. Then is the unique
valuation of 
that extends
and we have
for all in .
Proof. Proposition 7.2 ensures that
is irreducible. By setting
to infinity we obtain that is a valuation of
. The uniqueness and the
resultant-based expression are well known; for instance, see [59,
chapter XII, Corollary 6.2].
Let be monic in and
clustered at an effectively separable, regular, and irreducible contact
tower . We assume that is larger than or equal to the smallest slope of the
Newton polygon of . As
before, stands for the image 
of in ,
whose degree in is written .
Proof. Poisson's formula for resultants yields
Thanks to Lemma 5.7, we deduce:
 |
|||
|
 |
||
|
 |
(by Lemma 9.1) | |
|
 |
||
|
 |
|
Next, we consider and
monic in . Let and stand for the canonical
representatives of and
in , of respective degrees
and 
in . In the sequel, we define 
to be the constant coefficient of ,
when regarded as a univariate polynomial in .
are and the slopes
of the Newton polygon of are 
, then we have
Proof. Again, we use Poisson's formula for the resultants:
It follows that
Let 
be the distinct-slope factors of (as in Definition 7.11) and let 
stand for their image in .
We verify that:
By Lemma 9.1, if 
is a root of 
then 
is larger or equal to
the opposite of the slope of the single edge of the Newton polygon of
, that is
It follows that
 |
|
 |
|
|
 |
||
|
 |
(by Lemma 4.3)
|
In the rest of the section, we study the precision loss encountered in
each Newton factorization. For a partial factorization 
with monic and ,
the following well known formula will be used several times:
 |
(9.1) |
In the sequel represents the precision at which
the irreducible factors of the input polynomial are required. Let in be given modulo with
where 
. We assume that the
Newton polygon of has been computed. Following
Definition 7.11, we let stand for
the product of factors of with slopes and let stand for the product of
factors of with slopes 
, hence 
.
Let 
and 
,
let represent the normalized initial inverse of
.
According to Corollary 4.11, we may obtain with precision 
,
where
Setting 
for ,
equation
Since 
we have 
,
that yields
We also compute with precision 
, where 
,
and the same calculation yields
be given
with precision such that
Then, Algorithm 7.1 computes truncations of the
distinct slope factors of
modulo some 
such that
for .
Proof. We apply the above precision analysis in
the “divide and conquer” fashion used in Algorithm 7.1.
Now we examine the precision loss during the equal-slope factorization.
The input is a polynomial clustered at and which has a single slope and
known with precision such that
Let represent the equal slope factors of as in Definition 7.15, and set 
. By Corollary 4.23
the contact polynomial can be computed with
relative precision where
for 
. Setting 
and 
for , Lemma 9.4 implies that
Since
and 
, we obtain that
for .
be given
with precision
Then Algorithm 7.2 computes the equal-slope factors
modulo such that
Proof. In fact Algorithm 7.2
computes the equal-slope factors of with a
precision higher than the one requested here, but the above discussion
leads to the lower bounds.
We are now ready to prove Theorem 1.3. We assume that is monic and separable of degree
in and known modulo
where 
. We combine Theorem 1.1 with the above precision analyses.
Proof of Theorem 1.3. We apply
Algorithm 8.2 with entry modulo
, and with the trivial
contact tower of height zero. The above precision analyses for the
intermediate steps of the contact factorization algorithm, namely Lemmas
9.5 and 9.6, show by induction that all
intermediate factors of
occurring in the top level algorithm are computed along with a contact
tower of degree with
precision such that
Such a factor is proved to be irreducible when it has degree one in
. In this case, by inequality
(3.3), the coefficients of are
uniquely determined up to precision in at least
which equals
by Lemma 5.4. On the other hand, Lemma 9.3 yields
so the precision of is at least
as claimed. Note that the central shift algorithm does not produce
factors, so it does not involve any loss of precision.
The contact factorization presented in this paper is subject to further
improvements. A first research direction concerns the design of a
contact factorization algorithm that would not rely on univariate
irreducible factorization, by using the directed evaluation
paradigm of [52] instead; so the computed contact towers
would not be necessarily irreducible any longer. Another research
direction concerns the design of fast algorithms for the contact
coordinates in the vein of [51, 52]: we could
avoid the conversions to plain coordinates and their precision loss.
Another research direction concerns fields of small positive
characteristic 
.
S. Abelard, E. Berardini, A. Couvreur, and G. Lecerf. Computing Riemann–Roch spaces via Puiseux expansions. J. Complexity, 73:101666, 2022.
S. S. Abhyankar. Irreducibility criterion for germs of analytic functions of two complex variables. Adv. Math., 74(2):190–257, 1989.
S. S. Abhyankar and T. Moh. Newton–Puiseux expansion and generalized Tschirnhausen transformation. I. J. Reine Angew. Math., 260:47–83, 1973.
S. S. Abhyankar and T. Moh. Newton–Puiseux expansion and generalized Tschrinhausen transformation. II. J. Reine Angew. Math., 261:29–54, 1973.
M. Alberich-Carramiñana, J. Guàrdia, E. Nart, A. Poteaux, J. Roé, and M. Weimann. Polynomial factorization over henselian fields. Found. Comput. Math., 2024. https://doi.org/10.1007/s10208-024-09646-x.
M. E. Alonso, F. J. Castro-Jiménez, and H. Hauser. Encoding algebraic power series. J. Found. Comput. Math., 18(3):789–833, 2018.
M. Aschenbrenner, L. van den Dries, and J. van der Hoeven. Asymptotic Differential Algebra and Model Theory of Transseries. Number 195 in Annals of Mathematics studies. Princeton University Press, 2017.
J.-D. Bauch, E. Nart, and H. D. Stainsby. Complexity of OM factorizations of polynomials over local fields. LMS J. Comput. Math., 16:139–171, 2013.
J. Berthomieu, G. Lecerf, and G. Quintin. Polynomial root finding over local rings and application to error correcting codes. Appl. Algebra Engrg. Comm. Comput., 24(6):413–443, 2013.
A. Bostan, G. Christol, and Ph. Dumas. Fast computation of the Nth term of an algebraic series over a finite prime field. In M. Rosenkranz, editor, Proceedings of the 2016 ACM International Symposium on Symbolic and Algebraic Computation, ISSAC '16, pages 119–126. New York, NY, USA, 2016. ACM.
A. Bostan, F. Chyzak, G. Lecerf, B. Salvy, and É. Schost. Differential equations for algebraic functions. In C. W. Brown, editor, Proceedings of the 2007 International Symposium on Symbolic and Algebraic Computation, ISSAC '07. New York, NY, USA, 2007. ACM.
A. Bostan, G. Lecerf, B. Salvy, É. Schost, and B. Wiebelt. Complexity issues in bivariate polynomial factorization. In J. Schicho, editor, Proceedings of the 2004 International Symposium on Symbolic and Algebraic Computation, ISSAC '04, pages 42–49. New York, NY, USA, 2004. ACM Press.
A. Campillo and J. I. Farrán. Symbolic Hamburger–Noether expressions of plane curves and applications to AG codes. Math. Comp., 71(240):1759–1780, 2002.
D. G. Cantor and D. M. Gordon. Factoring polynomials
over -adic fields. In
W. Bosma, editor, Algorithmic Number Theory. 4th
International Symposium, ANTS-IV Leiden, The Netherlands, July
2-7, 2000. Proceedings, volume 1838 of Lecture Notes in
Comput. Sci., pages 185–208. Springer-Verlag, 2000.
D. G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Inform., 28:693–701, 1991.
D. G. Cantor and H. Zassenhaus. A new algorithm for factoring polynomials over finite fields. Math. Comput., 36(154):587–592, 1981.
A. L. Chistov. Polynomial complexity of the Newton–Puiseux algorithm. In Mathematical Foundations of Computer Science 1986. Proceedings of the 12th Symposium Bratislava, Czechoslovakia August 25–29, 1986, volume 233 of Lecture Notes in Comput. Sci., pages 247–255. Springer-Verlag, 1986.
A. L. Chistov. Efficient factoring polynomials over local fields and its applications. In Proceedings of the International Congress of Mathematicians, Kyoto, Japan, 1990, volume 1, pages 1509–1519. Springer-Verlag, 1991.
D. V. Chudnovsky and G. V. Chudnovsky. On expansion of algebraic functions in power and Puiseux series, I. J. Complexity, 2(4):271–294, 1986.
D. V. Chudnovsky and G. V. Chudnovsky. On expansion of algebraic functions in power and Puiseux series, II. J. Complexity, 3(1):1–25, 1987.
H. Cohen. A course in computational algebraic number theory. Graduate Texts in Mathematics. Springer, Berlin, Heidelberg, 1993.
V. Cossart and G. Moreno-Socías. Racines approchées, suites génératrices, suffisance des jets. Annales de la Faculté des sciences de Toulouse 6e série, 14(3):353–394, 2005.
D. Duval. Rational Puiseux expansions. Compos. Math., 70(2):119–154, 1989.
A. Dwivedi and N. Saxena. Computing Igusa's local zeta function of univariates in deterministic polynomial-time. In S. D. Galbraith, editor, ANTS XIV. Proceedings of the Fourteenth Algorithmic Number Theory Symposium, volume 4 of The Open Book Series, pages 197–214. Berkeley, CA, USA, 2020. MSP.
J. Fernández, J. Guàrdia, J. Montes, and E. Nart. Residual ideals of MacLane valuations. J. Algebra, 427:30–75, 2015.
D. Ford and P. Letard. Implementing the Round Four maximal order algorithm. J. Théor. Nombres Bordeaux, 6(1):39–80, 1994.
D. Ford, S. Pauli, and X.-F. Roblot. A fast algorithm
for polynomial factorization over .
J. Théor. Nombres Bordeaux, 14(1):151–169,
2002.
D. Ford and O. Veres. On the complexity of the Montes ideal factorization algorithm. In G. Hanrot, F. Morain, and E. Thomé, editors, Algorithmic Number Theory. 9th International Symposium, ANTS-IX, Nancy, France, July 19-23, 2010. Proceedings, volume 6197 of Lecture Notes in Comput. Sci., pages 174–185. Springer-Verlag, 2010.
A. Fröhlich and J. C. Shepherdson. On the factorisation of polynomials in a finite number of steps. Math. Z., 62:331–334, 1955.
A. Fröhlich and J. C. Shepherdson. Effective procedures in field theory. Philos. Trans. Roy. Soc. London. Ser. A., 248:407–432, 1956.
J. von zur Gathen and J. Gerhard. Modern computer algebra. Cambridge University Press, New York, 3rd edition, 2013.
J. von zur Gathen and V. Shoup. Computing Frobenius maps and factoring polynomials. Comput. complexity, 2(3):187–224, 1992.
G.-M. Greuel and G. Pfister. A Singular introduction to commutative algebra. Springer-Verlag Berlin Heidelberg, 2002.
J. Guàrdia, J. Montes, and E. Nart. Okutsu invariants and Newton polygons. Acta Arith., 145(1):83–108, 2010.
J. Guàrdia, J. Montes, and E. Nart. Higher Newton polygons in the computation of discriminants and prime ideal decomposition in number fields. J. Théor. Nombres Bordeaux, 23(3):667–696, 2011.
J. Guàrdia, J. Montes, and E. Nart. Newton polygons of higher order in algebraic number theory. Trans. Amer. Math. Soc., 364(1):361–416, 2012.
J. Guàrdia, J. Montes, and E. Nart. A new computational approach to ideal theory in number fields. Found. Comput. Math., 13(5):729–762, 2013.
J. Guàrdia, J. Montes, and E. Nart. Higher Newton polygons and integral bases. J. Number Theory, 147:549–589, 2015.
J. Guàrdia, E. Nart, and S. Pauli. Single-factor lifting and factorization of polynomials over local fields. J. Symbolic Comput., 47(11):1318–1346, 2012.
D. Harvey and J. van der Hoeven. Polynomial
multiplication over finite fields in time 
. J. ACM, 69(2):1–40, 2022.
Article 12.
J. P. G. Henry and M. Merle. Complexity of computation of embedded resolution of algebraic curves. In J. H. Davenport, editor, Eurocal '87. European Conference on Computer Algebra. Leipzig, GDR, June 2–5, 1987. Proceedings, volume 378 of Lect. Notes Comput. Sci., pages 381–390. Springer Berlin Heidelberg, 1989.
H. Hironaka. Resolution of singularities of an algebraic variety over a field of characteristic zero. Annals of Math., 79:109–326, 1964.
J. van der Hoeven. Automatic asymptotics. PhD thesis, École polytechnique, Palaiseau, France, 1997.
J. van der Hoeven. Relax, but don't be too lazy. J. Symbolic Comput., 34:479–542, 2002.
J. van der Hoeven. Newton's method and FFT trading. J. Symbolic Comput., 45(8):857–878, 2010.
J. van der Hoeven. Faster Chinese remaindering. Technical Report, HAL, 2016. https://hal.archives-ouvertes.fr/hal-01403810.
J. van der Hoeven. Computing with D-algebraic power series. Appl. Algebra Engrg. Comm. Comput., 30(1):17–49, 2019.
J. van der Hoeven. Effective power series computations. Found. Comput. Math., 19(3):623–651, 2019.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
J. van der Hoeven and G. Lecerf. Modular composition via factorization. J. Complexity, 48:36–68, 2018.
J. van der Hoeven and G. Lecerf. Accelerated tower arithmetic. J. Complexity, 55:101402, 2019.
J. van der Hoeven and G. Lecerf. Directed evaluation. J. Complexity, 60:101498, 2020.
J. van der Hoeven and G. Lecerf. Univariate polynomial factorization over finite fields with large extension degree. Appl. Algebra Eng. Commun. Comput., 35:121–149, 2024.
E. Kaltofen and V. Shoup. Fast polynomial factorization over high algebraic extensions of finite fields. In Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation, ISSAC '97, pages 184–188. New York, NY, USA, 1997. ACM.
E. Kaltofen and V. Shoup. Subquadratic-time factoring of polynomials over finite fields. Math. Comput., 67(223):1179–1197, 1998.
K. S. Kedlaya. On the algebraicity of generalized power series. Beitr. Algebra Geom., 58:499–527, 2017.
K. S. Kedlaya and C. Umans. Fast polynomial factorization and modular composition. SIAM J. Comput., 40(6):1767–1802, 2011.
H. T. Kung and J. F. Traub. All algebraic functions can be computed fast. J. ACM, 25(2):245–260, 1979.
S. Lang. Algebra, volume 211 of Graduate Texts in Mathematics. Springer-Verlag, New York, 3rd edition, 2002.
G. Lecerf. Fast separable factorization and applications. Appl. Algebra Engrg. Comm. Comput., 19(2):135–160, 2008.
G. Lecerf. New recombination algorithms for bivariate polynomial factorization based on Hensel lifting. Appl. Algebra Engrg. Comm. Comput., 21(2):151–176, 2010.
S. MacLane. A construction for absolute values in polynomial rings. Trans. Am. Math. Soc., 40(3):363–395, 1936.
S. MacLane. A construction for prime ideals as absolute values of an algebraic field. Duke Math. J., 2(3):492–510, 1936.
J. Montes. Polígonos de Newton de orden superior y aplicaciones aritméticas. PhD thesis, Universitat de Barcelona, Spain, 1999.
F. Mora. An algorithm to compute the equations of tangent cones. In J. Calmet, editor, Computer Algebra. EUROCAM '82, European Computer Algebra Conference, Marseilles, France, April 5-7, 1982, volume 144 of Lect. Notes in Computer Sc., pages 158–165. Springer-Verlag Berlin Heidelberg, 1982.
G. Moroz. New data structure for univariate polynomial approximation and applications to root isolation, numerical multipoint evaluation, and other problems. In 2021 IEEE 62nd Annual Symposium on Foundations of Computer Science (FOCS), pages 1090–1099. Los Alamitos, CA, USA, 2022. IEEE.
G. Moroz and É. Schost. A fast algorithm for computing the truncated resultant. In M. Rosenkranz, editor, Proceedings of the ACM on International Symposium on Symbolic and Algebraic Computation, ISSAC '16, pages 341–348. New York, NY, USA, 2016. ACM.
E. Nart. Okutsu–Montes representations of prime ideals of one-dimensional integral closures. Publicacions Matemàtiques, 55(2):261–294, 2011.
V. Neiger, J. Rosenkilde, and É. Schost. Fast computation of the roots of polynomials over the ring of power series. In Proceedings of the 2017 ACM on International Symposium on Symbolic and Algebraic Computation, ISSAC '17, pages 349–356. New York, NY, USA, 2017. ACM Press.
I. Newton. De methodis serierum et Fluxionum. Manuscript, 1671.
K. Okutsu. Construction of integral basis. I. Proc. Japan Acad. Ser. A Math. Sci., 58(1):47–49, 1982.
K. Okutsu. Construction of integral basis. II. Proc. Japan Acad. Ser. A Math. Sci., 58(2):87–89, 1982.
K. Okutsu. Construction of integral basis. III. Proc. Japan Acad. Ser. A Math. Sci., 58(3):117–119, 1982.
K. Okutsu. Construction of integral basis. IV. Proc. Japan Acad. Ser. A Math. Sci., 58(4):167–169, 1982.
Ö. Ore. Zur Theorie der Algebraischen Körper. Acta Math., 44:219–314, 1923.
Ö. Ore. Bestimmung der Diskriminanten algebraischer Körper. Acta Math., 45:303–344, 1925.
Ö. Ore. Newtonsche Polygone in der Theorie der algebraischen Körper. Math. Ann., 99:84–117, 1928.
A. M. Ostrowski. Über die Bedeutung der Theorie der konvexen Polyeder für die formale Algebra. Jahresber. Deutsch. Math.-Verein., 30(2):98–99, 1921. Talk given at Der Deutsche Mathematikertag vom 18–24 September 1921 in Jena.
A. M. Ostrowski. On multiplication and factorization of polynomials. I. Lexicographic orderings and extreme aggregates of terms. Aequationes Math., 13(3):201–228, 1975.
A. M. Ostrowski. On the significance of the theory of convex polyhedra for formal algebra. SIGSAM Bull., 33(1):5, 1999. Translated from [78].
V. Y. Pan. Univariate polynomials: nearly optimal algorithms for numerical factorization and root-finding. J. Symbolic Comput., 33(5):701–733, 2002.
S. Pauli. Factoring polynomials over local fields. J. Symbolic Comput., 32(5):533–547, 2001.
A. Poteaux. Calcul de développements de Puiseux et application au calcul de groupe de monodromie d'une courbe algébrique plane. PhD thesis, Université de Limoges, France, 2008.
A. Poteaux and M. Rybowicz. Improving complexity bounds for the computation of Puiseux series over finite fields. In Proceedings of the 2015 ACM on International Symposium on Symbolic and Algebraic Computation, ISSAC'15, pages 299–306. New York, NY, USA, 2015. ACM.
A. Poteaux and É. Schost. Modular composition modulo triangular sets and applications. Comput. Complex., 22(3):463–516, 2013.
A. Poteaux and M. Weimann. Using approximate roots
for irreducibility and equi-singularity issues in 
. Technical Report, arXiv:1904.00286,
2019.
A. Poteaux and M. Weimann. Computing Puiseux series: a fast divide and conquer algorithm. Ann. Henri Lebesgue, 5:1061–1102, 2021.
A. Poteaux and M. Weimann. A quasi-linear
irreducibility test in 
.
Comput. Complex., 31:6, 2022.
A. Poteaux and M. Weimann. Local polynomial factorisation: improving the Montes algorithm. In A. Hashemi, editor, Proceedings of the 2022 International Symposium on Symbolic and Algebraic Computation, ISSAC '22, pages 149–157. New York, NY, USA, 2022. ACM.
M. V. Puiseux. Recherches sur les fonctions algébriques. J. Math. Pures et Appliquées, 15:365–480, 1850.
P. Russell. Hamburger–Noether expansions and approximate roots of polynomials. Manuscripta Math., 31:25–95, 1980.
A. Schönhage. Schnelle Multiplikation von Polynomen über Körpern der Charakteristik 2. Acta Inform., 7:395–398, 1977.
A. Schönhage. The fundamental theorem of algebra in terms of computational complexity. Technical Report, Math. Inst. Univ. of Tübingen, 1982.
V. Shoup. New algorithms for finding irreducible polynomials over finite fields. Math. Comp., 54(189):435–447, 1990.
S. Smith. On the higher singularities of plane curves. Prod. London Math. Soc., 6:153–182, 1875.
E. W. von Tschirnhaus. Nova methodus auferendi omnes terminos intermedios ex data æquatione. Acta Eriditorium, 2:204–207, 1683.
B. L. van der Waerden. Algebra. Springer, 7th edition, 1991. Based in part on lectures by E. Artin and E. Noether.
R. J. Walker. Algebraic Curves, volume 13 of Princeton mathematical series. Princeton University Press, 1950.
P. Walsh. A polynomial-time complexity bound for the computation of the singular part of a Puiseux expansion of an algebraic function. Math. Comp., 69(231):1167–1182, 2000.
P. G. Walsh. On the complexity of rational Puiseux expansions. Pacific J. Math., 188(2):369–387, 1999.
S. M. Watt. A fixed point method for power series computation. In P. Gianni, editor, Symbolic and Algebraic Computation. International Symposium ISSAC' 88, Rome, Italy, July 4-8, 1988. Proceedings, volume 358 of Lect. Notes in Computer Sc., pages 206–217. Springer-Verlag, 1989.
O. Zariski. Le problème des modules pour les branches planes. Hermann, Paris, 1986.
polynomials in of
degree 3
cost function for univariate polynomial
factorization 3
homogeneous component of
of degree 
10
homogeneous components of
from degree to 
10
initial form of
11
valuation semi-group of the -th level of a contact tower
17
group generated by
17
ramification index of
17
-th
defining polynomial of a contact tower 17
defining ideal of a contact tower of height
18
level of a contact
tower 18
degree of with
respect to the contact variable
22
polynomials at the level
of a contact tower 24
expression of in
terms of the plain coordinates 24
conversion to plain coordinates
24
valuation of with
respect to 27
derivative of with
respect to 42
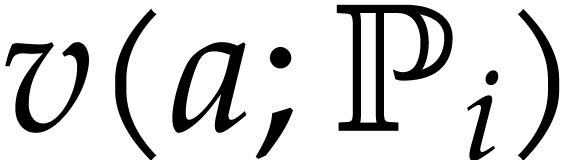valuation of
regarded in 53
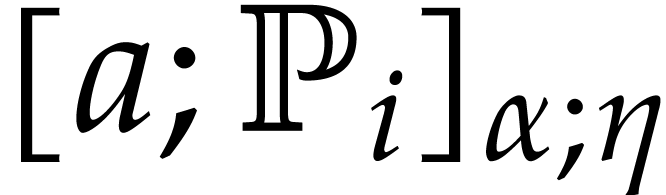homogeneous components of
regarded in 53
algebraic tower 3
approximate root 71
canonical representation 21
central shift 65
clustered polynomial 22
contact coordinates 17
contact factorization 56
contact polynomial 24
contact representation 24
contact slope 17
contact tower 17
degree 17
irreducible 54
reduced 17
regular 45
separable 41
distinct-slope factorization 60
equal-slope factorization 63
graded ring 10
Hensel context 36
initial 36
homogeneous component 10
initial expansion 46
initial form 11
initial root 65
initially reducible 54
leading monomial 18
monic in 22
Newton polygon 11
contact 56
regular 56
Newton polynomial 11
normalized inverse
initial 29
modulo 29
plain coordinates 24
regular
effectively 45
relative precision 11
semi-valuation 11
separable
effectively 41
slope 11
standard basis 18
reduced 18
uniformizing parameter 47
Weierstraß context 31
initial 32
Weierstraß
normalization 28
part 33
and
.
for 
,
in 
and 
for 
.
is a standard basis of
for some 
.
.
.
and 
holds for all 
in 
,
,
,
,
,
.
,
,
,
,
and 
.
:
we have
be such that
is a
root of 
