Implementing number theoretic
transforms  |
|
| Preliminary version of December 16, 2024 |
|
 . Grégoire
Lecerf has been supported by the French ANR-22-CE48-0016
NODE project. Joris van der Hoeven has been supported by an
ERC-2023-ADG grant for the ODELIX project (number 101142171).
. Grégoire
Lecerf has been supported by the French ANR-22-CE48-0016
NODE project. Joris van der Hoeven has been supported by an
ERC-2023-ADG grant for the ODELIX project (number 101142171).
Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. |
 |
 . This article has
been written using GNU TeXmacs [16].
. This article has
been written using GNU TeXmacs [16].
We describe a new, highly optimized implementation of number
theoretic transforms on processors with SIMD support (AVX,
AVX-512, and Neon). For any prime modulus
|
Number theoretic transforms (NTTs) were introduced by Pollard [21]. He used them as a tool to design practical algorithms for the efficient multiplication of very large integers. Technically speaking, a number theoretic transform is simply a discrete Fourier transform (DFT) over a finite field. Traditional DFTs work over the complex numbers. A fast algorithm to compute such DFTs was published a few years earlier by Cooley and Tukey [4], although the idea goes back to Gauss [14].
As of today, fast practical algorithms for multiplying large integers are based on number theoretic transforms, complex DFTs [23, first algorithm], or Schönhage-Strassen's algorithm [23, second algorithm]. All three strategies are very competitive and the winner depends on hardware and the application. Since the race is very close, it is interesting to heavily optimize each of the three approaches.
In this paper, we will describe a high performance implementation for
number theoretic transforms. We focus on modern general purpose CPUs
with support for SIMD (Single Instruction Multiple Data) instructions.
Our current implementation was written in 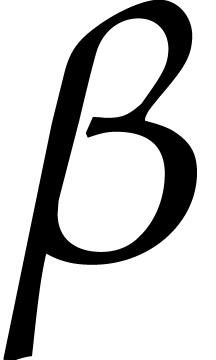 -version of it
has been released this year). It fully exploits SIMD accelerations and
we started experimentations with multi-threading.
-version of it
has been released this year). It fully exploits SIMD accelerations and
we started experimentations with multi-threading.
A first way to optimize NTTs is to design faster modular arithmetic. Let
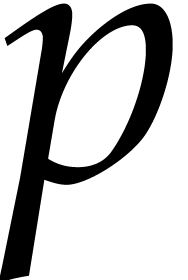 be a prime number. Traditionally, the result of
any arithmetic operation modulo
be a prime number. Traditionally, the result of
any arithmetic operation modulo 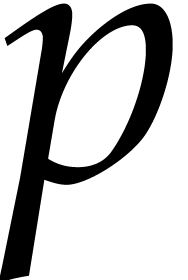 is always
normalized, e.g. to make it lie in
is always
normalized, e.g. to make it lie in 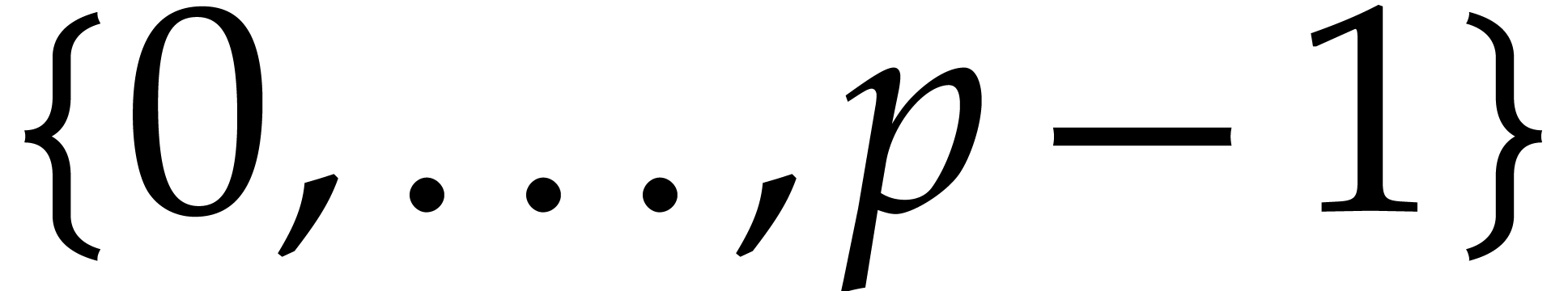 . It was first observed by Harvey [13]
that some of these normalizations can be delayed when computing NTTs and
that this can lead to significant speed-ups. In section 3,
we show how to take this idea one step further, which allows us to delay
even more normalizations.
. It was first observed by Harvey [13]
that some of these normalizations can be delayed when computing NTTs and
that this can lead to significant speed-ups. In section 3,
we show how to take this idea one step further, which allows us to delay
even more normalizations.
While we were working on our implementation
1. We started our implementation in 2019, but it remained
private due to the experimental nature of the new
The optimization of traditional DFTs is the subject of an extensive
literature. The most efficient implementations are based on so-called
“codelets” [8, 9, 22].
For a given target order  ,
the idea is to automatically generate a highly optimized program (called
a codelet) for DFTs of order
,
the idea is to automatically generate a highly optimized program (called
a codelet) for DFTs of order  .
Such codelets can optimize the use of registers and memory, which makes
them in particular cache-efficient. For small orders, we can also unroll
the loops, which minimizes the overhead of control structures. In
section 4, we apply the codelet approach to number
theoretic transforms and discuss some specific issues that arise for
this application. Similar experiments have recently been carried out in
the
.
Such codelets can optimize the use of registers and memory, which makes
them in particular cache-efficient. For small orders, we can also unroll
the loops, which minimizes the overhead of control structures. In
section 4, we apply the codelet approach to number
theoretic transforms and discuss some specific issues that arise for
this application. Similar experiments have recently been carried out in
the
The last section 5 is dedicated to timings. We implemented
our algorithms on five different systems that support SIMD arithmetic of
three different widths: 128-bit (ARM Neon), 256-bit (AVX-2), and 512-bit
(AVX-512). For orders 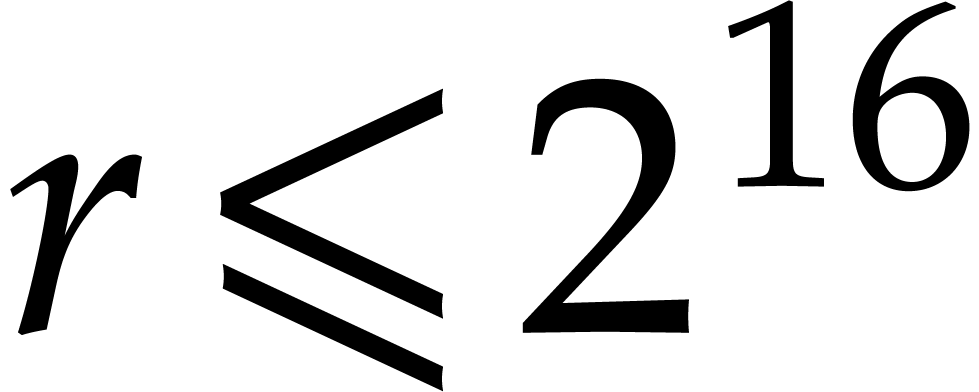 , we
achieve speed-ups that are proportional to the SIMD width. For higher
orders, the x86-based systems start to suffer from memory access costs,
whereas the performance of ARM-based systems remains stable. We also
experimented with multi-threaded versions of our algorithms, but without
pushing our optimization efforts as far as for the mono-threaded case.
, we
achieve speed-ups that are proportional to the SIMD width. For higher
orders, the x86-based systems start to suffer from memory access costs,
whereas the performance of ARM-based systems remains stable. We also
experimented with multi-threaded versions of our algorithms, but without
pushing our optimization efforts as far as for the mono-threaded case.
The application of the fast NTTs to integer multiplication requires a wrapper for Chinese remaindering and Kronecker segmentation. This turns out to be highly non-trivial to implement with the same level of optimization as our new NTTs. We plan to address this issue in a separate future work.
Let  be a field with a primitive root of unity
be a field with a primitive root of unity
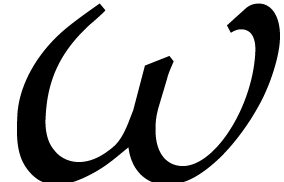 of order
of order  and assume that
and assume that
 is invertible in
is invertible in  .
We define the discrete Fourier transform (or DFT) of an
.
We define the discrete Fourier transform (or DFT) of an  -tuple
-tuple 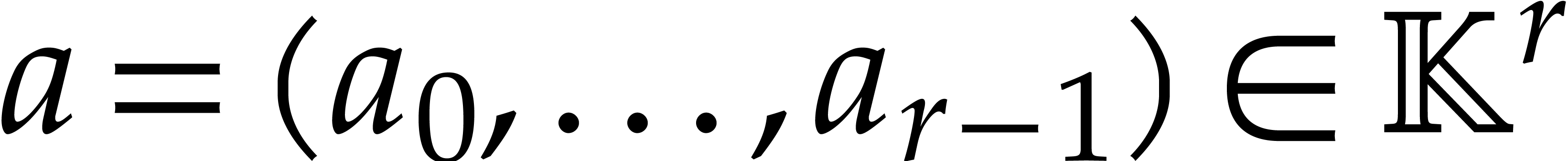 with
respect to
with
respect to 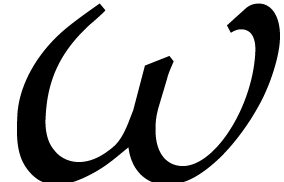 to be
to be 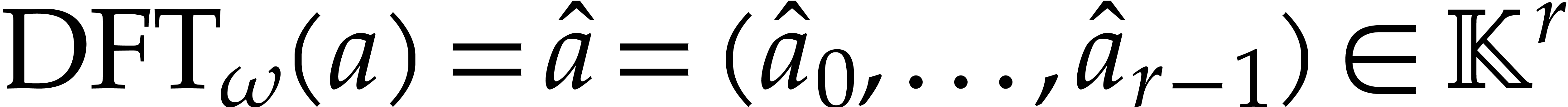 where
where
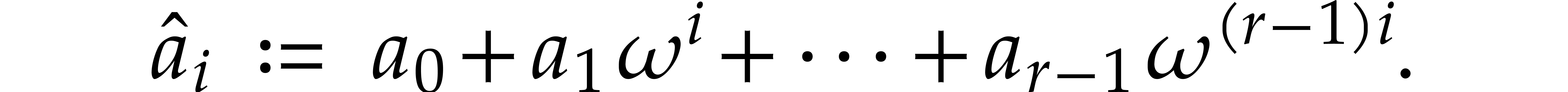
That is, 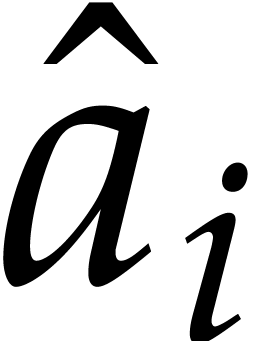 is the evaluation of the polynomial
is the evaluation of the polynomial
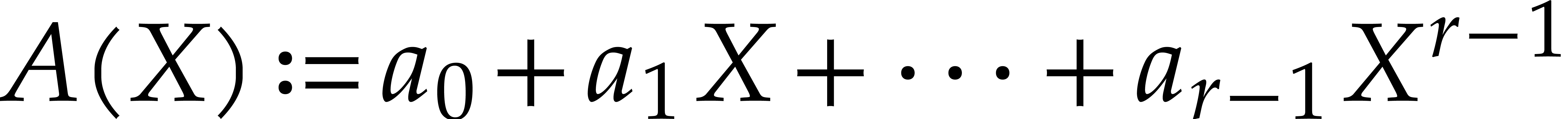 at
at  .
If
.
If  is a primitive
is a primitive  -th
root of unity, then so is its inverse
-th
root of unity, then so is its inverse  ,
and we have
,
and we have
Indeed, writing  , we have
, we have
where 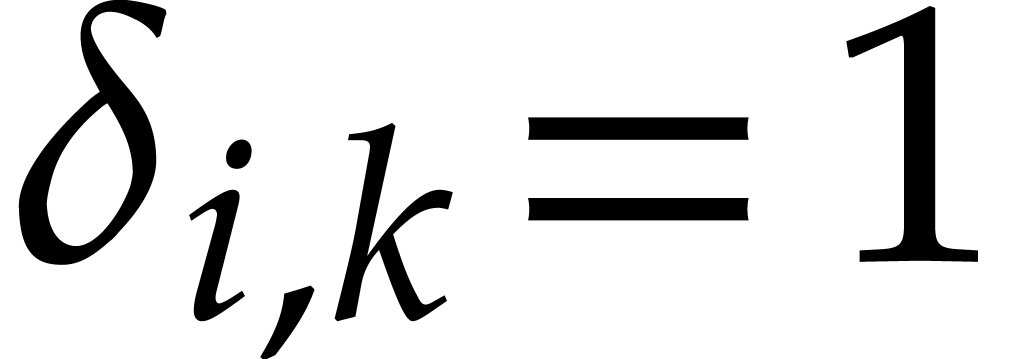 if
if 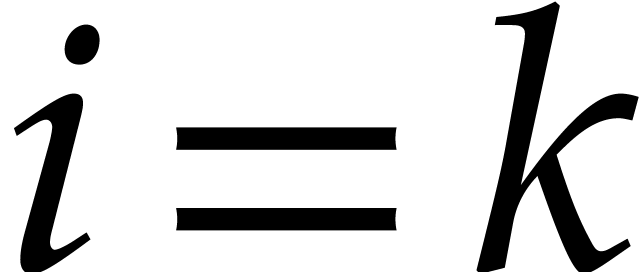 and
and 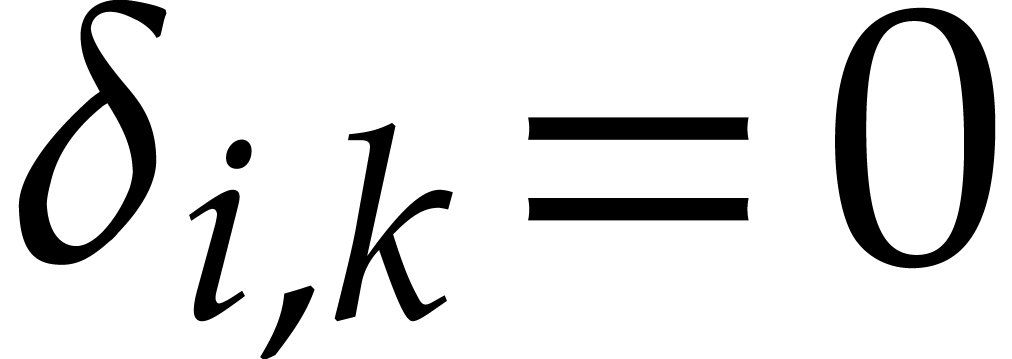 otherwise.
otherwise.
The DFT induces a ring homomorphism from 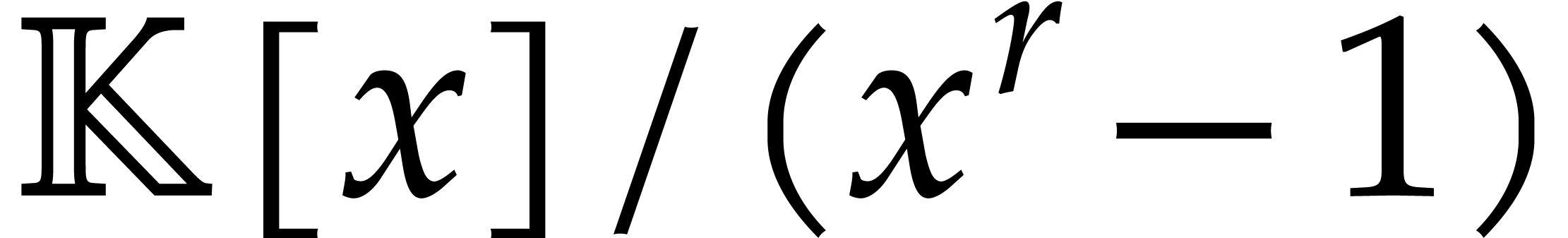 into
into
 , by sending
, by sending 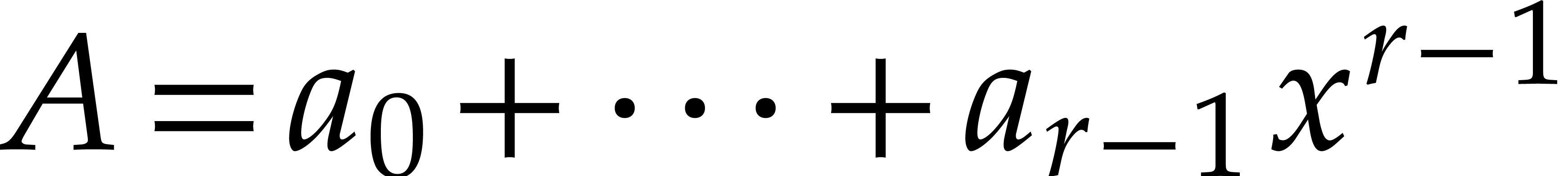 to
to 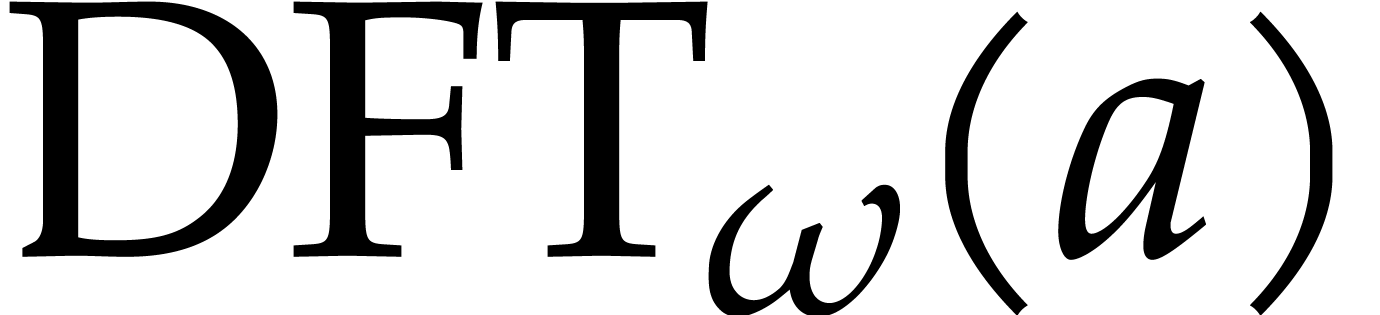 . Since the DFT is
invertible, this map (that we will still denote by
. Since the DFT is
invertible, this map (that we will still denote by  ) is actually an isomorphism. If we have a fast
way to compute DFTs, this yields an efficient way to multiply
“cyclic” polynomials
) is actually an isomorphism. If we have a fast
way to compute DFTs, this yields an efficient way to multiply
“cyclic” polynomials 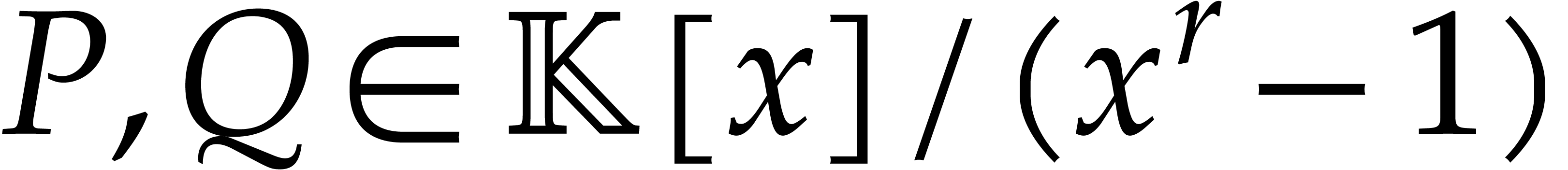 :
:
 |
(2) |
Here the multiplication 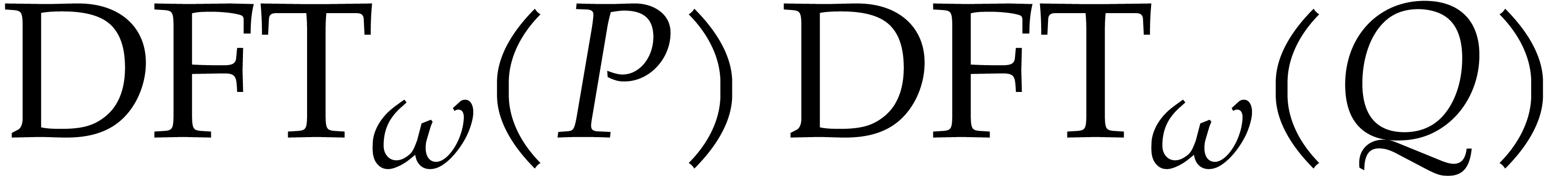 in
in  is done entry-wise. Given two polynomials
is done entry-wise. Given two polynomials 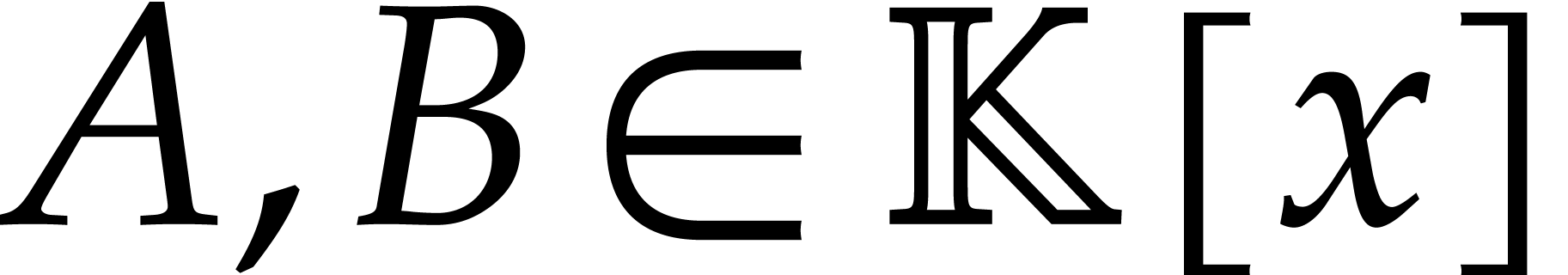 with
with
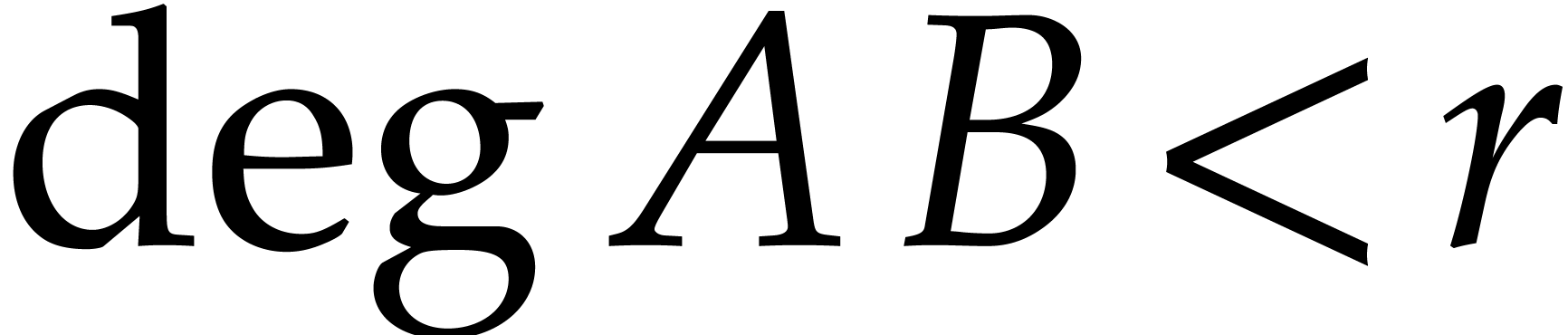 , we have
, we have

and the product  can be read off from
can be read off from 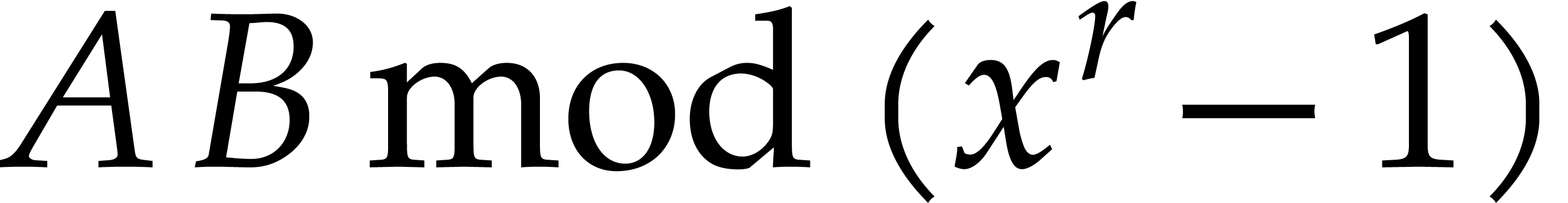 . Hence we also obtained an
algorithm for the multiplication of
. Hence we also obtained an
algorithm for the multiplication of  and
and 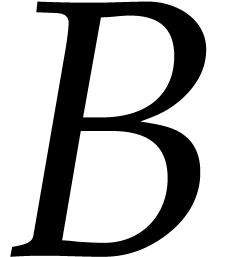 . This is called
FFT-multiplication.
. This is called
FFT-multiplication.
Let 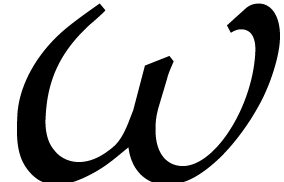 be a primitive
be a primitive  -th
root of unity, with
-th
root of unity, with 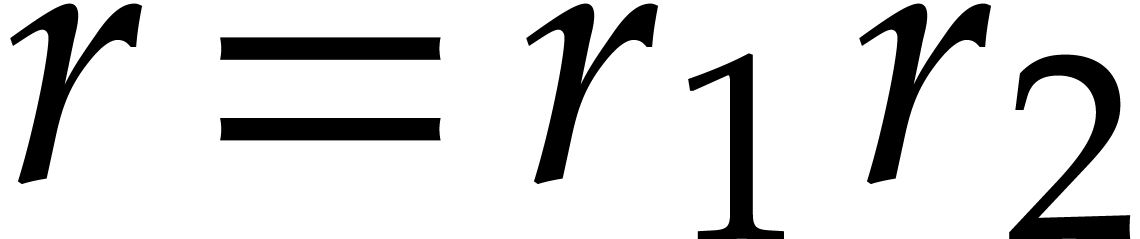 for
for 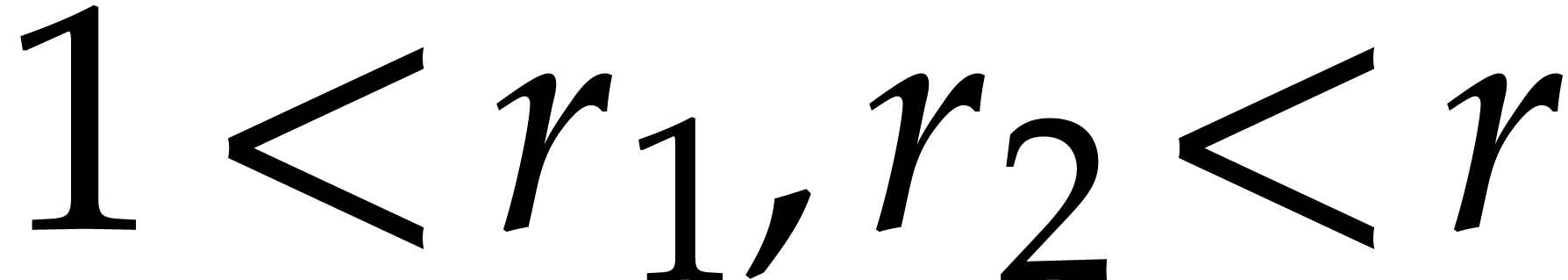 . Then
. Then 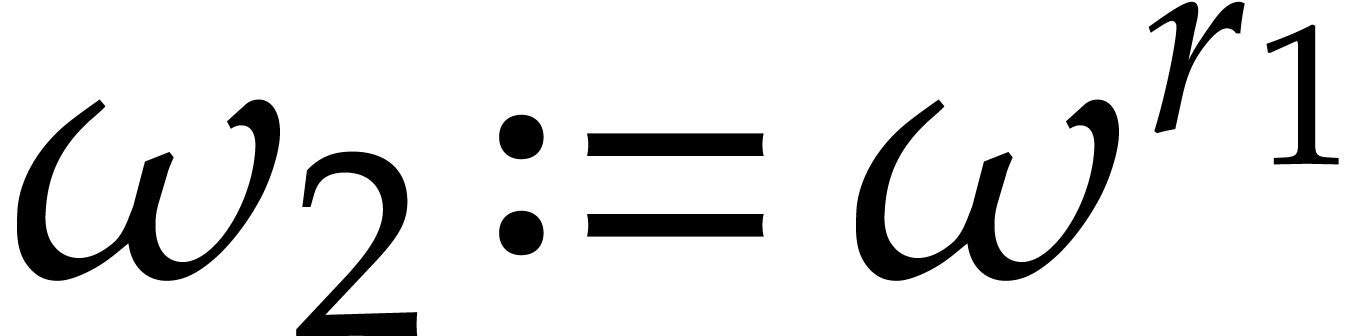 is a primitive
is a primitive 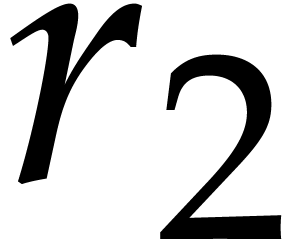 -th root of unity and
-th root of unity and 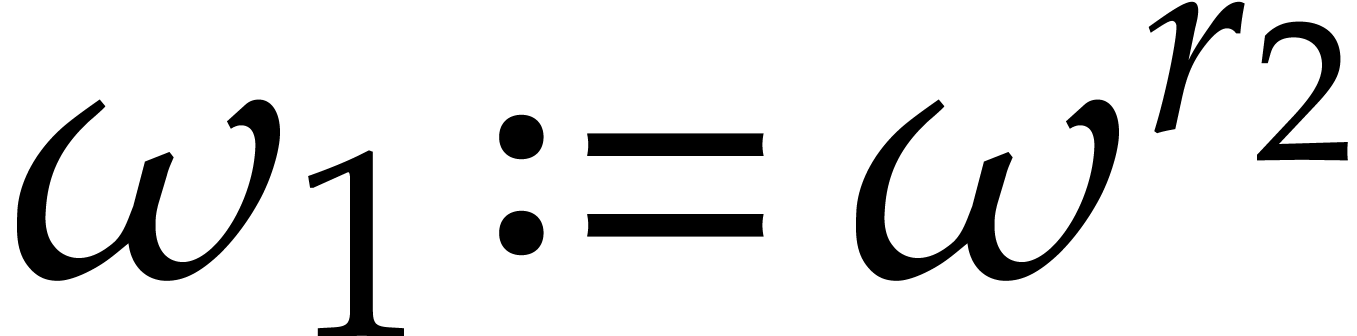 is a primitive
is a primitive 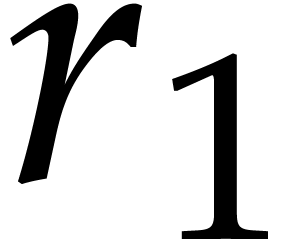 -th
root of unity. Moreover, for any
-th
root of unity. Moreover, for any  and
and  , we have
, we have
This formula can be decomposed in four steps:
Given a linear map 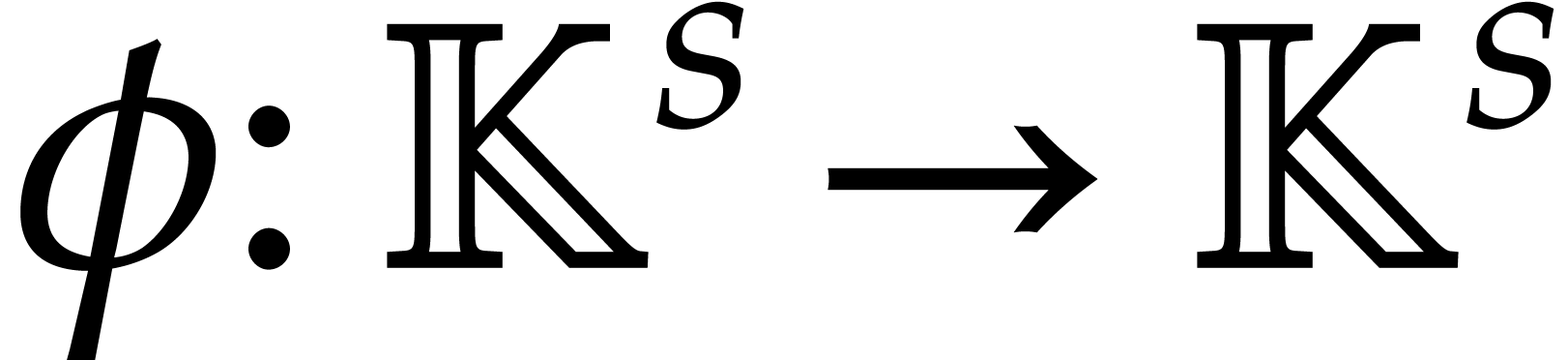 and
and 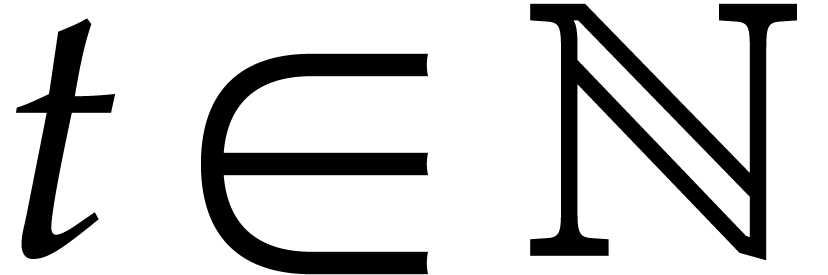 , it will be convenient to use the Kronecker
products
, it will be convenient to use the Kronecker
products 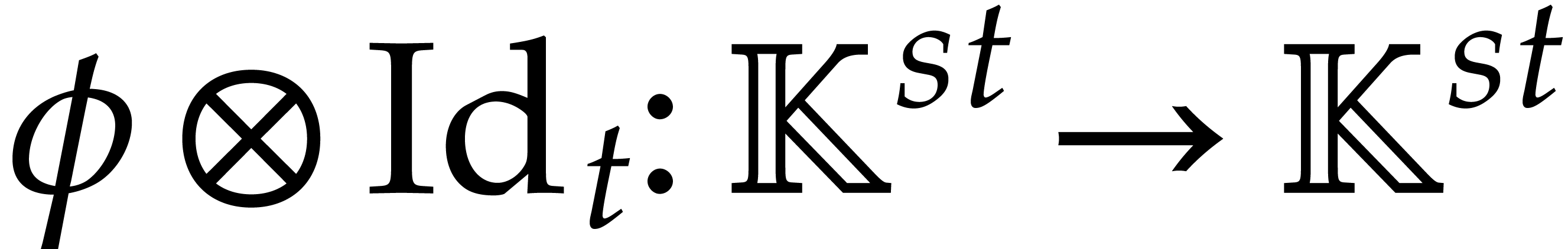 and
and 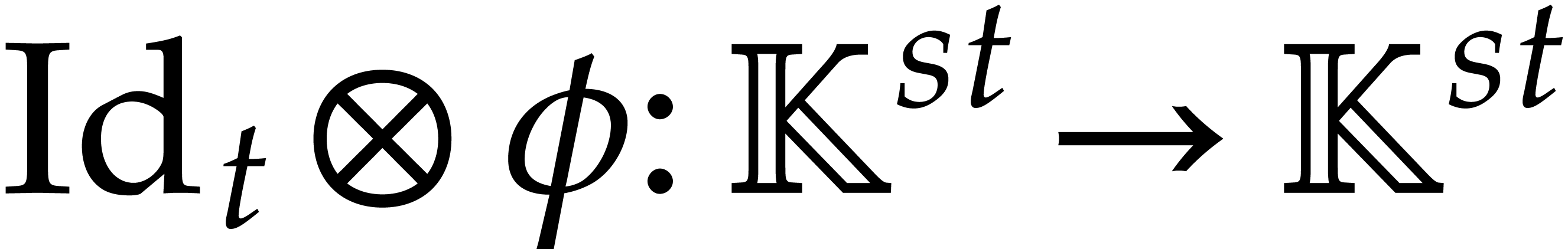 ,
that are defined by
,
that are defined by
Using these notations, we may rewrite (4) and (6) as
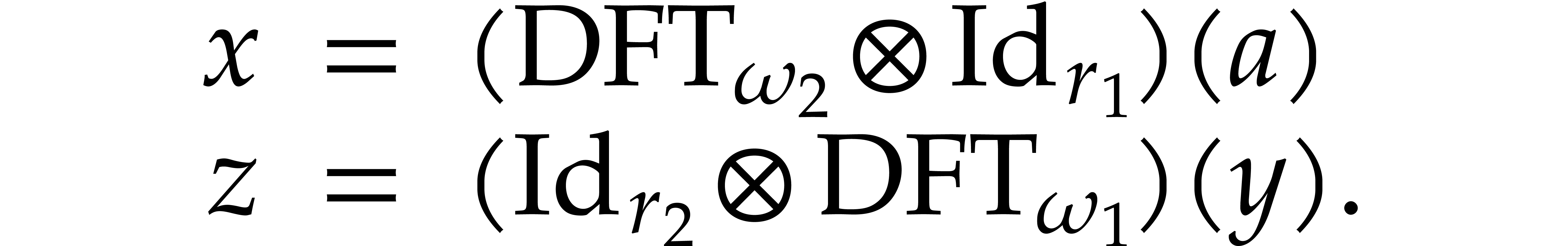
Step (5) consists of  scalar
multiplications by so-called twiddle factors
scalar
multiplications by so-called twiddle factors 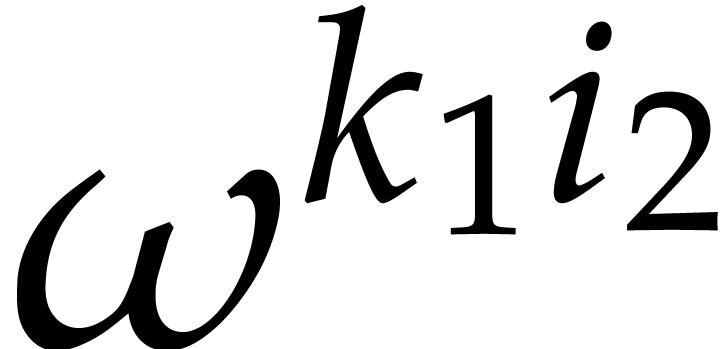 . We will denote this twiddling map by
. We will denote this twiddling map by
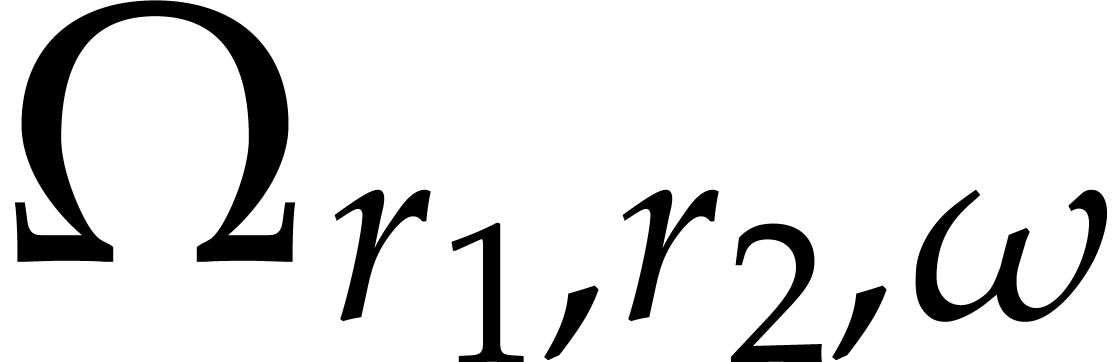 :
:
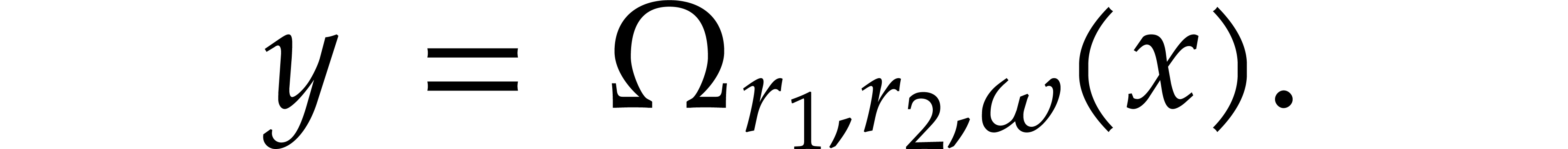
The last step corresponds to the transposition of an  matrix. Denoting this transposition map by
matrix. Denoting this transposition map by 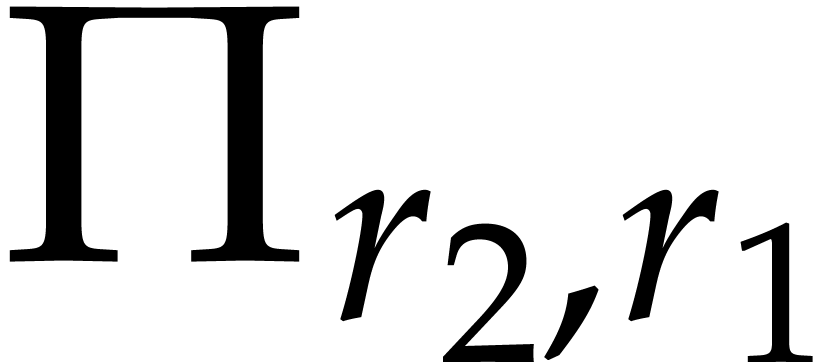 ,
the relation (3) becomes
,
the relation (3) becomes
 |
(8) |
If 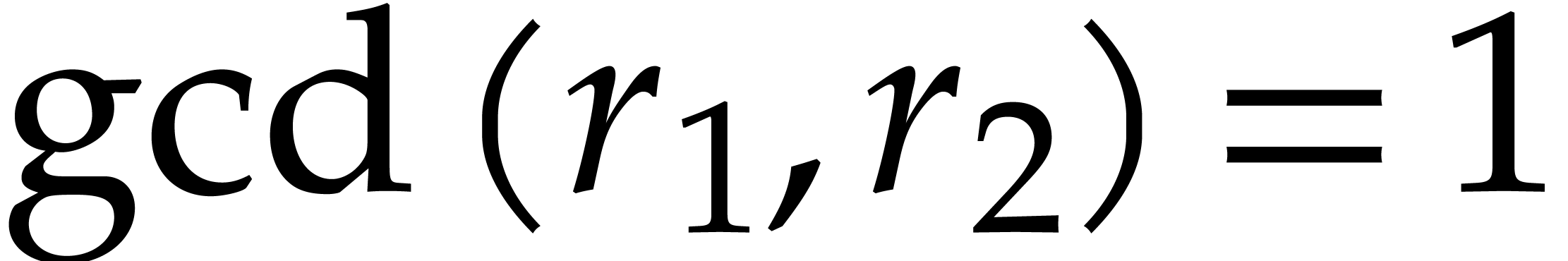 in the previous subsection, then it is
actually possible to avoid the twiddling step (5), as first
noted by Good in [11]. Consider the Bezout relation
in the previous subsection, then it is
actually possible to avoid the twiddling step (5), as first
noted by Good in [11]. Consider the Bezout relation
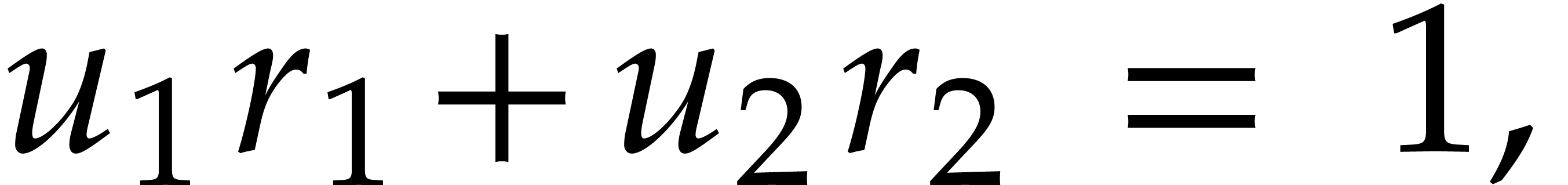
where 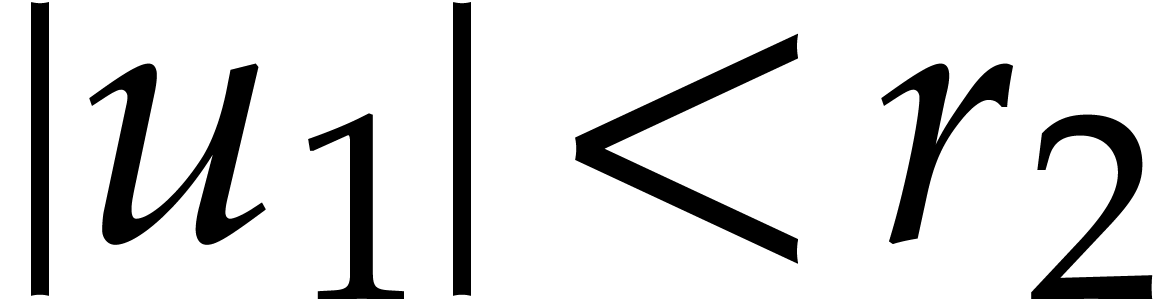 and
and 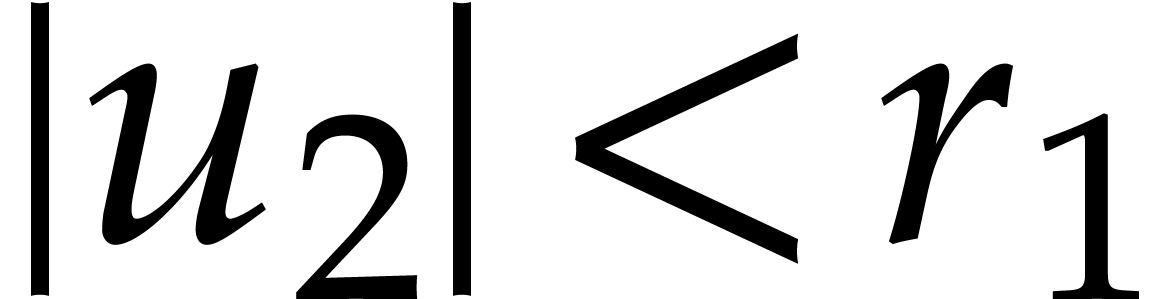 .
Then we have the isomorphism of abelian groups
.
Then we have the isomorphism of abelian groups
This Chinese remainder isomorphism induces an isomorphism of  -algebras
-algebras
Representing cyclic polynomials 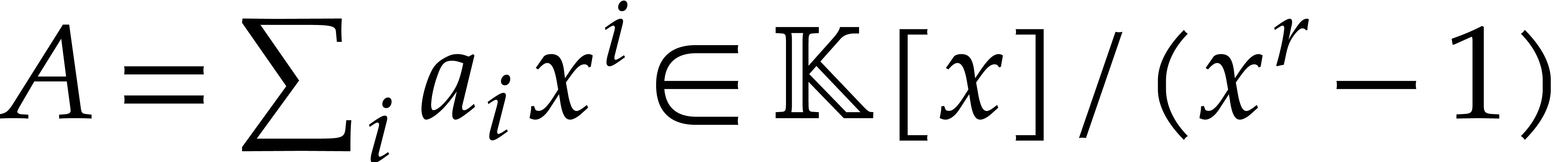 and
and

by the vectors  of their coefficients, the map
of their coefficients, the map
 acts as a permutation
acts as a permutation 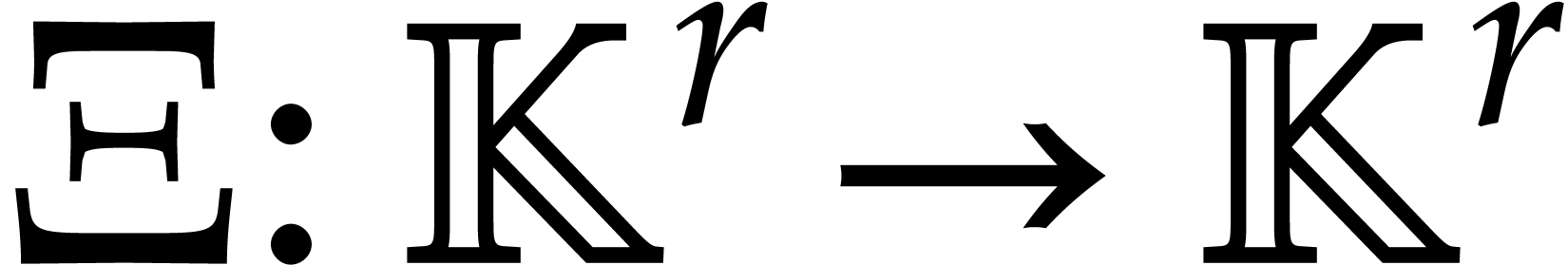 : if
: if  then
then 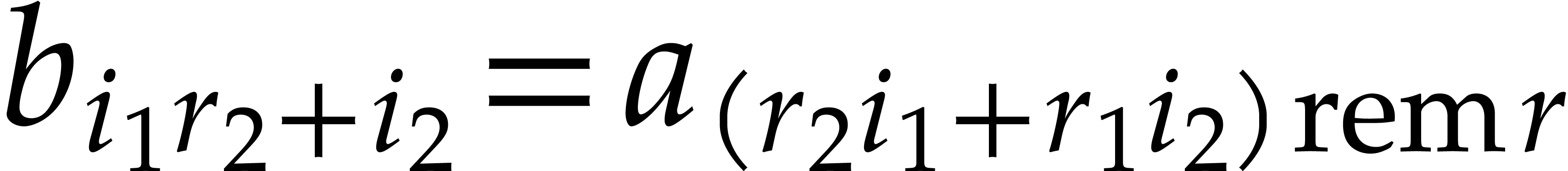 , for
, for 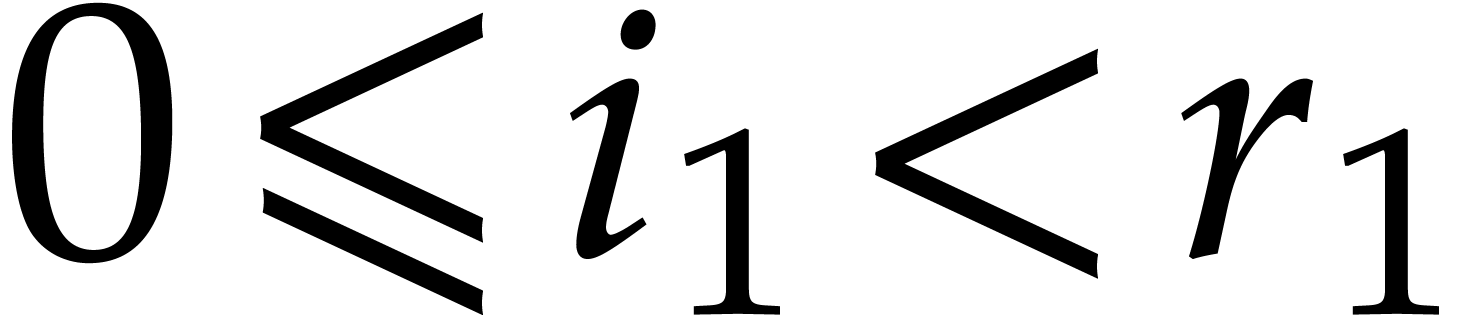 and
and 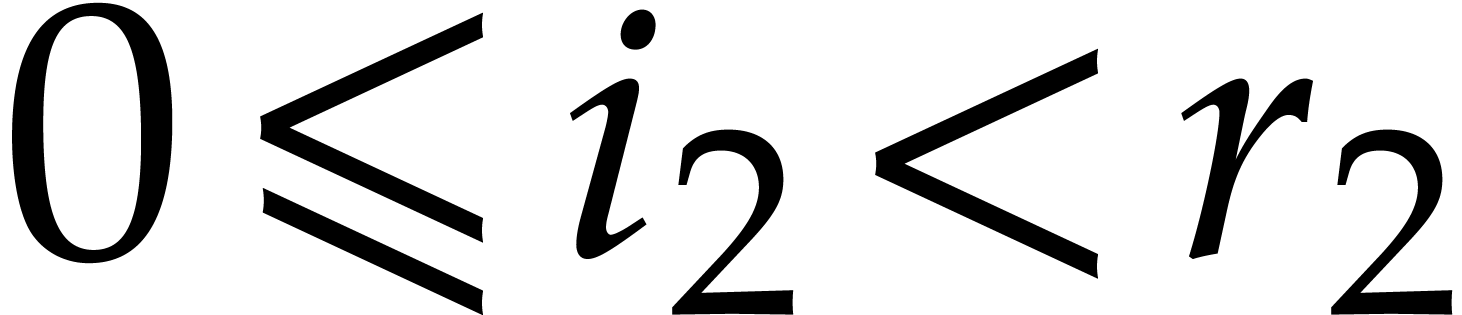 . The bivariate DFT
. The bivariate DFT
sends 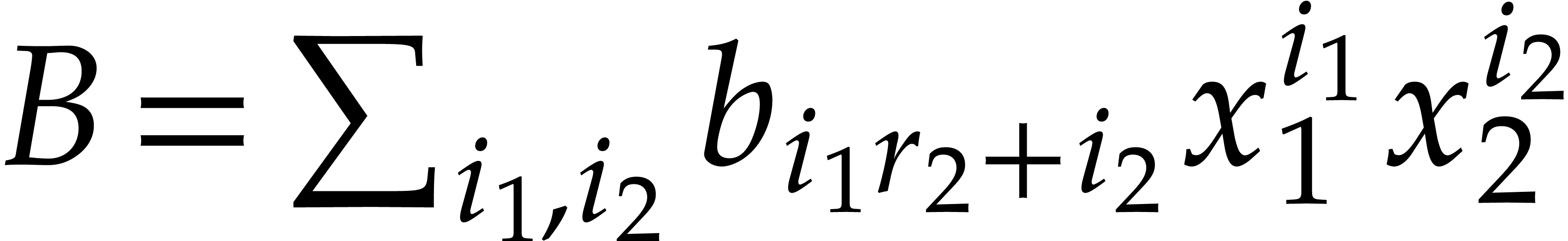 to the vector
to the vector  with
with
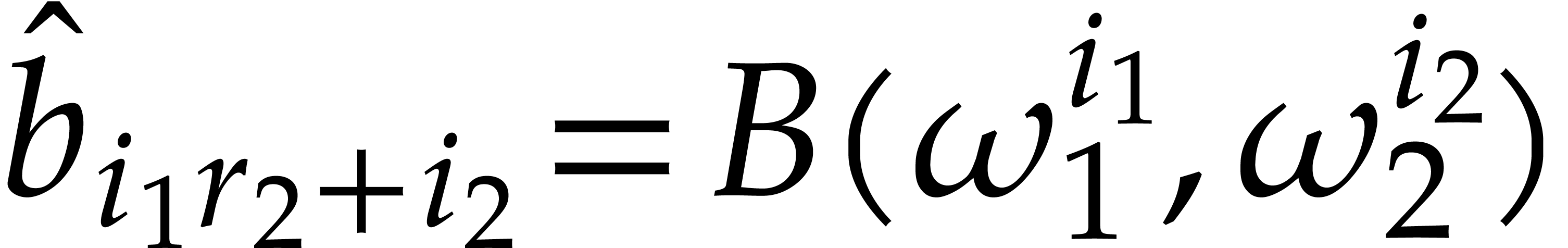 . If
. If  and
and  , then
, then
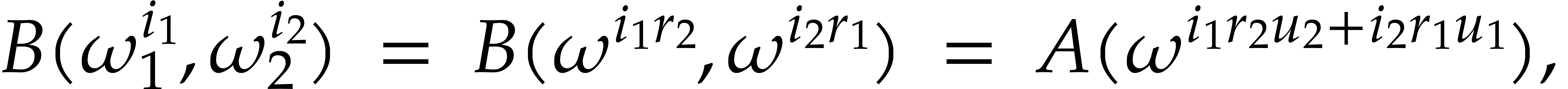
so 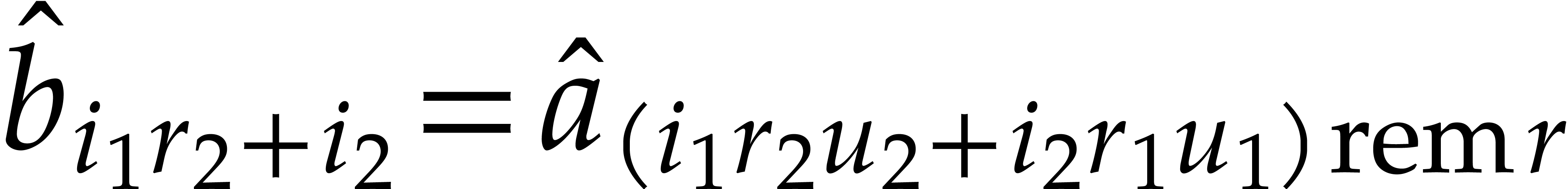 and
and  for some
permutation
for some
permutation 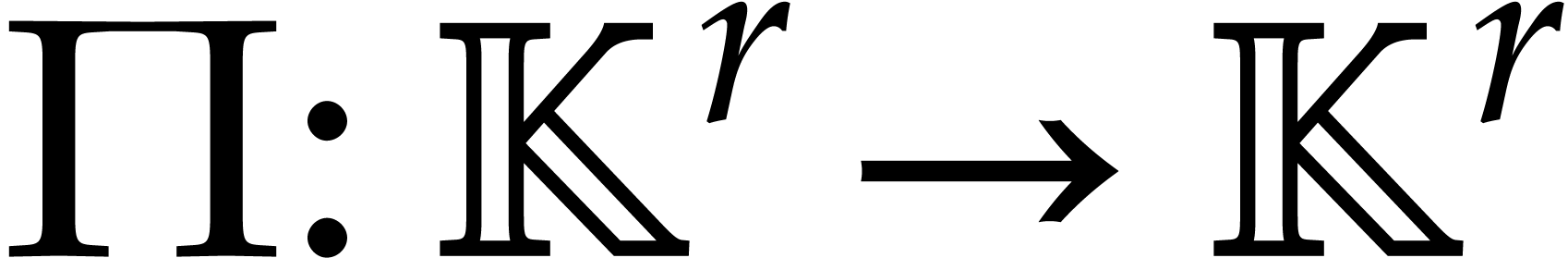 . Altogether,
this yields
. Altogether,
this yields
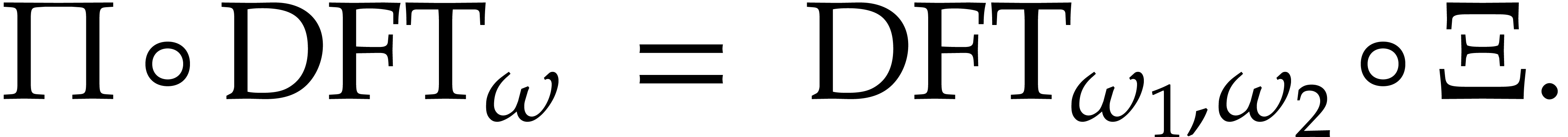
The above two subsections show that efficient algorithms for DFTs often
only compute them up to permutations. For some applications, it is
actually not required to perform all these permutations. Assume for
instance that we have an efficient algorithm for the computation of the
“twisted” 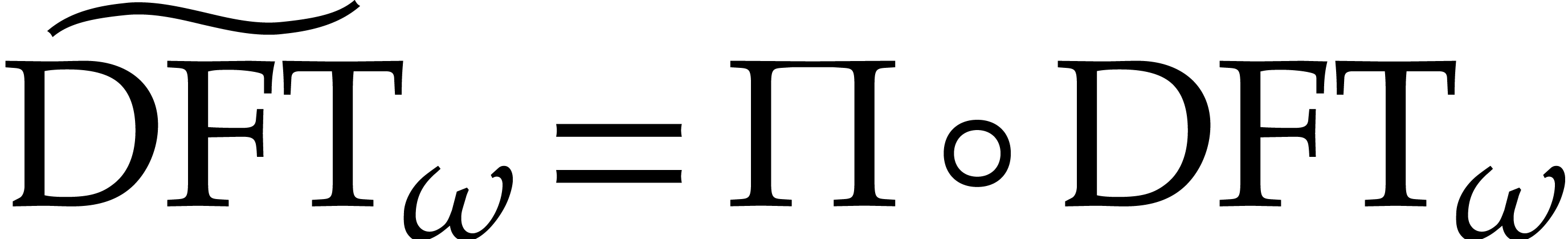 for some permutation
for some permutation  . Then the variant
. Then the variant

of (2) still yields an efficient method for
FFT-multiplication. This technique requires the inverse transform  to be implemented with more care, since one cannot
directly use the formula (1). Instead, one typically uses a
similar algorithm as for
to be implemented with more care, since one cannot
directly use the formula (1). Instead, one typically uses a
similar algorithm as for  ,
but with all steps reversed.
,
but with all steps reversed.
The twisting technique can be combined recursively with the algorithms
from the previous two subsections. Assume for instance that 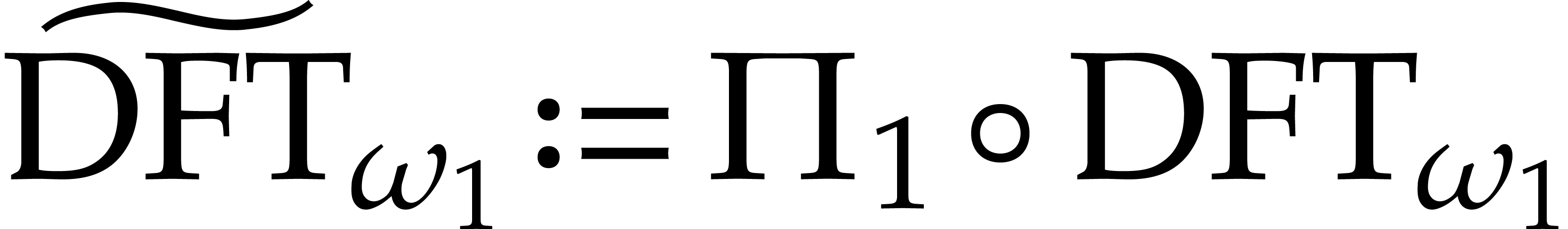 and
and 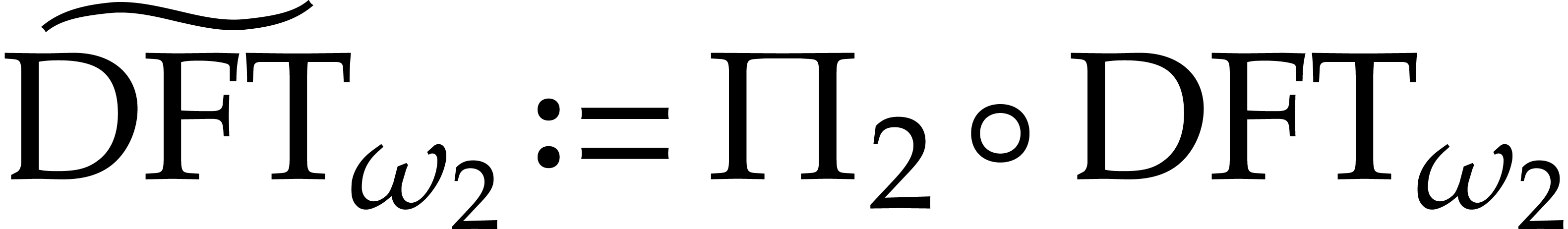 for some permutations
for some permutations 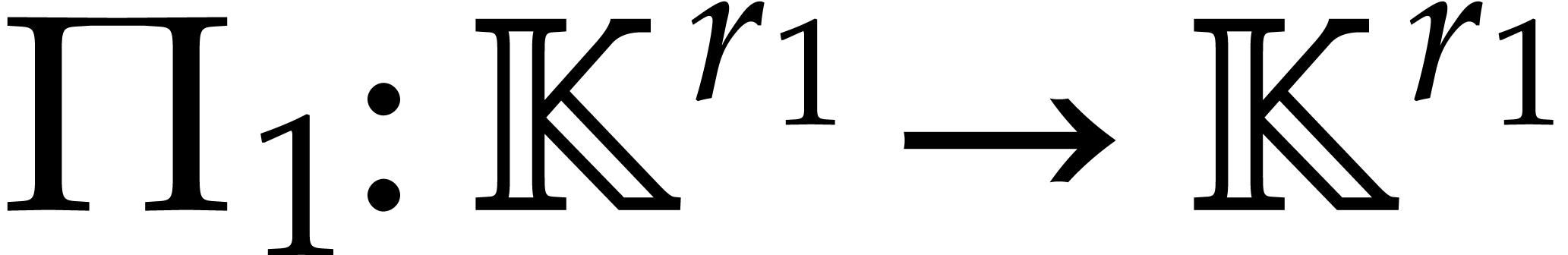 and
and  , and
let
, and
let
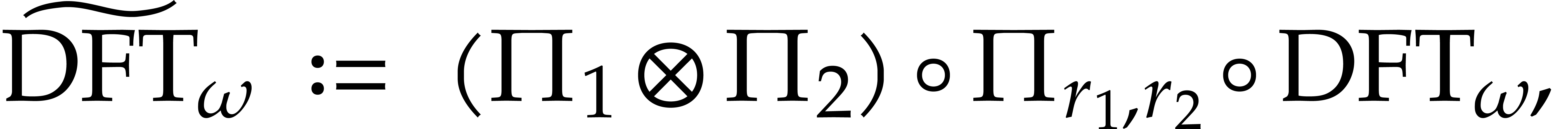
with the notation of (8). Then, equation (8) implies that
where 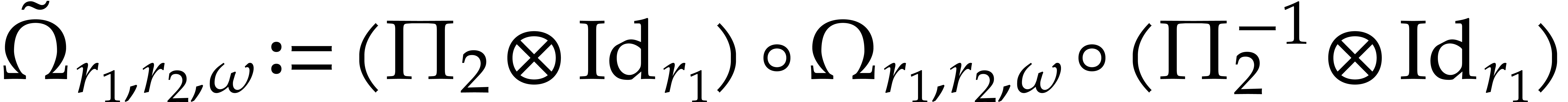 . For some table
. For some table  of precomputable twiddling factors, we have
of precomputable twiddling factors, we have 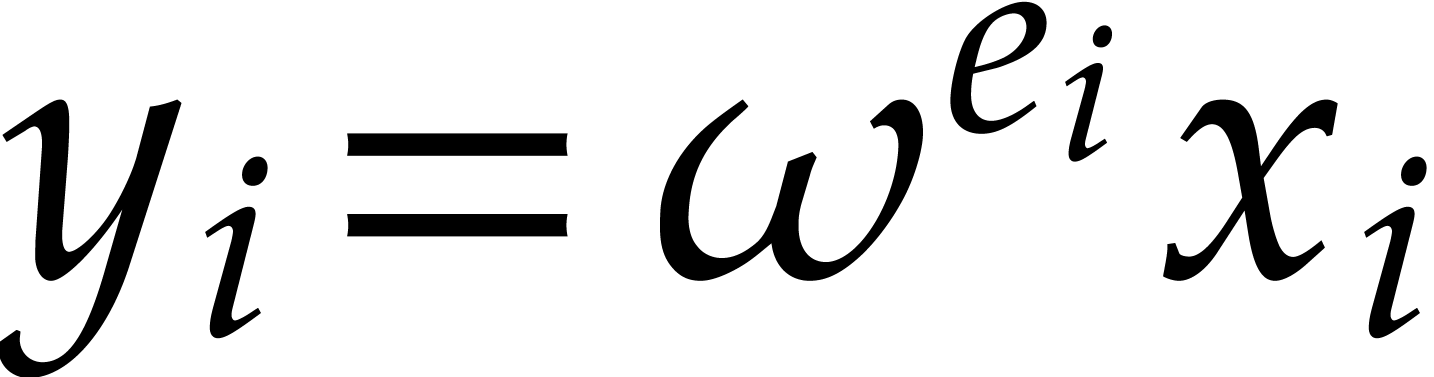 for any
for any  with
with 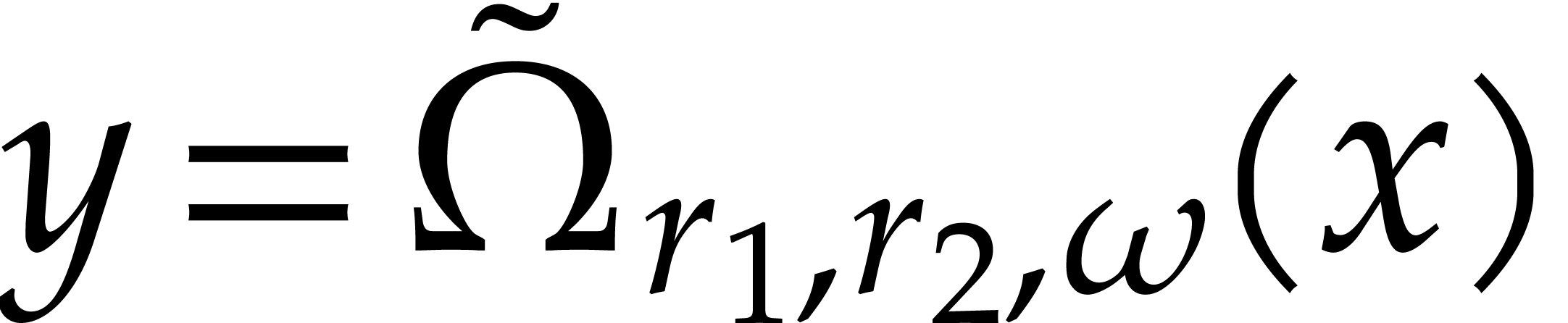 .
.
For DFTs of small orders, we also note that permutations of the input and output coefficients can be achieved without cost. As will be explained in sections 4.1 and 4.2, we will regard such DFTs as completely unrolled straight-line programs (SLPs); see definition in [3] for instance. Instead of explicitly permuting the input and output coefficients, it then suffices to appropriately rename all local variables in the SLP. This is particularly useful for the algorithm from section 2.3, which requires permutations of both the input and output coefficients.
In the special case when  is a finite field
is a finite field 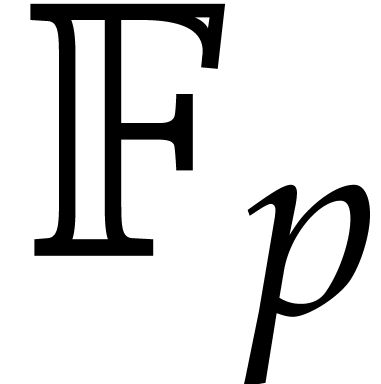 for some prime number
for some prime number  ,
a discrete Fourier transform is also called a number theoretic
transform (NTT). The most favorable case is when
,
a discrete Fourier transform is also called a number theoretic
transform (NTT). The most favorable case is when  is of the form
is of the form 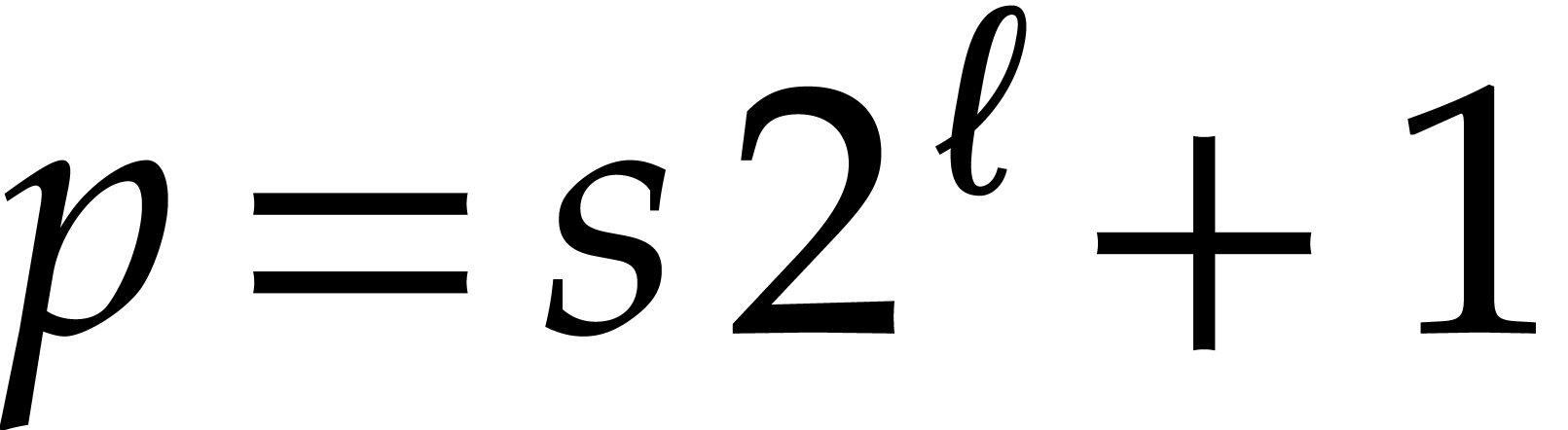 or
or  ,
where
,
where  is small. Indeed, since the multiplicative
group of
is small. Indeed, since the multiplicative
group of  is cyclic of order
is cyclic of order 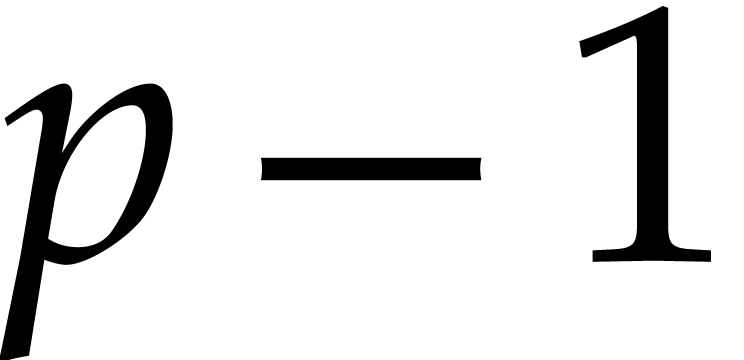 , this ensures the existence of primitive roots
of unity
, this ensures the existence of primitive roots
of unity 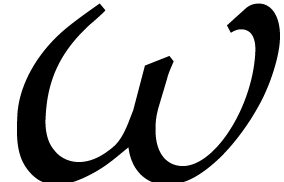 of large orders of the form
of large orders of the form 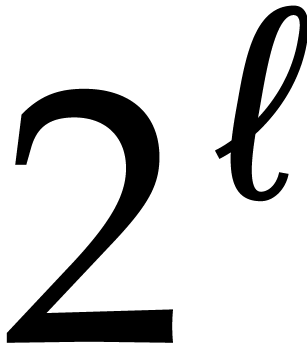 or
or 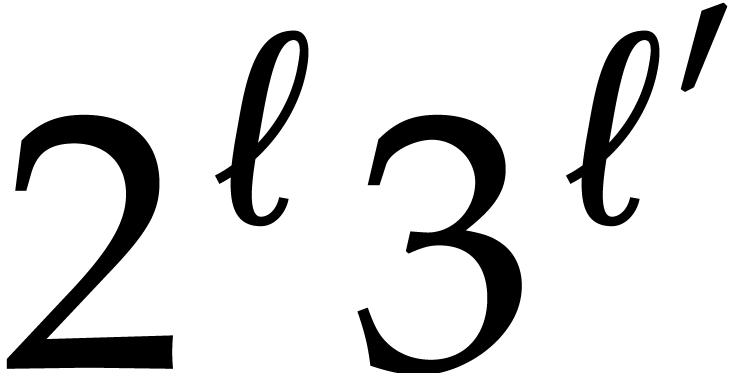 . Nice
primes
. Nice
primes 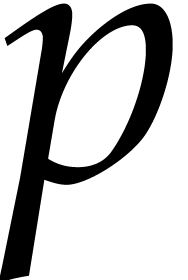 like this are sometimes called FFT
primes. In what follows, for any order
like this are sometimes called FFT
primes. In what follows, for any order 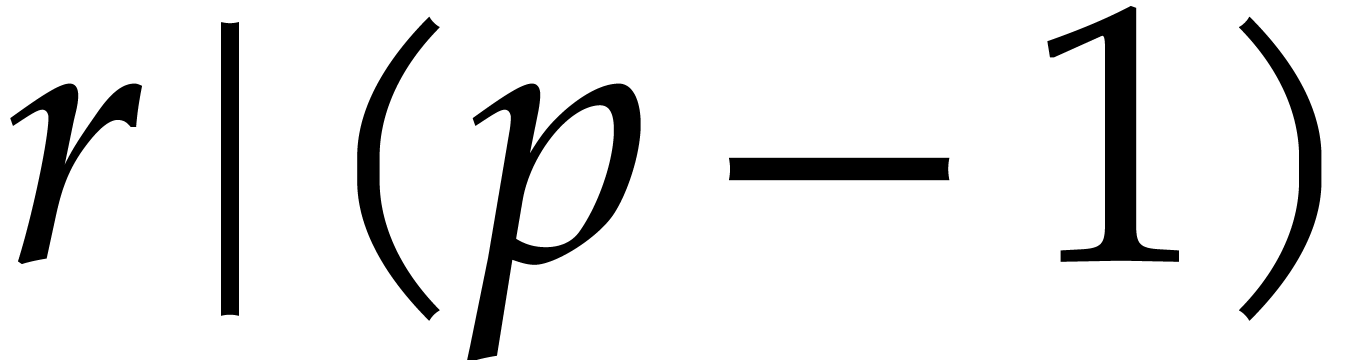 , we will denote by
, we will denote by  a number
theoretic transform of the form
a number
theoretic transform of the form 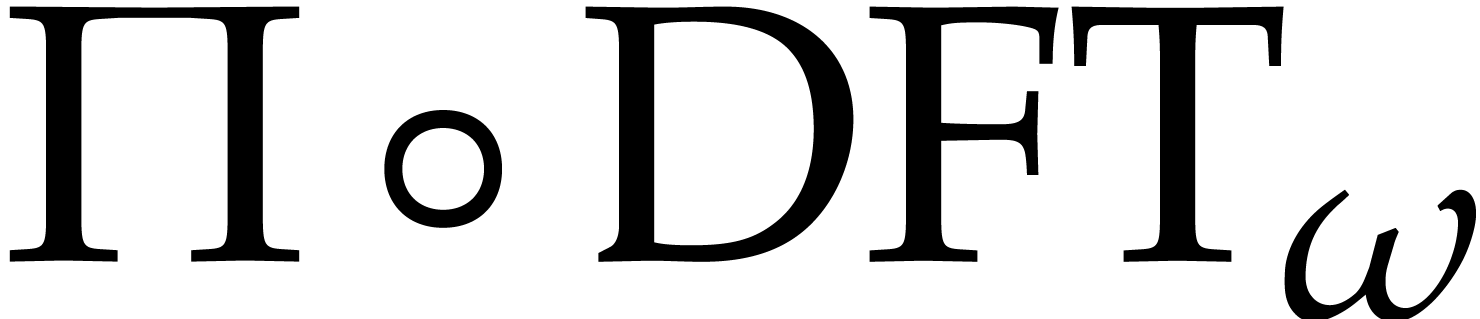 for some
suitable permutation
for some
suitable permutation  and primitive
and primitive  -th root of unity
-th root of unity 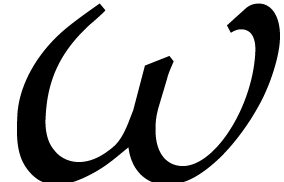 .
.
Pollard first noted [21] that NTTs can be used to devise
efficient practical algorithms for multiplying large integers: using
Kronecker segmentation, the two multiplicands 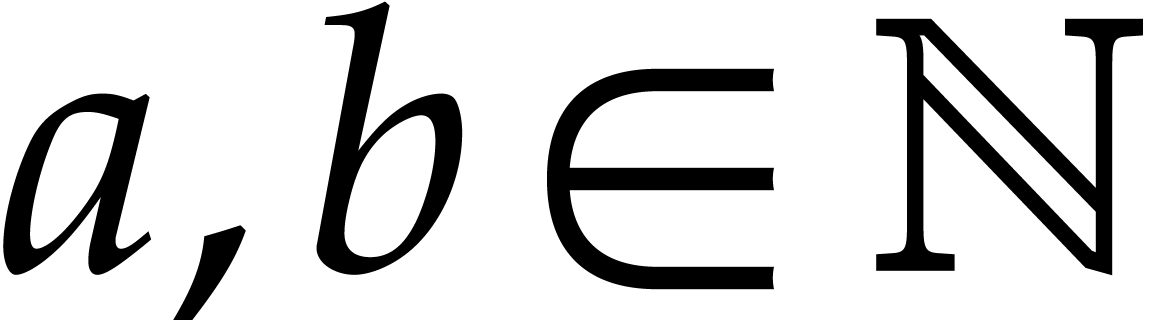 can be rewritten as special values
can be rewritten as special values
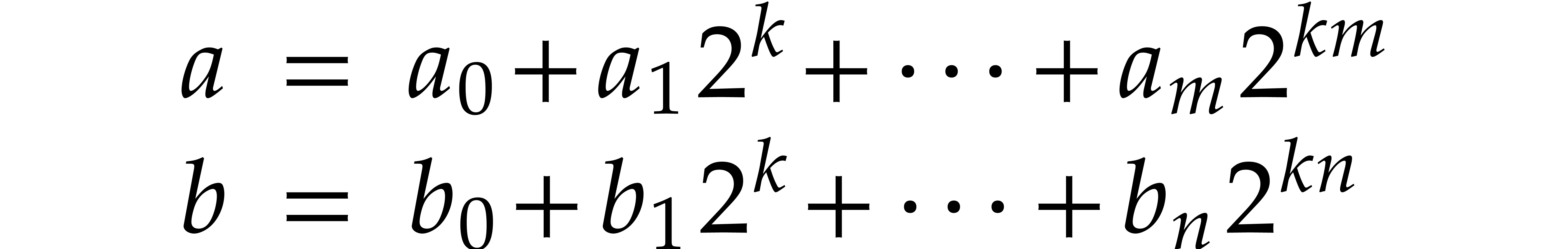
of integer polynomials 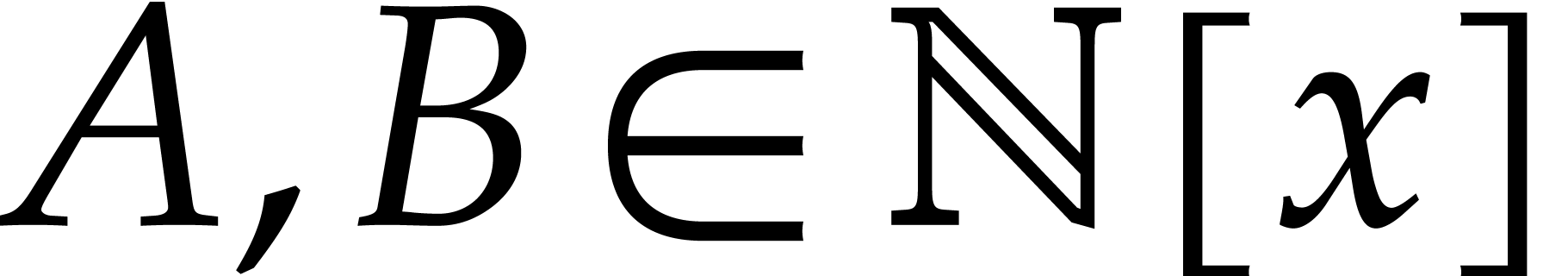 with small coefficients
with small coefficients
 . Then
. Then 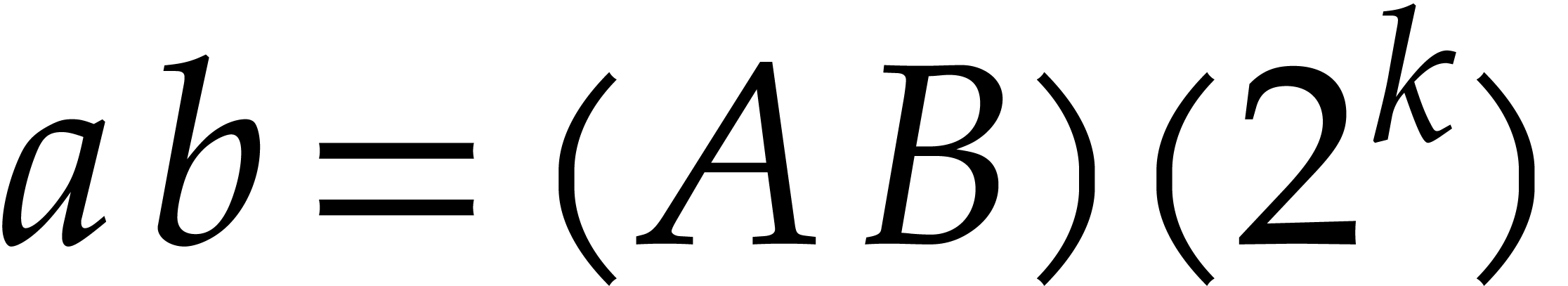 and the product
and the product  has coefficients in
has coefficients in 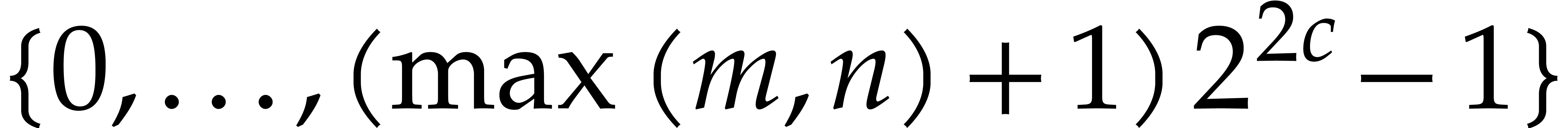 . If
. If
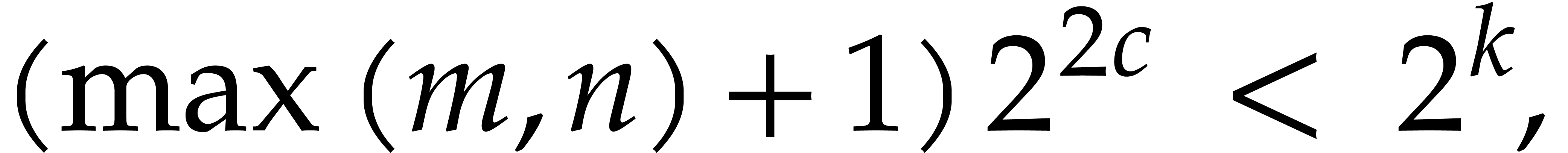 |
(9) |
then  can be read off from its reduction modulo
can be read off from its reduction modulo
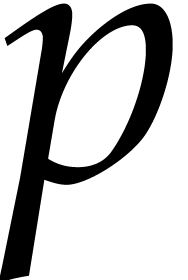 . If we also have
. If we also have 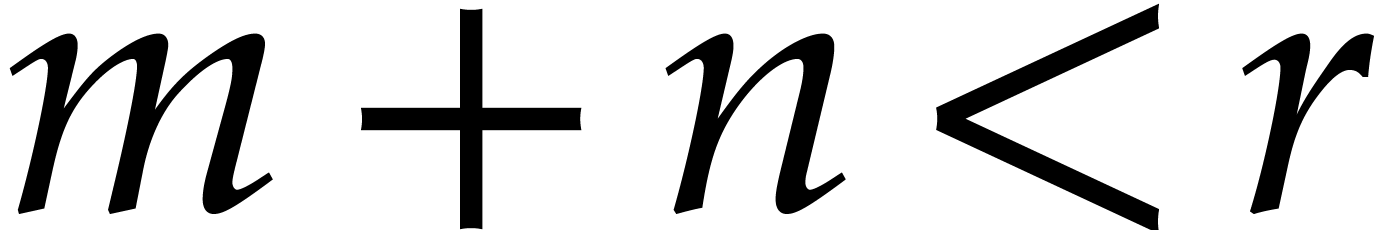 , then the product
, then the product  modulo
modulo 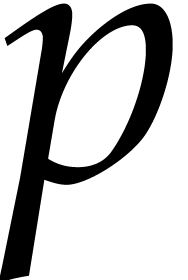 can be computed fast using
FFT-multiplication.
can be computed fast using
FFT-multiplication.
For the application to integer multiplication, Pollard's technique is
most efficient when 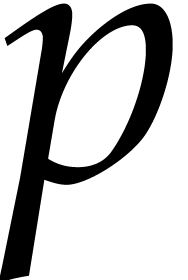 nicely fits into a machine
integer or floating point number. As soon as
nicely fits into a machine
integer or floating point number. As soon as  gets large (say
gets large (say  ), this
constraints
), this
constraints  to become fairly small
(e.g.
to become fairly small
(e.g. 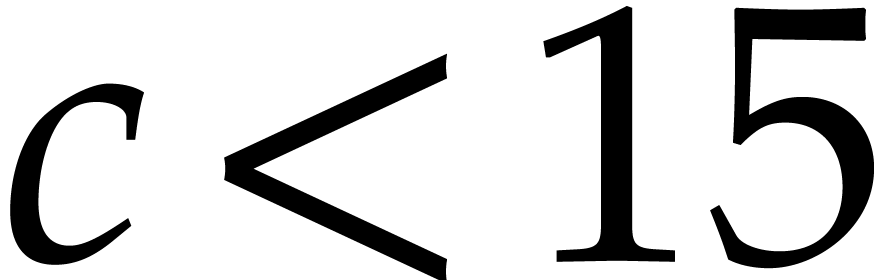 when using double precision
floating point arithmetic with
when using double precision
floating point arithmetic with 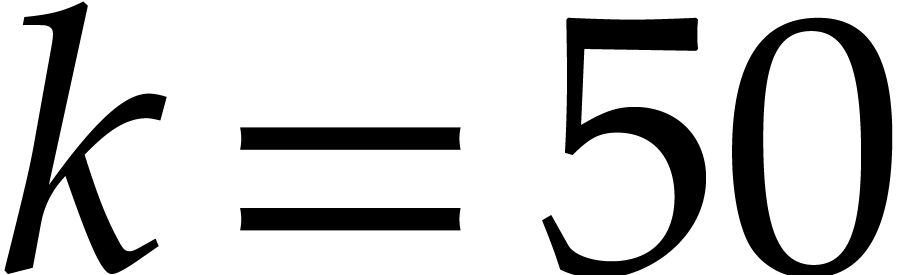 ).
In order to increase
).
In order to increase  , and
reduce the negative impact of
, and
reduce the negative impact of  in the constraint
(9), Pollard suggested to reduce modulo three FFT-primes
in the constraint
(9), Pollard suggested to reduce modulo three FFT-primes
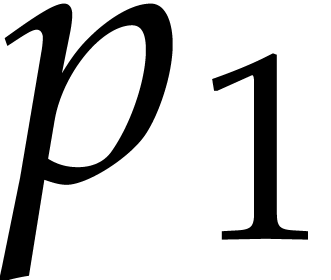 ,
, 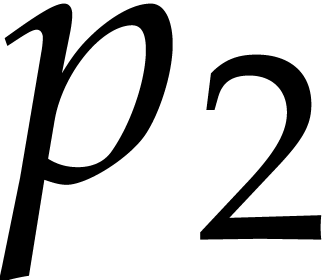 , and
, and  instead of a single
one and use Chinese remaindering to work modulo
instead of a single
one and use Chinese remaindering to work modulo 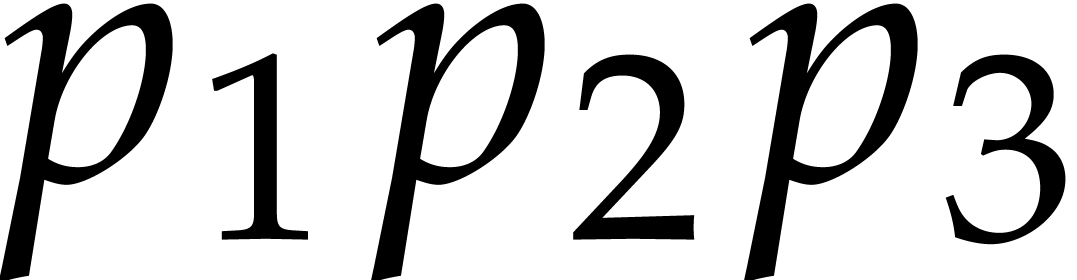 instead of
instead of 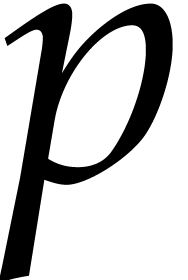 . For instance,
when using double precision floating point arithmetic, this allows us to
take
. For instance,
when using double precision floating point arithmetic, this allows us to
take 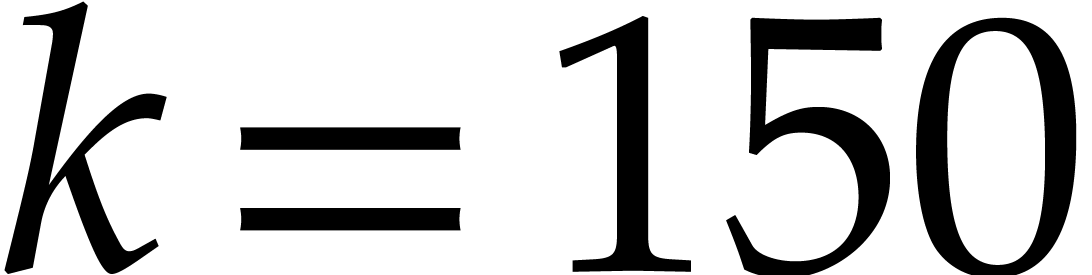 and
and 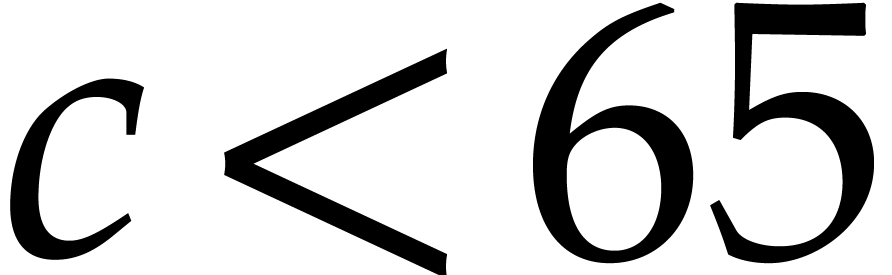 instead of
instead of 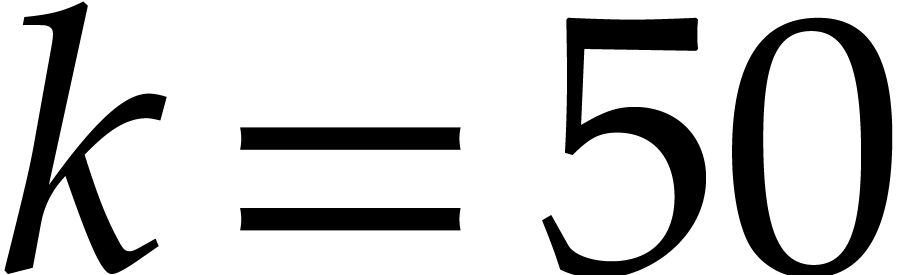 and
and  . As
of today, this is one of the fastest practical methods for integer
multiplication [13].
. As
of today, this is one of the fastest practical methods for integer
multiplication [13].
We refer to [7, 19] for previous work on the implementation of SIMD versions of modular arithmetic. Before starting such an implementation, one first has to decide whether one wishes to rely on floating point or integer arithmetic. In principle, integer arithmetic should be most suitable, since no bits are wasted on the storage of exponents. However, for large moduli of more than 32 bits, floating point arithmetic tends to be supported better by current hardware.
First of all, at least in the case of  32 bit integer products;
although there is an SIMD instruction for 64
32 bit integer products;
although there is an SIMD instruction for 64 64 bit integer multiplication, the high part of the
64 bit integer multiplication, the high part of the
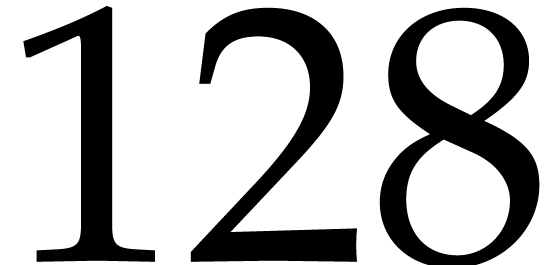 bit result is lost. In comparison, with floating
point arithmetic, the full product of a
bit result is lost. In comparison, with floating
point arithmetic, the full product of a  bit
integer multiplication can be obtained using two fused multiply add
instructions.
bit
integer multiplication can be obtained using two fused multiply add
instructions.
Based on these hardware considerations, we have decided to implement our
NTT with floating point arithmetic. Our implementation focusses on odd
moduli 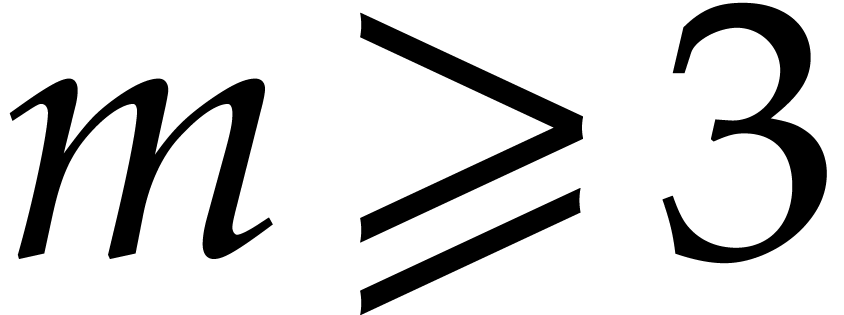 that fit into double precision numbers
and works for SIMD widths up to
that fit into double precision numbers
and works for SIMD widths up to 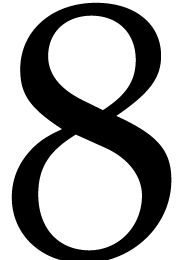 ,
as allowed by processors with AVX-512 support.
,
as allowed by processors with AVX-512 support.
Our approach further extends known ideas. On the one hand, for the
normalized representation of integers modulo 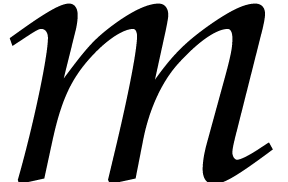 , we use signed residues in
, we use signed residues in  ; this provides us with a cheap way to gain one bit
of precision and it also simplifies the mathematical analysis. On the
other hand, we will allow the results of certain intermediate
computations to be non-normalized. The latter idea was already used with
success in [13], but we push it further by taking the
modulus a bit smaller (thereby sacrificing a few bits of precision),
which allows us to redundantly represent modular integers
; this provides us with a cheap way to gain one bit
of precision and it also simplifies the mathematical analysis. On the
other hand, we will allow the results of certain intermediate
computations to be non-normalized. The latter idea was already used with
success in [13], but we push it further by taking the
modulus a bit smaller (thereby sacrificing a few bits of precision),
which allows us to redundantly represent modular integers 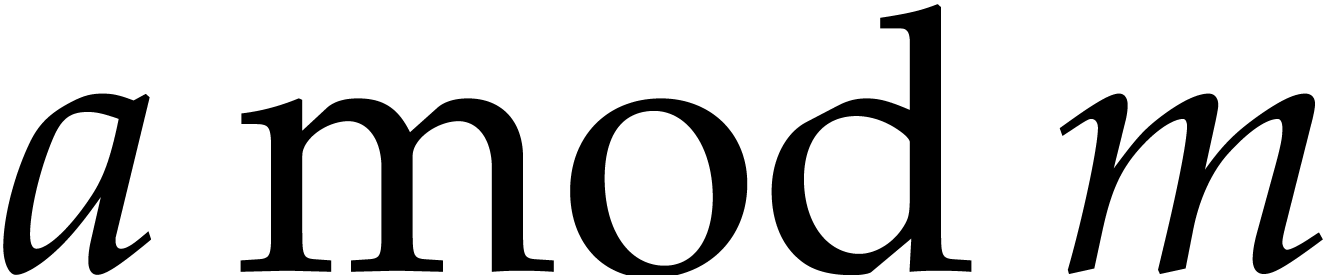 by integers
by integers  that can be several
times larger than
that can be several
times larger than 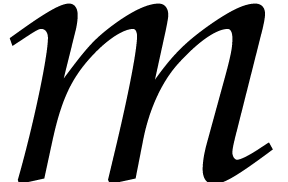 (this allows for several
speed-ups, as we shall see). Several recent implementations [2,
24] also use this kind of super-redundant representations
in order to perform basic NTTs of order
(this allows for several
speed-ups, as we shall see). Several recent implementations [2,
24] also use this kind of super-redundant representations
in order to perform basic NTTs of order  and
and 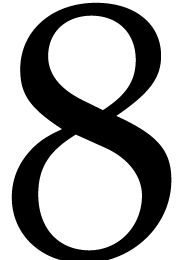 without unnecessary reductions. In this paper we will
present a generalization to arbitrary orders.
without unnecessary reductions. In this paper we will
present a generalization to arbitrary orders.
In what follows, we will write 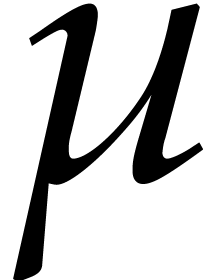 for the machine
precision and assume that
for the machine
precision and assume that  .
Then any real number in the interval
.
Then any real number in the interval 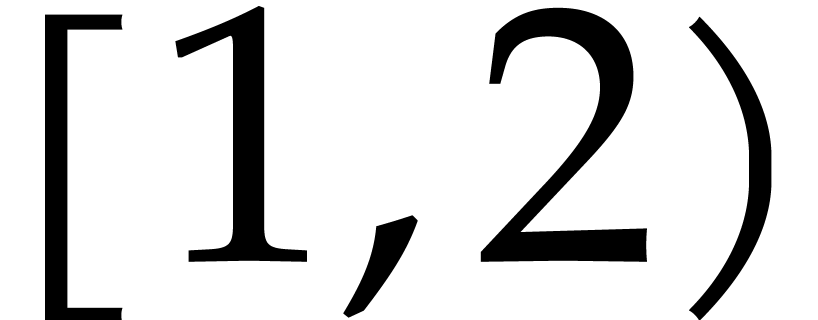 is a
floating point number if and only if it is a multiple of
is a
floating point number if and only if it is a multiple of  . Floating point number can be scaled by powers
. Floating point number can be scaled by powers
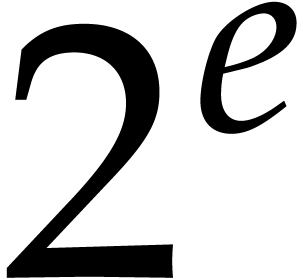 with exponents
with exponents 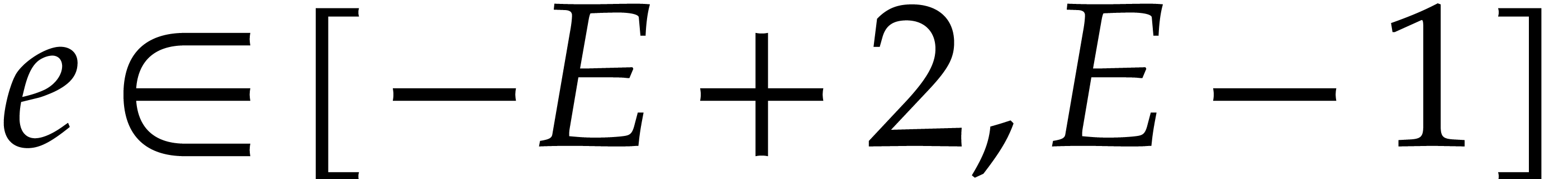 .
Here
.
Here  is assumed to satisfy
is assumed to satisfy 
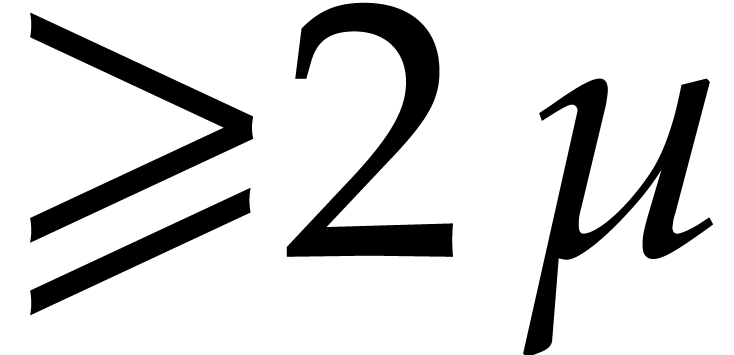 . Finally, zero is a special
floating point number.
. Finally, zero is a special
floating point number.
When rounding to nearest, the rounding error of a floating point
operation with an exact result in 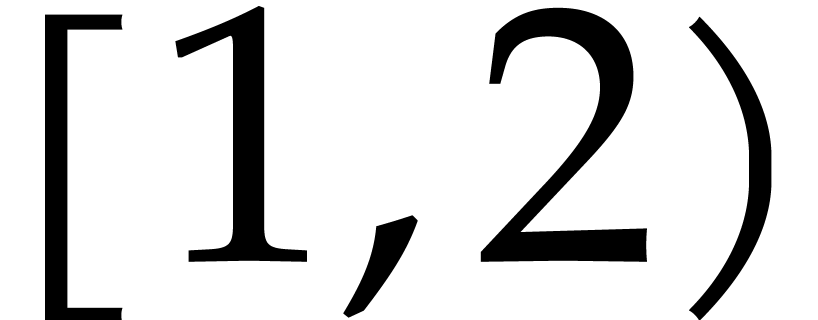 is always
bounded by
is always
bounded by 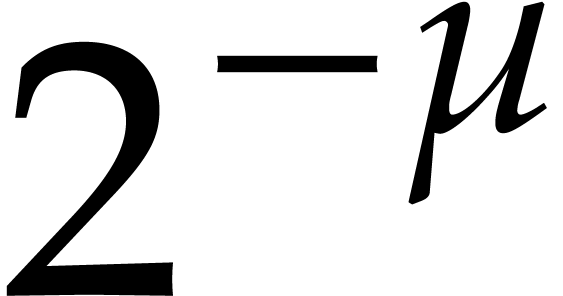 . Given a general
operation with an exact result
. Given a general
operation with an exact result  and rounded
result
and rounded
result 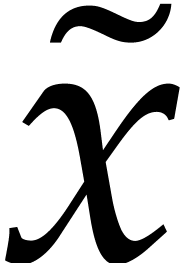 , this means that
, this means that
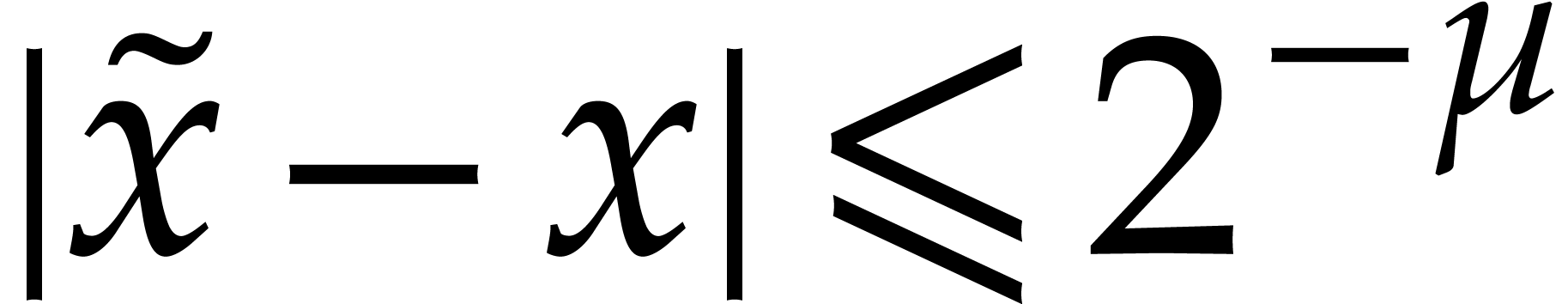 . Note also that
. Note also that 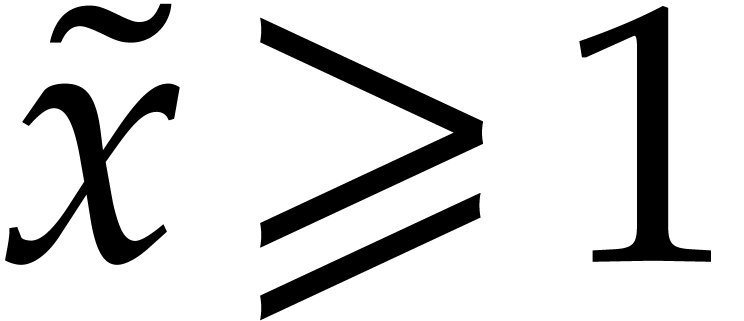 necessarily holds in this case. Consequently, we have
necessarily holds in this case. Consequently, we have
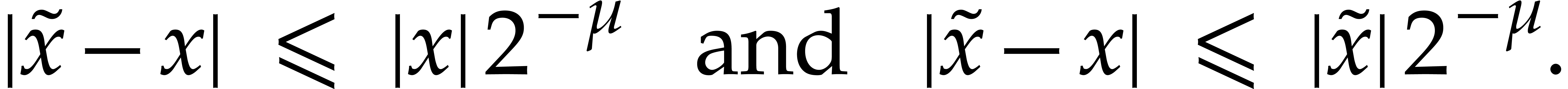 |
(10) |
More generally, these two inequalities hold whenever the exponent of
 does not overflow or underflow. Our current
implementation is limited to double precision, for which
does not overflow or underflow. Our current
implementation is limited to double precision, for which 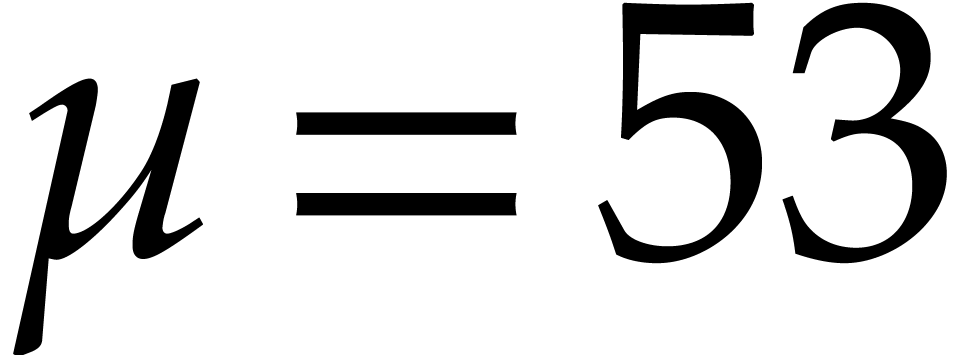 and
and 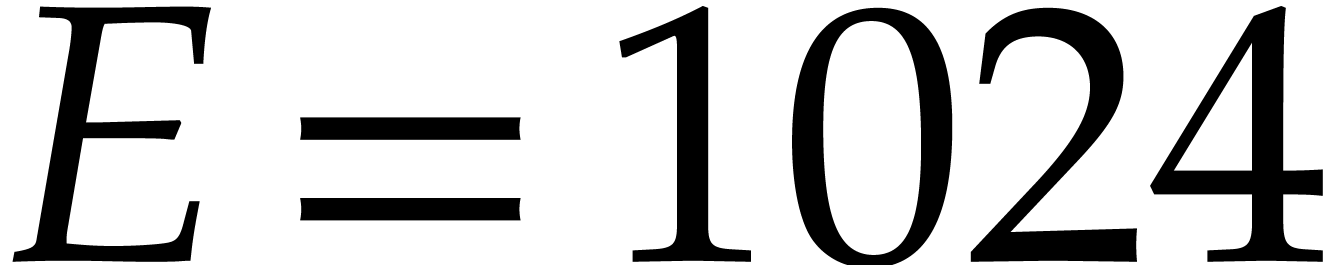 , but it
could easily be extended to single and other precisions. We assume
correct IEEE 754 style rounding to the nearest [1].
, but it
could easily be extended to single and other precisions. We assume
correct IEEE 754 style rounding to the nearest [1].
We will present our implementation of modular arithmetic using pseudo
machine code. The only data type that we will use are SIMD vectors of
width 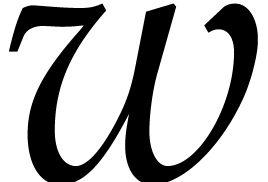 with floating point entries
(e.g.
with floating point entries
(e.g. 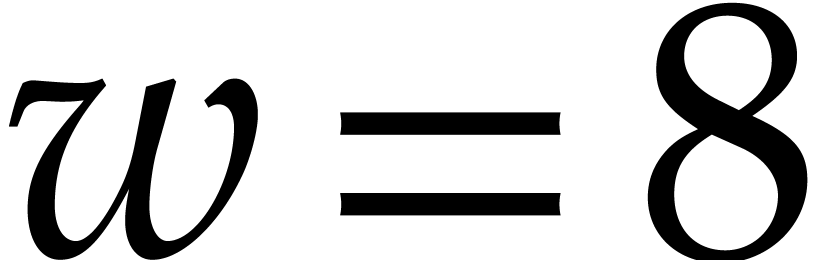 for processors with AVX-512
support, for double precision). Such vectors are typically stored in
hardware registers. The first argument of all our algorithms will be the
destination register and the subsequent arguments the source registers.
For instance, the instruction
for processors with AVX-512
support, for double precision). Such vectors are typically stored in
hardware registers. The first argument of all our algorithms will be the
destination register and the subsequent arguments the source registers.
For instance, the instruction  adds two SIMD
vectors
adds two SIMD
vectors 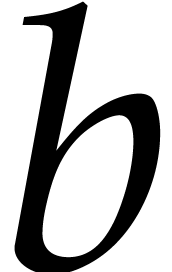 and
and  and puts the
result in
and puts the
result in  . In the
pseudo-code, the modulus
. In the
pseudo-code, the modulus 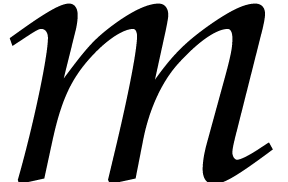 stands for a SIMD
vector of
stands for a SIMD
vector of 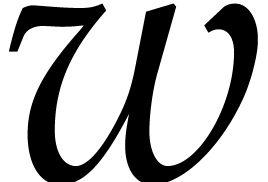 potentially different moduli. We also
denote by
potentially different moduli. We also
denote by 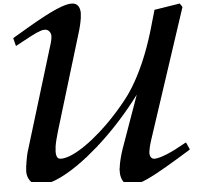 its floating point inverse
its floating point inverse 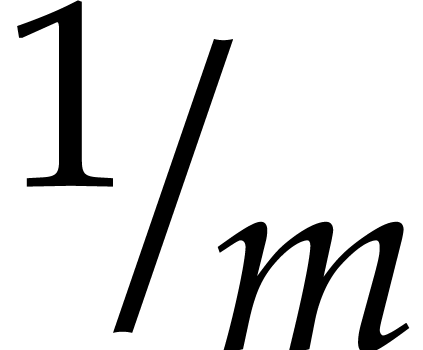 , rounded to nearest.
, rounded to nearest.
We assume that basic instructions for SIMD floating point arithmetic are provided by the hardware, namely addition (add), subtraction (sub), multiplication (mul), fused multiply add (fma) and its variants (fms, fnma, fnms), as well as an instruction for rounding to the nearest integer (round). Precisely, the fused operators are defined as follows:
On processors with AVX-512 support, one may implement  using the intrinsic _mm512_roundscale_pd.
using the intrinsic _mm512_roundscale_pd.
The modular analogues for the basic arithmetic operations are suffixed
by 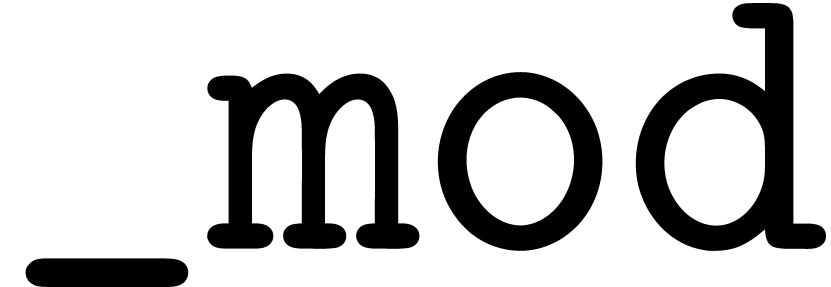 . For instance,
. For instance,  computes
computes 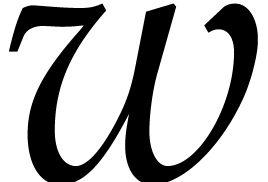 products modulo
products modulo 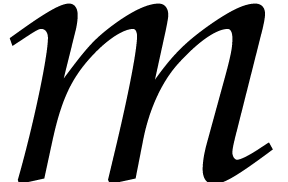 . The results of these analogues
are not required to be normalized. The modular ring operations, as well
as a separate operation
. The results of these analogues
are not required to be normalized. The modular ring operations, as well
as a separate operation  for normalization, can
be implemented as follows:
for normalization, can
be implemented as follows:
Algorithm
|
Algorithm
|
|
|
Algorithm
|
Algorithm
|
Here 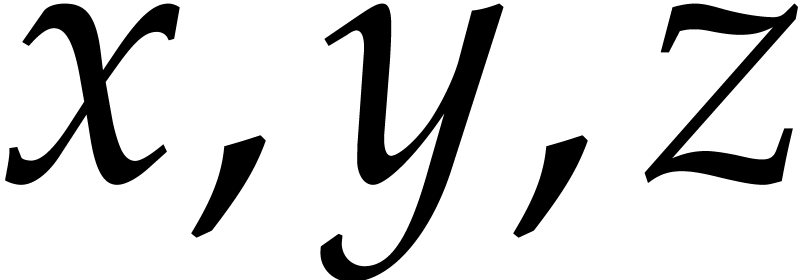 are temporary variables. Modular analogues
of the fused operations fma, fms, fnma, and fnms turn out to be of limited
use, since non-normalized addition and subtraction take only one
operation.
are temporary variables. Modular analogues
of the fused operations fma, fms, fnma, and fnms turn out to be of limited
use, since non-normalized addition and subtraction take only one
operation.
For the analysis of our algorithms, it suffices to consider the scalar
case 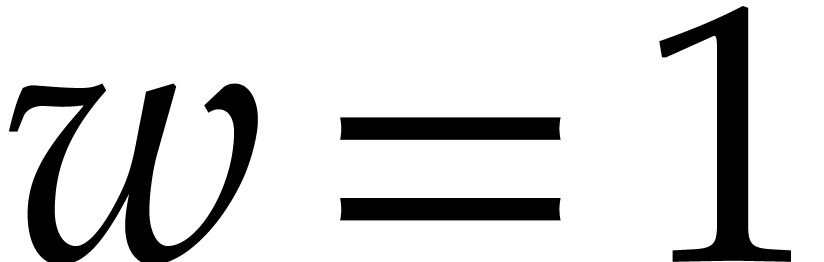 . Consider a modular
integer
. Consider a modular
integer 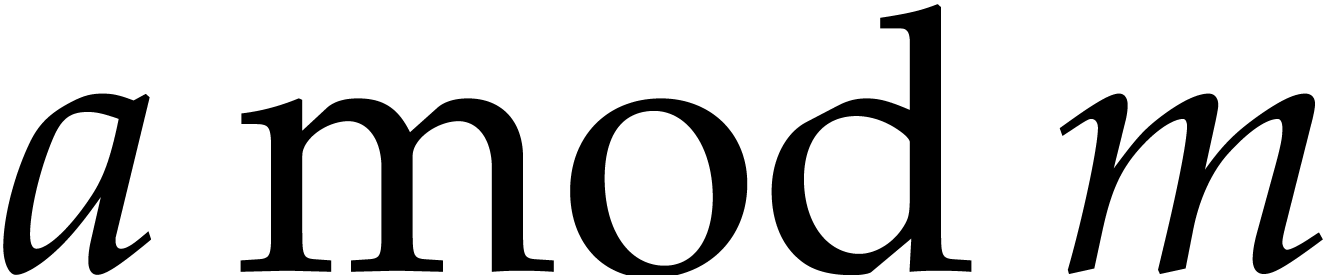 represented by an integer
represented by an integer  that fits into a floating point number of precision
that fits into a floating point number of precision 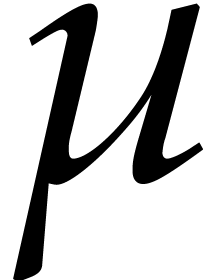 . Let
. Let
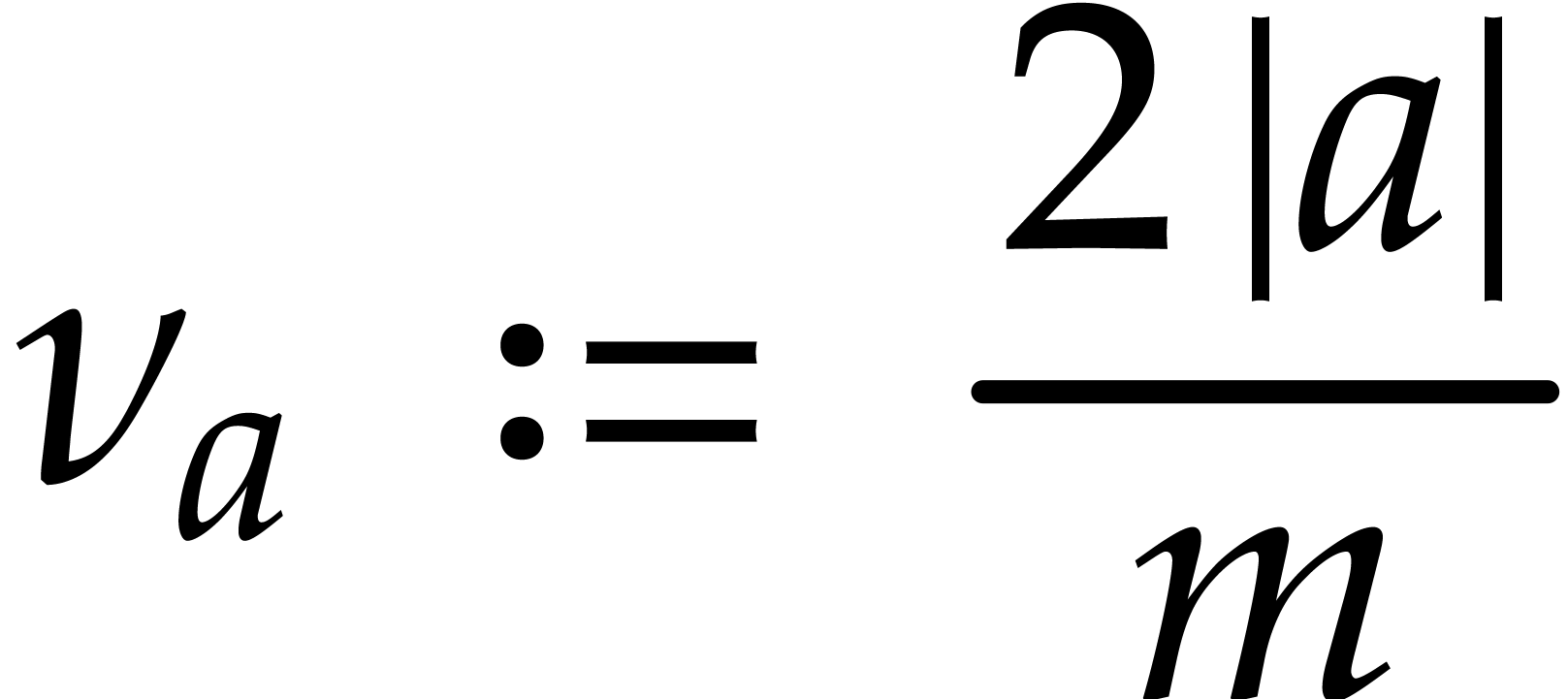
and note that 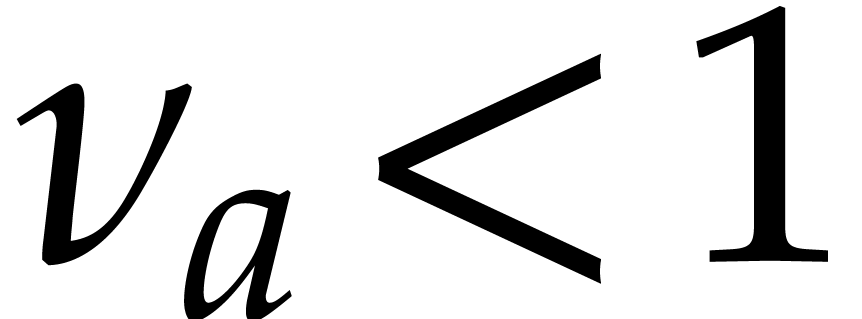 if and only if
if and only if 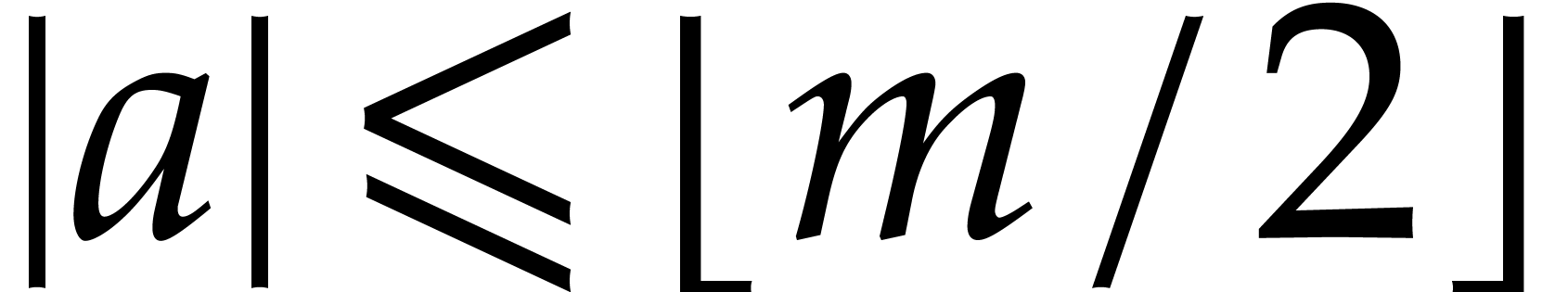 , i.e. if and only if
, i.e. if and only if  is normalized. If
is normalized. If 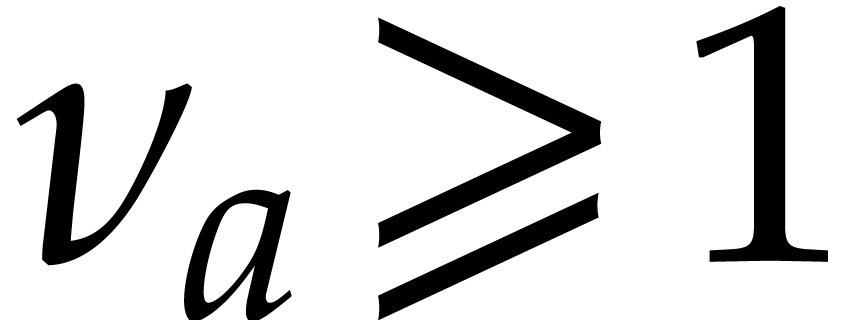 ,
then we regard
,
then we regard 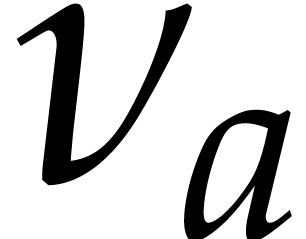 as a measure for how
non-normalized
as a measure for how
non-normalized  really is. For each of our
algorithms add_mod, sub_mod, mul_mod,
and normalize it is interesting to analyze
really is. For each of our
algorithms add_mod, sub_mod, mul_mod,
and normalize it is interesting to analyze 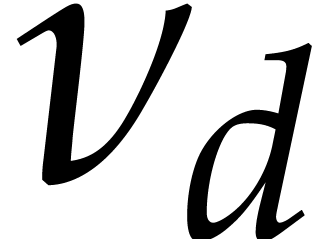 as a function of
as a function of 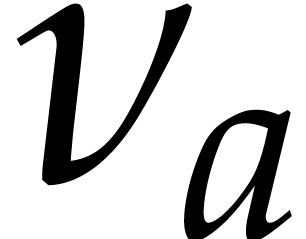 and
and 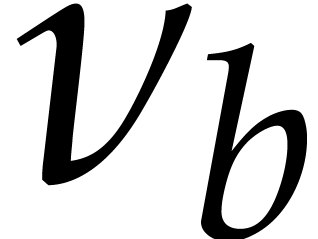 .
.
Note that 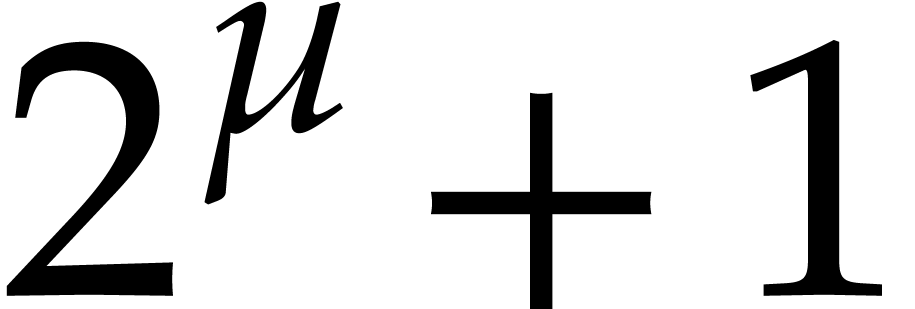 is the smallest integer that cannot be
represented exactly using a floating point number. For this reason, we
always assume that the source arguments
is the smallest integer that cannot be
represented exactly using a floating point number. For this reason, we
always assume that the source arguments  and
and 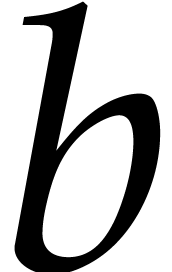 of our algorithms as well as the modulus
of our algorithms as well as the modulus 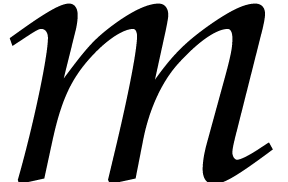 satisfy
satisfy 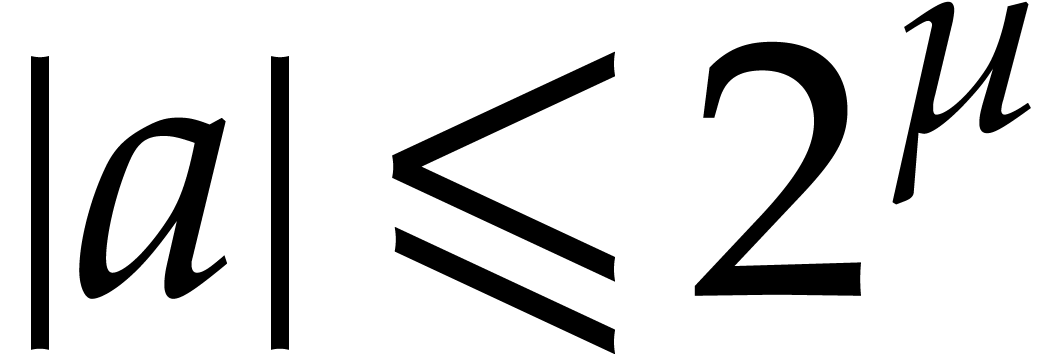 ,
, 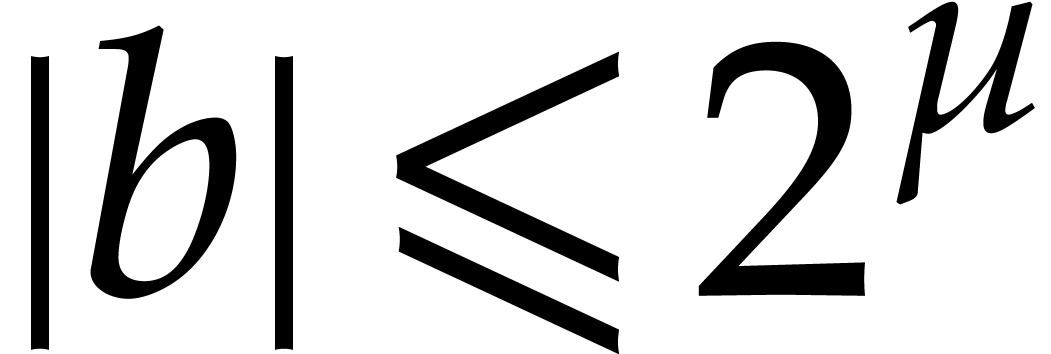 , and
, and 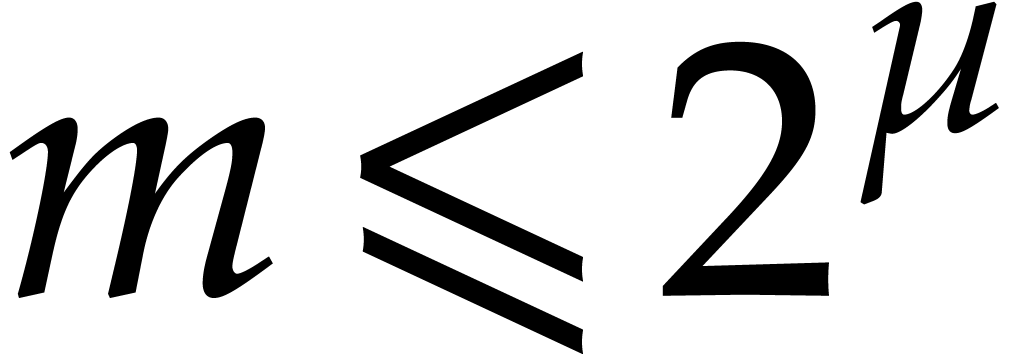 .
Each of our algorithms is easily seen to be correct, provided that
.
Each of our algorithms is easily seen to be correct, provided that  . In what follows, we will in
particular study under which circumstances this can be guaranteed.
. In what follows, we will in
particular study under which circumstances this can be guaranteed.
In the cases of addition and subtraction, the analysis is simple, since
we clearly have 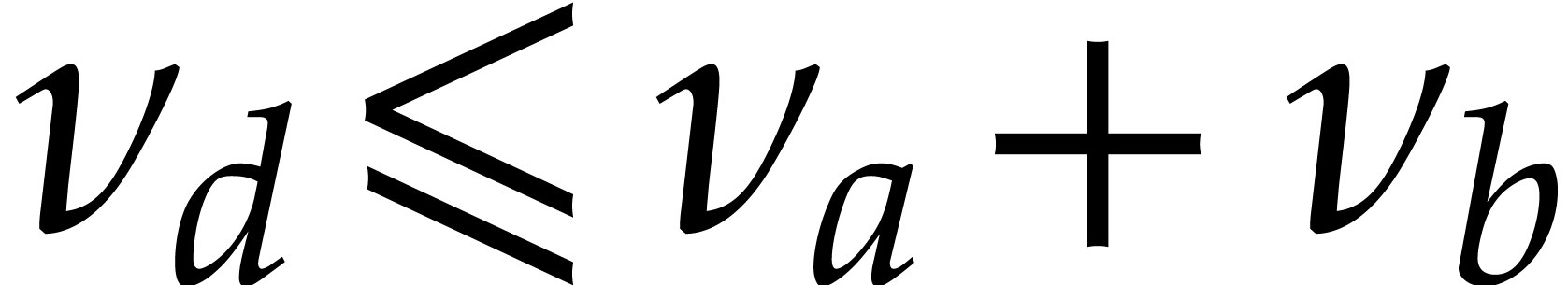 and
and  , provided that
, provided that 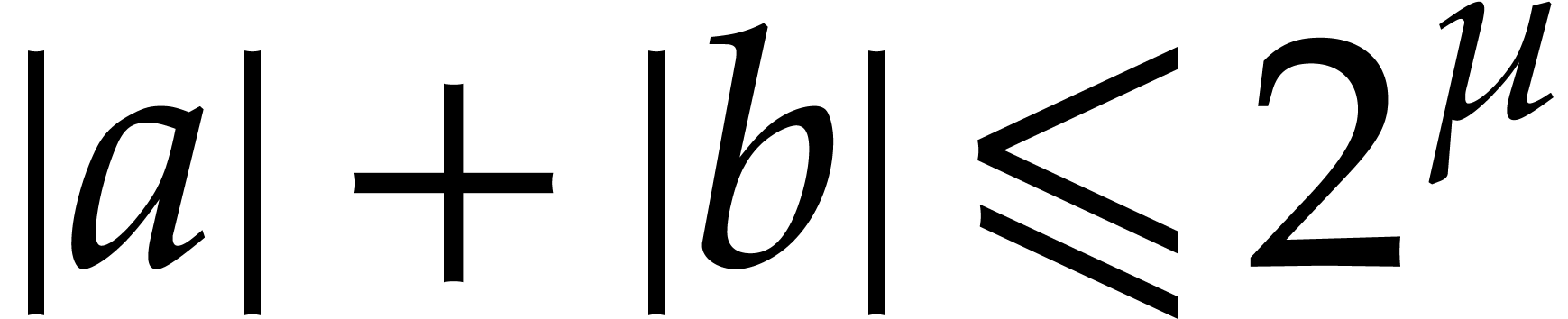 (or
(or 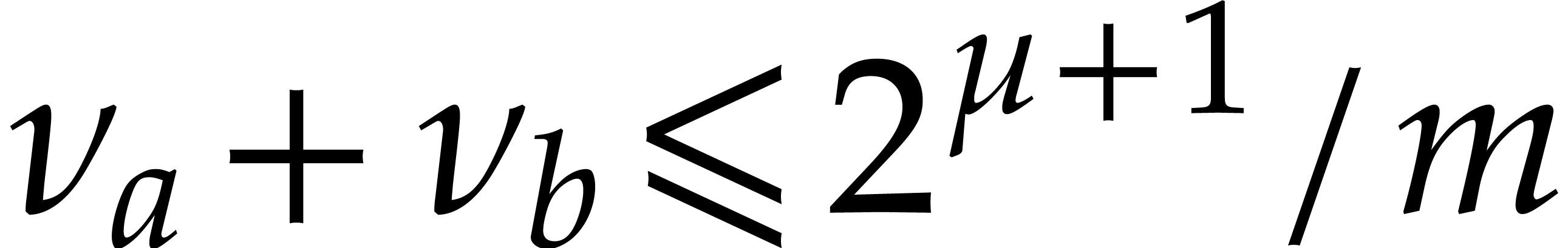 , equivalently).
, equivalently).
Proof. Let  and
and  be the errors for the computations of
be the errors for the computations of  and
and  :
:
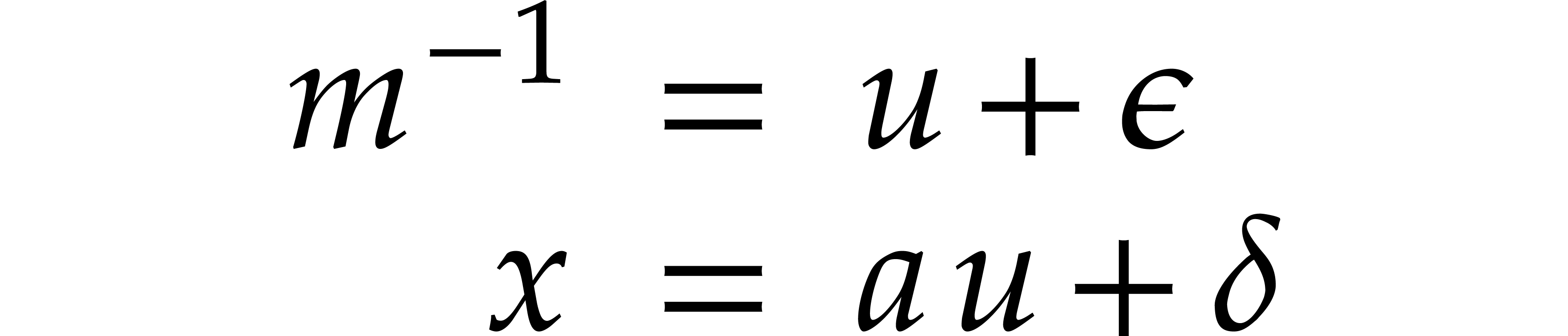
and recall that 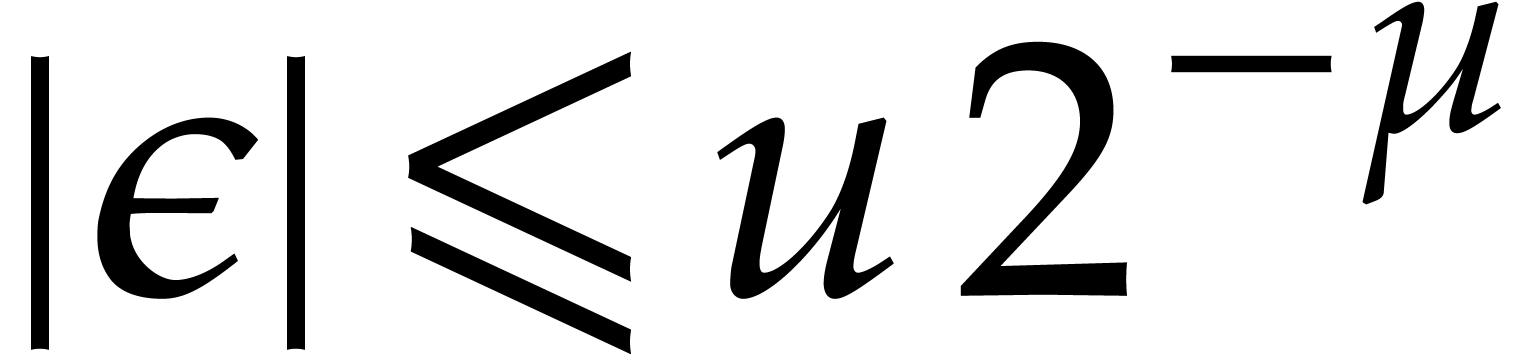 ,
, 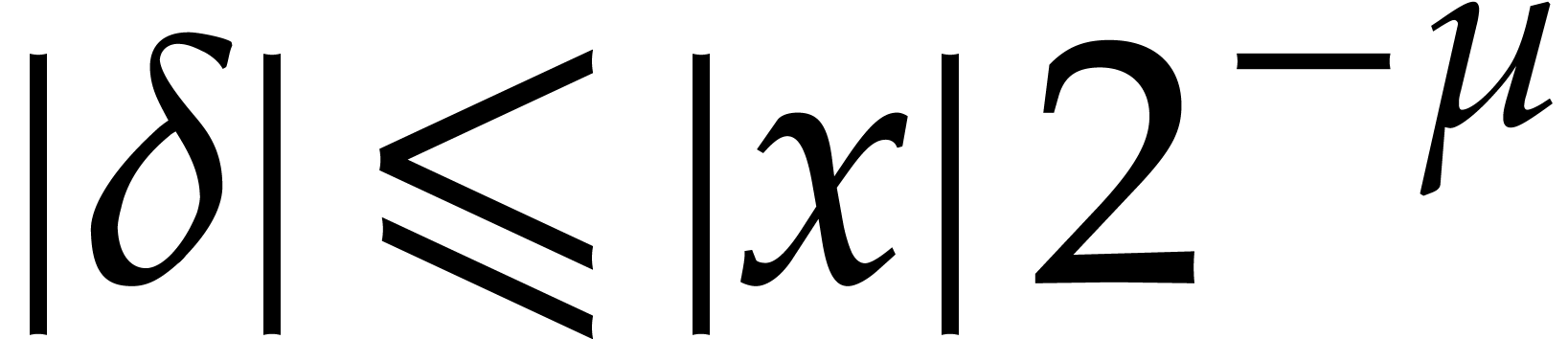 ,
, 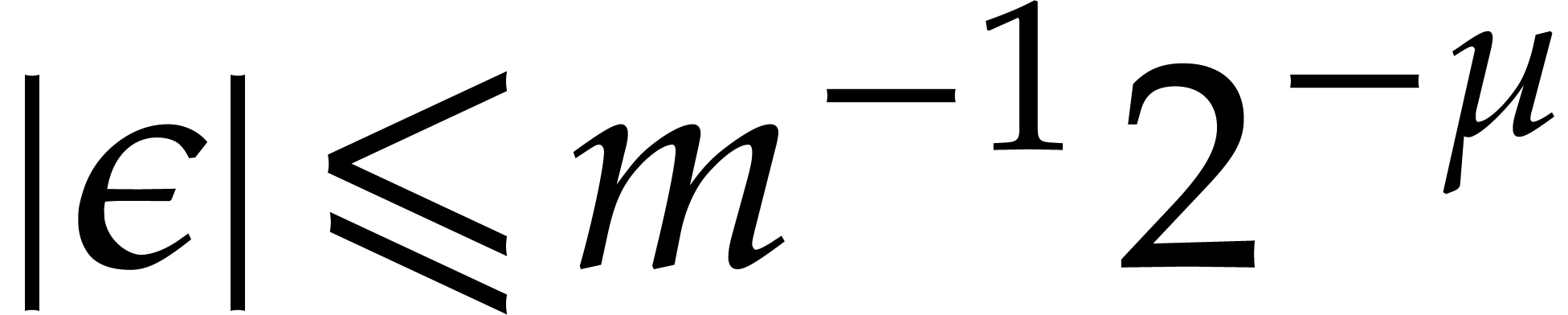 ,
and
,
and 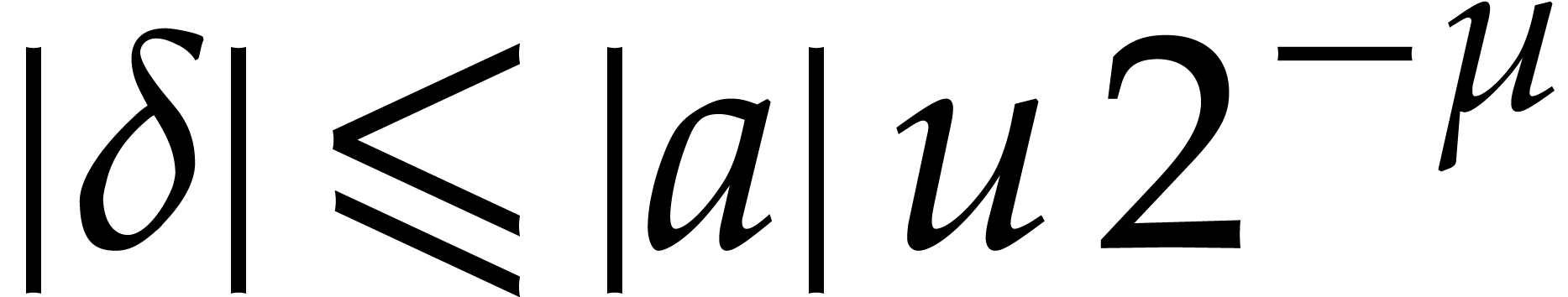 , using
, using
Let 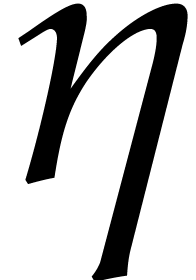 be the distance between
be the distance between  and the set
and the set 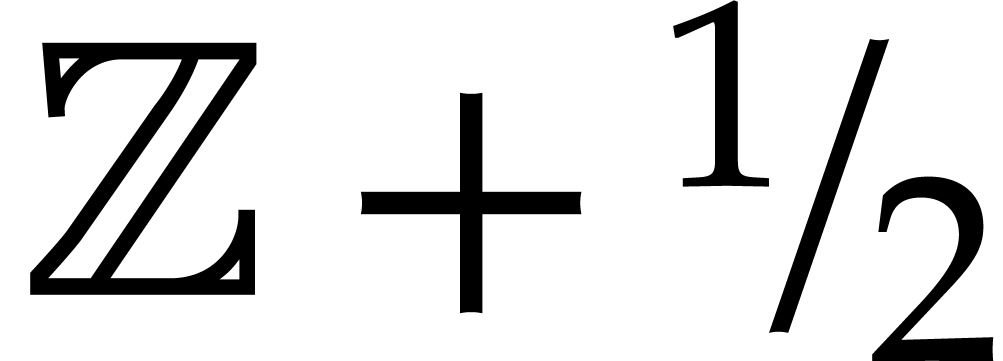 . Since
. Since 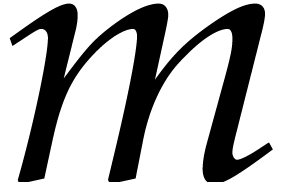 is odd, we must have
is odd, we must have  .
If
.
If 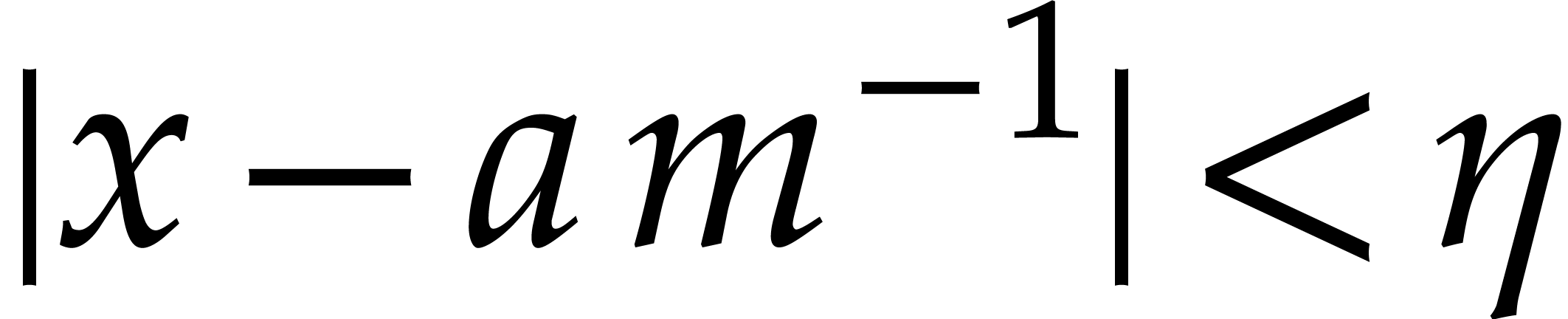 , then we necessarily have
, then we necessarily have
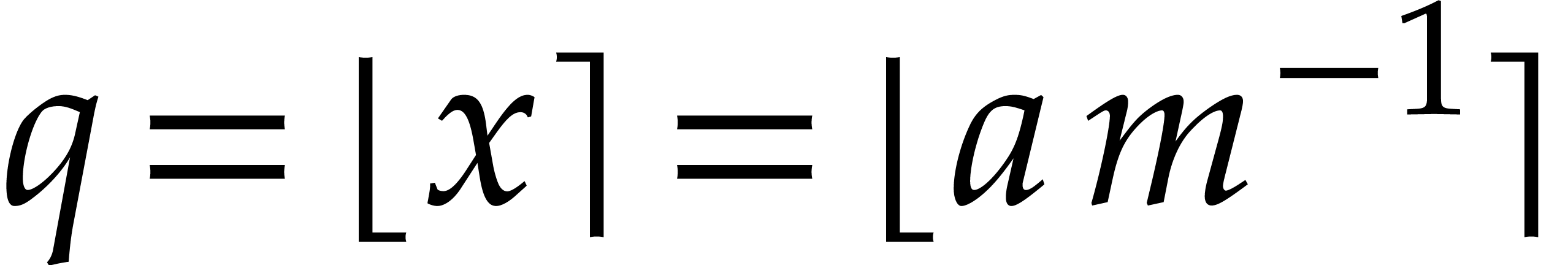 , and the end-result
, and the end-result  will indeed be normalized. Here
will indeed be normalized. Here 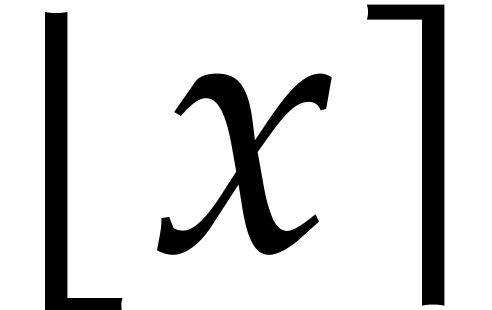 stands for the nearest integer to
stands for the nearest integer to  .
The condition
.
The condition 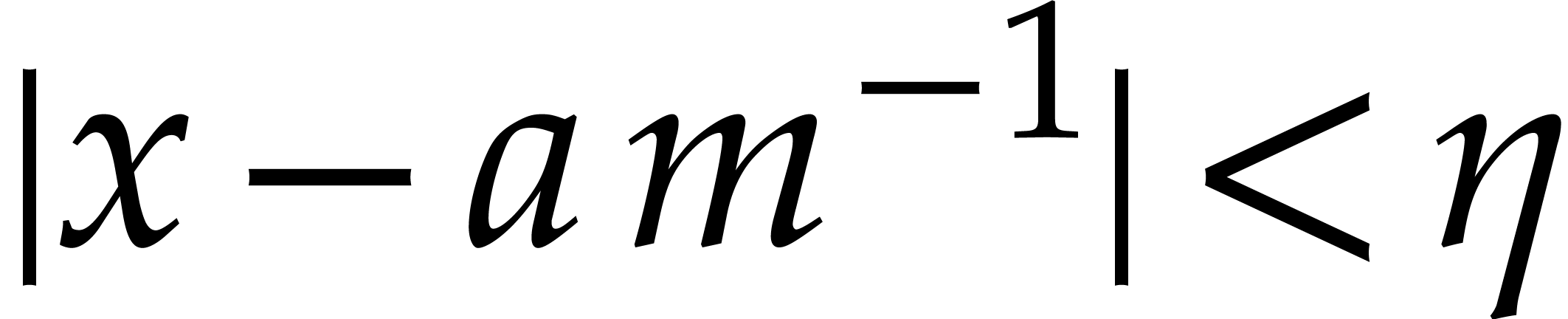 is satisfied as soon as
is satisfied as soon as 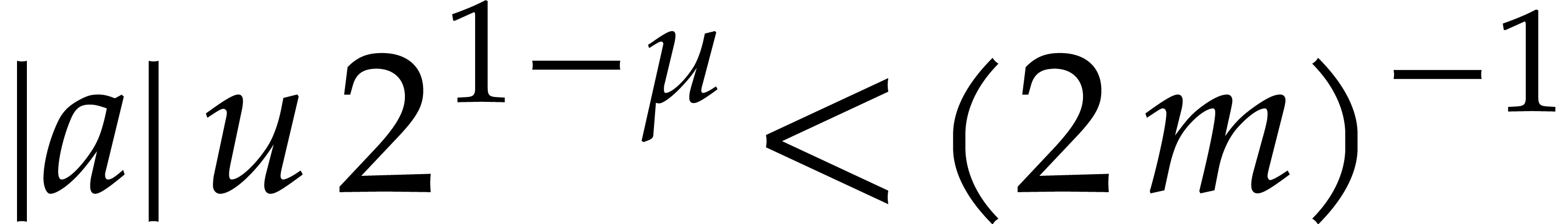 , i.e. if
, i.e. if 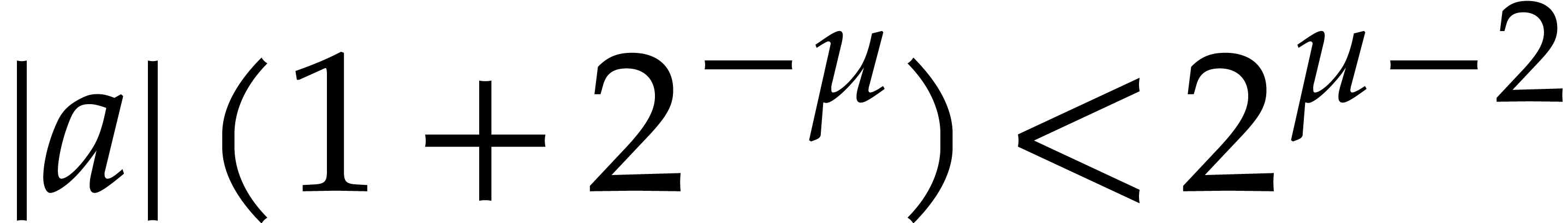 . Since
. Since  is an integer
and there are no integers between
is an integer
and there are no integers between 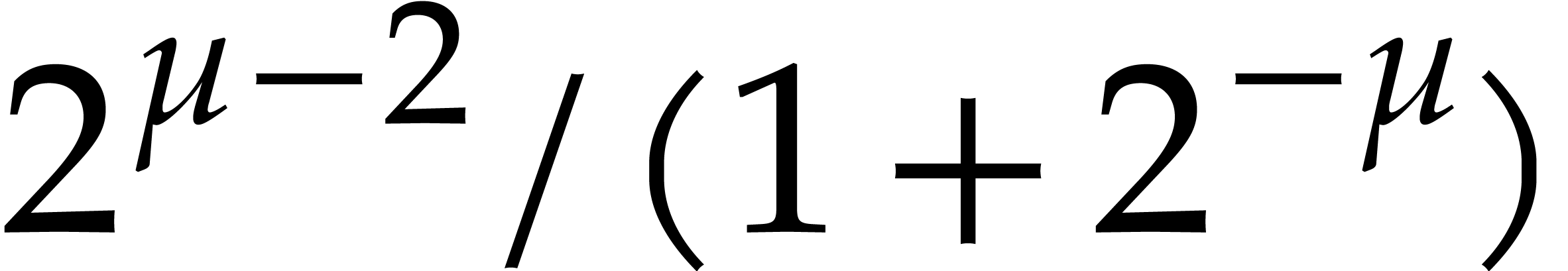 and
and 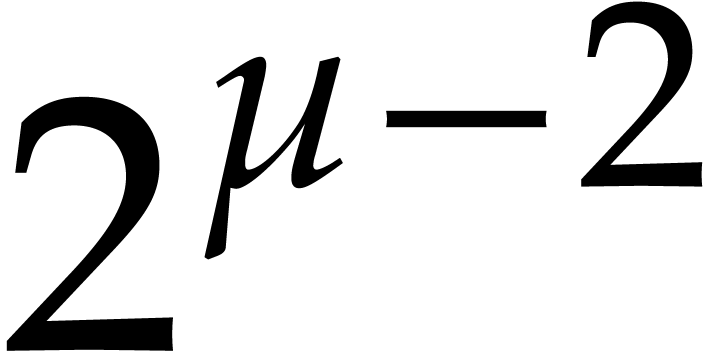 , this condition further simplifies
into
, this condition further simplifies
into 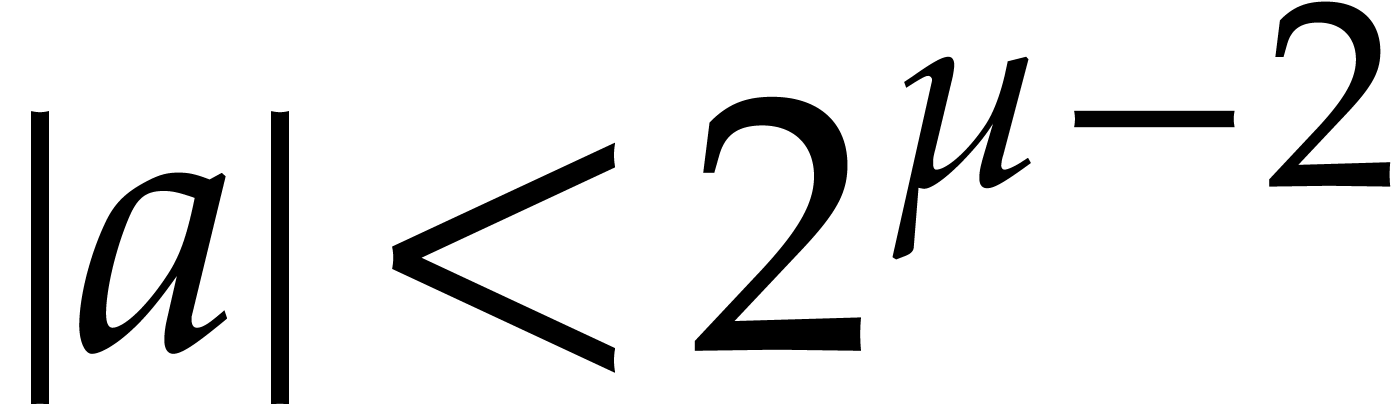 . This proves
(a).
. This proves
(a).
If  , then the above
calculations still yield
, then the above
calculations still yield 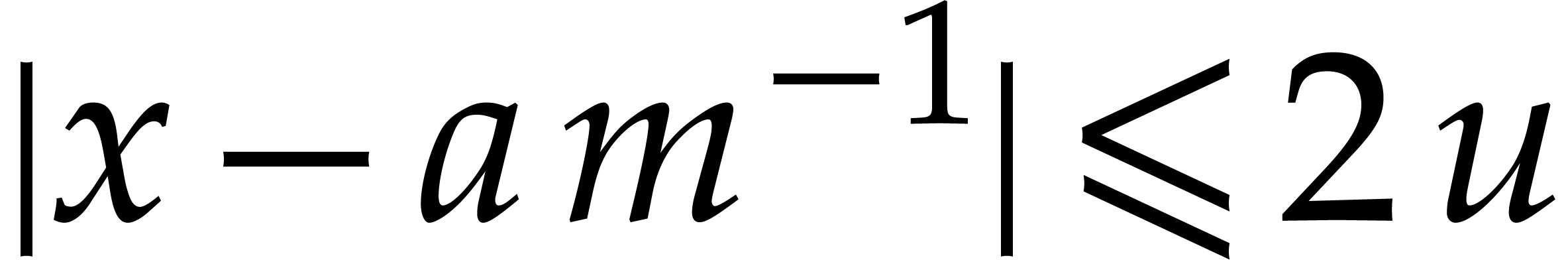 ,
whence
,
whence
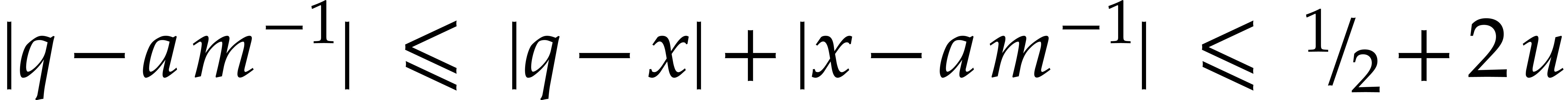
and
This in particular implies (b).
Remark  and
and 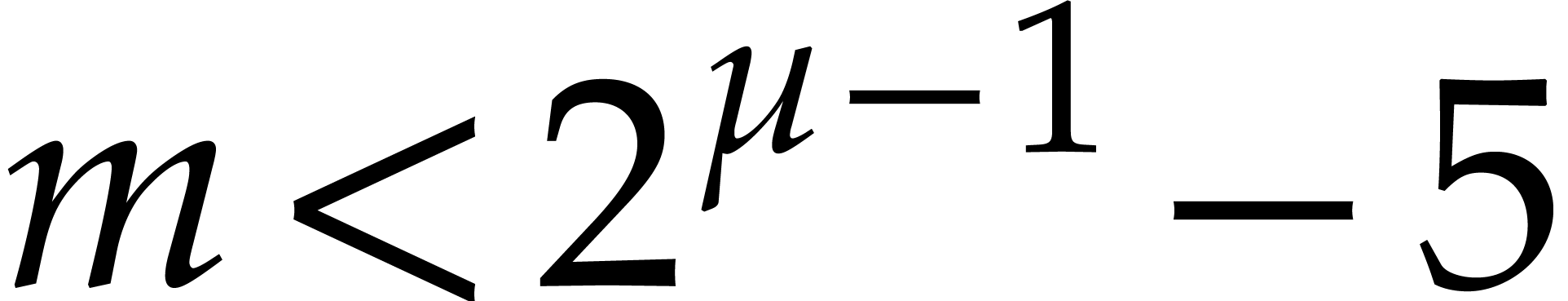 , then
, then
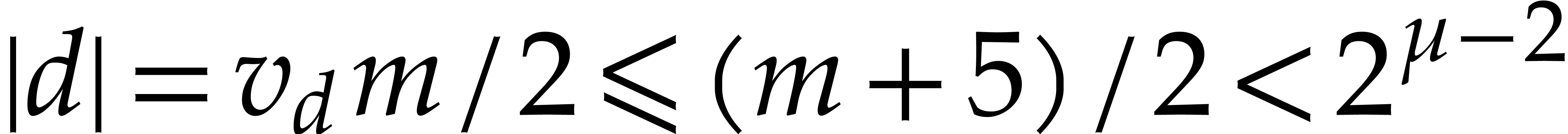 , so a second application of
normalize will achieve to normalize
, so a second application of
normalize will achieve to normalize  .
.
Proof. We first note that the product 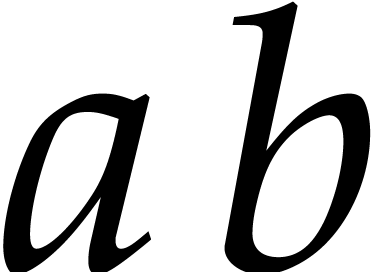 is represented exactly by
is represented exactly by 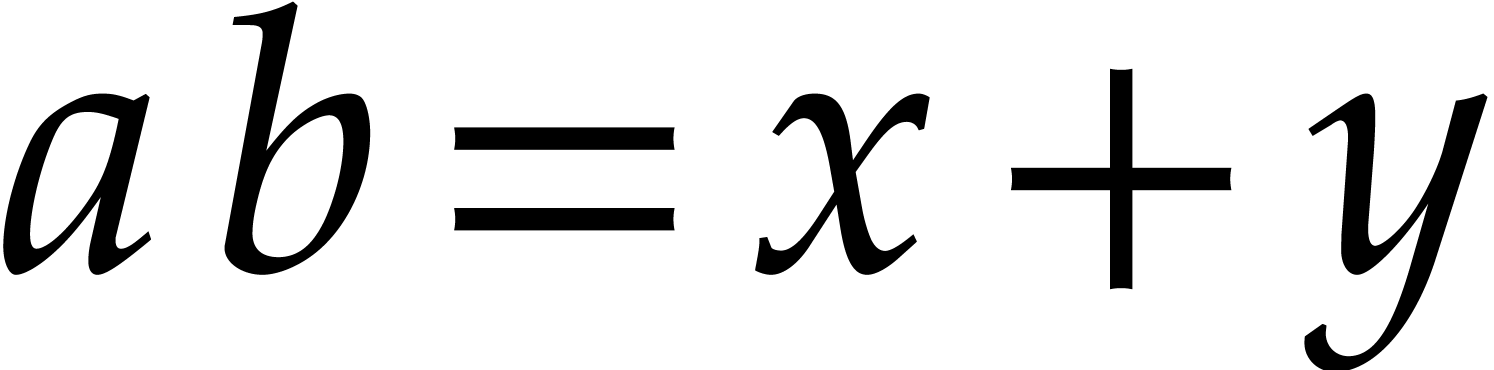 ,
where
,
where  and
and 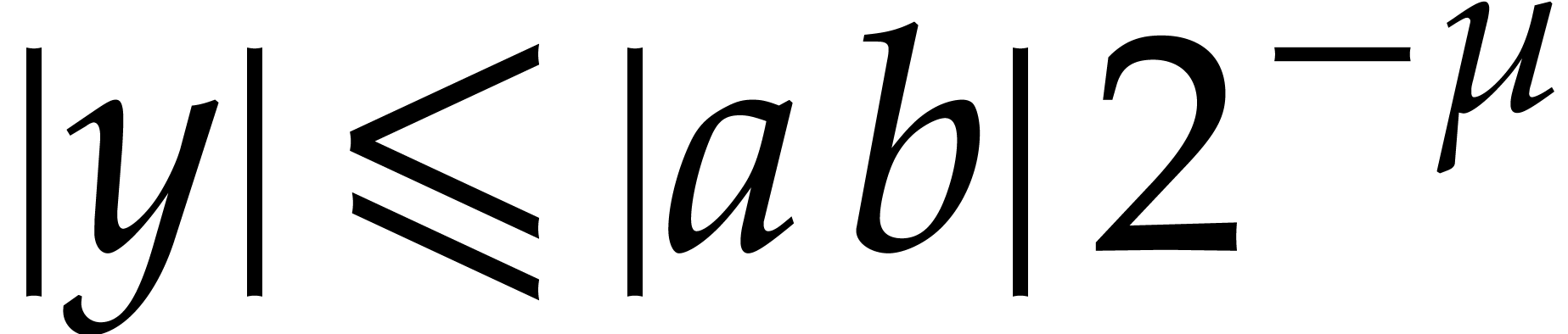 .
By a similar reasoning as in the beginning of the proof of Proposition
1, we have
.
By a similar reasoning as in the beginning of the proof of Proposition
1, we have
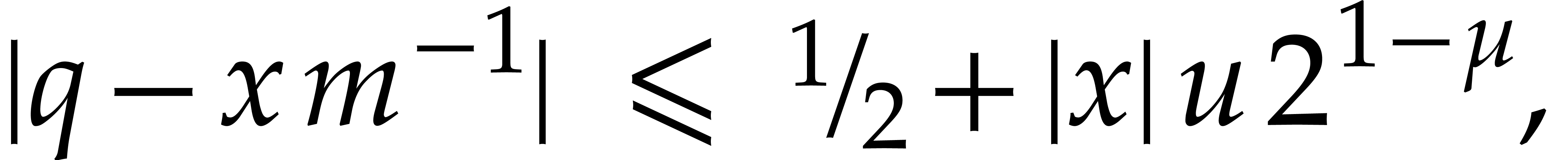
whence

Note that  implies
implies 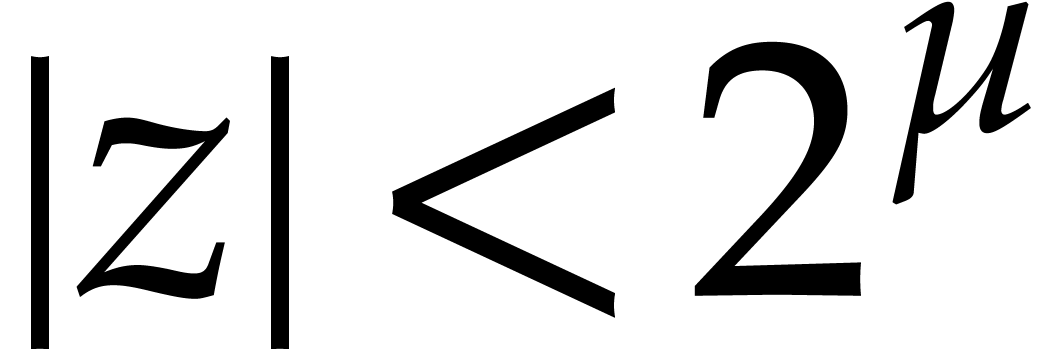 so
so
 is the exact value. We deduce that
is the exact value. We deduce that
This relation in particular yields (a). If 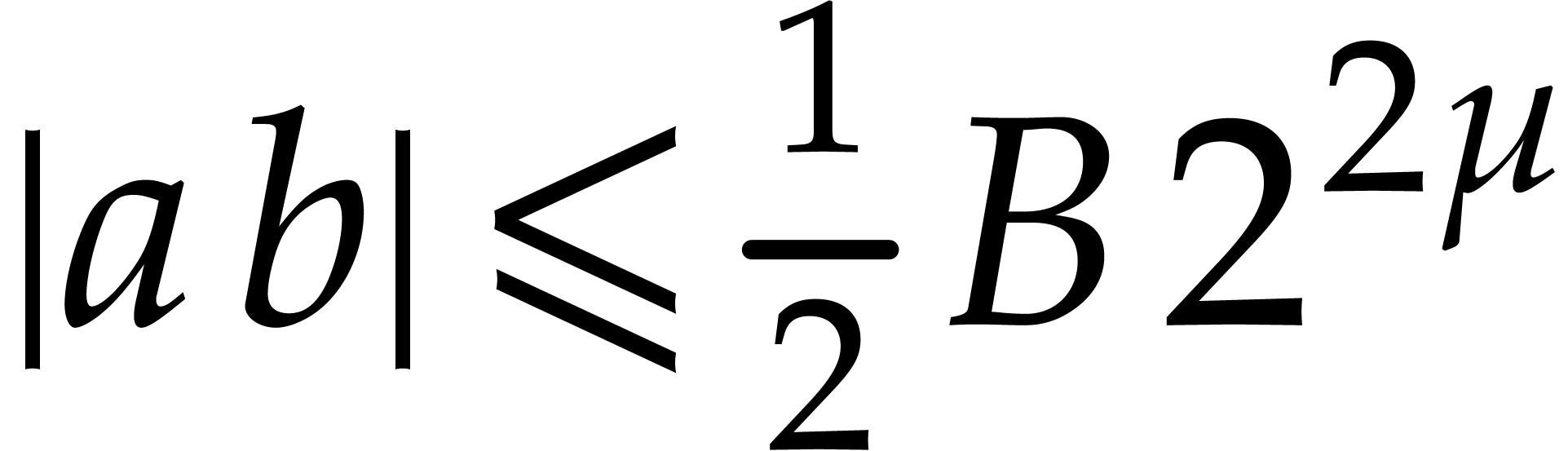 , then we also obtain
, then we also obtain
which proves (b). Assume finally that 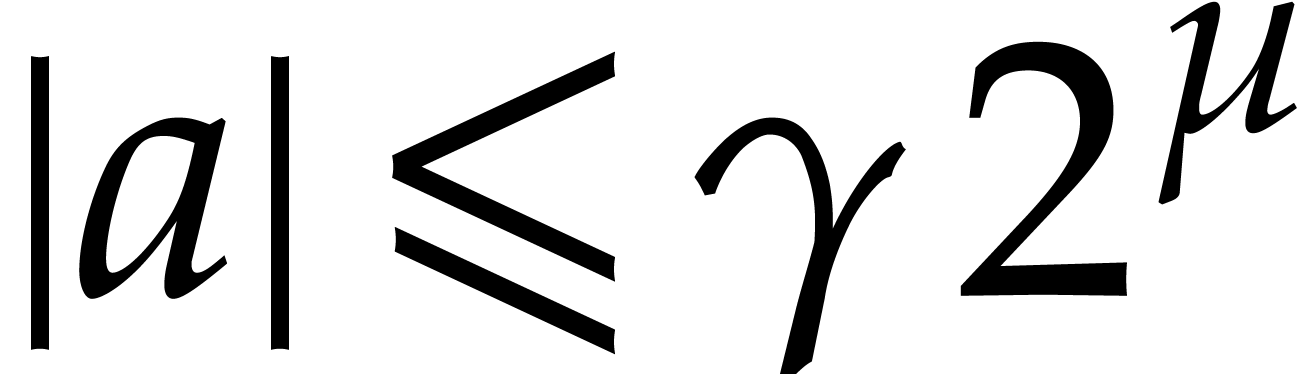 and
and 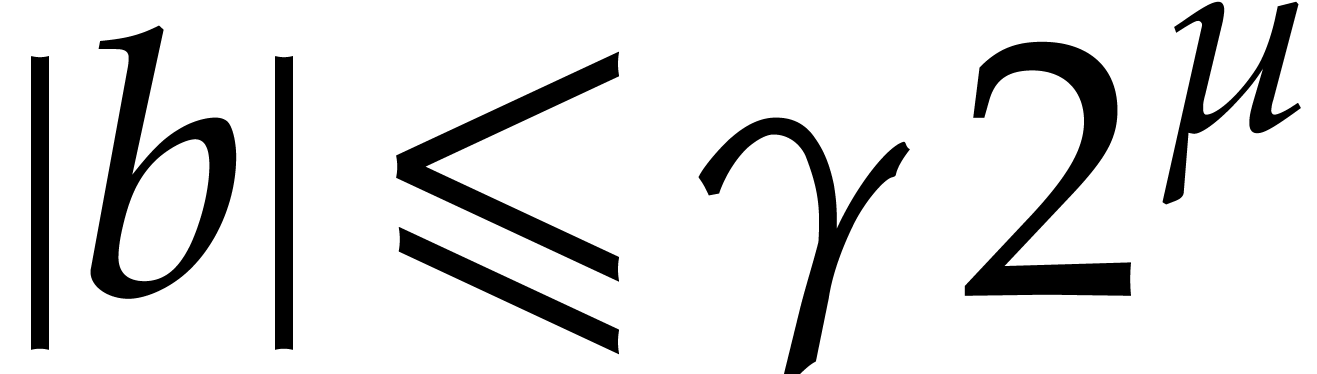 . Then
. Then
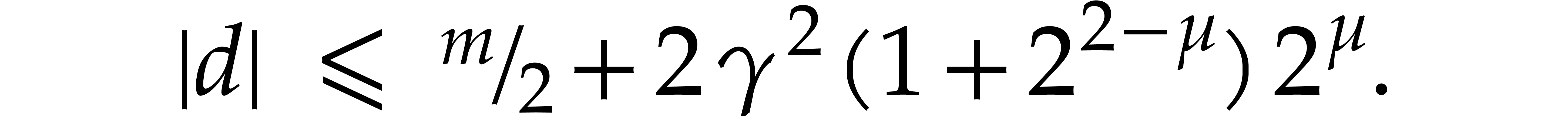
Since 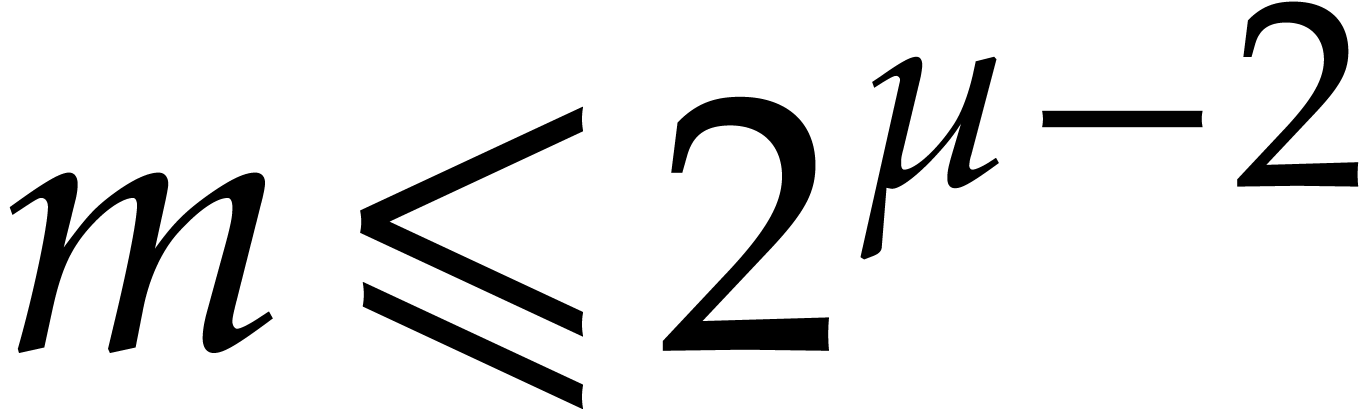 is odd, we have
is odd, we have 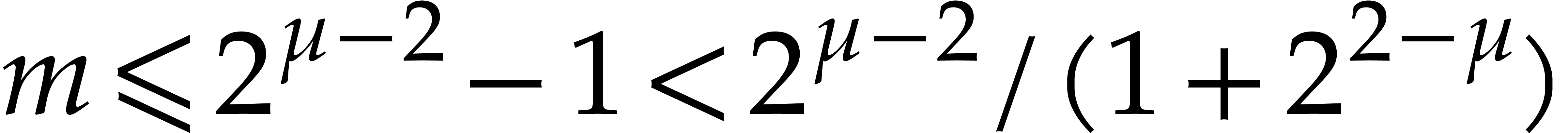 , whence the equation
, whence the equation
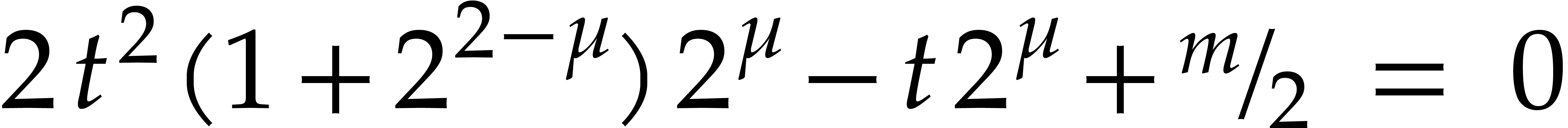
has two positive roots
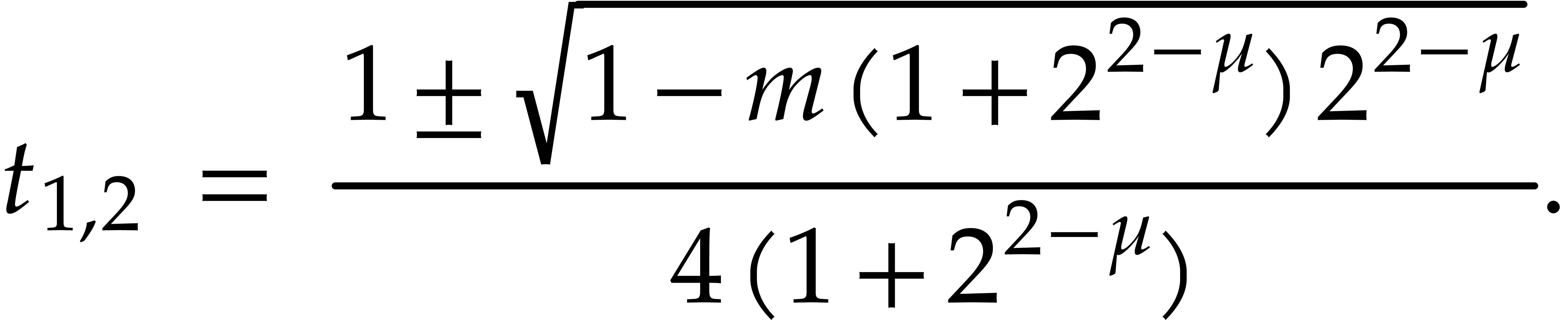
We took  to be the largest of these two roots.
This implies (c).
to be the largest of these two roots.
This implies (c).
Remark 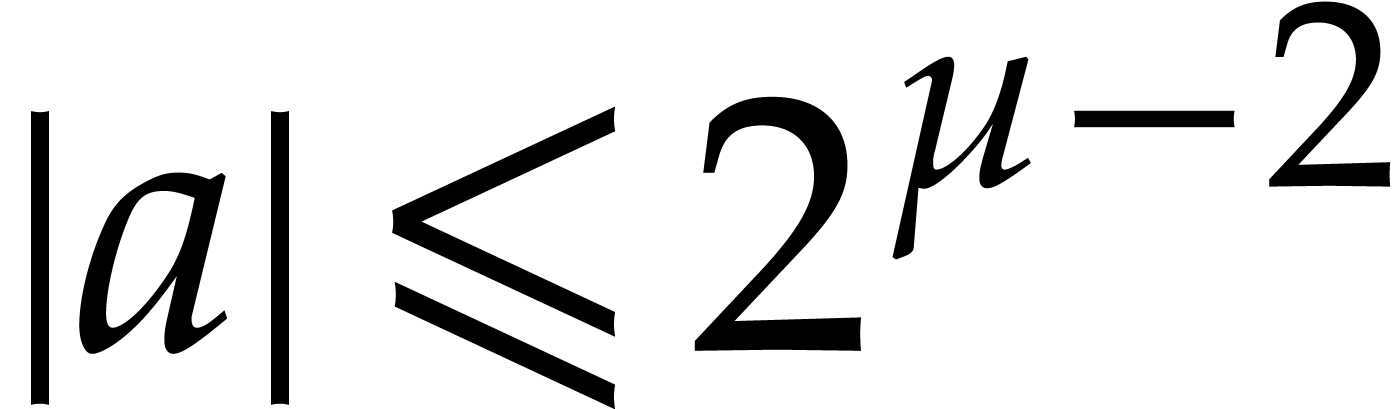 ,
, 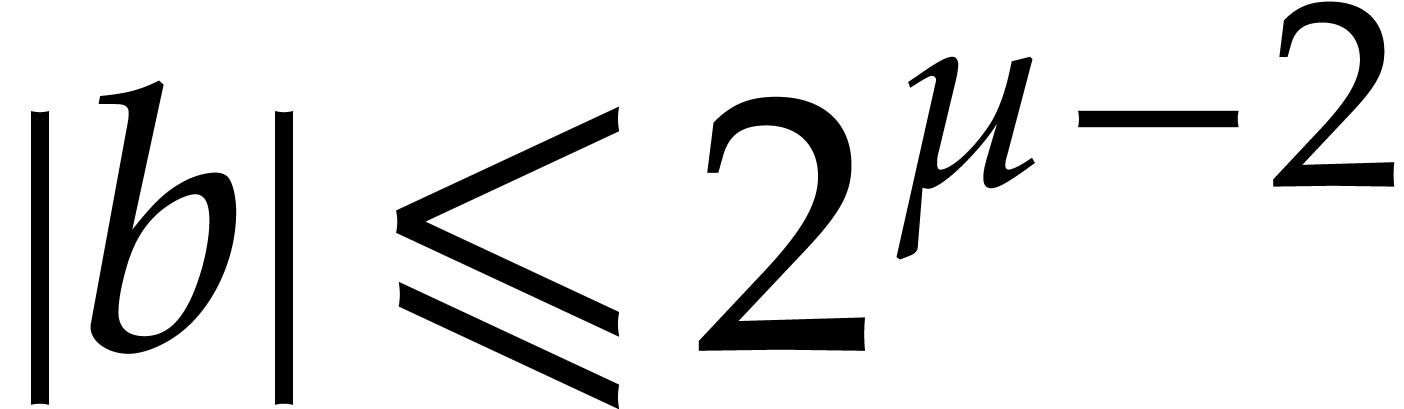 ,
and
,
and 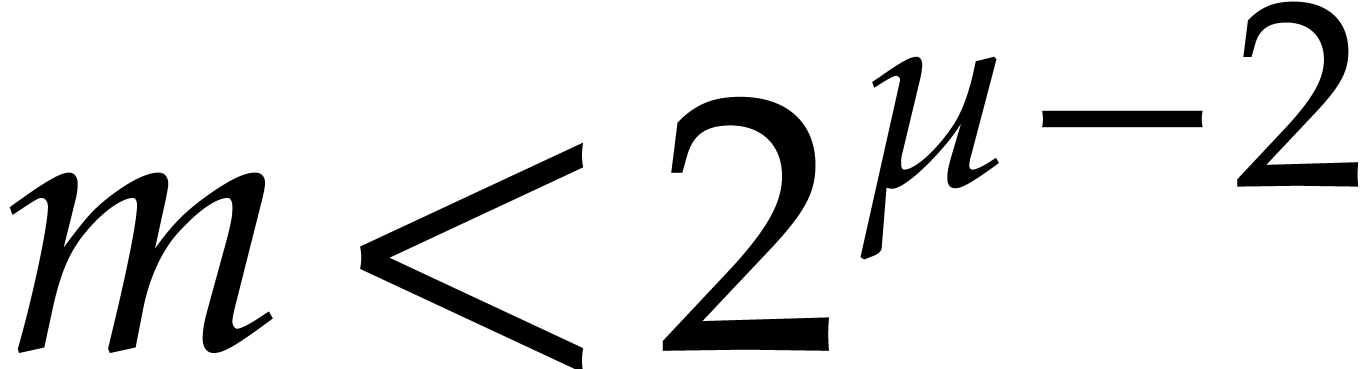 , then (c)
implies
, then (c)
implies 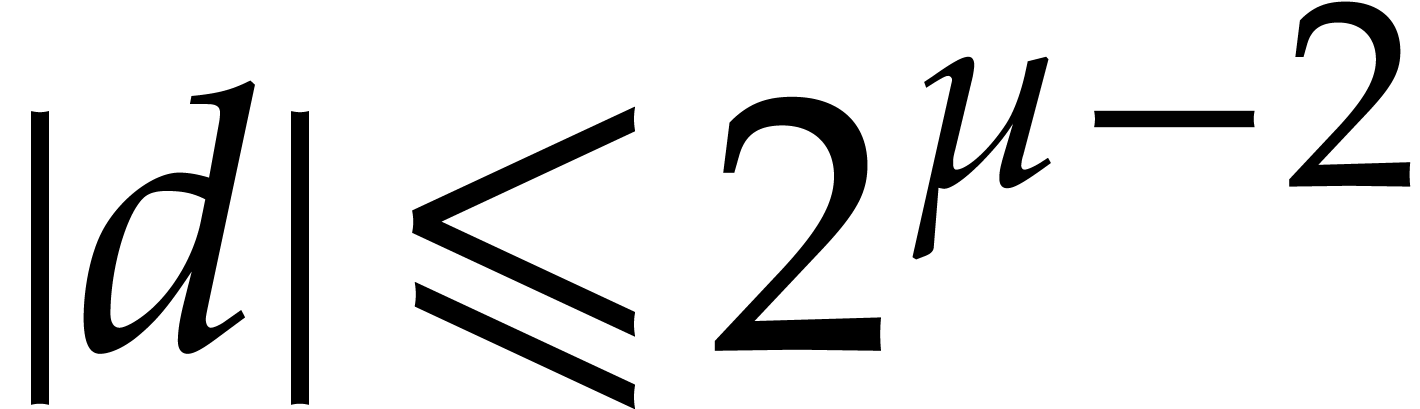 . Indeed,
. Indeed, 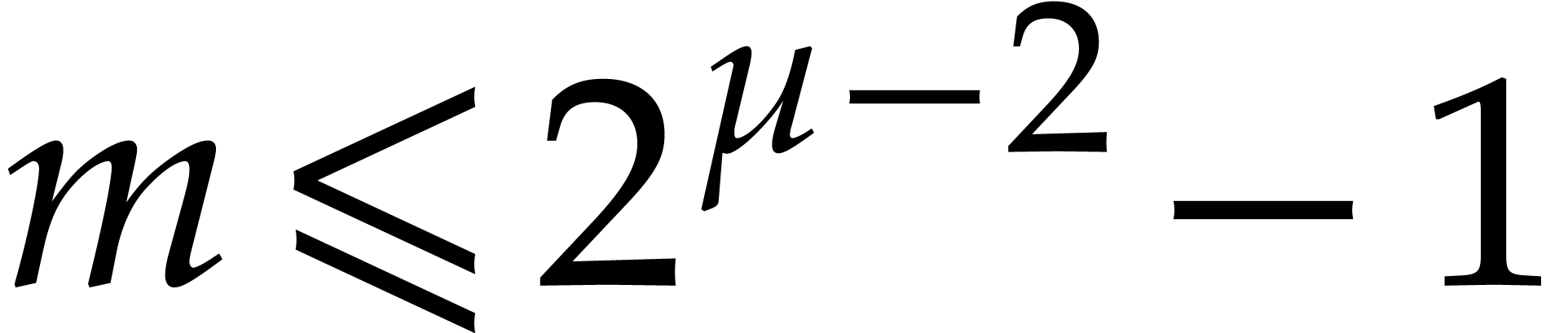 in that case, whence
in that case, whence 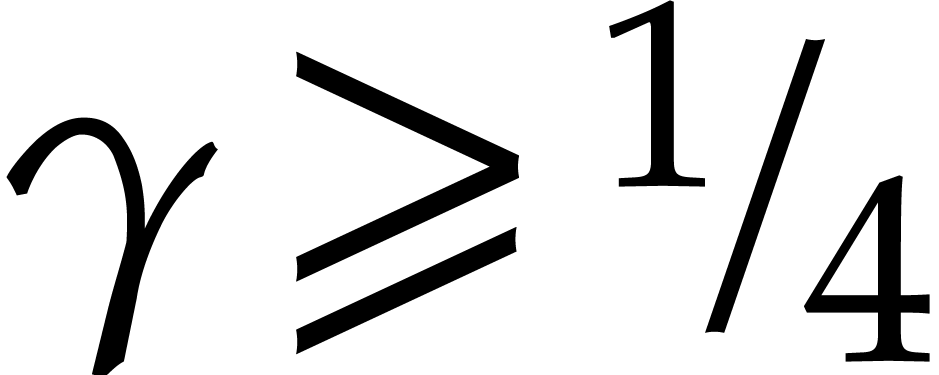 .
.
Remark 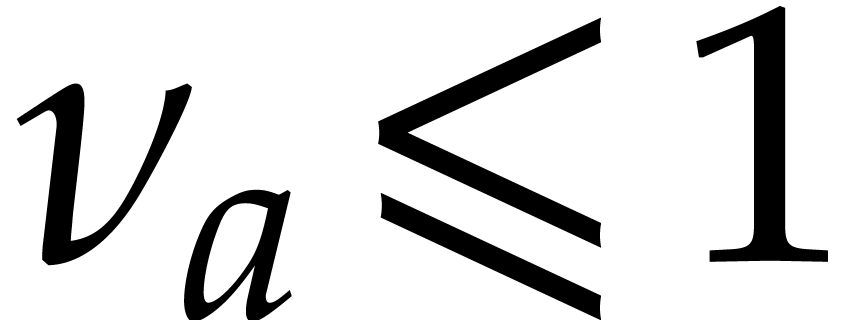 and
and  , then
(a) yields
, then
(a) yields
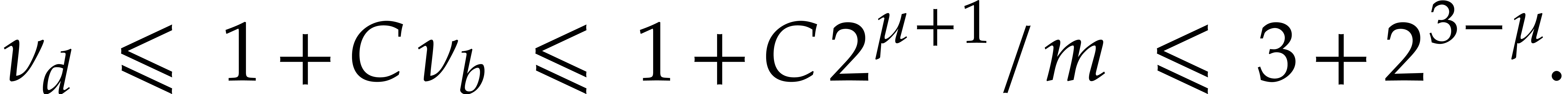
If 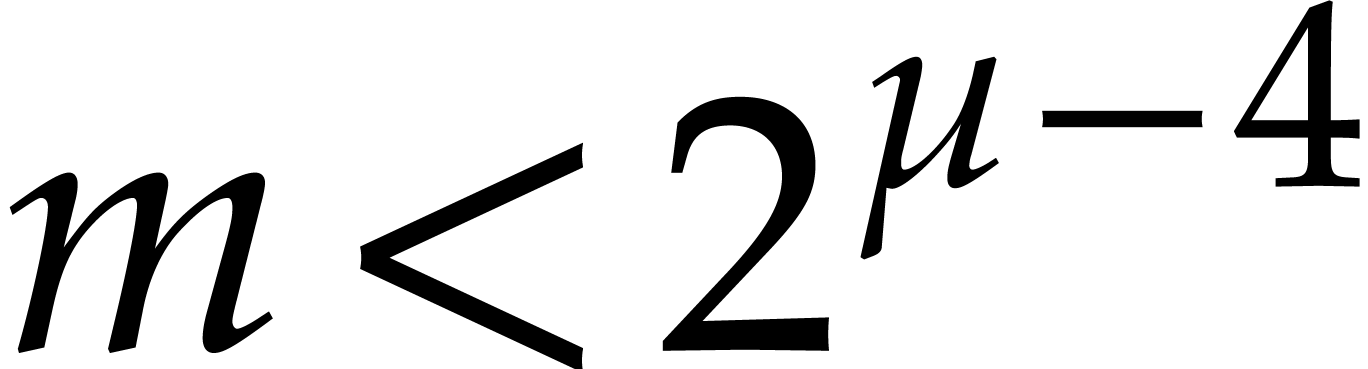 ,
,  , and
, and 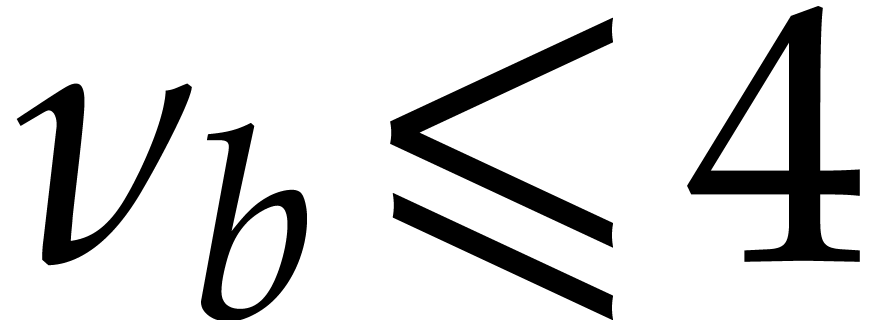 ,
then (a) yields
,
then (a) yields
since  .
.
The easiest way to implement DFTs is to write a single routine that
takes the order  and the coefficients as input
and then applies, say, Cooley and Tukey's algorithm using a double loop.
However, this strategy is register-inefficient for small orders and
cache-inefficient for large orders. Suboptimal loop unrolling may be
another problem.
and the coefficients as input
and then applies, say, Cooley and Tukey's algorithm using a double loop.
However, this strategy is register-inefficient for small orders and
cache-inefficient for large orders. Suboptimal loop unrolling may be
another problem.
For our implementation, we use the alternative strategy based on
“codelets”. For a given finite field 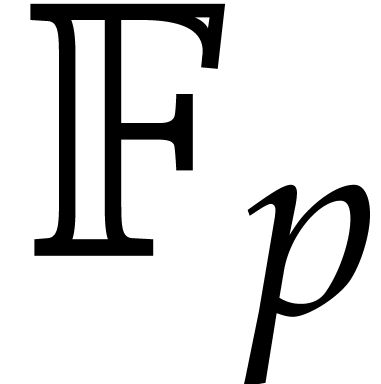 and a given target order
and a given target order  ,
the idea is to automatically generate a highly optimized program
,
the idea is to automatically generate a highly optimized program  for number theoretic transforms of order
for number theoretic transforms of order  over
over 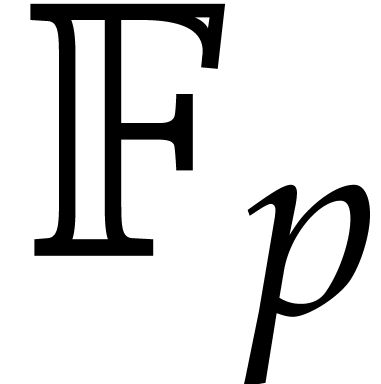 (up to permutations as
explained in section 2.4). Such highly optimized programs
that are dedicated to one specific task are called codelets. We
refer to [8, 9, 22] for early
work on codelets in the more traditional context of DFTs over
(up to permutations as
explained in section 2.4). Such highly optimized programs
that are dedicated to one specific task are called codelets. We
refer to [8, 9, 22] for early
work on codelets in the more traditional context of DFTs over  .
.
For small orders, codelets are typically designed by hand. For large
orders, they are generated automatically in terms of codelets of smaller
lengths. We developed a small “codelet library” inside
There are often multiple solutions to a given task. For instance, for an
NTT of composite order  ,
there may be multiple ways to factor
,
there may be multiple ways to factor 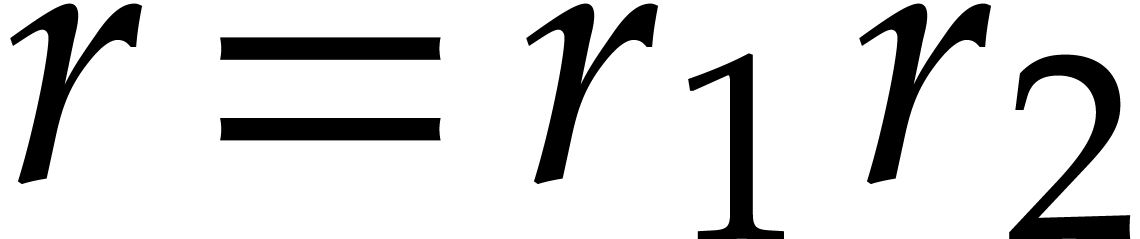 and then
apply one of the algorithms from section 2.2 or 2.3.
One advantage of codelets is that we may generate codelets for each
solution, do some benchmarking at runtime, and then select the most
efficient solution. For large orders, when benchmarking becomes more
expensive, the most efficient tactics can be cached on disk. Our codelet
library exploits this kind of ideas.
and then
apply one of the algorithms from section 2.2 or 2.3.
One advantage of codelets is that we may generate codelets for each
solution, do some benchmarking at runtime, and then select the most
efficient solution. For large orders, when benchmarking becomes more
expensive, the most efficient tactics can be cached on disk. Our codelet
library exploits this kind of ideas.
A straight-line program (SLP) over 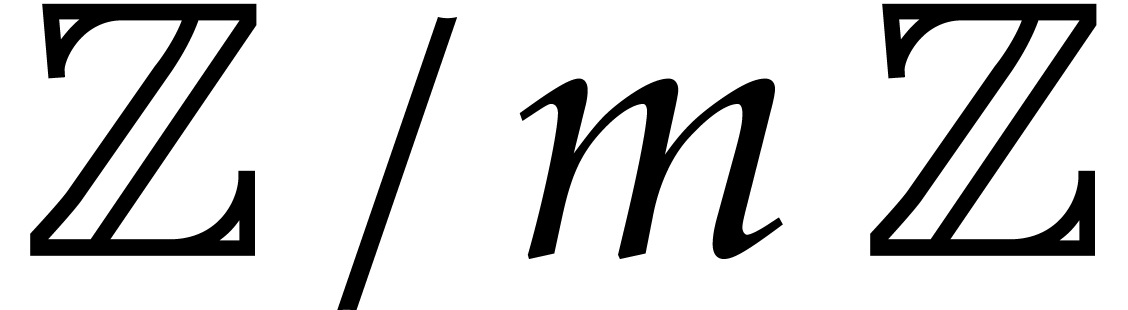 is a map
is a map 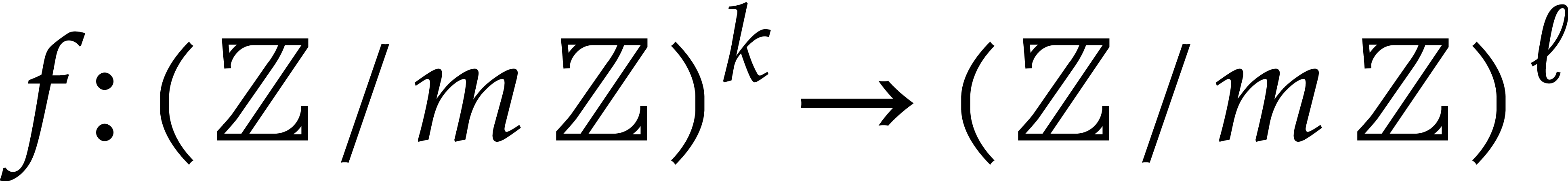 that can be implemented using a sequence of ring
operations in
that can be implemented using a sequence of ring
operations in 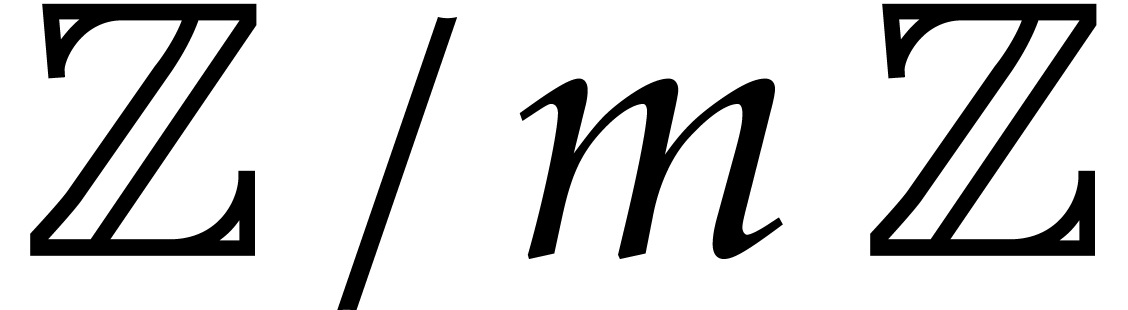 . For instance,
if
. For instance,
if  is a primitive root of unity of order
is a primitive root of unity of order  , then the following SLP with input
, then the following SLP with input
 and output
and output 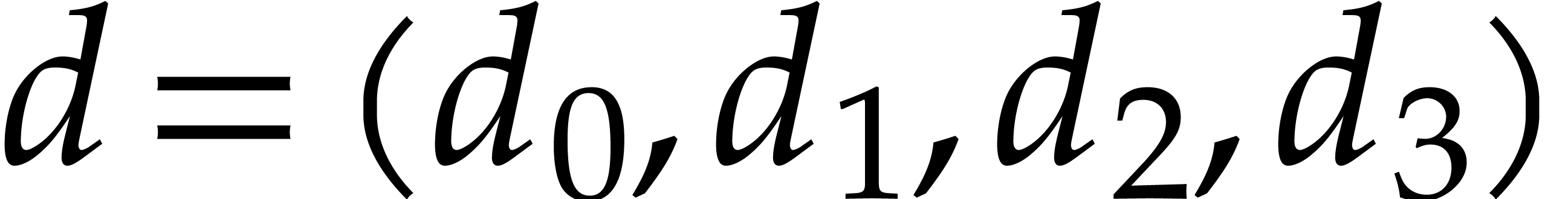 computes an
NTT of order
computes an
NTT of order  :
:
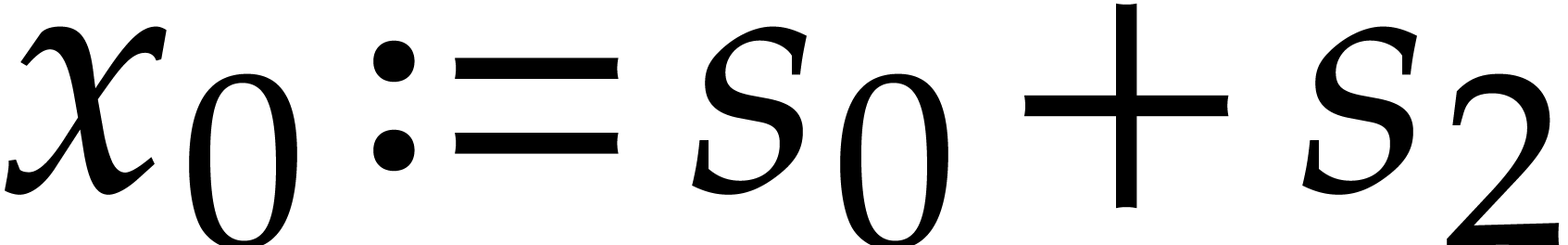

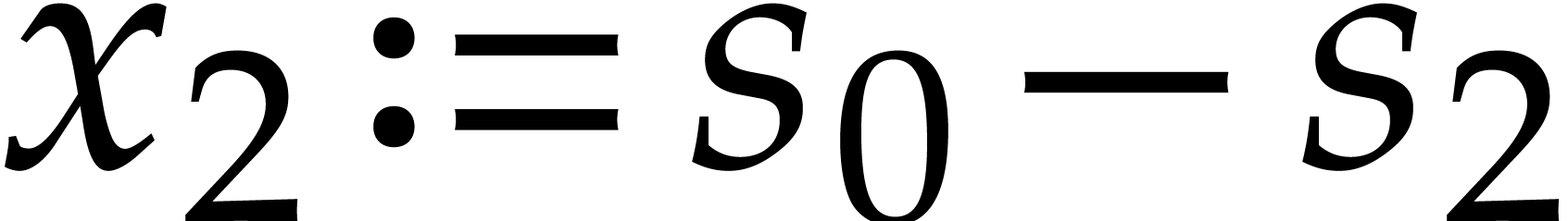

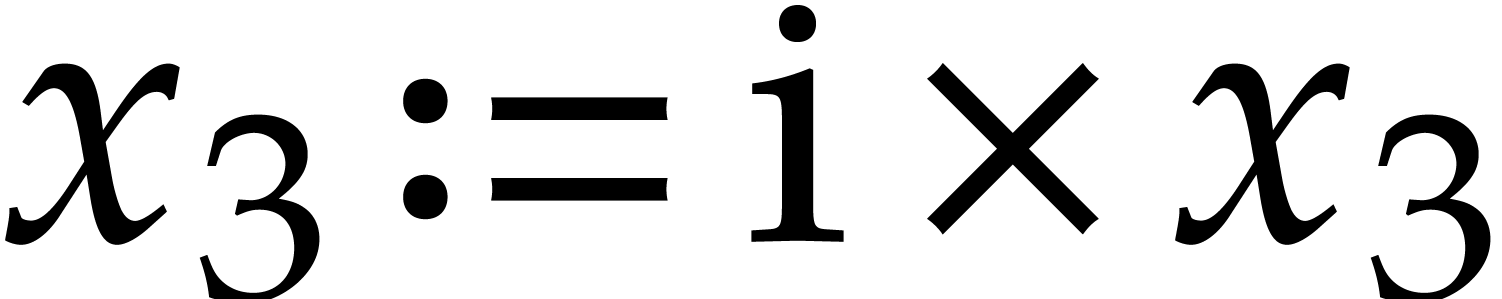
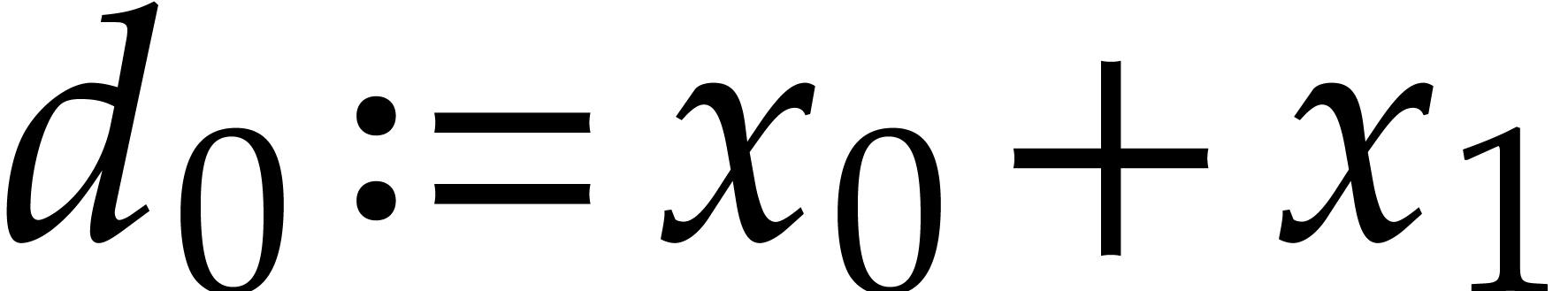
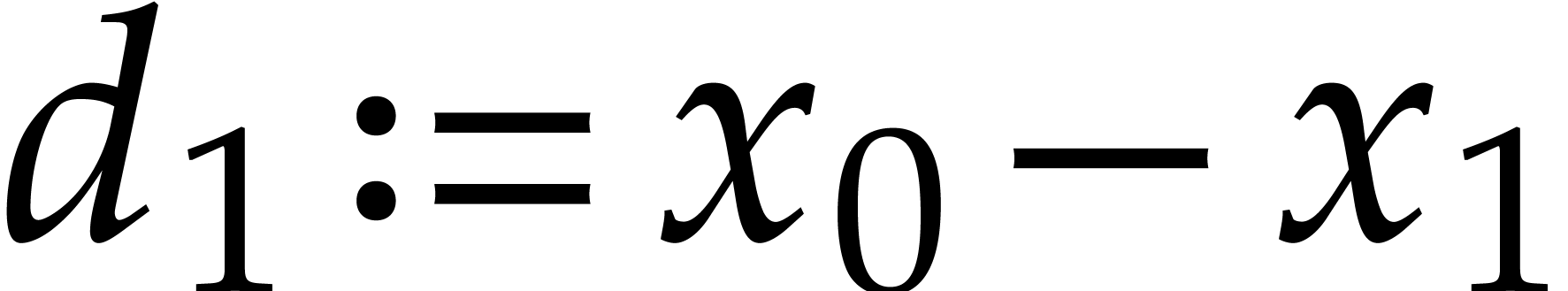
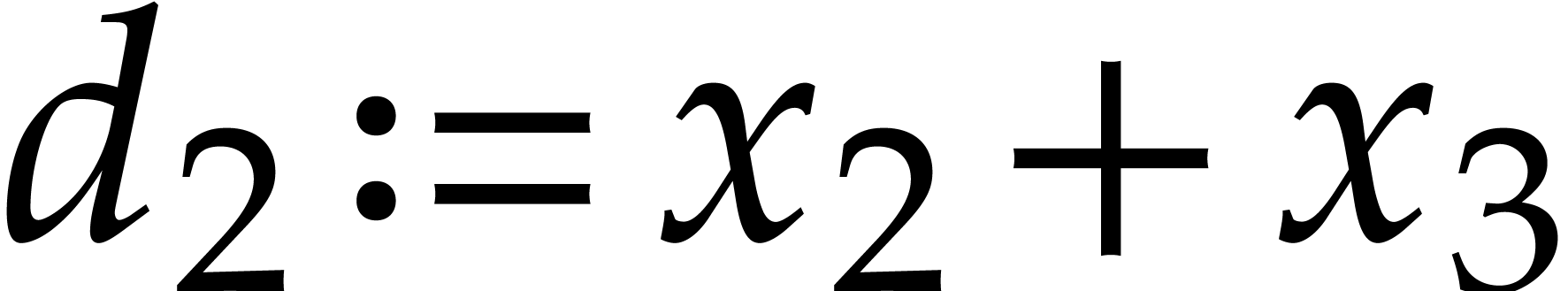
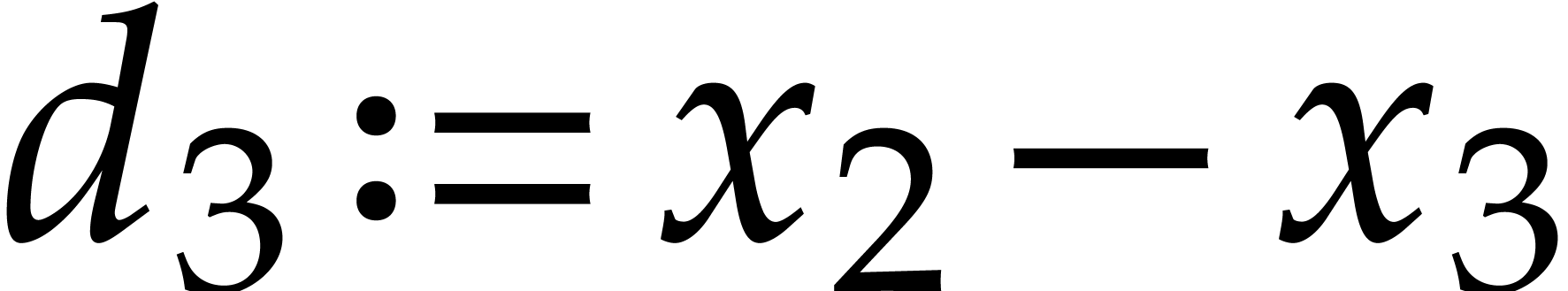
Here 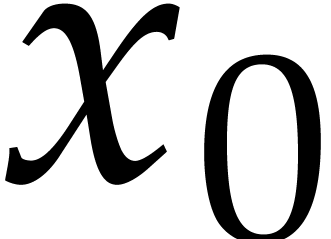 ,
, 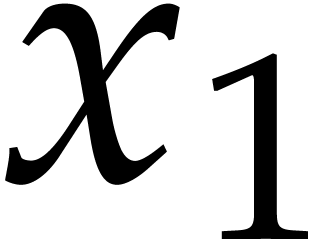 ,
, 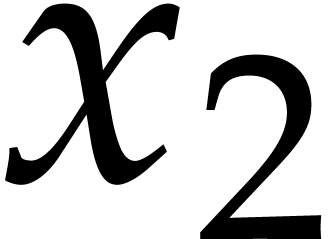 ,
, 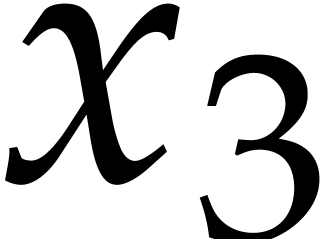 are auxiliary variables. Note also that the output
has been re-indexed in bit-reversed order: if
are auxiliary variables. Note also that the output
has been re-indexed in bit-reversed order: if  , then
, then 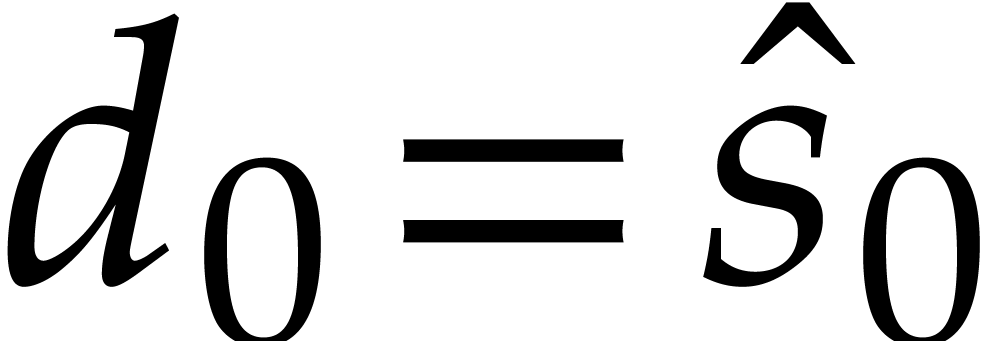 ,
,
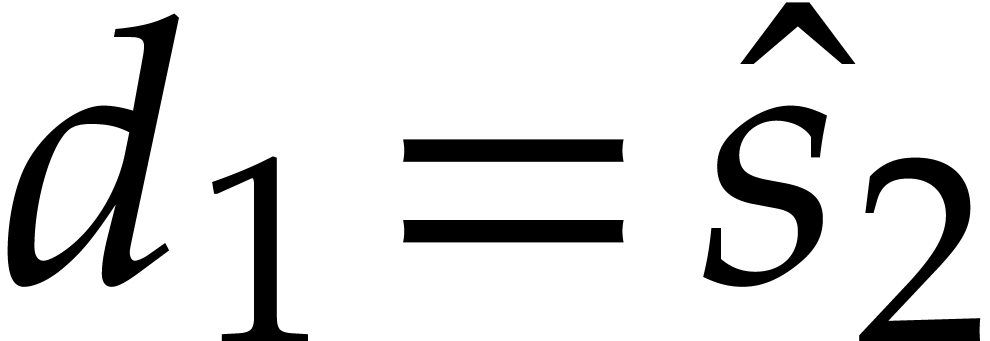 ,
, 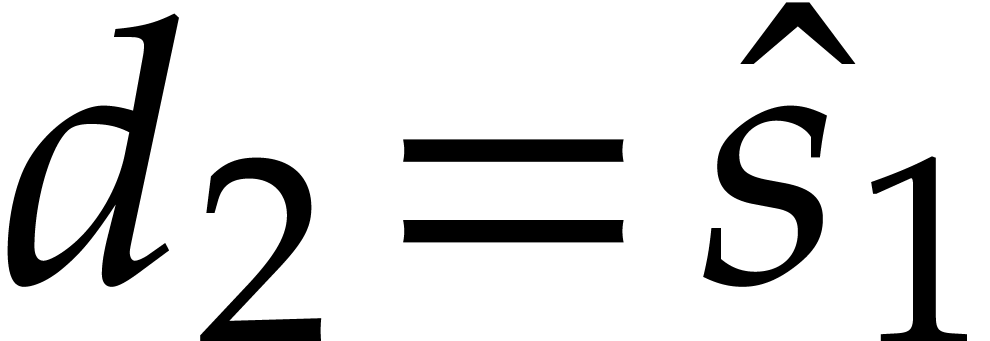 , and
, and 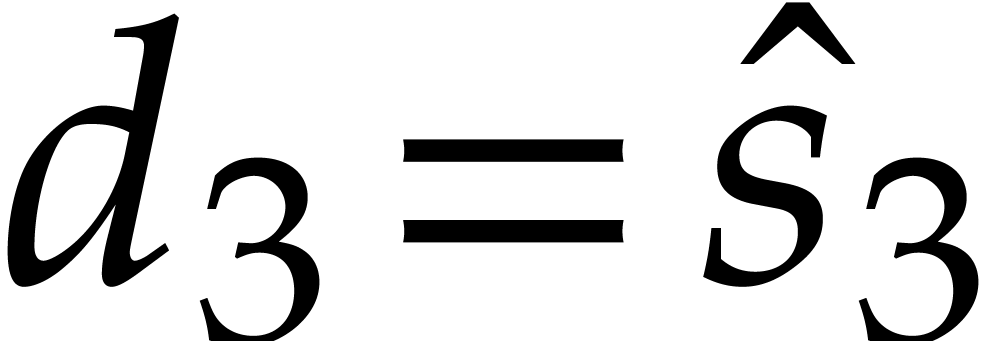 .
.
For an actual machine implementation of such an SLP, we may replace the
ring operations by the algorithms 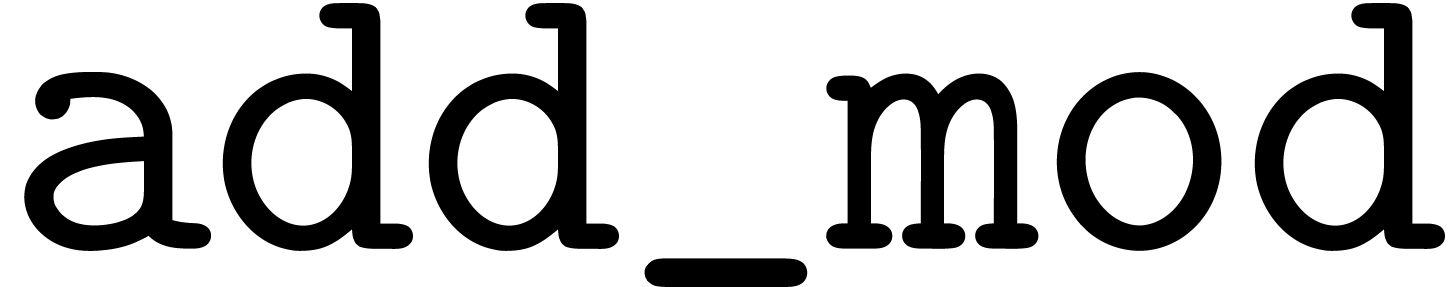 ,
,
 , and
, and 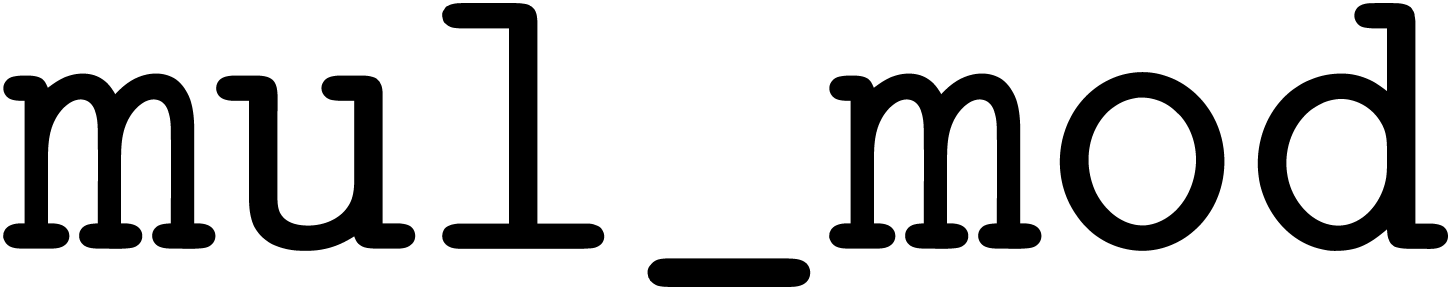 from the previous section. However, we have to be careful that all
non-normalized intermediate results fit into
from the previous section. However, we have to be careful that all
non-normalized intermediate results fit into 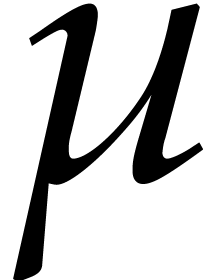 bit
integers. An easy linear-time greedy algorithm to ensure this is to
insert
bit
integers. An easy linear-time greedy algorithm to ensure this is to
insert  instructions whenever some intermediate
result might not fit.
instructions whenever some intermediate
result might not fit.
More precisely, for every intermediate result  of
a binary operation on
of
a binary operation on  and
and 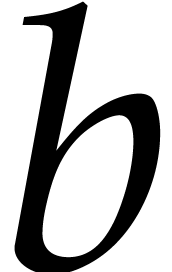 , we use the results from section 3.2
to compute a bound for
, we use the results from section 3.2
to compute a bound for 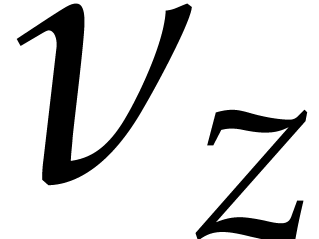 .
Whenever this bound exceeds
.
Whenever this bound exceeds 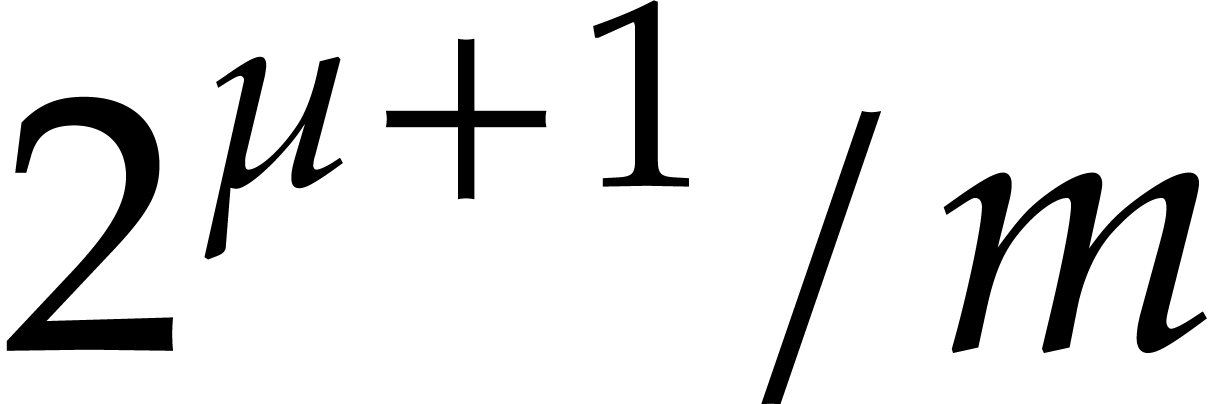 ,
we insert an instruction to normalize
,
we insert an instruction to normalize  or
or 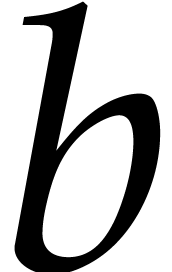 (we pick
(we pick  if
if  and
and 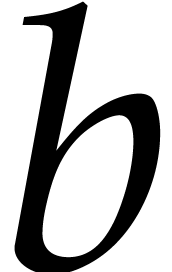 otherwise). For instance, if
otherwise). For instance, if 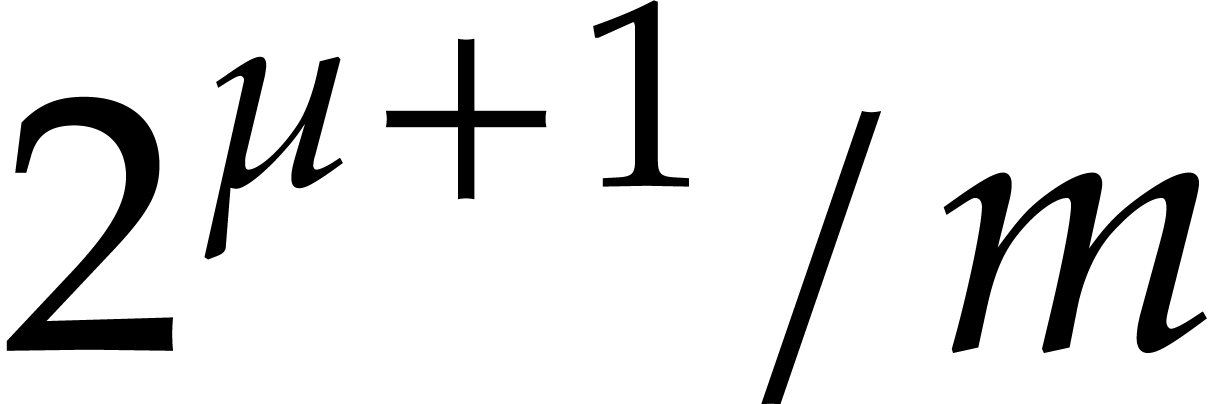 is slightly larger than
is slightly larger than 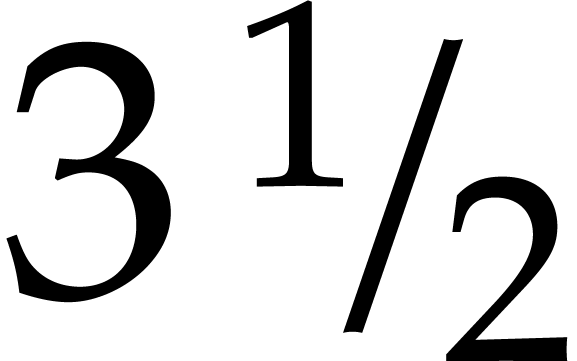 ,
then applying this strategy to the above SLP yields
,
then applying this strategy to the above SLP yields
Here we implicitly assumed that the input arguments 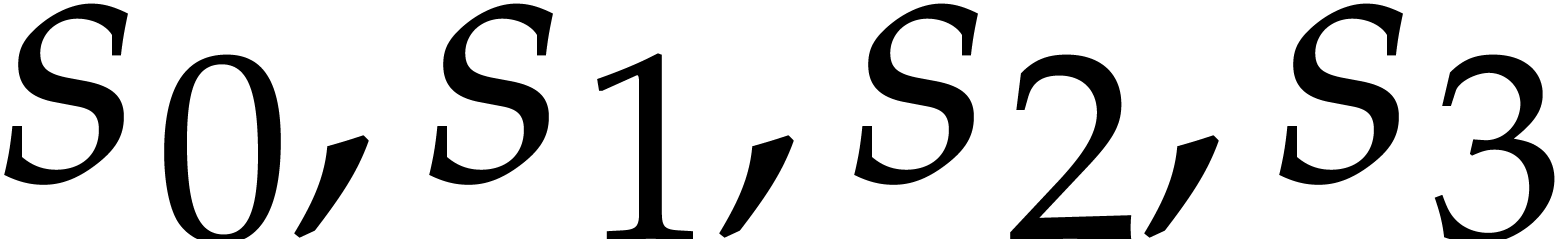 are normalized. We also wrote
are normalized. We also wrote  for a number that
is slightly larger than
for a number that
is slightly larger than 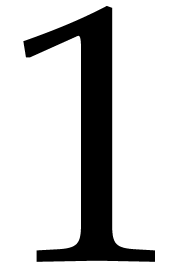 (e.g.
(e.g. 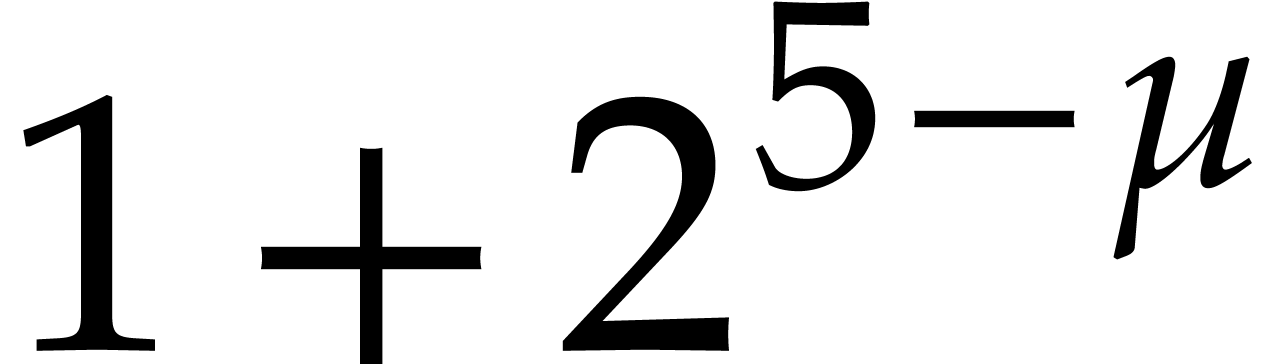 will do). We indeed had to normalize
will do). We indeed had to normalize 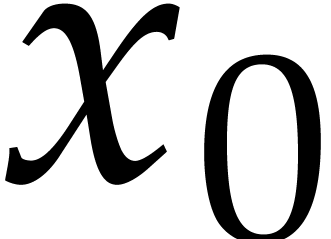 or
or 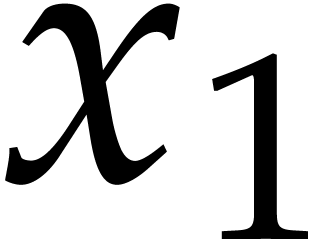 before the instruction
before the instruction 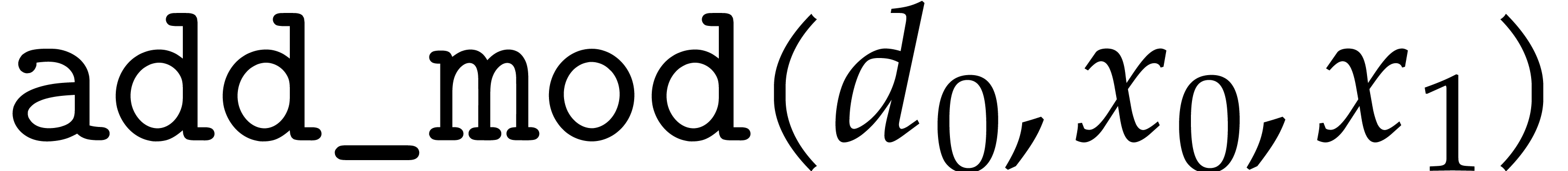 , since otherwise
, since otherwise 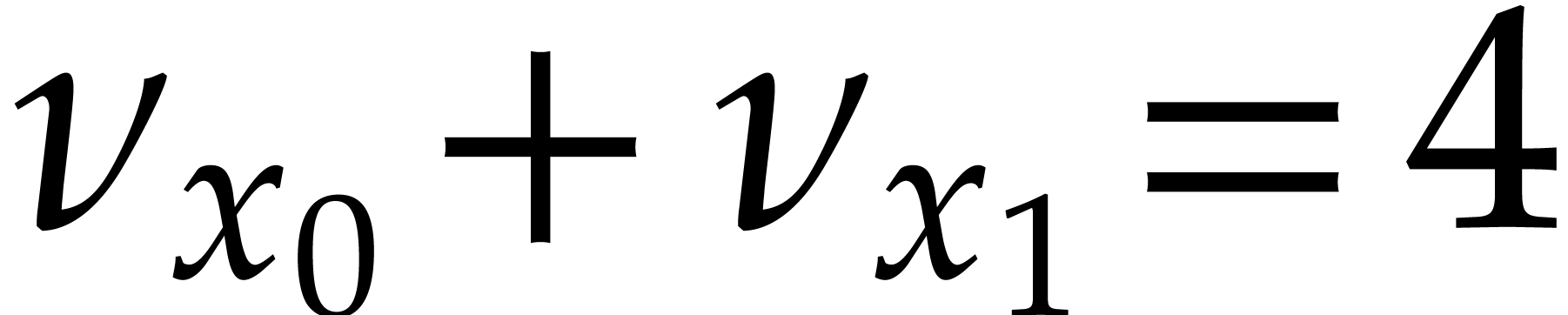 would
exceed
would
exceed 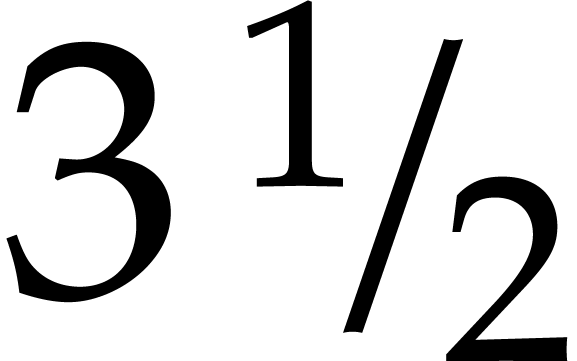 . Similarly, we
normalized
. Similarly, we
normalized 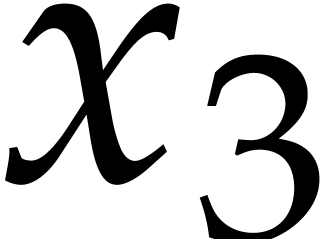 , since
, since 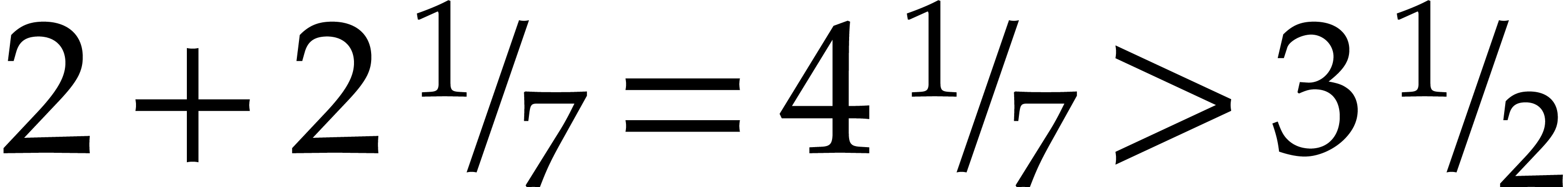 . On the other hand, after these
normalizations, we did not need to normalize
. On the other hand, after these
normalizations, we did not need to normalize 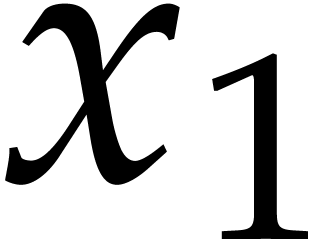 and
and
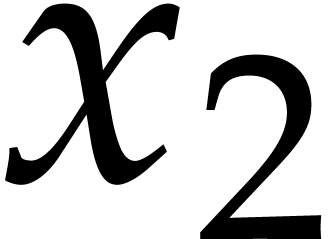 , since
, since 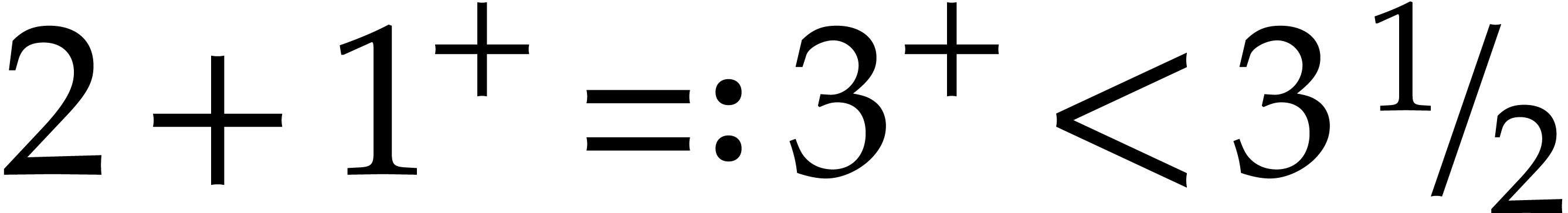 .
.
A few remarks about this approach.
The greedy strategy is not optimal in the sense that we might have
prevented overflows by inserting an even smaller number of
normalization instructions. One obvious optimization is to do the
normalization of 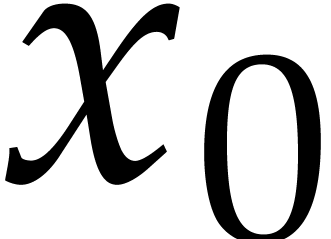 right after its
computation, which may improve subsequent bounds and avoid other
normalizations. One may iterate the greedy algorithm a few times
after applying this optimization. It is an interesting question how
to design even better algorithms.
right after its
computation, which may improve subsequent bounds and avoid other
normalizations. One may iterate the greedy algorithm a few times
after applying this optimization. It is an interesting question how
to design even better algorithms.
We may choose to normalize the output  or
not. If we allow for non-normalized output, then it may be
interesting to also allow for non-normalized input. The greedy
algorithm generalizes to this case as long as we know bounds for
or
not. If we allow for non-normalized output, then it may be
interesting to also allow for non-normalized input. The greedy
algorithm generalizes to this case as long as we know bounds for
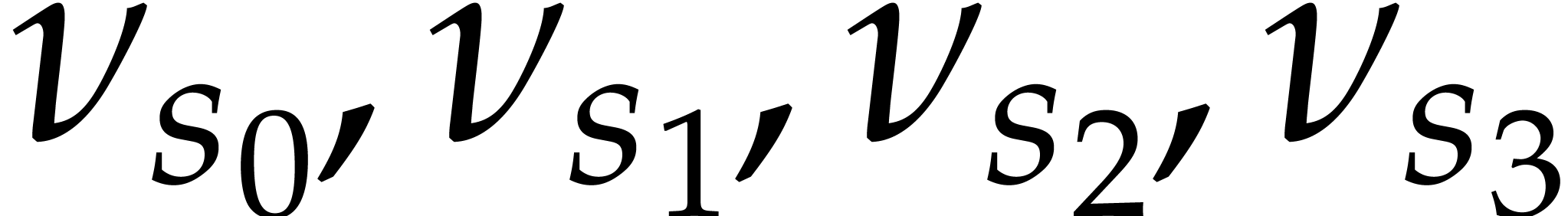 .
.
The bound for 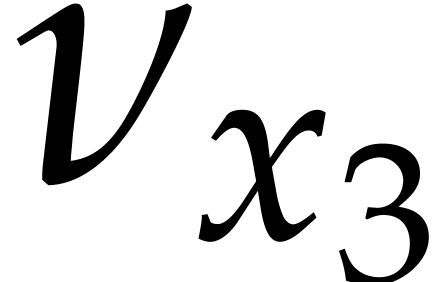 after multiplication with
after multiplication with  is suboptimal: since
is suboptimal: since  is a
constant,
is a
constant,  is also a known constant in
is also a known constant in 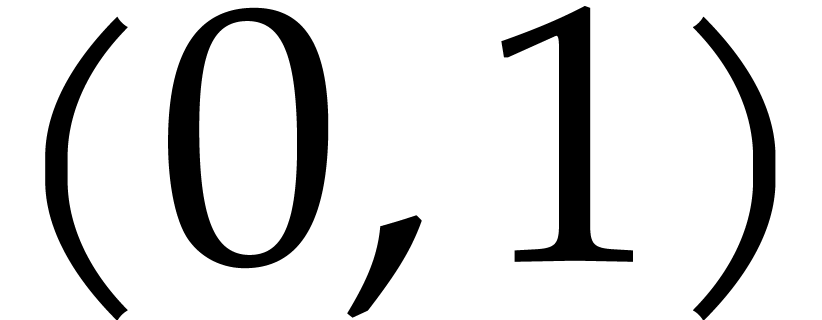 . We may use this constant
instead of the rough bound
. We may use this constant
instead of the rough bound 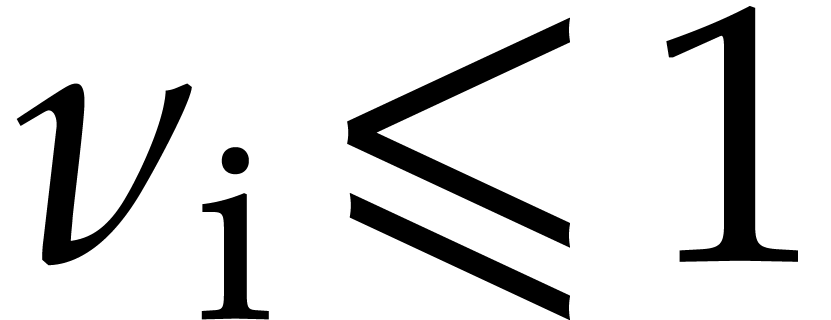 .
For instance, if
.
For instance, if 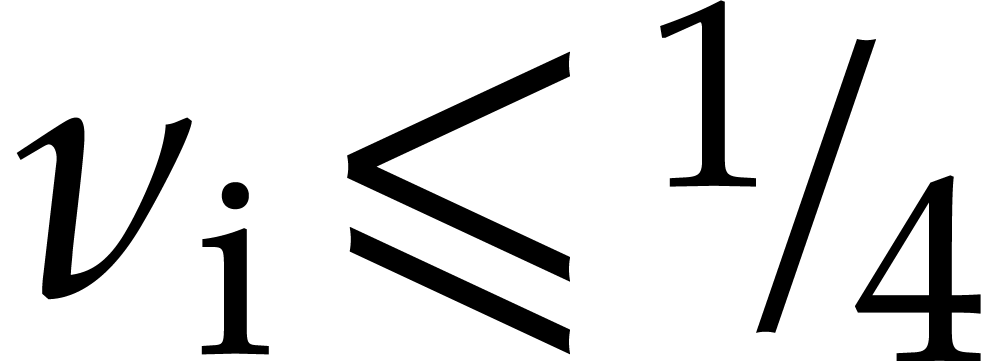 , then
, then
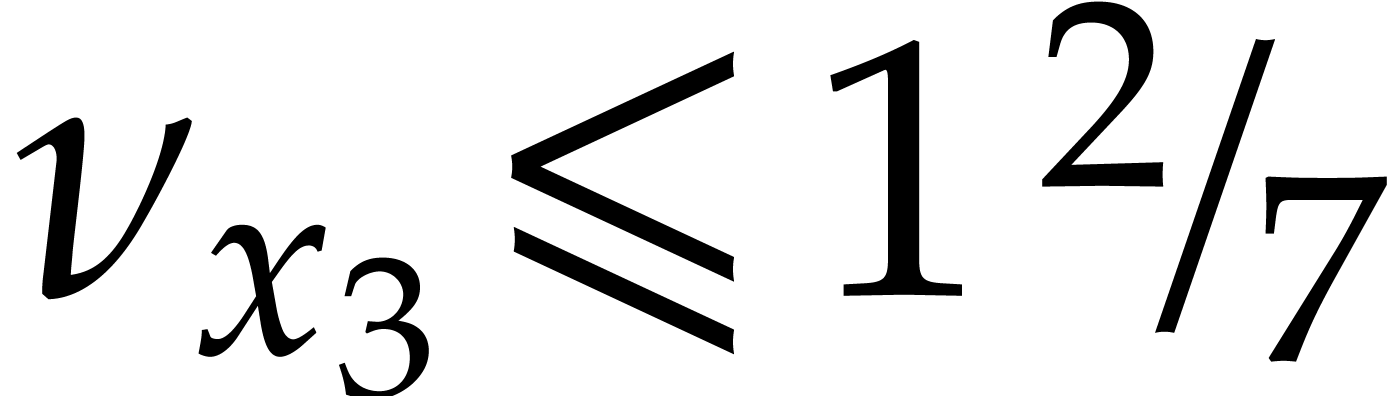 after the multiplication of
after the multiplication of 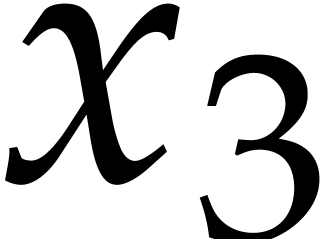 with
with  . Consequently,
. Consequently,
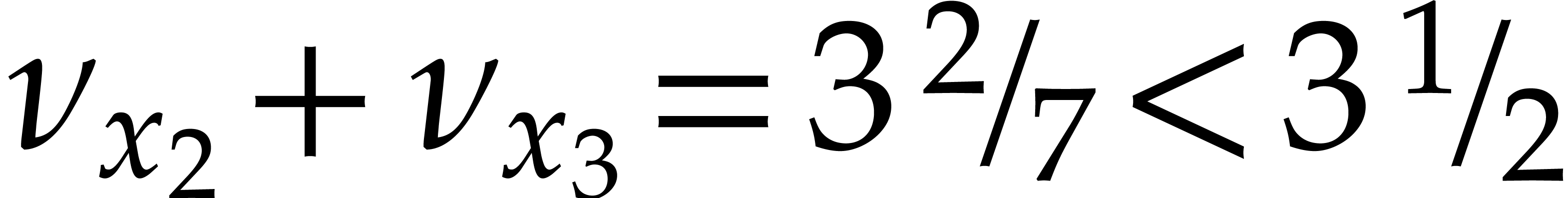 , which makes it no
longer necessary to normalize
, which makes it no
longer necessary to normalize 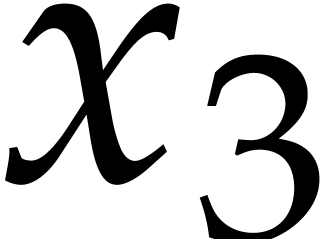 .
.
For NTTs of order up to  , it
is efficient to use unrolled codelets that can be regarded as SLPs.
Throughout our implementation, we assumed that
, it
is efficient to use unrolled codelets that can be regarded as SLPs.
Throughout our implementation, we assumed that 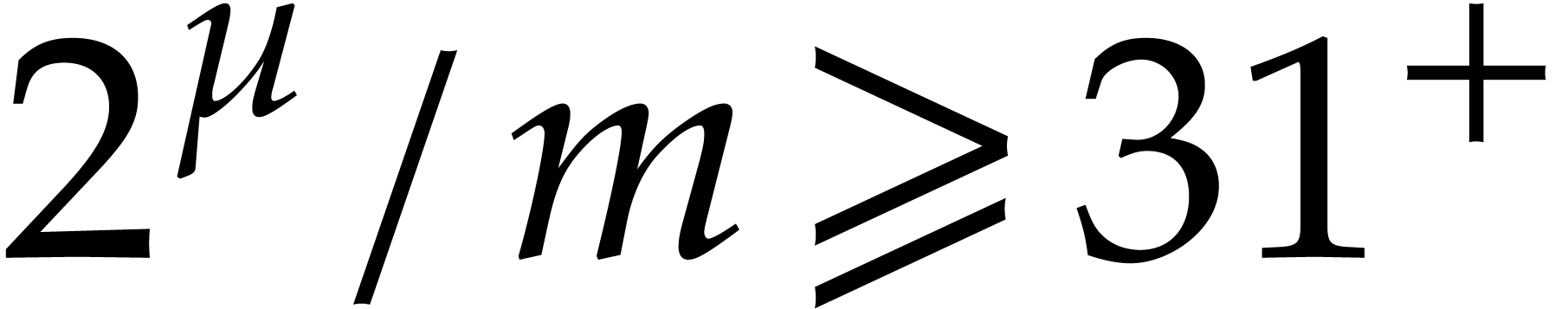 . This allows for moduli
. This allows for moduli 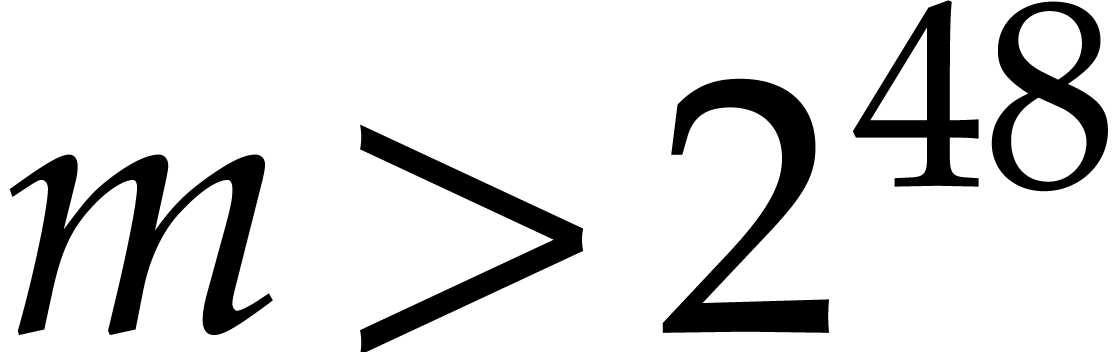 with a “capacity” of 48 bits. We wrote our transforms by
hand and manually determined the best spots for normalizations. Although
this means that we did apply the general greedy algorithm from the
previous section, we did use the same strategy to determine bounds for
the
with a “capacity” of 48 bits. We wrote our transforms by
hand and manually determined the best spots for normalizations. Although
this means that we did apply the general greedy algorithm from the
previous section, we did use the same strategy to determine bounds for
the 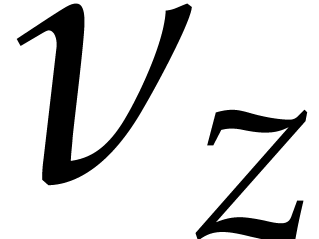 , where
, where  ranges over the intermediate results, and verify that we always have
ranges over the intermediate results, and verify that we always have
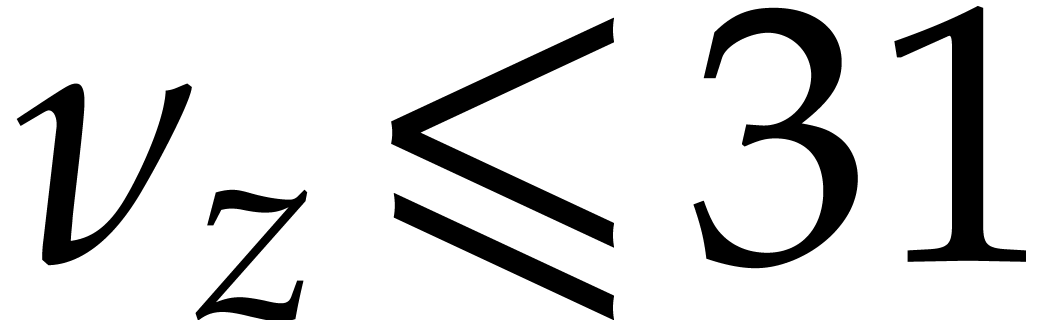 .
.
For small power of two orders 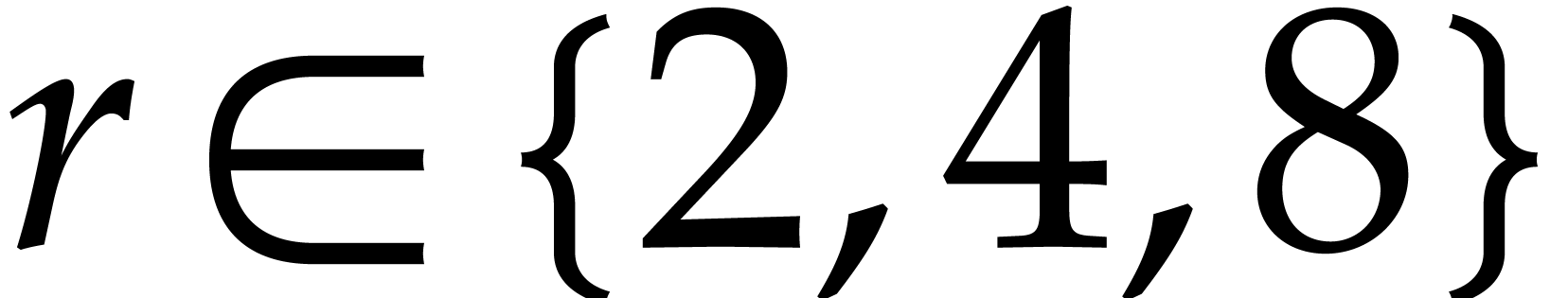 ,
we use the classical Cooley–Tukey algorithm without any
normalization. Writing
,
we use the classical Cooley–Tukey algorithm without any
normalization. Writing  and
and  for the input and output vectors in
for the input and output vectors in 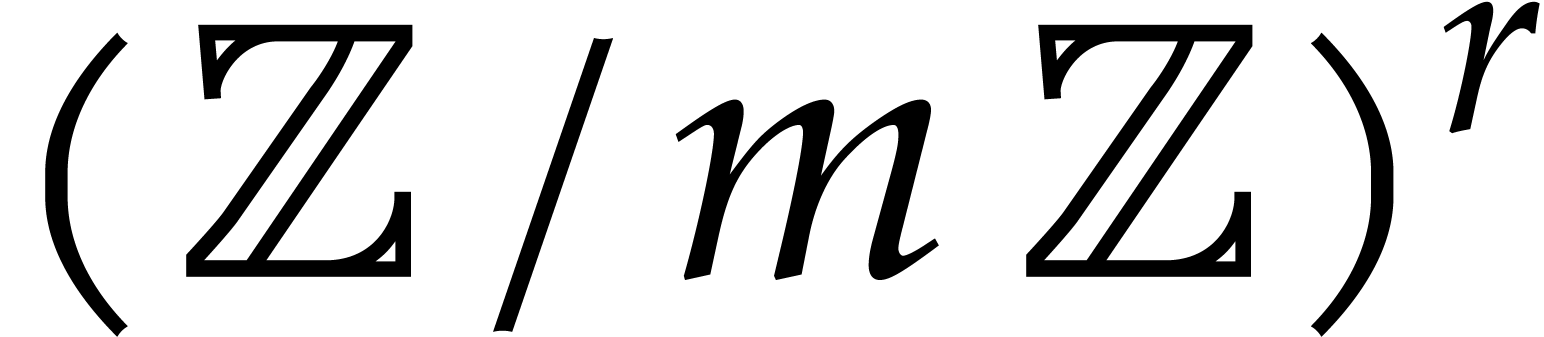 ,
and setting
,
and setting  , Proposition 3 implies
, Proposition 3 implies  . In view
of Remark 5, the worst case
. In view
of Remark 5, the worst case  may
only occur for evaluations at
may
only occur for evaluations at  and
and  (which only involve additions and subtractions).
(which only involve additions and subtractions).
NTTs of medium-size power of two orders 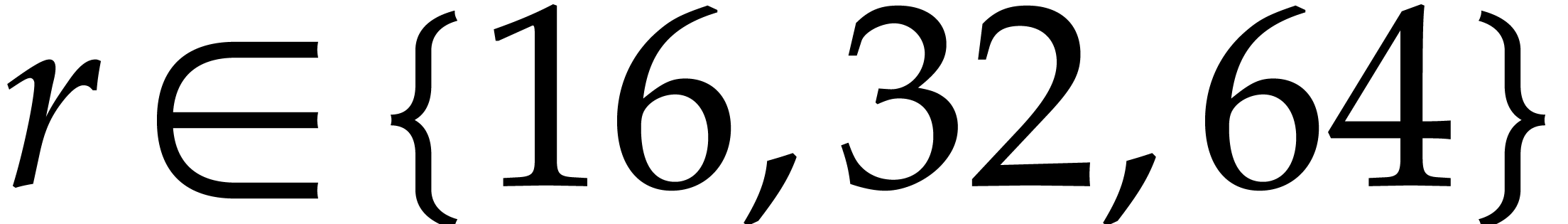 are
decomposed into smaller NTTs with one intermediate twiddling stage:
writing
are
decomposed into smaller NTTs with one intermediate twiddling stage:
writing  for a number theoretic transform of
order
for a number theoretic transform of
order  (while assuming the usual bit-reverse
indexing), we apply the formulas
(while assuming the usual bit-reverse
indexing), we apply the formulas
for suitable diagonal linear twiddle maps 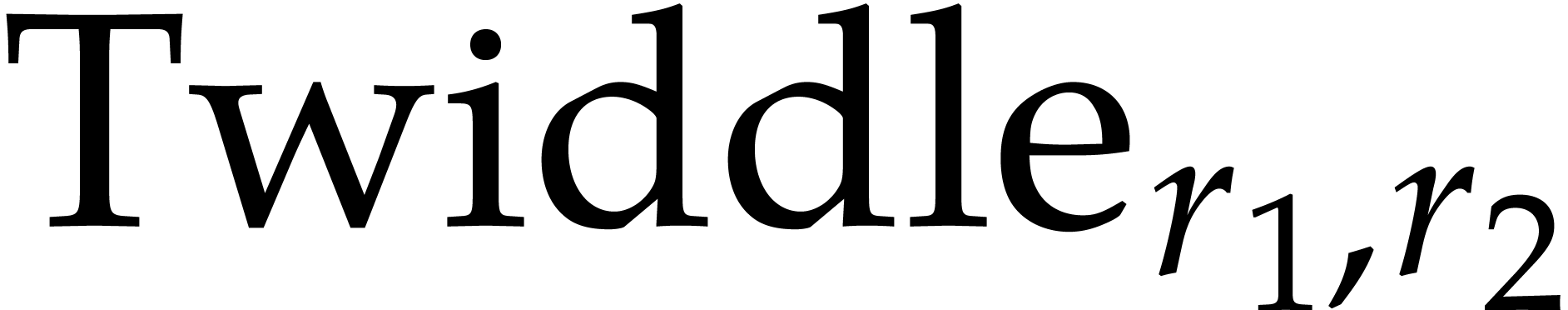 .
Our implementation automatically generates completely unrolled codelets
for
.
Our implementation automatically generates completely unrolled codelets
for  ,
,  , and
, and  .
The twiddling step has the advantage of partially normalizing the
intermediate results (see Remark 5). For instance, if
.
The twiddling step has the advantage of partially normalizing the
intermediate results (see Remark 5). For instance, if 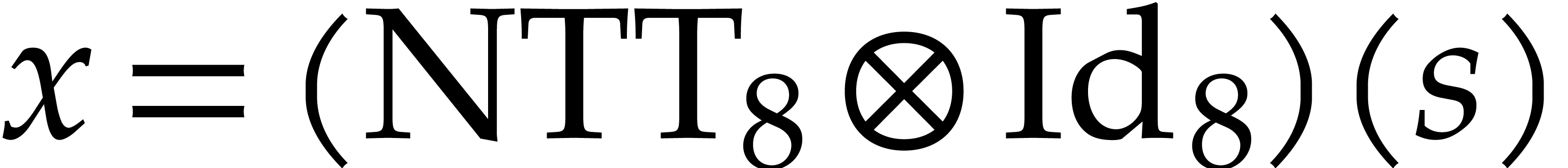 ,
, 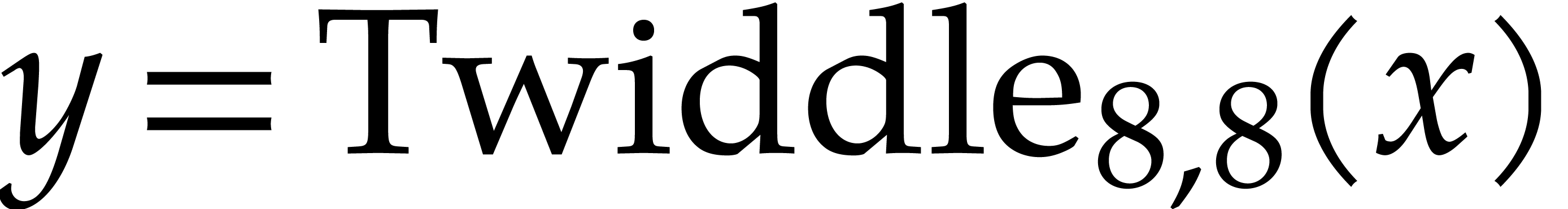 ,
,
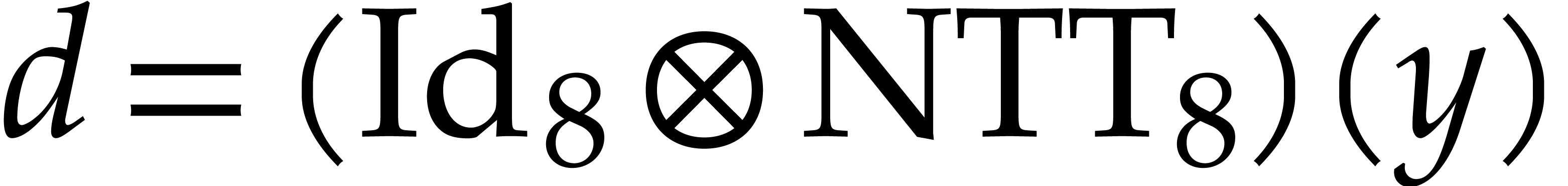 , and
, and 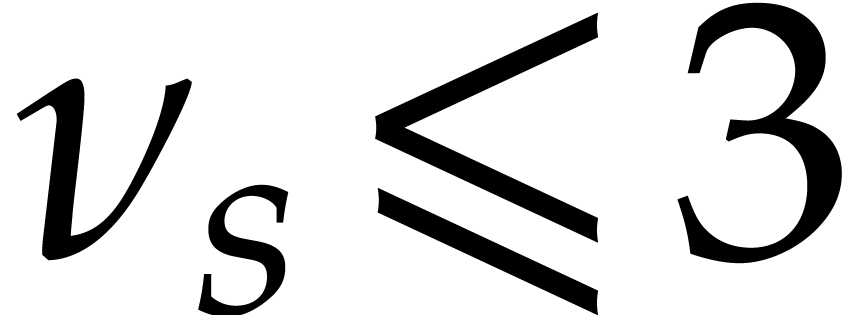 , then
, then  ,
,
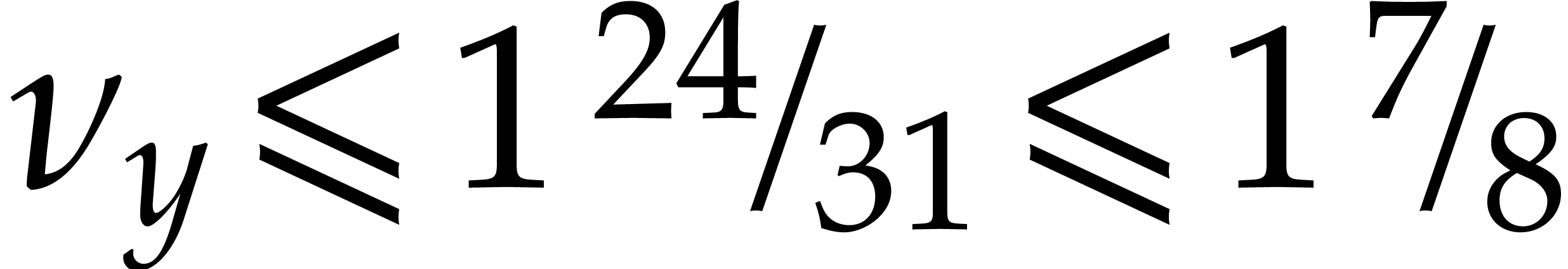 , and
, and 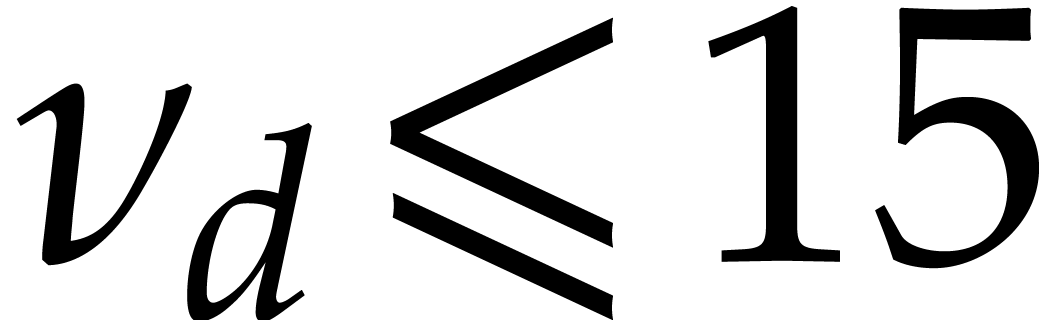 , using part (a) of Proposition 3.
Furthermore, the fact that several twiddle factors are equal to one
allows for an optimization: whenever we need to multiply
, using part (a) of Proposition 3.
Furthermore, the fact that several twiddle factors are equal to one
allows for an optimization: whenever we need to multiply  with one, we simply normalize
with one, we simply normalize  instead. In the case of
instead. In the case of  , the
error bounds are a bit better, and we only need to perform two
normalizations.
, the
error bounds are a bit better, and we only need to perform two
normalizations.
We also implemented hand-coded NTTs for some mixed-radix orders of the
form 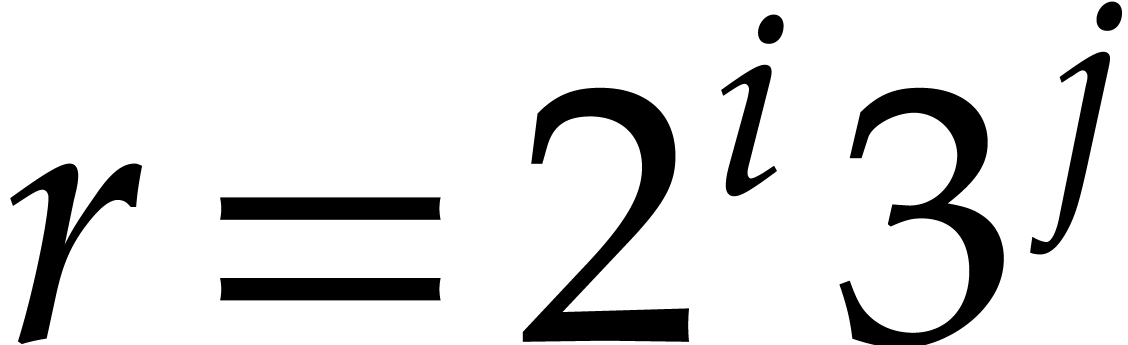 . If
. If  , and assuming that
, and assuming that 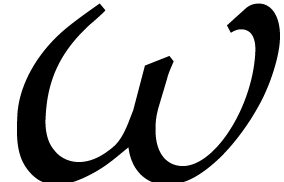 is
a primitive third root of unity, we use the following algorithm, without
normalization:
is
a primitive third root of unity, we use the following algorithm, without
normalization:
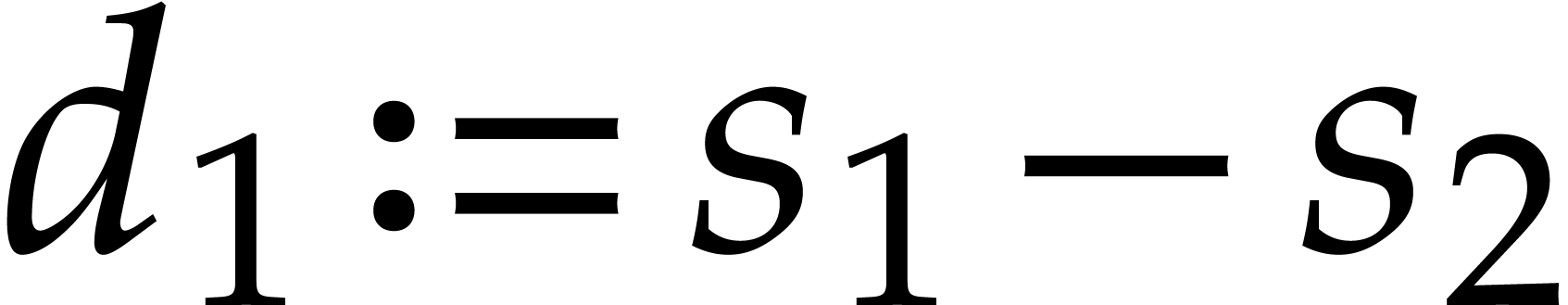
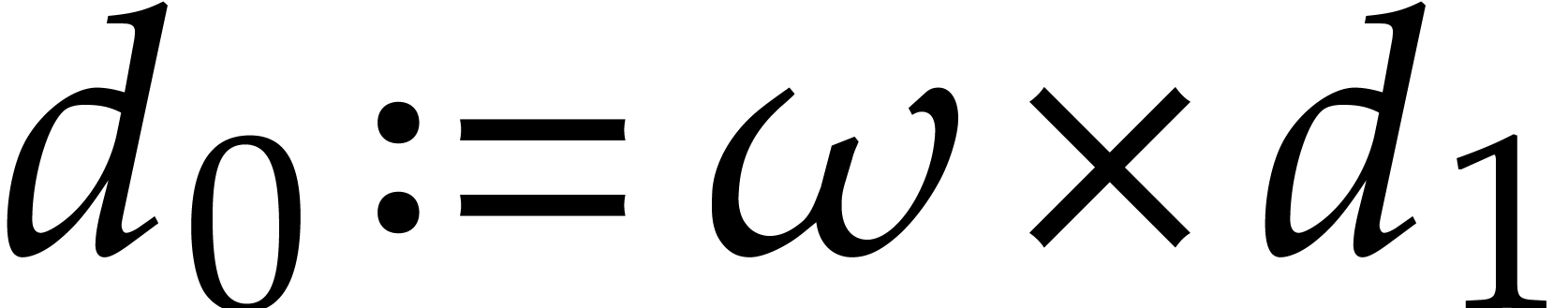

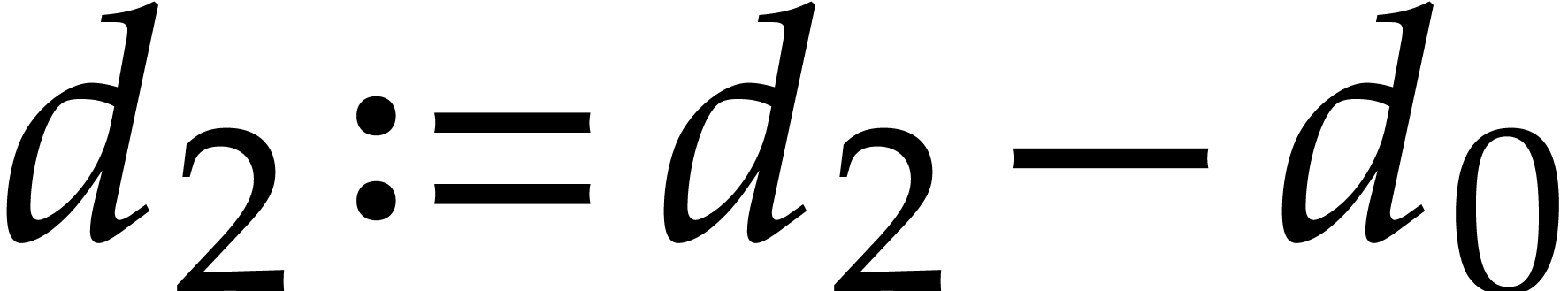



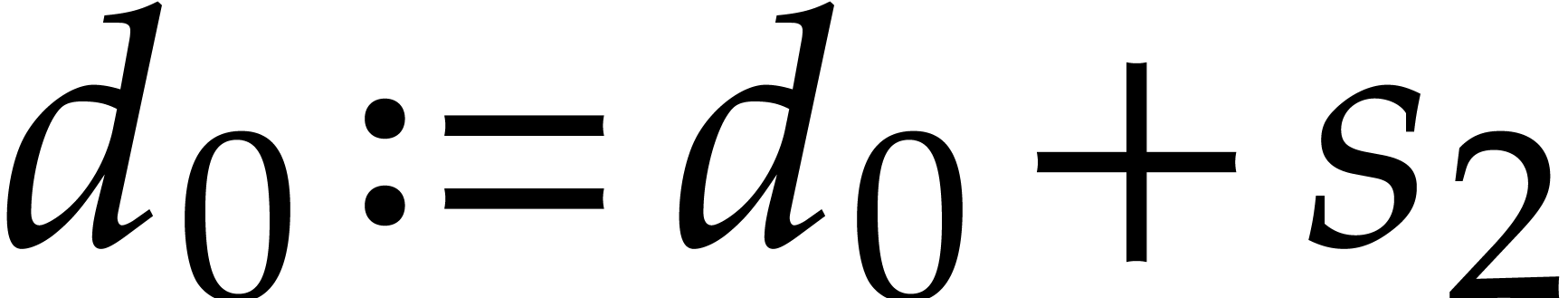
One verifies that 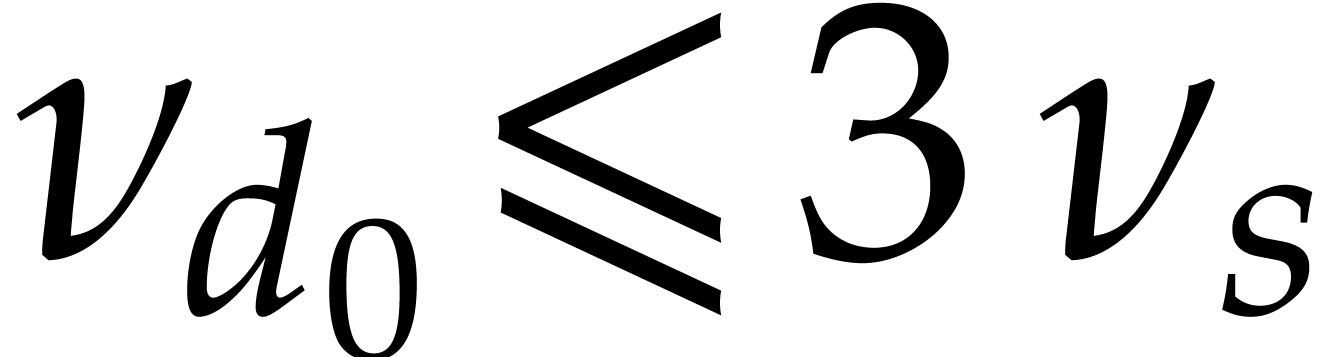 and
and 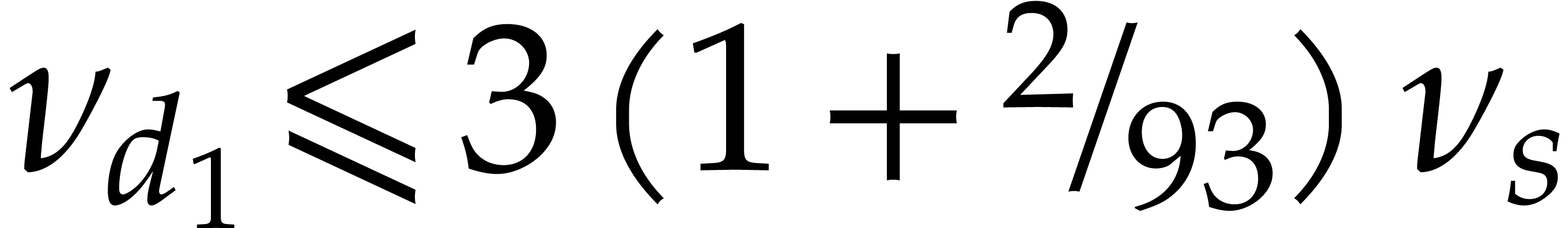 . For
. For 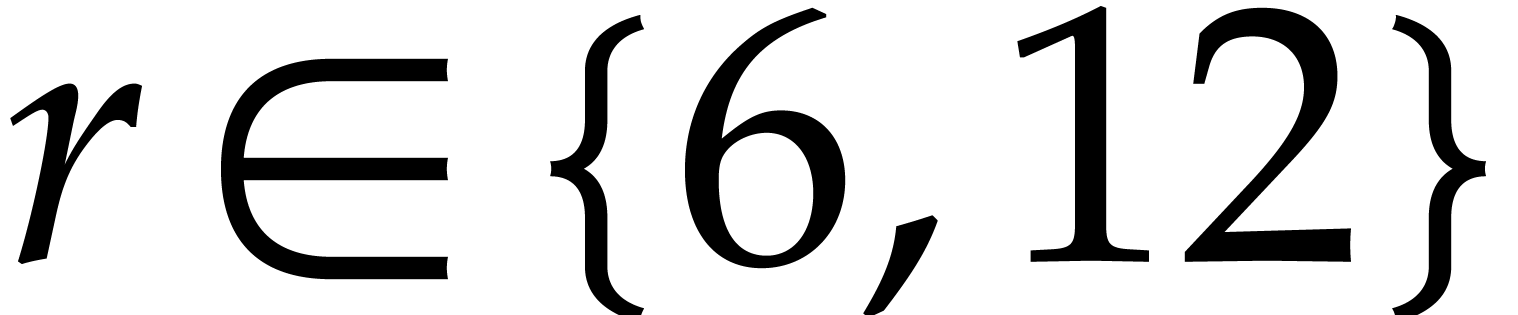 ,
we use Good's algorithm to decompose
,
we use Good's algorithm to decompose  in terms of
in terms of
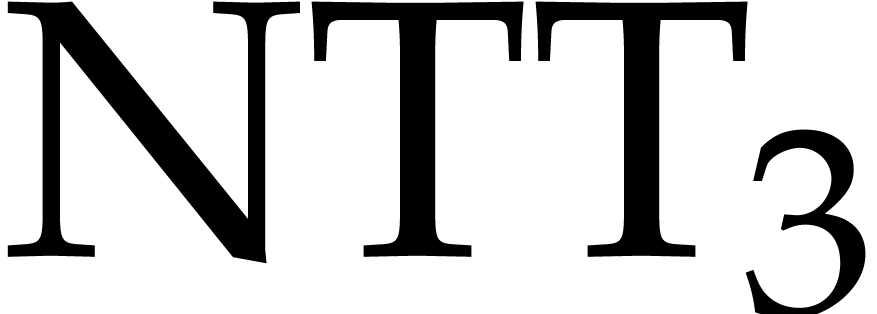 and
and 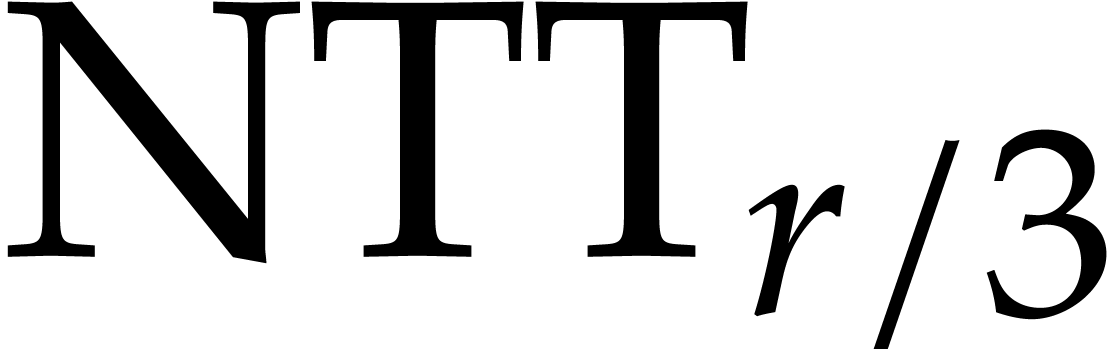 .
This yields
.
This yields 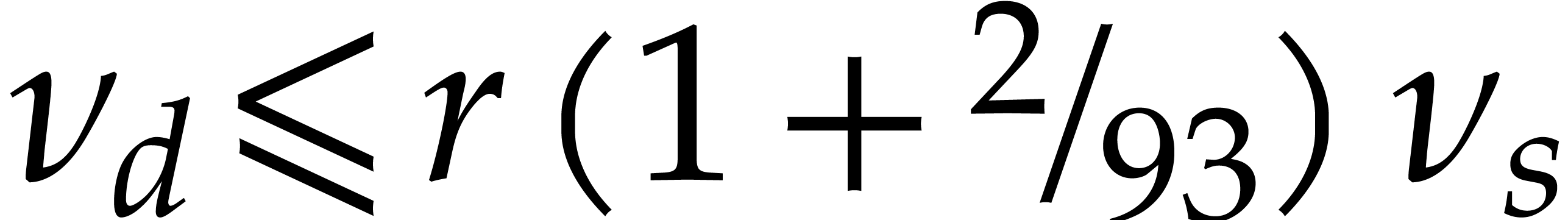 . For
. For  , we use the formula
, we use the formula
without normalization, which yields 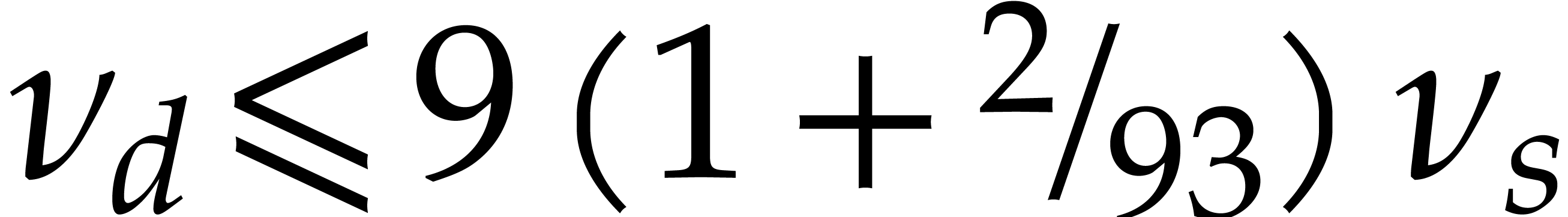 .
For
.
For 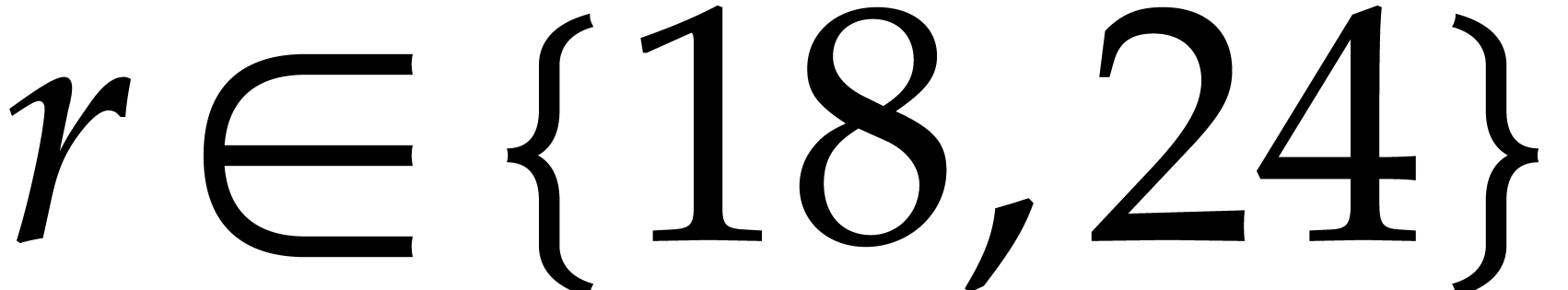 , we use Good's algorithm
with an intermediate normalization step. For
, we use Good's algorithm
with an intermediate normalization step. For 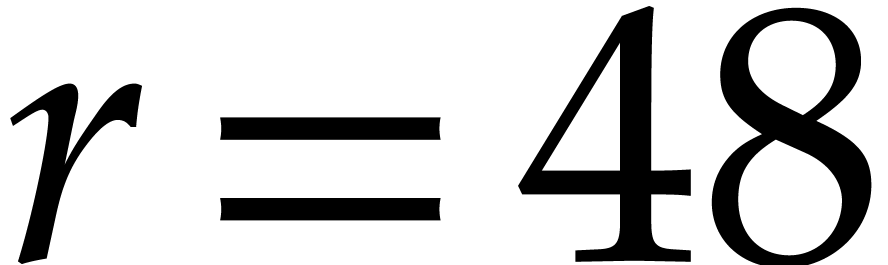 , we use the formula
, we use the formula
while taking benefit of the partial normalization of the twiddling step.
Now assume that we wish to compute an NTT of large order  with
with 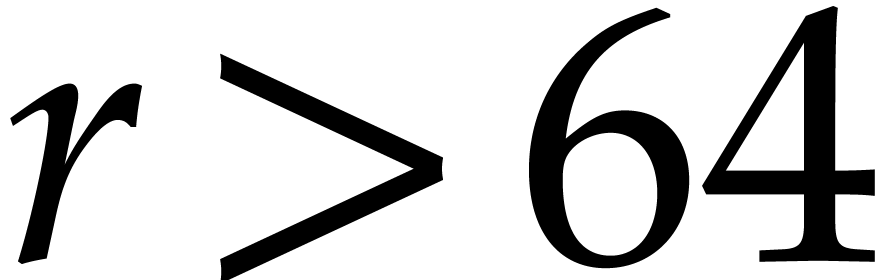 . For
input and output vectors
. For
input and output vectors 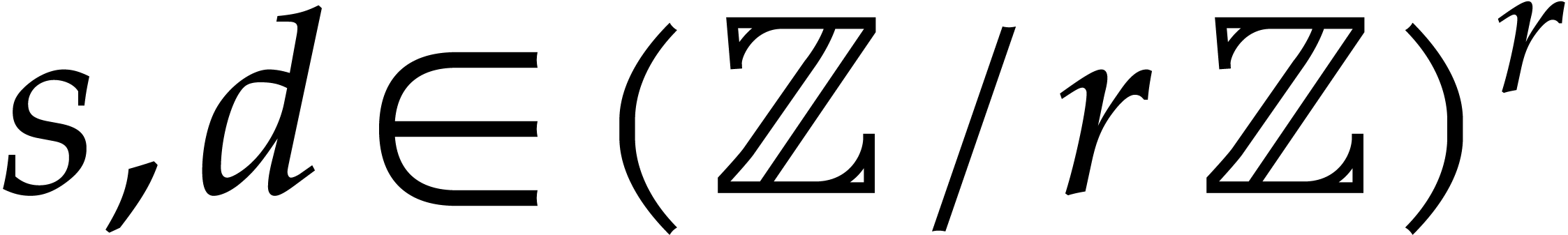 , we
require that
, we
require that 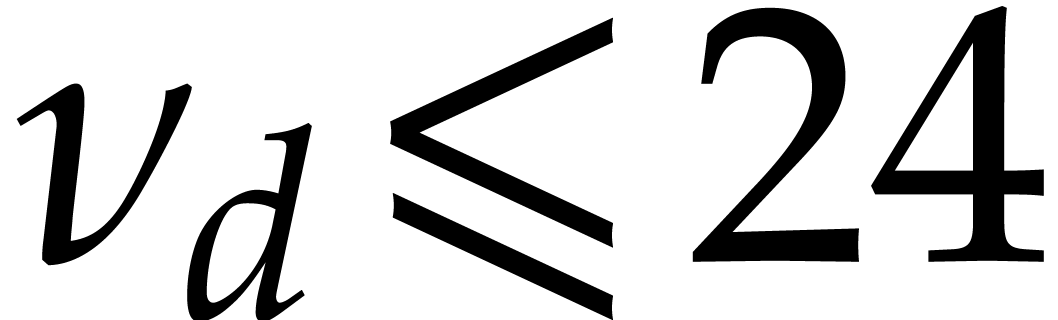 whenever
whenever 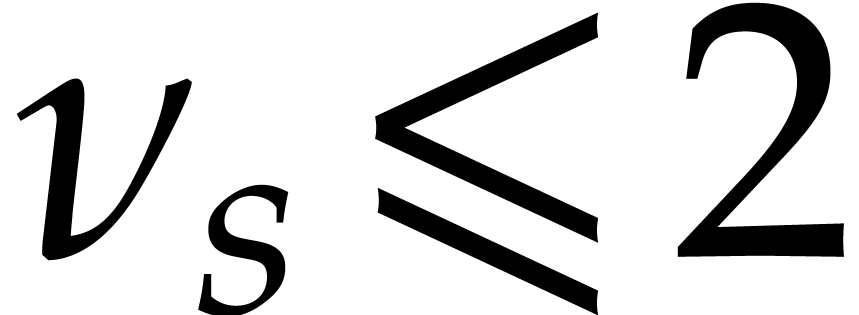 . This is indeed the case for all codelets from the
previous subsection.
. This is indeed the case for all codelets from the
previous subsection.
Let 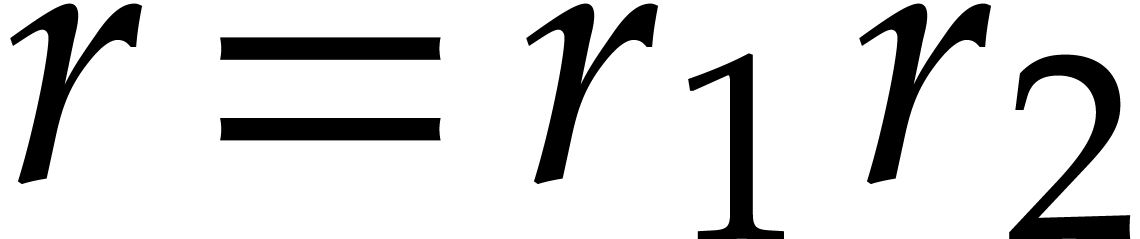 be a decomposition of
be a decomposition of  with
with 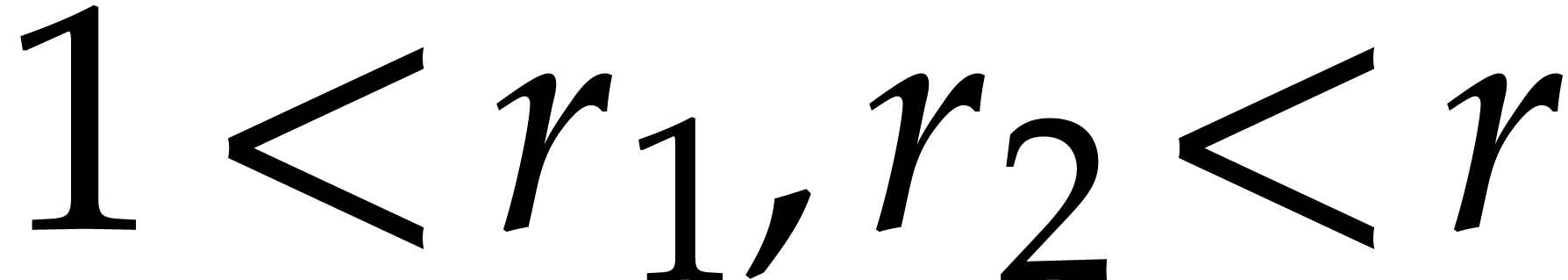 . We recursively assume
that we know how to compute codelets for
. We recursively assume
that we know how to compute codelets for  and
and
 . Now we compute
. Now we compute  using the formula
using the formula
 |
(11) |
Following (4), we compute 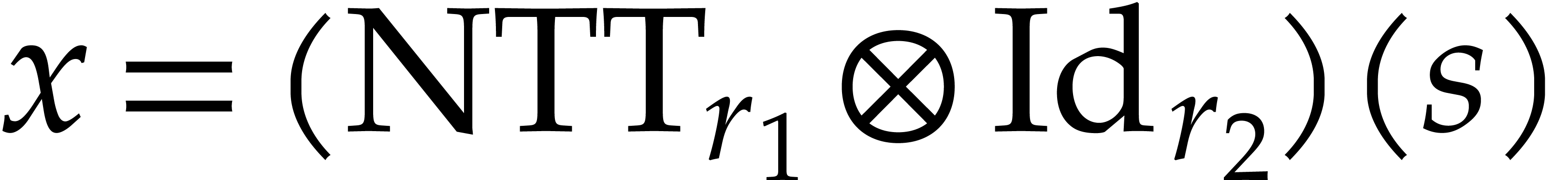 using
using
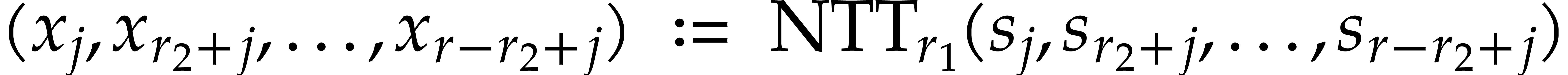 |
(12) |
for 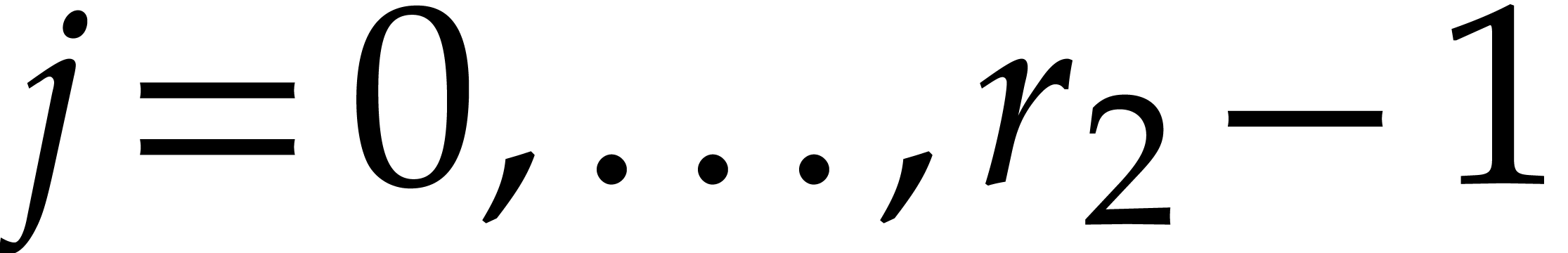 . Note that this yields
. Note that this yields
 whenever
whenever  ,
by our assumption on
,
by our assumption on  .
Setting
.
Setting  , let
, let 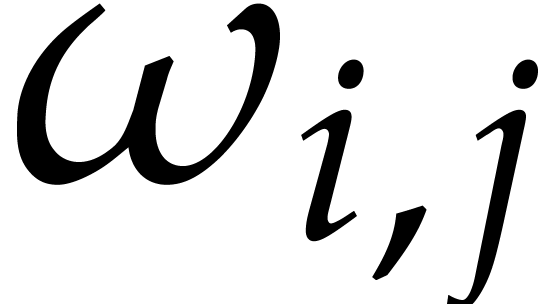 be the twiddle factors with
be the twiddle factors with
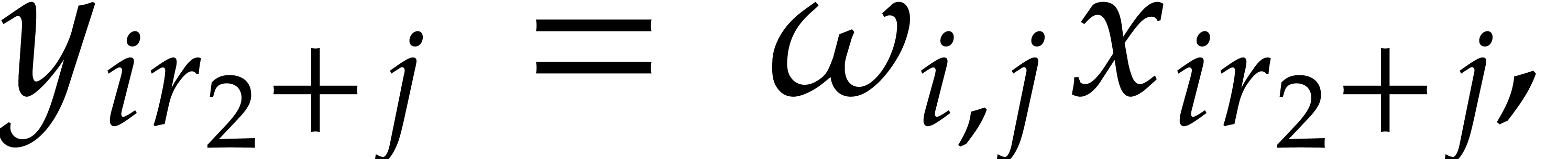
for  and
and 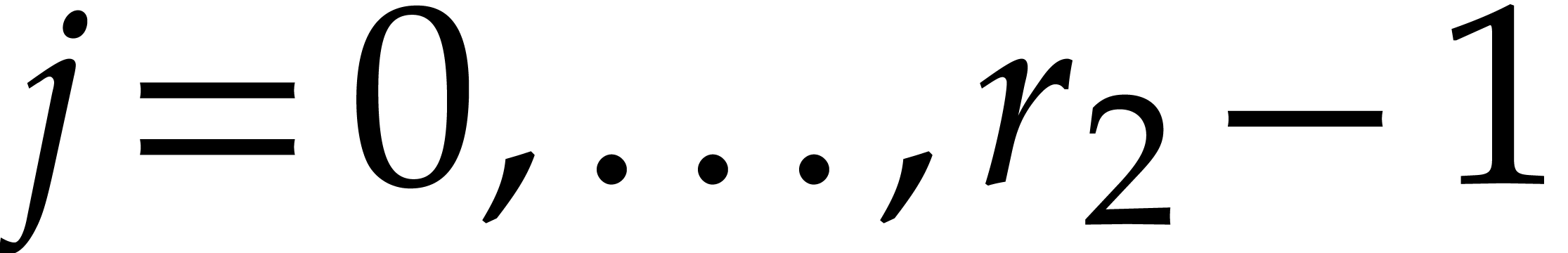 .
For
.
For  , we next compute
, we next compute
 |
(13) |
which corresponds to combining (5) and (6). If
 , then
, then 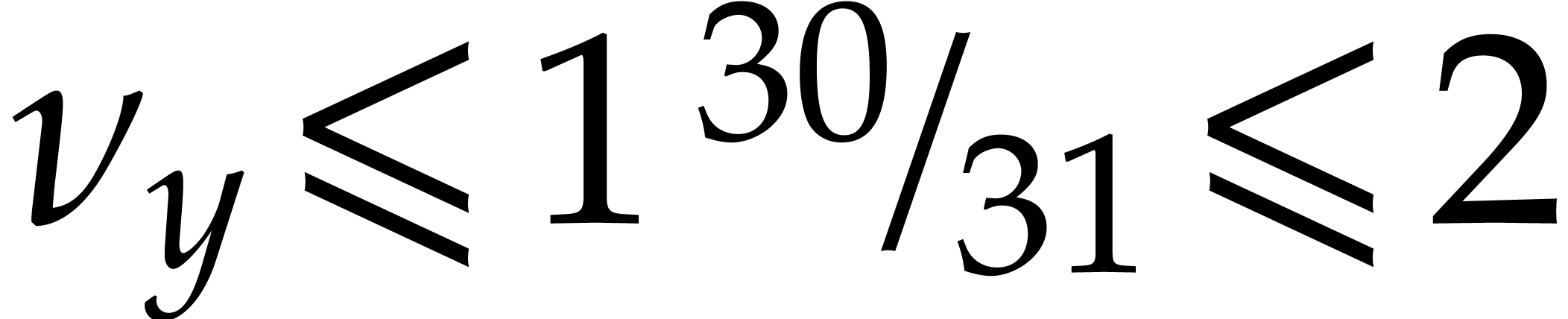 and
and  , by our assumption on
, by our assumption on
 . This proves our inductive
requirement that
. This proves our inductive
requirement that  whenever
whenever  .
.
It is important to keep an eye on the cache efficiency for the actual
implementation. In the formula (12), we precompute the
twiddle factors and store the vectors 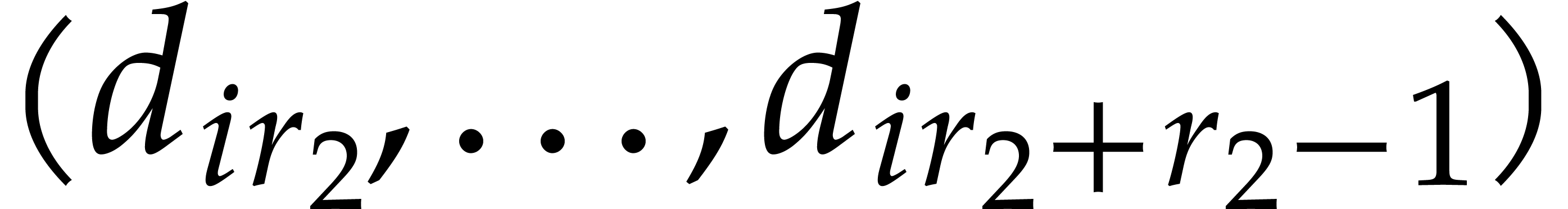 ,
,
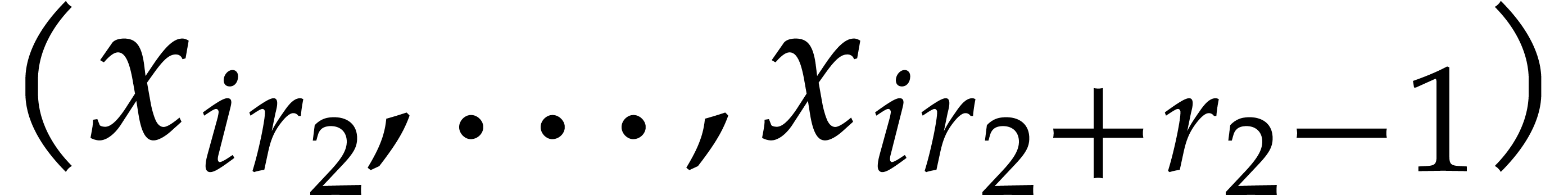 , and
, and 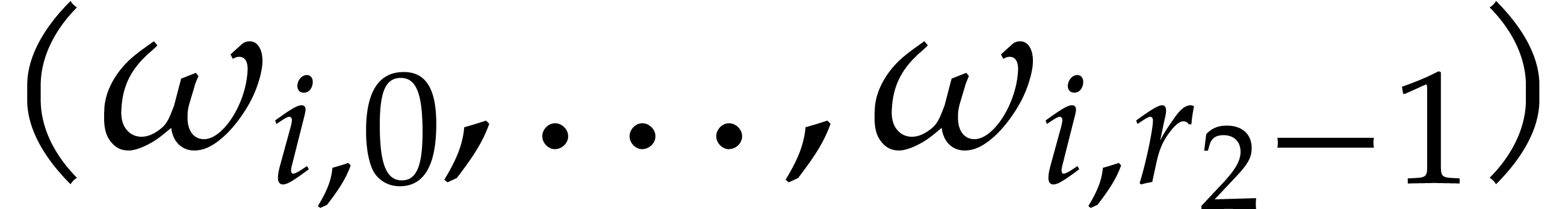 in contiguous segments of memory. Instead of applying a global twiddling
step
in contiguous segments of memory. Instead of applying a global twiddling
step 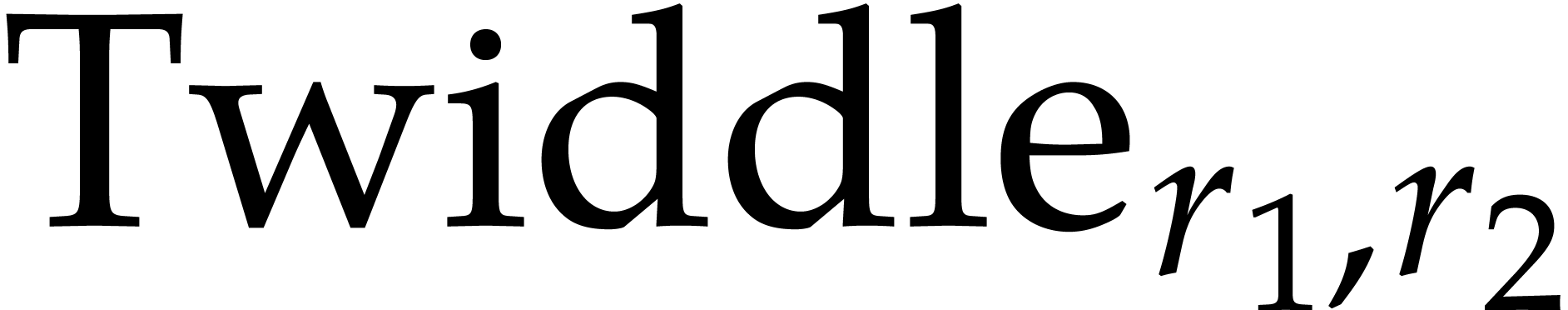 , we use a loop over
, we use a loop over
 and mix the twiddling step with the NTTs of
length
and mix the twiddling step with the NTTs of
length 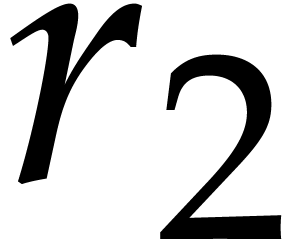 ; this avoids
traversing
; this avoids
traversing  elements in memory twice and thereby
improves the cache efficiency. If
elements in memory twice and thereby
improves the cache efficiency. If 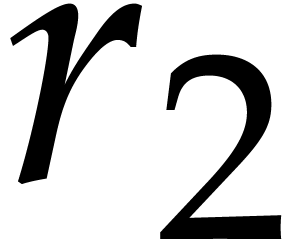 is really
large, then we might rewrite
is really
large, then we might rewrite  in terms of smaller
NTTs and move the twiddling step even further inside.
in terms of smaller
NTTs and move the twiddling step even further inside.
As to (12), we first need to move the input slices  with “stride”
with “stride” 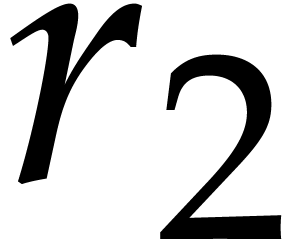 into contiguous memory. After applying the NTT, we also need to put the
result back in the slice
into contiguous memory. After applying the NTT, we also need to put the
result back in the slice  with stride
with stride 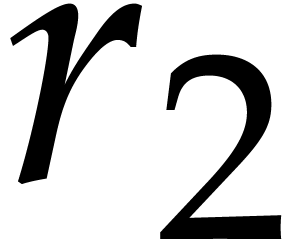 . These memory rearrangements
correspond to two
. These memory rearrangements
correspond to two  and
and  matrix transpositions. For cache efficiency, we need to minimize the
number of full traversals of vectors of size
matrix transpositions. For cache efficiency, we need to minimize the
number of full traversals of vectors of size  , so it is again better to use a loop over
, so it is again better to use a loop over 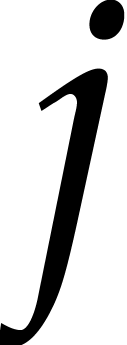 . However, entries of the form
. However, entries of the form 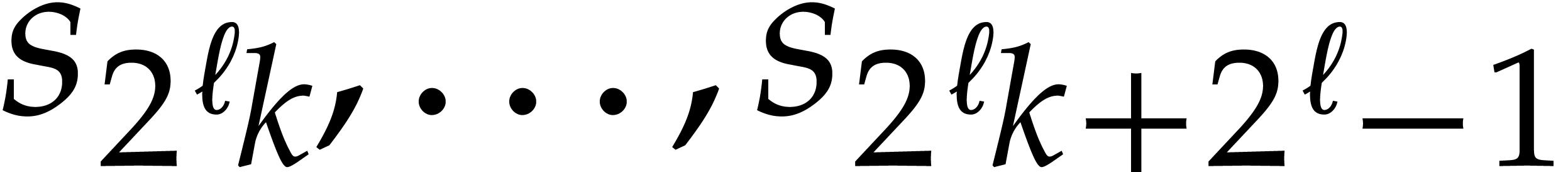 are typically stored in the same cache line for some
are typically stored in the same cache line for some
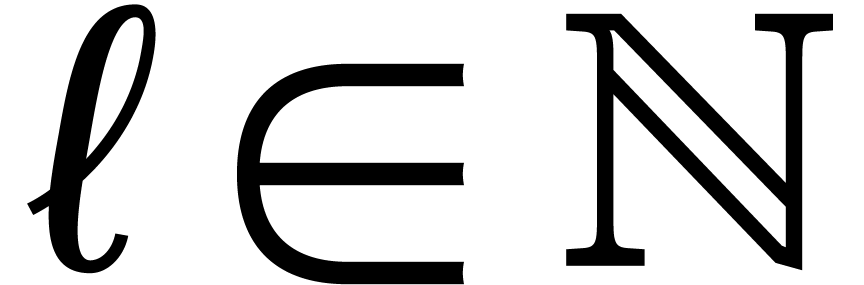 that depends on the hardware. It is better to
treat these contiguous entries together, which can be achieved by
cutting the loop over
that depends on the hardware. It is better to
treat these contiguous entries together, which can be achieved by
cutting the loop over  into chunks of size
into chunks of size 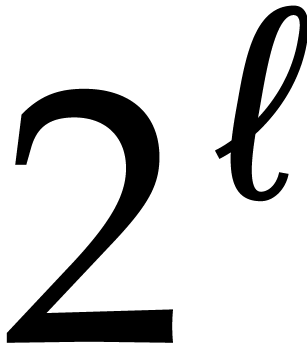 (in fact, slightly different chunk sizes may perform
even better). This corresponds to rewriting the
(in fact, slightly different chunk sizes may perform
even better). This corresponds to rewriting the  matrix transposition into
matrix transposition into 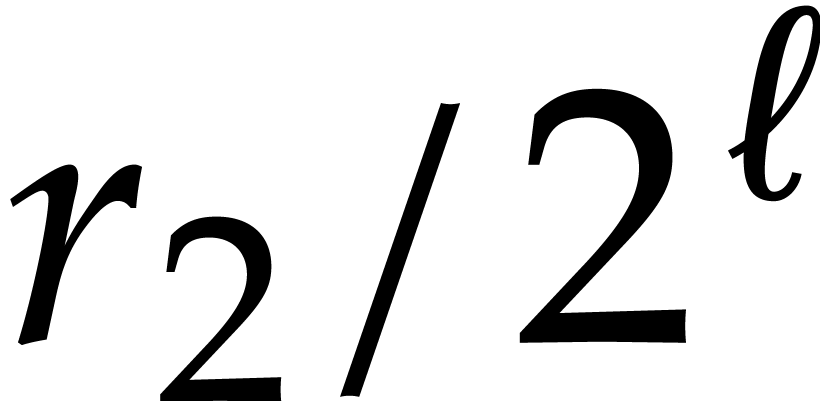 transpositions of
transpositions of 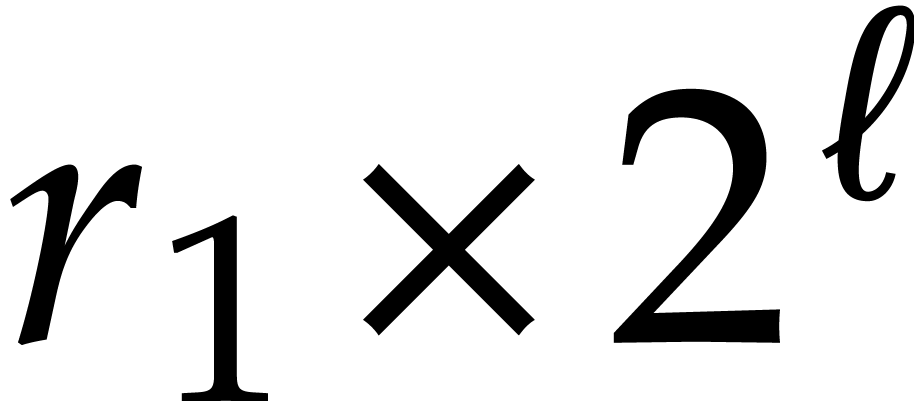 matrices (and similar for the inverse transposition).
matrices (and similar for the inverse transposition).
Assume now that we are on hardware that supports SIMD vectors of width
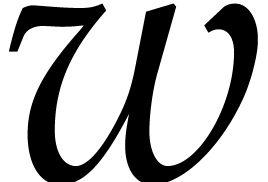 and let us investigate how to vectorize the
algorithm (11) from the previous subsection.
and let us investigate how to vectorize the
algorithm (11) from the previous subsection.
Let us first consider the case when 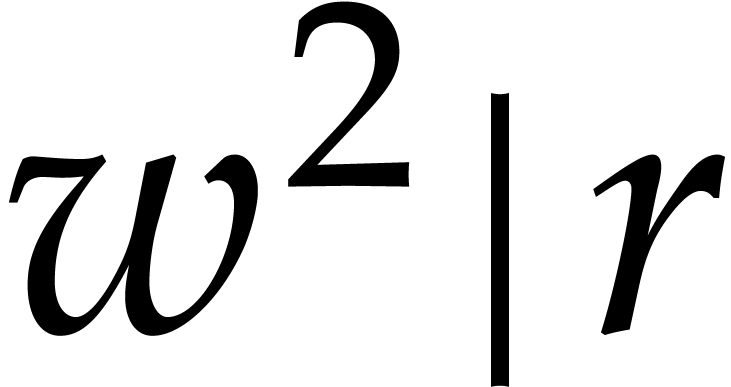 and
and  . The first step (12)
is easy to vectorize: we may reinterpret the map
. The first step (12)
is easy to vectorize: we may reinterpret the map 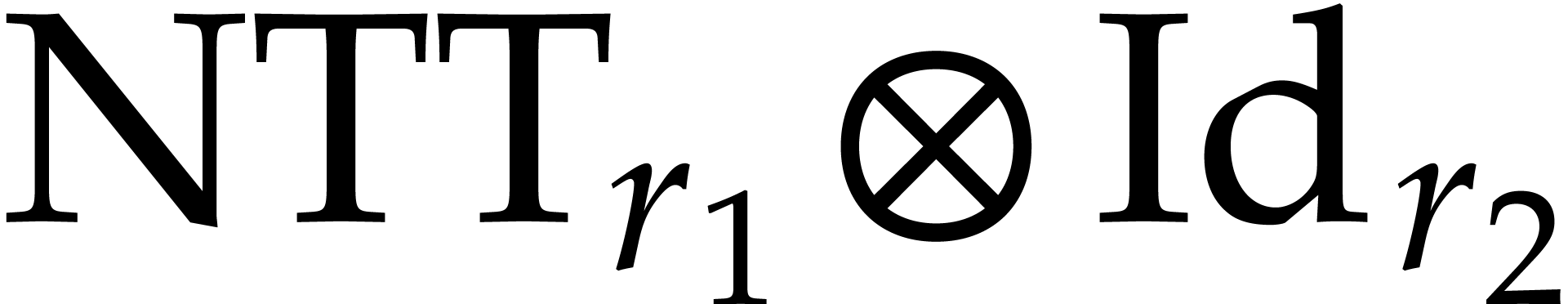 on vectors of size
on vectors of size  with entries in
with entries in 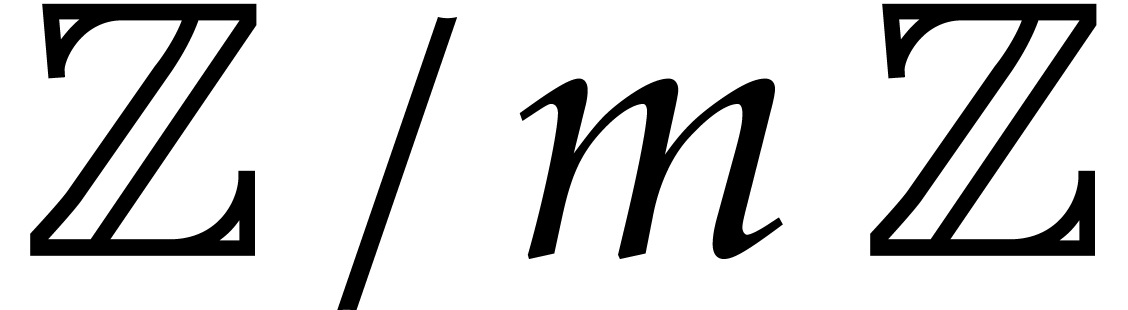 as the map
as the map  on vectors of size
on vectors of size 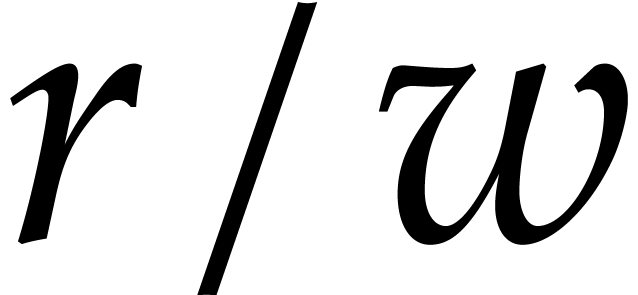 with SIMD entries in
with SIMD entries in 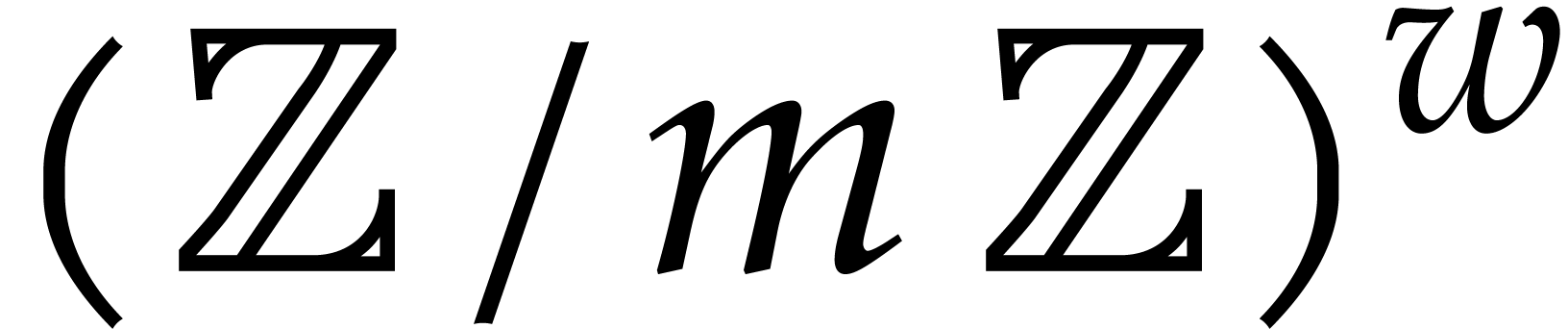 .
As to the second step (13), we have
.
As to the second step (13), we have 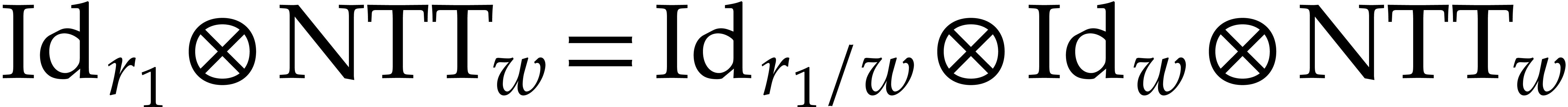 and the computation of the map
and the computation of the map 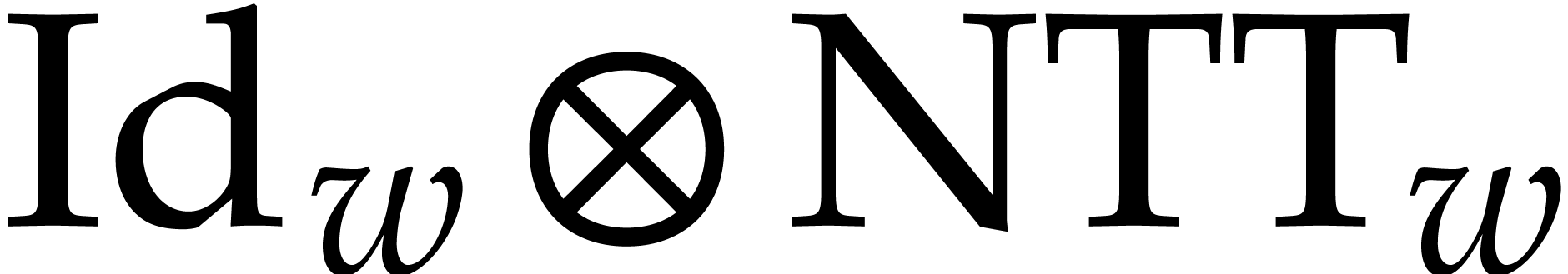 reduces to the
computation of
reduces to the
computation of  , using a
, using a  matrix transposition. In order to compute the map
matrix transposition. In order to compute the map
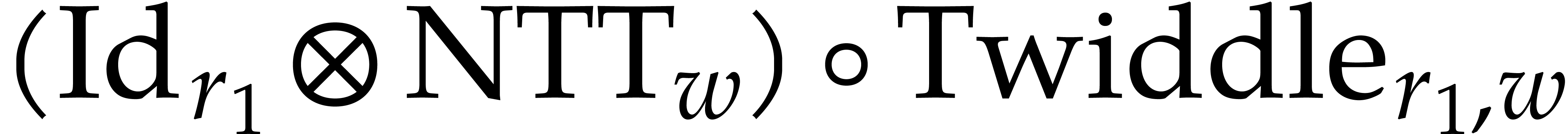 , this leads us to use a loop
of length
, this leads us to use a loop
of length 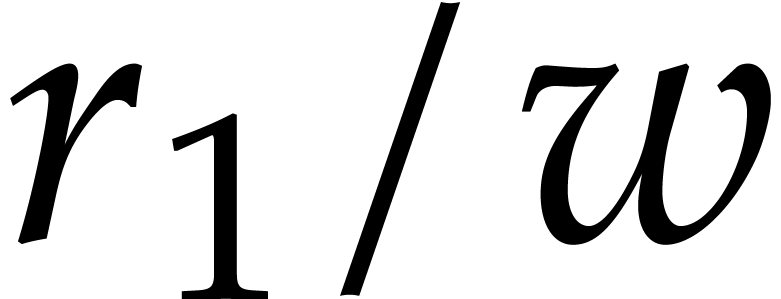 that treats blocks of
that treats blocks of 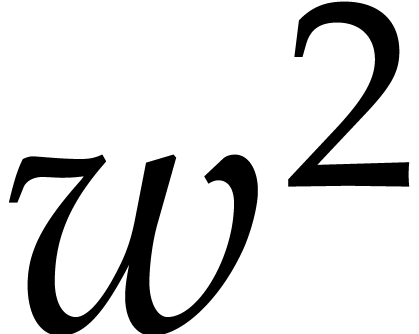 coefficients at the time. On each block, we first multiply with the
twiddle factors, then apply a
coefficients at the time. On each block, we first multiply with the
twiddle factors, then apply a  matrix
transposition, and finally an inline codelet for
matrix
transposition, and finally an inline codelet for  for SIMD coefficients of width
for SIMD coefficients of width 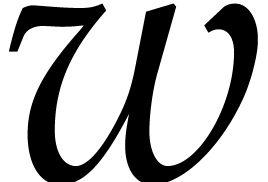 .
.
The idea behind SIMD implementations of  matrix
transposition is to recursively reduce this operation to two
matrix
transposition is to recursively reduce this operation to two  transpositions in different lanes, followed by a linear
number of operations to combine the results. This leads to an algorithm
that does the full transposition in
transpositions in different lanes, followed by a linear
number of operations to combine the results. This leads to an algorithm
that does the full transposition in 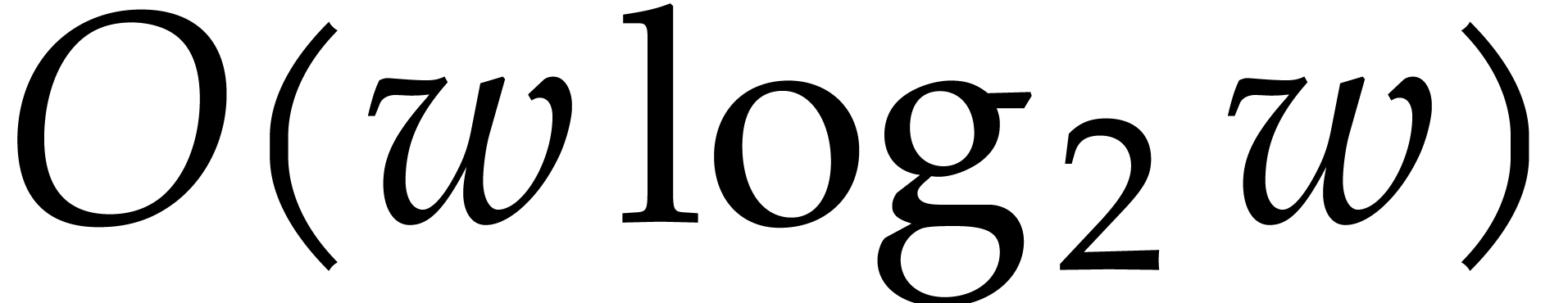 steps.
Concrete implementations on existing hardware are a bit tricky: every
next generation or brand of SIMD processors (SSE, AVX2, AVX-512, Neon,
...) tends to provide another set of instructions that are
useful for this application (permute, blend,
shuffle, etc.). Instead of covering all cases, we
illustrate the above recursive meta-algorithm by showing how to perform
a
steps.
Concrete implementations on existing hardware are a bit tricky: every
next generation or brand of SIMD processors (SSE, AVX2, AVX-512, Neon,
...) tends to provide another set of instructions that are
useful for this application (permute, blend,
shuffle, etc.). Instead of covering all cases, we
illustrate the above recursive meta-algorithm by showing how to perform
a  matrix transposition using
matrix transposition using 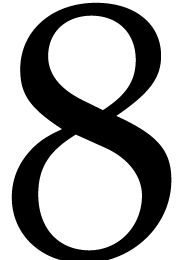 SIMD instructions on machines with AVX2 support:
SIMD instructions on machines with AVX2 support:
Let us now turn to the case when 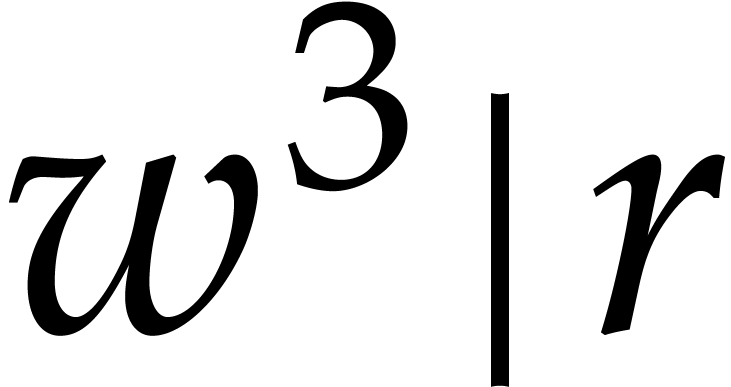 .
For any decomposition
.
For any decomposition 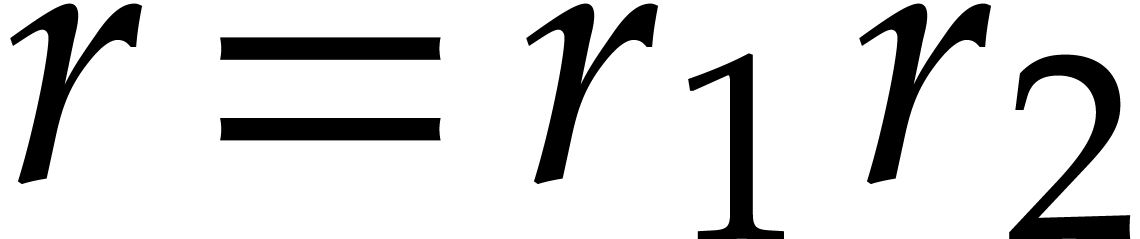 with
with 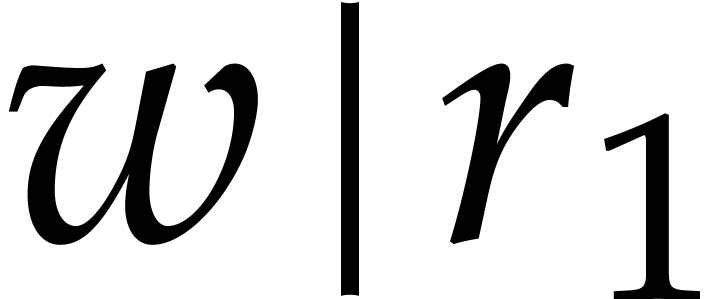 and
and 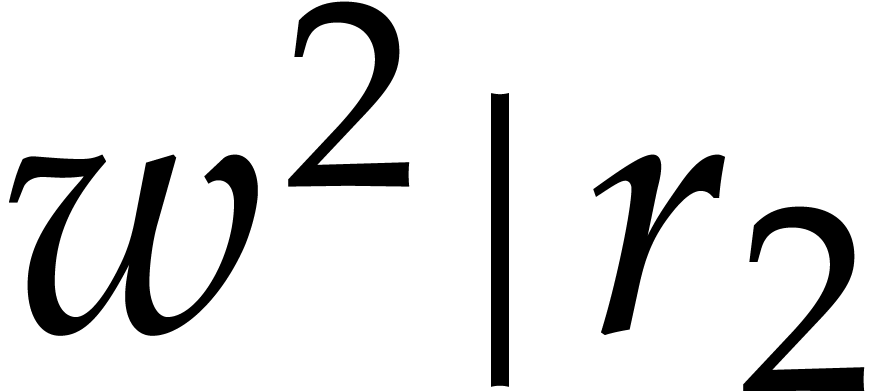 , we may apply the above
vectorization technique for the computation of
, we may apply the above
vectorization technique for the computation of  . Using the loop (13), this also allows
us to vectorize
. Using the loop (13), this also allows
us to vectorize 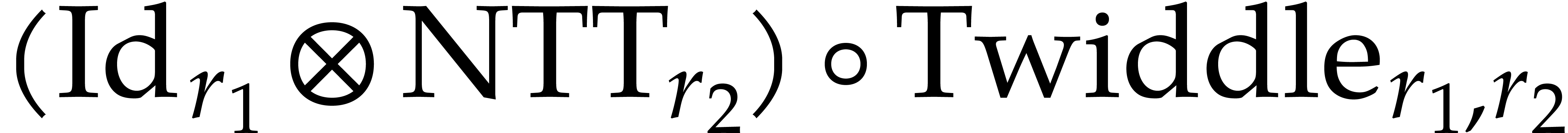 . Combined
with the fact that the map
. Combined
with the fact that the map 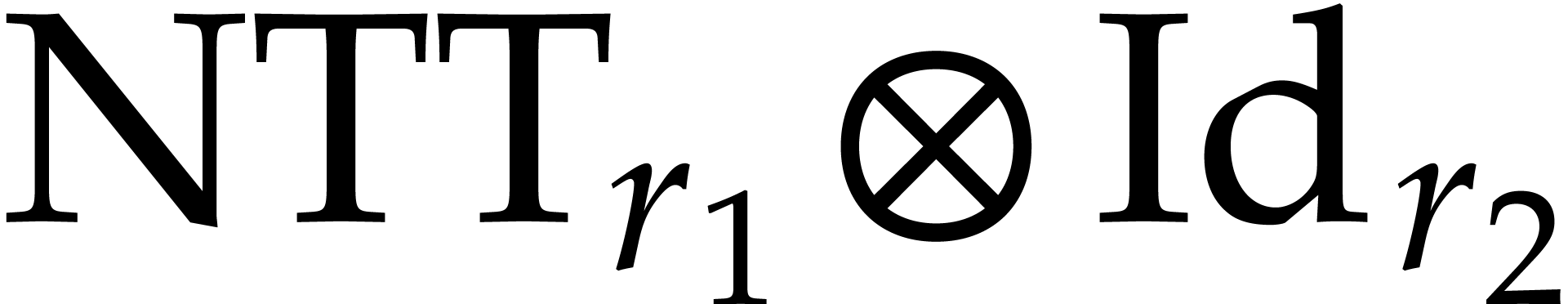 trivially vectorizes,
this provides us with an alternative vectorization of the formula (11). This technique has the advantage of providing more
flexibility for the choices of
trivially vectorizes,
this provides us with an alternative vectorization of the formula (11). This technique has the advantage of providing more
flexibility for the choices of 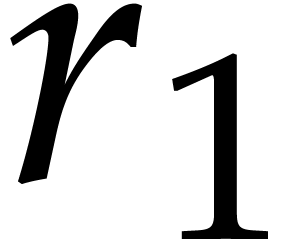 and
and 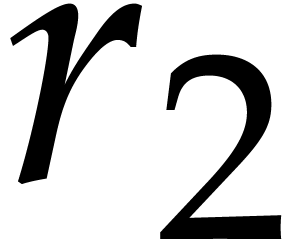 . In particular, for large orders
. In particular, for large orders  , taking
, taking 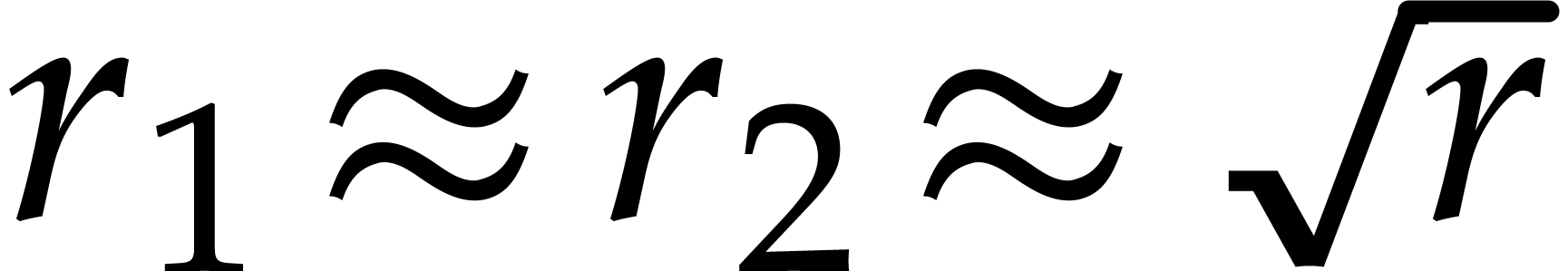 tends to
ensure a better cache efficiency.
tends to
ensure a better cache efficiency.
For our actual implementation, we emulate an SIMD width 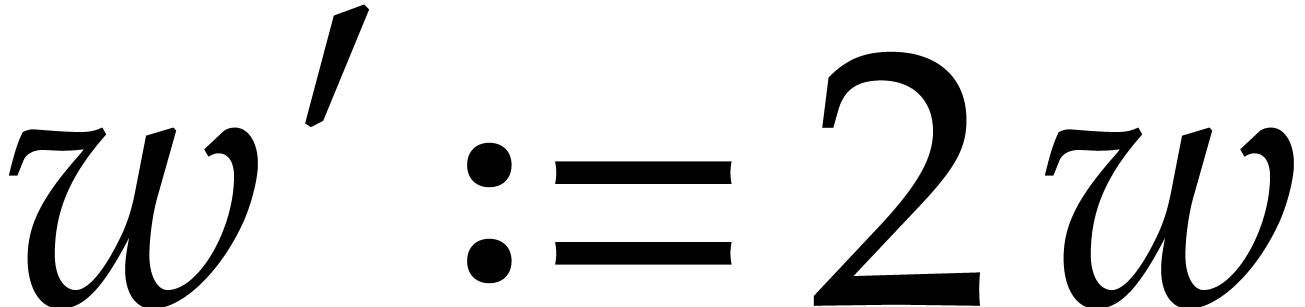 of twice the hardware SIMD width
of twice the hardware SIMD width 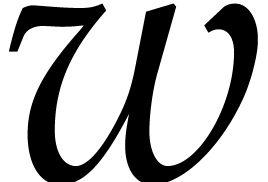 for the given
floating point type. This means that every instruction is
“duplexed” for the “low” and “high”
parts. For instance, the codelet for
for the given
floating point type. This means that every instruction is
“duplexed” for the “low” and “high”
parts. For instance, the codelet for 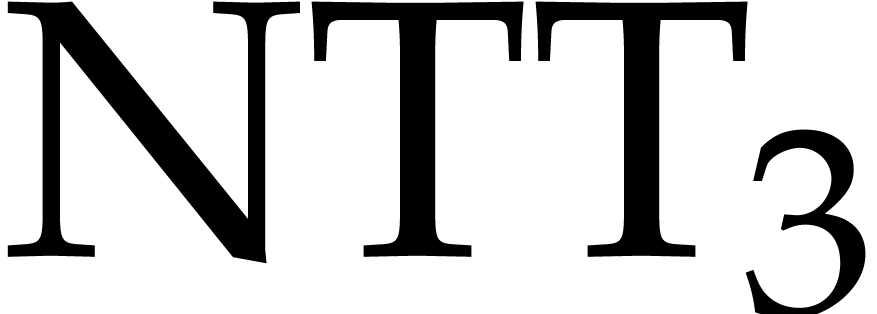 from
section 4.2 gives rise to the following duplex version for
coefficients in
from
section 4.2 gives rise to the following duplex version for
coefficients in 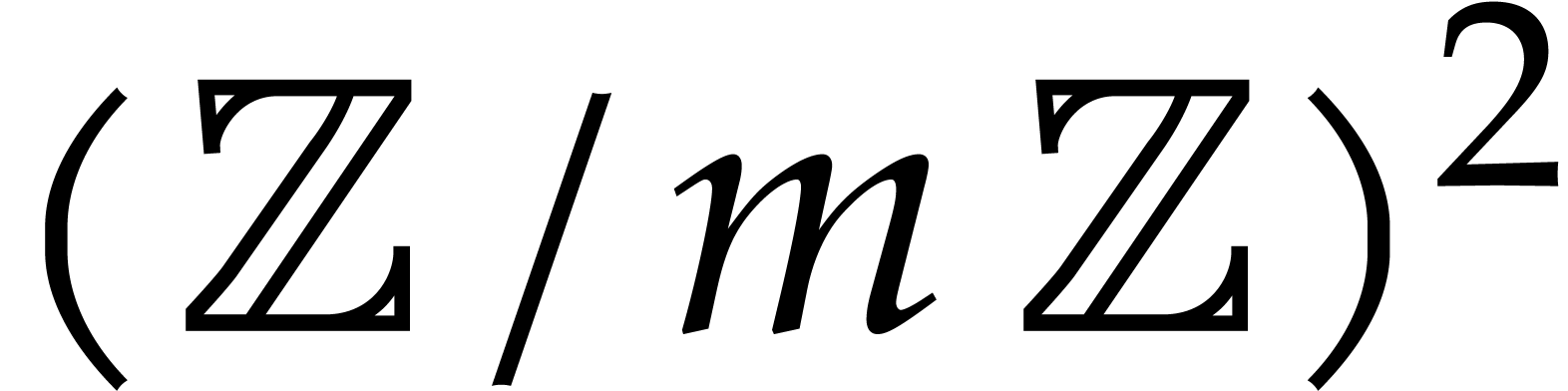 :
:
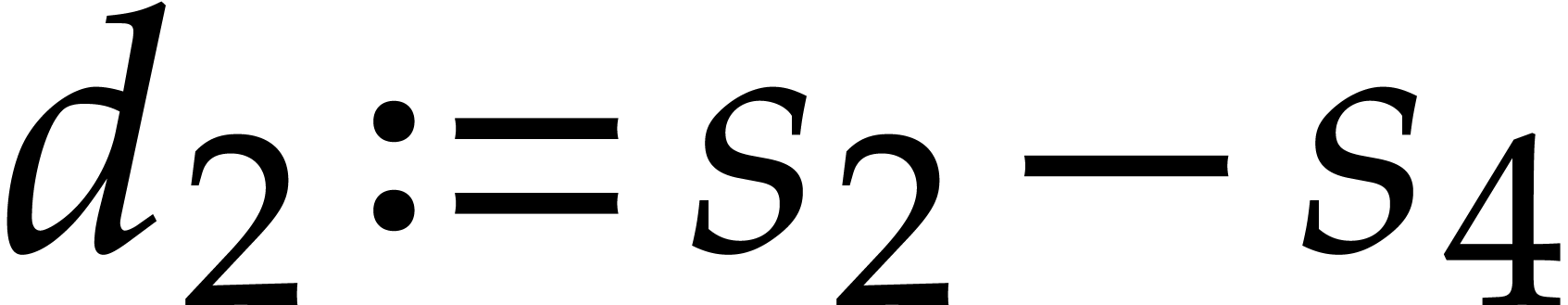
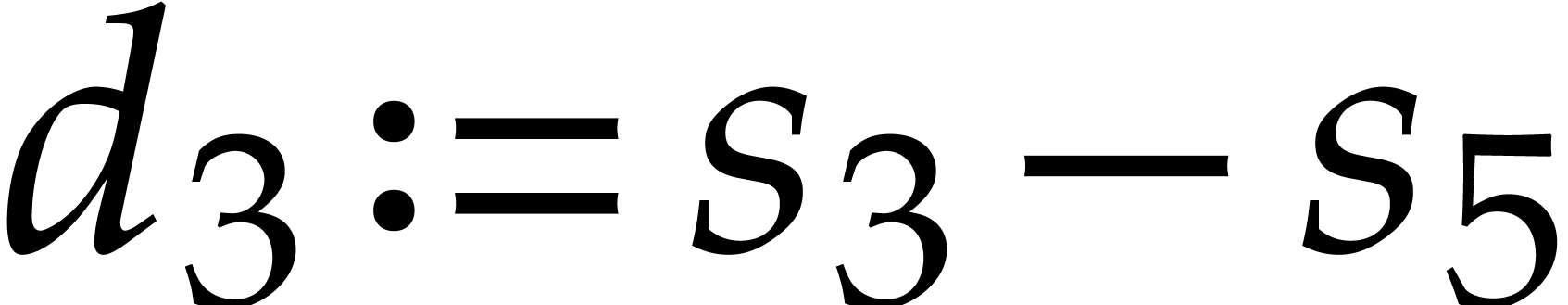
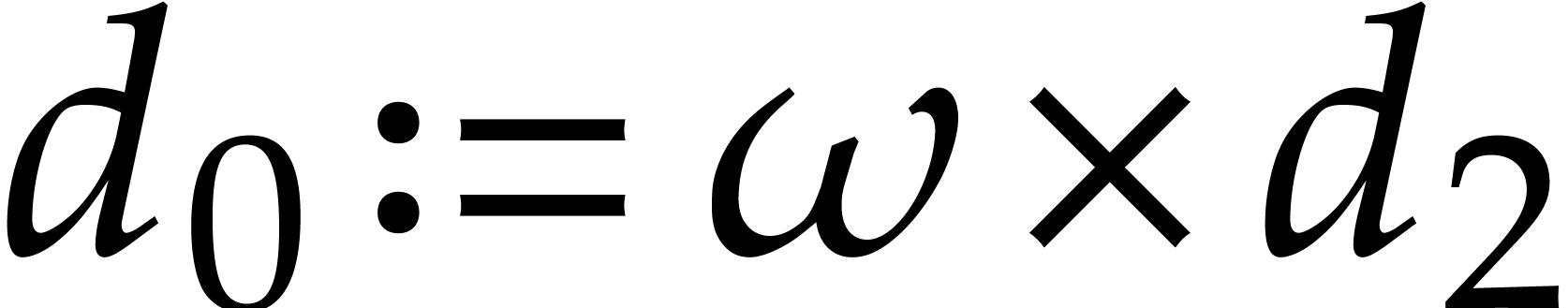
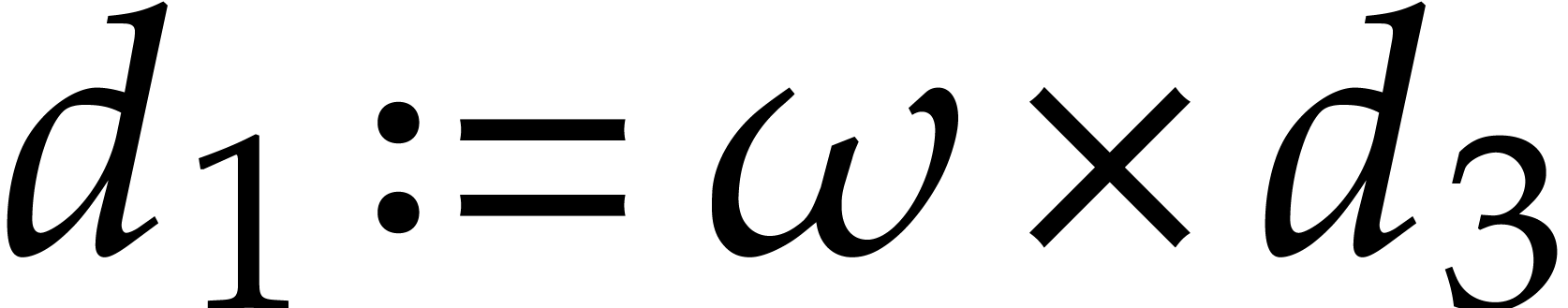

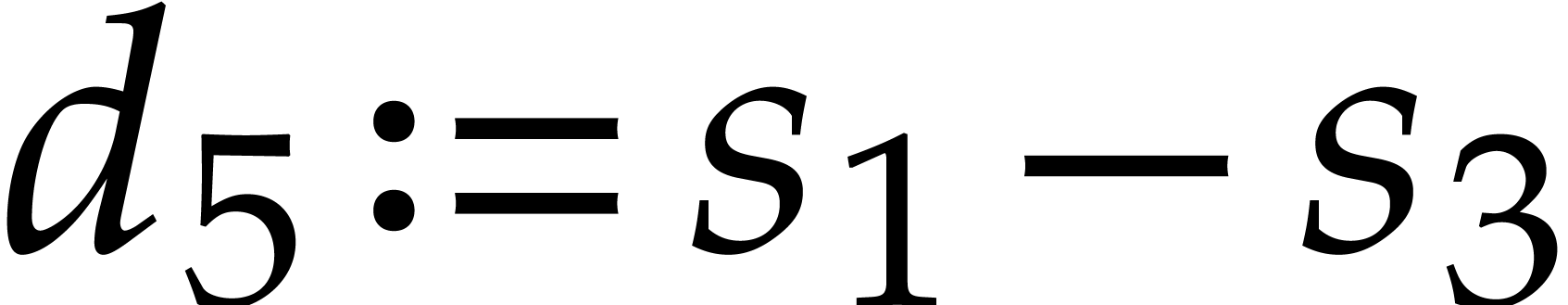
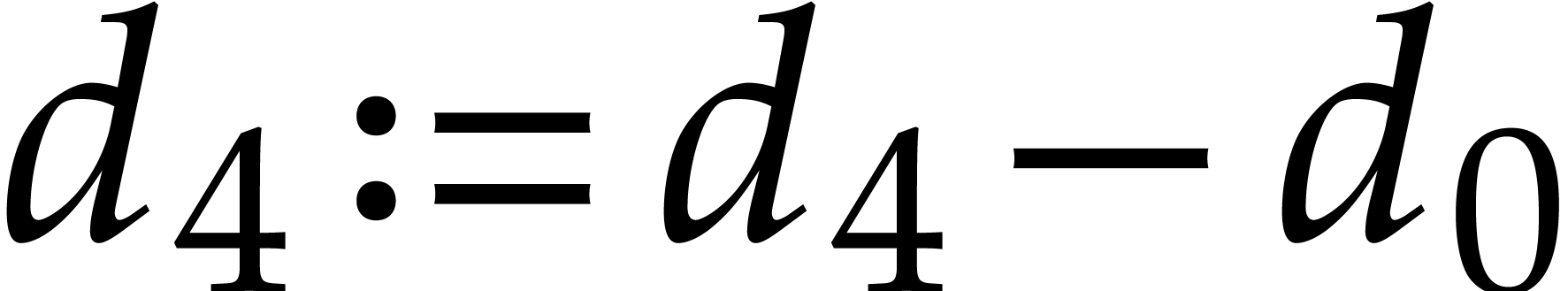
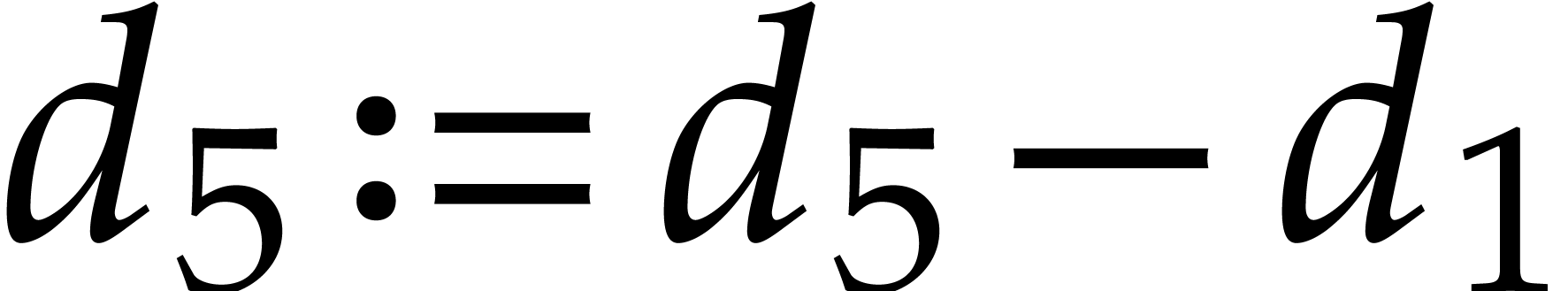

The main advantage of this technique is that it spreads data dependencies. This makes the code less vulnerable to delays caused by instructions with high latencies. One disadvantage of duplexing is that it doubles the pressure on hardware registers. Nevertheless, this is less of a problem on modern processors with many SIMD registers.
We implemented the algorithms described in this paper in the
mmcomp –optimize hpc/bench/dft_best_mixed_bench.mmx
We systematically use the fixed prime number 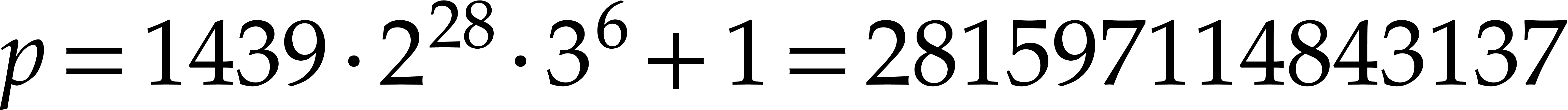 as
our modulus for all NTTs. Consequently,
as
our modulus for all NTTs. Consequently, 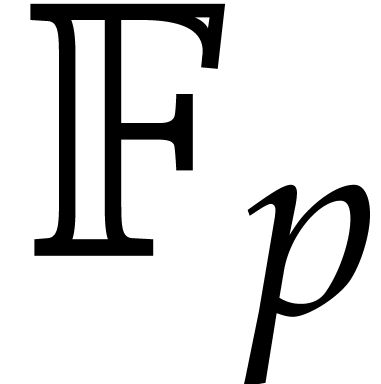 has
power of two roots of unity of orders up till
has
power of two roots of unity of orders up till  , which is also an upper bound for our main
benchmarks. For orders
, which is also an upper bound for our main
benchmarks. For orders 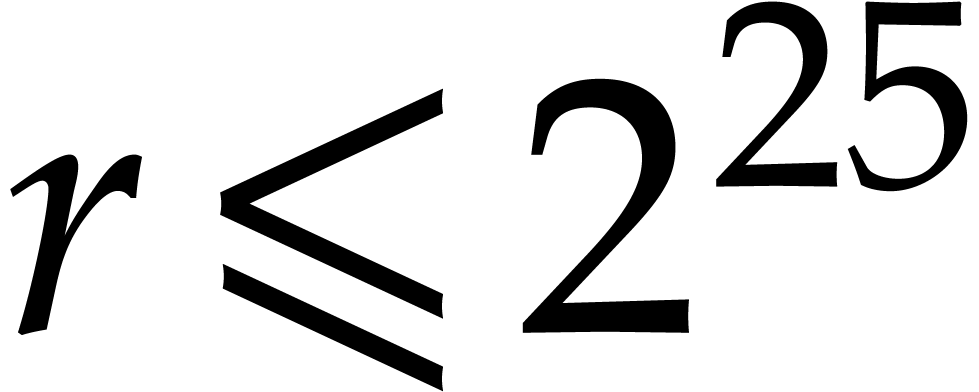 , our
implementation does an extensive search for the best strategy. For
larger orders, we make a suboptimal guess based on the best observed
strategies for orders
, our
implementation does an extensive search for the best strategy. For
larger orders, we make a suboptimal guess based on the best observed
strategies for orders  .
.
We tested our implementation on five different systems whose characteristics are specified in Table 1. These systems cover three SIMD widths:
Note that the AVX-512 support on the AMD RYZEN9 7950X3D processor is “double pumped” in the sense that certain instructions (like FMA) are done in two parts of 256 bits each
|
||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The main focus of this paper is on a mono-threaded implementation of
number theoretic transforms, while exploiting SIMD instruction-level
parallelism. We optimized our code for orders
 with
with
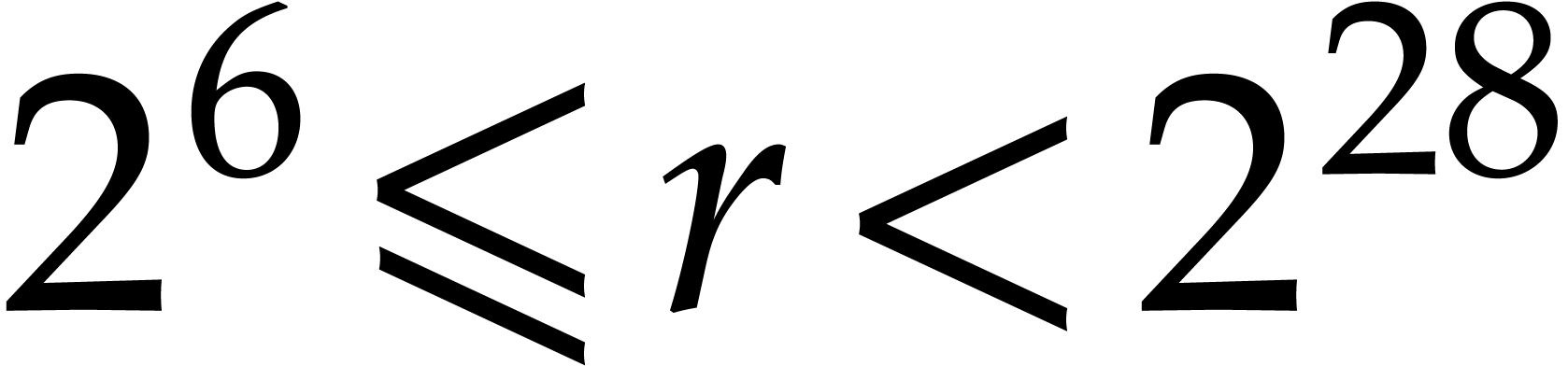 and
and
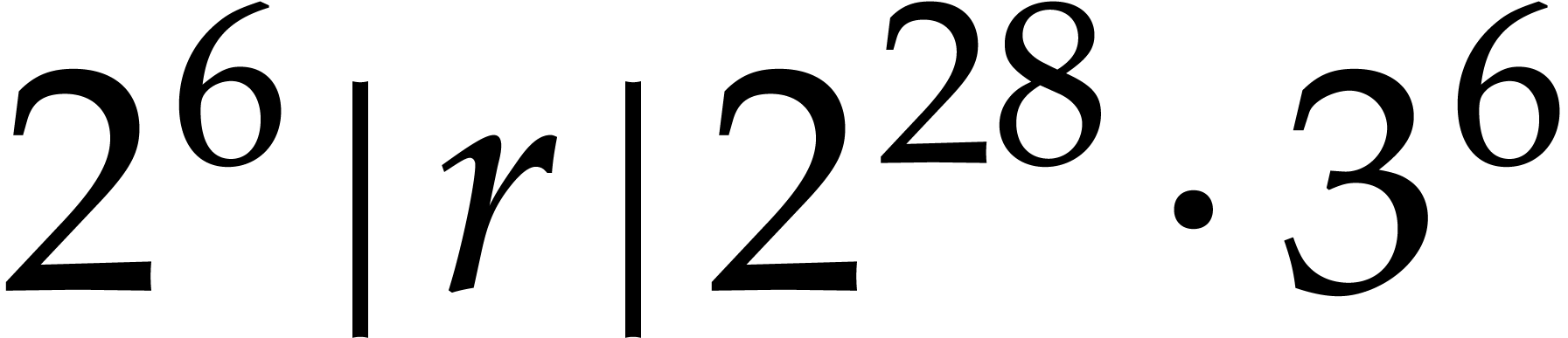 .
For reference and completeness, a full table with all observed timings
is provided in Table
2
. For each entry, we computed three timings and reported the median one.
In Figure
1
, we also plotted the corresponding graph. For readability, this graph
is limited to the x86-based architectures. The graph shows a familiar
nearly affine behavior for the computation time in the double
logarithmic scale. The sudden increase of the timings of the xeon curve
near
.
For reference and completeness, a full table with all observed timings
is provided in Table
2
. For each entry, we computed three timings and reported the median one.
In Figure
1
, we also plotted the corresponding graph. For readability, this graph
is limited to the x86-based architectures. The graph shows a familiar
nearly affine behavior for the computation time in the double
logarithmic scale. The sudden increase of the timings of the xeon curve
near
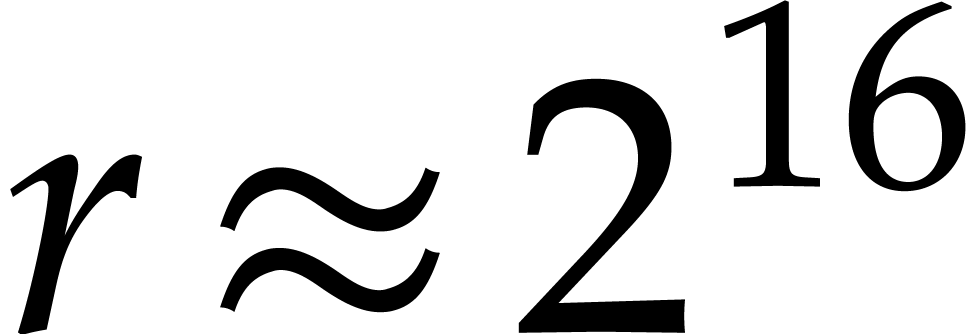 is due to an inefficient memory hierarchy on this computer.
is due to an inefficient memory hierarchy on this computer.
 |
Figure 1. Graphical representation of the timings from Table 2, for the first three columns only. |
Now one NTT of a power of two length 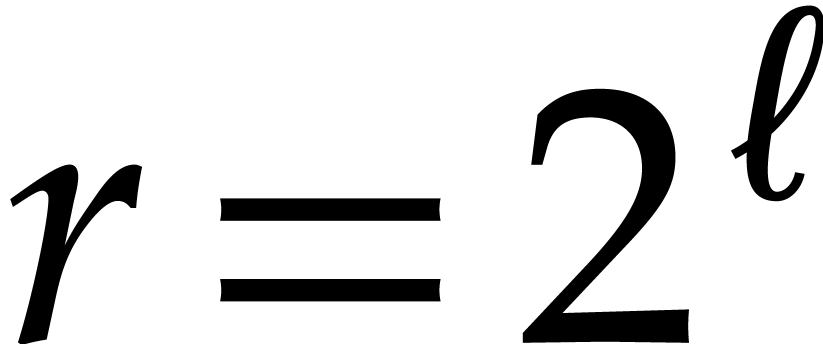 consists of
consists of
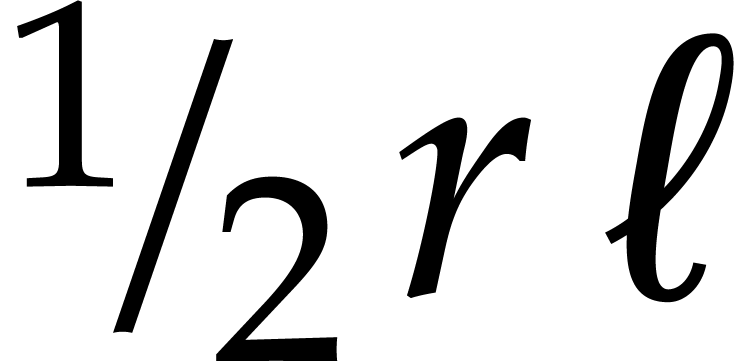 butterflies. For a better understanding of the
efficiency of our implementation it is therefore useful to divide our
timings by
butterflies. For a better understanding of the
efficiency of our implementation it is therefore useful to divide our
timings by 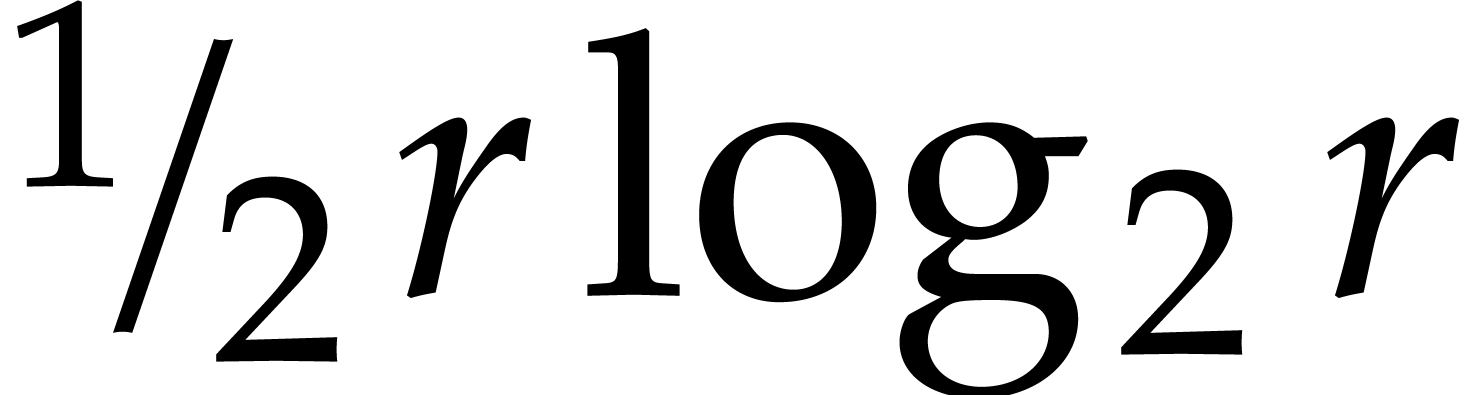 , even when
, even when  is not a power of two. Figure 2 shows
the resulting normalized timings. In addition, Figure 3
shows these normalized timings when measuring the cost of a butterfly in
cycles instead of nanoseconds.
is not a power of two. Figure 2 shows
the resulting normalized timings. In addition, Figure 3
shows these normalized timings when measuring the cost of a butterfly in
cycles instead of nanoseconds.
From Figure 3, we can read off that a doubled SIMD width
indeed makes the implementation approximately twice as fast on x86-based
architectures. Although Apple's M1 and M3 chips only support 128-bit
wide SIMD, they actually behave more like CPUs with 256-bit wide SIMD.
This is probably due to the fact that Apple chips provide four instead
of two FMA units, which potentially doubles the instruction-level
parallelism. For large  , the
M1 and M3 perform even better, thanks to a more efficient memory
hierarchy.
, the
M1 and M3 perform even better, thanks to a more efficient memory
hierarchy.
When multiplying the cost in cycles with the SIMD width 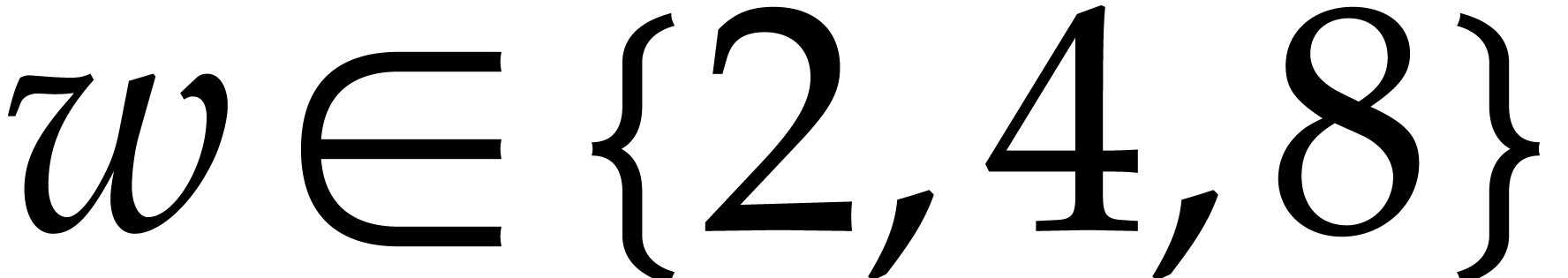 (while taking
(while taking 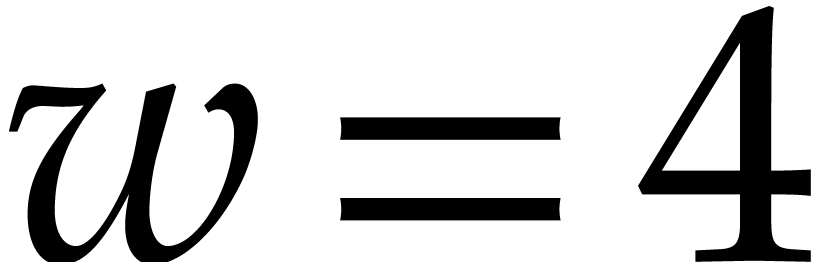 for the M1 and M3 chips in view of
what precedes), then we note that the cost of a single butterfly stays
between 5 and 8 cycles for
for the M1 and M3 chips in view of
what precedes), then we note that the cost of a single butterfly stays
between 5 and 8 cycles for 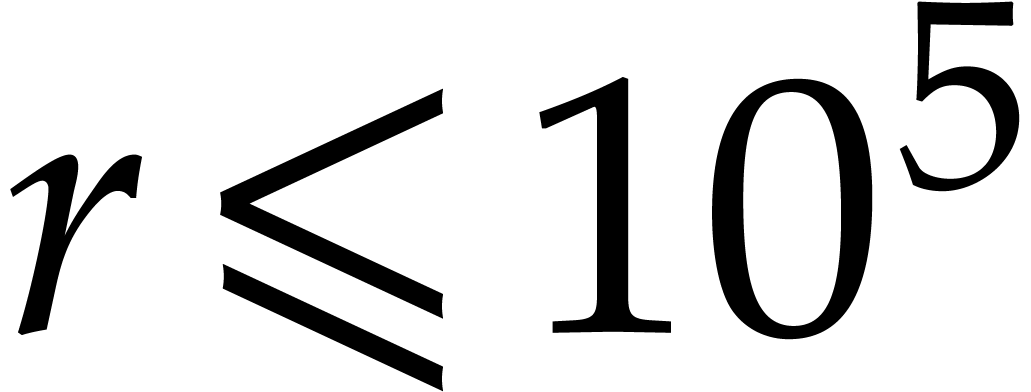 ;
this is similar to the performance of traditional scalar NTTs. For
larger orders
;
this is similar to the performance of traditional scalar NTTs. For
larger orders  , the cost on
x86-based platforms slowly increases to 12 cycles per butterfly (and
even to 15 cycles per butterfly for the Xeon W system and
, the cost on
x86-based platforms slowly increases to 12 cycles per butterfly (and
even to 15 cycles per butterfly for the Xeon W system and 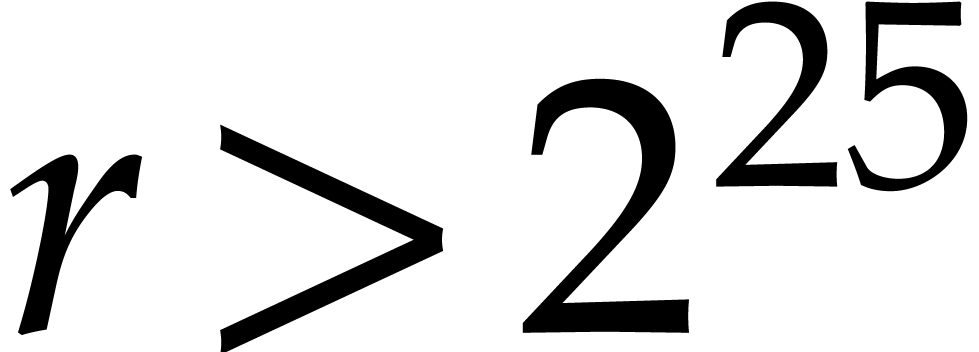 , but we recall that our implementation was not
optimized as heavily in this range).
, but we recall that our implementation was not
optimized as heavily in this range).
We also note the somewhat irregular behavior of the graphs in Figures 2 and 3, with discrepancies as large as 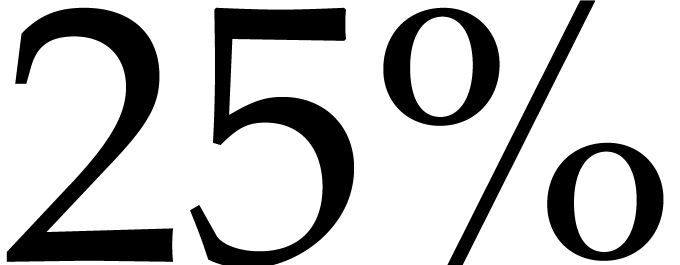 for close orders
for close orders  .
This is not due to inaccurate or irreproducible timings: it
turns out that the efficiency of the generated codelets is highly
dependent on the combinatorics of the divisors of
.
This is not due to inaccurate or irreproducible timings: it
turns out that the efficiency of the generated codelets is highly
dependent on the combinatorics of the divisors of  . In particular, if
. In particular, if  is a
power of two, then the “pool of available strategies” is
somewhat smaller than if
is a
power of two, then the “pool of available strategies” is
somewhat smaller than if  is divisible by a few
powers of
is divisible by a few
powers of  . Consequently, the
average costs in cycles tend to be slightly higher for power of two
lengths. When using NTTs as the workhorse of evaluation-interpolation
strategies (e.g. for integer multiplication), then it may
be interesting to use truncated Fourier transforms (TFTs) from [15,
20]: this should allow us to smooth out the graphs from
Figures 2 and 3, and benefit from the best
possible NTTs for close orders
. Consequently, the
average costs in cycles tend to be slightly higher for power of two
lengths. When using NTTs as the workhorse of evaluation-interpolation
strategies (e.g. for integer multiplication), then it may
be interesting to use truncated Fourier transforms (TFTs) from [15,
20]: this should allow us to smooth out the graphs from
Figures 2 and 3, and benefit from the best
possible NTTs for close orders 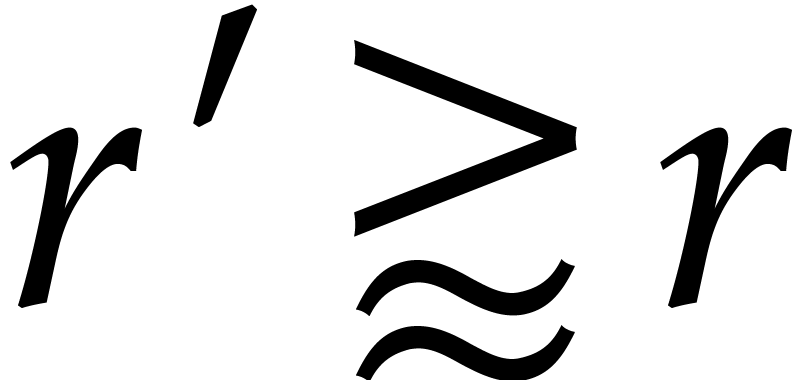 .
.
 |
 |
Figure 3. Variant of Figure 2 when using the cycle time as a unit instead of nanoseconds. |
We also compared our new algorithm to the one from [
13
]. For this purpose, we slightly adapted the companion C code from [
13
] to work also on M1 and M3 platforms and to support orders
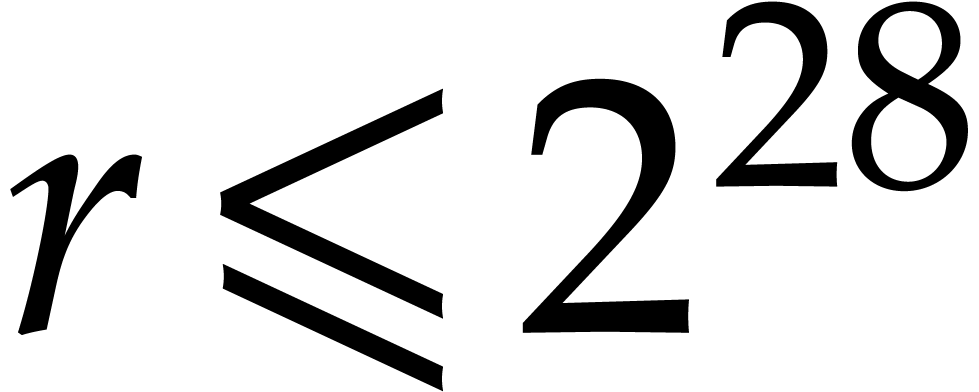 .
The timings for both implementations are shown in Table
3
. We recall that the algorithm from [
13
] uses a 62 bit prime and unsigned integer arithmetic, instead of a 49
bit prime and double precision floating point arithmetic. We have also
indicated the appropriately rescaled timings.
.
The timings for both implementations are shown in Table
3
. We recall that the algorithm from [
13
] uses a 62 bit prime and unsigned integer arithmetic, instead of a 49
bit prime and double precision floating point arithmetic. We have also
indicated the appropriately rescaled timings.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 3. Comparison of the
number of clock cycles per butterfly between our new
implementation and the implementation from [13].
We recall that the implementation from [13]
uses a prime |
In the previous subsection, we explored the cost of computing a single
NTT of order  over
over 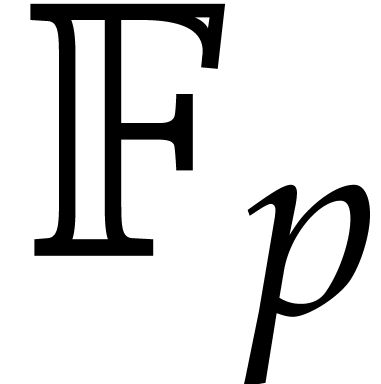 ,
while exploiting SIMD support in the processor. However, in order to
fully benefit from hardware SIMD support of width
,
while exploiting SIMD support in the processor. However, in order to
fully benefit from hardware SIMD support of width 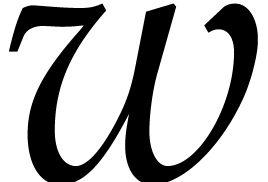 , it is better to compute
, it is better to compute 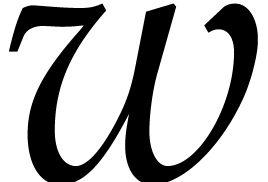 NTTs in parallel, as a single NTT of order
NTTs in parallel, as a single NTT of order  over
over
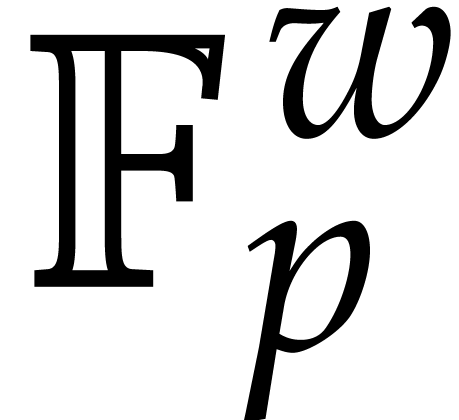 . Here
. Here 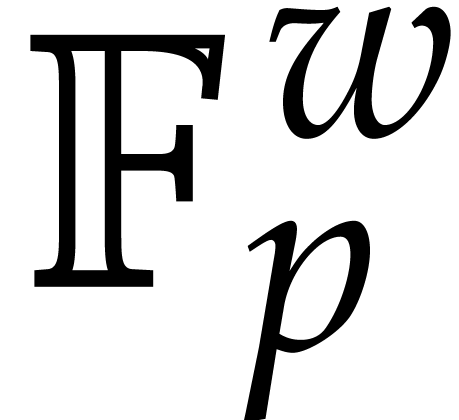 stands for the set of SIMD vectors of length
stands for the set of SIMD vectors of length 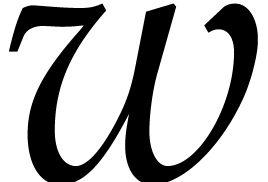 over
over 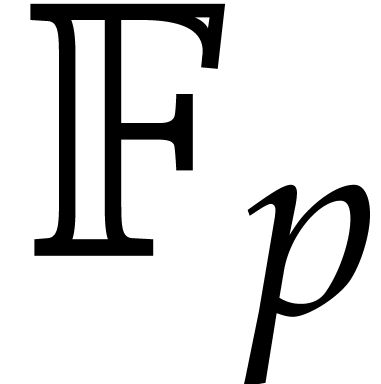 . Such a vector fits
exactly into a single hardware SIMD register. We will say that we are in
pure SIMD mode when we can compute
. Such a vector fits
exactly into a single hardware SIMD register. We will say that we are in
pure SIMD mode when we can compute 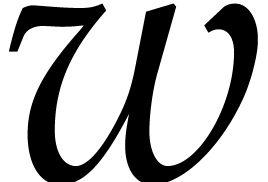 NTTs
in parallel in this way. This typically happens when we need to compute
many NTTs (e.g. when doing an integer matrix product as in
[13]), in chunks of
NTTs
in parallel in this way. This typically happens when we need to compute
many NTTs (e.g. when doing an integer matrix product as in
[13]), in chunks of 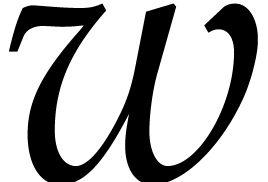 NTTs at a time.
By contrast, we are in thwarted SIMD mode if we want to compute
a single or less than
NTTs at a time.
By contrast, we are in thwarted SIMD mode if we want to compute
a single or less than 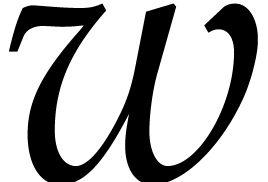 NTTs, as in the previous
subsection. Although this mode may still benefit from SIMD arithmetic,
this typically requires non-trivial data rearrangements as described in
section 4.4.
NTTs, as in the previous
subsection. Although this mode may still benefit from SIMD arithmetic,
this typically requires non-trivial data rearrangements as described in
section 4.4.
In order to compare the pure and thwarted modes, it is useful to compare the following three costs:
the cost of a single NTT of length  over
over
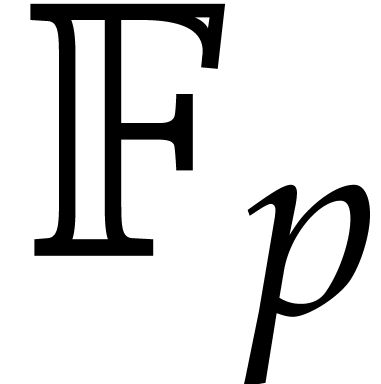 ,
,
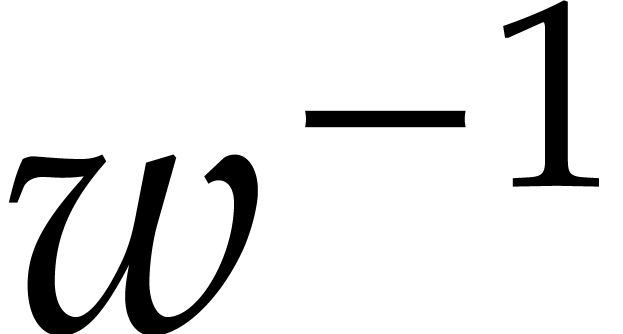 times the cost of
times the cost of  NTTs of length
NTTs of length  over
over  , and
, and
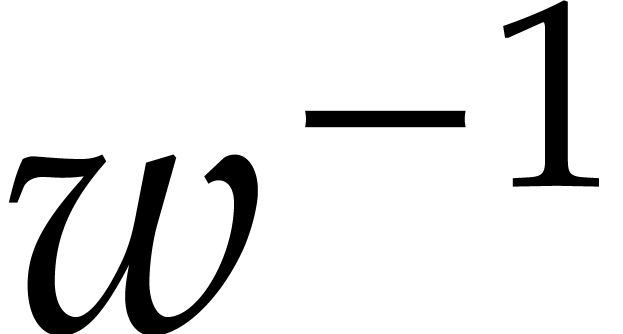 times the cost of a single NTT of length
times the cost of a single NTT of length
 over
over 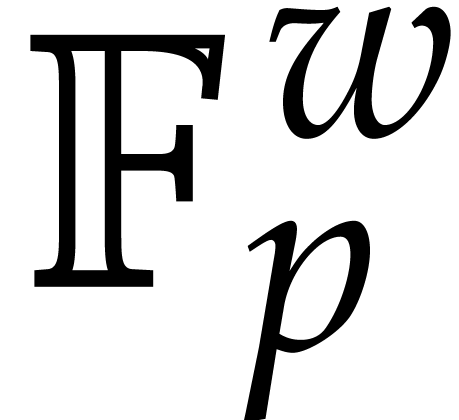 .
.
Although the first two costs ought to be similar most of the time, this
is not necessarily the case when
 is close to one of the (L1, L2, L3,
.
.
.
) cache sizes. In Table
4
, we show a detailed comparison of these costs for power of two lengths.
The overhead of thwarted with respect to pure SIMD is most important for
small orders
is close to one of the (L1, L2, L3,
.
.
.
) cache sizes. In Table
4
, we show a detailed comparison of these costs for power of two lengths.
The overhead of thwarted with respect to pure SIMD is most important for
small orders
 .
.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The main focus of this paper has been on an almost optimal
implementation of the NTT using SIMD double precision arithmetic, but in
the mono-threaded case. Naturally, we were curious about the performance
of our work when using multiple threads. In this last subsection, we
report on some preliminary experiments, while emphasizing that this is
work in progress which has not yet benefited from a similar level of
optimization. We recompiled
Before measuring the thread efficiency of our implementation, it is useful to analyze the maximal theoretical speed-up that multi-threading may provide on our testing platforms. For this, we created a simple loop that calls many times an empty function, and measured the speed-up when executing this loop in a multi-threaded fashion. The results have been reported in Table 5. For the x86-based platforms, we note that the number of logical threads is twice as high as the number of physical threads, due to hyperthreading. It turns out that our simple loop does benefit from hyperthreading, but that this is less likely to happen for highly optimized HPC code like our NTTs. For the M1 and M3 processors, efficiency cores tend to be much slower than performance cores, with similar pitfalls as in the case of hyperthreading. Note that the observed speed-ups always decreased when using a number of threads that exceeds the maximal number of logical threads for the platform.
For our main experiments, the number of threads  is fixed for each individual timing. The main codelets that benefit from
multi-threaded execution are of the form
is fixed for each individual timing. The main codelets that benefit from
multi-threaded execution are of the form 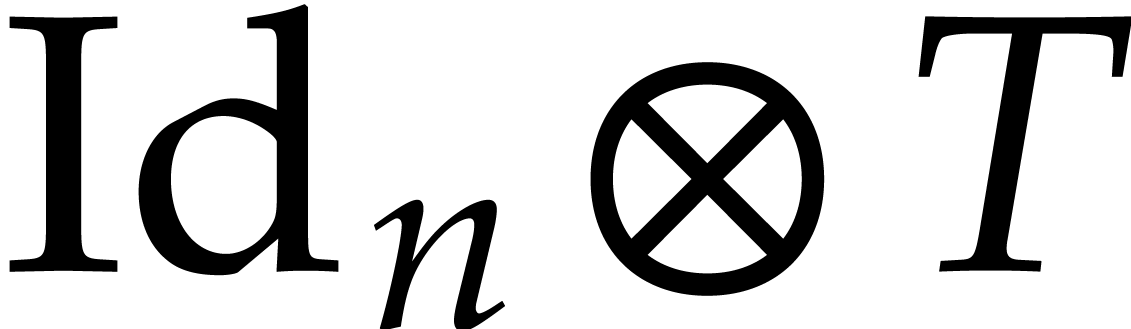 or
or 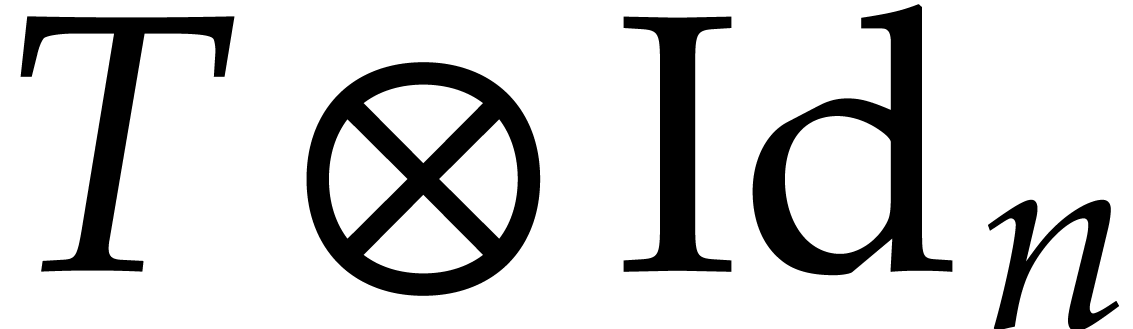 for some other codelet
for some other codelet  and
some large integer
and
some large integer 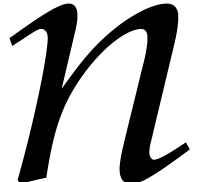 . For a
parameter
. For a
parameter  (that we call the flooding
factor), let us write
(that we call the flooding
factor), let us write 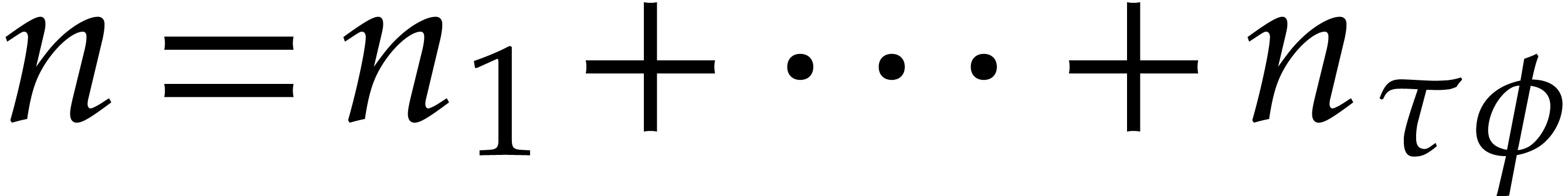 with
with  . Now we subdivide the execution of, say,
. Now we subdivide the execution of, say, 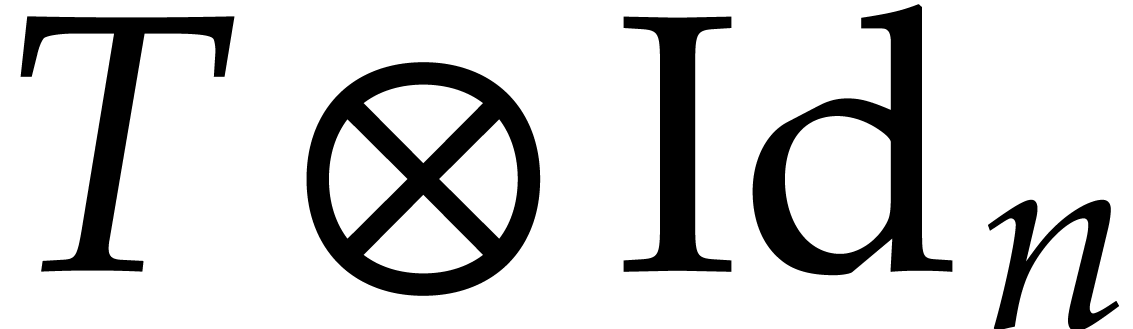 into the execution of chunks
into the execution of chunks 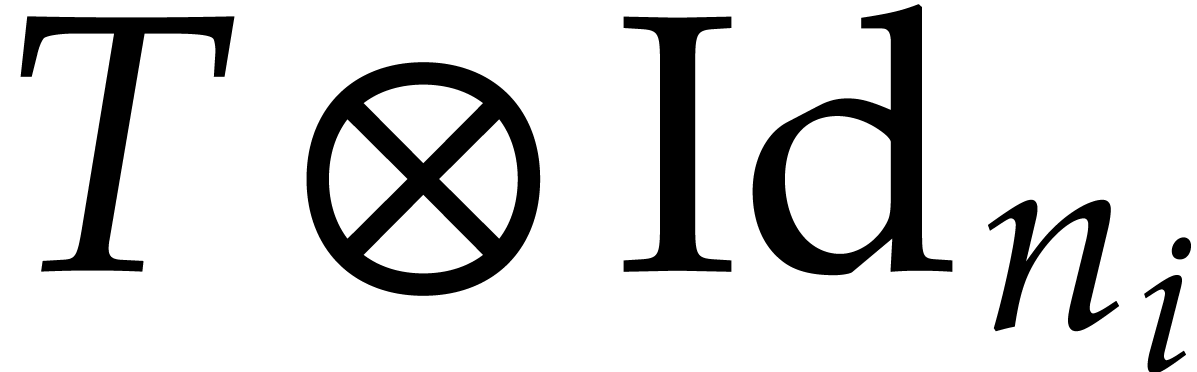 for
for  . These chunks are
executed by our
. These chunks are
executed by our  threads using the work stealing
paradigm. In our codelet factory, the most appropriate flooding factor
threads using the work stealing
paradigm. In our codelet factory, the most appropriate flooding factor
 for given
for given 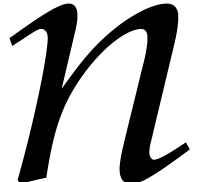 and
and  is determined dynamically.
is determined dynamically.
The first scenario we tested is that of a single NTT of length
 ,
while using
,
while using
 threads. For each platform, we investigate three values for
threads. For each platform, we investigate three values for
 :
the number of physical or performance cores, the number of logical or
performance plus efficiency cores, and an intermediate value. The
resulting timings are shown in Table
6
. We observed a large variance, especially on x86 platforms. We consider
the speed-ups on the m1 and m3 platforms to be reasonably satisfactory
for a first implementation. The timings for the other platform are far
from optimal. We omitted the results for the zen4 platform, since they
were so absurd that they require further investigation.
:
the number of physical or performance cores, the number of logical or
performance plus efficiency cores, and an intermediate value. The
resulting timings are shown in Table
6
. We observed a large variance, especially on x86 platforms. We consider
the speed-ups on the m1 and m3 platforms to be reasonably satisfactory
for a first implementation. The timings for the other platform are far
from optimal. We omitted the results for the zen4 platform, since they
were so absurd that they require further investigation.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The second scenario is when we wish to compute a large number
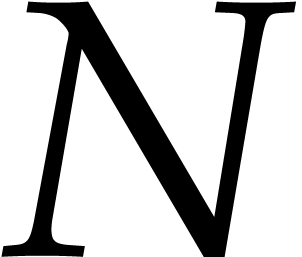 of NTTs of the same order
of NTTs of the same order
 .
This is similar to the pure SIMD mode that we investigated in
subsection
5.2
. We use a similar work stealing approach as above. Each individual
thread repeatedly computes NTTs of order
.
This is similar to the pure SIMD mode that we investigated in
subsection
5.2
. We use a similar work stealing approach as above. Each individual
thread repeatedly computes NTTs of order
 over
over
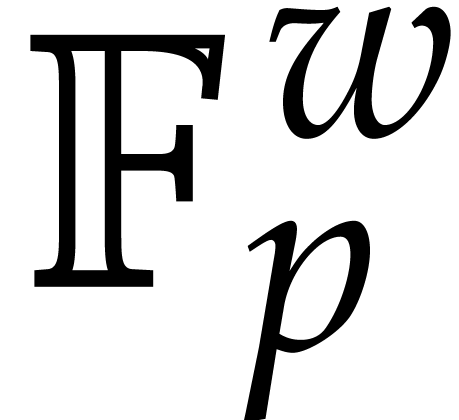 .
In Table
7
, we reported detailed timings in the single case when
.
In Table
7
, we reported detailed timings in the single case when
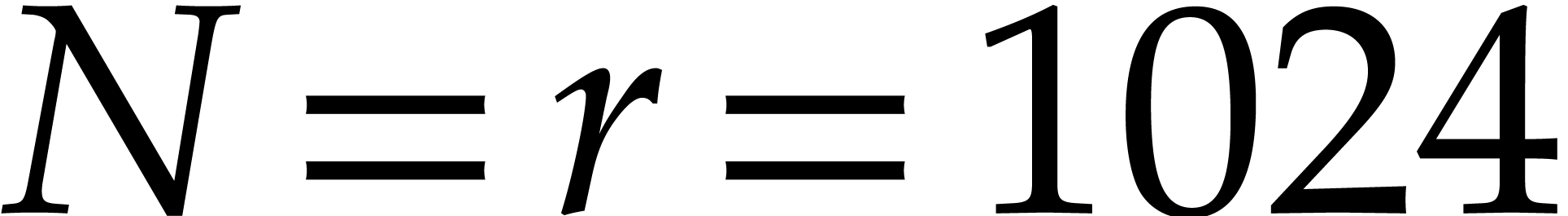 and only for the m3 platform. The table also indicates the best
flooding factor
and only for the m3 platform. The table also indicates the best
flooding factor
 as a function of the number of threads
as a function of the number of threads
 .
.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 7. Speed-ups on an M3
processor for |
ANSI/IEEE. IEEE standard for binary floating-point arithmetic. Technical Report, ANSI/IEEE, New York, 2008. ANSI-IEEE Standard 754-2008. Revision of IEEE 754-1985, approved on June 12, 2008 by IEEE Standards Board.
J. Bradbury, N. Drucker, and M. Hillenbrand. NTT software optimization using an extended Harvey butterfly. Cryptology ePrint Archive, Paper 2021/1396, 2021. https://eprint.iacr.org/2021/1396.
P. Bürgisser, M. Clausen, and M. A. Shokrollahi. Algebraic complexity theory. Springer-Verlag, Berlin, 1997.
J. W. Cooley and J. W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Comput., 19:297–301, 1965.
J.-G. Dumas, P. Giorgi, and C. Pernet. FFPACK: finite field linear algebra package. In J. Schicho, editor, Proceedings of the 2004 International Symposium on Symbolic and Algebraic Computation, ISSAC '04, pages 119–126. New York, NY, USA, 2004. ACM.
J.-G. Dumas, P. Giorgi, and C. Pernet. Dense linear algebra over word-size prime fields: the FFLAS and FFPACK packages. ACM Trans. Math. Softw., 35(3):19–1, 2008.
P. Fortin, A. Fleury, F. Lemaire, and M. Monagan. High-performance SIMD modular arithmetic for polynomial evaluation. Concurr. Comput. Pract. Exp., 33(16):e6270, 2021.
M. Frigo. A fast Fourier transform compiler. In Proceedings of the ACM SIGPLAN 1999 Conference on Programming Language Design and Implementation, PLDI '99, pages 169–180. New York, NY, USA, 1999. ACM.
M. Frigo and S. G. Johnson. The design and implementation of FFTW3. Proc. IEEE, 93(2):216–231, 2005.
S. Fu, N. Zhang, and F. Franchetti. Accelerating high-precision number theoretic transforms using Intel AVX-512. 2024. https://spiral.ece.cmu.edu/pub-spiral/pubfile/PACT_2024_AVX_371.pdf.
I. J. Good. The interaction algorithm and practical Fourier analysis. J. R. Stat. Soc. Series B, 20(2):361–372, 1958.
W. Hart and the FLINT Team. FLINT: Fast Library for Number Theory. From 2008. Software available at http://www.flintlib.org.
D. Harvey. Faster arithmetic for number-theoretic transforms. J. Symbolic Comput., 60:113–119, 2014.
M. T. Heideman, D. H. Johnson, and C. S. Burrus. Gauss and the history of the fast Fourier transform. Arch. Hist. Exact Sci., 34(3):265–277, 1985.
J. van der Hoeven. The truncated Fourier transform and applications. In J. Gutierrez, editor, Proceedings of the 2004 International Symposium on Symbolic and Algebraic Computation, ISSAC '04, pages 290–296. New York, NY, USA, 2004. ACM.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
J. van der Hoeven and G. Lecerf. Mathemagix User Guide. HAL, 2013. https://hal.archives-ouvertes.fr/hal-00785549.
J. van der Hoeven and G. Lecerf. Evaluating straight-line programs over balls. In P. Montuschi, M. Schulte, J. Hormigo, S. Oberman, and N. Revol, editors, 2016 IEEE 23nd Symposium on Computer Arithmetic, pages 142–149. IEEE, 2016.
J. van der Hoeven, G. Lecerf, and G. Quintin. Modular SIMD arithmetic in Mathemagix. ACM Trans. Math. Softw., 43(1):5–1, 2016.
R. Larrieu. The truncated Fourier transform for mixed radices. In M. Burr, editor, Proceedings of the 2017 ACM International Symposium on Symbolic and Algebraic Computation, ISSAC '17, pages 261–268. New York, NY, USA, 2017. ACM.
J. M. Pollard. The fast Fourier transform in a finite field. Math. Comput., 25(114):365–374, 1971.
M. Püschel, J. M. F. Moura, J. Johnson, D. Padua, M. Veloso, B. Singer, J. Xiong, F. Franchetti, A. Gacic, Y. Voronenko, K. Chen, R. W. Johnson, and N. Rizzolo. SPIRAL: code generation for DSP transforms. Proc. IEEE, 93(2):232–275, 2005. Special issue on “Program Generation, Optimization, and Adaptation”.
A. Schönhage and V. Strassen. Schnelle Multiplikation großer Zahlen. Computing, 7:281–292, 1971.
D. Takahashi. An implementation of parallel number-theoretic transform using Intel AVX-512 instructions. In F. Boulier, M. England, T. M. Sadykov, and E. V. Vorozhtsov, editors, Computer Algebra in Scientific Computing. CASC 2022., volume 13366 of Lect. Notes Comput. Sci., pages 318–332. Springer, Cham, 2022.
N. Zhang, A. Ebel, N. Neda, P. Brinich, B. Reynwar, A. G. Schmidt, M. Franusich, J. Johnson, B. Reagen, and F. Franchetti. Generating high-performance number theoretic transform implementations for vector architectures. In 2023 IEEE High Performance Extreme Computing Conference (HPEC), pages 1–7. Los Alamitos, CA, USA, 2023. IEEE.