Computing one billion roots using the tangent Graeffe method Joris van der Hoevenabc, Michael Monaganad a. Department of Mathematics Simon Fraser University 8888 University Drive Burnaby, British Columbia V5A 1S6, Canada b. CNRS, École polytechnique, Institut Polytechnique de Paris Laboratoire d'informatique de l'École polytechnique (LIX, UMR 7161) 1, rue Honoré d'Estienne d'Orves Bâtiment Alan Turing, CS35003 91120 Palaiseau, France c. Email: vdhoeven@lix.polytechnique.fr d. Email: mmonagan@cecm.sfu.ca November 3, 2023

1.Introduction

Consider a polynomial function over a field given through a black box capable of evaluating at points in . The problem of sparse interpolation is to recover the representation of in its usual form, as a linear combination

(1)

of monomials . One popular approach to sparse interpolation is to evaluate at points in a geometric progression. This approach goes back to work of Prony in the eighteen's century [41] and became well known after Ben-Or and Tiwari's seminal paper [2]. It has widely been used in computer algebra, both in theory [7, 30, 32-35, 39] and in practice [11, 14, 24, 25, 29, 31]; see [43] for a nice survey.

More precisely, if a bound for the number of terms is known, then we first evaluate at pairwise distinct points , where and for all . The generating function of the evaluations at satisfies the identity

where and is of degree . The rational function can be recovered from using fast Padé approximation [6, 37]. For well chosen points , it is often possible to recover the exponents from the values . If the exponents are known, then the coefficients can also be recovered using a transposed version of fast multipoint interpolation [5, 7]. This leaves us with the question how to compute the roots of in an efficient way.

For practical applications in computer algebra, we usually have , in which case it is most efficient to use a multi-modular strategy. This means that we rather work with coefficients in a finite field , where is a prime number that we are free to choose. It is well known that polynomial arithmetic over can be implemented most efficiently using FFTs when the order of the multiplicative group is smooth. In practice, this prompts us to choose of the form for some small and such that fits into a machine word.

The traditional way to compute roots of polynomials over finite fields is using Cantor and Zassenhaus' method [8]. In [19, 20], alternative algorithms were proposed for our case of interest when is smooth. The fastest algorithm was based on the tangent Graeffe transform and it gains a factor with respect to Cantor–Zassenhaus' method. The aim of the present paper is to report on a parallel implementation of this new algorithm and on a few improvements that allow for a further constant speed-up. A preliminary version of this paper was published at ICMS 2020 [27]. The new contributions in this paper include the theoretical contributions in sections 3.4, 3.5, 3.6 and 3.7, the implementation details in section 4 and the (parallel) timing results in section 5.

In section 2, we start by recalling generalities about the Graeffe transform and the heuristic root finding method based on the tangent Graeffe transform from [19]. In section 3, we present the main new theoretical improvements, which all rely on optimizations in the FFT-model for fast polynomial arithmetic. Our contributions are threefold:

• In the FFT-model, one backward transform out of four can be saved for Graeffe transforms of order two (see section 3.2).

• When composing a large number of Graeffe transforms of order two, “FFT caching” [3] can be used to gain another factor of (see section 3.3).

  All optimizations still apply in the TFT model, which can save a factor between one and two, depending on the number of roots (see section 3.5).

In section 3.4 we also indicate how to generalize our methods to Graeffe transforms of general orders. In section 3.7 we determine how much faster the tangent Graeffe algorithm is than the Cantor–Zassenhaus algorithm. To do this, we determine the constant factors in the complexities of both algorithms, under the assumption that arithmetic in is done using FFT-based algorithms.

We first implemented a sequential version of the tangent Graeffe method in C, with the optimizations from sections 3.2 and 3.3; see [27]. Section 4 is devoted to a more elaborate parallel implementation in Cilk C. We detail how we parallelized the different steps of the algorithm, and how we organized the memory so we could factor a polynomial of degree over , for . We believe we are the first to factor such large polynomials. Our code is available here

In the last section 5, we give timings. We used a multi-core computer with two 10 core Intel Xeon E5 2680 v2 CPUs and 128 gigabytes of RAM. The above factorization of a polynomial of degree then takes just under 4,000 seconds on 10 cores and uses 121 gigabytes of RAM.

2.Root finding using the tangent Graeffe transform

Let be an effective field. Throughout the paper, time complexities count arithmetic operations in the field and space complexities are for elements of . We use to denote the time for multiplying two polynomials in of degree . We make the customary assumption that is a non-decreasing function that tends to infinity.

We will chiefly be interested in the case when , where is a prime of the form with small. We call primes of this form smooth Fourier primes. Some examples that we use and their bit lengths are as follows:

For and of this form and , we have , by using FFT-multiplication.

Let be a polynomial of degree in which has distinct roots in . The tangent Graeffe algorithm computes the roots of . The cost of the algorithm depends on a parameter with . The parameter determines what proportion of the roots are found in each iteration of the algorithm. The space complexity of the algorithm is and the average time complexity is

Theoretically, choosing yields the best time complexity. However, because we want to factor polynomials with very large , our implementation chooses a smaller in the interval to save space. For the time complexity is

In this section, we recall the tangent Graeffe algorithm from [19]. In the next section, we will analyze its complexity in the FFT-model and present several improvements.

2.1.Graeffe transforms

Let be a general field. The traditional Graeffe transform of a monic polynomial of degree is the unique polynomial of degree such that

(2)

If is monic, then so is . If splits over into linear factors , then one has

More generally, given , we define the Graeffe transform of order to be the polynomial of degree given by

If , then

If is a primitive -th root of unity in , then we also have

(3)

If , then we finally have

(4)

2.2.Root finding using tangent Graeffe transforms

Let be a formal indeterminate with . Elements in are called tangent numbers. They are of the form with and basic arithmetic operations go as follows:

Now let be a monic polynomial of degree that splits over :

where are pairwise distinct. Then the tangent deformation satisfies

The definitions from the previous subsection readily extend to coefficients in instead of . Given , we call the tangent Graeffe transform of of order . We have

where

Now assume that we have an efficient way to determine the roots of . For some polynomial , we may decompose

For any root of , we then have

Whenever happens to be a single root of , it follows that

If , this finally allows us to recover as

2.3.Heuristic root finding over smooth finite fields

Assume now that is a finite field, where is a prime number of the form for some small . Assume also that is a primitive element of order for the multiplicative group of .

Let be as in the previous subsection. The tangent Graeffe method can be used to efficiently compute those of for which is a single root of . In order to guarantee that there are a sufficient number of such roots, we first replace by for a random shift , and use the following heuristic:

H

For any subset of cardinality and any , there exist at least elements such that contains at least elements.

For a random shift and any , the assumption ensures with probability at least that has at least single roots.

Now take to be the largest power of two such that and let . By construction, note that . The roots of are all -th roots of unity in the set , where . We may thus determine them by evaluating at for . Since , this can be done efficiently using a discrete Fourier transform. Combined with the tangent Graeffe method from the previous subsection, this leads to the following probabilistic algorithm for root finding:

Algorithm 1 Input: of degree and only order one factors, Output: the set of roots of Note: time complexities for the main steps are indicated on the right

If then return Let be largest such that and let Pick at random and compute Compute For , set Let be of order and write Compute , , and for If , then set , else set For do If and , then set Compute Compute Recursively determine the set of roots of and return

Remark 1. To compute we may use , which requires three polynomial multiplications in of degree . In total, step 5 therefore performs such multiplications. We discuss how to perform step 5 efficiently in the FFT model in section 3.

Remark 2. For practical implementations, one may vary the threshold for and the resulting threshold for . For larger values of , the computations of the DFTs in step 6 get more expensive, but the proportion of single roots goes up, so more roots are determined at each iteration. From an asymptotic complexity perspective, it would be best to take . In practice, we actually preferred to take the lower threshold , because the constant factor of our implementation of step 6 (based on Bluestein's algorithm [4]) is significant with respect to our highly optimized implementation of the tangent Graeffe method. A second reason we prefer of size instead of is that the total space used by the algorithm is linear in .

Remark 3. For the application to sparse interpolation, it is possible to further speed up step 5 for the top-level iteration, which is the most expensive step. More precisely, for a polynomial with terms, the idea is to take and of order instead of for some constant with . This reduces (and the cost of the top-level iteration) by a factor of . For the recursive calls, we still need to work with a primitive root of unity of order and random shifts.

3.Computing Graeffe transforms

3.1.Reminders about discrete Fourier transforms

Assume that is invertible in and let be a primitive -th root of unity. Consider a polynomial . Then the discrete Fourier transform (DFT) of order of the sequence is defined by

We will write for the cost of one discrete Fourier transform in terms of the number of operations in . We assume that . For any , we have

(5)

If is invertible in , then it follows that . The costs of direct and inverse transforms therefore coincide up to a factor .

If is composite, , and , then we have

			(6)

This shows that a DFT of length reduces to transforms of length plus transforms of length plus multiplications in :

In particular, if , then .

It is sometimes convenient to apply DFTs directly to polynomials as well; for this reason, we also define . Given two polynomials with , we may then compute the product using

In particular, we obtain , where we recall that stands for the cost of multiplying two polynomials of degree .

Remark 4. In Algorithm 1, we note that step 6 comes down to the computation of three DFTs of length . Since is a power of two, this length is of the form for some . In view of (6), we may therefore reduce step 6 to DFTs of length plus DFTs of length . If is very small, then we may use a naive implementation for DFTs of length . In general, one may use Bluestein's algorithm [4] to reduce the computation of a DFT of length into the computation of a product in , which can in turn be computed using FFT-multiplication and three DFTs of length a larger power of two.

3.2.Graeffe transforms of order two

Let be a field with a primitive -th root of unity . Let be a polynomial of degree . Then the relation (2) yields

(7)

For any , we further note that

(8)

so can be obtained from using transpositions of elements in . Concerning the inverse transform, we also note that

for . Plugging this into (7), we conclude that

This leads to the following algorithm for the computation of :

Algorithm 2 Input: with and a primitive -th root of unity Output:

Compute For , compute Return

Proposition 5. Let be a primitive -th root of unity in and assume that is invertible in . Given a monic polynomial with , we can compute in time

Proof. We have already explained the correctness of Algorithm 2. Step 1 requires one forward DFT of length and cost . Step 2 can be done in linear time . Step 3 requires one inverse DFT of length and cost . The total cost of Algorithm 2 is therefore .

Remark 6. In terms of the complexity of multiplication, we obtain This gives a improvement over the previously best known bound that was used in [19]. Note that the best known algorithm for computing squares of polynomials of degree is . It would be interesting to know whether squares can also be computed in time .

3.3.Graeffe transforms of power of two orders

In view of (4), Graeffe transforms of power of two orders can be computed using

(9)

Now assume that we computed the first Graeffe transform using Algorithm 2 and that we wish to apply a second Graeffe transform to the result. Then we note that

(10)

is already known for . We can use this to accelerate step 1 of the second application of Algorithm 2. Indeed, in view of (6) for and , we have

(11)

for . In order to exploit this idea in a recursive fashion, it is useful to modify Algorithm 2 so as to include in the input and in the output. This leads to the following algorithm:

Algorithm 3 Input: with , a primitive -th root of unity , and Output: and

Set Set For , compute Return and

Proposition 7. Let be a primitive -th root of unity in and assume that is invertible in . Given a monic polynomial with and , we can compute in time

Proof. It suffices to compute and then to apply Algorithm 3 recursively, times. Every application of Algorithm 3 now takes operations in , whence the claimed complexity bound.

Remark 8. In [19], Graeffe transforms of order were directly computed using the formula (9), using operations in . The new algorithm is twice as fast for large .

3.4.Graeffe transforms of arbitrary smooth orders

The algorithms from subsections 3.2 and 3.3 readily generalize to Graeffe transforms of order for arbitrary , provided that we have an -th root of unity . For convenience of the reader, we specified the generalization of Algorithm 3 below, together with the resulting complexity bounds.

Algorithm 4 Input: with , , a primitive -th root of unity , and Output: and

Set For , set For , compute Return and

Proposition 9. Let be a primitive -th root of unity in , where is invertible in . Given a monic polynomial with and , we can compute in time

Proof. Straightforward generalization of Proposition 7.

Corollary 10. Let be a primitive -th root of unity in , where are invertible in . Given a monic polynomial with and , we can compute in time

Proof. Direct consequence of (4).

Remark 11. In our application to root finding, we are interested in the efficient computation of Graeffe transforms of high order . In terms of the size of , it is instructive to observe that the “average cost”

is minimal for . This suggests that it might be interesting to use Graeffe transforms of order three whenever possible. In the application of Algorithm 1, this would lead us to take primes of the form , with small and close to . This still allows us to use radix 2 FFTs, while at the same time benefitting from radix 3 Graeffe transforms.

3.5.Truncated Fourier transforms

If is a fixed finite field, then DFTs are most efficient for sizes that divide . For our root finding application, it is often convenient to take , in which case should be a power of two or three times a power of two. The truncated Fourier transform was developed for the multiplication of polynomials such that the degree of the product does not have a nice size of this type. It turns out that we may also use it for the efficient computation of Graeffe transforms of polynomials of arbitrary degrees. Moreover, the optimizations from the previous subsections still apply.

Let us briefly describe how the truncated Fourier transform can be used for the computation of Graeffe transforms of power of two orders. With the notations from subsections 3.2 and 3.3, we assume that is a power of two as well and that we wish to compute the Graeffe transform of a polynomial of degree with . Let denote the reversal of a binary number of bits. For instance, and . Then the truncated Fourier of at order is defined by

It has been shown in [22] that and can both be computed in time . More generally, for direct transforms, one may compute

in time , whenever . For generalizations to arbitrary radices, we refer to [36].

Taking , we note that

for . This provides us with the required counterpart of (8) for retrieving efficiently from . The relation (10) also has a natural counterpart:

for . This leads to the following refinement of Algorithm 3:

Algorithm 5 Input: with , a primitive -th root of unity , and Output: and

Set Set For , compute Return and

Proposition 12. Let be a primitive -th root of unity in , where , and assume that is invertible in . Given a monic polynomial with and , we can compute in time

Proof. Straightforward adaptation of the proof of Proposition 7, while using [22].

3.6.Taylor shifts

In step 3 of Algorithm 1, we still need an algorithm to compute the Taylor shift . If the characteristic of exceeds , then it is (not so) well known [1, Lemma 3] that this can be done in time , using the following reduction to a single polynomial multiplication of degree :

Algorithm 6 Input: of degree and Output:

Return

It is interesting to observe that Taylor shifts can still be computed in time in small characteristic, as follows:

Algorithm 7 Input: of degree and Output:

Define for where Rewrite with for For , replace Return

3.7.Comparison with Cantor–Zassenhaus' algorithm

We give a theoretical comparison of Algorithm 1 with the Cantor–Zassenhaus algorithm [8], where both algorithms have been optimized in the “FFT model” [44]. For this comparison, it is convenient to replace the “worst case” heuristic H by a more empirical assumption. More precisely, if we take for , then the expected proportion of single roots is (see e.g. [23]). This expected proportion is indeed observed in practice: see Table 3. In Algorithm 1, we took .

Proposition 13. Consider Algorithm 1 with the modification that we take instead of for some fixed . Then the expected cost of Algorithm 1 is bounded by

(12)

Proof. We first analyze the cost of step 9. Let be the cost of the polynomial multiplications in the product tree algorithm, where is the size of . Exercise 10.3 of [17] shows that . The recurrence for is for and . Solving this recurrence while using the assumption that is non-decreasing yields . Now let be the successive sizes of for the recursive calls of the algorithm, so that . Thus the cost of all executions of step 9 is . Using again that is non-decreasing, we have .

Let us next analyze the cost of the other steps until step 10 inclusive, but without the recursive calls in step 11. Set .

• To compute in step 3 costs ; using [1, Lemma 3].

• Step 4 takes to compute .

• By Proposition 7, step 5 costs , which is equivalent to .

• Step 6 is using [4].

• The division in step 10 is using fast division [17].

Altogether, the cost of these steps is .

We now need to account for the cost of the recursive calls in step 11. For the tangent Graeffe algorithm will, under our hypothesis, on average, obtain at least of the roots in each recursive call, leaving slightly less than of them to be found. Since and is non-decreasing, the total cost of Algorithm 1 is therefore as claimed.

Remark 14. In the asymptotic region where , the bound (12) reduces to . Since we may pick as large as we want, the complexity of Algorithm 1 is then bounded by for any .

Assume from now on that we are in the asymptotic region where . Then Remark 14 shows that the cost of the tangent Graeffe method is for any . The bottleneck of Cantor–Zassenhaus' algorithm in this region is modular exponentiation, which accounts for a total cost of [17]. We wish to determine the constant factor in order to give an accurate comparison between the two algorithms. Given polynomials with , one modular exponentiation does modular squarings

in a loop. However, in the first few iterations, the degree of is less then so no division is needed. The number of steps with divisions is . Using fast division [17], the remainder can be computed with two multiplications of size assuming the required inverse of , the reciprocal of , is precomputed. In the FFT model, one forward transform of may be saved and the forward transform of the inverse of may be cached [44]. This costs , i.e. at least , since . The cost of the top-level modular exponentiation is therefore equivalent to . Using a similar recursion as for in the proof of Proposition 13, the total cost of all modular compositions in CZ is equivalent to (strictly speaking, this is really an upper bound; but we indeed obtain an equivalence for common values of , such as or ). Altogether, this means that the tangent Graeffe algorithm is about times faster than Cantor–Zassenhaus.

Remark 15. In practice, we often have , and the complexity of Cantor–Zassenhaus also involves another term due to gcd computations. The corresponding constant factor is fairly high, which makes the tangent Graeffe algorithm even more favorable in this asymptotic region.

4.Implementing the tangent Graeffe algorithm

For our implementation, we have been pursuing three goals. We first wanted to reimplement the tangent Graeffe algorithm from scratch using FFT-based polynomial arithmetic and compare it with a good implementation of the Cantor–Zassenhaus algorithm. Second, we wanted to factor a polynomial of degree . For this, it is important to consider space efficiency. Third, we wanted to parallelize the tangent Graeffe algorithm for a multi-core computer. Unlike the Cantor–Zassenhaus algorithm, the tangent Graeffe algorithm is gcd-free which makes it easier to parallelize. We first tried parallelizing only the FFTs that appear in steps 3, 5, 6, 9, and 10 of Algorithm 1 to see if this alone is sufficient to obtain good parallel speedup. It isn't.

Our main practical challenge is, however, space, not time. For a 64 bit prime , and an input polynomial of degree , the input polynomial and output roots alone need 16 gigabytes of storage. Our first implementation exceeded the virtual memory of our machine which has 128 gigabytes of RAM plus 240 gigabytes of SSD swap space.

To reduce space we use in-place algorithms. In-place algorithms do not allocate new space (memory). They work in the input and output space and we allow them to be given additional working space. To parallelize a recursive in-place algorithm, we must partition the input, output and the temporary memory (if any) for recursive parallel calls. Our design is such that the space used does not increase with more cores. We refer the reader to Giorgi, Grene and Roche [18] for examples of in-place serial algorithms in computer algebra and a bibliography.

4.1.Parallelizing the FFTs

Number theoretic FFTs over were first introduced by Pollard [40]. Let us first explain how we parallelized such FFTs using Cilk C. The strategy is classical, but it is convenient to detail it here, since we use the same strategy for parallelizing the other steps in Algorithm 1. Cilk [16] was designed to support the parallelization of recursive divide and conquer algorithms like the FFT for multi-core computers. To parallelize recursive algorithms using Cilk we first modify the code so that the memory locations that are updated in the recursive calls do not overlap.

Figure 1 shows our sequential C code for two radix 2 FFTs that we use. In the vernacular fft1 is known as the “decimation-in-time” FFT and fft2 as the “decimation-in-frequency” FFT. We refer the reader to Chu and George [9] for a discussion of the two FFTs. We note that Geddes, Czapor, and Labahn present only fft1 in their book on computer algebra [10], whereas von zur Gathen and Gerhard present only fft2 [17].

In the code in Figure 1, LONG is a macro for long long int, a 64 bit signed integer. The C functions addmod, submod, mulmod implement in respectively for . For multiplication in we use Roman Pearce's implementation of Möller and Granlund [38]. The input array of size is the main input to and output from the FFT. The input is an array of size containing powers of , a primitive -th root of unity in . We precompute

Precomputing saves asymptotically half of the multiplications in the FFT. For , fft1 and fft2 both do multiplications. Duplicating of powers of means all recursive calls in fft1 and fft2 access sequentially.

Codes like these where the recursive calls update separate parts of the array are easy to parallelize using Cilk. To parallelize fft1 in Cilk C we first make a new subroutine fft1cilk which executes the two recursive calls in parallel. In Figure 2 the two Cilk spawn directives do this. For small we do not want to start two new processes because of the cost of process management overhead. Thus for , fft1cilk calls fft1 which runs sequentially.

   cilk void block1( LONG n2, LONG *A, LONG b, LONG W, LONG p ) {
      LONG i,s,t;
      for( i=0; i<b; i++ ) {
         s = A[i];
         t = mulmod(W[i],A[n2+i],p);
         A[   i] = addmod(s,t,p);
         A[n2+i] = submod(s,t,p);
      }
      return;
   }
   #define B 65536
   #define FFTCUTOFF 32768
   cilk void fft1cilk( LONG *A, LONG n, LONG *W, LONG p ) {
      LONG q,r,i;
      if( n<=FFTCUTOFF ) { fft1(A,n,W,p); return; }
      spawn fft1cilk( A,    n2, W+n2, p );
      spawn fft1cilk( A+n2, n2, W+n2, p );
      sync; // wait for the two fft1cilk calls to finish
      n2 = n/2; q = n2/B; r = n2-q*B;
      for( i=0; i<q; i++ ) spawn block1( n2, A+i*B, B, W+i*B, p );
      if( r>0 ) spawn block1( n2, A+q*B, r, W+q*B, p );
      sync; // wait for all blocks to complete
      return;
   }

To obtain good parallel speedup we also need to parallelize the for loop in fft1 because it does multiplications out of a total of multiplications. We do this by executing large contiguous blocks of the loop in parallel. We could use Cilk's parallel for loop construct cilk_for and let Cilk determine what block size to use but this does not allow us to tune the block size for best performance. Instead we choose a blocksize B and parallelize the loop explicitly as shown in Figure 2. To get best performance, we reduced B until the Cilk process overhead takes more than 1% say of the total time for the FFT. This yields good parallel speedup for many cores when is large.

An alternative way to parallelize an FFT is to use a recursive FFT for creating parallel tasks for large as we have but use a non-recursive FFT for smaller . These and other strategies for parallelizing the FFT for multi-core computers are discussed in [9, 13].

4.2.Step 4: the Taylor shift

Steps 1, 2, 3, 5, and 6 of Algorithm 6 require time. Steps 3 and 6 involve inverses in which, because they require many divisions, are relatively very expensive. All the inverses can be replaced with multiplications as follows. After computing ! in step 1, we compute the inverse . For steps 3 and 6, we run the loop backwards and multiply by to get the next inverse as follows.

for( i=d; i>1; i-- ) { Pi[i] = mulmod(Pi[i],finv,p); finv = mulmod(finv,i,p); }

We parallelized only the polynomial multiplication in step 4. To multiply two polynomials of degree at most our FFT multiplication needs three arrays , , and of size where satisfies .

The data in Table 4 shows that the best parallel speedup for step 3 is 4.12. A factor of 4.12 on 10 cores is not very good and due to the fact that we did not paralellize steps 1, 3 and 6 which involve , and multiplications in , respectively. We did not do this because computing is not a bottleneck of Algorithm 1.

Of course, it is possible to paralellize steps 1, 3 and 6. For blocks of size we would need to compute the factorials in parallel. We could do this by first computing partial products in parallel and then compute . Now we can execute step 1 in blocks in parallel. Next we would compute the inverses of so we can execute steps 3 and 6 in parallel.

4.3.Step 5: the tangent Graeffe loop

Step 5 of Algorithm 1 is the main computation in Algorithm 1. It has complexity . We successfully parallelized the FFTs and all loops in blocks except the following data movement:

  for( i=0; i<n/2; i++ ) A[i] = A[2*i];   // compress
  for( i=0; i<n/2; i++ ) A[n/2+i] = A[i]; // duplicate

We tried parallelizing the above code by moving the even entries of into a temporary array , in blocks, in parallel, then copying them back to , twice, in blocks, in parallel. On 6 cores, the parallel code is slower than the serial code so we have left this pure data movement not parallelized.

4.4.Step 6: parallelizing the evaluations

Each of the three evaluations , and for in step 6 of Algorithm 1 can be done using the Bluestein transform [4] in time. Although step 6 does not dominate the time complexity it needs the most space. We need at least units of storage to store the values of , and . For and , the requirement implies . This is gigabytes. We chose to save half of this by choosing instead. This increases the time a little (see Table 3) because we obtain a smaller portion of the roots at each recursive call of Algorithm 1.

The Bluestein transform does one multiplication of two polynomials of degree plus work. For a multiplication of degree we need an FFT of size and our FFT uses units of temporary storage. For , and we have so we need 192 gigabytes. We do not evaluate of , and in parallel as that would triple the 192 gigabytes to 576 gigabytes.

For with small, because for some , we can save time and space by applying (6). We do DFTs of size , in blocks, in parallel, then multiplications by powers of , in blocks in parallel, followed by FFTs of size which we do in parallel. This reduces the time for an evaluation by a factor between 6 and 12 since we replace 3 FFTs of size where by FFTs of size which is equivalent to one FFT of size .

We need an additional units of storage for storing the inputs of size for the FFTs and an additional units for the required array. Thus applying (6) reduces the temporary storage needed from units to units. For and , with , this is gigabytes of temporary storage instead of 192 gigabytes.

We can now state the total storage needed by our implementation of Algorithm 1. We need to store the input of degree and an array of size for the output roots . We need space for three temporary polynomials of degree . Including the memory for step 6, our implementation uses units, which, for , and is 121 gigabytes.

4.5.Step 9: parallelizing the product tree multiplication algorithm

In step 9 we need to expand the polynomial . Let and suppose is stored in an array of size and in an array of size . We can compute in using fast multiplication and divide and conquer. The obvious way to do this is to split the roots in into two equal size groups, of size and , then recursively compute

and finally multiply by using fast multiplication for large . In the literature this approach is called the product tree multiplication algorithm; see [17, Algorithm 10.3]. In Appendix A, the function mult implements the product tree algorithm in Magma. We use it to create the input polynomial to get Magma timings. However, mult is inefficient because all recursive calls allocate new memory for the inputs and products in the product tree.

For large products we use our FFT based polynomial multiplication FFTpolmul64s which needs a temporary array of size units of storage where . We do not want to allocate space for in each recursive call. Fortunately, is a power of 2 so we can divide into two halves and execute the two recursive calls in parallel using the two halves of . But the size of plus is . They don't fit in . The remedy is to note that and are both monic, so we do not need to store their leading coefficients.

Figure 3 presents C code for an in-place product tree algorithm which uses the input space of size , the output space of size and a temporary array of size for all polynomial multiplications in the product tree. Our solution splits asymmetrically into a “large” set of size where and a “small” set of size . For example, for we use and . To multiply we first recursively compute in and in . We copy the contents of to the input array and we compute the product in . For small , we use polmul64s an in-place multiplication with quadratic complexity. Then we add and to so that contains . Thus we have the following result.

In Figure 3 , because the memory for , and in the two recursive calls is separated, we may execute the two recursive calls to treemul in parallel. This also holds recursively, so we can keep executing recursive calls in parallel, which is ideal for Cilk. In our parallel implementation of treemul we parallelize the two recursive calls if . We also parallelize FFTmul64s and the FFTs (both the subalgorithms and their calls inside treemul ). We do not parallelize the two polynomial additions.

#include <stdlib.h>
#define LONG long long int

// Input polynomials a and b mod p of degree da and db respectively.
// Output array c is space for the sum a + b mod p (product a b mod p)
LONG poladd64s( LONG *a, LONG *b, LONG *c, LONG da, LONG db, LONG p );
LONG polmul64s( LONG *a, LONG *b, LONG *c, LONG da, LONG db, LONG p );
LONG FFTmul64s( LONG *a, LONG *b, LONG *c, LONG da, LONG db, LONG *T, LONG p );

void treemul( LONG *S, LONG n, LONG *Q, LONG *T, LONG p ) {
  LONG i,m,d;
  if( n==1 ) { Q[0] = submodp(0,S[0],p); return; }
  for( m=1; 2*m<n; m=2*m );
  d = n-m;
  treemul(S,m,Q,T,p);  // compute a(x)-x^m in Q[0..m-1] using S[0..m-1] and T[0..3m-1]
  treemul(S+m,d,Q+m,T+3*m,p);  // and b(x)-x^d in Q[m..n-1] using S[m..n-1] and T[3m..]
  for( i=0; i<n; i++ ) S[i] = Q[i];   // S = [a0,a1,…,am-1,b0,b1,…,bd-1]
  if( d<10 ) polmul64s(S,S+m,Q,m-1,d-1,p); // in-place classical multiplication
  else FFTmul64s(S,S+m,Q,m-1,d-1,T,p);  // FFT multiplication using T[0..6m-1]
  Q[n-1] = 0;
  poladd64s(Q+d,S,Q+d,m-1,m-1,p);    // add x^m (b-x^d) to Q[d..n-1]
  poladd64s(Q+m,S+m,Q+m,d-1,d-1,p);  // add x^d (a-x^m) to Q[m..n-1]
  // Q[n] = 1; is okay for this sequential code but not for a parallel code
  return;
}

LONG *array64s(LONG n); // return an array of size n
void treeproduct( LONG *S, LONG n, LONG *Q, LONG p ) {
  // S is an array of size n and Q of size n+1
  LONG N,*T;
  for( N=1; N<n; N=2*N );
  T = array64s(3*N);
  treemul(S,n,Q,T,p);
  free(T);
  Q[n] = 1;
  return;
}

Remark 17. By dividing the input asymmetrically so that the FFTs are fully utilized, we gain upto a factor of 2 in speed when is much smaller then . Thus we get the benefit of using a truncated FFT [22] for the polynomial multiplications without using it.

Remark 18. If we insert the statement Q[n] = 1; before the return statement in treemul, then the sequential code will still work. However, since both recursive calls update Q[n], the memory is no longer separated, so the two recursive calls cannot be executed in parallel.

5.Timing Results

We want to compare our new tangent Graeffe implementation with an implementation of the Cantor–Zassenhaus algorithm [8] which uses fast polynomial arithmetic. One of the best implementations that we know of is Magma's Factorize command. Magma uses an implementation of Shoup's work [44] by Allan Steel [45]. For of degree with distinct roots in , Magma uses the Cantor–Zassenhaus algorithm which has time complexity .

The timings in Tables 1 and 2 were obtained on an 8 core Intel Xeon E5-2660 CPU which runs at at 2.2 GHz base and 3.0 GHz turbo. The input polynomials in Tables 1 and 2 of degree were created with random distinct roots in . Table 1 is for the 28.8 bit prime and Table 2 is for the 62.4 bit prime .

The timings in column NewTG are for our C implementation of Algorithm 1 with the parameter chosen in . The timings in column Magma are for the Factorize command for Magma version V2.25-5. Magma code for creating and factoring it is given in Appendix A. We note that older versions of Magma have a quadratic sub-algorithm; this problem was fixed by Steel for version V2.25-5. We also note that Magma has faster arithmetic for primes .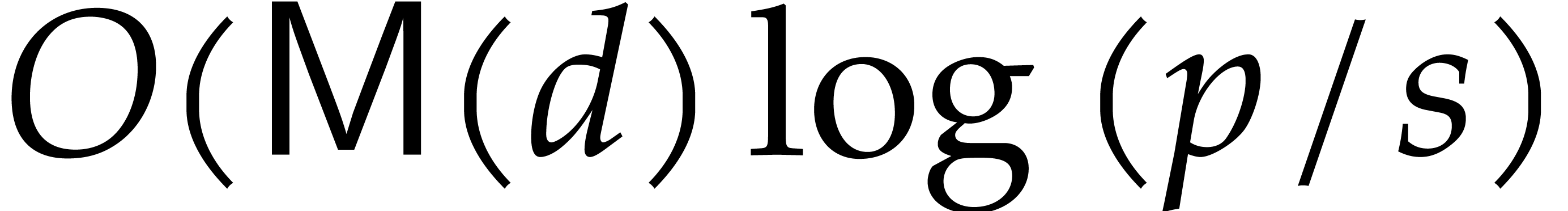

The columns in Tables 1 and 2 labeled Step5, Step6, Step9, and report the time spent in steps 5 , 6 , 9 , and 10 , respectively, in the top level call of Algorithm 1 . They show that initially step 5 , which costs , dominates the cost of steps 6 and 9 which cost and respectively. As increases, so does , and the number of iterations of step 5 in Algorithm 1 drops; ultimately, the computation of the product in step 9 dominates.

Magma NewTG Step5 Step6 Step9 first %roots FFT 3.38s 0.07s 0.02s 0.01s 0.01s 0.00s 0.05s 75.0% 14 0.41ms 7.34s 0.17s 0.05s 0.03s 0.01s 0.01s 0.11s 74.4% 13 0.86ms 16.96s 0.32s 0.10s 0.05s 0.03s 0.02s 0.23s 75.1% 12 1.84ms 39.05s 0.64s 0.20s 0.10s 0.08s 0.03s 0.46s 75.7% 11 3.85ms 88.65s 1.21s 0.37s 0.19s 0.17s 0.06s 0.92s 75.3% 10 7.93ms 203.0s 2.54s 0.71s 0.43s 0.41s 0.12s 1.94s 75.2% 9 16.8ms 462.5s 5.16s 1.34s 0.90s 0.91s 0.25s 3.94s 75.1% 8 35.2ms 1050.s 10.5s 2.51s 1.84s 2.03s 0.52s 8.01s 75.2% 7 74.7ms 2407.s 21.2s 4.55s 3.80s 4.41s 1.11s 16.1s 75.4% 6 157.5ms — 43.0s 8.14s 8.06s 9.62s 2.31s 32.7s 75.7% 5 333.7ms — 86.2s 13.7s 16.3s 21.1s 4.91s 64.4s 76.3% 4 697.5ms — 174.0s 22.4s 33.5s 46.3s 10.2s 132.s 77.5% 3 1460.ms — 342.8s 32.2s 67.2s 99.7s 20.7s 258.s 80.1% 2 3055.ms

Table 1. Timings in CPU seconds for using .

Magma NewTG Step5 Step6 Step9 first %roots FFT 18.94s 0.21s 0.08s 0.04s 0.01s 0.00s 0.14s 69.8% 48 0.41ms 44.07s 0.46s 0.18s 0.08s 0.01s 0.01s 0.30s 68.8% 47 0.86ms 103.5s 0.98s 0.37s 0.17s 0.03s 0.02s 0.64s 69.2% 46 1.83ms 234.2s 2.06s 0.77s 0.35s 0.08s 0.05s 1.33s 68.9% 45 3.83ms 534.5s 4.15s 1.54s 0.72s 0.17s 0.08s 2.67s 69.2% 44 7.93ms 1219.s 8.90s 3.24s 1.53s 0.38s 0.18s 5.70s 69.2% 43 16.6ms 2809.s 18.69s 6.75s 3.24s 0.87s 0.40s 12.0s 69.2% 42 35.2ms 6428.s 38.76s 13.9s 6.79s 1.93s 0.85s 24.9s 69.2% 41 74.7ms — 79.88s 28.3s 14.2s 4.11s 1.77s 51.4s 69.2% 40 157.5ms — 165.5s 57.6s 29.8s 9.01s 3.71s 106.s 69.2% 39 333.5ms — 335.4s 115.s 60.8s 19.2s 7.66s 215.s 69.2% 38 697.5ms — 702.5s 238.s 129.s 42.4s 16.3s 451.s 69.2% 37 1460.ms

Table 2. Timings in CPU seconds for using .

The column labeled %roots reports the percentage of the roots found in the first tangent Graeffe application. Column is the value of in step 5. Step 5 does FFTs of size . Column FFT reports the time for one of those FFTs. For example, in Table 2, for , 13.9 seconds was spent in step 5. The code did FFTs of size which took seconds.

The timings in Table 1 show that the tangent Graeffe method is 100 times faster than Magma's implementation of Cantor–Zassenhaus at degree . For the larger prime in Table 2 the tangent Graeffe method is 166 times faster at degree .

Table 3 shows the effect of different choices for the parameter in Algorithm 1. If the roots of under the Graeffe transform are uniformly distributed among the -th roots of unity, then the proportion of them that remain distinct is . Thus doubling increases the proportion of roots found at each recursive level of Algorithm 1, which saves time, but it also doubles the cost of the evaluations in step 6. Recall that the theoretically optimal performance is obtained by taking , where we note that and for .

Column gives the expected proportion of roots that will be found. Column %roots is the actual percentage of roots found by Algorithm 1 . Columns Step5, Step6, and Total are the time in step 5 , step 6 , and the total time. The data in Table 3 suggests choosing to minimize time. For the algorithm is expected to obtain between and of the roots. Our actual choice of increases the time by about 10% but saves a factor of 2 in space.

Choice of %roots Step5 Step6 Total %roots Step5 Step6 Total 0.432 43.3% 27.6s 0.54s 64.53s 0.586 58.5% 27.4s 0.96s 67.10s 0.657 65.7% 27.3s 1.16s 44.71s 0.766 76.5% 26.7s 2.39s 47.17s 0.811 81.1% 26.7s 2.40s 39.86s 0.875 87.4% 25.9s 4.92s 43.14s 0.900 90.0% 25.9s 4.92s 39.47s 0.935 93.5% 24.0s 10.2s 45.34s 0.949 94.9% 25.2s 10.3s 43.16s 0.967 96.7% 24.4s 21.2s 55.12s

Table 3. Tangent Graeffe timings in CPU seconds for for various .

Table 4 shows the results for our parallel implementation including timings for of degree . The timings in Table 4 were obtained on a server with a 10 core Intel E5 2680 v2 CPU with 128 gigabytes of RAM running at 3.0GHz base, 3.6GHz turbo. The input polynomial is created as before by choosing random distinct values from with .

cores Step3 Step5 Step6 Step8 Step9 first Total Space 1 1.931 0.393 8.446 0.841 0.624 1.233 0.562 12.11 19.44 120 MiB 10 0.292 0.135 1.320 0.147 0.078 0.190 0.157 2.035 5.627 120 MiB speedup 6.61x 2.91x 6.40x 5.72x 8.00x 6.49x 3.58x 5.95x 3.45x 1 3.975 0.817 17.18 1.671 1.246 2.683 1.180 24.79 39.97 240 MiB 10 0.538 0.261 2.421 0.297 0.150 0.397 0.273 3.823 8.336 240 MiB speedup 7.39x 3.13x 7.10x 5.63s 8.31x 6.76x 4.32x 6.48x 4.79x 1 8.458 1.713 35.00 3.533 2.512 5.826 2.475 51.09 82.31 488 MiB 10 1.110 0.533 5.043 0.625 0.300 0.797 0.521 7.845 16.25 488 MiB speedup 7.62x 3.21x 6.94x 5.65x 8.37x 7.31x 4.75x 6.51x 5.07x 1 18.16 3.533 70.75 7.244 5.001 12.63 5.220 104.4 168.6 0.95 GiB 10 2.383 1.070 10.07 1.218 0.599 1.680 1.045 15.74 27.66 0.95 GiB speedup 7.62x 3.30x 7.03x 5.95x 8.35x 7.52x 5.00x 6.63x 6.10x 1 819.4 133.3 2316 274.2 157.2 574.0 203.4 3660 5815 30.3 GiB 10 102.7 37.49 319.7 45.75 18.54 74.29 38.50 536.1 850.4 30.3 GiB speedup 7.98x 3.56x 7.23x 5.99x 8.48x 7.73x 5.28x 6.83x 6.84x 1 1752 274.9 4631 566.6 316.7 1228 422.5 7442 11820 60.6 GiB 10 219.7 75.66 636.0 92.46 37.35 159.7 76.92 1082 1719.3 60.6 GiB speedup 7.79x 3.63x 7.28x 6.12x 8.48x 7.69x 5.49x 6.88x 6.88x 1 3739 645.2 10486 1423 682.6 2795.5 1017 17057 26889 121 GiB 10 465.2 156.5 1366 243.8 83.03 341.5s 180.7 2379 3714.7 121 GiB speedup 8.04x 4.12x 7.67x 5.88x 8.22x 8.19x 5.63x 7.17x 7.23x

Table 4. Real timings (in seconds) for using .

Timings in column are for computing the input polynomial using our in-place parallel product tree multiplication from section 3.4. The total time for computing the roots of is in column Total. Roughly speaking, our software takes 10 times longer to compute the roots of (less for larger ) than it does to create !

Timings in columns Step4, Step5, Step6, Step9, and are the times for those steps for the top-level call of Algorithm 1. Speedups are given for each computation. The reader can see that the parallel speedup is not as good for Step4 and the division . This is because we have only parallelized the FFTs in them; none of steps of linear cost are parallelized.

6.Conclusion

The motivation for our work is the problem of sparse polynomial interpolation where one seeks to recover the coefficients and monomials of a polynomial with terms from values of . The popular approach by Prony and Ben-Or–Tiwari needs only values of but it needs to factor a polynomial of degree which has distinct roots in . Using the Cantor–Zassenhaus (CZ) algorithm, computing the roots of takes time. Because this is the most expensive step in Ben-Or/Tiwari sparse interpolation, and because CZ does gcd computations which are difficult to parallelize, research in sparse interpolation has tried different approaches that do not require root finding.

If we choose the prime of the form with small, the new tangent Graeffe (TG) algorithm factors in time. This is faster than CZ, but the constants actually matter in practice. In this work we improved the main step of TG by a factor of 2 and we showed that for large , TG is faster than CZ by a factor of . Our new C implementation of TG is over 100 times faster than Magma's C implementation of CZ for on the tests we made. So TG really is a lot faster than CZ.

Another goal was to see if we could parallelize TG for multi-core computers. We found that it was not sufficient to only parallelize the underlying FFT. We also had to parallelize many sub-algorithms to get good parallel speedup. Here we contributed a new parallel in-place product tree algorithm. We were also successful in reducing the space needed so that we could compute the roots of of degree one billion on a 10 core computer with 128 gigabytes of RAM in about one hour. It should be possible to reduce the time further by using vectorization [12, 26]. The sequential implementation of the FFTs could also be further improved using techniques from [15, 42] and Harvey's approach for number theoretic FFTs [21].

Appendix A.Magma code

  p := 3*29*2^56+1;
  p := 7*2^26+1;
  Fp := FiniteField(p);
  R<x> := PolynomialRing(Fp);

  mult := function( L )
    n := #L;
    if n eq 1 then return x-L[1];
    else
       m := n div 2;
       f := $$( L[1..m] ) * $$( L[m+1..n] );
       return f;
    end if;
  end function;

  d := 2^12-1;
  S := { Random(Fp) : i in [1..d] };
  while #S lt d do S := S join { Random(Fp) : i in [1..d-#S] }; end while;
  #S;
  L := [ x : x in S ];
  time f := mult( L );
  time g := Factorization(f);

Bibliography