Optimizing the half-gcd
algorithm |
|
| December 23, 2022 |
|
 . This article has
been written using GNU TeXmacs [18].
. This article has
been written using GNU TeXmacs [18].
In this paper, we propose a carefully optimized “half-gcd” algorithm for polynomials. We achieve a constant speed-up with respect to previous work for the asymptotic time complexity. We also discuss special optimizations that are possible when polynomial multiplication is done using radix two FFTs. |
The computation of greatest common divisors is the key operation to be
optimized when implementing a package for rational number arithmetic.
For integers of small bit-length  ,
one may use Euclid's algorithm, which has a quadratic time complexity
,
one may use Euclid's algorithm, which has a quadratic time complexity
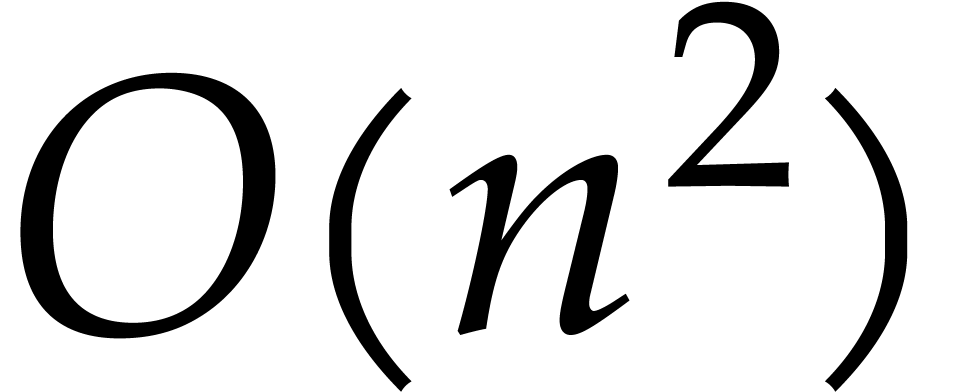 . Asymptotically faster
algorithms were first proposed by Knuth [20] and
Schönhage [29], based on earlier ideas by Lehmer [22]. Schönhage's algorithm has a logarithmic
. Asymptotically faster
algorithms were first proposed by Knuth [20] and
Schönhage [29], based on earlier ideas by Lehmer [22]. Schönhage's algorithm has a logarithmic  overhead with respect to integer multiplication, which is
believed to be asymptotically optimal. Many variants and improvements
have been proposed since, mainly aiming at faster practical
implementations [36, 32, 23, 26, 4, 27]. All these subquadratic
algorithms are based on a recursive reduction to half of the precision;
for this reason it is convenient to regroup them under the name
“half-gcd algorithms”.
overhead with respect to integer multiplication, which is
believed to be asymptotically optimal. Many variants and improvements
have been proposed since, mainly aiming at faster practical
implementations [36, 32, 23, 26, 4, 27]. All these subquadratic
algorithms are based on a recursive reduction to half of the precision;
for this reason it is convenient to regroup them under the name
“half-gcd algorithms”.
An analogous story can be told about the history of polynomial gcd computations. The polynomial counterpart of Euclid's algorithm was first described by Stevin [33, p. 241]. The first algorithms for polynomial half-gcds are due to Moenck [25] and Brent–Gustavson–Yun [5]; several variants have been developed since [35, 36, 4].
We refer to [10, chapter 11] for a gentle exposition of the
polynomial half-gcd algorithm. This exposition also contains a careful
analysis of the constant factor in the asymptotic time complexity. More
precisely, let 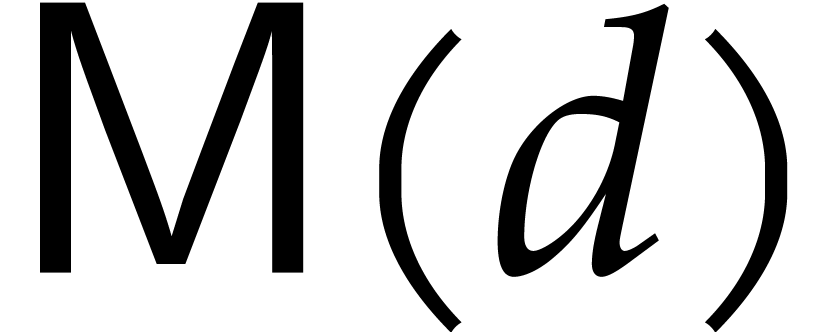 be the complexity to multiply two
polynomials of degree
be the complexity to multiply two
polynomials of degree 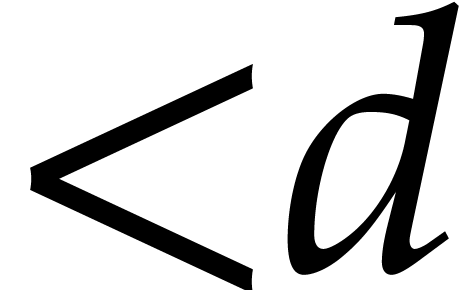 over an abstract effective
field
over an abstract effective
field  . Then the gcd of two
polynomials of degree
. Then the gcd of two
polynomials of degree 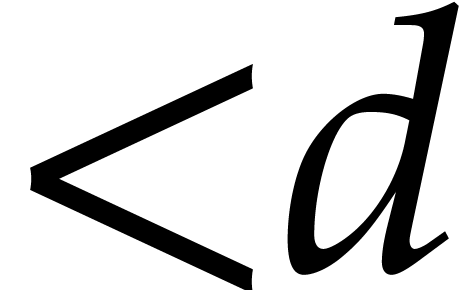 can be computed using
can be computed using 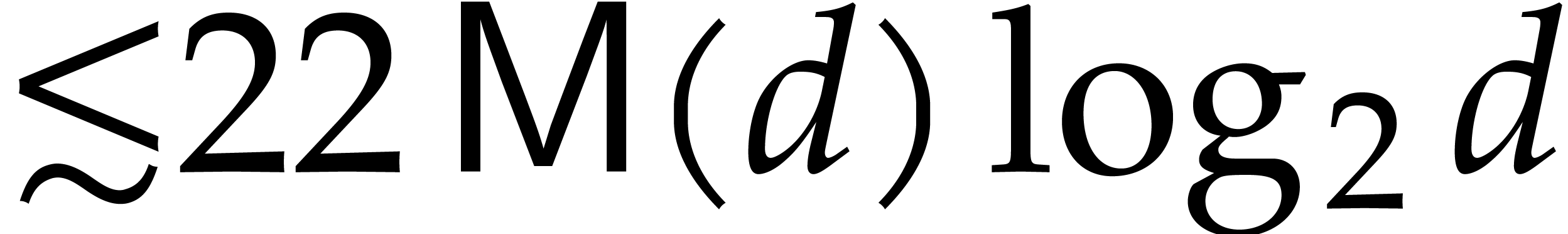 operations in
operations in  .
This complexity further drops to
.
This complexity further drops to 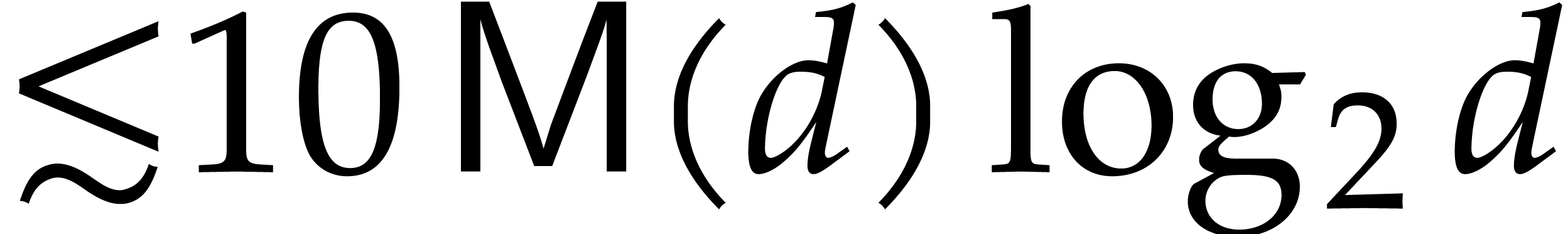 if the
corresponding Euclidean remainder sequence is “normal” (all
quotients in the ordinary Euclidean algorithm are of degree one). The
authors declare that they made no particular efforts to optimize these
constants
if the
corresponding Euclidean remainder sequence is “normal” (all
quotients in the ordinary Euclidean algorithm are of degree one). The
authors declare that they made no particular efforts to optimize these
constants 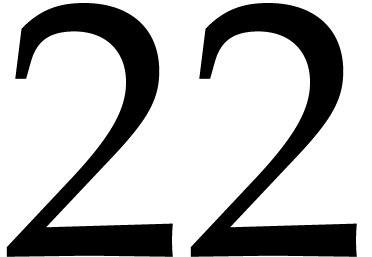 and
and  ;
in [10, Research problem 11.11], they ask the question how
far these constants can be lowered. This main goal of the present paper
is to make progress on this question.
;
in [10, Research problem 11.11], they ask the question how
far these constants can be lowered. This main goal of the present paper
is to make progress on this question.
One major motivation for optimizing constant factors in time complexity bounds is the development of faster implementations. Now practical algorithms for multiplying large polynomials usually rely on fast Fourier techniques. We will also investigate optimizations that are only possible when multiplications are done in this way. Indeed, this so-called FFT model allows for various specific optimizations that typically help to reduce constant factors. We refer to [3] for a nice survey of such tricks and mention NTL [31] as a software library that was early to exploit them in a systematic way.
A particularly favorable case is when the ground field  has primitive
has primitive  -th roots of
unity for all sufficiently large
-th roots of
unity for all sufficiently large  .
We will call this the “binary FFT model”. A good example is
the finite field
.
We will call this the “binary FFT model”. A good example is
the finite field  for a prime
for a prime 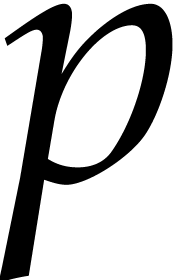 of the form
of the form 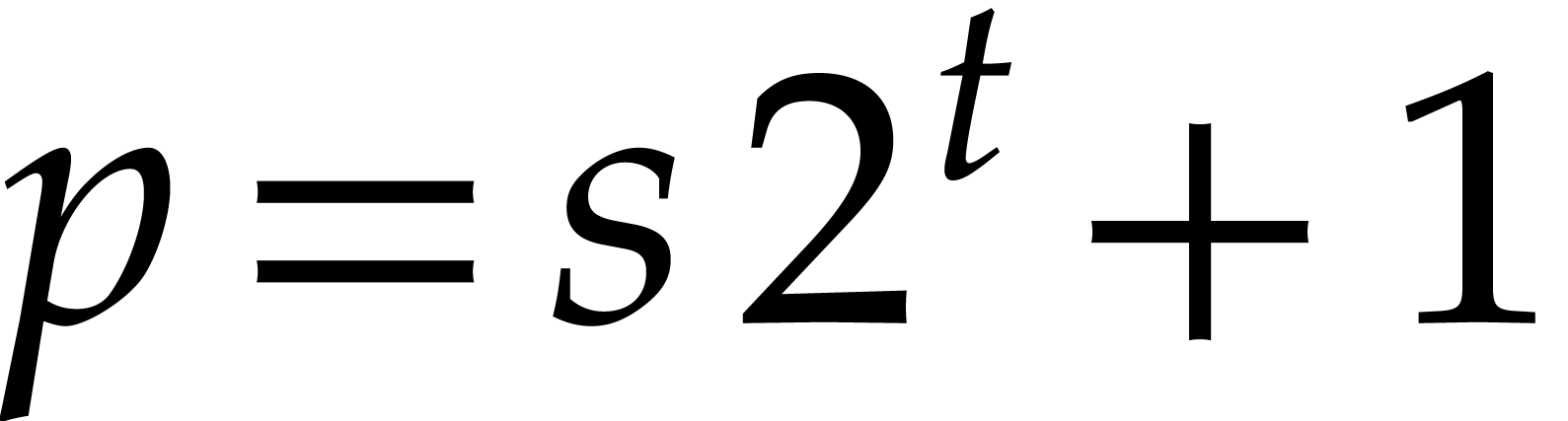 , where
, where  is large. Such finite fields arise naturally after modular
reduction, provided that
is large. Such finite fields arise naturally after modular
reduction, provided that 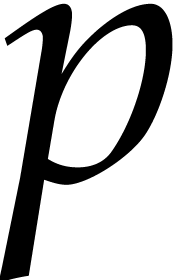 can be chosen freely.
The binary FFT model allows for additional tricks and is particularly
useful for dichotomic algorithms such as the half-gcd. We refer to
section 2 for those results that will be required in this
paper. Note that large polynomial multiplications over general finite
fields are fastest using FFT-based techniques, although one may not
necessarily use radix two FFTs; see [14, 15]
and references therein for the fastest current algorithms.
can be chosen freely.
The binary FFT model allows for additional tricks and is particularly
useful for dichotomic algorithms such as the half-gcd. We refer to
section 2 for those results that will be required in this
paper. Note that large polynomial multiplications over general finite
fields are fastest using FFT-based techniques, although one may not
necessarily use radix two FFTs; see [14, 15]
and references therein for the fastest current algorithms.
For convenience of the reader, we will first describe our new half gcd
algorithms in the normal case (see section 4). This will
allow us to avoid various technical complications and focus on the new
optimizations. The first idea behind our new half gcd is to make the
update step after the first recursive call particularly efficient, by
using a  matrix variant of the middle product
algorithm [12]. This leads to an algorithm of time
complexity
matrix variant of the middle product
algorithm [12]. This leads to an algorithm of time
complexity  in general and
in general and 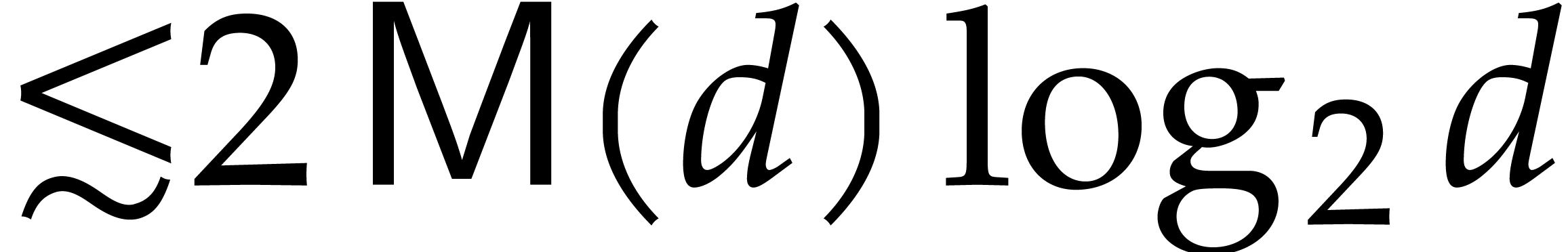 in the FFT model (Proposition 6). The second idea is to
combine this with known optimizations for the (binary) FFT model, such
as FFT doubling, FFT caching, and Harvey's variant of the middle product
[13]. In the binary FFT model, this allows us to compute
half gcds in time
in the FFT model (Proposition 6). The second idea is to
combine this with known optimizations for the (binary) FFT model, such
as FFT doubling, FFT caching, and Harvey's variant of the middle product
[13]. In the binary FFT model, this allows us to compute
half gcds in time 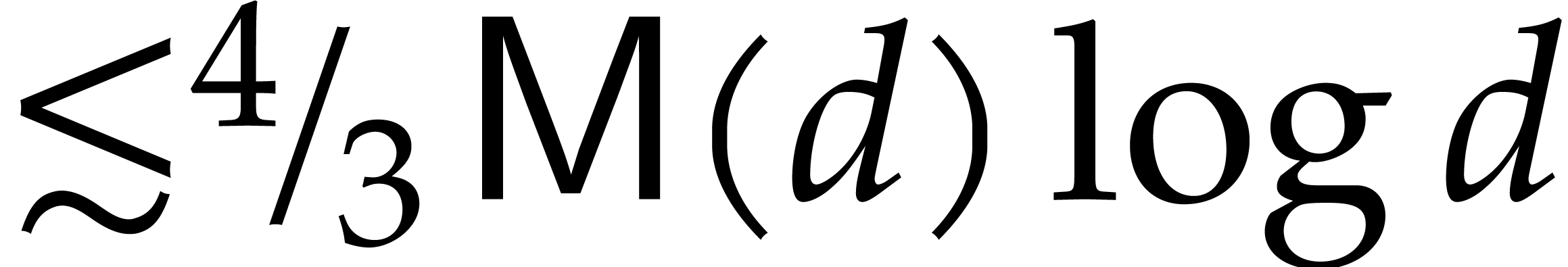 (Proposition 7
and Corollary 9).
(Proposition 7
and Corollary 9).
When dropping the normality assumption, the algorithm becomes more
technical, but it turns out that the middle product trick can still be
generalized. This is explained in section
5
and leads to the bound
 for general gcds and
for general gcds and
 in the FFT model (Theorem
15
). In the binary FFT model, special efforts are needed in order to
enforce the use of DFTs of power of two lengths. We prove the bound
in the FFT model (Theorem
15
). In the binary FFT model, special efforts are needed in order to
enforce the use of DFTs of power of two lengths. We prove the bound
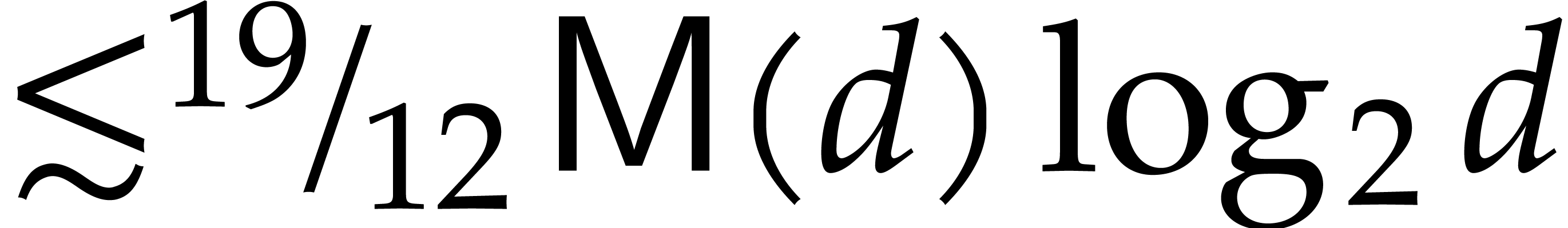 in this last case (Theorem
17
). See Table
1
for a summary of the new constant factors
in this last case (Theorem
17
). See Table
1
for a summary of the new constant factors
|
|||||||||||||||
It is well known that polynomial gcds have many applications: fast
arithmetic on rational functions, fast reconstruction of rational
functions [10, section 5.7], polynomial factorization [7], fast decoding of error-correcting codes [2,
24, 9], sparse interpolation [1,
28], etc. Personally, we were mainly motivated by the last
application to sparse interpolation. After the introduction of the
tangent Graeffe algorithm [11, 17], gcd
computations have often become one of the main practical bottlenecks.
For this application, it is typically possible to work modulo a prime of
the form 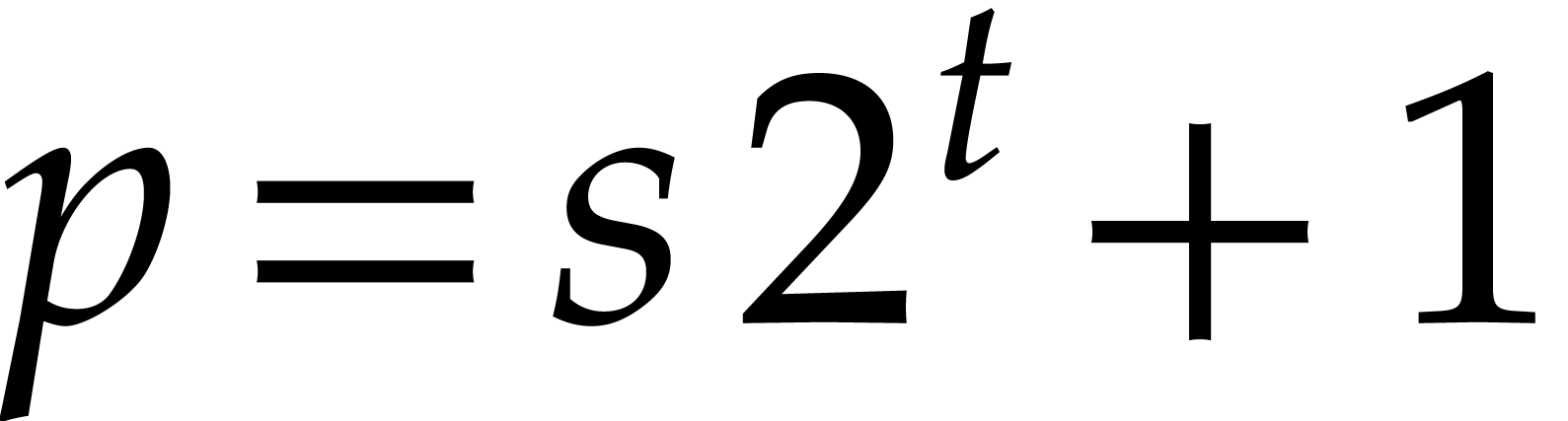 , which allows us to
exploit our optimizations for the binary FFT model.
, which allows us to
exploit our optimizations for the binary FFT model.
We made a first implementation of the new algorithm and also programmed the customary extension to the computation of subresultants (see [10, section 11.2] and also [21] for this extension). Work is in progress on HPC implementations of our algorithms and all required subalgorithms.
A few questions remain for future work. It is likely that the ideas in
this paper can be applied to integer gcds as well, except for the
optimizations that are specific to the binary FFT model. It would also
be nice to have counterparts for the “ternary FFT model”,
which could be used for fields  of characteristic
two (see [17, section 3.4] for an algorithm of this kind in
the case of iterated Graeffe transforms). Finally, in view of Bernstein
and Yang's recent ideas from [4], as well as Remark 16, one may wonder whether the bounds for the normal case can
actually be extended to the general case.
of characteristic
two (see [17, section 3.4] for an algorithm of this kind in
the case of iterated Graeffe transforms). Finally, in view of Bernstein
and Yang's recent ideas from [4], as well as Remark 16, one may wonder whether the bounds for the normal case can
actually be extended to the general case.
Acknowledgments. We are grateful to Michael
The best bounds in this paper will be proved for the so-called
“binary FFT model”, which requires special assumptions on
the ground field
 .
First of all, this model requires
.
First of all, this model requires
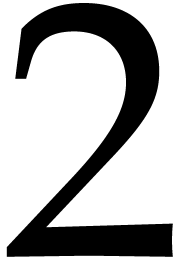 to be invertible in
to be invertible in
 .
Secondly, for any polynomial
.
Secondly, for any polynomial
 that occurs during computations, we assume that
that occurs during computations, we assume that
 has a primitive
has a primitive
 -th
root of unity
-th
root of unity
 with
with
 .
For convenience, we also assume that
.
For convenience, we also assume that
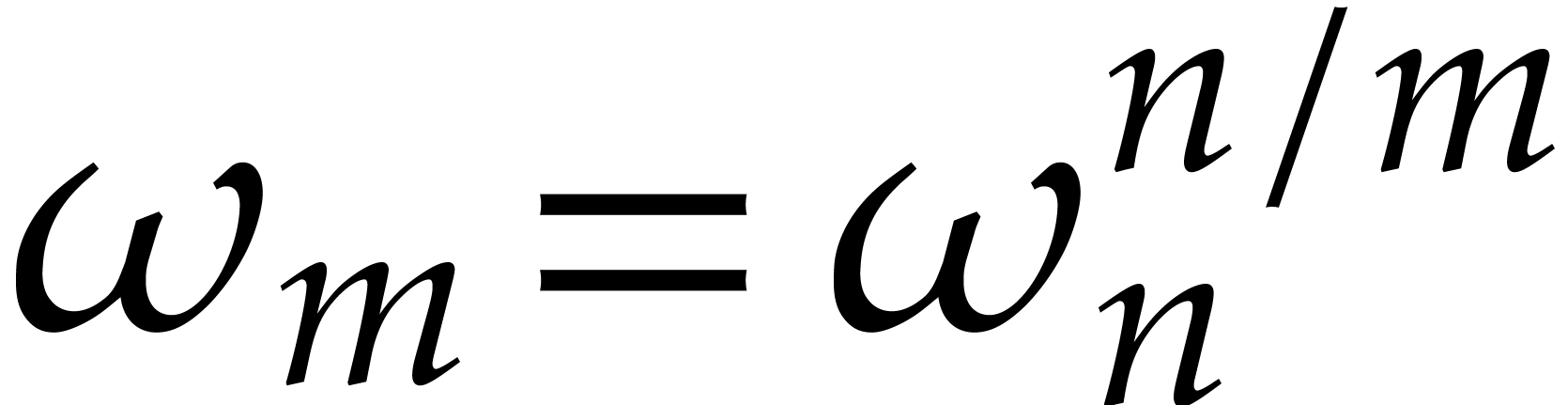 whenever
whenever
 divides
divides
 .
We measure computational complexity in terms of the number of required
field
.
We measure computational complexity in terms of the number of required
field
1. Using an easy refinement of the analysis, it turns out that
the main half gcd algorithms in this paper involve only a
linear number of divisions, so the bulk of the operations are
actually ring operations in  .
.
 .
Given
.
Given
 with
with
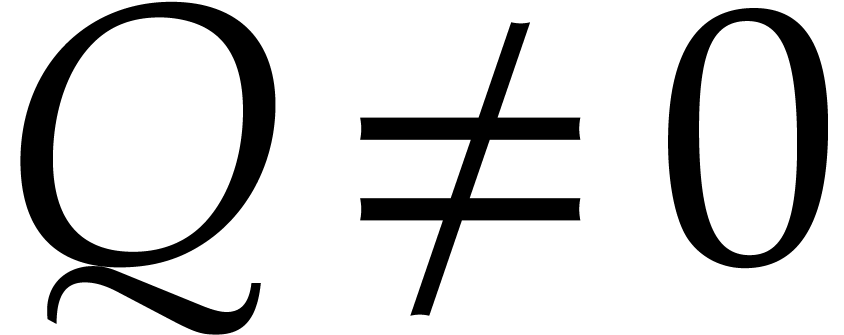 ,
we write
,
we write
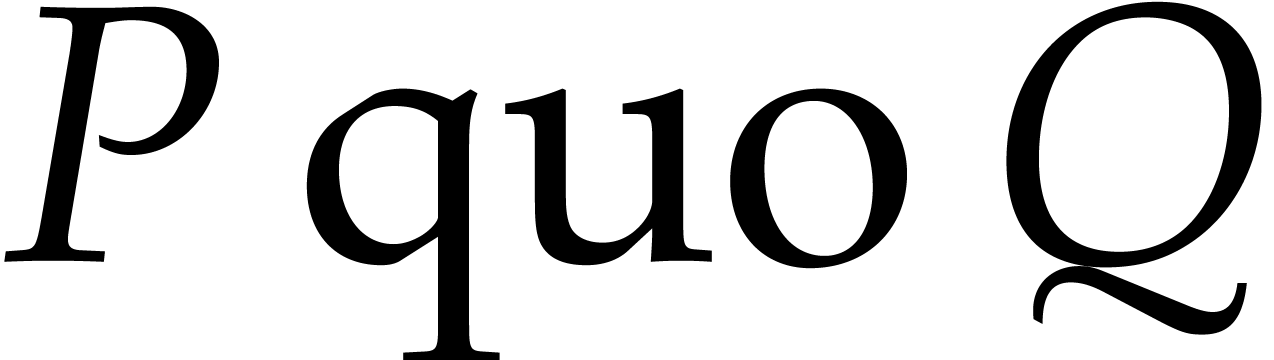 and
and
 for the quotient and the remainder of the Euclidean division of
for the quotient and the remainder of the Euclidean division of
 by
by
 ,
respectively.
,
respectively.
Let 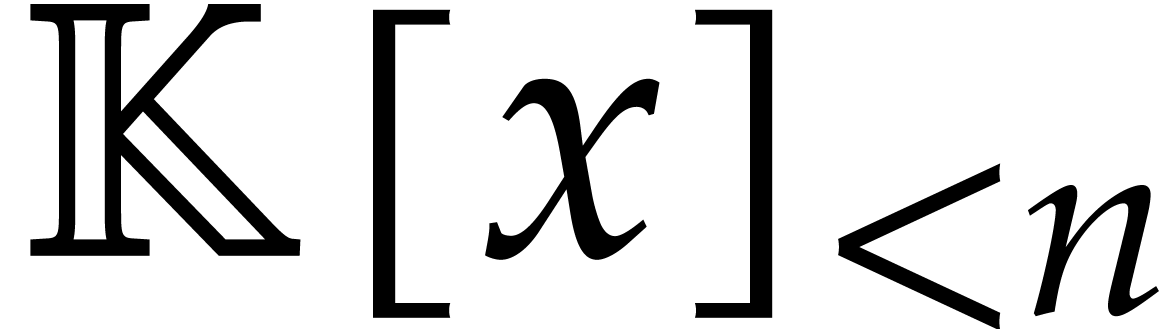 denote the space of polynomials of degree
denote the space of polynomials of degree
 . Given
. Given 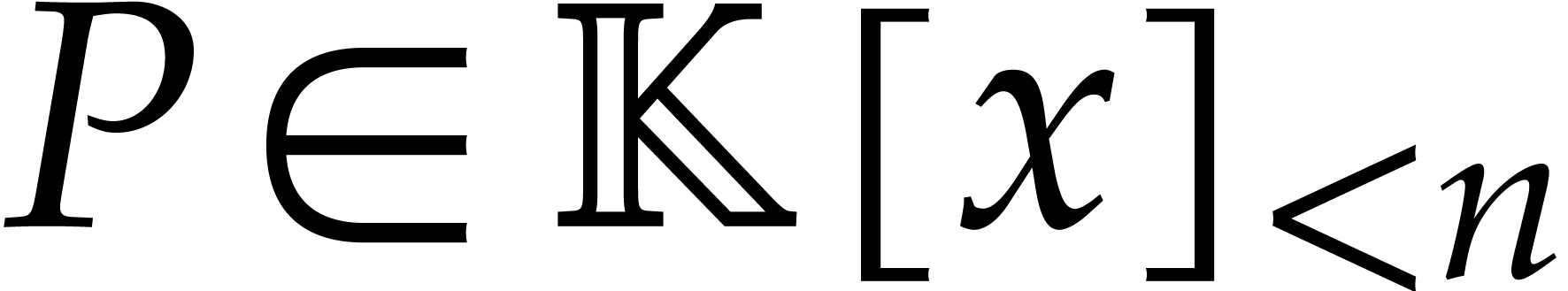 with
with  , we define its
discrete Fourier transform
, we define its
discrete Fourier transform 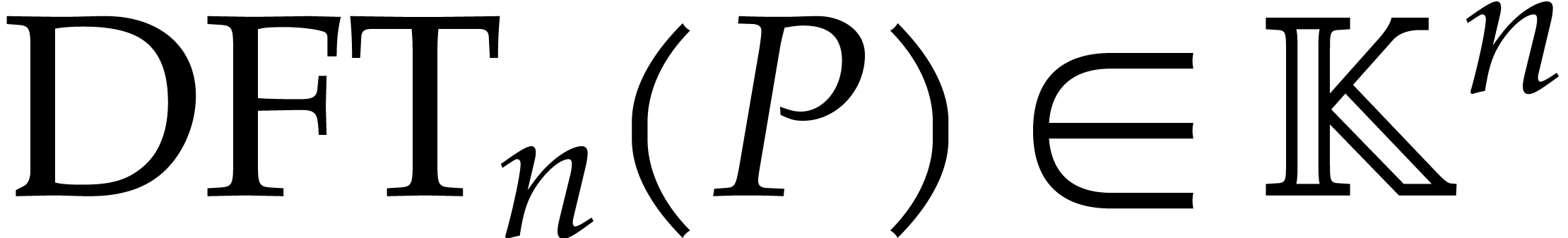 by
by

We will write  for the maximum cost of computing
a discrete Fourier transform of order
for the maximum cost of computing
a discrete Fourier transform of order  or the
inverse transformation
or the
inverse transformation 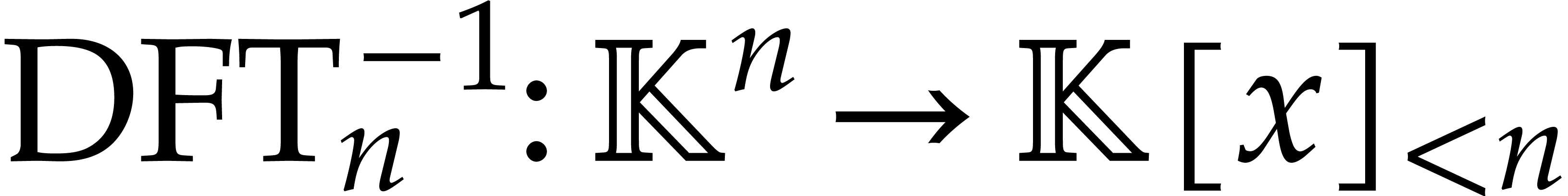 . It
is well known [8] that
. It
is well known [8] that 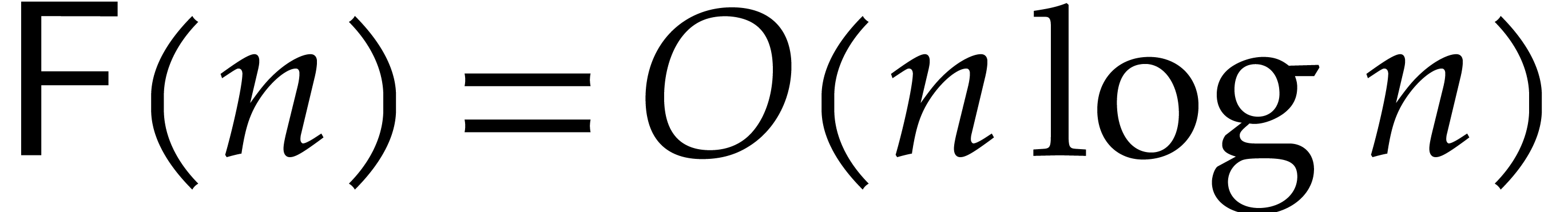 .
In what follows, we will always assume that
.
In what follows, we will always assume that 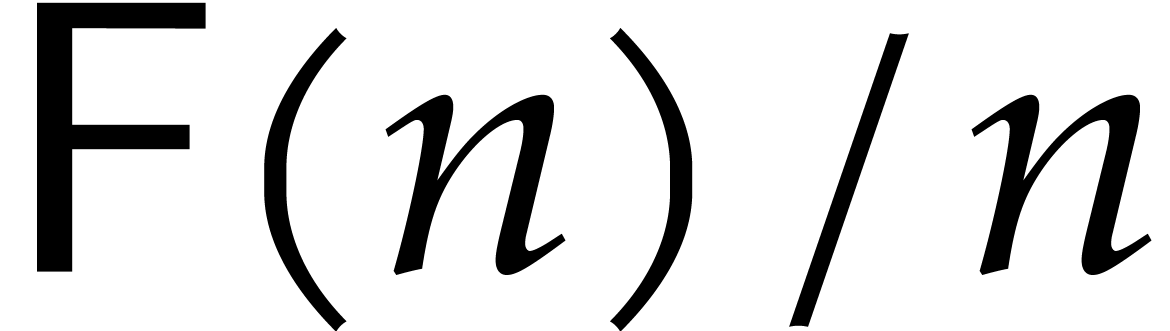 , and
, and  are non-decreasing
(for
are non-decreasing
(for  and
and  ,
respectively). Therefore, we may just as well take
,
respectively). Therefore, we may just as well take 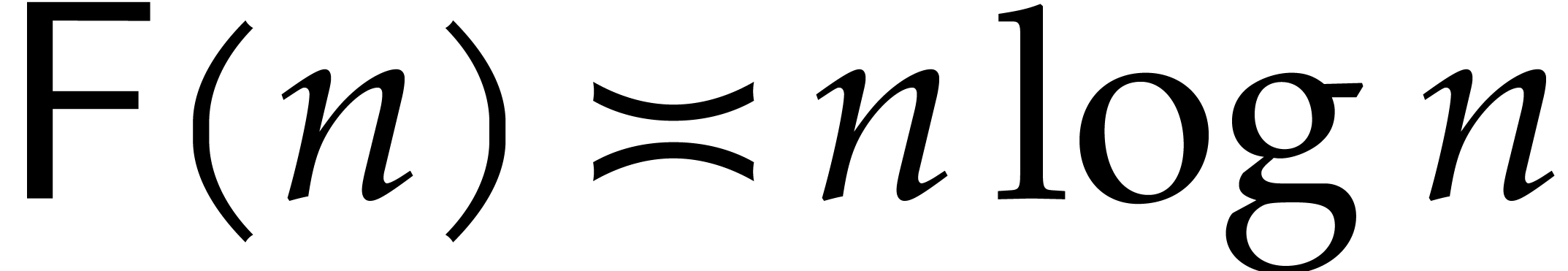 , but it is instructive to keep the notation
, but it is instructive to keep the notation
 to indicate where we use Fourier transforms.
to indicate where we use Fourier transforms.
If  and the discrete Fourier transform of
and the discrete Fourier transform of 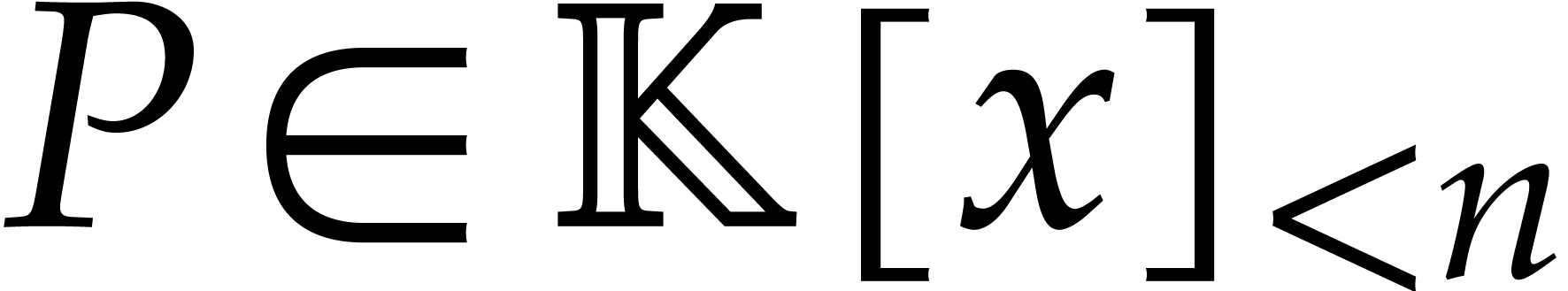 at order
at order  with respect to
with respect to 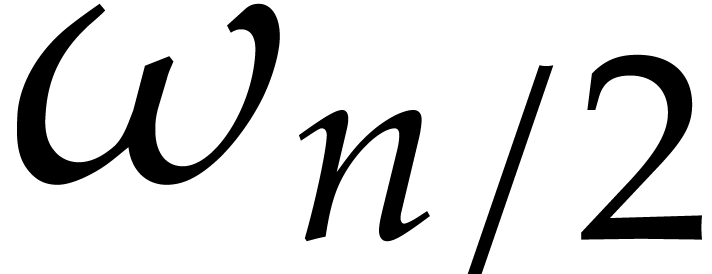 is known, then it costs
is known, then it costs 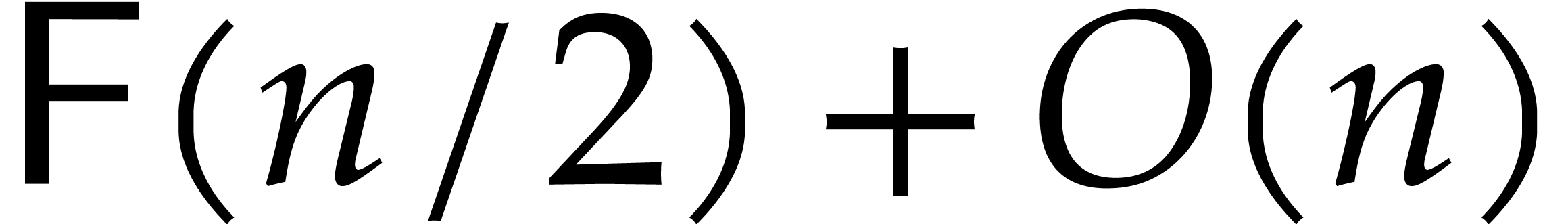 to
compute
to
compute  . Indeed, we already
know
. Indeed, we already
know 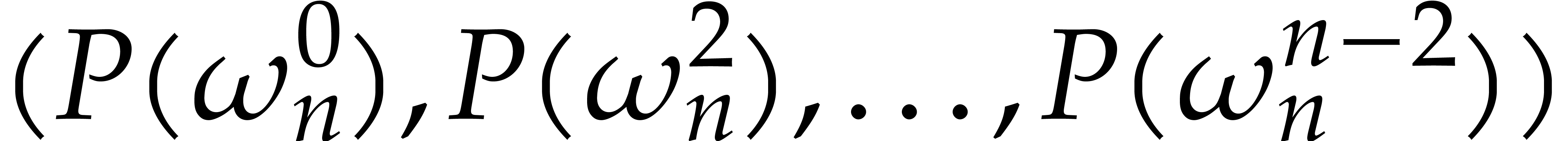 , so it remains to
compute
, so it remains to
compute 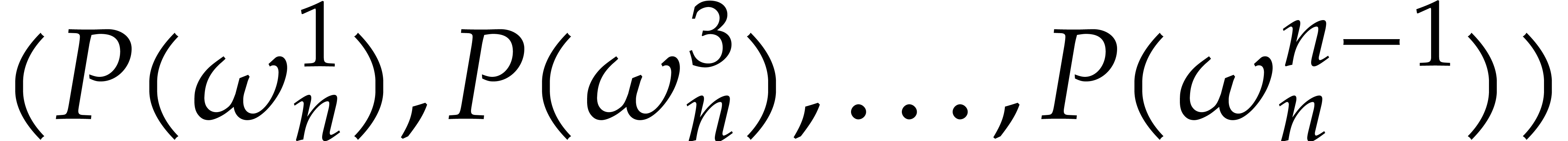 . But this is the DFT
of
. But this is the DFT
of 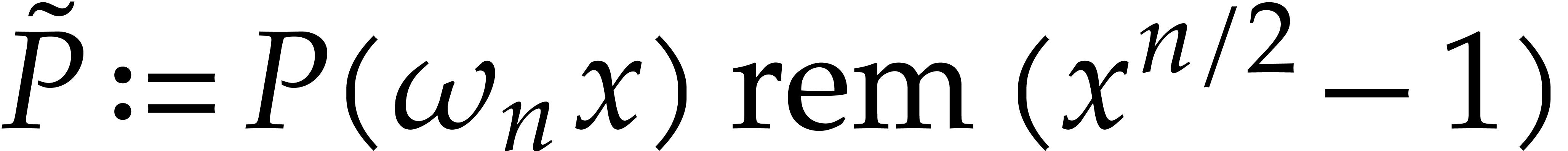 at order
at order  and it takes
a linear number of operations to compute
and it takes
a linear number of operations to compute  in
terms of
in
terms of  . We call this trick
FFT doubling.
. We call this trick
FFT doubling.
Given  with
with  ,
we may use the discrete Fourier transform to compute the product
,
we may use the discrete Fourier transform to compute the product  using
using
This is called FFT multiplication. If we fix  of degree
of degree 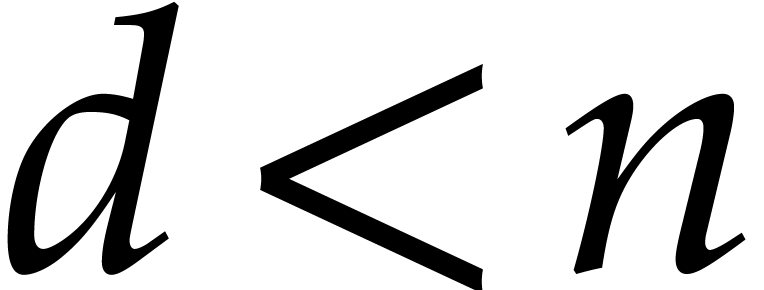 , then we may
consider the multiplication map with
, then we may
consider the multiplication map with  as a linear
map
as a linear
map 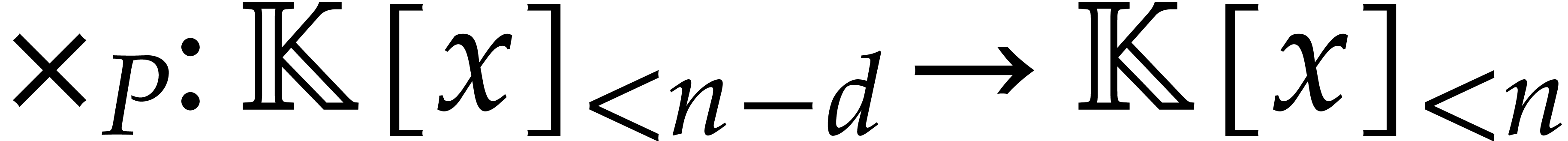 . We have
. We have

where  stands for componentwise multiplication by
stands for componentwise multiplication by
 in
in  and
and  for the injection of
for the injection of 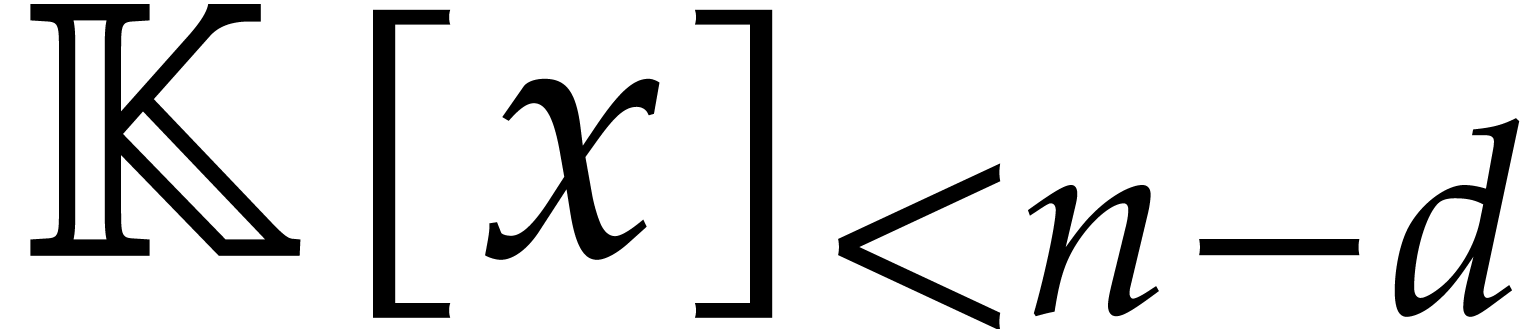 into
into 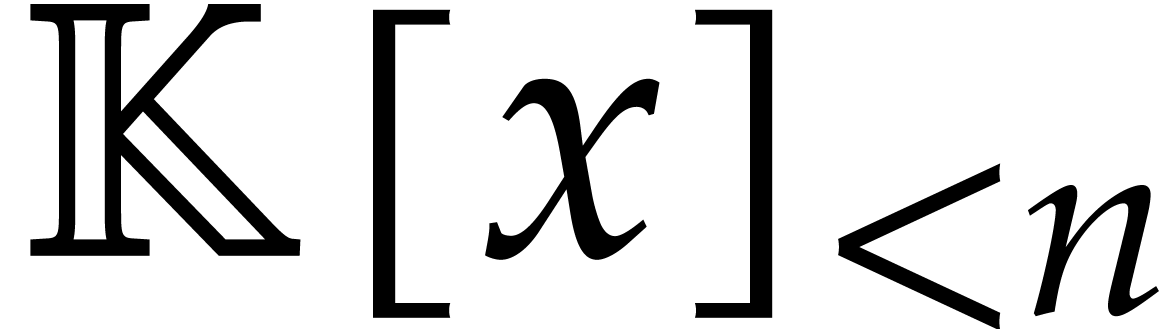 .
.
Given 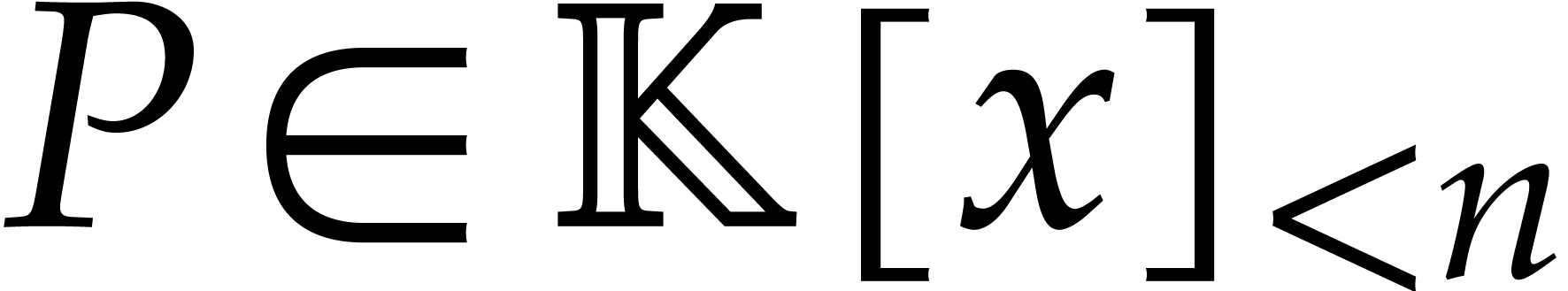 of degree
of degree  and
and
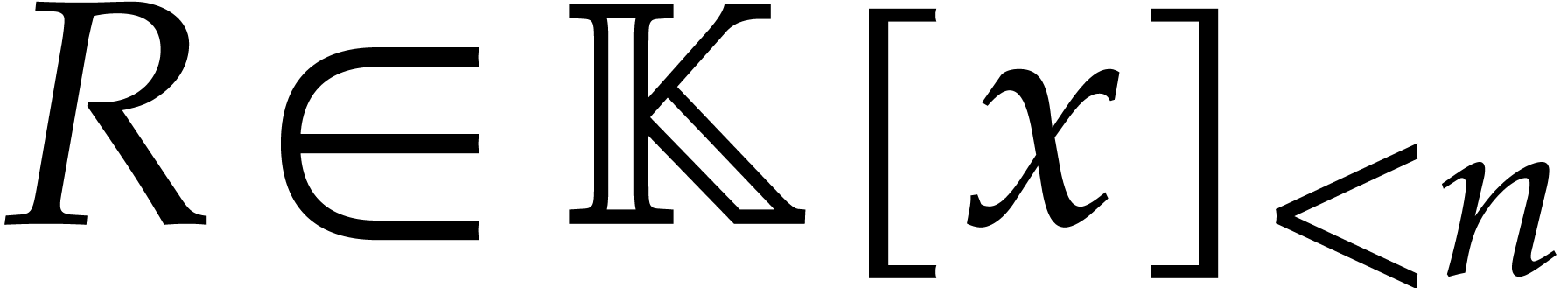 , we define their middle
product
, we define their middle
product 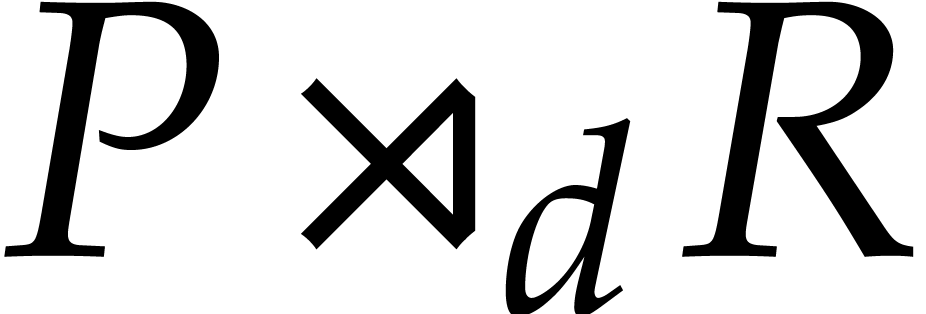 by
by
Let us recall how 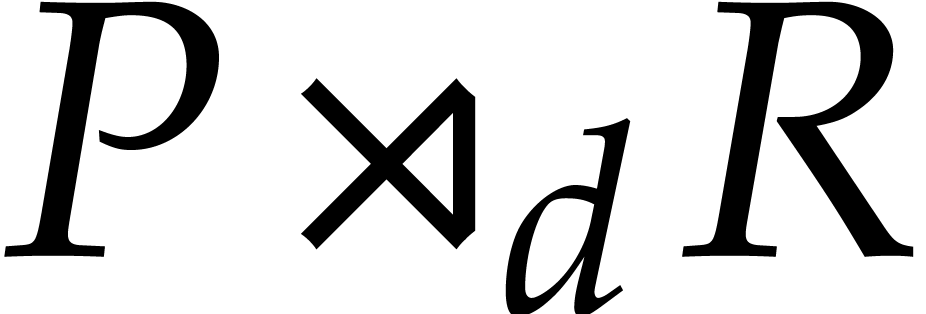 can be computed efficiently
using FFT multiplication.
can be computed efficiently
using FFT multiplication.
Let  be of degree
be of degree  ,
let
,
let  and
and 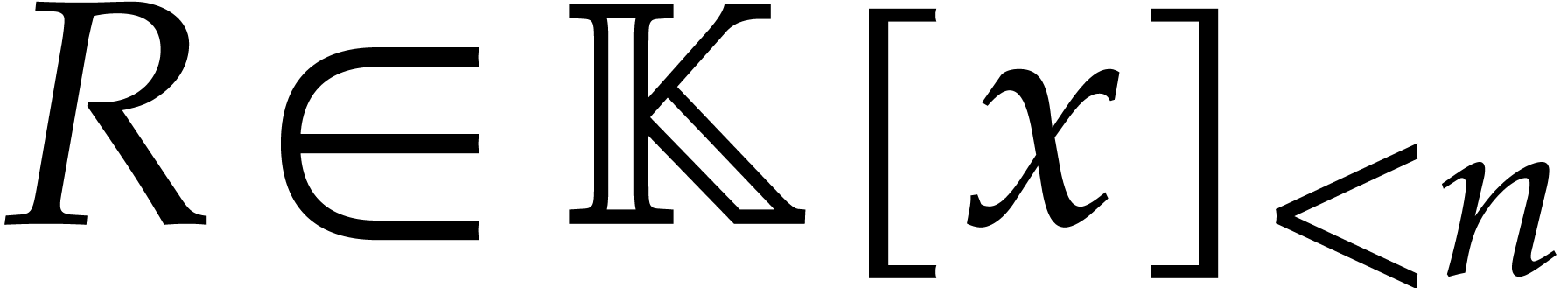 .
If
.
If  , then we observe that
, then we observe that
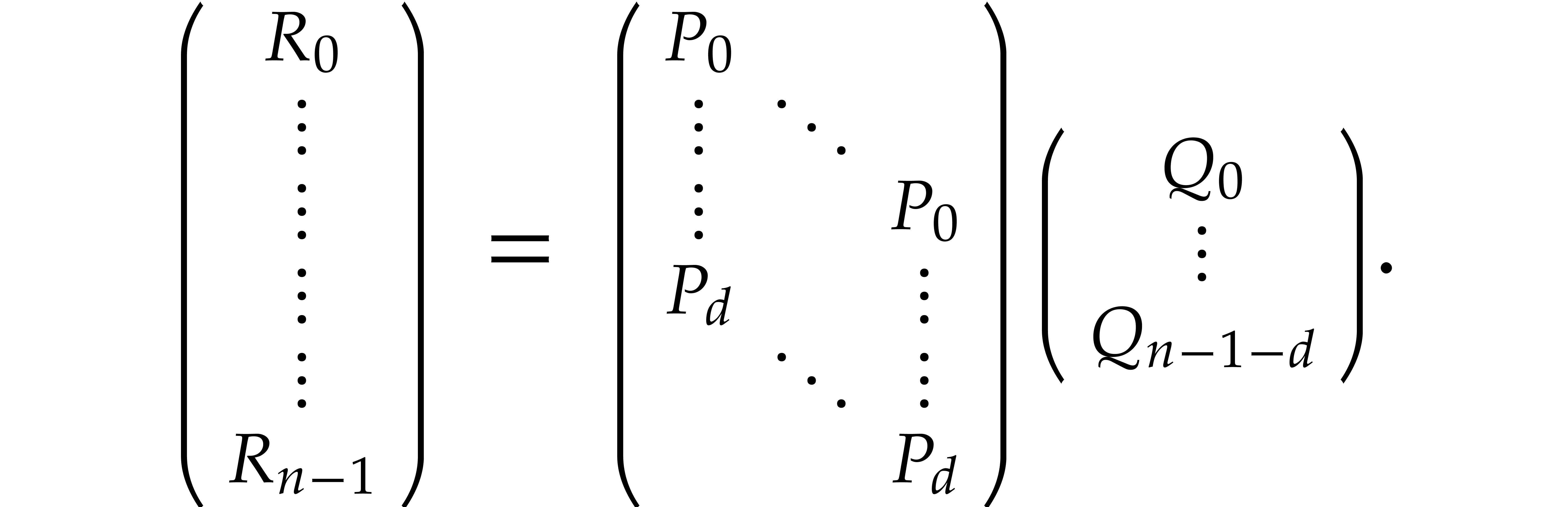
The matrix in the middle has  rows and
rows and 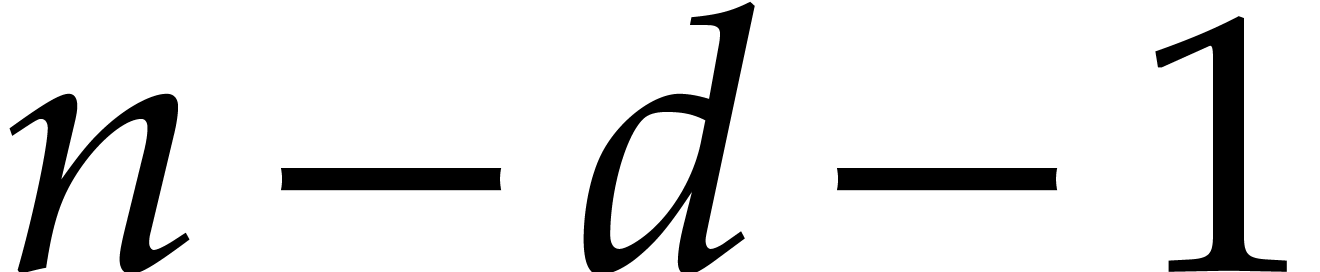 columns and we may think of it as the matrix of the map
columns and we may think of it as the matrix of the map
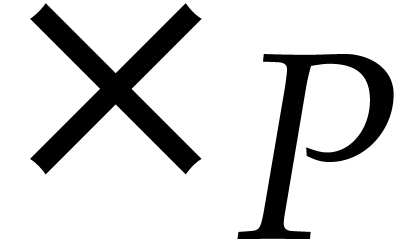 . If
. If 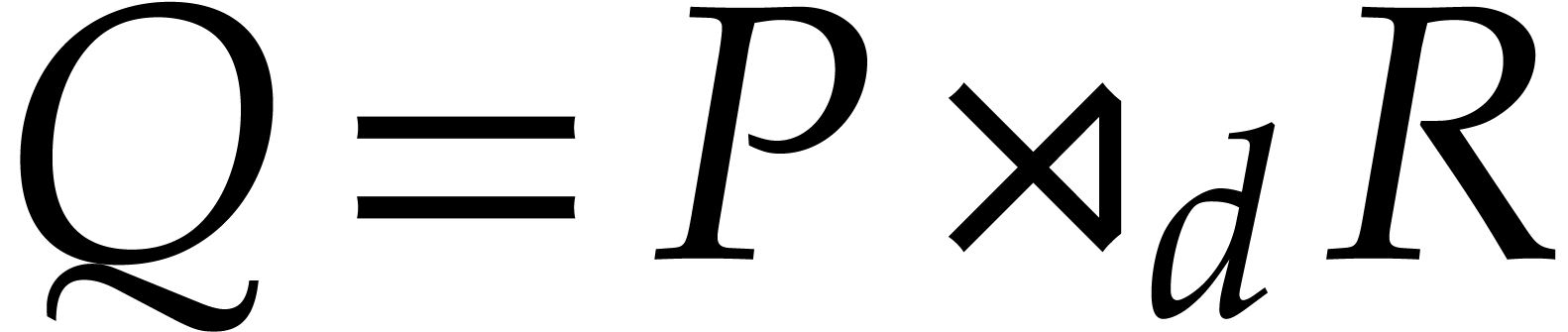 , then we note that
, then we note that
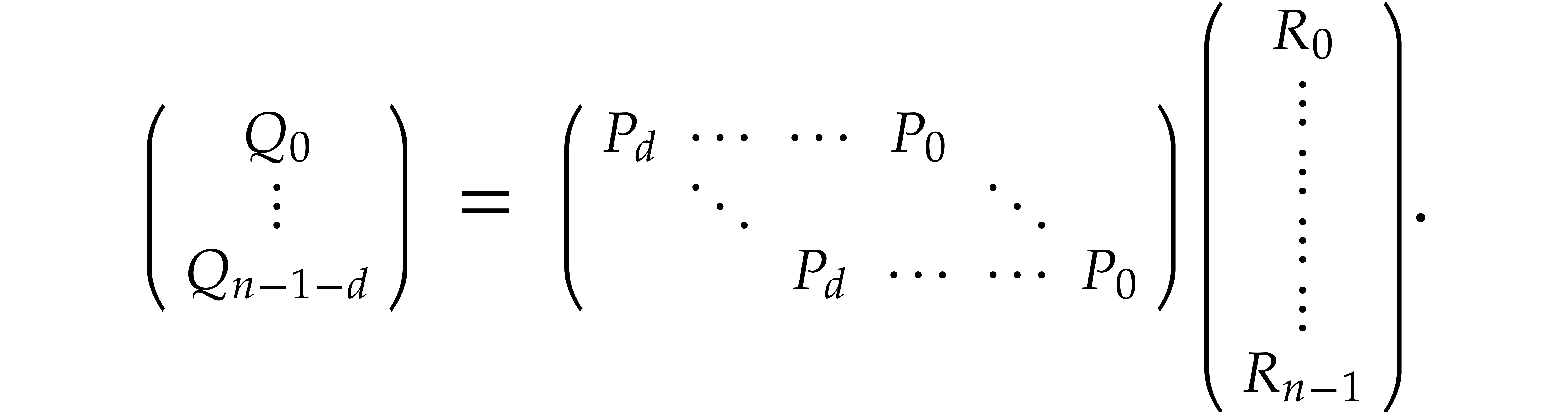
In other words 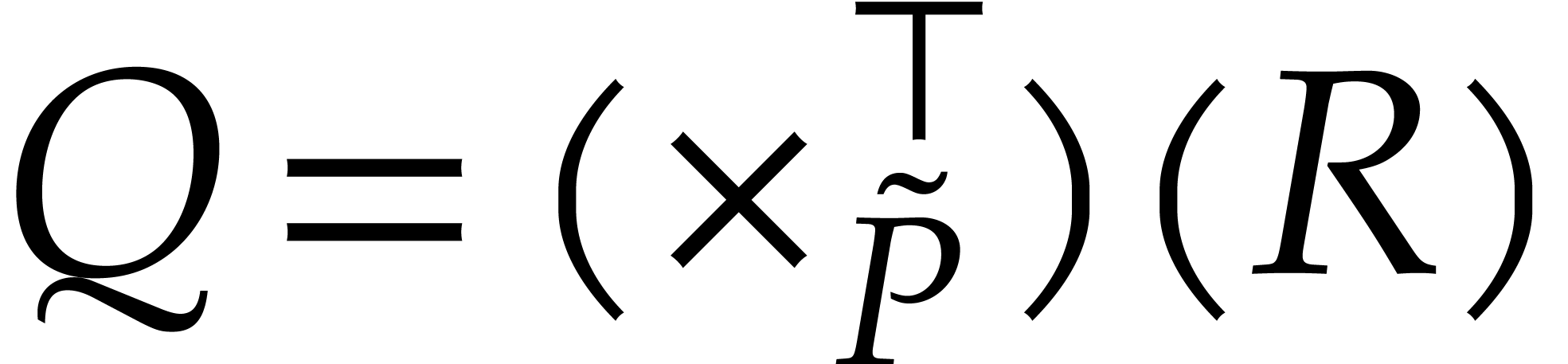 , where
, where 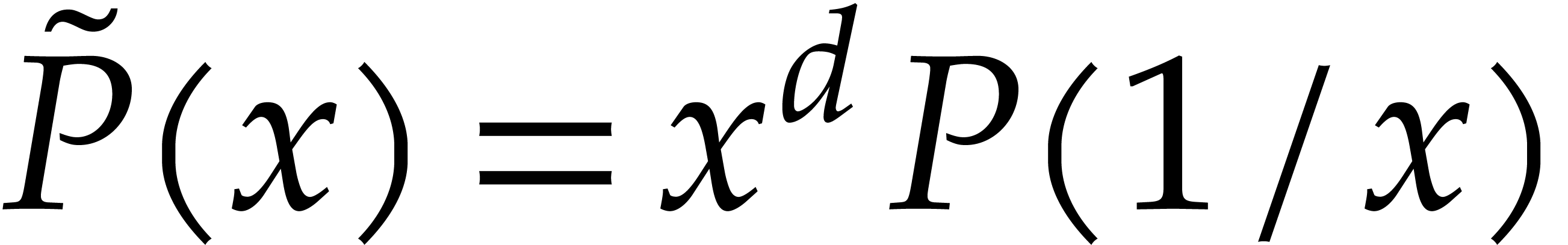 and
and 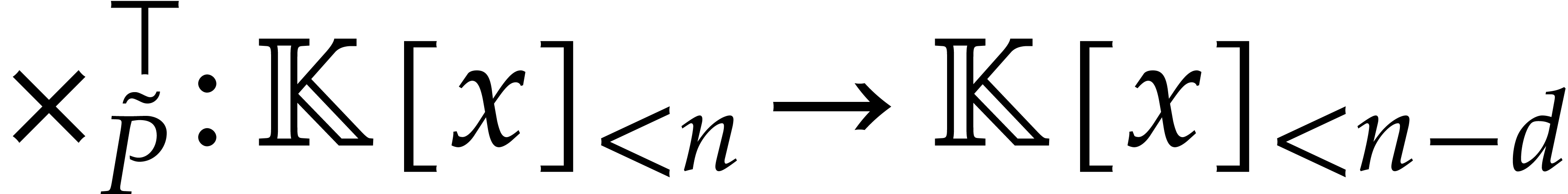 stands for the transpose
of
stands for the transpose
of 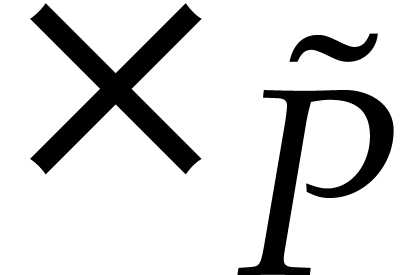 . Since
. Since

where 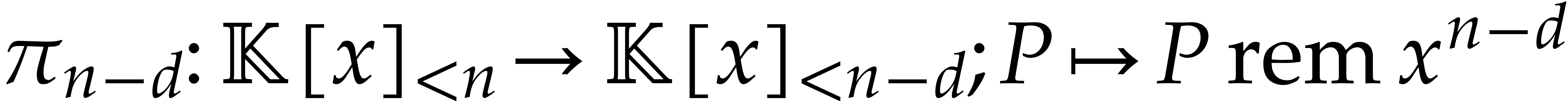 , it follows that
, it follows that

Taking DFTs with respect to 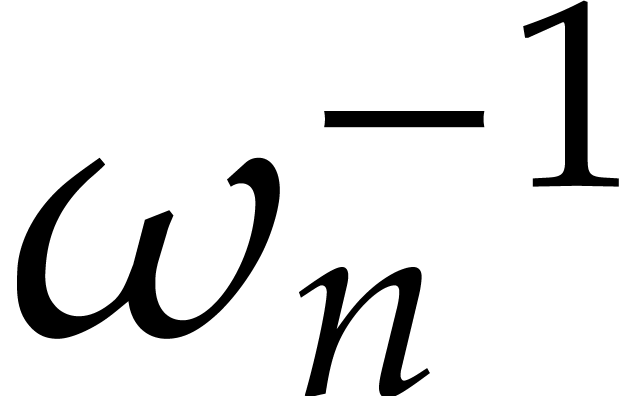 instead of
instead of  and using that
and using that 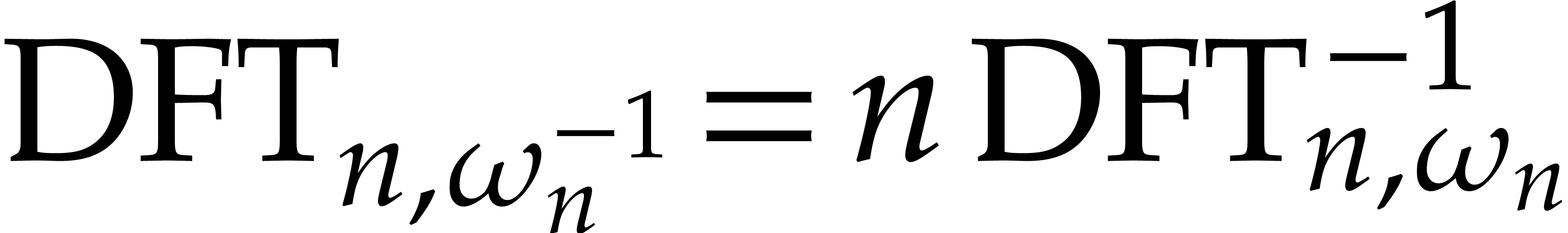 ,
we also obtain
,
we also obtain
This is the alternative formula from [13] that we will use.
From the complexity perspective, let 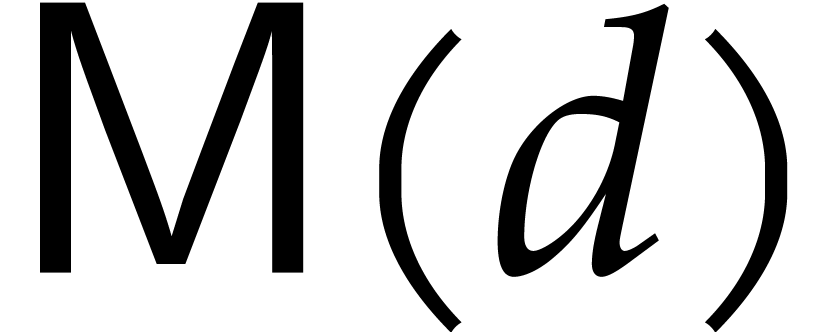 be the cost
to multiply two polynomials in
be the cost
to multiply two polynomials in 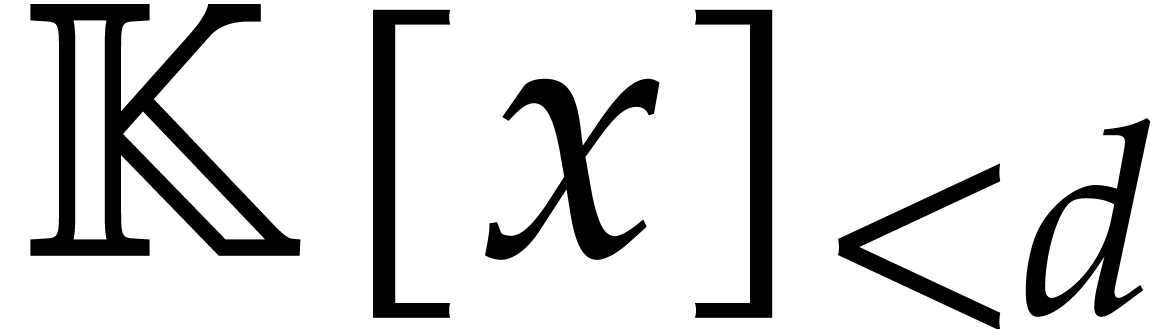 .
Using FFT multiplication, we see that
.
Using FFT multiplication, we see that 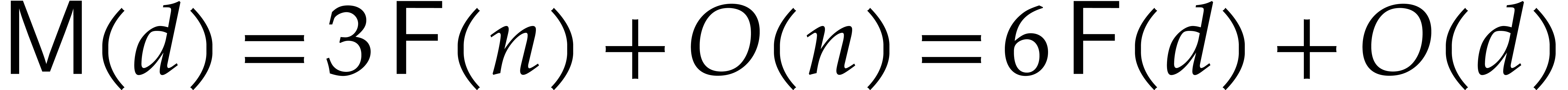 in the
binary FFT model. More generally, if
in the
binary FFT model. More generally, if  is even,
then any two polynomials
is even,
then any two polynomials  with
with  can be multiplied in time
can be multiplied in time 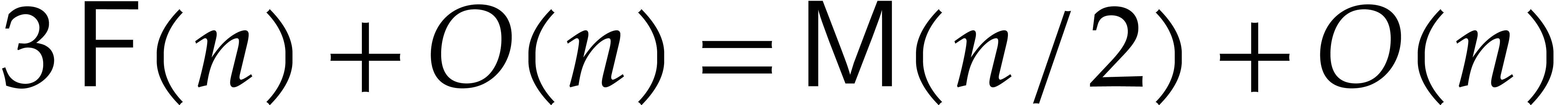 using this method.
Similarly, the cost
using this method.
Similarly, the cost 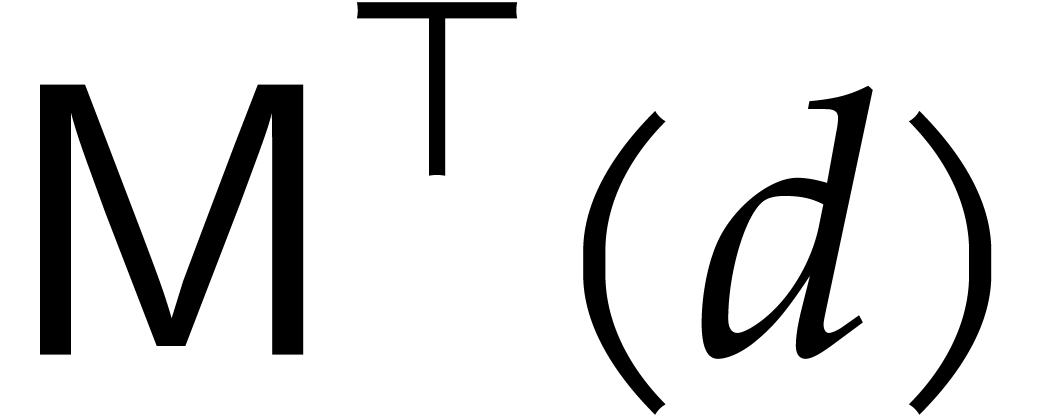 to compute a middle product
(2) with
to compute a middle product
(2) with 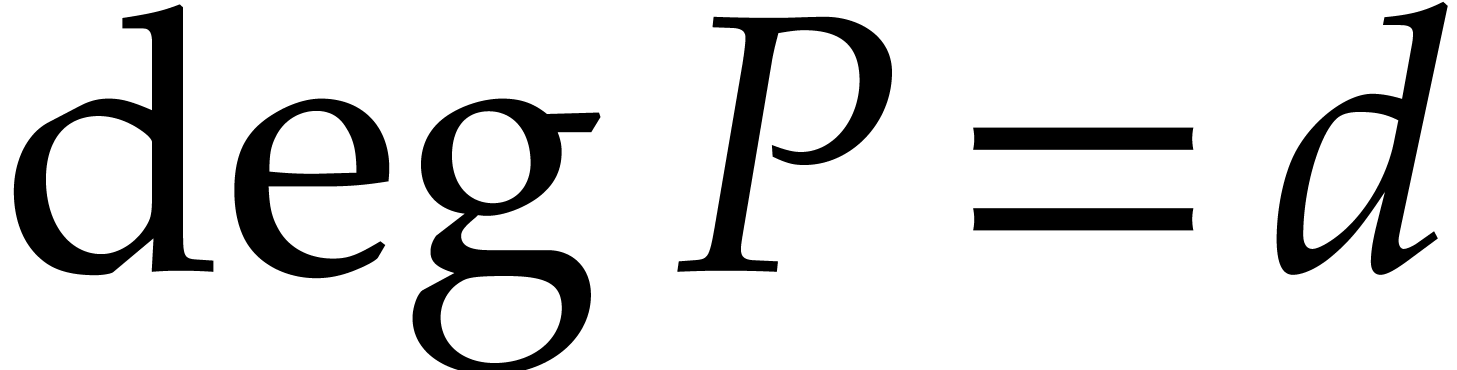 and
and 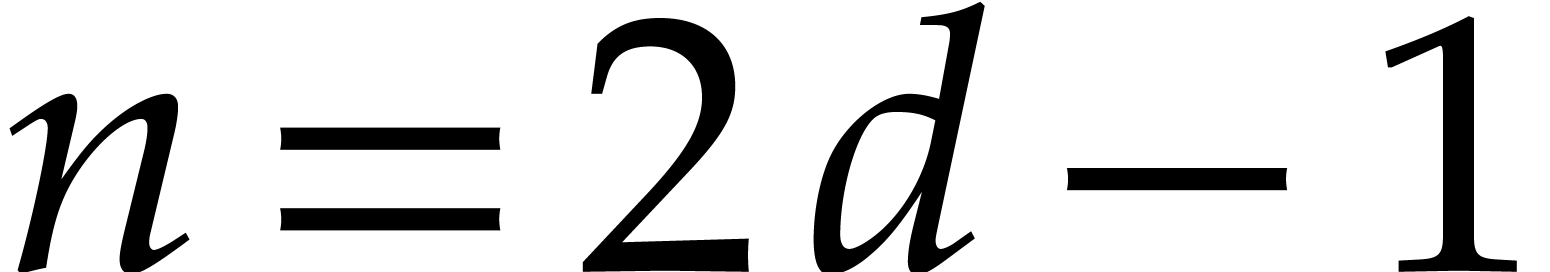 satisfies
satisfies 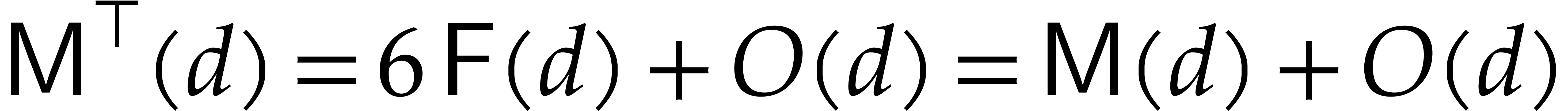 . If
. If  is even and
is even and  is general, then
is general, then 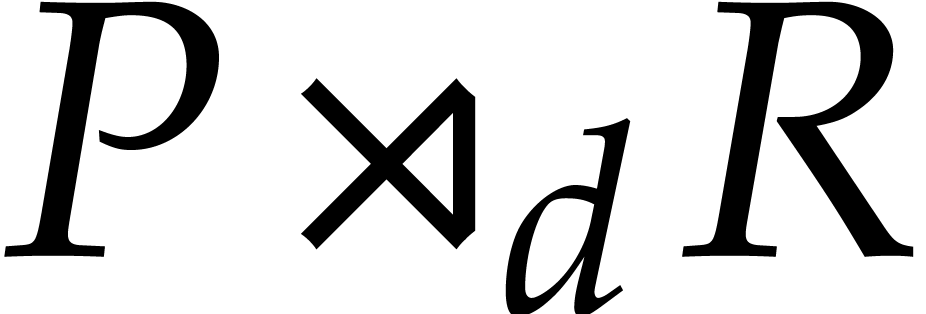 can be computed in time
can be computed in time 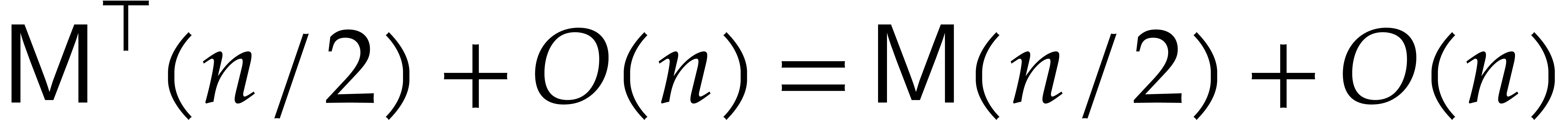 .
.
It is important to note that the above results all generalize to the
case when the coefficient field  is replaced by
the algebra
is replaced by
the algebra 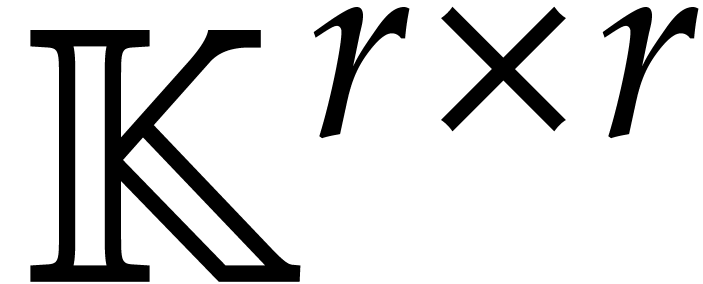 of
of  matrices
with entries in
matrices
with entries in  . For
instance, assume that
. For
instance, assume that 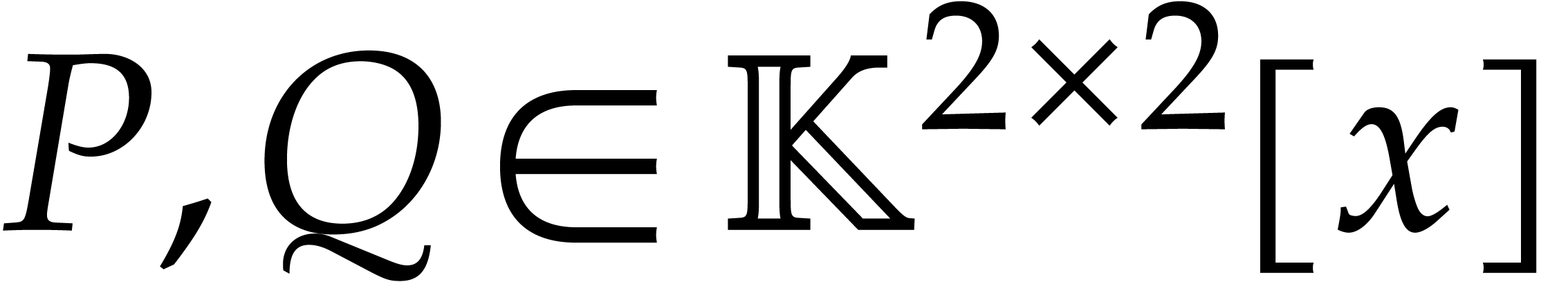 with
with  . Then (1) allows us to compute
. Then (1) allows us to compute
 using
using  DFTs,
DFTs,  inverse DFTs, and
inverse DFTs, and  multiplications
of
multiplications
of  matrices in
matrices in 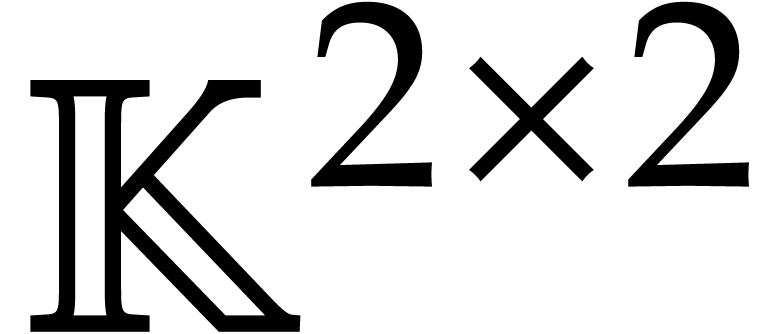 ,
for a total cost of
,
for a total cost of  .
.
Although the main focus in this paper is on the binary FFT model, we
will also consider other types of polynomial multiplication. In that
case, we will still denote by 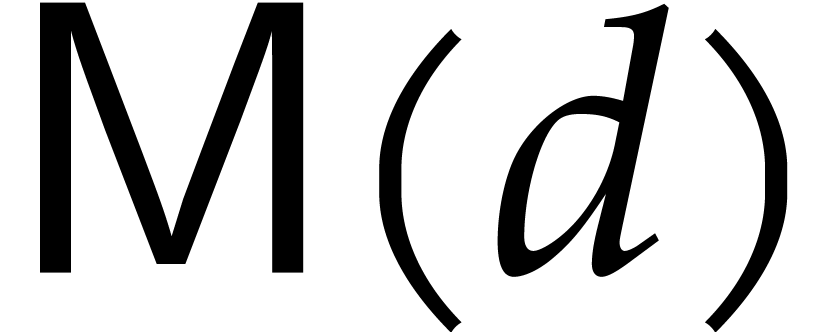 and
and 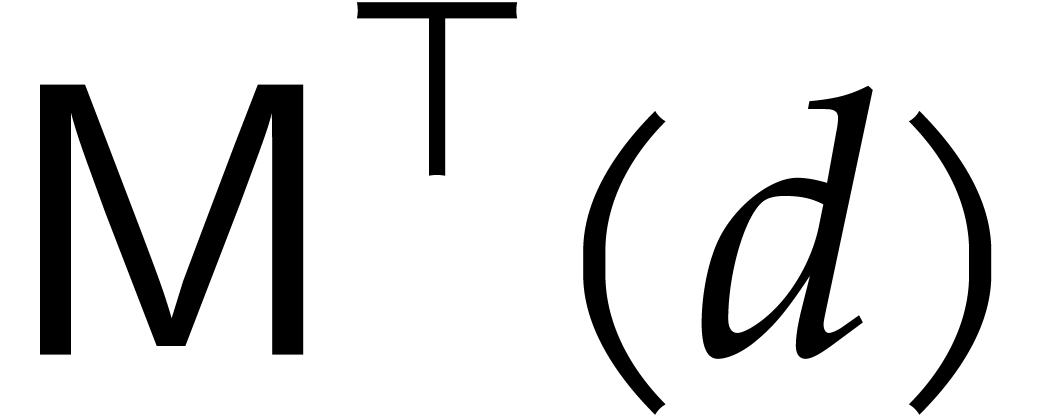 the complexities of multiplying two polynomials in
the complexities of multiplying two polynomials in 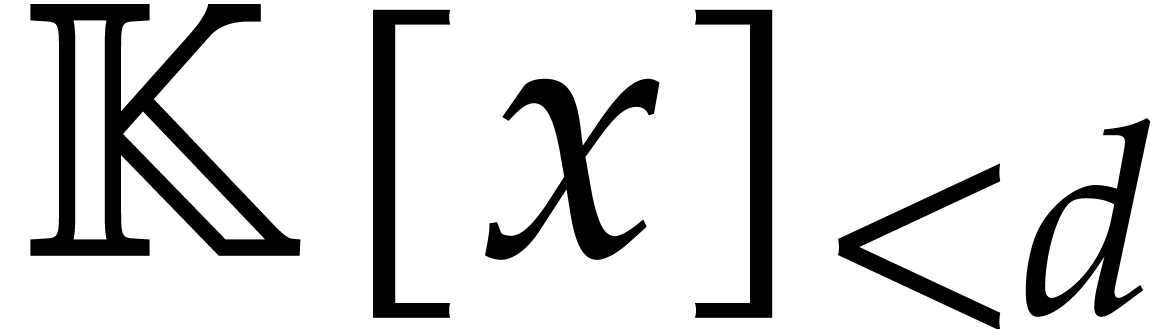 and to compute the middle product
and to compute the middle product  for
for  of degree
of degree  and
and 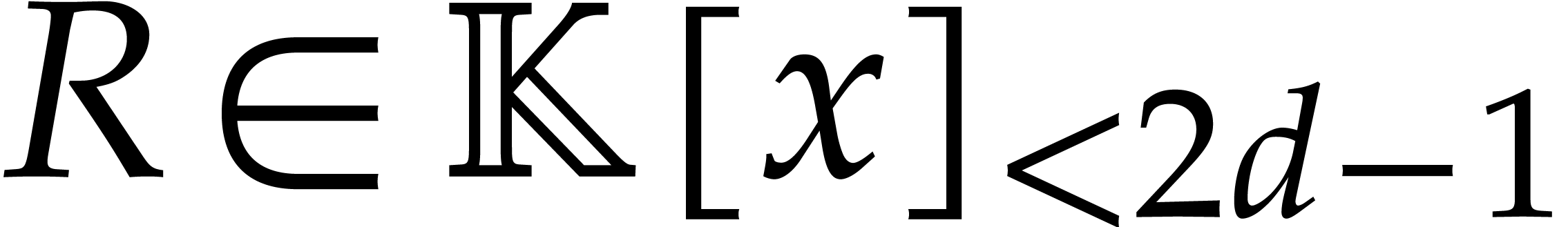 . Moreover, we make the following
assumptions on these cost functions:
. Moreover, we make the following
assumptions on these cost functions:
We have  .
.
The product of any  with
with  can be computed in time
can be computed in time 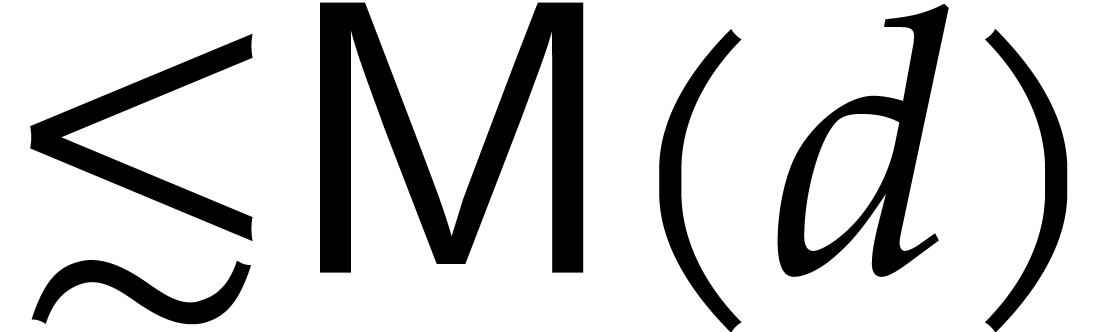 and similarly for
the middle product
and similarly for
the middle product 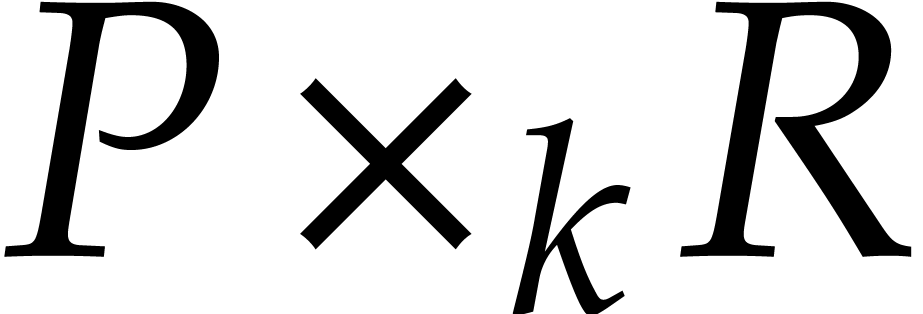 of
of  with
with  and
and 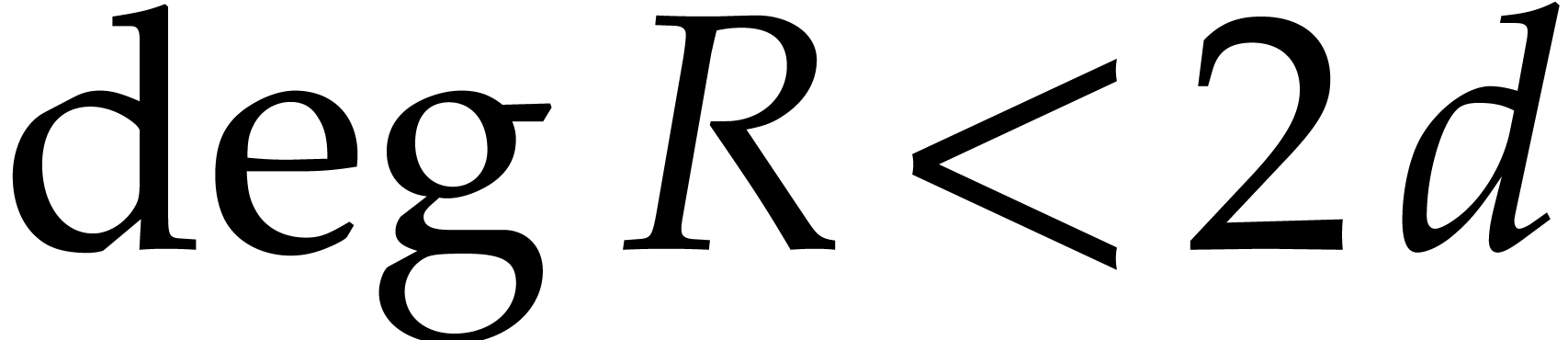 .
.
The functions 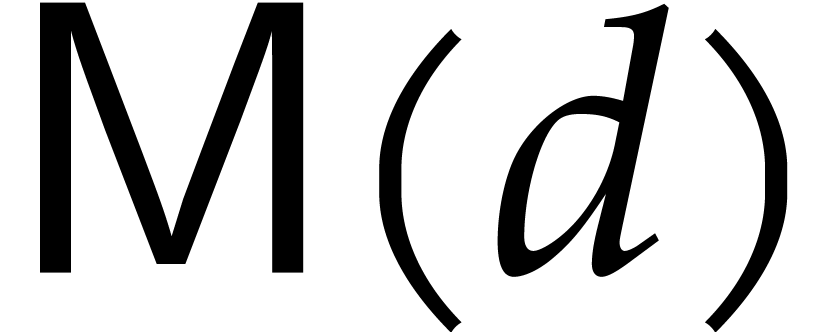 ,
,  , and
, and 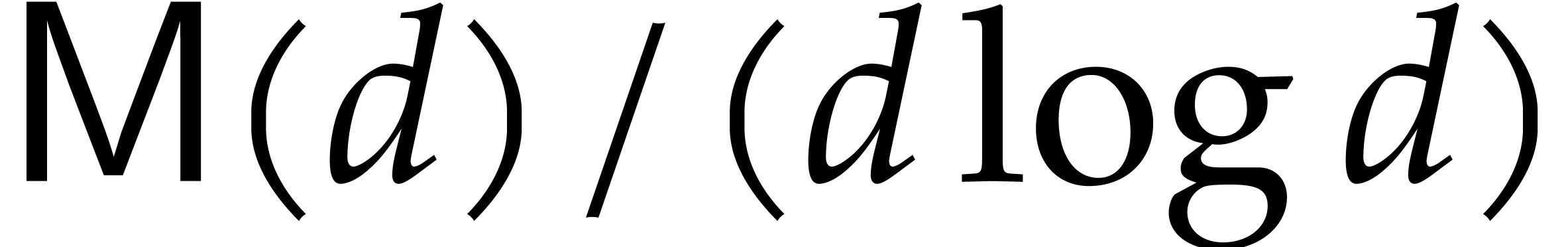 are non-decreasing (for
are non-decreasing (for  ,
,
 , and
, and 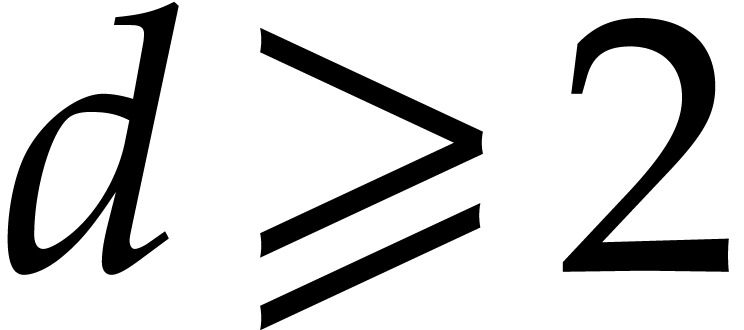 , respectively).
, respectively).
We also make the same assumptions for the analogue cost functions  and
and 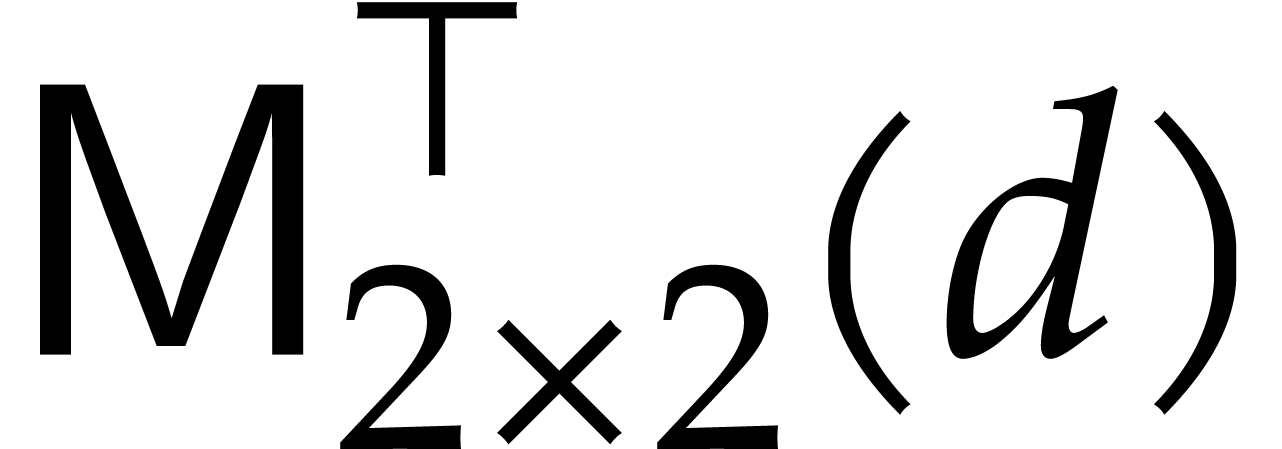 when taking coefficients
in
when taking coefficients
in 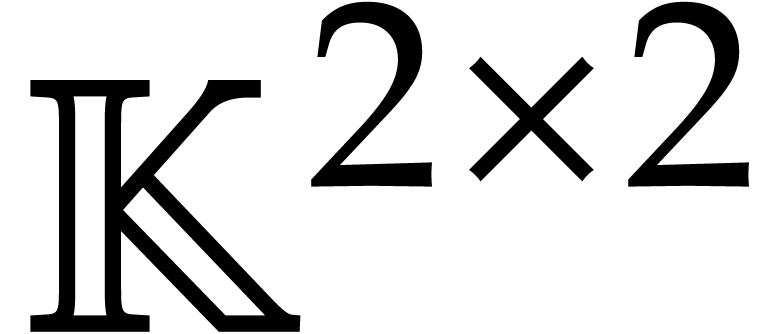 instead of
instead of  .
In the binary FFT model we have seen that we may take
.
In the binary FFT model we have seen that we may take 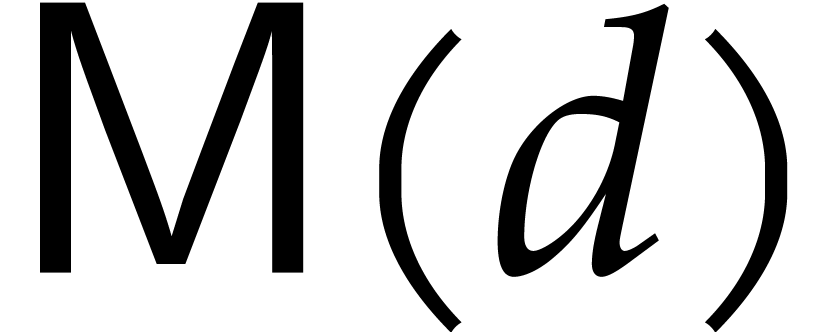 and
and 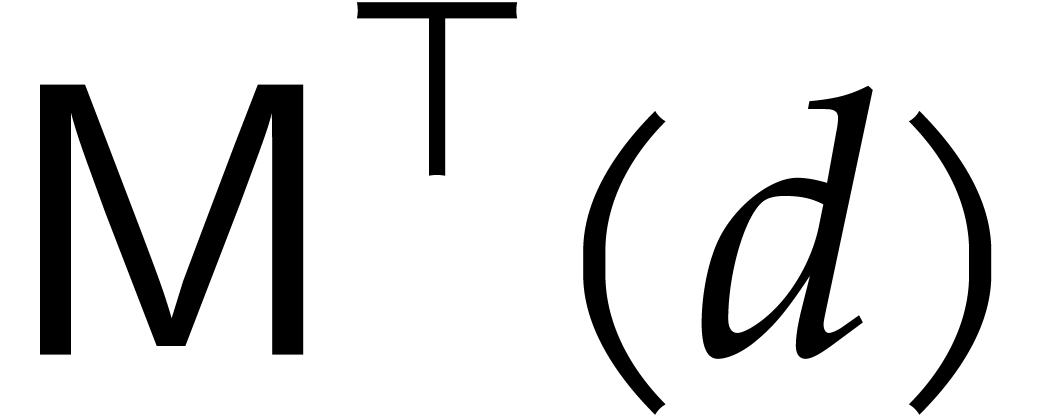 to be of the form
to be of the form 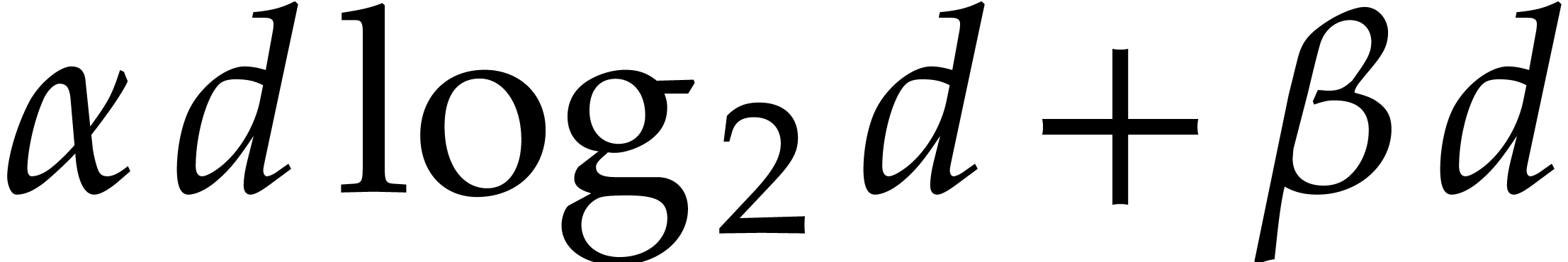 for suitable constants
for suitable constants 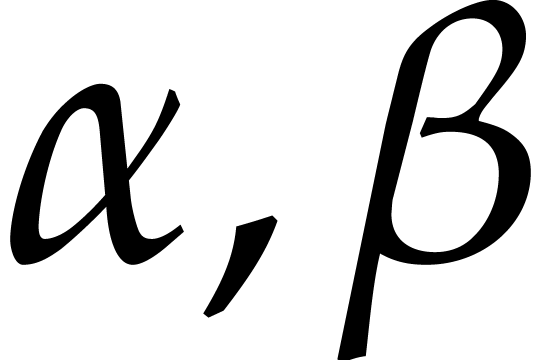 ,
after which the above assumptions are satisfied (if
,
after which the above assumptions are satisfied (if  is not a power of two, then one may use the truncated Fourier transform
[16], for instance). They are also verified for all other
commonly used types of multiplication, such as Karatsuba's and Toom's
methods [19, 37], or FFT-based methods for
arbitrary radices [30, 6, 15].
is not a power of two, then one may use the truncated Fourier transform
[16], for instance). They are also verified for all other
commonly used types of multiplication, such as Karatsuba's and Toom's
methods [19, 37], or FFT-based methods for
arbitrary radices [30, 6, 15].
In addition, we define  to be a constant such
that
to be a constant such
that  . We have seen that we
may take
. We have seen that we
may take  in the binary FFT model; this
generalizes to arbitrary FFT models. Using Strassen's method for
in the binary FFT model; this
generalizes to arbitrary FFT models. Using Strassen's method for  matrix multiplication [34], we may
always take
matrix multiplication [34], we may
always take 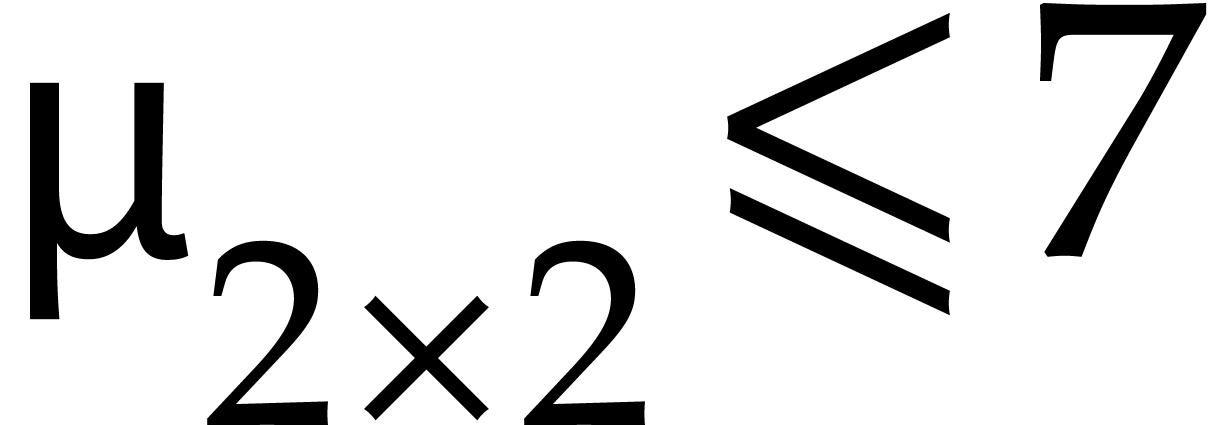 . From a
practical point of view, we usually have
. From a
practical point of view, we usually have  .
.
Let us examine the constant  a bit more closely
in the case of Karatsuba multiplication. The complexity of this method
satisfies
a bit more closely
in the case of Karatsuba multiplication. The complexity of this method
satisfies

for certain constants  and
and 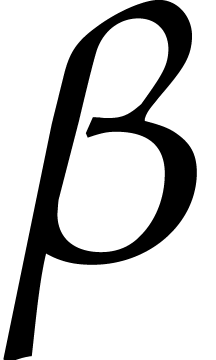 , which yields
, which yields 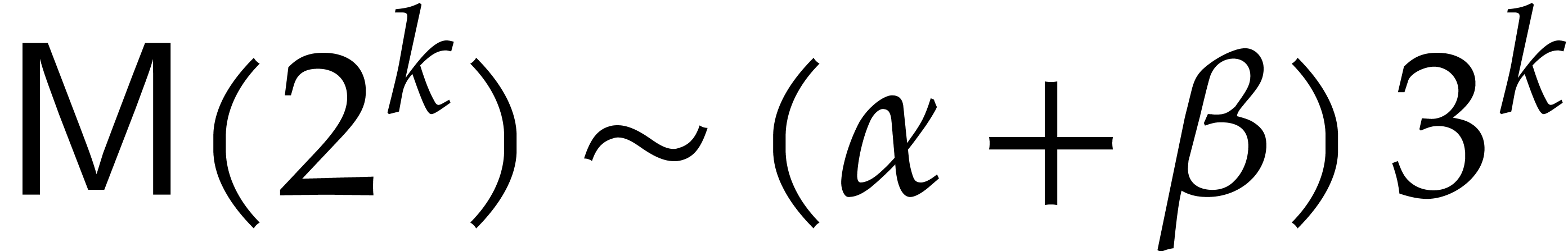 .
Similarly, when using Karatsuba's method to multiply
.
Similarly, when using Karatsuba's method to multiply  matrices, the complexity
matrices, the complexity  satisfies
satisfies
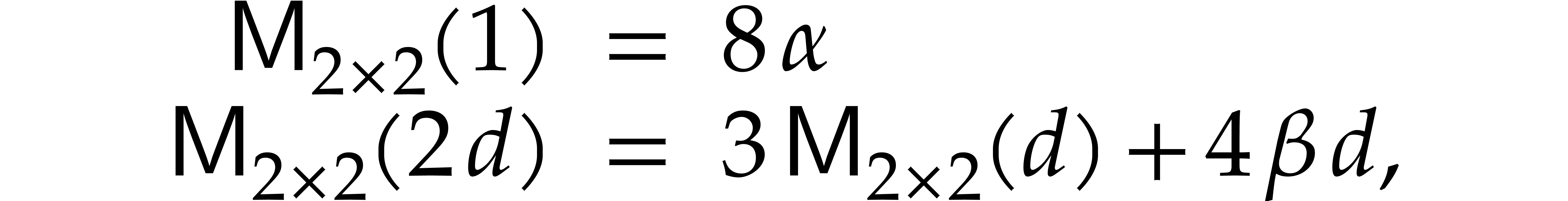
which leads to 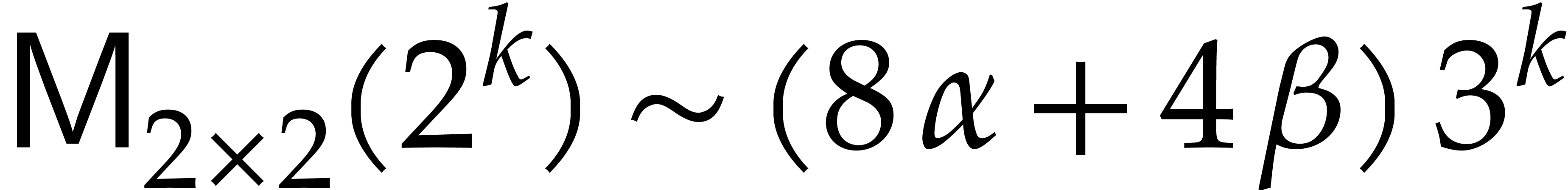 and
and
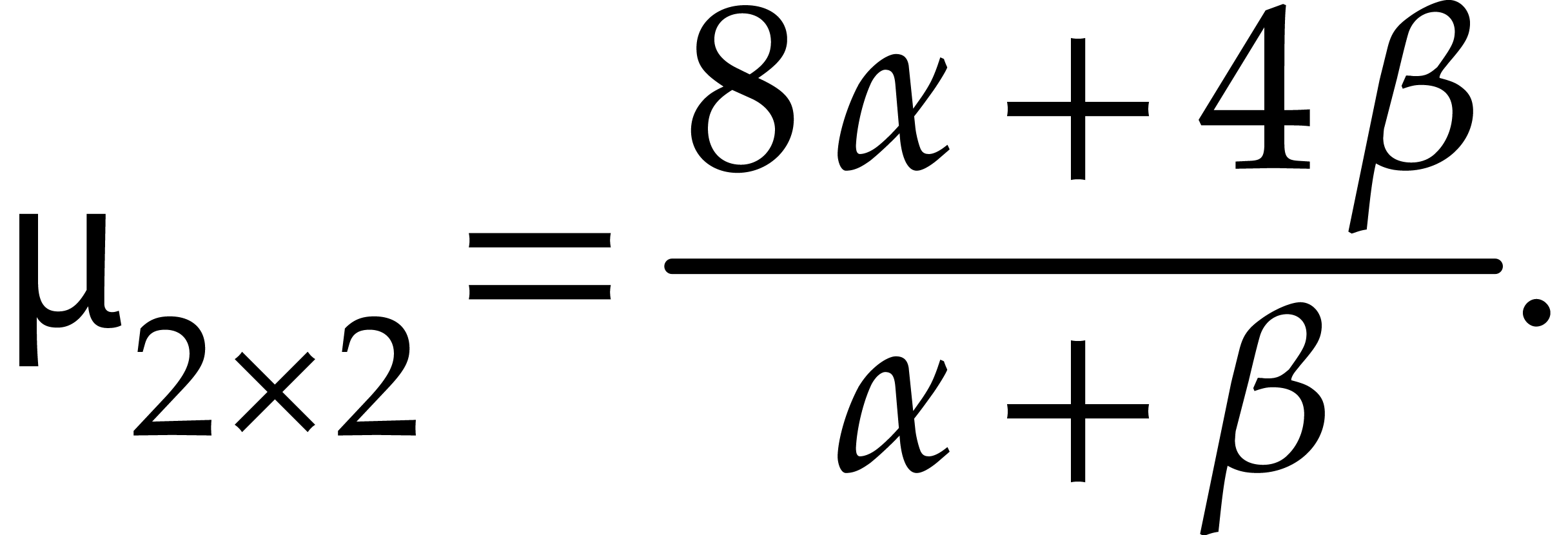
This analysis can be generalized to general lengths  and to the case when we only use Karatsuba's method for degrees above a
certain threshold. In the latter case, it is usually favorable to choose
the threshold over
and to the case when we only use Karatsuba's method for degrees above a
certain threshold. In the latter case, it is usually favorable to choose
the threshold over 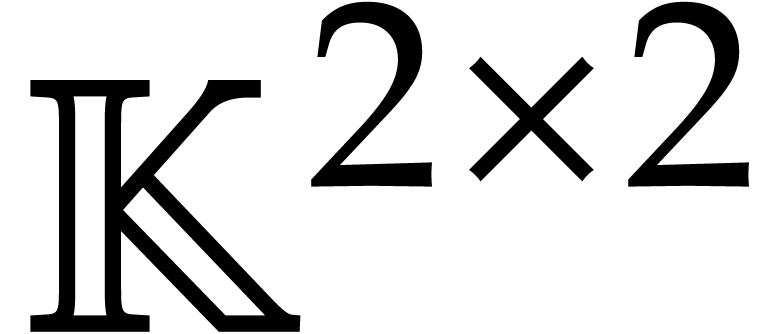 to be slightly lower than the
threshold over
to be slightly lower than the
threshold over  .
.
Let  be such that
be such that 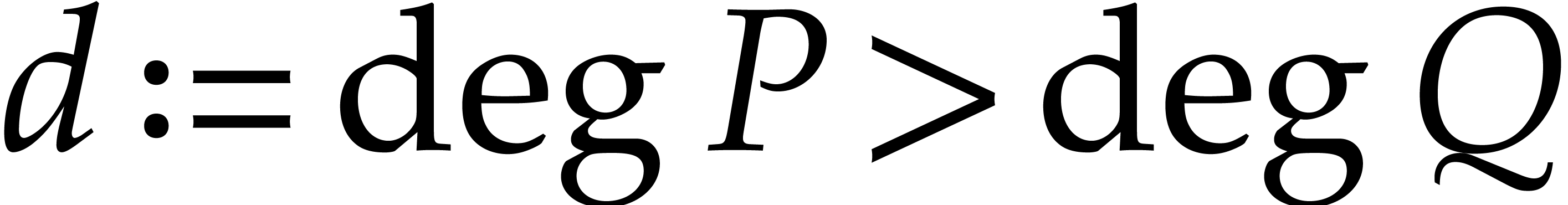 .
The Euclidean remainder sequence
.
The Euclidean remainder sequence 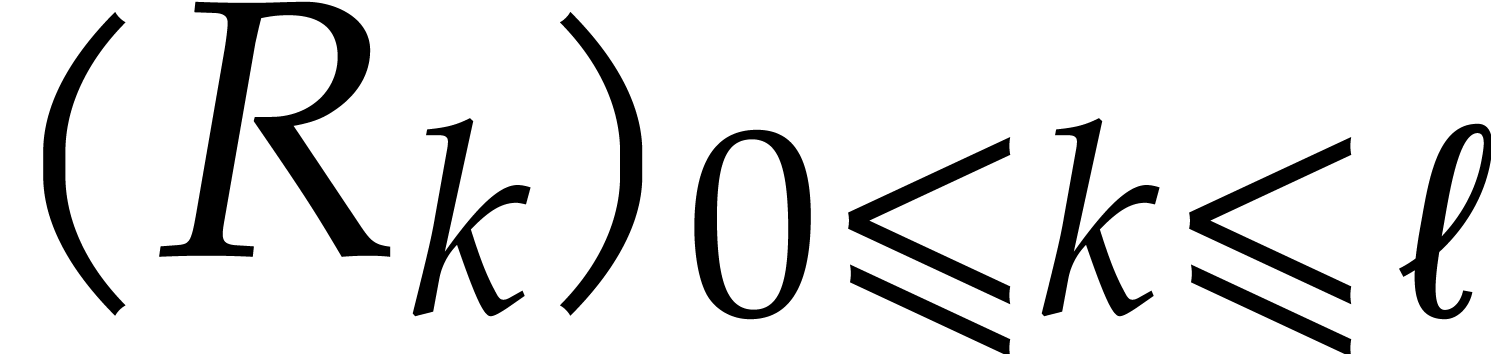 is
defined by
is
defined by
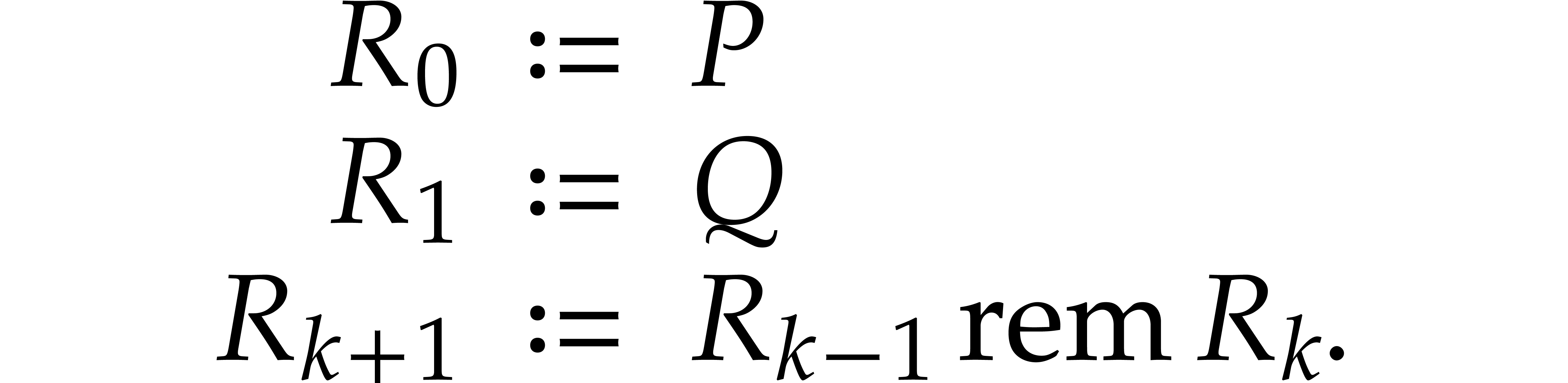
The length of the sequence is the smallest index  for which
for which  . For
. For
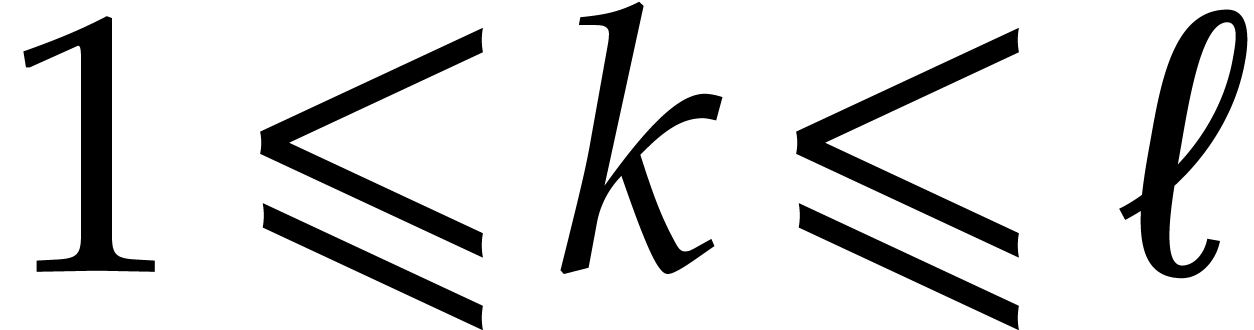 , we set
, we set
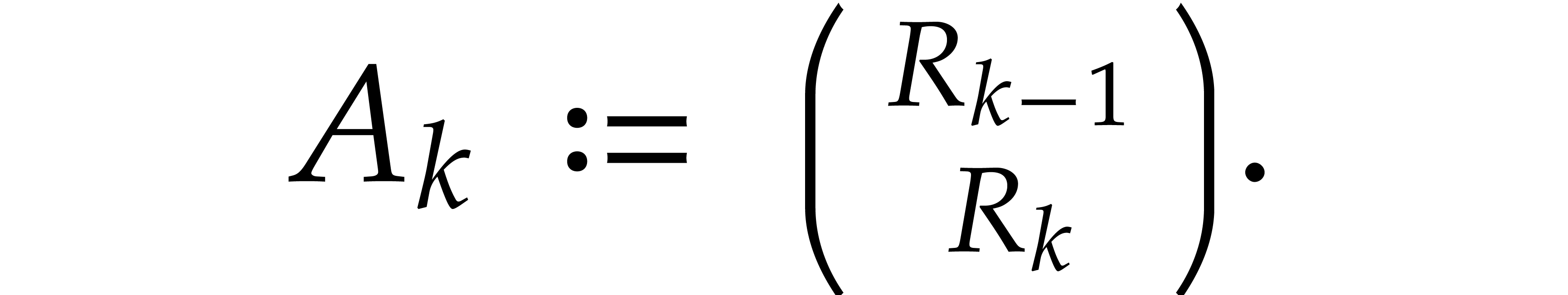
We also define the sequence of Bezout matrices 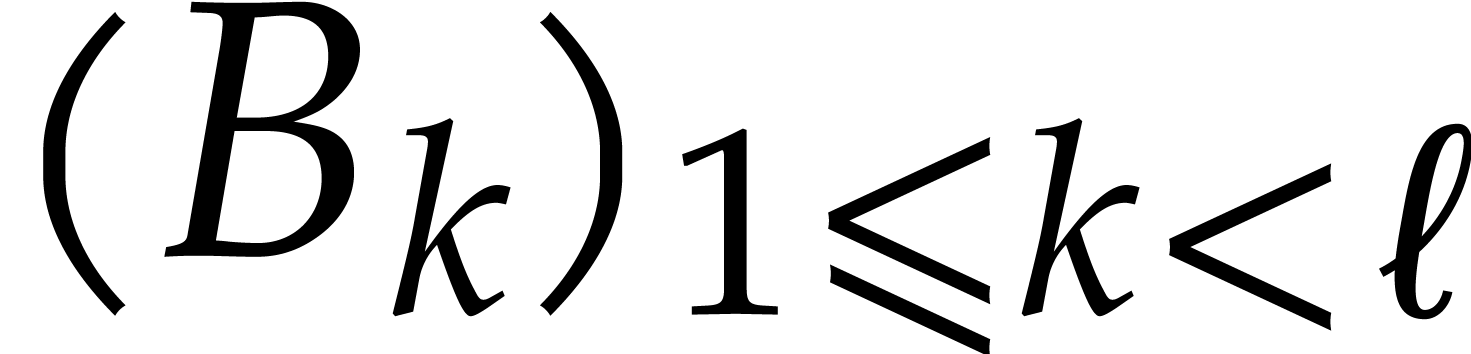 by
by
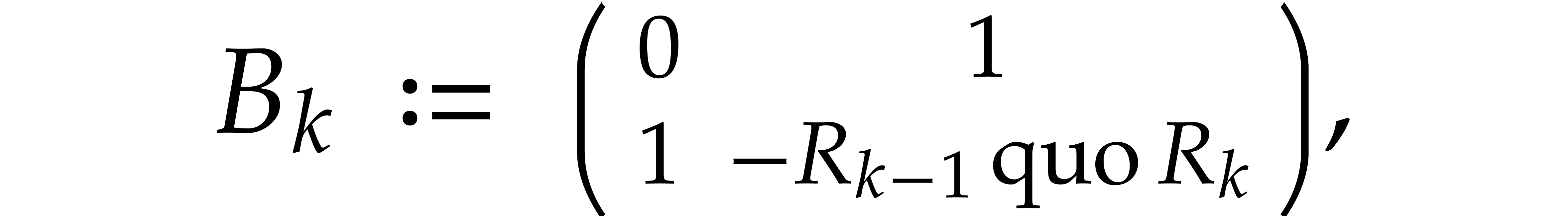
so that

for 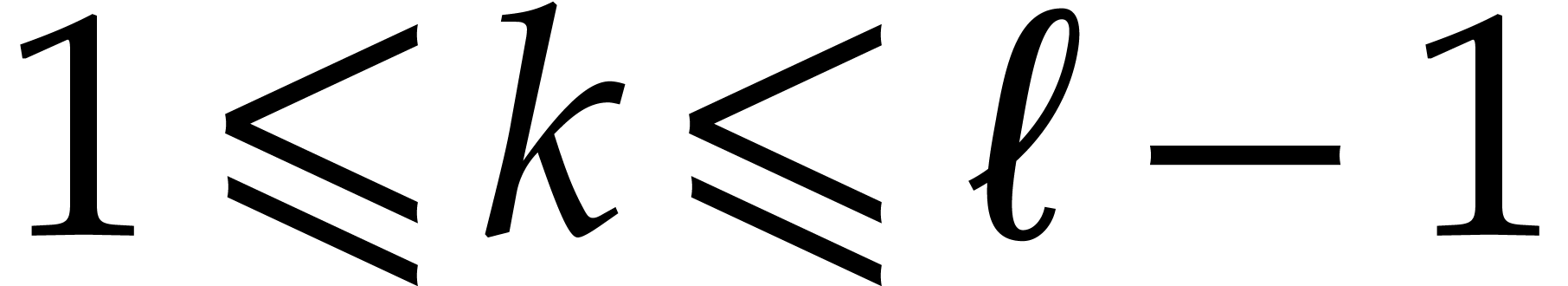 . We have
. We have 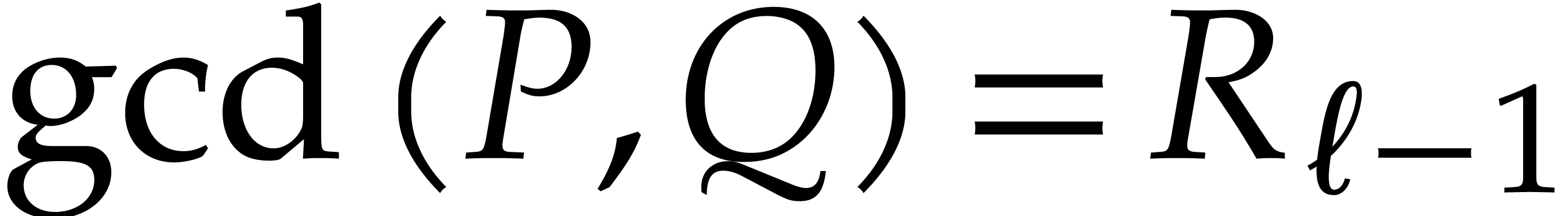 .
.
We regard  as a matrix polynomial in
as a matrix polynomial in 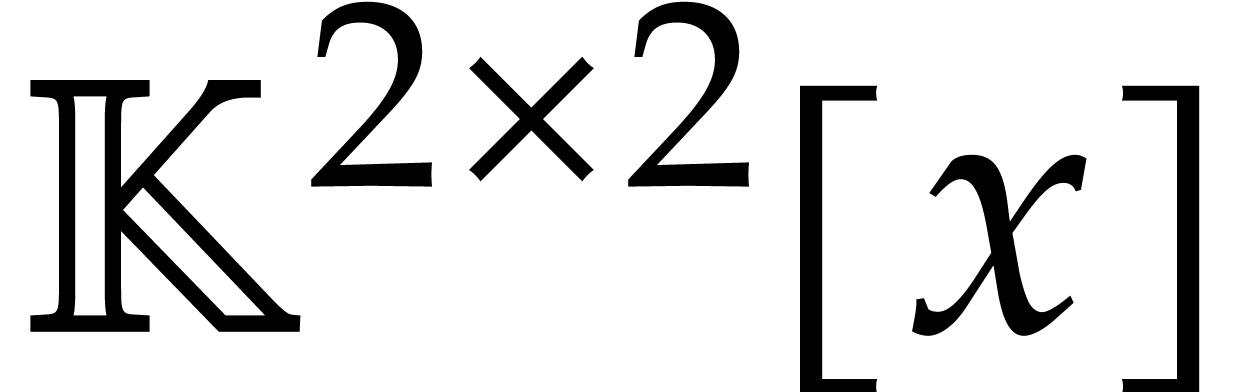 and say that
and say that 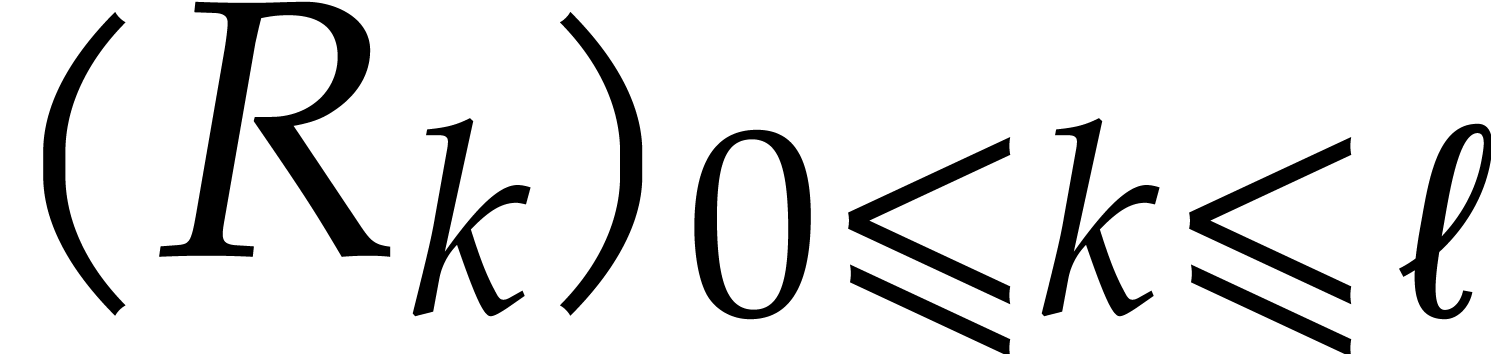 and
and 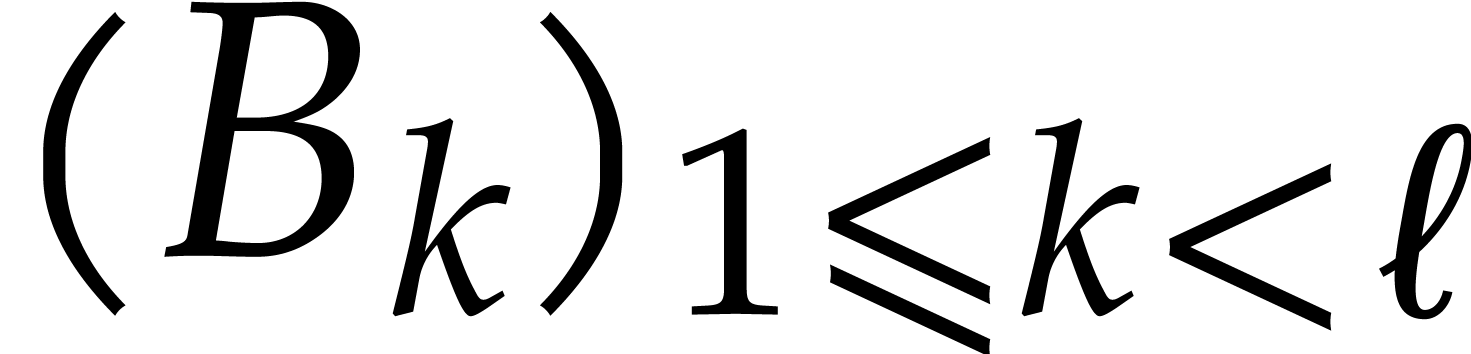 are normal if
are normal if 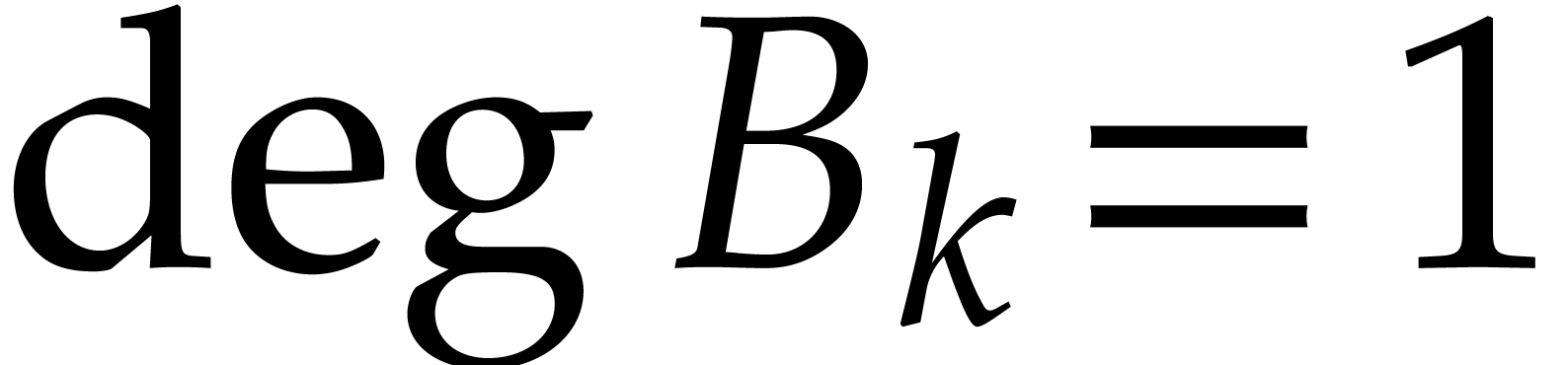 for all
for all  . This is the case if and only if
. This is the case if and only if  and
and 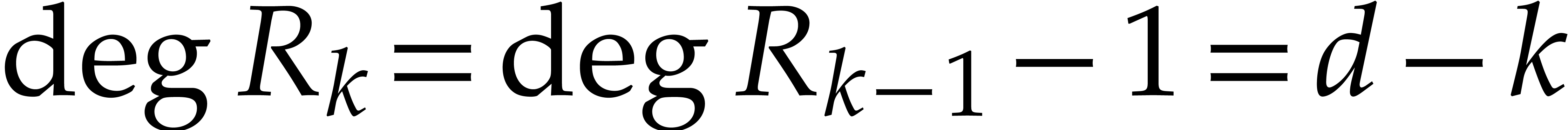 for all
for all 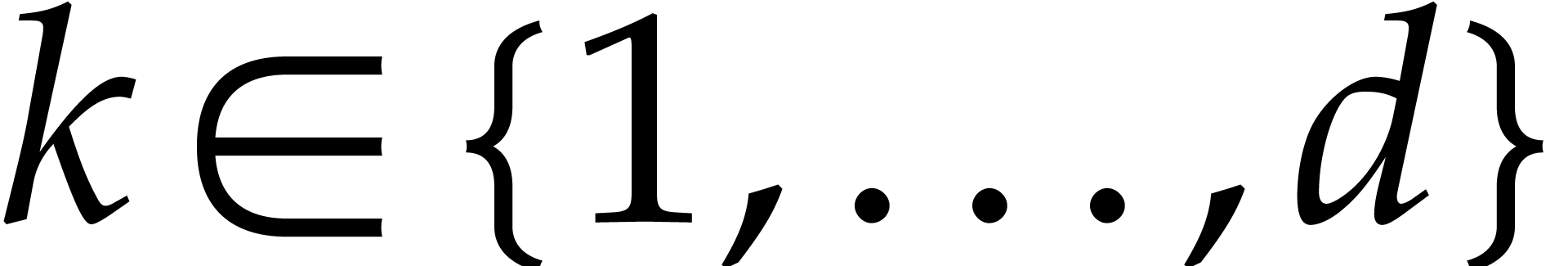 . For
. For 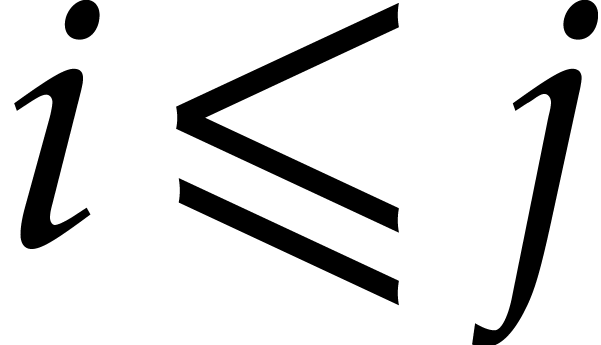 ,
we also define
,
we also define
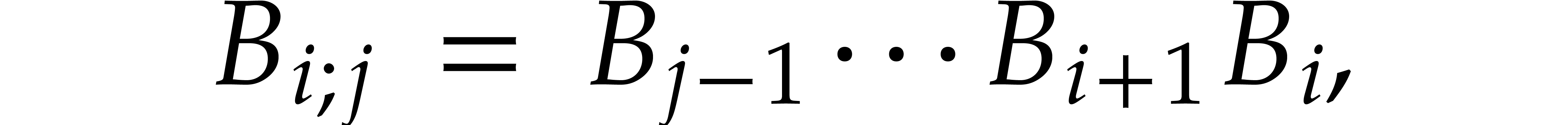
so that
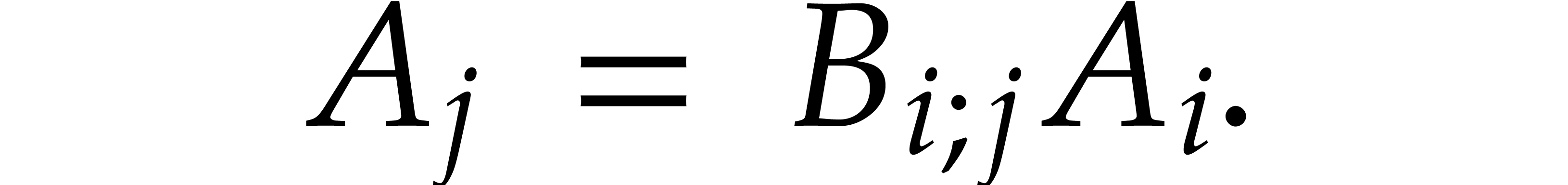
(We understand that 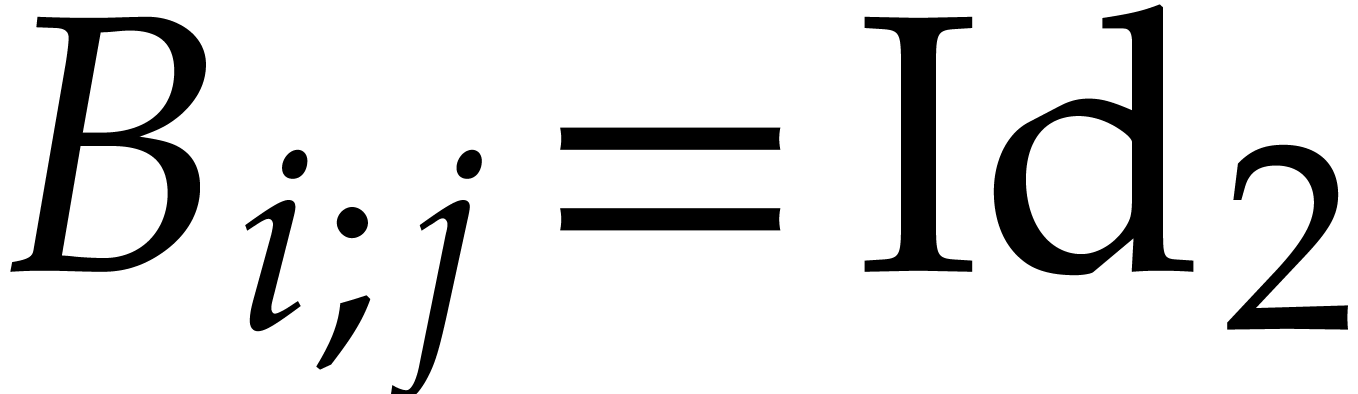 if
if 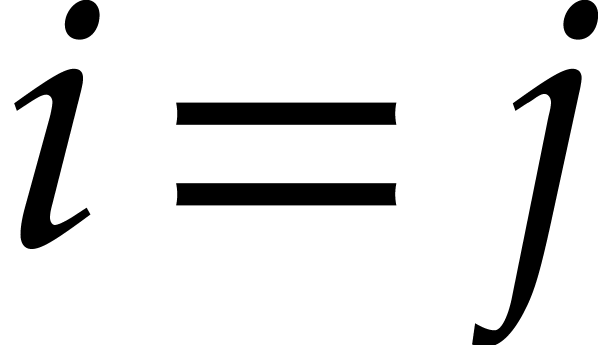 .) In particular,
.) In particular,

so an extended gcd computation essentially boils down to the computation
of the matrix product  . In
the case of a normal remainder sequence, this is done most efficiently
using binary splitting:
. In
the case of a normal remainder sequence, this is done most efficiently
using binary splitting:
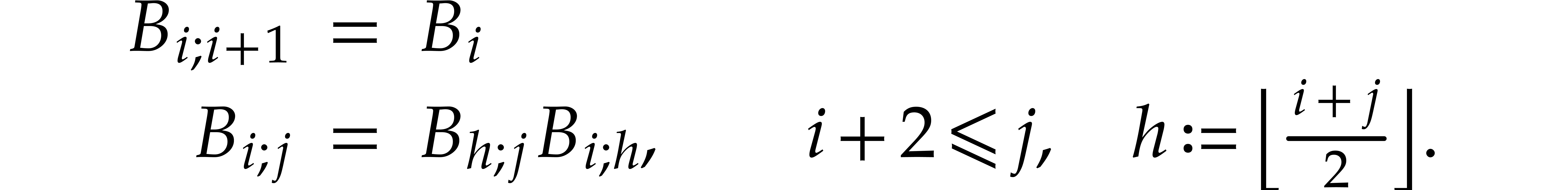
In essence, this is also how the half-gcd algorithm works.
 , we have
, we have
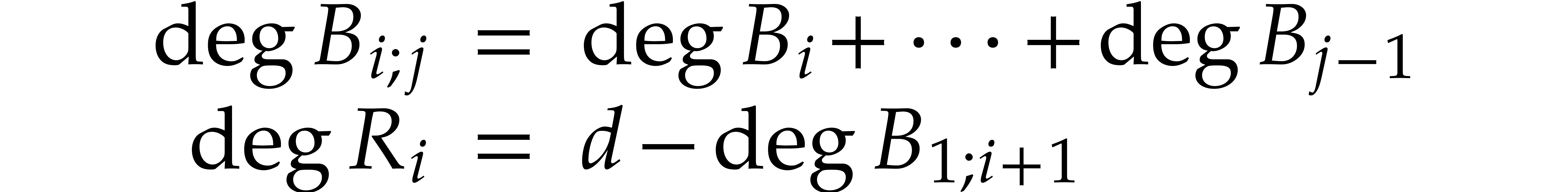
In particular, if  is normal, then
is normal, then 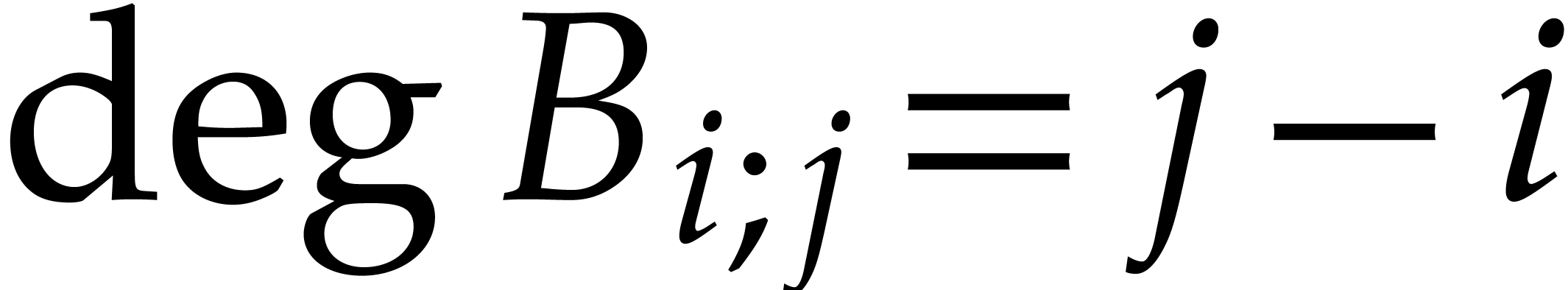 and
and 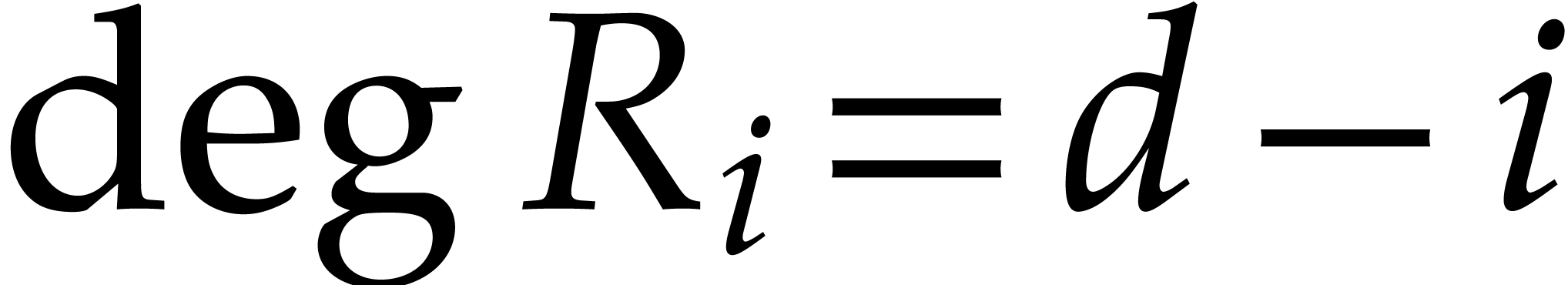 .
.
Proof. Let us show by induction on 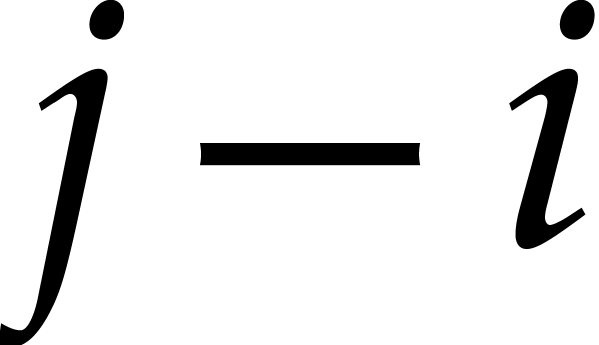 that
that
for any  . This is clear if
. This is clear if
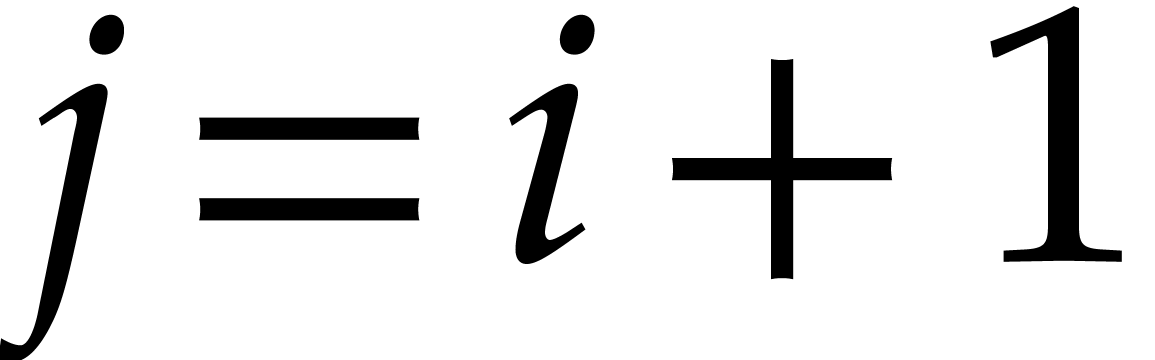 , so assume that
, so assume that  and let
and let  . Then
. Then
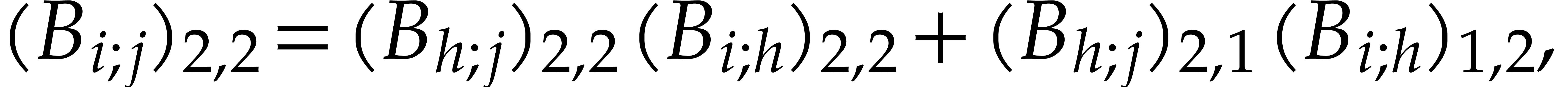
so the induction hypothesis yields

whence 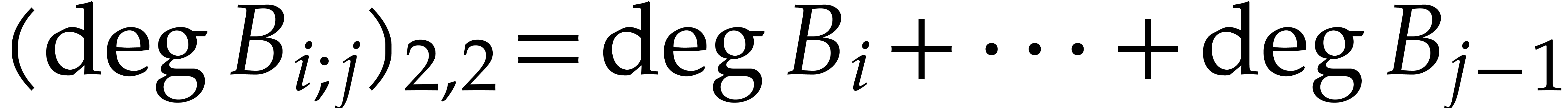 . In a similar way,
the induction hypothesis yields
. In a similar way,
the induction hypothesis yields 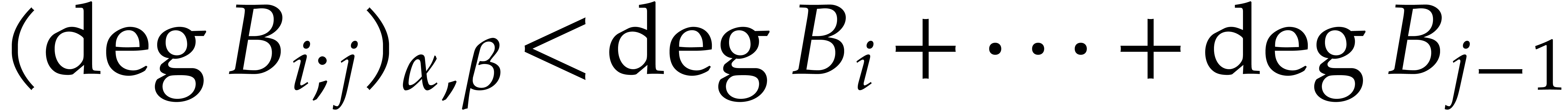 for all
for all  .
.
As to the second relation, we note that

whence 

Example 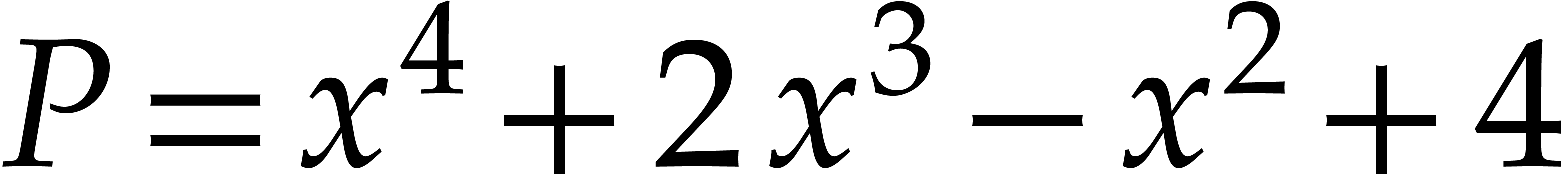 and
and  , we
obtain the following normal remainder sequence:
, we
obtain the following normal remainder sequence:
In the irnormal case, it is convenient to work with an alternative
indexation of remainder sequences for which  , as in the normal case. Note that we will not
consider abnormal remainder sequences until section 5
below, so the reader may safely skip this subsection until there.
, as in the normal case. Note that we will not
consider abnormal remainder sequences until section 5
below, so the reader may safely skip this subsection until there.
Let us now explain our reindexation in detail. For any  , let
, let
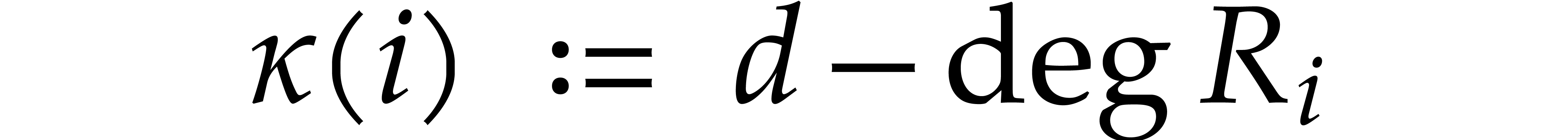
We also take

Then we set
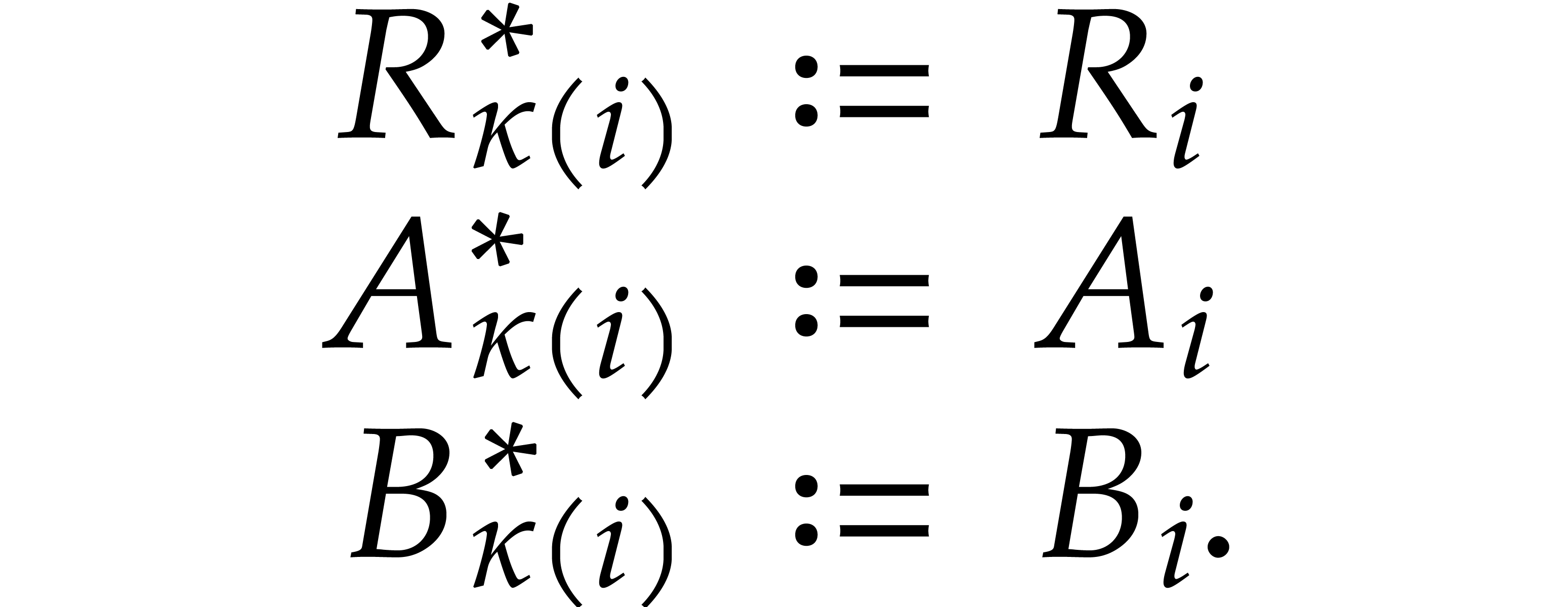
Moreover, for any  , we define
, we define
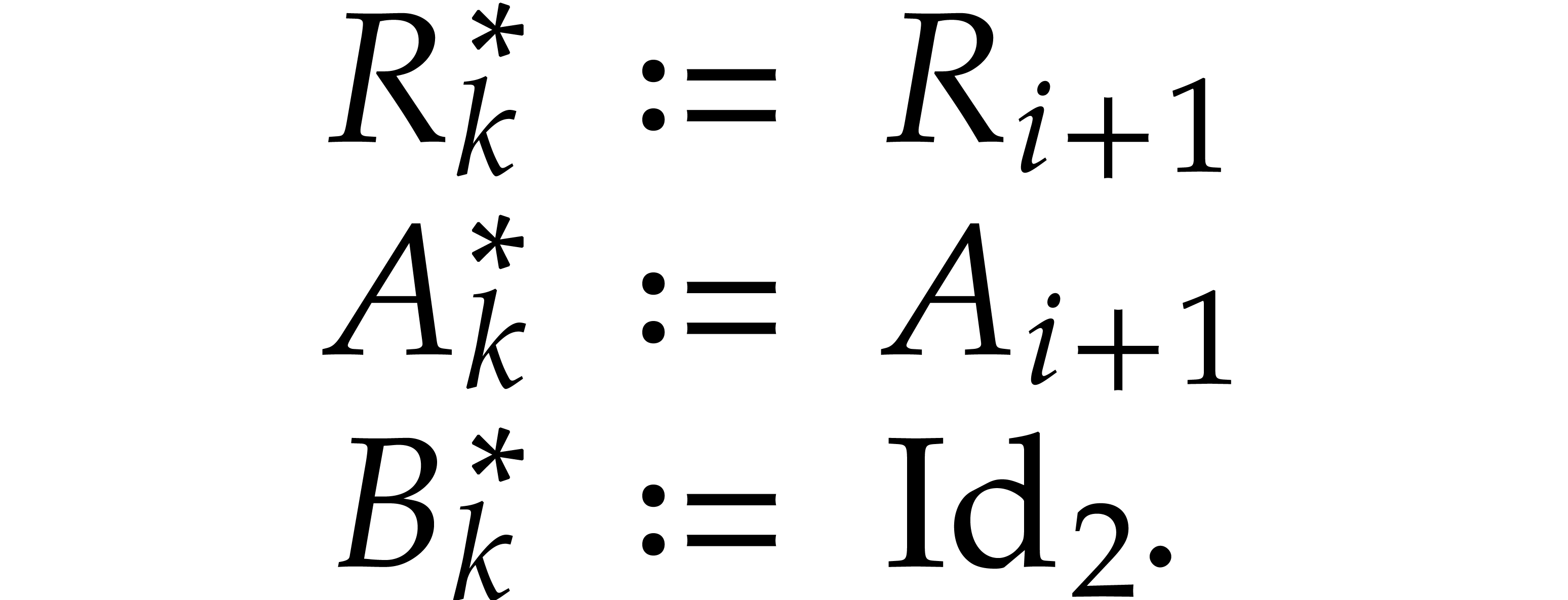
For  , we also define
, we also define
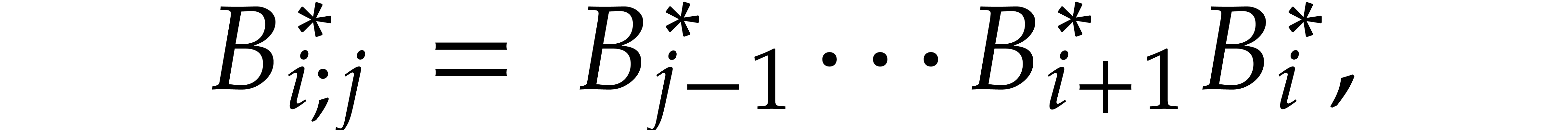
so that we still have
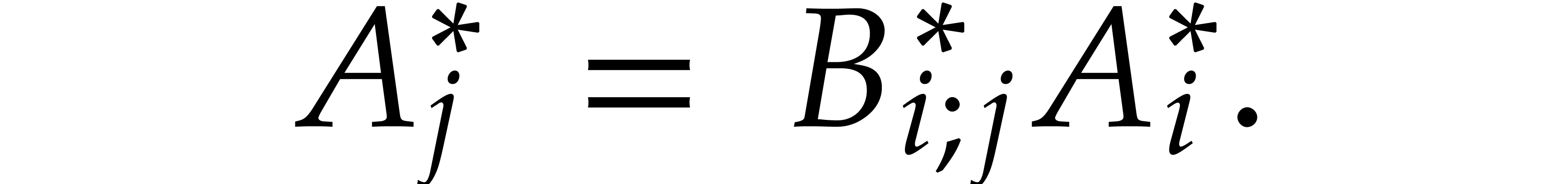
By construction, for 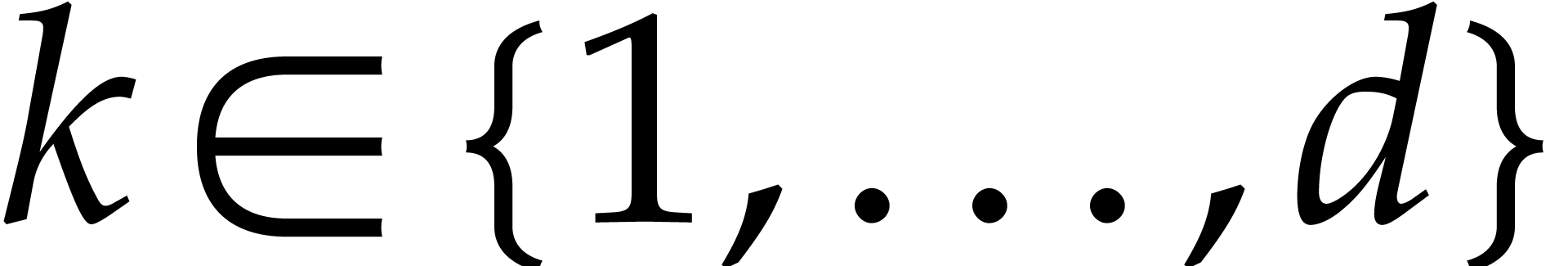 , we
have
, we
have

As before, we will sometimes write 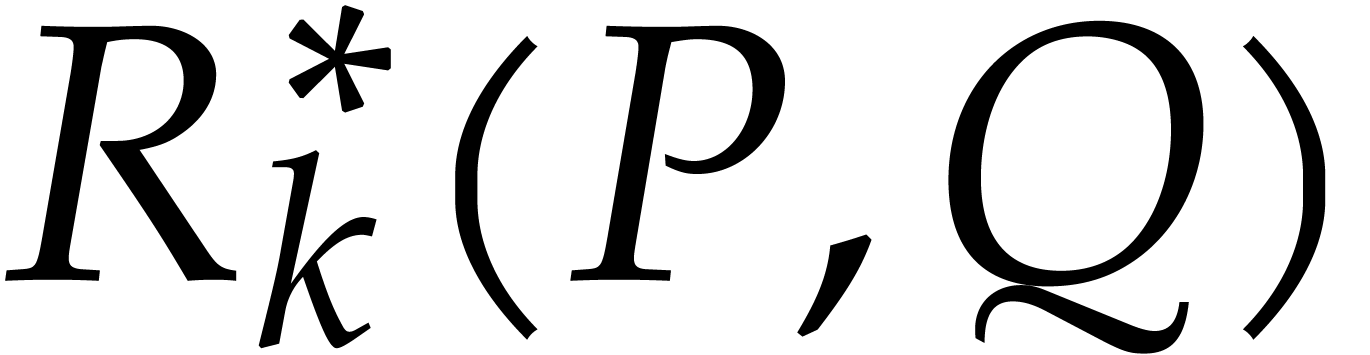 instead of
instead of
 in order to emphasize the dependence on
in order to emphasize the dependence on  and
and  , and
similarly for
, and
similarly for  , etc.
Occasionally, when
, etc.
Occasionally, when  is not clear from the
context, we also write
is not clear from the
context, we also write 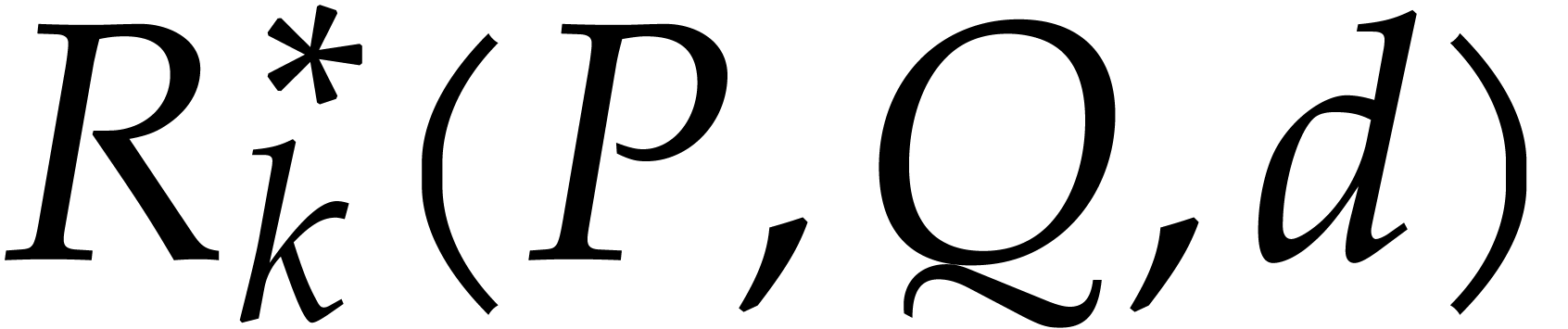 ,
,
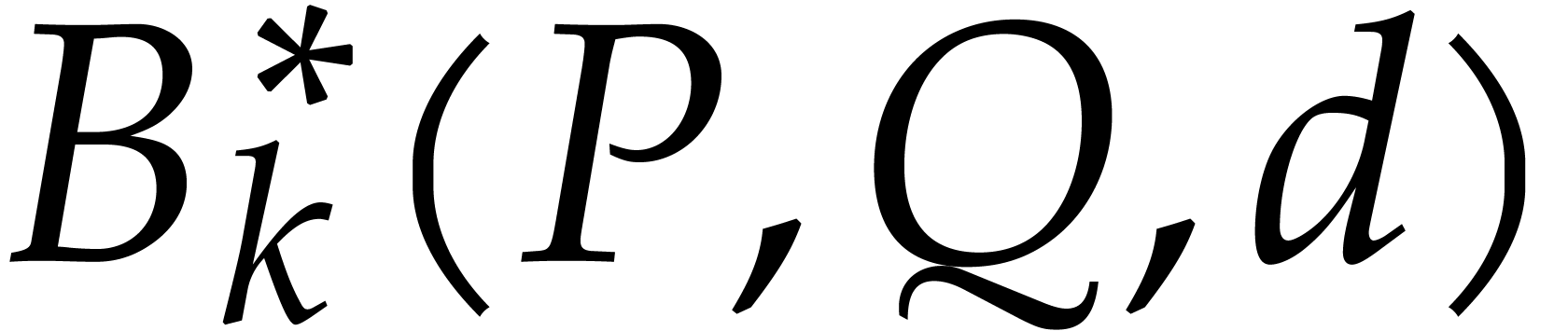 , etc.
, etc.
Example  and
and  , we
have
, we
have
After reindexation 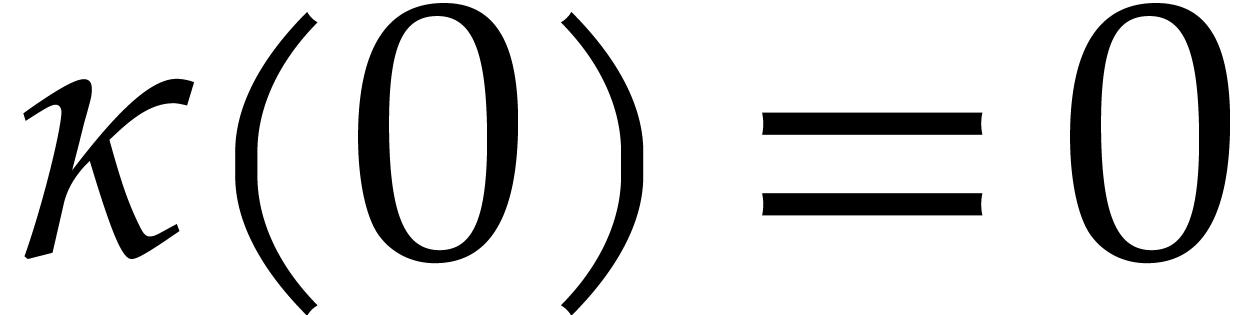 ,
,  ,
,  ,
,
 , and
, and 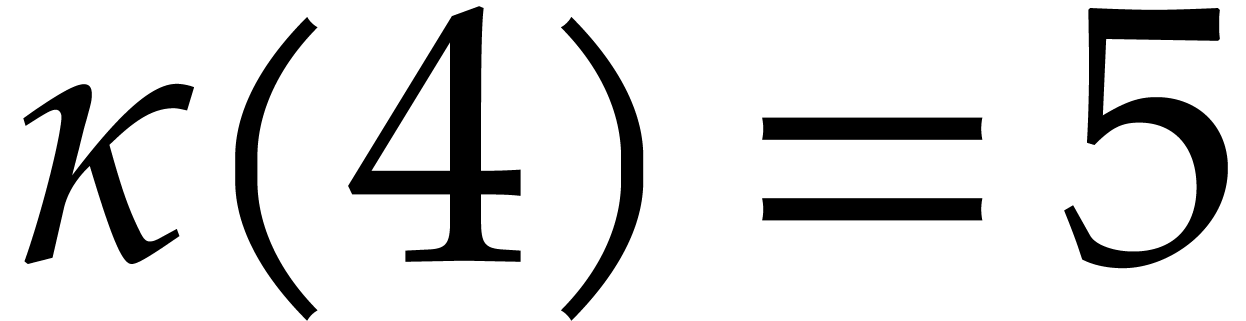 , we obtain
, we obtain
Let  be as in the previous section with remainder
sequence
be as in the previous section with remainder
sequence 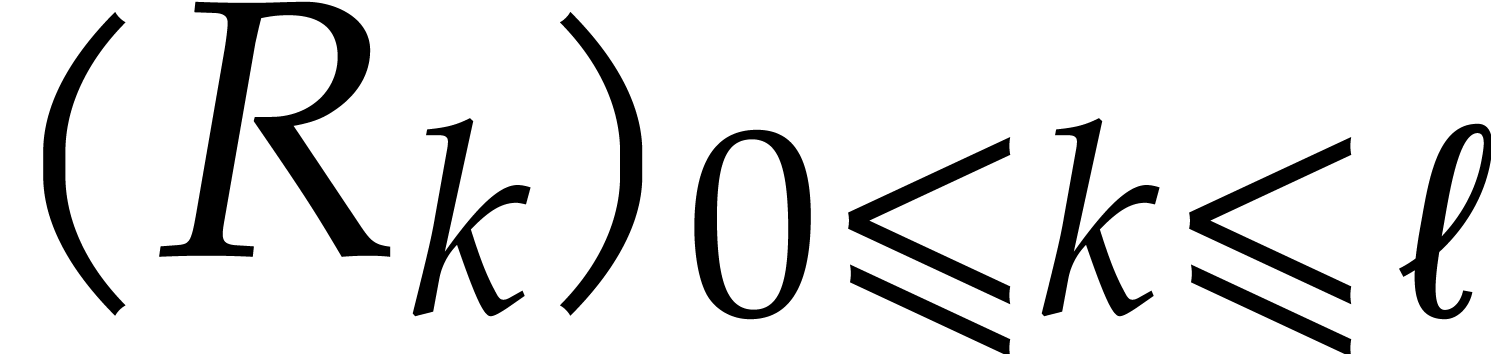 . We will write
. We will write 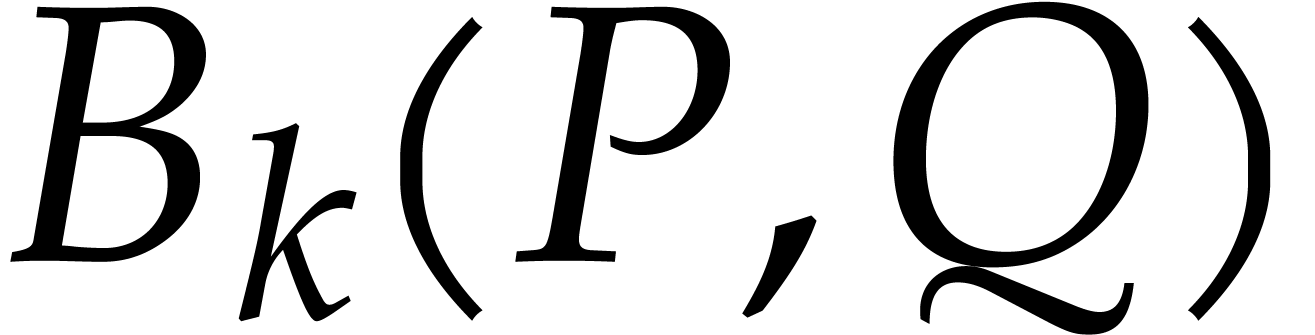 for the corresponding
for the corresponding  -th
Bezout matrix
-th
Bezout matrix  in case we wish to make the
dependency on
in case we wish to make the
dependency on  and
and  clear.
Similarly, we define
clear.
Similarly, we define 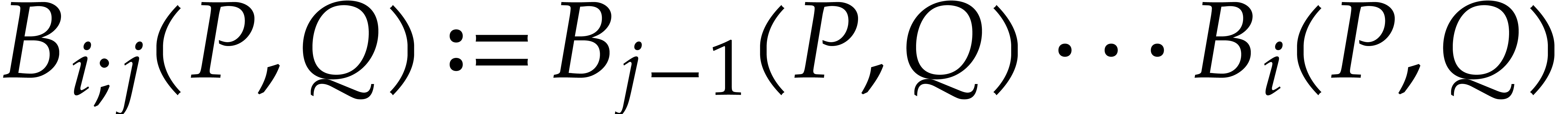 and
and 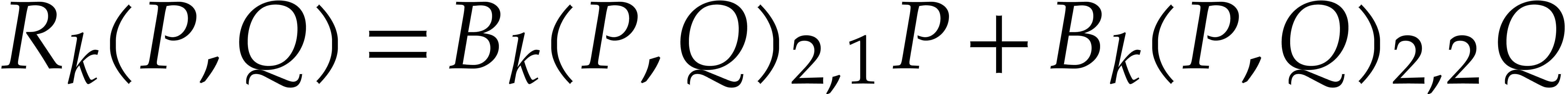 . Given a polynomial
. Given a polynomial  and
indices
and
indices  , it will also be
convenient to define
, it will also be
convenient to define

Here we understand that 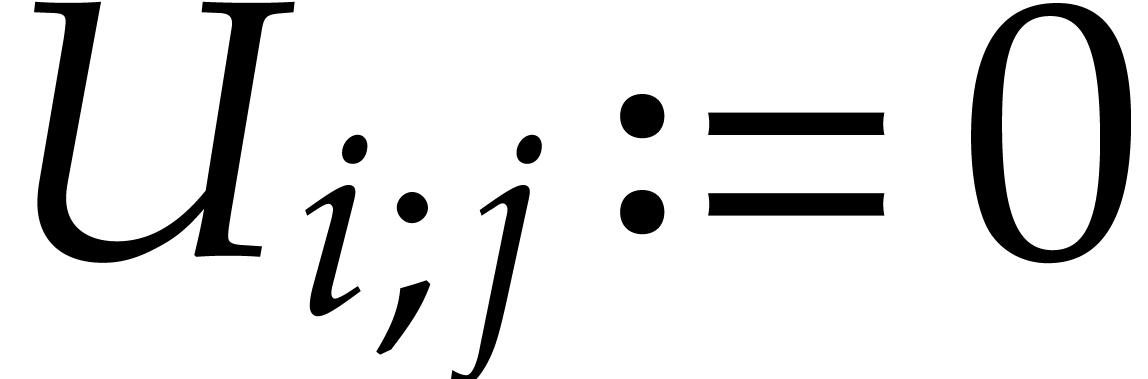 whenever
whenever  .
.
Proof. We have 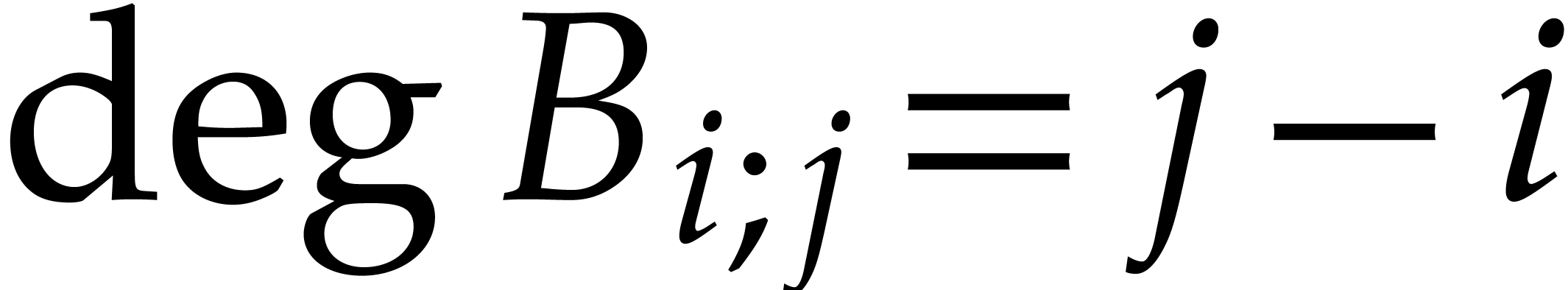 for all
for all
 . For
. For  , the relation
, the relation

thus shows that the coefficient 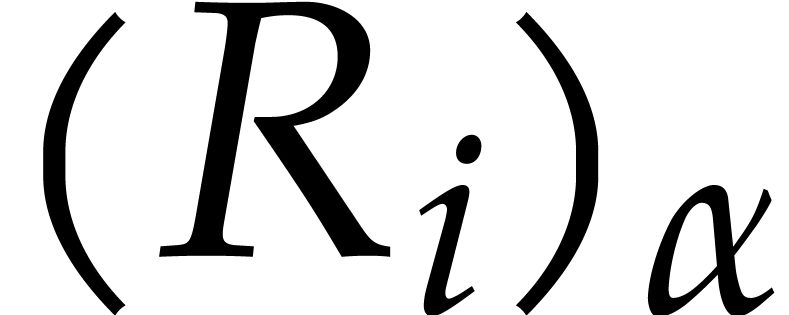 of degree
of degree  in
in 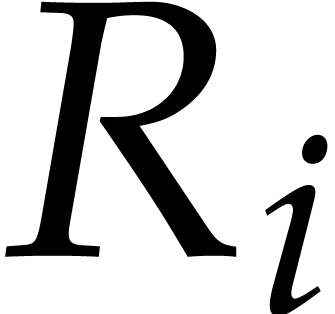 only depends on
coefficients
only depends on
coefficients  and
and  of
of  and
and  with
with 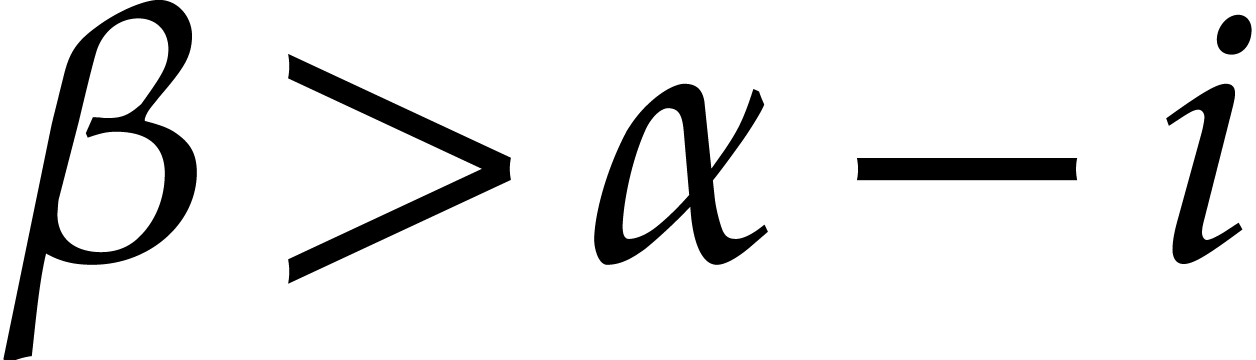 . In particular,
. In particular,

and
since 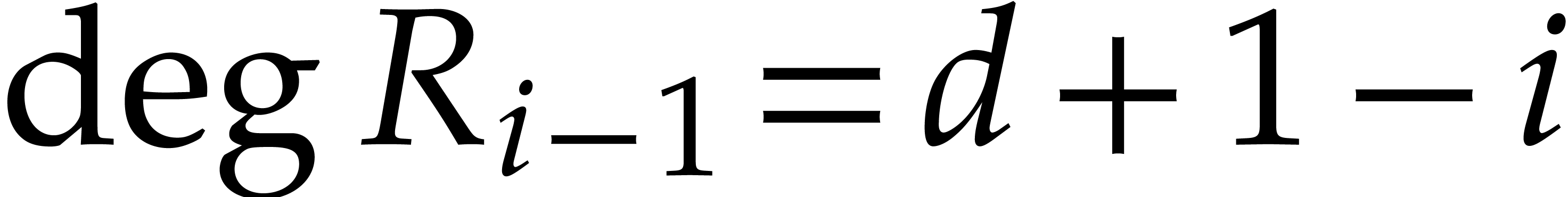 and
and 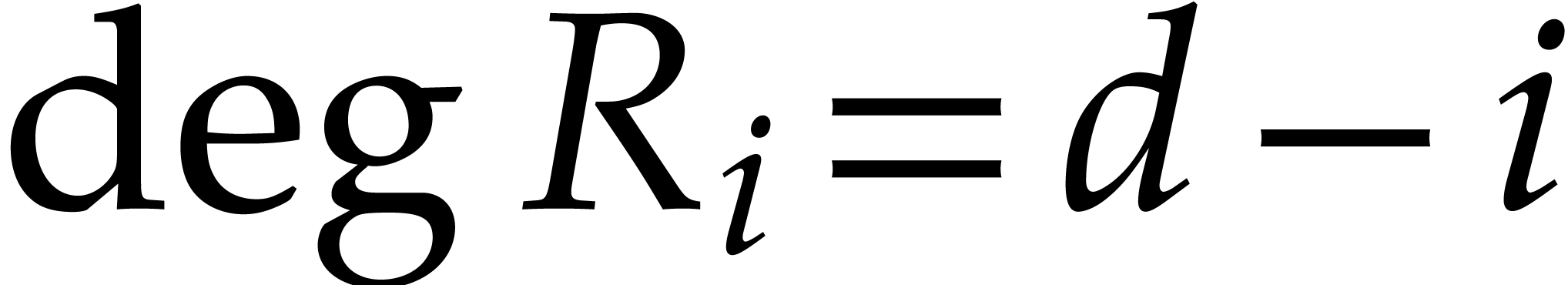 .
This shows that
.
This shows that

By induction on  , we also
obtain
, we also
obtain 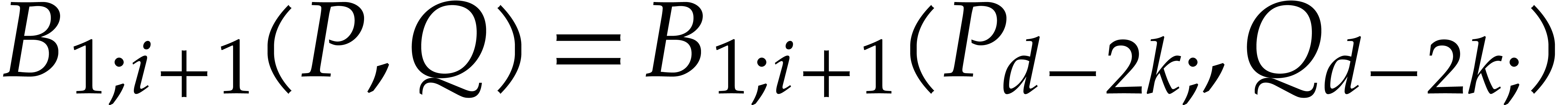 . We conclude by
taking
. We conclude by
taking 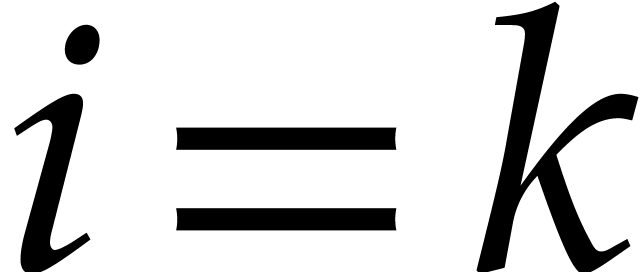 .
.
The lemma leads to the following recursive algorithm for the computation
of  :
:
Algorithm
Output: |
Proof. If  ,
then the result follows from Lemma 4. If
,
then the result follows from Lemma 4. If 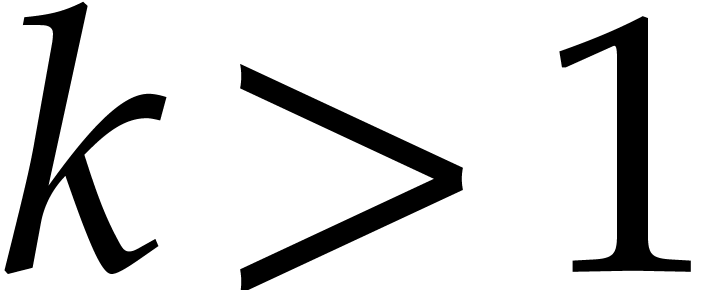 , then Lemma 4 implies
, then Lemma 4 implies 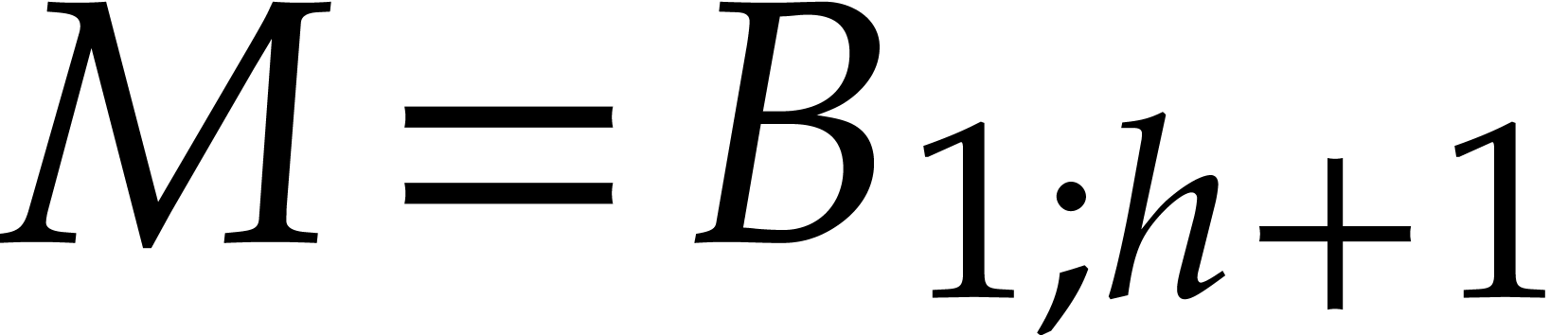 , whence
, whence 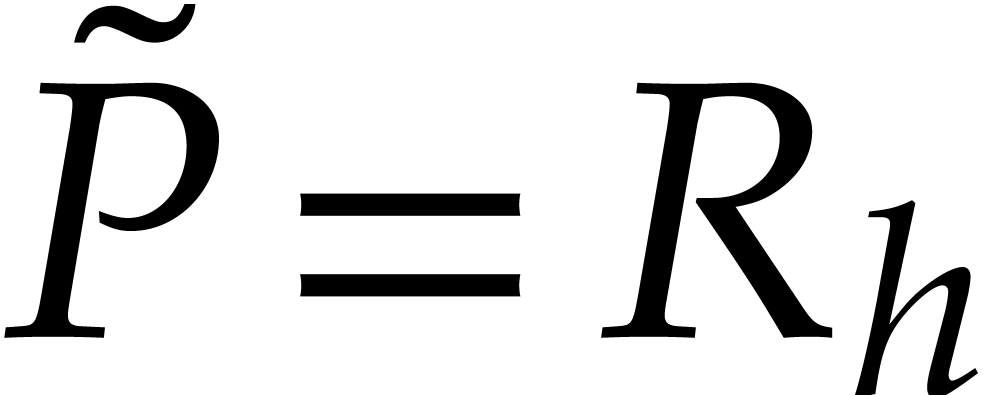 and
and 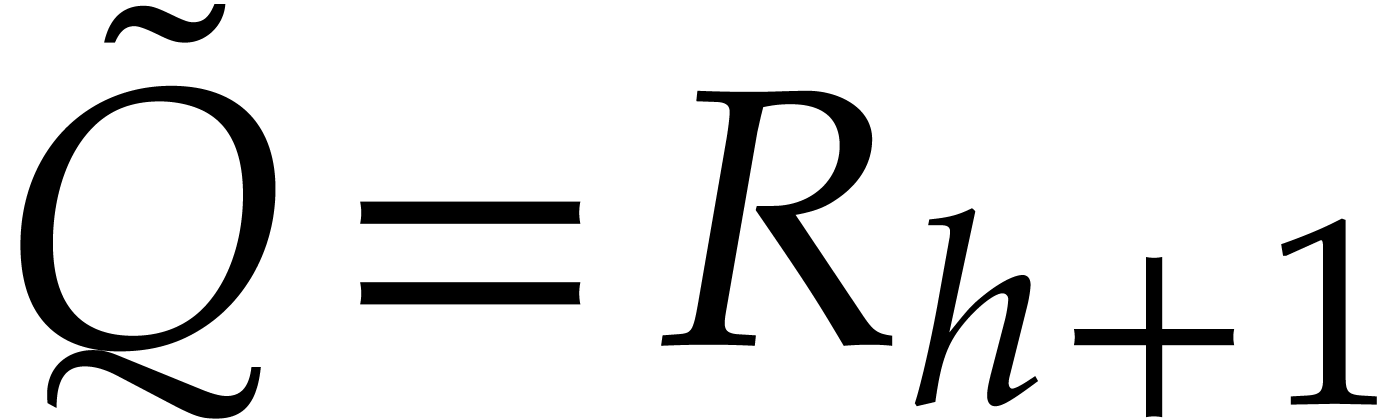 . For
. For 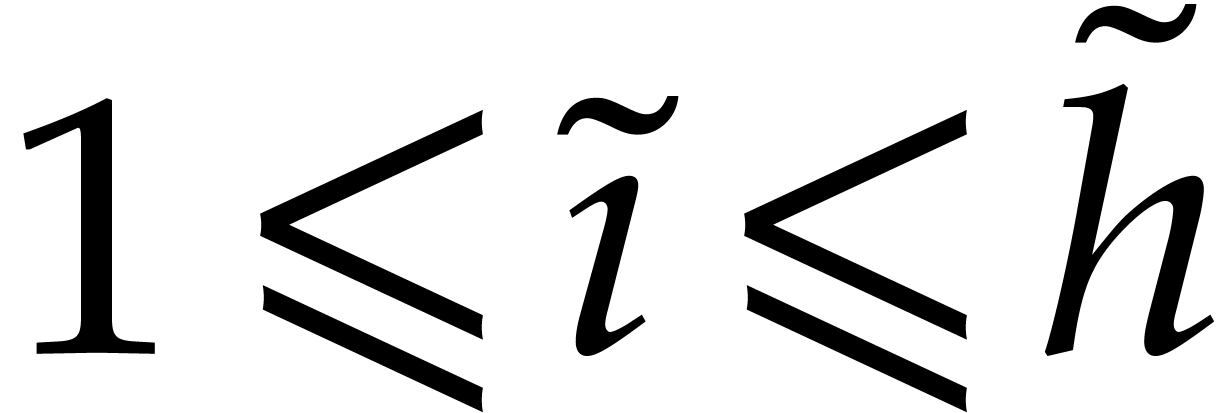 , we have
, we have  .
This allows us to apply Lemma 4 once more, and obtain
.
This allows us to apply Lemma 4 once more, and obtain  . We conclude by noting that
. We conclude by noting that 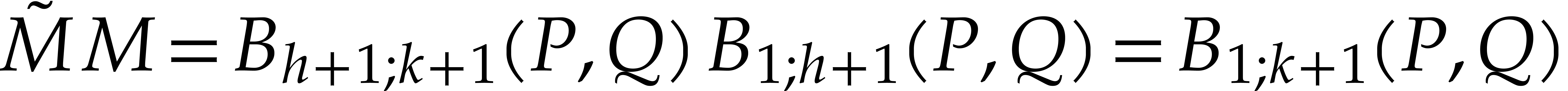 .
.
Let us now show how to compute  and
and 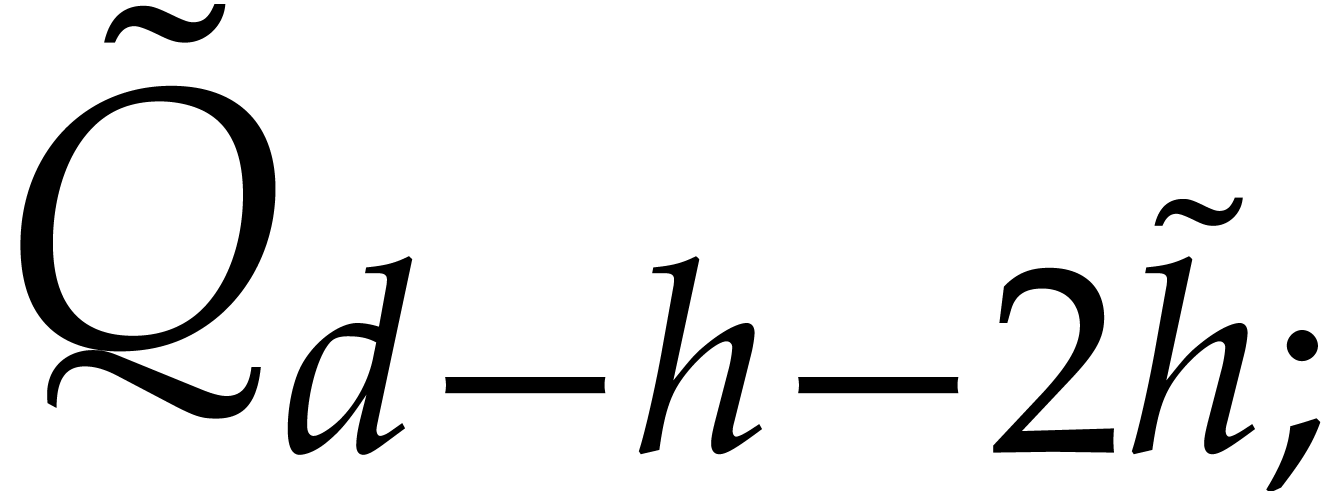 efficiently in step 4 using a middle product
of
efficiently in step 4 using a middle product
of  matrix polynomials. In order to simplify the
exposition, we assume that
matrix polynomials. In order to simplify the
exposition, we assume that  is a power of two; in
subsection 4.4 we will consider arbitrary lengths. We first
decompose all polynomials into blocks of degree
is a power of two; in
subsection 4.4 we will consider arbitrary lengths. We first
decompose all polynomials into blocks of degree 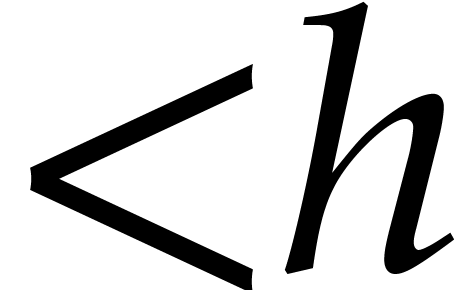 . More precisely, let
. More precisely, let

so that

and
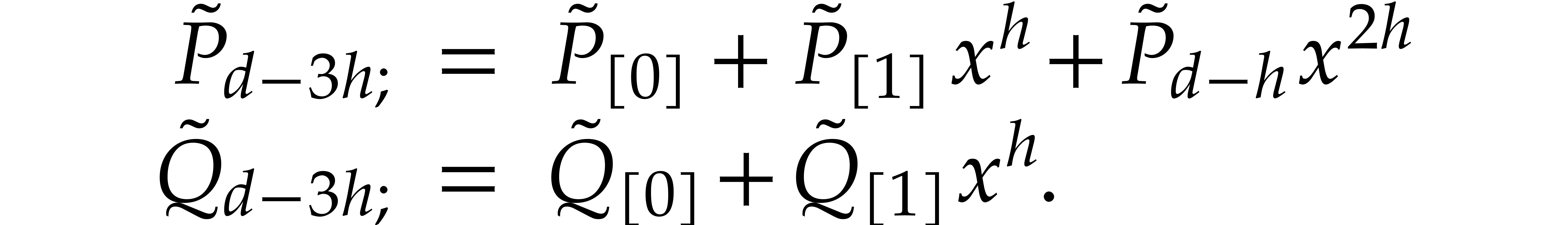
Then we observe that
where the left hand matrix has degree
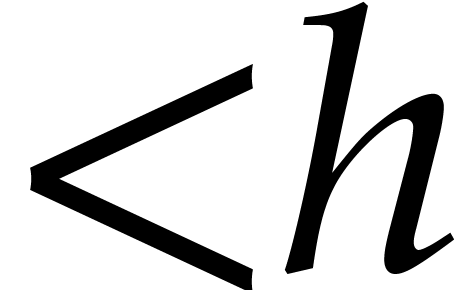 ,
where
,
where
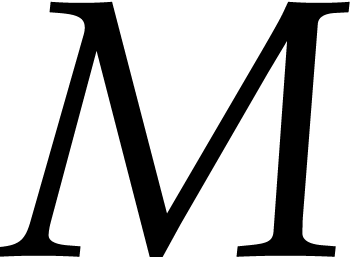 has degree
has degree
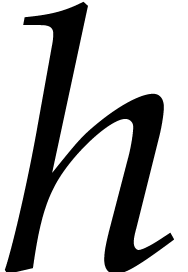 ,
and where the right hand matrix has degree
,
and where the right hand matrix has degree
 ;
see also Figure
1
.
;
see also Figure
1
.
 can be recovered in linear time using
can be recovered in linear time using
Before we discuss further optimizations that are specific to the binary FFT model, let us first consider a general multiplication scheme (that satisfies the assumptions from section 2.2), and analyze the complexity of Algorithm 1 with the middle product optimization.

Moreover, for a multiplication with  for
some
for
some  , the cost is
, the cost is

Proof. Recall that we assumed  to be a power of two. Then the running time of the algorithm satisfies
the recurrence inequality
to be a power of two. Then the running time of the algorithm satisfies
the recurrence inequality
Unrolling this relation while using the assumption that  is non-decreasing yields the first bound. If
is non-decreasing yields the first bound. If 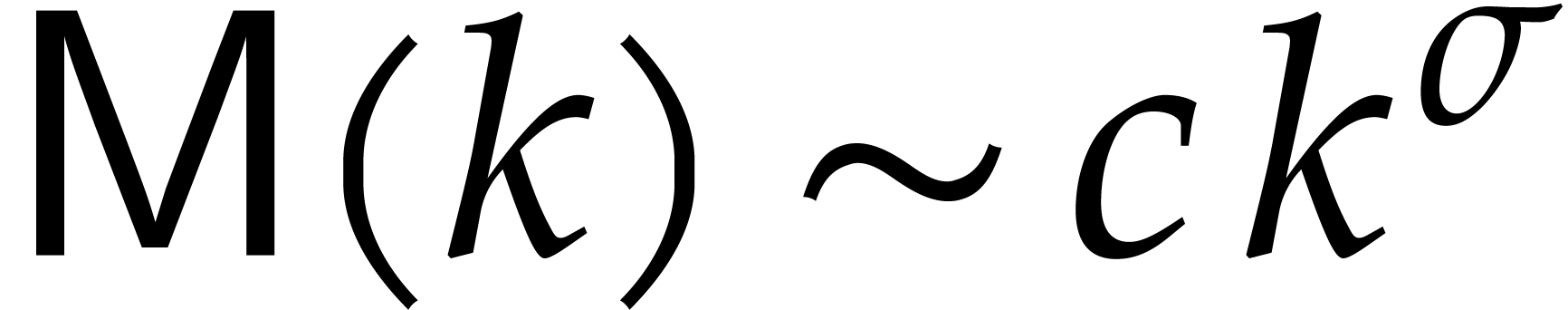 for
some
for
some  and
and  ,
then the relation (6) yields
,
then the relation (6) yields 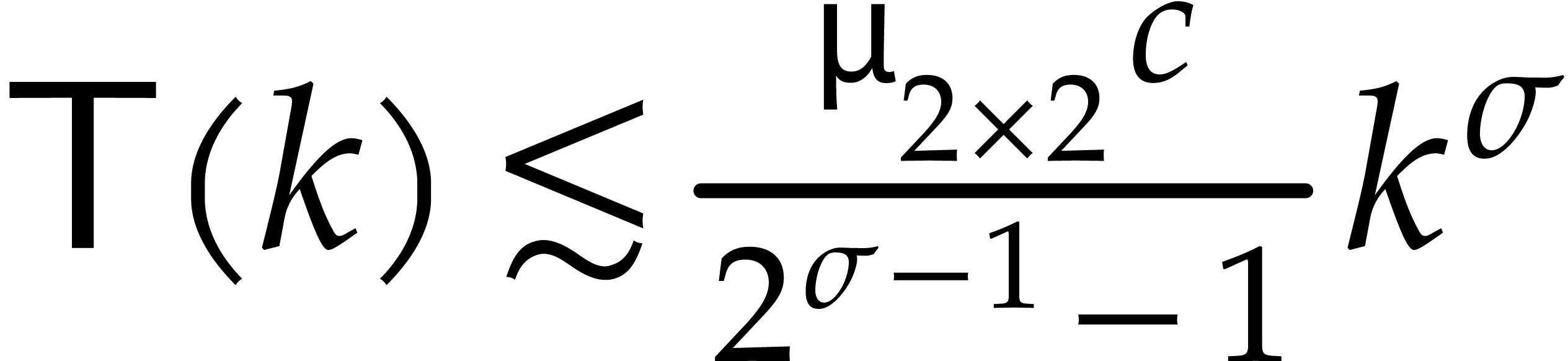 .
.
In order to efficiently implement Algorithm 1 with the
optimizations from the previous subsection in the binary FFT model, let
us again assume that  is a power of two. We
essentially have to compute a
is a power of two. We
essentially have to compute a  matrix middle
product in step 4 and a
matrix middle
product in step 4 and a  matrix
product in step 6. We will do all these computations using
DFTs of length
matrix
product in step 6. We will do all these computations using
DFTs of length 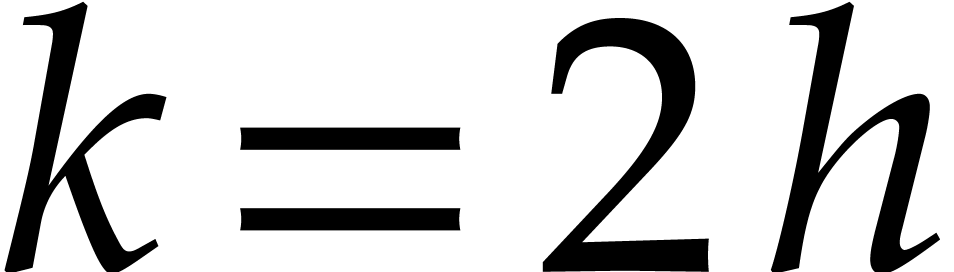 .
.
Let us first consider the middle product (4). We have  in (4) and the right hand side matrix
has degree
in (4) and the right hand side matrix
has degree 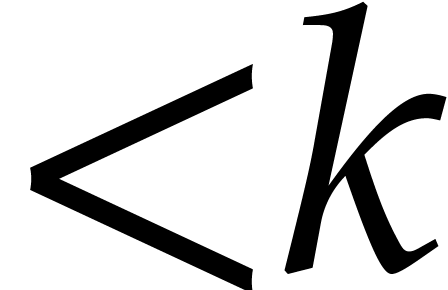 . Consequently, we
may apply (3) and compute the middle product using FFT
multiplication:
. Consequently, we
may apply (3) and compute the middle product using FFT
multiplication:
We also recall that the individual term  can be
recovered separately using (5).
can be
recovered separately using (5).
As to the matrix product 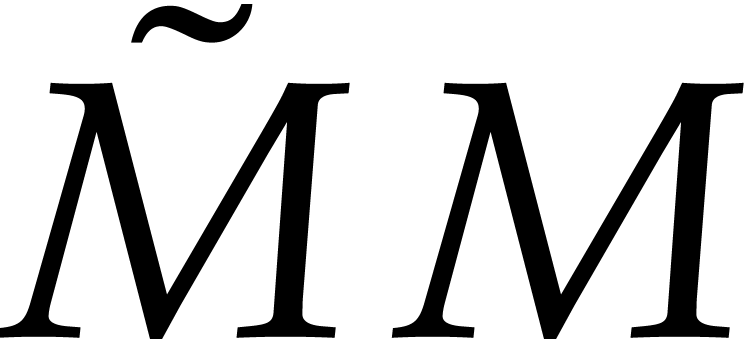 ,
its degree is
,
its degree is  , which is just
one too large to use FFT multiplication directly. Nevertheless, FFT
multiplication still allows us to compute
, which is just
one too large to use FFT multiplication directly. Nevertheless, FFT
multiplication still allows us to compute 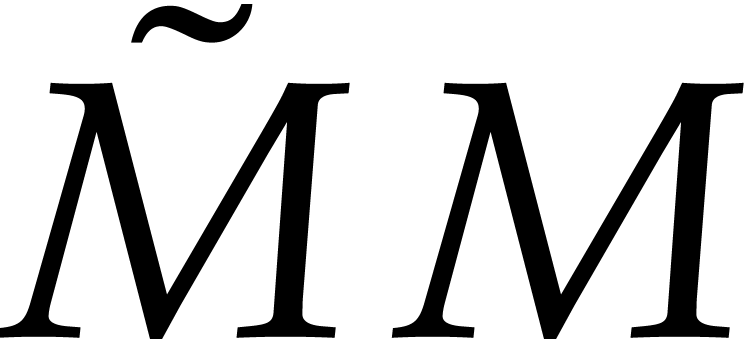 modulo
modulo
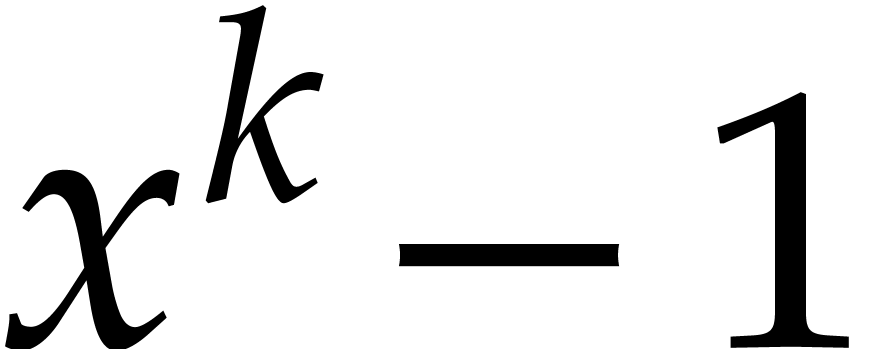 . Then we may simply recover
. Then we may simply recover
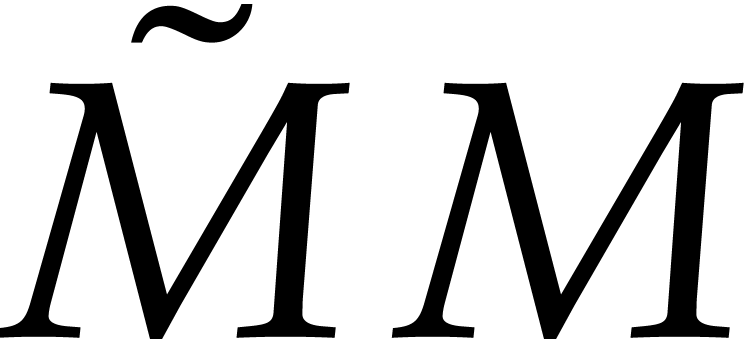 by computing the leading coefficient
by computing the leading coefficient 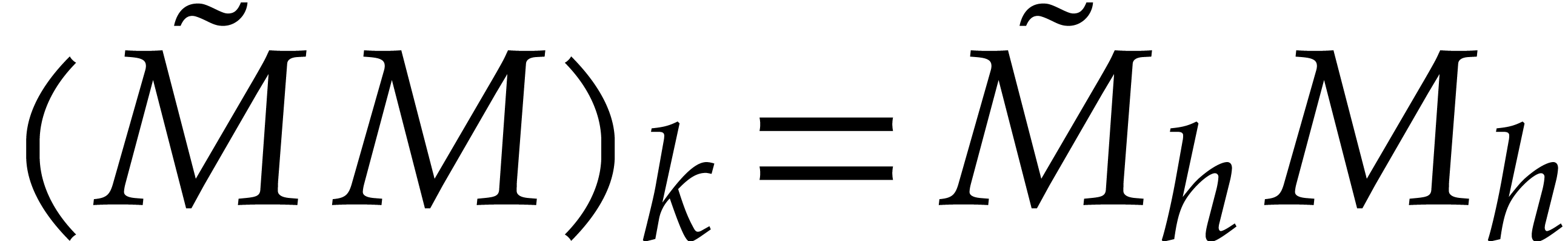 separately.
separately.
Now the FFT model also allows for “FFT caching” when doing
the recursive calls. In addition to 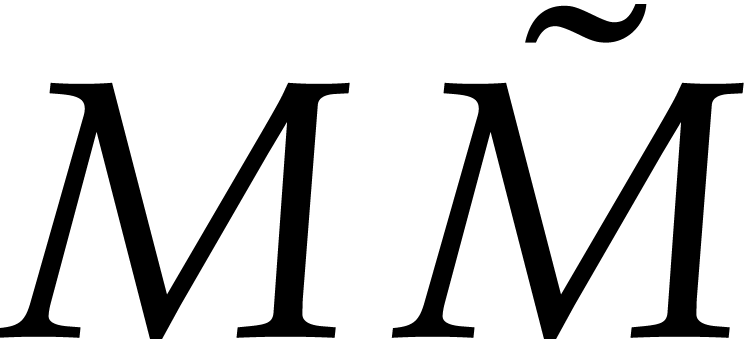 ,
we return its DFT transform at the end of the algorithm. When computing
the DFT transforms of
,
we return its DFT transform at the end of the algorithm. When computing
the DFT transforms of 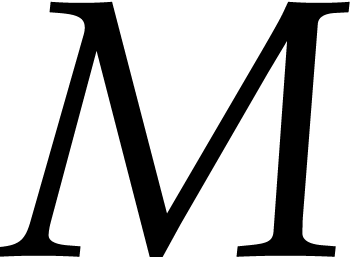 and
and 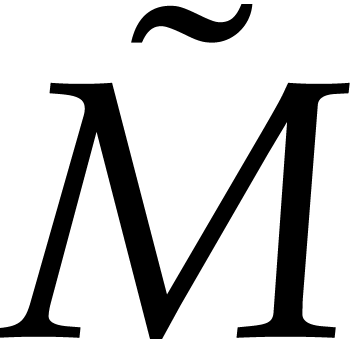 at length
at length  , this means that
we already know their DFT transforms at length
, this means that
we already know their DFT transforms at length  , and thereby save half of the work.
, and thereby save half of the work.
Summarizing, this leads to the following algorithm:
Proof. Since the algorithm is simply an adaptation of Algorithm 1 to the binary FFT model, it is correct by Proposition 5. Let us analyze the costs of the various steps without the recursive calls.
The cost of the DFTs in step 3 is bounded by  .
.
The cost of step 4 is bounded by 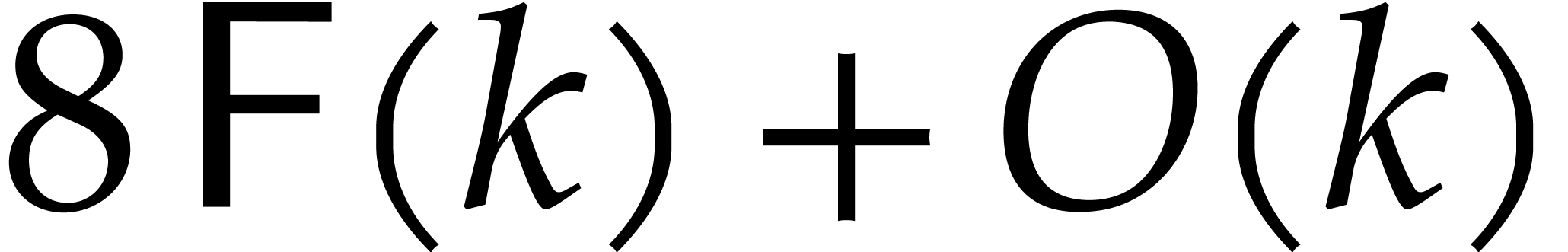 .
.
The cost of the DFTs in step 5 is again bounded by
 .
.
The cost of step 6 is bounded by  .
.
The total cost of the top-level of the algorithm is therefore bounded by
 . Consequently, the cost of
our algorithm satisfies the recurrence inequality
. Consequently, the cost of
our algorithm satisfies the recurrence inequality
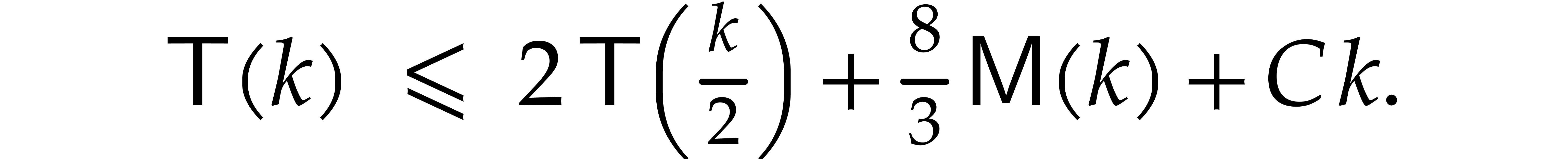
Unrolling this relation while using the assumption that 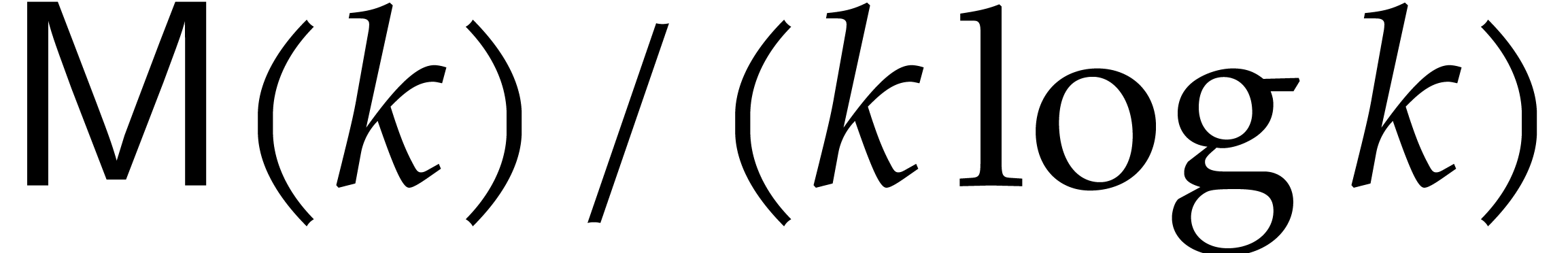 is non-decreasing yields the desired complexity bound.
is non-decreasing yields the desired complexity bound.

Let us now generalize Algorithm 2 to the case when  is not necessarily a power of two.
is not necessarily a power of two.
Algorithm
Input:
Output: |
|
Proof. The correctness is proved in the same way
as for Algorithm 1. For some universal constant  , the cost
, the cost 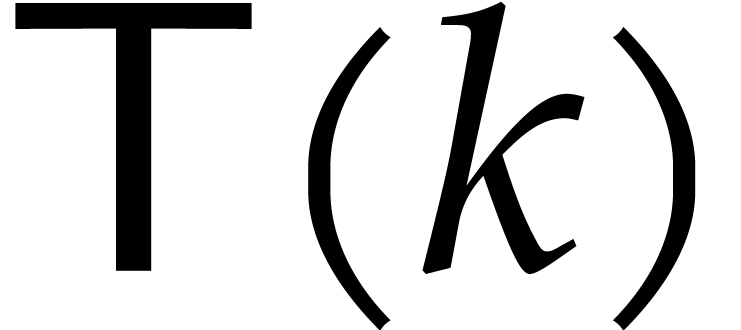 of the algorithm satisfies the recurrence relation
of the algorithm satisfies the recurrence relation
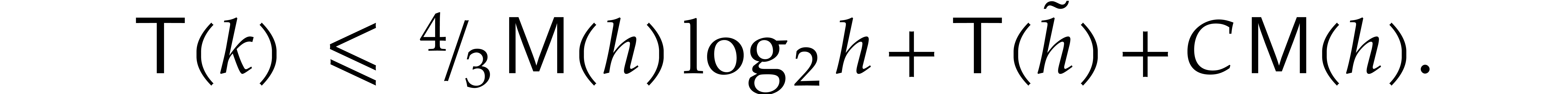
Writing 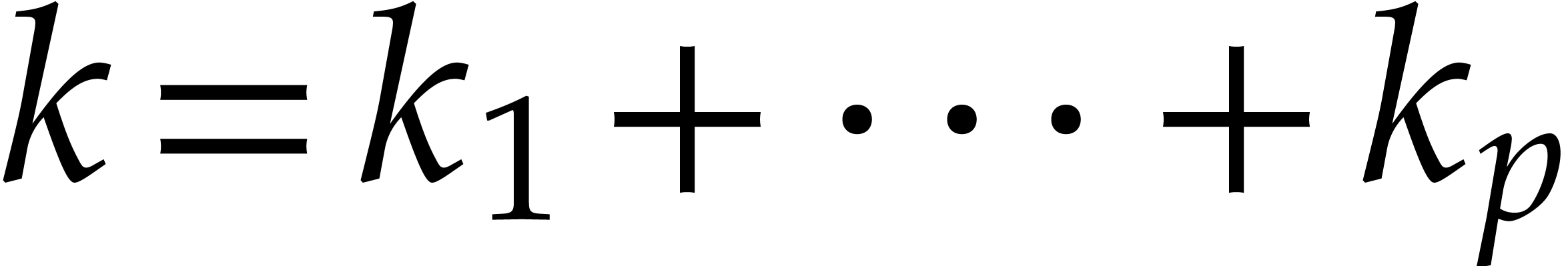 with
with  and
and  , it follows that
, it follows that
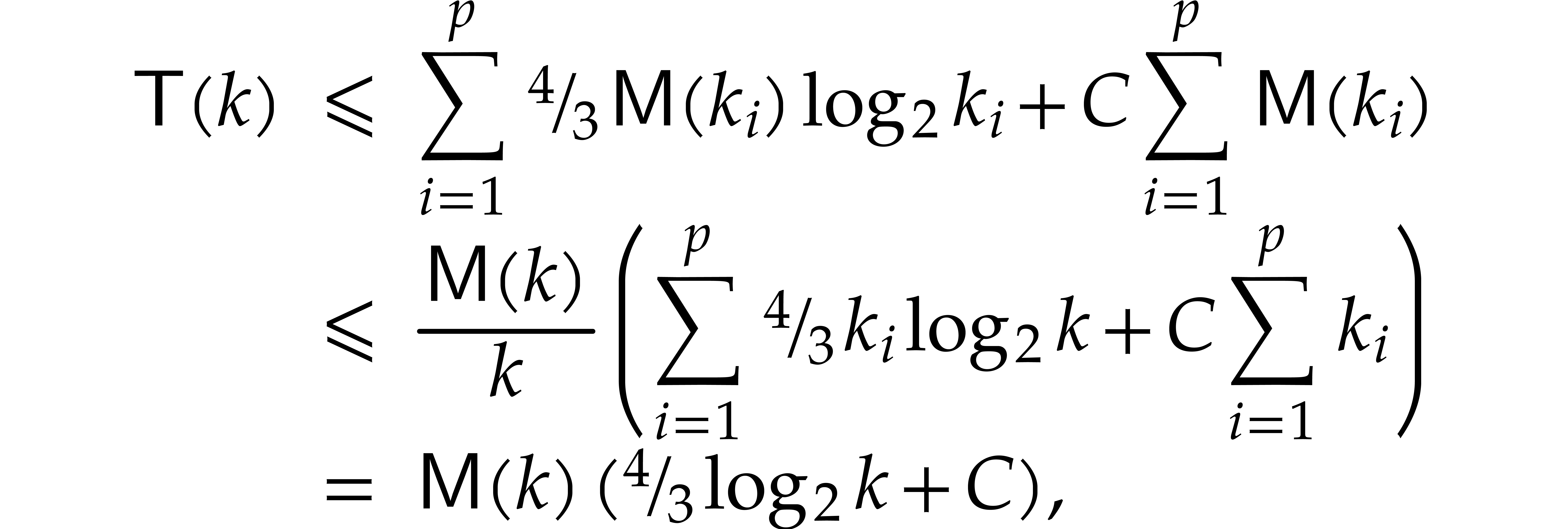
where we used our assumption that  is
non-decreasing.
is
non-decreasing.
Proof. Modulo multiplication of  and
and  with
with 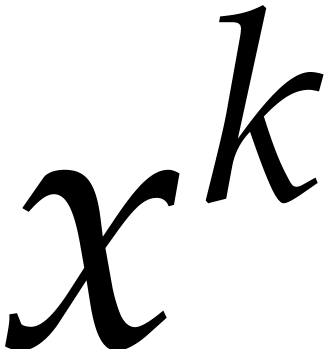 ,
we may assume without loss of generality that
,
we may assume without loss of generality that 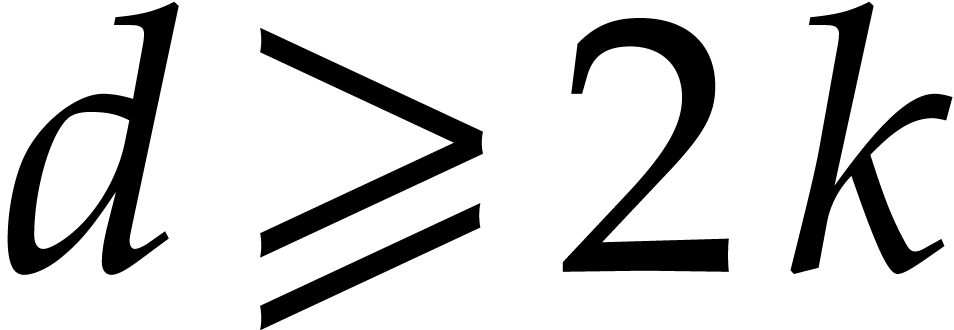 .
.
Remark
Algorithms 1 and 2 generalize to the abnormal case, modulo several technical adjustments. In this section we describe how to do this.
Let us first show how to adapt Algorithm 1. Lemma 4 now becomes:
Proof.
We have
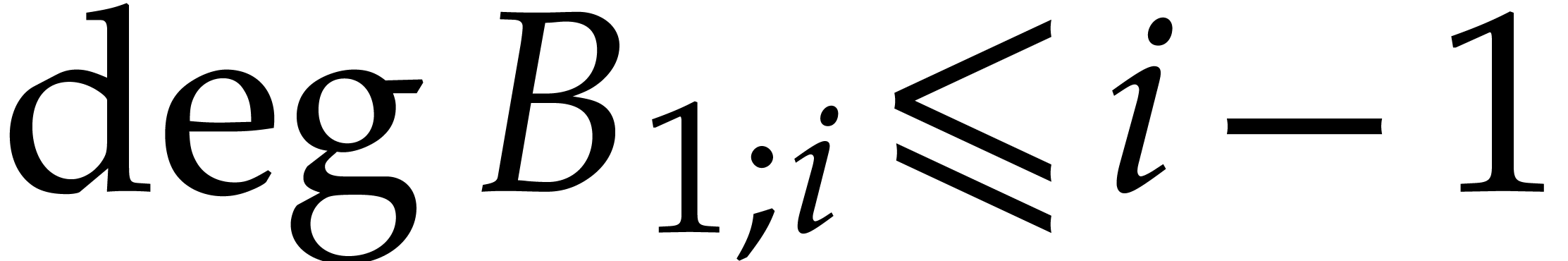 for
for
 ,
whence the relation
,
whence the relation
 shows that the coefficient
shows that the coefficient
 of degree
of degree
 in
in
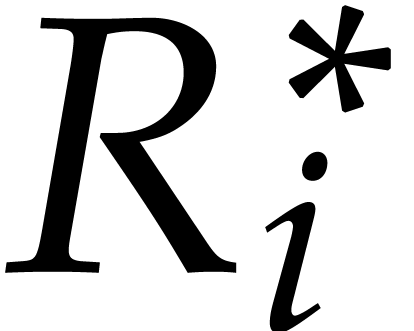 only depends on coefficients
only depends on coefficients
 and
and
 of
of
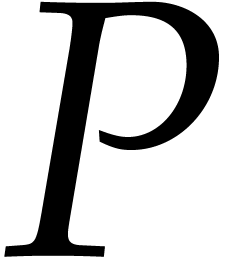 and
and
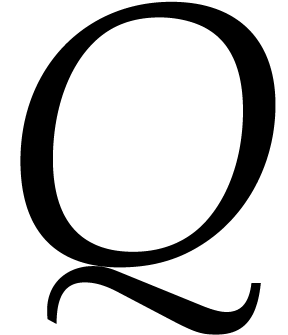 with
with
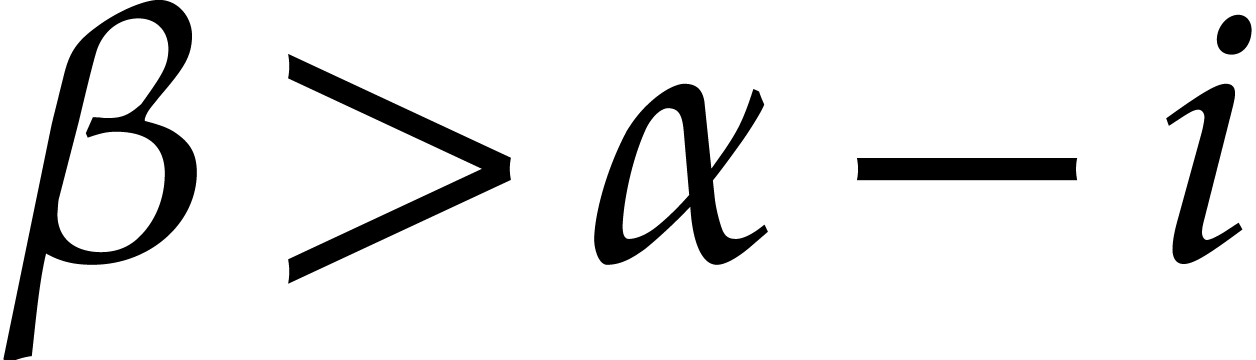 .
We next proceed in a similar way as in the proof of Lemma
4
.
.
We next proceed in a similar way as in the proof of Lemma
4
.

Proof. If  ,
then the result is obvious. If
,
then the result is obvious. If  and
and 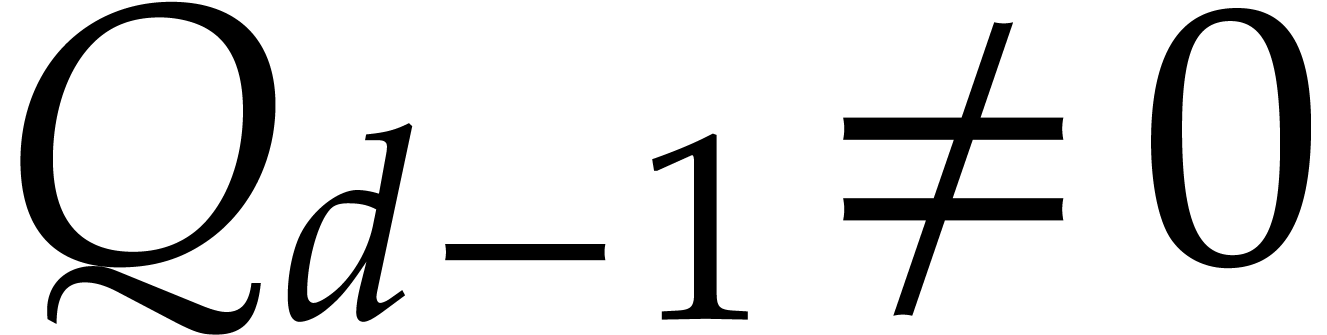 , then the result follows from Lemma 11.
Assume from now on that
, then the result follows from Lemma 11.
Assume from now on that 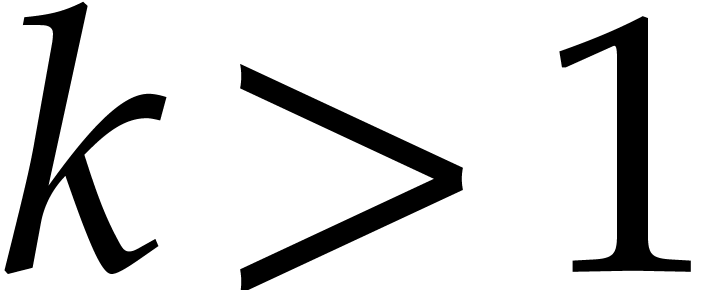 and
and  . Then Lemma 11 implies
. Then Lemma 11 implies 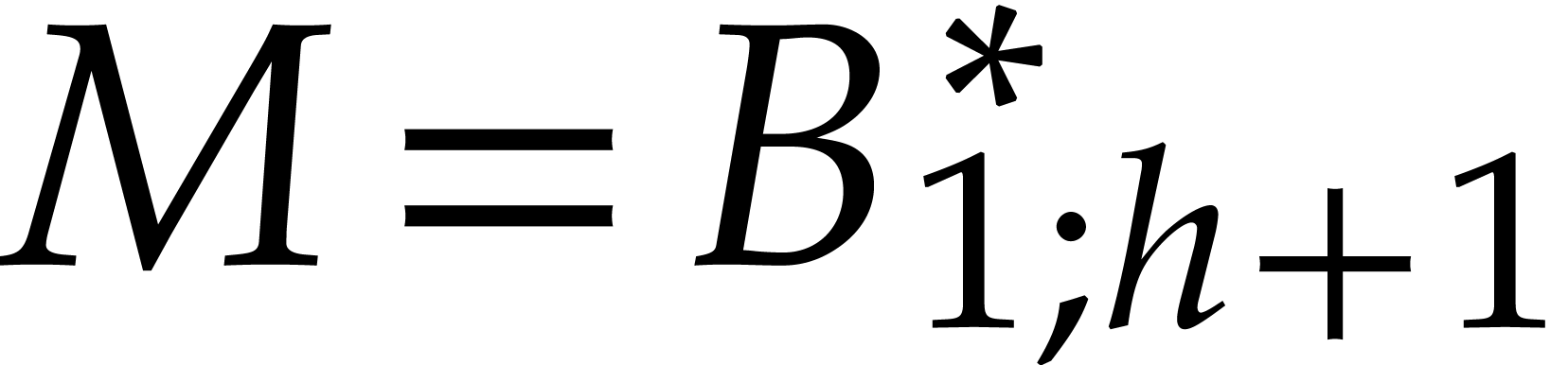 , whence
, whence  and
and 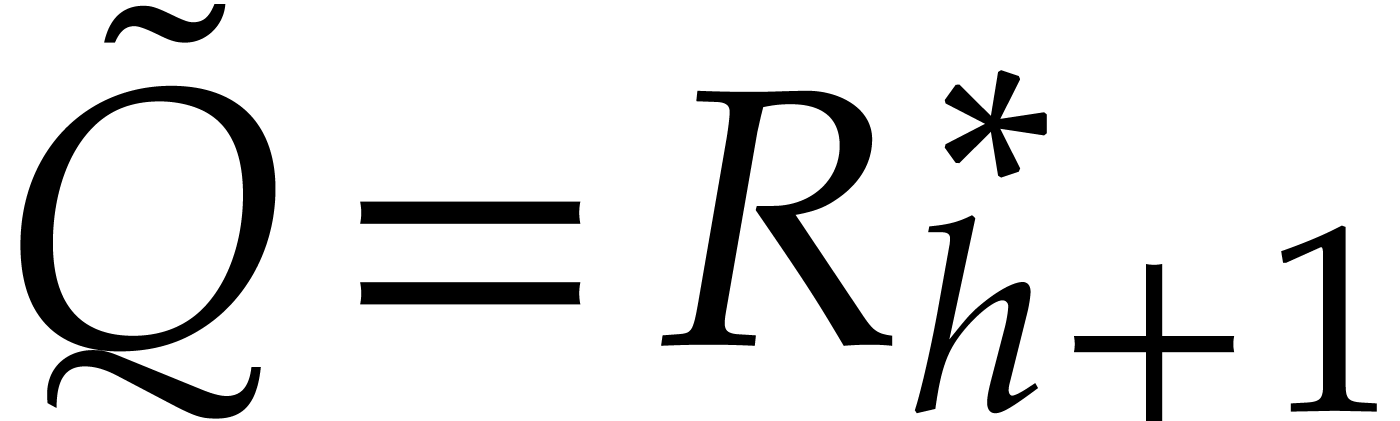 .
.
Let  be largest with
be largest with 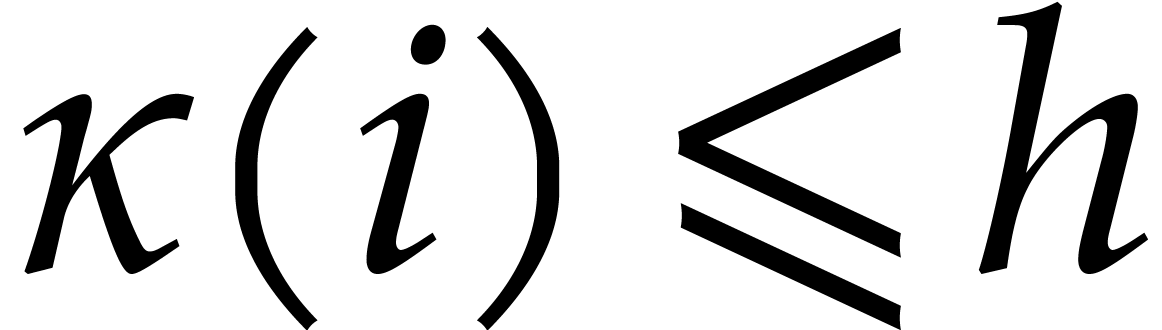 . If
. If 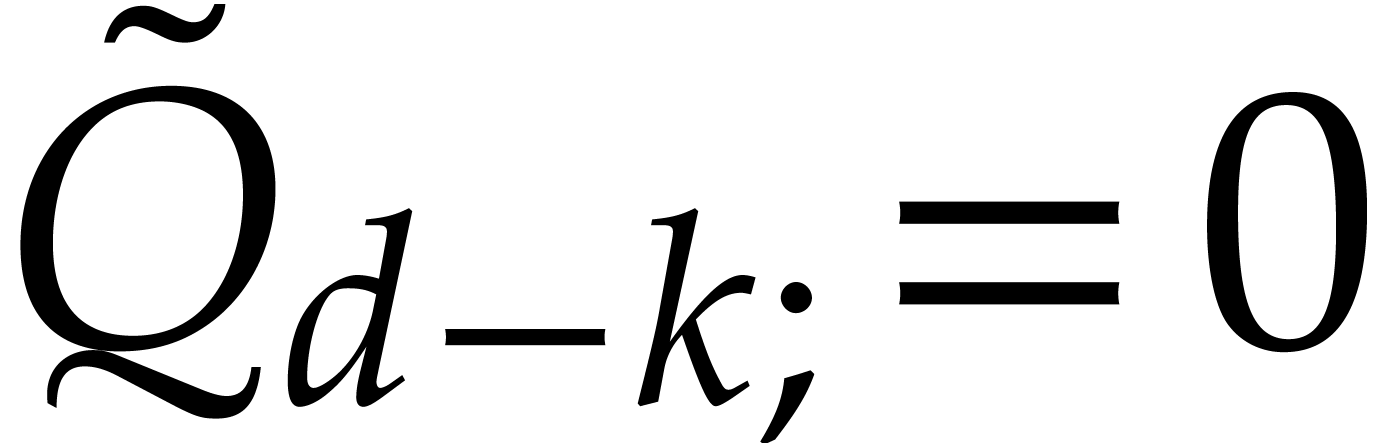 in step 6,
then
in step 6,
then  , so
, so 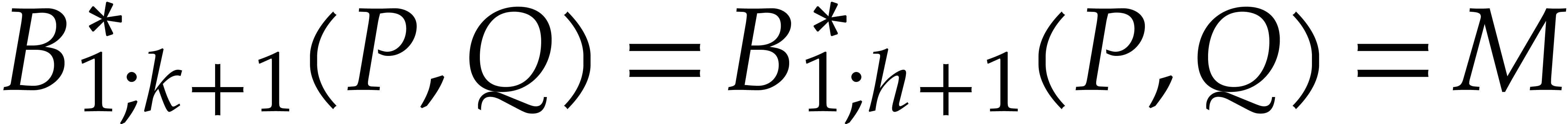 and our algorithm returns the correct answer. Assume from now on that
and our algorithm returns the correct answer. Assume from now on that
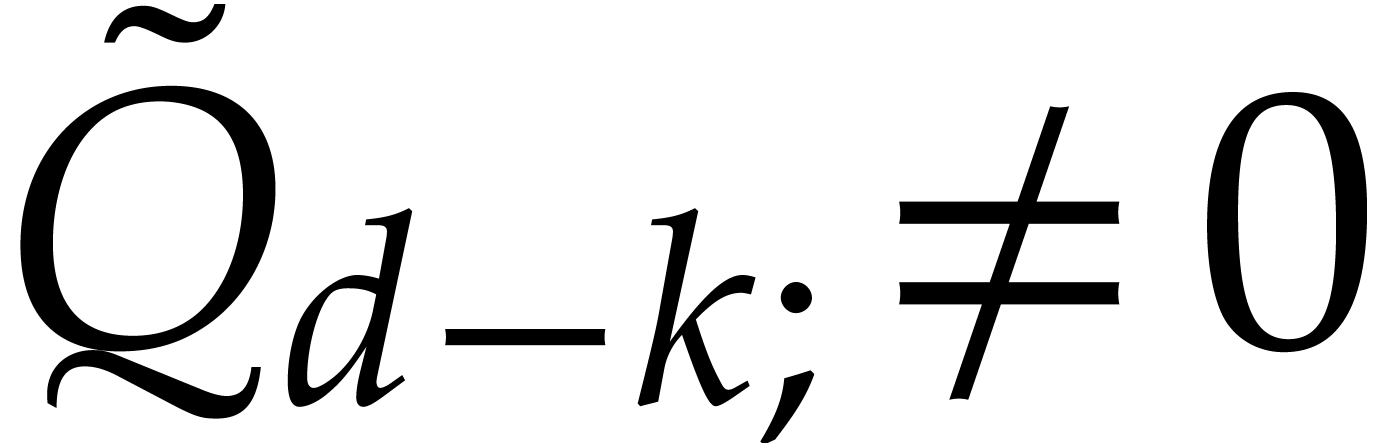 .
.
We call 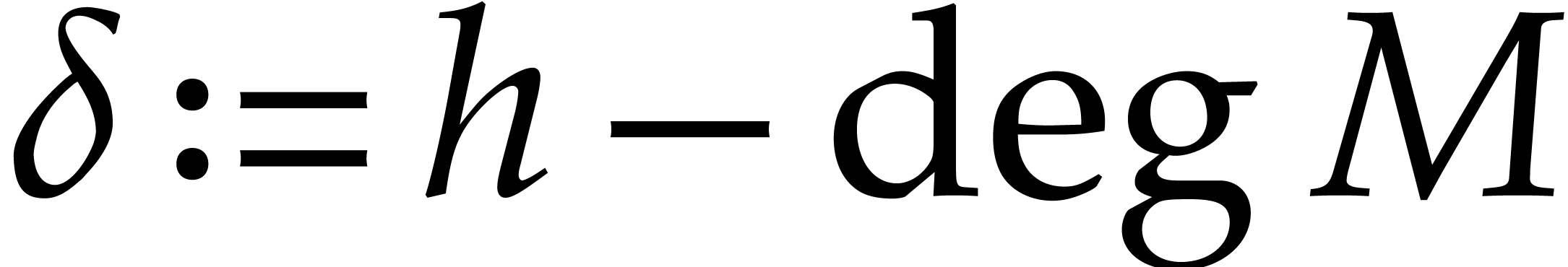 the degeneracy after
the degeneracy after 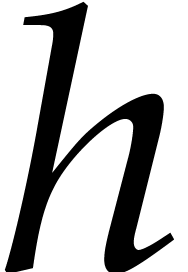 steps. Let
steps. Let  still be largest with
still be largest with
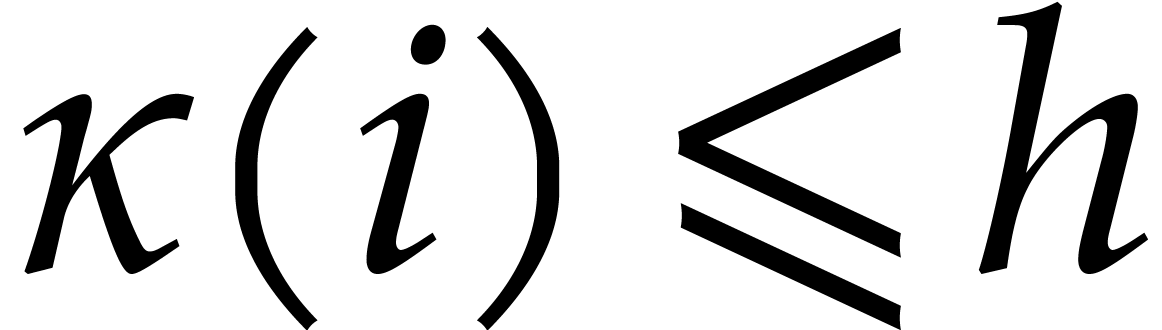 . Then we have
. Then we have 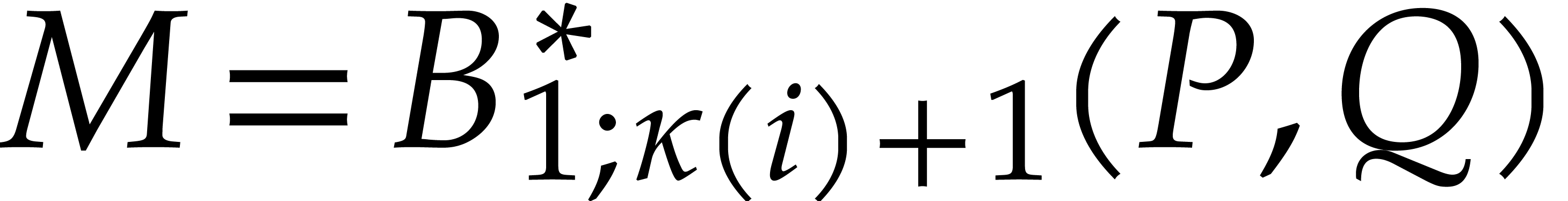 and
and 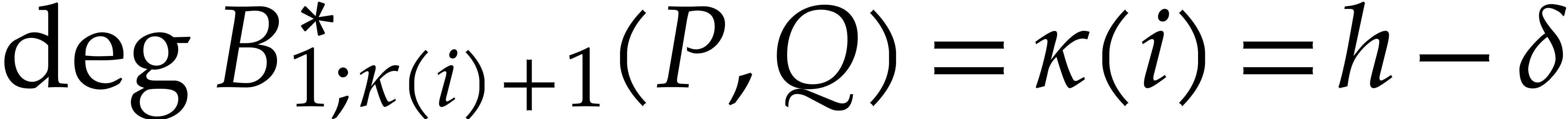 . In
particular, we see that
. In
particular, we see that 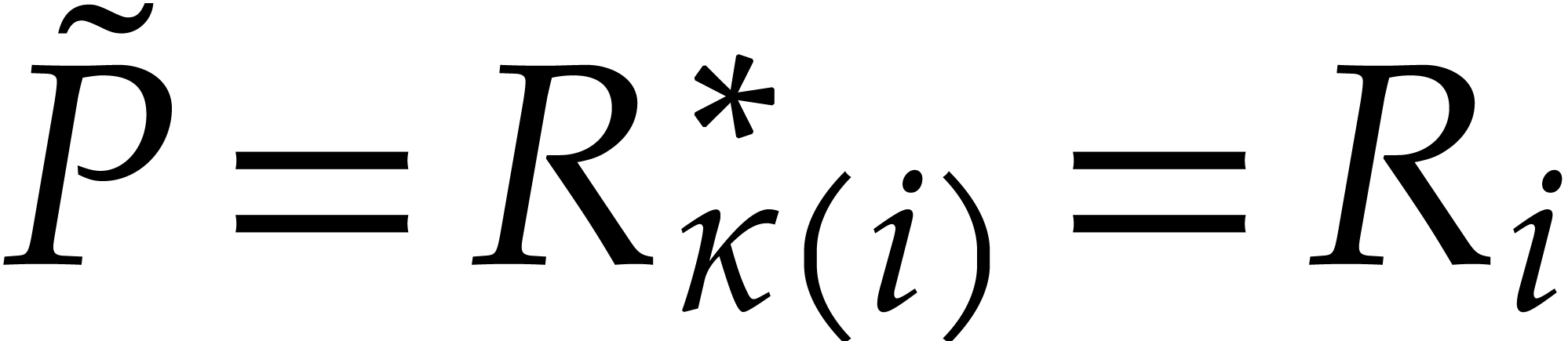 ,
,
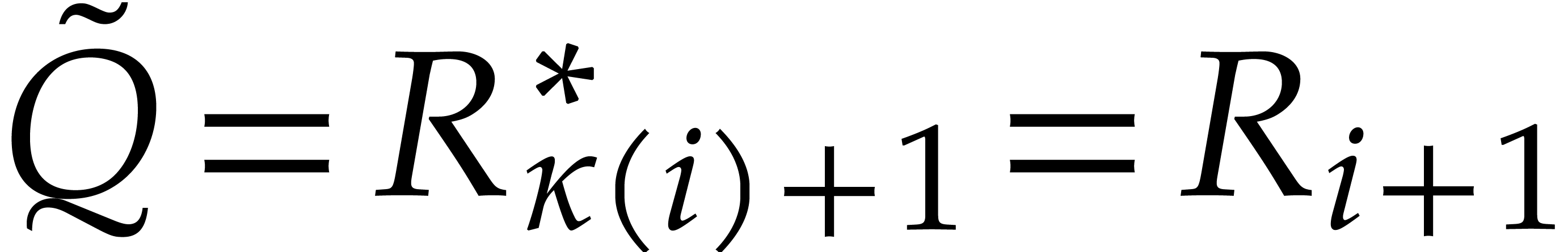 , and
, and  . Furthermore,
. Furthermore, 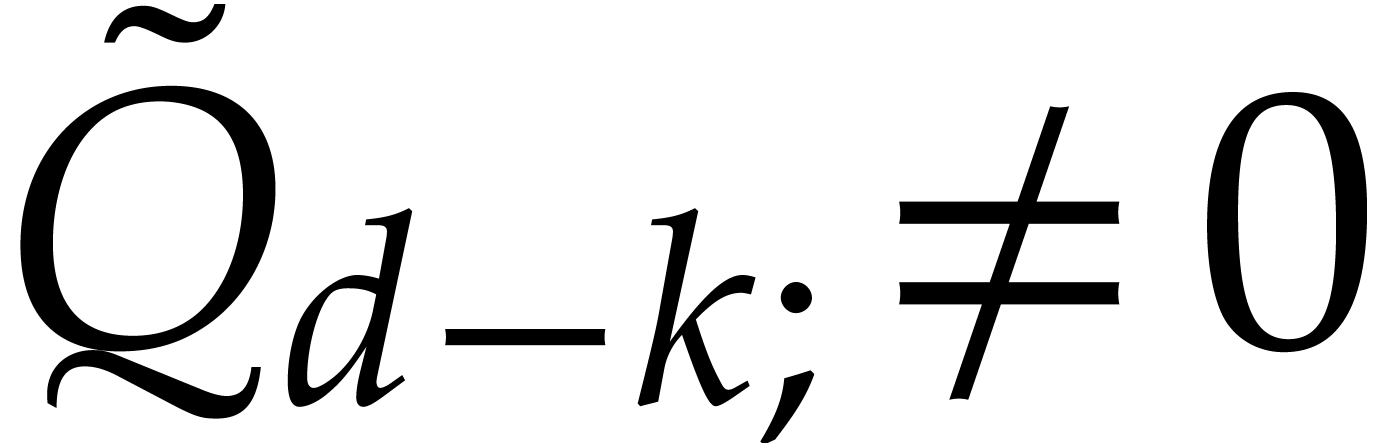 implies that
implies that
 , so
, so  . Therefore, we computed the
. Therefore, we computed the 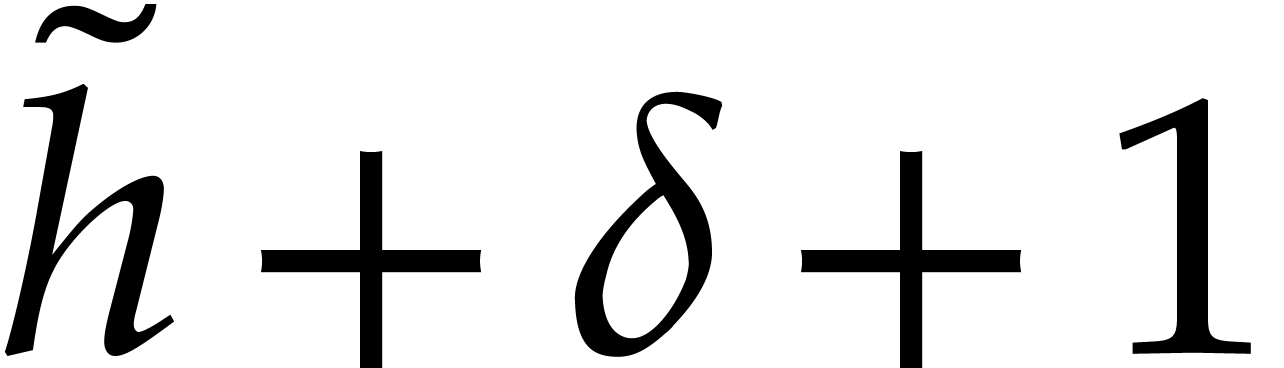 leading terms of
leading terms of  as part of
as part of 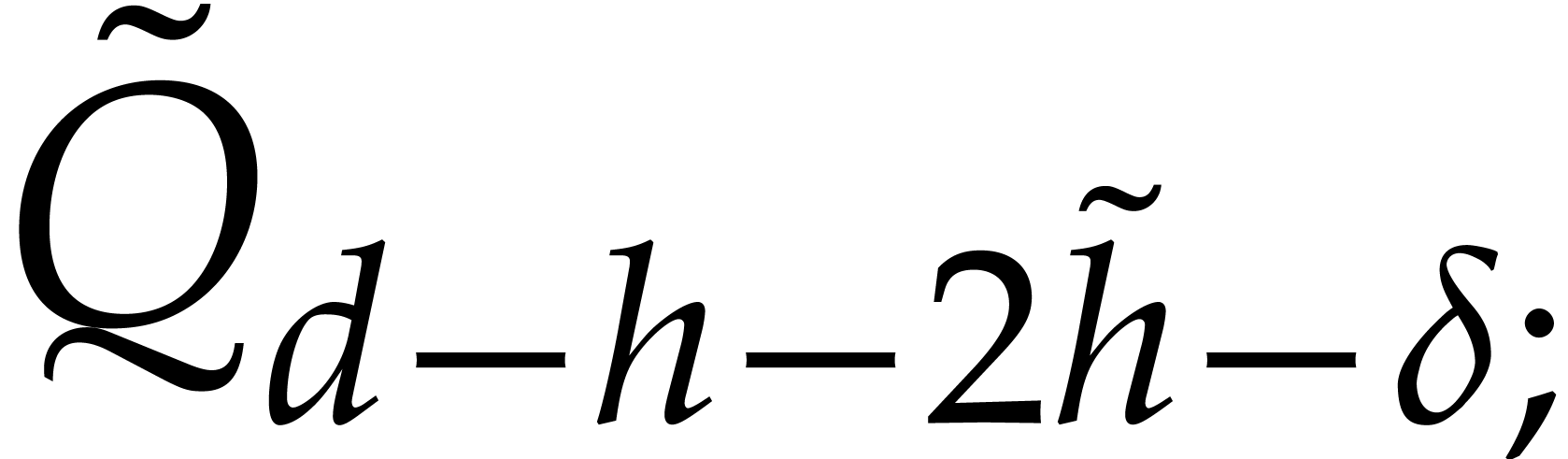 . Now
. Now  ,
so we only need the
,
so we only need the 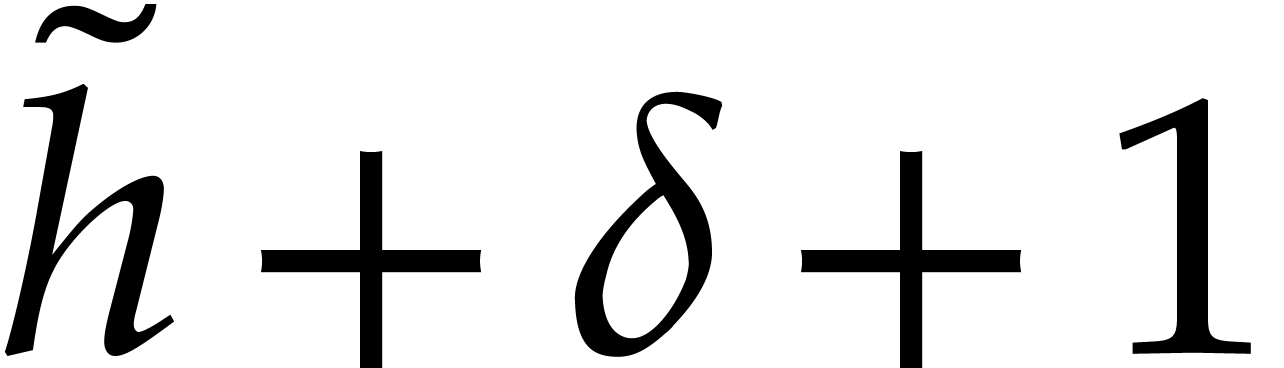 leading coefficients of
leading coefficients of 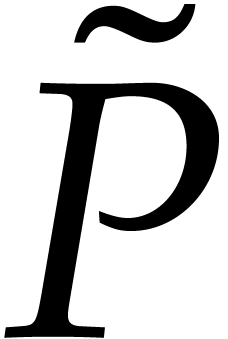 and
and  in order to compute
in order to compute  . This proves our claim that
. This proves our claim that  .
.
After step 7, we thus have  ,
,
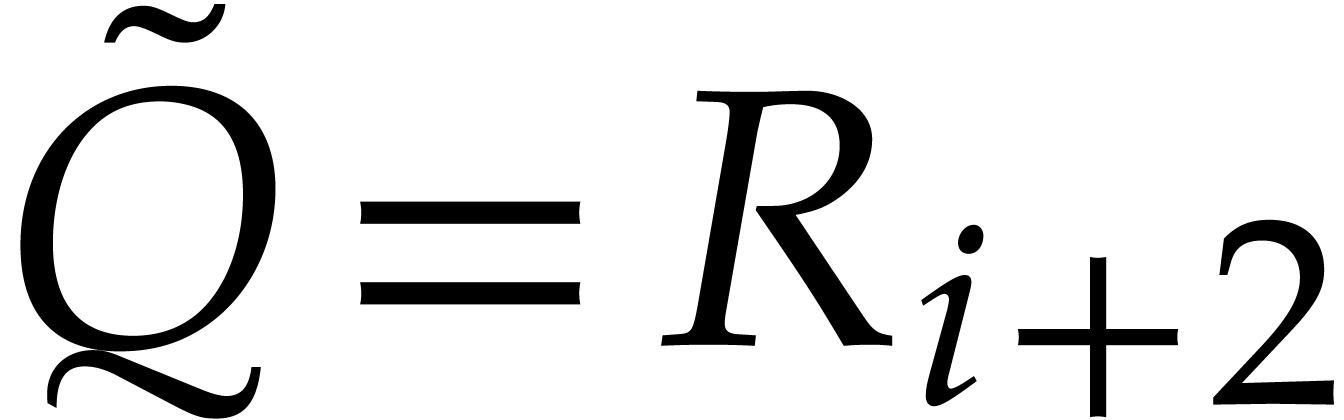 , and
, and 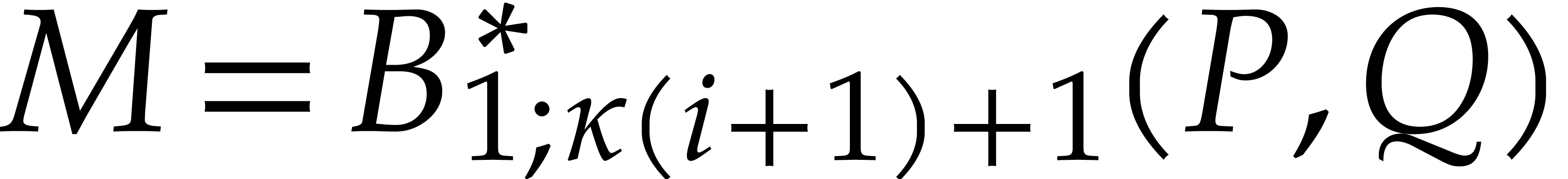 , where
, where 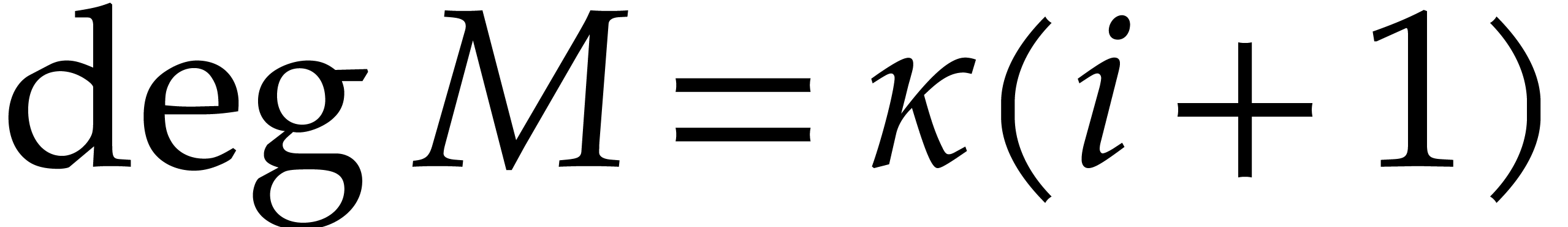 .
Moreover,
.
Moreover, 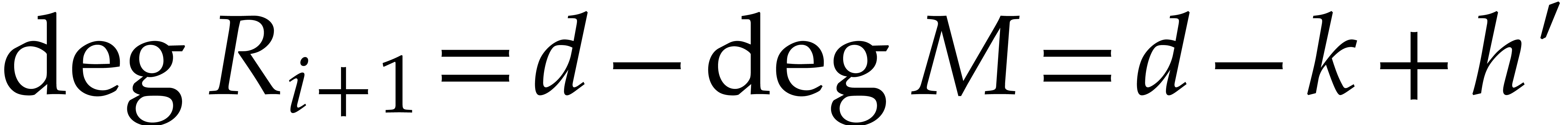 and
and 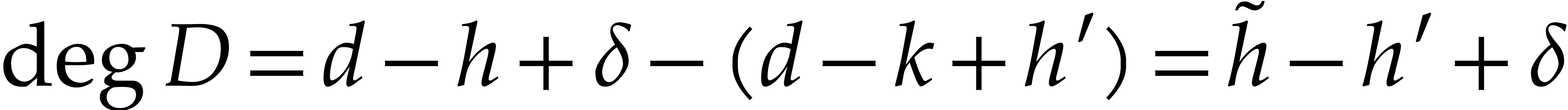 .
In particular, we may indeed retrieve the new value of
.
In particular, we may indeed retrieve the new value of 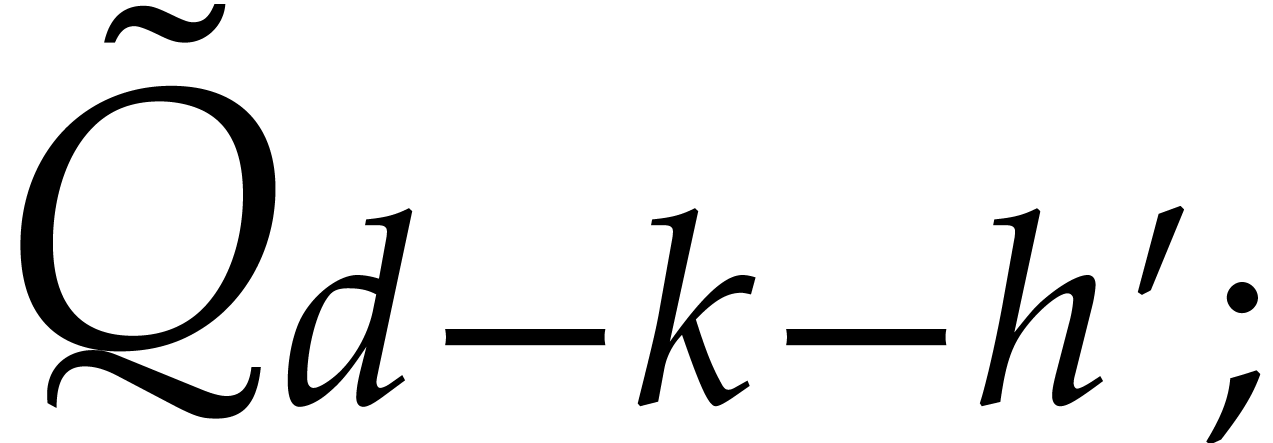 from
from 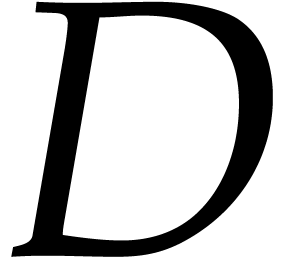 and the old values of
and the old values of 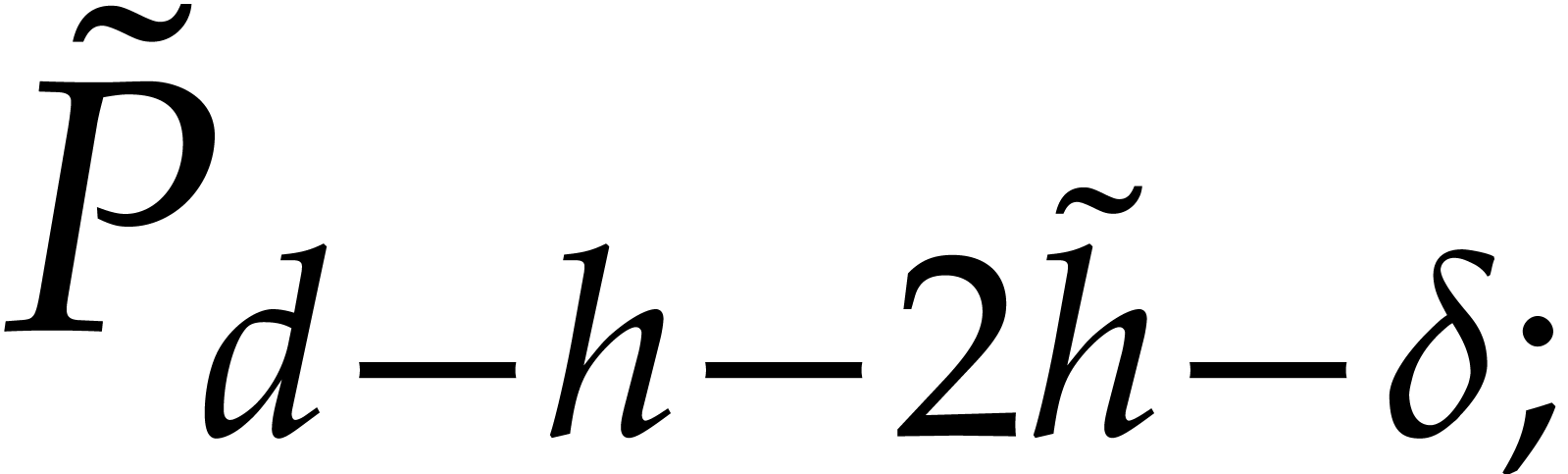 and
and 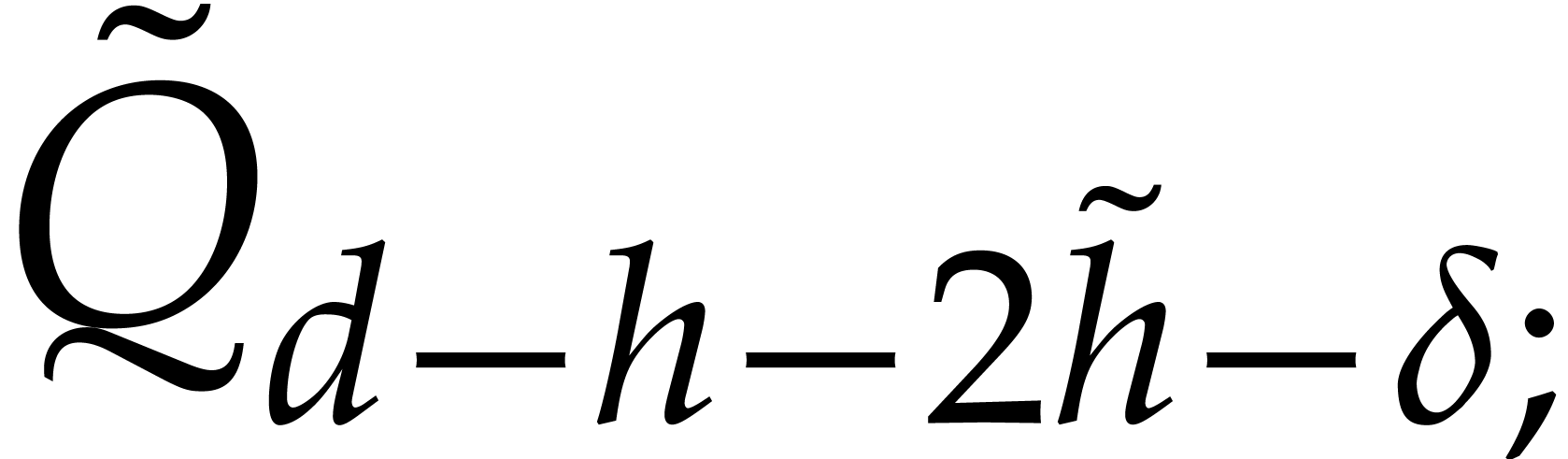 at the end of step 7, since
at the end of step 7, since
 . Furthermore,
. Furthermore, 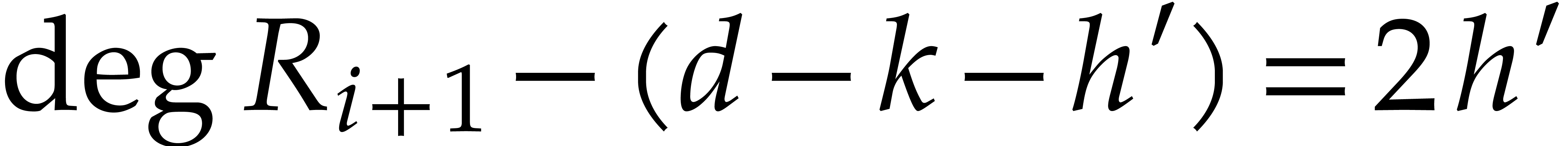 , which allows to apply Lemma 11,
and obtain
, which allows to apply Lemma 11,
and obtain  . We conclude that
. We conclude that
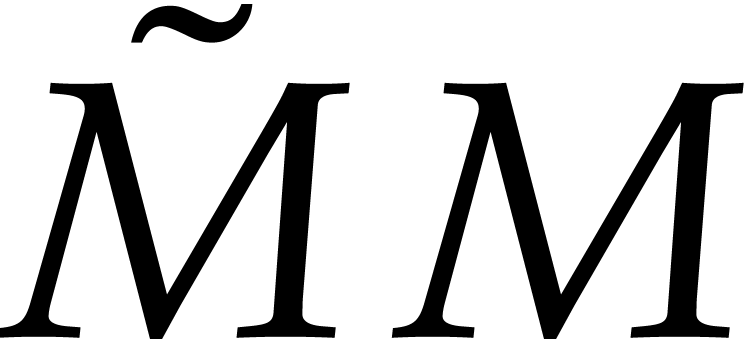 |
 |
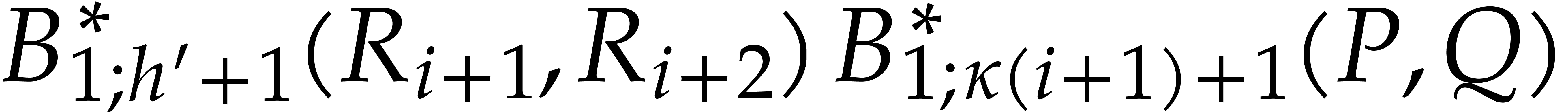 |
|
 |
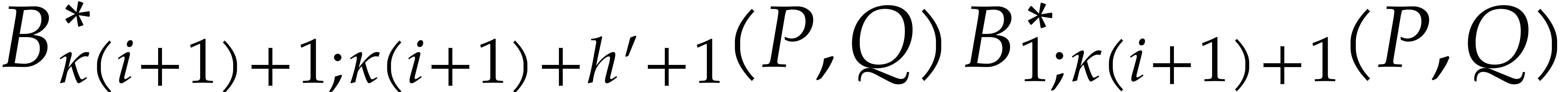 |
||
 |
 |
||
 |
 |
 |
Remark  in step 3, but
it is interesting to note that the above correctness proof actually
works for any choice of
in step 3, but
it is interesting to note that the above correctness proof actually
works for any choice of  with
with 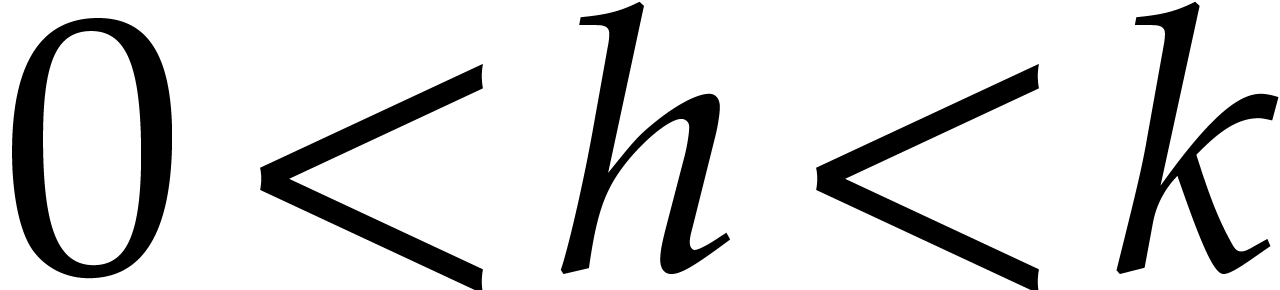 . We will use this property for our FFT version
in section 5.3 below, where we will take
. We will use this property for our FFT version
in section 5.3 below, where we will take 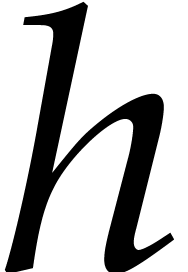 to be a power of two.
to be a power of two.
Contrary to what we did in section 4.2, we do not require
 to be a power of two in this subsection. In
fact, it is possible to efficiently implement step 5 in
general, using middle products. This time, we break up our input and
output polynomials as follows:
to be a power of two in this subsection. In
fact, it is possible to efficiently implement step 5 in
general, using middle products. This time, we break up our input and
output polynomials as follows:

Then we have (see See Figure 1
)
As before, the coefficient  is computed
separately using
is computed
separately using
Remark 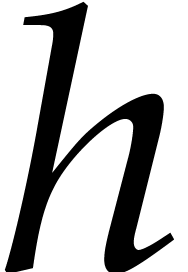 with
with
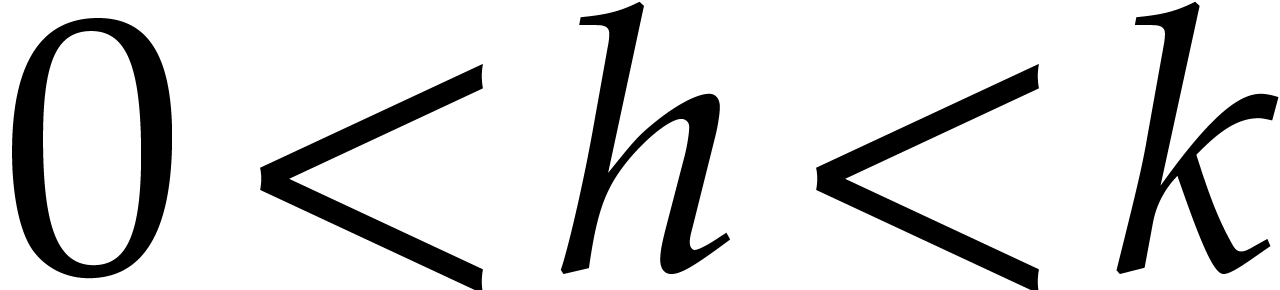 .
.
Let  be as in section 4.2. For the
multiplication method that we selected, assume that the middle product
(8) and the final product
be as in section 4.2. For the
multiplication method that we selected, assume that the middle product
(8) and the final product 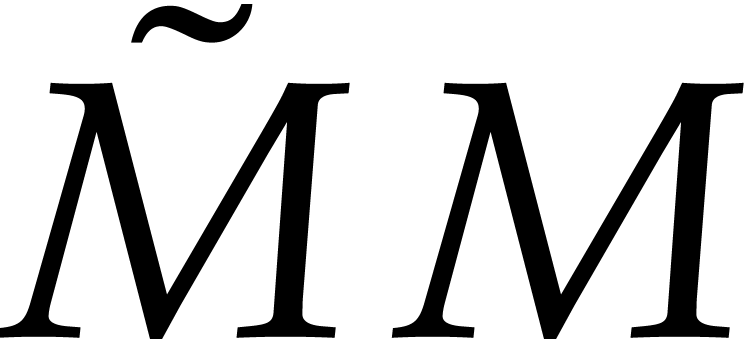 can each
be computed in time
can each
be computed in time  . Then we
have the following generalization of Proposition 6:
. Then we
have the following generalization of Proposition 6:
 be as in Proposition 6.
Then Algorithm 4 with the middle product optimization
runs in time at most
be as in Proposition 6.
Then Algorithm 4 with the middle product optimization
runs in time at most
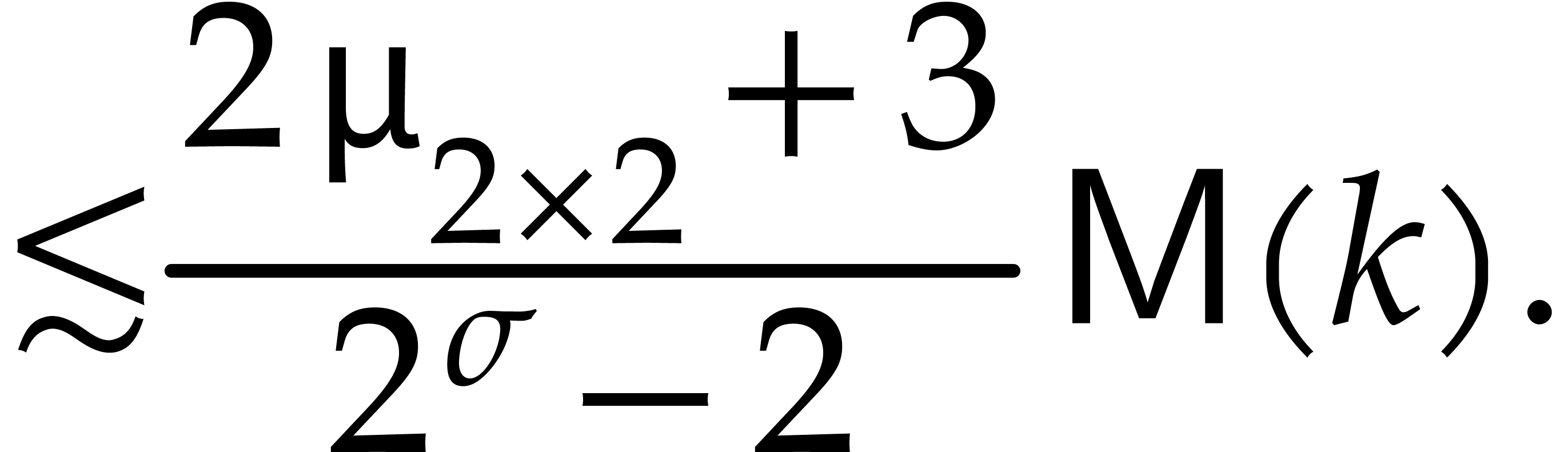
Moreover, for a multiplication with  for
some
for
some  , the cost is
, the cost is
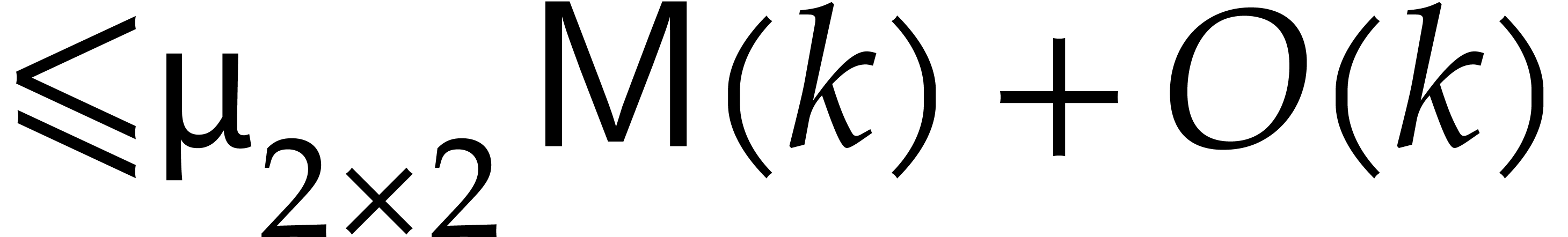
Proof. The cost of steps 5 and 9 is bounded by 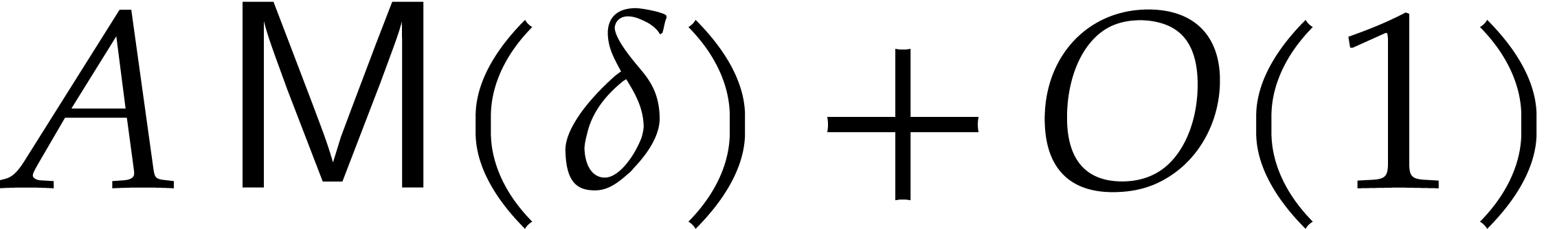 ,
according to the assumption just above this proposition. In step 7, the computation of
,
according to the assumption just above this proposition. In step 7, the computation of 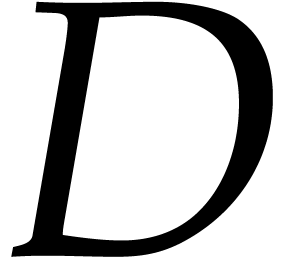 can be done in
time
can be done in
time 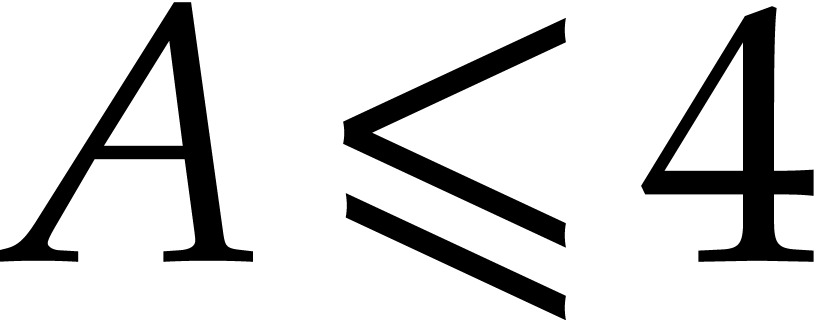 with
with 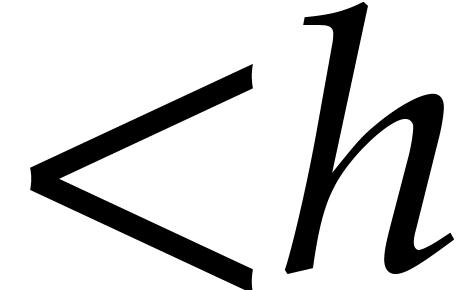 ,
using Newton's method for fast power series inversion; see,
e.g. [3, section 6]. The update of
,
using Newton's method for fast power series inversion; see,
e.g. [3, section 6]. The update of  amounts to two products of degrees
amounts to two products of degrees 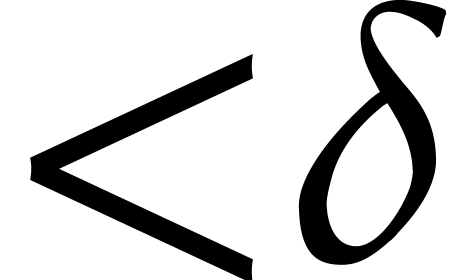 by
by  , which can certainly be
computed in time
, which can certainly be
computed in time  . The update
of
. The update
of 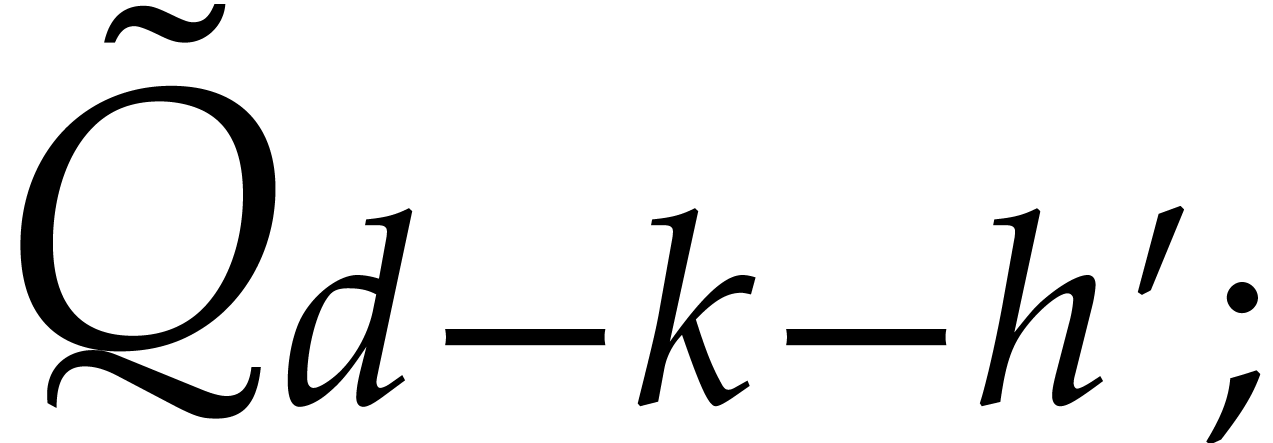 can be computed efficiently using a middle
product that takes
can be computed efficiently using a middle
product that takes  additional operations.
Altogether, the cost
additional operations.
Altogether, the cost 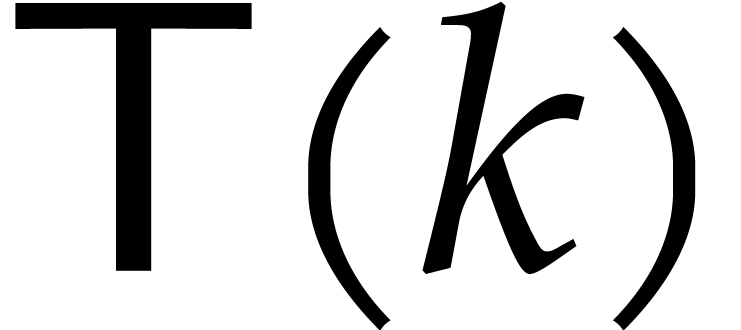 of the algorithm satisfies
of the algorithm satisfies
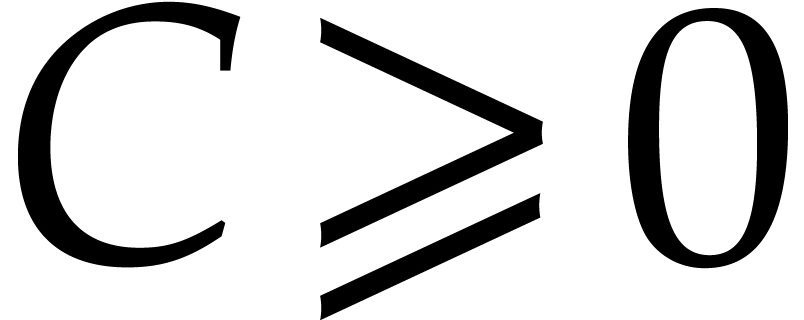
for some constant 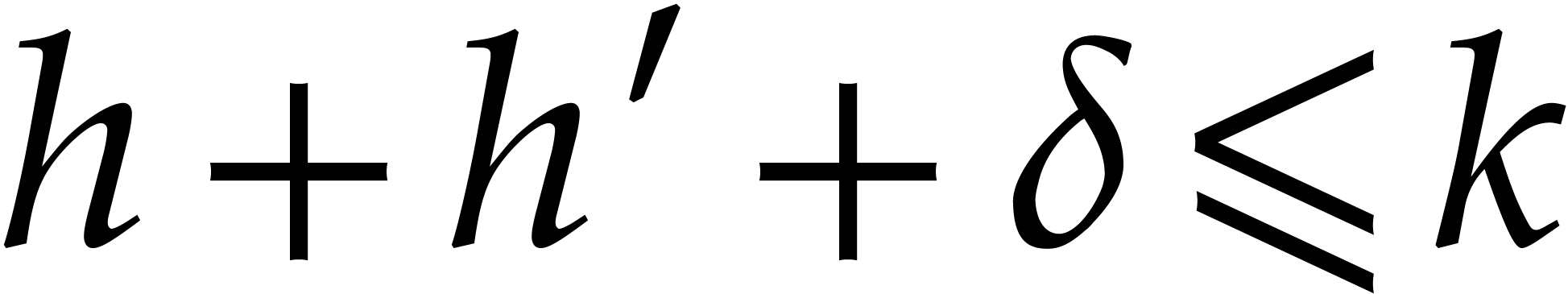 . Note also
that
. Note also
that 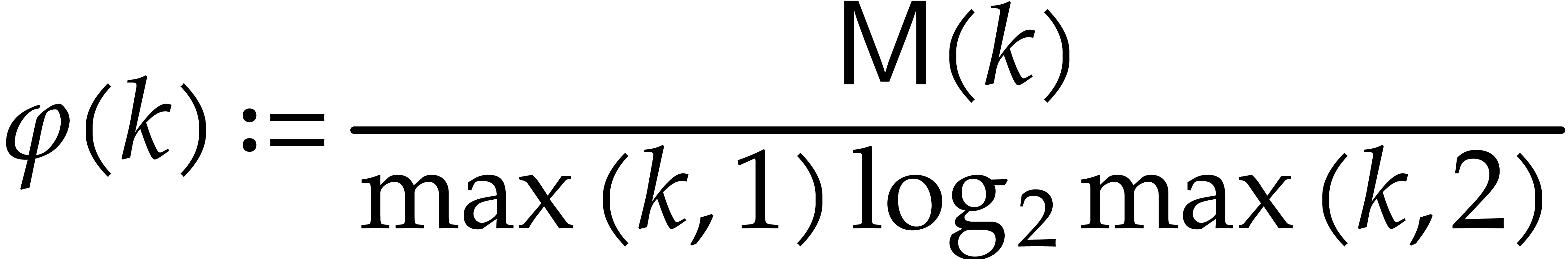 and that
and that

is a non-decreasing function. Let  and
and  be such that
be such that
for all 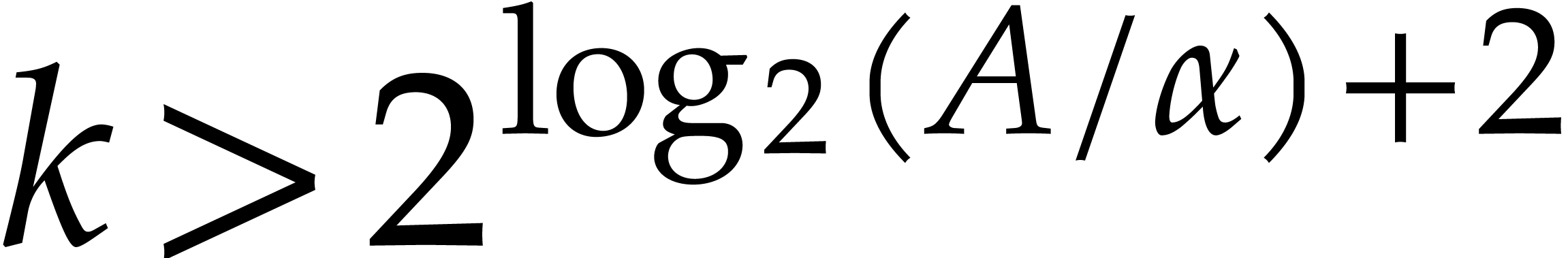 . Let us show by
induction on
. Let us show by
induction on  that (10) holds for
all
that (10) holds for
all  as well. Indeed,
as well. Indeed,
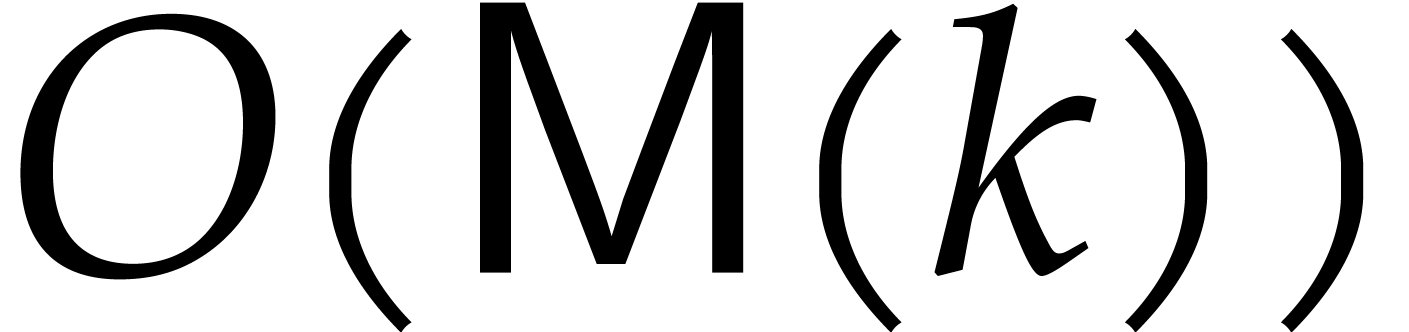
This completes the proof of the first bound. We skip the proof of the
second one, which is based on similar arguments.
Remark 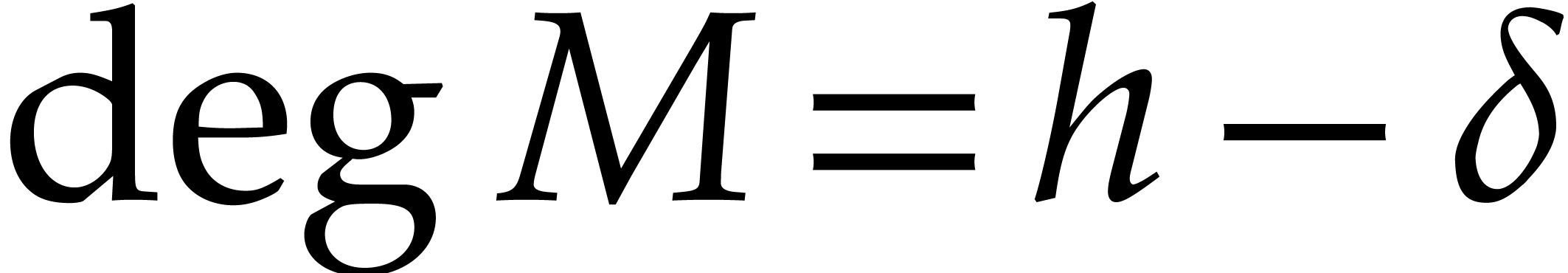 . If, on the contrary, some of the quotients
have exceptionally large degrees, then many of the recursive calls will
terminate early at step 6. This will actually make the
constants decrease instead of increase. The only problematic
case therefore seems to be when many of the quotients have moderately
large degrees; it would be interesting to know more about the precise
worse case scenario.
. If, on the contrary, some of the quotients
have exceptionally large degrees, then many of the recursive calls will
terminate early at step 6. This will actually make the
constants decrease instead of increase. The only problematic
case therefore seems to be when many of the quotients have moderately
large degrees; it would be interesting to know more about the precise
worse case scenario.
One important feature of Algorithm 2 is that we use the
same length  for all our DFTs. If
for all our DFTs. If  is a power of two, then we may conserve this property in
the abnormal case. Indeed, the final product
is a power of two, then we may conserve this property in
the abnormal case. Indeed, the final product 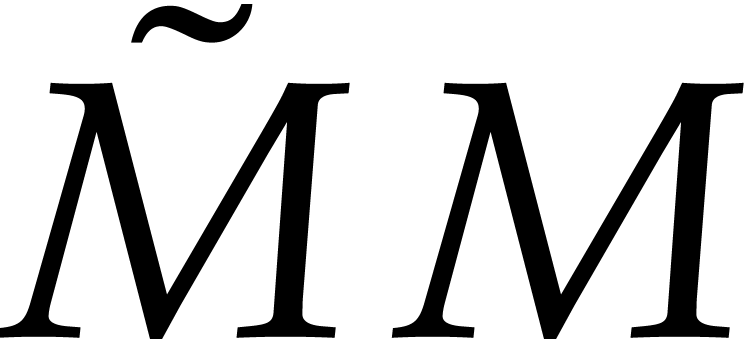 causes no problem since its degree is still
causes no problem since its degree is still 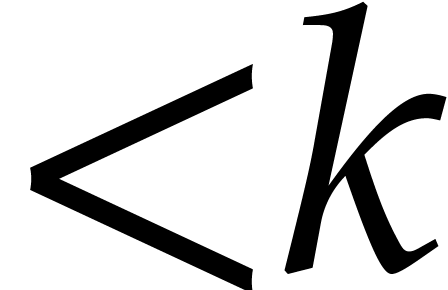 . As to the middle product (8), we now
have
. As to the middle product (8), we now
have  and the degree of the right hand side is
still
and the degree of the right hand side is
still 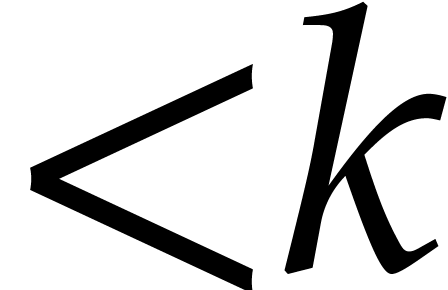 . This allows us to
apply (3), which yields
. This allows us to
apply (3), which yields
However, there is no reason why  should be a
power of two for the second recursive call. In order to remedy to this
problem, we introduce a new parameter
should be a
power of two for the second recursive call. In order to remedy to this
problem, we introduce a new parameter  that we
assume to be a power of two and that we will use for the lengths of our
DFTs. This requires a minor adjustment of (11):
that we
assume to be a power of two and that we will use for the lengths of our
DFTs. This requires a minor adjustment of (11):
We are now in a position to adapt Algorithm 4 to the binary FFT model: see Algorithm 5 .
Algorithm
Output: |
|
For the complexity analysis, it will be convenient to assume that 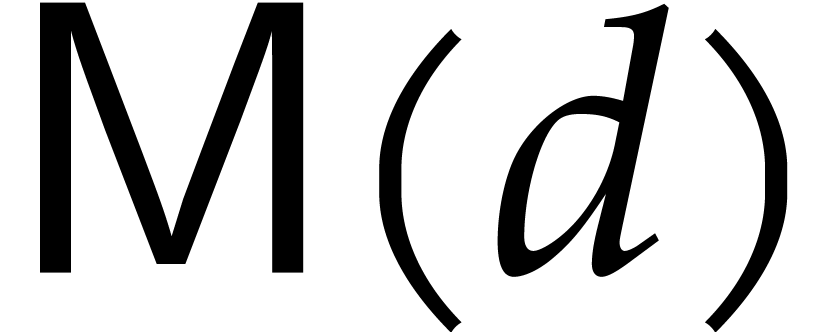 satisfies the properties from section 2.2.
In particular, the assumption that
satisfies the properties from section 2.2.
In particular, the assumption that  is
non-decreasing implies that
is
non-decreasing implies that 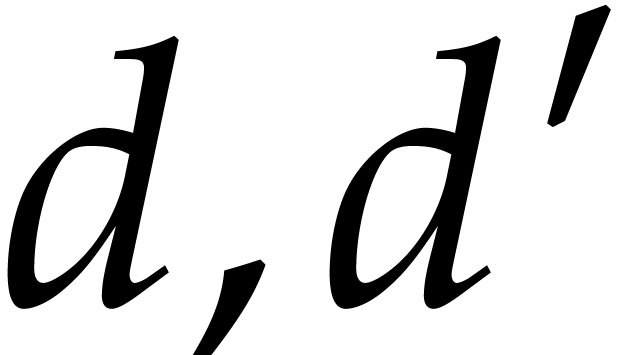 for all
for all  . Conversely, in the binary FFT model, it will
be convenient to also assume that
. Conversely, in the binary FFT model, it will
be convenient to also assume that 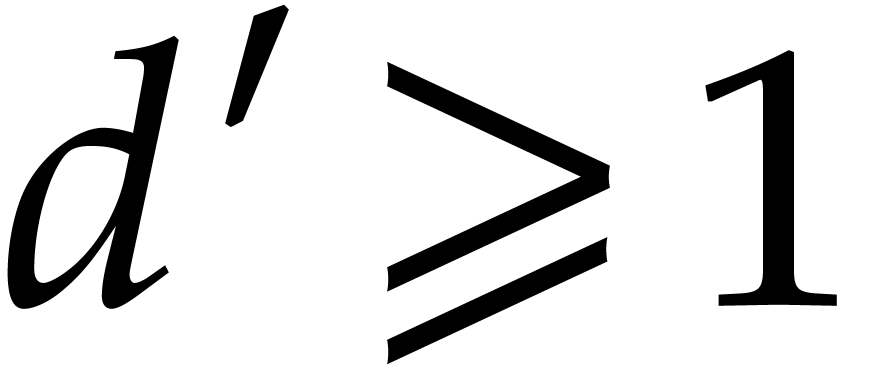 for all
for all  ,
,  ,
and some fixed constant
,
and some fixed constant 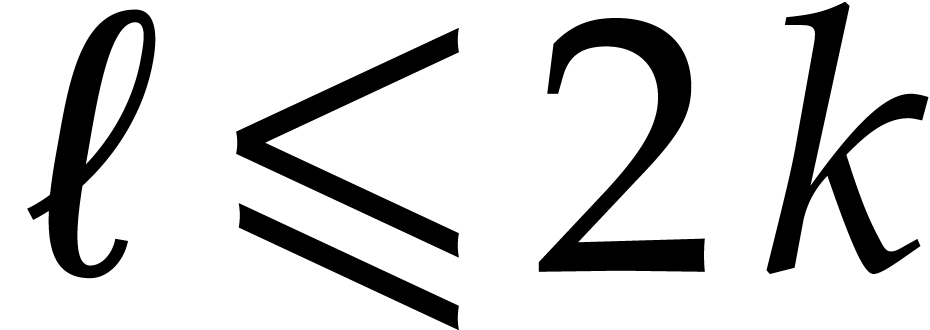 .
.
Proof. The correctness is proved in a similar way as the correctness of Proposition 12, while using Remarks 13 and 14.
The total cost of steps 5, 6, 9,
and 10 is 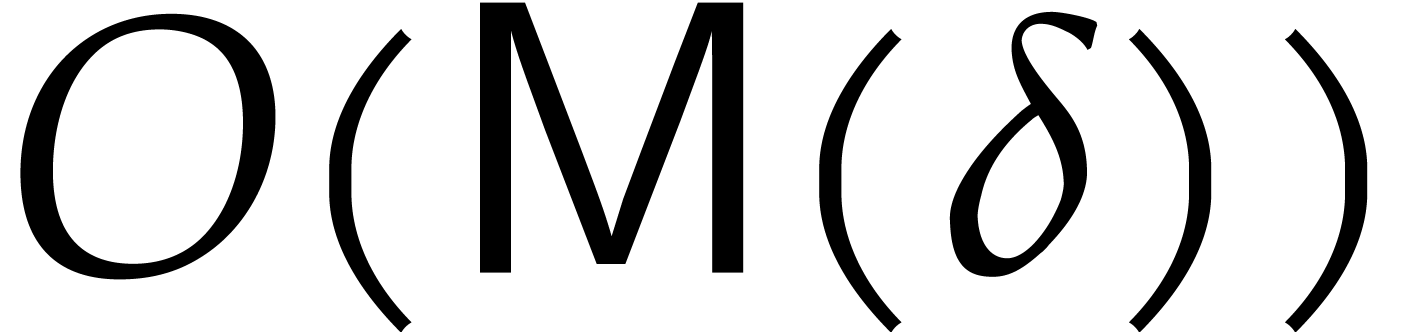 , as
in the proof of Proposition 7. As to the update step 8, the computation of
, as
in the proof of Proposition 7. As to the update step 8, the computation of 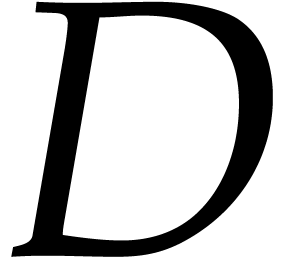 requires
requires 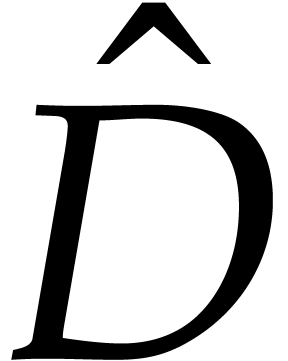 operations. The computation of
operations. The computation of 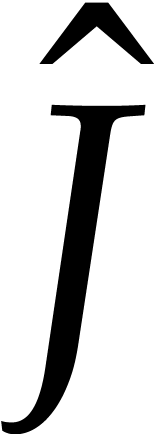 and
and  costs
costs 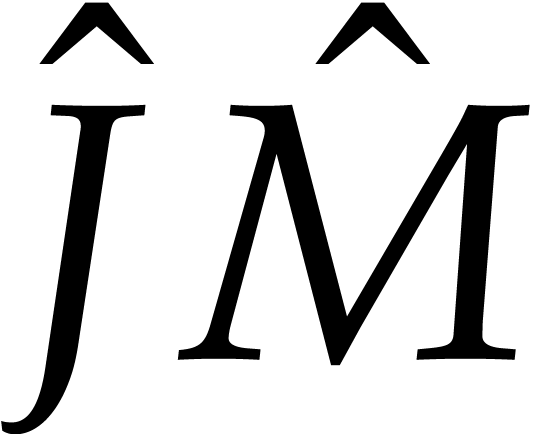 ,
whereas the multiplication
,
whereas the multiplication  takes linear time.
takes linear time.
Now let 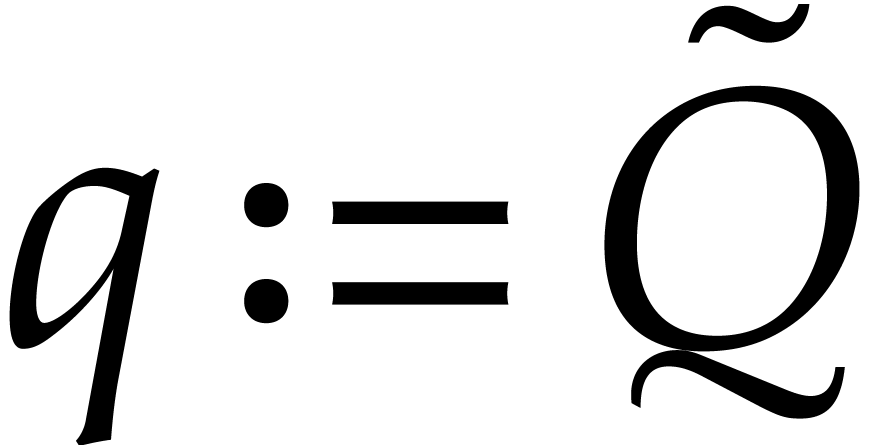 and
and  before the
updates, so that
before the
updates, so that  with
with 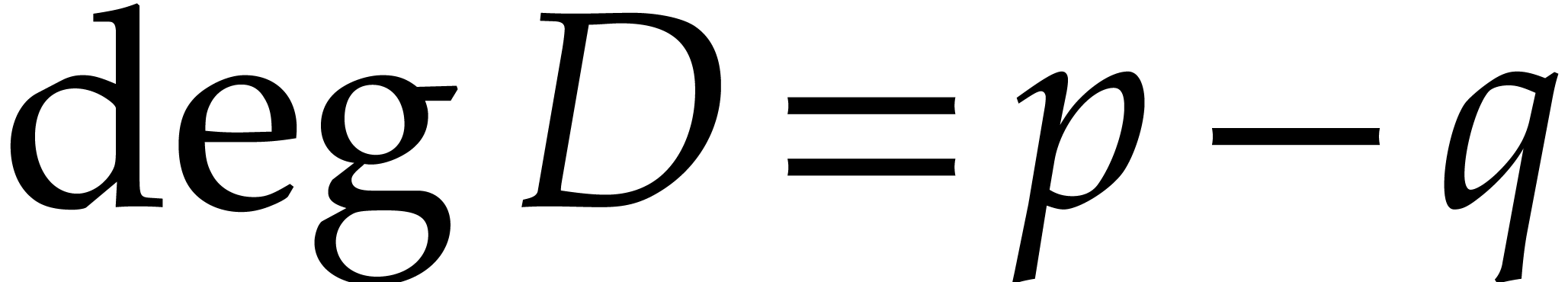 and
and 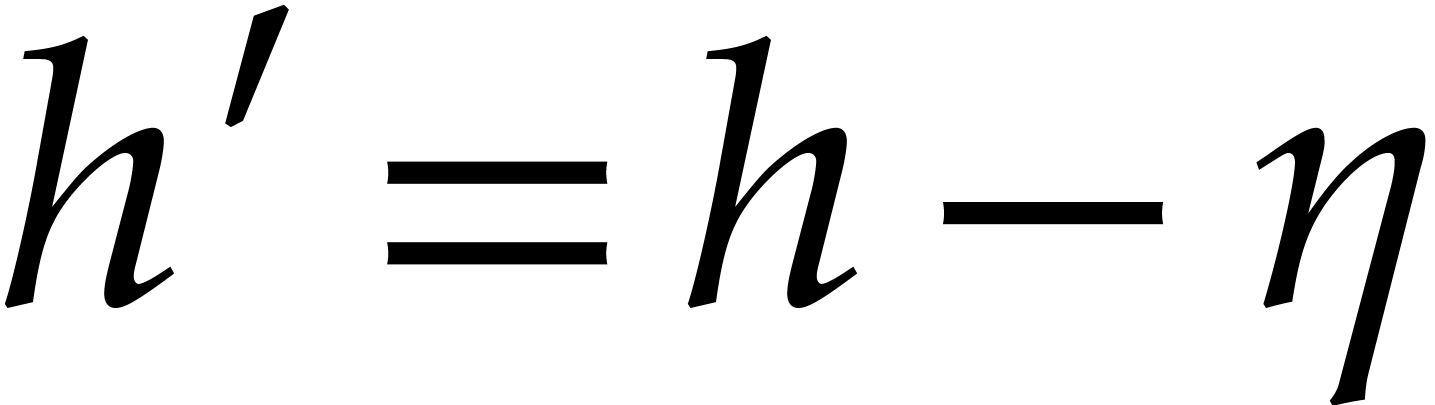 . Since
. Since 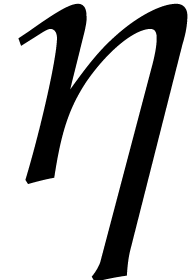 , the lowest
, the lowest  coefficients of
coefficients of 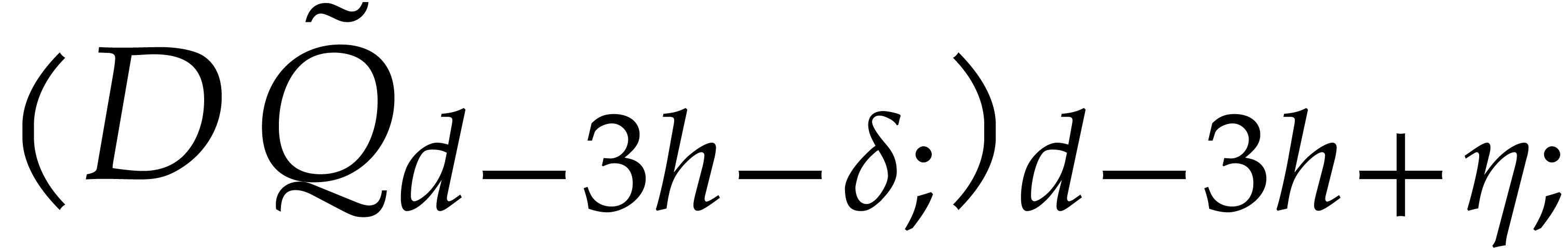 do not matter in step 9.
During the update, this means that we essentially need to compute
do not matter in step 9.
During the update, this means that we essentially need to compute 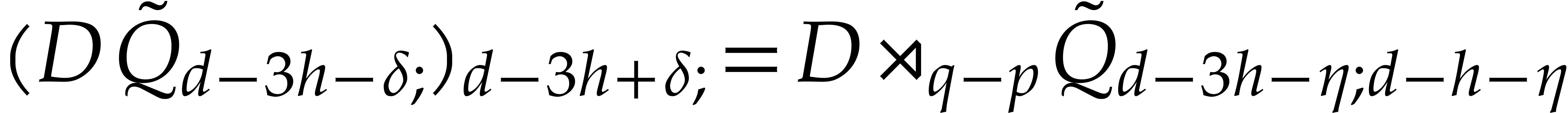 . Now, using FFT multiplication,
the computation of
. Now, using FFT multiplication,
the computation of
takes one direct and one inverse DFT of length  of total cost
of total cost 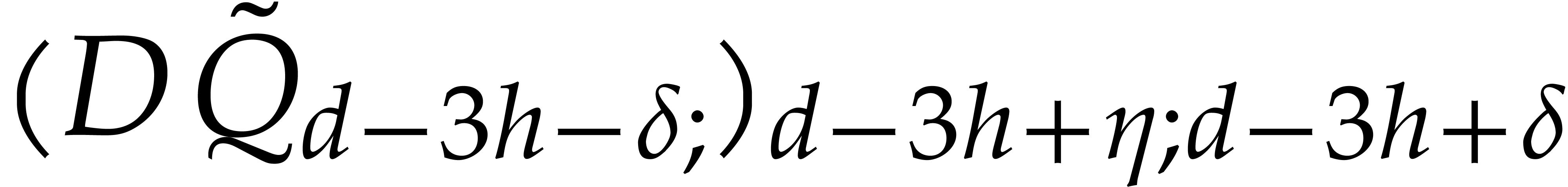 , since we
already know
, since we
already know 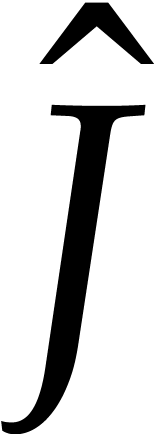 . The remaining
coefficients
. The remaining
coefficients  can be computed in time
can be computed in time 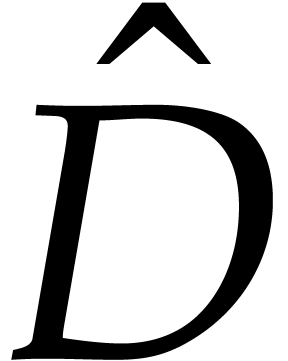 .
.
If 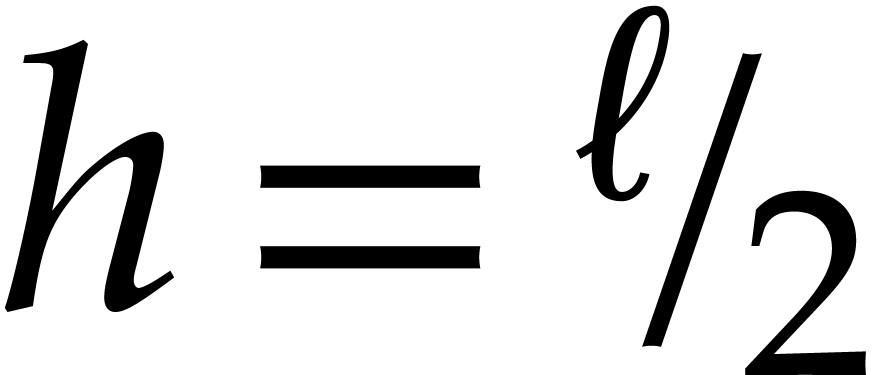 , then
, then 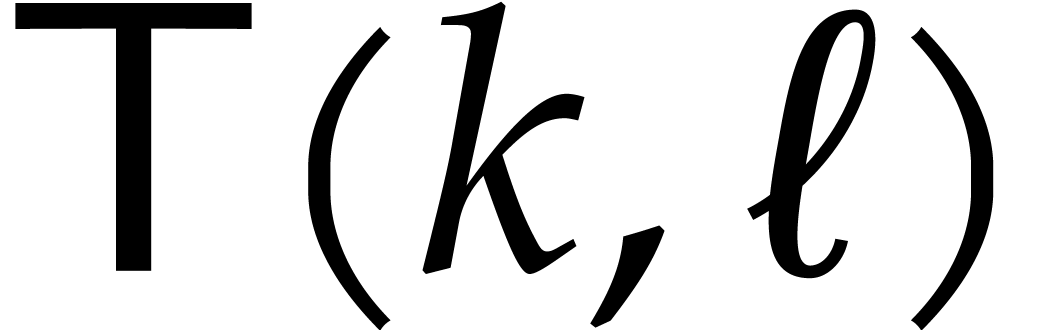 and the above analysis shows that the time complexity
and the above analysis shows that the time complexity  of the algorithm satisfies
of the algorithm satisfies

for suitable constants 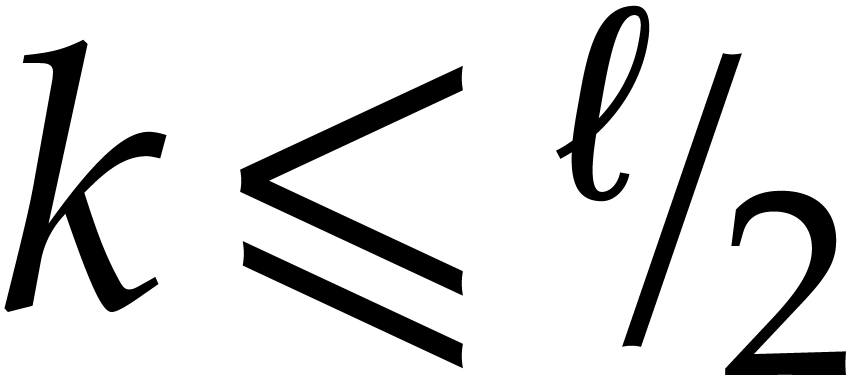 and
and  . If
. If 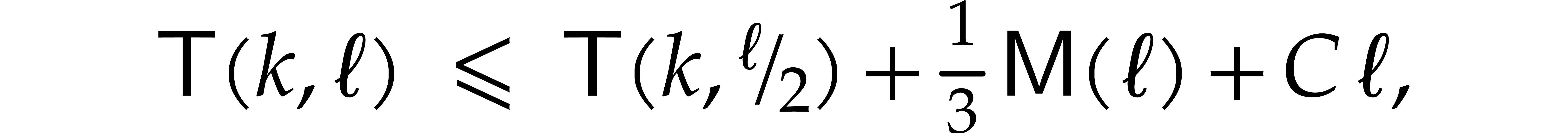 ,
then the FFT doubling in step 3 can be done in time
,
then the FFT doubling in step 3 can be done in time 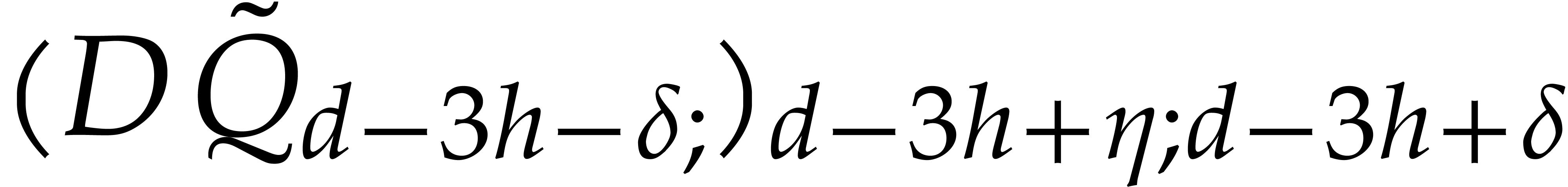 , so
, so

by increasing  if necessary. In the bound for
if necessary. In the bound for
 when
when 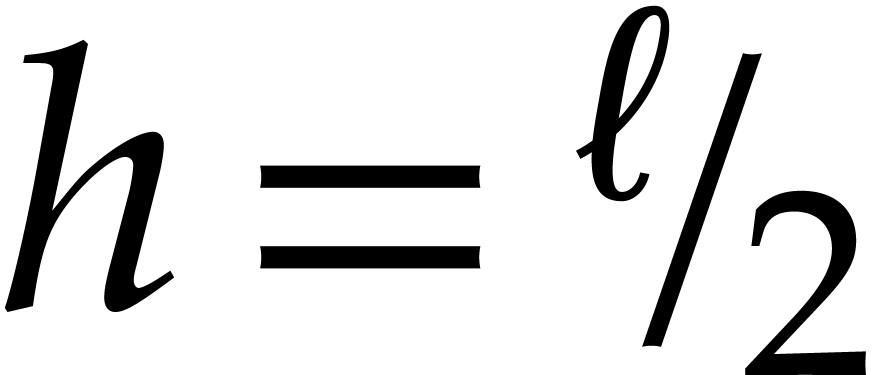 ,
the term
,
the term 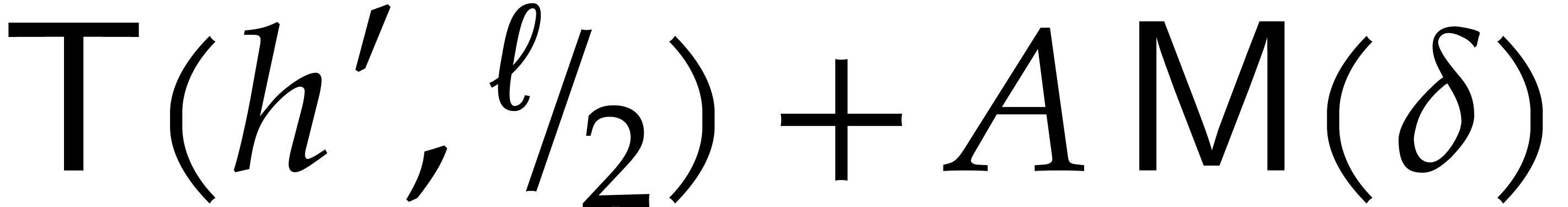 pollutes the complexity analysis. Our
next objective is to reduce to the case when the sum
pollutes the complexity analysis. Our
next objective is to reduce to the case when the sum  is replaced by
is replaced by 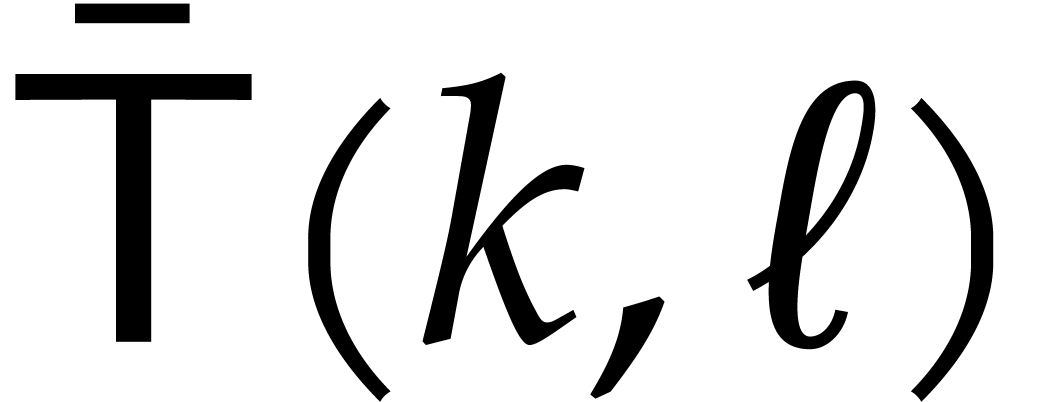 .
.
We start with the definition of an upper bound 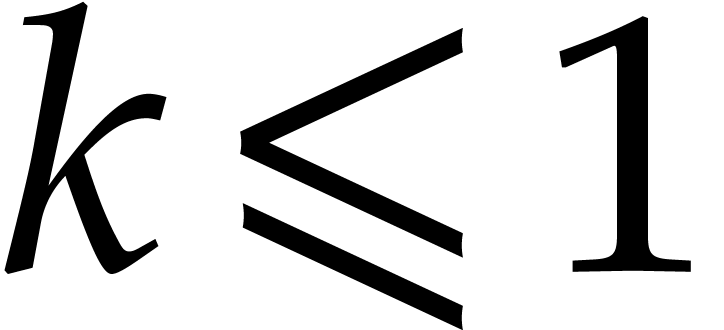 for
for  as follows. For
as follows. For  , we take
, we take  .
For
.
For 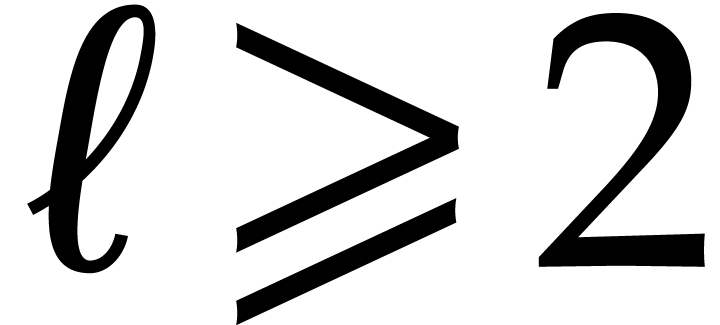 with
with  ,
we define
,
we define

For 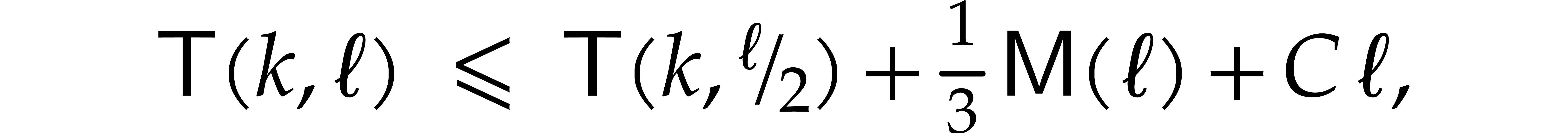 with
with  ,
we take
,
we take
Using an easy induction, we note that 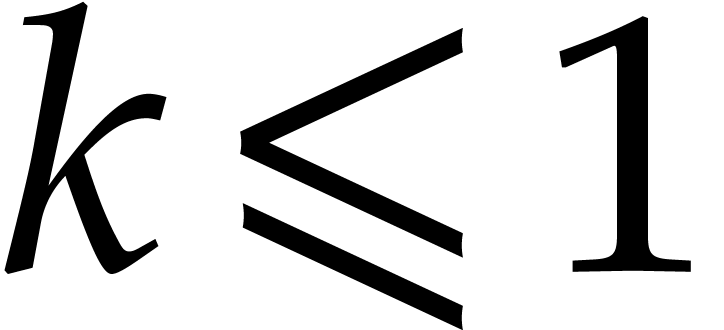 is
increasing in
is
increasing in  for fixed
for fixed 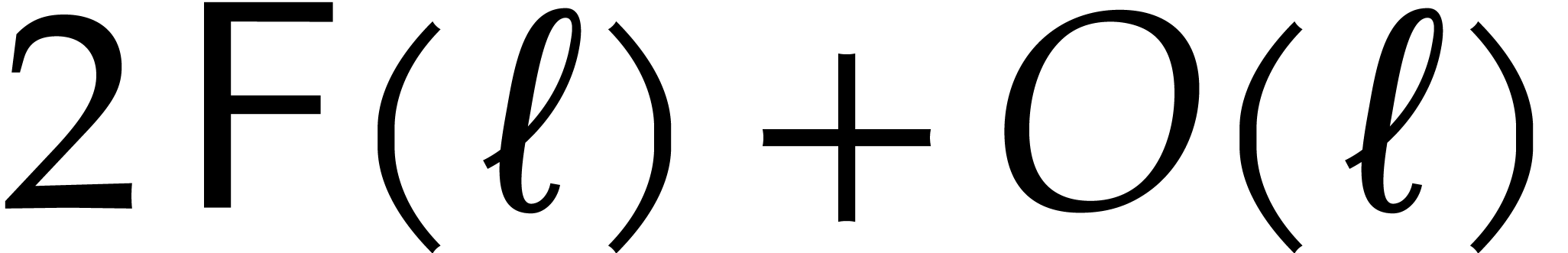 . If
. If  and
and  , then there exist
, then there exist  and
and
 with
with  such that
such that
Given 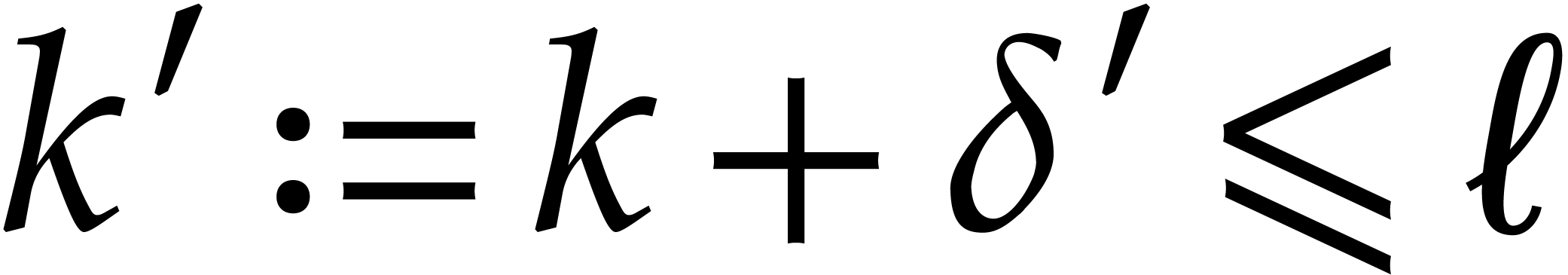 with
with  ,
it follows that
,
it follows that

More generally, for any 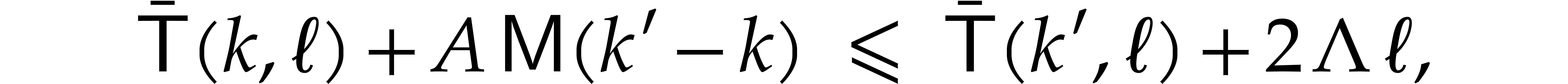 , we
claim that
, we
claim that

where 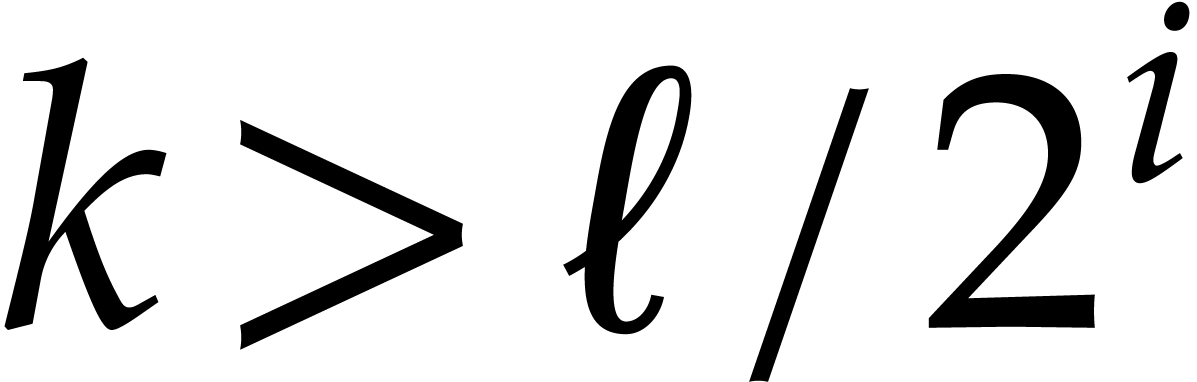 is the constant from before the statement
of this theorem.
is the constant from before the statement
of this theorem.
We prove our claim by induction on the smallest  with
with  . We already dealt with
the case when
. We already dealt with
the case when 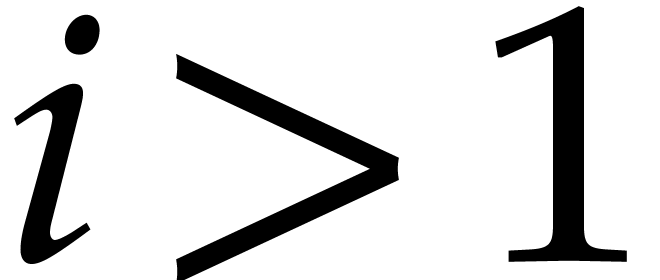 , so assume
that
, so assume
that  . If
. If 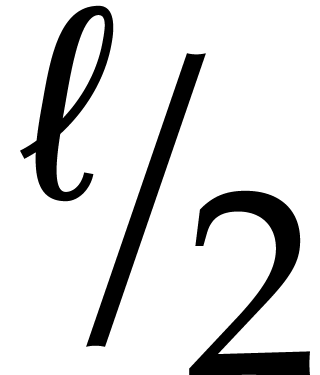 , then (13) and the induction
hypothesis with
, then (13) and the induction
hypothesis with 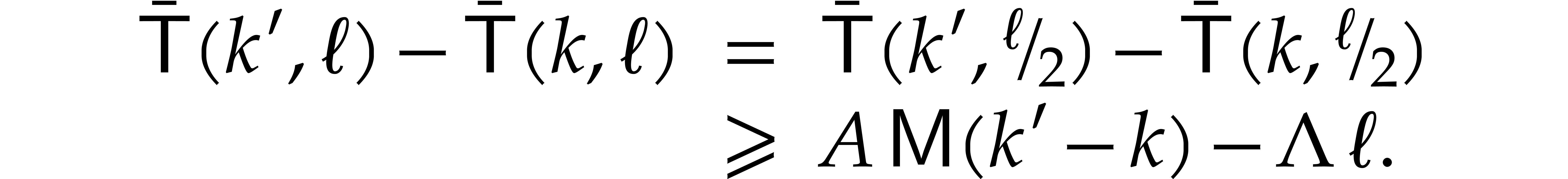 in the role of
in the role of 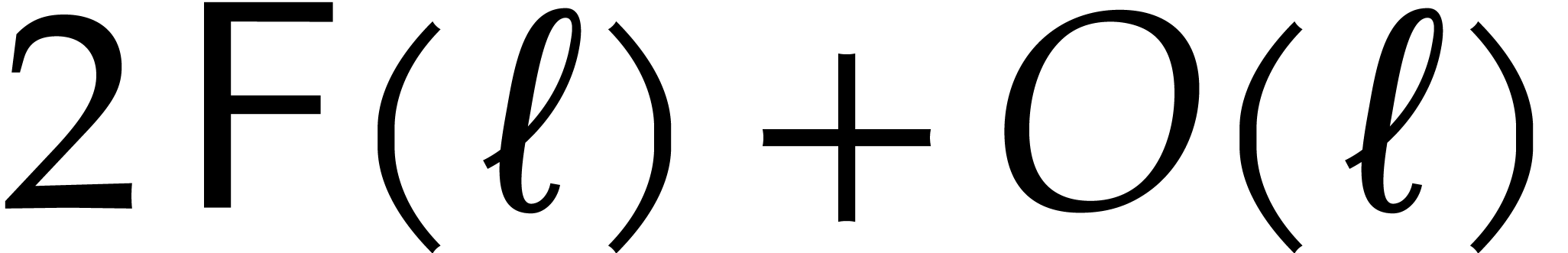 yield
yield

In particular,
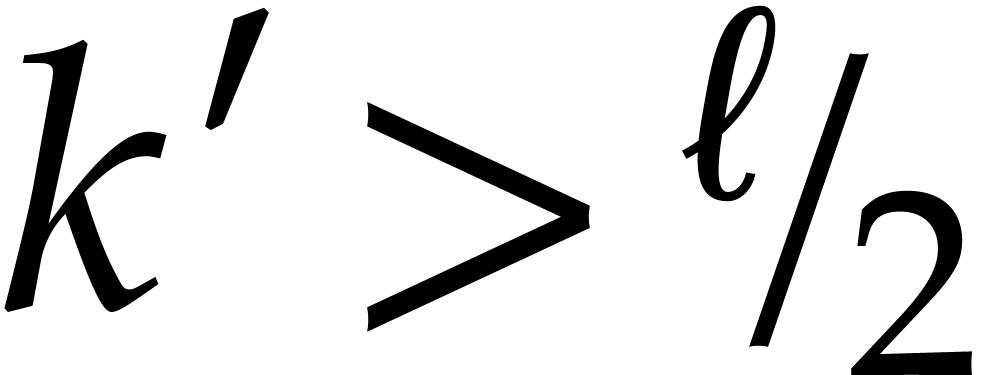
If  , then we have shown above
(with
, then we have shown above
(with 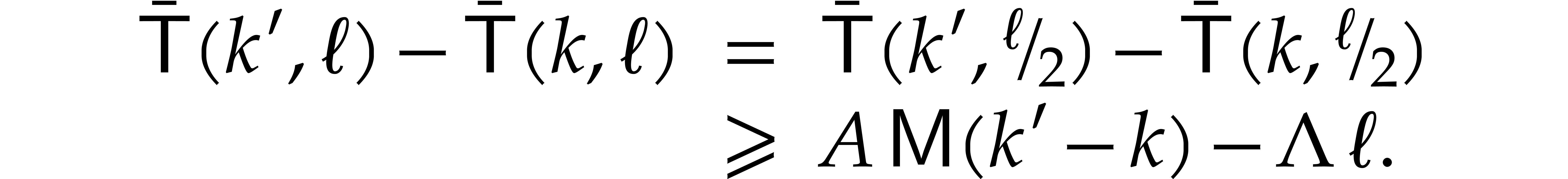 in the role of
in the role of  ) that
) that

whence
as claimed.
Now consider 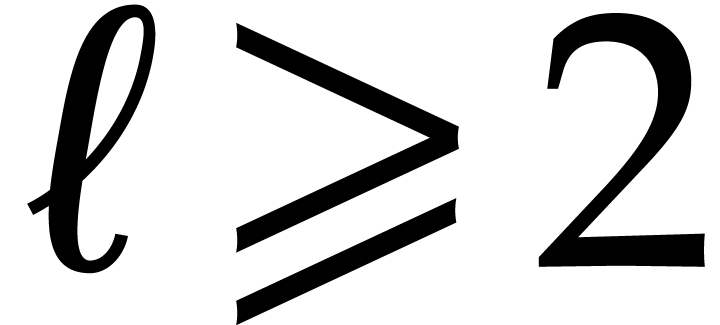 with
with  and
let
and
let  and
and  be such that
be such that
 . Then our claim implies
. Then our claim implies
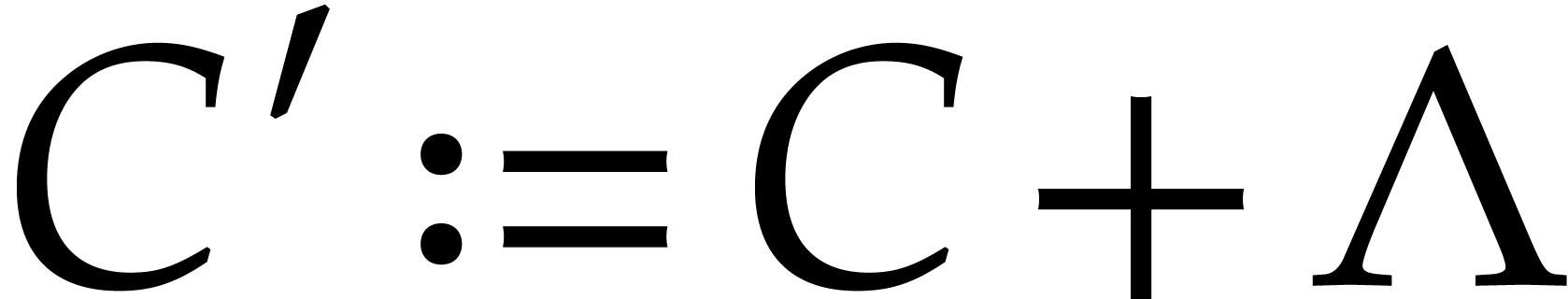
Plugging this into (14), while setting  , we obtain
, we obtain
for all  and
and  .
Unrolling this inequality for
.
Unrolling this inequality for  ,
we deduce that there exists a constant
,
we deduce that there exists a constant 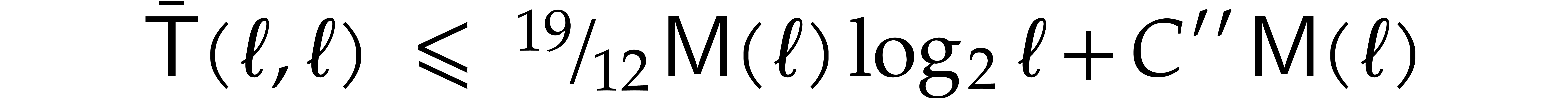 with
with
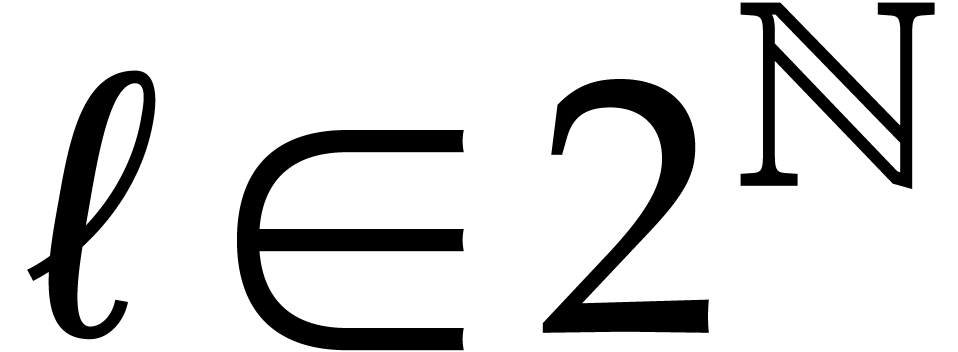
for all  . For general
. For general 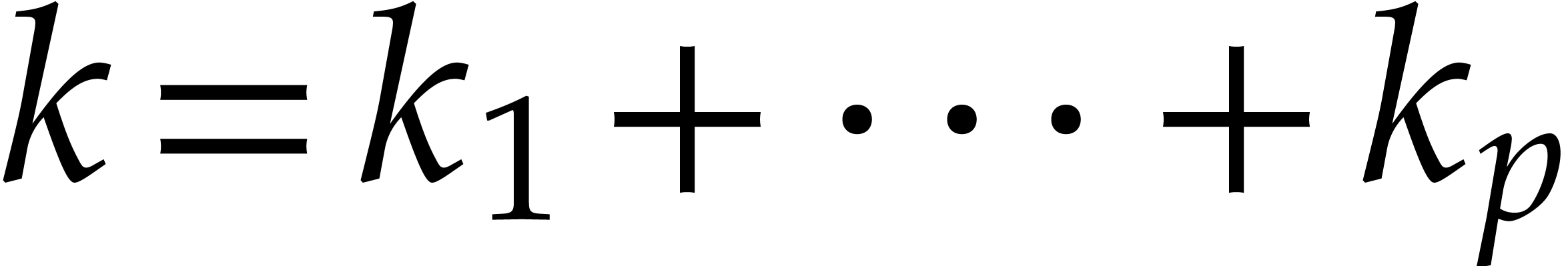 with
with  and
and  , combining this bound with (13)
and (15) yields
, combining this bound with (13)
and (15) yields
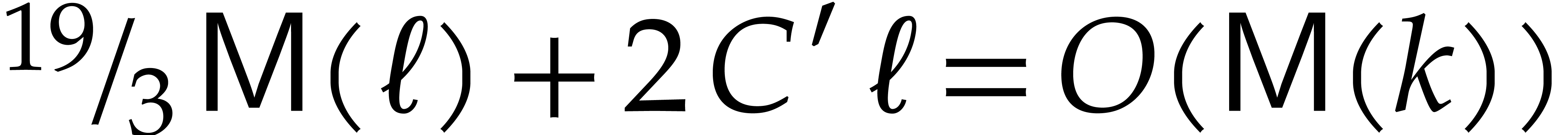
Under the assumption that 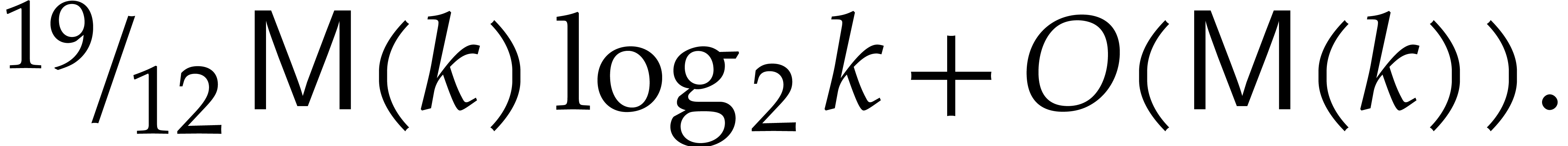 ,
we have
,
we have 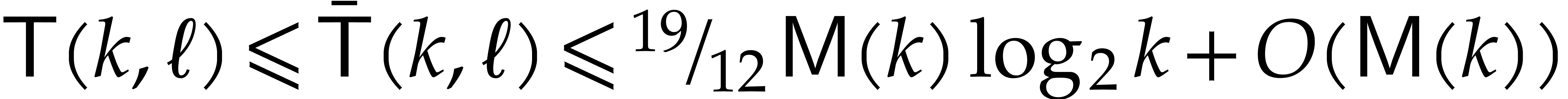 , whence
, whence 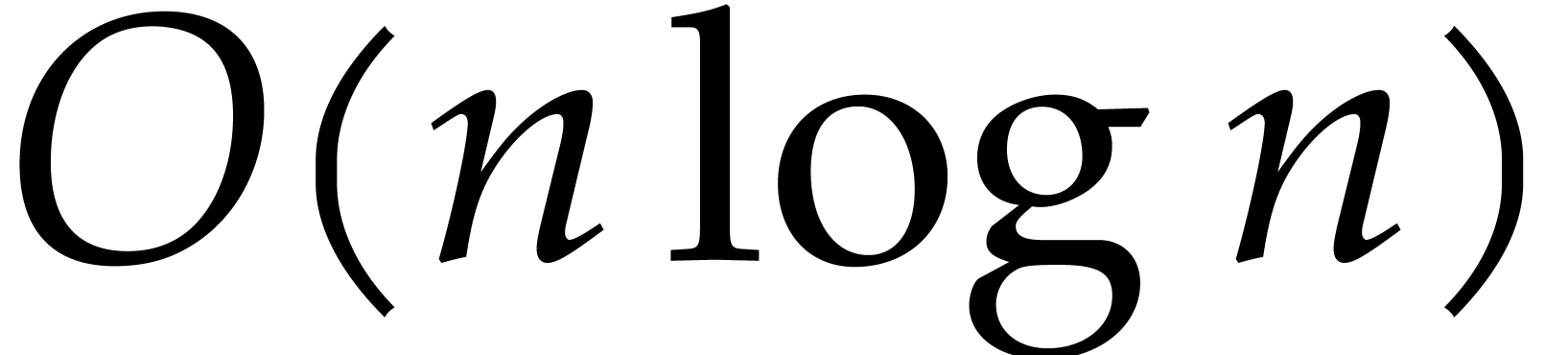 .
.
M. Ben-Or and P. Tiwari. A deterministic algorithm for sparse multivariate polynomial interpolation. In Proc. ACM STOC '88, pages 301–309. New York, NY, USA, 1988.
E. R. Berlekamp. Algebraic coding theory. McGraw-Hill, 1968.
D. J. Bernstein. Fast multiplication and its applications, pages 325–384. Mathematical Sciences Research Institute Publications. Cambridge University Press, United Kingdom, 2008.
D. J. Bernstein and B.-Y. Yang. Fast constant-time gcd computation and modular inversion. IACR Trans. Cryptogr. Hardw. Embed. Syst., 3:340–398, 2019.
R. P. Brent, F. G. Gustavson, and D. Y. Y. Yun. Fast solution of Toeplitz systems of equations and computation of Padé approximants. J. Algorithms, 1(3):259–295, 1980.
D. G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Informatica, 28:693–701, 1991.
D. G. Cantor and H. Zassenhaus. A new algorithm for factoring polynomials over finite fields. Math. Comp., 36(154):587–592, 1981.
J. W. Cooley and J. W. Tukey. An algorithm for the machine calculation of complex Fourier series. Math. Computat., 19:297–301, 1965.
J. L. Dornstetter. On the equivalence between Berlekamp's and Euclid's algorithms. IEEE Transactions on Information Theory, 33:428–431, 1987.
J. von zur Gathen and J. Gerhard. Modern Computer Algebra. Cambridge University Press, New York, NY, USA, 3rd edition, 2013.
B. Grenet, J. van der Hoeven, and G. Lecerf. Randomized root finding over finite fields using tangent Graeffe transforms. In Proc. ISSAC '15, pages 197–204. New York, NY, USA, 2015. ACM.
G. Hanrot, M. Quercia, and P. Zimmermann. The middle product algorithm I. speeding up the division and square root of power series. AAECC, 14:415–438, 2004.
D. Harvey. Faster algorithms for the square root and reciprocal of power series. Math. Comp., 80:387–394, 2011.
D. Harvey and J. van der Hoeven. Faster polynomial multiplication over finite fields using cyclotomic coefficient rings. J. of Complexity, 54, 2019. Article ID 101404, 18 pages.
D. Harvey and J. van der Hoeven. Polynomial
multiplication over finite fields in time 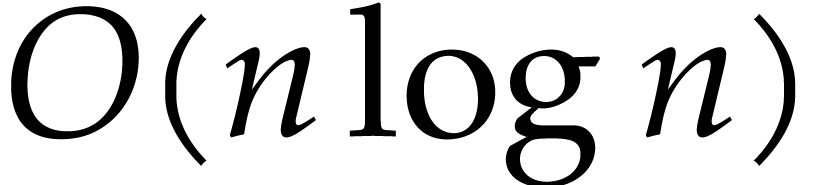 . Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02070816.
. Technical Report, HAL, 2019. http://hal.archives-ouvertes.fr/hal-02070816.
J. van der Hoeven. The truncated Fourier transform and applications. In Proc. ISSAC 2004, pages 290–296. Univ. of Cantabria, Santander, Spain, July 2004.
J. van der Hoeven and M. Monagan. Computing one billion roots using the tangent Graeffe method. ACM SIGSAM Commun. Comput. Algebra, 54(3):65–85, 2021.
J. van der Hoeven et al. GNU TeXmacs. https://www.texmacs.org, 1998.
A. Karatsuba and J. Ofman. Multiplication of multidigit numbers on automata. Soviet Physics Doklady, 7:595–596, 1963.
D. E. Knuth. The analysis of algorithms. In Actes du congrès international des matheématiciens 1970, volume 3, pages 269–274. Gauthier-Villars, 1971.
G. Lecerf. On the complexity of the Lickteig–Roy subresultant algorithm. J. Symbolic Comput., 2018. https://doi.org/10.1016/j.jsc.2018.04.017.
D. H. Lehmer. Euclid's algorithm for large numbers. Amer. Math. Monthly, pages 227–233, 1938.
D. Lichtblau. Half-GCD and fast rational recovery. In Proc. ISSAC '05, pages 231–236. 2005.
J. Massey. Shift-register synthesis and bch decoding. IEEE Transactions on Information Theory, 15:122–127, 1969.
R. Moenck. Fast computation of GCDs. In Proc. of the 5th ACM Annual Symposium on Theory of Computing, pages 142–171. New York, 1973. ACM Press.
N. Möller. On Schönhage's algorithm and subquadratic integer gcd computation. Math. Comp., 77(261):589–607, 2008.
F. Morain. Implementing the Thull-Yap algorithm for computing euclidean remainder sequences. In Proc. ISSAC '22, pages 197–205. 2022.
R. Prony. Essai expérimental et analytique sur les lois de la dilatabilité des fluides élastiques et sur celles de la force expansive de la vapeur de l'eau et de la vapeur de l'alkool, à différentes températures. J. de l'École Polytechnique Floréal et Plairial, an III, 1:24–76, 1795. Cahier 22.
A. Schönhage. Schnelle Berechnung von Kettenbruchentwicklungen. Acta Informatica, 1(2):139–144, 1971.
A. Schönhage. Schnelle Multiplikation von Polynomen über Körpern der Charakteristik 2. Acta Informatica, 7:395–398, 1977.
V. Shoup. NTL: a library for doing number theory. 1996. www.shoup.net/ntl.
D. Stehlé and P. Zimmermann. A binary recursive gcd algorithm. In D. Buell, editor, Algorithmic Number Theory, pages 411–425. Springer Berlin Heidelberg, 2004.
S. Stevin. L'arithmétique. Imprimerie de Christophle Plantin, 1585.
V. Strassen. Gaussian elimination is not optimal. Numer. Math., 13:352–356, 1969.
V. Strassen. The computational complexity of continued fractions. In Proc. of the Fourth ACM Symp. on Symbolic and Algebraic Computation, pages 51–67. 1981.
K. Thull and C. K. Yap. A unified approach to HGCD algorithms for polynomials and integers. https://cs.nyu.edu/yap/papers/SYNOP.htm#hgcd.
A. L. Toom. The complexity of a scheme of functional elements realizing the multiplication of integers. Soviet Mathematics, 4(2):714–716, 1963.