|
Joris van der
Hoevena, Robin
Larrieub
|
|
CNRS, Laboratoire d'informatique
École polytechnique
91128 Palaiseau Cedex
France
|
|
a. Email:
vdhoeven@lix.polytechnique.fr
|
|
b. Email:
larrieu@lix.polytechnique.fr
|
|
|
Abstract
Let  be the finite field with
be the finite field with  elements and let
elements and let  be a primitive
be a primitive  -th root of unity in an extension field
-th root of unity in an extension field  of
of  . Given
a polynomial
. Given
a polynomial  of degree less than
of degree less than  , we will show that its discrete Fourier
transform
, we will show that its discrete Fourier
transform  can be computed essentially
can be computed essentially  times faster than the discrete Fourier transform of a
polynomial
times faster than the discrete Fourier transform of a
polynomial  of degree less than
of degree less than  , in many cases. This result is achieved by
exploiting the symmetries provided by the Frobenius automorphism of
, in many cases. This result is achieved by
exploiting the symmetries provided by the Frobenius automorphism of  over
over  .
.
Keywords
FFT; finite field; complexity bound; Frobenius automorphism
A.C.M. subject classification: G.1.0
Computer-arithmetic, F.2.1 Number-theoretic computations
A.M.S. subject classification:
68W30
,
68Q17
,
68W40
1.Introduction
Let  and let
and let  be a
primitive
be a
primitive  -th root of unity
in
-th root of unity
in  . The traditional
algorithm for computing discrete Fourier transforms [7]
takes a polynomial
. The traditional
algorithm for computing discrete Fourier transforms [7]
takes a polynomial  of degree
of degree  on input and returns the vector
on input and returns the vector  .
If
.
If  actually admits real coefficients, then we
have
actually admits real coefficients, then we
have  for all
for all  ,
so roughly
,
so roughly  of the output values are superfluous.
Because of this symmetry, it is well known that such “real
FFTs” can be computed roughly twice as fast as their complex
counterparts [3, 25].
of the output values are superfluous.
Because of this symmetry, it is well known that such “real
FFTs” can be computed roughly twice as fast as their complex
counterparts [3, 25].
More generally, there exists an abundant literature on the computation
of FFTs of polynomials with various types of symmetry.
Crystallographic FFT algorithms date back to [26],
with contributions as recent as [20], but are dedicated to
crystallographic symmetries. So called lattice FFTs have been
studied in a series of papers initiated by [11] and
continued in [27, 4]. A more general framework
due to [1] was recently revisited from the point of view of
high-performance code generation [18]. Further symmetric
FFT algorithms and their truncated versions were developed in [16].
In this paper, we focus on discrete Fourier transforms of polynomials
 with coefficients in the finite field with
with coefficients in the finite field with  elements. In general, primitive
elements. In general, primitive  -th roots of unity
-th roots of unity  only
exist in extension fields of
only
exist in extension fields of  ,
say
,
say  . This puts us in a
similar situation as in the case of real FFTs: our primitive root of
unity
. This puts us in a
similar situation as in the case of real FFTs: our primitive root of
unity  lies in an extension field of the
coefficient field of the polynomial. This time, the degree of the
extension is
lies in an extension field of the
coefficient field of the polynomial. This time, the degree of the
extension is  instead of
instead of  . As in the case of real FFTs, it is natural to
search for algorithms that allow us to compute the DFT of a polynomial
in
. As in the case of real FFTs, it is natural to
search for algorithms that allow us to compute the DFT of a polynomial
in  approximately
approximately  times
faster than the DFT of a polynomial in
times
faster than the DFT of a polynomial in  .
.
The main purpose of this paper is to show that such a speed-up by an
approximate factor of  can indeed be achieved.
The idea is to use the Frobenius automorphism
can indeed be achieved.
The idea is to use the Frobenius automorphism  as
the analogue of complex conjugation. If
as
the analogue of complex conjugation. If  ,
then we will exploit the fact that
,
then we will exploit the fact that  for all
for all  and
and  . This
means that it suffices to evaluate
. This
means that it suffices to evaluate  at only one
element of each orbit for the action of the Frobenius automorphism on
the cyclic group
at only one
element of each orbit for the action of the Frobenius automorphism on
the cyclic group  generated by
generated by  . We will give an efficient algorithm for doing
this, called the Frobenius FFT.
. We will give an efficient algorithm for doing
this, called the Frobenius FFT.
Our main motivation behind the Frobenius FFT is the development of
faster practical algorithms for polynomial multiplication over finite
fields of small characteristic. In [12], we have shown how
to reduce multiplication in  to multiplication in
to multiplication in
 , while exploiting the fact
that efficient DFTs are available over
, while exploiting the fact
that efficient DFTs are available over  .
Unfortunately, this reduction involves an overhead of a factor
.
Unfortunately, this reduction involves an overhead of a factor  for zero padding. The Frobenius FFT can be thought of as a
more direct way to use evaluation-interpolation strategies over
for zero padding. The Frobenius FFT can be thought of as a
more direct way to use evaluation-interpolation strategies over  for polynomial multiplication over
for polynomial multiplication over  . We have not yet implemented the algorithms in
the present paper, but the ultimate hope is to make such multiplications
twice as efficient as in [12].
. We have not yet implemented the algorithms in
the present paper, but the ultimate hope is to make such multiplications
twice as efficient as in [12].
Let us briefly detail the structure of this paper. In section 2,
we first recall some standard complexity results for finite field
arithmetic. We pursue with a quick survey of the fast Fourier transform
(FFT) in section 3. The modern formulation of this
algorithm is due to Cooley and Tukey [7], but the algorithm
was already known to Gauß [9].
In section 4, we introduce the discrete Frobenius
Fourier transform (DFFT) and describe several basic algorithms to
compute DFFTs of prime order. There are essentially two efficient ways
to deal with composite orders. Both approaches are reminiscent of
analogue strategies for real FFTs [25], but the technical
details are more complicated.
The first strategy is to reduce the computation of  discrete Fourier transforms of polynomials
discrete Fourier transforms of polynomials  of
degree
of
degree  to a single discrete Fourier transform of
a polynomial
to a single discrete Fourier transform of
a polynomial  of degree
of degree  . This elegant reduction is the subject of section
5, but it is only applicable if we need to compute many
transforms. Furthermore, at best, it only leads to the gain of a factor
. This elegant reduction is the subject of section
5, but it is only applicable if we need to compute many
transforms. Furthermore, at best, it only leads to the gain of a factor
 instead of
instead of  ,
due to numerous applications of the Frobenius automorphism
,
due to numerous applications of the Frobenius automorphism  .
.
The second strategy, to be detailed in section 6, is to
carefully exploit the symmetries in the usual Cooley–Tukey FFT; we
call the resulting algorithm the Frobenius FFT (FFFT). The
complexity analysis is more intricate than for the algorithm from
section 5 and the complete factor  is only regained under certain conditions. Fortunately, these conditions
are satisfied for the most interesting applications to polynomial
multiplication in
is only regained under certain conditions. Fortunately, these conditions
are satisfied for the most interesting applications to polynomial
multiplication in  or when
or when  becomes very large with respect to
becomes very large with respect to  .
.
In this paper, we focus on direct DFFTs and FFFTs. Inverse FFFTs can be
computed in a straightforward way by reversing the main algorithm from
section 6. Inverting the various algorithms from section 4 for DFFTs of prime orders requires a bit more effort, but
should not raise any serious difficulties. The same holds for the
algorithms to compute multiple DFFTs from section 5.
Besides inverse transforms, it is possible to consider truncated
Frobenius FFTs, following [14, 15, 21],
but this goes beyond the scope of this paper. It might also be worth
investigating the use of Good's algorithm [10] as an
alternative to the Cooley–Tukey FFT, since the order  usually admits many distinct prime divisors in our
setting.
usually admits many distinct prime divisors in our
setting.
2.Finite field arithmetic
Throughout this paper and unless stated otherwise, we will assume the
bit complexity model for Turing machines with a finite number of tapes
[23]. Given a field  ,
we will write
,
we will write  for the set of polynomials in
for the set of polynomials in  of degree
of degree  .
.
Let us write  for some prime number
for some prime number  and
and  . Elements
in the finite field
. Elements
in the finite field  are usually represented as
elements of
are usually represented as
elements of  , where
, where  is a monic irreducible polynomial of degree
is a monic irreducible polynomial of degree  . We will denote by
. We will denote by  the
cost to multiply two polynomials in
the
cost to multiply two polynomials in  .
Multiplications in
.
Multiplications in  can be reduced to a constant
number of multiplications of polynomials in
can be reduced to a constant
number of multiplications of polynomials in  via
the precomputation of a “pre-inverse” of
via
the precomputation of a “pre-inverse” of  . The multiplication of two polynomials in
. The multiplication of two polynomials in  can be reduced to the multiplication of two
polynomials in
can be reduced to the multiplication of two
polynomials in  using Kronecker substitution [8, Corollary 8.27]. In other words, we have
using Kronecker substitution [8, Corollary 8.27]. In other words, we have  .
.
The best currently known bound for  was
established in [13]. It was shown there that
was
established in [13]. It was shown there that
 |
(2.1) |
uniformly in  , where
, where
Sometimes, we rather need to perform  multiplications
multiplications  with
with  . The complexity of this operation will be denoted
by
. The complexity of this operation will be denoted
by  . Throughout this paper,
it will be convenient to assume that
. Throughout this paper,
it will be convenient to assume that  is
increasing in both
is
increasing in both  and
and  . In other words,
. In other words,  is
increasing in both
is
increasing in both  and
and  .
.
The computation of the Frobenius automorphism  in
in
 requires
requires  multiplications
in
multiplications
in  when using binary powering, so this operation
has complexity
when using binary powering, so this operation
has complexity  . This cost
can be lowered by representing elements in
. This cost
can be lowered by representing elements in  with
respect to so-called normal bases [5]. However,
multiplication in
with
respect to so-called normal bases [5]. However,
multiplication in  becomes more expensive for
this representation.
becomes more expensive for
this representation.
The discrete Frobenius Fourier transform potentially involves
computations in all intermediate fields  where
where
 divides
divides  .
The necessary minimal polynomials
.
The necessary minimal polynomials  for these
fields and the corresponding pre-inverses can be kept in a table. The
bitsize of this table is bounded by
for these
fields and the corresponding pre-inverses can be kept in a table. The
bitsize of this table is bounded by  .
It is known [22] that
.
It is known [22] that  .
Consequently, the bitsize of the table requires
.
Consequently, the bitsize of the table requires  storage.
storage.
Another important operation in finite fields is modular
composition: given  and a monic polynomial
and a monic polynomial
 of degree
of degree  ,
the aim is to compute the remainder
,
the aim is to compute the remainder  of the
euclidean division of
of the
euclidean division of  by
by  . If
. If  is the minimal
polynomial of the finite field
is the minimal
polynomial of the finite field  ,
then this operation also corresponds to the evaluation of the polynomial
,
then this operation also corresponds to the evaluation of the polynomial
 at a point in
at a point in  .
If
.
If  and
and  are two distinct
monic irreducible polynomials in
are two distinct
monic irreducible polynomials in  of degree
of degree  , then the conversion of an element
in
, then the conversion of an element
in  to an element in
to an element in  also
boils down to one modular composition of degree
also
boils down to one modular composition of degree  over
over  .
.
We will denote by  the cost of a modular
composition as above. Theoretically speaking, Kedlaya and Umans proved
that
the cost of a modular
composition as above. Theoretically speaking, Kedlaya and Umans proved
that  [19]. From a practical point
of view, one rather has
[19]. From a practical point
of view, one rather has  . If
. If
 is smooth and one needs to compute several
modular compositions for the same modulus, then algorithms of
quasi-linear complexity do exist [17].
is smooth and one needs to compute several
modular compositions for the same modulus, then algorithms of
quasi-linear complexity do exist [17].
Given primitive elements  and
and  with
with  , the paper [17]
also contains efficient algorithms for conversions between
, the paper [17]
also contains efficient algorithms for conversions between  and
and  . Using
modular composition, we notice that this problem reduces in time
. Using
modular composition, we notice that this problem reduces in time  to the case where we are free to choose primitive
elements
to the case where we are free to choose primitive
elements  and
and  that suit
us. We let
that suit
us. We let  be a cost function for conversions
between
be a cost function for conversions
between  and
and  and denote
and denote
 .
.
3.Fast Fourier transforms
3.1The discrete Fourier
transform
Let  be any field and let
be any field and let  be a primitive
be a primitive  -th root of
unity for some
-th root of
unity for some  . Now consider
a polynomial
. Now consider
a polynomial  , where
, where

The discrete Fourier transform  of
of  with respect to
with respect to  is the vector
is the vector

If  is a small number, then
is a small number, then  can be computed by evaluating
can be computed by evaluating  directly for
directly for  , using Horner's method for
instance. If
, using Horner's method for
instance. If  is a prime number, then Rader and
Bluestein have given efficient methods for the computation of discrete
Fourier transforms of order
is a prime number, then Rader and
Bluestein have given efficient methods for the computation of discrete
Fourier transforms of order  ;
see [24, 6] and subsection 3.2
below.
;
see [24, 6] and subsection 3.2
below.
In subsection 3.4, we are interested in the case when  is composite. In that case, one may compute
is composite. In that case, one may compute  using the fast Fourier transform (or FFT). The
modern formulation of this algorithm is due to Cooley and Tukey [7], but the algorithm was already known to Gauß [9]. The output
using the fast Fourier transform (or FFT). The
modern formulation of this algorithm is due to Cooley and Tukey [7], but the algorithm was already known to Gauß [9]. The output  of the FFT uses a
mirrored indexation
of the FFT uses a
mirrored indexation  that we will introduce in
subsection 3.3 below.
that we will introduce in
subsection 3.3 below.
We will denote by  the cost of computing a FFT in
the field
the cost of computing a FFT in
the field  .
.
3.2Rader reduction
Assume that we wish to compute a DFT of large prime length  . The multiplicative group
. The multiplicative group  is cyclic, of order
is cyclic, of order  . Let
. Let
 be such that
be such that  is a
generator of this cyclic group. Given a polynomial
is a
generator of this cyclic group. Given a polynomial  and
and  with
with  ,
we have
,
we have

Setting

it follows that  , when
regarding
, when
regarding  ,
,  and
and  as elements of
as elements of

In other words, we have essentially reduced the computation of a
discrete Fourier transform of length  to a
so-called cyclic convolution of length
to a
so-called cyclic convolution of length  .
.
3.3Generalized bitwise mirrors
Let  be a positive integer with a factorization
be a positive integer with a factorization
 such that
such that  for each
for each  . Then any index
. Then any index  can uniquely be written in the form
can uniquely be written in the form

where  for all
for all  .
We call
.
We call  the digits of
the digits of  when written in the mixed base
when written in the mixed base  .
We also define the
.
We also define the  -mirror
of
-mirror
of  by
by

Whenever  is clear from the context, we simply
write
is clear from the context, we simply
write  instead of
instead of  .
.
If  has length one, then we notice that
has length one, then we notice that

Setting  , we also have
, we also have

Finally, given  , let
, let  ,
,  ,
,
 and
and  ,
so that
,
so that  and
and  .
Then it is not hard to see that for all
.
Then it is not hard to see that for all  and
and
 , we have
, we have

3.4The Cooley–Tukey FFT
We are now in a position to recall how the FFT works. Let  ,
,  ,
,
 and
and  be as at the end of
the previous subsection. We denote
be as at the end of
the previous subsection. We denote  and notice
that
and notice
that  is a primitive
is a primitive  -th root of unity. Similarly,
-th root of unity. Similarly,  is a primitive
is a primitive  -th root of
unity. Recall that
-th root of
unity. Recall that  for
for  . For any
. For any  and
and  , we have
, we have

so that
 |
(3.1) |
In this formula, one recognizes two polynomial evaluations of orders
 and
and  .
More precisely, we may decompose the polynomial
.
More precisely, we may decompose the polynomial  as
as

where  and
and  .
This allows us to rewrite (3.1) as
.
This allows us to rewrite (3.1) as
 |
(3.2) |
For each  , we may next
introduce the polynomial
, we may next
introduce the polynomial  by
by

The relation (3.2) now further simplifies into
 |
(3.3) |
This leads to the following recursive algorithm for the computation of
discrete Fourier transforms.
Algorithm 
Input: 
Output:  .
.
if  then
compute the answer using a direct algorithm and return it
then
compute the answer using a direct algorithm and return it
Decompose 
for  do
do
Compute 
for  do
do
Let 
Let 
Compute 
return 
If the  are all bounded, then this algorithm
requires
are all bounded, then this algorithm
requires  operations in
operations in  . For practical purposes it is best though to pick
. For practical purposes it is best though to pick
 such that
such that  and
and  are as close to
are as close to  as possible. This
approach is most “cache friendly” in the sense that it keeps
data as close as possible in memory [2].
as possible. This
approach is most “cache friendly” in the sense that it keeps
data as close as possible in memory [2].
4.Frobenius Fourier transforms
4.1The discrete Frobenius Fourier
transform
Let  be an extension of finite fields. Let
be an extension of finite fields. Let  denote the Frobenius automorphism of
denote the Frobenius automorphism of  over
over  . We recall that the
group
. We recall that the
group  generated by
generated by  has
size
has
size  and that it coincides with the Galois group
of
and that it coincides with the Galois group
of  over
over  .
.
Let  be a primitive
be a primitive  -th
root of unity with
-th
root of unity with  . Recall
that
. Recall
that  and
and  .
We will write
.
We will write  for the cyclic group of size
for the cyclic group of size  generated by
generated by  .
The Frobenius automorphism
.
The Frobenius automorphism  naturally acts on
naturally acts on
 and we denote by
and we denote by  the
order of an element
the
order of an element  under this action. Notice
that
under this action. Notice
that  . A subset
. A subset  is called a cross section if for every
is called a cross section if for every  , there exists exactly one
, there exists exactly one  such that
such that  for some
for some  . We will denote this element
. We will denote this element  by
by  . We
will also denote the corresponding set of indices by
. We
will also denote the corresponding set of indices by  .
.
Now consider a polynomial  .
Recall that its discrete Fourier transform with respect to
.
Recall that its discrete Fourier transform with respect to  is defined to be the vector
is defined to be the vector

Since  admits coefficients in
admits coefficients in  , we have
, we have

for all  . For any
. For any  , this means that we may retrieve
, this means that we may retrieve
 from
from  .
Indeed, setting
.
Indeed, setting  with
with  , we obtain
, we obtain  .
We call
.
We call

the discrete Frobenius Fourier transform of  with respect to
with respect to  and the section
and the section  .
.
Let  and
and  .
Then
.
Then  leaves
leaves  invariant,
whence
invariant,
whence  . Since
. Since  is the subfield of
is the subfield of  that is fixed
under the action of
that is fixed
under the action of  , this
yields
, this
yields

It follows that the number of coefficients in  needed to represent
needed to represent  is given by
is given by
 |
(4.1) |
In particular, the output and input size  of the
discrete Frobenius Fourier transform coincide.
of the
discrete Frobenius Fourier transform coincide.
4.2Twiddled transforms
In the Cooley–Tukey algorithm from section 3.4, the
second wave of FFTs operates on “twiddled” polynomials  instead of the polynomials
instead of the polynomials  . An alternative point of view is to directly
consider the evaluation of
. An alternative point of view is to directly
consider the evaluation of  at the points
at the points  with
with  and where
and where  . We will call this operation a twiddled
DFT.
. We will call this operation a twiddled
DFT.
The twiddled DFFT is defined in a similar manner. More precisely, assume
that we are given an  -th root
of unity
-th root
of unity  such that the set
such that the set  is stable under the action of
is stable under the action of  .
Assume also that we have a cross section
.
Assume also that we have a cross section  of
of  under this action and the corresponding set of
indices
under this action and the corresponding set of
indices  . Then the
twiddled DFFT computes the family
. Then the
twiddled DFFT computes the family

Again, we notice that
 |
(4.2) |
We will denote by  the complexity of computing a
twiddled DFFT of this kind.
the complexity of computing a
twiddled DFFT of this kind.
4.3The naive strategy
If  is a small number, then we recall from
section 3.1 that it is most efficient to compute ordinary
DFTs of order
is a small number, then we recall from
section 3.1 that it is most efficient to compute ordinary
DFTs of order  in a naive fashion, by evaluating
in a naive fashion, by evaluating
 for
for  using Horner's
method. From an implementation point of view, one may do this using
specialized codelets for various small
using Horner's
method. From an implementation point of view, one may do this using
specialized codelets for various small  .
.
The same naive strategy can also be used for the computation of DFFTs
and twiddled DFFTs. Given a cross section  and
the corresponding set of indices
and
the corresponding set of indices  ,
it suffices to evaluate
,
it suffices to evaluate  separately for each
separately for each
 . Let
. Let  be the order of
be the order of  under the action of
under the action of  . Then
. Then  actually belongs
to
actually belongs
to  , so the evaluation of
, so the evaluation of
 can be done in time
can be done in time  . With the customary assumption that
. With the customary assumption that  is increasing as a function of
is increasing as a function of  , it follows using (4.2) that the
complete twiddled DFFT can be computed in time
, it follows using (4.2) that the
complete twiddled DFFT can be computed in time

Assuming that full DFTs of order  over
over  are also computed using the naive strategy, this yields
are also computed using the naive strategy, this yields
 |
(4.3) |
In other words, for small  ,
we have achieved our goal to gain a factor
,
we have achieved our goal to gain a factor  .
.
4.4Full Frobenius action
The next interesting case for study is when  is
prime and the action of
is
prime and the action of  on
on  is either transitive, or has only two orbits and one of them is trivial.
If
is either transitive, or has only two orbits and one of them is trivial.
If  , then
, then  always forms an orbit of its own in
always forms an orbit of its own in  ,
but we can have
,
but we can have  . If
. If  , then it can happen that
, then it can happen that  is a singleton. This happens for instance for a
is a singleton. This happens for instance for a  -th primitive root of unity
-th primitive root of unity  , for
, for  ,
and
,
and  .
.
If  is a singleton, say
is a singleton, say  , then we necessarily have
, then we necessarily have  and the DFFT reduces to a single evaluation
and the DFFT reduces to a single evaluation  with
with
 and
and  .
This is precisely the problem of modular composition that we encountered
in section 2, whence
.
This is precisely the problem of modular composition that we encountered
in section 2, whence  .
The speed-up
.
The speed-up  with respect to a full DFT is
comprised between
with respect to a full DFT is
comprised between  and
and  , depending on the efficiency of our algorithm for
modular composition. Theoretically speaking, we recall that
, depending on the efficiency of our algorithm for
modular composition. Theoretically speaking, we recall that  , which allows us to gain a factor
, which allows us to gain a factor  for any
for any  .
.
In a similar way, if  and
and  , then the computation of one DFFT reduces to
, then the computation of one DFFT reduces to  additions (in order to compute
additions (in order to compute  ) and one composition modulo a polynomial of degree
) and one composition modulo a polynomial of degree
 (instead of
(instead of  ).
).
Remark 4.1. Assume that  is prime,
is prime,  and
and  . If we are free to choose the representation
of elements in
. If we are free to choose the representation
of elements in  , then the
DFFT becomes particularly efficient if we take
, then the
DFFT becomes particularly efficient if we take  . In other words, if
. In other words, if  is the
monic minimal polynomial of
is the
monic minimal polynomial of  over
over  (so that
(so that  ),
then we represent elements of
),
then we represent elements of  as polynomials in
as polynomials in
 modulo
modulo  .
Given
.
Given  , just writing down
, just writing down
 then yields the evaluation of
then yields the evaluation of  at
at  , whence
, whence  .
.
4.5Rader reduction
For large prime orders  and
and  , let us now show how to adapt Rader reduction
to the computation of DFFTs in favourable cases. With the notations from
section 3.2, we have
, let us now show how to adapt Rader reduction
to the computation of DFFTs in favourable cases. With the notations from
section 3.2, we have

for all  , where
, where  is such that
is such that  .
The action of
.
The action of  therefore induces an action
therefore induces an action  on
on  .
.
Let us assume for simplicity that the order  of
the additive subgroup generated by
of
the additive subgroup generated by  in
in  is comprime with
is comprime with  .
Then there exists an element
.
Then there exists an element  of order
of order  in
in  and
and  . Consequently,
. Consequently,

We may thus regard the product  as a bivariate
polynomial in
as a bivariate
polynomial in  and
and  .
Let
.
Let  be the constant term in
be the constant term in  of this bivariate polynomial. From
of this bivariate polynomial. From  ,
we can recover
,
we can recover  for every
for every  . By construction, the
. By construction, the  with
with
 actually form a section of
actually form a section of  under the action of
under the action of  . This
reduces the computation of a DFFT for the section
. This
reduces the computation of a DFFT for the section  to the computation of
to the computation of  .
.
As to the computation of  ,
assume for simplicity that
,
assume for simplicity that  contains a primitive
contains a primitive
 -th root of unity. Recall
that
-th root of unity. Recall
that  has coefficients in
has coefficients in  whereas
whereas  admits coefficients in
admits coefficients in  . Notice also that
. Notice also that  does
not depend on the input
does
not depend on the input  ,
whence it can be precomputed. We compute
,
whence it can be precomputed. We compute  as
follows in the FFT-model with respect to
as
follows in the FFT-model with respect to  .
We first transform
.
We first transform  and
and  into two vectors
into two vectors  and
and  . The computation of
. The computation of  may
again be regarded as a precomputation. The computation of the Fourier
transform
may
again be regarded as a precomputation. The computation of the Fourier
transform  now comes down to
now comes down to  modular compositions of degree
modular compositions of degree  over
over  . We finally transform the result back into
. We finally transform the result back into
 . Altogether, this yields
. Altogether, this yields

It is instructive to compare this with the cost of a full DFT of length
 over
over  using Rader's
algorithm:
using Rader's
algorithm:

Depending on the efficiency of modular composition, the speed-up for
DFFTs therefore varies between  and
and  . Notice that the algorithm from the previous
subsection becomes a special case with parameters
. Notice that the algorithm from the previous
subsection becomes a special case with parameters  and
and  .
.
5.Multiple Fourier transforms
5.1Parallel lifting
Let  be an extension of
be an extension of  and assume that its elements are represented as polynomials in a
primitive element
and assume that its elements are represented as polynomials in a
primitive element  of degree
of degree  . Given
. Given  polynomials
polynomials
 , we may then form the
polynomial
, we may then form the
polynomial

If  and
and  is a primitive
is a primitive
 -th root of unity in the base
field
-th root of unity in the base
field  , then we notice that
, then we notice that
 |
(5.1) |
In other words, the discrete Fourier transform operates coefficientwise
with respect to the basis  of
of  .
.
Recall that  stands for the cost of computing
stands for the cost of computing
 Fourier transforms of length
Fourier transforms of length  over
over  . The maps
. The maps  and its inverse boil down to matrix transpositions in
memory. On a Turing machine, they can therefore be computed in time
and its inverse boil down to matrix transpositions in
memory. On a Turing machine, they can therefore be computed in time
 . From (5.1), it
follows that
. From (5.1), it
follows that
 |
(5.2) |
This relation does not give us anything really new, since we made the
assumption in section 2 that  is
increasing in both
is
increasing in both  and
and  . Nevertheless, it provides us with an elegant and
explicit algorithm in a special case.
. Nevertheless, it provides us with an elegant and
explicit algorithm in a special case.
5.2Symmetric multiplexing
Let us next consider an  -th
root of unity
-th
root of unity  and a primitive
and a primitive  -th root of unity
-th root of unity  .
Given
.
Given  , we have for all
, we have for all  ,
,

Abbreviating  and setting
and setting


it follows that

Now given the twiddled discrete Fourier transform  of
of  , we in particular know
the values
, we in particular know
the values  . Letting the
Frobenius automorphism
. Letting the
Frobenius automorphism  act on these values, we
obtain the vector
act on these values, we
obtain the vector  . Using one
matrix-vector product
. Using one
matrix-vector product  , we
may then retrieve the values of the individual twiddled transforms
, we
may then retrieve the values of the individual twiddled transforms  at
at  . Doing
this for each
. Doing
this for each  in a cross section of
in a cross section of  under the action of
under the action of  ,
this yields a way to retrieve the twiddled DFFTs of
,
this yields a way to retrieve the twiddled DFFTs of  from the twiddled DFT of
from the twiddled DFT of  .
.
Recall that  denotes the complexity of computing
the DFFTs of
denotes the complexity of computing
the DFFTs of  elements of
elements of  over
over  . Since
. Since  is a Vandermonde matrix, the matrix-vector product
is a Vandermonde matrix, the matrix-vector product  can be computed in time
can be computed in time  using polynomial
interpolation [8, Chapter 10]. Given
using polynomial
interpolation [8, Chapter 10]. Given  , we may compute each individual vector
, we may compute each individual vector  in time
in time  using the Frobenius
automorphism
using the Frobenius
automorphism  . Since there
are
. Since there
are  orbits in
orbits in  under the
action of
under the
action of  , we may thus
retrieve the
, we may thus
retrieve the  from
from  in
time
in
time  . In other words,
. In other words,
 |
(5.3) |
5.3Multiplexing over an intermediate
field
In the extreme case when  ,
every
,
every  has order one under the action of
has order one under the action of  and
and  . In
that case, the bound (5.3) is not very sharp, but (5.2)
already provides us with a good alternative bound for this special case.
For
. In
that case, the bound (5.3) is not very sharp, but (5.2)
already provides us with a good alternative bound for this special case.
For  with
with  ,
let us now consider the case when
,
let us now consider the case when  has order at
most
has order at
most  under the action of
under the action of  for all
for all  , so that
, so that  . Let
. Let  be a
primitive element in
be a
primitive element in  over
over  , so that
, so that  and
and  . Given our
. Given our  polynomials
polynomials
 , we may form
, we may form

Then we have

Moreover, we may compute  from
from  for each
for each  , using the
algorithm from the previous subsection, but with the additional property
that at least one
, using the
algorithm from the previous subsection, but with the additional property
that at least one  has maximal order
has maximal order  under the action of
under the action of  .
.
If  is prime and
is prime and  ,
then the above discussion shows that, without loss of generality, we may
assume that
,
then the above discussion shows that, without loss of generality, we may
assume that  has order
has order  under the action of
under the action of  . This
means that
. This
means that  has maximal order
has maximal order  for every
for every  , whereas
, whereas  has order one. Hence,
has order one. Hence,  .
Similarly, if
.
Similarly, if  is prime and
is prime and  , then we obtain a reduction to the case when
, then we obtain a reduction to the case when
 has maximal order
has maximal order  for
all
for
all  , whence
, whence  . In both cases, we obtain the following:
. In both cases, we obtain the following:
Proposition 5.1. If
 is prime, then
is prime, then

Remark 5.2. We recall that  , whence
, whence  .
When using the best known bound (2.1) for
.
When using the best known bound (2.1) for  and
and  , it follows for some
constant
, it follows for some
constant  that
that

In other words, we cannot hope to gain more than an asymptotic factor of
 with respect to a full DFT.
with respect to a full DFT.
If  is not necessarily prime, then the technique
from this section can still be used for every individual
is not necessarily prime, then the technique
from this section can still be used for every individual  . However, the rewritings of elements in
. However, the rewritings of elements in  as elements in
as elements in  and
and  have to be done individually for each
have to be done individually for each  using modular compositions. Denoting by
using modular compositions. Denoting by  the
order of
the
order of  under
under  ,
it follows that
,
it follows that

Notice that conversions of the same type correspond to modular
compositions with the same modulus. If  is
smooth, then it follows that we may use the algorithms from [17]
and keep the cost of the conversions quasi-linear.
is
smooth, then it follows that we may use the algorithms from [17]
and keep the cost of the conversions quasi-linear.
6.The Frobenius FFT
Let  and
and  be as in section
3.3 and let
be as in section
3.3 and let  be a primitive
be a primitive  -th root of unity. In this section
we present an analogue of the FFT from section 3.4: the
Frobenius FFT (or FFFT). This algorithm uses the same mirrored
indexation as the Cooley–Tukey FFT: given
-th root of unity. In this section
we present an analogue of the FFT from section 3.4: the
Frobenius FFT (or FFFT). This algorithm uses the same mirrored
indexation as the Cooley–Tukey FFT: given  , it thus returns the family
, it thus returns the family  . We start with the description of the index set
. We start with the description of the index set
 that corresponds to the so-called
“privileged cross section”
that corresponds to the so-called
“privileged cross section”  of
of  .
.
6.1Privileged cross sections
Given  , consider the orbit
, consider the orbit
 of
of  under the action of
under the action of
 . We define
. We define

Then  is a cross section of
is a cross section of  under the action of
under the action of  ; we call
it the privileged cross section for
; we call
it the privileged cross section for  (and
(and  ).
).
Now let  ,
,  ,
,  ,
,
 and
and  be as above. Then
be as above. Then
 is a primitive
is a primitive  -th
root of unity. Let
-th
root of unity. Let  be the corresponding
privileged cross section of
be the corresponding
privileged cross section of  .
.
Proposition 6.1. We
have

Proof. Let  and
and  with
with  and
and  be such that
be such that  for some
for some  . Since
. Since

and similarly  , it follows
that
, it follows
that  .
.
Inversely, given  with
with  for some
for some  , we claim that
there exists a
, we claim that
there exists a  such that
such that  for
for  . Indeed,
. Indeed,  implies that
implies that  ,
whence
,
whence  is an
is an  -th
root of unity. This means that there exists a
-th
root of unity. This means that there exists a  with
with  , i.e.
, i.e.
 .
.
Now assume that 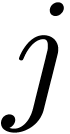 is minimal with
is minimal with  for some
for some  . Given
. Given  such that
such that  , the
above claim shows that there exists a
, the
above claim shows that there exists a  such that
such that
 for
for  .
But then
.
But then  , whence
, whence  . This shows that
. This shows that  implies
implies  .
.
Inversely, assume that  is minimal such that
is minimal such that
 . Then the above claim
implies that there exists a
. Then the above claim
implies that there exists a  such that
such that  for
for  . Without
loss of generality we may assume that
. Without
loss of generality we may assume that  was chosen
minimal while satisfying this property. Given
was chosen
minimal while satisfying this property. Given  ,
,  and
and  with
with  , we have
, we have  . Consequently,
. Consequently,  and
and
 whenever
whenever  .
In other words,
.
In other words,  . This shows
that
. This shows
that  implies the existence of a
implies the existence of a  with
with  and
and  .
.
6.2The main algorithm
We are now in a position to adapt the Cooley–Tukey FFT. In the
case when  or
or  is prime,
we will use one of the algorithms from section 4 for the
computation of twiddled DFFTs.
is prime,
we will use one of the algorithms from section 4 for the
computation of twiddled DFFTs.
Algorithm 
Input: 
Output:  .
.
if  then
return
then
return 
Let 
Decompose 
for  do
do
for  do
do
Let 
Notice that  ,
,
where  is the order of
is the order of 
Let 
if  then
then
Let 
Compute 
Compute 
return 
For the usual FFT, it was possible to choose  in
such a way that
in
such a way that  , and we
recall that this improves the cache efficiency of practical
implementations. However, this optimization is more problematic in our
setting since it would require the development of an efficient recursive
algorithm for twiddled FFFTs. This is an interesting topic, but beyond
the scope of the present paper.
, and we
recall that this improves the cache efficiency of practical
implementations. However, this optimization is more problematic in our
setting since it would require the development of an efficient recursive
algorithm for twiddled FFFTs. This is an interesting topic, but beyond
the scope of the present paper.
6.3Complexity analysis
Let us now perform the complexity analysis of  . For
. For  ,
we first focus on all FFTs and twiddled DFFTs that are computed at
“stage
,
we first focus on all FFTs and twiddled DFFTs that are computed at
“stage  ” using a
fallback algorithm. These FFTs and twiddled DFFTs are all of length
” using a
fallback algorithm. These FFTs and twiddled DFFTs are all of length
 . Given
. Given  , let
, let  be the number of
transforms of a polynomial in
be the number of
transforms of a polynomial in  over
over  . From (4.2), it follows that
. From (4.2), it follows that

Now a naive bound for the cost of an FFT or twiddled DFFT of a
polynomial in  over
over  is
is
 |
(6.1) |
This means that the cost of all FFTs and twiddled DFFTs at stage  is bounded by
is bounded by

Now  can only be non zero if
can only be non zero if  . Consequently,
. Consequently,

The total cost of all FFTs and twiddled DFFTs of prime length is
therefore bounded by

where  .
.
Strictly speaking, if  is a proper divisor of
is a proper divisor of
 , then the output of a
twiddled DFFT of a polynomial in
, then the output of a
twiddled DFFT of a polynomial in  over
over  does not use the “standard” representation for
does not use the “standard” representation for
 , so the result must be
converted. The cost of all such conversions at stage
, so the result must be
converted. The cost of all such conversions at stage  is bounded by
is bounded by

For a number  with prime factorization
with prime factorization  , let
, let  .
We also denote
.
We also denote  and notice that
and notice that  . Let us show by induction over
. Let us show by induction over  that
that

This is clear for  , since
, since
 and
and  for
for  . Assuming that the relation holds for a given
. Assuming that the relation holds for a given
 , we get
, we get

This completes the induction and we conclude that the total conversion
cost is bounded by

This concludes the proof of the following result:
Theorem 6.2. If
 are all prime, then
are all prime, then

where  .
.
Remark 6.3. If the  are very small, then we have shown in section 4.3
that (6.1) can be further sharpened into
are very small, then we have shown in section 4.3
that (6.1) can be further sharpened into

As a consequence, the bound for  becomes
becomes

Remark 6.4. It is also possible to treat
the case when  apart in the bound for
apart in the bound for  , thereby avoiding the factor
, thereby avoiding the factor  whenever possible. A similar analysis as for the cost
of the conversions then yields
whenever possible. A similar analysis as for the cost
of the conversions then yields

Whenever we can manage to keep  and
and  small with respect to
small with respect to  ,
this means that we gain a factor
,
this means that we gain a factor  with respect to
a full DFT.
with respect to
a full DFT.
6.4Frobenius FFTs over 
Let us now study the special case when  and
and  . This case is useful for the
multiplication of polynomials
. This case is useful for the
multiplication of polynomials  with
with  . The idea is to compute the Frobenius FFTs
. The idea is to compute the Frobenius FFTs
 and
and  ,
to perform the pointwise multiplications
,
to perform the pointwise multiplications  and to
retrieve
and to
retrieve  by doing one inverse Frobenius FFT.
by doing one inverse Frobenius FFT.
Modulo zero padding, we have some flexibility in the choice of  , which should divide
, which should divide  . In particular, for polynomials
. In particular, for polynomials  and
and  of large degree, we may choose
of large degree, we may choose
 to be a multiple of
to be a multiple of  and
take
and
take  and
and  (instead of
(instead of
 ) for the top call of the
algorithm FFFT from section 6.2. By selecting the
representation of
) for the top call of the
algorithm FFFT from section 6.2. By selecting the
representation of  as explained in Remark 4.1, this means that
as explained in Remark 4.1, this means that  for a single
for a single  and
and  for the remaining
for the remaining  indices
indices  .
In other words, one Frobenius FFT of length
.
In other words, one Frobenius FFT of length  reduces to one Frobenius FFT of length
reduces to one Frobenius FFT of length  and one
full FFT over
and one
full FFT over  of length
of length  .
.
We choose the remaining  to be small prime
numbers, so as to minimize the cost of the full FFT over
to be small prime
numbers, so as to minimize the cost of the full FFT over  of length
of length  . For
the remaining FFFT of length
. For
the remaining FFFT of length  ,
we may then apply Theorem 6.2 and Remark 6.3.
From a practical point of view, the computation of this remaining FFFT
should take about
,
we may then apply Theorem 6.2 and Remark 6.3.
From a practical point of view, the computation of this remaining FFFT
should take about  times the time the computation
of a full FFT of length
times the time the computation
of a full FFT of length  for some small constant
for some small constant
 .
.
We conclude that one entire FFFT of length  can
be performed approximately
can
be performed approximately 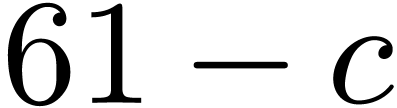 times faster as a
full FFT of length
times faster as a
full FFT of length  . We hope
that this will lead to practical implementations for polynomial
multiplication in
. We hope
that this will lead to practical implementations for polynomial
multiplication in  that are approximately twice
as efficient as the implementation from [12].
that are approximately twice
as efficient as the implementation from [12].
7.References
-
[1]
-
L. Auslander, J. R. Johnson, and R. W. Johnson. An
equivariant Fast Fourier Transform algorithm. Drexel
University Technical Report DU-MCS-96-02, 1996.
-
[2]
-
David H Bailey. Ffts in external of hierarchical
memory. In Proceedings of the 1989 ACM/IEEE conference on
Supercomputing, pages 234–242. ACM, 1989.
-
[3]
-
G.D. Bergland. A fast Fourier transform algorithm
for real-valued series. Communications of the ACM,
11(10):703–710, 1968.
-
[4]
-
R. Bergmann. The fast Fourier transform and fast
wavelet transform for patterns on the torus. Applied and
Computational Harmonic Analysis, 2012. In Press.
-
[5]
-
Dieter Blessenohl. On the normal basis theorem.
Note di Matematica, 27(1):5–10, 2007.
-
[6]
-
Leo I. Bluestein. A linear filtering approach to
the computation of discrete Fourier transform. IEEE
Transactions on Audio and Electroacoustics,
18(4):451–455, 1970.
-
[7]
-
J.W. Cooley and J.W. Tukey. An algorithm for the
machine calculation of complex Fourier series. Math.
Computat., 19:297–301, 1965.
-
[8]
-
J. von zur Gathen and J. Gerhard. Modern
Computer Algebra. Cambridge University Press, New York,
NY, USA, 3rd edition, 2013.
-
[9]
-
C. F. Gauss. Nachlass: Theoria interpolationis
methodo nova tractata. In Werke, volume 3, pages
265–330. Königliche Gesellschaft der
Wissenschaften, Göttingen, 1866.
-
[10]
-
I. J. Good. The interaction algorithm and practical
Fourier analysis. Journal of the Royal Statistical
Society, Series B. 20(2):361–372, 1958.
-
[11]
-
A. Guessoum and R. Mersereau. Fast algorithms for
the multidimensional discrete Fourier transform. IEEE
Transactions on Acoustics, Speech and Signal Processing,
34(4):937–943, 1986.
-
[12]
-
D. Harvey, J. van der Hoeven, and G. Lecerf. Fast
polynomial multiplication over 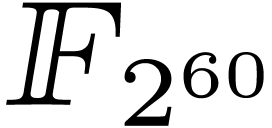 .
In Proc. ISSAC '16, pages 255–262, New York, NY,
USA, 2016. ACM.
.
In Proc. ISSAC '16, pages 255–262, New York, NY,
USA, 2016. ACM.
-
[13]
-
D. Harvey, J. van der Hoeven, and G. Lecerf. Faster
polynomial multiplication over finite fields. J. ACM,
63(6), 2017. Article 52.
-
[14]
-
J. van der Hoeven. The truncated Fourier transform
and applications. In J. Gutierrez, editor, Proc. ISSAC
2004, pages 290–296, Univ. of Cantabria, Santander,
Spain, July 4–7 2004.
-
[15]
-
J. van der Hoeven. Notes on the Truncated Fourier
Transform. Technical Report 2005-5, Université
Paris-Sud, Orsay, France, 2005.
-
[16]
-
J. van der Hoeven, R. Lebreton, and É.
Schost. Structured FFT and TFT: symmetric and lattice
polynomials. In Proc. ISSAC '13, pages 355–362,
Boston, USA, June 2013.
-
[17]
-
J. van der Hoeven and G. Lecerf. Modular
composition via factorization. Technical report, HAL, 2017. http://hal.archives-ouvertes.fr/hal-01457074.
-
[18]
-
J. Johnson and X. Xu. Generating symmetric DFTs and
equivariant FFT algorithms. In ISSAC'07, pages
195–202. ACM, 2007.
-
[19]
-
K. S. Kedlaya and C. Umans. Fast polynomial
factorization and modular composition. SIAM J. Comput.,
40(6):1767–1802, 2011.
-
[20]
-
A Kudlicki, M. Rowicka, and Z. Otwinowski. The
crystallographic Fast Fourier Transform. Recursive symmetry
reduction. Acta Cryst., A63:465–480, 2007.
-
[21]
-
R. Larrieu. The truncated fourier transform for
mixed radices. Technical report, HAL, 2016. http://hal.archives-ouvertes.fr/hal-01419442.
-
[22]
-
Jean-Louis Nicolas and Guy Robin. Highly composite
numbers by Srinivasa Ramanujan. The Ramanujan Journal,
1(2):119–153, 1997.
-
[23]
-
C.H. Papadimitriou. Computational
Complexity. Addison-Wesley, 1994.
-
[24]
-
C.M. Rader. Discrete Fourier transforms when the
number of data samples is prime. Proc. IEEE,
56:1107–1108, 1968.
-
[25]
-
H.V. Sorensen, D.L. Jones, M.T. Heideman, and C.S.
Burrus. Real-valued fast Fourier transform algorithm. IEEE
Transactions on Acoustics, Speech and Signal Processing,
35(6):849–863, 1987.
-
[26]
-
L. F. Ten Eyck. Crystallographic Fast Fourier
Transform. Acta Cryst., A29:183–191, 1973.
-
[27]
-
A. Vince and X. Zheng. Computing the Discrete
Fourier Transform on a hexagonal lattice. Journal of
Mathematical Imaging and Vision, 28:125–133, 2007.
 be the finite field with
be the finite field with  elements and let
elements and let  be a primitive
be a primitive  -th root of unity in an extension field
-th root of unity in an extension field  of
of  . Given
a polynomial
. Given
a polynomial  of degree less than
of degree less than  , we will show that its discrete Fourier
transform
, we will show that its discrete Fourier
transform  can be computed essentially
can be computed essentially  times faster than the discrete Fourier transform of a
polynomial
times faster than the discrete Fourier transform of a
polynomial  of degree less than
of degree less than  , in many cases. This result is achieved by
exploiting the symmetries provided by the Frobenius automorphism of
, in many cases. This result is achieved by
exploiting the symmetries provided by the Frobenius automorphism of  over
over  .
.
 and let
and let  be a
primitive
be a
primitive  -th
-th .
. of degree
of degree  on input and returns the vector
on input and returns the vector  .
. actually admits real coefficients, then we
have
actually admits real coefficients, then we
have  for all
for all  ,
, of the output values are superfluous.
Because of this symmetry, it is well known that such “real
FFTs” can be computed roughly twice as fast as their complex
counterparts [
of the output values are superfluous.
Because of this symmetry, it is well known that such “real
FFTs” can be computed roughly twice as fast as their complex
counterparts [ elements. In general, primitive
elements. In general, primitive  only
exist in extension fields of
only
exist in extension fields of  .
. instead of
instead of  .
. approximately
approximately  times
faster than the DFT of a polynomial in
times
faster than the DFT of a polynomial in  .
. as
the analogue of complex conjugation. If
as
the analogue of complex conjugation. If  for all
for all  and
and  .
. generated by
generated by  to multiplication in
to multiplication in
 ,
, .
. for zero padding. The Frobenius FFT can be thought of as a
more direct way to use evaluation-interpolation strategies over
for zero padding. The Frobenius FFT can be thought of as a
more direct way to use evaluation-interpolation strategies over  .
. of
degree
of
degree  of degree
of degree  instead of
instead of  .
. ,
, for the set of polynomials in
for the set of polynomials in  of degree
of degree  for some prime number
for some prime number  and
and  .
. ,
, is a monic irreducible polynomial of degree
is a monic irreducible polynomial of degree  .
. the
cost to multiply two polynomials in
the
cost to multiply two polynomials in  .
. via
the precomputation of a “pre-inverse” of
via
the precomputation of a “pre-inverse” of  .
. using Kronecker substitution [
using Kronecker substitution [ .
.





 multiplications
multiplications  with
with  .
. .
. is
increasing in both
is
increasing in both  is
increasing in both
is
increasing in both  multiplications
in
multiplications
in  .
. where
where
 divides
divides  .
. .
. storage.
storage.
 and a monic polynomial
and a monic polynomial
 of degree
of degree  of the
euclidean division of
of the
euclidean division of  by
by  .
. ,
, at a point in
at a point in  .
. are two distinct
monic irreducible polynomials in
are two distinct
monic irreducible polynomials in  to an element in
to an element in  also
boils down to one modular composition of degree
also
boils down to one modular composition of degree  the cost of a modular
composition as above. Theoretically speaking, Kedlaya and Umans proved
that
the cost of a modular
composition as above. Theoretically speaking, Kedlaya and Umans proved
that  [
[ .
. and
and  with
with  ,
, and
and  .
. to the case where we are free to choose primitive
elements
to the case where we are free to choose primitive
elements  and
and  that suit
us. We let
that suit
us. We let  be a cost function for conversions
between
be a cost function for conversions
between  .
. be a primitive
be a primitive  .
. ,
,
 of
of 
 directly for
directly for  ,
, of the FFT uses a
mirrored indexation
of the FFT uses a
mirrored indexation  that we will introduce in
subsection
that we will introduce in
subsection  the cost of computing a FFT in
the field
the cost of computing a FFT in
the field  is cyclic, of order
is cyclic, of order  .
. be such that
be such that  is a
generator of this cyclic group. Given a polynomial
is a
generator of this cyclic group. Given a polynomial  and
and  with
with  ,
,

 ,
, ,
, and
and  as elements of
as elements of

 such that
such that  for each
for each  .
. can uniquely be written in the form
can uniquely be written in the form

 for all
for all  .
. the digits of
the digits of  .
. -mirror
-mirror
 .
. has length one, then we notice that
has length one, then we notice that

 ,
,
 ,
, ,
, ,
, and
and  ,
, and
and  .
. and
and
 ,
,
 ,
, and notice
that
and notice
that  is a primitive
is a primitive  -th
-th is a primitive
is a primitive  -th
-th for
for  ,
,


 and
and  .
.
 by
by



 then
compute the answer using a direct algorithm and return it
then
compute the answer using a direct algorithm and return it
 ,
, ,
,






 are all bounded, then this algorithm
requires
are all bounded, then this algorithm
requires  operations in
operations in  such that
such that  as possible. This
approach is most “cache friendly” in the sense that it keeps
data as close as possible in memory [
as possible. This
approach is most “cache friendly” in the sense that it keeps
data as close as possible in memory [ be an extension of finite fields. Let
be an extension of finite fields. Let  generated by
generated by  .
. and
and  .
. the
order of an element
the
order of an element  under this action. Notice
that
under this action. Notice
that  .
. is called a cross section if for every
is called a cross section if for every  ,
, such that
such that  for some
for some  .
. .
. .
.

 .
. from
from  .
. with
with  .
.
 .
. .
. leaves
leaves  .
. is the subfield of
is the subfield of 
 is given by
is given by

 .
. at the points
at the points  with
with  .
. -th
-th such that the set
such that the set  is stable under the action of
is stable under the action of  .
.

 the complexity of computing a
twiddled DFFT of this kind.
the complexity of computing a
twiddled DFFT of this kind.
 and
the corresponding set of indices
and
the corresponding set of indices  ,
, separately for each
separately for each
 .
. be the order of
be the order of  actually belongs
to
actually belongs
to  ,
, .
. is increasing as a function of
is increasing as a function of 

 ,
, always forms an orbit of its own in
always forms an orbit of its own in  .
. ,
, -th
-th ,
, ,
, .
. ,
, and the DFFT reduces to a single evaluation
and the DFFT reduces to a single evaluation  with
with
 .
. .
. with respect to a full DFT is
comprised between
with respect to a full DFT is
comprised between  and
and  for any
for any  .
. )
) is the
monic minimal polynomial of
is the
monic minimal polynomial of  ),
), .
. then yields the evaluation of
then yields the evaluation of  at
at  .
.
 ,
, is such that
is such that  .
. on
on  .
. of
the additive subgroup generated by
of
the additive subgroup generated by  in
in  .
. of order
of order  in
in  .
.
 and
and  .
. be the constant term in
be the constant term in  ,
, for every
for every  .
. with
with
 under the action of
under the action of  to the computation of
to the computation of  -th
-th .
. and
and  .
. may
again be regarded as a precomputation. The computation of the Fourier
transform
may
again be regarded as a precomputation. The computation of the Fourier
transform  now comes down to
now comes down to 
 using Rader's
algorithm:
using Rader's
algorithm:

 and
and  and
and  .
. ,
,
 and
and 
 of
of  stands for the cost of computing
stands for the cost of computing
 and its inverse boil down to matrix transpositions in
memory. On a Turing machine, they can therefore be computed in time
and its inverse boil down to matrix transpositions in
memory. On a Turing machine, they can therefore be computed in time
 .
.
 and a primitive
and a primitive  ,
, ,
,
 and setting
and setting



 of
of  .
. .
. ,
, at
at  .
. in a cross section of
in a cross section of  from the twiddled DFT of
from the twiddled DFT of  denotes the complexity of computing
the DFFTs of
denotes the complexity of computing
the DFFTs of  is a Vandermonde matrix, the matrix-vector product
is a Vandermonde matrix, the matrix-vector product  can be computed in time
can be computed in time  using polynomial
interpolation [
using polynomial
interpolation [ ,
, using the Frobenius
automorphism
using the Frobenius
automorphism  orbits in
orbits in  from
from  .
.
 ,
, has order one under the action of
has order one under the action of  .
. with
with  ,
, under the action of
under the action of  .
. be a
primitive element in
be a
primitive element in  and
and  .
.

 from
from  for each
for each  ,
, has maximal order
has maximal order  under the action of
under the action of  ,
, .
. ,
, .
.
 ,
, .
. and
and  ,
, that
that

 with respect to a full DFT.
with respect to a full DFT.
 and
and  the
order of
the
order of 
 and
and  be as in section
be as in section
 .
. that corresponds to the so-called
“privileged cross section”
that corresponds to the so-called
“privileged cross section”  of
of  under the action of
under the action of

 is a cross section of
is a cross section of  be the corresponding
privileged cross section of
be the corresponding
privileged cross section of  .
.
 and
and  with
with  and
and  be such that
be such that  for some
for some  .
.
 ,
, .
. with
with  such that
such that  for
for  ,
, is an
is an  ,
, .
.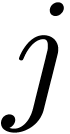 is minimal with
is minimal with  such that
such that  ,
, such that
such that
 for
for  .
. ,
, .
. implies
implies  .
. .
. for
for  .
. was chosen
minimal while satisfying this property. Given
was chosen
minimal while satisfying this property. Given  whenever
whenever  .
. implies the existence of a
implies the existence of a 
 or
or 

 ,
,

 do
do
 ,
, is the order of
is the order of 

 then
then



 ,
, .
. ,
, .
. ,
, be the number of
transforms of a polynomial in
be the number of
transforms of a polynomial in  over
over  .
.


 .
.

 .
. ,
,
 with prime factorization
with prime factorization  ,
, .
. and notice that
and notice that  .
.
 ,
, and
and  for
for  .
.

 are all prime, then
are all prime, then

 .
.
 becomes
becomes

 apart in the bound for
apart in the bound for  ,
, whenever possible. A similar analysis as for the cost
of the conversions then yields
whenever possible. A similar analysis as for the cost
of the conversions then yields

 and
and  small with respect to
small with respect to  ,
, and
and  .
. with
with  .
. ,
, and to
retrieve
and to
retrieve  by doing one inverse Frobenius FFT.
by doing one inverse Frobenius FFT.
 .
. of large degree, we may choose
of large degree, we may choose
 and
take
and
take  and
and  (instead of
(instead of
 )
) for a single
for a single  and
and  for the remaining
for the remaining  indices
indices  .
. and one
full FFT over
and one
full FFT over  to be small prime
numbers, so as to minimize the cost of the full FFT over
to be small prime
numbers, so as to minimize the cost of the full FFT over  times the time the computation
of a full FFT of length
times the time the computation
of a full FFT of length  .
.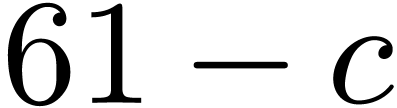 times faster as a
full FFT of length
times faster as a
full FFT of length 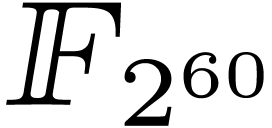 .
.