Directed evaluation |
|
| Final version of October 2020 |
|
. This paper is
part of a project that has received funding from the French
“Agence de l'Innovation de Défense”.
Let
|
Let 
be an effective field. Here,
effective means that elements of can be
represented by concrete data structures and that algorithms for the
field operations are at our disposal, including a zero-test. Effective
rings are defined in a similar way.
The aim of the present paper is the fast computation with algebraic numbers. We start by recalling various known strategies, including the most prominent one: dynamic evaluation. Our first main problem will be to develop a more efficient variant of dynamic evaluation. We next recall how to represent algebraic numbers using towers of algebraic extensions. Our second main problem is to develop efficient algorithms for computations in such towers.
be a monic separable polynomial of degree
in 
,
not necessarily irreducible, and let 
represent
a root of in the algebraic closure 
of . Given an
algorithm 
that runs over a generic effective
field, consider the question of running
efficiently over 
.
A natural first approach begins with the computation of the defining
polynomial of over :
this essentially corresponds to factoring into
irreducible polynomials. Unfortunately this task is not feasible over a
generic field [19, 20]. Of course, when is explicitly finitely generated over its prime
sub-field, such factorizations can be computed. However, no general
efficient algorithms (i.e. running in softly linear time)
are currently known for this task; see [21].
Another approach consists in computing in 
while
regarding 
as a parameter constrained by 
. So any element 
in is represented by a polynomial 
in of degree 
, such that 
.
With this representation, additions, subtractions and products can
easily be performed in 
, with
seen as the class of 
. On the other hand, testing whether 
is zero or not requires us to distinguish the following
cases:
If is the zero polynomial, then 
is zero for any root of
, so the result of the
test is “
”;
If the resultant 
is non-zero, then is non-zero for any root
of , so the result of
the test is “
”;
Otherwise, 
is not a constant polynomial
and has degree . A
proper decomposition of is thus
discovered: 
. We
split the current computation, into the two following
ones:
In the first branch, is subjected to
the constraint 
; in
this branch, the result of the zero-test 
becomes “”.
In the second branch, is subjected to
the constraint 
and the result of the
zero-test becomes “”.
If the inverse of is requested, then we first
test if is zero or not. If
is identically zero (in the resulting branch), then an exception is
raised; if is non-zero, then the inverse can be
computed from the Bézout relation for and
, which can itself be
computed using the extended gcd algorithm.
This manner of evaluating a program is called dynamic
evaluation. It finishes after a necessarily finite number of
splittings. At the end of all the computations, we obtain a
factorization of 
, not
necessarily into irreducible polynomials, along with one output value
for each of the 
cases when 
for 
. In other words, instead
of working with a specific root of ,
the program is evaluated for a generic root of . For this reason, is
sometimes called an algebraic parameter: the program is
executed as if were a field, and cases are
distinguished only when inconsistencies actually occur during the
execution. After a zero test 
or an inversion
that gives rise to a splitting, the element is enforced to be identically zero or invertible in
each branch. Notice that the separability assumption on
is important, since it ensures that 
and 
are coprime in the above decomposition .
Example 
be a parameter with for 
, and consider the computation of
the gcd of
Using dynamic evaluation, this gives rise to three branches, and the result
Dynamic evaluation is very attractive from a conceptual point of view,
but rather tricky to implement: splittings correspond to
non-deterministic control structures that are typically implemented
using continuations [41]. Dynamic evaluation is also
difficult to analyze from the complexity perspective. In particular, it
is hard to determine the amount of computation that can be shared
between several branches. At any rate, the worst case complexity of
dynamic evaluation is much higher than the number of steps of the
program multiplied by the cost of operations in .
The first aim of this paper is to design an alternative, so-called
directed evaluation strategy, with the same abstract
specification, but with a quasi-linear computational complexity in . The key idea is to run the entire
program, while systematically opting for the “principal”
branch in case of splittings. This principal branch is the one for which
the defining polynomial of is maximal. At every
splitting, we also store the defining polynomial for the other
“residual” branch. Once the computation for the principal
branch has been completed, we recursively apply the same algorithm for
each residual branch, on the reduced input data modulo the corresponding
defining polynomial. The required reductions are computed simultaneously
for all residual branches, using a fast divide-and-conquer algorithm for
multi-modular reduction.
using the dynamic evaluation
strategy. More generally, one may wish to compute with a finite number
of parameters 
that are introduced successively
as follows: 
is subjected to the constraint
for some monic polynomial 
, then 
is subjected
to 
with 
monic in 
, then 
is
subjected to 
with 
monic in 
, and so on. The
second aim of the present paper is the design of fast algorithms for
computing dynamically in 
as if it were a
field. The main difficulties arise when 
is
allowed to be arbitrarily large.
The parameters naturally induce a tower
of effective algebraic extensions
where
The parameter 
corresponds to the class of 
in 
for 
. A tower of this type is written 
and we call its height. Throughout this
paper, we write 
and 
. The 
are called the
defining polynomials of the tower, and
its degree. Elements in are naturally
represented by univariate polynomials in over
of degree 
.
In order to reduce computational costs, it will be convenient to assume
that the tower is explicitly separable in the sense that 
and that we have explicit Bézout cofactors
with 
for . In particular, each 
is reduced. This means that 
contains no non-zero
nilpotent elements or, equivalently, that is a
product of separable field extensions of .
Towers of algebraic extensions are related to “triangular
sets”. In fact, we may see the preimage of
over as a multivariate polynomial 
in 
such that
has degree 
in ,
degrees 
in 
for 
, and 
.
The sequence 
then forms a special regular case
of a triangular set. The separability of
translates into the requirement that 
is
separable for all roots 
of 
for .
The second main aim of this paper is to generalize the directed
evaluation strategy from the univariate case, while ensuring that the
complexity remains bounded by the number of steps in our algorithm
multiplied by 
(which corresponds roughly
speaking to the cost of arithmetic operations in the tower [29]).
Intuitively speaking, we use the univariate strategy in a recursive
fashion, but the analysis becomes far more technical due to the fact
that splittings can occur at any level of the tower. This difficulty
will be countered through the development of suitable data structures.
means that 
;
see [21, chapter 25, section 7] for technical details.
The notation 
means that there exist 
such that 
for 
sufficiently large. The least integer larger or equal to is written 
;
the largest one smaller or equal to is written
.
Given an effective ring 
, we
use 
as a notation for the cost of multiplying
two polynomials of degree ,
in terms of the number of operations in .
It is known [6] that 
.
We will also denote
In particular, given 
for some monic polynomial
of degree ,
elements in 
may be represented as classes of
polynomials in 
modulo , additions in require additions in ,
whereas multiplications in can be done using
ring operations in .
We let 
denote an exponent such that two 
matrices over a commutative ring
can be multiplied with 
operations in . The constant 
denotes another exponent such that a rectangular 
matrix over a commutative ring can be multiplied
with a square 
matrix with 
operations in . Le Gall has
shown in [34] that one may take 
; Huang and Pan have shown in [31] that
one may take 
. Throughout
this paper, in order to simplify complexity analyses, we assume that
and 
.
Recall that an element 
is said to be
primitive if 
. If
is a reduced -algebra,
then it is well known that a sufficiently generic -linear combination of 
is a
primitive element of 
. It may
thus seem odd, at first sight, to manipulate towers
of height 
whenever an isomorphic algebra 
exists. The problem is that both the computations of
primitive elements and conversions between representations are usually
expensive.
Over a general field , no
efficient algorithm is currently known for finding a primitive element
together with its minimal polynomial 
,
and polynomials 
such that 
for . It is known that this
problem can efficiently be reduced to a multivariate version of the
problem of modular composition using a randomized Las Vegas algorithm.
The corresponding conversions between tower and primitive element
representations can also be done using modular composition. All this is
a consequence of the transposition principle and Le Verrier's method; we
refer to [29, 30, 33, 38,
39] for more details. Unfortunately, no softly linear
algorithm is known for modular composition over a generic field,
although efficient algorithms have recently been designed for specific
cases [9, 27, 28]. If is a finite field, then Kedlaya–Umans and followers
have established almost optimal theoretical bit complexity bounds [30, 33, 38].
Without primitive elements, using a naive induction on , the multiplication in
can be performed in time 
for some constant 
. It is well known that, for a
sufficiently large constant 
,
such products can actually be carried out in time 
using Kronecker substitution; see for instance [21, chapter
8]. If many of the individual degrees are small,
then can become as large as 
, which leads to an overall complexity bound of
the form 
. Unfortunately,
this bound is far from linear if 
is much larger
than 
. Lebreton has shown
that one may take 
; see [35] and [29, Proposition 2.4].
Substantial improvements for the value of seem
difficult to achieve, and it might not even be possible to reach values
that are arbitrarily close to .
An alternative approach for efficient computations in a given tower is
to produce an equivalent, so-called accelerated tower of small
height, such that conversions between both towers are reasonably cheap.
This approach was first proposed in [29]: when the are all irreducible, we have shown how to multiply
elements in with 
operations in , for any fixed
real 
.
Dynamic evaluation has been developed by Della Dora, Dicrescenzo and Duval [10, 13-15] as a way to compute with algebraic parameters without irreducible factorizations. The approach is sometimes called the “D5 principle”, after the initials of the authors of [10]. One may regard dynamic evaluation as a computer algebra counterpart of the concept of non-deterministic evaluation from theoretical computer science. The strategy of dynamic evaluation has been extended to transcendental parameters [17, 22], real algebraic numbers in [16], and more general algebraic structures [25, chapter 8].
Several implementations have been proposed for parameters that are constrained by triangular sets. Early implementations simply handled splittings by redoing the entire computation under stricter constraints [13]. Unnecessary recomputations can be avoided through the use of high-level control structures such as continuations [4]. Unfortunately, efficient implementations of such control structures are rarely available for common programming languages. In this paper, we mostly leave implementation issues aside and focus on the complexity of computations with parameters.
In his PhD thesis, Dellière has investigated the relationship
between dynamic evaluation and decompositions of constructible sets into
triangular sets [11, 12]: the central
operation is the computation of gcds with coefficients in products of
fields, such as . Let us
further mention that dynamic evaluation has influenced several
polynomial system solvers relying on triangular sets [3],
and is now involved in various other algorithms in computer algebra; see
for instance [7, 26, 36].
Dedicated algorithms over dynamic fields such as
have been proposed by Dahan et al. [8]. Without
appealing to the general dynamic evaluation paradigm, they designed
efficient algorithms for quasi-inversion in , as well as gcd computations and coprime
factorization in 
.
Recomputations induced by splittings are handled using fast ad
hoc techniques.
In the worst case, it is known that dynamic evaluation over suffers from an overhead of the order 
: see Examples 4.4 and 4.6.
To our knowledge, this paper is first to propose a general strategy for
removing this overhead.
The main contribution of the present paper is a new evaluation paradigm to compute with algebraic parameters in an asymptotically fast manner. In section 2, we recall the concept of computation trees as a formalization for the cost of algebraic algorithms. In section 3, we introduce the concepts of unpermissive, panoramic, and directed evaluation. This provides us with precise terminology for analyzing subtle differences between the complexities of various evaluation strategies.
Informally speaking, the unpermissive evaluation of a computation tree
simply aborts the usual evaluation whenever a zero-divisor needs to be
inverted or tested to zero. If a zero-divisor is discovered in this way,
then a proper factorization 
of one of the
defining polynomials can be deduced. This leads to a decomposition of
into the direct sum of two proper subalgebras,
defined by the towers 
and 
.
A panoramic evaluation of a computation tree returns all possible
results when considering as algebraic
parameters, and thereby constitutes our main objective. The unpermissive
evaluation model gives rise to the following naive panoramic evaluation
strategy: whenever the unpermissive evaluation produces a proper
splitting of , we restart the
evaluation over each of the two subalgebras of . The problem with this rather naive approach is
that the evaluation may need to be restarted as many as 
times, which turns out to be suboptimal from a complexity point of view:
see Example 4.4.
The directed evaluation is meant to remedy this situation by ensuring a
sharp decrease of every time that we need to
restart the evaluation. More precisely, we will show that the
reevaluation depth remains bounded by 
.
Section 4.2 contains our main complexity result in the case
of a single parameter, i.e. 
.
We prove a softly linear complexity bound for panoramic evaluation and
provide a detailed comparison with various implementations of dynamic
evaluation.
In section 5, we turn to the case of an arbitrary number of
parameters . With respect to
the univariate case, the main difference is that 
is not necessarily a field, although we still conduct our computation as
if it were (e.g. during gcds computations in 
). Consequently, zero-tests and inversions of
elements in 
may lead to additional case
distinctions according to the possible values of 
. Despite these technical complications, we again
prove a quasi-linear complexity bound for the cost of panoramic
evaluation, under the assumption that is fixed
(this means that is not allowed to grow with
).
For arbitrary, not necessarily bounded heights , the complexity analysis becomes tedious. We need
to revisit the construction of accelerated towers of fields, introduced
in [29], in the context of directed evaluation. The key
idea is as follows: before the directed evaluation of a given
computation tree, we perform the directed computation of an accelerated
version of the current tower, so the computation tree can subsequently
benefit from accelerated arithmetic. Overall, in section 7,
we achieve an overhead of the form 
for the
panoramic evaluation, where 
represents any fixed
positive real number.
Our techniques are more general than those of [8]: they
turn out to be applicable in all contexts that involve dynamic
evaluation with algebraic numbers. In addition, thanks to our
accelerated tower arithmetic, we improve the complexity bounds for the
specific tasks studied in [8], whenever
is allowed to be arbitrarily large.
Section 7.4 contains two important additional examples. We
first show that products in a separable tower can be done in time 
, which extends [29].
We next present a less straightforward application of fast panoramic
evaluation to matrix multiplication with entries in .
This section gathers known definitions and results about elementary operations in computer algebra, to be used in this paper.
Let us recall the notion of a computation tree; we essentially follow
the presentation from [5, chapter 4, section 4]. In the
present paper, all computation trees manipulate data in -algebras over an effective field , and only the following operations are
allowed:
The binary arithmetic operations 
in the
algebra.
The unary operation 
of inversion, which is
partially defined in the algebra.
The unary zero-test, written 
.
For each constant 
, the
nullary constant function 
and the unary
function 
of scalar multiplication by 
. We denote the corresponding
sets of constant functions and scalar multiplications by 
and 
.
We write 
for the set of all arithmetic
operations.
of the sets 
,
, 
, and 
of input
nodes, computation nodes, branching nodes and
output nodes. We assume that the input nodes form an initial
segment of unary nodes starting at the root, that the output nodes are
leafs (of arity zero), that computation nodes admit arity one, and
that branching nodes admit arity two. A computation tree over is such a binary tree,
together with an instruction function that
assigns an instruction of the form
to every computation node 
,
where 
has arity 
, and 
are nodes in 
that are predecessors of (i.e. nodes in the path ascending from
to the root of the tree);
assigns an instruction of form
to every branching node ,
where 
is a predecessor of
in ;
assigns a return value 
to every
output node , where are predecessors of in
, and 
may depend on .
be a computation tree as above with 
input nodes. Let be a -algebra and let us show how gives rise to an evaluation function
The value 
is a new symbol that is returned
whenever an arithmetic operation cannot be executed. In the present
framework this can only happen for inversions.
Given an input value 
, the
evaluation of at
proceeds by constructing a path 
from the root of
the tree, along with the function
that associates a value to each node of the path, as follows:
The path begins with the input nodes 
of ,
and we set 
for 
.
The next node of the path is set to the successor of 
.
If the current node of the path is a computation node of the form 
then we set 
. If this calculation is well
defined, then the next node of the path is set to the successor of
. Otherwise, the
evaluation path ends at ,
we say that the computation tree is undefined at , and we set 
.
If the current node of the path is a branching node
of the form 
, then we set
. If 
is then the next node of the path is set to
the left successor of ,
otherwise the next node is the right successor of .
If the current node of the path is an output node
with return value , then
we set 
. The path ends at
and we set 
.
. Given a path of length 
with leaf 
in ,
we define 
to be its cost. The maximal cost of
a path is called the operational cost of
and we denote it by 
. We
may use as a bound for the number of
operations in that are required for the
evaluation of over .
Since additions, multiplications and inversions typically admit different costs, it is convenient to introduce the following more detailed quantities:
stands for the number of input nodes,
i.e. 
.
stands for the maximal arity of a return
value, i.e. 
.
stands for the maximal number of operations
in 
for a path in .
stands for the maximal number of
multiplications for a path in .
stands for the maximal number of inversions
or zero-tests for a path in .
We will call 
the detailed cost of and notice that 
.
Taking 
in Example 2.1, we have
, 
, 
, 
, 
.
Usually, we are really interested in the maximal number 
of scalar operations in that are needed to
evaluate over .
If and are clear from
the context, this is simply called the cost of
or the time needed to evaluate .
It will be useful to introduce the following additional quantities:
stands for the maximal number of elements in
that are needed to represent an element in
. Throughout this paper,
we assume that operations in can all be
computed using 
operations in .
stands for the number of operations in that are needed to multiply two elements in .
stands for the maximal number of operations
in that are needed to perform a zero-test or
inversion in .
We clearly have
Remark
negations 
are implemented as 
;
divisions 
are implemented as 
;
equality tests 
are implemented as 
.
These restrictions are harmless, in the sense that they only affect the
constants hidden in the “
”
of complexity estimates.
Remark
Remark 
. Roughly speaking, it is a natural
extension of the Turing machine model for which the tapes are allowed to
contain elements in . The BSS
model is more powerful than the computation tree model in the sense that
it allows for loops, subroutines, lookup tables, etc. Nevertheless, an
arbitrary program in the BSS model that admits a finite number of
execution flows may be emulated by a computation tree. This amounts to
“unrolling” all possible executions as in Example 2.1
above.
Remark
A polynomial in 
of degree
is represented by the vector of its coefficients
from degree 
to 
.
Polynomial additions (resp. subtractions) in take at most additions
(resp. subtractions) in .
Determining the degree of a polynomial in
requires at most zero-tests.
be an effective commutative ring with
unity. We denote by a cost function for
multiplying two polynomials 
by a straight-line
program over . We make the
following assumptions:
is a nondecreasing function in —this assumption is customary;
is sufficiently close to linear, in
the sense that
 |
(2.1) |
holds whenever 
. This
assumption is less common, but it is only used within Propositions
2.6 and 7.7. Notice that (2.1)
is equivalent to 
.
For general , it has been
shown in [6] that one may take
If has positive characteristic, then it was
shown in [23, 24] that one may even take
where 
.
be of degree 
and
let 
be monic of degree 
. The quotient of the Euclidean division of 
by can be computed by a
straight-line program in time 
.
Given this quotient 
, the
remainder 
can be computed using 
additional operations. If necessary, the degree of 
can be determined using at most 
further zero-tests.
and 
in 
can be computed
in time 
; see [21,
chapter 11]. But we will need to be more precise in section 5.3
in order to analyze the complexity of “directed inversions in
towers”. Following the notation of [37], let 
and 
be in
of respective degrees 
and 
, and consider the extended Euclidean
sequence defined as follows:
, 
, 
,
;
, 
, 
,
where 
is the quotient of 
by 
.
Consequently we have 
, that
is the remainder in the division of by 
, and 
for
all 
. The sequence ends after
division steps with 
for
, and 
. The last non-zero polynomial 
is 
and the Bézout relation is 
.
The fast extended Euclidean algorithm applied to 
and 
does not compute the complete Euclidean
sequence, but only the sequence of the quotients 
in a divide and conquer fashion. This is enough to permit the efficient
recovery of the Bézout relation .
For 
, let 
. We claim that the number of zero-tests in the
fast extended Euclidean algorithm is exactly 
. This claim is a consequence of the two following
observations about the fast extended Euclidean algorithm (see for
instance [37, Algorithm 18]):
Computing the quotients 
does not involve any
zero-tests or inversions. On the other hand the determination of
requires testing the coefficients of 
from degree 
to , which involves 
zero-tests. This totalizes
zero-tests.
The degrees of the cofactors 
and 
, but also of all the entries
of the “transition matrices” are explicitly determined
from the 
; see [37,
Lemma 10]. So the computation of the transition matrices also does
not involve any zero-tests or inversions.
In order to perform polynomial divisions, the inverses of the leading
coefficients of the are needed. This requires at
most 
inversions.
To summarize the discussion, the extended gcd of
and of degree 
takes additions, subtractions and products in , plus zero-tests and
inversions. In addition, every inversion of an
element is preceded by an unsuccessful zero-test for that element.
Elements of a tower are in fine
represented by vectors of coordinates in 
.
So additions, subtractions, and products by scalars in
can be done by straight-line programs with linear costs. We recall the
following result, where 
represents the cost of
one product in .
such that one product
in can be computed by a straight-line program
in time
In addition, the product of two polynomials in 
can be computed by a straight-line program in time
Proof. This result is essentially due to
Lebreton [35]; see also [29, Proposition
2.4].
In the introduction, we have informally discussed computations with parameters and various strategies for automating case distinctions. In this section, we formalize these ideas in the specific situation of algebraic parameters.
Let be an effective field and let 
be an ideal of 
such that:
is a -algebra
of finite dimension 
,
is absolutely radical, which means radical
over the algebraic closure of .
In the context of the present paper, it will be convenient to call a parametric algebra over
with parameters, and is
said to be its defining ideal, written 
. The respective images of 
in are denoted by ;
they are regarded as parameters over , subject to the relations in . Geometrically speaking, the tuple 
represents a generic point in the set 
of the
zeros of in 
. This setting is more general than the one of
the introduction, but it is intended to be applied later to ideals generated by triangular sets.
Let be a second parametric algebra over with parameters. As a
shorthand, we write 
whenever
is a quotient algebra of .
This is the case if, and only if, 
,
or, equivalently, if 
. If
, then we write 
for the canonical projection 
,
and notice that 
represents a generic point in
the set 
of the zeros of 
in . With a slight abuse of
notation, is extended in a coefficient-wise
manner to 
.
Two parametric algebras 
and 
are said to be disjoint if 
.
In that case, we have
More generally, given pairwise disjoint 
, we have
We will call such a decomposition a splitting of .
Now consider the prime decomposition
of the defining ideal of , and define 
for . Then we have 
and there exists a natural isomorphism
 |
(3.1) |
It is convenient to call this relation the total splitting of
. The corresponding zero-set
is a disjoint union:
Given a zero-divisor 
, we
have
Indeed, we clearly have 
.
Conversely, given 
with 
, we have 
,
whence 
since is radical,
and 
. Setting
we obtain a natural isomorphism
Such a decomposition is called an atomic splitting of . We have
From an effective point of view, the computation of total splittings requires an algorithm for polynomial factorization, whereas atomic splittings can be computed using standard techniques from effective polynomial algebra, such as Gröbner bases, triangular sets, or geometric resolutions.
Let us now describe an abstract way to formalize computations in
parametric algebras modulo splittings. Consider a set 
of parametric algebras over .
We say that is a parametric framework
if the following conditions are satisfied:
Each 
is an effective -algebra.
Given 
, we can test
whether is invertible and compute if so.
Given 
with ,
we have an algorithm for the projection .
Given 
, we can
effectively compute 
and 
.
For any 
with 
,
we have algorithms for both directions of this isomorphism.
Using Gröbner basis techniques, the above conditions are in
particular verified if is the set of all
parametric algebras that are explicitly given by
a finite set of generators of .
Indeed, a Gröbner basis of induces a basis
of over along with the
multiplication matrices by ,
so the above operations boil down to linear algebra. This observation is
convenient from a conceptual point of view, but, of course, not very
efficient from the asymptotic complexity perspective. Sections 4,
5, and 7 are devoted to more specific
parametric frameworks that allow for asymptotically faster
implementations.
From now on, denotes a parametric algebra, and
we will use the notations from section 2.1 for computation
trees. The unpermissive evaluation of a computation tree with input nodes as above at
is defined as follows. Informally speaking, the
tree is evaluated in the usual way over
concerning ring operations, but the evaluation aborts whenever a
zero-divisor needs to be inverted or tested to zero.
More precisely, we write 
for the
unpermissive path, and 
for the
unpermissive evaluation function. We introduce a new output
value, written 
, in order to
indicate that the evaluation process detects that the current algebra
is not a field. We define 
by induction:
If the current node of the path is a
computation node of the form 
,
then we distinguish the following cases:
If 
is zero in , then the path ends at
with 
.
If is invertible, then 
and the next node of the path becomes the successor of .
Otherwise, is a zero-divisor in , and the evaluation
aborts; the path ends at ,
we set 
, and record
the zero-divisor for future use.
If the current node in the path is a
branching node , then we
distinguish the following cases:
If is zero in , then 
,
and the next node of the path becomes the right successor of
.
If is invertible in , then we set 
, and the next node of the path becomes the
left successor of .
Otherwise, is a zero-divisor in , and the evaluation
aborts; the path ends at ,
we set , and record
the zero-divisor for future use.
For the other types of nodes, the evaluation rules remain the same as for the standard evaluation described in section 2.1.
.
If 
, then the evaluation
paths and 
coincide and
holds, under the natural convention that 
.
Proof. The proof is straightforward from the
definitions.
for a computation
tree 
, we say that
is a panoramic splitting of 
for the pair 
if 
for
. A panoramic
value of at 
is a set of pairs 
such that 
is a panoramic splitting of and 
for 
.
denote the total splitting of , and let be a
panoramic value of at . Then, for each 
,
we have
where 
is the unique integer such that 
.
Proof. Since 
is a field,
any non-zero element in is invertible.
Consequently,
and Lemma 3.1 implies that 
.
On the other hand,
and Lemma 3.1 implies that
Example from Example 2.1
for some 
, and let
, and 
, with 
.
If represents the image of 
in , then a possible
panoramic splitting of at
is
where
,
and 
,
for 
,
and 
.
Notice that the associated primes of 
are 
for 
, and
the total splitting of is
The following naive algorithm for the computation of panoramic values was already sketched in the introduction:
Algorithm
Compute the unpermissive evaluation 
.
If , then return
.
Otherwise a non-trivial zero-divisor has
been recorded, which allows us to compute proper subalgebras
and 
such that
and 
.
Recursively apply the algorithm to 
for
and return the union the panoramic
values obtained in this way.
Proof. The algorithm finishes since is finite dimensional. As for the correctness it suffices
to verify that the output in step 2 is correct, which is straightforward
from the definitions.
From now we focus on the development of a faster alternative for
Algorithm 3.1. The idea is to impose a finer control over
the dimension of the components of splittings. Informally speaking,
computation trees over will be evaluated
entirely, while restricting operations to suitable subalgebras of : when a zero test or an inversion
occurs for a value , the
current subalgebra is further restricted to its largest subalgebra where
the projection of is either invertible or zero.
In order to formalize this idea, we need some definitions and the underlying directed arithmetic operations.
,
we say that a splitting
is directed if
and 
for 
,
for .
A directed evaluation of
takes as input:
a directed splitting of 
,
a point 
,
and returns
a refined directed splitting of 
,
such that 
.
We introduce a directed variant of the inversion in , that takes a directed splitting
as input, the value in
to be inverted, and that returns a directed
splitting 
such that
is either zero or invertible;
The result of the directed inversion of is
respectively or 
.
We also introduce a directed variant of the zero-test in , that takes a directed splitting
and the value in to be tested as input, and that returns a directed
splitting such that
is either zero or invertible;
If is invertible, then
has been computed and recorded;
The result is 
.
Remark do not imply uniqueness of the output
splittings.
Remark for these operations, so
splittings never occur.
Let us now define the directed evaluation of a tree . As input, we take a directed splitting and .
Informally speaking, this evaluation simply applies the above directed
operations in sequence, so we evaluate the entire computation tree while
restricting the current algebra when encountering zero-tests and
inversions. The list of the residual subalgebras is maintained
throughout the evaluation process. For consistency, the evaluation takes
a directed splitting as input, but only the
summand will be decomposed during the evaluation
process.
Formally speaking, the directed evaluation path is written 
. To each node 
,
we both associate a directed splitting
of , so
and a value
The directed evaluation of is defined
inductively as follows:
The path starts with the input nodes of .
We set 
and 
,
for 
. The next node of
the path is set to the successor of .
If the current node of the path is the root
of the path, and is a computation node ,
then we necessarily have 
and 
, we set 
and 
. The next node of the path is
set to the successor of .
If the current node of the path is a
computation node with 
, whose direct predecessor is 
, then we set 
and
The next node of the path is set to the successor of .
If the current node of the path is a
computation node , whose
direct predecessor is ,
then we apply the directed inversion to 
for
the splitting 
. This
yields a new splitting 
that we assign to
.
If 
, then we set
, and the path ends
at .
Otherwise 
, and the
next node of the path becomes the successor of .
If the current node of the path is a
branching node , whose
direct predecessor is ,
then we apply the directed zero-test to for
the splitting . This
yields a new splitting ,
that we assign to .
If , then 
, and the current node of
the path becomes the right successor of .
Otherwise, 
, and the
current node of the path becomes the left successor of . We also record the
inverse 
.
If the current node of the path is an output
node , whose predecessor
is , then we set 
and
Whenever 
are such that
is a successor of , the
splittings of at and
satisfy 
.
It can be checked by induction over the path
that 
and 
are well
defined.
represent the
directed splitting returned by the directed
evaluation of at as
above. Then, for all 
, we
have
Proof. We verify by induction on paths that and 
coincide, and that 
holds for all that is not a
branching node.
Example from
Example 2.1, and let
, and , with .
Consider the directed evaluation of at 
, where
represents the image of in . The first zero-test that we encounter is
, which yields the directed
splitting
After the 
zero-tests 
, we end up with the directed decomposition
and the value 
. This is due
to the requirement that directed evaluation always privileges the
“branch of highest degree”. If 
,
then the last zero-test potentially leads to another directed
decomposition
and the value 
. In general,
we recall that directed evaluation is a non-deterministic process: the
output may depend on internal splitting choices that are made during the
directed zero-tests and inversions.
We are now in a position to state a central algorithm of this paper, which performs panoramic evaluations using directed ones. The presentation is abstract, in terms of general parametric frameworks. In the remainder of the paper we will study various concrete instantiations of this algorithm.
Algorithm
Perform the directed evaluation of at
for the trivial directed splitting 
of .
Let be the directed splitting obtained
in return.
Compute the projections 
for .
Recursively call the algorithm in order to evaluate at for .
Return the union of 
and of the panoramic
values obtained in step 3.
Proof. Algorithm 3.2 finishes because the dimension of the input algebra strictly decreases throughout the recursive calls in step 3. At the end of step 1, we have
by Proposition 3.9. Therefore the singleton 
is a panoramic value of at 
. We conclude by observing that the
union of the panoramic values in step 4 gives a panoramic value of at .
Example 
, and 
for 
. After the recursive calls
in step 3, we obtain the panoramic value
In the next sections, Algorithm 3.2 will lead to nearly linear asymptotic complexity bounds. So it turns out to be much faster than the naive Algorithm 3.1.
From the complexity point of view, there is still a problem
with naive implementations of Algorithm 3.2: the directed
evaluation approach involves many potentially expensive conversions of
the form 
. A general solution
to this issue is tedious, but for the concrete parametric frameworks
from this paper, a natural and efficient approach is to delay these
conversions. This can be done at the price of performing arithmetic
operations in the input algebra instead of its subalgebras.
Consider for instance the simplest case when 
, where is monic of degree
. Let 
with 
and 
.
Then one projection 
corresponds to a division by
of cost 
,
when using the standard representation for elements in . This means that additions during the directed
evaluation of a tree typically admit a cost
instead of 
, which is
suboptimal.
A natural remedy to this problem is to delay reductions modulo . This strategy naturally fits in
our setting of parametric frameworks through the use of redundant
representations. More precisely, consider some
within a parametric framework .
Then we may define a new parametric framework 
whose objects are algebras in , with this modification that elements in are represented by elements in . Given 
,
this means that projections 
are free of charge
in . The arithmetic
operations on elements in
are also performed in . The
inversion of 
is done by computing the projection
in and then performing
the inversion of 
in ; zero-tests are done similarly.
Of course, at the end of a directed evaluation that uses this kind of
redundant representations, we may wish to convert the result to the
standard representation in .
This can be done by inserting a “finalization” step at the
end of step 1 in Algorithm 3.2.
This section is devoted to parametric algebras with one
algebraic parameter, that is of the form 
with
monic, separable, and of degree . For our complexity bounds it will be
convenient to assume that 
.
Elements in are represented as remainder classes
with 
.
The univariate situation is notably simple but already useful enough to
be treated separately. We first specify the parametric framework and the
directed operations, then we analyze the cost of our fast panoramic
evaluation, and finally we compare the directed evaluation strategy with
dynamic evaluation.
For efficiency reasons, we further assume that
is explicitly separable in the sense that we are given the
cofactors 
and 
in 
in the Bézout relation
 |
(4.1) |
Computing this relation from the outset only requires
operations in .
Let us first specify the required operations of the univariate parametric framework, and explicit their complexity.
Additions and subtractions in can clearly be
performed by straight-line programs in linear time , whereas multiplications take time .
An element 
with is
invertible if and only if 
and, in that case,
can be computed using the extended Euclidean
algorithm. Both the test and the computation of
can be done by a computation tree in time .
We have if and only if 
. In that case, we have
for all ; the projection
can thus be computed in time by a straight-line program (below, we will rather use
the technique of delayed reductions from section 3.7 in
order to avoid projections altogether).
Given 
with 
,
we have 
and 
.
This shows that we can compute 
and 
in time using computation
trees.
Given univariate parametric algebras 
,
we have if, and only if, 
(which in particular implies that the 
are
pairwise coprime). In this case, the isomorphism
in both directions can be computed in time 
by using the usual subproduct tree of 
;
see [21, chapter 10].
The directed zero-tests and inversions of an element 
with preimage can be computed in time , as follows:
The input is a directed splitting of ,
the Bézout relation 
,
and an element 
with preimage 
.
If 
, then the result of
the zero-test is and the result of the
inversion is . The input
directed splitting is left unchanged in return.
We compute 
along with the Bézout
relation 
.
If 
, then the result of
the zero-test is and the result of the
inversion is 
. The input
directed splitting is left unchanged in return.
We compute 
, and deduce
the Bézout relations of 
and , and of 
and 
by Lemma 4.1 below.
If 
then we return the directed splitting
and the image of is zero in 
. The value of the zero-test is , and the result of the
inversion is .
Otherwise, we return the splitting
and the image of in 
is invertible. The latter splitting is actually directed since 
implies
The inverse of modulo
is obtained as follows:
From the Bézout relation ,
we deduce 
and then
From the Bézout relation ,
we get 
, and deduce
The value of the zero-test is ,
and the result of the inversion is 
.
be monic and separable of degree
, and let 
and 
be non-constant monic polynomials in such that 
.
Given the Bézout relation 
,
the Bézout relations for and , and and
can be computed by a straight-line program in
time .
Proof. From the given Bézout relation we have
Since 
and 
are strictly
less than 
, reduction of this
relation modulo 
yields
This is the desired Bézout relation for
and . By symmetry, the
Bézout relation for and
can be computed in a similar way.
We are now ready to present the main complexity bound of this section, in terms of the detailed cost functions defined in section 2.1.
be an explicitly separable
extension of of degree 
, and let be a computation
tree over -algebras of
detailed cost 
. Then the
panoramic evaluation of over
by Algorithm 3.2 takes time
Proof. We use Algorithm 3.2 in
combination with the technique of delayed reductions from section 3.7. This means that we avoid the cost of conversions, at the
price of performing arithmetic operations in subalgebras of in the algebra itself. More
precisely, the cost of one directed evaluation of
over is the sum of:
operations in for
the nodes of type in ,
operations in for
the nodes of type 
,
operations in for
the directed zero-tests and inversions,
operations in for
the reductions in the output nodes of the path (i.e.
the “finalization step” in the terminology of section 3.7).
Let denote the directed splitting obtained at
the end of step 1 of Algorithm 3.2. By construction we have
 |
(4.2) |
Fast multi-remaindering yields for in time 
.
We recursively perform the panoramic evaluation of
over 
for all .
Let 
be the cost of one panoramic evaluation of
over an algebra of dimension . We have shown that there exists a universal
constant 
such that
In view of (4.2), we conclude by unrolling this inequality
at most 
times.
Example performs 
operations in
. One directed evaluation of
over 
takes time 
, for .
In this example, the resulting cost of Algorithm 3.2 is
which is better than the bound of Theorem 4.2 because the
recursive depth is constant. If is a field, then
we notice that the usual evaluation of at takes time 
.
Let us now compare the complexity of directed evaluation with the
complexities of other known strategies for a single algebraic parameter.
One problem with dynamic evaluation is that it is hard to implement in
common programming languages without support for parallelism or high
level control structures such as continuations [41]. Early
implementations of dynamic evaluation were therefore naive [13],
the computation tree essentially being reevaluated for every separate
case: see subsection 4.3.1. In theory, using
When using common sequential programming languages, dynamic evaluation is usually implemented as in Algorithm 3.2, with the following two differences:
Splittings are no longer required to be directed. In other words, at
each evaluation step, the splitting at node
of is not required
to satisfy the conditions 
for 
. Consequently, whenever a zero-test or an
inversion triggers a basic splitting for 
, the branch where we continue the evaluation is
chosen non-deterministically. Such evaluations are said to be
undirected in the sequel.
Once the undirected evaluation is finished, the projections in step 2 of Algorithm 3.2 are done naively, without fast multi-remaindering.
Adapting the cost analysis of Algorithm 3.2 leads to the complexity bound
for naive dynamic evaluation, in terms of the detailed cost functions from section 2.1.
The following example shows that the latter bound is tight in the worst case. So naive dynamic evaluation is in general less efficient than fast panoramic evaluation.
Example
with , , , and
let represent the image of
in . Then a possible
undirected evaluation of at 
performs a basic splitting and may select the splitting
So a possible undirected evaluation ends with the latter splitting and
output value 
.
A possible undirected evaluation of over 
may end with the splitting
and value 
. Doing so for the
rest of the evaluation, we may end with the splitting
and the value of over is
for ,
and is 
over 
.
The total execution time therefore grows at least with
In comparison to Example 4.3, it turns out that dynamic evaluation may be significantly more expensive than our fast panoramic evaluation based on directed evaluation.
The naive implementation of dynamic evaluation using reevaluations of
the entire computation tree leads to unnecessary recomputations.
High-level control structures such as continuations can be used to avoid
this kind of recomputations, by resuming the
“recomputations” directly at the points where the splittings
occurred.
Example be a computation tree of the family introduced in Example
2.1, and let us again consider
with , , ,
and let represent the image of
in . The dynamic evaluation
of at encounters an
inconsistency when testing whether 
is zero
modulo 
. One computation
continues modulo 
, and so
returns . Another computation
continues modulo 
and a new splitting occurs at
the zero-test of 
, etc.
Counting common computations in branches only once, the total cost of
the dynamic evaluation is bounded by
which is essentially the same as the cost of our fast panoramic evaluation: see Example 4.3.
Example 
-algebras:
for from to
do
for from to do
if 
then 
Evaluated over a field of degree over , the
total cost of this program is
Let us now take with as
in the previous example. The dynamic evaluation executes the first loop
sequentially with cost 
. Then
it splits at the zero-test of 
modulo into two branches:
The first branch works modulo and reduces
modulo ,
which amounts to 
operations in . The costs of the zero-tests totalize
.
The second branch works modulo .
The zero-test of 
costs 
, and causes the present branch to split up
into two:
The first branch works modulo 
and
reduces 
, which
amounts to 
operations in . The costs of the zero-tests totalize
.
The second branch works modulo 
.
The zero-test of 
costs 
, and causes the present branch to
split up into two:
...
The total execution time when using dynamic evaluation is therefore
By Theorem 4.2, the execution time using fast panoramic
evaluation is 
, which is
significantly better.
The bottleneck of dynamic evaluation in Example 4.6 lies in the projections of data from parametric algebras into smaller ones. It is important to stress that this cost cannot be reduced by executing the branches in a judicious order or by cleverly factoring out common computations in branches using continuations. In our fast panoramic evaluation strategy, this means that fast multi-remaindering plays a crucial role for handling these projections efficiently.
The above examples show that determining the best strategy to compute a panoramic value for a given computation tree is not an obvious problem: in fact, computation trees and more general programs may often be modified in order to accelerate panoramic evaluations. Let us now consider some specific computation trees for which efficient ad hoc strategies have been developed.
For panoramic quasi-inversions in ,
gcds, and coprime factorizations in 
,
Dahan et al. have designed fast algorithms in [8].
For instance, they showed that a panoramic gcd in 
could be obtained with cost
 |
(4.3) |
see [8, Propositions 2.4 and 4.1]. For this problem, Theorem 4.2 leads to the cost
which can be further improved to
 |
(4.4) |
by using Kronecker substitution to multiply polynomials in 
in time 
. If
, then this cost is slightly
higher than (4.3). If 
,
then (4.4) simplifies to 
,
which is slightly better than (4.3).
Another interesting application of fast panoramic evaluation is the
computation of the determinant 
of an matrix 
with entries in . By means of Berkowitz' algorithm
[1], such a determinant can be computed in time 
by a straight-line program over , and therefore in time 
by a
straight-line program over .
This cost decreases to 
by using [32],
and even to 
thanks to [40],
whenever inverses of 
are given in . We can do better with fast panoramic
evaluation: we first compute the determinant of
over as if it were a field by means of a
computation tree that performs ring operations
and 
zero-tests and inversions. By Theorem 4.2, this can be done in time
The resulting panoramic value corresponds to the residues of modulo several pairwise coprime factors of . Chinese remaindering finally allows to
recover the actual determinant using additional operations in .
From now on, we focus on the complexity of panoramic evaluation for algebraic parameters. Such a tower is determined by
algebraic parameters , where
is constrained by an algebraic equation over
, and
is constrained by an algebraic equation over 
for
. It is natural to apply the
method of the previous sections for a single algebraic parameter in a
recursive manner. But we have to face a new difficulty: directed
zero-tests and inversions in will involve
occasional zero-tests and inversions in 
,
that will themselves involve occasional zero-tests and inversions in
, etc. The first goal of this
section is to design data structures that allow us to create new
branches for free during directed evaluation. At the end of a directed
evaluation we need to project input data into all the residual branches.
Performing this task efficiently is the second goal of this section.
Data structures play an important role in the efficiency of operations
required by parametric frameworks. From now on, we will only manipulate
parametric algebras whose defining ideals are generated by triangular
sets. In other words, all parametric algebras will be represented by
towers over 
,
as in section 1.1. We recall that
is also assumed to be absolutely reduced, i.e. is a product of fields. A tower is
said to be explicitly separable if we are given the
Bézout cofactors 
and 
in 
such that 
for .
In order to simplify complexity analyses, it is convenient to assume
that 
for .
In particular, 
. This
restriction is harmless, since extensions of degree 
can be discarded without cost in our model of computation trees.
Consider two towers and 
of the same height and over the same base field
. Let 
and 
denote the respective defining polynomials
of and .
We say that is a factor tower of if 
. This
is the case if, and only if, there exist natural projections 
(that naturally extend to projections 
in a coefficient-wise manner) such that:
divides 
for .
sends an element 
represented by 
to
for .
Given such a factor tower of 
, let us now study the cost 
of computing one projection 
of an element 
with 
.
be a factor tower of . The projection 
of
an element 
can be computed by a straight-line
program in time
Proof. Let 
denote the
preimage of . We recursively
apply 
to the coefficients of 
. Then, the reduction of 
modulo 
can be done by a straight-line program
with cost 
. Consequently,
there exists a universal constant such that the
cost function 
satisfies
Unrolling this inequality yields
Taking 
from Proposition 2.6
concludes the proof.
In the sequel, “()” stands for the empty tuple. Let 
be an index set of 
-tuples
of integers with 
and
for integers 
and 
.
Consider a family 
of factor towers of with the property that 
only
depends on 
for all 
,
and write 
. We say that such
a family of factors forms a tree factorization of if the variety 
is partitioned into
. If 
and 
, then we also write 
for the defining polynomial of 
over 
.
It is convenient to represent such a factorization by a labeled tree (see Figure 5.1): the nodes are identified with the index set made of the disjoint union
and each node
is labeled with the algebraic extension
.
The parent of the node
with
is simply the node
.
Each individual factor tower
corresponds to a path from the root to a leaf.
Given 
and ,
let
Projecting the equality
on the first coordinates, we observe that the
projection of 
, for given
, is the same for all 
, and equals 
, whence 
.
Consequently, 
forms a tree factorization of the
sub-tower 
. From an algebraic
point of view, this means that we have a natural isomorphism
Consider an explicitly separable tower and
assume that we wish to compute the panoramic evaluation of a computation
tree over .
In order to apply Algorithm 3.2 in this multivariate
context, it would be natural to specify a parametric framework, as we
did in the univariate case. Since we will exclusively focus on the
directed approach from now on, it turns out to be simpler and more
straightforward to describe how to perform the directed evaluation and
the projections in steps 1 and 2.
Informally speaking, we want to work with respect to a “factor of
highest possible degree” at each level. This leads to special
types of factorizations of that are illustrated
in Figure 5.2. The actual computations are done in the
algebras from the highlighted “principal branch”. The other
“residual branches” are dealt with at a next iteration, when
the computations for the principal branch have been completed.
Technically speaking, a directed splitting of
will be represented by:
Vectors 
of polynomials in
for , such that:
are the defining polynomials of a factor
tower of , written
, and called the
principal branch.
for .
for 
.
The Bézout relations 
for , so is explicitly
separable.
Each factor 
with 
and
gives rise to a factor tower 
of , called a residual
branch, as follows:
For 
, we set 
.
.
For 
, the defining
polynomial of 
over 
is the projection of 
in 
.
The tree representation of the resulting tower factorization is summarized in Figure 5.2
represented in this manner is
Notice that a directed splitting 
of naturally induces a directed splitting 
of 
for .
Now the main idea is to perform the directed evaluation of a computation tree over the principal branch, while postponing evaluations over residual branches. With our representation of directed splittings, creating residual branches is essentially free of charge; the corresponding tower representations will only be computed after completion of the entire directed evaluation, using a dedicated “finalization” procedure that will be detailed in subsection 5.4 below. After the finalization, the projections from step 2 of Algorithm 3.2 can be carried out efficiently using fast multi-remaindering; this will also be detailed in subsection 5.4.
As in the univariate case, it will be convenient to use the technique of
delayed reductions from section 3.7. During directed
evaluations, this means that we will actually represent elements in 
by elements in ,
for . In particular,
operations in 
on elements in 
are really performed in . We
recall that the main benefit of this representation is that projections
are free of charge, whenever 
is a quotient algebra of whose elements are also
redundantly represented by elements in .
On the other hand, we will resort to reduced representations for
directed zero-tests and inversions. We will also systematically reduce
all output values. Notice that elements in can
be reduced in time 
, by Lemma
5.1. In the next subsection, we detail how to perform
directed zero-tests and inversions.
In the case of a single algebraic parameter, we reduced directed
inversions and zero-tests to extended gcd computations. With several
parameters the problem is more difficult. An element
in can be tested to be invertible by means of a
straight-line program over with polynomial cost
and a single zero-test in :
it essentially suffices to compute the determinant of the multiplication
endomorphism 
using Berkowitz' algorithm [1]. But the cost of this approach is more than quadratic in
, which is not satisfactory
for our purposes. We now develop a more efficient strategy based on
recursive calls of the fast extended gcd algorithm in the directed
evaluation model. Note that a similar recursive approach was previously
used in the contexts of dynamic evaluation and triangular sets.
Algorithm
If 
then return
if 
or and otherwise. The directed splitting is left
unchanged.
Let 
denote the preimage of , and recursively compute the extended
monic gcd of and 
over 
, using directed
evaluation of a computation tree for extended gcds, with the
directed splitting 
as extra input.
Let 
denote the directed splitting
obtained in return and let 
be its
principal branch. This extended gcd computation also returns a
monic polynomial 
,
and 
in 
such that
the following Bézout relation holds:
where 
and 
.
Let 
, 
, so that the Bézout relation
holds. Compute the reduced
representations of 
,
, 
, 
,
and (recall that we delayed these
reductions), and then compute 
.
Deduce the Bézout relations 
and
by means of Lemma 4.1.
If 
, then return
true, along with the directed splitting 
, and the Bézout
relation of 
and .
If , then return
, along with the
directed splitting 
,
the Bézout relation of and , and the inverse 
of 
.
If 
, then return
true, along with the directed splitting 
, and the Bézout
relation of and .
Otherwise return ,
along with the directed splitting 
,
the Bézout relation of and , and the inverse 
of .
Until the end of the paper, 
represents a cost
function for products in 
where 
can be any principal branch encountered in the directed evaluation model
over . Similarly, 
is a cost function for reduced projections from onto .
operations in ,
where 
.
Proof. In step 8 we have
Consequently, the splittings in the output are directed.
In step 8, the fact that 
taken modulo is the inverse of 
in 
can be verified as follows, in the same way as in section
4.1: the Bézout relation of 
and gives
which simplifies to 
thanks to the Bézout
relation of and .
The correctness of the algorithm follows from these facts.
Let us write 
for the cost of the algorithm and
recall that we are using the technique of delayed reductions. If 
then the cost is 
.
Otherwise, when computing extended gcds using the fast algorithm from
section 2.2, step 2 takes
operations in . Step 3 takes
further operations, and step 4 takes time 
,
by Lemma 4.1. Steps 5 to 8 require 
operations in . Therefore,
there exists a universal constant 
such that
 |
(5.1) |
Proposition 2.6 and Lemma 5.1 lead to
whence
for some universal constant 
.
Using 
, unrolling the latter
inequality leads to the claimed bound.
As before, let be a separable tower with
defining polynomials of degree 
, and denote .
At the end of a directed evaluation, we must recover the tower
factorization of induced by the directed
splitting. We also need efficient routines for projecting onto the
residual branches. In this subsection (and contrary to the previous
subsection), we use the traditional, reduced representations for
elements in towers. We begin with a simple lemma for the computation of
Bézout relations induced by factorizations.
be monic and separable of degree
, and let 
be non constant monic polynomials in such that
. Given the Bézout
relation of 
and 
, the Bézout relations of
and 
for 
can be computed by a straight-line program in time .
Proof. We first construct the subproduct tree of
: it is defined as the set of
the sub-products defined recursively as follows:
the set 
if 
,
the union of 
and the subproduct trees of
and 
if 
.
A straightforward divide and conquer algorithm computes all these
products with arithmetic operations in . Then, we obtain the Bézout
relations for 
and 
,
as well as for 
and 
,
in time by Lemma 4.1. We conclude
using a standard induction argument on 
.
as above,
the explicitly separable factor towers 
for
and 
can be computed in
time by a straight-line program, where . In addition, both directions of
the isomorphism
 |
(5.2) |
can be computed by straight-line programs in time .
Proof. Until the end of the proof, it is convenient to keep in mind the notation for the tree factorization in Figure 5.2, associated to the directed splitting. Let us write:
for the cost of the construction of the
explicitly separable factor towers ;
for the cost of the projections from onto 
;
for the cost of the Chinese remaindering
from to .
The proof is done by induction on 
.
If , then the costs are zero.
Assume now that 
and that explicitly separable
factor towers 
have been constructed. We thus
have the following effective isomorphism:
 |
(5.3) |
We first project 
and the Bézout relation
onto 
and 
for 
and
with cost 
. This already
gives the defining polynomials of 
over 
for and , along with the corresponding Bézout
relations.
We next project the polynomials of 
onto , namely
for 
, using
operations in (it is better to use Lemma 5.1 in practice, but the present bound in terms of 
simplifies the analysis). From the already computed 
, 
,
and 
, we deduce the
Bézout relations of 
and 
for , by means of Lemma 5.3, in time
Overall, we have shown that there exists a universal constant such that
 |
(5.4) |
Let us now consider both directions of the isomorphism (5.2).
Given , represented by , we compute the projections 
and 
for
and in time ;
this already gives the images of into 
for and . Then we compute the remainders of 
modulo for 
in time 
. So there exists a universal
constant 
such that
 |
(5.5) |
For the inverse Chinese remaindering problem, we are given 
for , and 
for and . We have at our disposal , its factors for and the Bézout relation of 
and . We compute 
whose projections are 
for :
where 
(resp. 
)
is the canonical preimage of 
(resp. of ). Computing
costs ; see [21,
Algorithm 10.20]. The isomorphism (5.3) gives rise to the
isomorphism
whose right-hand side contains 
.
We finally recover the image of this element in
using 
recursive calls of the Chinese
remaindering procedure. Altogether, this shows that there exists a
universal constant 
with
 |
(5.6) |
By using , inequality (5.5) and Proposition 2.6 give
Similarly, the relation (5.6) yields
Finally, using our assumption that for 
, the relation (5.4)
implies that
We are now ready the state the main complexity result of this section, in terms of the detailed cost functions from section 2.1.
be an explicitly separable tower
of degree , let , and let
be a computation tree over -algebras
of detailed cost 
. Then the
panoramic evaluation of over
using Algorithm 3.2, along with the computation of
auxiliary data, requires
operations in . Let 
denote the panoramic splitting in the output. By
means of the auxiliary data, conversions in both directions of this
isomorphism can be done in time
Proof. The proof is very similar to the one of
Theorem 4.2. It is straightforward whenever 
, so we may freely assume 
from now. Using redundant representations, the directed evaluation of
over requires the
following operations in :
operations for the nodes of type in ;
operations for the nodes of type by Proposition 2.6;
operations for the zero-tests and inversions
by Lemma 5.1 and Proposition 5.2;
operations to reduce the output values, by
Lemma 5.1.
At the end, the directed splitting
 |
(5.7) |
satisfies
 |
(5.8) |
The finalization of the residual branches 
takes
time by Lemma 5.4. In step 2 of
Algorithm 3.2 we next project the
input values of the computation tree to the residual algebras . Again by Lemma 5.4,
this can be done in time 
.
Let denote the cost function of one panoramic
evaluation of over a -algebra of dimension 
.
The above analysis shows the existence of a universal constant such that
Unrolling this inequality at most times, thanks
to (5.8), the claimed complexity bound follows.
Let 
denote the cost function of the conversions
between and a panoramic splitting. Using Lemma
5.4, we conclude that
again thanks to (5.8).
Before we turn to the more technical topic of speeding up computations in algebraic towers, we will have a short intermezzo to study primitive tower representations. The results in this section are essentially from [29, sections 3 and 4.1], although we slightly generalized some of them.
Let be an effective -algebra and let be an
effective -algebra with an
explicit basis 
. We start by
recalling the main result from [29, section 3] about the
evaluation of multivariate polynomials in 
at
points in 
. This can in
particular be used in order to compute so-called multivariate modular
compositions. We recall that (resp.
) stands for the number of
operations in that are required in order to
multiply two elements in (resp.
). We assume that 
and that additions and subtractions in
and are cheaper than multiplications.
be an effective
-algebra of rank 
, whose basis is explicitly
given. Let 
with 
for
, and let 
. If 
,
then A(a1,…,at) can be computed by a
straight-line program in time
Proof. The case 
corresponds to the classical baby-step giant-step algorithm over ; see for instance [29,
section 3.1]. The extension to 
has been designed
in [29, section 3.2]. In [29, Proposition
3.3], the assumption for
was used for convenience. But if for some , then does
not actually appear in , so
discarding is free of charge in the
straight-line program model.
The main difference with [29] is that we will consider
primitive tower over arbitrary -algebras
instead of fields .
In the same spirit as section 3.7, it will also be
convenient to also integrate the idea of redundant representations in
the definition.
From an abstract point of view, given two effective -algebras and , we may use elements in as a redundant representation of elements in if we have an effective monomorphism 
and an effective epimorphism 
such that 
is the identity map of .
We say that is an effective retract of
. We will write 
(resp. 
)
for the cost of one evaluation of 
(resp. 
), and we
denote 
.
From now on, assume that is a product of
separable field extensions of .
We consider a tower of ring extensions of of the
form 
, 
for , where
is monic and explicitly separable of degree , which means that there exists a Bézout
relation with 
and 
.
consists of:
A -algebra , a monomorphism , and an epimorphism
such that is the identity map of .
Linear forms 
, 
with 
,
for .
Monic polynomials 
, for
.
, for
and 
.
Writing 
for the class of 
in 
, we assume that these
data satisfy the following properties for :
The following map 
is a
monomorphism that extends :
 |
 |
 |
|
 |
 |
 |
(j=1,…,i). |
The following map 
with 
is an epimorphism that extends :
The polynomials 
are called
parametrizations of the 
in
terms of .
In terms of the triangular set defined in the
introduction ( is the canonical preimage of in 
), an
element is represented by a polynomial 
with 
defined modulo 
. So the conversion of
into an element of 
boils down to evaluating 
modulo 
.
The backward conversion consists in evaluating the image 
of a univariate polynomial 
at
. Both conversions are
instances of multivariate modular composition problems that can be
handled using Proposition 6.1. More precisely:
in terms of the defining polynomials , and
in terms of 
,
and 
,
such that is a primitive tower
representation of . Then
there exist straight-line programs for which:
One evaluation of 
takes 
operations in .
The images 
for
can be computed in time 
.
Given 
, one
evaluation of 
can be done in time 
.
Proof. If for some , then does
not actually appear in polynomial representations of elements in . In the computation tree model, we
may suppress such indices without any cost. Without loss of generality
we may therefore assume that for .
The complexity bound for one evaluation of with
is a direct consequence of Proposition 6.1.
Indeed, any element in can be represented as
, where
admits partial degrees in
for 
. Now we can compute
in time
since . We finally notice
that 
.
For , the map 
extends coefficientwise into a map 
. We may thus convert the minimal polynomial 
of over
into a polynomial 
in time
The computation of then takes time , since for all .
In order to evaluate 
at an element 
in , we write
for the preimage of and
observe that
We first evaluate 
at 
in
, where 
is the class of 
in 
.
This takes time 
by Proposition 6.1
and yields a polynomial
Since 
, we next notice that
so the preimage in 
of 
is
which represents 
. Applying
to the 
coefficients of
costs 
.
Altogether, this proves the existence of a universal constant such that
We conclude that can be computed in time
using our assumptions that and
for all .
If 
is a field, then our definition of primitive
tower representations of coincides with the one
from [29, Definition 2.2] whenever the
are isomorphisms. If has sufficiently many
elements, then primitive tower representations can for instance be
computed using linear algebra techniques. For efficiency reasons, we
will rely on the following result that will be used later with a
parametric algebra in the role of .
is a field of cardinality 
. Then a primitive tower representation of
can be computed using 
inversions and zero-tests in ,
plus 
ring operations in .
Remark
Remark 
, then a primitive
tower representation of can be computed by a
randomized Las Vegas algorithm using an expected number of inversions and zero-tests in plus
arithmetic ring operations in .
It is more subtle to regard such randomized variants as computation
trees. Although our model does not provide us with an instruction to
compute random elements of ,
nothing prevents us from adding a “pool” of randomly chosen
elements to the input. Since randomized Las Vegas algorithms may fail
for certain random choices, they typically loop until suitable random
numbers are drawn. As explained in Remark 2.4, we may
unroll such loops to make things fit in our computation tree model,
provided that we can provide an absolute bound on the number of
times that we have to run the loop.
In our case, we claim that such an absolute bound indeed exists.
Following [29, Proposition 4.3], the construction is
incremental in : assuming
that 
already found, one has to pick up a
suitable value of 
in a subset 
of of cardinality 
.
The crucial observation is that a suitable value always exists in this
finite set , which bounds the
number of random values that have to be tried. With
ordered randomly, can actually be found with a
bounded number of expected trials.
The suboptimality of the complexity bounds of Proposition 2.6
and of Theorem 5.5 appears when the height
of the tower gets as large as 
.
In fact, if indeed gets large, then many of the
are necessarily small. This section is devoted
to an efficient solution to this issue.
Roughly speaking, as long as a product of the form 
is reasonably small, it turns out to be favorable to change the given
representation of 
into a more efficient
primitive element representation 
.
Repeating this operation as many times as necessary, the original tower
is replaced by an equivalent tower 
of much smaller height and for which all defining
polynomials have sufficiently large degree. Such accelerated
towers were first introduced in [29, section 4.2]. In
this section, we will further refine the concept and show how to use
such towers in combination with directed evaluation.
Throughout this section, we carry on with the notations from section 5: the original tower is explicitly
defined by 
, and we set for . As
before, we will assume that and that for . In
particular, .
In this subsection, we extend the notion of accelerated towers from [29, Definition 4.6] and study accelerated tower arithmetic.
Let be an explicitly separable tower over , and let 
. By [29, Lemma 4.7], there exists a
sequence of integers 
of length
 |
(7.1) |
such that, for 
, we have
 |
(7.2) |
where 
. In this subsection,
we assume that the sequence 
has been fixed once
and for all.
and consider a
factor tower 
of 
.
Then the subsequence 
induces a family of
towers 
over 
for 
. An accelerated
tower for , and
with respect to the sub-sequence ,
consists of a family of primitive tower representations of these
towers for .
More precisely, these representations comprise the following data:
A tower 
over with
defining polynomials 
,
where 
and 
,
and such that 
. The
class of 
in 
is
written 
.
For 
:
Linear forms 
, 
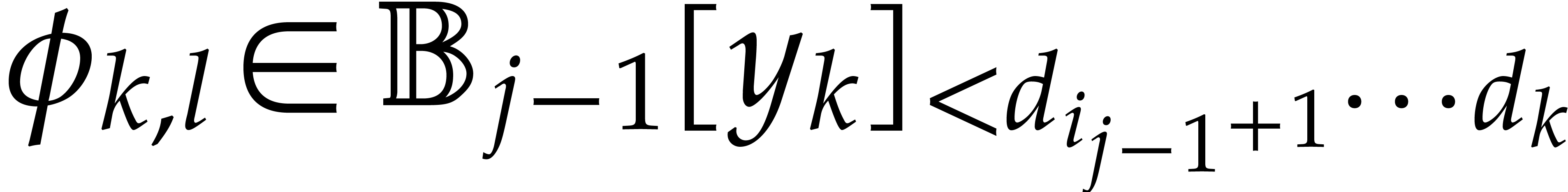over for 
,
for 
,
for 
and 
.
Let represent the identity map of . For and
, these data induce the
following monomorphism that extends 
:
Let represent the identity map of . For and
, we also have the
following epimorphism that extends 
:
and 
. For and , we
finally have
In particular, for , we have
the following monomorphism that extends :
 |
|
 |
|
 |
|
 |
(l=ij-1+1,…,ij) |
 |
|
 |
When 
, taking
 |
(7.3) |
yields
 |
(7.4) |
whence products in 
can be computed using 
operations in ,
by Proposition 2.6. The worst case complexity of products
in is therefore asymptotically better than in
, which explains the
terminology of “accelerated towers”. Let us now detail how
to make elements in benefit from this
acceleration.
be an accelerated tower for as in Definition 7.1. Given 
and 
,
conversions between 
and
via and can
be done by straight-line programs in time 
.
Proof. The proof is adapted from [29,
Lemma 4.8]. Let us first assume that the polynomials 
have been precomputed for 
.
By Proposition 2.6,
and by Proposition 6.3, we have
If 
then such conversions simply cost 
. Otherwise we have 
by (7.2). In both cases it follows that
for some universal constant .
Unrolling the latter inequality, while taking into account that 
and , we
deduce that
Finally, given 
, we notice
that can be precomputed in time
by Proposition 6.3, again by distinguishing the cases when
and 
.
Consequently, the total cost of these precomputations is
be an accelerated
tower for as in Definition 7.1.
Given and ,
products in can be computed by a straight-line
program in time
Two polynomials of degree 
over can be multiplied by a straight-line program in time
Proof. One conversion between
and 
can be done in time
by Lemma 7.2. On the other hand, Proposition 2.6 yields
Combining the latter costs, we deduce that
and the claimed cost for 
corresponds to setting
.
One motivation behind Definitions 6.2 and 7.1 with respect to the less general definitions from [29] is to allow for redundant representations. More precisely, we have:
be an accelerated tower for as in Definition 7.1. Then is an accelerated tower for any factor tower of .
Proof. A tower factor 
of
is a tower factor of 
. Let 
denote the canonical
monomorphism, then 
is the identity of 
. Setting 
we first verify by induction that
 |
|
 |
|
 |
|
 |
(l=ij-1+1,…,k) |
is a monomorphism that extends 
,
for , since 
.
Let 
represent the identity map of . For ,
we define the epimorphism 
,
for , that extends 
:
Since 
, we deduce that 
is the identity map of .
Notice that the tower is only used for the
acceleration of arithmetic operations; we do not require this tower to
be separable. Writing 
for the image of 
in , our use of
redundant representations also makes it unnecessary to determine the
defining polynomials of 
.
Although the computation of such defining polynomials 
along with Bézout relations for and 
would be convenient for speeding up multiplications
in 
, it seems tricky to
integrate these computations without deteriorating the overall
complexity.
When reduced, non-redundant representations are explicitly required, we will resort to the following counterpart of Lemma 5.1:
be a factor tower of , and let 
be an
accelerated tower for as in Definition 7.1. Given and , the projection of an element onto can be computed by a
straight-line program in time 
.
Proof. The proof is the same as in Lemma 5.1, except that we appeal to accelerated products 
of Proposition 7.3. The cost of the
projection thus becomes:
Now (7.2) yields 
for 
. Since ,
the claimed bound follows.
be a principal
branch encountered in a directed evaluation over , and let be an
accelerated tower of , as
in Definition 7.1. Given and
, one directed zero-test or
inversion can be done in time
Proof. We adapt the proof of Proposition 5.2 so as to benefit from accelerated products. From Proposition 7.3 we have
and from Lemma 7.5 we have
Consequently, the relation (5.1) implies the existence of a
universal constant such that
Unrolling the latter inequality yields
while using the facts that and
for , by (7.2).
Now that we have seen how to benefit from accelerated arithmetic, let us show how to construct accelerated towers. We use induction on the height, in combination with Proposition 6.4. As usual, all computations in the directed model are done using the redundant representation.
Algorithm
If 
, then return 
for the directed splitting along with an
empty accelerated tower.
Otherwise 
;
recursively apply the algorithm to 
and
. Let 
represent the directed splitting of obtained in return, let 
be
the principal branch, and let 
be the
accelerated tower for .
Let 
be the canonical preimages of 
in 
;
compute 
,...,
.
By directed evaluation over 
,
starting with the directed splitting , compute a primitive tower representation
for
seen as a tower over 
.
Let 
be the directed splitting obtained
in return and let 
be the corresponding
principal branch.
The latter primitive tower representation consists of
Linear forms 
,
over for
;
for ;
for and
.
With the notation of Definition 7.1, we set 
for and 
for and .
Compute 
and define, for 
:
as 
regarded
as in 
;
.
Complete the tower with the projections
of the Bézout relations of 
and
over 
;
return this tower, 
,
and .
,
then Algorithm 7.1 is correct and runs in time
for a sequence of integers 
that satisfies
Proof. When entering step 5,
is an accelerated tower for ;
so we have the monomorphism 
and the epimorphism
such that 
is the
identity map of . We also
have the following isomorphisms for :
 |
 |
 |
|
|
|
 |
(l=is-1+1,…,k). |
So the following morphisms are monomorphisms that extend , for 
:
 |
|
 |
|
|
|
|
(l=is-1+1,…,k) |
 |
|
 |
Let
We observe that 
extends 
and that
This completes the correctness proof.
Step 1 takes constant time. In step 3, the projections require
operations in , by Lemma 7.5 and the assumption that for . Notice that the same bound holds
for step 6.
Step 4 is free of charge whenever 
.
Otherwise 
holds by (7.2). During
the directed evaluation of step 4, one product in the principal branch
takes 
operations in by
Proposition 7.3, and the cost of one directed inversion is
by Proposition 7.6. Consequently,
step 4 runs in time
In step 5 we perform
conversions from to 
, which amount to
operations in by Lemma 7.2.
Remark , then the randomized Las
Vegas version of Proposition 6.4 (see Remark 6.6)
may be used in Algorithm 7.1, so that step 4 has an
expected cost
which still dominates the cost of Algorithm 7.1 in this model.
In order to make the directed evaluation benefit from accelerated
arithmetic, we first need to compute an accelerated tower. Then, the
complexity of accelerated divisions is simply adjusted according to
Proposition 7.6. At the end of a computation, we use the
following lemma in order to recover the extended tower factorization of
, as in section 5.4.
as above,
and an accelerated tower for its principal branch, the explicitly
separable factor towers for
and can be computed in time 
by a straight-line program, where .
In addition, both directions of the isomorphism
can be computed by straight-line programs in time 
.
Proof. The algorithm is the same as in the proof
of Lemma 5.4. We only revisit the cost analysis when using
accelerated arithmetic. Given ,
Proposition 7.3 yields
whence
In a similar way, we obtain
We deduce that
 |
|
be an explicitly separable tower
of degree , let , and let
be a computation tree over -algebras
of detailed cost , as
defined in section 2.1. Assume that . Then the panoramic evaluation of over using Algorithm 3.2,
along with the computation of auxiliary data, requires
 |
(7.5) |
operations in ,
where
Let denote the panoramic splitting in the
output. Using the auxiliary data, conversions in both directions of
this isomorphism can be done in time
 |
(7.6) |
Proof. The directed construction of the accelerated tower takes
by Proposition 7.7. Then, we project the input values onto
the principal branch, written ,
in time
by Lemma 7.5.
Let us summarize the number of operations in
needed for the directed evaluation of over , when using redundant
representations in :
operations for the nodes of type in ;
for the nodes of type
by Proposition 7.3;
for the zero-tests and inversions by Lemma
7.5 and Proposition 7.6,
for the reduction of the output node by
Lemma 7.5.
At the end, the directed splitting 
satisfies
 |
(7.7) |
Then we finalize the construction of the residual branches in time
by Proposition 7.9. We next project the
input values of the tree to ,
in time
again by Proposition 7.9. We finally perform the recursive
panoramic evaluations of over . The conclusion follows as in the proof of
Theorem 5.5.
Remark 
, then the factor 
in the definition of 
can be replaced by an
expected 
in Theorem 7.10, by using
the randomized variant from Remark 7.8 for the directed
construction of the accelerated tower.
The following corollary simplifies the above complexity bound by tuning
the parameters 
and .
, the bound
and the bound 
.
Proof. It suffices to take
and as in (7.3) and (7.4).
The main result of [29] is an efficient algorithm to compute products in separable towers of field extensions. We are now in a position to generalize this result to arbitrary explicitly separable towers.
be an explicitly separable tower
as in the introduction of this section. If , then products in can be
computed in time
Proof. Let 
.
Applying Theorem 7.10 to the straight-line program that
simply computes a product, it requires 
operations to compute a parametric splitting 
, auxiliary data, and the projections 
for . Using the
auxiliary data, the theorem also allows us to recover 
from these projections using 
further operations
in . We conclude by taking
and as in (7.3)
and (7.4).
Another interesting application that has already been discussed in the univariate case at the end of section 4.3.3 is the computation of determinants.
be an explicitly separable
tower as in the introduction of this section. If , then the determinant of an 
matrix in 
can be computed in time
Proof. The proof is similar to the one of
Theorem 7.13.
As a final application, we revisit the matrix product. We need the following generalization of Proposition 2.6:
, assume that 
. Then the product of two matrices in can be computed
in time
Proof. We proceed along the same lines as
Lebreton in [35, section 3.2]; see also [29,
Proposition 2.4]. Consider two matrices 
,
we first lift the matrices to multivariate polynomial matrices in 
of partial degrees in for . We
next convert these polynomial matrices to univariate polynomial matrices
in 
using Kronecker substitution. We multiply
these matrices using the evaluation-interpolation technique. Since admits at least distinct
evaluation points, this can be done in time
We finally convert the result back to a polynomial matrix in , and we reduce each of the entries
with respect to using the algorithm from [35, section 3.2]. This reduction step requires 
operations in .
Now our assumption that for
implies 
and 
.
Using (2.1), we conclude that the total running time is
bounded by
 |
|||
 |
|
|
The next proposition is an example of a less straightforward use of
Theorem 7.10, where we adapt the “acceleration
factor” to a specific situation, and where
we wish to decrease the overhead of the accelerated towers. Precisely,
after a directed construction of an accelerated tower, we obtain a
directed splitting 
that satisfies
As a byproduct, we have an accelerated tower of
of degree at our disposal. The recursive calls
to panoramic evaluations over for 
then lead to accelerated towers for each of the factor
towers of . Let 
denote a bound for the sum of the degrees of all these
accelerated towers. Then we have
Unrolling this inequality leads to 
,
which is slightly suboptimal.
We may modify the construction of accelerated towers, described in
Algorithm 7.1, in order to ensure that the degree of the
accelerated tower is never more than twice the degree of the principal
branch before entering the evaluation of the given computation tree.
This is done as follows. At the end of Algorithm 7.1, we
compare the degree of the accelerated tower to
the degree of the principal branch .
If 
then we are done. Otherwise, the principal
branch is much smaller than in the sense that
, and we use again Algorithm
7.1 in order to compute an accelerated tower for . We carry on computing a new
accelerated tower of the current principal branch in the directed model
over until the condition
is met. By Proposition 7.7, the total cost of this process
is roughly only twice as much as a single run of Algorithm 7.1
since
With these modifications in hand, we ensure that 
.
be an explicitly separable
tower as in the introduction of this section. If 
and 
, then two matrices in can be multiplied in
time 
.
Proof. Let 
be a fixed
positive constant. Take 
and fix a sequence such that (7.1) and (7.2)
hold. Since , we observe that
.
We first compute a single product in with the
sole purpose of retrieving a parametric splitting , together with the auxiliary data for efficient
conversions in both directions, and an accelerated tower of height for each 
of degree 
, where 
; as discussed above. This precomputation takes time
One conversion between and 
also take time
Now assume that we wish to multiply two matrices . This problem is reduced to 
multiplication problems of matrices in 
that we
further transform into matrix multiplications within the corresponding
accelerated towers, so Proposition 7.15, yields the cost
using the assumptions that 
and .
Remark . It is an
interesting question how to adapt the setting of this paper so that
complexity bounds of this type can be derived.
Theorems 4.2, 5.5, and 7.10 show that the approach of directed evaluation allows us to compute panoramic evaluations in a time that is arbitrarily close to linear. We chose the setting of computation trees as our complexity model and it is natural to ask whether similar results hold in the RAM and Turing models. This seems plausible, although technical difficulties are likely to arise in the efficient implementation of data structures on Turing machines; see [30] for a detailed analysis of a similar kind, but for another problem.
So far, we have only addressed the sequential complexity of dynamic
evaluation and its variants. It would be interesting to conduct a
similar study for parallel computation models. Dynamic evaluation lends
itself particularly well to parallel execution: whenever we encounter a
splitting, it is natural to continue the execution of each of the
branches in parallel. In the directed setting, we a priori have
to complete the execution of the principal branch in order to benefit
from the fastest possible multi-remaindering. Nevertheless, this is
really a trade-off, and we may very well start to execute some
“sufficiently thick” residual branches before completion of
the principal branch. It is also important to notice that these
considerations have only minor impact from the worst case complexity
perspective: the opportunities for this kind of parallelism only arise
when splittings actually occur. In the absence of splittings, we have to
evaluate the computation tree over the full
original algebra , so the
parallel complexity is really a function of the amount of parallelism
that is available in and in the algebra
operations of .
For our presentation, we restricted our towers to be explicitly
separable from the outset. In practice, towers are usually constructed
by adding new parameters that satisfy polynomial constraints one by one.
These polynomials may contain multiple factors, in which case one is
usually only interested in the radical ideal generated by the
constraints. This more general setting can actually also be covered
efficiently using our techniques. Indeed, consider an explicitly
separable tower and a new algebraic parameter
that is subjected to 
, where 
is a monic
polynomial that is not necessarily separable. Then we simply compute the
separable factorization 
as if
were a field (here assuming that the characteristic is zero or
sufficiently large), using panoramic evaluation, together with the
requested Bézout relations for the non-trivial factors 
. Let be
the resulting splitting. Then any pair 
with gives rise to a new explicitly separable tower of
height 
, which allows us to
recurse.
In this paper, we only considered parameters that satisfy polynomial
constraints, but the technique of directed evaluation naturally
generalizes to various other settings. For instance, for an integer
parameter 
, one may compute
in 
as if it were a field, so
is partially factored during directed evaluations. This situation is
commonly encountered in number theory and computer algebra, where the
deterministic construction of “large” prime numbers is
rather expensive. Another possible extension of our work concerns real
algebraic numbers in the continuation of [16].
Another direction for future work concerns the particular kind of tower
arithmetic that we build on. In this paper, we essentially combined the
best previously known generic algorithms from Theorem 2.6
with the idea of accelerated towers. For specific base fields , such as finite fields or
subfields of 
, other
efficient algorithms have been proposed for tower arithmetic [9,
27, 28]. It should not be hard to combine
directed evaluation with these algorithms in order to improve on Theorem
7.10 and Corollary 7.12 for such more specific
base fields .
Finally, the recent new theoretical ideas from [27-29] and this paper should also allow for more efficient software implementations, although it remains a major challenge to make this happen. In particular, this requires to implement all available approaches with care and determine the thresholds for which they are most efficient. For particularly long parametric evaluations, one may also wish to switch to towers of smaller height, and to spend more time on factoring the defining polynomials.
S. J. Berkowitz. On computing the determinant in small parallel time using a small number of processors. Inform. Process. Lett., 18:147–150, 1984.
L. Blum, F. Cucker, M. Shub, and S. Smale. Complexity and real computation. Springer Science & Business Media, 2012.
F. Boulier, F. Lemaire, and M. Moreno Maza. Well known theorems on triangular systems and the D5 principle. In J.-G. Dumas, editor, Proceedings of Transgressive Computing 2006: a conference in honor of Jean Della Dora, pages 79–92. U. J. Fourier, Grenoble, France, 2006.
P. A. Broadbery, T. Gómez-Díaz, and S. M. Watt. On the implementation of dynamic evaluation. In A. H. M. Levelt, editor, Proceedings of the 1995 International Symposium on Symbolic and Algebraic Computation, ISSAC '95, pages 77–84, New York, NY, USA, 1995. ACM.
P. Bürgisser, M. Clausen, and M. A. Shokrollahi. Algebraic complexity theory, volume 315 of Grundlehren der Mathematischen Wissenschaften. Springer-Verlag, 1997.
D. G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Inform., 28:693–701, 1991.
M. Coste, H. Lombardi, and M.-F. Roy. Dynamical method in algebra: Effective nullstellensätze. Ann. Pure Appl. Logic, 111(3):203–256, 2001.
X. Dahan, M. Moreno Maza, É. Schost, and Yuzhen Xie. On the complexity of the D5 principle. In J.-G. Dumas, editor, Proceedings of Transgressive Computing 2006: a conference in honor of Jean Della Dora, pages 149–168. U. J. Fourier, Grenoble, France, 2006.
L. De Feo, J. Doliskani, and É. Schost. Fast
algorithms for -adic
towers over finite fields. In Proceedings of the 38th
International Symposium on Symbolic and Algebraic
Computation, ISSAC '13, pages 165–172, New York, NY,
USA, 2013. ACM.
J. Della Dora, C. Dicrescenzo, and D. Duval. About a new method for computing in algebraic number fields. In B. F. Caviness, editor, EUROCAL '85: European Conference on Computer Algebra Linz, Austria, April 1–3 1985 Proceedings Vol. 2: Research Contributions, pages 289–290. Springer Berlin Heidelberg, 1985.
S. Dellière. Triangularisation de systèmes constructibles : application à l'évaluation dynamique. PhD thesis, Université de Limoges. Faculté des sciences et techniques, 1999.
S. Dellière. On the links between triangular sets and dynamic constructible closure. J. Pure Appl. Algebra, 163(1):49–68, 2001.
C. Dicrescenzo and D. Duval. Algebraic extensions and algebraic closure in Scratchpad II. In P. Gianni, editor, Symbolic and Algebraic Computation. International Symposium ISSAC '88. Rome, Italy, July 4–8, 1988. Proceedings, number 358 in Lect. Notes Comput. Sci., pages 440–446. Springer-Verlag, 1989.
D. Duval. Rational Puiseux expansions. Compos. Math., 70(2):119–154, 1989.
D. Duval. Algebraic numbers: An example of dynamic evaluation. J. Symbolic Comput., 18(5):429–445, 1994.
D. Duval and L. González-Vega. Dynamic evaluation and real closure. Math. Comput. Simul., 42(4-6):551–560, 1996.
D. Duval and J.-C. Reynaud. Sketches and computation – II: dynamic evaluation and applications. Math. Structures Comput. Sci., 4(2):239–271, 1994.
H. Friedman. Algorithmic procedures, generalized Turing algorithms, and elementary recursion theory. In R. O. Gandy and C. M. E. Yates, editors, Logic Colloquium '69, volume 61 of Studies in Logic and the Foundations of Mathematics, pages 361–389. Elsevier, 1971.
A. Fröhlich and J. C. Shepherdson. On the factorisation of polynomials in a finite number of steps. Math. Z., 62:331–334, 1955.
A. Fröhlich and J. C. Shepherdson. Effective procedures in field theory. Philos. Trans. Roy. Soc. London. Ser. A., 248:407–432, 1956.
J. von zur Gathen and J. Gerhard. Modern computer algebra. Cambridge University Press, New York, 3rd edition, 2013.
T. Gómez-D
az.
Examples of using dynamic constructible closure. Math.
Comput. Simul., 42(4-6):375–383, 1996.
D. Harvey and J. van der Hoeven. Faster polynomial multiplication over finite fields using cyclotomic coefficient rings. J. Complexity, 54:101404, 2019.
D. Harvey, J. van der Hoeven, and G. Lecerf. Faster polynomial multiplication over finite fields. J. ACM, 63(6), 2017. Article 52.
J. van der Hoeven. Automatic asymptotics. PhD thesis, École polytechnique, Palaiseau, France, 1997.
J. van der Hoeven and G. Lecerf. Composition modulo powers of polynomials. In M. Blurr, editor, Proceedings of the 2017 ACM on International Symposium on Symbolic and Algebraic Computation, ISSAC '17, pages 445–452, New York, NY, USA, 2017. ACM.
J. van der Hoeven and G. Lecerf. Modular composition via complex roots. Technical report, CNRS & École polytechnique, 2017. http://hal.archives-ouvertes.fr/hal-01455731.
J. van der Hoeven and G. Lecerf. Modular composition via factorization. J. Complexity, 48:36–68, 2018.
J. van der Hoeven and G. Lecerf. Accelerated tower arithmetic. J. Complexity, 55:101402, 2019.
J. van der Hoeven and G. Lecerf. Fast multivariate multi-point evaluation revisited. J. Complexity, 56:101405, 2020.
Xiaohan Huang and V. Y. Pan. Fast rectangular matrix multiplication and applications. J. Complexity, 14(2):257–299, 1998.
E. Kaltofen. On computing determinants of matrices without divisions. In P. S. Wang, editor, ISSAC 92 International Symposium on Symbolic Algebraic Computation, ISSAC '92, pages 342–349, New York, NY, USA, 1992. ACM.
K. S. Kedlaya and C. Umans. Fast polynomial factorization and modular composition. SIAM J.Comput., 40(6):1767–1802, 2011.
F. Le Gall. Powers of tensors and fast matrix multiplication. In K. Nabeshima, editor, ISSAC'14: International Symposium on Symbolic and Algebraic Computation, pages 296–303, New York, NY, USA, 2014. ACM.
R. Lebreton. Relaxed Hensel lifting of triangular sets. J. Symbolic Comput., 68(2):230–258, 2015.
G. Lecerf. Computing the equidimensional decomposition of an algebraic closed set by means of lifting fibers. J. Complexity, 19(4):564–596, 2003.
G. Lecerf. On the complexity of the Lickteig–Roy subresultant algorithm. J. Symbolic Comput., 92:243–268, 2019.
A. Poteaux and É. Schost. Modular composition modulo triangular sets and applications. Comput. Complex., 22(3):463–516, 2013.
A. Poteaux and É. Schost. On the complexity of computing with zero-dimensional triangular sets. J. Symbolic Comput., 50:110–138, 2013.
F. P. Preparata and D. V. Sarwate. An improved parallel processor bound in fast matrix inversion. Inform. Process. Lett., 7(3):148–150, 1978.
J. C. Reynolds. The discoveries of continuations. LISP and Symbolic Computation, 6:233–247, 1993.
and a single input node. Let 
represent the 
then return 
is shown on the
right-hand side. The input node is a circle, computation nodes are
long rectangles, output nodes are shorter rectangles, and branching
nodes are diamond-shaped.
,
,
.
.
of
,
of 
,
,
is either zero or invertible in 
whenever 
.
.