Faster multi-point evaluation over any
field  |
|
| August 11, 2025 |
|
 . Grégoire
Lecerf has been supported by the French ANR-22-CE48-0016
NODE project. Joris van der Hoeven has been supported by an
ERC-2023-ADG grant for the ODELIX project (number 101142171).
. Grégoire
Lecerf has been supported by the French ANR-22-CE48-0016
NODE project. Joris van der Hoeven has been supported by an
ERC-2023-ADG grant for the ODELIX project (number 101142171).
Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. |
 |
 . This article has
been written using GNU TeXmacs [11].
. This article has
been written using GNU TeXmacs [11].
The evaluation of a polynomial at several points is called the problem of multi-point evaluation. We design new faster deterministic algorithms to solve this problem for an algebraic computational model. For this purpose, we analyze the precomputation costs of recent amortized evaluation algorithms, and then study the complexity of the problem as a function of the number of evaluation points.
|
Let  be an effective field, so that we have
algorithms for the field operations. Given a polynomial
be an effective field, so that we have
algorithms for the field operations. Given a polynomial 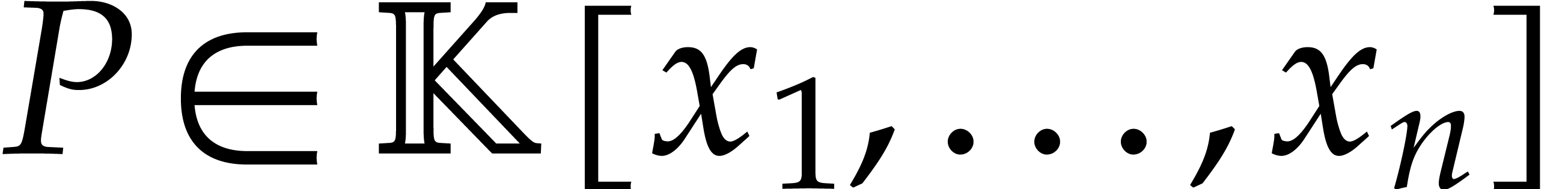 and a tuple
and a tuple 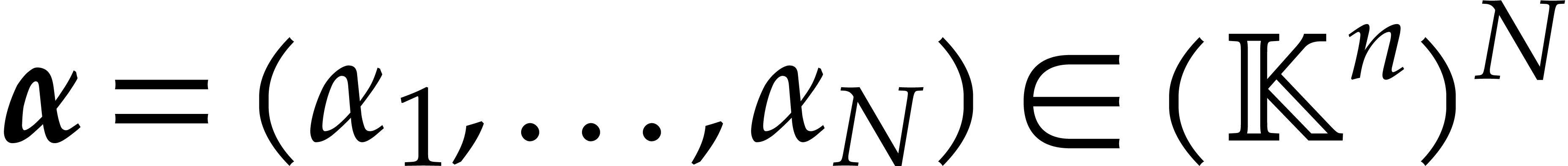 of points, the computation of
of points, the computation of  is called the problem of multi-point
evaluation. The converse problem is called interpolation
and takes a candidate support of
is called the problem of multi-point
evaluation. The converse problem is called interpolation
and takes a candidate support of 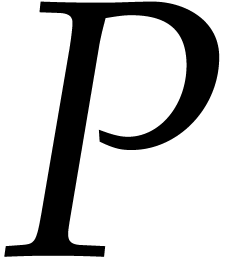 as input.
as input.
These problems naturally occur in several areas of applied algebra. For
instance in [16], we have shown that fast multi-point
evaluation leads to fast polynomial system solving. Multi-point
evaluation with a large number of variables also leads to fast modular
composition [20]. The more specific bivariate case 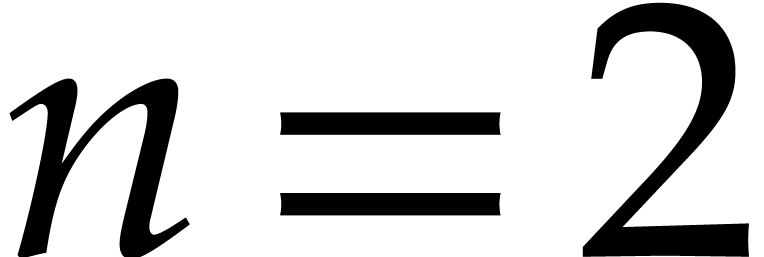 appears for example in the computation of generator
matrices of algebraic geometry error correcting codes [21].
appears for example in the computation of generator
matrices of algebraic geometry error correcting codes [21].
The problem of multi-point evaluation is typically studied in the case
when  , where
, where  is the total degree of
is the total degree of 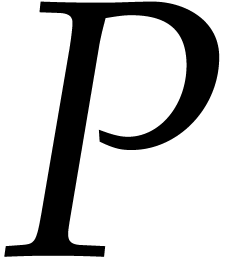 . One
particularity of this paper is that, besides this classical case, we
also study the complexity when
. One
particularity of this paper is that, besides this classical case, we
also study the complexity when 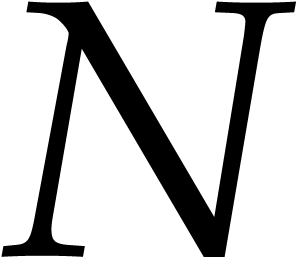 and
and 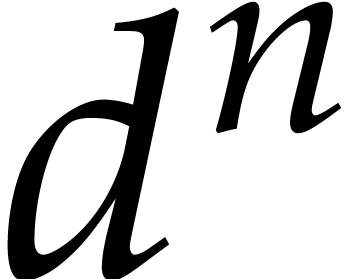 have different orders of magnitude. Especially in the case
when
have different orders of magnitude. Especially in the case
when 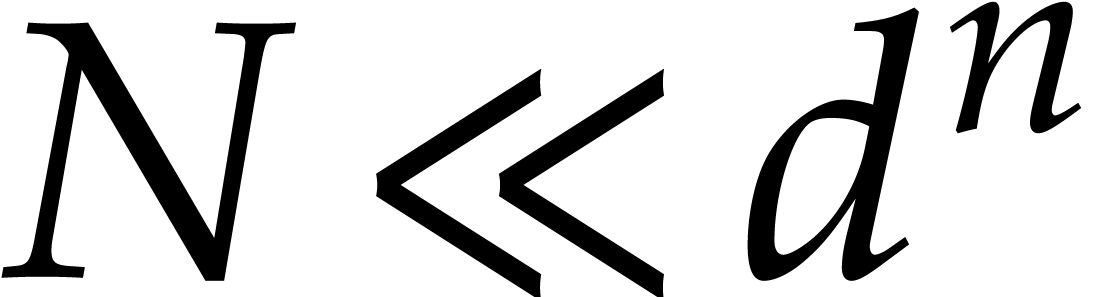 , our recent work [14, 17] on amortized multi-point
evaluation (when the set of points is fixed) turns out to be very
useful; this application was also one of our motivations for the present
work.
, our recent work [14, 17] on amortized multi-point
evaluation (when the set of points is fixed) turns out to be very
useful; this application was also one of our motivations for the present
work.
In this paper, the number 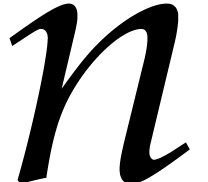 of variables is always
assumed to be fixed, so the constants hidden in the “
of variables is always
assumed to be fixed, so the constants hidden in the “ ” of our complexity bounds depend on
” of our complexity bounds depend on
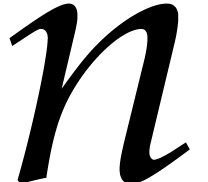 . For complexity analyses, we
will only consider algebraic complexity models like computation trees or
RAM machines [5]. The time complexity then measures the
number of arithmetic operations and zero-tests in
. For complexity analyses, we
will only consider algebraic complexity models like computation trees or
RAM machines [5]. The time complexity then measures the
number of arithmetic operations and zero-tests in  . The soft-Oh notation
. The soft-Oh notation 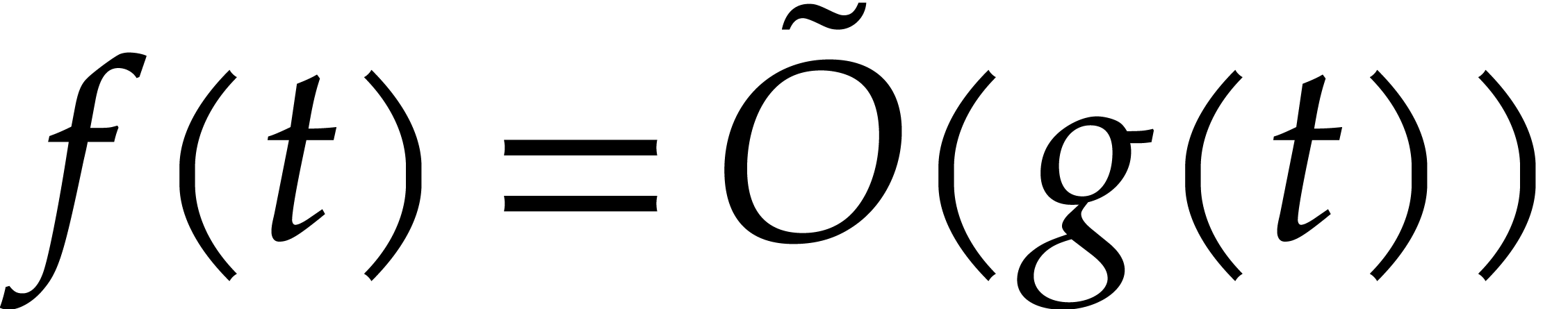 is a shorthand for
is a shorthand for 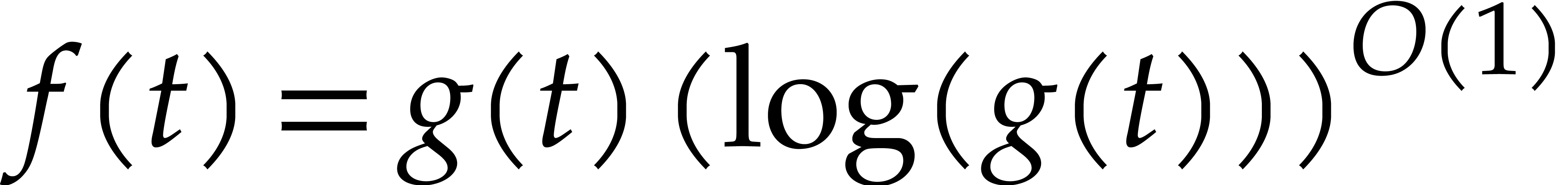 ; see [9, chapter 25, section 7] for technical details.
; see [9, chapter 25, section 7] for technical details.
The constant  will denote a real value between
will denote a real value between
 and
and  such that two
such that two  matrices over a commutative ring can be multiplied
with
matrices over a commutative ring can be multiplied
with 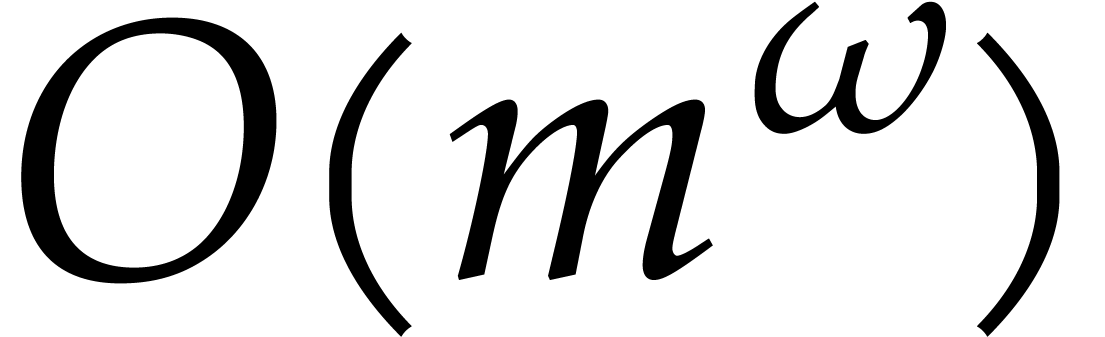 ring operations. The current best known
bound is
ring operations. The current best known
bound is 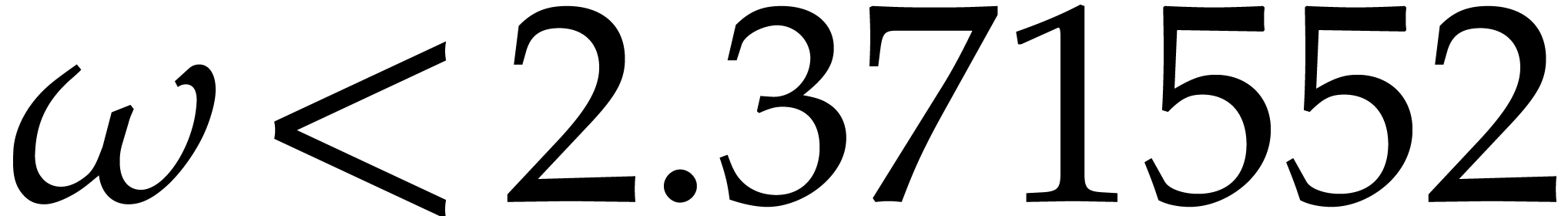 [30]. The constant
[30]. The constant 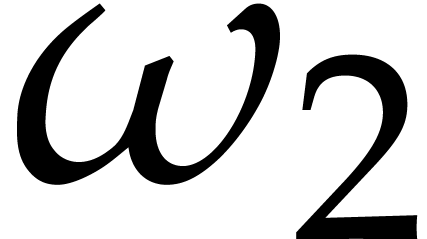 will be a real value between 3 and 4 such that the
product of a
will be a real value between 3 and 4 such that the
product of a 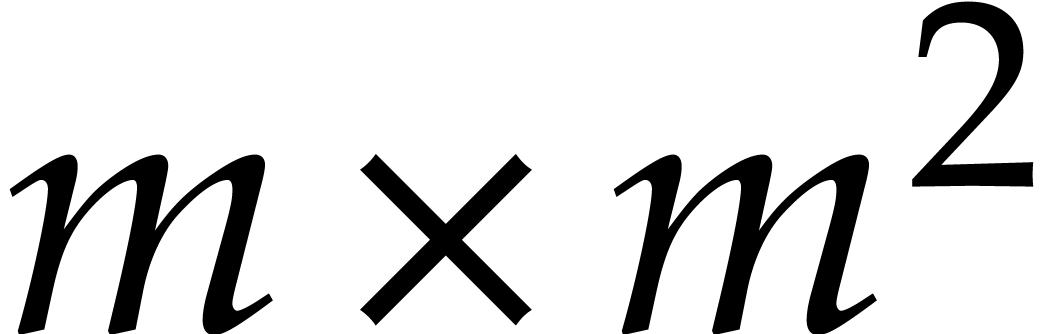 matrix by a
matrix by a 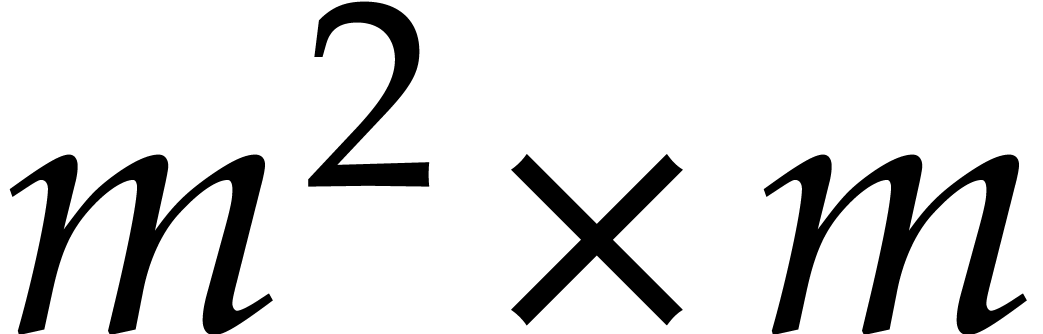 matrix takes
matrix takes 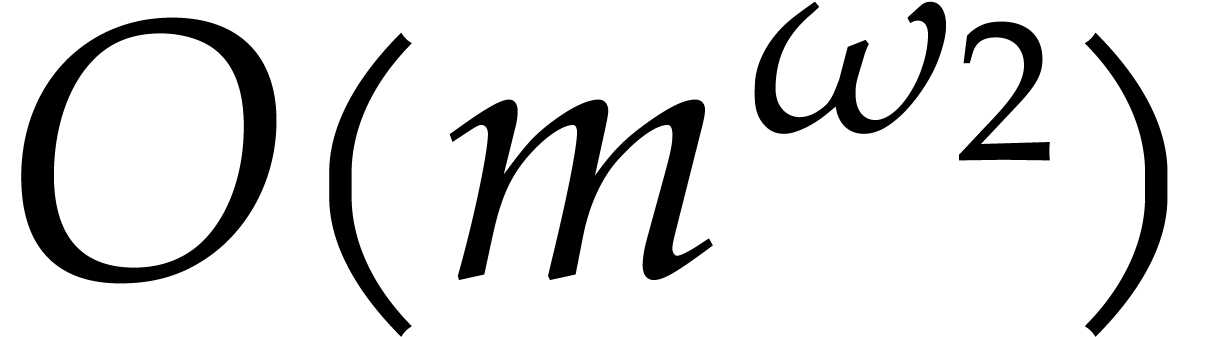 operations; one may take
operations; one may take 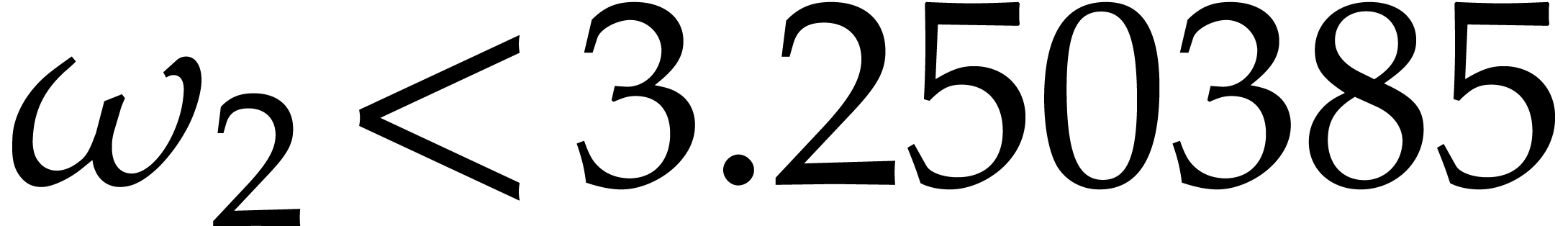 [30].
[30].
The first line of results, presented in section 2, concerns
the derandomization of the Nüsken–Ziegler algorithm [26].
When  our new deterministic bound coincides with
their probabilistic one; see Theorem 2.6. For
our new deterministic bound coincides with
their probabilistic one; see Theorem 2.6. For 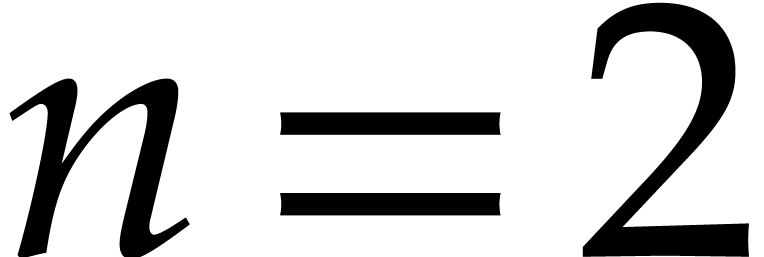 our deterministic evaluation in degree
our deterministic evaluation in degree  at
at 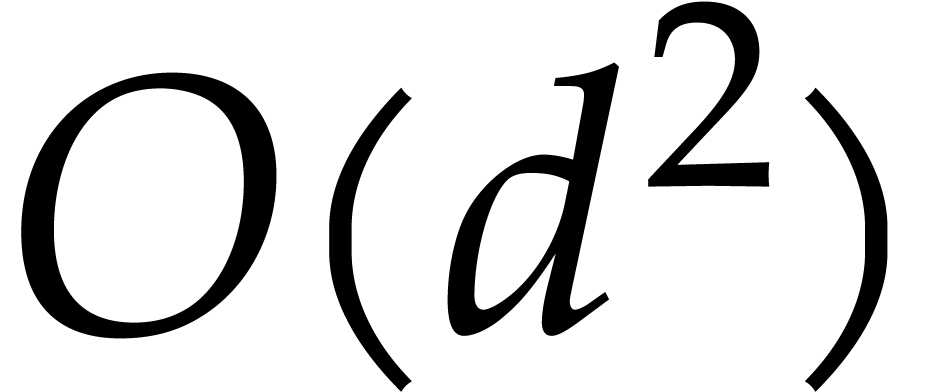 points costs
points costs 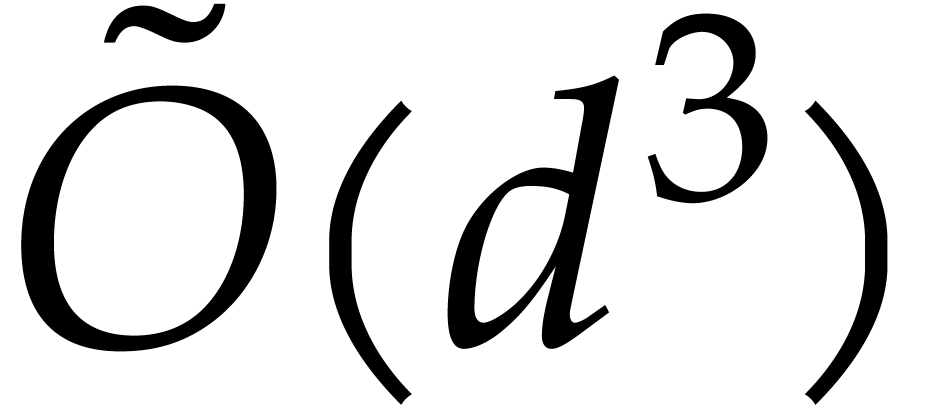 operations in
operations in  , whereas the
probabilistic version of [26] takes
, whereas the
probabilistic version of [26] takes 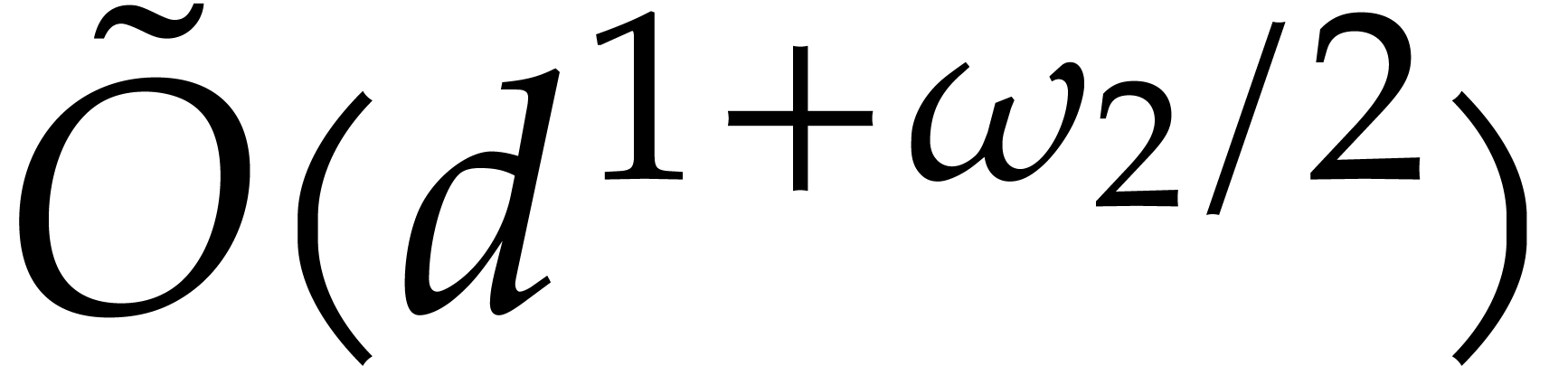 , which tends to
, which tends to 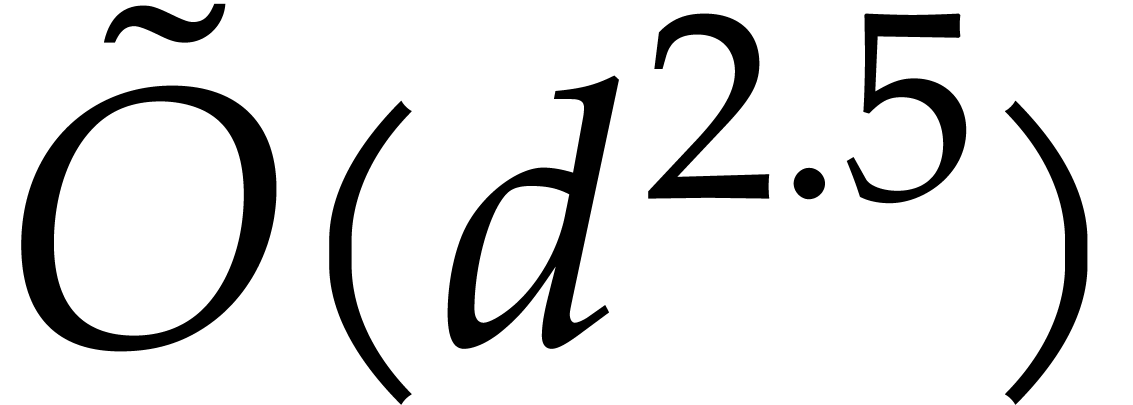 when
when 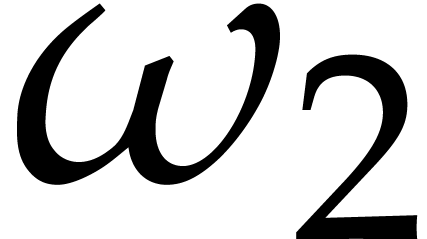 tends to the lower bound
tends to the lower bound 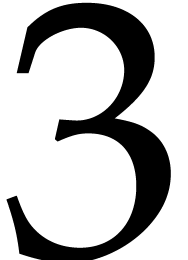 ; see Theorems 2.7 and 2.8,
and Remark 2.4.
; see Theorems 2.7 and 2.8,
and Remark 2.4.
In section 3 we turn to the amortized multi-point
evaluation of multivariate polynomials. For such algorithms, the set of
evaluation points is fixed, so we may use potentially expensive
precomputations as a function of these points. A softly optimal
algorithm for amortized multi-point evaluation was first given in [17]. Still in section 3 we provide a careful
analysis of the cost of the precomputations. Building on algorithms from
[23], it turns out that this can be done with a complexity
exponent below the one of linear algebra: see Lemma 3.6. We
next use this to derive our main complexity bounds for non-amortized
multi-point evaluation: Theorems 3.9 and 3.13.
The latter theorem slightly improves upon the Nüsken–Ziegler
algorithm when 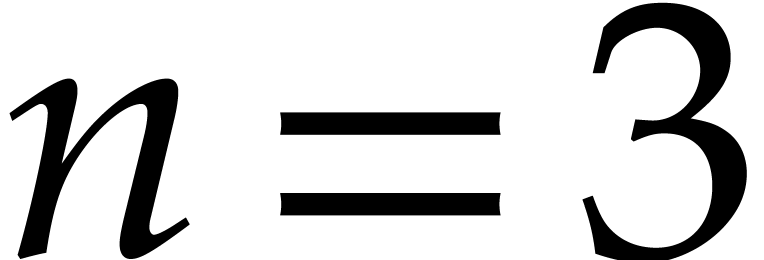 or
or  ;
see Remark 3.16 for details. We also show that the
evaluation at
;
see Remark 3.16 for details. We also show that the
evaluation at 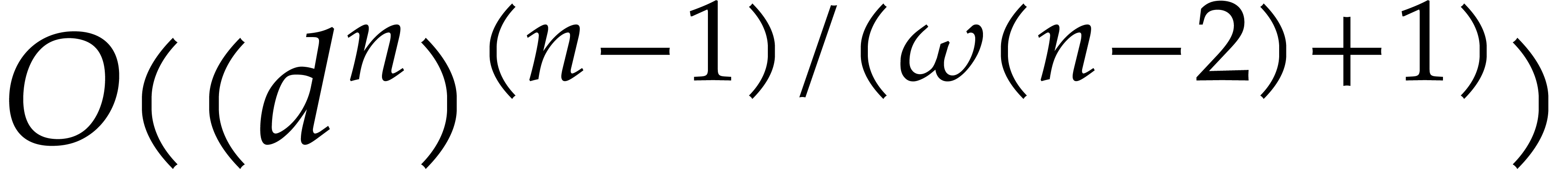 points can be performed in softly
linear time, which again improves upon the Nüsken–Ziegler
algorithm.
points can be performed in softly
linear time, which again improves upon the Nüsken–Ziegler
algorithm.
If 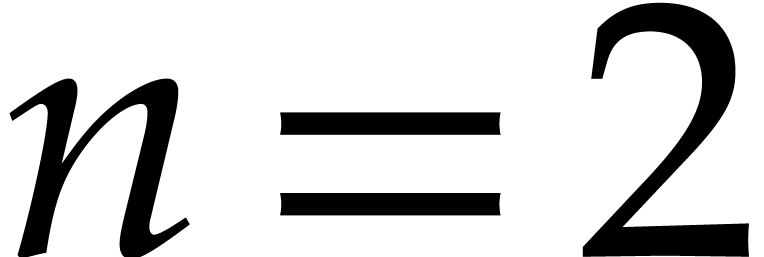 , then Theorem 3.9
also improves on our deterministic version of the
Nüsken–Ziegler algorithm from Theorem 2.7; see
Remark 3.10. The comparison with the randomized version is
given in Remark 3.11.
, then Theorem 3.9
also improves on our deterministic version of the
Nüsken–Ziegler algorithm from Theorem 2.7; see
Remark 3.10. The comparison with the randomized version is
given in Remark 3.11.
Most of our new complexity bounds rely on theoretical complexity bounds for matrix multiplication, which are known to be hard to observe in practice. Consequently, we do not expect our bounds to lead to competitive software implementations. On the other hand, we expect that our deterministic version of the Nüsken–Ziegler algorithm may be implemented in a practically efficient way.
In order to design the above deterministic algorithms for any effective
field  , we frequently need to
assume that the cardinality of
, we frequently need to
assume that the cardinality of  is sufficiently
large or that we explicitly know an element of a sufficiently large
multiplicative order. This subtlety only concerns finite fields and is
usually addressed by computing over an algebraic extension of
is sufficiently
large or that we explicitly know an element of a sufficiently large
multiplicative order. This subtlety only concerns finite fields and is
usually addressed by computing over an algebraic extension of  . Since we work over an arbitrary
effective field in this paper, we need to deal with this extension issue
in detail. In particular, we may not assume that the cardinality or
characteristic of
. Since we work over an arbitrary
effective field in this paper, we need to deal with this extension issue
in detail. In particular, we may not assume that the cardinality or
characteristic of  are known. In Appendix A, we present a general way to address these issues. Our
solution can be implemented with programming languages that support
generic programming, such as
are known. In Appendix A, we present a general way to address these issues. Our
solution can be implemented with programming languages that support
generic programming, such as
Achieving quasi-linear complexity for the general problem of
multivariate multi-point evaluation seems to be difficult. If 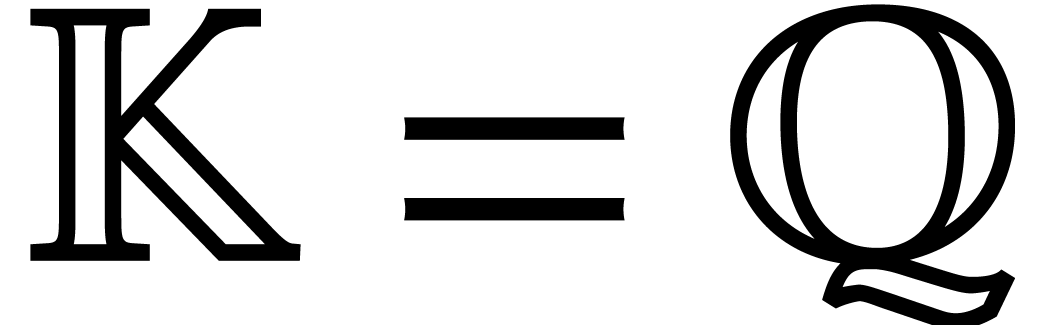 or
or  is a field of finite
characteristic, then algorithms due to Kedlaya and Umans [20]
achieve a complexity exponent
is a field of finite
characteristic, then algorithms due to Kedlaya and Umans [20]
achieve a complexity exponent  ,
where
,
where 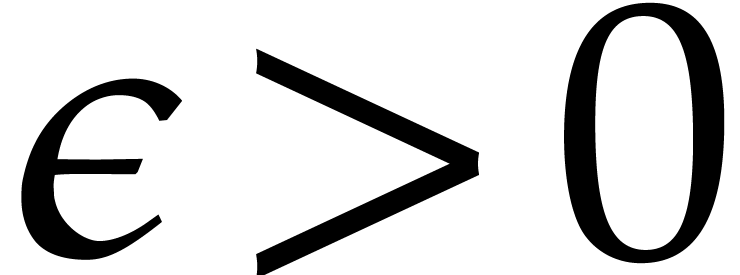 is a constant that can be taken
arbitrarily close to zero. Unfortunately, to our best knowledge, these
algorithms do not seem suitable for practical purposes [13,
Conclusion]. Recent advances in this vein are to be found in [2,
3].
is a constant that can be taken
arbitrarily close to zero. Unfortunately, to our best knowledge, these
algorithms do not seem suitable for practical purposes [13,
Conclusion]. Recent advances in this vein are to be found in [2,
3].
The best previously known complexity bound for 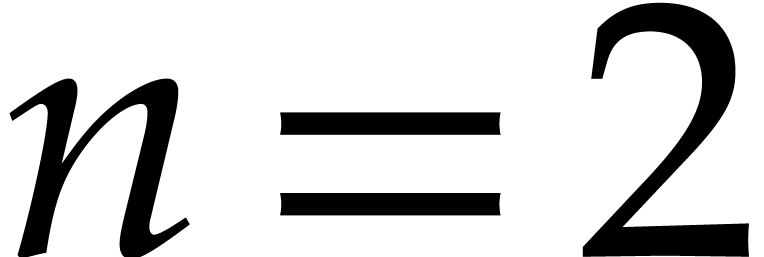 and for general fields and input is due to Nüsken and Ziegler [26]: the evaluation of
and for general fields and input is due to Nüsken and Ziegler [26]: the evaluation of  at
at 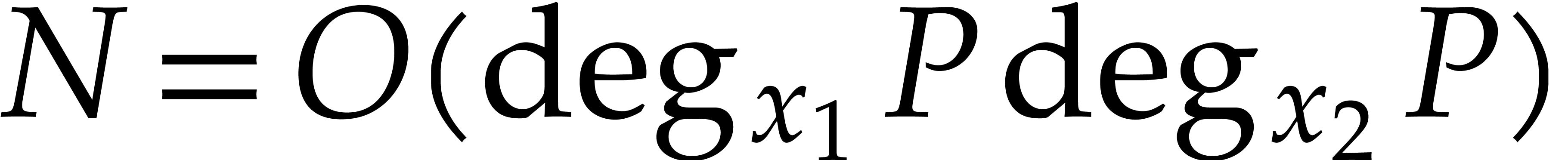 points can be done using
points can be done using 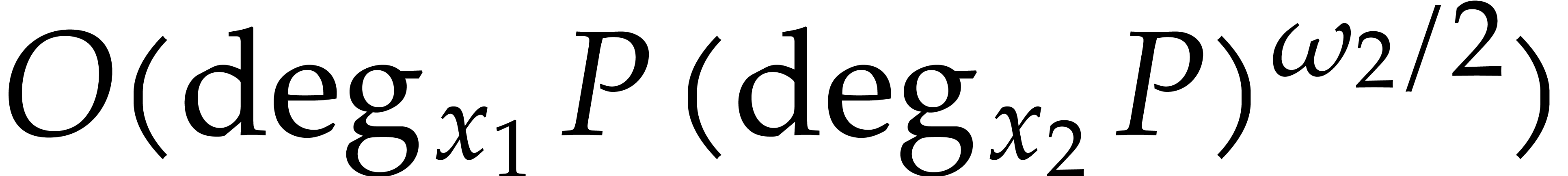 operations in
operations in  , assuming that
the
, assuming that
the  -coordinates of the
points are pairwise distinct. So, for
-coordinates of the
points are pairwise distinct. So, for 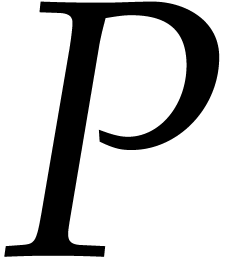 of total
degree
of total
degree  , the cost is an
expected number of
, the cost is an
expected number of 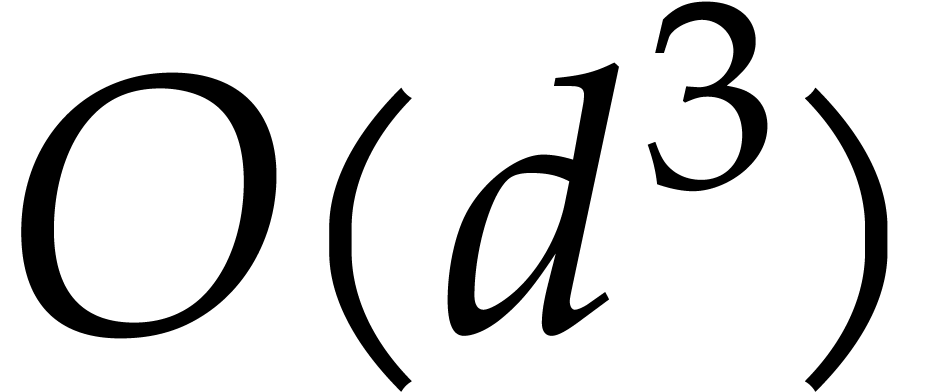 operations in
operations in  , that equals
, that equals 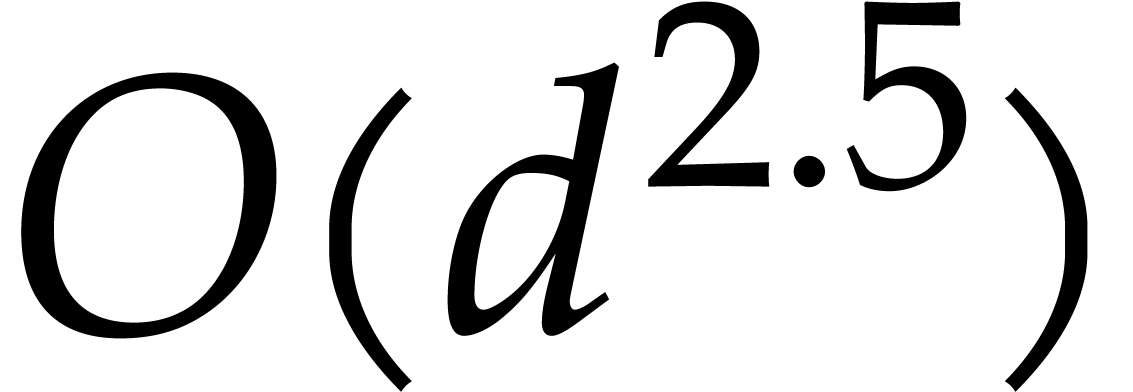 without
fast linear algebra, and that tends to
without
fast linear algebra, and that tends to  when
when 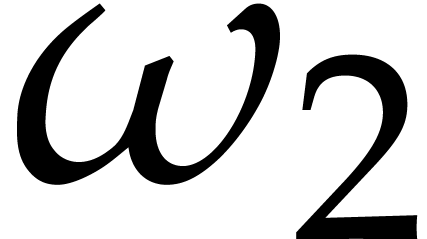 tends to
tends to 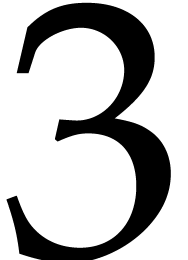 .
We further mention [19] for efficient algorithms for
special sets of points
.
We further mention [19] for efficient algorithms for
special sets of points  .
.
Another recent result for any field  ,
and for
,
and for 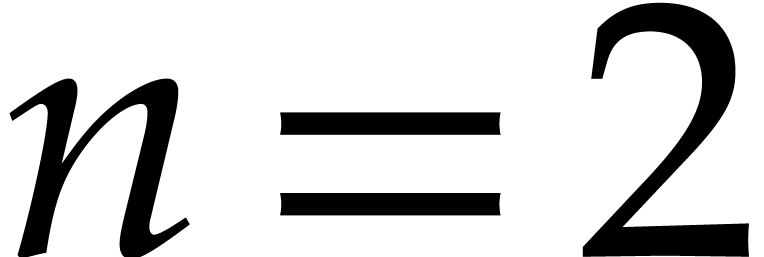 , is due to Neiger,
Salvy, Schost, and Villard [25]. Their algorithm is derived
from their fast modular composition algorithm. Given
, is due to Neiger,
Salvy, Schost, and Villard [25]. Their algorithm is derived
from their fast modular composition algorithm. Given  ,
,  ,
and
,
and 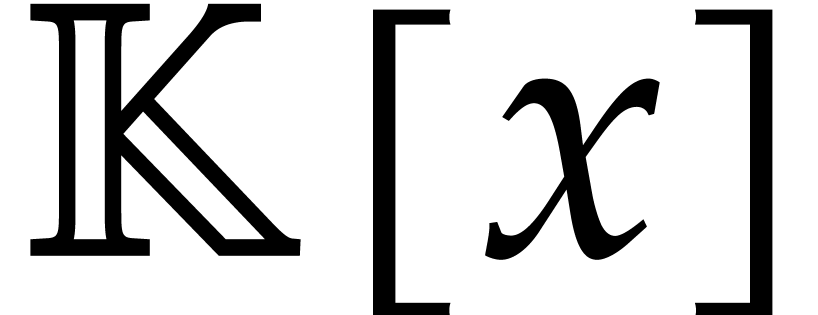 in
in  of degree
of degree  , they show how to compute the
polynomial
, they show how to compute the
polynomial 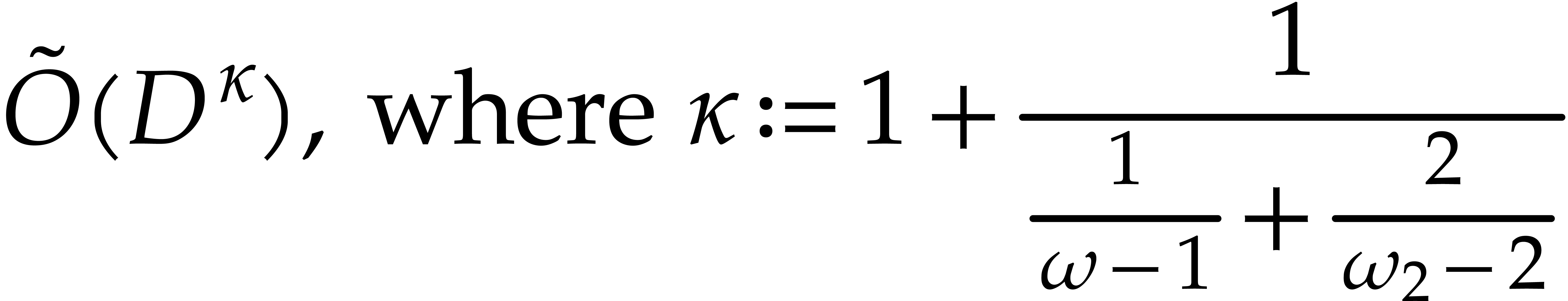 by a probabilistic algorithm of Las
Vegas type using an expected number of
by a probabilistic algorithm of Las
Vegas type using an expected number of

operations in  ; see [25,
Theorem 1.1]. Then the bivariate evaluation problem reduces to modular
composition in the following way. First, up to a sufficiently generic
linear change of the coordinates, there exist
; see [25,
Theorem 1.1]. Then the bivariate evaluation problem reduces to modular
composition in the following way. First, up to a sufficiently generic
linear change of the coordinates, there exist  of
degree
of
degree 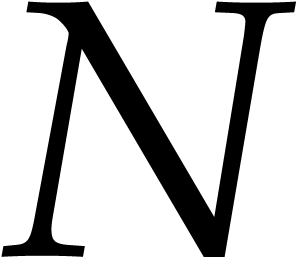 and
and 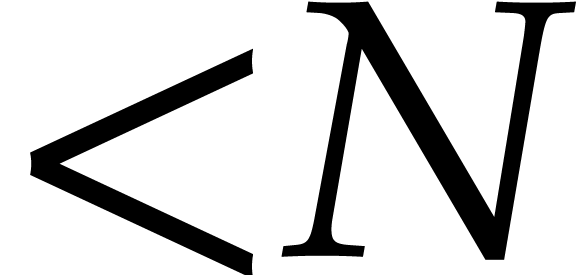 of degree
of degree
 such that
such that 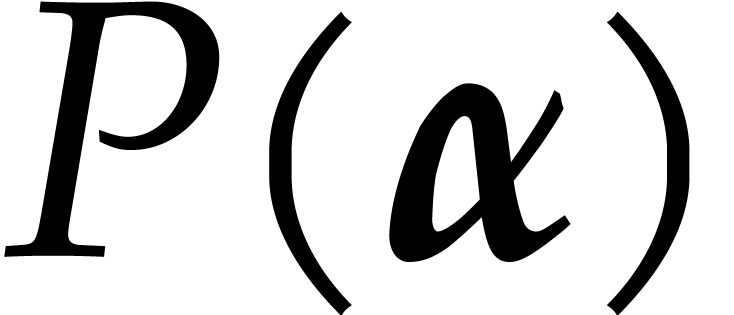 ,
so
,
so 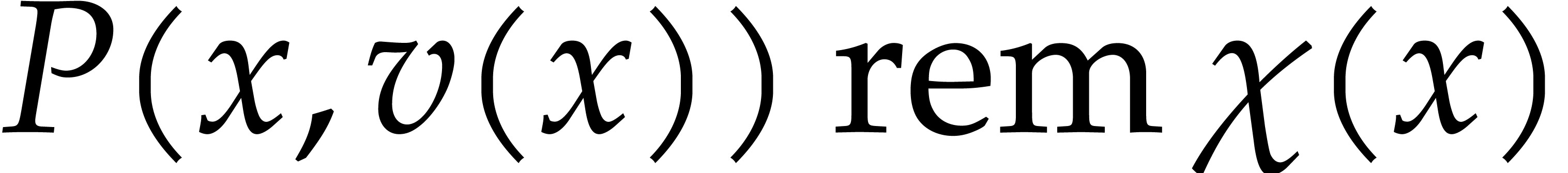 can easily be recovered from
can easily be recovered from 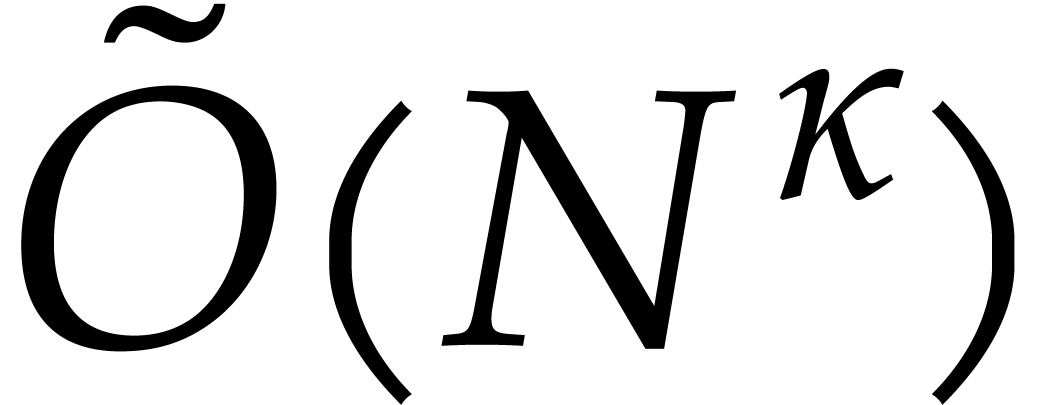 . In [25, section 10.3] it is
shown that
. In [25, section 10.3] it is
shown that 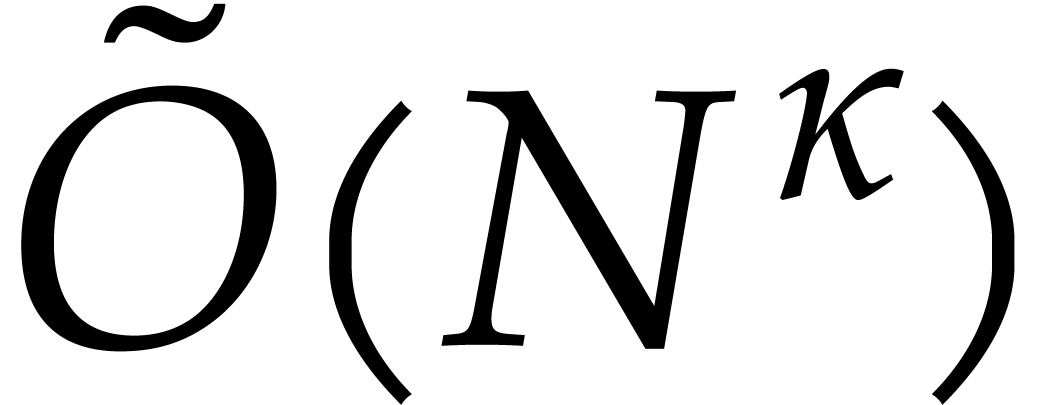 can be computed using
can be computed using 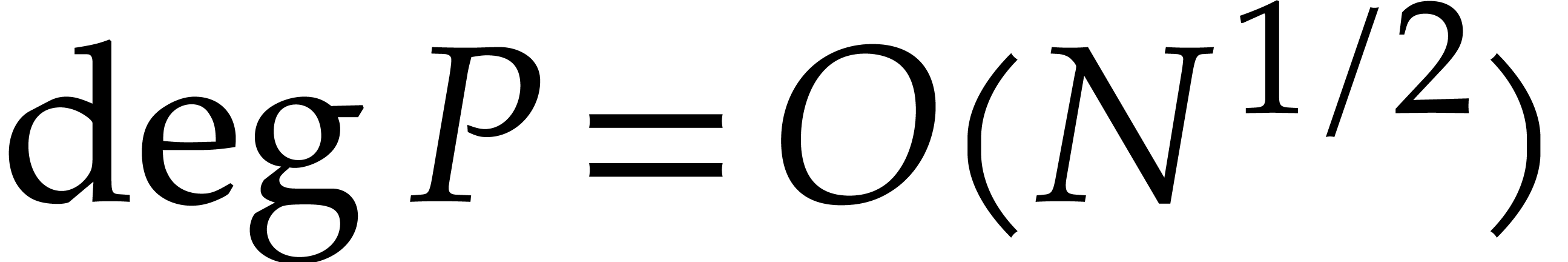 operations in
operations in  ,
whenever
,
whenever 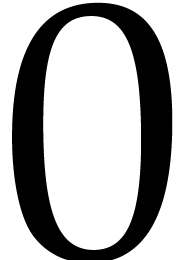 ,
,  has characteristic
has characteristic 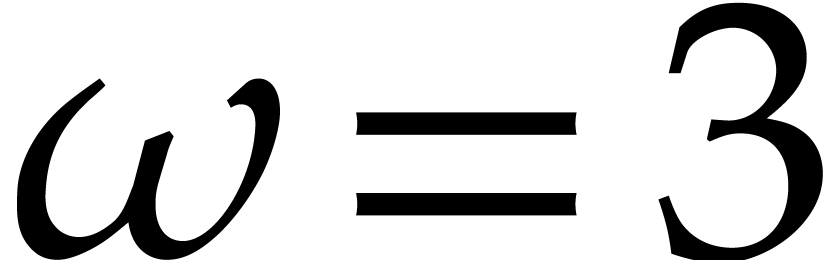 , and the
input is sufficiently generic. Without fast linear algebra, that is when
, and the
input is sufficiently generic. Without fast linear algebra, that is when
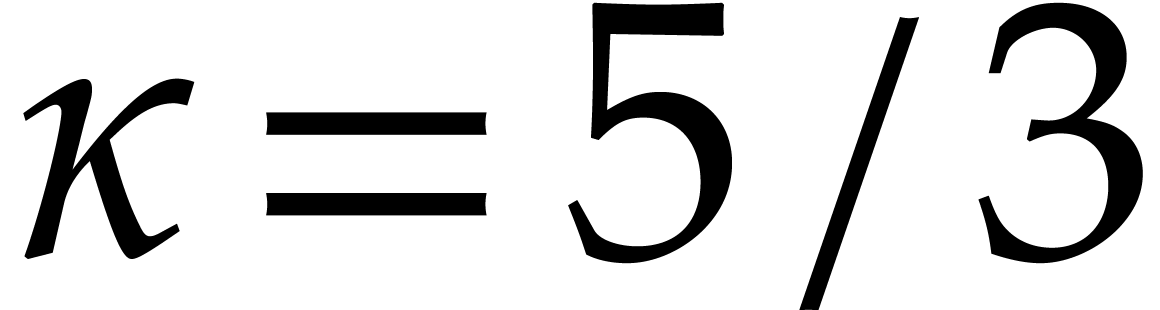 , one has
, one has  . With the best known value for
. With the best known value for 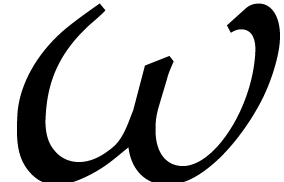 , one has
, one has  .
If
.
If 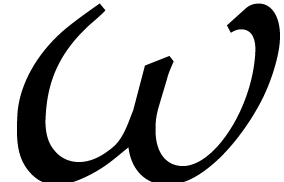 and
and 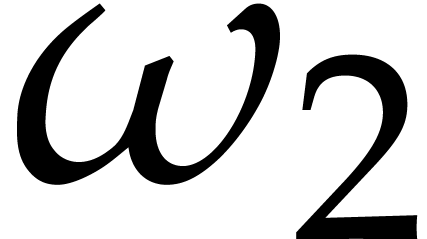 tend to their
trivial lower bounds
tend to their
trivial lower bounds  and 3, then
and 3, then 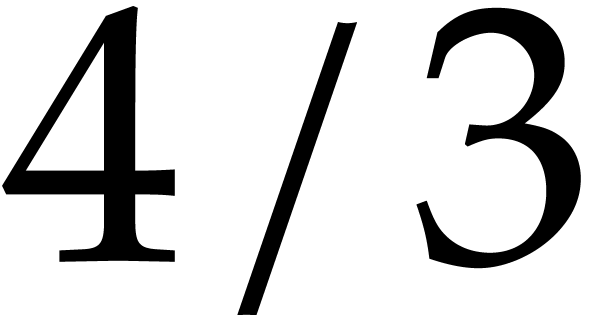 tends to
tends to 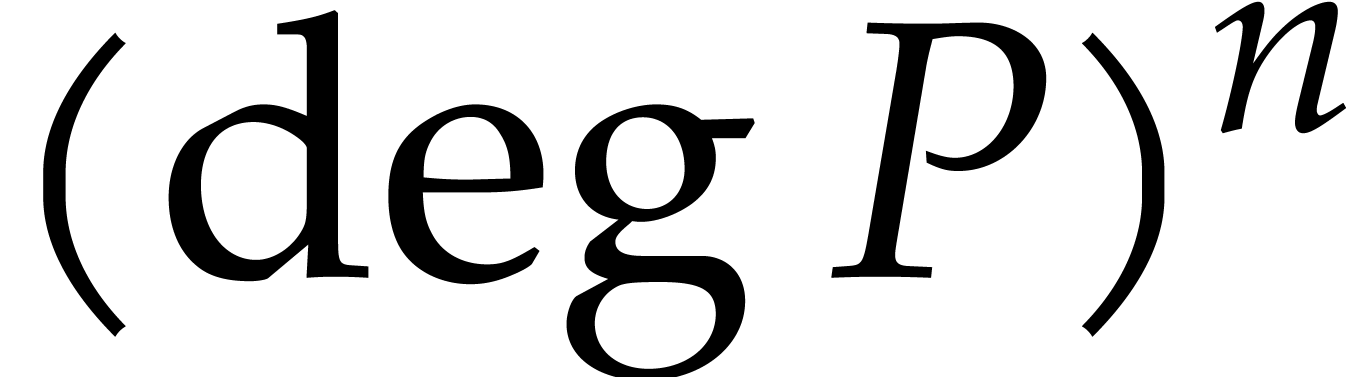 .
.
In recent years, softly linear time has been achieved for multi-point
evaluation and interpolation when  is a fixed
generic tuple of points [15, 24]. These
algorithms are amortized in the sense that potentially
expensive precomputations as a function of
is a fixed
generic tuple of points [15, 24]. These
algorithms are amortized in the sense that potentially
expensive precomputations as a function of  are
allowed. When the dimension
are
allowed. When the dimension 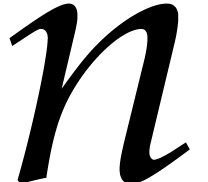 is arbitrary but
fixed, the amortized algorithms from [15] generalize the
classical univariate “divide and conquer” approach, as
presented for instance in [9, chapter 10]. The results in
[24] restrict to the case
is arbitrary but
fixed, the amortized algorithms from [15] generalize the
classical univariate “divide and conquer” approach, as
presented for instance in [9, chapter 10]. The results in
[24] restrict to the case 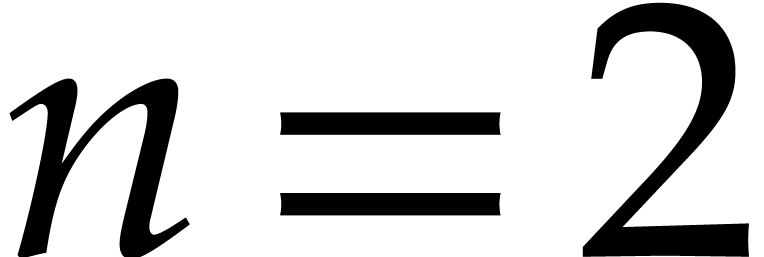 .
They take into account the partial degrees of
.
They take into account the partial degrees of  and are based on changes of polynomial bases that are similar to the
ones of [12, section 6.2].
and are based on changes of polynomial bases that are similar to the
ones of [12, section 6.2].
The article [14] handles arbitrary (i.e. possibly
non-generic) tuples of evaluation points  ,
while restricting to the amortized bivariate case
,
while restricting to the amortized bivariate case 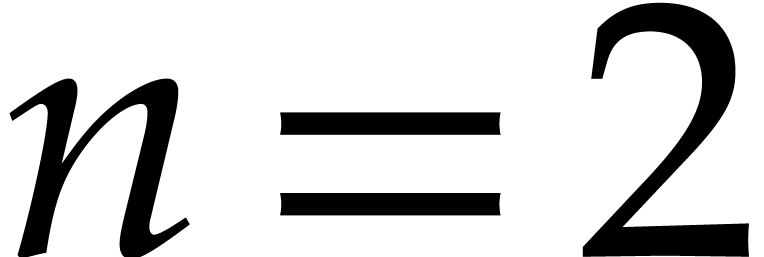 and
and 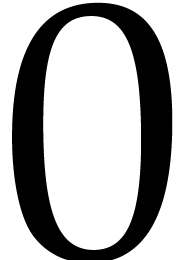 . New techniques for
general dimensions
. New techniques for
general dimensions 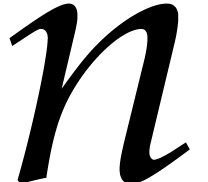 were presented in [17].
In the present paper we analyze the cost of the precomputations needed
in [17]. This is key for our improved complexity bounds for
non-amortized multi-point evaluation, especially when
were presented in [17].
In the present paper we analyze the cost of the precomputations needed
in [17]. This is key for our improved complexity bounds for
non-amortized multi-point evaluation, especially when  is substantially smaller than
is substantially smaller than  .
.
Throughout this paper, we assume the dimension 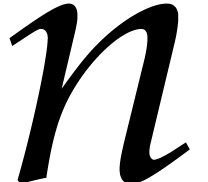 to be fixed. So the constants hidden in the
to be fixed. So the constants hidden in the  of
the complexity estimates will depend on
of
the complexity estimates will depend on 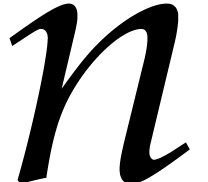 .
We recall that
.
We recall that 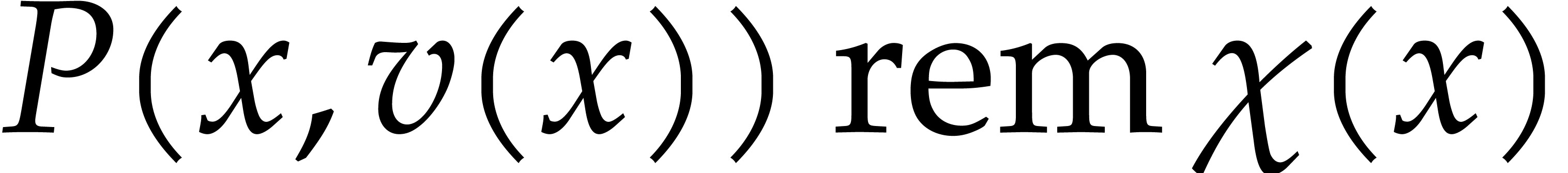 denotes the tuple of values
denotes the tuple of values 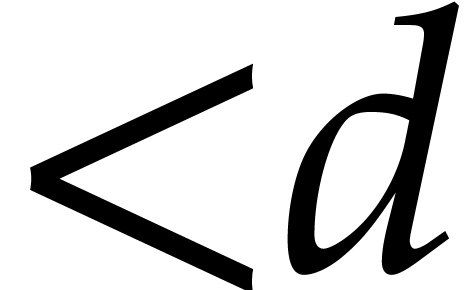 . The
. The  -vector
space of the polynomials of total degree
-vector
space of the polynomials of total degree 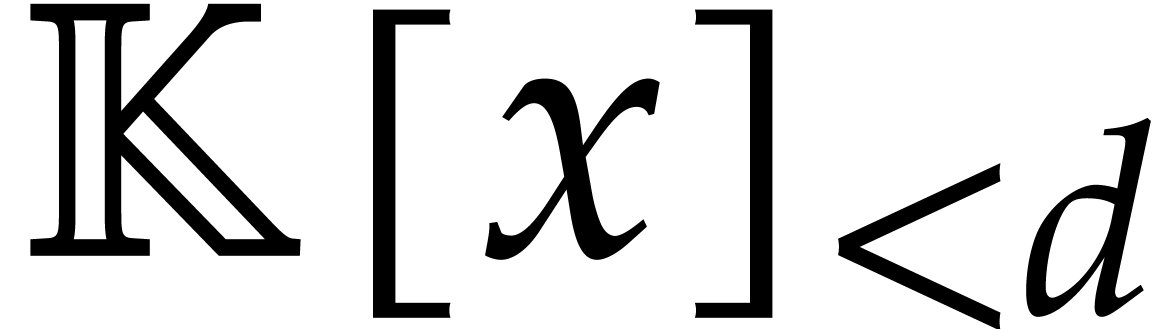 in
in  will be written
will be written  .
The cardinality of
.
The cardinality of  is written
is written  .
.
We denote by  the time that is needed to compute
a product
the time that is needed to compute
a product 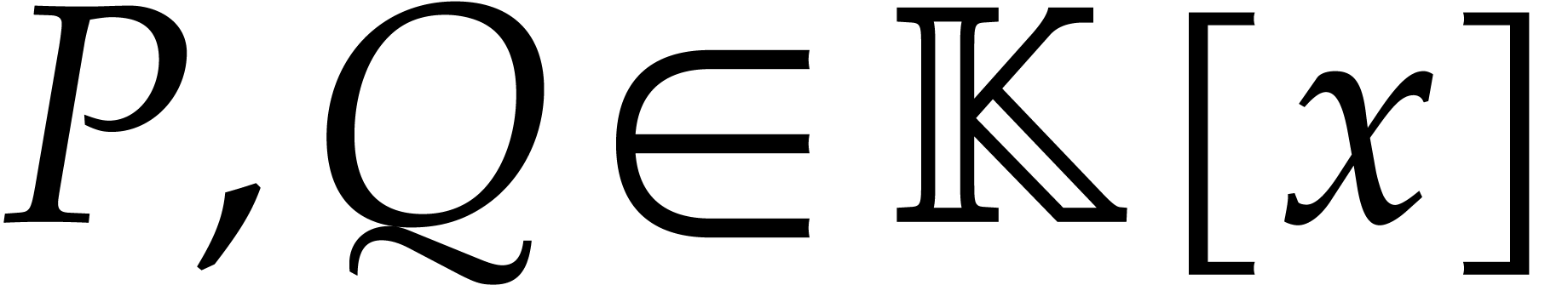 of two polynomials
of two polynomials 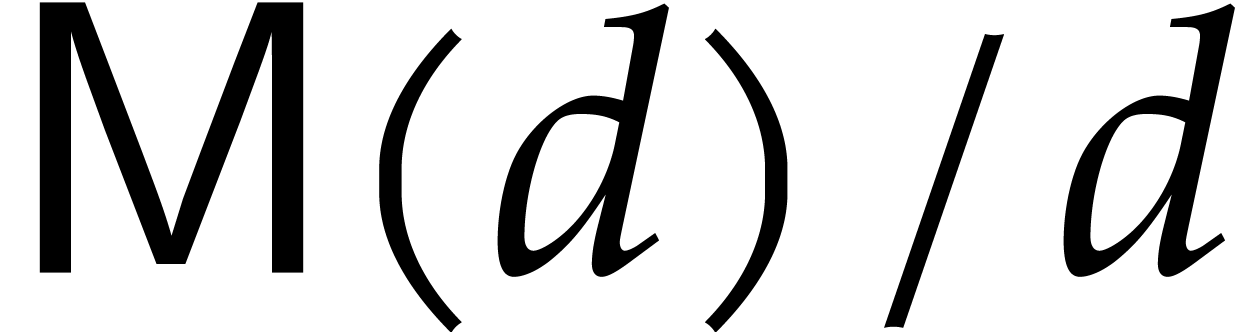 of degree
of degree 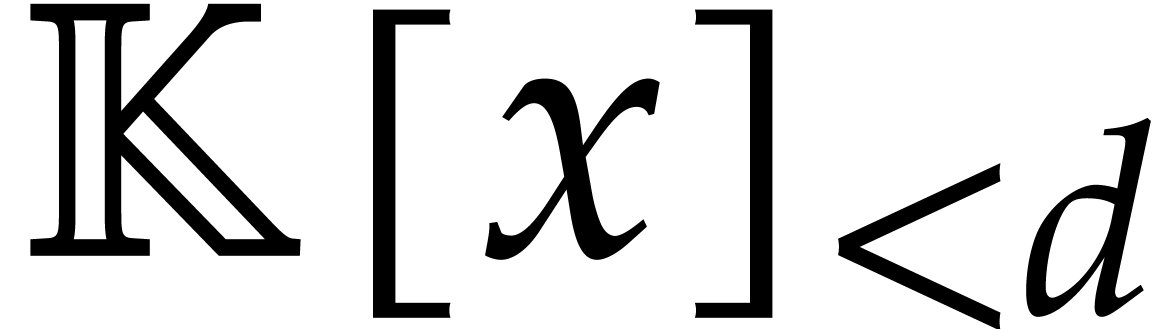 . We make the usual
assumptions that
. We make the usual
assumptions that  is non-decreasing as a function
of
is non-decreasing as a function
of  and that
and that  whenever
whenever
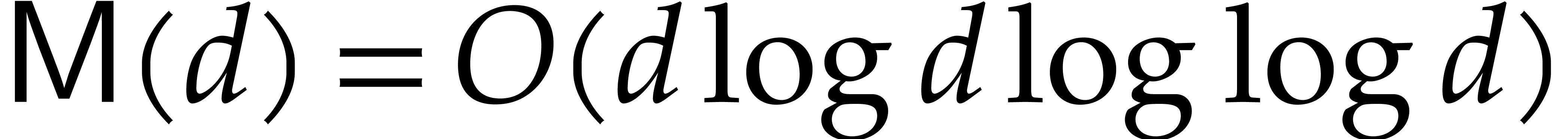 . Using a variant of the
Schönhage–Strassen algorithm [6], it is well
known that
. Using a variant of the
Schönhage–Strassen algorithm [6], it is well
known that 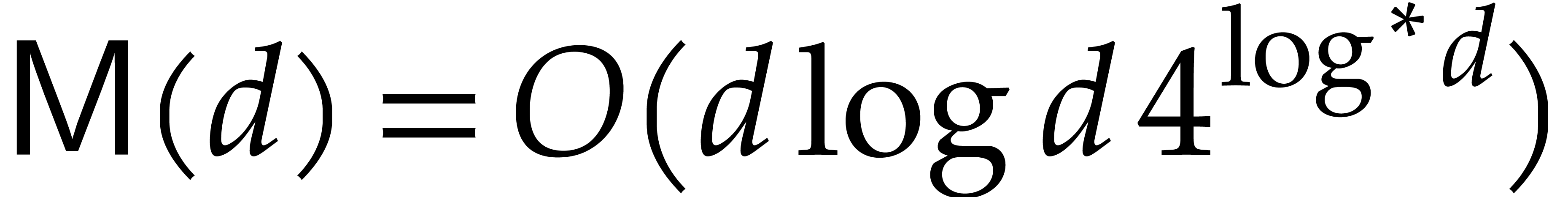 . If we restrict
our attention to fields
. If we restrict
our attention to fields  of positive
characteristic, then we may even take
of positive
characteristic, then we may even take 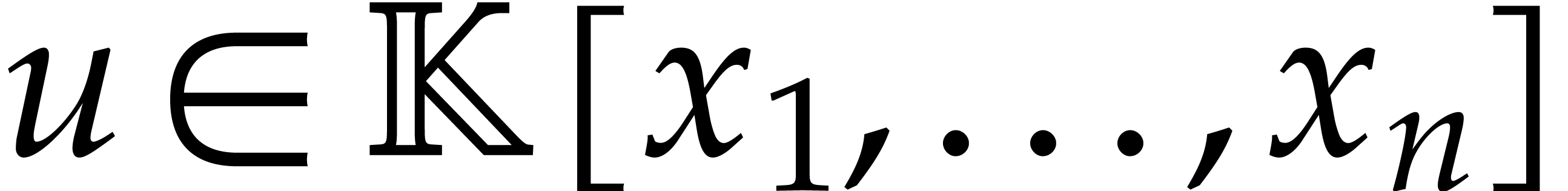 [10],
where
[10],
where  denotes the iterated logarithm.
denotes the iterated logarithm.
A linear form  is said to
separate the points
is said to
separate the points  if it takes
pairwise different values at pairwise different points of
if it takes
pairwise different values at pairwise different points of  . It will often be convenient to split
. It will often be convenient to split  into non-empty subsequences
into non-empty subsequences  . A joined separating form for
. A joined separating form for  is a separating form for each
is a separating form for each  for
for 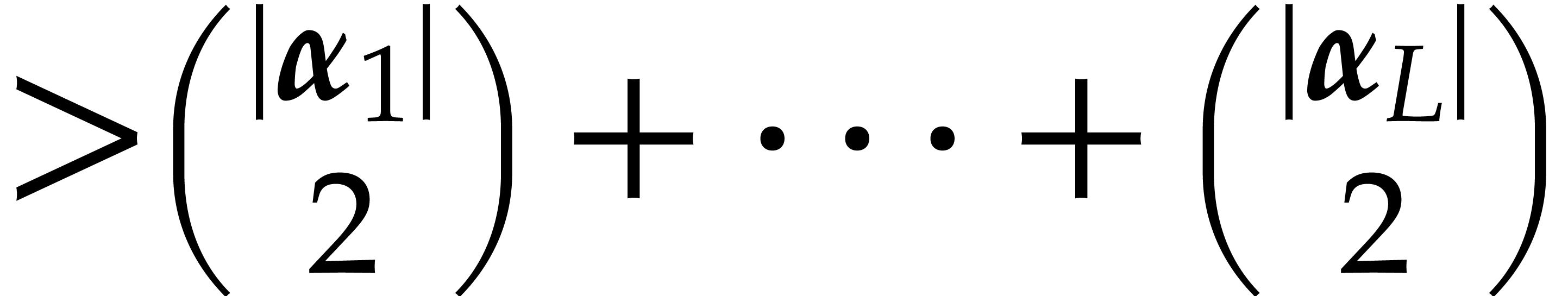 . It may be computed as
follows.
. It may be computed as
follows.
 be a set of
be a set of  elements in
elements in  . We can
compute a joined separating form
. We can
compute a joined separating form 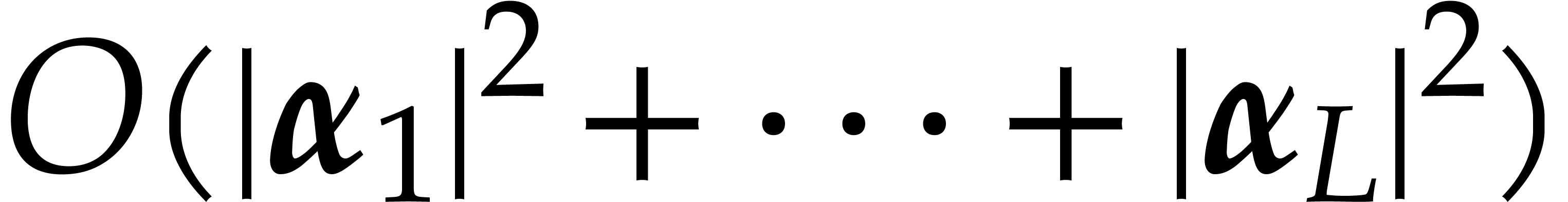 for
for  with
with  using
using
operations in  .
.
Proof. Recall that  is
constant. We proceed by induction on
is
constant. We proceed by induction on  .
If
.
If 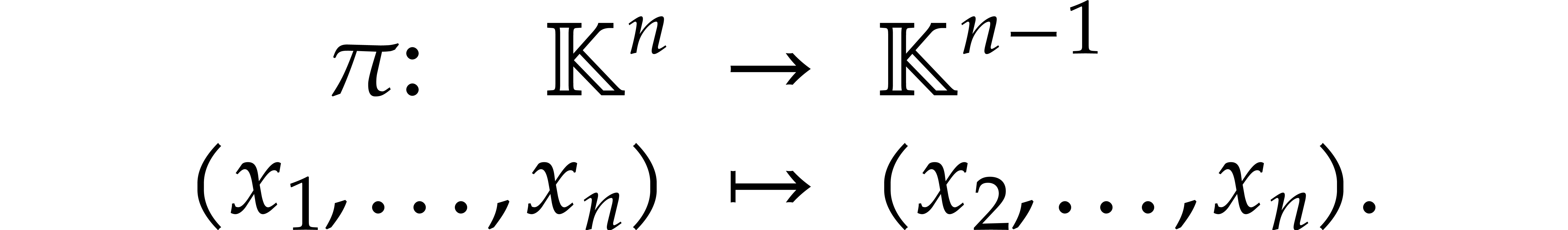 then the proof is immediate. Assume that
then the proof is immediate. Assume that 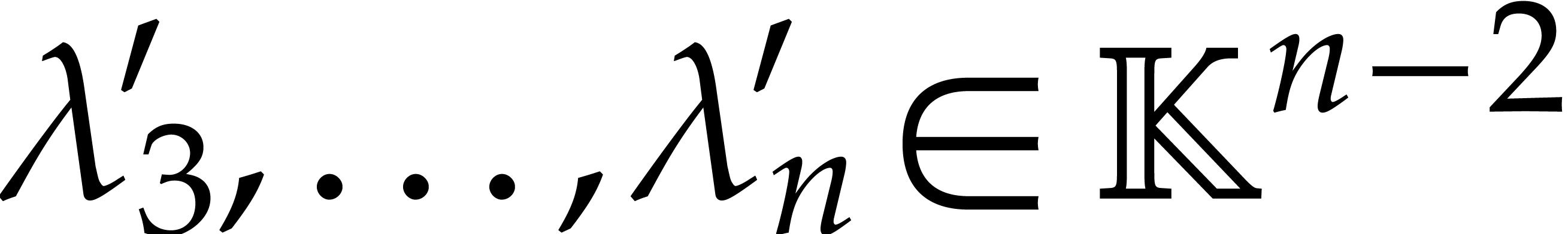 and let
and let
By the induction hypothesis, we may compute 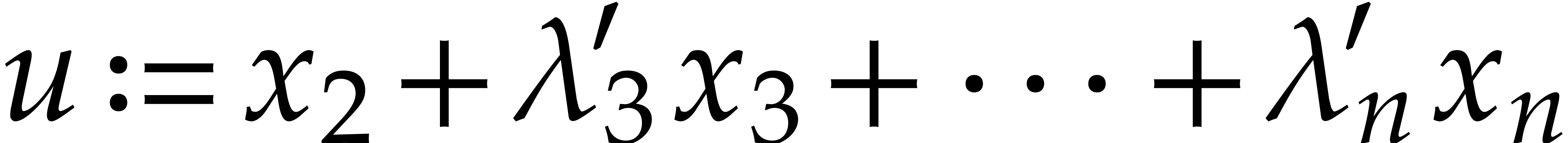 in
time
in
time  , such that
, such that  is a joined separating form for
is a joined separating form for 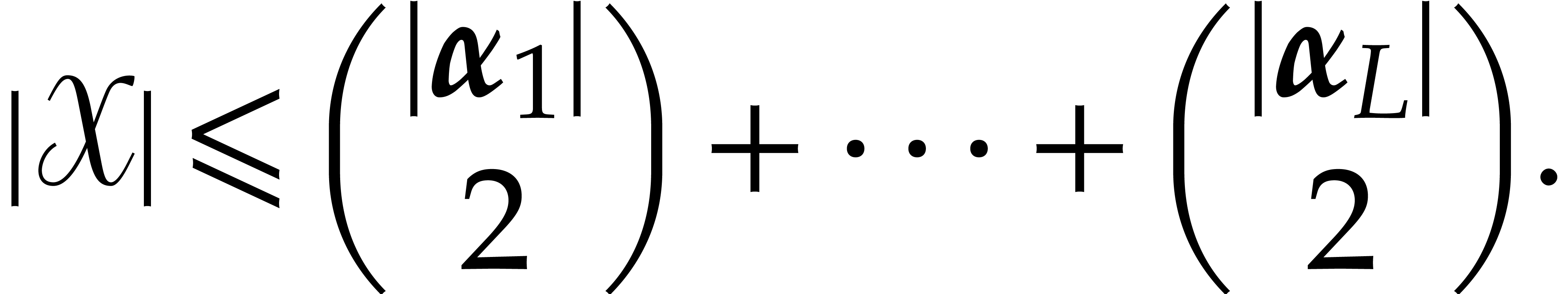 . Let
. Let
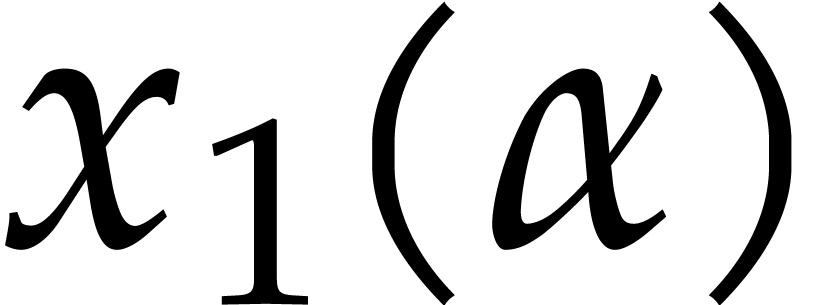
with

Here 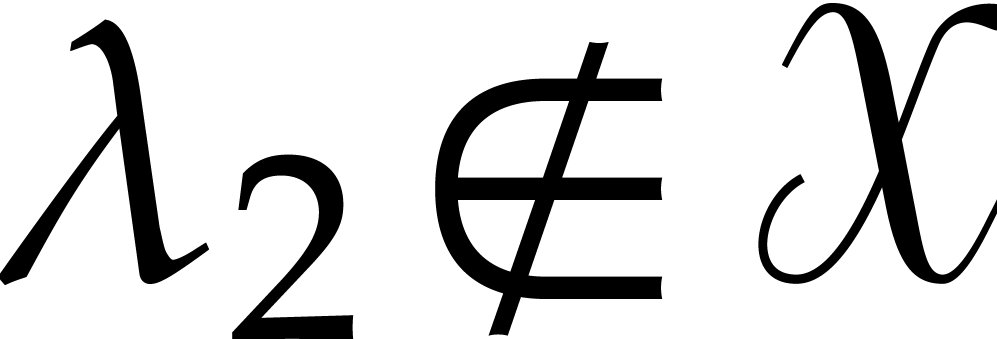 stands for the first coordinate of
stands for the first coordinate of 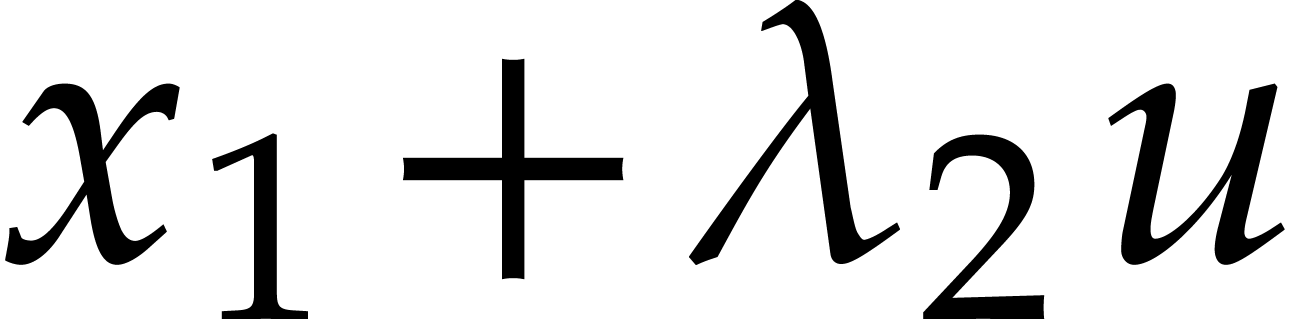 . If
. If 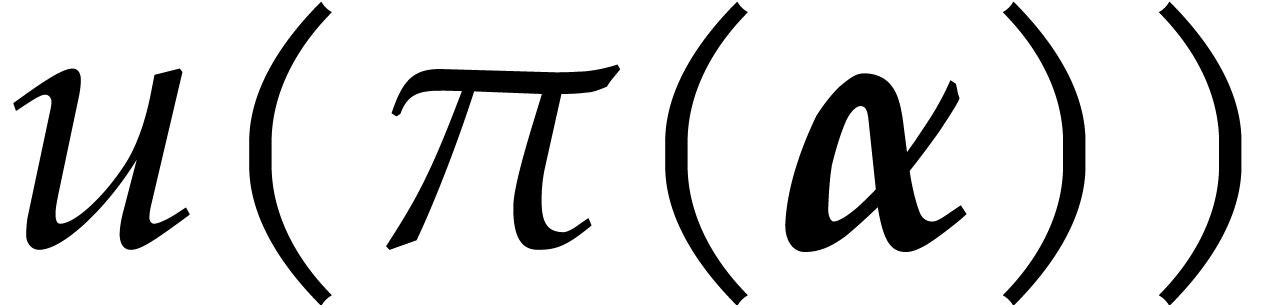 ,
then
,
then  is a joined separating form for
is a joined separating form for  . We may compute
. We may compute  using
using  operations in
operations in  and
then
and
then  using
using  further
operations. We finally pick
further
operations. We finally pick  and derive the
required joined separating form
and derive the
required joined separating form  (so
(so 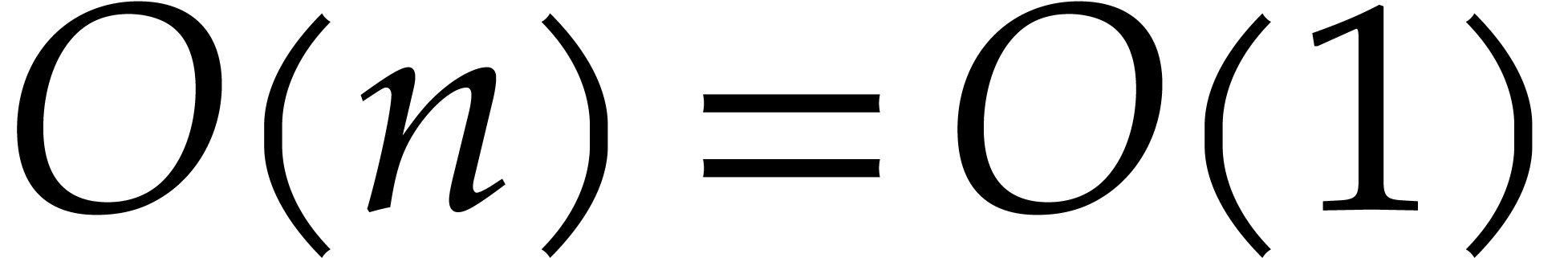 for
for  ) using
) using
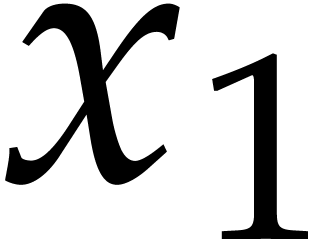 operations in
operations in  .
.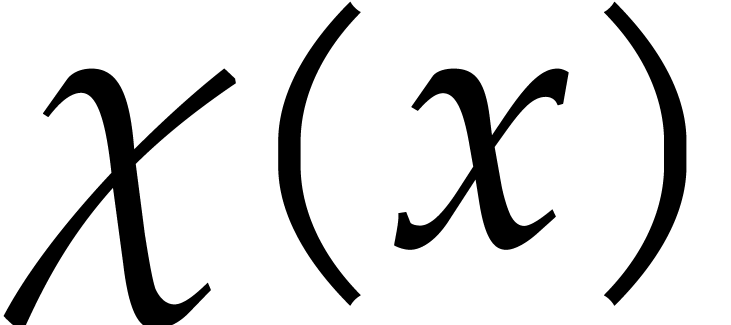
If  is a separating form for
is a separating form for  , then there exist a monic separable polynomial
, then there exist a monic separable polynomial
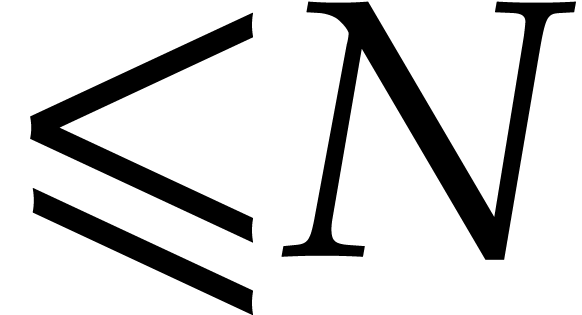 of degree
of degree 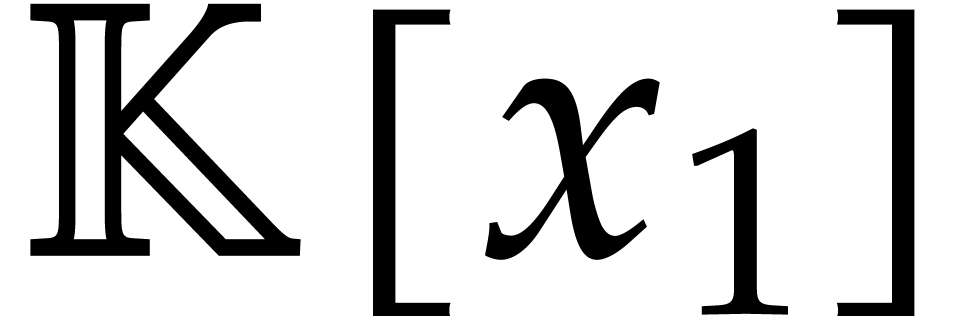 in
in  and
and 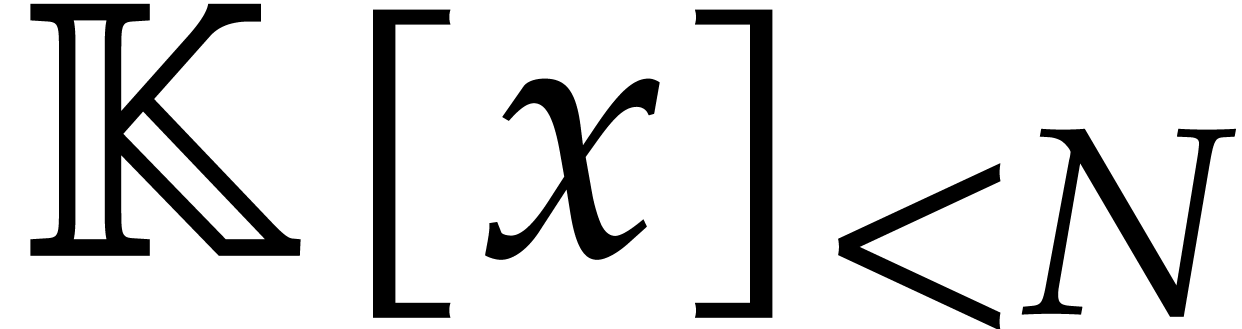 other polynomials in
other polynomials in 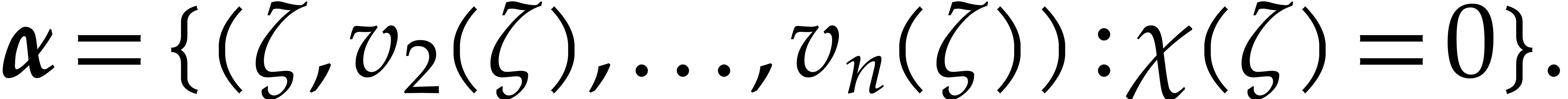 such that
such that
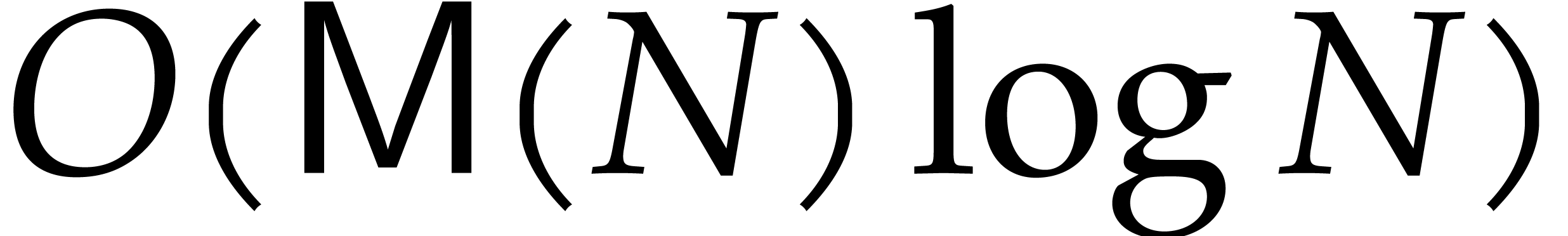
The polynomials  are called a univariate
representation of
are called a univariate
representation of  .
If the points of the sequence
.
If the points of the sequence  are pairwise
distinct, then it is well-known that these polynomials can be computed
using
are pairwise
distinct, then it is well-known that these polynomials can be computed
using  operations in
operations in  , thanks to sub-product tree algorithms; see [9, chapter 10] or [4], for instance. Otherwise we
will rely on the following lemma.
, thanks to sub-product tree algorithms; see [9, chapter 10] or [4], for instance. Otherwise we
will rely on the following lemma.
 is a separating form for
is a separating form for 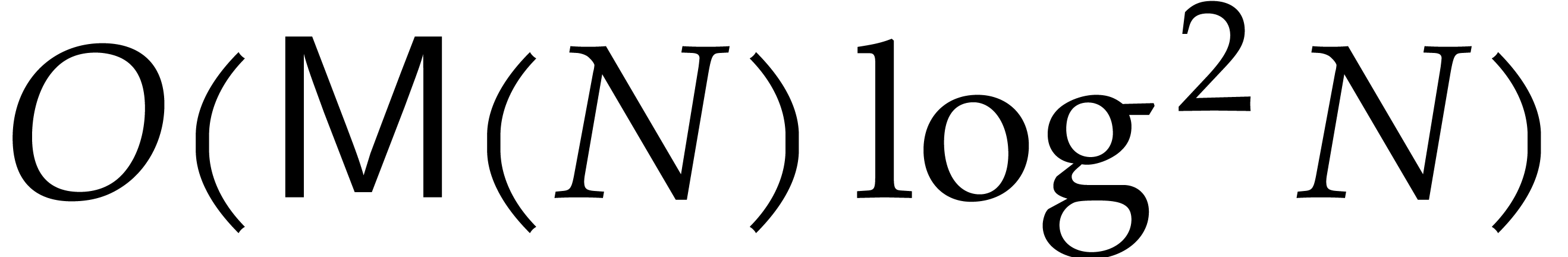 , then the univariate
representation of
, then the univariate
representation of 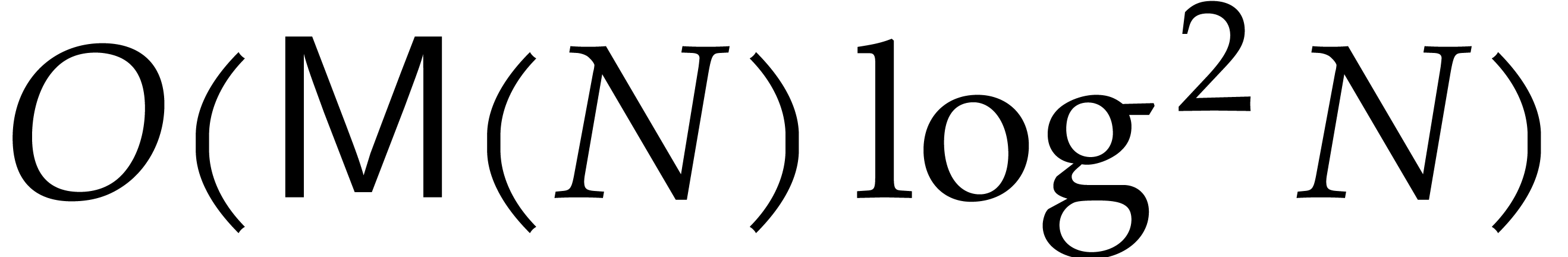 can be computed using
can be computed using 
 operations in
operations in  .
.
Proof. We proceed recursively as follows. If
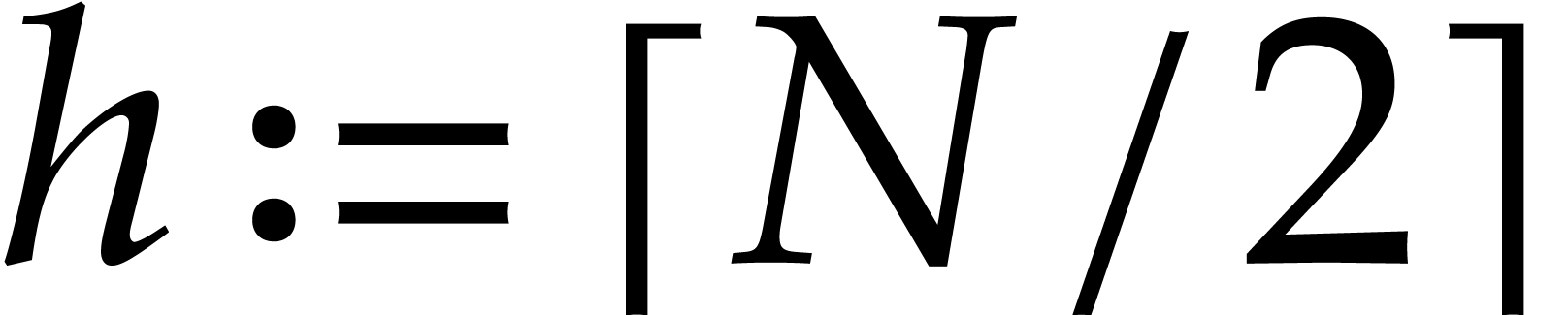 then the univariate representation is obtained
easily in time
then the univariate representation is obtained
easily in time 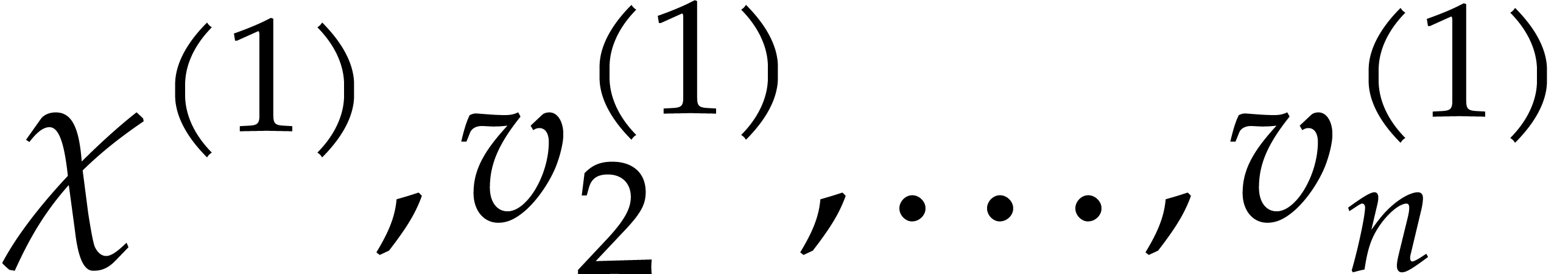 . Otherwise,
we let
. Otherwise,
we let  and we recursively compute the univariate
representations
and we recursively compute the univariate
representations 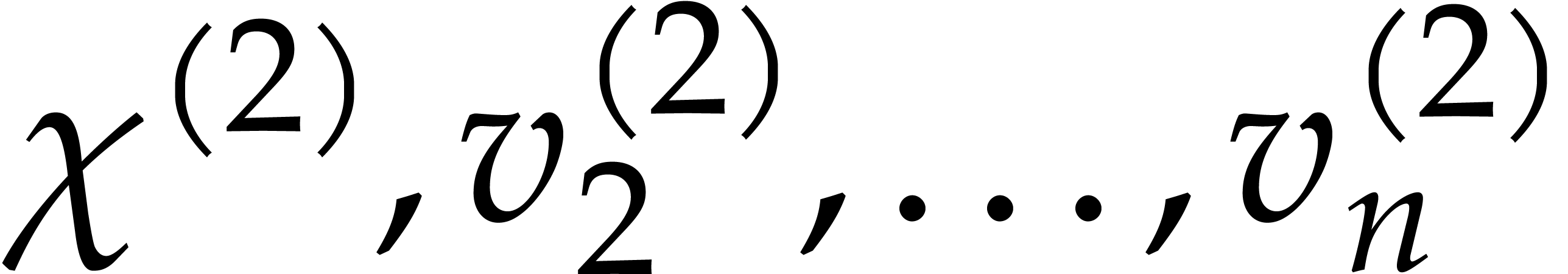 of
of 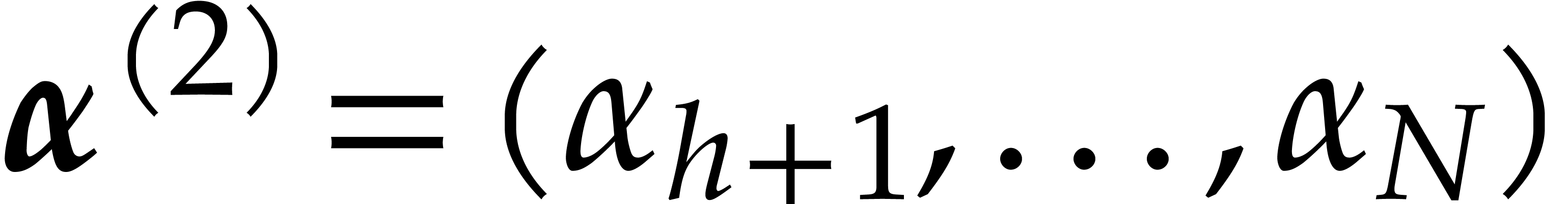 and
and
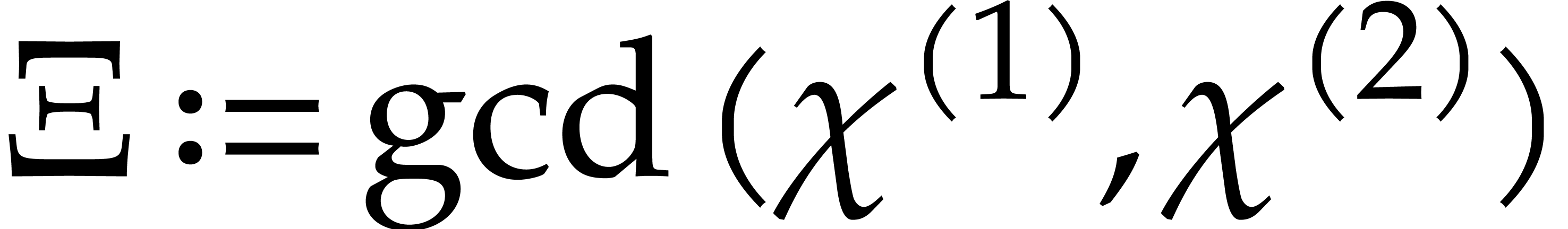 of
of 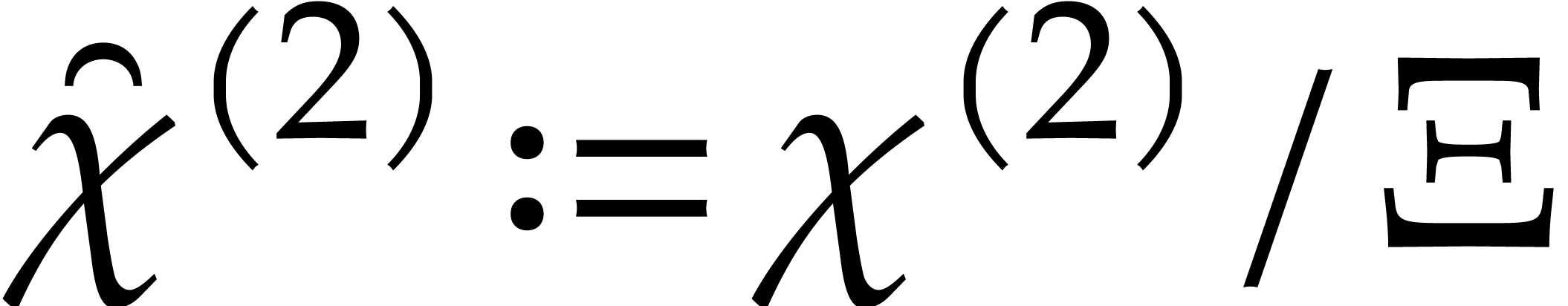 .
We next compute
.
We next compute  ,
,  , and
, and 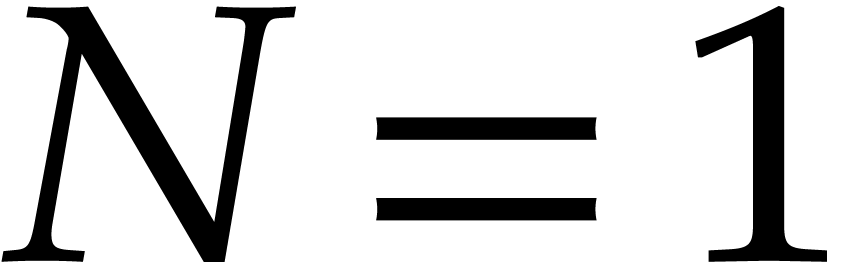
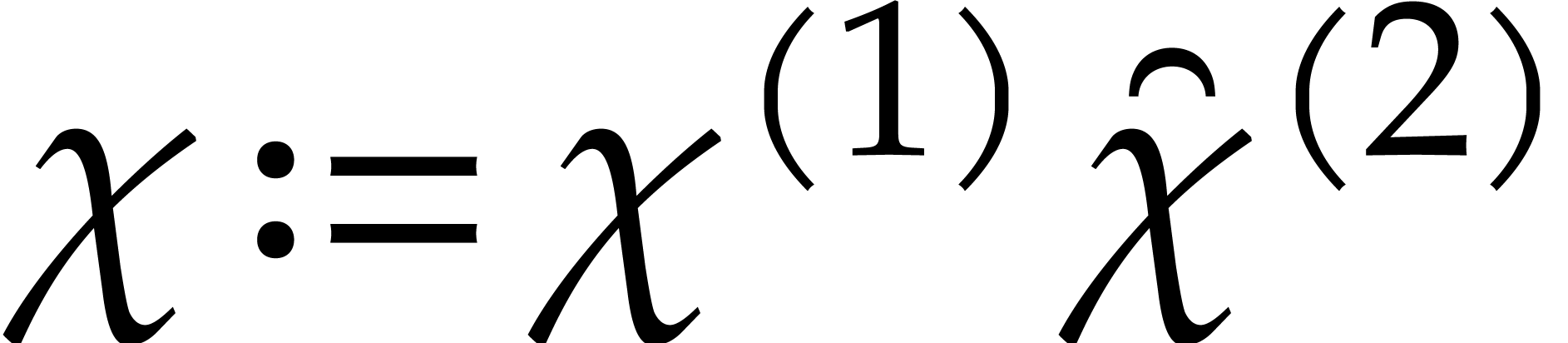 for
for 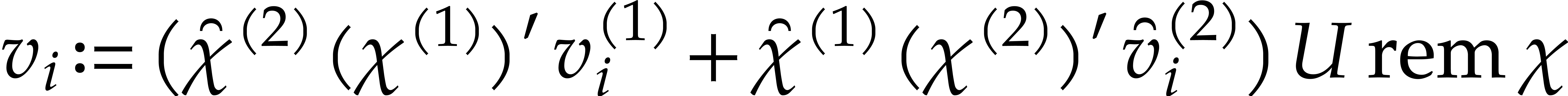 . In
this way, the univariate representation of
. In
this way, the univariate representation of 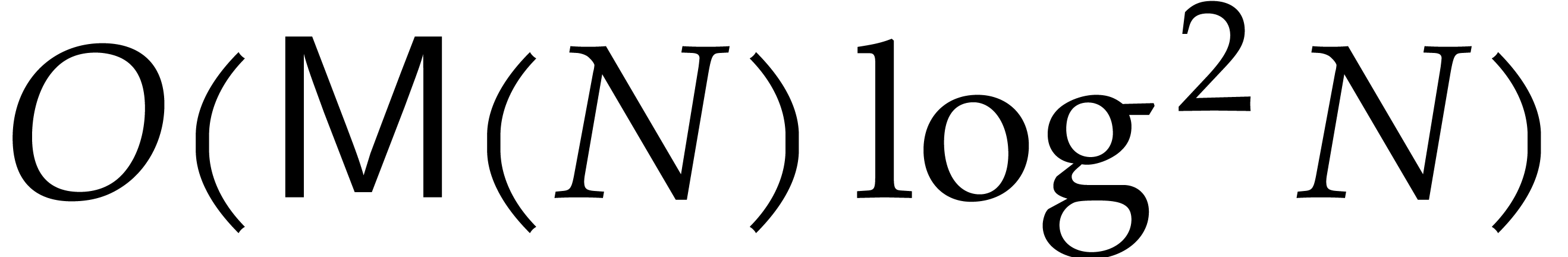 can
be obtained as
can
be obtained as 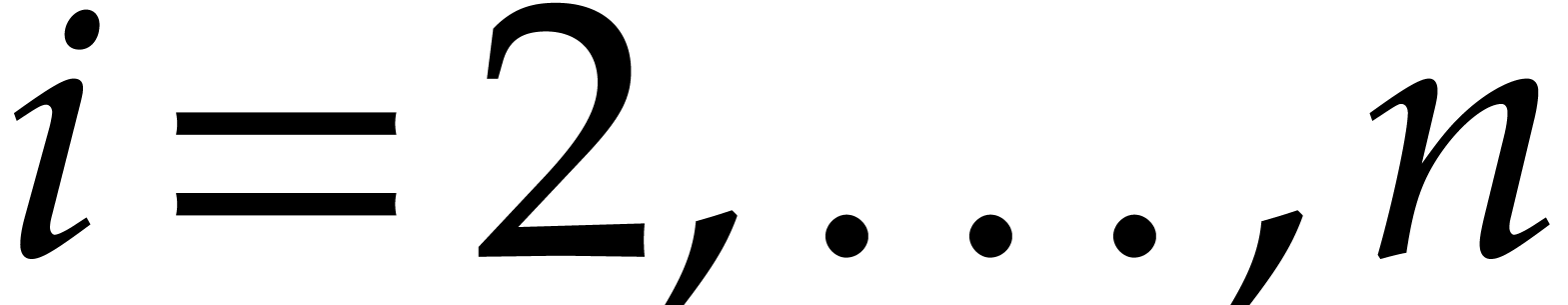 , and
, and

for 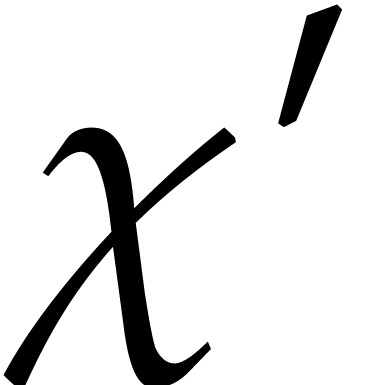 , where
, where 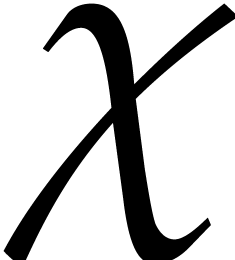 is the inverse of
is the inverse of 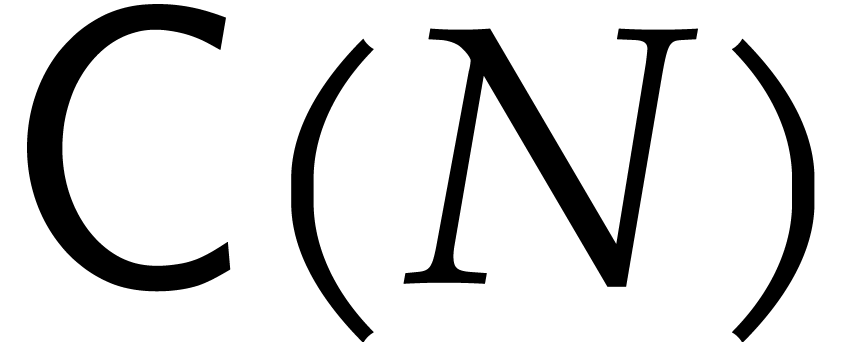 modulo
modulo 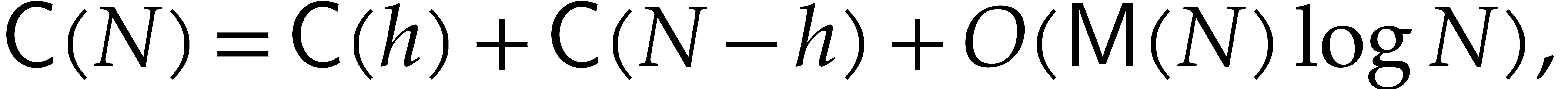 . The cost
. The cost 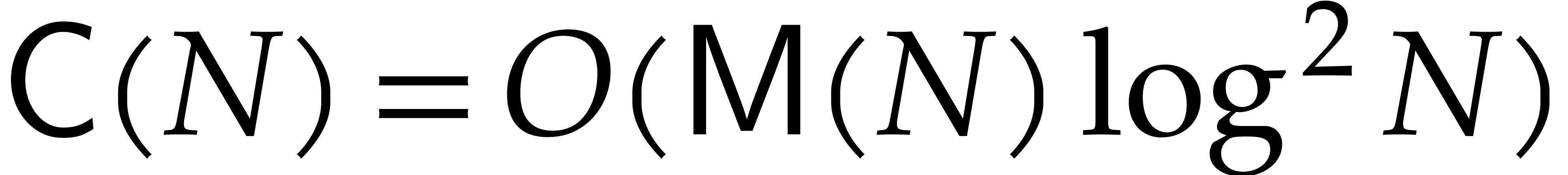 of this method
satisfies
of this method
satisfies
which yields 
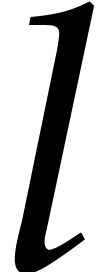 .
.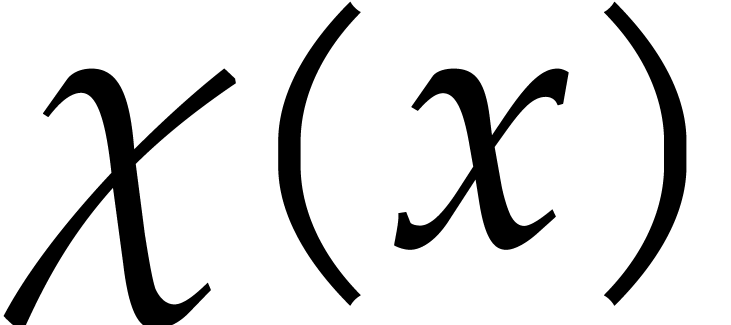
 is
a separating form
is
a separating form
Nüsken and Ziegler focused on the case where  . The case where
. The case where  is only
mentioned in the conclusion of [26]. Our next algorithm
encompasses both cases and benefits from joined separating forms.
is only
mentioned in the conclusion of [26]. Our next algorithm
encompasses both cases and benefits from joined separating forms.
Let  and
and 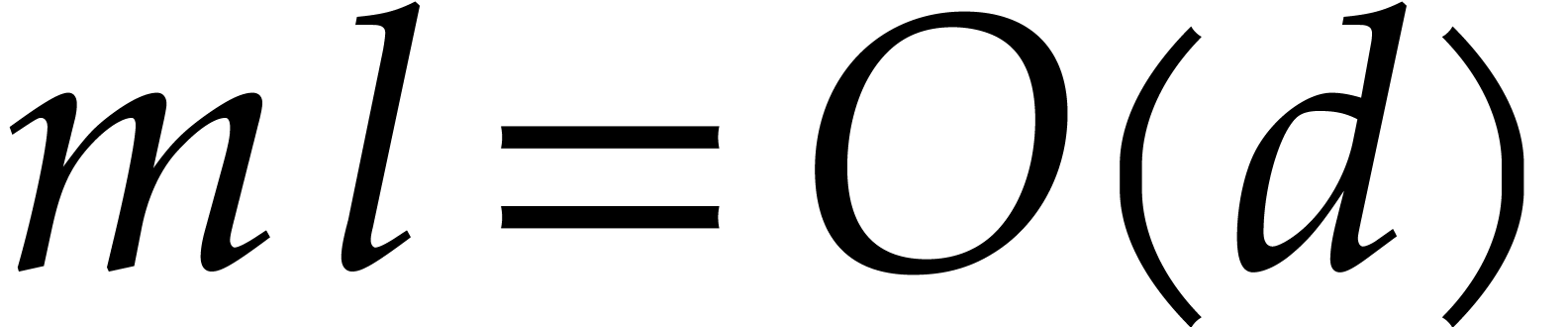 be positive
integer parameters such that
be positive
integer parameters such that 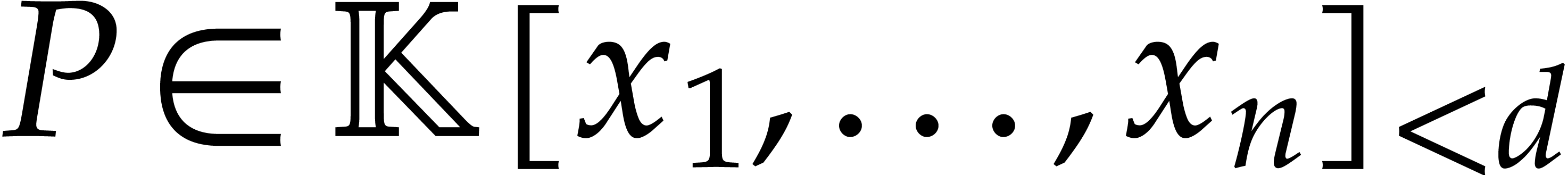 and
and  . We expand the polynomial
. We expand the polynomial 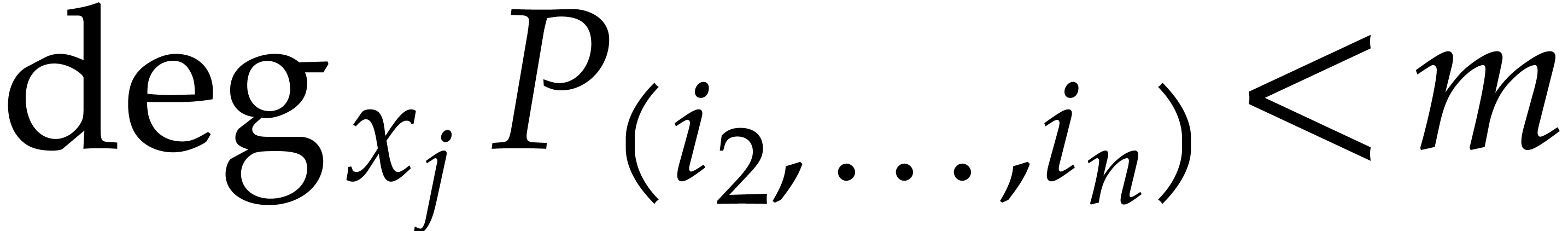 to be evaluated as
to be evaluated as
 |
(2.1) |
where 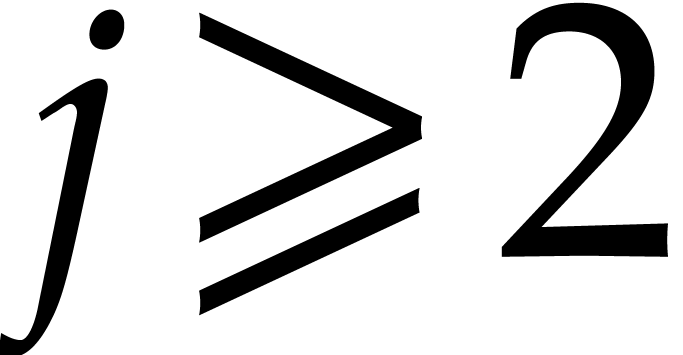 for
for 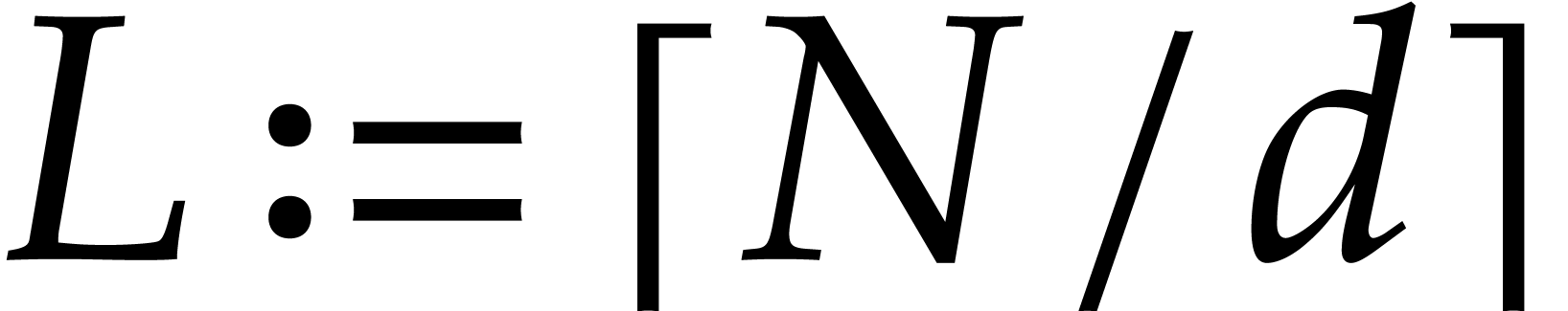 and
and 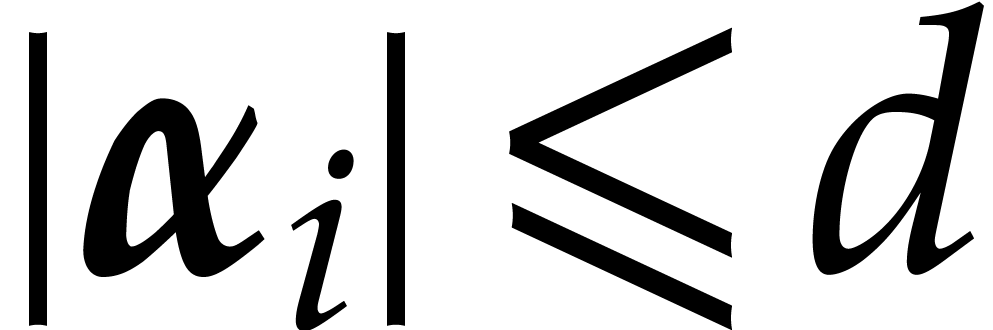 .
.
We partition  into subsequences
into subsequences  with
with  and
and 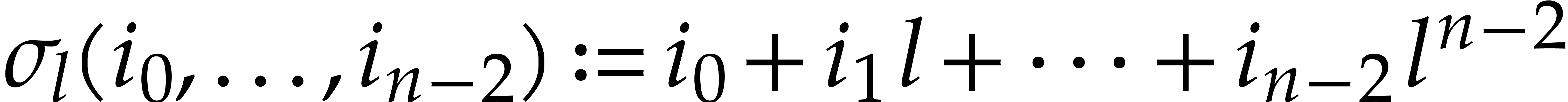 for
for  . Let
. Let
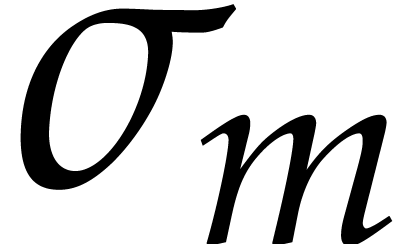
be arbitrary bijections, e.g.  and
similarly for
and
similarly for 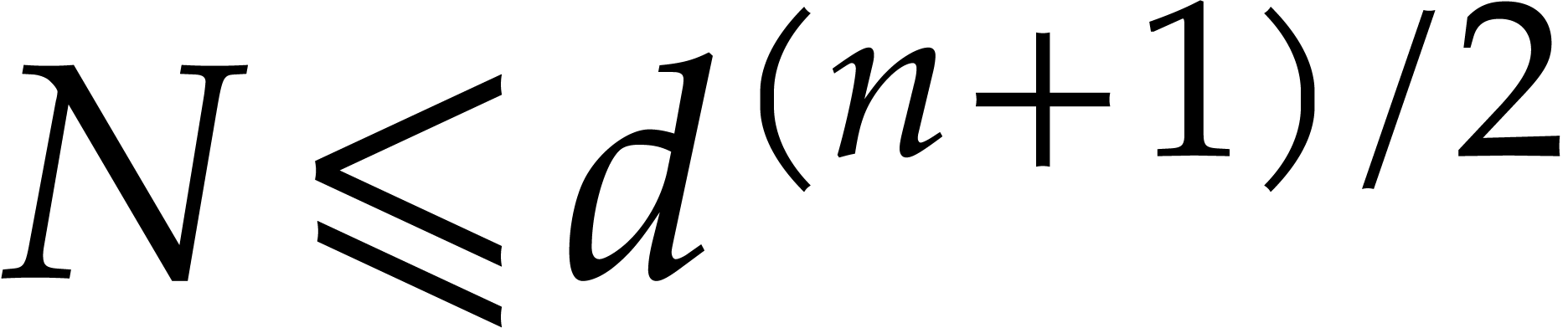 .
.
Algorithm
If 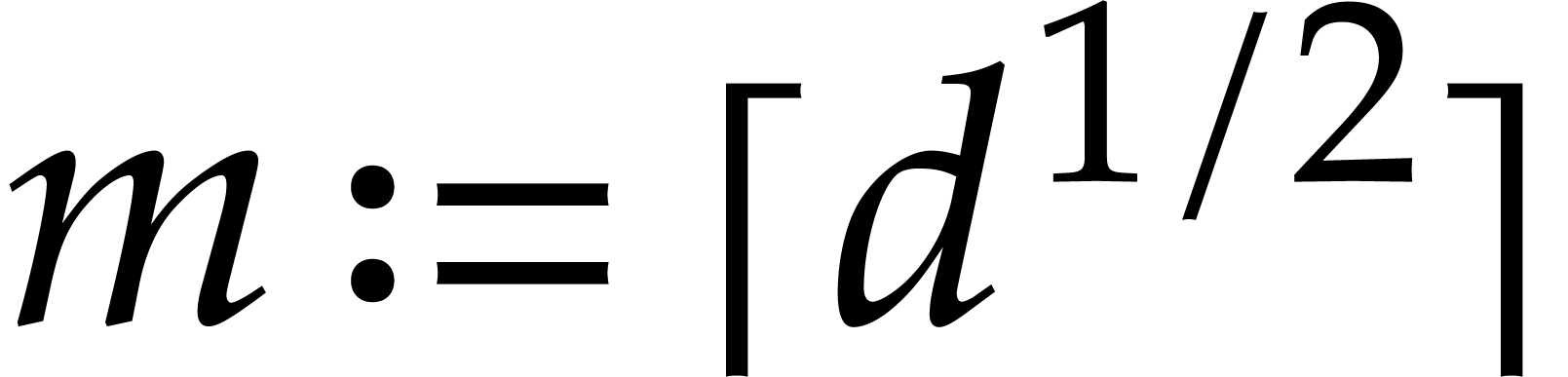 then set
then set  . Otherwise set
. Otherwise set 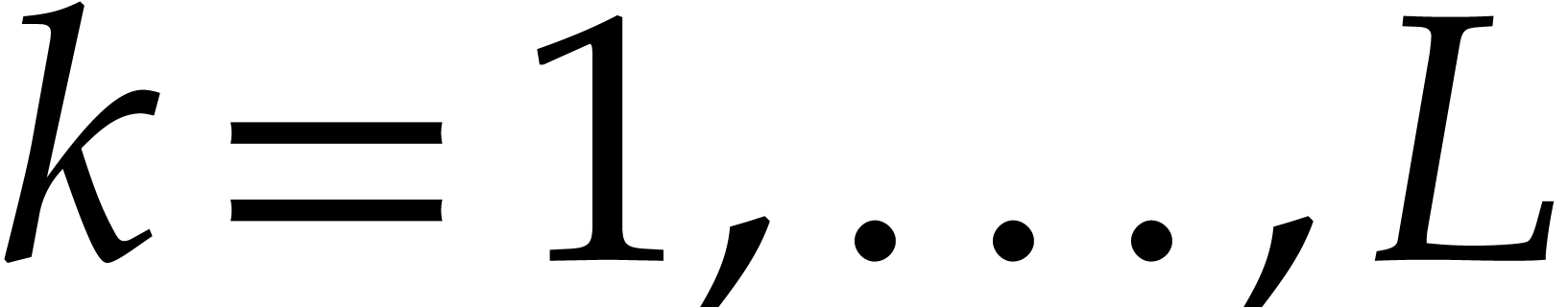 .
.
Set 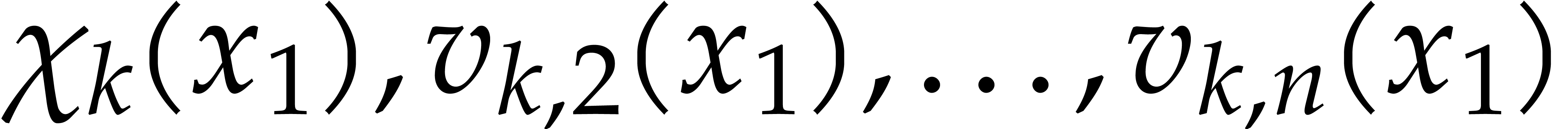 .
.
For 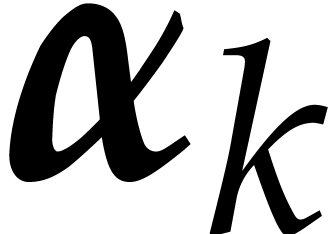 , compute the
univariate representation
, compute the
univariate representation 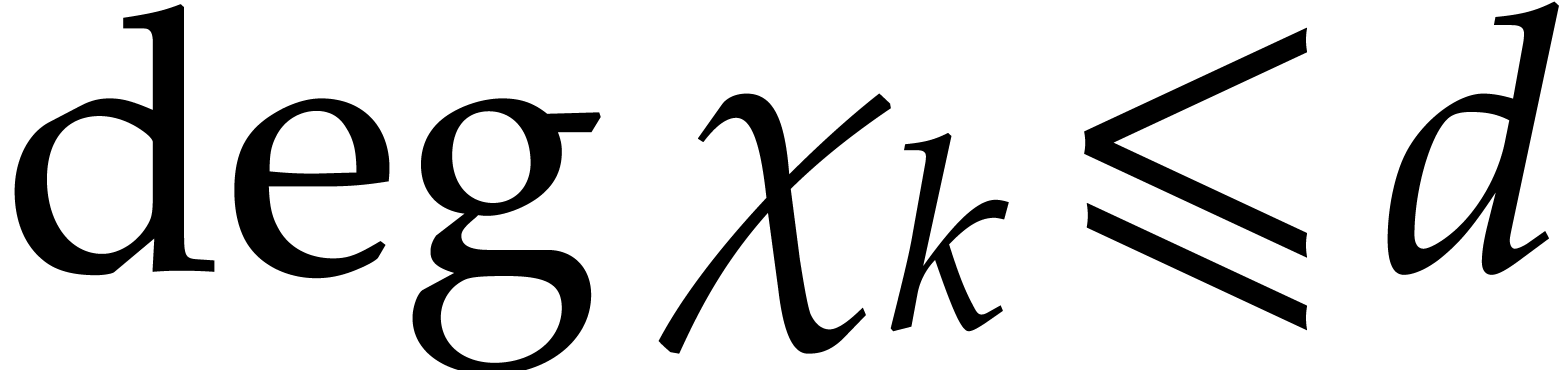 of
of 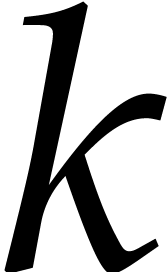 . Note that
. Note that  for all
for all  .
.
For 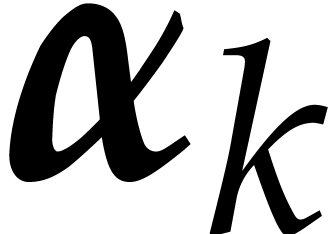 and
and 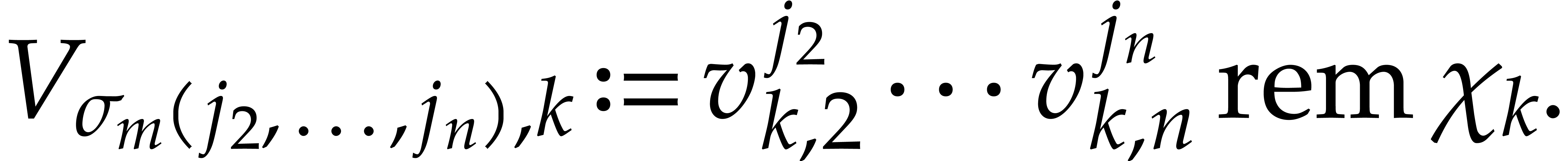 ,...,
,...,  ,
compute
,
compute
We regard  as a
as a 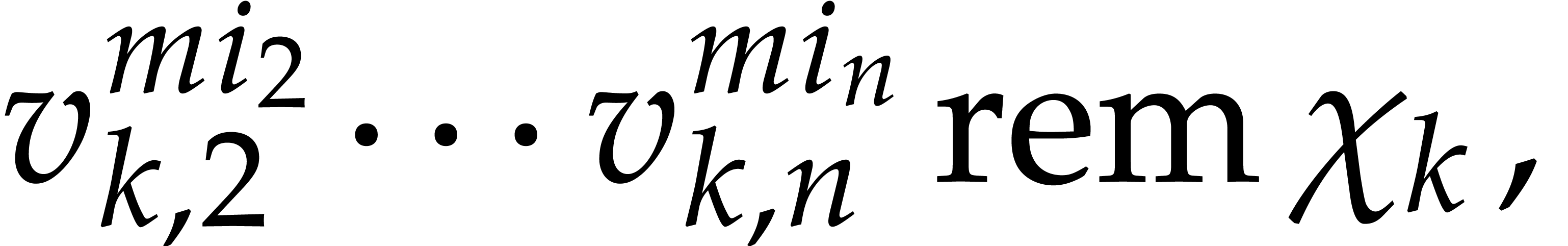 matrix over
matrix over  , with
entries of degrees
, with
entries of degrees  .
.
For  , compute
, compute  and then
and then

for  ,...,
,..., 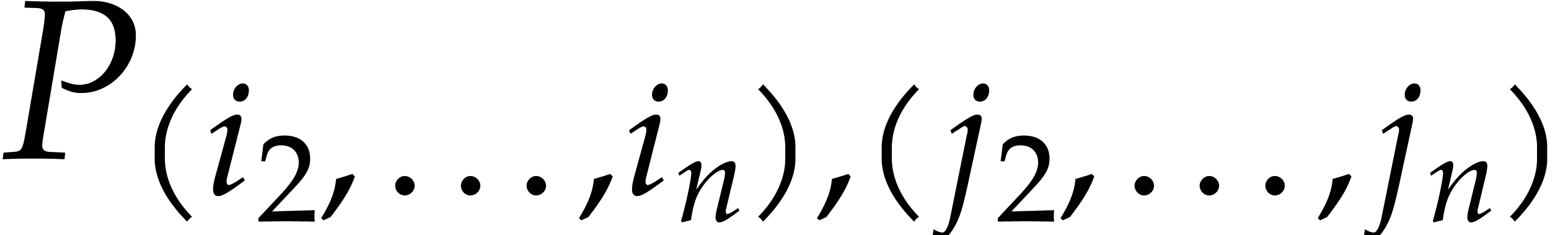 .
.
For 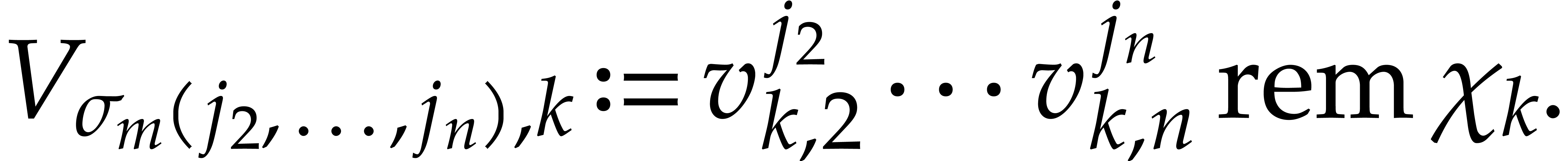 ,...,
,...,  , let
, let  denote the coefficient
denote the coefficient 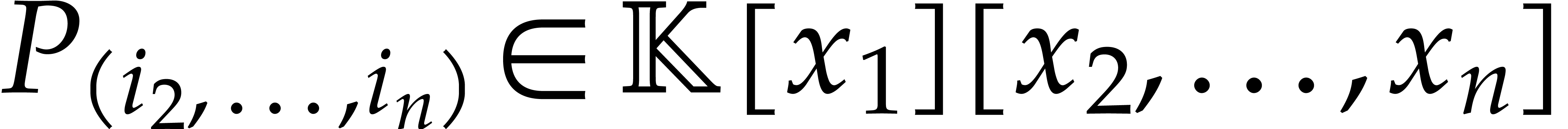 of
of  in
in 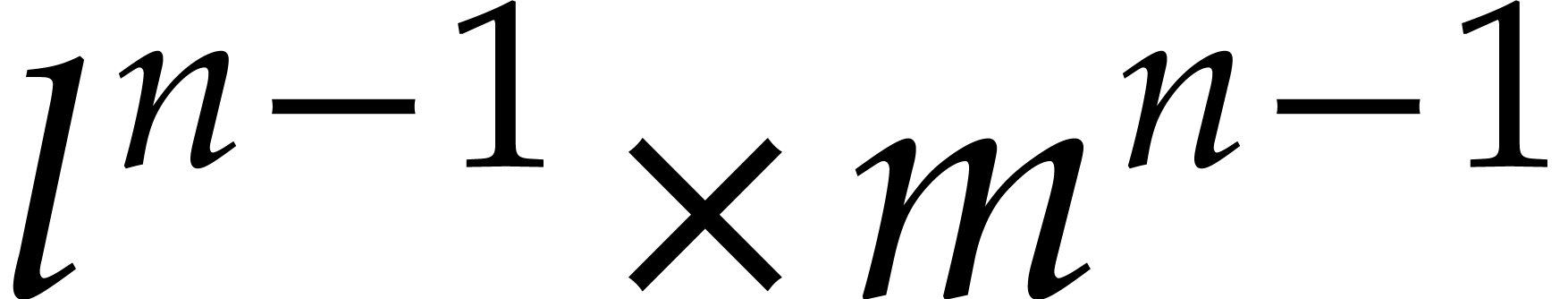 . We
regard
. We
regard 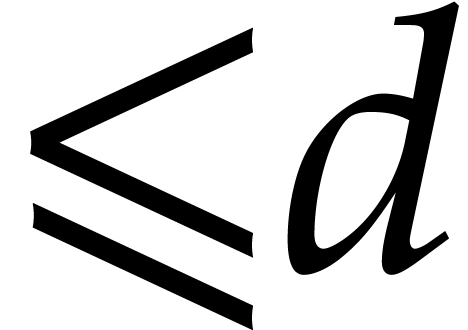 as a
as a  matrix over
matrix over  , with
entries of degrees
, with
entries of degrees 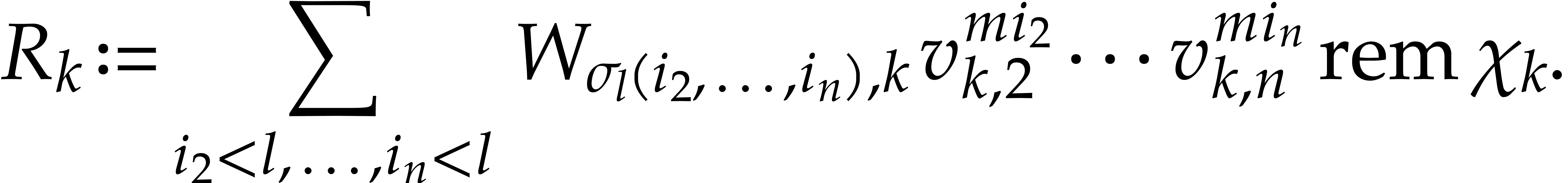 .
Compute
.
Compute
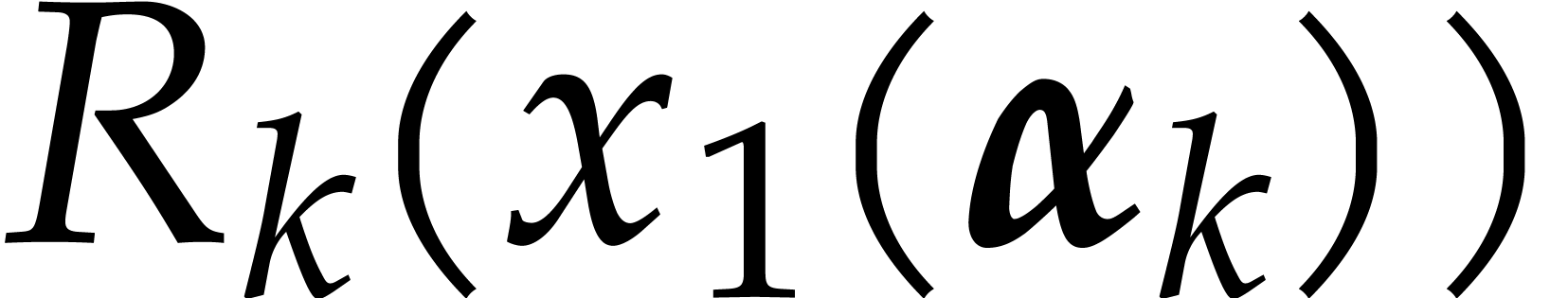
For 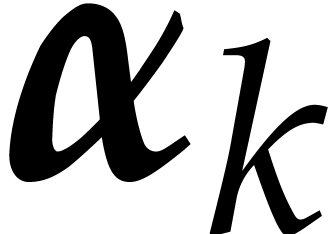 , compute
, compute

Return the concatenation of the vectors  for
for 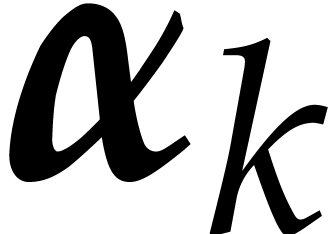 , where
, where 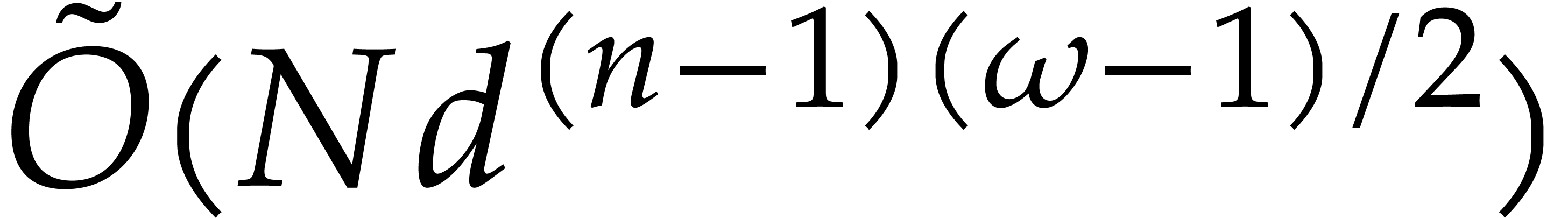 stands for the vector with the first coordinates
of the points in
stands for the vector with the first coordinates
of the points in 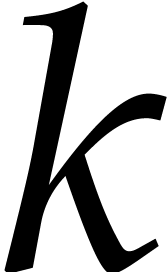 .
.
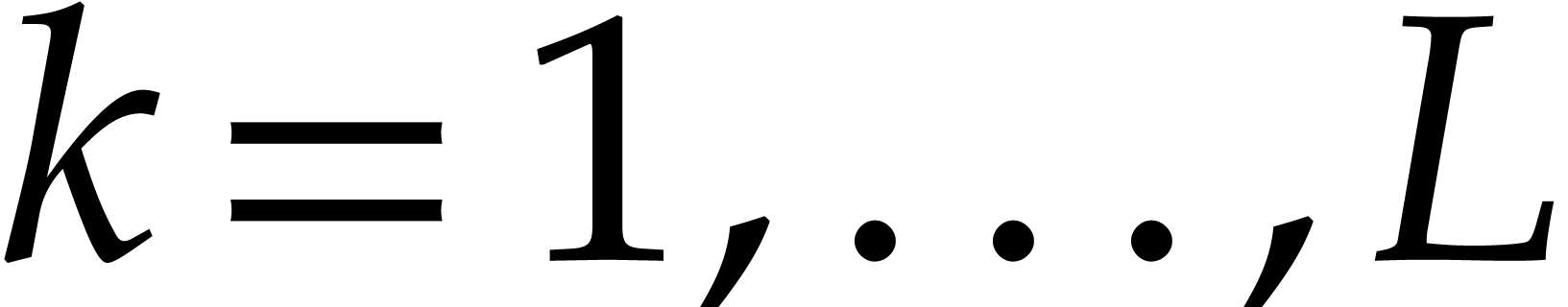 operations in
operations in  if
if 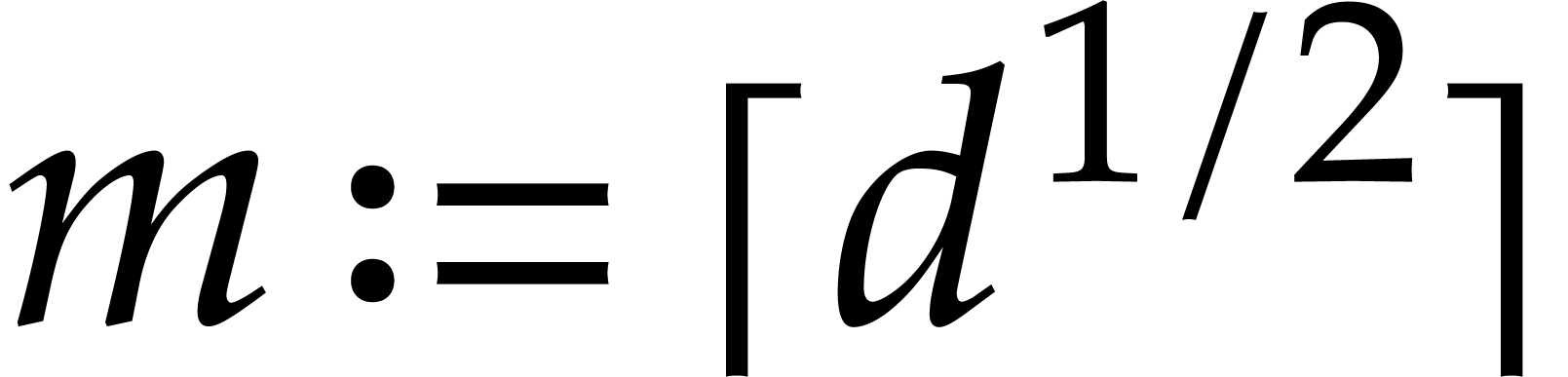 and
and  operations
otherwise.
operations
otherwise.
Proof. The assumption on  is needed for step 2. For all
is needed for step 2. For all 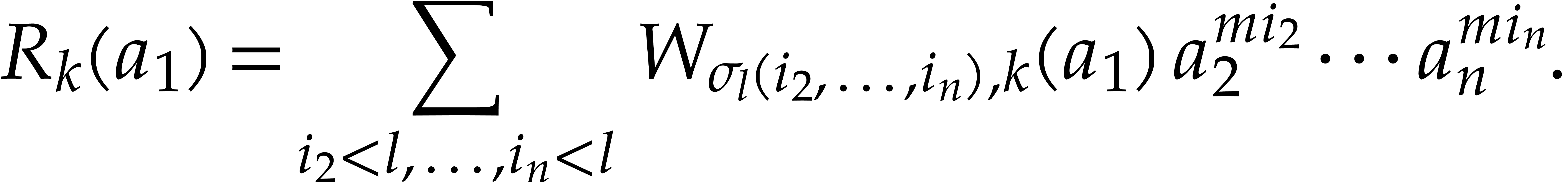 and all points
and all points
 in
in  we verify in step 6
that
we verify in step 6
that
In step 5 we have

From the expansion 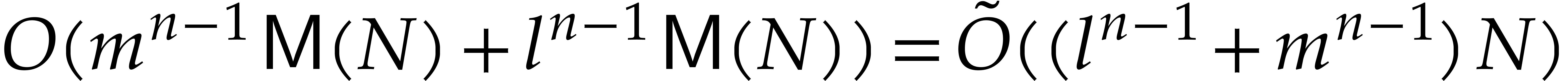 .
.
By Lemma 2.2, step 2 takes 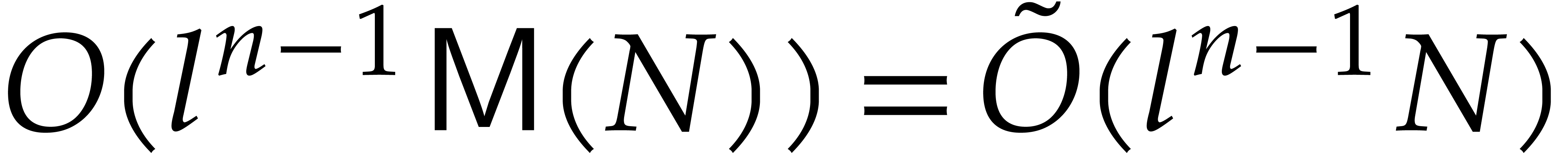 operations in
operations in  . Steps 3 and 4
take
. Steps 3 and 4
take
operations. Step 6 contributes  to the cost. Step
7 performs univariate multi-point evaluations in total time
to the cost. Step
7 performs univariate multi-point evaluations in total time  . For the complexity of step 5 we distinguish
the following cases:
. For the complexity of step 5 we distinguish
the following cases:
If 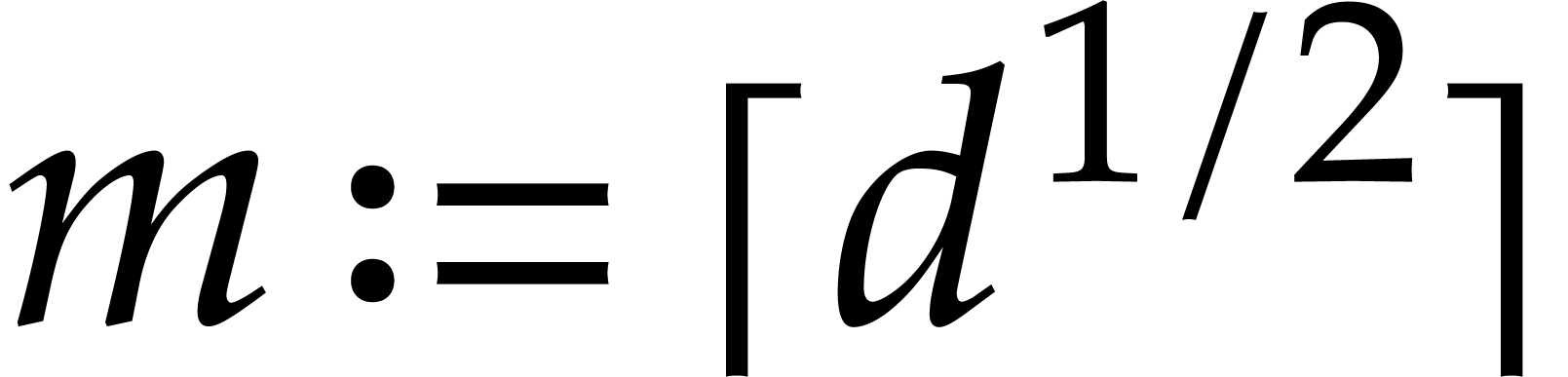 , then
, then 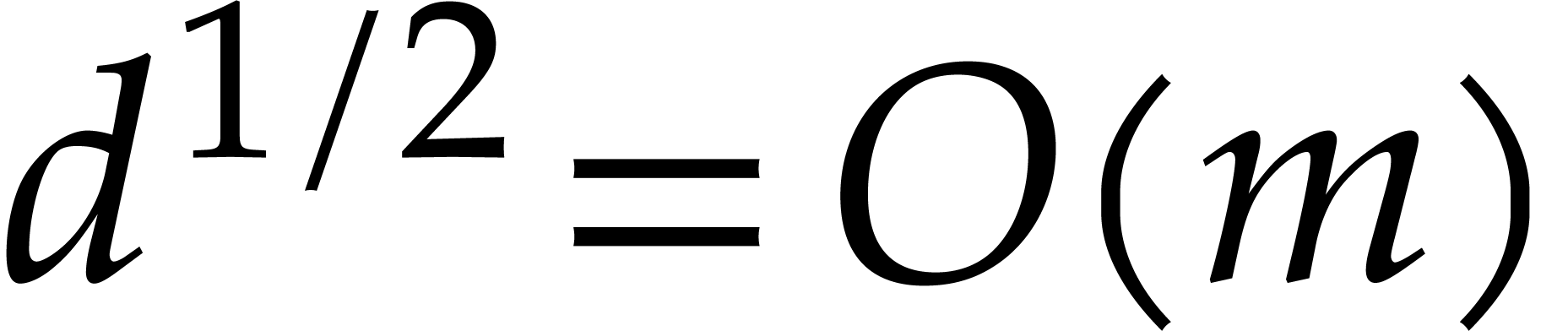 ,
, 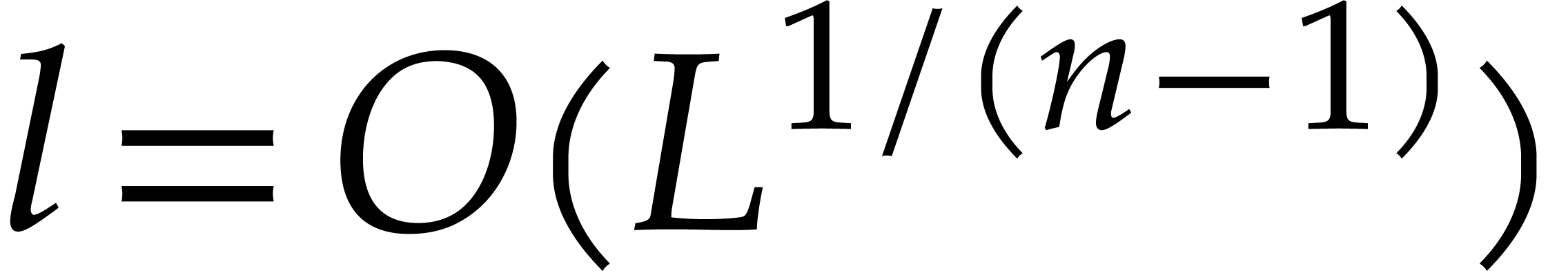 ,
,
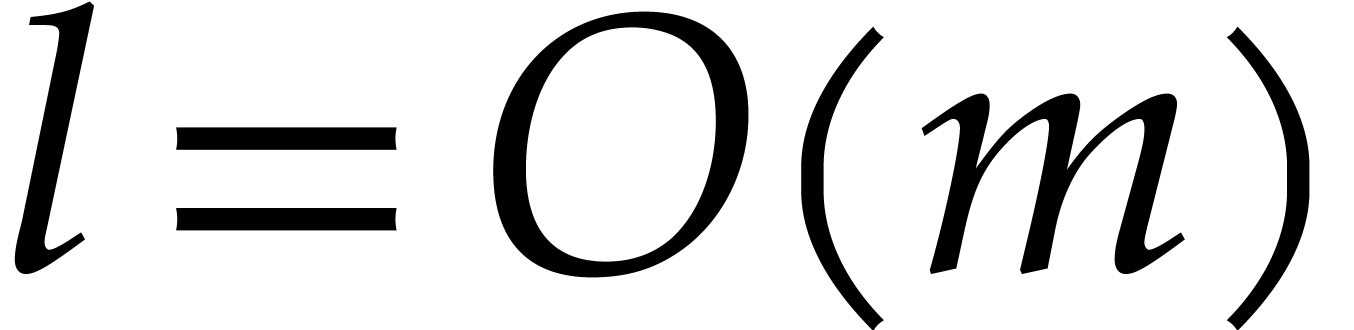 ,
, 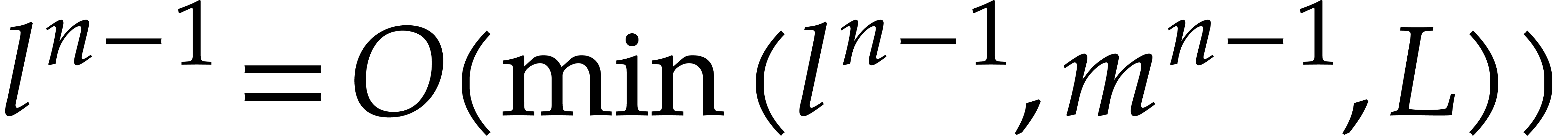 , and
, and  .
Consequently,
.
Consequently,  , so the
product
, so the
product  can be split into products of
can be split into products of  matrices, and the cost of step 5 is
matrices, and the cost of step 5 is
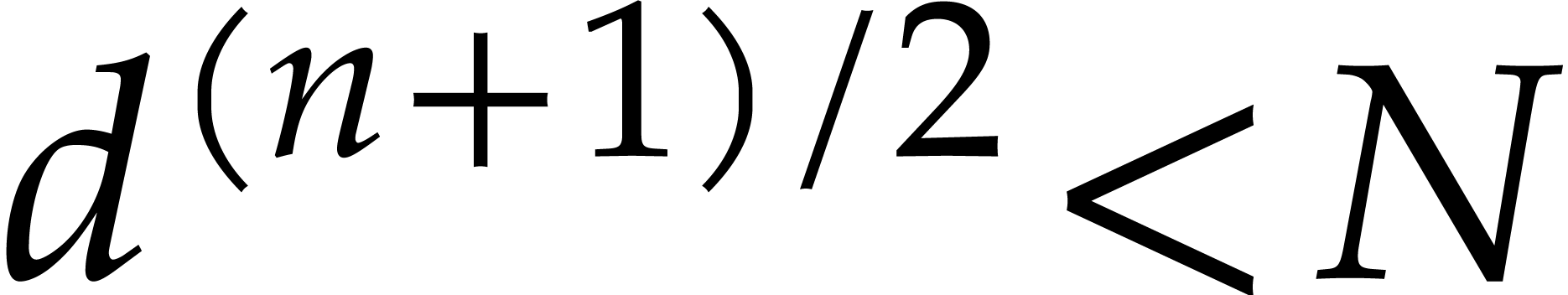
In this case, the total cost of the algorithm is
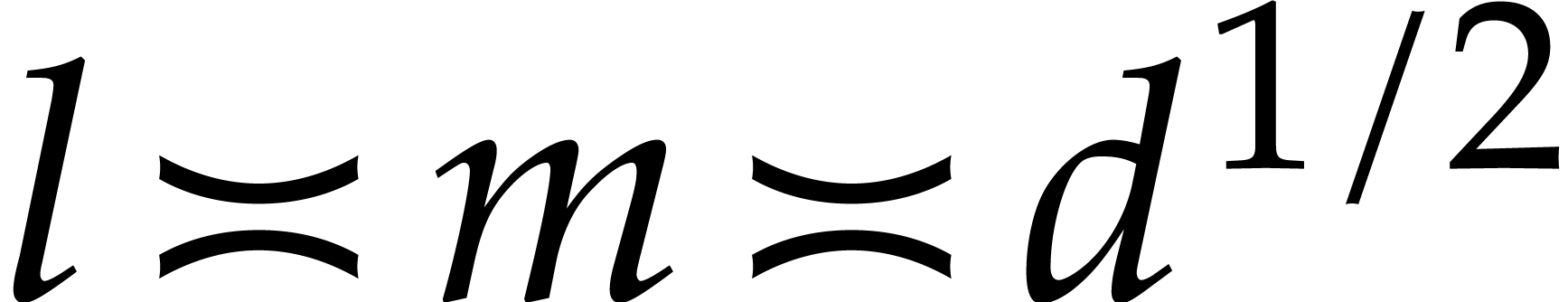
Otherwise, we have 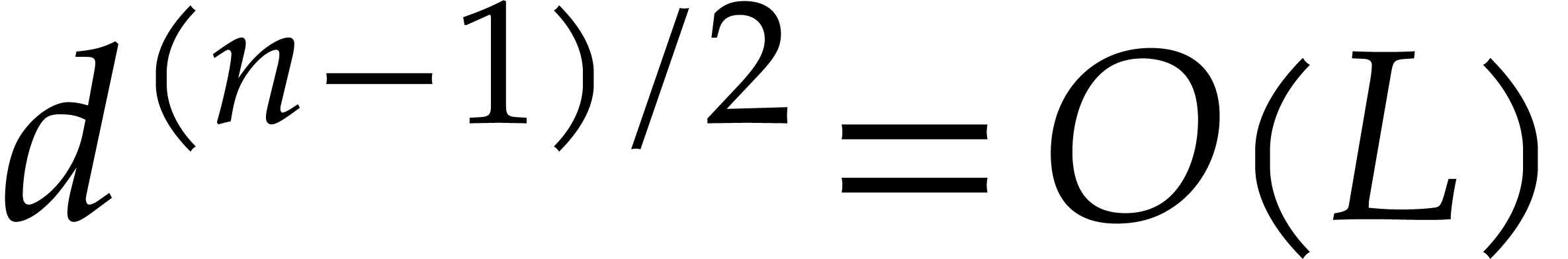 ,
,
 , and
, and 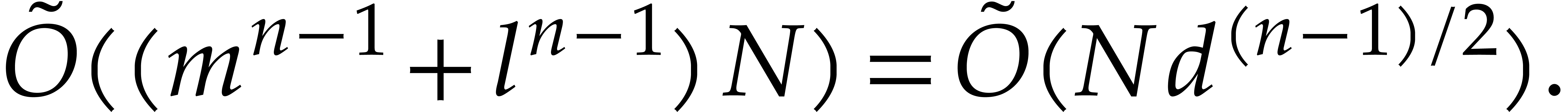 . Consequently,
. Consequently,  , the product
, the product  can again
be split into products of
can again
be split into products of  matrices, and the
cost of step 5 becomes
matrices, and the
cost of step 5 becomes
This dominates the total cost of the algorithm since

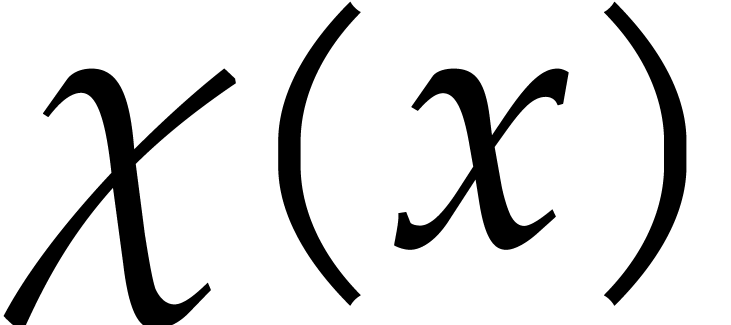
Remark  in step 5 of Algorithm
2.1 actually depends on the ratios of the dimensions of
in step 5 of Algorithm
2.1 actually depends on the ratios of the dimensions of
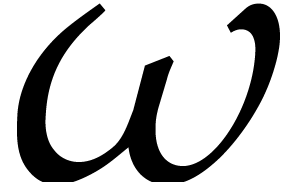 and
and  .
For simplicity, we have reduced this product to several products of
.
For simplicity, we have reduced this product to several products of  matrices, whence a complexity bound in terms of
matrices, whence a complexity bound in terms of  . This choice is slightly
sub-optimal if
. This choice is slightly
sub-optimal if 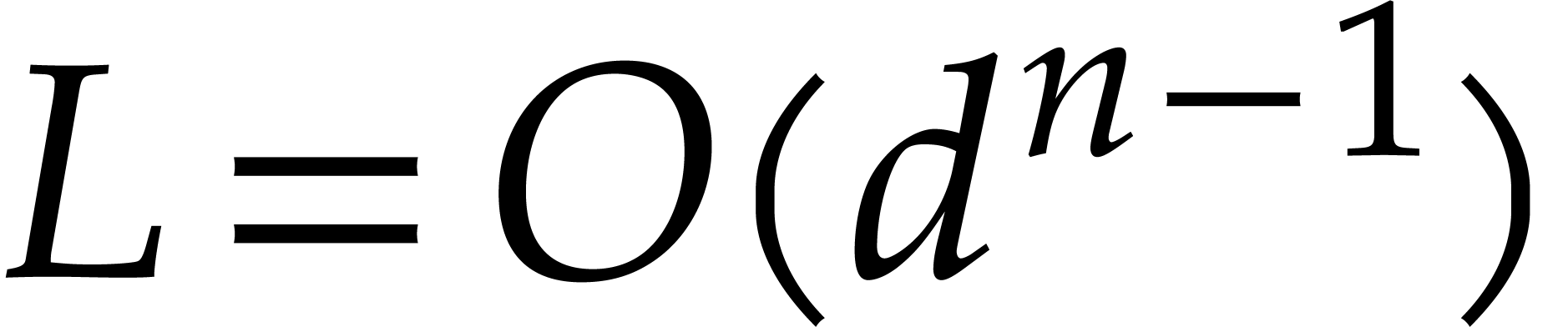 ; see [30]. For instance, if
; see [30]. For instance, if 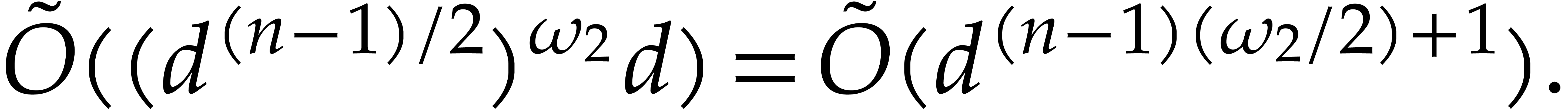 ,
then
,
then 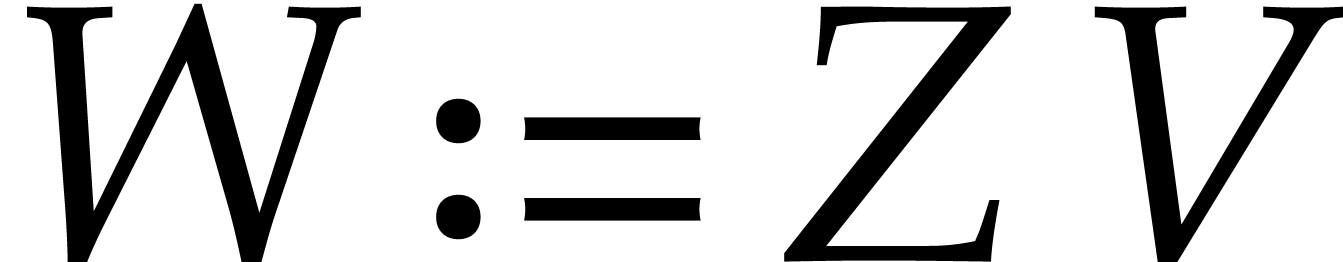 and the product
and the product  can
be done faster, using only
can
be done faster, using only
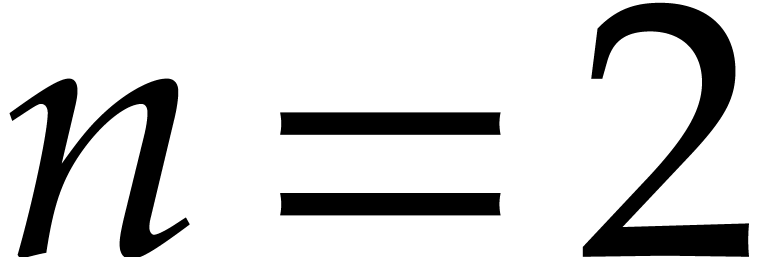
operations in  . The product
. The product
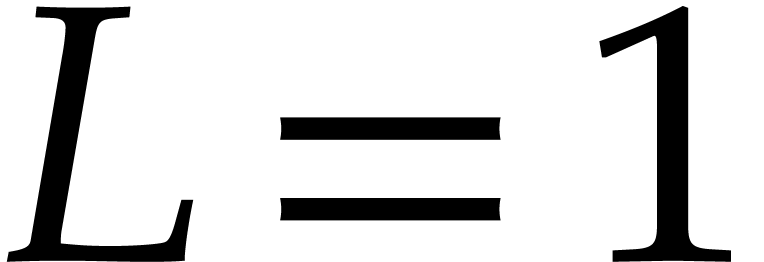 still dominates the total cost of Algorithm 2.1.
still dominates the total cost of Algorithm 2.1.
Remark 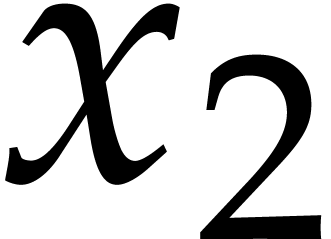 and
and  ; see [26,
Theorem 8]. They give the complexity bound in terms of
; see [26,
Theorem 8]. They give the complexity bound in terms of 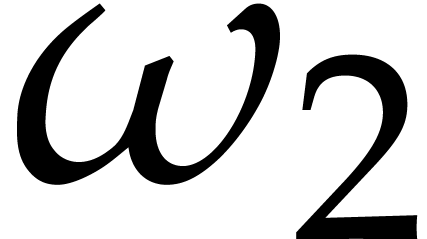 , recalled in Remark 2.4, but also
in terms of the partial degrees in
, recalled in Remark 2.4, but also
in terms of the partial degrees in  and
and 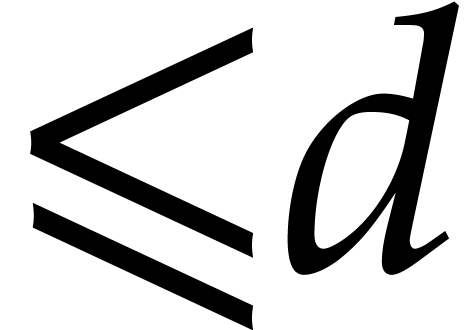 . The case where
. The case where 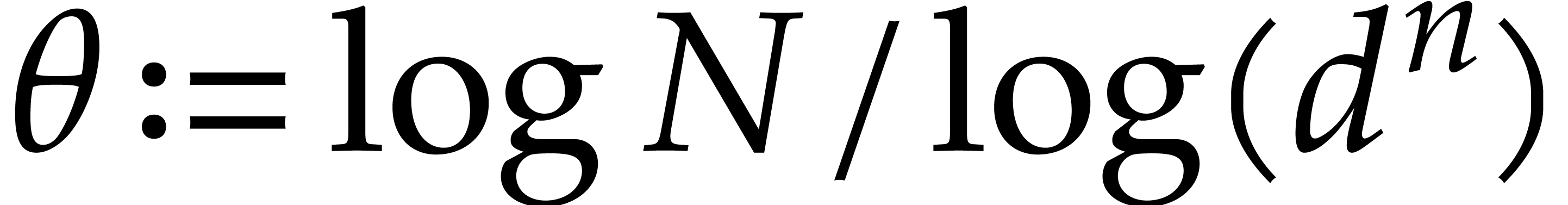 is only mentioned in the conclusion of [26].
is only mentioned in the conclusion of [26].
In general, the form  does not necessarily
separate all the
does not necessarily
separate all the  for
for  . In such degenerate situations, one may apply a
suitable change of coordinates before using Algorithm 2.1,
provided that the cardinality of
. In such degenerate situations, one may apply a
suitable change of coordinates before using Algorithm 2.1,
provided that the cardinality of  is sufficiently
large. In [26, section 6], Nüsken and Ziegler use a
randomized method to compute such a change of coordinates. In this
section, our first contribution is an alternative deterministic method,
that takes advantage of the splitting of
is sufficiently
large. In [26, section 6], Nüsken and Ziegler use a
randomized method to compute such a change of coordinates. In this
section, our first contribution is an alternative deterministic method,
that takes advantage of the splitting of  into
into
 . Another contribution is the
complexity analysis in terms of the number of evaluation points. The
following theorem summarizes the cost of our deterministic version of
the Nüsken–Ziegler algorithm for
. Another contribution is the
complexity analysis in terms of the number of evaluation points. The
following theorem summarizes the cost of our deterministic version of
the Nüsken–Ziegler algorithm for  .
.
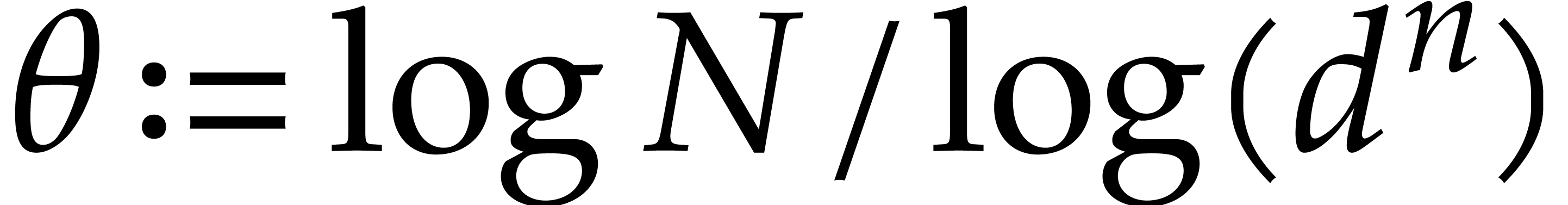 be a fixed dimension, let
be a fixed dimension, let  be of total degree
be of total degree 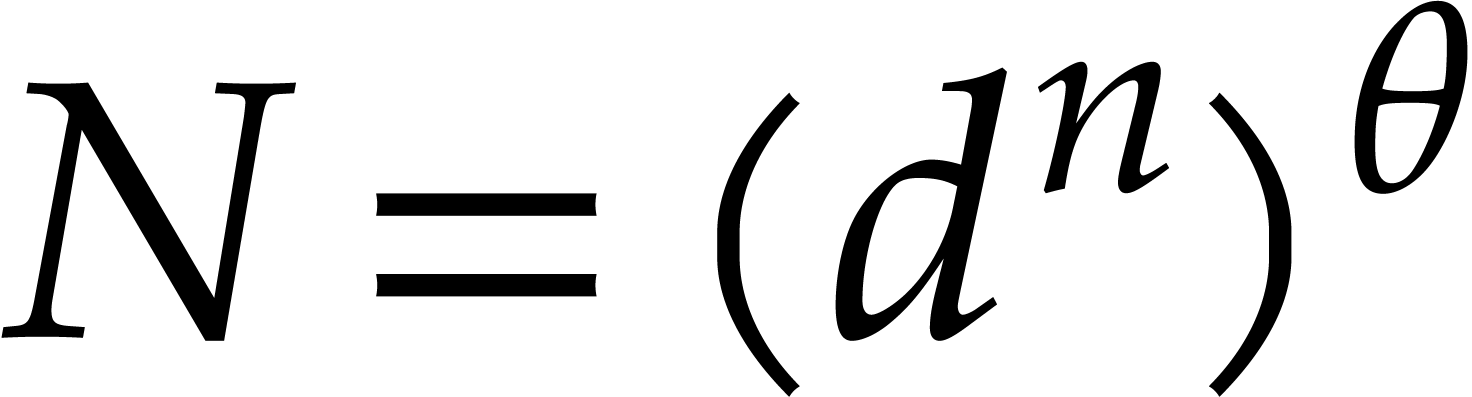 ,
let
,
let 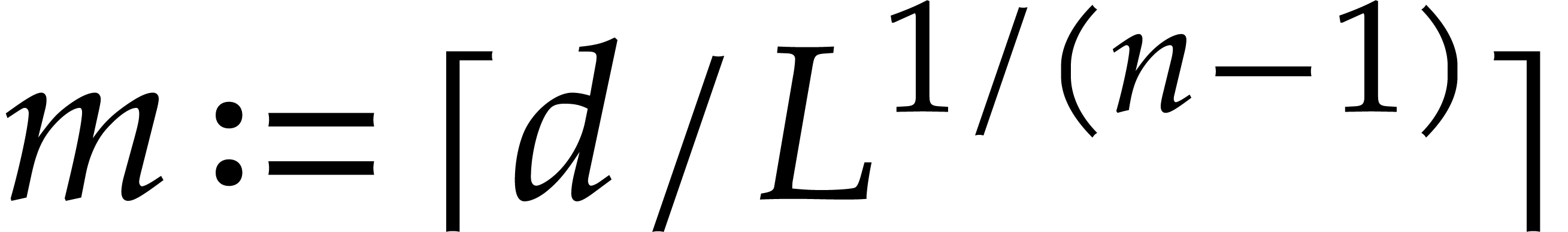 , and let
, and let 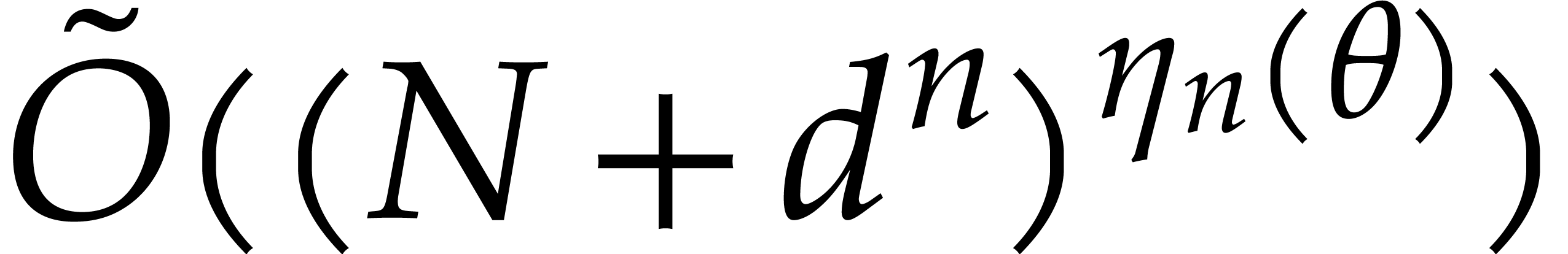 , that is
, that is 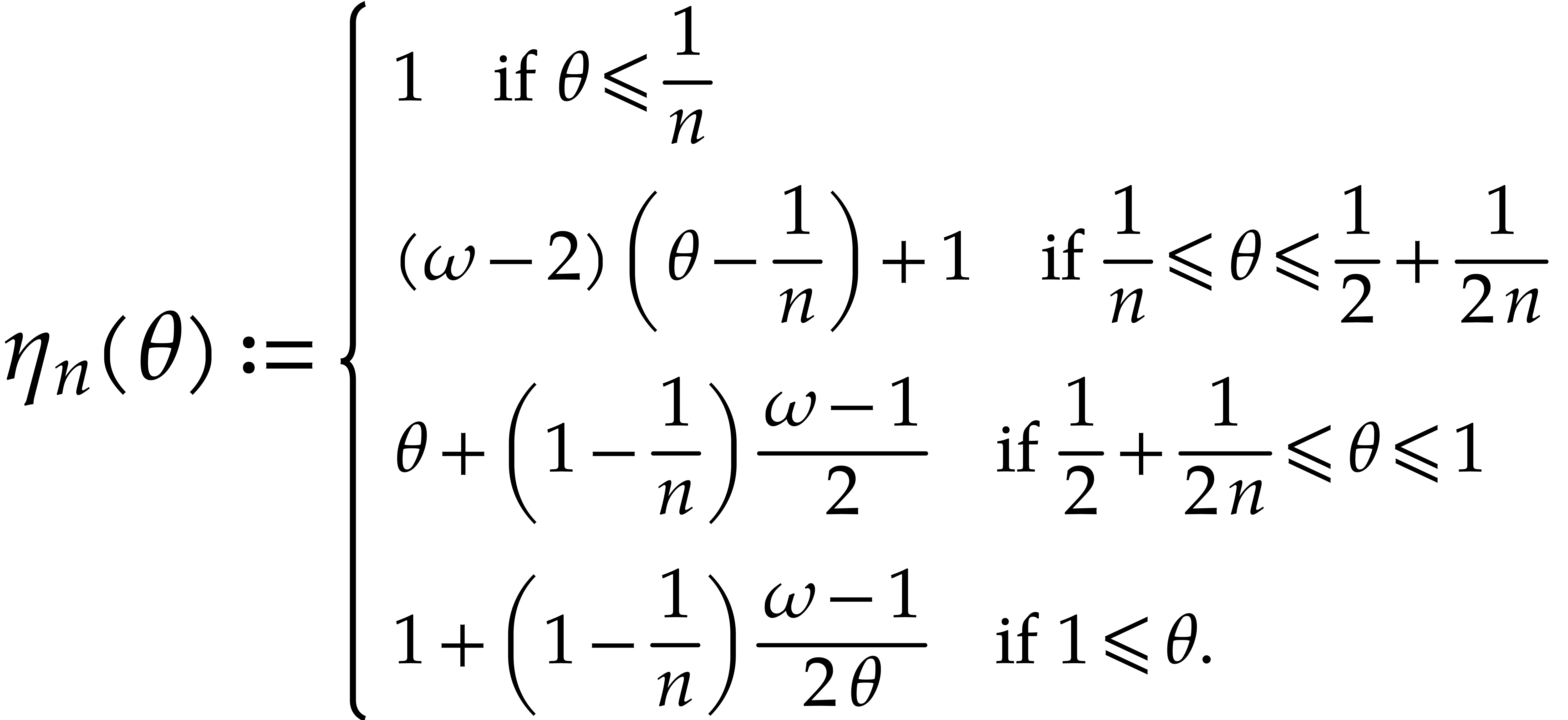 .
Then
.
Then 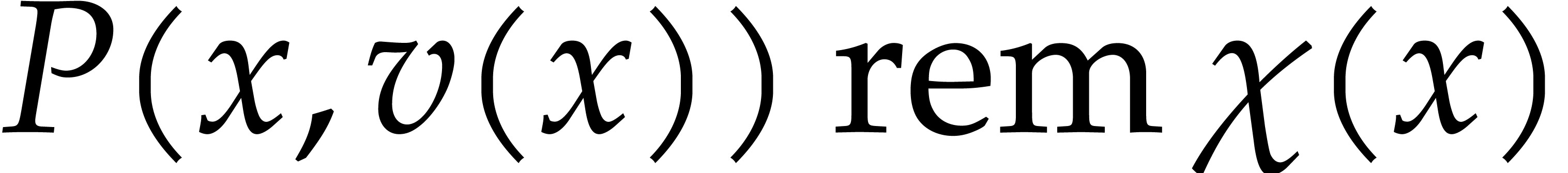 can be computed using
can be computed using 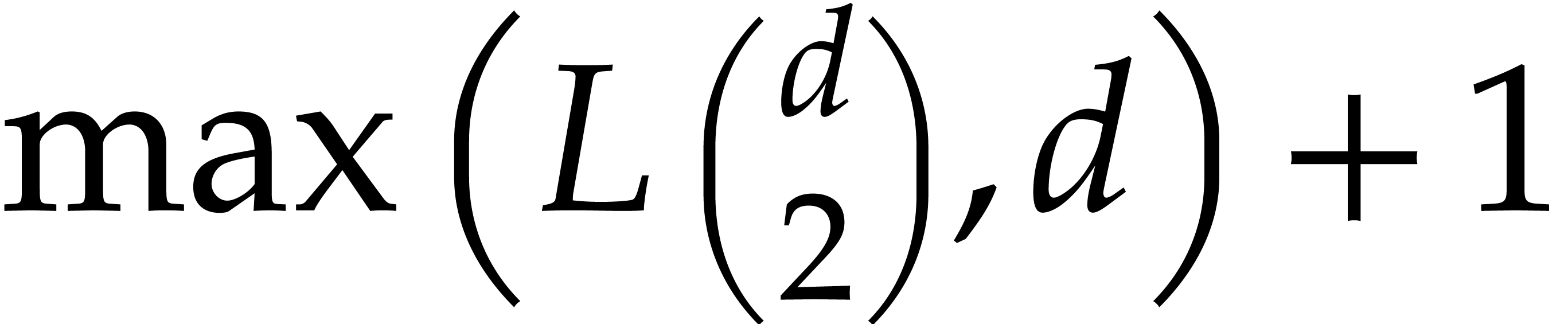 operations in
operations in  , where
, where
Proof. Assume first that we are given  distinct elements in
distinct elements in  .
By Lemma 2.1, we may compute a joined separating form
.
By Lemma 2.1, we may compute a joined separating form 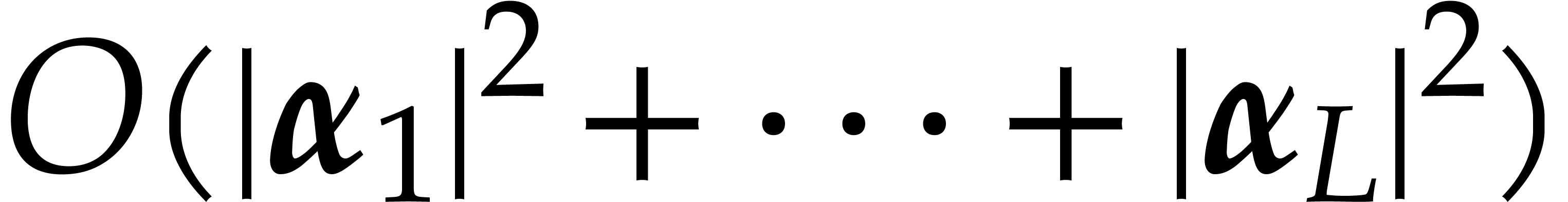 for
for  using
using
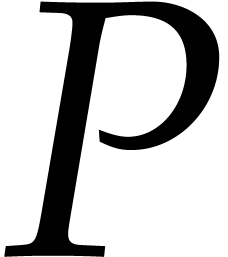 |
(2.2) |
operations in  . Let
. Let
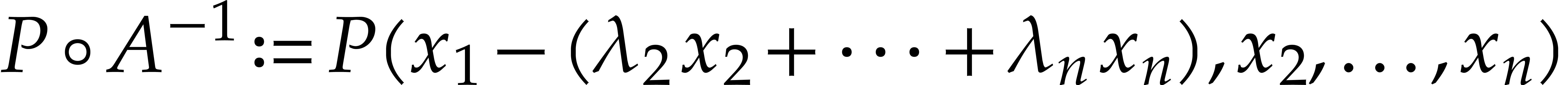
We replace 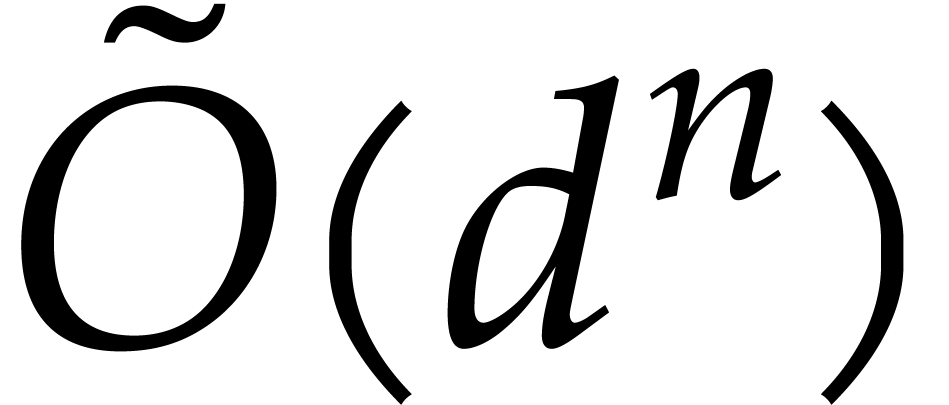 by
by  .
This takes
.
This takes 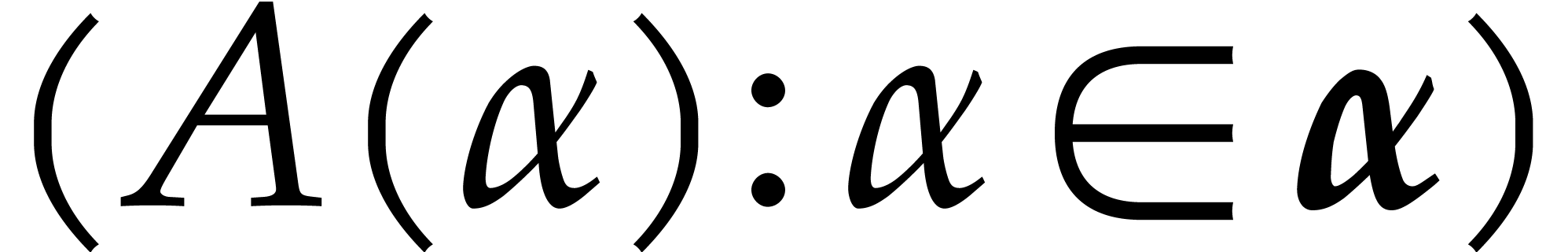 operations in
operations in  thanks to [16, Appendix A, Proposition A.5] and the
thanks to [16, Appendix A, Proposition A.5] and the 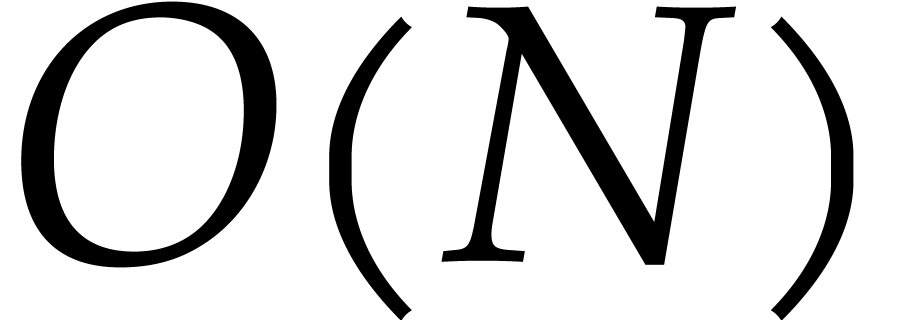 distinct elements in
distinct elements in  .
We next replace
.
We next replace 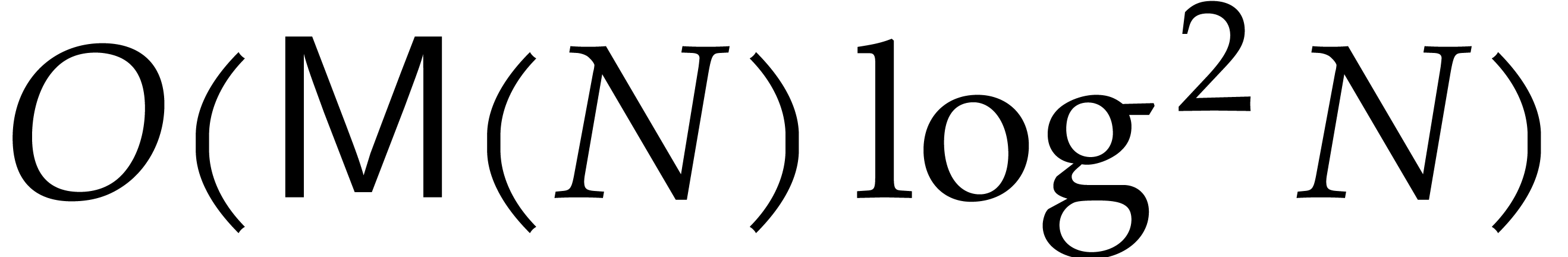 by
by  ,
using
,
using 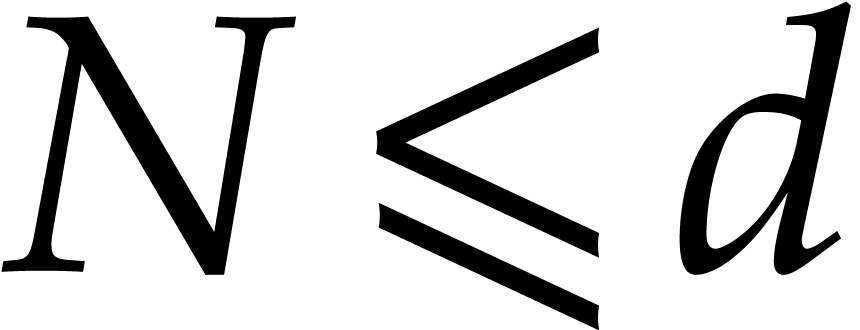 further operations. In this way, we reduce
the problem to the case where
further operations. In this way, we reduce
the problem to the case where  separates
separates 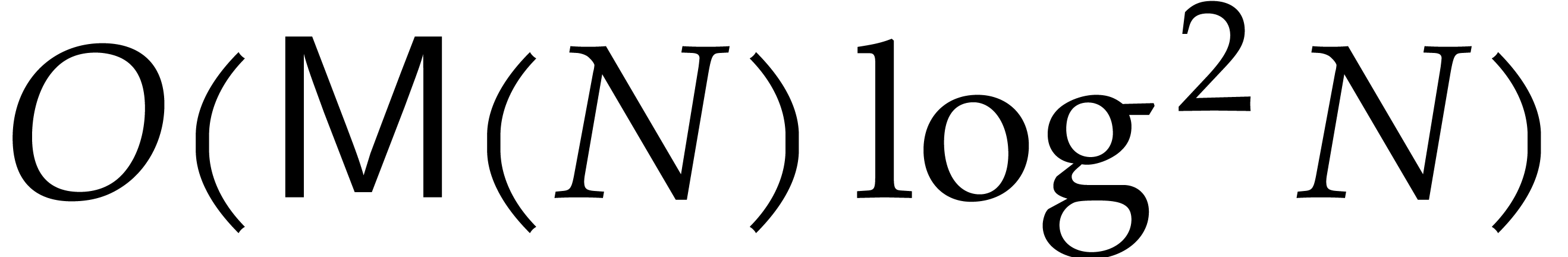 . It remains to compute
. It remains to compute  via Proposition 2.3.
via Proposition 2.3.
If  , that is
, that is 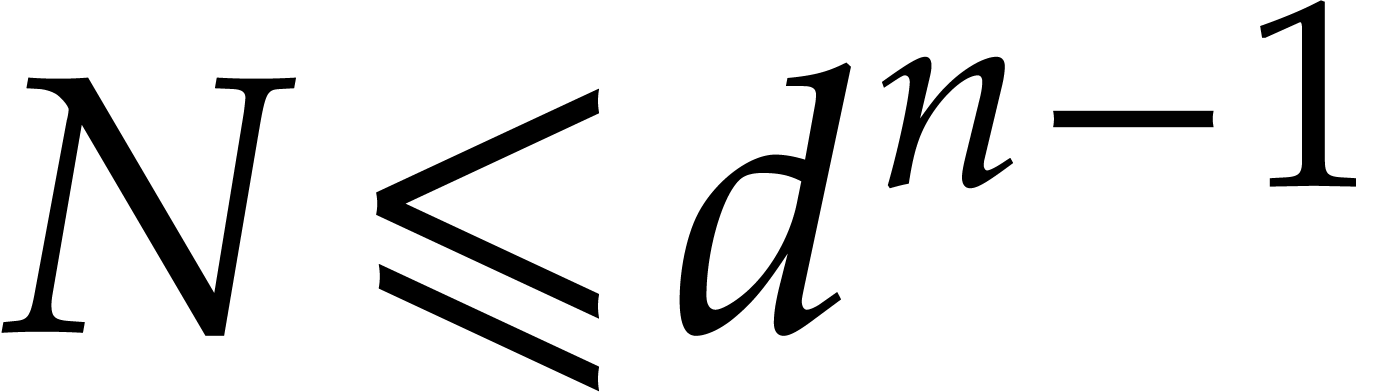 , then the cost of Algorithm 2.1
is
, then the cost of Algorithm 2.1
is 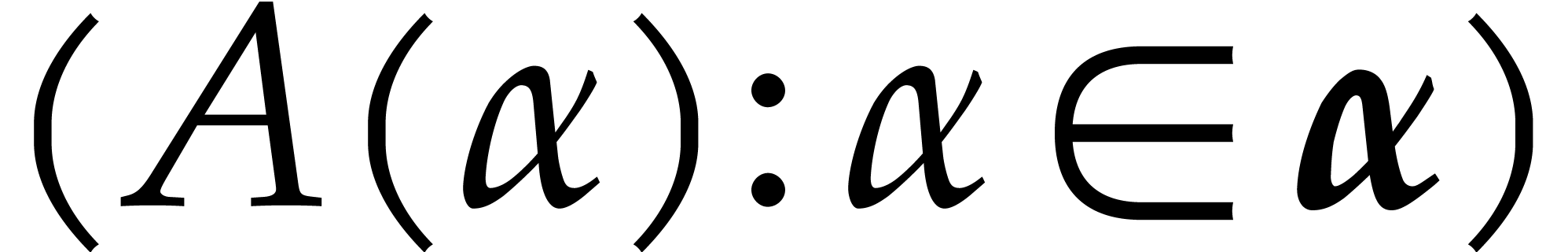 . If
. If  and
and  then
then  (since
(since 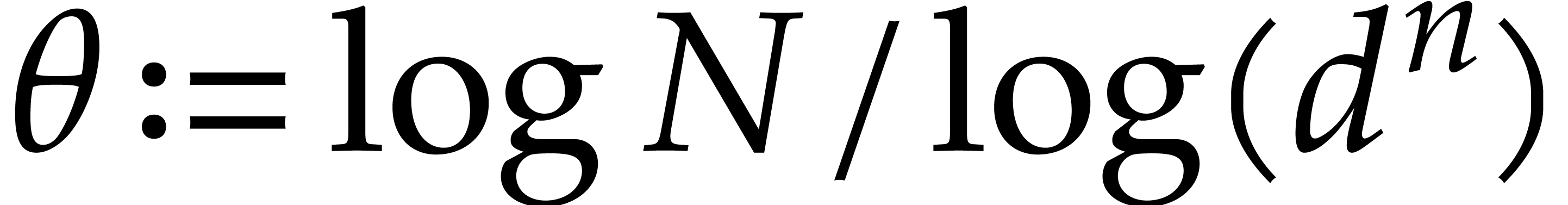 ) and the cost of Algorithm 2.1 becomes
) and the cost of Algorithm 2.1 becomes
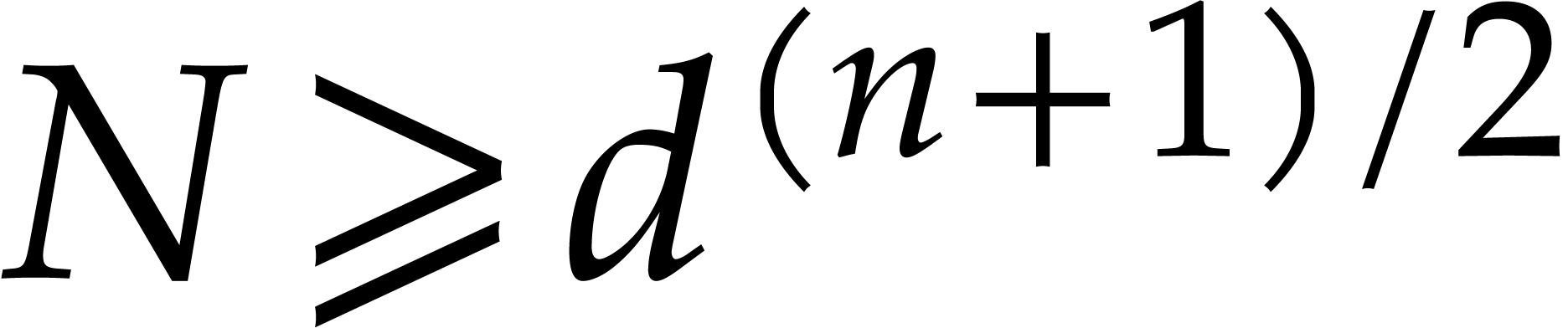
This dominates the contribution
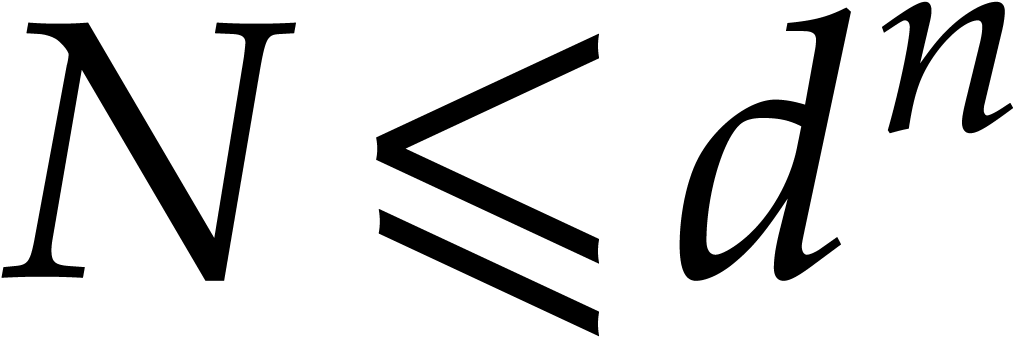
If 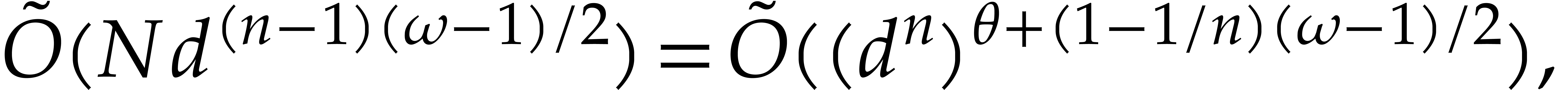 and
and 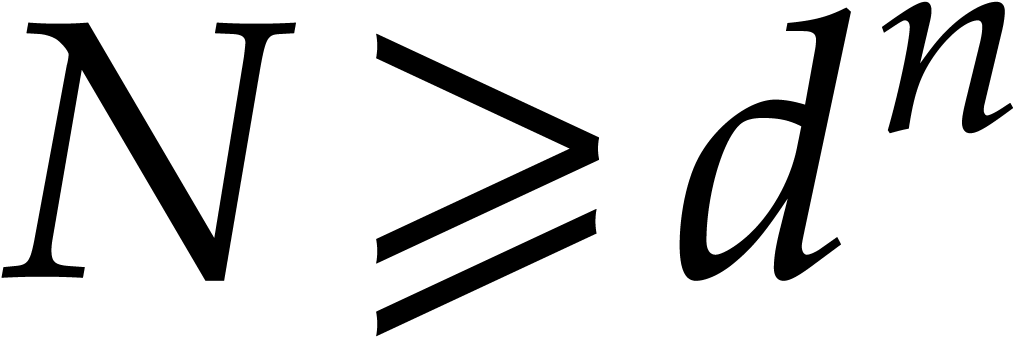 ,
then the cost of Algorithm 2.1 becomes
,
then the cost of Algorithm 2.1 becomes
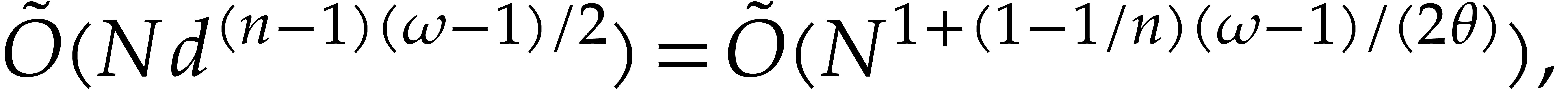
which again dominates the contribution  then the cost is
then the cost is
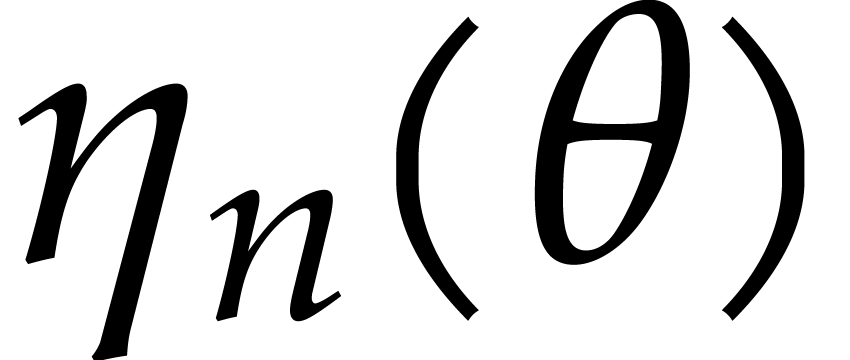
still dominating the contribution
It remains to deal with the case where  distinct
elements in
distinct
elements in  are not given. We appeal to
Proposition A.2: the hypotheses are met since the values
returned by the present evaluation algorithm are independent of the
are not given. We appeal to
Proposition A.2: the hypotheses are met since the values
returned by the present evaluation algorithm are independent of the  given elements of
given elements of  or of an
algebraic extension of it. The complexity overhead does not exceed
or of an
algebraic extension of it. The complexity overhead does not exceed
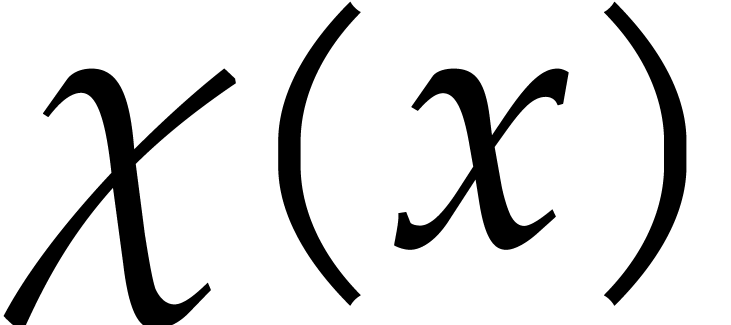
 |
Figure 2.1. Complexity exponent
|
 introduced in Theorem
2.6
.
introduced in Theorem
2.6
.
The bivariate case  behaves differently from the
general one, because the deterministic search of a separating form
becomes the bottleneck. The following theorem summarizes the cost of our
deterministic bivariate version of the Nüsken–Ziegler
algorithm.
behaves differently from the
general one, because the deterministic search of a separating form
becomes the bottleneck. The following theorem summarizes the cost of our
deterministic bivariate version of the Nüsken–Ziegler
algorithm.
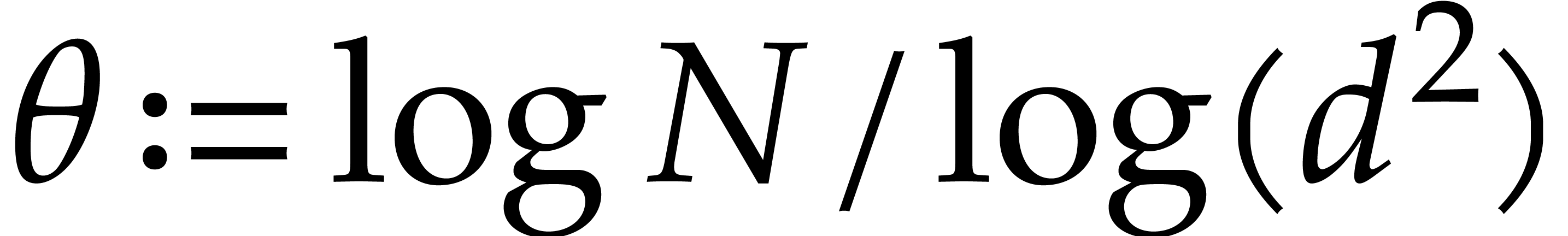 be of total degree
be of total degree 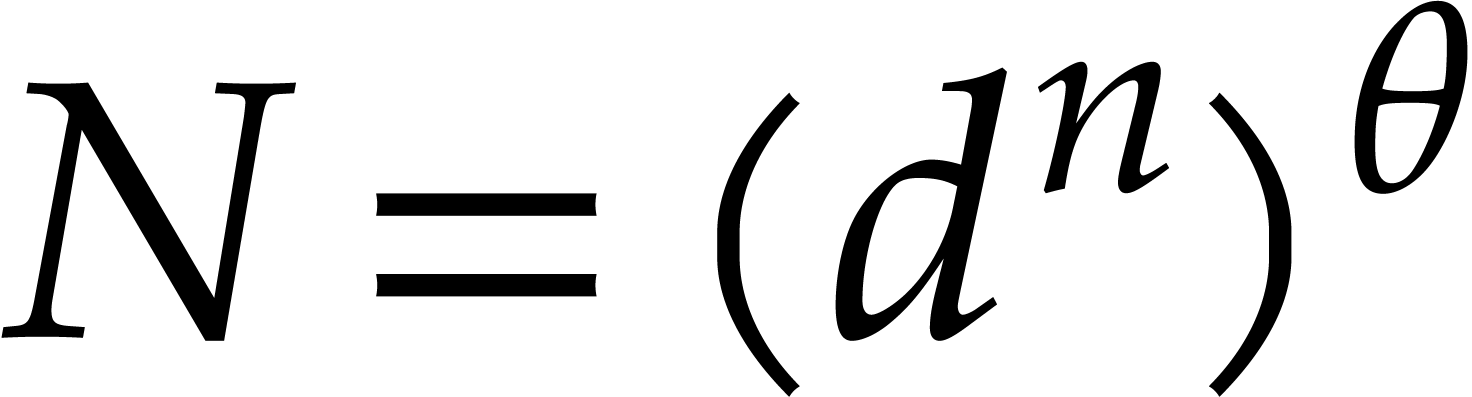 , let
, let 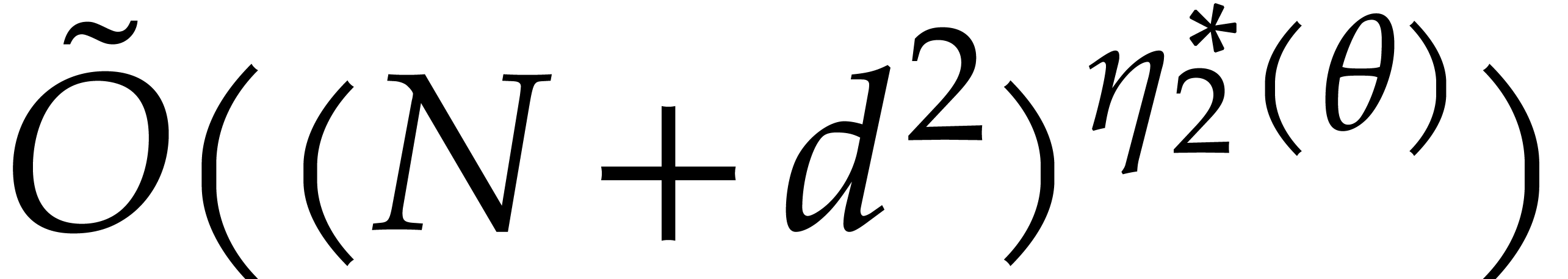 ,
and let
,
and let 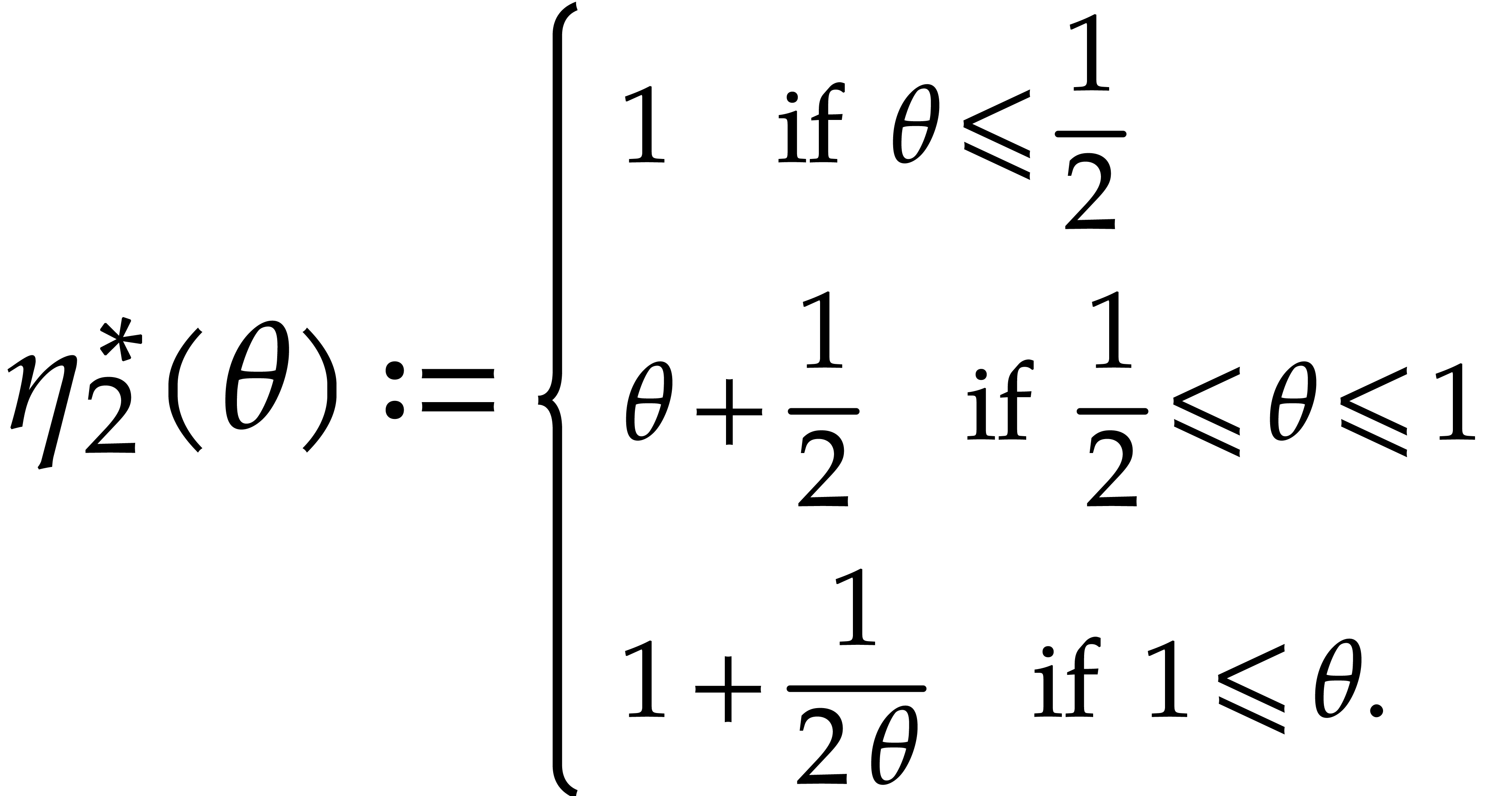 . Then
. Then 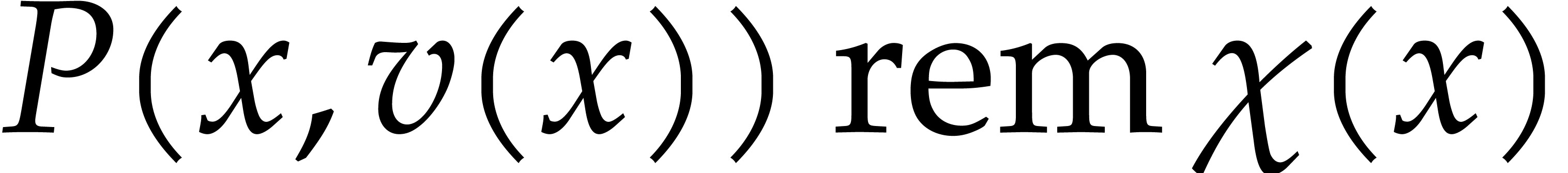 can be computed using
can be computed using  operations
in
operations
in  , where
, where
Proof. Assume first that we are given  elements in
elements in  .
By Lemma 2.1, a joined separating form
.
By Lemma 2.1, a joined separating form 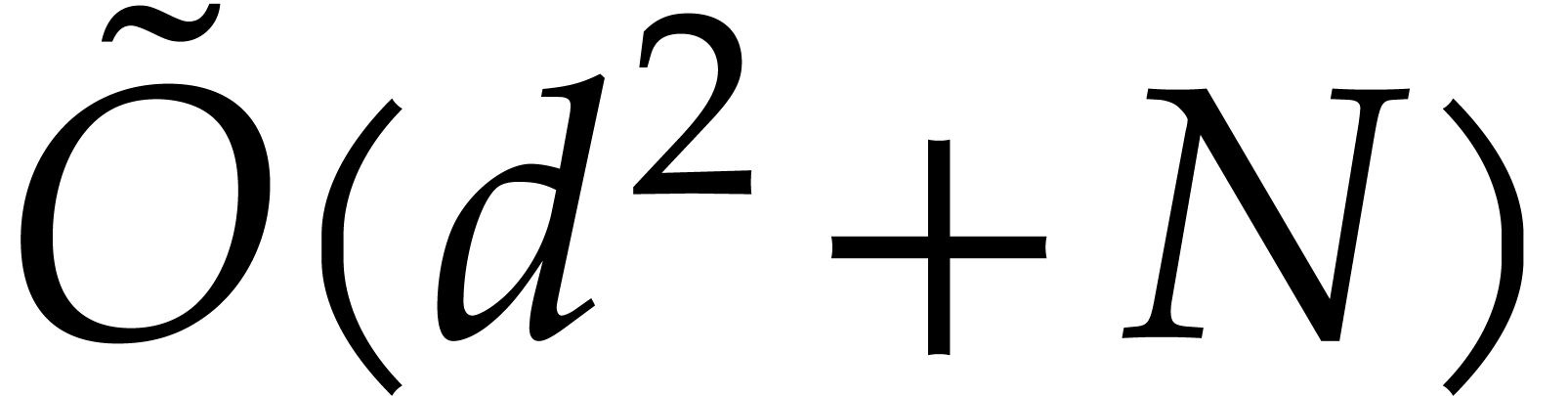 for
for  can be obtained in time
can be obtained in time
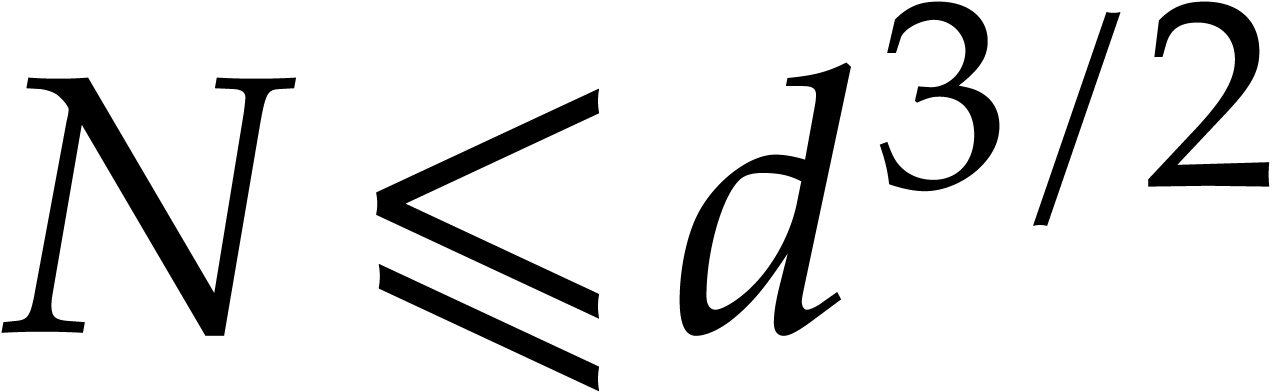 |
(2.3) |
Applying the linear change of coordinates to 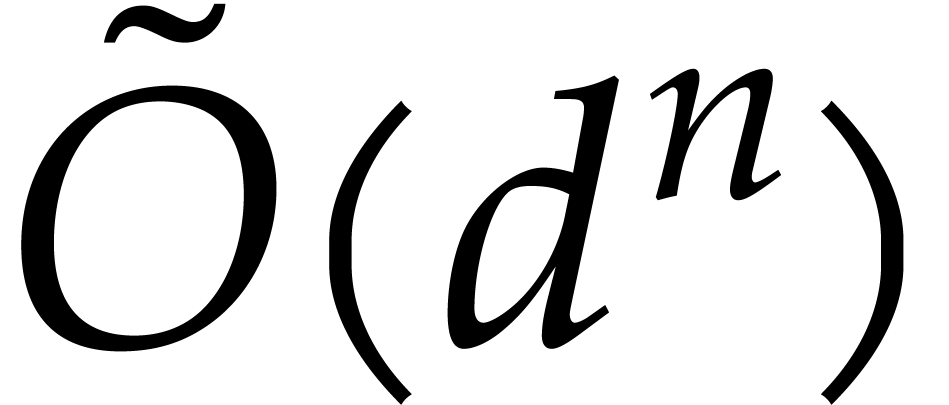 and
and
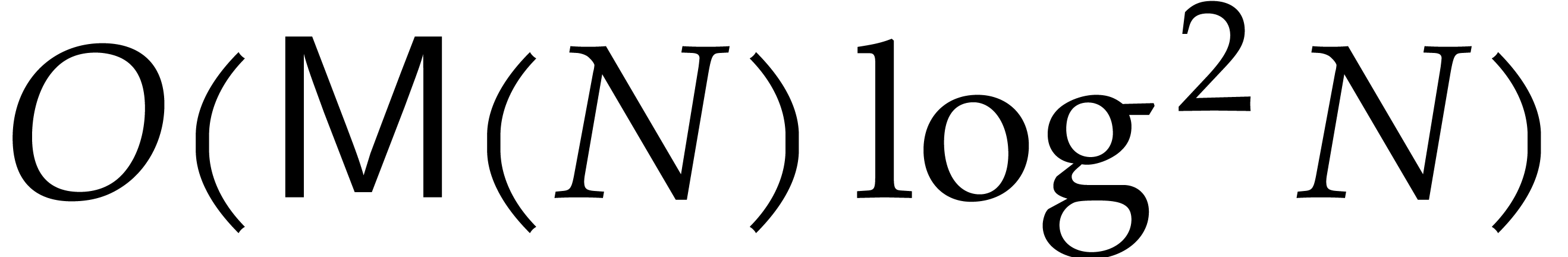 takes
takes 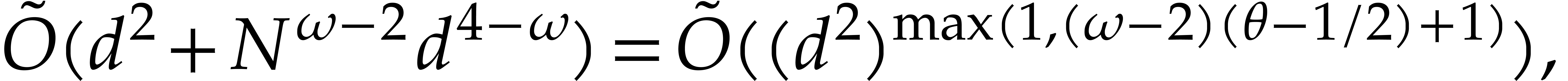 operations: here
we may use [1, Lemma 1] to change the variables
independently of the cardinality of
operations: here
we may use [1, Lemma 1] to change the variables
independently of the cardinality of  .
.
If  , then the cost of
Algorithm 2.1 is
, then the cost of
Algorithm 2.1 is
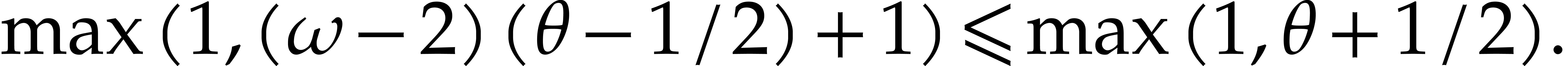
by Proposition 2.3. Since  ,
we also verify that
,
we also verify that
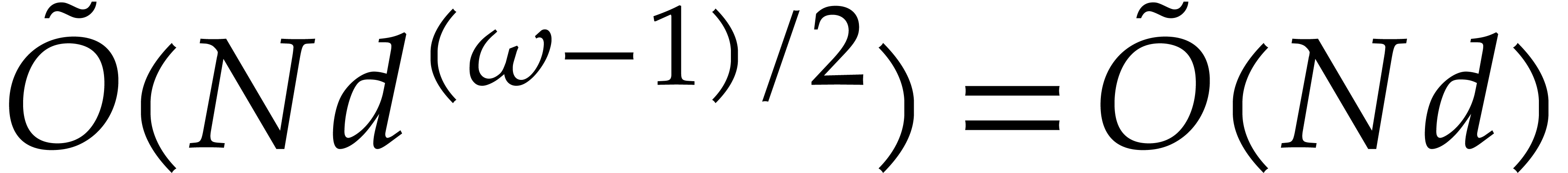
If 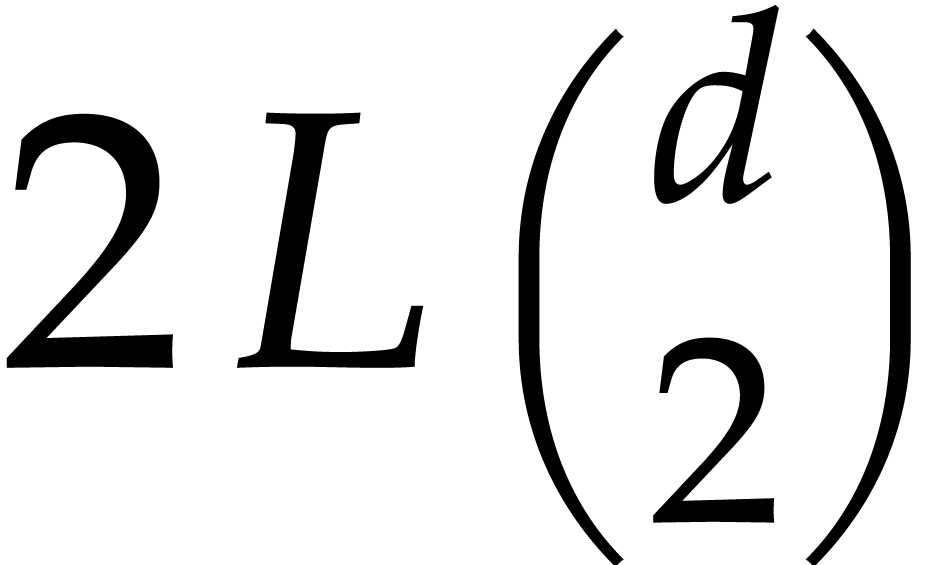 , then the cost of
Algorithm 2.1 is
, then the cost of
Algorithm 2.1 is 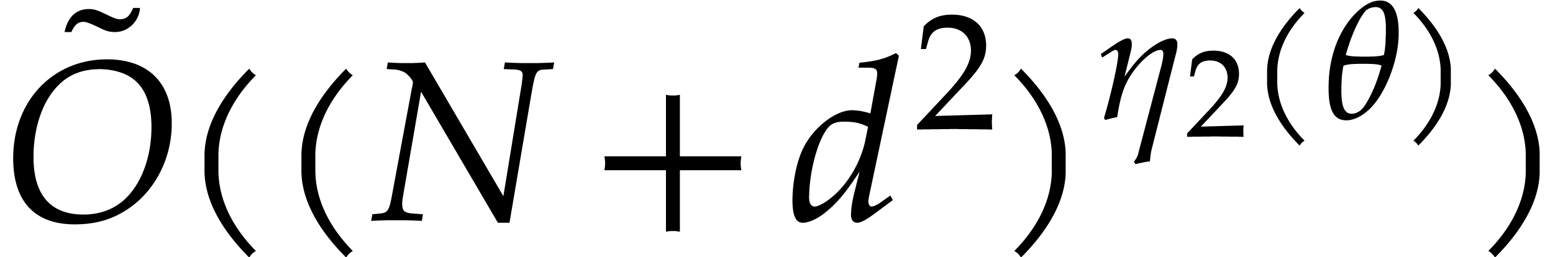 ,
which is again dominated by
,
which is again dominated by
Finally, if we are not given 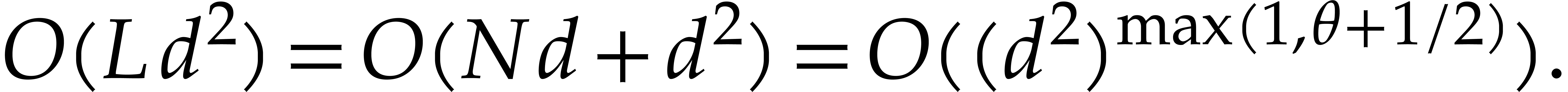 elements in
elements in  , then we apply Proposition A.2, as in the proof of Theorem 2.6.
, then we apply Proposition A.2, as in the proof of Theorem 2.6.
The next theorem rephrases the probabilistic version of Nüsken and
Ziegler for two variables and when 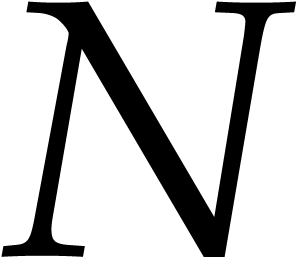 varies.
varies.
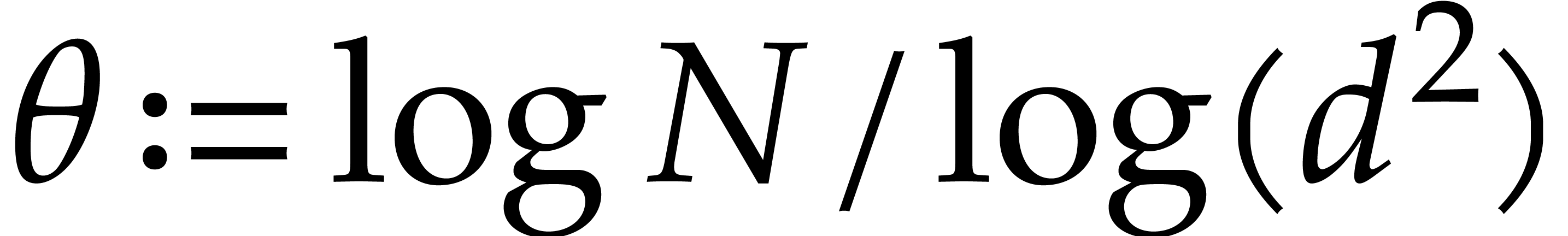 be of total degree
be of total degree 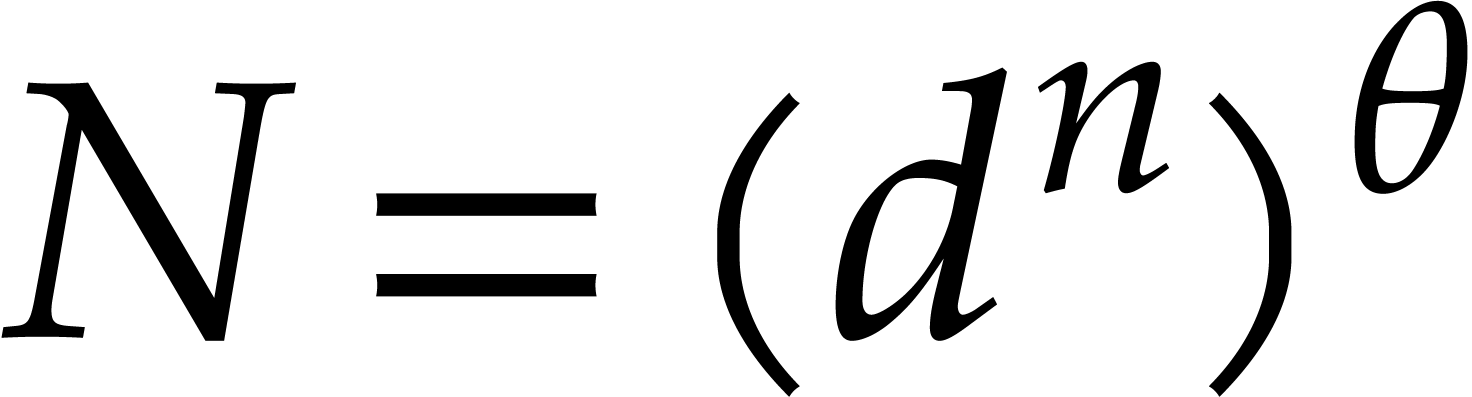 , let
, let 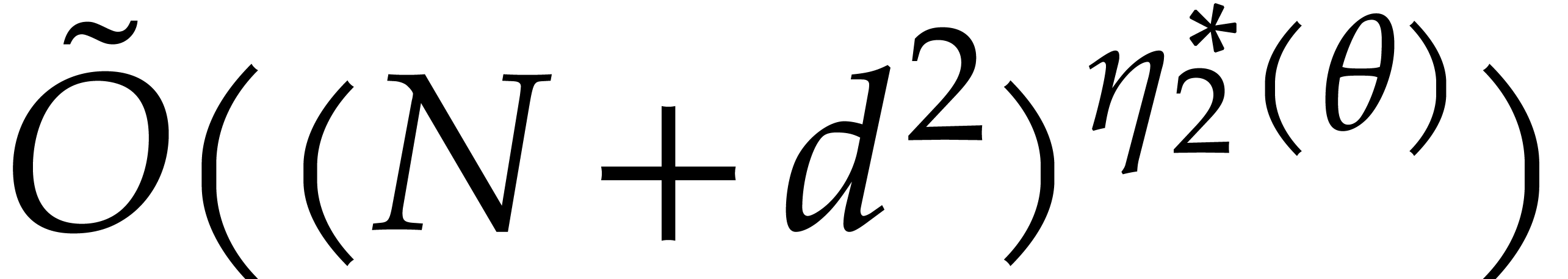 ,
let
,
let 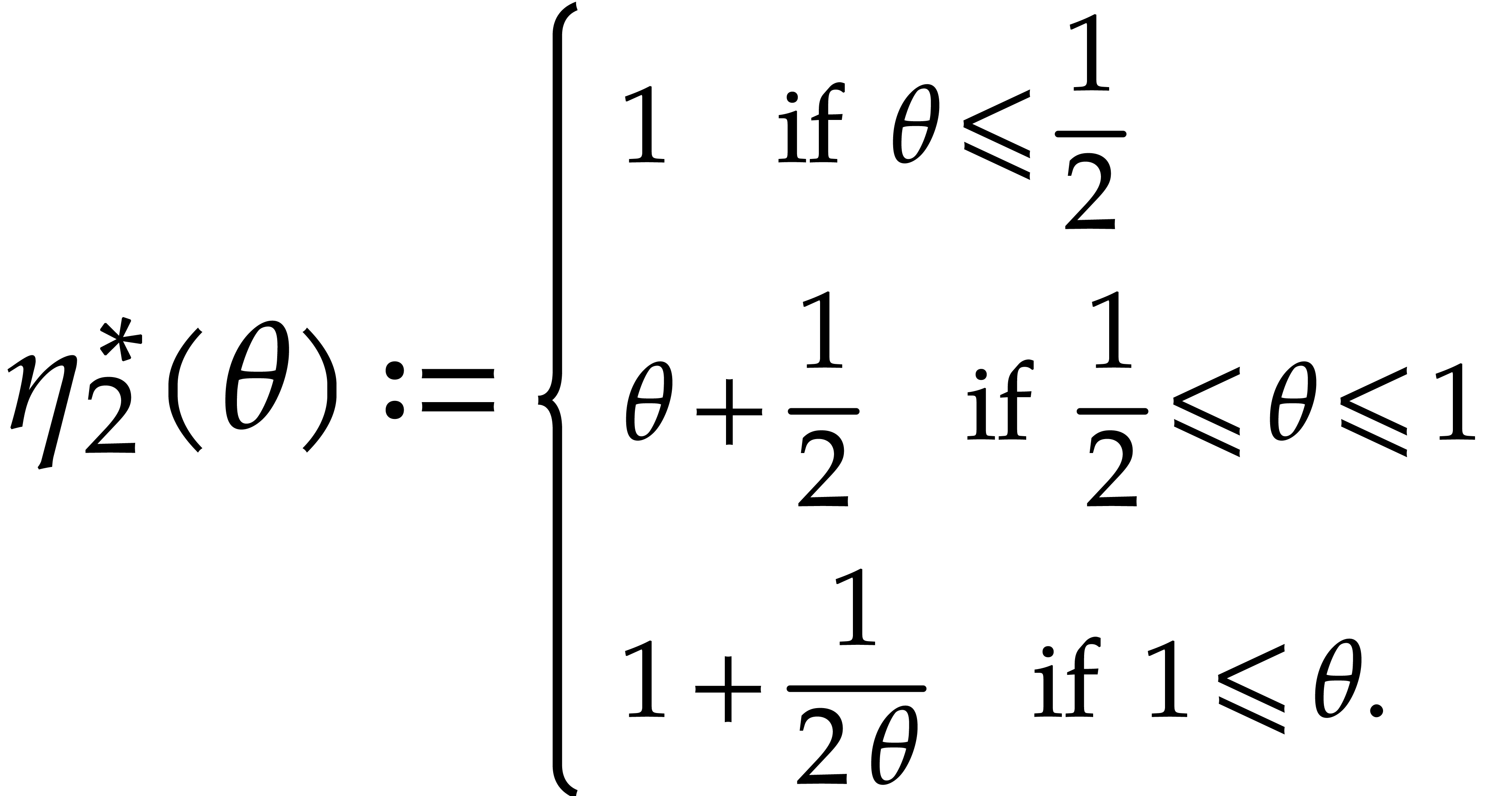 , and assume that we
are given
, and assume that we
are given 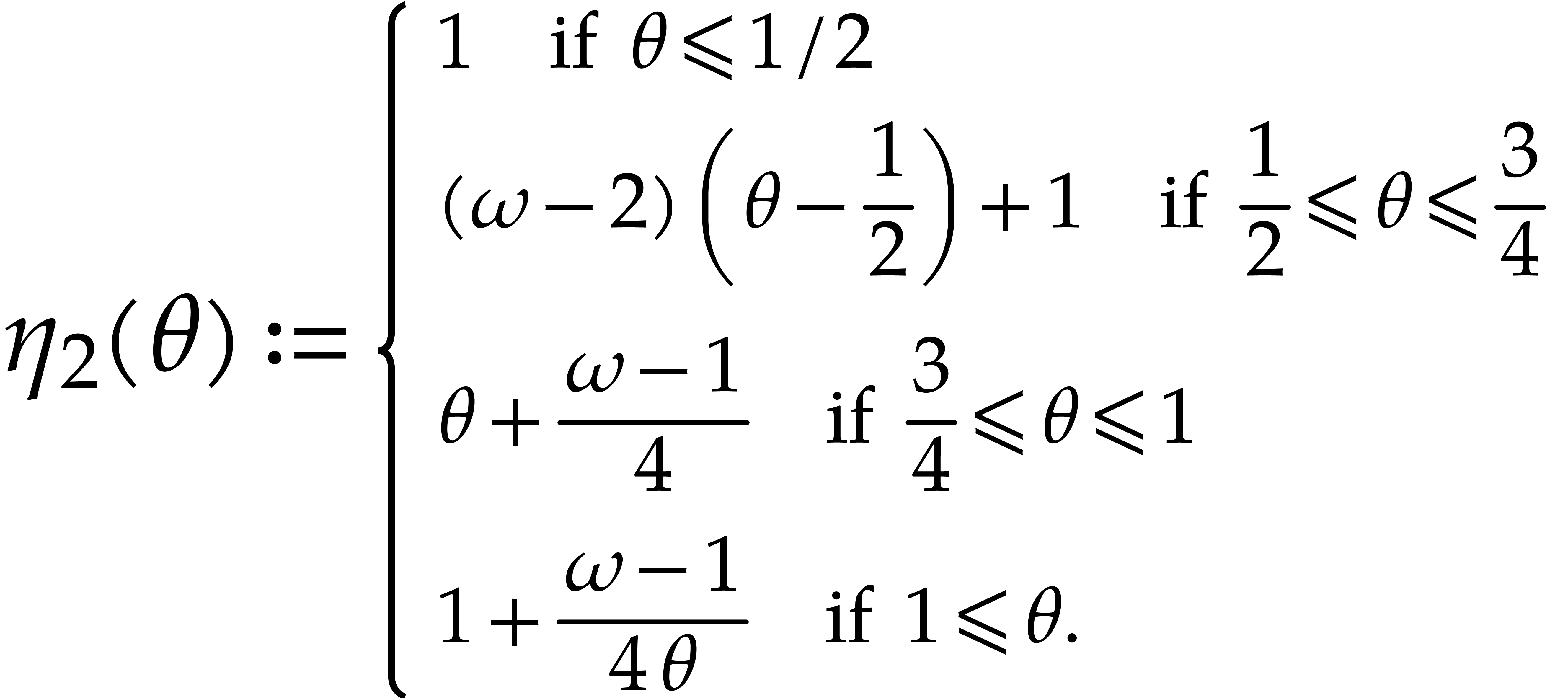 distinct elements in
distinct elements in  . Then
. Then  can be
computed by a probabilistic algorithm of Las Vegas type using an
expected number of
can be
computed by a probabilistic algorithm of Las Vegas type using an
expected number of 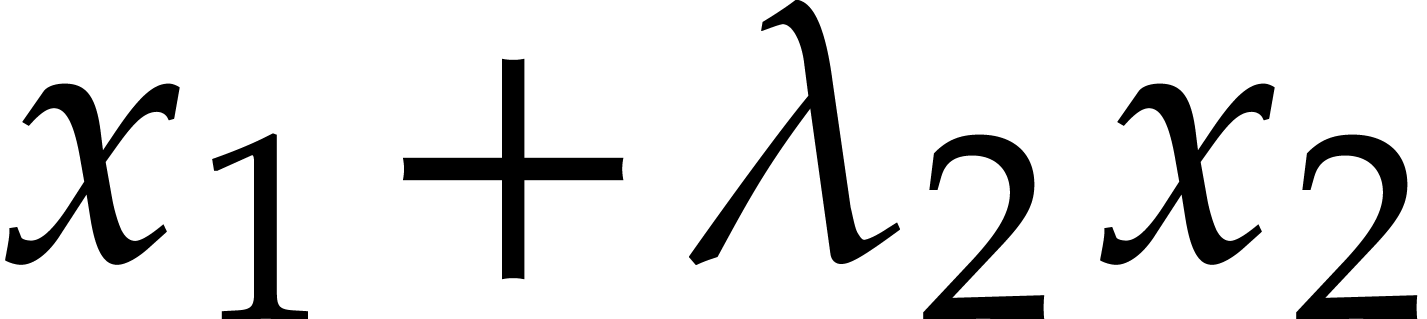 operations in
operations in  , where
, where
Proof. In order to find a joined separating form
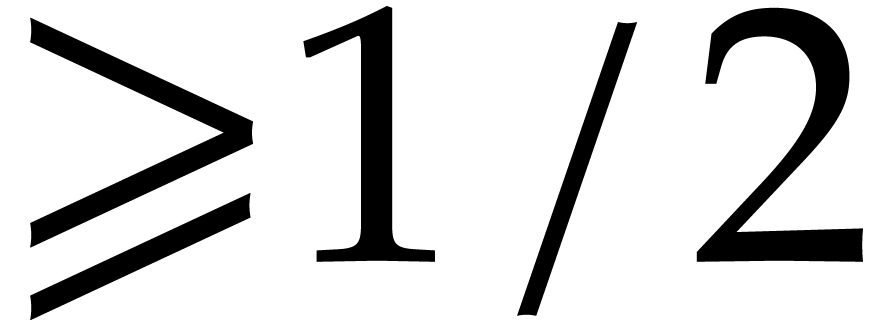 for
for  ,
it suffices to take a random
,
it suffices to take a random 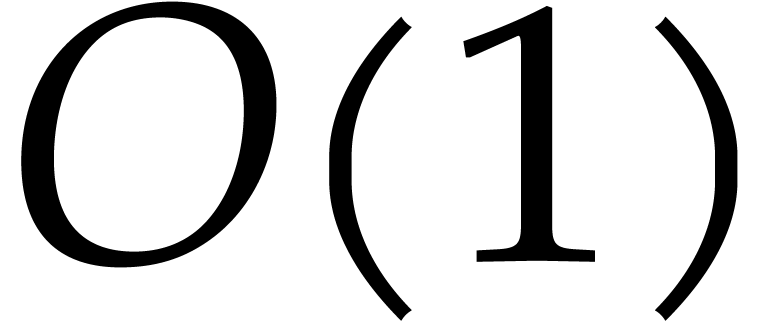 in the given subset
of
in the given subset
of  . The probability of
success for each trial is
. The probability of
success for each trial is  ;
see the proof of Lemma 2.1. So the expected number of
trials is
;
see the proof of Lemma 2.1. So the expected number of
trials is  . The rest of the
proof is adapted from the one of Theorem 2.7.
Alternatively, one may adapt the proof of Theorem 2.6, by
noting that the cost to compute a separating form is negligible, if we
are allowed to use a randomized algorithm.
. The rest of the
proof is adapted from the one of Theorem 2.7.
Alternatively, one may adapt the proof of Theorem 2.6, by
noting that the cost to compute a separating form is negligible, if we
are allowed to use a randomized algorithm.
 when
when
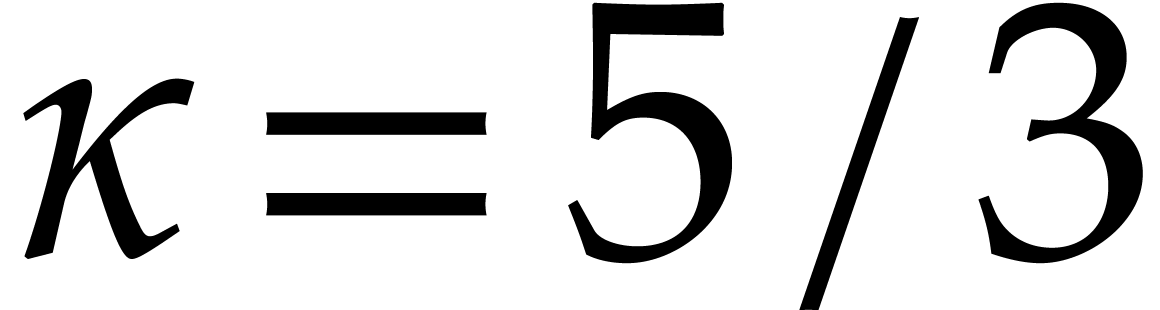 .
.
In this section, we refine our complexity analysis of the amortized
algorithm for the evaluation of multivariate polynomials from [17].
Here amortized means that the set of evaluation points is considered to
be fixed and that several polynomials need to be evaluated at these same
points. The method of [17] first computes so-called
“heterogeneous bases” for the vanishing ideals of suitable
subsets of these evaluation points. These computations only depend on
the fixed set of evaluation points and this first step can therefore be
regarded as a precomputation. Then any given polynomial 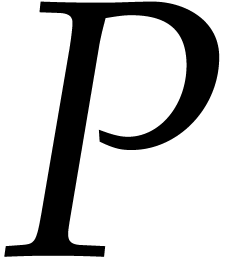 can be evaluated in quasi-linear time at the fixed set of points. This
second step makes intensive use of the precomputed heterogeneous bases.
can be evaluated in quasi-linear time at the fixed set of points. This
second step makes intensive use of the precomputed heterogeneous bases.
The main novelty of this section is a precise analysis of the cost of
the required precomputations. From this, we will be able to derive new
complexity bounds for non-amortized multi-point evaluation, by balancing
the costs of the precomputation and evaluation steps. Throughout this
section 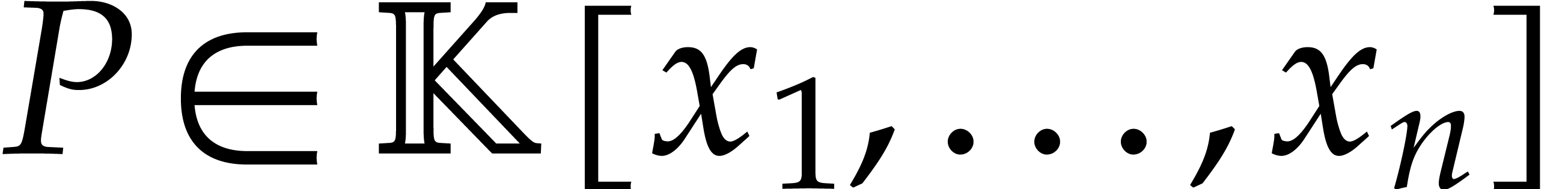 and
and 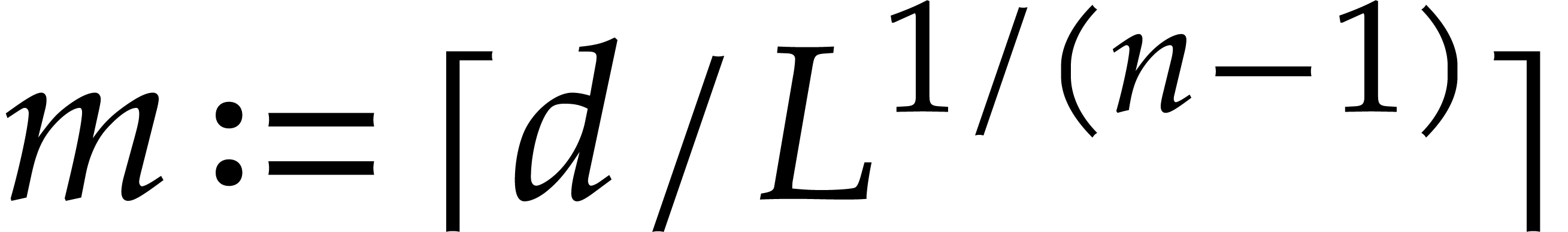 denote the
polynomial and the tuple of evaluation points, respectively. We also
write
denote the
polynomial and the tuple of evaluation points, respectively. We also
write 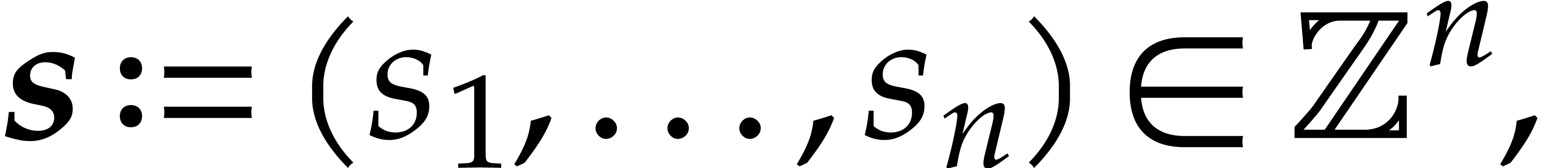 for the ideal of
for the ideal of  that consists of all polynomials that vanish at
that consists of all polynomials that vanish at  . We recall that the dimension
. We recall that the dimension 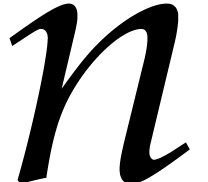 is fixed.
is fixed.
Let us consider a vector
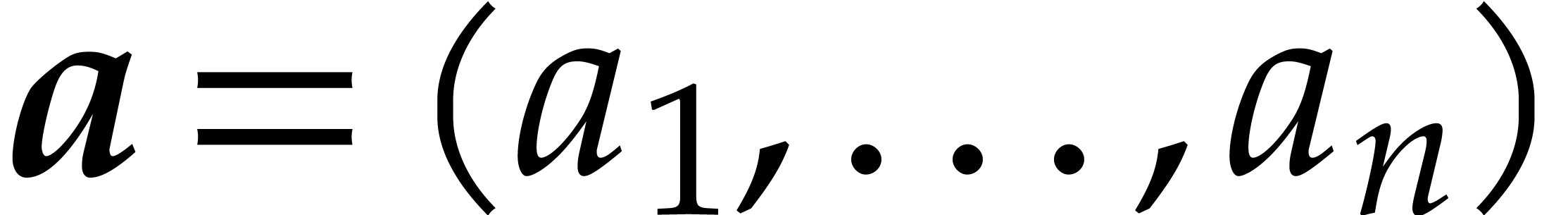
called a shift for the degrees, the 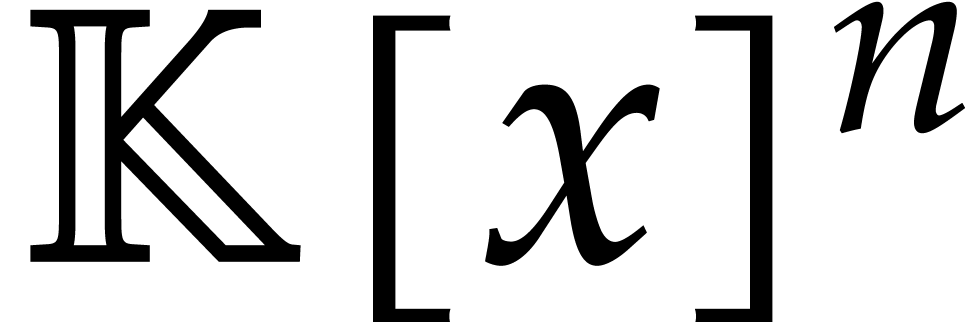 -degree of a row vector
-degree of a row vector 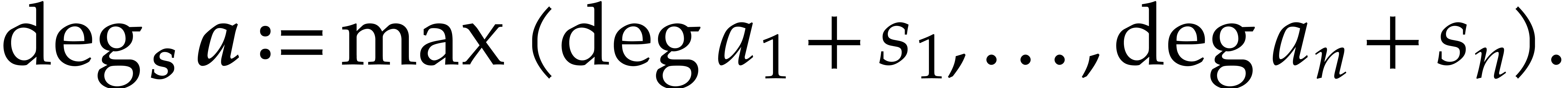 in
in  is defined as
is defined as

If  is non-zero, then the
is non-zero, then the  -pivot index of
-pivot index of  is the largest index
is the largest index  for which the latter
maximum is reached. The entry
for which the latter
maximum is reached. The entry 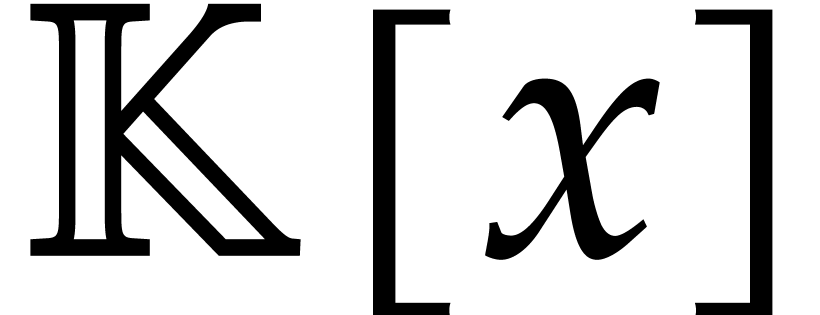 is called the
is called the
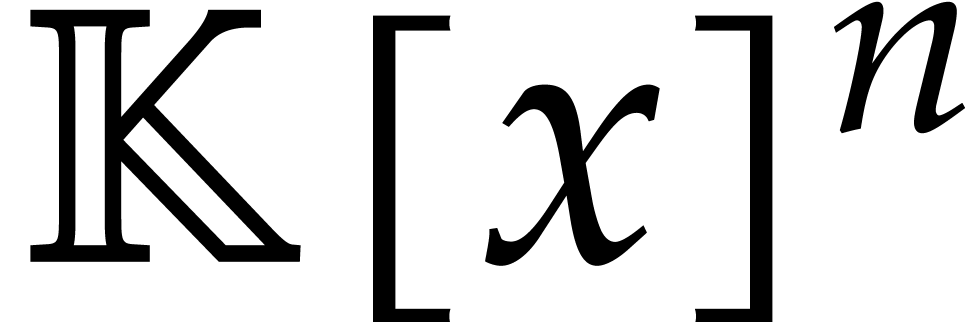 -pivot, and
its degree is the
-pivot, and
its degree is the 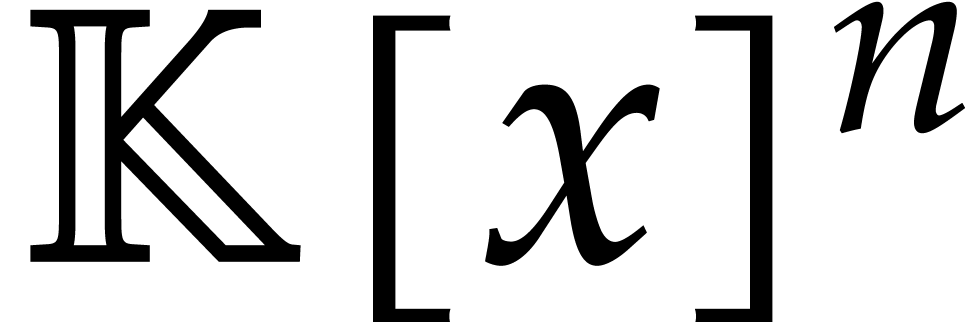 -pivot
degree. If
-pivot
degree. If  is zero, then its
is zero, then its 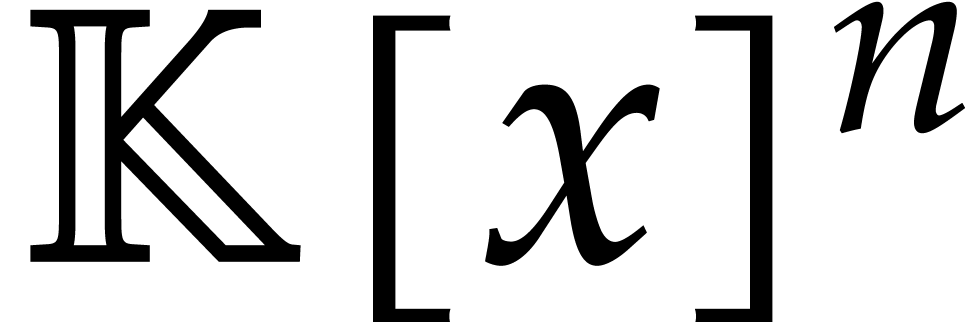 -pivot index is defined to be zero.
-pivot index is defined to be zero.
Let  denote a
denote a  matrix with
entries in
matrix with
entries in  . The matrix
. The matrix  is in
is in 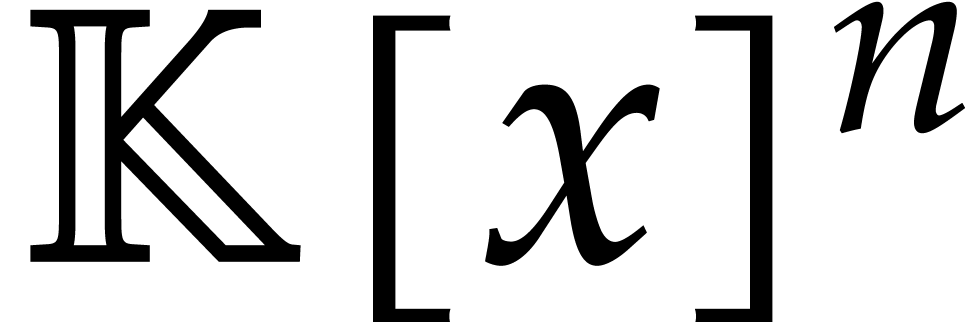 -Popov
form if the following properties are satisfied:
-Popov
form if the following properties are satisfied:
The non-zero 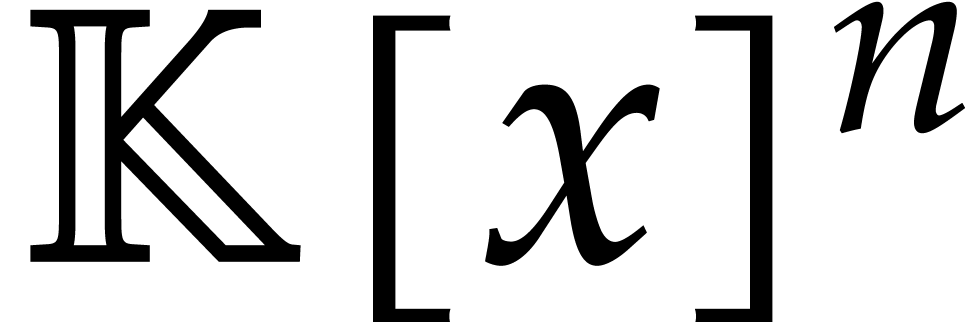 -pivot
indices of the rows of
-pivot
indices of the rows of  are in increasing
order;
are in increasing
order;
The 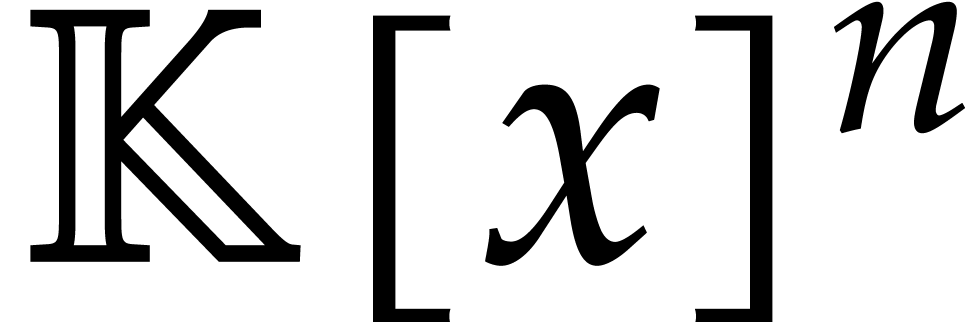 -pivots of the rows
of
-pivots of the rows
of  are monic (i.e. have leading
coefficient
are monic (i.e. have leading
coefficient  );
);
The 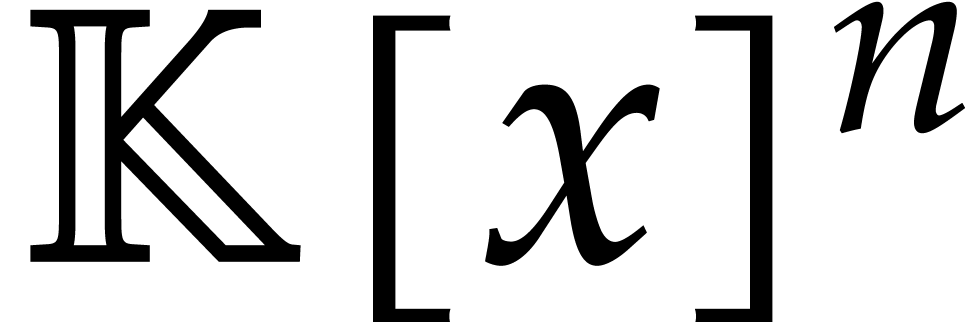 -pivots of
-pivots of  have a degree strictly larger than the other elements
in their column.
have a degree strictly larger than the other elements
in their column.
If 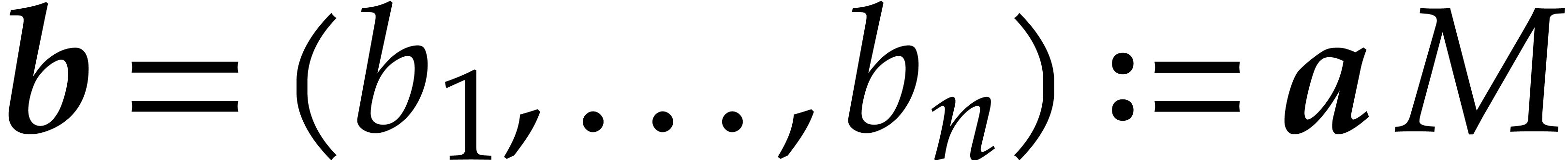 and
and  is non-singular,
then its
is non-singular,
then its 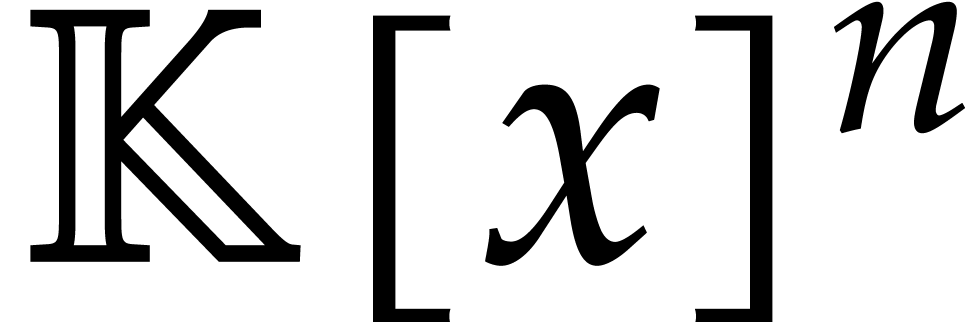 -pivots are the
diagonal elements, because none of its rows are zero. In this case,
-pivots are the
diagonal elements, because none of its rows are zero. In this case,  satisfies the “predictable degree”
property:
satisfies the “predictable degree”
property:
 be a non-singular
be a non-singular 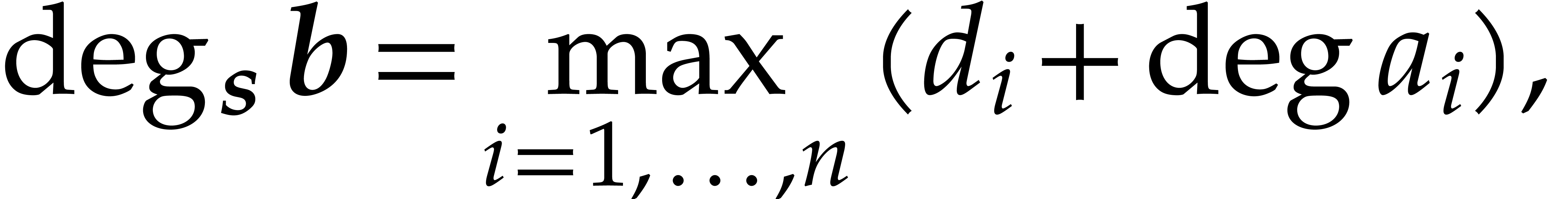 matrix in
matrix in  -Popov form. If
-Popov form. If
 for some row vector
for some row vector  , then
, then

where  denotes the
denotes the  -degree of the
-degree of the  -th
row of
-th
row of  .
.
Proof. See [22, Theorem 1.1], for
instance.
Given non-constant polynomials  in
in  , and given an
, and given an 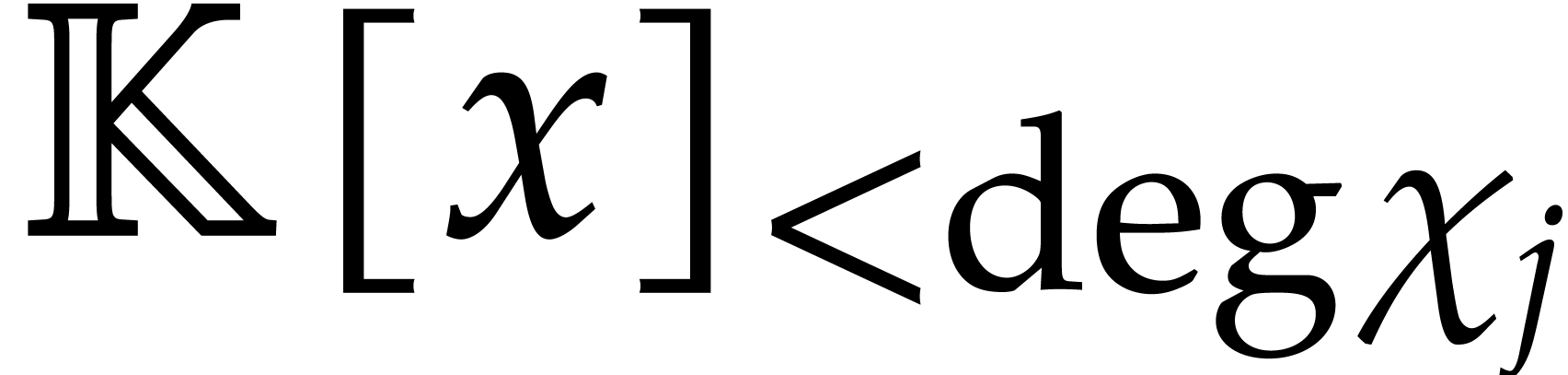 matrix
matrix
 with entries
with entries  in
in 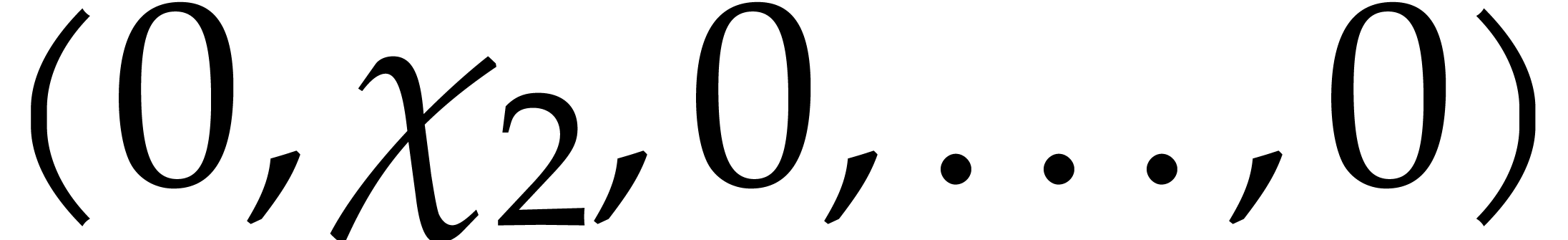 ,
, 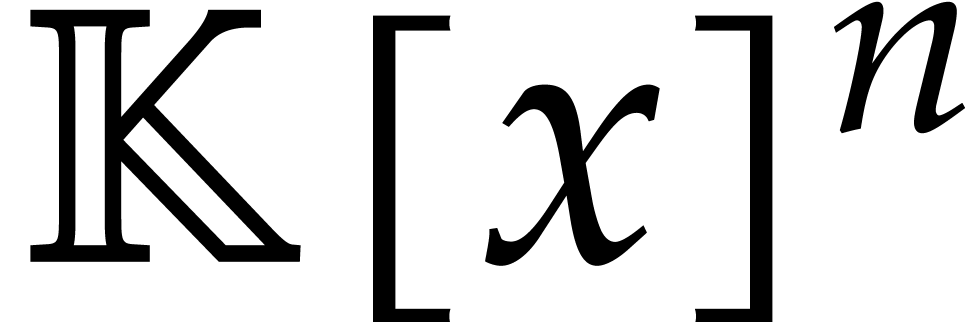 -Popov
forms will be used to compute the kernel of the map
-Popov
forms will be used to compute the kernel of the map
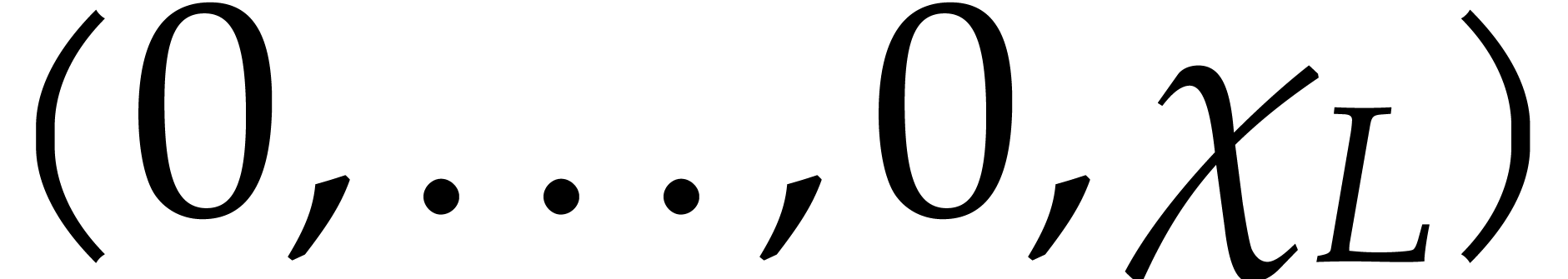
With  , the vectors
, the vectors  ,
,  ,...,
,...,
 are a free family in
are a free family in  , so the kernel of
, so the kernel of  is a free
is a free
 -module of rank
-module of rank  .
.
 , non-constant polynomials
, non-constant polynomials  in
in  , and
an
, and
an 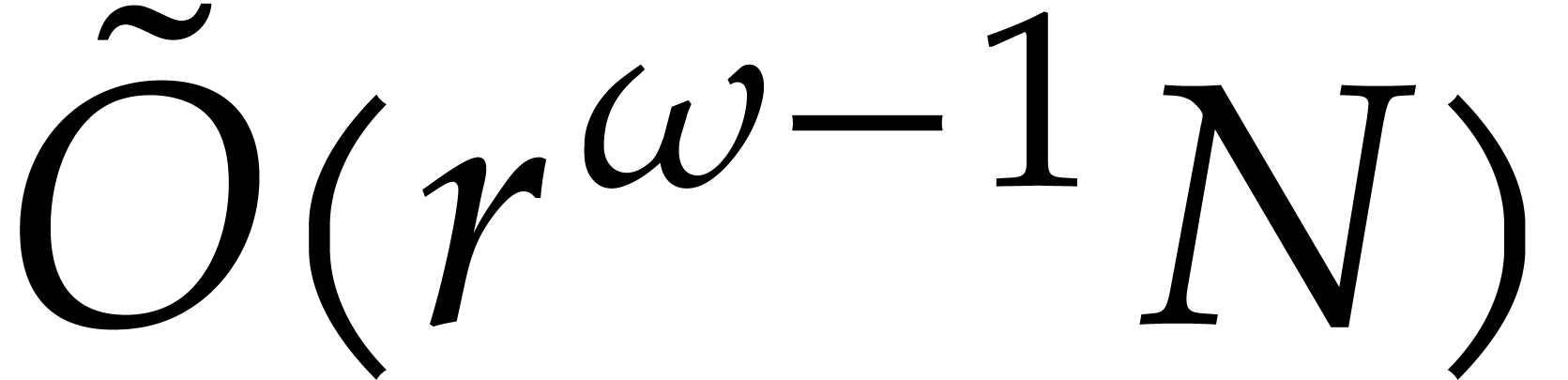 matrix
matrix 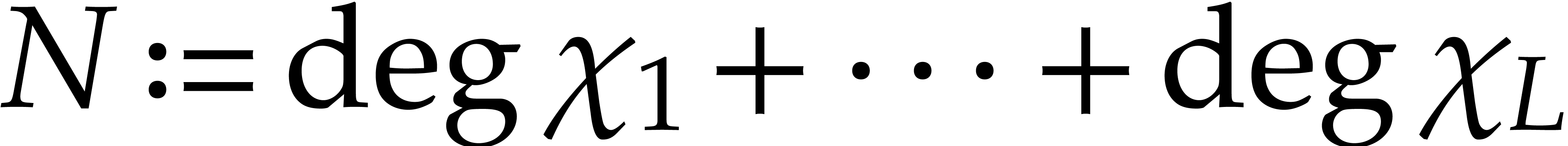 with entries
with entries
 in
in  ,
there exists a unique
,
there exists a unique  matrix
matrix  in s-Popov form such that the rows of
in s-Popov form such that the rows of 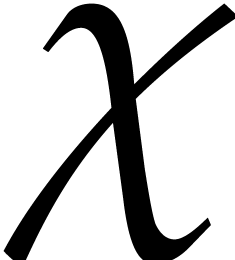 are a basis of ker
are a basis of ker  .
If
.
If 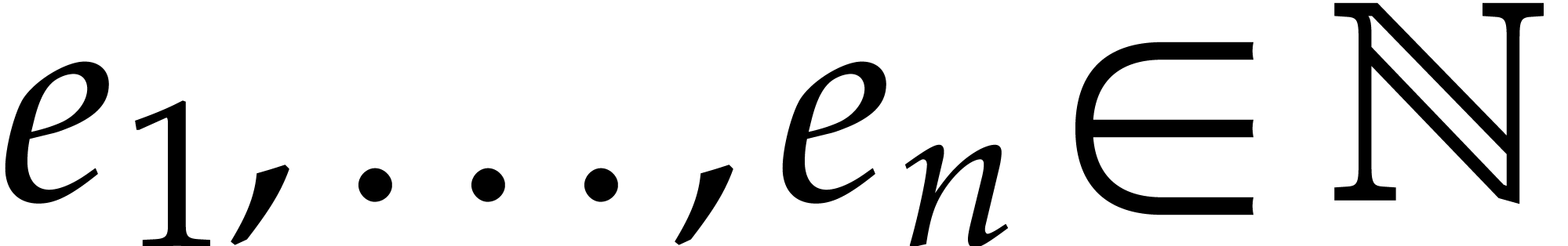 then
then 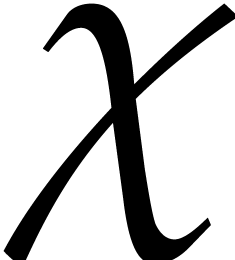 can be
computed using
can be
computed using 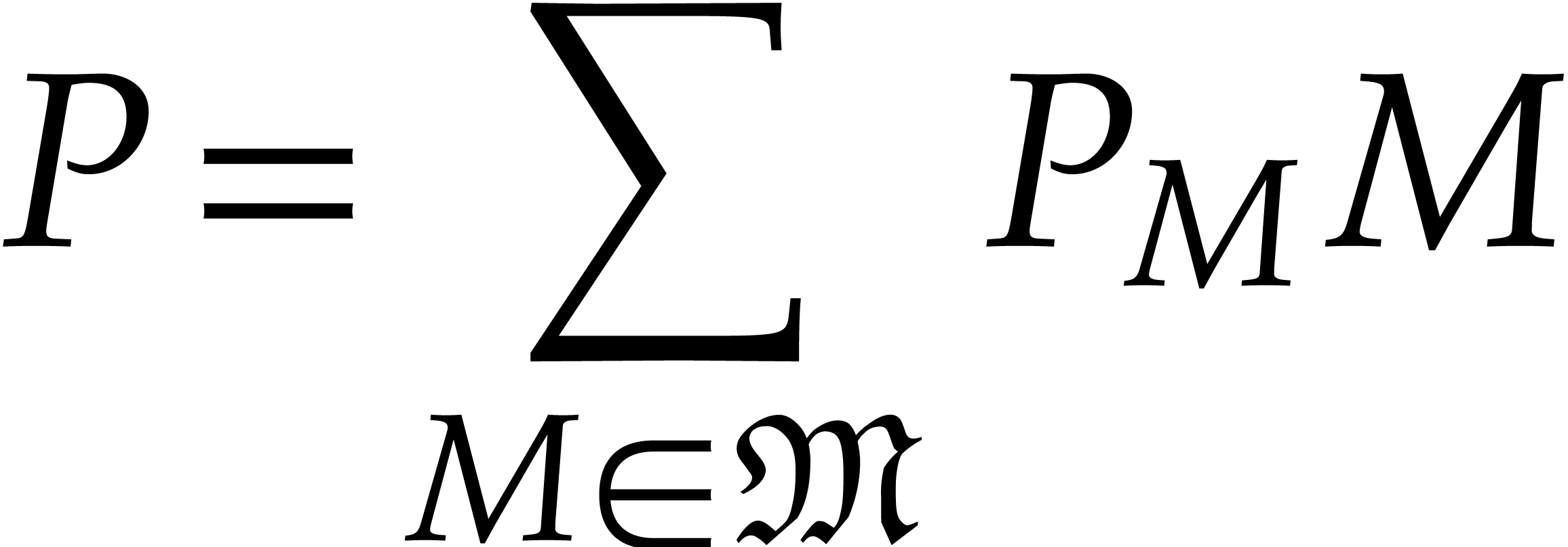 operations in
operations in  , where
, where 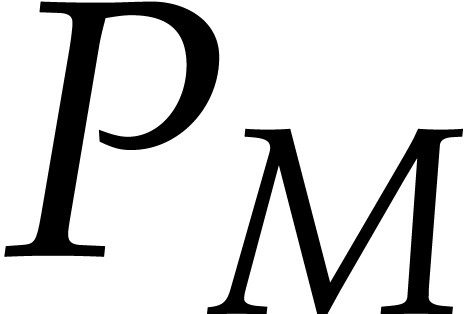 .
.
Let 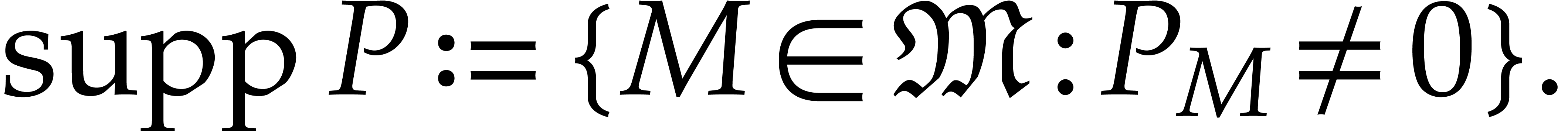 be the set of monomials
be the set of monomials  with
with  . Any polynomial
. Any polynomial  can uniquely be written as a linear combination
can uniquely be written as a linear combination
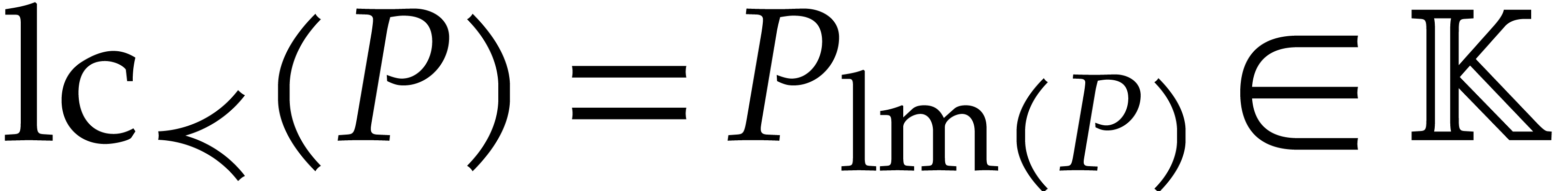
with coefficients  in
in  and
finite support
and
finite support
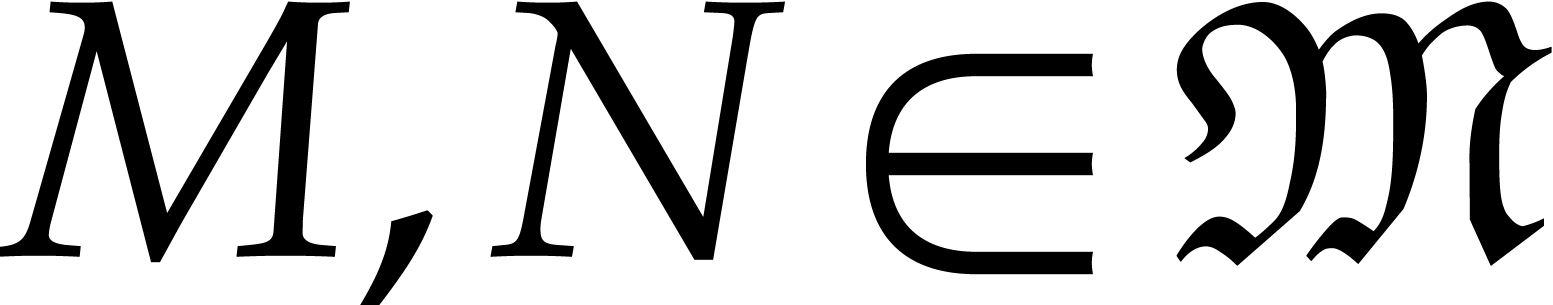
Given a total ordering  on
on 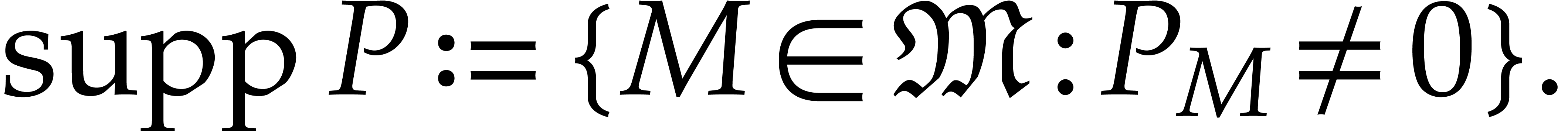 , the support of any non-zero polynomial
, the support of any non-zero polynomial  admits a unique maximal element
admits a unique maximal element 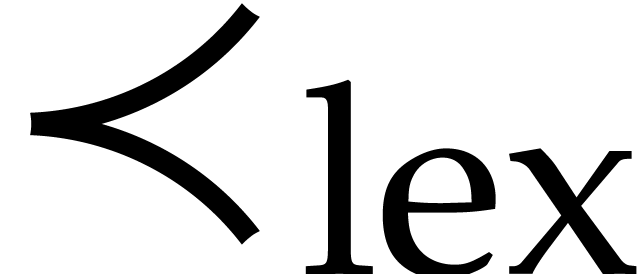 that is called the leading monomial of
that is called the leading monomial of  ; the corresponding coefficient
; the corresponding coefficient  is called the leading coefficient of
is called the leading coefficient of
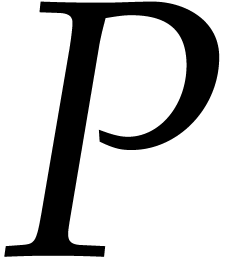 . A total ordering
. A total ordering 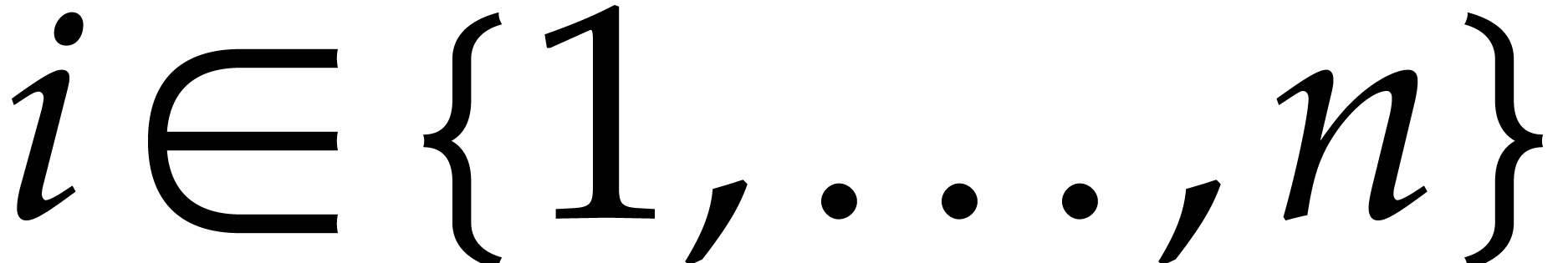 on
on 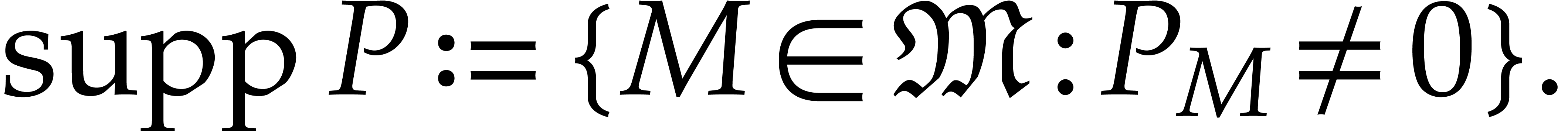 is said to be
admissible if
is said to be
admissible if
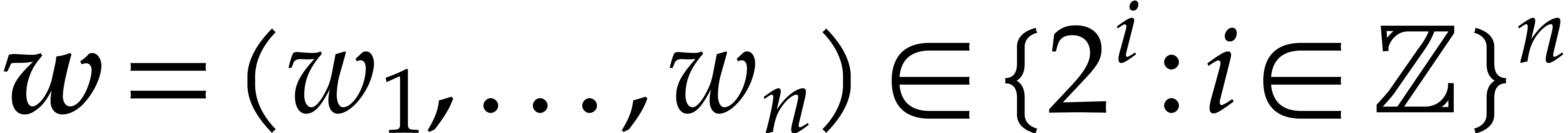
for all monomials 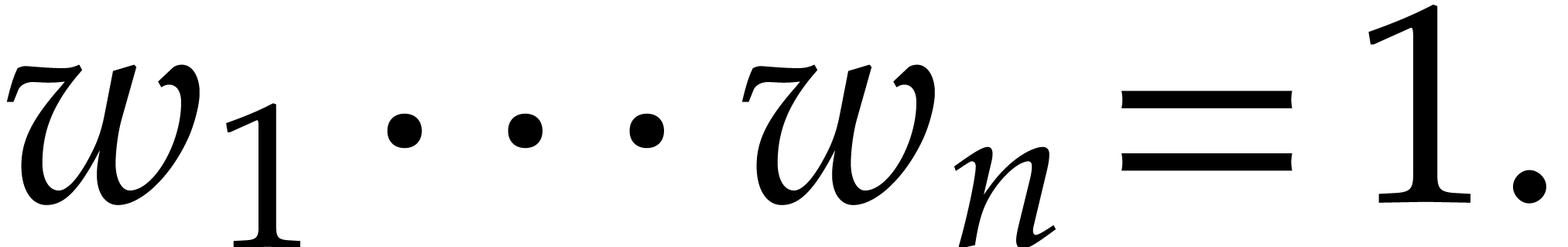 and
and  . In particular, the lexicographical ordering
. In particular, the lexicographical ordering 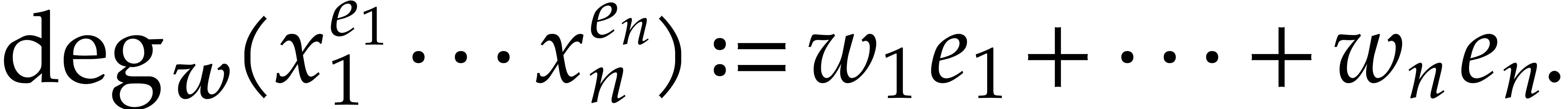 defined by
defined by
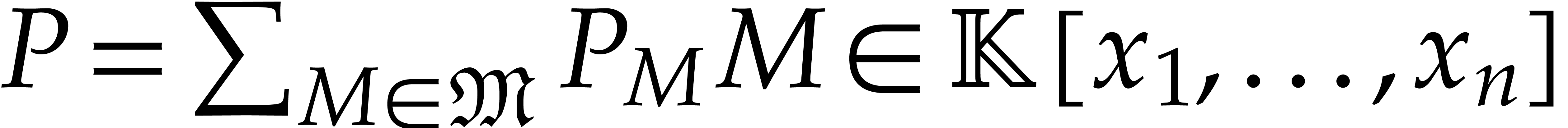
is admissible.
In the rest of the paper, an admissible weight will be
an 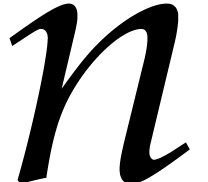 -tuple
-tuple
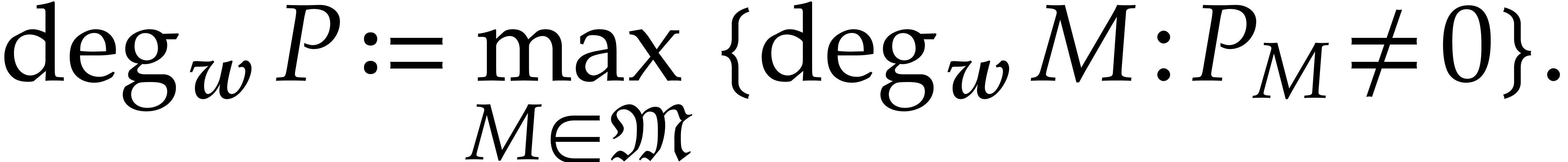
with
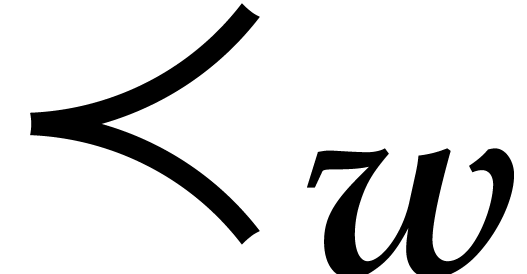 |
(3.1) |
Given a monomial  , we define
its
, we define
its  -degree by
-degree by
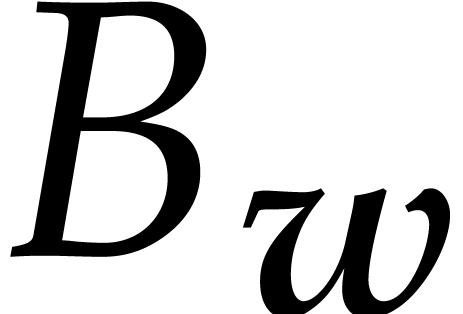
For a non-zero polynomial 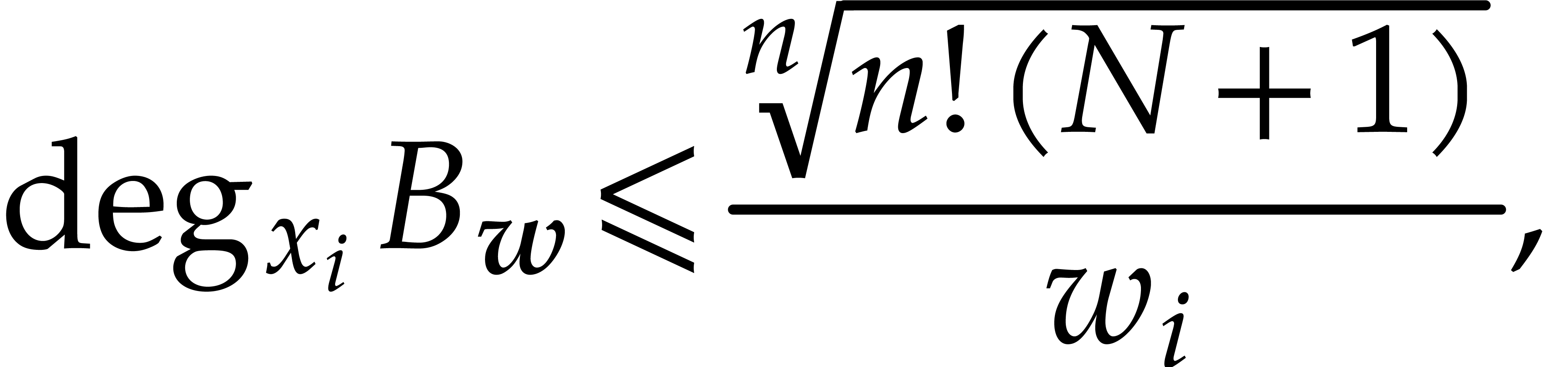 ,
we define its
,
we define its  -degree
by
-degree
by

We also define the ordering  on
on 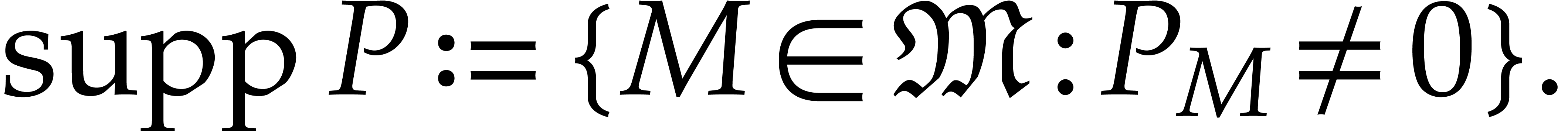 by
by

It is easy to check that  is an admissible
ordering. Given an admissible weight
is an admissible
ordering. Given an admissible weight  ,
there exists a unique non-zero polynomial
,
there exists a unique non-zero polynomial  in the
reduced Gröbner basis of
in the
reduced Gröbner basis of 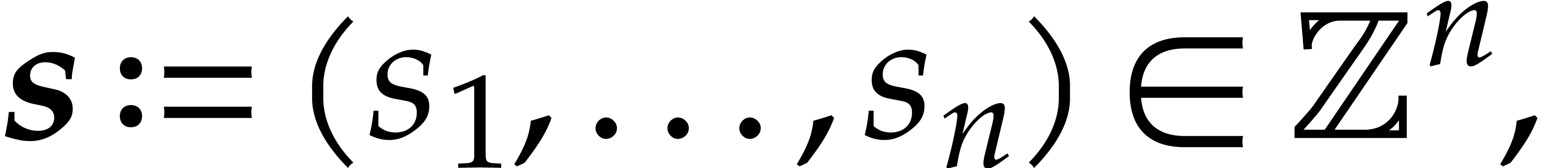 whose leading
monomial is minimal for
whose leading
monomial is minimal for  and whose leading
coefficient is one. We call
and whose leading
coefficient is one. We call  the
the  -simplest element of
-simplest element of 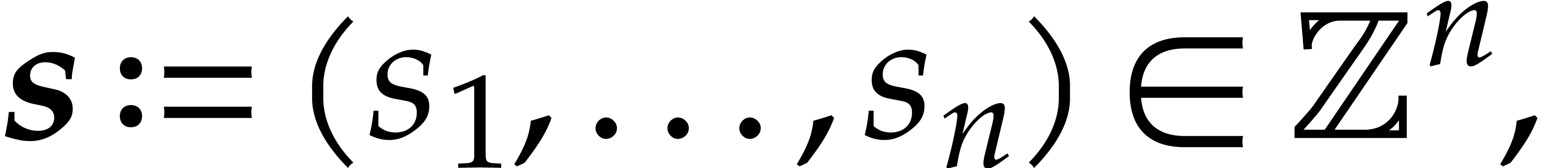 . Note that there are at most
. Note that there are at most 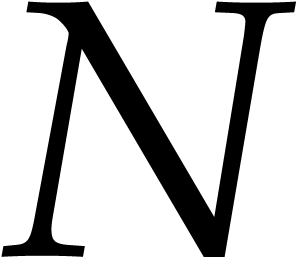 monomials less than the leading monomial of
monomials less than the leading monomial of  for
for  (otherwise there would exist a
smaller polynomial in the Gröbner basis). From [17,
Corollary 1], we know that
(otherwise there would exist a
smaller polynomial in the Gröbner basis). From [17,
Corollary 1], we know that
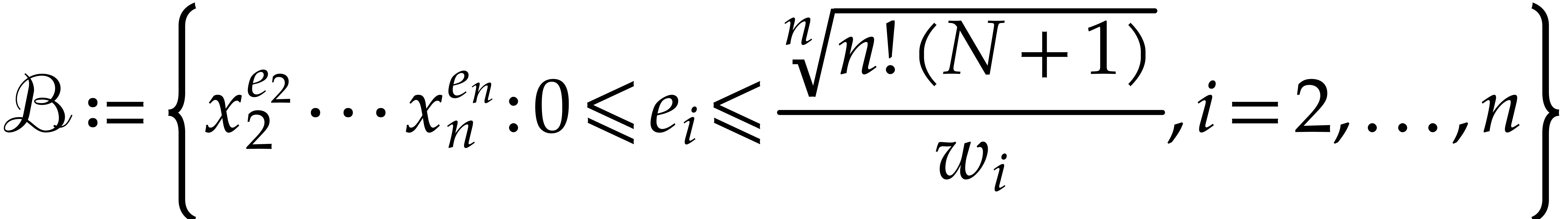 |
(3.2) |
for  . The main aim of this
section is an efficient algorithm for the computation of
. The main aim of this
section is an efficient algorithm for the computation of  . For this purpose, we may assume without loss
of generality that we ordered the coordinates such that
. For this purpose, we may assume without loss
of generality that we ordered the coordinates such that 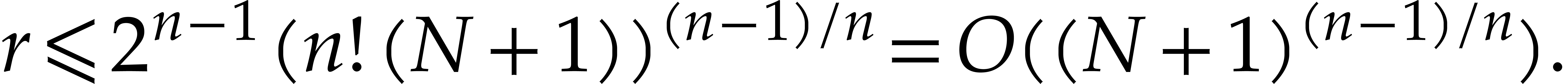 . By (3.1), this yields
. By (3.1), this yields  . Using also
. Using also
It follows that the set
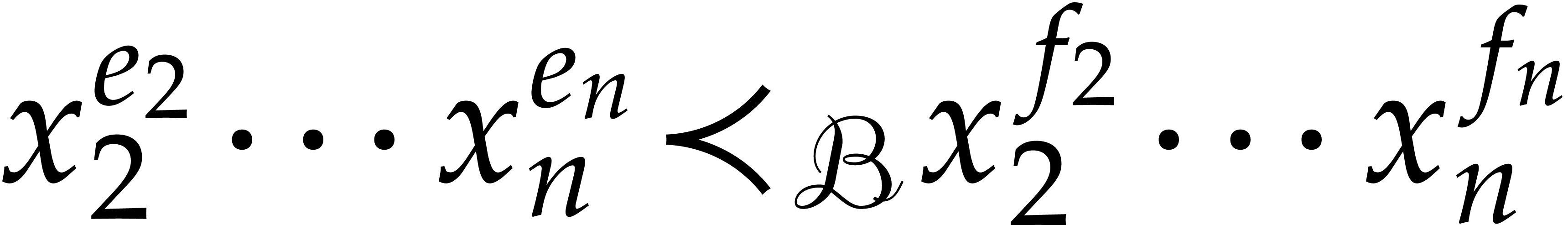
of monomials in 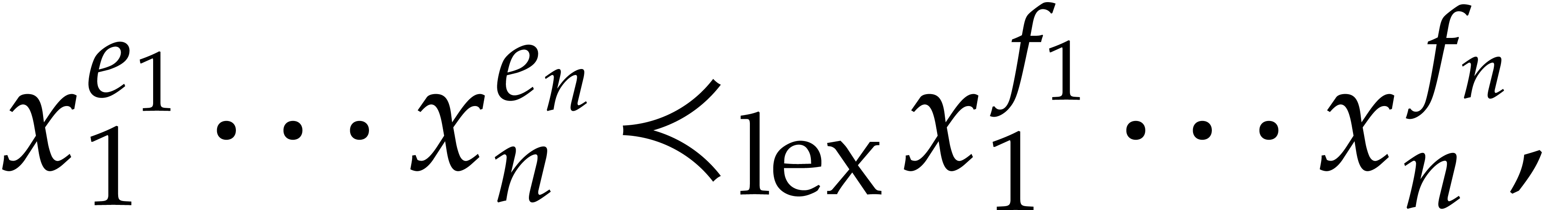 has cardinality
has cardinality
 |
(3.3) |
We sort the monomials of 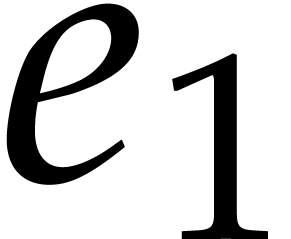 according to the
ordering
according to the
ordering 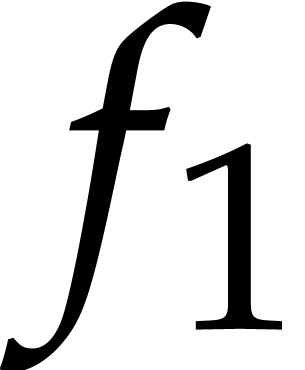 for which
for which
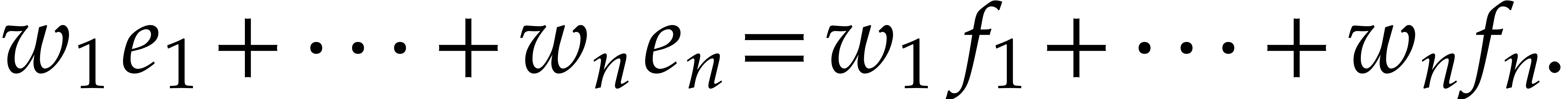
if and only if
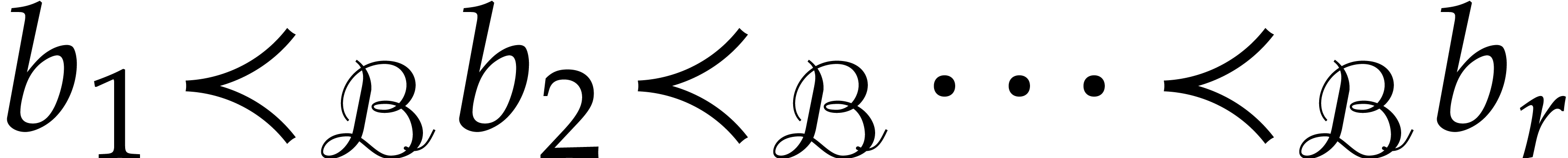
where
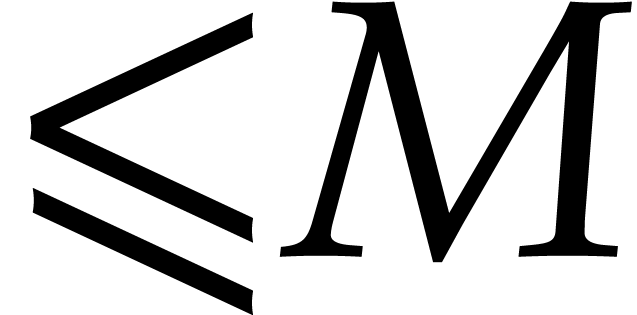
For this choice of  and
and 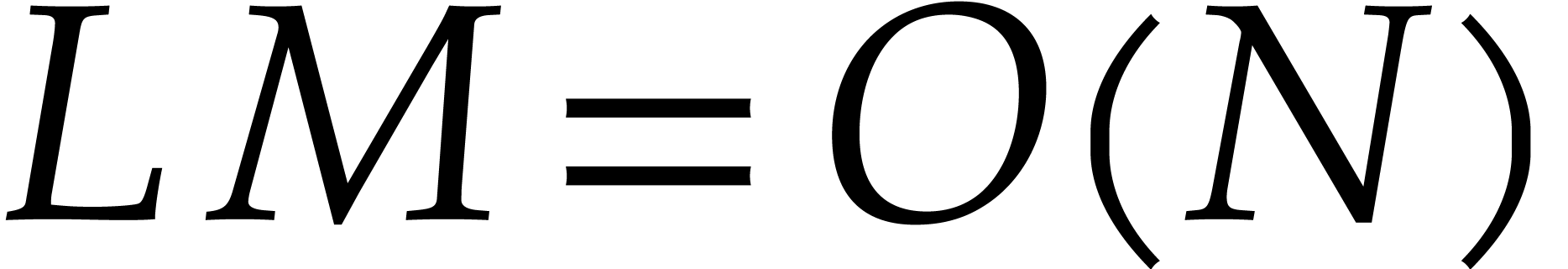 , we note that
, we note that

Let
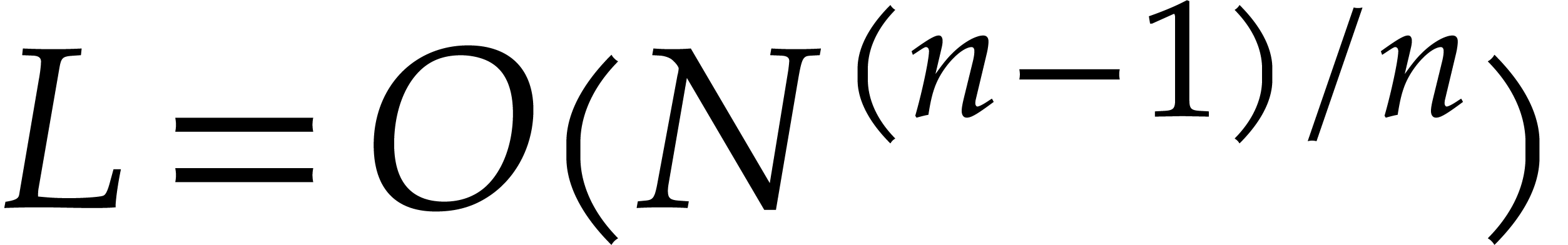
denote the monomials of 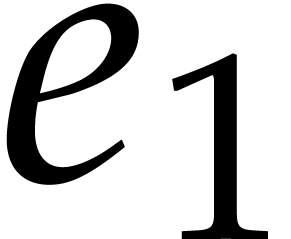 in increasing order.
in increasing order.
As in the previous sections, the sequence of points  will be split into subsequences
will be split into subsequences  of cardinality
of cardinality
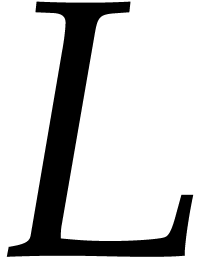 such that
such that  and
and 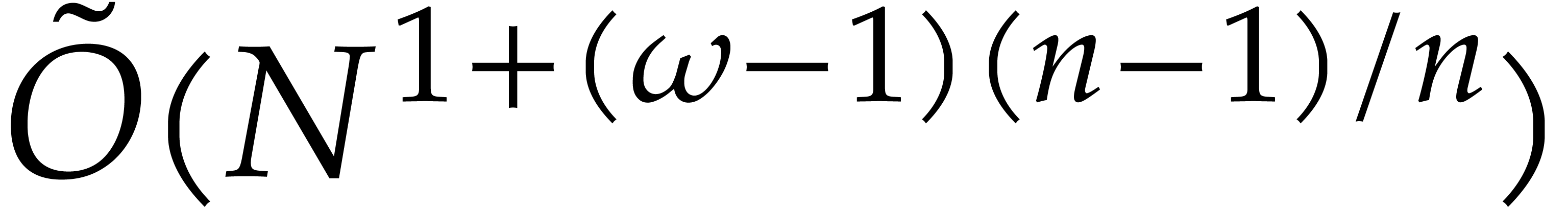 . More precisely, until section 3.6, we take
. More precisely, until section 3.6, we take
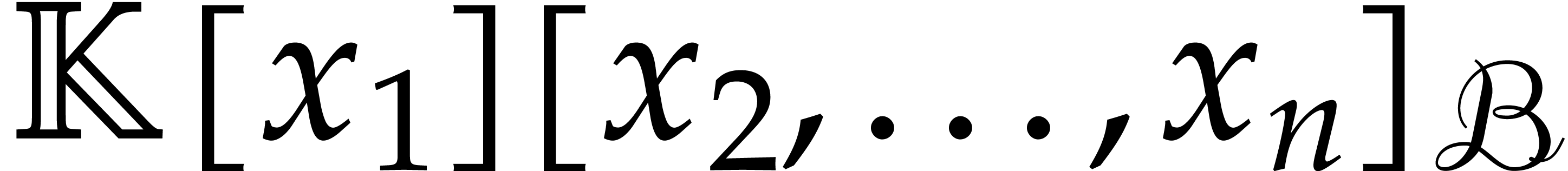 |
(3.4) |
so that  . Recall that
. Recall that  is the
is the  -simplest
element of
-simplest
element of 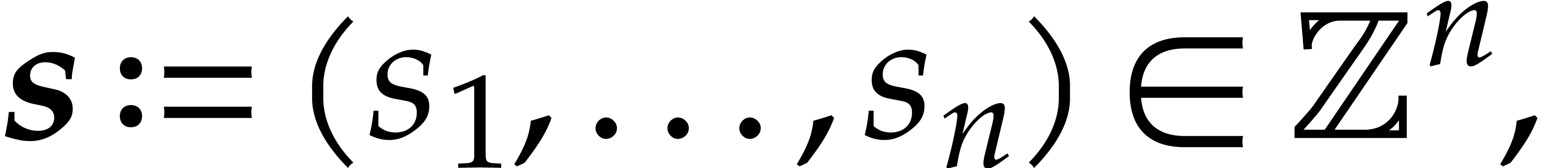 . The next idea is
to reexpress this minimality property in terms of
. The next idea is
to reexpress this minimality property in terms of 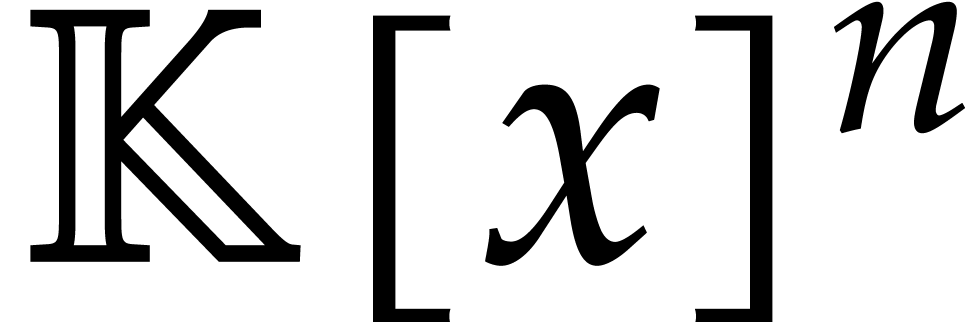 -Popov forms for an appropriate shift vector
-Popov forms for an appropriate shift vector 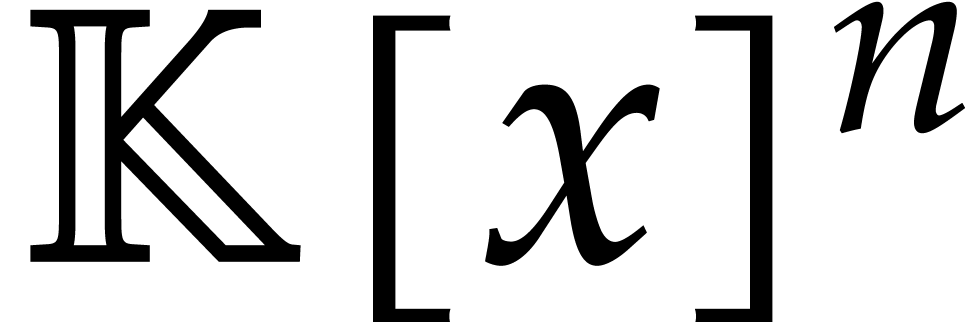 . Then the
. Then the 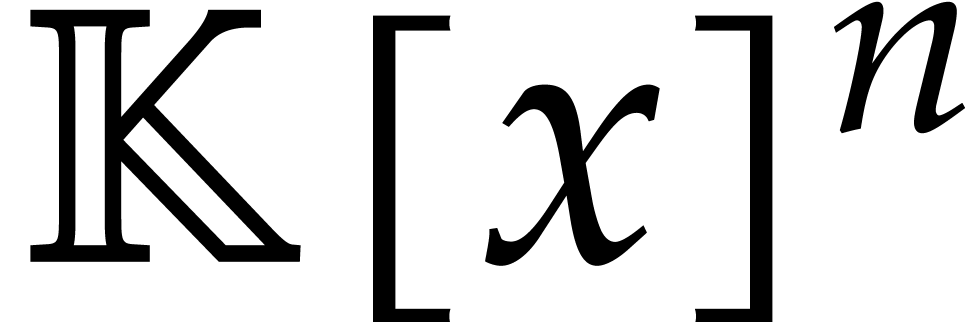 -Popov form
-Popov form  will be a matrix
with entries in
will be a matrix
with entries in  and support in
and support in  and
and  can be easily found among the
can be easily found among the 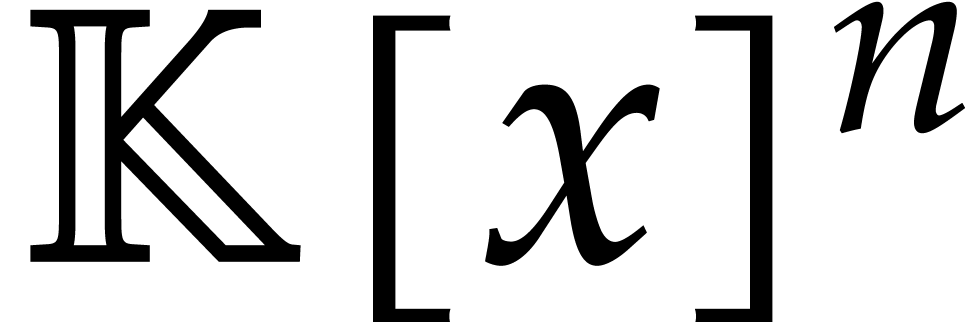 -smallest elements in
-smallest elements in  .
.
 and
and 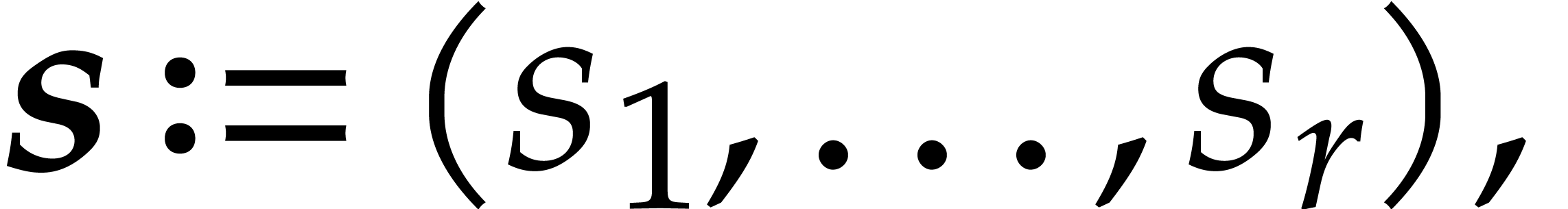 be as
in
be as
in 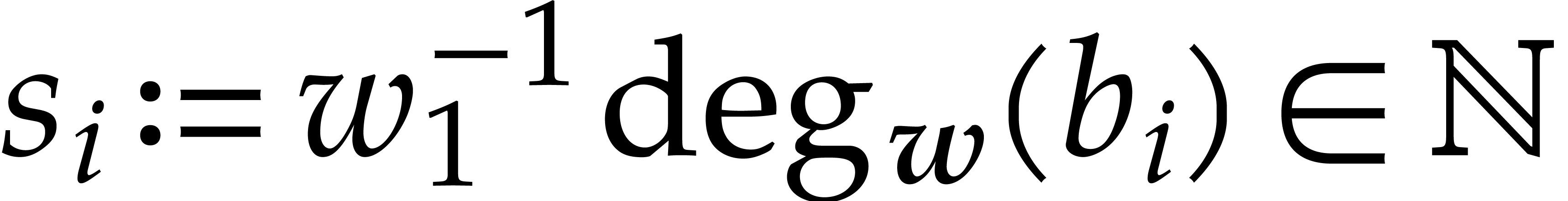 are joined separating forms for
are joined separating forms for
 . Then we can compute
. Then we can compute  using
using
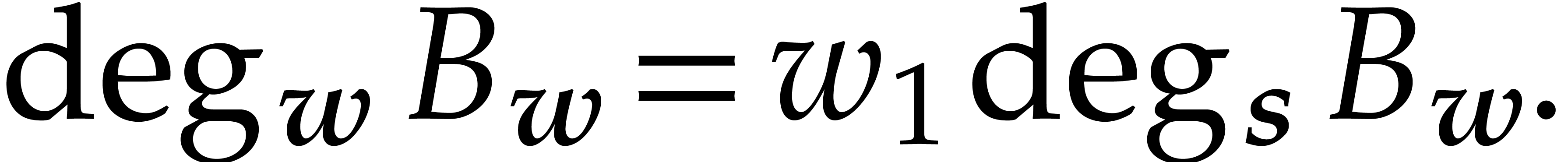
operations in  .
.
Proof. Without loss of generality, we may order
the coordinates such that 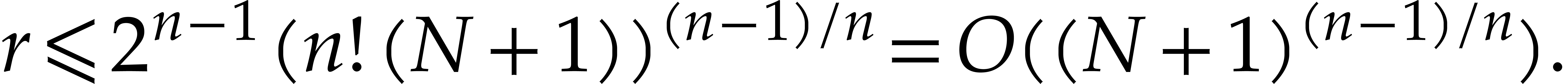 ,
after which we may use the above notation. We write
,
after which we may use the above notation. We write  for the set of polynomials over
for the set of polynomials over  with support in
with support in
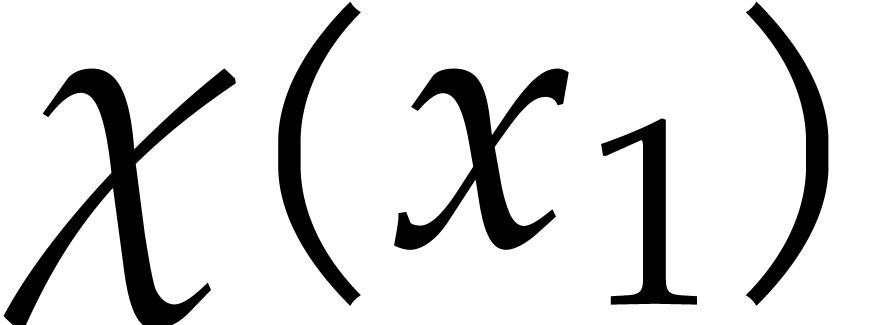 . Let
. Let 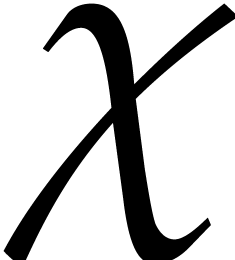 be the
be the  -Popov form of the
matrix representing the kernel of the projection
-Popov form of the
matrix representing the kernel of the projection
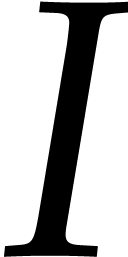
in the basis  and for the shift vector
and for the shift vector

where 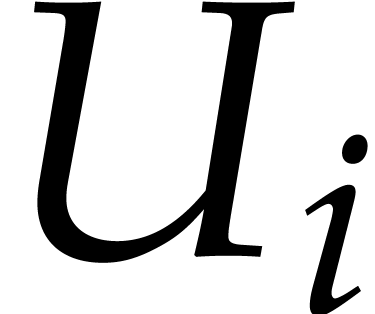 . Regarding
. Regarding  also as a
also as a  -vector
in
-vector
in  , we have
, we have
 |
(3.5) |
Since  is principal,
is principal, 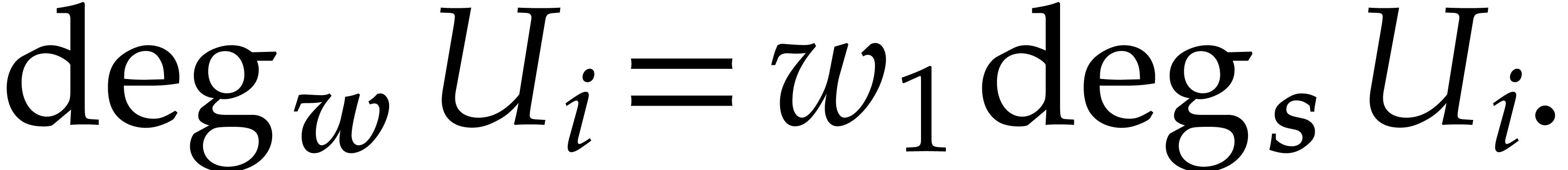 is a
free
is a
free  -module. Let
-module. Let  be the minimal polynomial of
be the minimal polynomial of  in
in
 . Since
. Since 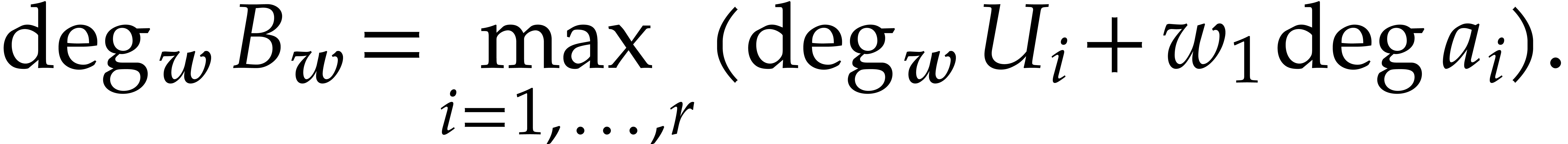 is a free family of
is a free family of 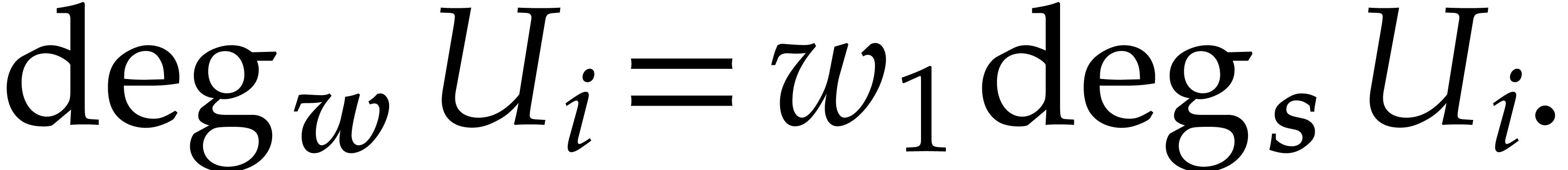 , the
rank of
, the
rank of 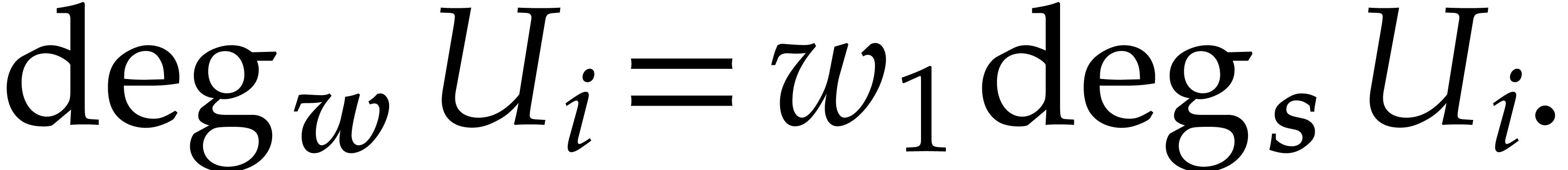 is
is  .
Consequently,
.
Consequently,  is a non-singular
is a non-singular  matrix.
matrix.
Every row 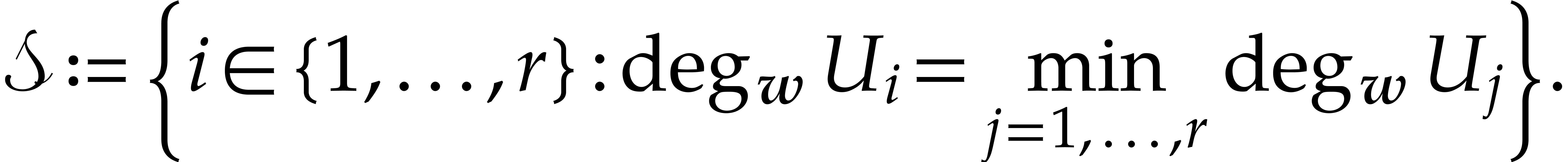 of
of  with
with 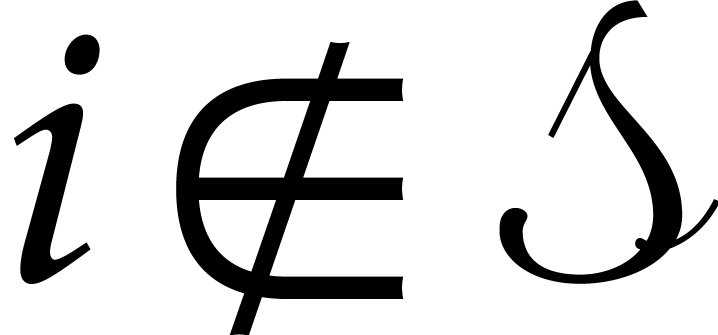 can also be regarded as a
polynomial in
can also be regarded as a
polynomial in  , which belongs
to
, which belongs
to  . We have
. We have
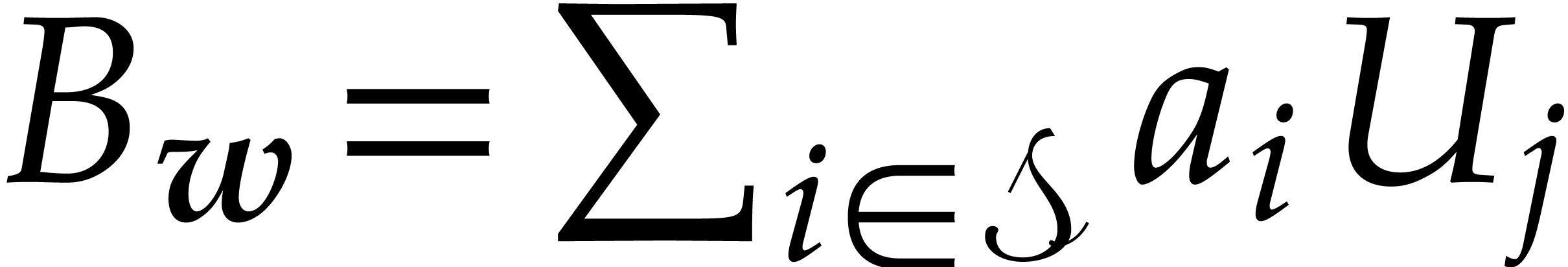 |
(3.6) |
By construction, there exist 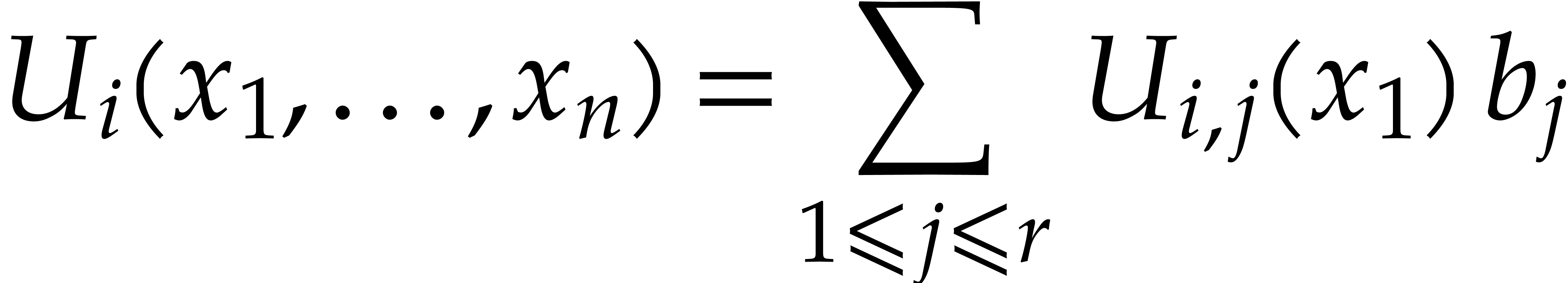 in
in  such that
such that
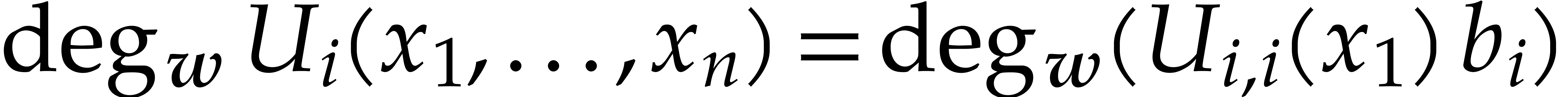
By Lemma 3.1,

Let  be the set of row indices
be the set of row indices  such that
such that  is minimal, that is
is minimal, that is

By the minimality of  and since the
and since the 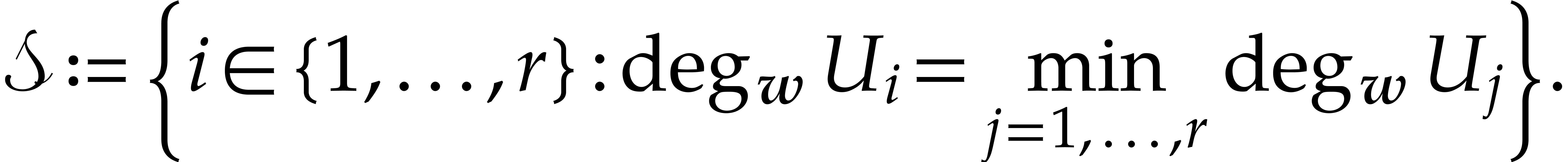 belong to
belong to  , the
polynomials
, the
polynomials  with
with  must be
zero and the others must be in
must be
zero and the others must be in  .
Consequently,
.
Consequently, 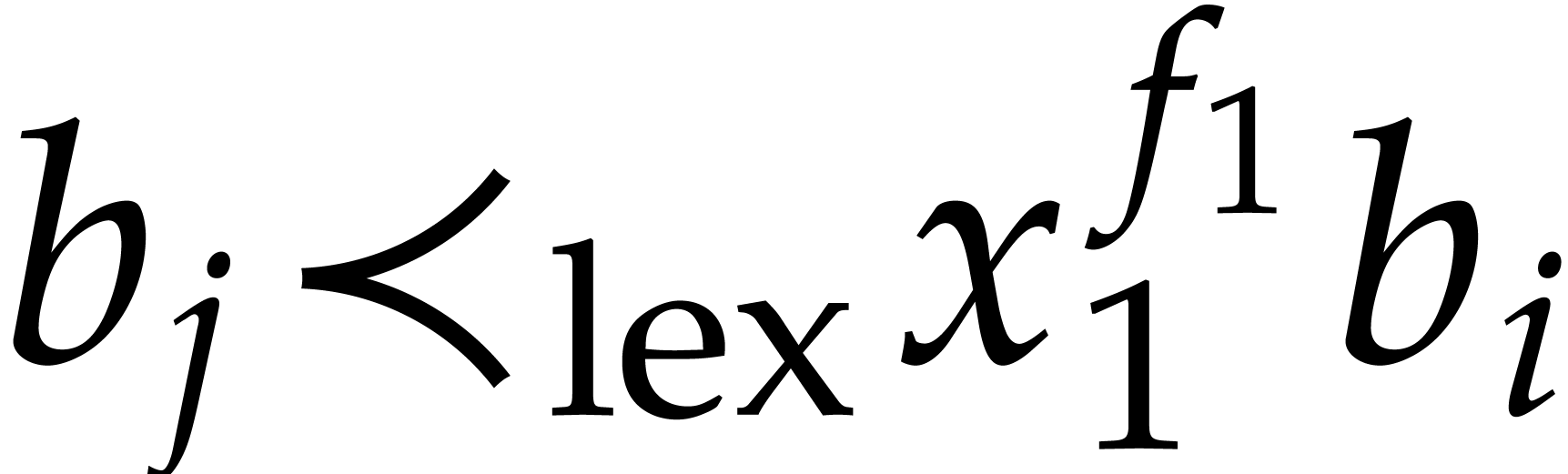 . By definition
(see section 3.1), the
. By definition
(see section 3.1), the  -pivot
index of
-pivot
index of
is  . This means that
. This means that
and
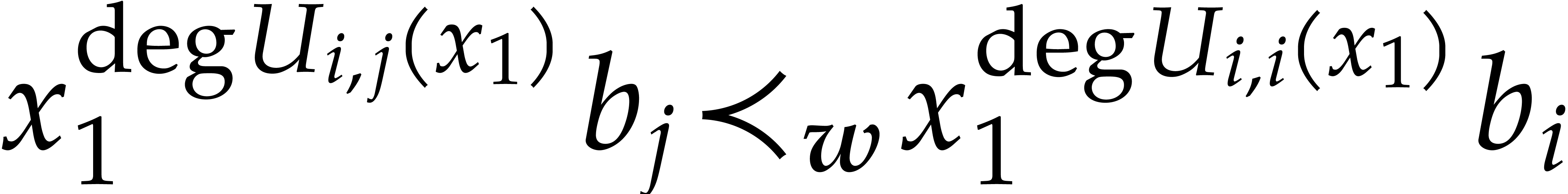
for all 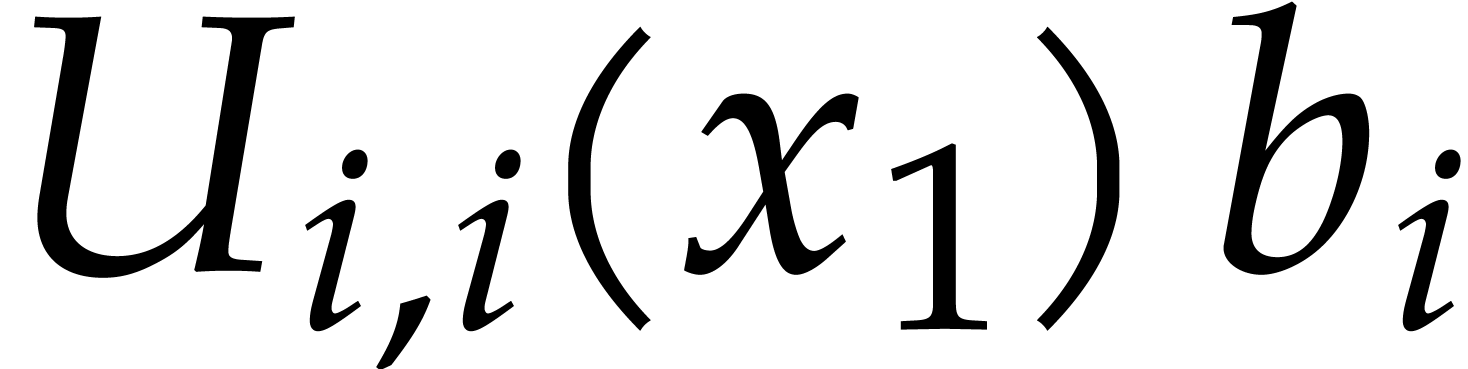 . If
. If 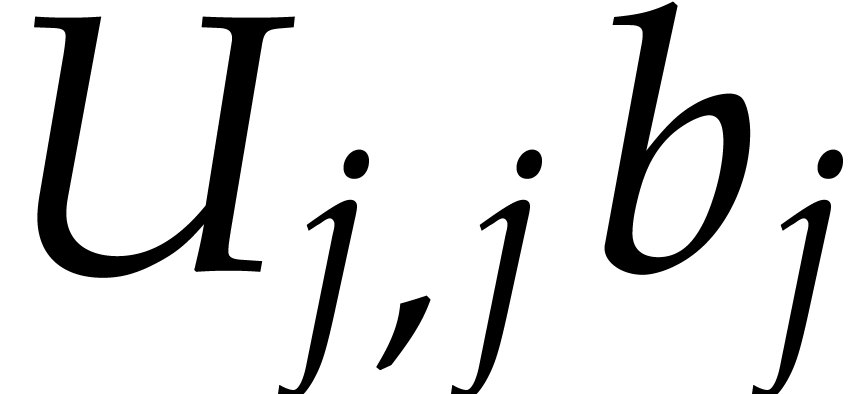 is such that
is such that 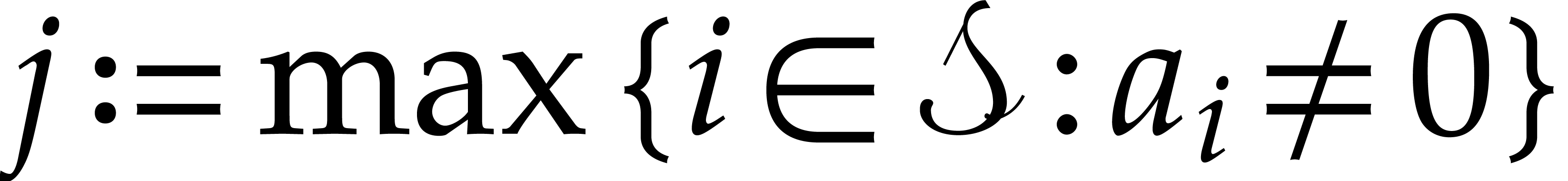 , then the
definition of the ordering
, then the
definition of the ordering  ensures that
ensures that  , where
, where  . It follows that
. It follows that 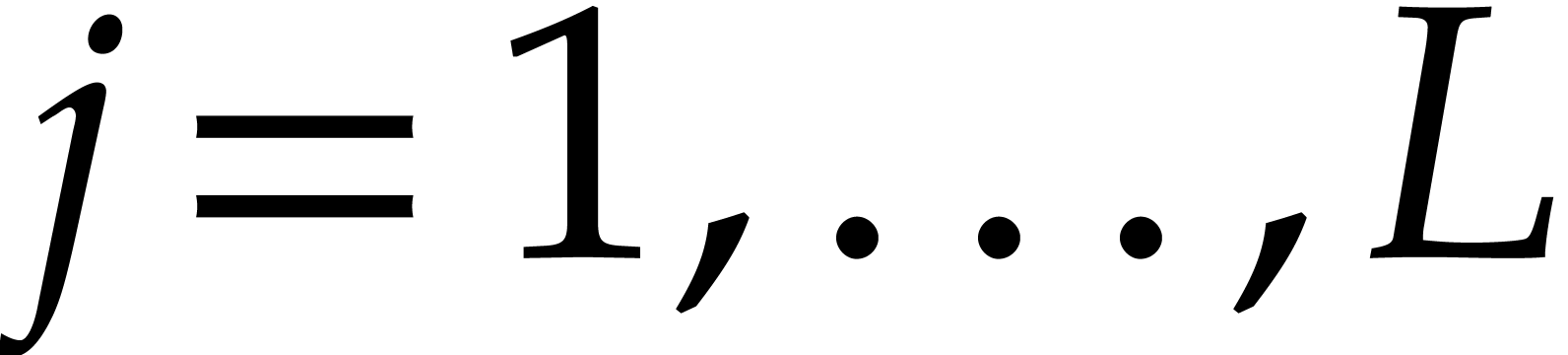 ,
whence
,
whence  . In other words, the
leading monomial of
. In other words, the
leading monomial of  for
for  is the leading monomial of
is the leading monomial of  .
Consequently, the leading monomial of
.
Consequently, the leading monomial of  is the
leading monomial of
is the
leading monomial of 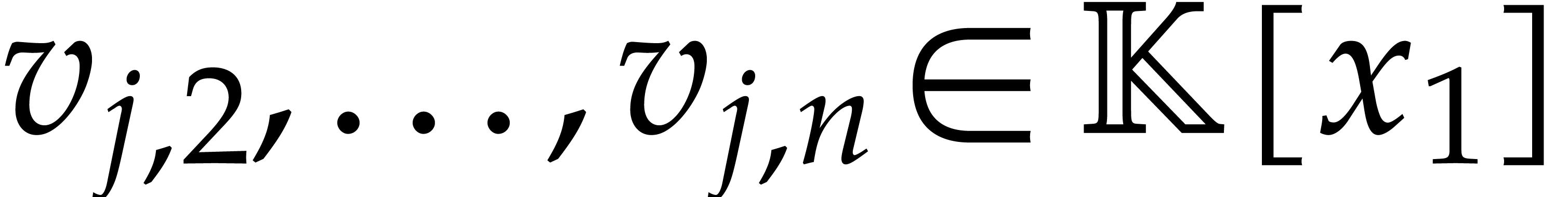 , where
, where
 . Finally, the minimality of
. Finally, the minimality of
 implies that
implies that  is
is  -proportional
-proportional 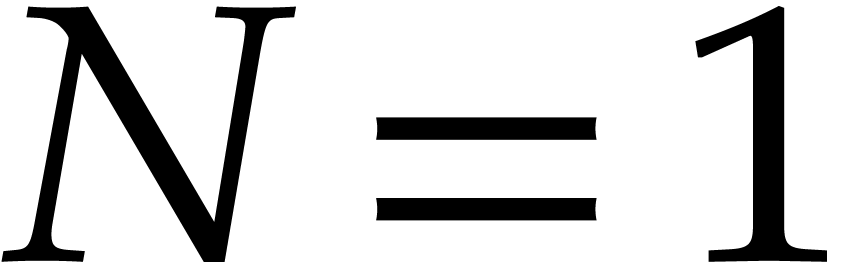 to
to 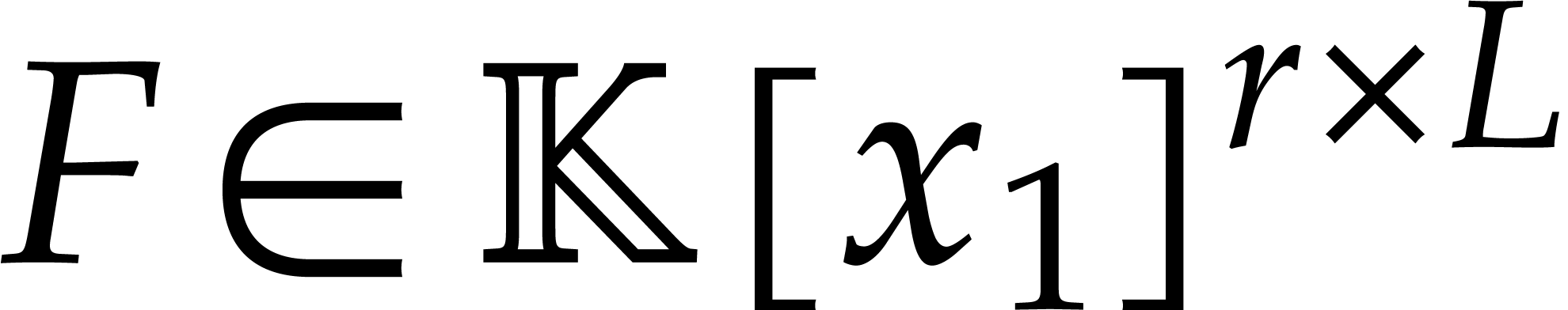 .
.
In order to obtain the  -Popov
form
-Popov
form  , we first compute the
univariate representations of
, we first compute the
univariate representations of  for
for 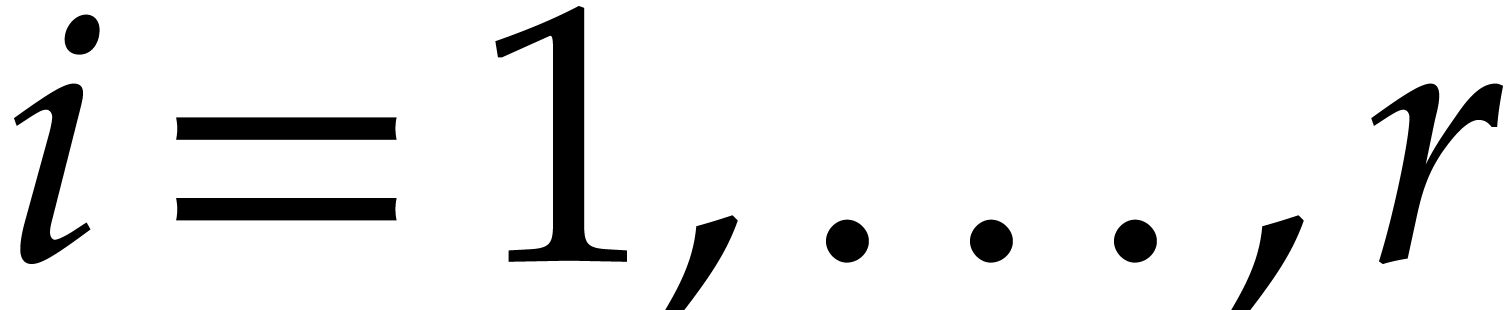 : this takes
: this takes 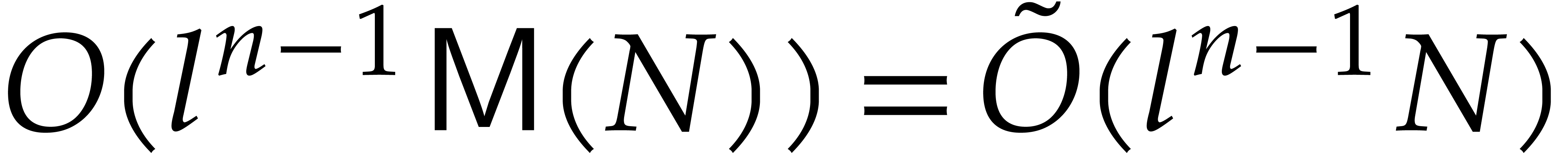 operations
in
operations
in  by Lemma 2.2. The univariate
representation of
by Lemma 2.2. The univariate
representation of  is given by a monic polynomial
is given by a monic polynomial
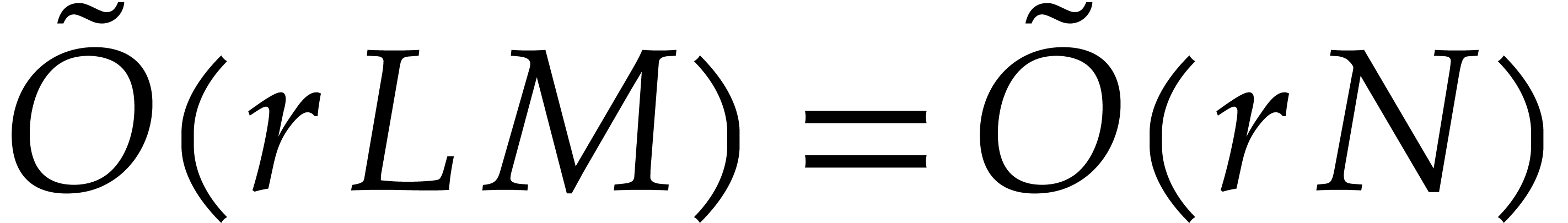 of degree
of degree  and
polynomials
and
polynomials  of degrees
of degrees  . Now consider the matrix
. Now consider the matrix  defined by
defined by
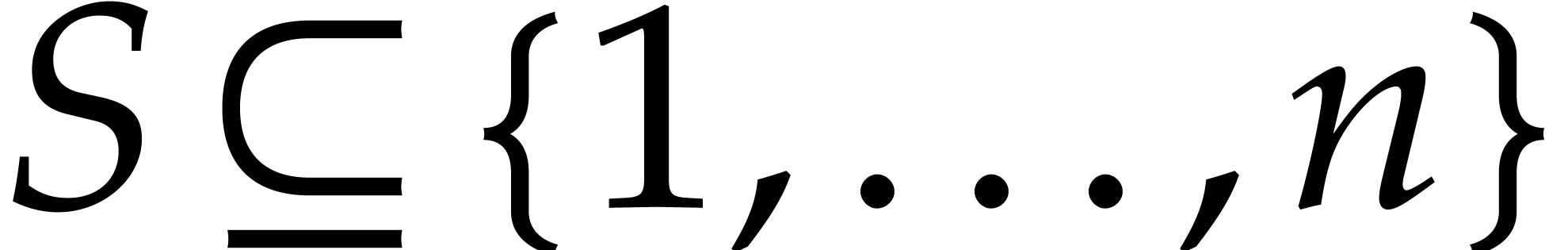
for  and
and 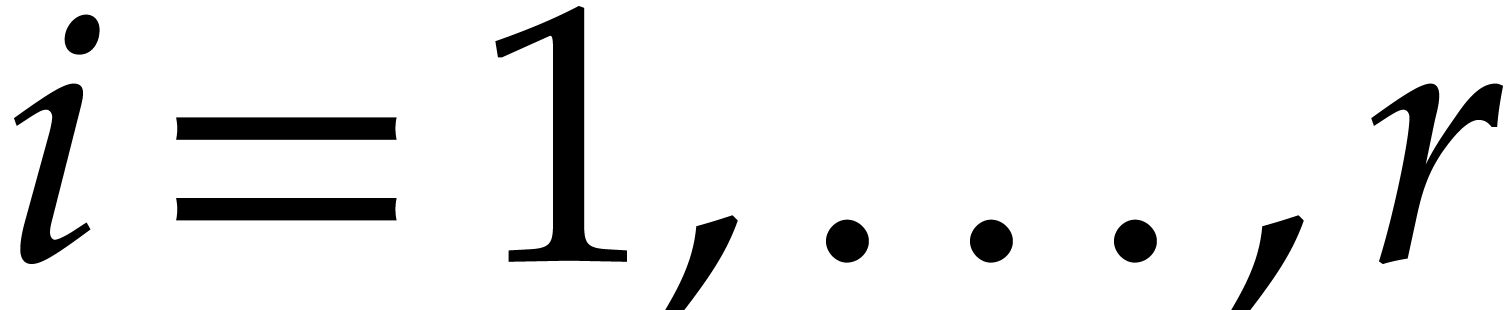 :
the entries
:
the entries 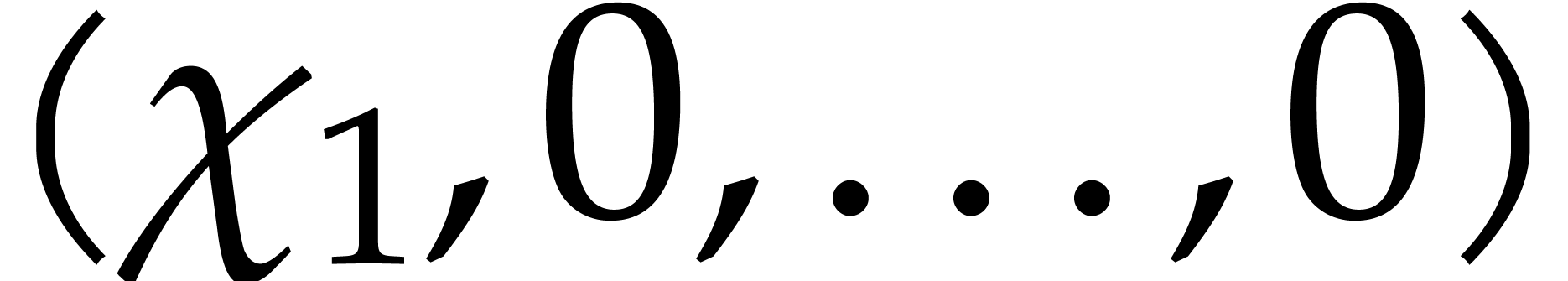 can be computed in softly linear
time
can be computed in softly linear
time 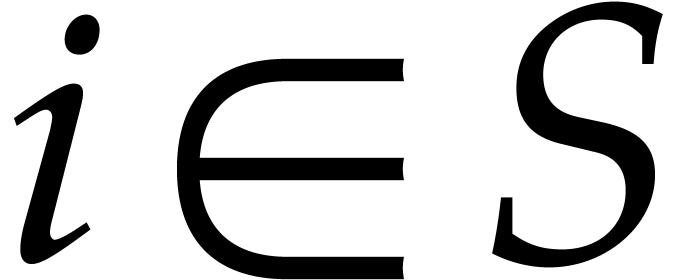 because the
because the 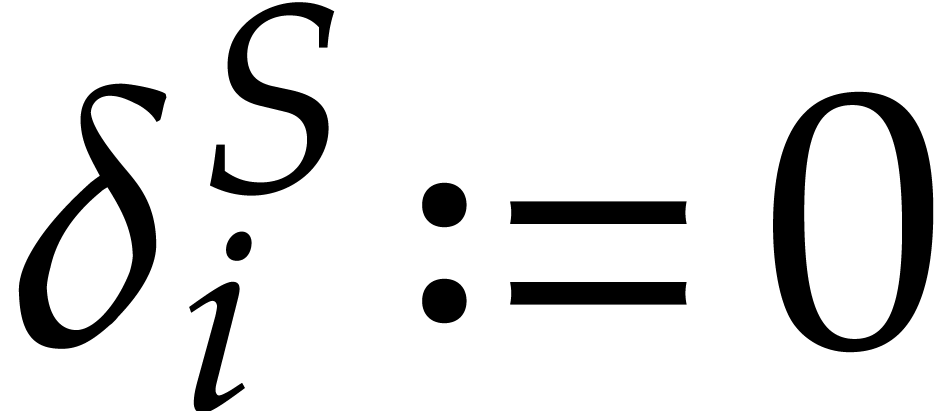 run
over the monomials of the block
run
over the monomials of the block 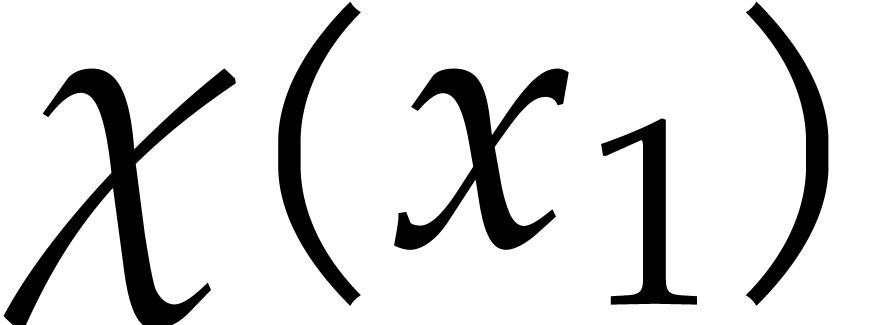 .
Since
.
Since 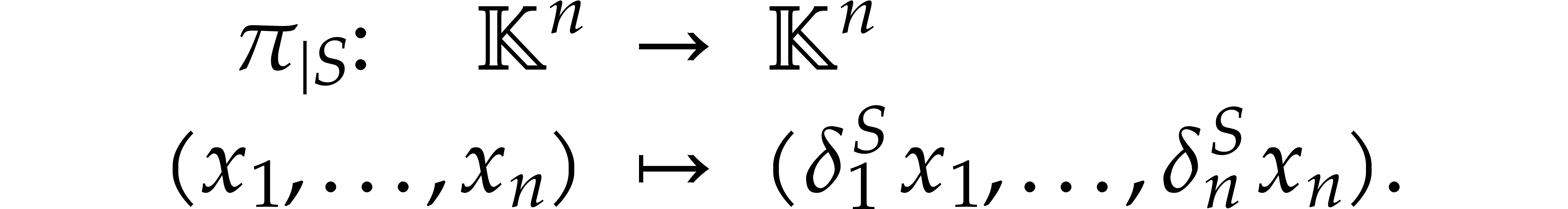 ,
we may apply Proposition 3.2. We conclude that
,
we may apply Proposition 3.2. We conclude that 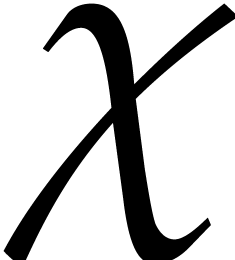 can be computed using
can be computed using

operations in  .
.
Given  , we define
, we define
Given a finite subset 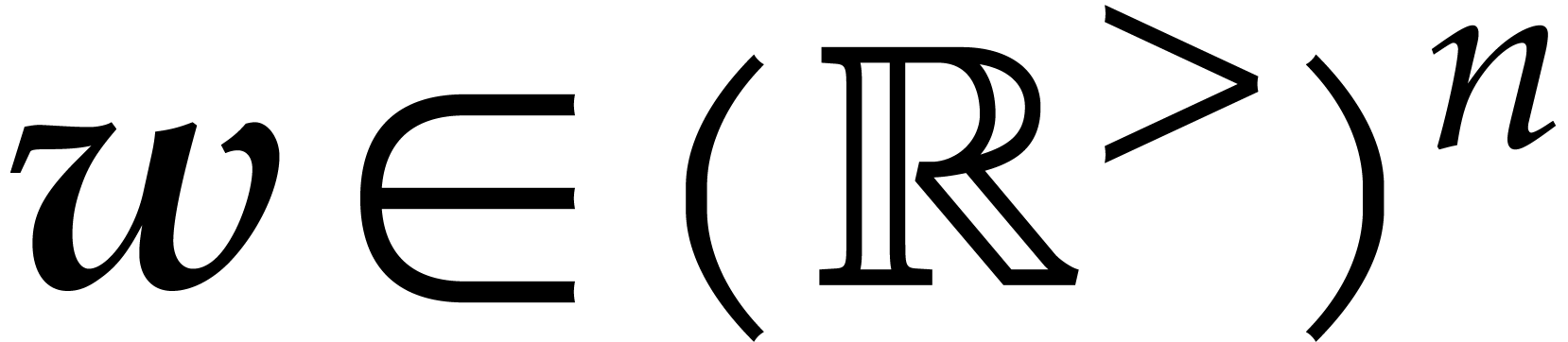 , we
write
, we
write 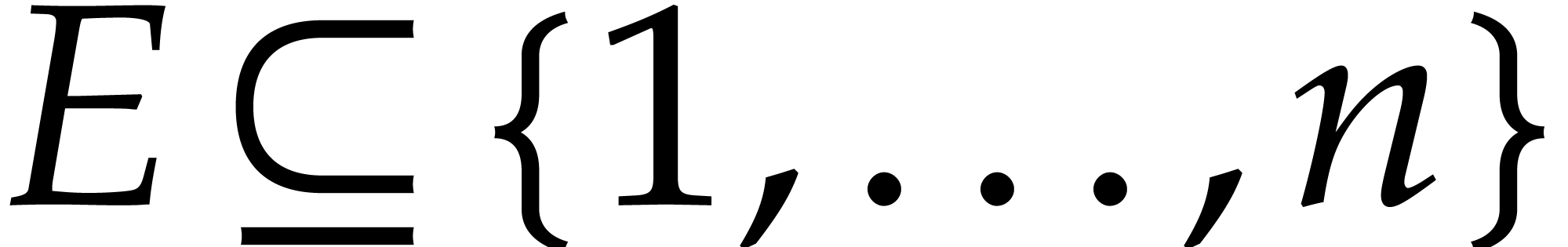 if
if 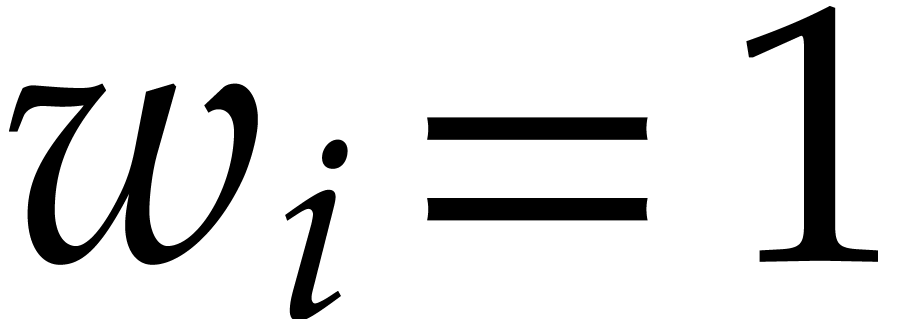 and
and  otherwise. We introduce
otherwise. We introduce
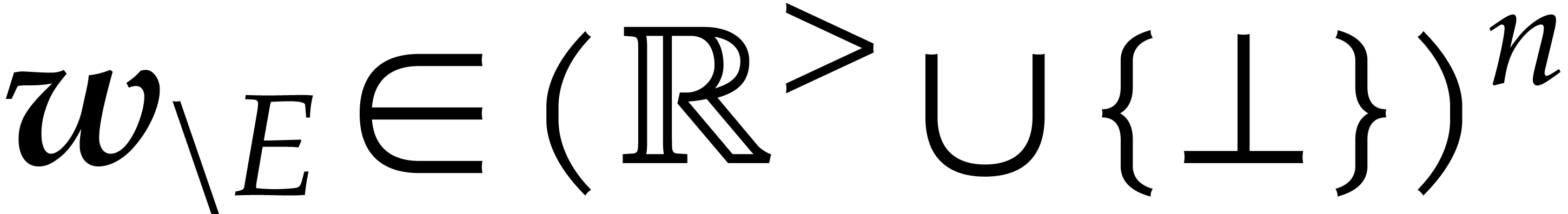
We denote by  the image of
the image of  under
under  and we define
and we define
Given a general weight 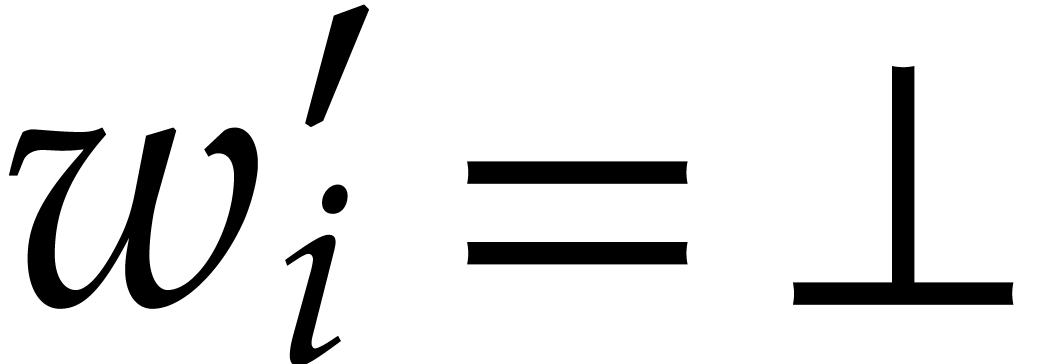 and a subset
and a subset  such that
such that  for all
for all  , we define
, we define  to be the
weight
to be the
weight  with
with  if
if  and
and 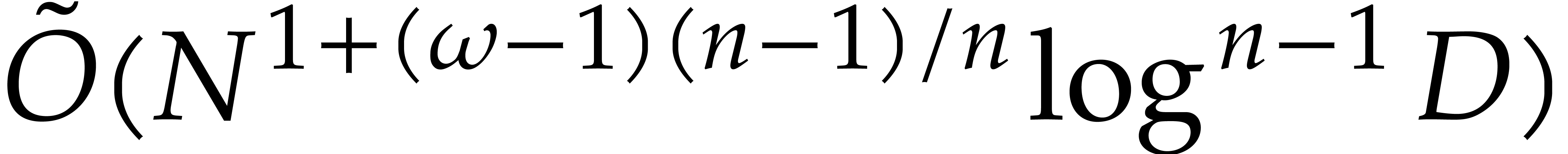 if
if  . If
. If  is admissible, then we
note that
is admissible, then we
note that 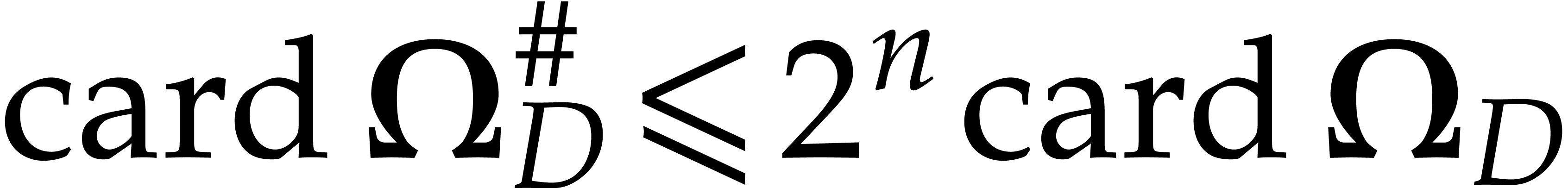 is again admissible for
is again admissible for 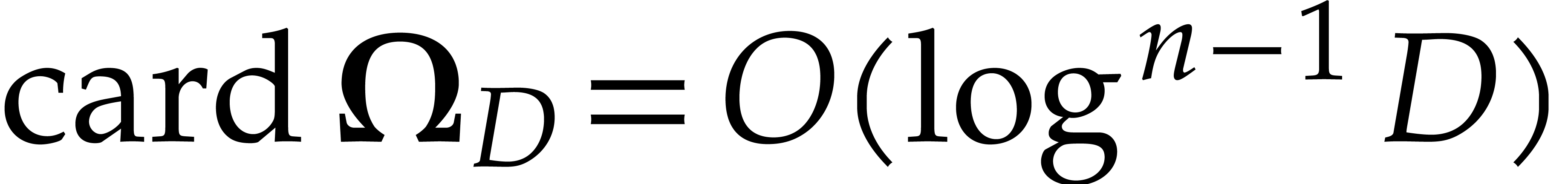 where
where  . We
further let
. We
further let
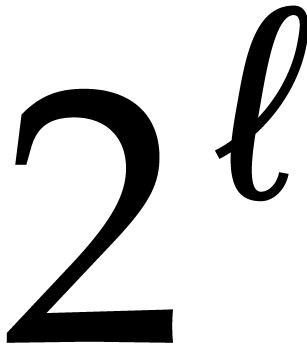
The family of simplest polynomials 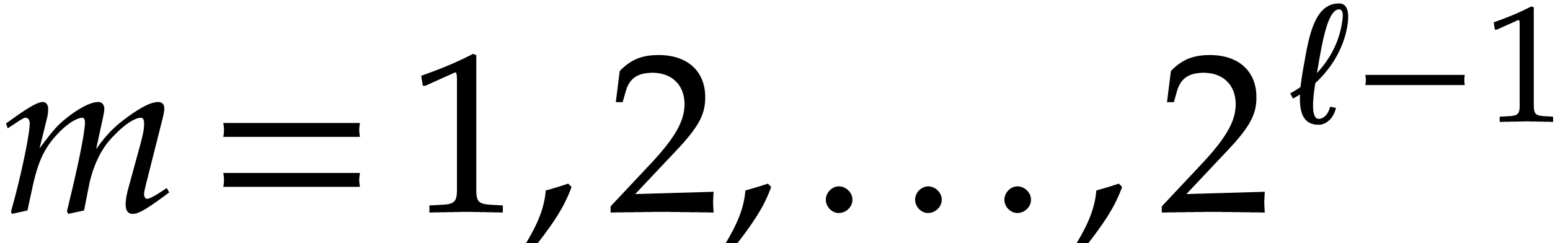 is called a
heterogenous basis for
is called a
heterogenous basis for  and
and
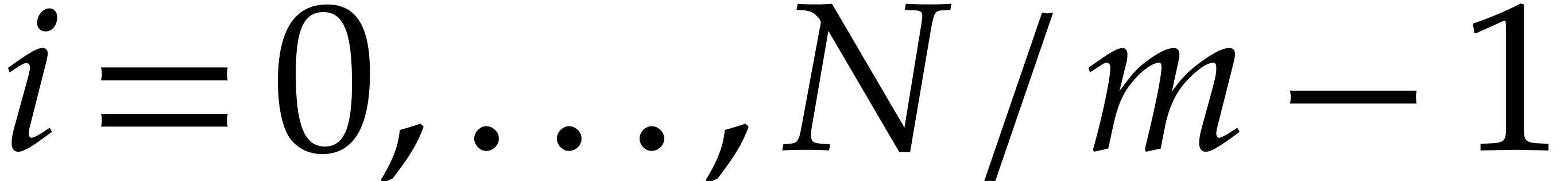 .
.
 and
and  be as
in
be as
in 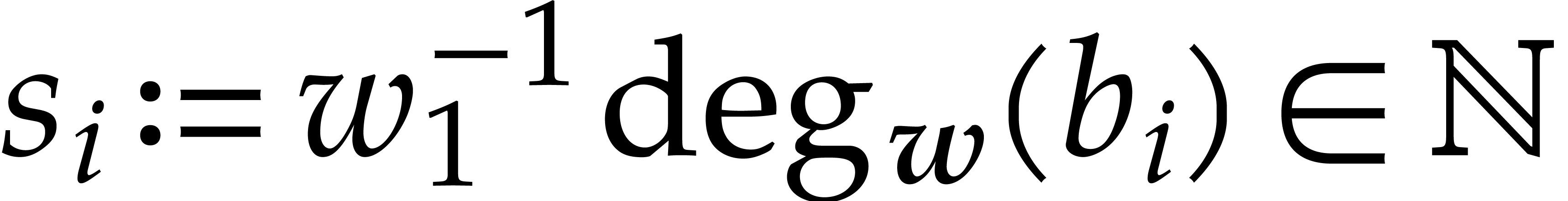 are joined separating forms for
are joined separating forms for  . Then a heterogenous basis
. Then a heterogenous basis  can be computed using
can be computed using
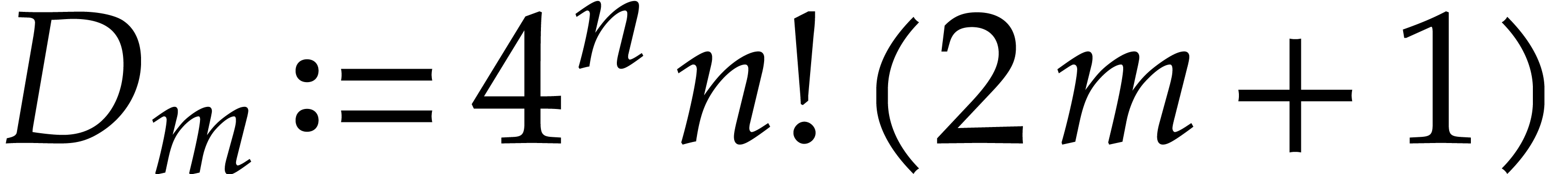
operations in  .
.
Proof. The cost for computing a single  is given in Lemma 3.3. On the other hand, we
have
is given in Lemma 3.3. On the other hand, we
have  , and
, and 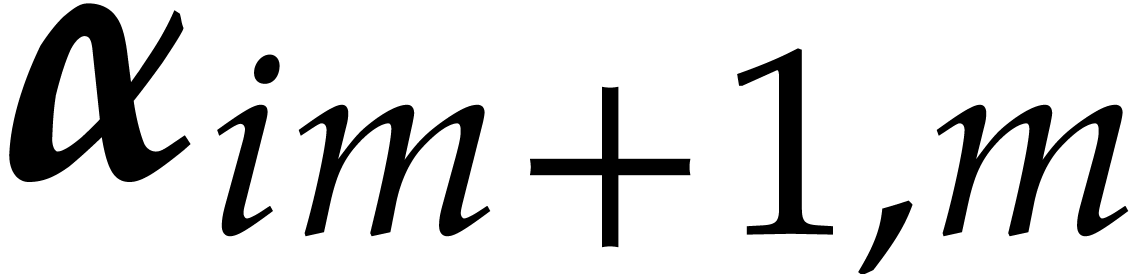 by [17, Lemma 2].
by [17, Lemma 2].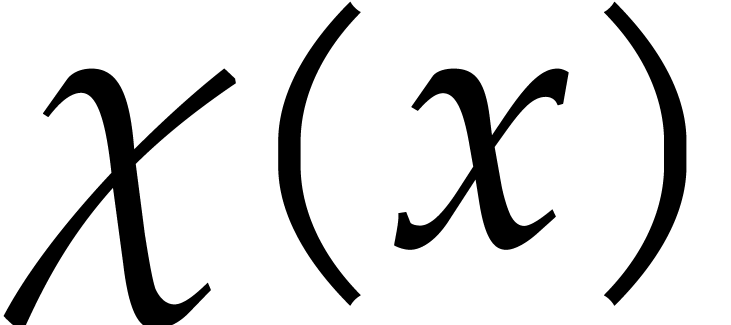
Let  and
and  are still as in
are still as in
 is a power
is a power 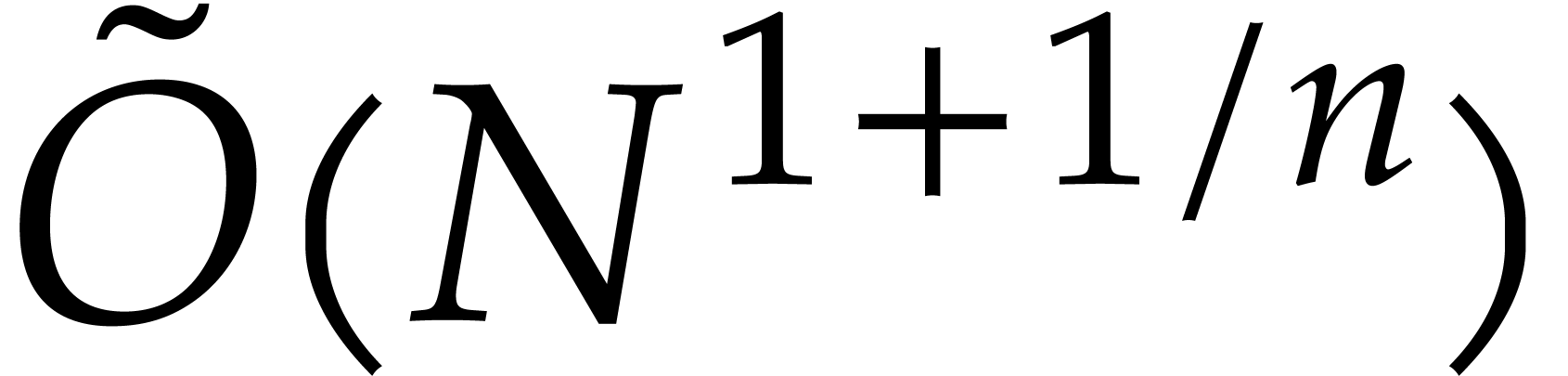 . A
recursive heterogeneous basis for
. A
recursive heterogeneous basis for  and
and 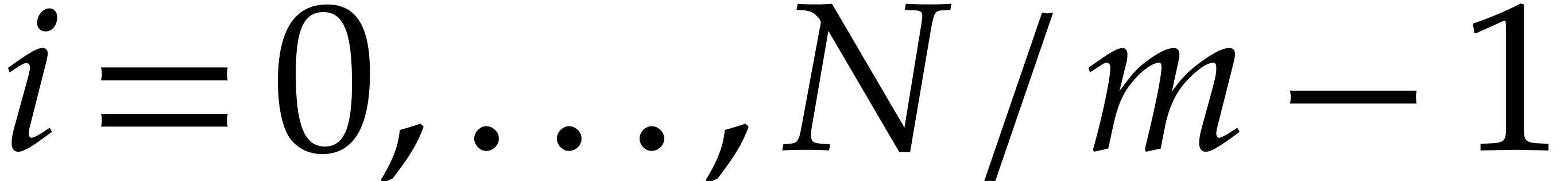 consists of the following data:
consists of the following data:
a heterogenous basis for  and
and 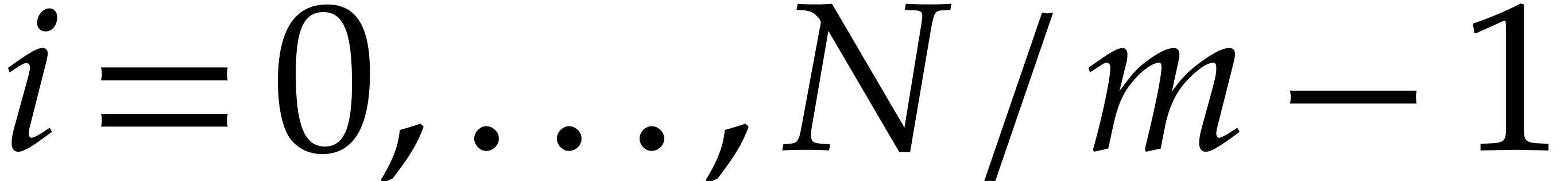 ,
,
for all  and
and  ,
a heterogeneous basis for
,
a heterogeneous basis for 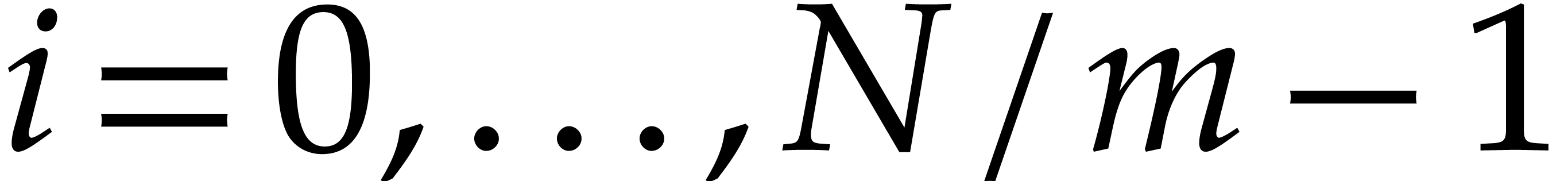 and
and 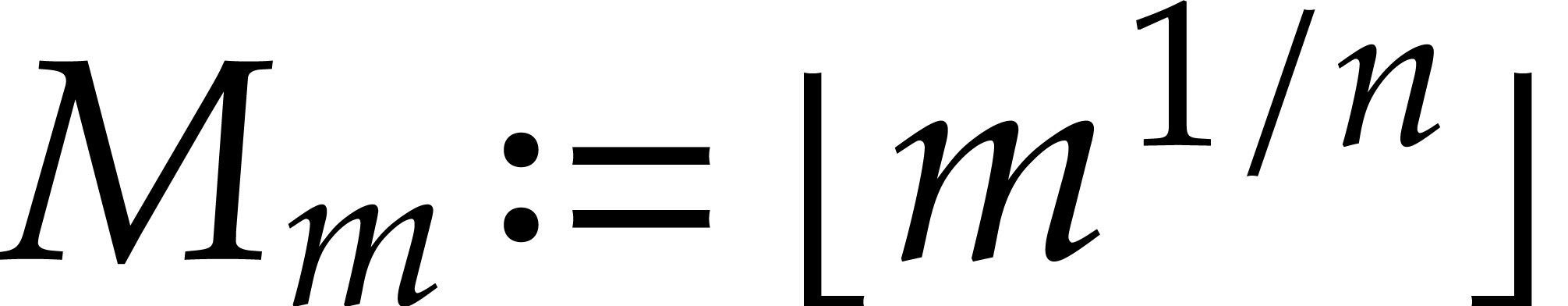 .
.
We say that linearly independent linear forms 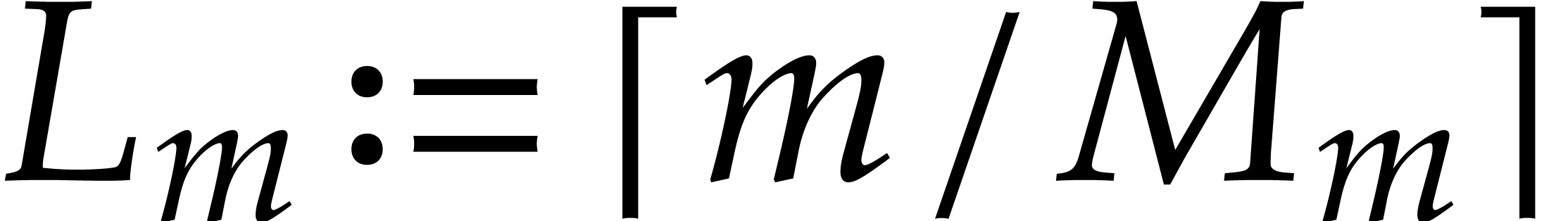 weakly separate
weakly separate  if each of them
is a joined separating form for
if each of them
is a joined separating form for  .
We say that they recursively weakly separate
.
We say that they recursively weakly separate  if they weakly separate each of the above
if they weakly separate each of the above 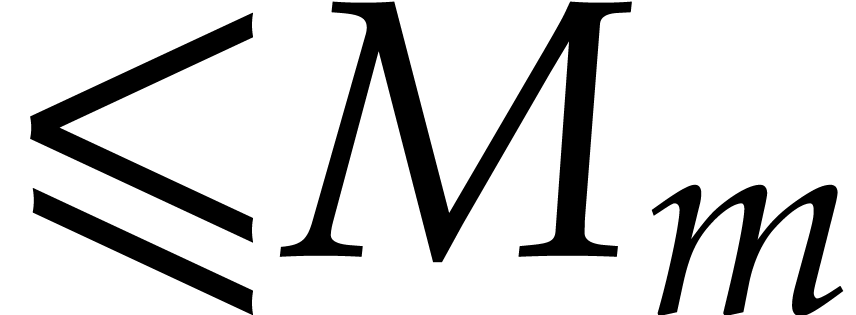 for
for  and
and  .
.
In order to construct recursive heterogeneous bases, we need
coordinates 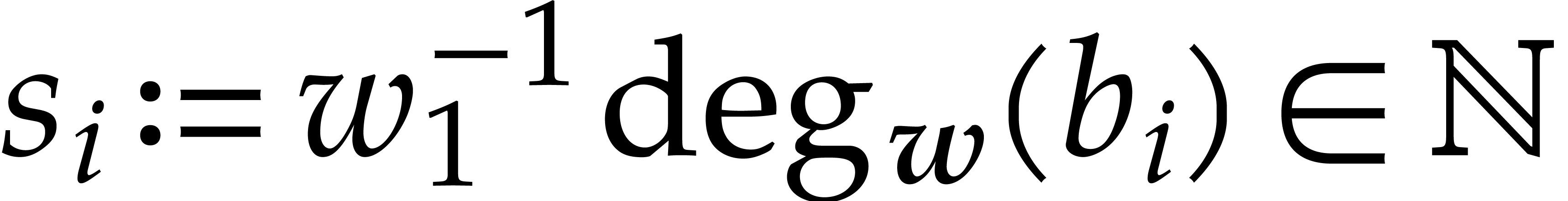 that recursively weakly separate
that recursively weakly separate
 . This is the purpose of the
following lemma.
. This is the purpose of the
following lemma.
 points in
points in
 . A basis
. A basis 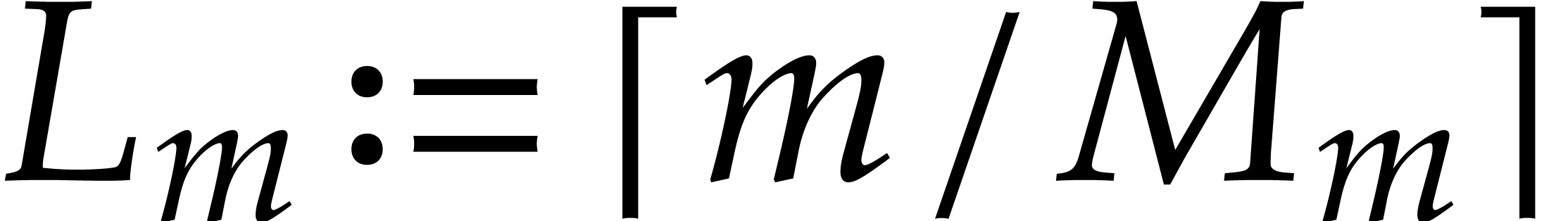 of linear forms that recursively weakly separate
of linear forms that recursively weakly separate 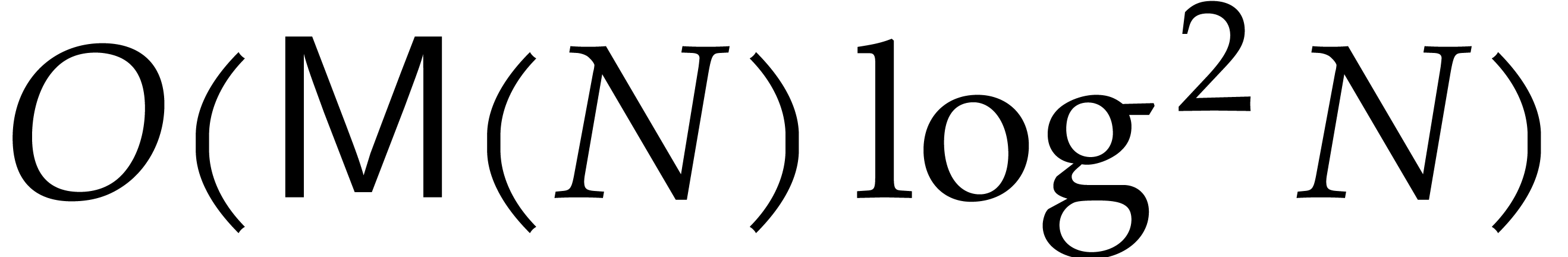 can be computed using
can be computed using  operations in
operations in  .
.
Proof. With  and
and 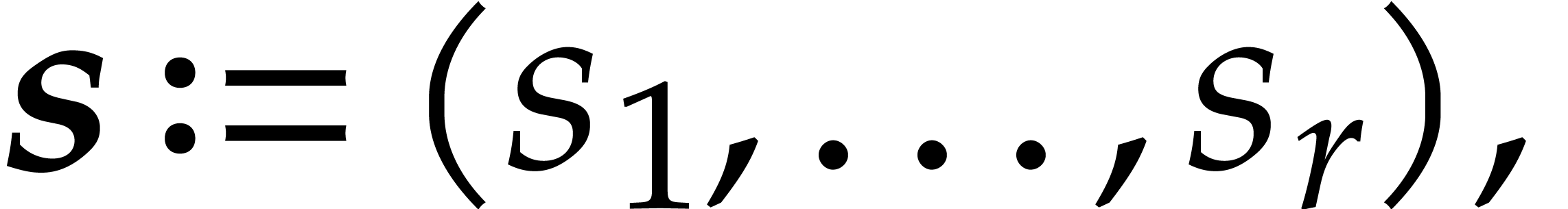 as in
as in
 |
(3.7) |
Let us call  the standard split of
the standard split of 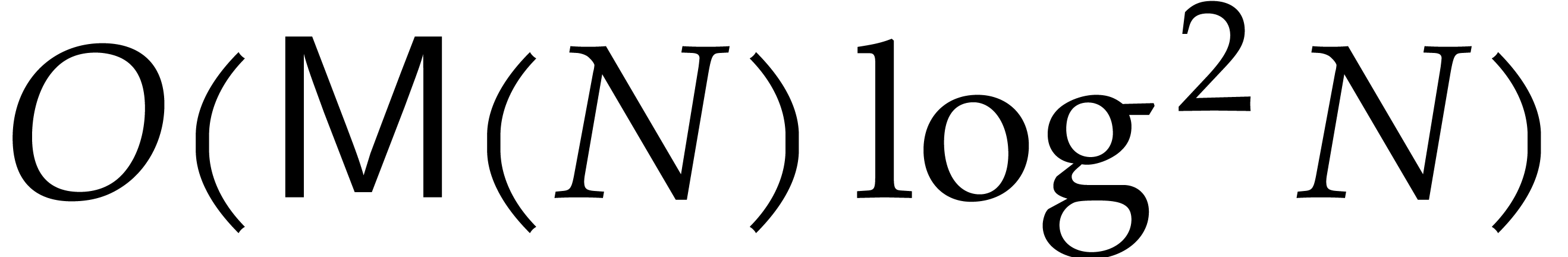 . We construct the sequence of sequences of
points
. We construct the sequence of sequences of
points  that consists of the standard split of
that consists of the standard split of
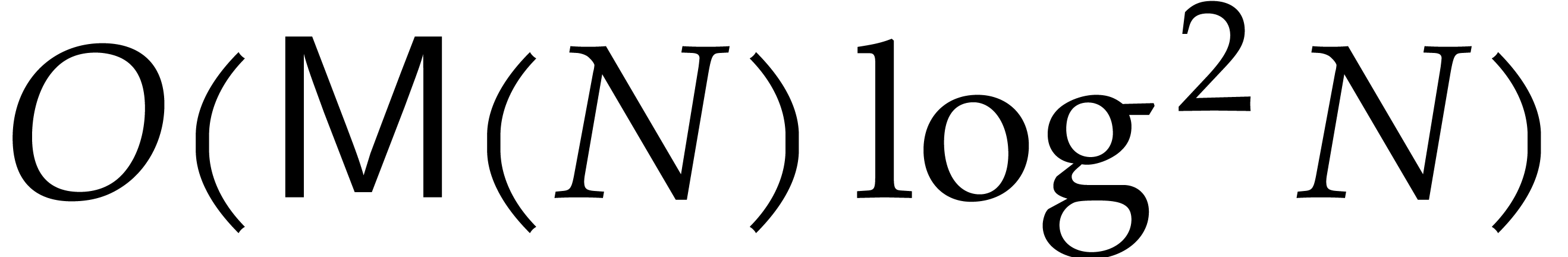 and the standard splits of
and the standard splits of  for
for  and
and 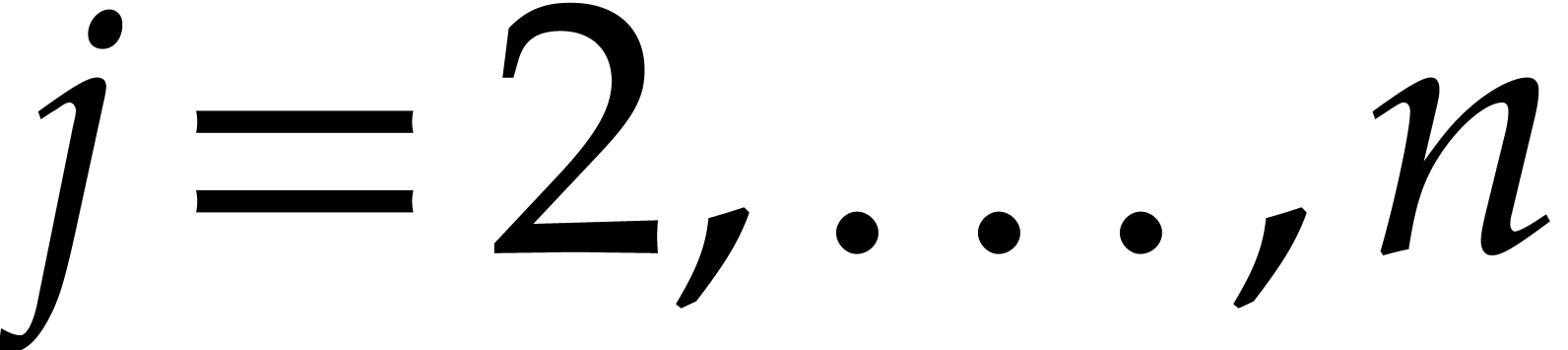 .
.
Let 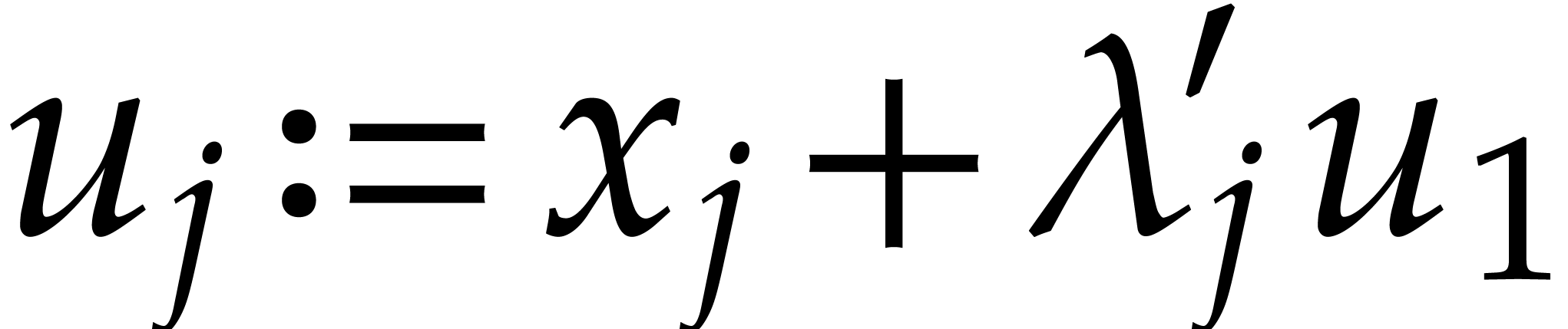 . The standard split of
. The standard split of
 consists of
consists of  sequences of
cardinality
sequences of
cardinality  . The total
number of points in
. The total
number of points in  is at most
is at most  . Using
. Using
By Lemma 2.1, we may compute a joined separating form 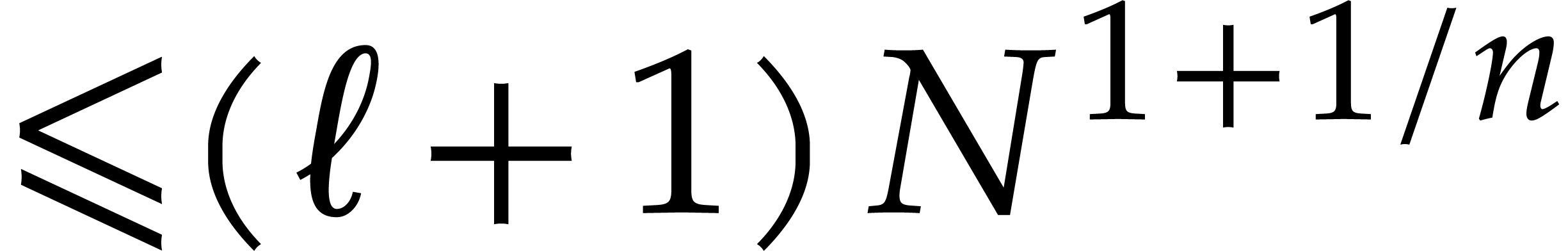 for
for 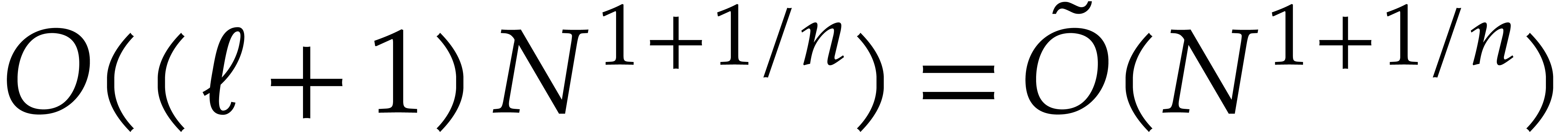 , in
time
, in
time 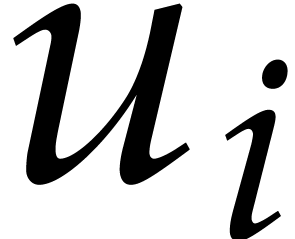 , using the given subset
of
, using the given subset
of  . For
. For 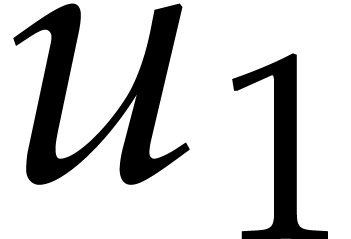 , we take
, we take  for some
for some 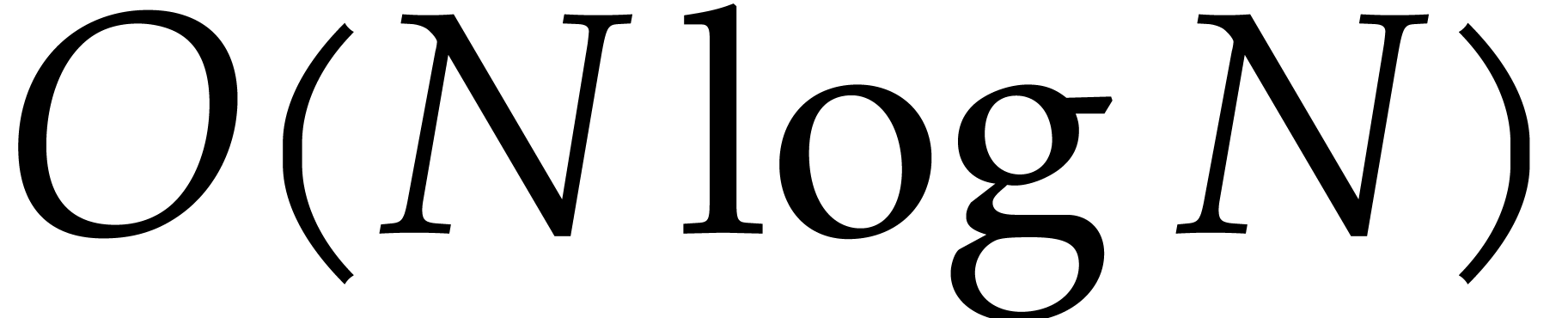 in
in  such that
such that
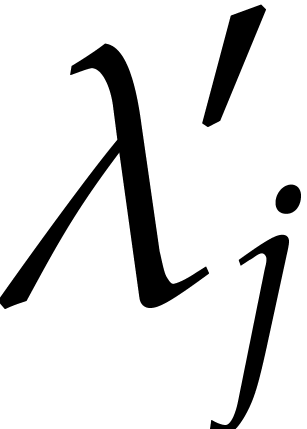
for all distinct points 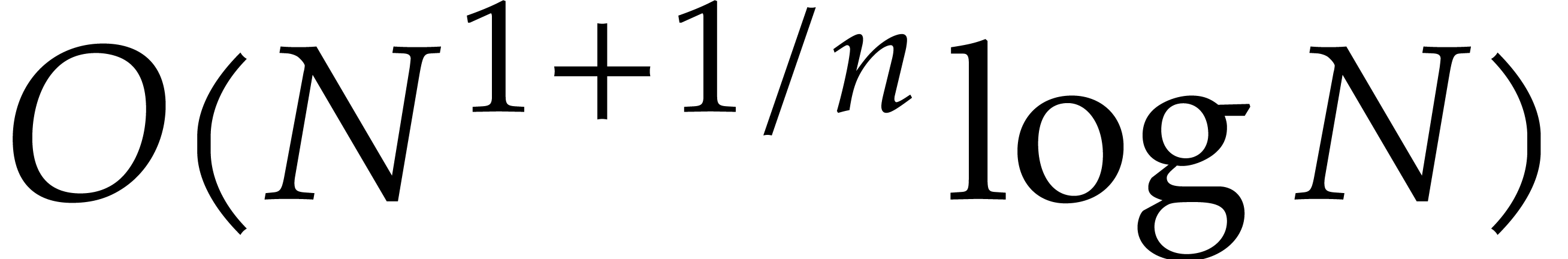 in
in  , for all
, for all  in
in 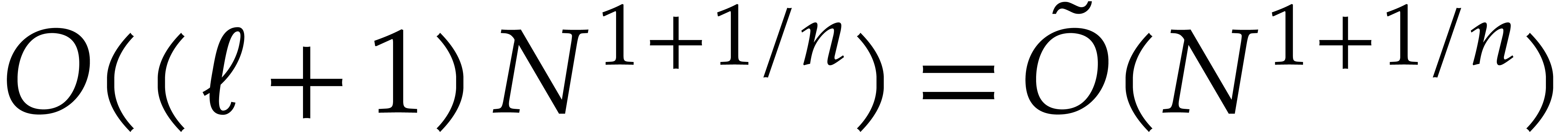 . Since
. Since 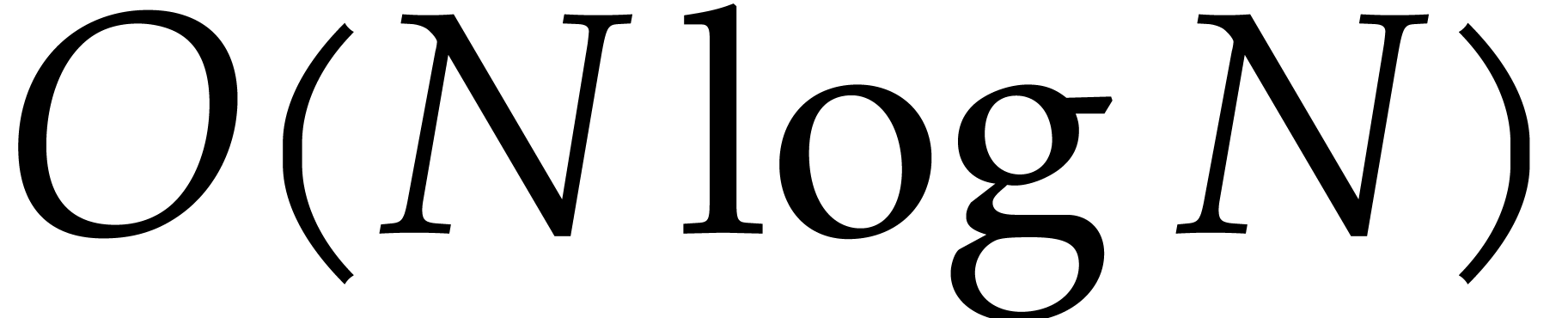 must be different from
must be different from  elements in
elements in  , a suitable
, a suitable 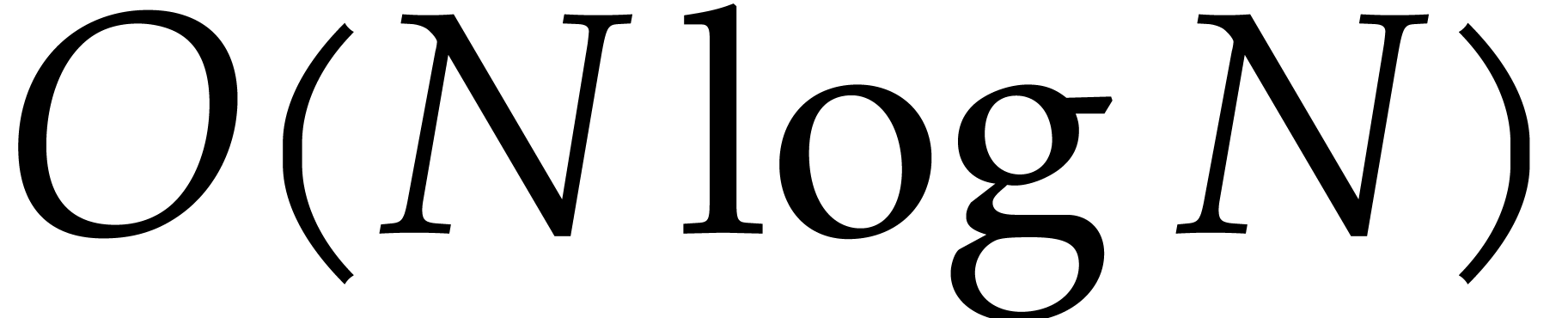 can be
found in the given subset of
can be
found in the given subset of  .
In this way,
.
In this way, 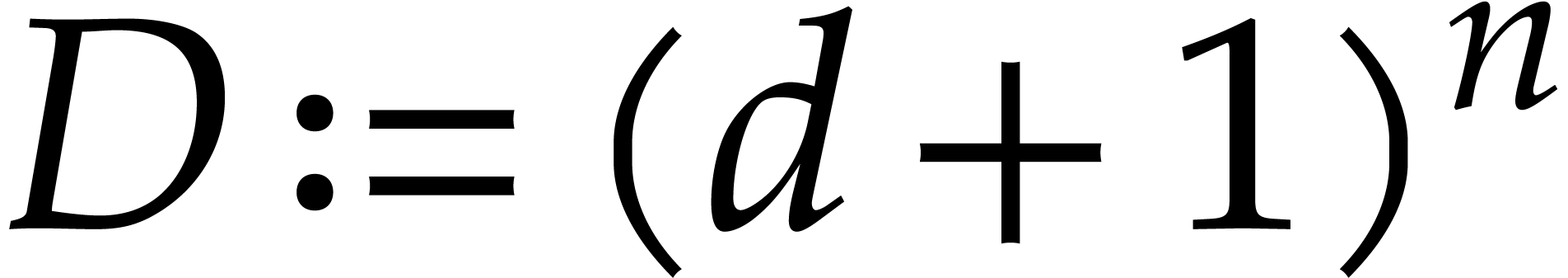 is a joined separating form for
is a joined separating form for
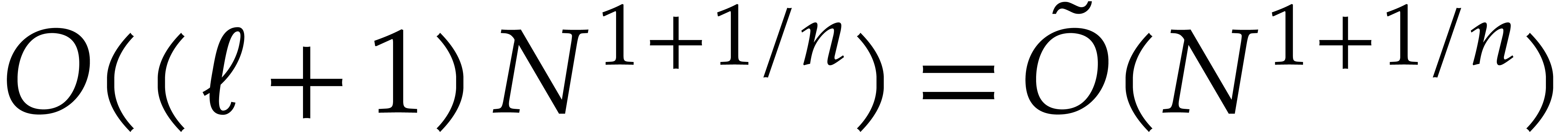 .
.
By construction, 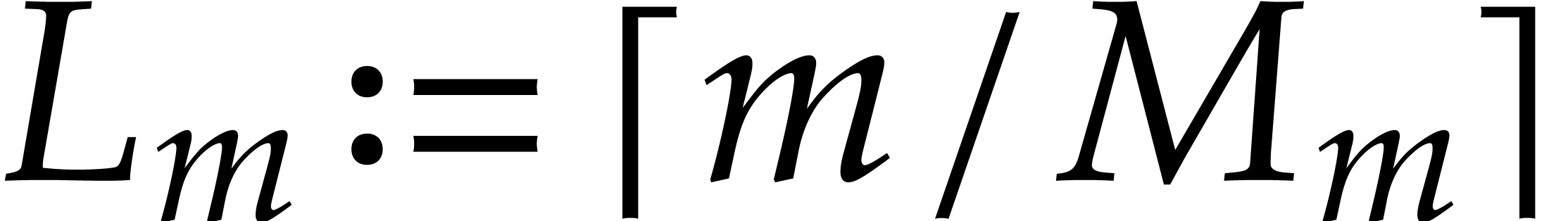 are
are  -linearly independent. The evaluation of
-linearly independent. The evaluation of 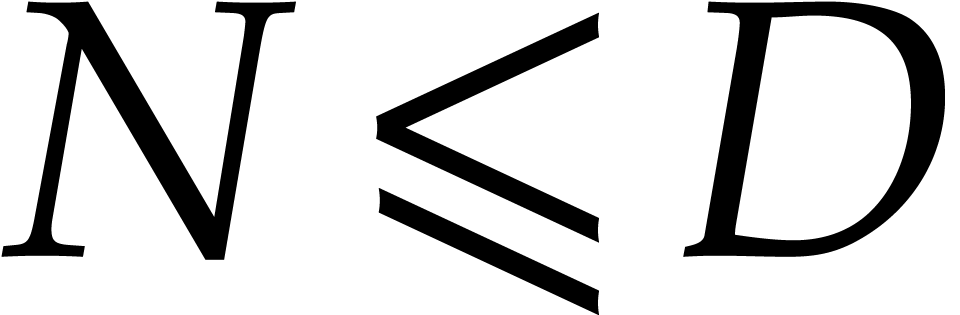 at all points
at all points 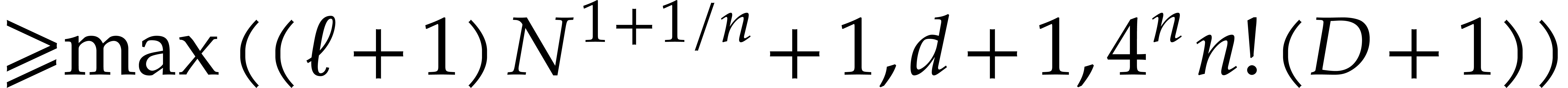 in
in 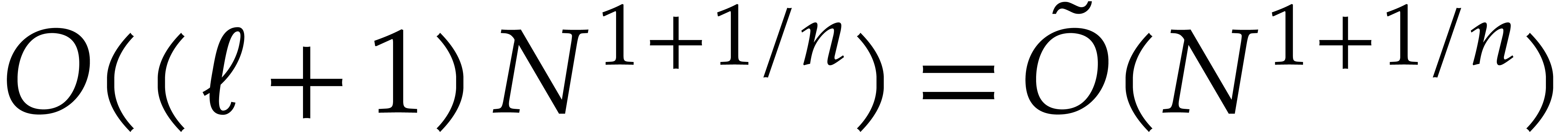 takes
takes  operations in
operations in  . For each
. For each  ,
the set of unsuitable values for
,
the set of unsuitable values for  can be computed
using
can be computed
using 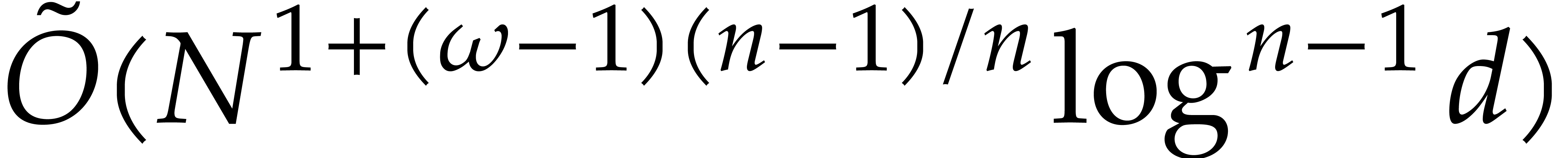 operations in
operations in  .
.
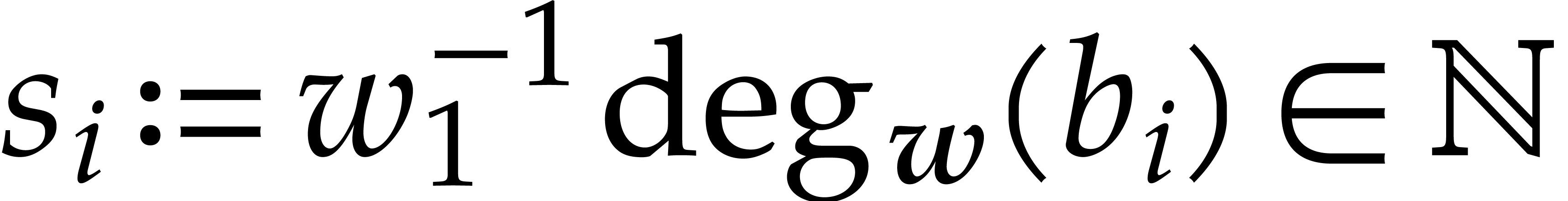 recursively weakly
separate
recursively weakly
separate 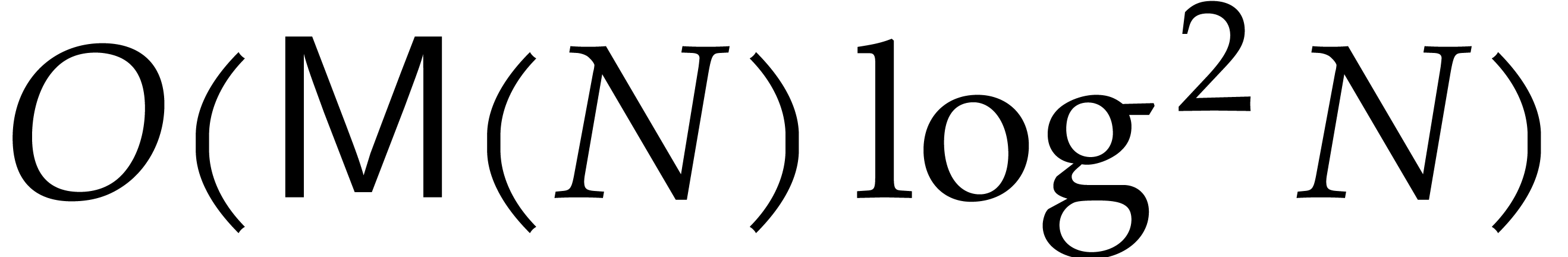 . Then a recursive
heterogeneous basis for
. Then a recursive
heterogeneous basis for 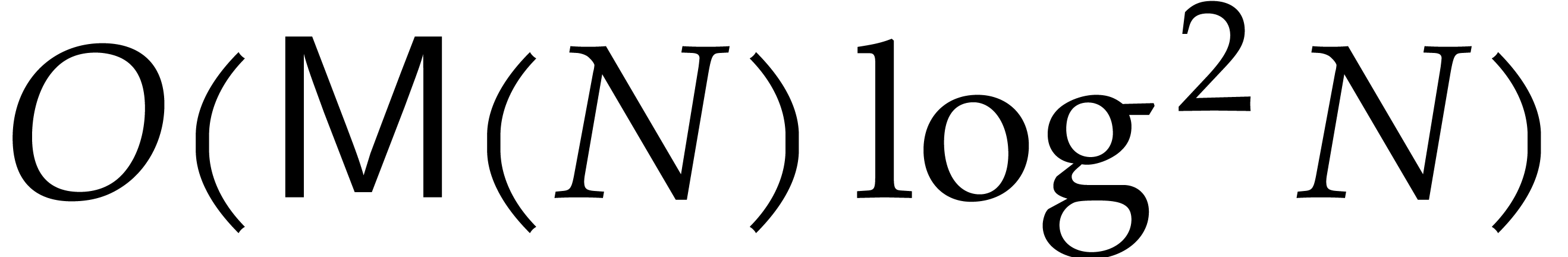 and
and 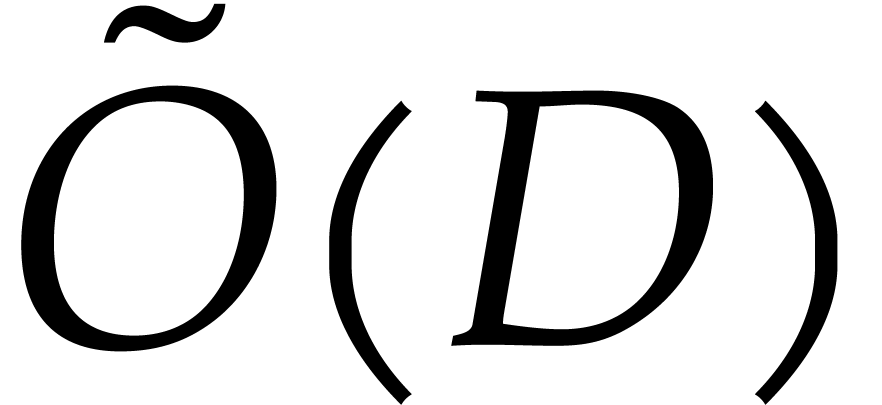 can be computed using
can be computed using
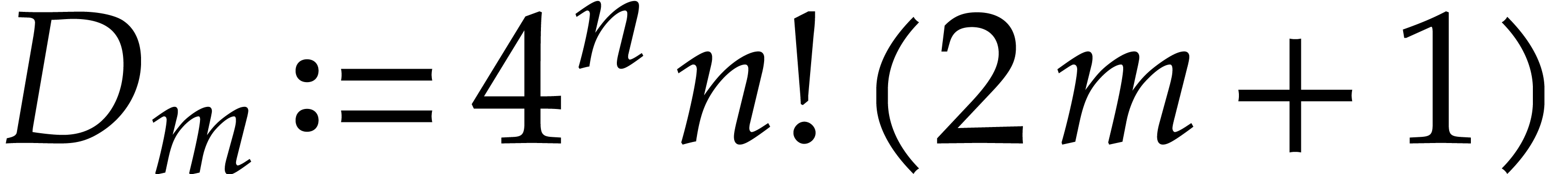
operations in  .
.
Proof. This is a direct consequence of Lemma 3.4; recall that  is fixed.
is fixed.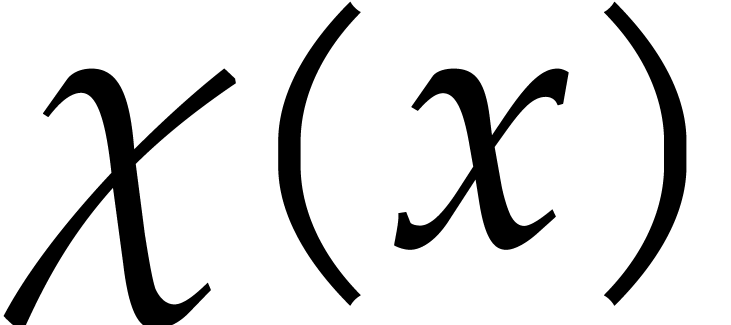
We gather the preceding results of this section into the following
statement. We will say that an element 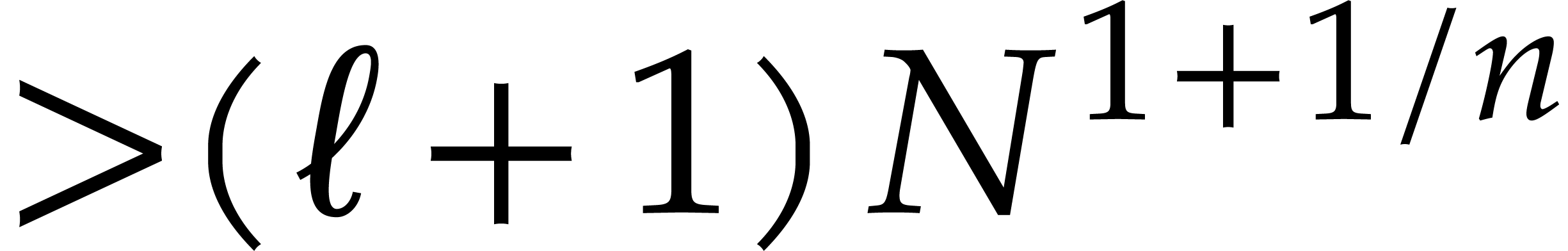 has
(multiplicative) order
has
(multiplicative) order 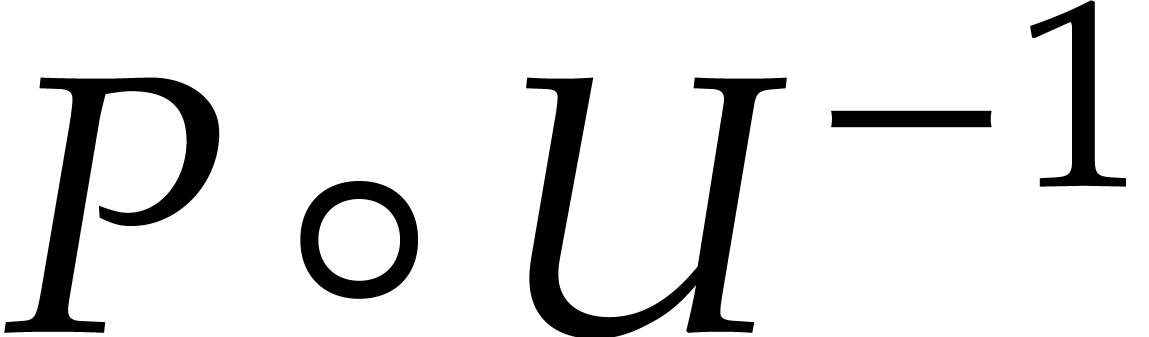 whenever
whenever 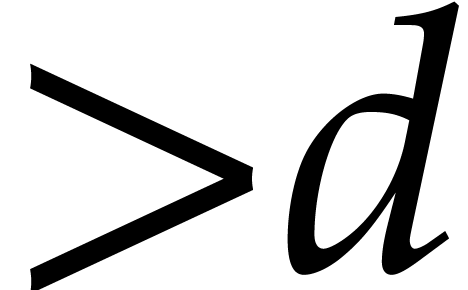 for all
for all  . The order equals
. The order equals
 if in addition
if in addition  .
.
 and
and  .
Assume that
.
Assume that  is a power
is a power 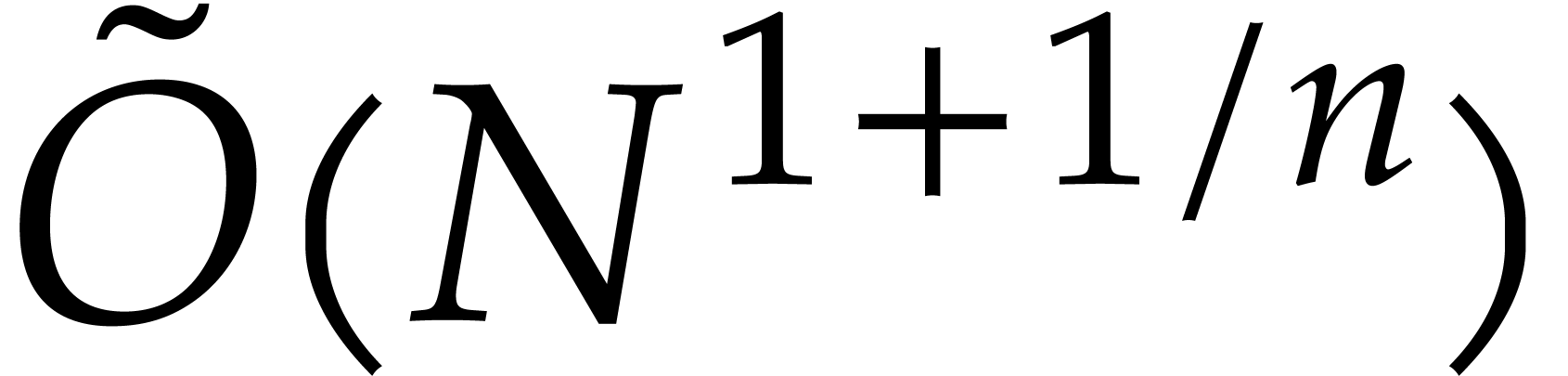 , and that we are given an element of order
, and that we are given an element of order
in  . Then we can compute
an invertible
. Then we can compute
an invertible 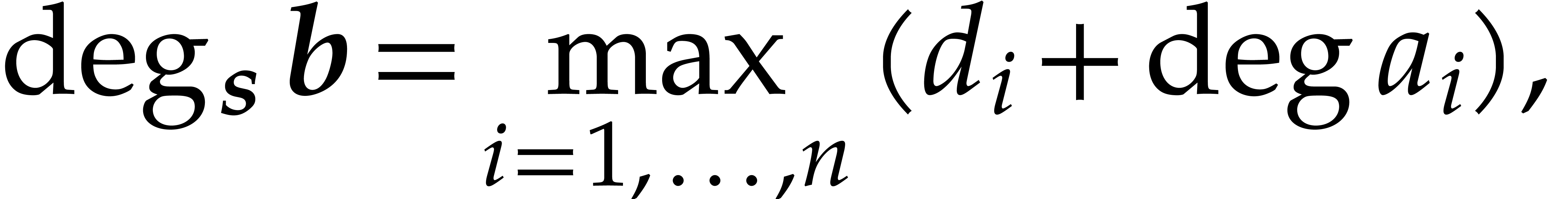 matrix
matrix  over
over  such that
such that 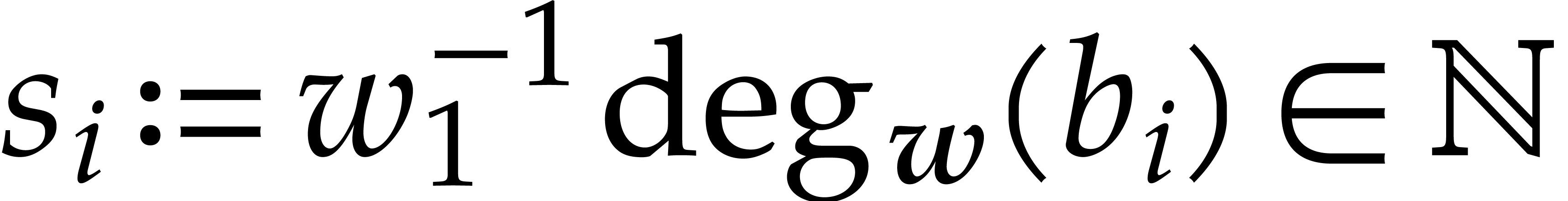 recursively weakly separate the
recursively weakly separate the 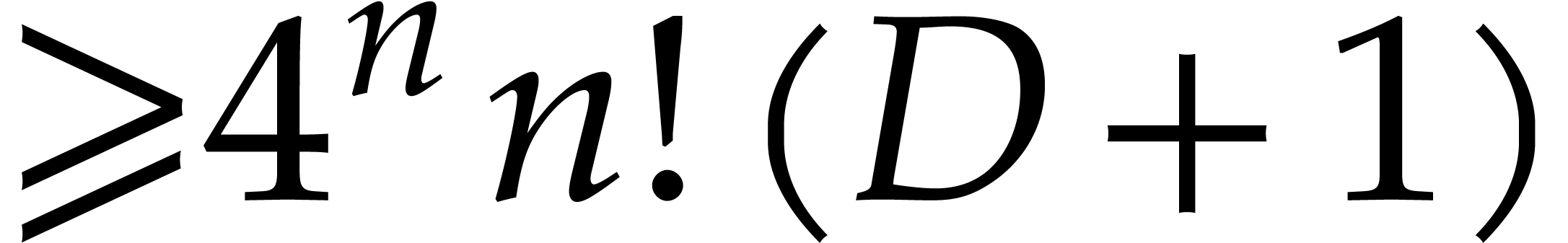 ,
together with a recursive heterogeneous basis for
,
together with a recursive heterogeneous basis for  and
and 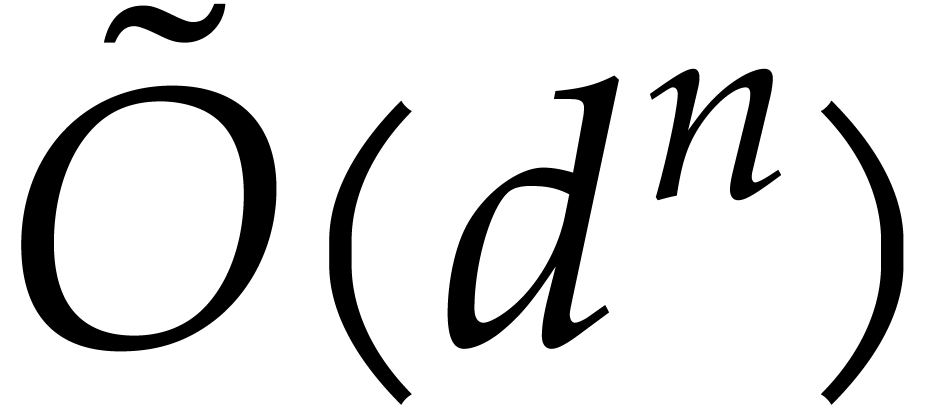 , using
, using
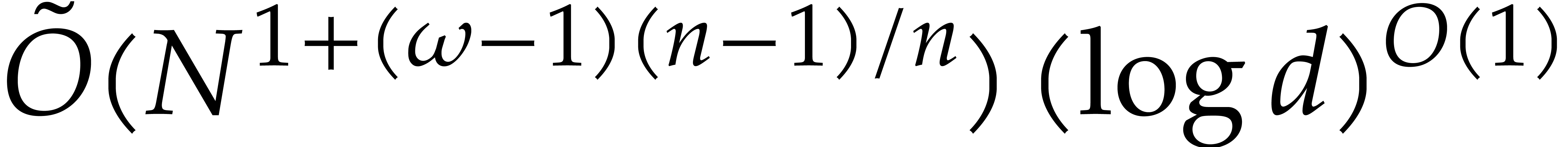
operations in  . Having
computed such a basis, any polynomial
. Having
computed such a basis, any polynomial 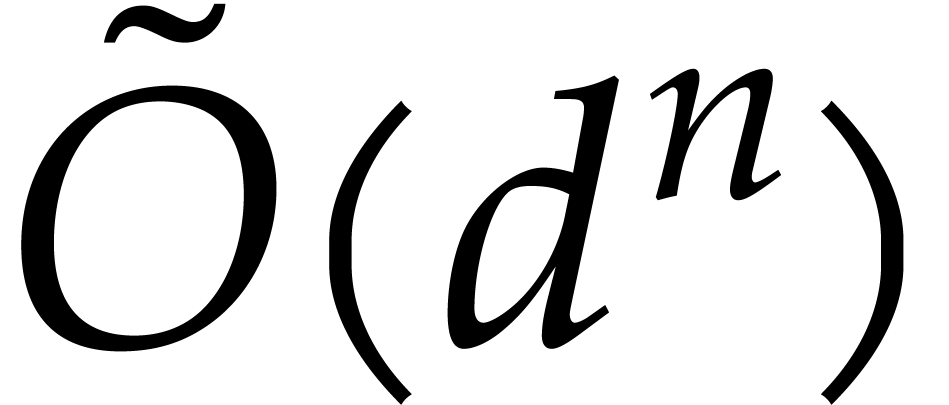 of total
degree
of total
degree  can be evaluated at
can be evaluated at  using
using  operations in
operations in  .
.
Proof. The case 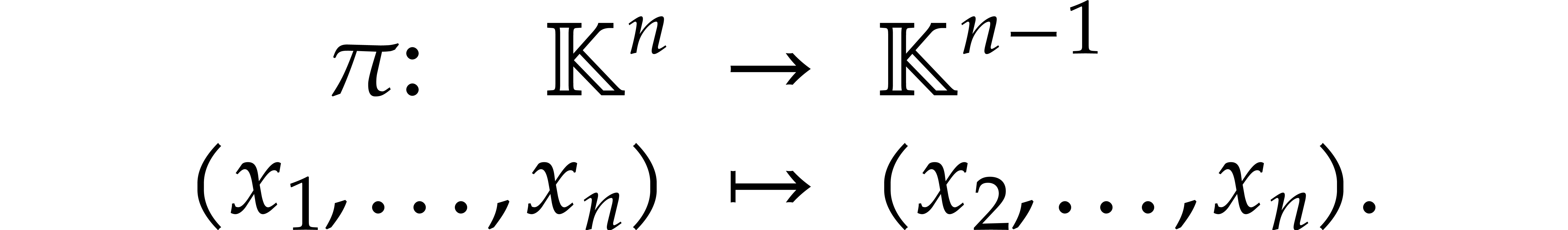 is
well-known; see [9, chapter 10]. So let us assume
is
well-known; see [9, chapter 10]. So let us assume 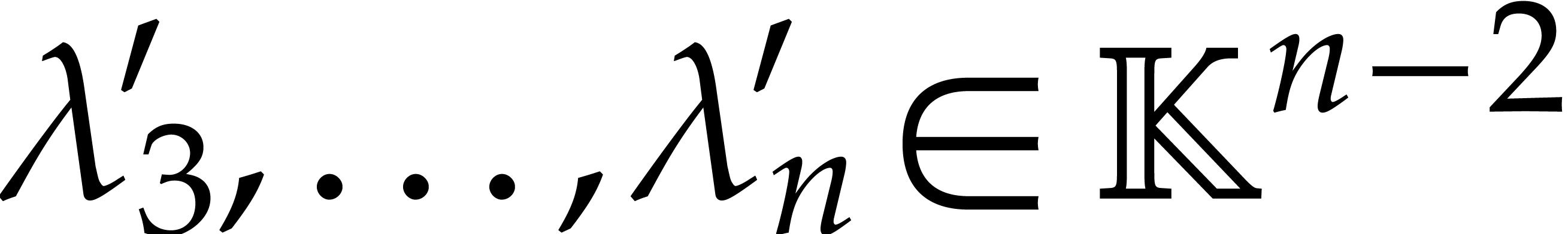 . The computation of
. The computation of  and of the recursive heterogeneous basis has been
addressed in Lemmas 3.5 (using the element of order
and of the recursive heterogeneous basis has been
addressed in Lemmas 3.5 (using the element of order  ) and Lemma 3.6.
) and Lemma 3.6.
Given  and
and  ,
the computation of the polynomial
,
the computation of the polynomial  takes
takes  operations in
operations in  thanks to [16, Appendix A, Proposition A.5] and the element of order
thanks to [16, Appendix A, Proposition A.5] and the element of order
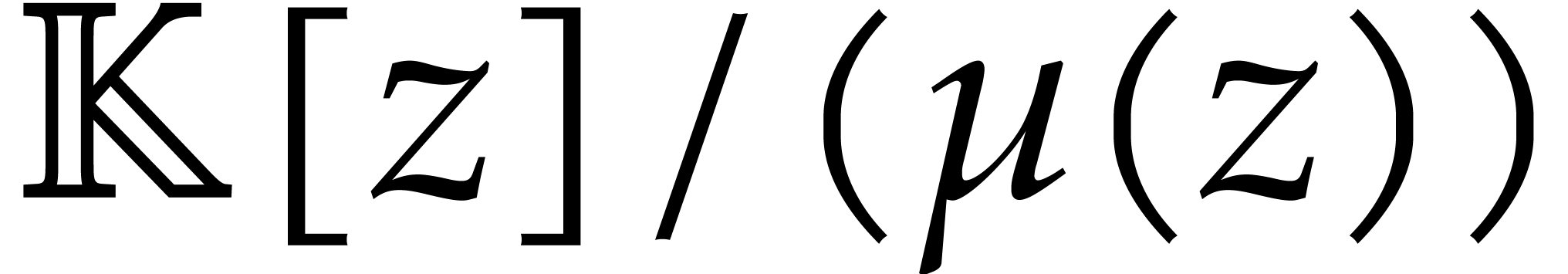 . By [17,
Theorem 5],
. By [17,
Theorem 5], 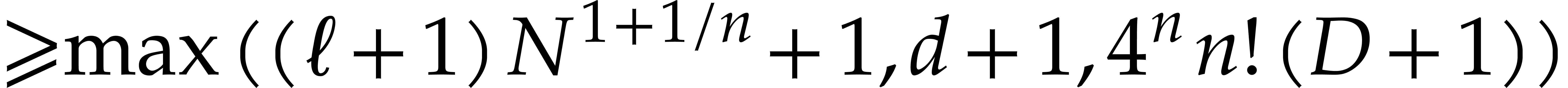 can be evaluated at
can be evaluated at  using
using 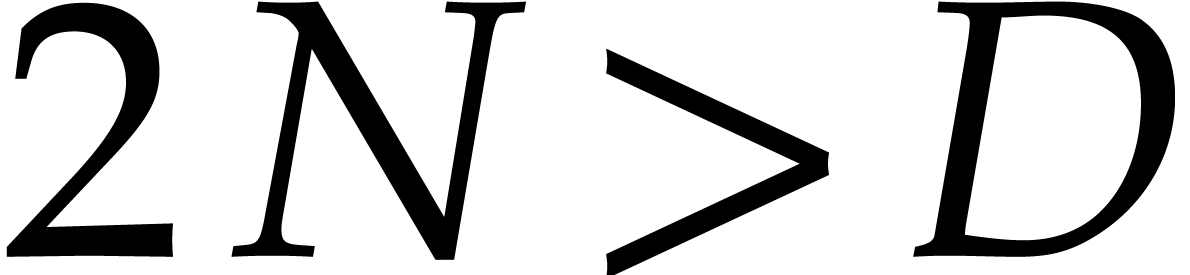 operations in
operations in  . Here
. Here  is a cost function
for multiplying two sparse polynomials
is a cost function
for multiplying two sparse polynomials 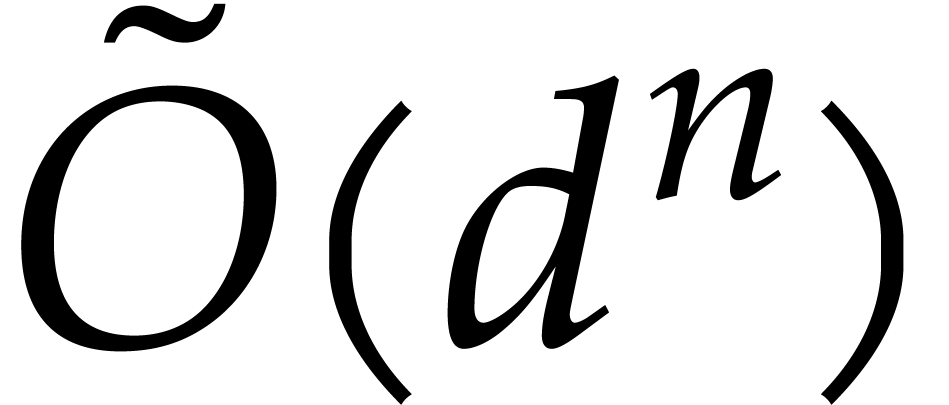 and
and  in
in  , where
, where
 is the maximum of the sizes of the supports of
is the maximum of the sizes of the supports of
 ,
,  , and
, and  .
As detailed in the proof of [17, Theorem 1], we may take
.
As detailed in the proof of [17, Theorem 1], we may take
 , thanks to the element of
order
, thanks to the element of
order  .
.
 be a fixed dimension, let
be a fixed dimension, let 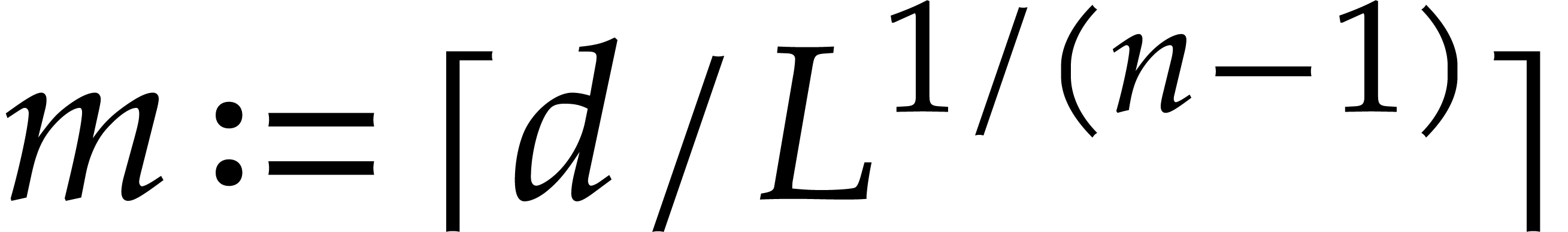 and
and  be such that
be such that  . After the precomputation of
suitable data, as a function of
. After the precomputation of
suitable data, as a function of 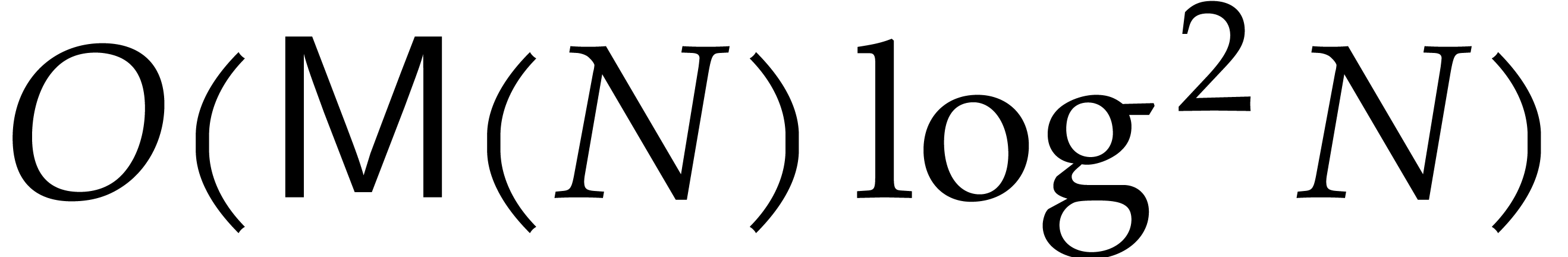 and
and 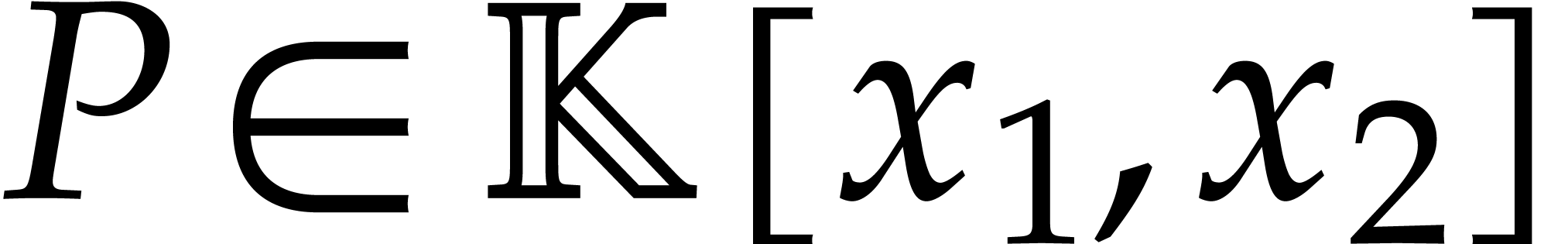 only, any polynomial
only, any polynomial 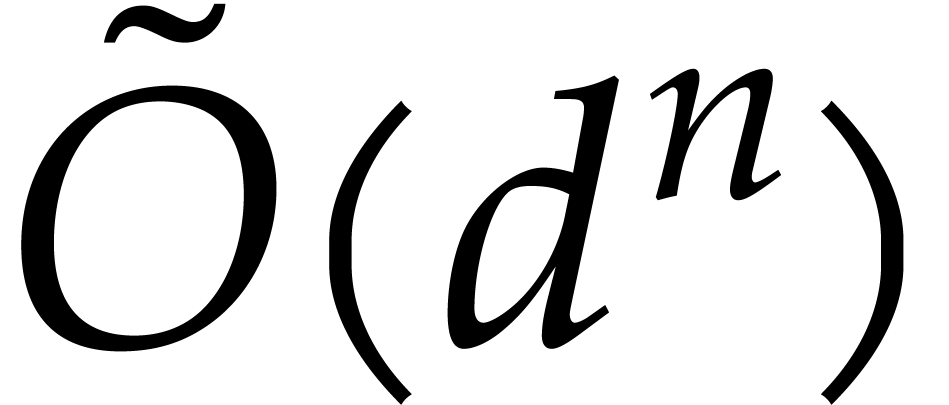 of total
degree
of total
degree 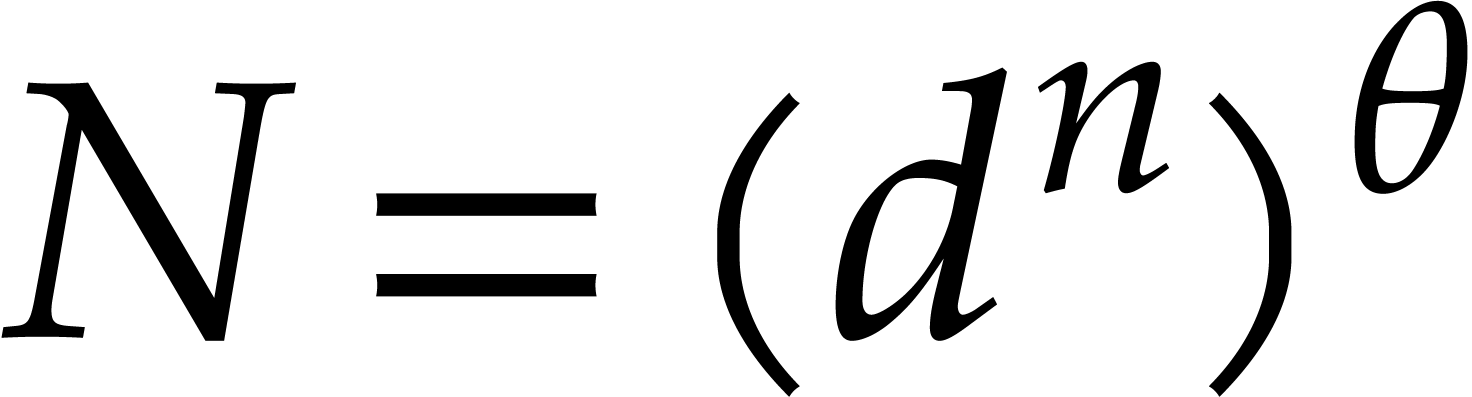 can be evaluated at
can be evaluated at 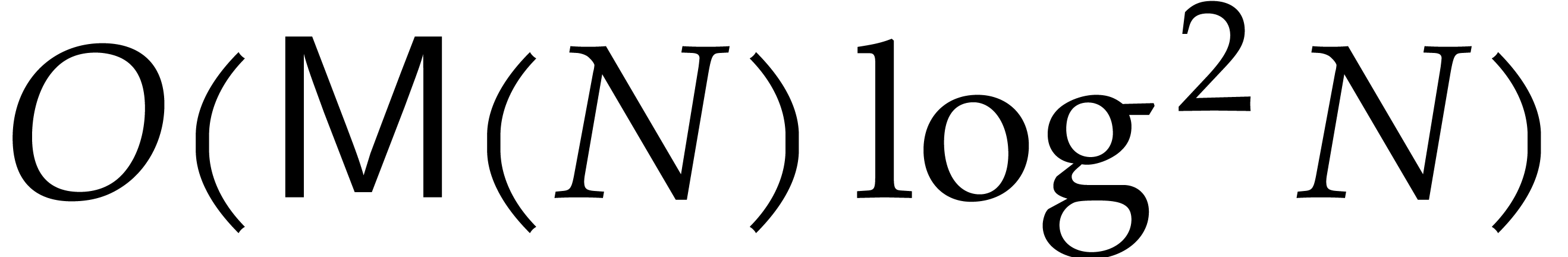 using
using
operations in  .
Moreover, the precomputation can be done using
.
Moreover, the precomputation can be done using
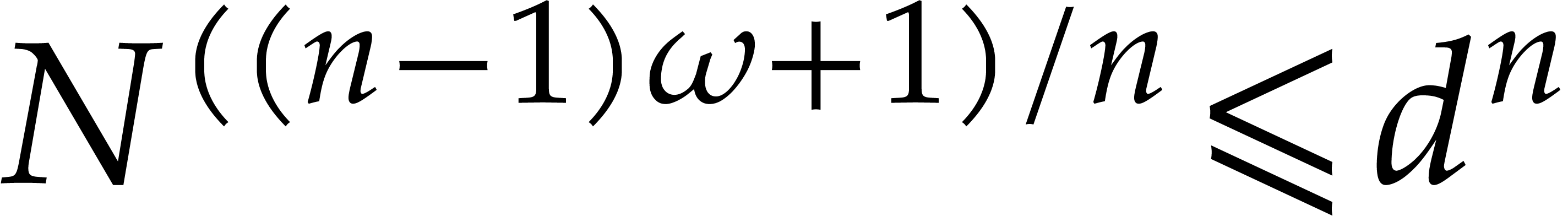
operations in  .
.
Proof. Let  .
We first handle the case where
.
We first handle the case where 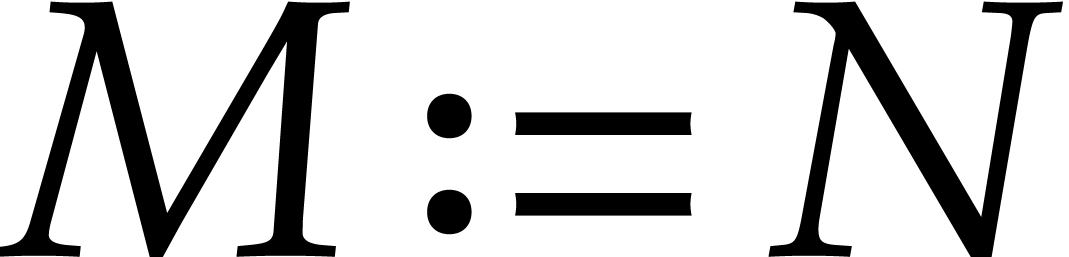 .
In this way, up to repeating some points in
.
In this way, up to repeating some points in 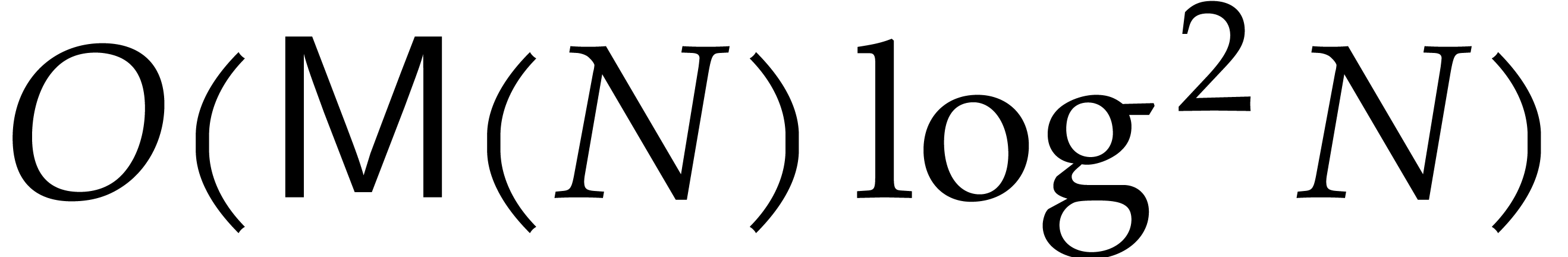 , we may assume that
, we may assume that 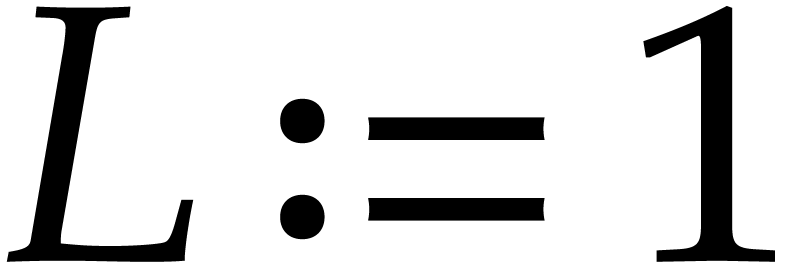 is a
power of two such that
is a
power of two such that 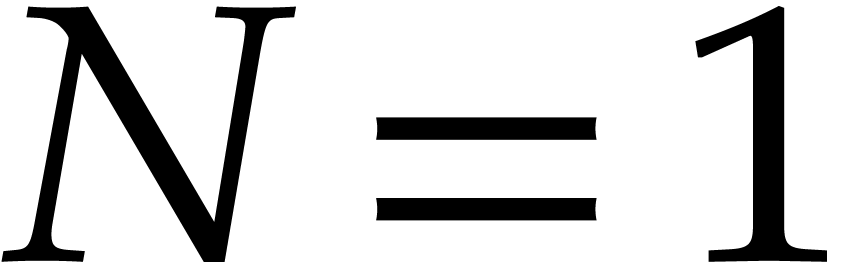
 .
.
If we are given an element of order 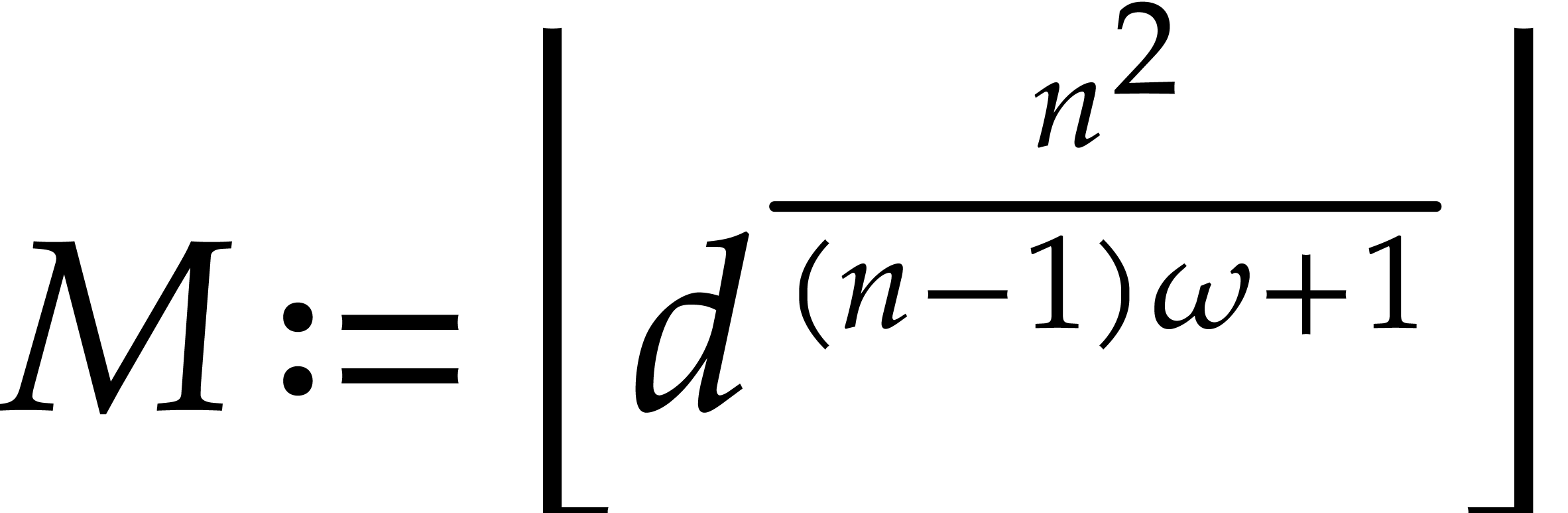 ,
then the complexity bounds follow from Lemma 3.7.
Otherwise, we may appeal to Proposition A.2 to ensure the
existence of this element of high order. In this way, note that the
precomputed data are in general defined over an extension of the form
,
then the complexity bounds follow from Lemma 3.7.
Otherwise, we may appeal to Proposition A.2 to ensure the
existence of this element of high order. In this way, note that the
precomputed data are in general defined over an extension of the form
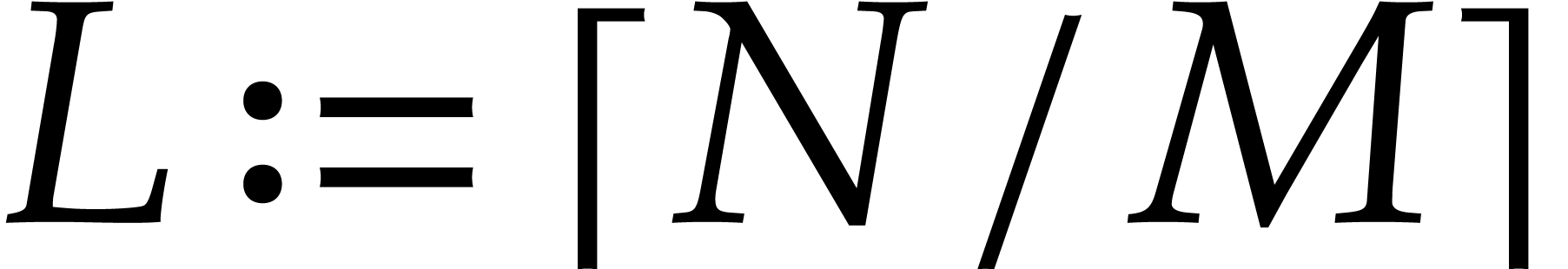 , and that
, and that 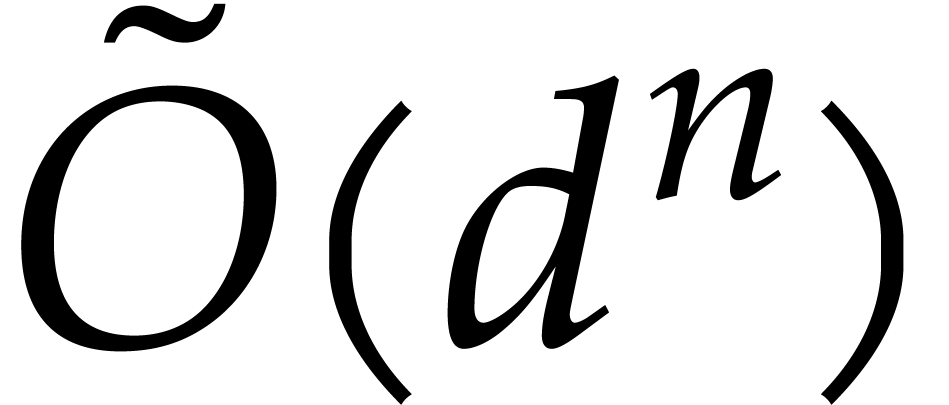 must then be evaluated over this extension, following the rules
described in the proof of Proposition A.2.
must then be evaluated over this extension, following the rules
described in the proof of Proposition A.2.
Finally, if  then we subdivide
then we subdivide 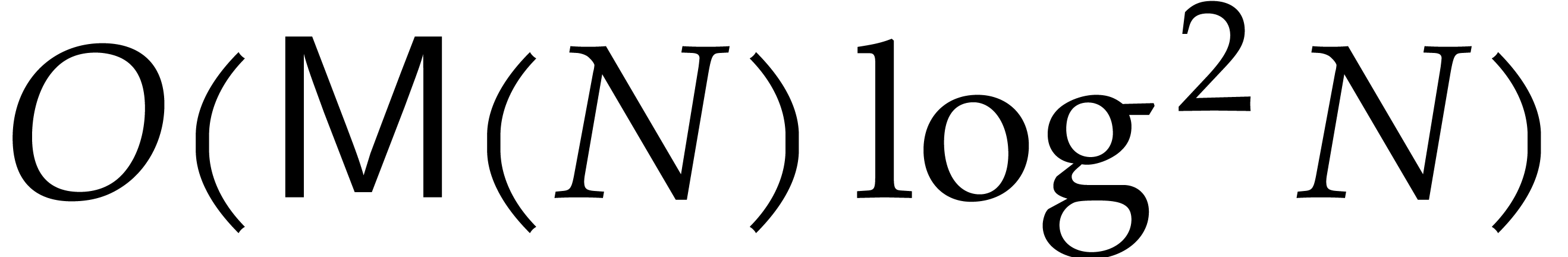 into
into  subsequences of size
subsequences of size 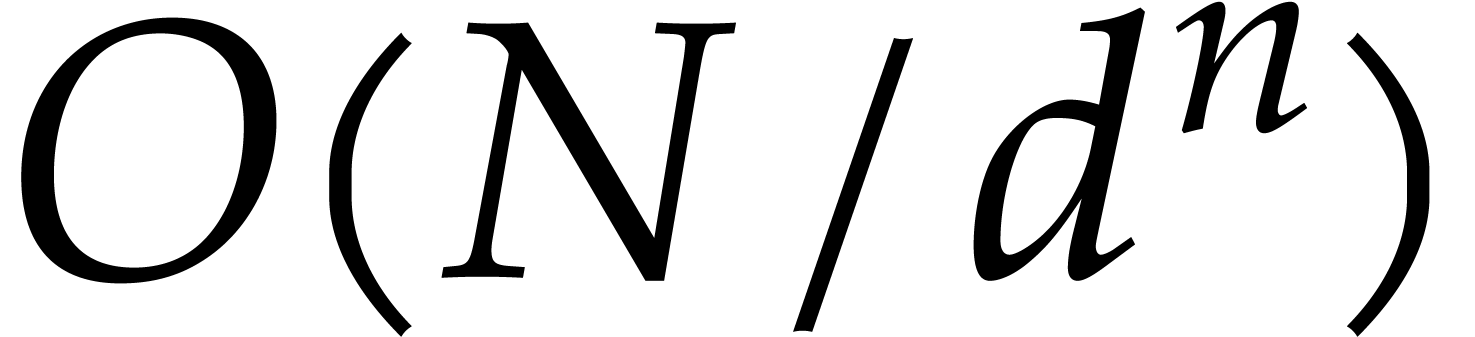 , and then repeat the precomputations and the
evaluations for each subsequence.
, and then repeat the precomputations and the
evaluations for each subsequence.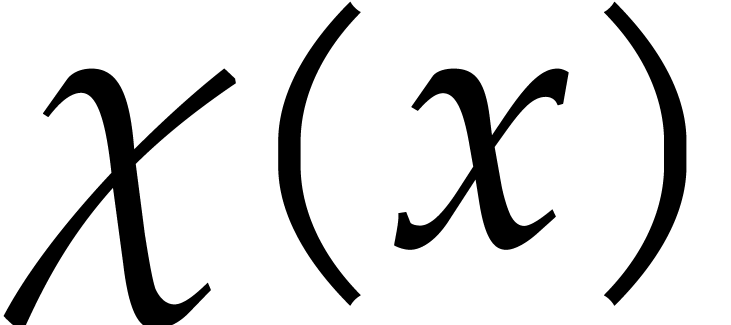
Using the preceding amortized evaluation strategy, we analyze the cost
of a single multi-point evaluation in 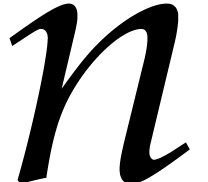 variables
as a function of
variables
as a function of 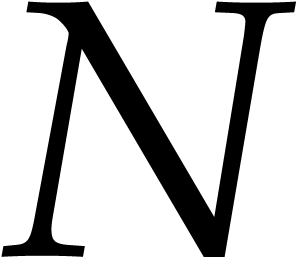 .
.
 be a fixed dimension. A polynomial
be a fixed dimension. A polynomial
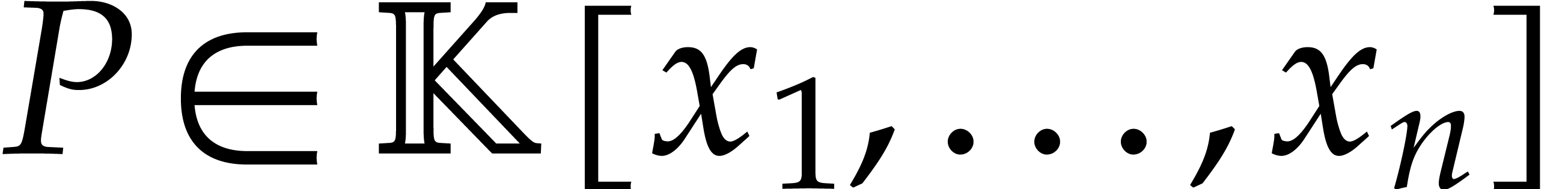 of total degree
of total degree  can be
evaluated at
can be
evaluated at  points in
points in 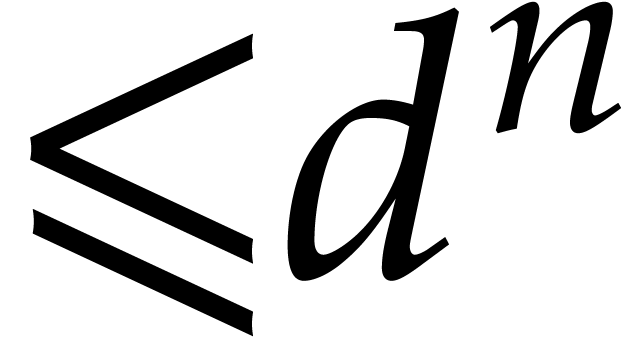 using
using 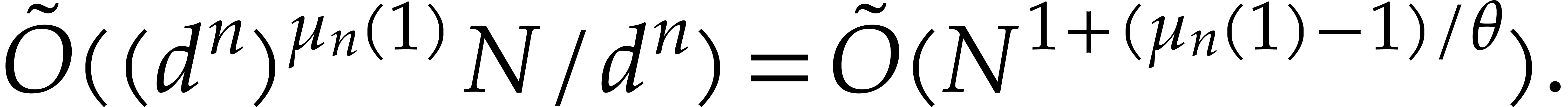 operations in
operations in  , where
, where
Proof. We start with the case 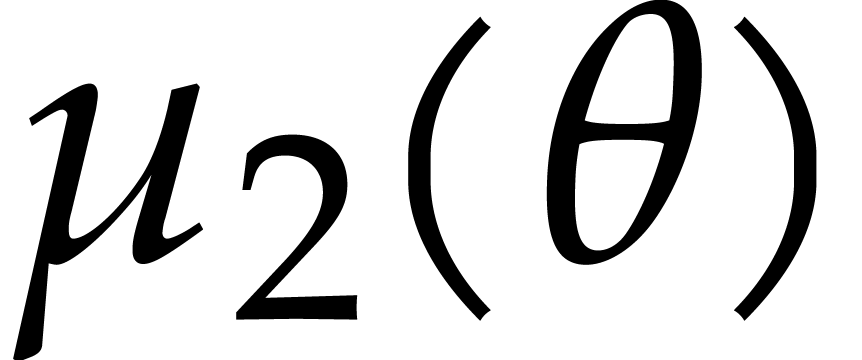 . We subdivide
. We subdivide  into
subsequences
into
subsequences  of cardinality
of cardinality  , where
, where 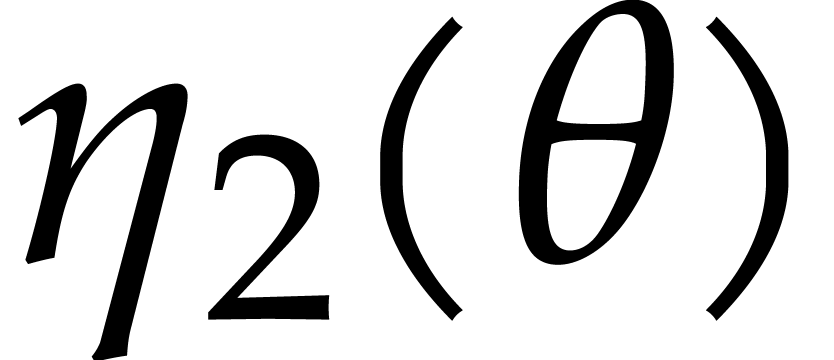 and
and 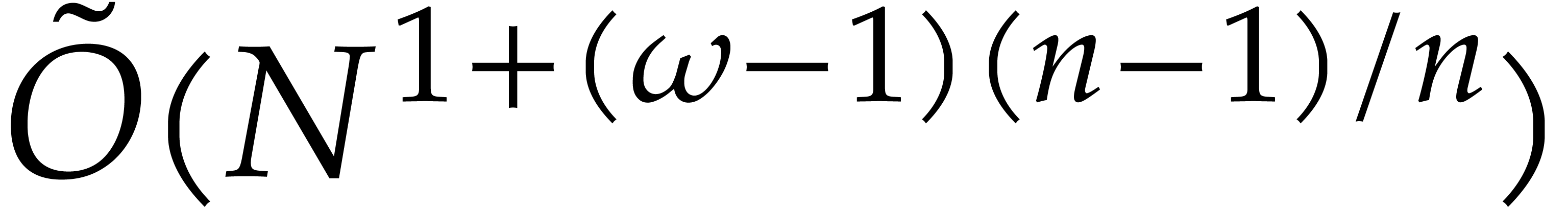 . The evaluations of
. The evaluations of 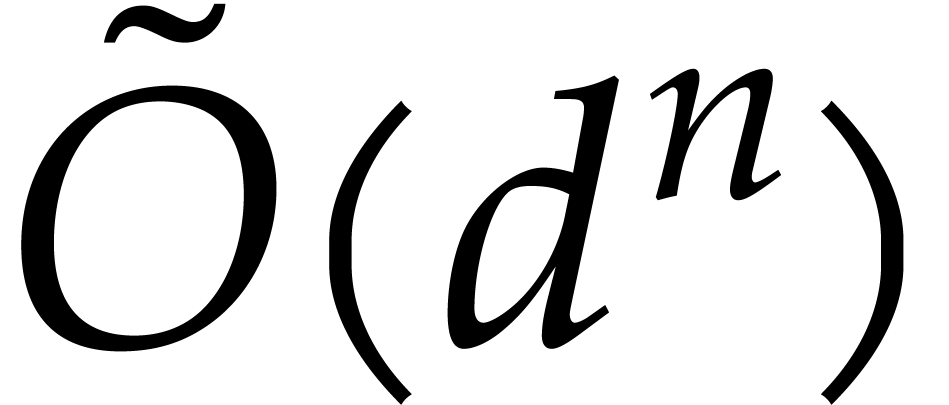 at
at  for
for  take
take
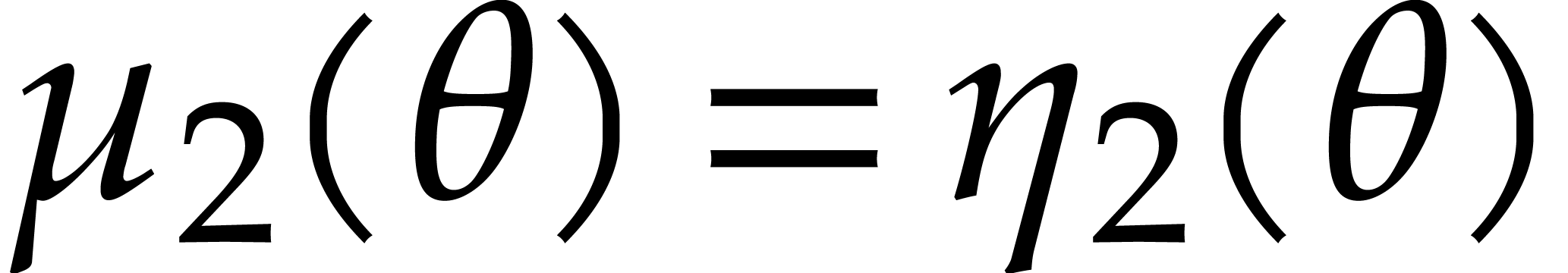 |
(3.8) |
operations in  by Theorem 3.8. We
distinguish the following cases:
by Theorem 3.8. We
distinguish the following cases:
If  , then we set
, then we set  and
and 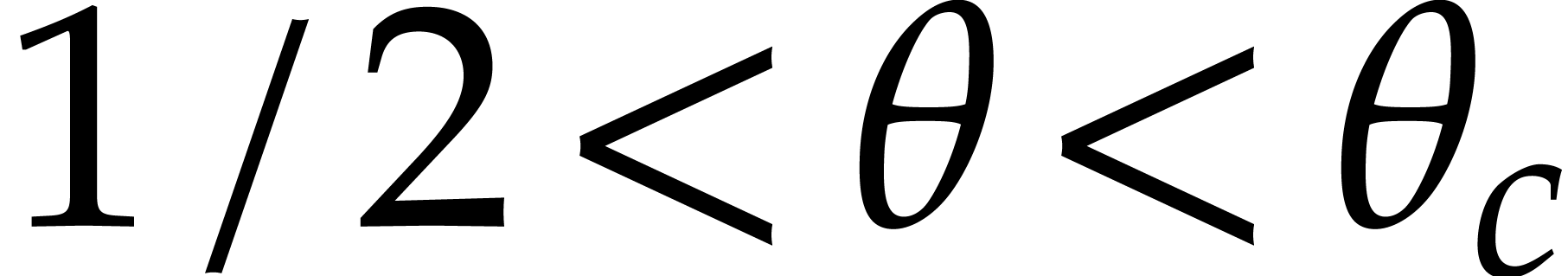 ,
so the cost
,
so the cost  .
.
Otherwise we take

and 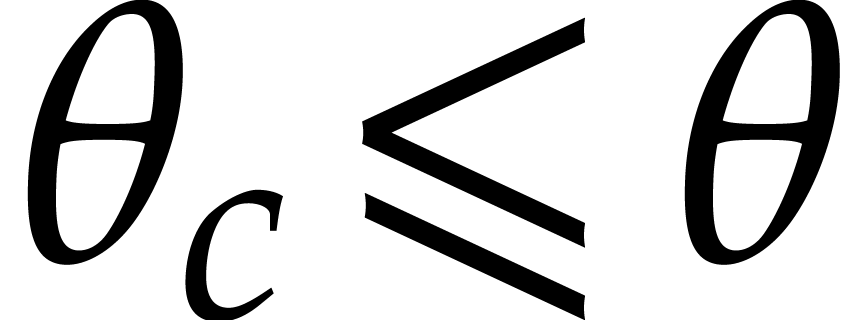 , so the cost
, so the cost
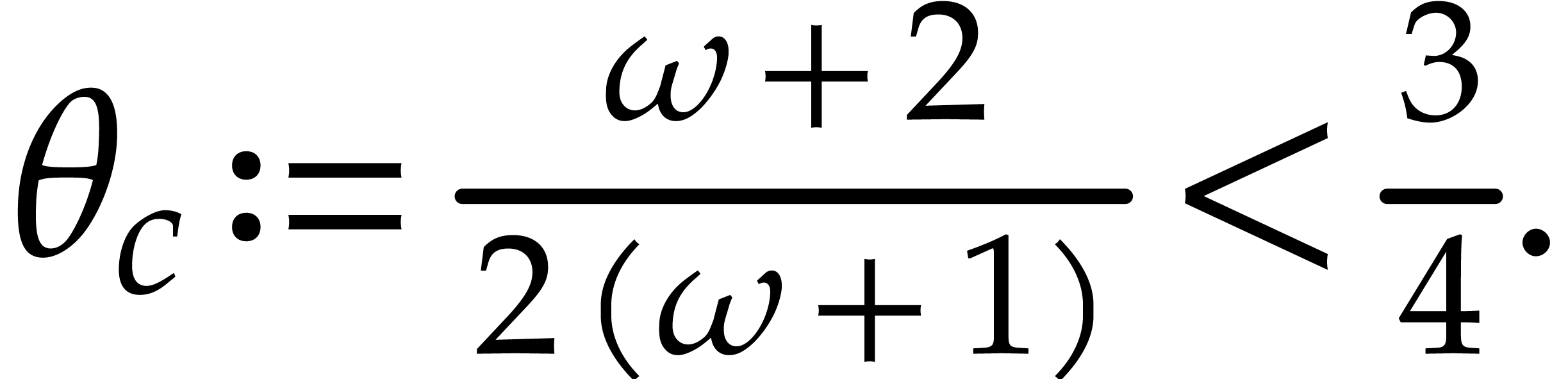
Finally, if 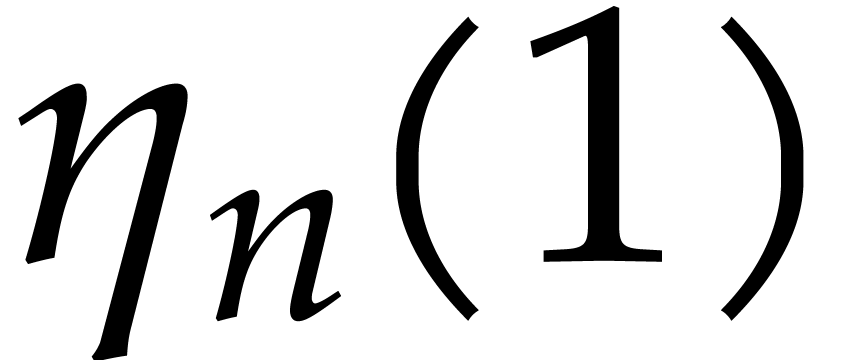 then we subdivide
then we subdivide 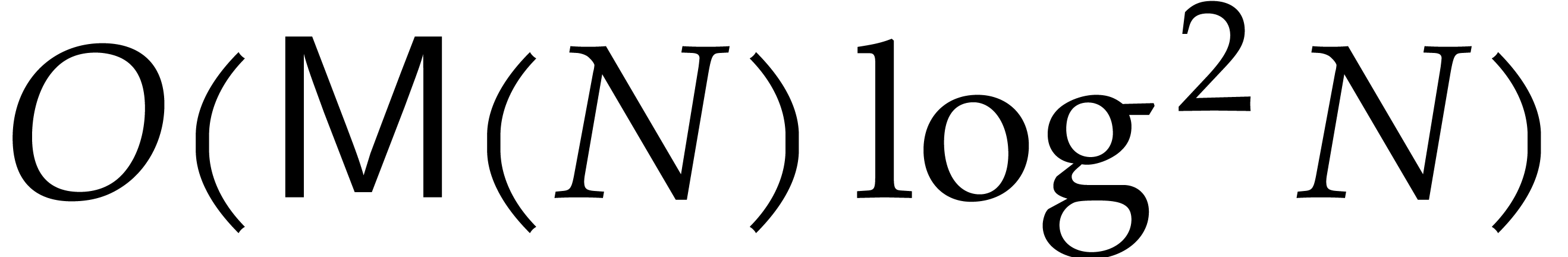 into
into  subsequences of size
subsequences of size 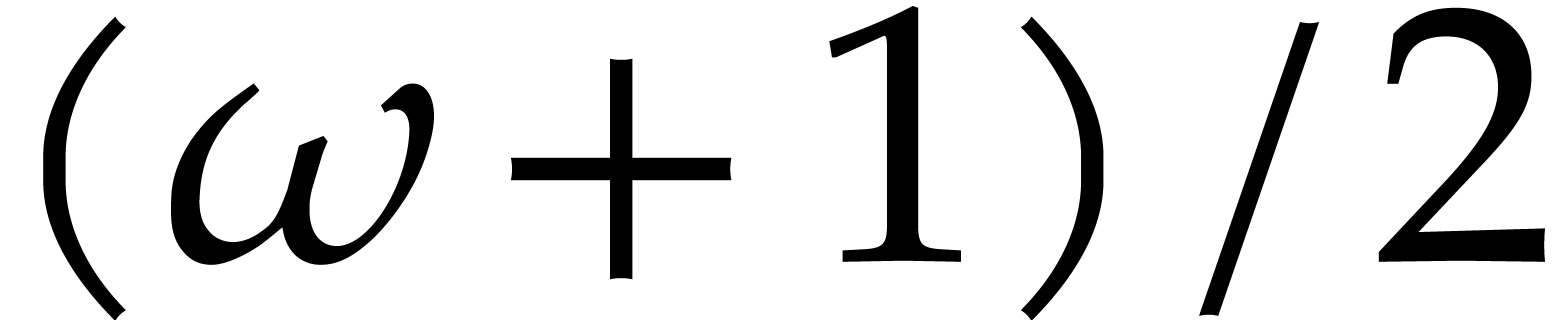 , so the evaluation cost becomes
, so the evaluation cost becomes
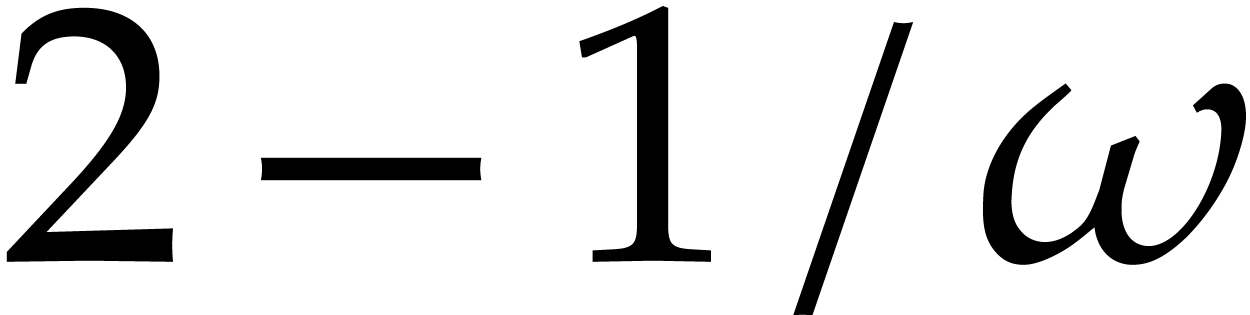
Remark  and
and  ,
then Theorem 3.9 always improves on Theorem 2.7.
,
then Theorem 3.9 always improves on Theorem 2.7.
Remark 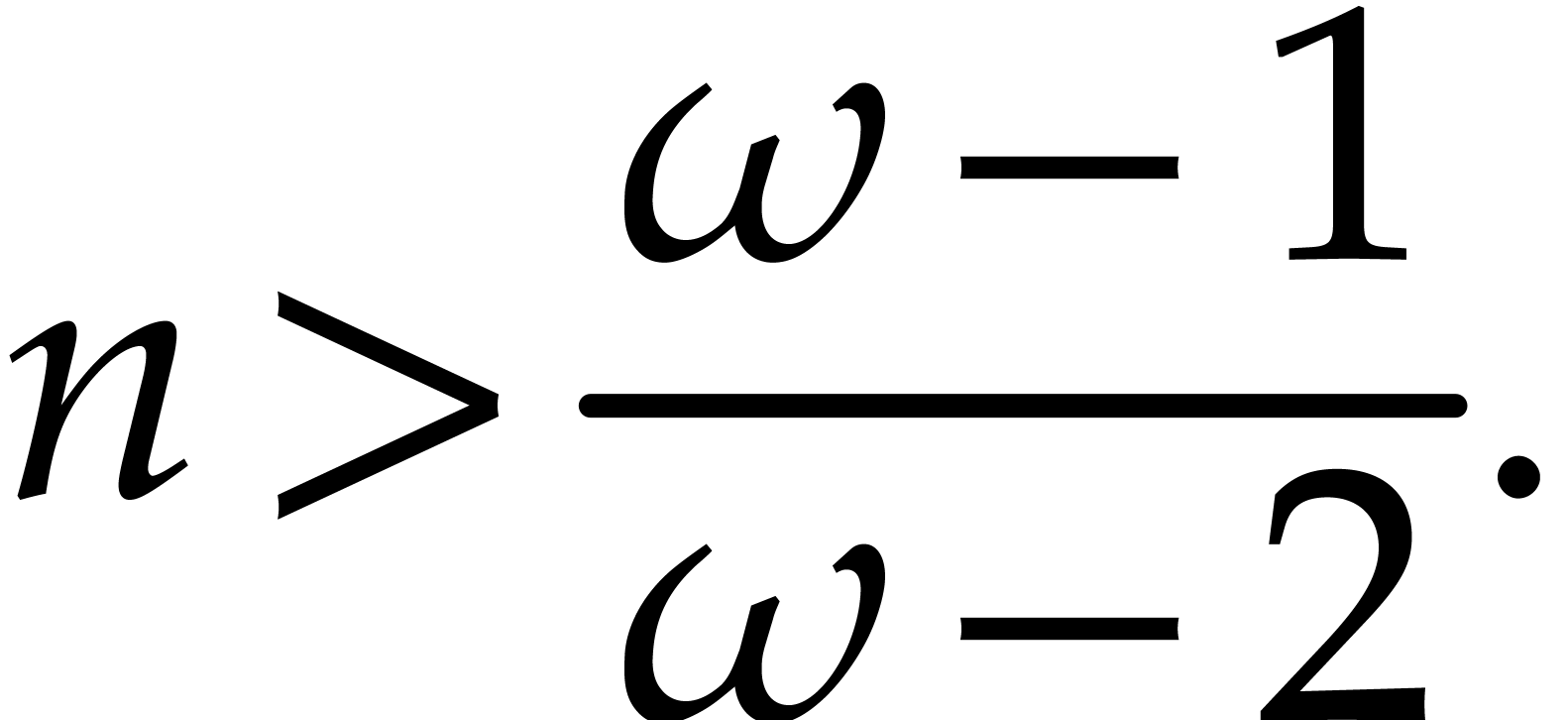 for bivariate multi-point evaluation in Figure
3.1
.
for bivariate multi-point evaluation in Figure
3.1
.
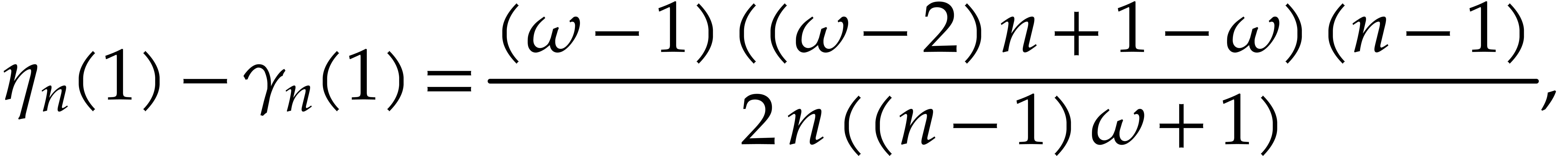 ,
we observe that
,
we observe that
 if
if  ,
,
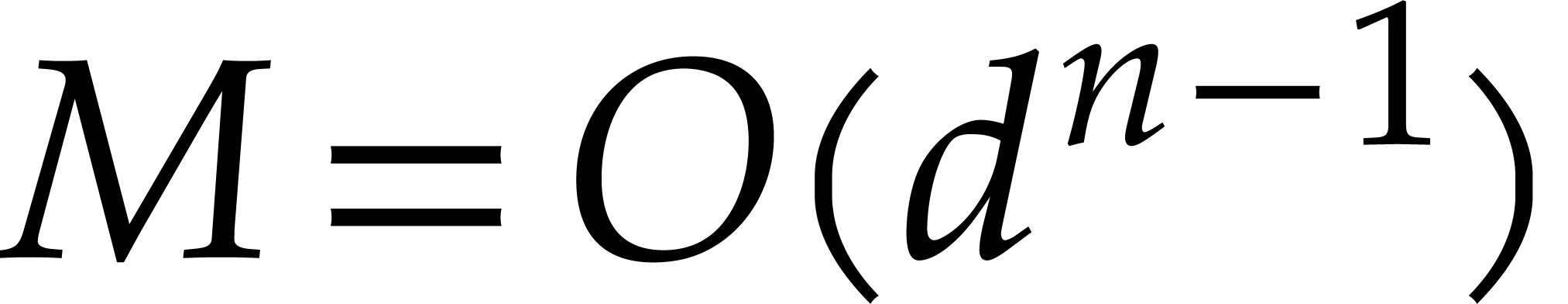 if
if 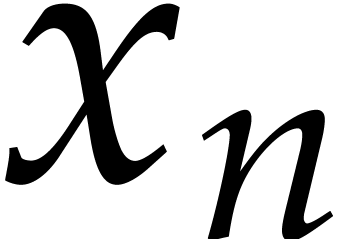 ,
,
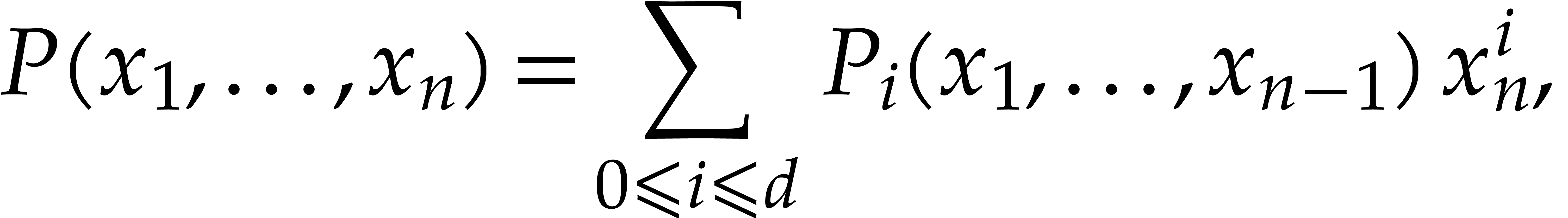 if
if  ,
where
,
where 
Remark 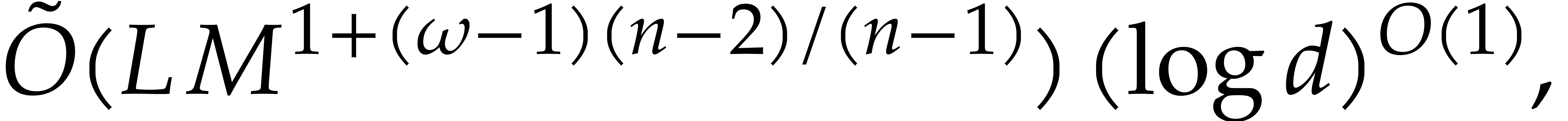 and
and  tend to
tend to 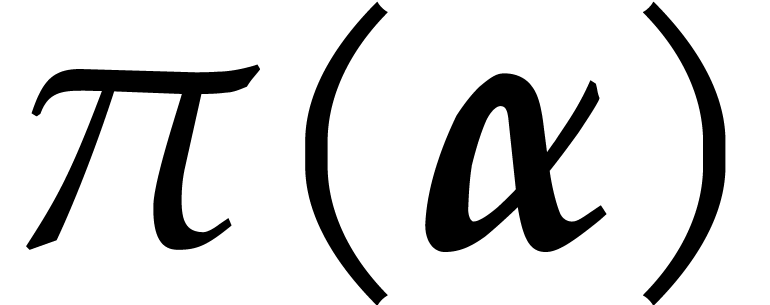 and
and 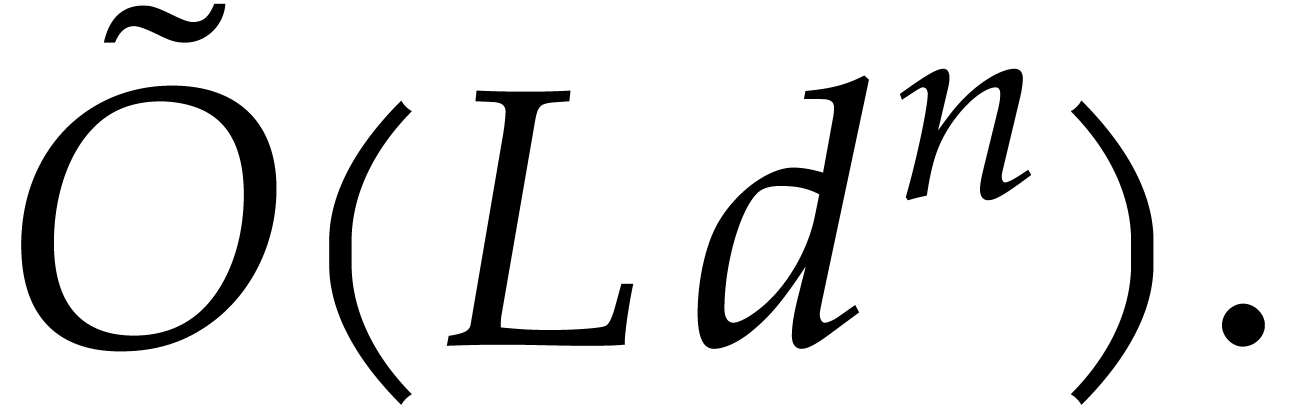 respectively, when
respectively, when  tends to
infinity. If
tends to
infinity. If 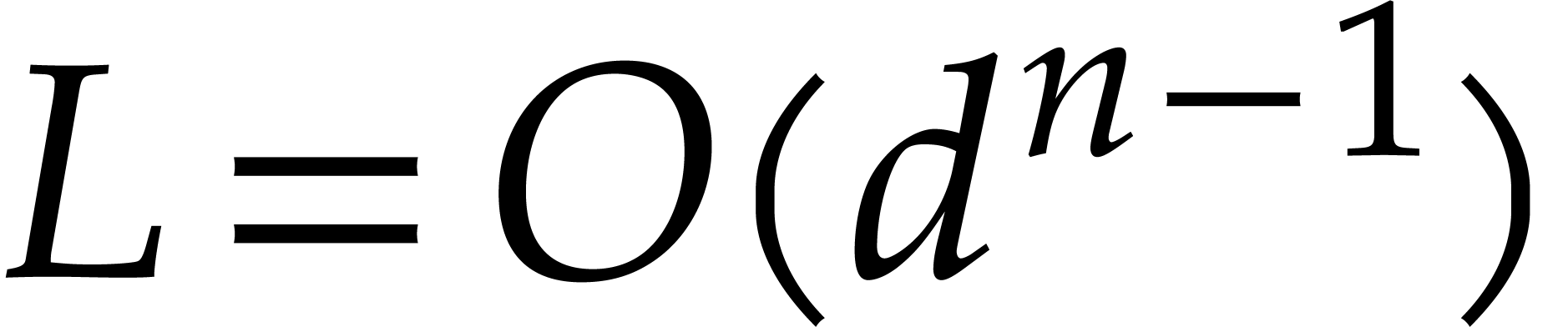 , then our new
bound improves on the Nüsken–Ziegler algorithm as soon as
, then our new
bound improves on the Nüsken–Ziegler algorithm as soon as
 is not too small. More precisely, we have
is not too small. More precisely, we have
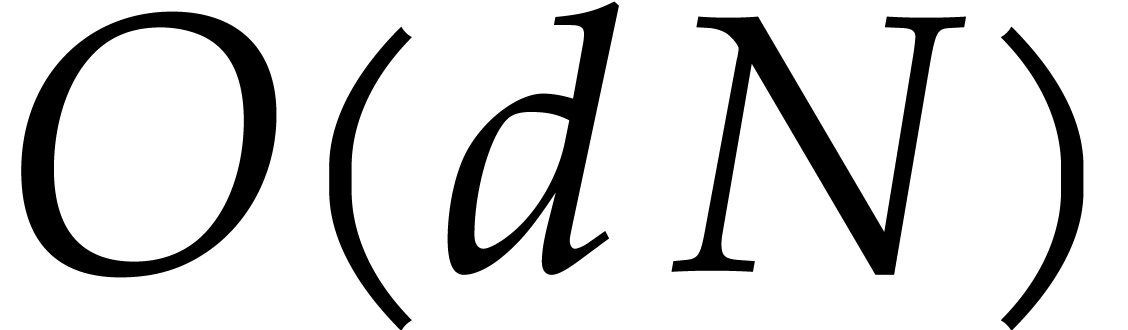
so our method is faster when
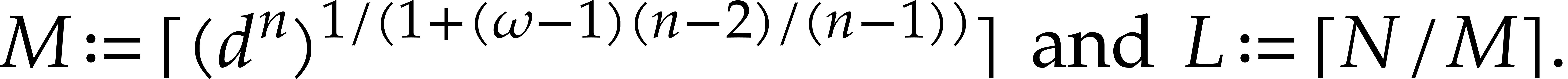
As in section 2.3, let us now analyze the variant when we
apply the amortized evaluation method for  variables to the non-amortized problem for
variables to the non-amortized problem for 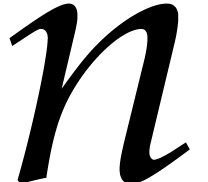 variables.
variables.
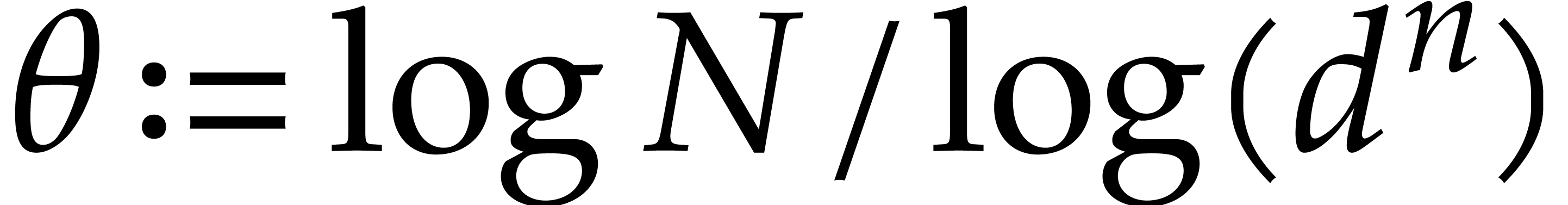 be a fixed dimension. A polynomial
be a fixed dimension. A polynomial
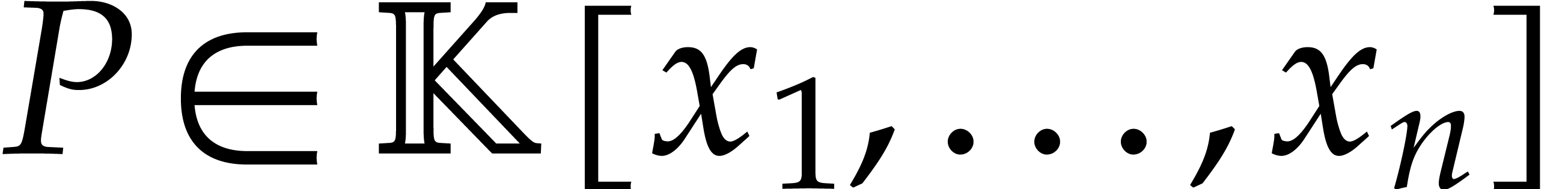 of total degree
of total degree 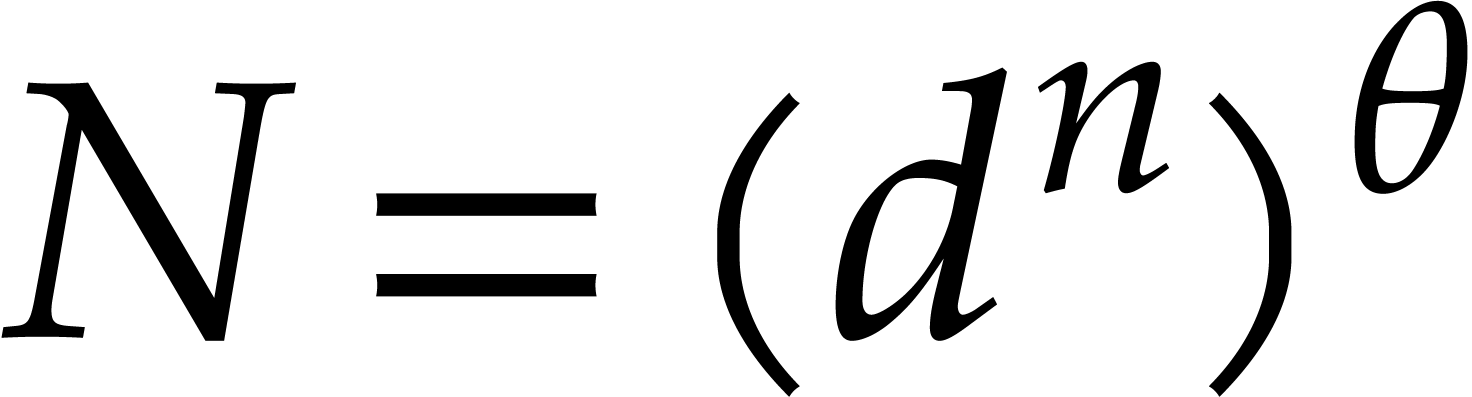 can be
evaluated at
can be
evaluated at  points in
points in 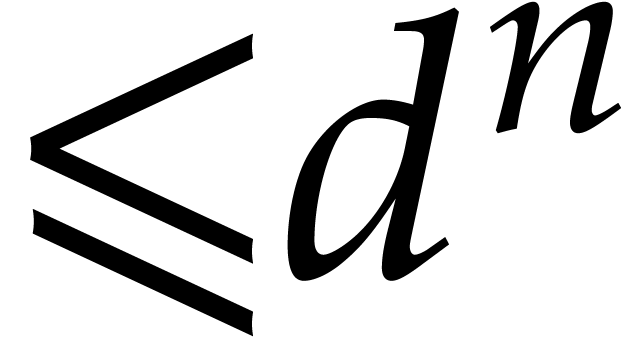 using
using 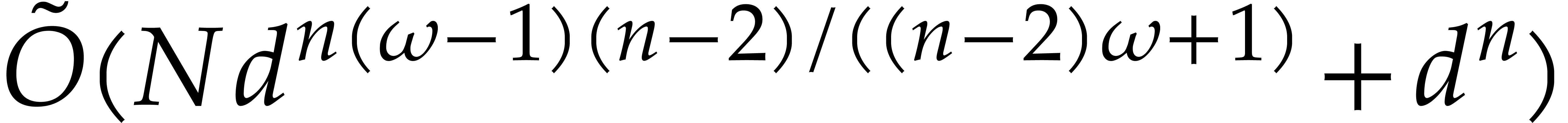 operations in
operations in  , where
, where
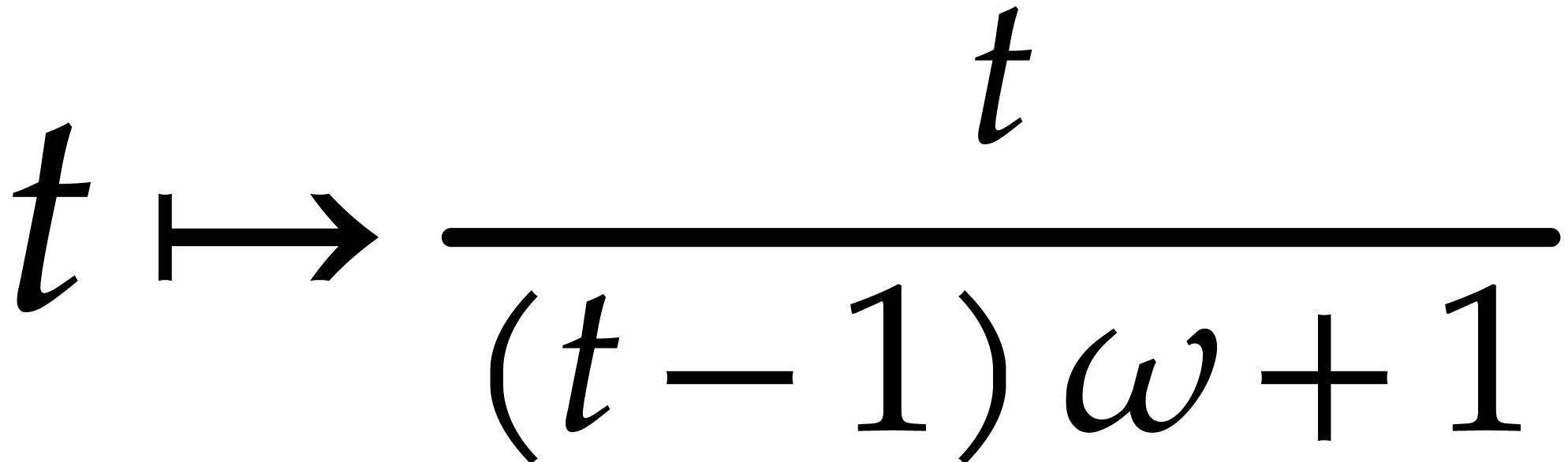
Proof. Again, we subdivide  into subsequences
into subsequences  of cardinality
of cardinality  such that
such that  . We
expand
. We
expand 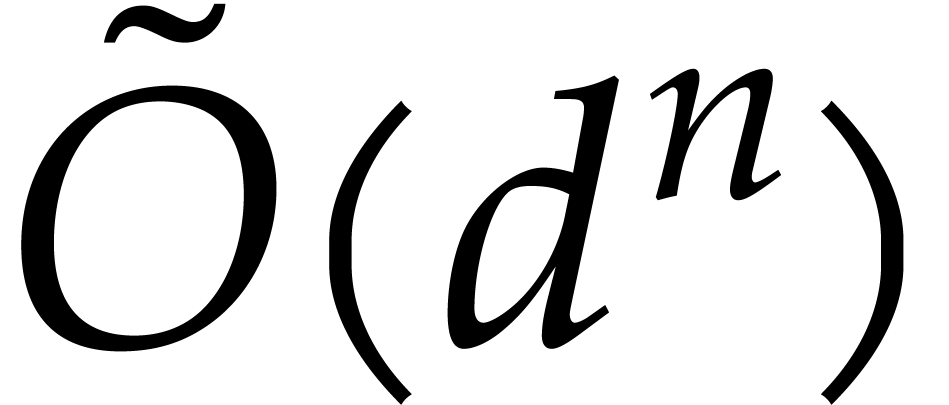 as a polynomial in
as a polynomial in 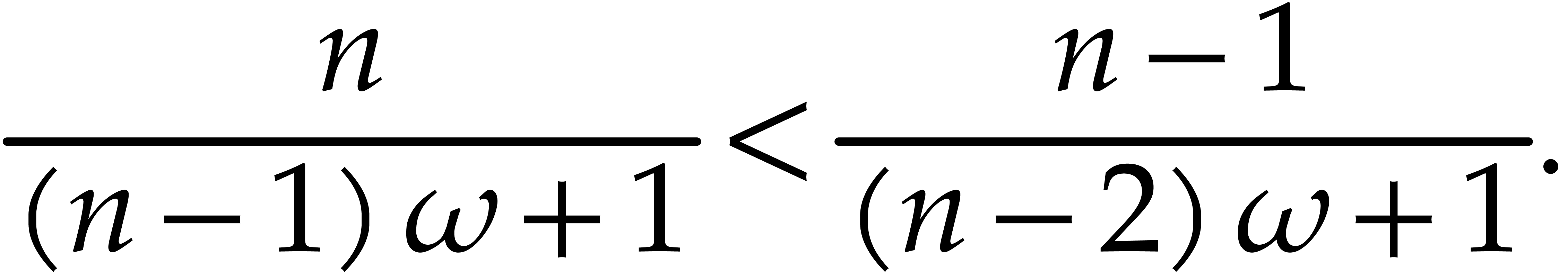 ,
,
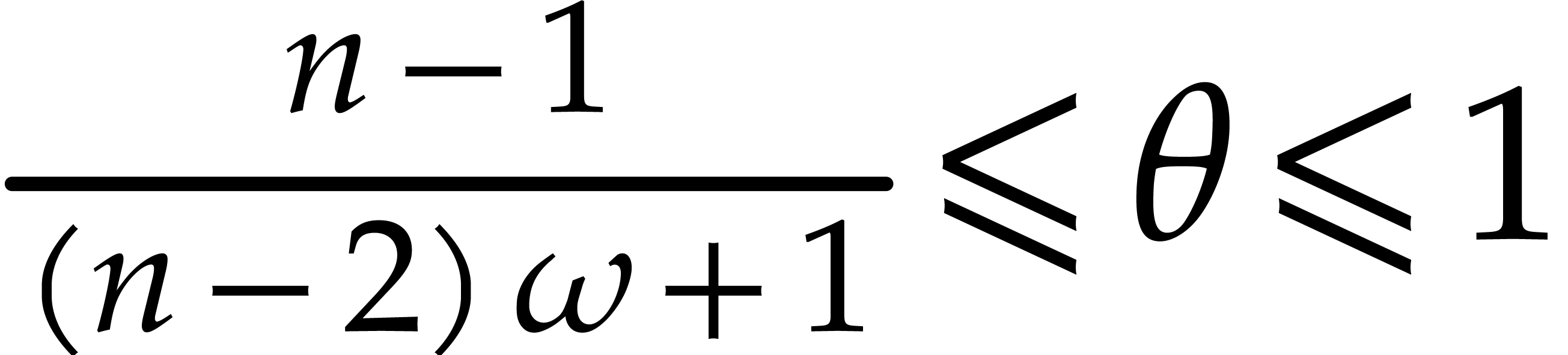
and let  denote the projection
denote the projection 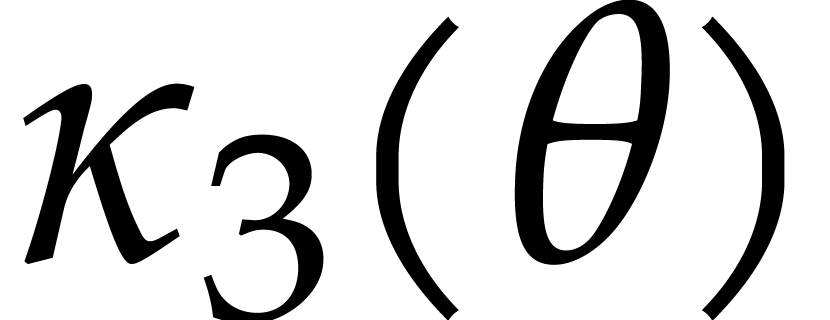 .
.
We apply Theorem 3.8 successively with  in the role of
in the role of  . The total
cost of the precomputations is
. The total
cost of the precomputations is

after which the cost of the evaluations of 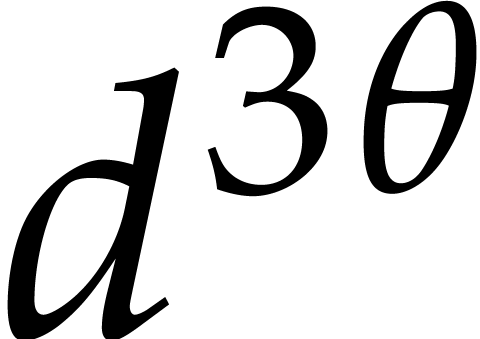 at
at
 becomes
becomes
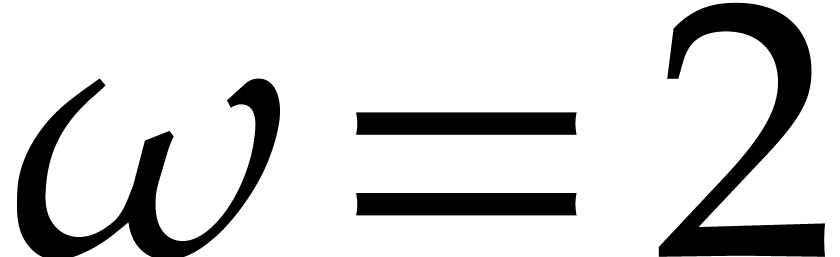
We deduce 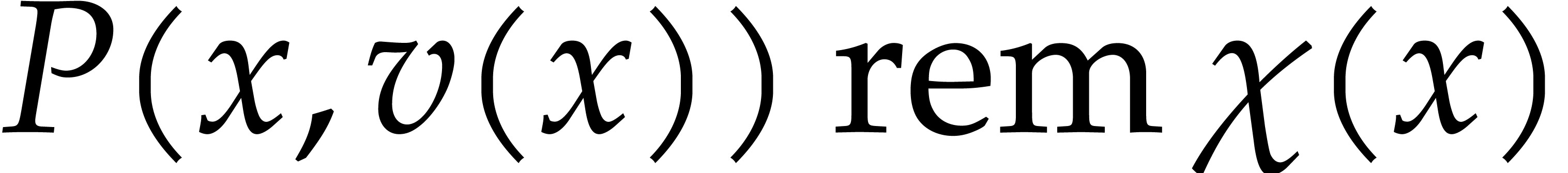 in time
in time  .
Now we set
.
Now we set
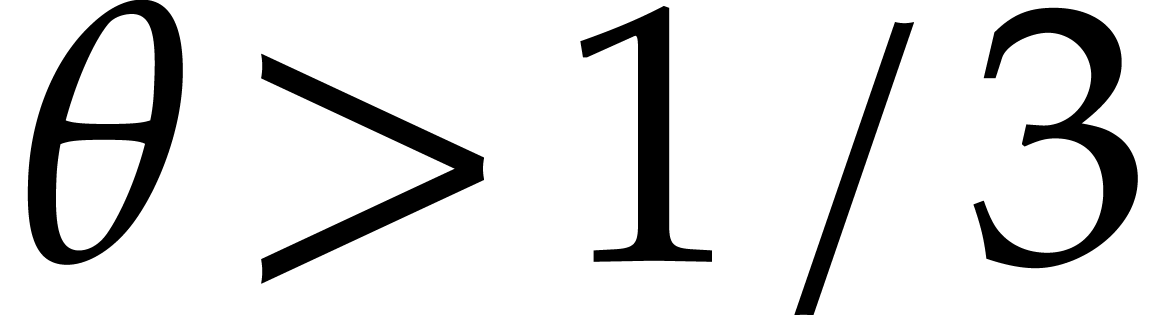
Using 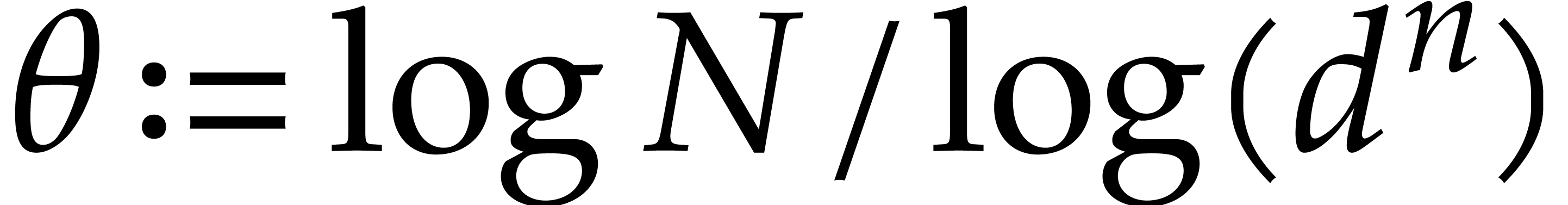 , we verify that
, we verify that  . In total, the computation of
. In total, the computation of 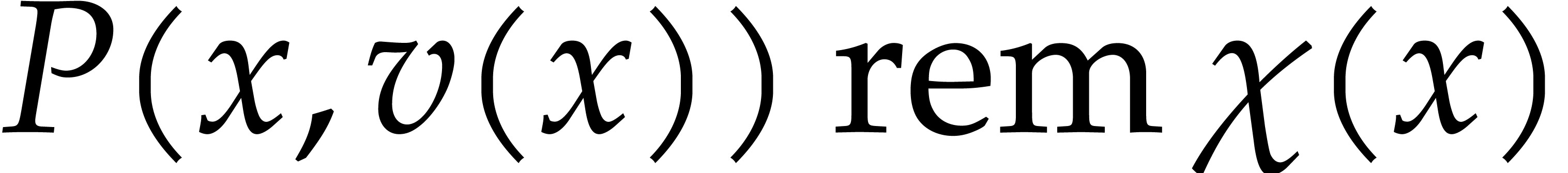 costs
costs
Still using  , we note that
, we note that
Consequently, the total cost simplifies to 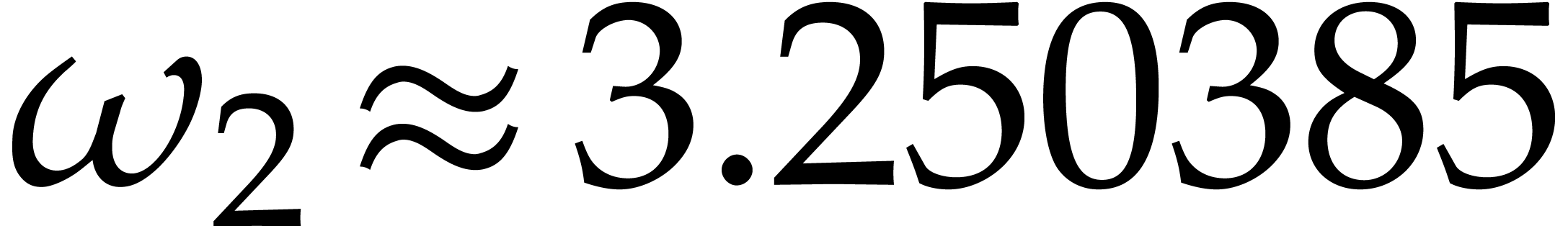 .
.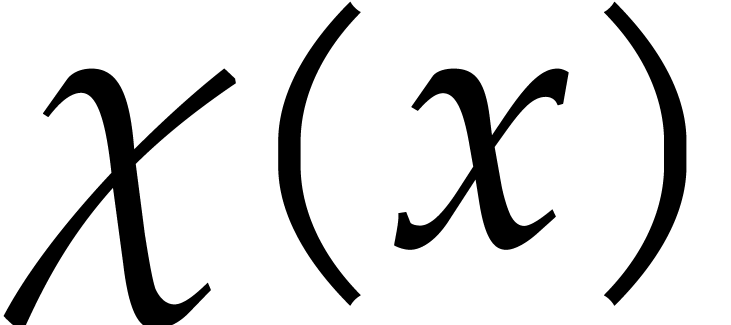
Remark  is decreasing for
is decreasing for 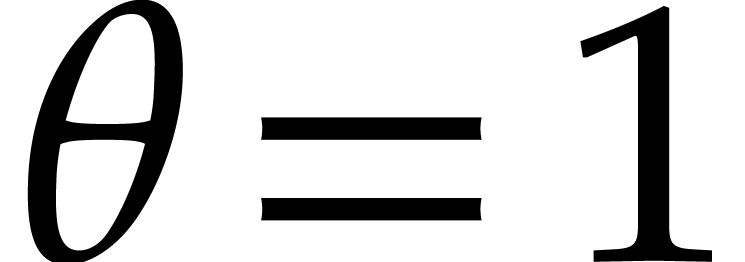 ,
we have
,
we have
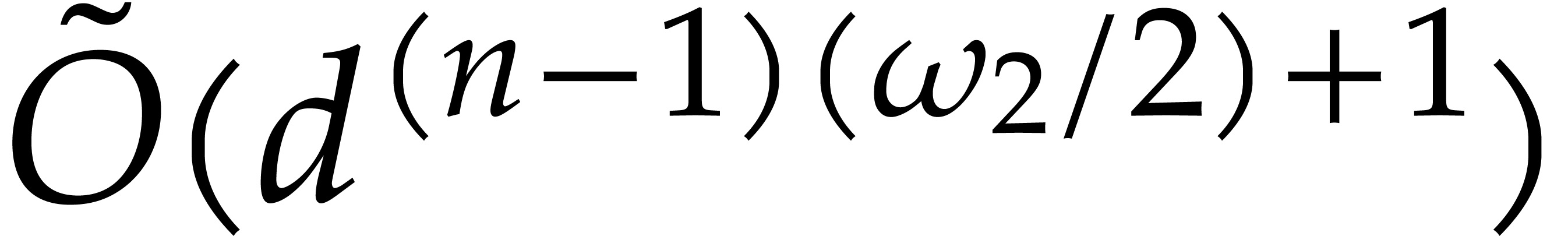
If 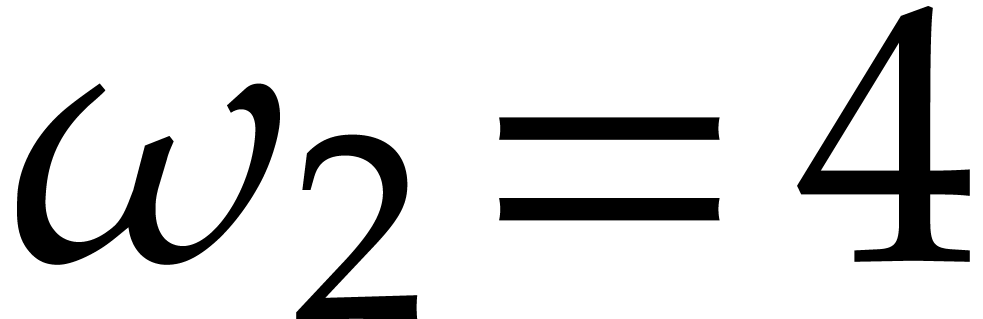 , then
, then
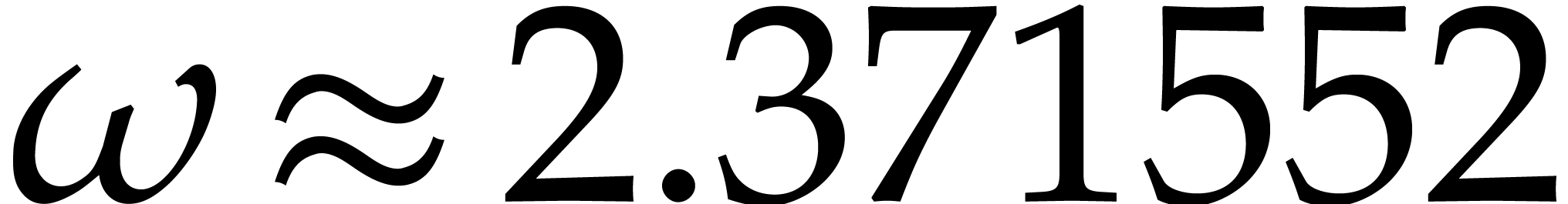
Consequently, if 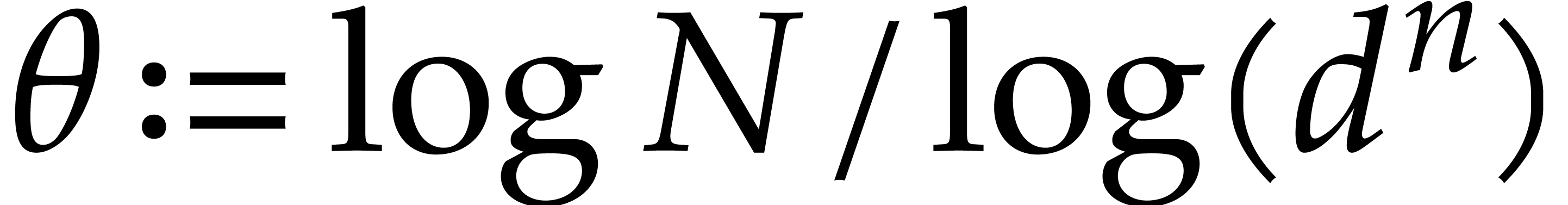 , then
Theorem 3.13 always improves upon Theorem 3.9.
, then
Theorem 3.13 always improves upon Theorem 3.9.
Remark 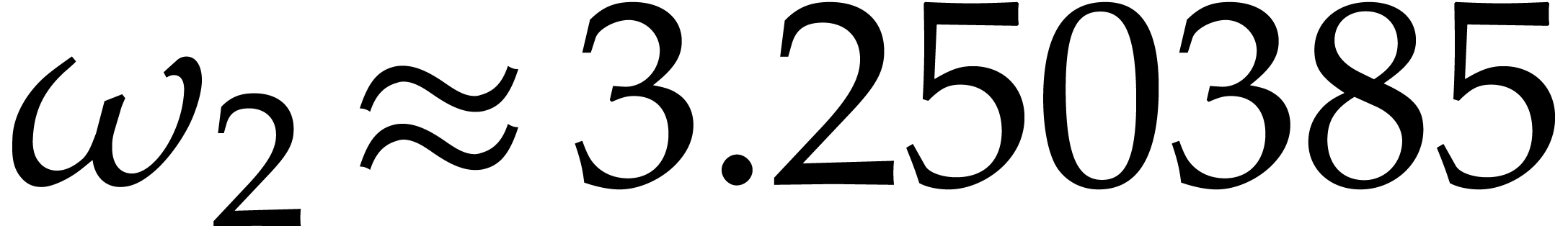 from Theorem
3.13
is plotted in Figure
3.2
.
from Theorem
3.13
is plotted in Figure
3.2
.
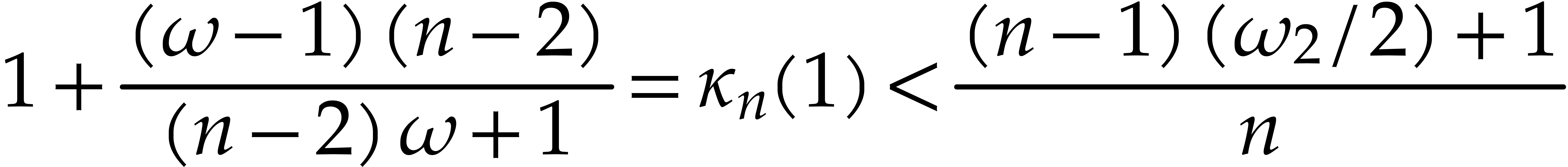 |
Figure 3.2. Complexity exponent
|
 at the limit when
at the limit when
 .
However, for the best currently known upper bound for
.
However, for the best currently known upper bound for
 ,
we have
,
we have
 for all
for all
 ,
even when taking into account Remark
2.4
. More precisely, for
,
even when taking into account Remark
2.4
. More precisely, for
 ,
we have
,
we have
 .
At the same time, for
.
At the same time, for
 ,
the exponent of the Nüsken–Ziegler algorithm is
,
the exponent of the Nüsken–Ziegler algorithm is
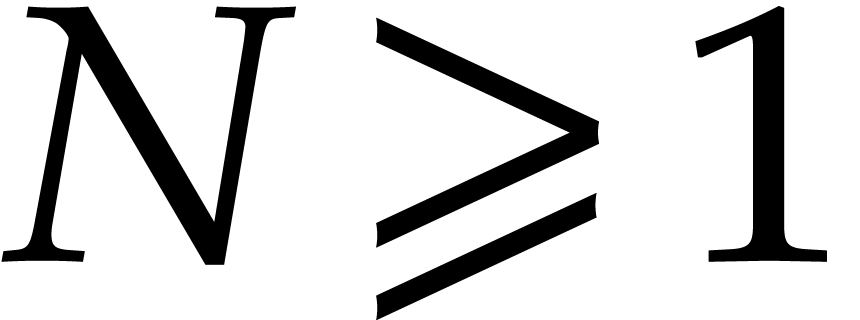 .
.
Remark 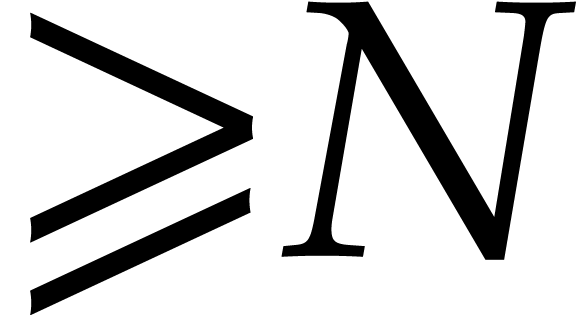 , it is instructive to
compare Theorem 3.13 with the best
Nüsken–Ziegler style complexity bound
, it is instructive to
compare Theorem 3.13 with the best
Nüsken–Ziegler style complexity bound 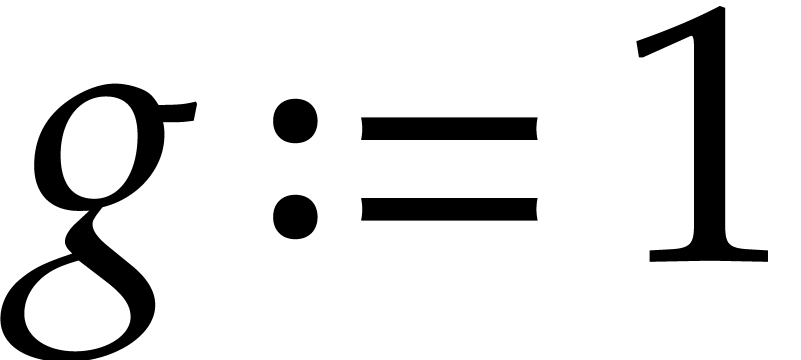 of Remark 2.4:
of Remark 2.4:
If 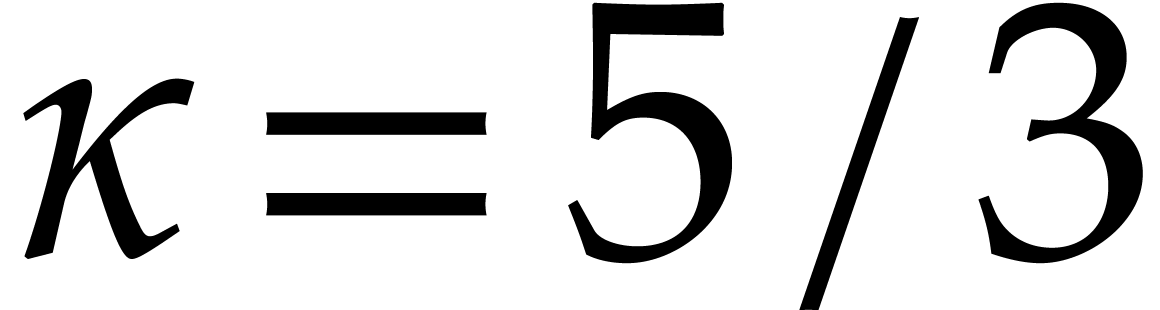 and
and 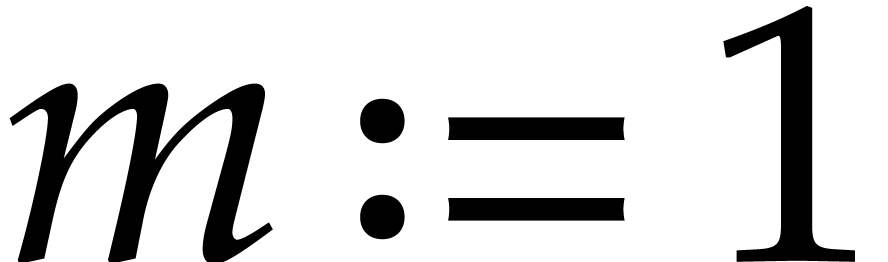 ,
then the bound from Theorem 3.13 is always better.
,
then the bound from Theorem 3.13 is always better.
For the best currently known values 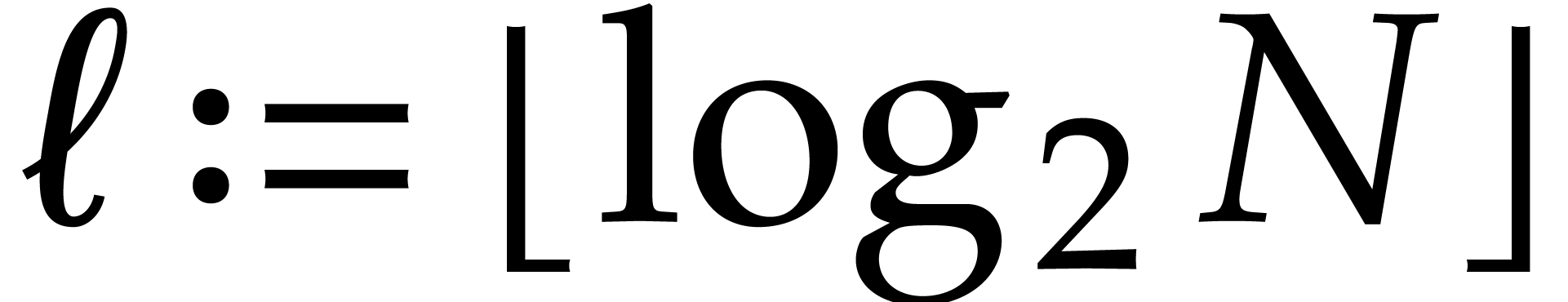 and
and
 , we verify numerically
that
, we verify numerically
that
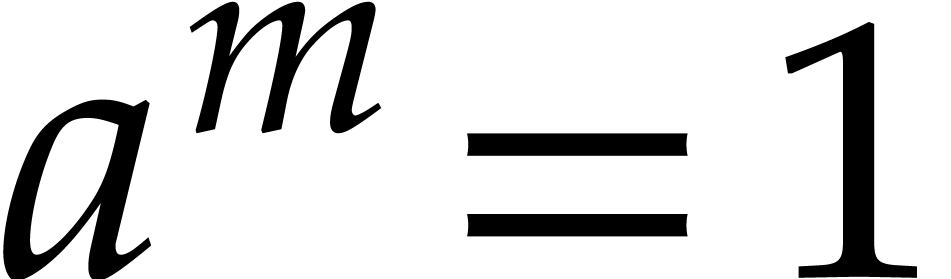
if and only if 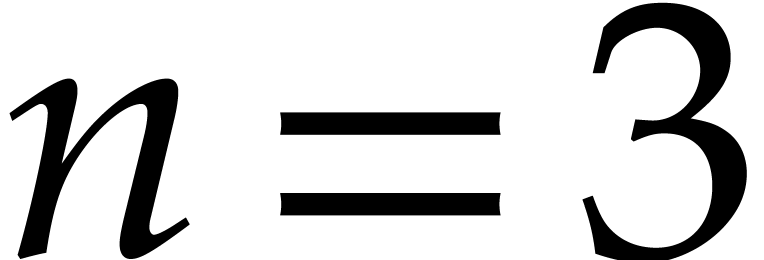 or
or  .
.
At the limit when 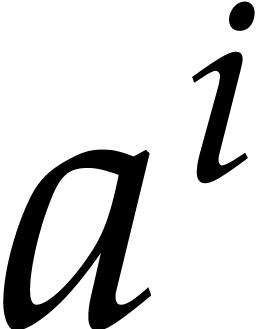 and
and  , we have
, we have 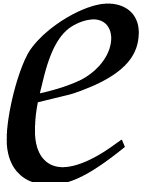 and
and 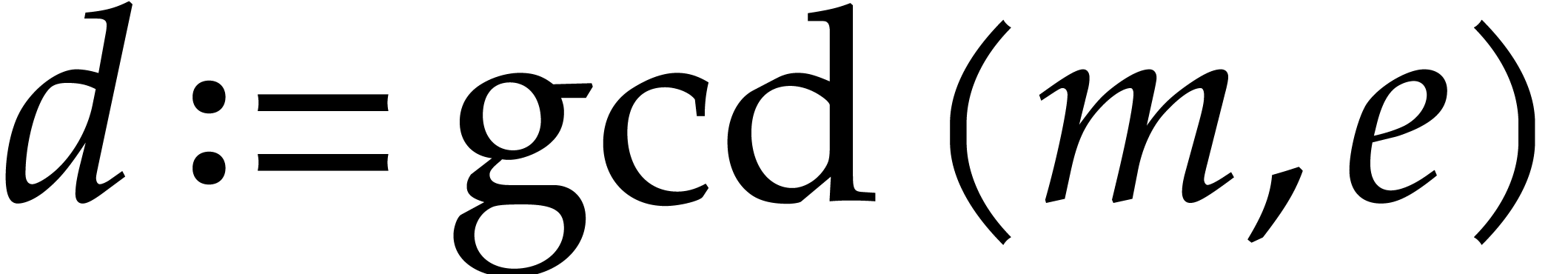 for
for 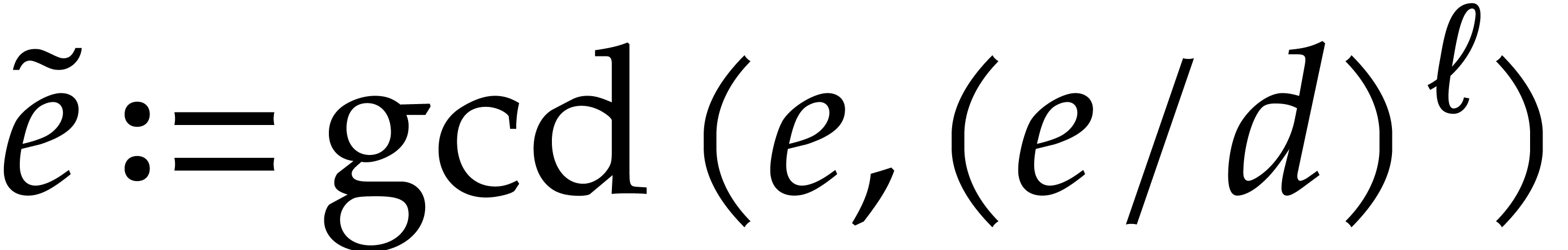 .
.
Let  be an effective field, and let
be an effective field, and let 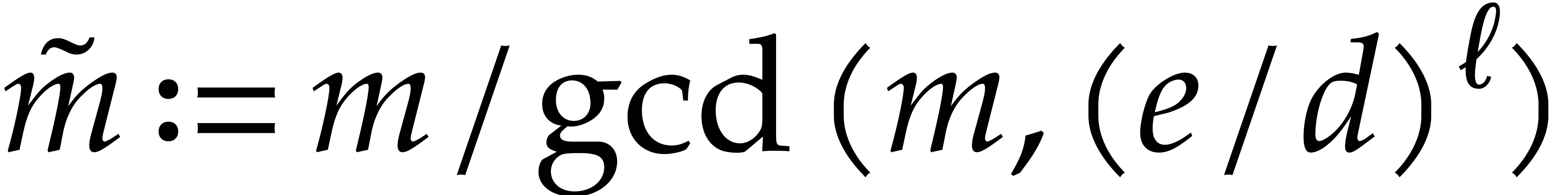 denote its multiplicative group. We are interested in
finding elements of
denote its multiplicative group. We are interested in
finding elements of 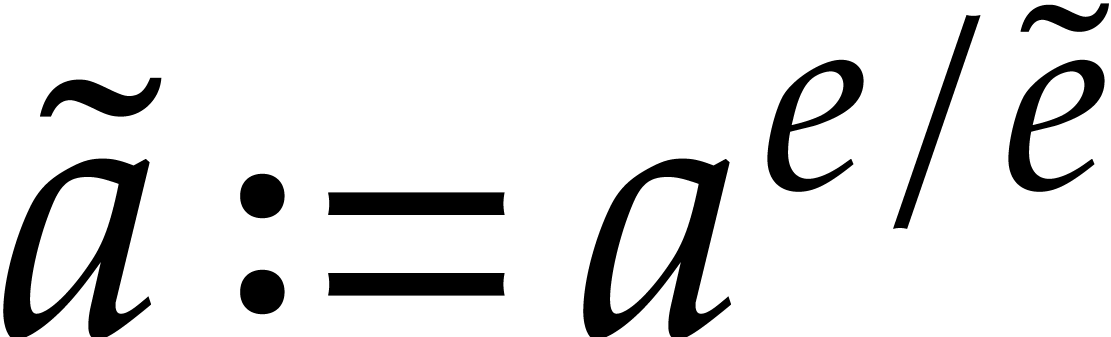 of a sufficiently high
order, possibly after replacing
of a sufficiently high
order, possibly after replacing  by a suitable
extension. The following algorithm finds such elements whenever the
cardinality of
by a suitable
extension. The following algorithm finds such elements whenever the
cardinality of  is sufficiently large.
is sufficiently large.
Algorithm
Set 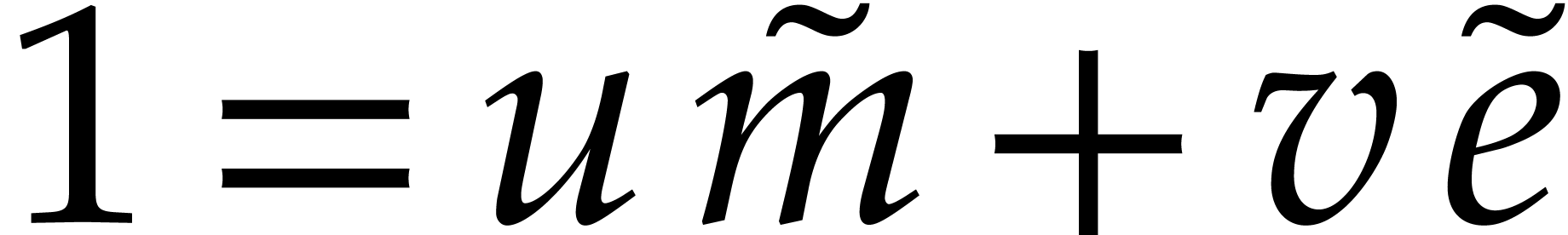 ,
, 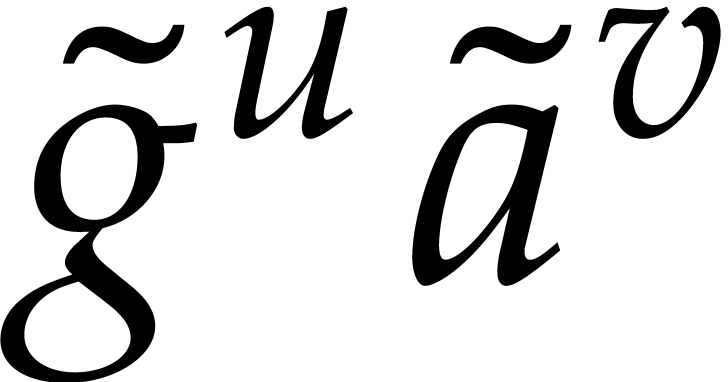 , and
, and 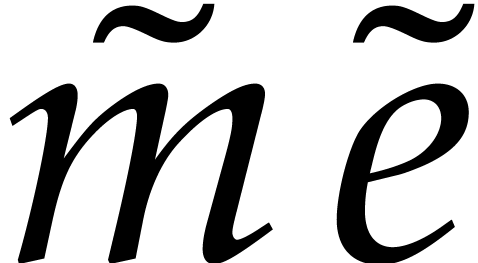 .
.
For each element  in
in  do:
do:
If  then continue the loop of step 2
with the next element in
then continue the loop of step 2
with the next element in  .
.
Compute  for
for  .
.
If the order  of
of 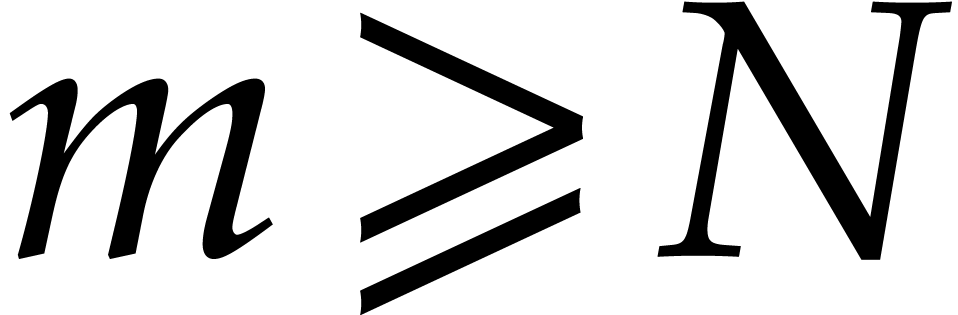 is
is  , then return
, then return
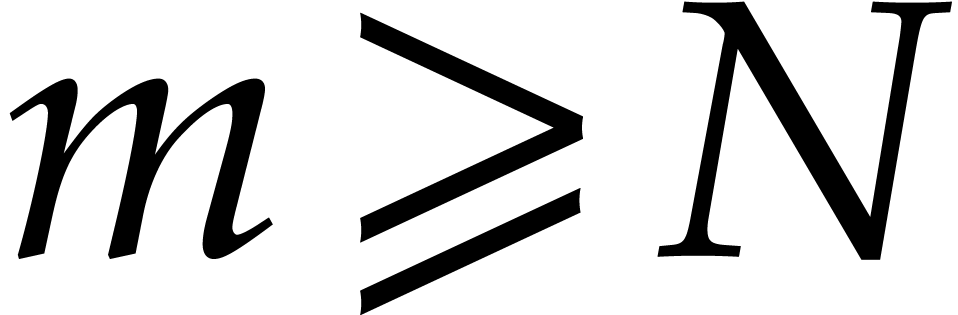 .
.
Compute 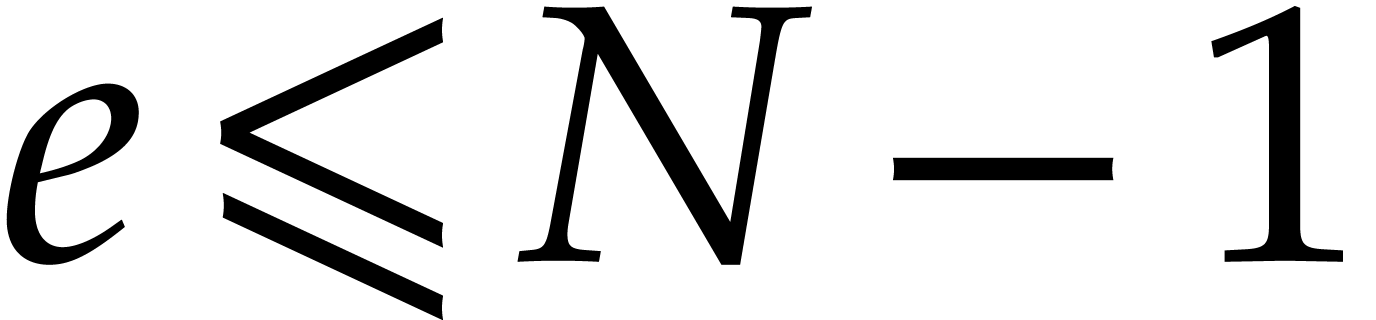 ,
,  ,
,  ,
, 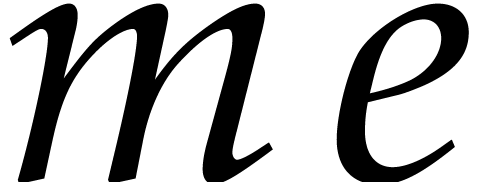 ,
and
,
and  .
.
Compute the integers 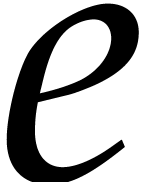 and
and  of the Bézout relation
of the Bézout relation 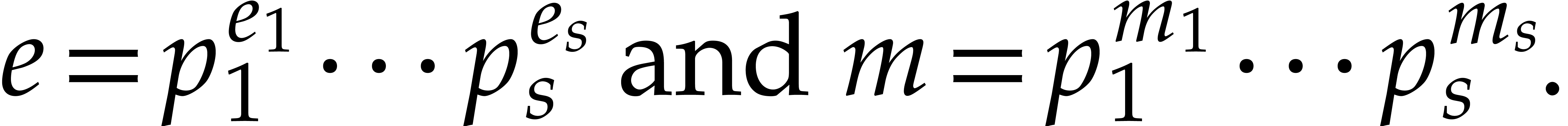 . Replace
. Replace 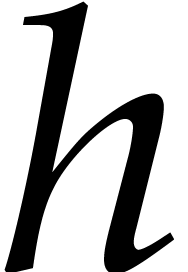 by
by  and
and  by
by
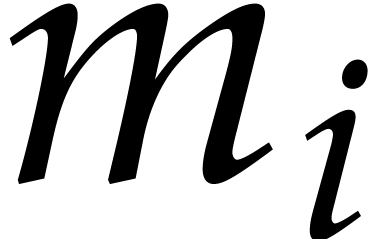 .
.
If 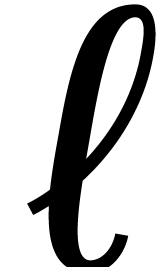 then return
then return 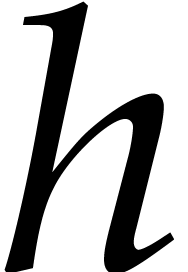 .
.
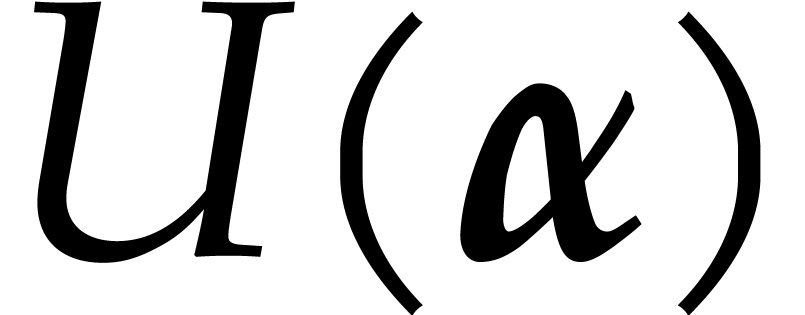 operations in
operations in  .
.
Proof. Let 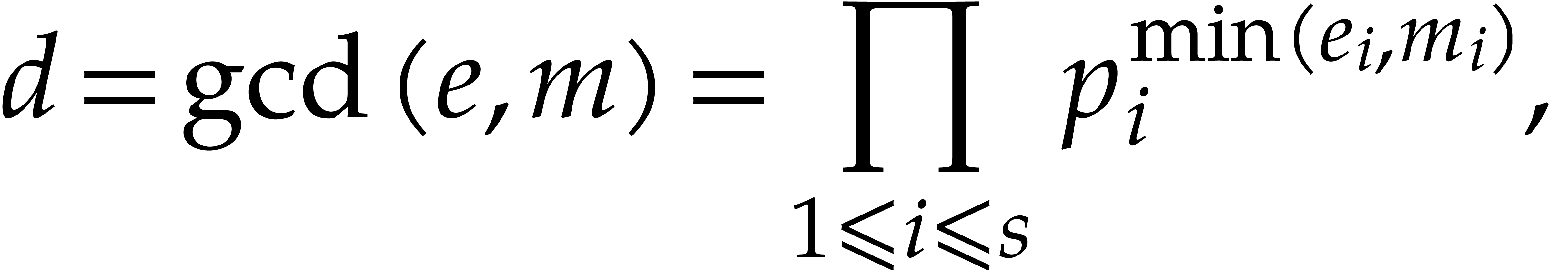 denote the
current subset of the elements of
denote the
current subset of the elements of  that have been
handled when entering step 2.a. We will show by induction that the
elements of
that have been
handled when entering step 2.a. We will show by induction that the
elements of 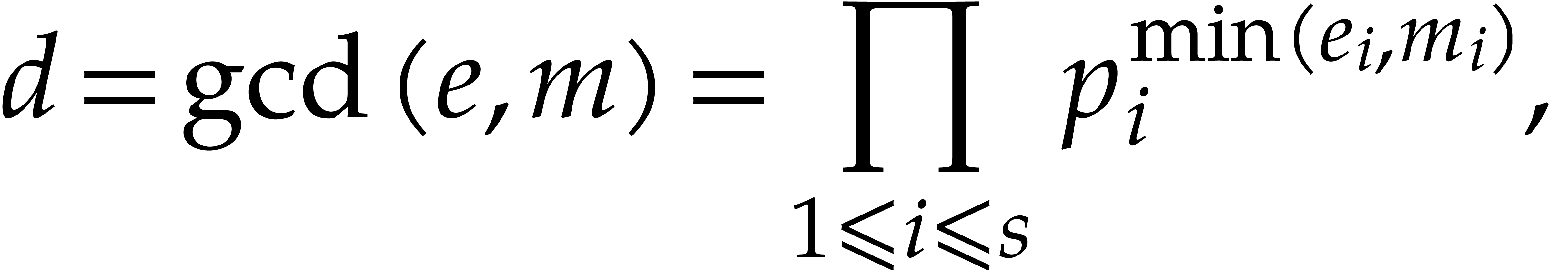 have order dividing
have order dividing 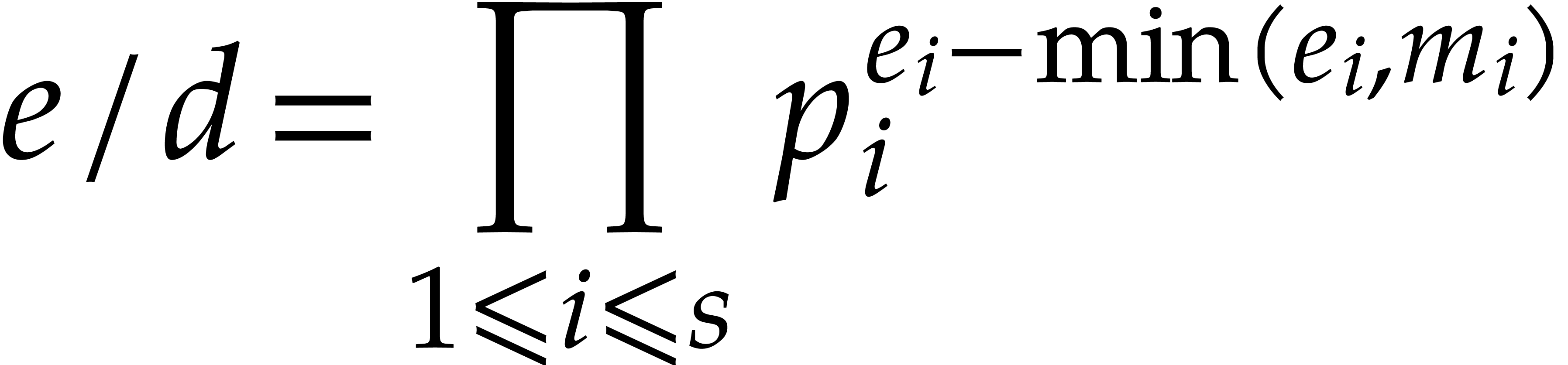 , and that
, and that  has order
has order
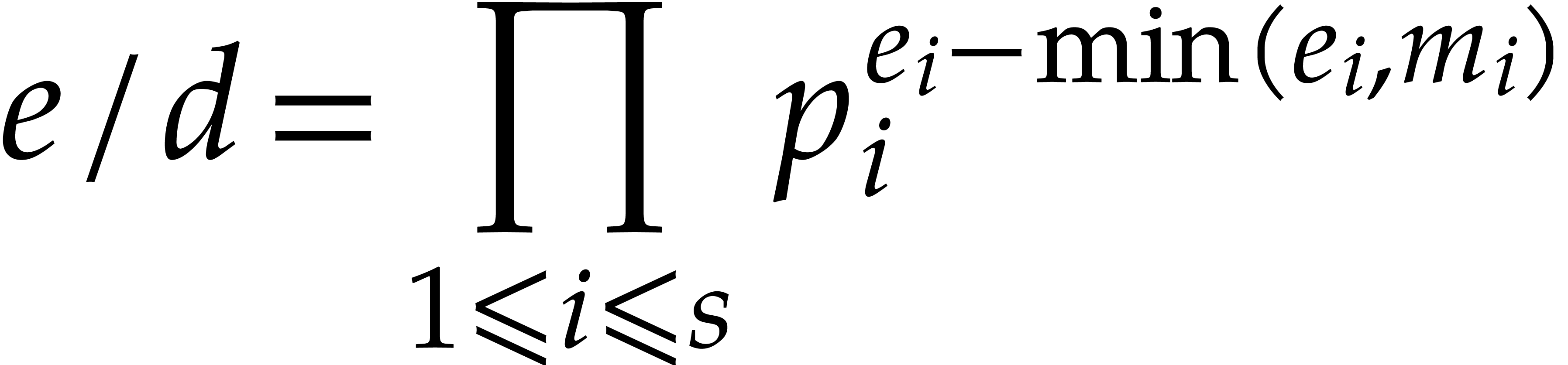 . Of course, these properties
hold at the beginning, when
. Of course, these properties
hold at the beginning, when 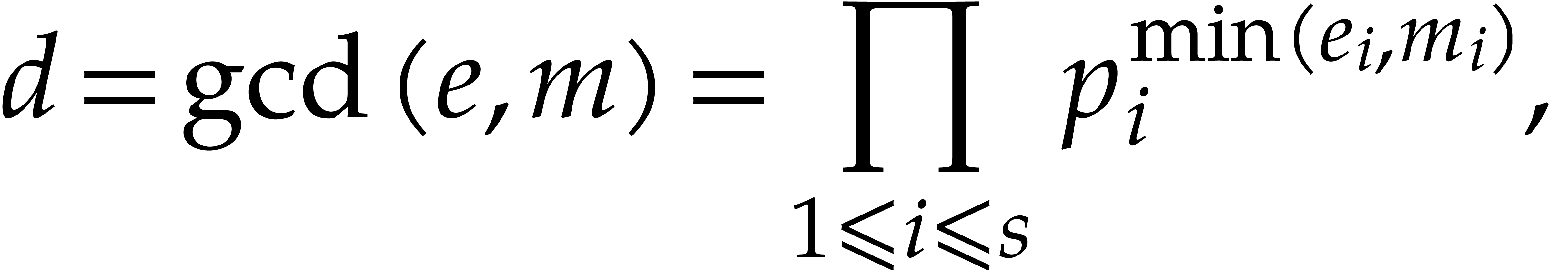 is empty.
is empty.
If  then the induction hypothesis is preserved.
If the algorithm exits at step 2.c, then the output is clearly correct.
Otherwise, the order
then the induction hypothesis is preserved.
If the algorithm exits at step 2.c, then the output is clearly correct.
Otherwise, the order 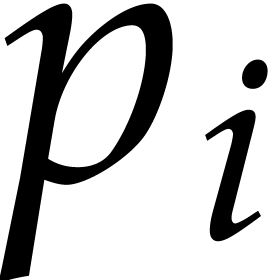 of
of 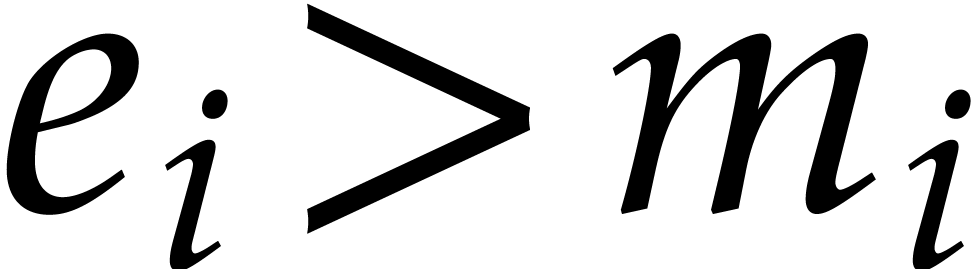 can be read off from the computations of step 2.b.
can be read off from the computations of step 2.b.
Let  be the prime numbers occurring in the
factorization of
be the prime numbers occurring in the
factorization of 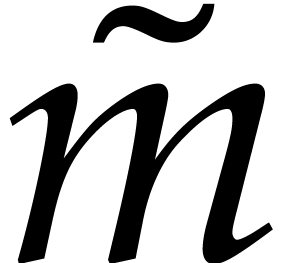 , of
respective multiplicities
, of
respective multiplicities  in
in 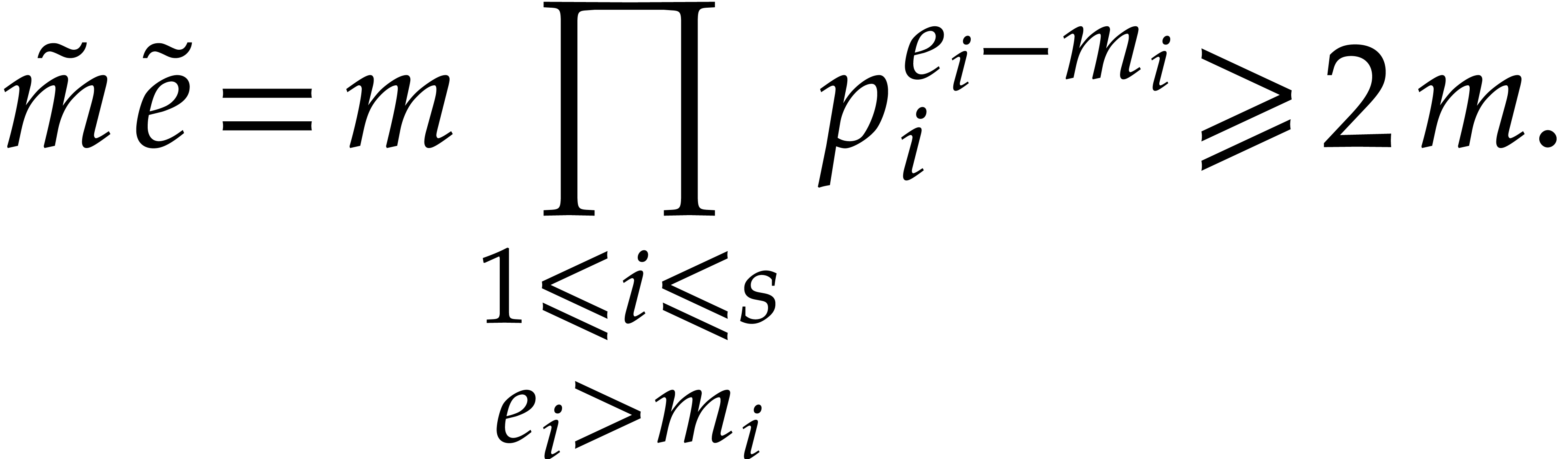 and
and  in
in 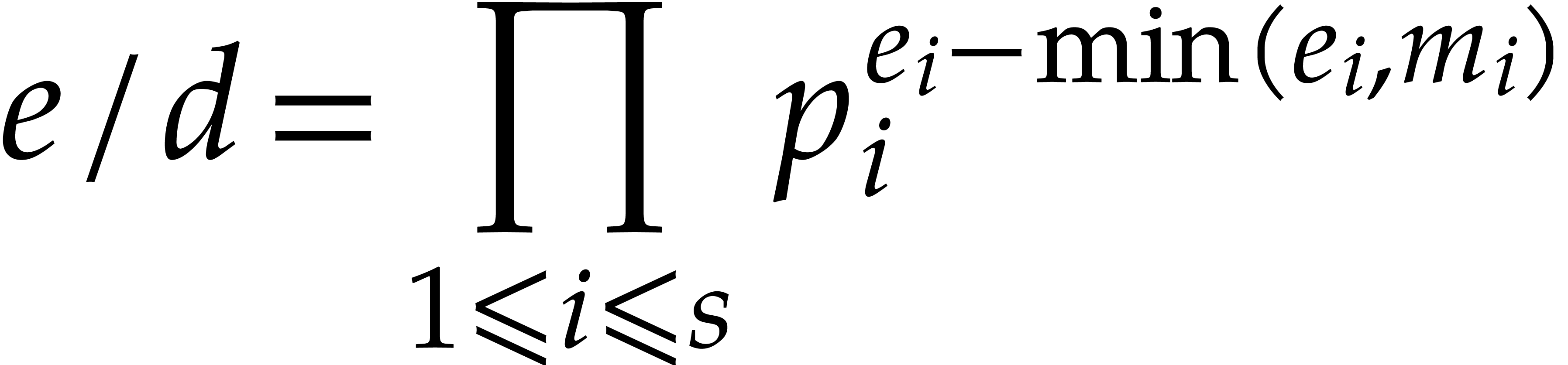 ,
so we have
,
so we have

Some of the 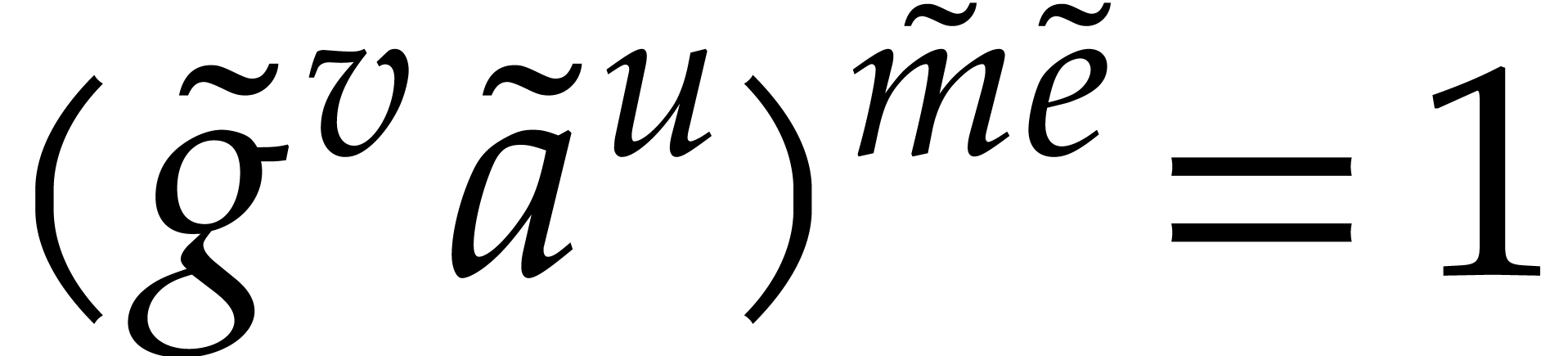 or
or 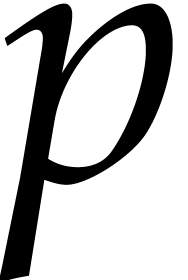 may be
zero here. Since
may be
zero here. Since 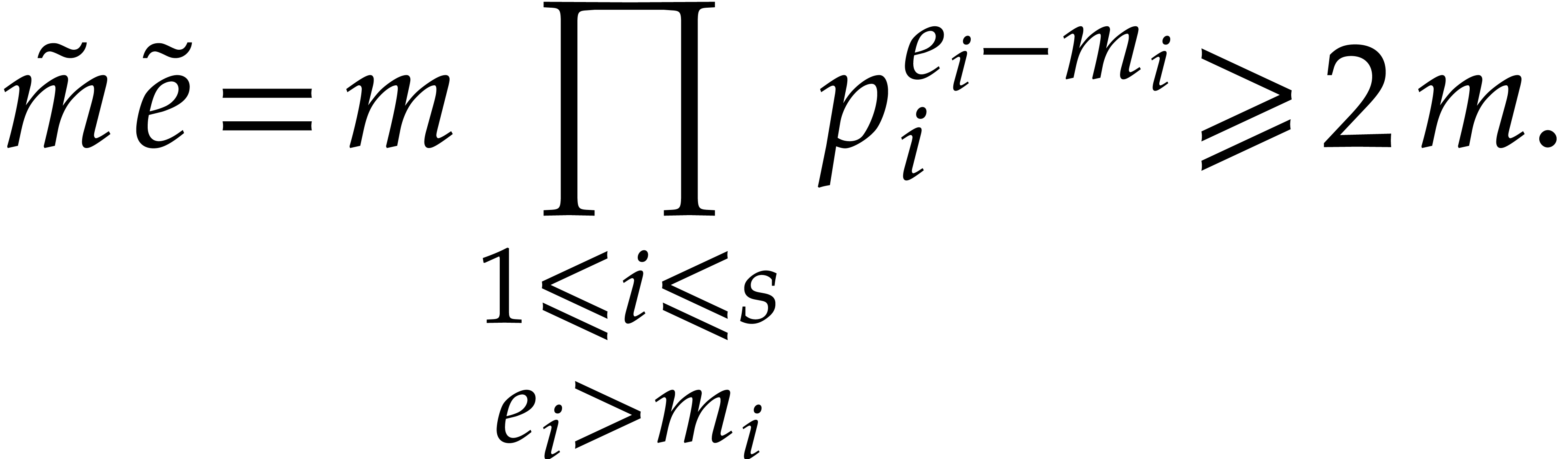 and
and 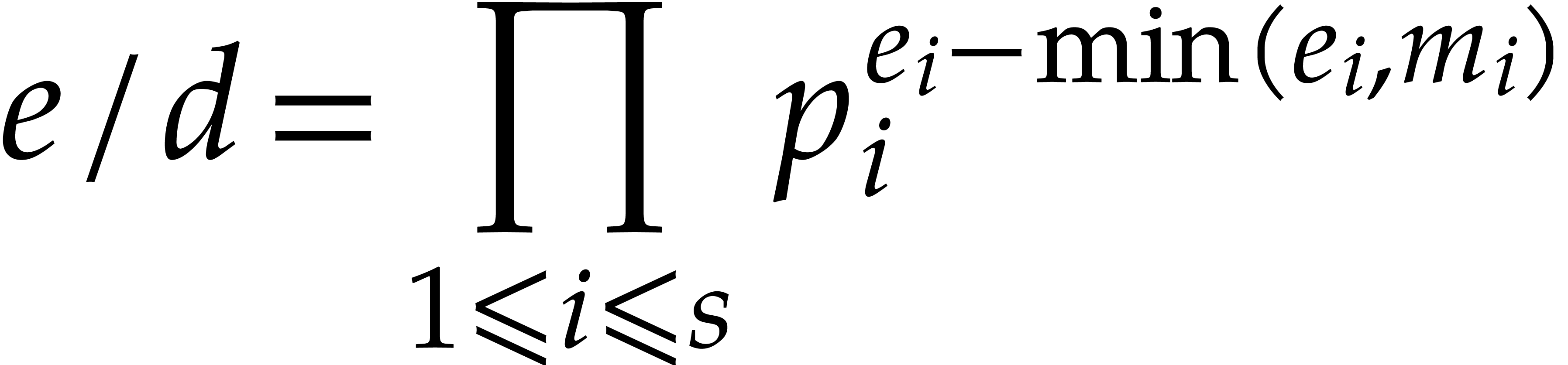 are
at most
are
at most  , the
, the 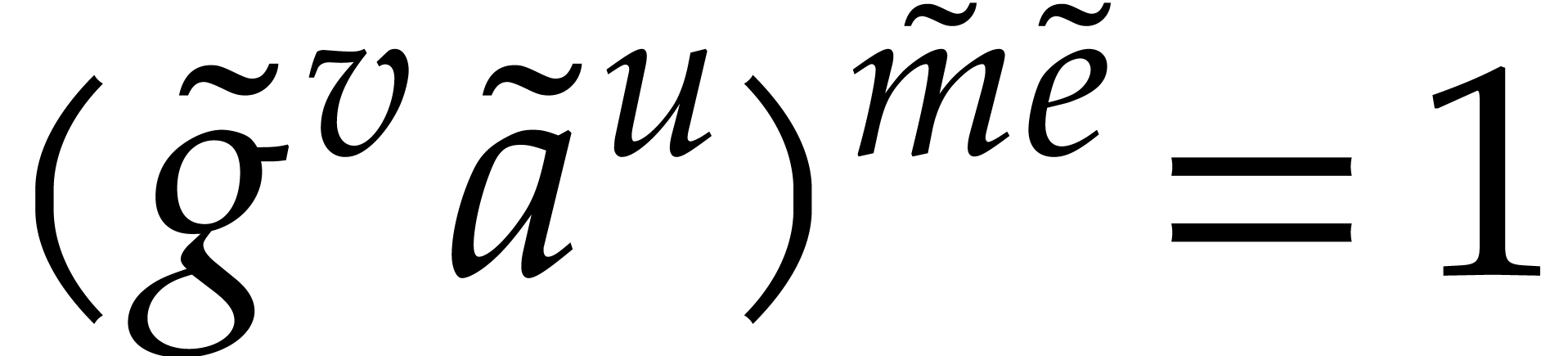 and
and  are at most
are at most  . From
. From
and since 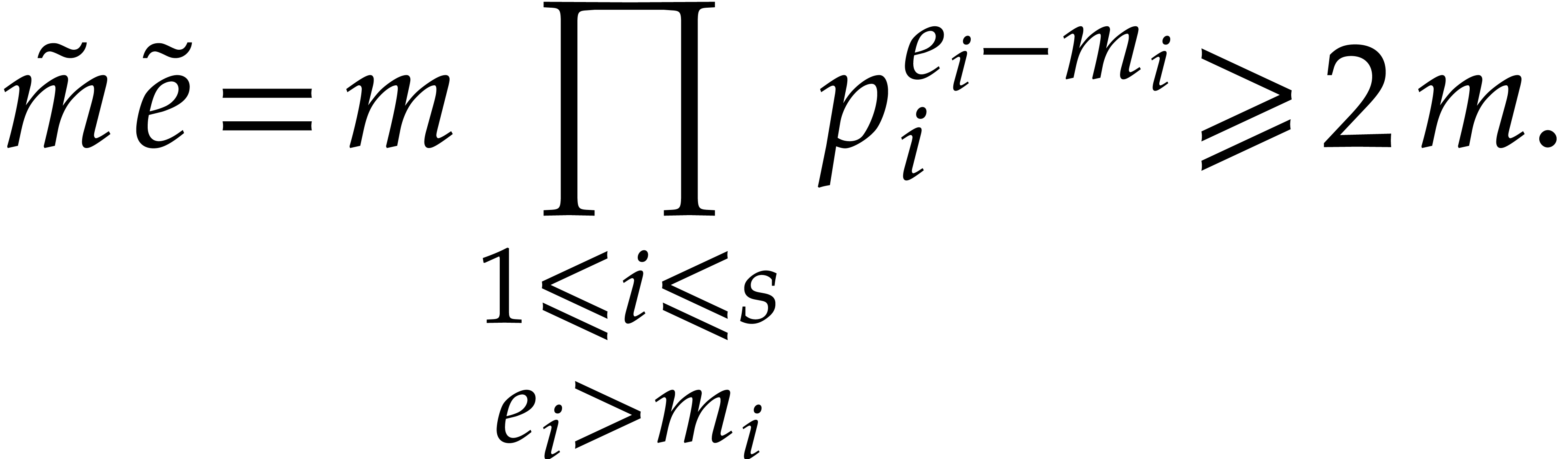 does not divide
does not divide  , we note that the integer
, we note that the integer
is at least  and only divisible by the primes
and only divisible by the primes
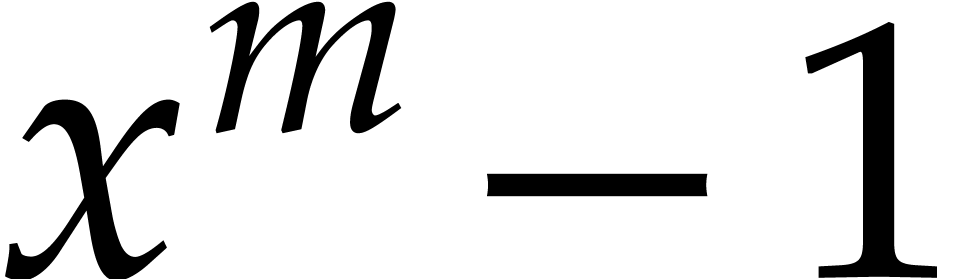 such that
such that 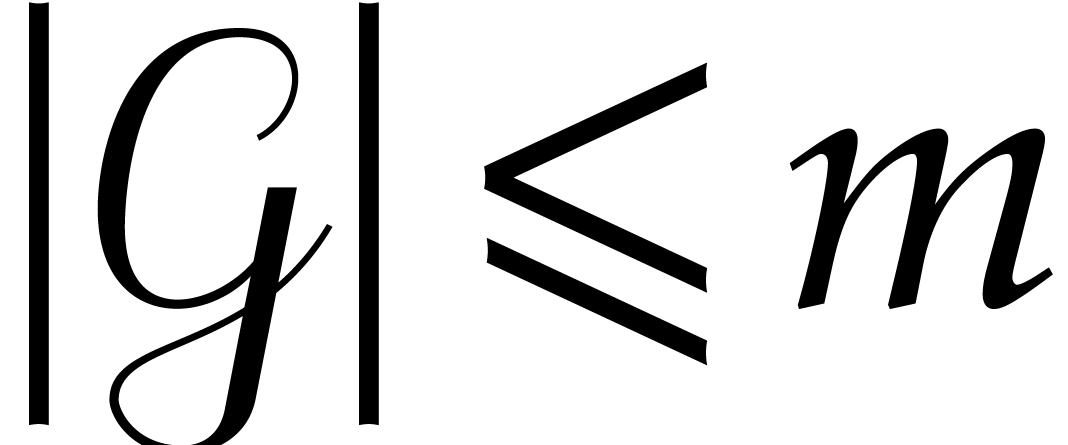 .
It follows that
.
It follows that
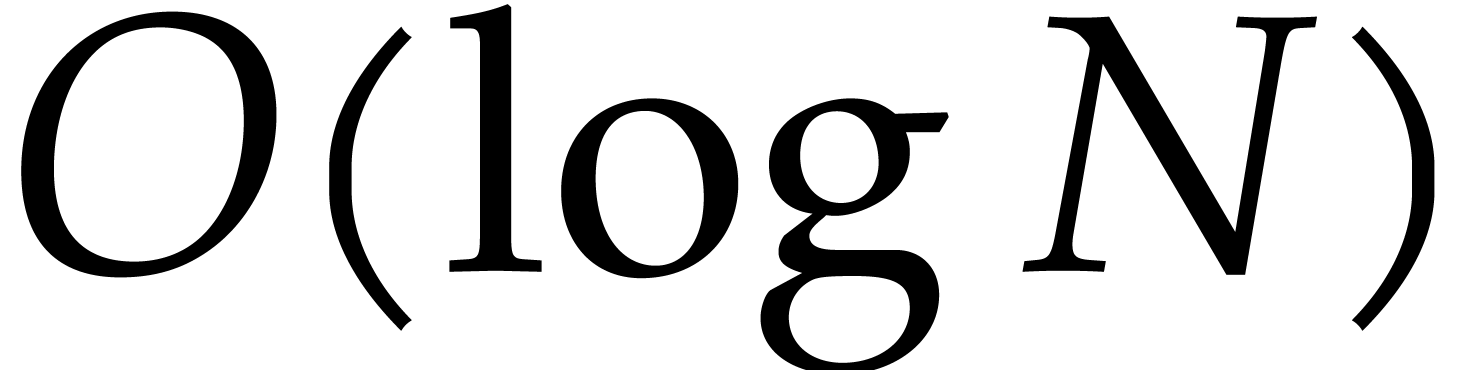
hence 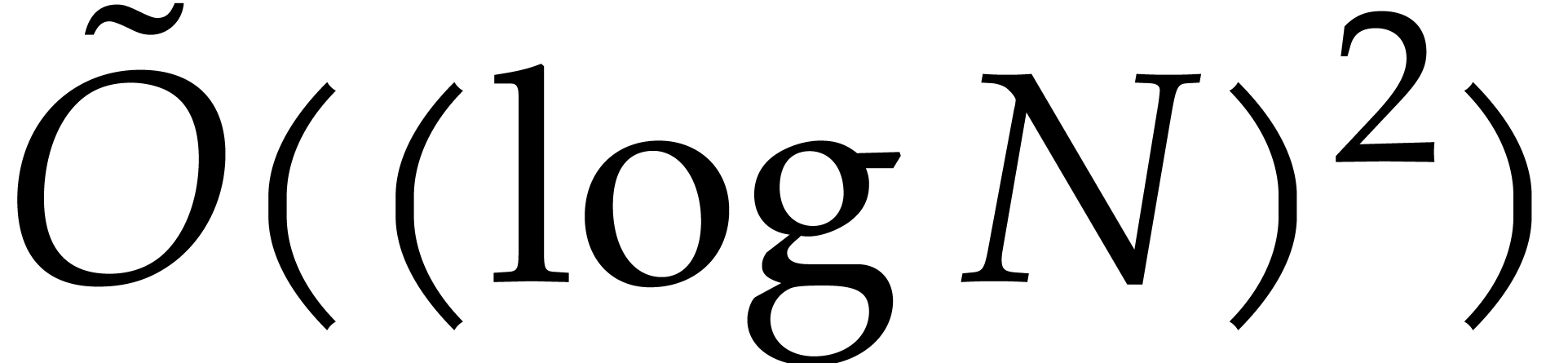 and
and 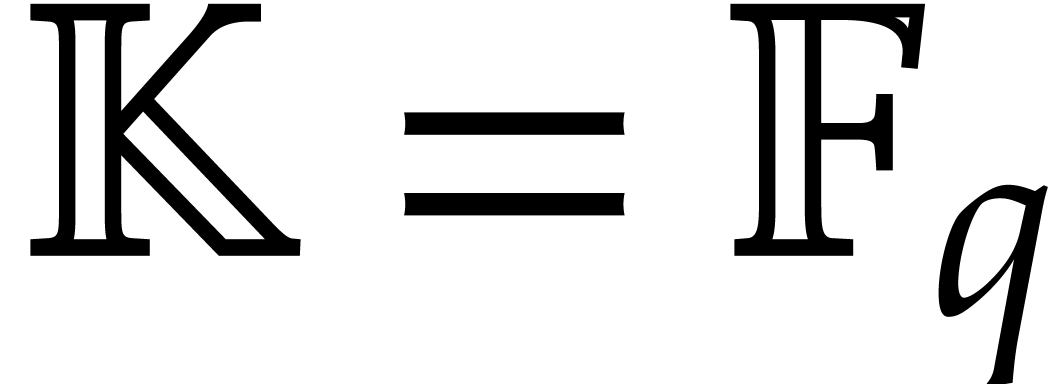 are coprime
and
are coprime
and

Now  has order
has order 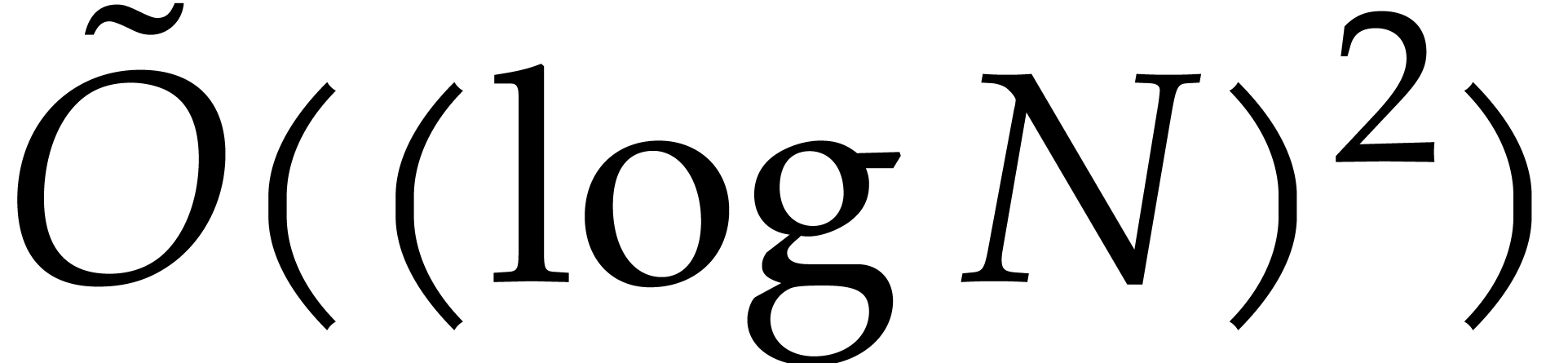 and
and  has order
has order 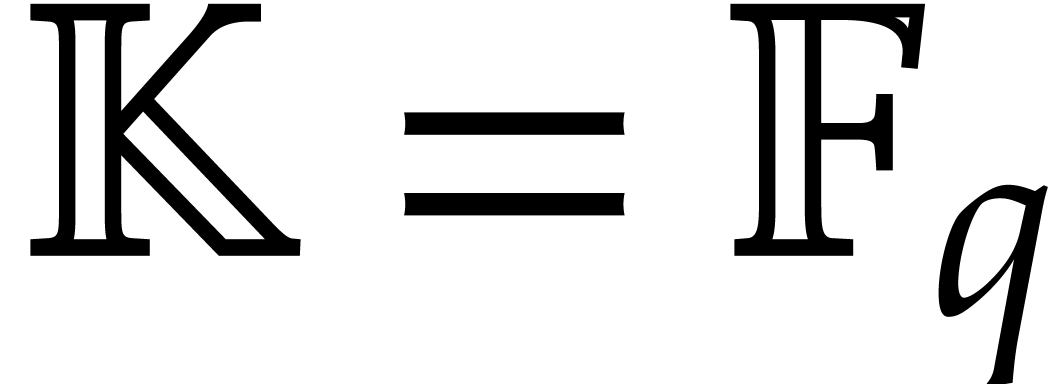 ,
whence
,
whence  . If
. If  is a prime divisor of
is a prime divisor of 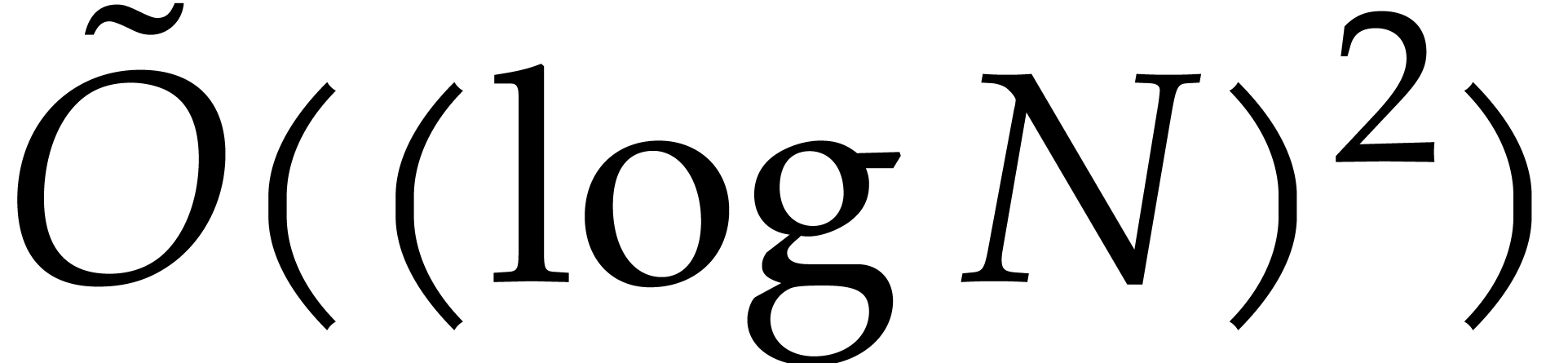 , then
, then
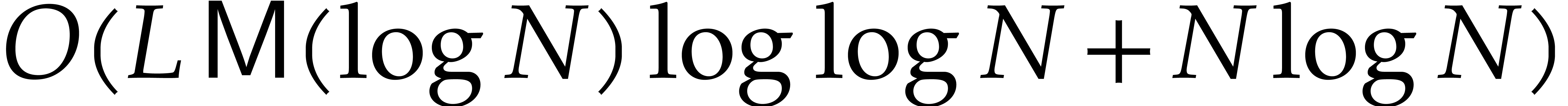
Similarly, if  is a prime divisor of
is a prime divisor of  , then
, then 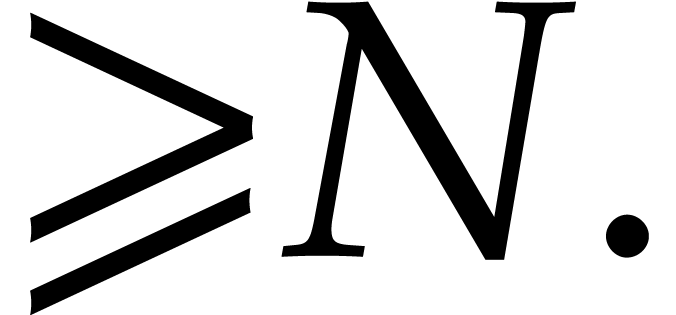 .
Consequently,
.
Consequently,  has order
has order 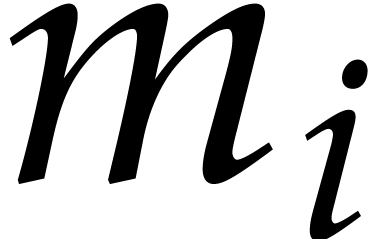 . In particular, if the algorithm exits in step 2.f,
then the output is correct. From
. In particular, if the algorithm exits in step 2.f,
then the output is correct. From

we note that 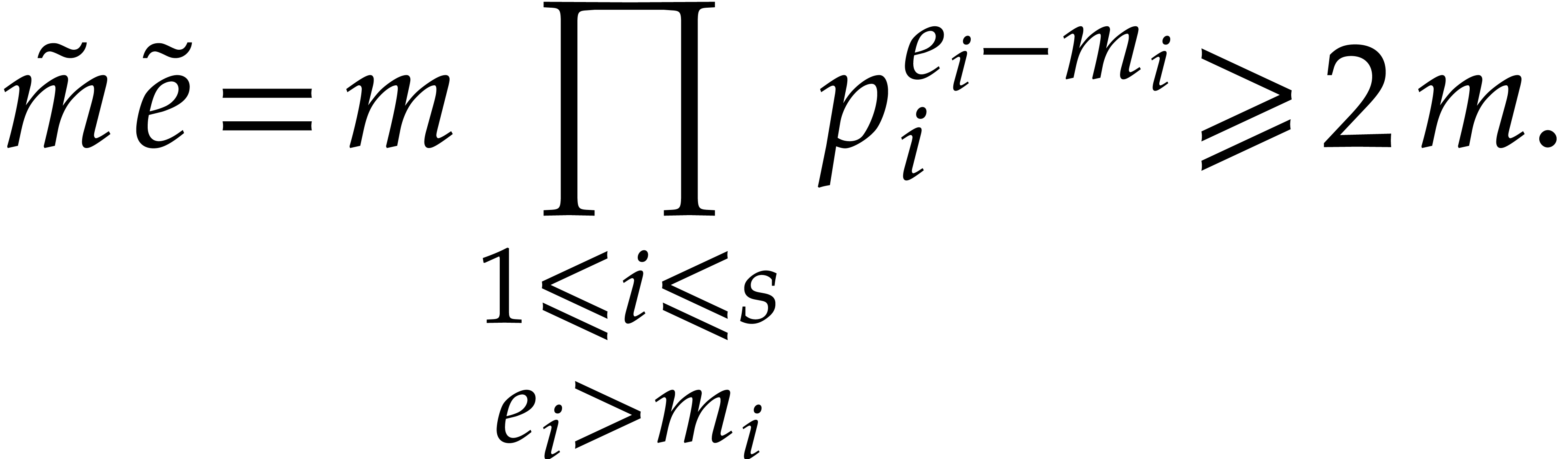 and
and 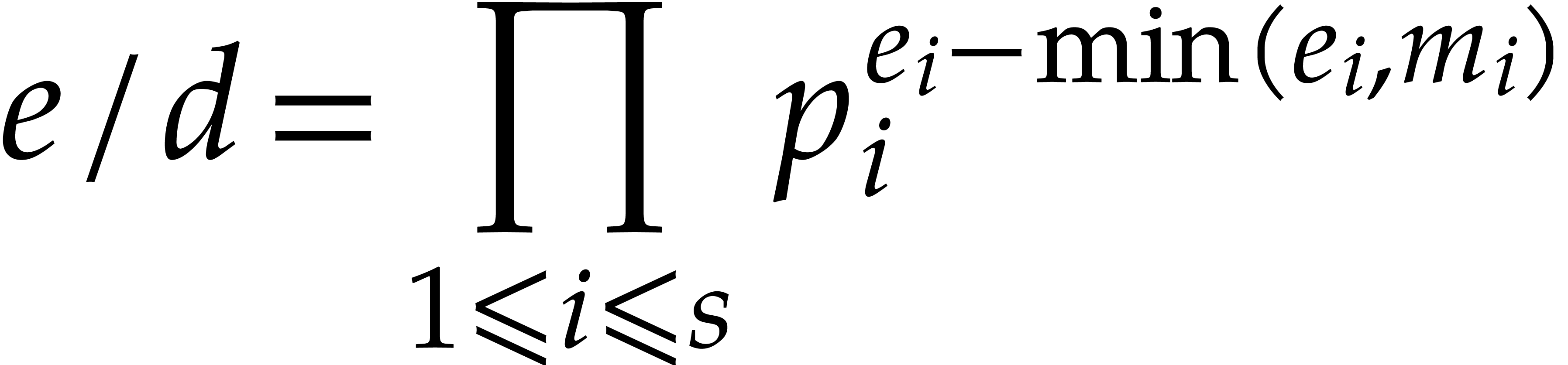 divide
divide
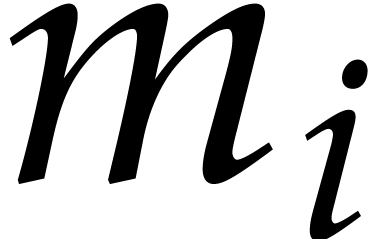 . Therefore the induction
hypothesis again holds at the end of step 2.
. Therefore the induction
hypothesis again holds at the end of step 2.
Since the orders of the elements of 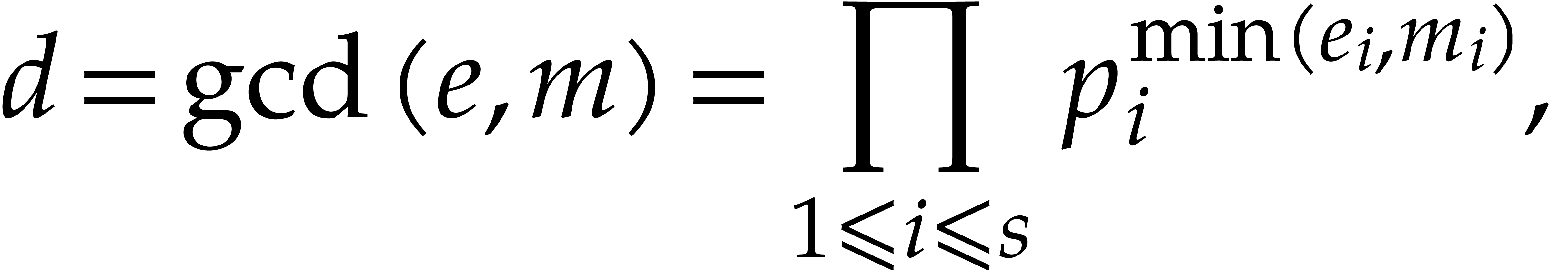 divide
divide 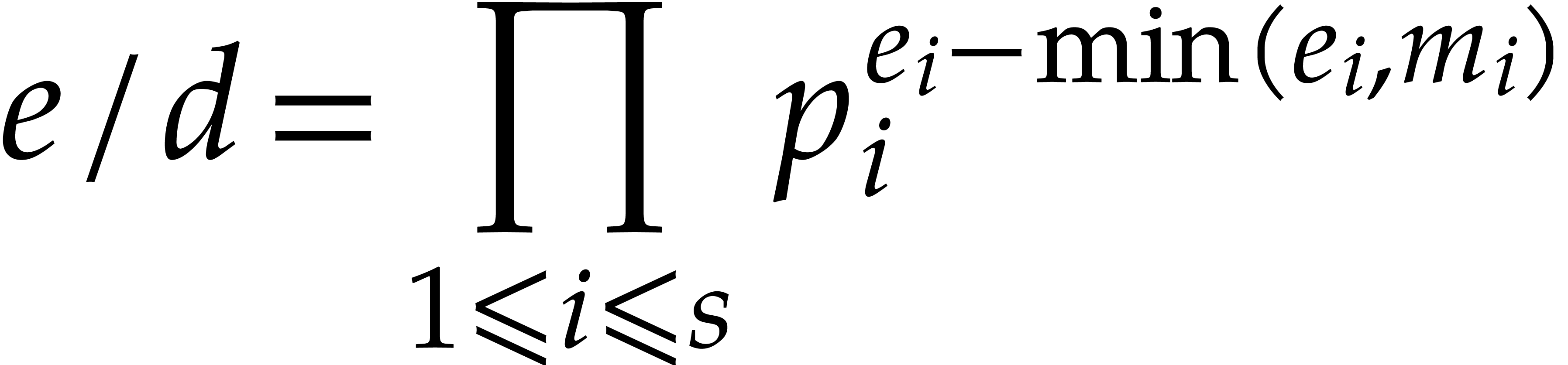 , they are roots of the polynomial
, they are roots of the polynomial
 , whence
, whence 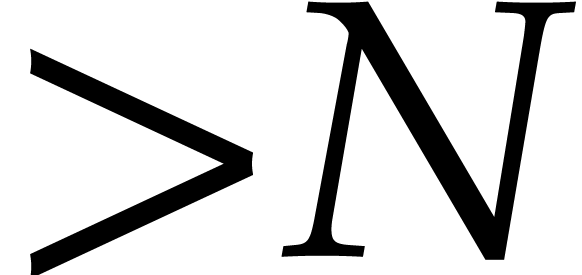 . This shows that the algorithm works as
expected.
. This shows that the algorithm works as
expected.
Steps 2.a, 2.d, and 2.e take  operations in
operations in  . Step 2.b takes
. Step 2.b takes  operations. In step 2.e, the integer
operations. In step 2.e, the integer 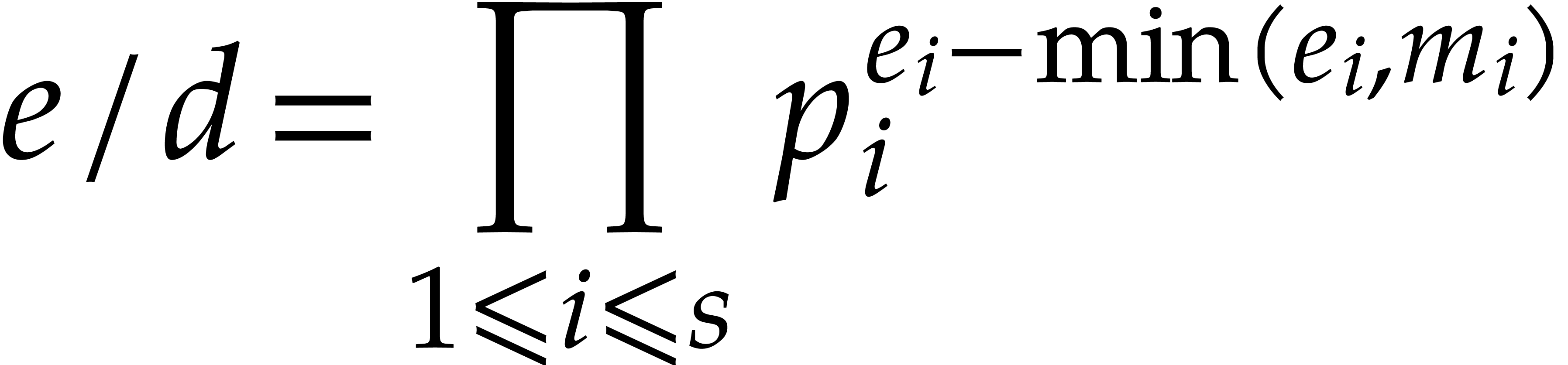 is at least
doubled, so step 2.b can occur only
is at least
doubled, so step 2.b can occur only  times.
Overall, the total cost is
times.
Overall, the total cost is 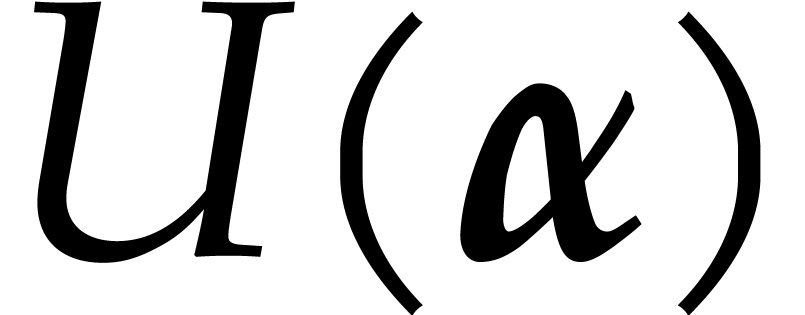 .
We finally observe that the gcds and the Bézout relations can be
computed using a negligible number of
.
We finally observe that the gcds and the Bézout relations can be
computed using a negligible number of  bit
operations. In order to be painstakingly precise, we note that such bit
operations can be emulated by operations over
bit
operations. In order to be painstakingly precise, we note that such bit
operations can be emulated by operations over  in
our algebraic complexity model.
in
our algebraic complexity model.
In many usual cases, it is known that Algorithm A.1 is
suboptimal. In particular, if the characteristic of  is zero, then
is zero, then  has always order
has always order  . If
. If 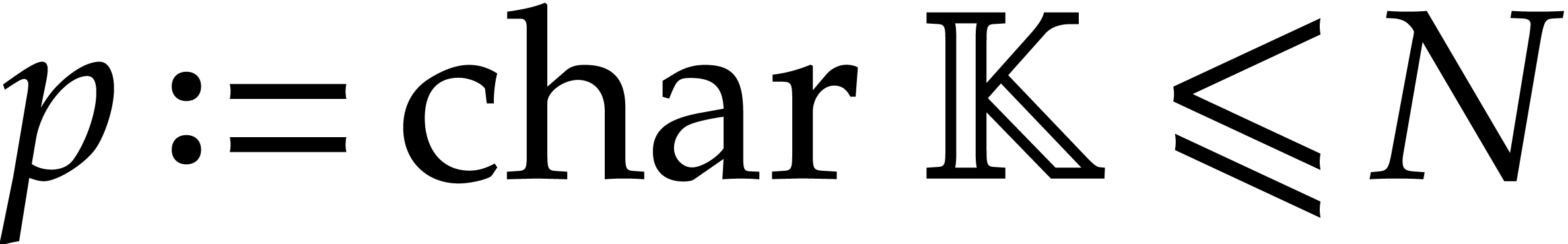 is a finite field,
then
is a finite field,
then 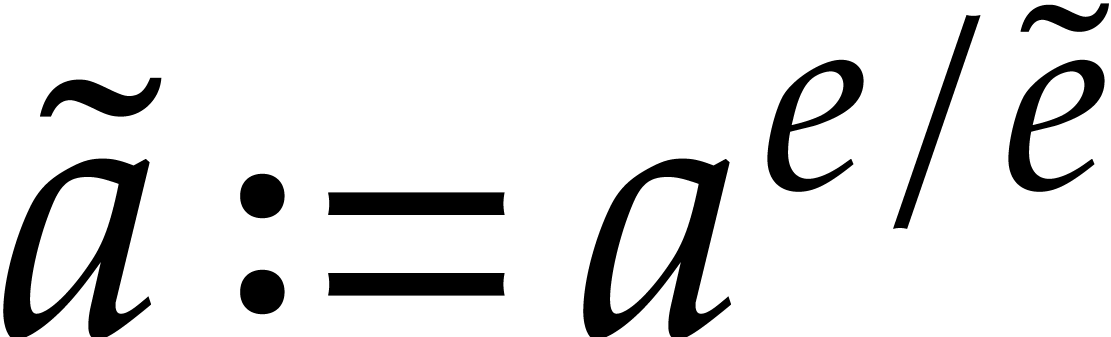 is cyclic and primitive elements can be
obtained more efficiently; see [8, 28, 29] for instance, but also the survey [7]. As an
advantage, Algorithm A.1 is field agnostic. This property
seems mostly of theoretical interest, but it turns out to be useful when
programming generic algorithms, that do not require specific properties
of
is cyclic and primitive elements can be
obtained more efficiently; see [8, 28, 29] for instance, but also the survey [7]. As an
advantage, Algorithm A.1 is field agnostic. This property
seems mostly of theoretical interest, but it turns out to be useful when
programming generic algorithms, that do not require specific properties
of  : for instance the
characteristic or the cardinality of
: for instance the
characteristic or the cardinality of  are not
computable. The following proposition explains how to use Algorithm A.1 even without any piece of information about
are not
computable. The following proposition explains how to use Algorithm A.1 even without any piece of information about  .
.
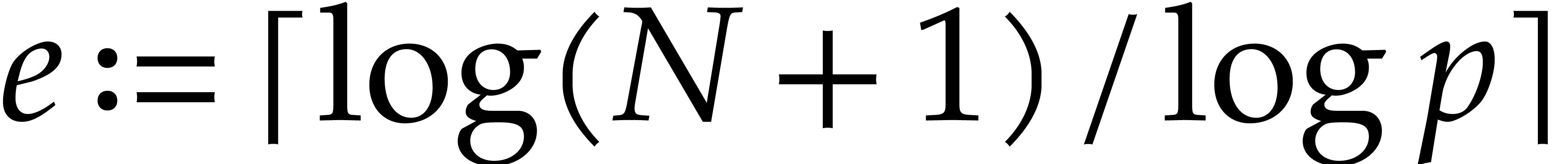 be a computation
tree of total cost
be a computation
tree of total cost 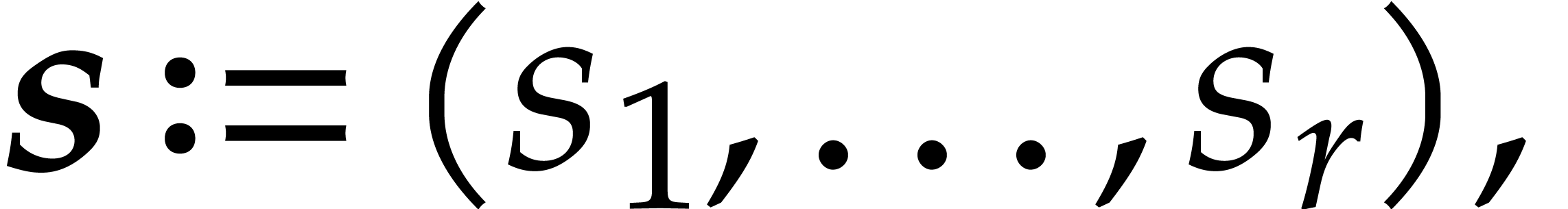 over
over  , such that
, such that
One of the input values of 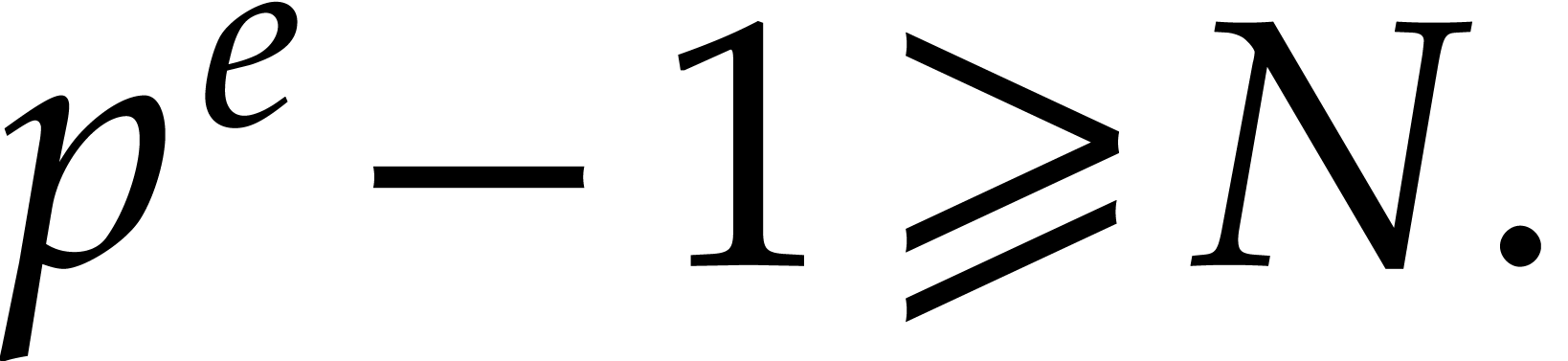 must contain an
element
must contain an
element  of order
of order  ;
;
The output values of 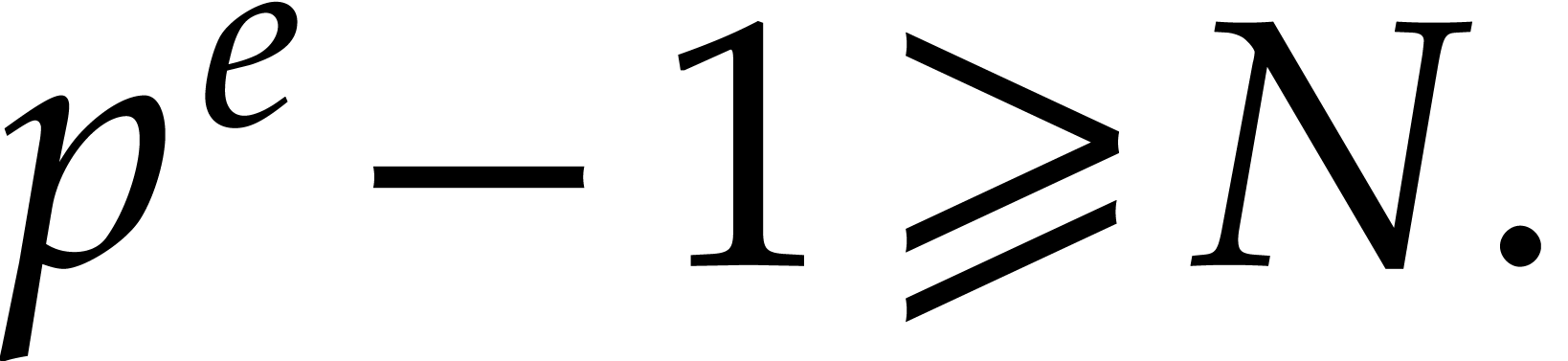 are independent of
the value taken for
are independent of
the value taken for  ,
even when
,
even when  is taken in an algebraic
extension
is taken in an algebraic
extension 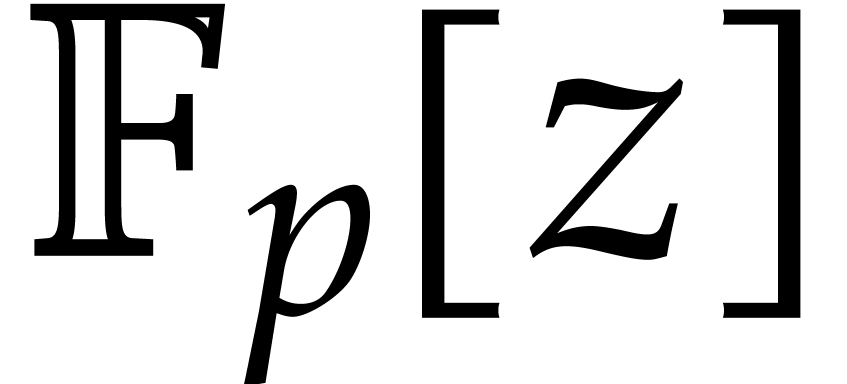 of
of  and
when
and
when 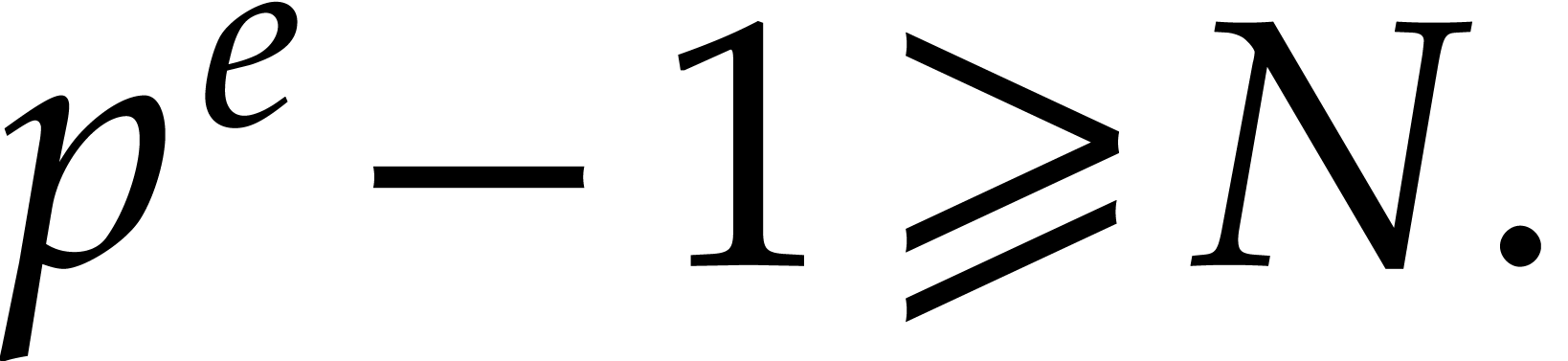 is evaluated over
is evaluated over 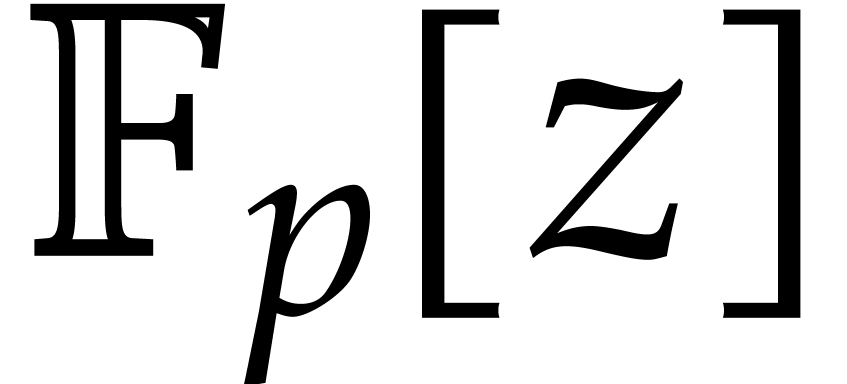 .
.
Then there exists a computation tree 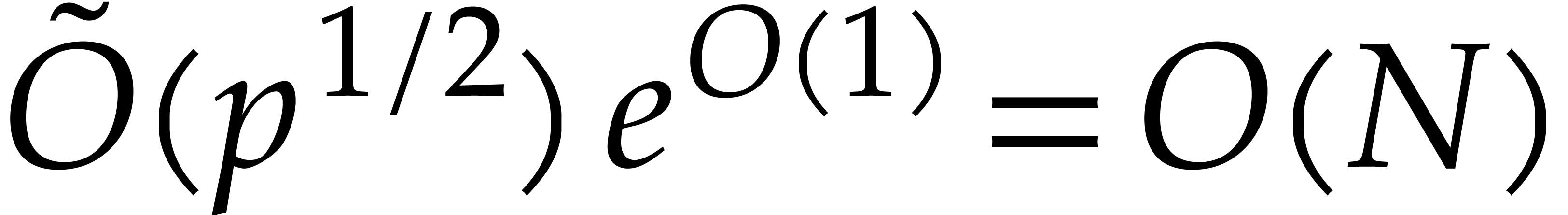 of
total cost
of
total cost
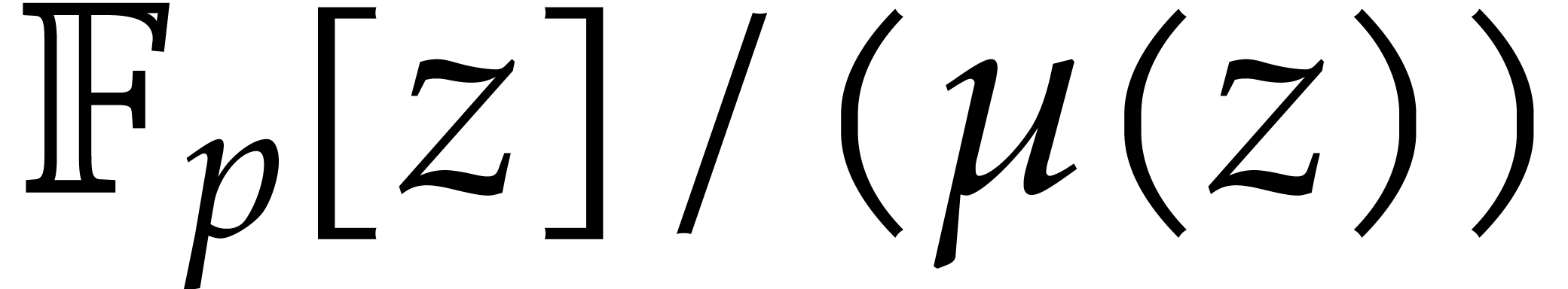
that computes the same as 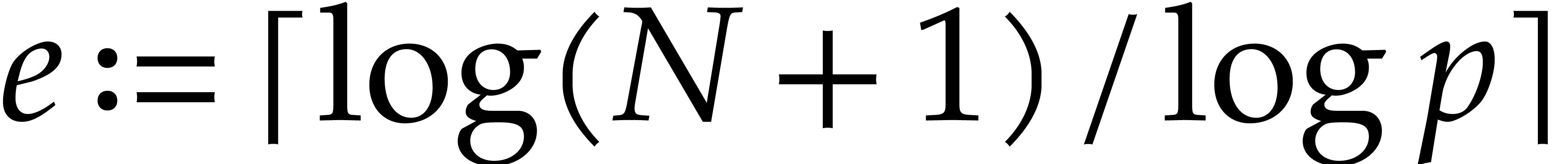 but without
requiring an input element of order
but without
requiring an input element of order 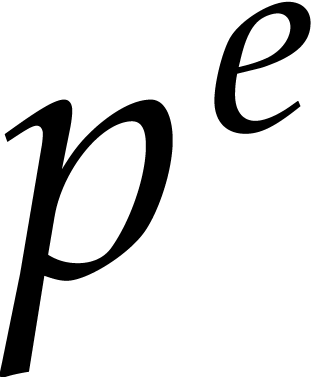
Proof. We are interested in computing an element
of order  . First, we can
compute the sequence of integers
. First, we can
compute the sequence of integers  in
in  using
using  additions, and then
determine whether
additions, and then
determine whether 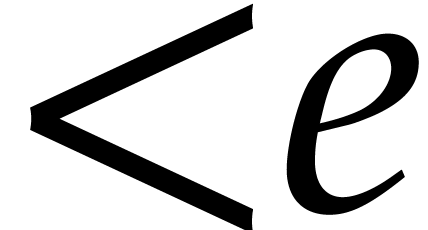 is
is  or
not. If
or
not. If  , then we can use
Algorithm A.1 in order to obtain an element
, then we can use
Algorithm A.1 in order to obtain an element  of
of  of order
of order  . In this case,
. In this case, 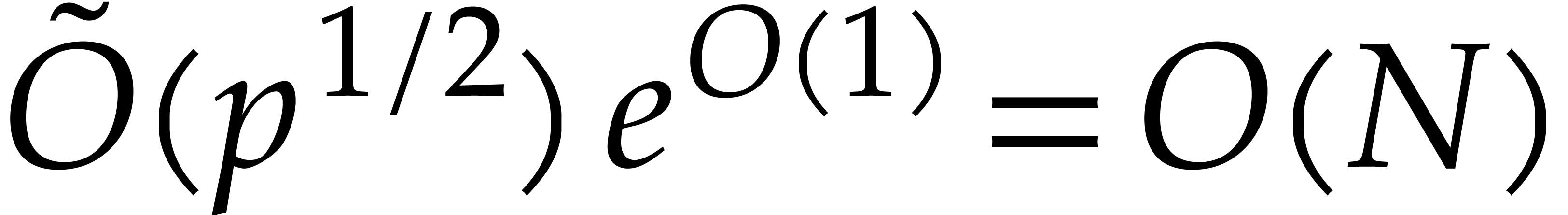 simply runs
simply runs
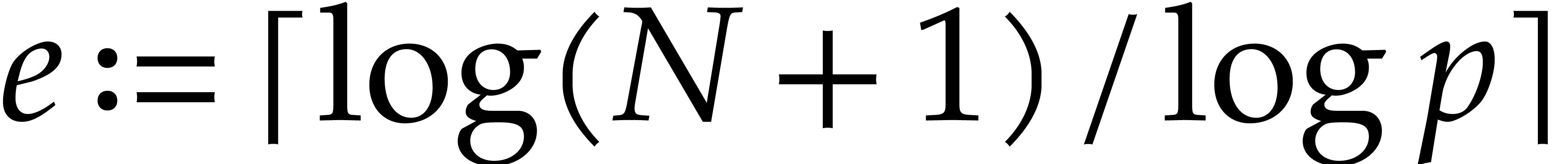 with
with  .
.
Otherwise,  . We shall compute
in a sufficiently large algebraic extension of
. We shall compute
in a sufficiently large algebraic extension of  as follows. Let
as follows. Let 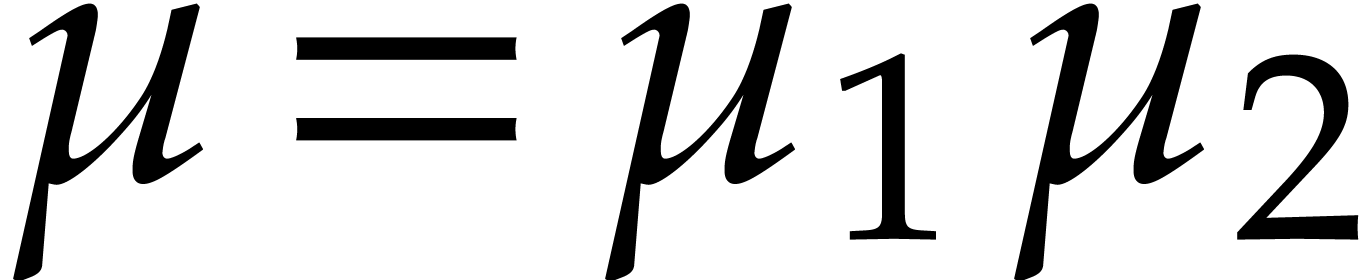 be the first integer such that
be the first integer such that
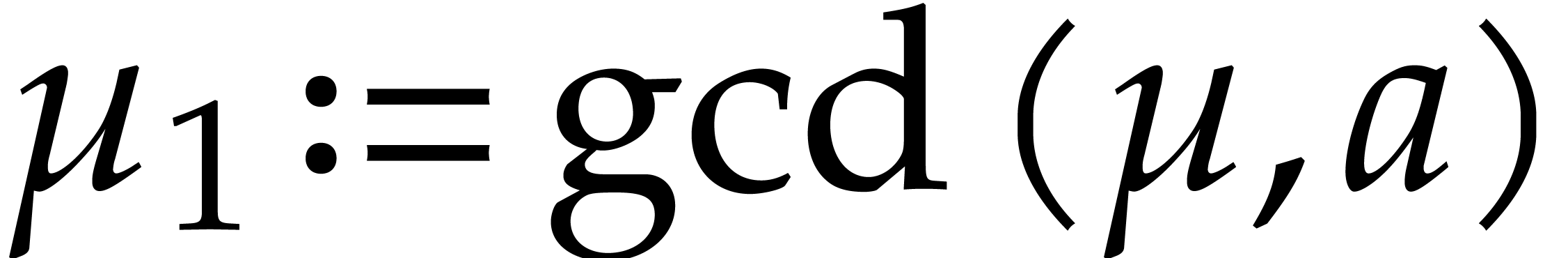
Thanks to [27, Theorem 3.2], we may deterministically
construct a monic irreducible polynomial 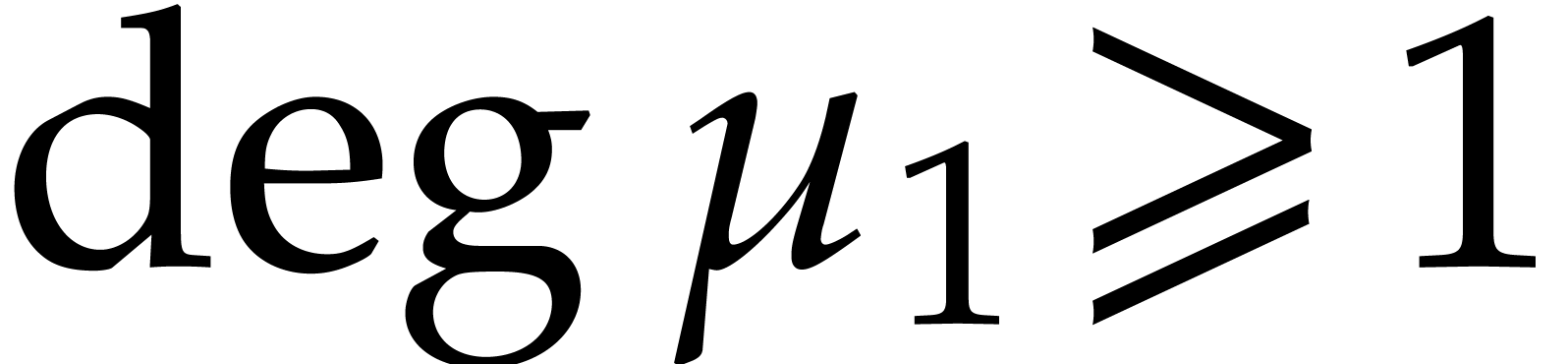 of
degree
of
degree 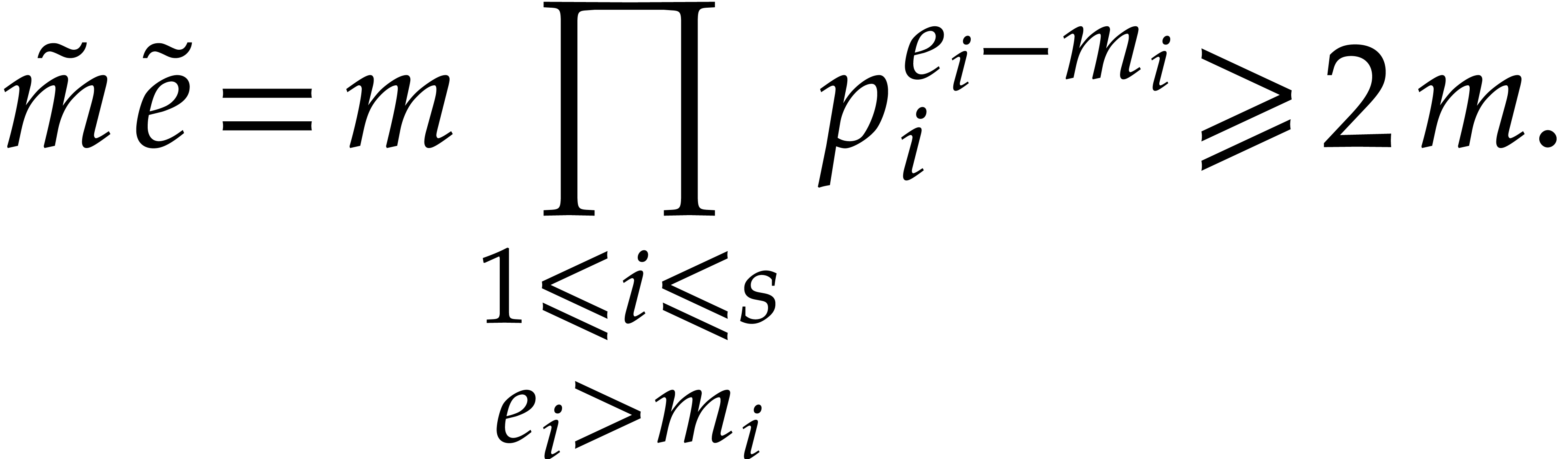 in
in 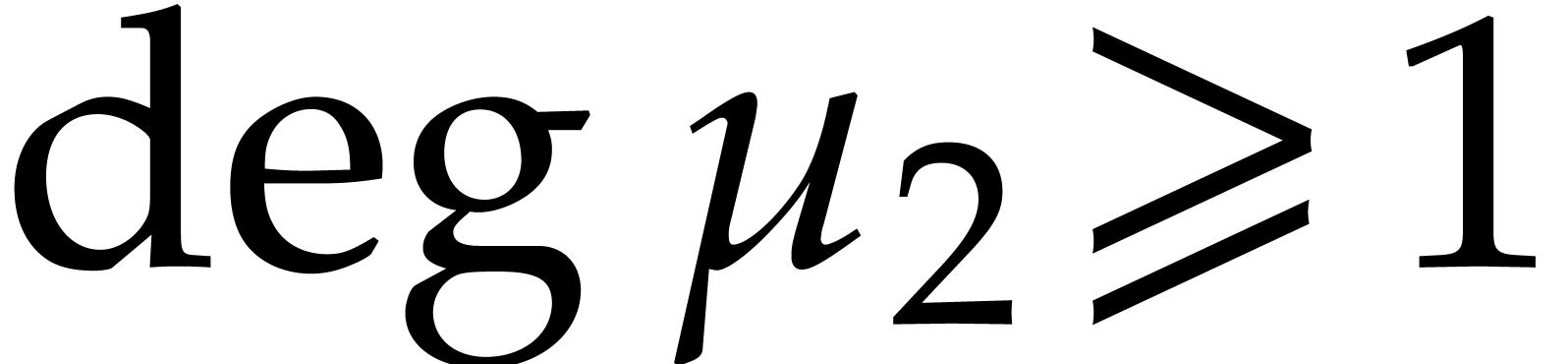 using
using 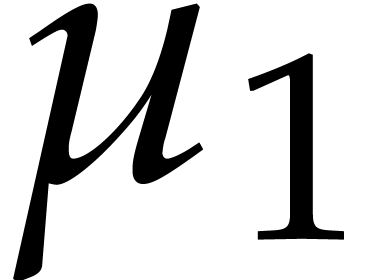 operations in
operations in  .
In this way,
.
In this way, 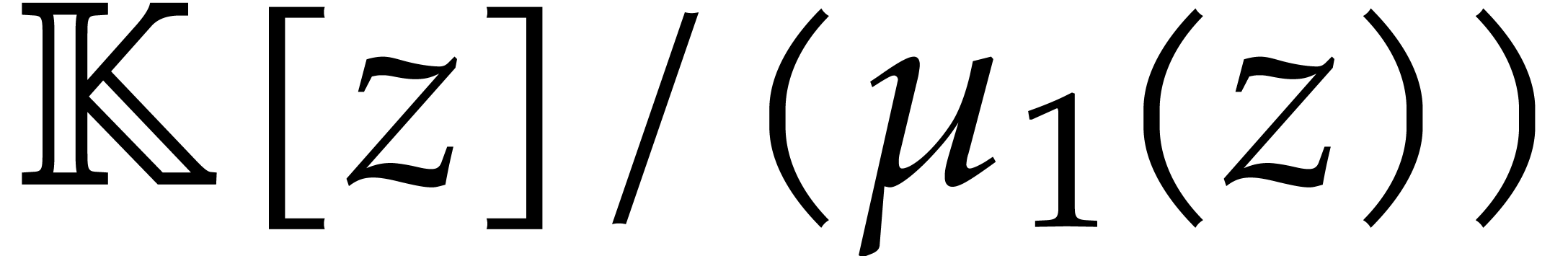 is the finite field with
is the finite field with  elements. We can enumerate
elements. We can enumerate  non-zero elements of
non-zero elements of 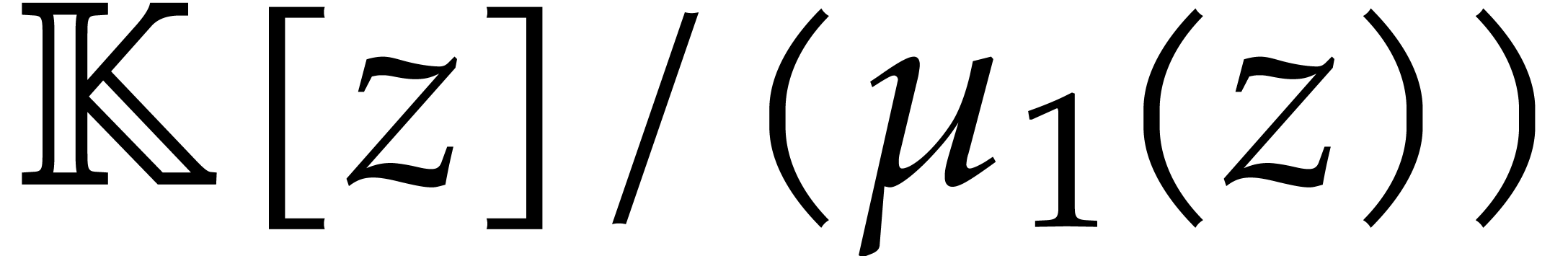 and then use Algorithm A.1 in order to obtain an element
and then use Algorithm A.1 in order to obtain an element  of
of
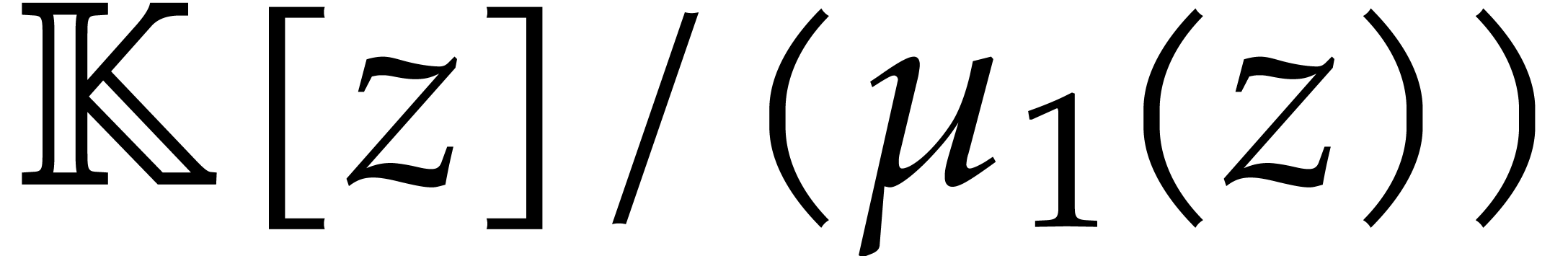
 of order
of order 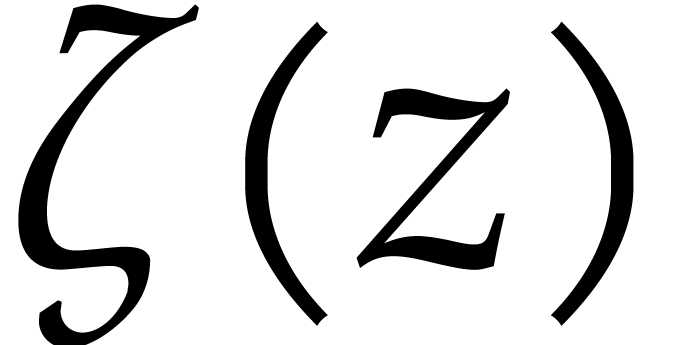 . We regard
. We regard 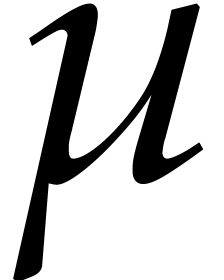 as a
polynomial in
as a
polynomial in 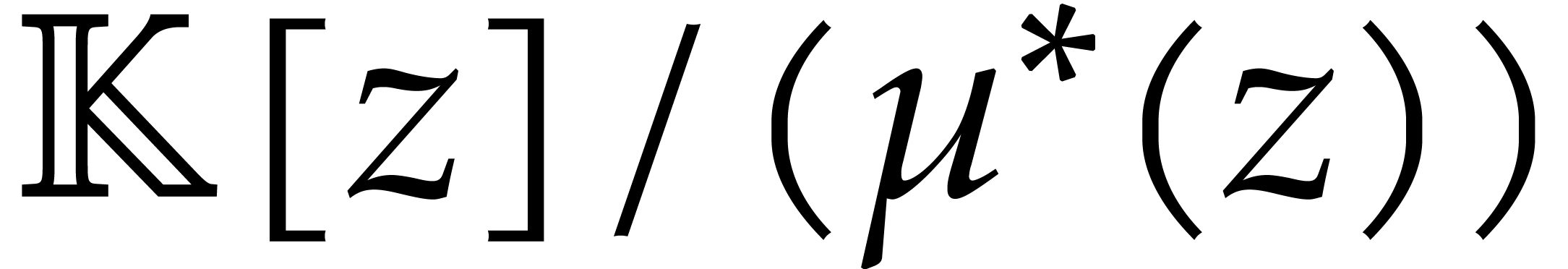 of degree
of degree 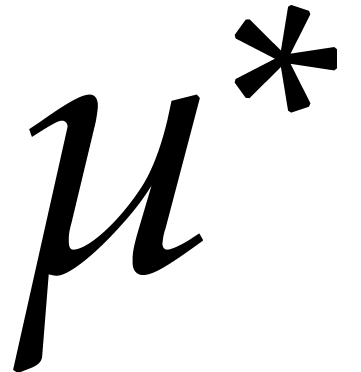 .
.
Now we regard 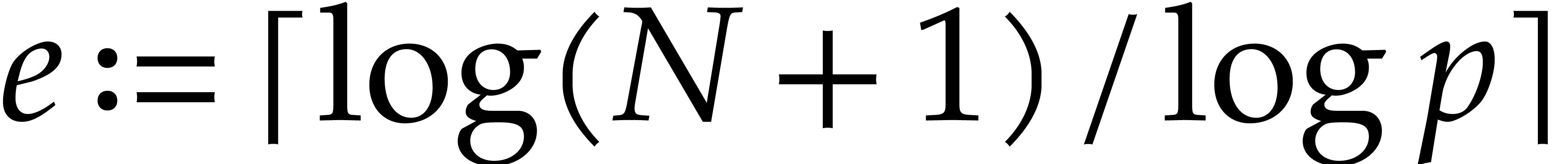 as a computation tree over
as a computation tree over 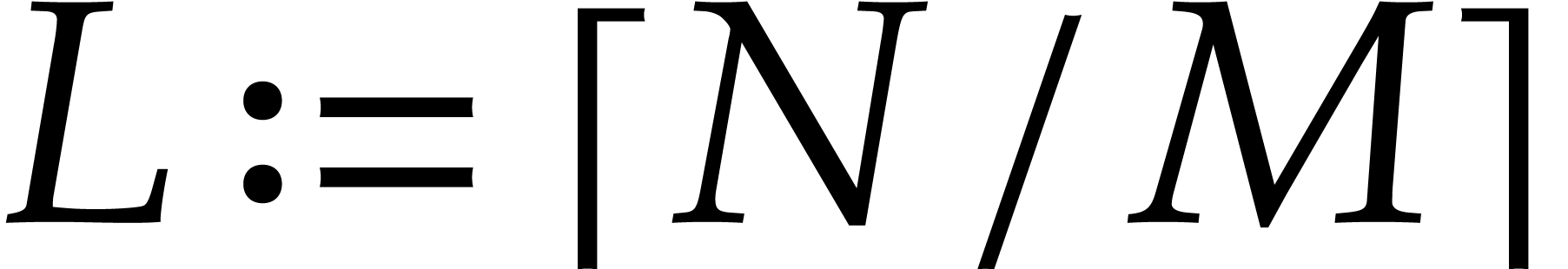 , using
, using 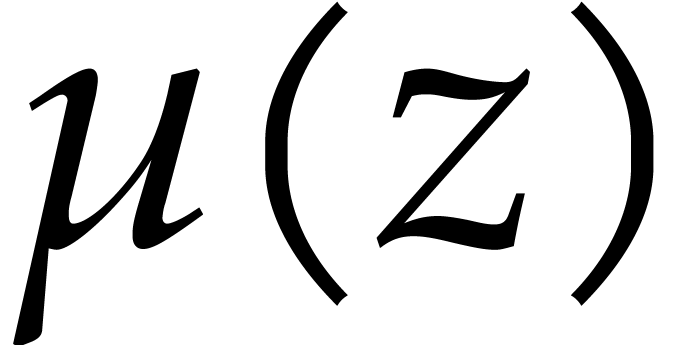 in
place of the input element of order
in
place of the input element of order 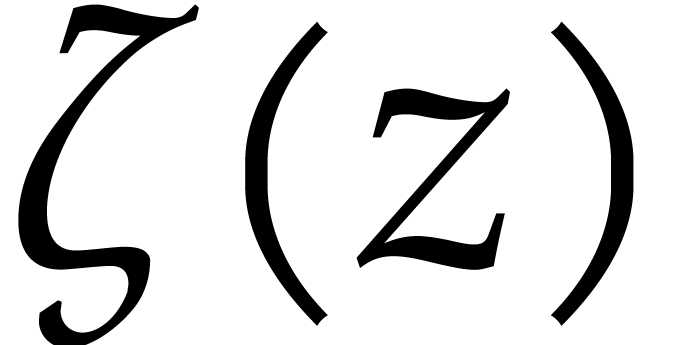 .
While executing
.
While executing 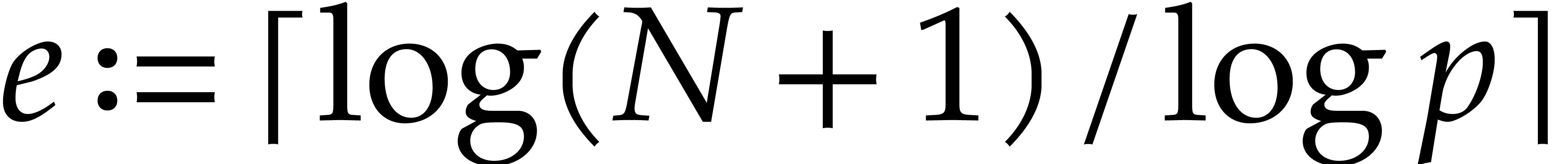 for given input in
for given input in  , sums and products can be lifted
straightforwardly to
, sums and products can be lifted
straightforwardly to 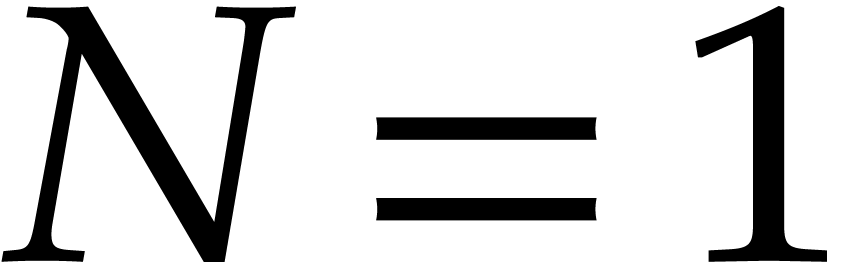
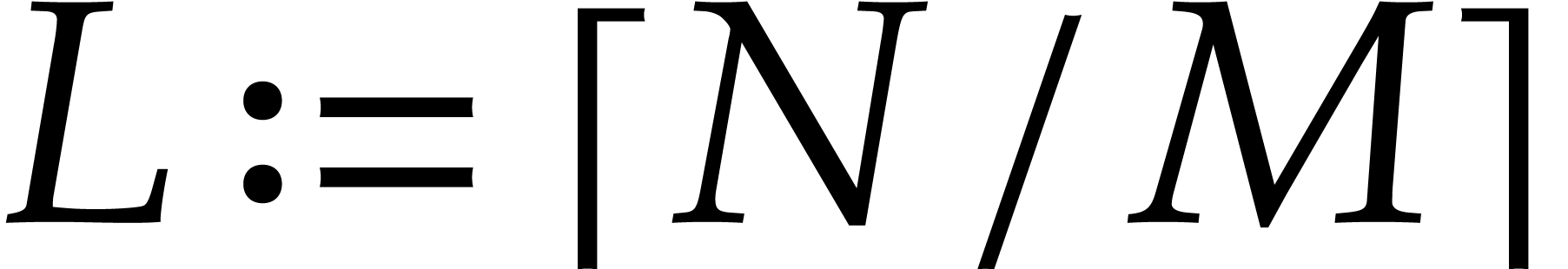 : elements of
: elements of 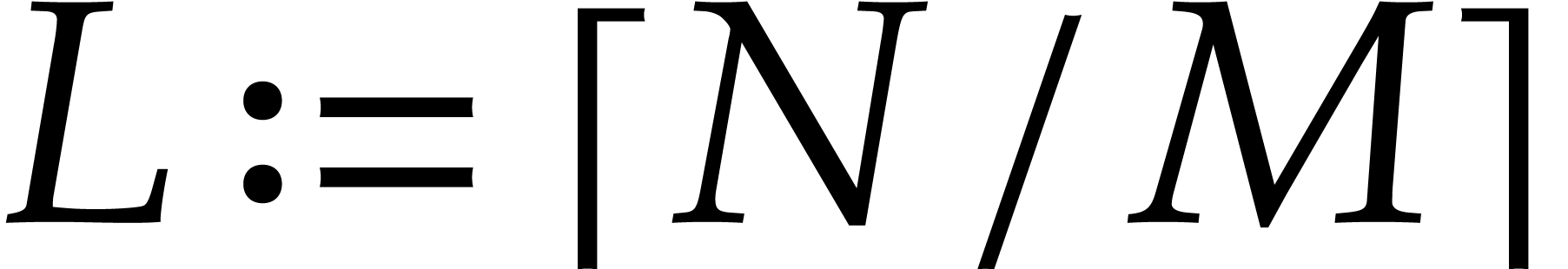 are
represented by polynomials of degree
are
represented by polynomials of degree  .
When testing whether an element
.
When testing whether an element
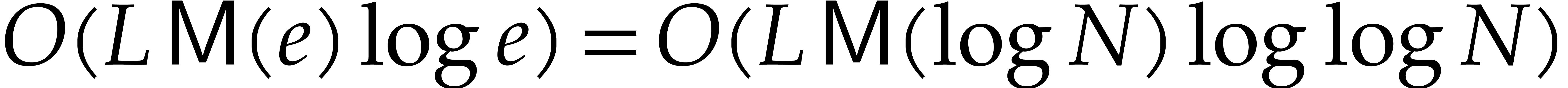
is invertible or not, we proceed as follows:
If  is identically zero, then the test
returns false.
is identically zero, then the test
returns false.
If  is invertible modulo
is invertible modulo  , then the test returns true.
, then the test returns true.
Otherwise,  can be factored
can be factored  , with
, with  ,
,
 , and
, and  . We continue our computations with
. We continue our computations with  in the role of
in the role of  ,
while projecting all previously computed results from
,
while projecting all previously computed results from 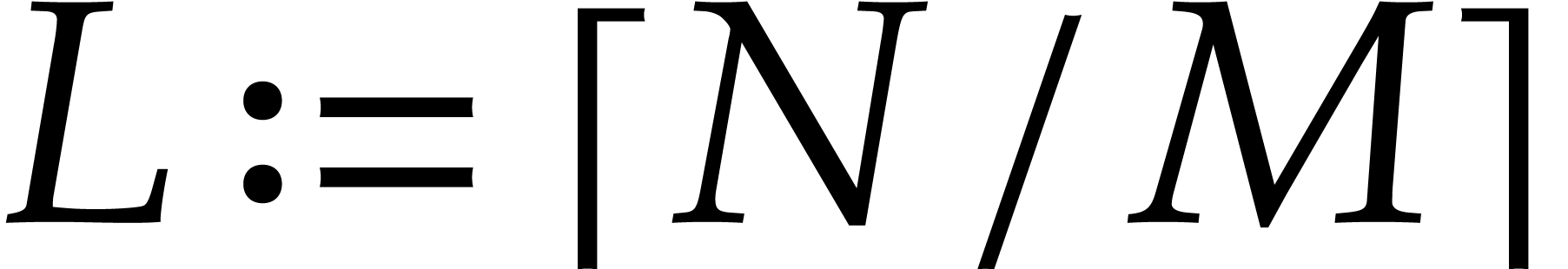 in
in  . In
particular,
. In
particular,  becomes identically zero after
this projection, and the test returns false.
becomes identically zero after
this projection, and the test returns false.
Note that  remains embedded in
remains embedded in 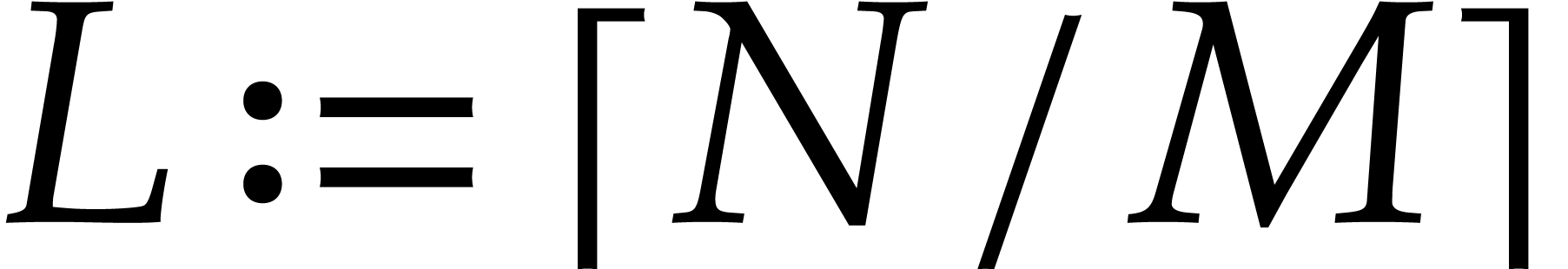 whenever
whenever  is replaced by any non-trivial factor
over
is replaced by any non-trivial factor
over  . In particular, the
order of
. In particular, the
order of 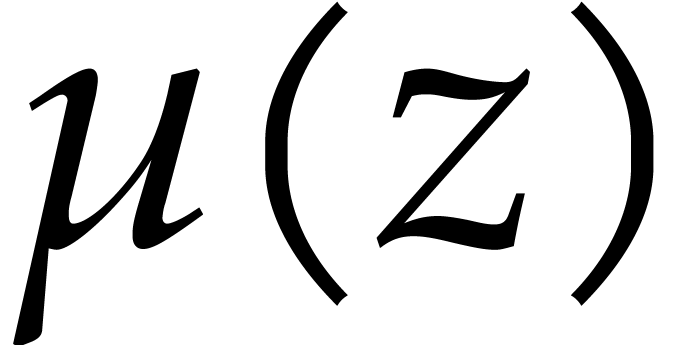 remains
remains 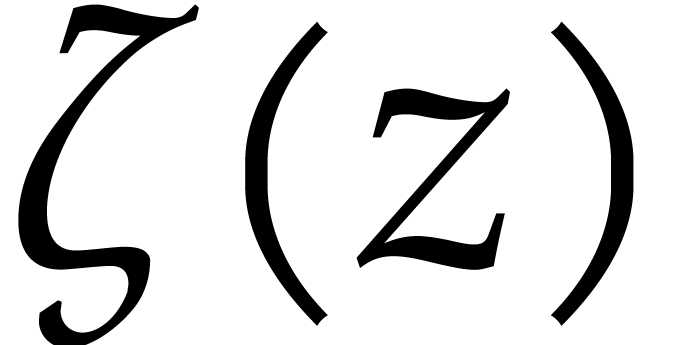 after
any such replacement. At the end, we thus obtain the evaluation of
after
any such replacement. At the end, we thus obtain the evaluation of 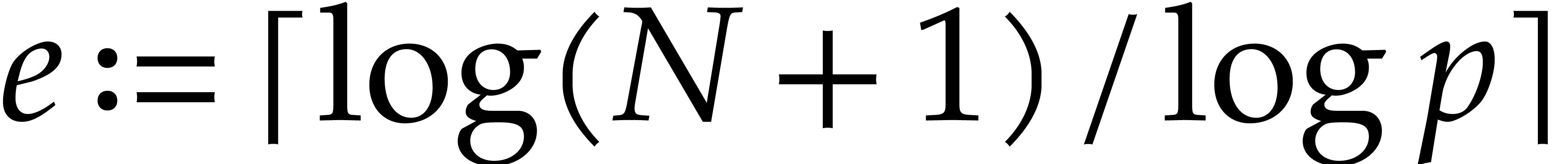 over
over  ,
where
,
where  is a non-constant factor of the original
is a non-constant factor of the original
 . This proves the correctness
of our method.
. This proves the correctness
of our method.
Computing 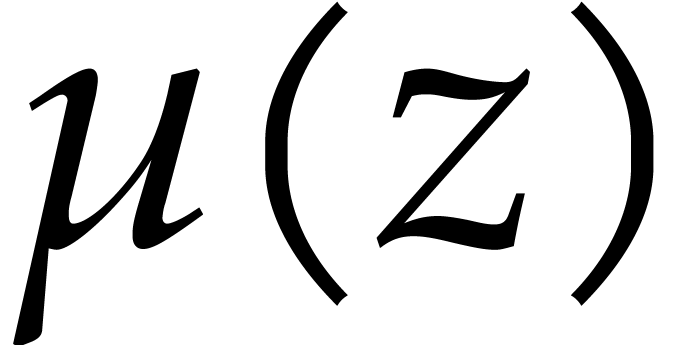 takes
takes 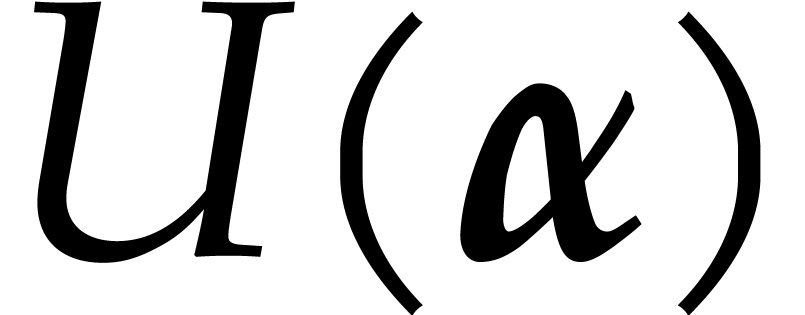 operations thanks to Proposition A.1. The evaluation of
operations thanks to Proposition A.1. The evaluation of
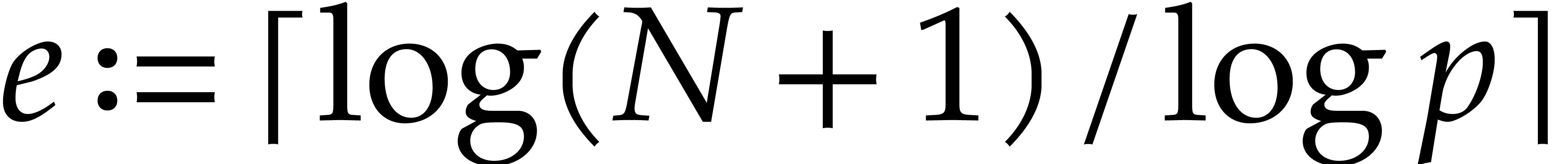 over
over  requires
requires  ring operations or extended gcd computations for
polynomials over
ring operations or extended gcd computations for
polynomials over  of degree at most
of degree at most 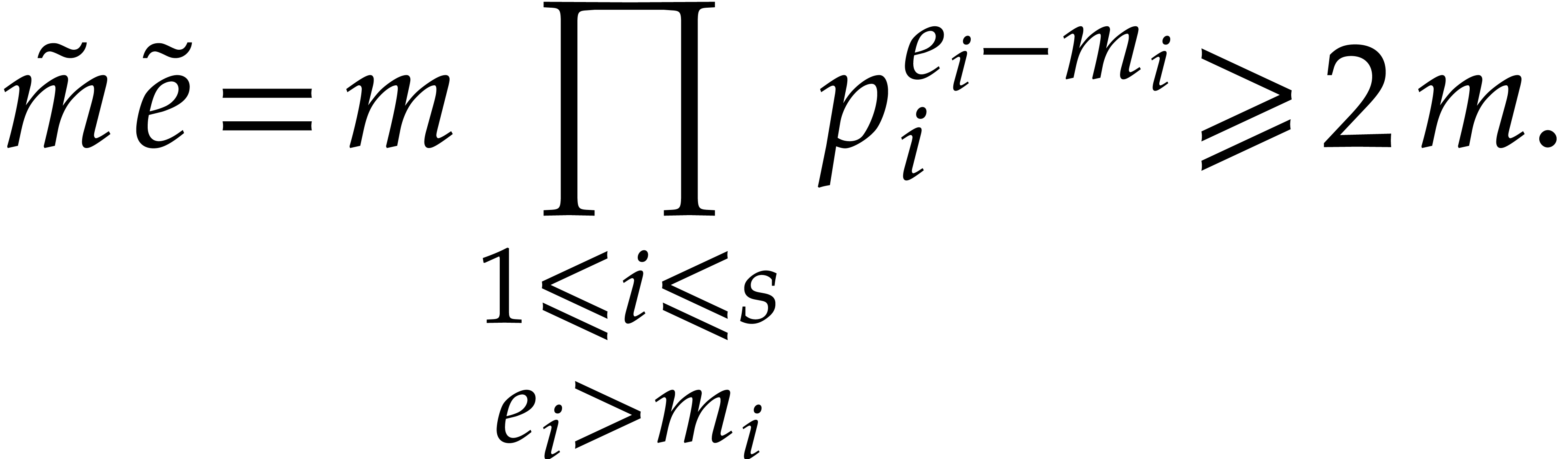 . This contributes
. This contributes  to
the cost. The overall cost is therefore as claimed.
to
the cost. The overall cost is therefore as claimed.
S. Abelard, A. Couvreur, and G. Lecerf. Efficient computation of Riemann–Roch spaces for plane curves with ordinary singularities. Appl. Algebra Eng. Commun. Comput., 35(6):739–804, 2024.
V. Bhargava, S. Ghosh, Z. Guo, M. Kumar, and C. Umans. Fast multivariate multipoint evaluation over all finite fields. In 2022 IEEE 63rd Annual Symposium on Foundations of Computer Science (FOCS), pages 221–232. New York, NY, USA., 2022. IEEE.
V. Bhargava, S. Ghosh, M. Kumar, and C. K. Mohapatra. Fast, algebraic multivariate multipoint evaluation in small characteristic and applications. J. ACM, 2023. Article 42.
A. Bostan, G. Lecerf, and É. Schost. Tellegen's principle into practice. In Proceedings of the 2003 International Symposium on Symbolic and Algebraic Computation, ISSAC '03, pages 37–44. New York, NY, USA, 2003. ACM.
P. Bürgisser, M. Clausen, and M. A. Shokrollahi. Algebraic Complexity Theory, volume 315 of Grundlehren der Mathematischen Wissenschaften. Springer-Verlag, 1997.
D. G. Cantor and E. Kaltofen. On fast multiplication of polynomials over arbitrary algebras. Acta Inform., 28:693–701, 1991.
Q. Cheng. On the construction of finite field elements of large order. Finite Fields their Appl., 11(3):358–366, 2005.
S. Gao. Elements of provable high orders in finite fields. Proc. Am. Math. Soc., 127(6):1615–1623, 1999.
J. von zur Gathen and J. Gerhard. Modern computer algebra. Cambridge University Press, New York, 3rd edition, 2013.
D. Harvey and J. van der Hoeven. Faster polynomial multiplication over finite fields using cyclotomic coefficient rings. J. Complexity, 54:101404, 2019.
J. van der Hoeven. The Jolly Writer. Your Guide to GNU TeXmacs. Scypress, 2020.
J. van der Hoeven and R. Larrieu. Fast reduction of bivariate polynomials with respect to sufficiently regular Gröbner bases. In C. Arreche, editor, Proceedings of the 2018 ACM International Symposium on Symbolic and Algebraic Computation, ISSAC '18, pages 199–206. New York, NY, USA, 2018. ACM.
J. van der Hoeven and G. Lecerf. Fast multivariate multi-point evaluation revisited. J. Complexity, 56:101405, 2020.
J. van der Hoeven and G. Lecerf. Amortized bivariate multi-point evaluation. In M. Mezzarobba, editor, Proceedings of the 2021 International Symposium on Symbolic and Algebraic Computation, ISSAC '21, pages 179–185. New York, NY, USA, 2021. ACM.
J. van der Hoeven and G. Lecerf. Fast amortized multi-point evaluation. J. Complexity, 67:101574, 2021.
J. van der Hoeven and G. Lecerf. On the complexity exponent of polynomial system solving. Found. Comput. Math., 21:1–57, 2021.
J. van der Hoeven and G. Lecerf. Amortized multi-point evaluation of multivariate polynomials. J. Complexity, 74:101693, 2022.
J. van der Hoeven, G. Lecerf, B. Mourrain et al. Mathemagix. 2002. http://www.mathemagix.org.
J. van der Hoeven and É. Schost. Multi-point evaluation in higher dimensions. Appl. Alg. Eng. Comm. Comp., 24(1):37–52, 2013.
K. S. Kedlaya and C. Umans. Fast polynomial factorization and modular composition. SIAM J. Comput., 40(6):1767–1802, 2011.
D. Le Brigand and J.-J. Risler. Algorithme de Brill–Noether et codes de Goppa. Bulletin de la société mathématique de France, 116(2):231–253, 1988.
V. Neiger. Bases of relations in one or several variables: fast algorithms and applications. PhD thesis, École Normale Supérieure de Lyon (France) – University of Waterloo (Canada), 2016. https://tel.archives-ouvertes.fr/tel-01431413.
V. Neiger. Fast computation of shifted Popov forms of polynomial matrices via systems of modular polynomial equations. In Proceedings of the ACM on International Symposium on Symbolic and Algebraic Computation, ISSAC '16, pages 365–372. New York, NY, USA, 2016. ACM.
V. Neiger, J. Rosenkilde, and G. Solomatov. Generic bivariate multi-point evaluation, interpolation and modular composition with precomputation. In A. Mantzaflaris, editor, Proceedings of the 45th International Symposium on Symbolic and Algebraic Computation, ISSAC '20, pages 388–395. New York, NY, USA, 2020. ACM.
V. Neiger, B. Salvy, É. Schost, and G. Villard. Faster modular composition. J. ACM, 71(2):1–79, 2023. Article No. 11.
M. Nüsken and M. Ziegler. Fast multipoint evaluation of bivariate polynomials. In S. Albers and T. Radzik, editors, Algorithms – ESA 2004. 12th Annual European Symposium, Bergen, Norway, September 14-17, 2004, volume 3221 of Lect. Notes Comput. Sci., pages 544–555. Springer Berlin Heidelberg, 2004.
V. Shoup. New algorithms for finding irreducible polynomials over finite fields. Math. Comp., 54(189):435–447, 1990.
V. Shoup. Searching for primitive roots in finite fields. Math. Comp., 58:369–380, 1992.
I. Shparlinski. On finding primitive roots in finite fields. Theor. Comput. Sci., 157(2):273–275, 1996.
V. V. Williams, Y. Xu, Z. Xu, and R. Zhou. New bounds for matrix multiplication: from alpha to omega. In D. P. Woodruff, editor, Proceedings of the 2024 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pages 3792–3835. Philadelphia, PA 19104 USA, 2024. SIAM.